Phase-field modeling of ductile fracture

Abstract

Phase-field modeling of brittle fracture in elastic solids is a well-established framework that overcomes the limitations of the classical Griffith theory in the prediction of crack nucleation and in the identification of complicated crack paths including branching and merging. We propose a novel phase-field model for ductile fracture of elasto-plastic solids in the quasi-static kinematically linear regime. The formulation is shown to capture the entire range of behavior of a ductile material exhibiting $J_2$-plasticity, encompassing plasticization, crack initiation, propagation and failure. Several examples demonstrate the ability of the model to reproduce some important phenomenological features of ductile fracture as reported in the experimental literature.

1 Introduction

In the past two decades, the ability to accurately predict fracture in ductile materials has gained increasing importance in several industrial fields, including e.g. the automotive, aerospace and marine sectors, due to the constant quest for optimal design and weight reduction of new components. The availability of computational predictive tools allows for substantial savings in the cost of experiments, especially in cases where these are extremely complex (such as e.g. for gas pipelines, aircraft fuselages, or nuclear vessels), as well as for design optimization. A computational model for ductile fracture is expected to predict a number of behavioral features, including state of stress, damage patterns, the stability of possibly existing cracks, crack propagation paths and corresponding load-carrying capacity.

Since the late sixties, several modeling approaches have been proposed for ductile fracture, see [1] for a comprehensive review. Following the classification in [1] but with a slight modification of the terminology, we will here distinguish between global and field approaches. In the former, one or a few parameters are assumed to completely characterize the crack tip conditions. Within this category, the classical choice is Rice’s J-integral which presents a number of important drawbacks [1]: i. it can assess the stability of pre-existing crack-like flaws but cannot predict crack initiation and propagation from a notch or other stress concentrators; ii. the critical value of the J integral is not a material property as it strongly depends on the specimen geometry [2, 3], which led to the proposal of the two-parameters J–Q approach [4]; iii. the method is not applicable to arbitrarily complex geometries. Subsequently developed alternatives using the so-called critical crack tip opening displacement or crack tip opening angle share the same limitations [5–7]. Global approaches are either adopted within analytical models or implemented with the finite element (FE) method (FEM), where crack propagation is typically dealt with using remeshing algorithms, which adapt the mesh topology to the crack geometry [8].

Field approaches [9, 10], rather than relying on global parameters, base the prediction of fracture on a detailed description of the damage phenomena in the process zone. In turn, within field approaches we can distinguish between continuum and discrete formulations, both typically implemented with the FEM. Continuum approaches refer the description of damage to the volume of the material bulk and consist in the use of constitutive equations coupling plasticity and damage at the material point level. A large number of models have been proposed in this framework, see [1] for a review. Here we just mention the micro-mechanically motivated model by Gurson [11], where the plastic yield surface depends on a damage variable associated to the void volume fraction (or porosity); its improved version known as the Gurson–Tvergaard–Needleman (GTN) model [12], which incorporates additional parameters to better describe the void growth kinetics; and the phenomenological (i.e. macroscopic), thermodynamically consistent damage mechanics modeling framework developed by Lemaitre [13, 14]. In all these models, the constitutive equations lead to a strong softening behavior as the damage level increases, which leads to strain and damage localization. This in turn determines the loss of ellipticity of the governing differential equations and, in a numerical discretized setting, a strong mesh sensitivity of the computational results. A few different solutions to this issue have been proposed, most notably the incorporation of a material length scale through non-local or gradient damage approaches [15, 16]. Being endowed with a length scale, these approaches are additionally capable of predicting size effects, which is not possible with local models. Non-local or gradient versions of the Gurson and of the GTN models have been proposed in [17, 18], respectively.

Continuum formulations are typically unable to describe the surface decohesion and crack propagation phase subsequent to the softening and damage localization phase. Conversely, this phase is naturally handled by the discrete formulations, which involve a surface description. In an FE framework the proper modelling of discrete cracks of arbitrary geometry requires either remeshing [8] or embedding techniques such as the extended FEM (XFEM) [19], both allowing for the (respectively explicit and implicit) tracking of discontinuities within an existing mesh. In both cases, additional assumptions are needed for the crack initiation and propagation criteria, as well as for crack growth direction criteria. Moreover, both approaches present significant implementational difficulties, such as the need for suitable transfer of the state variables in the case of remeshing [20] as well as integration, conditioning and data handling issues for the XFEM, most notably in the 3D setting. A widely used alternative is the so-called cohesive zone modeling approach, implemented through interface or generalized contact elements [21–23]. This approach describes explicitly the discrete fracture process and is straightforward for crack paths known a priori [24–26]. Its extension to unknown crack paths entails the insertion of cohesive elements between each pair of continuum elements in an FE mesh, which may lead to strong mesh dependency and over-estimated cracked areas [27]. XFEM and cohesive zone modeling can be possibly coupled [28]. All discrete approaches cannot describe diffuse ductile damage, which in metals typically precedes the localization of damage within a thin band, and their applications are currently largely limited to brittle fracture or small-scale yielding conditions.

Very recently, there have been attempts to combine the continuum and the discrete approaches to capture the transition between damage, localization, crack initiation and propagation. These attempts involved e.g. the combination of a Lemaitre-based non-local or gradient damage model [29, 30] or of the GTN model [31] with the XFEM. Obviously, the crack propagation phase inherits the difficulties of the XFEM framework, moreover additional complications arise from the need for a consistent and seamless transition between continuum and discrete descriptions in subsequent behavioral stages.

Phase-field modeling, which shares many features with continuum approaches, has recently emerged as a competitive alternative to discrete methods for the description of brittle fracture phenomena. In general, the phase-field approach to model systems with sharp interfaces consists in incorporating a continuous field variable—the so-called order parameter—which differentiates between multiple physical phases within a given system through a smooth transition. In the context of fracture, such order parameter (the crack phase field) describes the smooth transition between the fully broken and intact material phases, thus approximating the sharp crack discontinuity. The evolution of the crack phase field as a result of the external loading conditions models the fracture process. What makes the approach particularly attractive is its ability to elegantly simulate complicated fracture processes, including crack initiation, propagation, merging, and branching, in general situations and for 3D geometries, without the need for additional ad-hoc criteria. Propagating cracks are tracked automatically by the evolution of the smooth crack field on a fixed mesh. This leads to a significant advantage over the discrete fracture description methods outlined earlier. On the other hand, as mentioned earlier the approach shares several features with gradient-enhanced local continuum damage models. Therefore, it is the perfect candidate to enable a seamless transition between the description of continuum damage and discrete crack propagation phases.

Phase-field modeling of brittle fracture has been a topic of very intense research in the past few years and has already attained impressive results [32–39]. The currently available formulations encompass static and dynamic approaches to brittle fracture. The extension to ductile fracture has been the subject of very limited attempts. In [40, 41], fracture of ductile elastic–plastic solids was investigated under dynamic loading conditions. The focus was placed on reproducing the experimentally observed ductile to brittle failure mode transition with increasing loading speed. In these works, the total (free) energy functional is taken as the sum of elastic, plastic and fracture contributions. The elastic contribution takes the classical form, the fracture contribution contains only the component of the classical form involving the gradient of the phase-field, and the plastic contribution is a chosen function of the phase field and of the hardening variable. Recently, Duda et al. [42] proposed a phase field model for quasi-static brittle fracture in elasto-plastic solids, a phenomenon typical of metals below the ductile–brittle transition temperature. In this case, limited plastic deformation is assumed to take place in the vicinity of the notch root or crack tip. Also in this case the total energy is the sum of elastic, plastic and fracture contributions. The elastic and fracture contributions take the classical form used in available brittle fracture formulations, whereas the plastic contribution is a chosen function of the accumulated plastic strain including as parameters the elastic modulus, the yield stress and the strain hardening exponent.

Objective of this paper is to propose a new phase-field formulation of ductile fracture in elasto-plastic solids, in the quasi-static kinematically linear regime. The distinct feature of the proposed model is the introduction of a coupling between the degradation function applied to the tensile portion of the elastic energy and the plastic strain state. This coupling is shown to play a fundamental role for the correct prediction of some phenomenological aspects of ductile fracture evidenced from available experimental results, and is proved to be thermodynamically consistent. The paper is structured as follows. Section 2 revisits the main features of phase-field models of brittle fracture for elastic solids, which serves as a basis for the subsequent extension to the ductile regime. Section 3 illustrates the proposed model, whose algorithmic aspects are developed in Sect. 4. Section 5 presents several numerical examples to test the predictive ability of the model with respect to some effects evidenced by experimental tests in the literature. Finally, conclusions are drawn in Sect. 6.

2 Point of departure: phase-field models of brittle fracture of elastic solids revisited

Phase-field approaches to brittle fracture of elastic solids have been independently developed and investigated in the physics and mechanics communities starting from the late ’90s and the literature on the subject is wide. Our previous paper [39] provides an overview of the existing quasi-static and dynamic phase-field fracture formulations accepted in both communities. Herein, we focus on quasi-static fracture.

As follows, we recall particularly the phase-field models of brittle fracture which originate from the variational formulation of brittle fracture by Francfort and Marigo [43] and the related regularized formulation of Bourdin et al. [32]. All these formulations have been applied to linearly elastic materials in the small deformation framework.

In [43], the entire (quasi-static) process of crack initiation, propagation and branching is governed by a minimization problem of the free energy functional

$$\begin{aligned} E(\varvec{u},\Gamma )=\int _\Omega \Psi _\mathrm{e}(\varvec{\varepsilon }(\varvec{u})) d\mathbf{x} + G_c\int _\Gamma ds, \end{aligned}$$

(1)

where $\Psi _\mathrm{e}$ is the elastic energy density function defined as $\Psi _\mathrm{e}:=\frac{1}{2}{\varvec{\varepsilon }}:\mathbb {C}:{\varvec{\varepsilon }}$ $=\frac{1}{2}\lambda \mathrm{tr}^2({\varvec{\varepsilon }})+\mu \mathrm{tr}({\varvec{\varepsilon }}^2)$, with $\varvec{\varepsilon }$ as the second order infinitesimal strain tensor, $\mathbb {C}$ as the fourth-order elasticity tensor, $\lambda$ and $\mu$ as the Lamé constants, and $G_c$ as the material fracture toughness. The solution is an admissible crack set $\Gamma \subset \Omega$ and a displacement field $\varvec{u}:\Omega \rightarrow \mathbb {R}^n$, which is discontinuous across $\Gamma$. The shortcomings of the classical Griffith theory of brittle fracture are proven to be overcome by formulation (1), see [43] and also [44] for further details and a comprehensive overview.

To enable an efficient numerical treatment of (1), its regularized formulation was devised by Bourdin et al. [32]:

$$\begin{aligned} E_\ell (\varvec{u},s)= & {} \int _\Omega g(s)\Psi _\mathrm{e}(\varvec{\varepsilon }(\varvec{u})) d\mathbf{x}\nonumber \\&+ G_c \int _\Omega \left( \frac{1}{4\ell }(1-s)^2+\ell |\nabla s|^2\right) d\mathbf{x}, \end{aligned}$$

(2)

with a field variable $s$ which indicates the crack (the crack field parameter) and which varies smoothly from 1 (undamaged material) to 0 (totally broken). The transition zone of $s$ is controlled by the parameter $\ell >0$ with the dimension of a length. Function $g(s):=s^2+\eta$ couples $s$ with the elastic field and typically satisfies $g(s)>0$ for $0<s\le 1$. The small dimensionless parameter $\eta$ models an artificial residual stiffness of a totally broken phase ($s=0$) and is essentially needed to prevent numerical difficulties.

With $\ell \rightarrow 0$, the formulation (2) approximates (1) in the sense of $\Gamma$-convergence, thus establishing the link between regularized and free-discontinuity fracture energies. This implies that the zero set of the crack field $s$ indeed recovers the crack set $\Gamma$.

Using variational principles, the minimization problem (2) can be reformulated as the system of the stress equilibrium equation $\mathrm{div}\;\varvec{\sigma }(\varvec{u},s)=0$, with $\varvec{\sigma }$ as the second-order Cauchy stress tensor

$$\begin{aligned} \varvec{\sigma }(\varvec{u},s):=g(s)\displaystyle \frac{\partial \Psi _\mathrm{e}(\varvec{\varepsilon })}{\partial \varvec{\varepsilon }} =g(s)\mathbb {C}:\varvec{\varepsilon }, \end{aligned}$$

(3)

and the evolution equation for $s$:

$$\begin{aligned} 2\ell \Delta s+\frac{1-s}{2\ell }=\frac{g^\prime (s)}{G_c}\Psi _\mathrm{e}(\varvec{\varepsilon }), \end{aligned}$$

(4)

see e.g. [33, 34].

The formulation (2) does not distinguish between fracture behavior in tension and compression. Already in [32] examples of unrealistic crack patterns in compression were reported. To avoid such situations, and, additionally, to prevent the interpenetration of the crack faces under compression, a modified regularized formulation of (1) was proposed in Amor et al. [35] and Miehe et al. [36, 37],

$$\begin{aligned} E_\ell (\varvec{u},s)&= \int _\Omega \left[ g(s)\Psi _\mathrm{e}^{+}(\varvec{\varepsilon }) + \Psi _\mathrm{e}^{-}(\varvec{\varepsilon }) \right] d\mathbf{x} \nonumber \\&\quad \ + G_c \int _\Omega \left( \frac{1}{4\ell }(1-s)^2+\ell |\nabla s|^2\right) d\mathbf{x}, \end{aligned}$$

(5)

using a specific additive decomposition $\Psi _\mathrm{e}=\Psi _\mathrm{e}^{+}+\Psi _\mathrm{e}^{-}$ of the elastic energy density $\Psi _\mathrm{e}$. In contrast to (2), the degradation of only the positive energy part is allowed herein, whereas the negative part remains undegraded.

Two options for decomposition of $\Psi _\mathrm{e}$ can be found in the literature, namely, the split into volumetric and deviatoric contributions, see [35],

$$\begin{aligned} \Psi _\mathrm{e}^{+}(\varvec{\varepsilon }):= & {} \frac{1}{2}K_n\langle \mathrm{tr}(\varvec{\varepsilon }) \rangle _{+}^2 + \mu (\varvec{\varepsilon }_\mathrm{dev}:\varvec{\varepsilon }_\mathrm{dev}),\nonumber \\ \Psi _\mathrm{e}^{-}(\varvec{\varepsilon }):= & {} \frac{1}{2}K_n\langle \mathrm{tr}(\varvec{\varepsilon }) \rangle _{-}^2, \end{aligned}$$

(6)

where $K_n=\lambda +\frac{2\mu }{n},\, \langle a\rangle _{\pm }:=\frac{1}{2}(a\pm |a|)$ and $\varvec{\varepsilon }_\mathrm{dev}:=\varvec{\varepsilon }-\frac{1}{3}\mathrm{tr}(\varvec{\varepsilon })\varvec{I}$, as well as the split based on the spectral decomposition of the strain tensor $\varvec{\varepsilon }=\sum _{I=1}^3 \langle \varepsilon _I\rangle \varvec{n}_I\otimes \varvec{n}_I$, where $\{\varepsilon _I\}_{I=1}^3$ and $\{\varvec{n}_I\}_{I=1}^3$ are the principal strains and principal strain directions, respectively, see [36, 37]. In this case, $\varvec{\varepsilon }_{\pm }:=\sum _{I=1}^3\langle \varepsilon _I\rangle _{\pm }\varvec{n}_I\otimes \varvec{n}_I$ and, eventually,

$$\begin{aligned} \Psi _\mathrm{e}^{\pm }(\varvec{\varepsilon }):= \frac{1}{2}\lambda \langle \mathrm{tr}(\varvec{\varepsilon }) \rangle _{\pm }^2 + \mu \mathrm{tr}(\varvec{\varepsilon }_\pm ^2). \end{aligned}$$

(7)

The system of Euler–Lagrange equations of the functional $E_\ell$ in (5) involves the stress–strain relation and the evolution equation of the crack phase field reading as

$$\begin{aligned} \varvec{\sigma }(\varvec{u},s):=g(s)\frac{\partial \Psi _\mathrm{e}^{+}(\varvec{\varepsilon })}{\partial \varvec{\varepsilon }} +\frac{\partial \Psi _\mathrm{e}^{-}(\varvec{\varepsilon })}{\partial \varvec{\varepsilon }}, \end{aligned}$$

(8)

and

$$\begin{aligned} 2\ell \Delta s+\frac{1-s}{2\ell }=\frac{g^\prime (s)}{G_c}\Psi _\mathrm{e}^{+}(\varvec{\varepsilon }), \end{aligned}$$

(9)

respectively. By coupling $s$ with $\Psi _\mathrm{e}^{+}$ in $E_\ell$, the evolution of $s$ in (9) is driven only by the dilatational part of the volumetric strain, thus providing cracking in tension. On the other hand, the absence of $\Psi _\mathrm{e}^{-}$ in (9) prevents crack evolution in the (highly) compressed parts of a solid, in which $\Psi _\mathrm{e}^{-}$ is expected to dominate $\Psi _\mathrm{e}^{+}$. Also, since the $\Psi _\mathrm{e}^{-}$ part remains undegraded in $E_\ell$, resulting in the presence of $\partial \Psi _\mathrm{e}^{-}/\partial \varvec{\varepsilon }$ in the relation (8), it can be expected that in case of crack closure the crack lips interpenetration is also prevented. It can be noticed finally that regardless of the type of split used in (5), the constitutive relation (8) is non-linear which is in contrast to (3).

The results on $\Gamma$-convergence for the functional $E_\ell$ in (5) are not available. That is, strictly speaking, it is not clear what kind of functional (and hence what kind of ’physical’ process) is to be recovered when $\ell \rightarrow 0$ in this case. The formulation (5) using different kinds of split of $\Psi _\mathrm{e}$, however, has been shown to provide adequate simulation results for brittle fracture processes in elastic bodies, see e.g. [35–37].

To enhance the efficiency of phase-field computations, the so-called higher-order and hybrid formulations were recently proposed in [38] and [39], respectively. Extension of the quasi-static formulations (2) and (5) to the dynamic setting has been presented in numerous contributions, see e.g. [45–50].

3 Phase-field model of ductile fracture

3.1 The conceptual background

To illustrate the prime difficulties in deriving the phase-field model for elasto-plastic ductile fracture, we first summarize the conceptual scheme underlying the phase-field framework for brittle fracture in Fig. 1. The process ① (i.e. the pure linearly elastic regime) and the related (classical) formulation $E(\varvec{u})\rightarrow \mathrm{min}$, where

$$\begin{aligned} E(\varvec{u}):=\int _\Omega \Psi _\mathrm{e}(\varvec{\varepsilon }(\varvec{u})) d\mathbf{x}, \end{aligned}$$

(10)

can naturally be viewed as an embedded part of the process ② (linear elasticity, followed by fracture) and of the corresponding variational formulation $E(\varvec{u},\Gamma )\rightarrow \mathrm{min}$, with $E(\varvec{u},\Gamma )$ as in (1). In the figure, we use the sign $\Longrightarrow$ to indicate the ’extension’ of case (10) to (1) both in terms of the process and of the formulation. The relation between the ’sharp crack’ and the ’phase-field’/’diffusive crack’ formulations—the latter being given by (2) or, more generally, by (5)—is indicated by the symbol . In practice, with a reasonably small $\ell$ in (2) and (5), the computed $\varvec{\sigma }\hbox {-}\varvec{\varepsilon }$ response in this case recovers the one from the process ②. Note that all functionals involved in the considered logical scheme

(11)

are available.

Fig. 1

From linear elasticity towards phase-field modeling of brittle fracture via the variational formulation

Using Fig. 1 as a conceptual layout, one difficulty in constructing the phase-field model for the ductile case becomes clear, see Fig. 2. The contents of the left plot in this figure—the process ① and the related energy description—are well-established: we may take e.g. the $J_2$-plasticity framework as a starting point, i.e.

$$\begin{aligned} E(\varvec{\varepsilon }^\mathrm{e},\varvec{\varepsilon }^\mathrm{p},\alpha ):=\int _\Omega \left[ \Psi _\mathrm{e}(\varvec{\varepsilon }^\mathrm{e}) + \Psi _\mathrm{p}(\alpha ) \right] d\mathbf{x}, \end{aligned}$$

(12)

where

$$\begin{aligned} \Psi _\mathrm{p}(\alpha ):=\sigma _\mathrm{y}\alpha +\frac{1}{2}h\alpha ^2, \end{aligned}$$

(13)

is the plastic energy density function assuming linear isotropic hardening, with yield stress $\sigma _\mathrm{y}$, hardening variable $\alpha$ and hardening modulus $h>0$. In (12), $\varvec{\varepsilon }^\mathrm{e}$ and $\varvec{\varepsilon }^\mathrm{p}$ are respectively the elastic and the plastic strain tensors, which are assumed to additively contribute to the total strain, $\varvec{\varepsilon }=\varvec{\varepsilon }^\mathrm{e}+\varvec{\varepsilon }^\mathrm{p}$. The plastic strain $\varvec{\varepsilon }^\mathrm{p}$ and the hardening variable $\alpha$ are treated as internal (state) variables, for which appropriate evolution equations are established, see e.g. Simo and Hughes [51] or Owen [52].

Fig. 2

From plasticity towards phase-field modeling of ductile fracture: the corresponding variational formulation is a missing link

Unfortunately, and in contrast to the previous case, we do not have here a variational theory that describes the ductile fracture process (the dashed line of the process ② in Fig. 2) in the way it was done in the brittle case. That is, within the logical scheme

(14)

which formally mimics (11), the functional $E(\varvec{\varepsilon }^\mathrm{e},\varvec{\varepsilon }^\mathrm{p},\alpha ,\Gamma )$ is not available. Therefore, we cannot derive its regularized counterpart $E_\ell (\varvec{\varepsilon }^\mathrm{e},\varvec{\varepsilon }^\mathrm{p},\alpha ,s)$ to be treated as the corresponding phase-field formulation.

To overcome this difficulty the following option may be considered: taking the elasto-plastic formulation (12)—as the one that is already capable of reproducing the process ① in Fig. 2—and ’enriching’ it by mimicking the regularization formalism (2) or (5). This implies introducing an appropriate coupling function $g$ into $E(\varvec{\varepsilon }^\mathrm{e},\varvec{\varepsilon }^\mathrm{p},\alpha )$ in (12), as well as adding the (original or modified) surface energy functional from (2) and (5). The resulting formulation should then be able to reproduce the process ②, most importantly, including its fracturing (dashed) part.

One of the first attempts in this direction can be found in [42]. The formulation proposed therein relies on the free energy functional

$$\begin{aligned} E_\ell (\varvec{\varepsilon }^\mathrm{e},\varvec{\varepsilon }^\mathrm{p},\alpha ,s)&:= \int _\Omega \left[ g(s)\Psi _\mathrm{e}^{+}(\varvec{\varepsilon }^\mathrm{e}) \!+\! \Psi _\mathrm{e}^{-}(\varvec{\varepsilon }^\mathrm{e}) \!+\! \Psi _\mathrm{p}(\alpha ) \right] d\mathbf{x} \nonumber \\&\ \quad + G_c \int _\Omega \left( \frac{1}{4\ell }(1-s)^2+\ell |\nabla s|^2\right) d\mathbf{x}, \end{aligned}$$

(15)

with $g(s)=s^2+\eta$ and $\Psi _\mathrm{p}(\alpha )$ slightly different from the one in (13). The formulation is termed by the authors a phase-field/gradient damage model for brittle fracture in elasto-plastic solids. To our understanding, the reference to brittle fracture is due to the choice of $g$, which corresponds to the original brittle model in elastic solids (2) and (5). As may be guessed, the fracture mechanism (i.e. the evolution of the phase-field) in this case will be driven primarily by the elastic strains, thus the contribution of the plastic strains will be minor. This will be illustrated by some of the numerical examples in Sect. 5.

From the above observation, it becomes clear that a cornerstone of the ductile phase-field model derivation is the appropriate choice of the function $g$ and, particularly, that this function should depend not only on the phase-field variable $s$ but also on a certain measure of the plastic strain state.

3.2 The proposed model

In this contribution, we propose the following free energy functional

$$\begin{aligned}&E_\ell (\varvec{\varepsilon }^\mathrm{e},\varvec{\varepsilon }^\mathrm{p},\alpha ,s)\nonumber \\&\quad := \int _\Omega \left[ g(s,p)\Psi _\mathrm{e}^{+}(\varvec{\varepsilon }^\mathrm{e}) + \Psi _\mathrm{e}^{-}(\varvec{\varepsilon }^\mathrm{e}) + \Psi _\mathrm{p}(\alpha ) \right] d\mathbf{x} \nonumber \\&\qquad \quad +\, G_c \int _\Omega \left( \frac{1}{4\ell }(1-s)^2+\ell |\nabla s|^2\right) d\mathbf{x}, \end{aligned}$$

(16)

where we define

$$\begin{aligned} g(s,p):=s^{2p}+\eta , \end{aligned}$$

(17)

with

$$\begin{aligned} p:=\frac{\varepsilon ^\mathrm{p}_\mathrm{eq}}{\varepsilon ^\mathrm{p}_\mathrm{eq,crit}}, \quad \varepsilon ^\mathrm{p}_\mathrm{eq}(t):= \sqrt{\frac{2}{3}}\int _{0}^t \sqrt{\dot{\varvec{\varepsilon }}^\mathrm{p}:\dot{\varvec{\varepsilon }}^\mathrm{p}} \;d\tau , \end{aligned}$$

(18)

and $\varepsilon ^\mathrm{p}_\mathrm{eq,crit}$ as a threshold value. $\varepsilon ^\mathrm{p}_\mathrm{eq}$ is often referred to as the von Mises equivalent plastic strain.

The variable $p$ accounts for accumulation and localization of plastic strains, and our idea of devising (17), i.e. incorporation of $p$ into the coupling function $g$, is to make $s$ dependent on $p$, thereby assuming that the fracture process is the result of the accumulation of the ductile damage.

As shown in the following, due to (17) $p$ enters the evolution equation for $s$, thus already providing their implicit relation. The explicit interaction between $s$ and $p$ (or rather the influence of $p$ upon $s$) is clarified in Appendix 1, using an asymptotic (perturbation) analysis, and is shown to obey

$$\begin{aligned} s \sim 1-\frac{4\ell }{G_c}p\Psi _\mathrm{e}^{+}(\varvec{\varepsilon }^\mathrm{e}). \end{aligned}$$

(19)

The latter particularly means that, owing to (17)–(18), the contribution of the plastic strains to the phase-field development should be, at least, competitive with the contribution of the elastic strains. In the numerical examples in Sect. 5, we will observe that $p$ takes even a dominating role over $\Psi _\mathrm{e}^{+}$, thus ’delaying’ the brittle-like fracture development and enabling the desired plasticity-driven fracture initiation and propagation mechanism, as depicted in Fig. 3.

Fig. 3

The conceptual backbone of the proposed model: a the plastic strain accumulation and localization zone within $\Omega$ and the related $p=p(\varvec{\varepsilon }^\mathrm{p}(\mathbf{x},t))$; $t$ stands for the pseudo-time; b the phase-field $s(\mathbf{x},t)$ triggered by $p$ and occurring in the plastic strain localization zone

The variational derivative of $E_\ell$ with respect to $\varvec{\varepsilon }^\mathrm{e}$ leads to the equilibrium equation $\mathrm{div}\;\varvec{\sigma }=\varvec{0}$, where the stress takes the form

$$\begin{aligned} \varvec{\sigma }(\varvec{\varepsilon }^\mathrm{e},s,p):=g(s,p)\frac{\partial \Psi _\mathrm{e}^{+}(\varvec{\varepsilon }^\mathrm{e})}{\partial \varvec{\varepsilon }^\mathrm{e}} + \frac{\partial \Psi _\mathrm{e}^{-}(\varvec{\varepsilon }^\mathrm{e})}{\partial \varvec{\varepsilon }^\mathrm{e}}. \end{aligned}$$

(20)

For the current formulation, we assume the material obeys $J_2$-plasticity with linear isotropic hardening, thus Eq. (13) holds. Moreover, the yielding function is defined as

$$\begin{aligned} f(\varvec{\sigma } ,\alpha ,s,p) = \sqrt{3 J_2(\varvec{\sigma }_\mathrm{dev})} + t_\alpha \le 0, \end{aligned}$$

(21)

where $J_2(\varvec{\sigma }_\mathrm{dev})$ is the second invariant of the deviatoric stress tensor $\varvec{\sigma }_\mathrm{dev}:=\varvec{\sigma }-\frac{1}{3} \mathrm{tr}(\varvec{\sigma })\varvec{I}$ and $t_\alpha$ is the hardening thermodynamical force obtained from (16) and (13) as

$$\begin{aligned} t_\alpha :=-\frac{\partial E_\ell }{\partial \alpha }=-(\sigma _\mathrm{y} + h\alpha ). \end{aligned}$$

(22)

Assuming associative plasticity, the evolution equation for the plastic strain $\varvec{\varepsilon }^\mathrm{p}$ and the internal hardening variable $\alpha$ are

$$\begin{aligned} \dot{\varvec{\varepsilon }}^\mathrm{p}(\varvec{\sigma },s,p) = \dot{\lambda } \; \frac{\partial f}{\partial \sigma }, \nonumber \\ \dot{\alpha }=\dot{\lambda } \; \frac{\partial f}{\partial t_\alpha }, \end{aligned}$$

(23)

where $\dot{\lambda }$ is the plastic consistency factor. Note that these evolution equations are the same of classical $J_2$-plasticity, where they automatically ensure satisfaction of the second law of thermodynamics. The fact that the same evolution equations can be used in the present model while still guaranteeing thermodynamic consistency is demonstrated in Appendix 2. Loading and unloading conditions are governed by the Kuhn–Tucker relations

$$\begin{aligned} \dot{\lambda }\ge 0, \quad f\le 0, \quad \dot{\lambda }f = 0. \end{aligned}$$

(24)

The evolution equation for the crack phase-field reads

$$\begin{aligned} 2\ell \Delta s+\frac{1-s}{2\ell }=\frac{g_{,s}(s,p)}{G_c}\Psi _\mathrm{e}^{+}(\varvec{\varepsilon }^\mathrm{e}), \end{aligned}$$

where $g_{,s}=\frac{\partial g}{\partial s}$ and with $g$ as in (17) it turns into

$$\begin{aligned} 2\ell \Delta s+\frac{1-s}{2\ell }=\frac{2s^{2p-1}}{G_c} p \Psi _\mathrm{e}^{+}(\varvec{\varepsilon }^\mathrm{e}) . \end{aligned}$$

(25)

As was already mentioned and as it can now be seen from (25), the phase-field $s$ is not only driven by the tensile part of the elastic energy but it also depends on the introduced plastic variable $p$. The explicit relation between $s$ and $p$ is given by (19), see Appendix 1 for the derivation details.

The irreversibility of the crack phase-field during loading/unloading is ensured by the introduction of the following local history variable into (25)

$$\begin{aligned} {\mathcal {H}}_\mathrm{e}(\mathbf{x},t):=\max _{\tau \in [0,t]}\Psi _\mathrm{e}^{+}(\varvec{\varepsilon }^\mathrm{e}(\mathbf{x},\tau )), \end{aligned}$$

(26)

This represents the maximum positive elastic energy obtained in a loading process and stems from the work of Miehe and co-workers on brittle fracture models [37]. Note that the introduction of (26) also enables algorithmic decoupling of the governing system of equations and the application of a staggered approach, which is extremely robust for computing phase-field models.

The system of governing equations of the proposed elasto-plastic ductile fracture model is summarized in Table 1.

Table 1 Governing equations of the proposed elasto-plastic ductile fracture model

The following Neumann and Dirichlet boundary conditions apply

$$\begin{aligned} \begin{aligned} \varvec{u} = \bar{\varvec{u}} \quad \mathrm{on} \quad \partial \Omega _{\bar{u}}, \\ \varvec{\sigma } \cdot \varvec{n} = \bar{\varvec{t}} \quad \mathrm{on} \quad \partial \Omega _{\bar{t}}, \\ \nabla s \cdot \varvec{n} = 0 \quad \mathrm{on} \quad \partial \Omega , \end{aligned} \end{aligned}$$

(27)

where $\bar{\varvec{u}}$ and $\bar{\varvec{t}}$ are prescribed on $\partial \Omega _{\bar{u}}$ and $\partial \Omega _{\bar{t}}$, respectively, $\partial \Omega =\partial \Omega _{\bar{u}}\cup \partial \Omega _{\bar{t}}$ and $\partial \Omega _{\bar{u}}\cap \partial \Omega _{\bar{t}}=\emptyset$. Finally, $\varvec{n}$ is the outward normal unit vector to the boundary.

Remark 1

Setting formally $p\equiv 1$ in (16) one recovers a formulation similar to the one in [42], which we will term elasto-plastic brittle fracture model. The corresponding governing system of equations is summarized in Table 2. The boundary conditions (27) apply in this case as well.

Note that the evolution equation (f) is the same as (9), which is valid for brittle fracture of elastic solids, where $s$ is driven only by the tensile part of the elastic stored energy. It has no interaction with the plastic flow mechanism and thus does not account for the plastic strain localization.

Table 2 Governing equations of the elasto-plastic brittle fracture model

3.3 Generalization of the coupling function

The coupling function $g(s,p)=s^{2p}+\eta$ introduced above can be generalized as follows

$$\begin{aligned} g(s,p):=s^{2p^m}+\eta , \end{aligned}$$

(28)

where $m\in \{1,2,3,...\}$. The purpose of introducing an additional parameter in $g$ is to enable a greater flexibility in controlling the ’speed’ of a ductile fracture mechanism. Indeed, the increase of the order of $p=\frac{\varepsilon _\mathrm{eq}^\mathrm{p}}{\varepsilon _\mathrm{eq,crit}^\mathrm{p}}$ is expected to slow down the accumulation of damage before reaching the threshold value $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$, that is when $p<1$, see Fig. 4, and to accelerate it when the threshold is exceeded ($p>1$). The effect of $m$ is studied in some of the examples in Sect. 5.

Fig. 4

The plastic variable $p^m$ for $m=1,2,3$ as a function of the equivalent plastic strain $\varepsilon _\mathrm{eq}^\mathrm{p}$

4 Algorithmic aspects

4.1 Staggered solution strategy

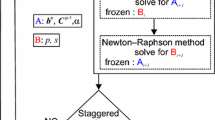
Following the ideas of algorithmic decoupling by Miehe et al. [37], we solve the weak formulations of equations (a) and (g) from Table 1, as well as of (a) and (f) from Table 2, using a staggered strategy. The strategy adopted for the proposed model is slightly different from the one of brittle fracture implementations, and is therefore illustrated in Figure 5.

Fig. 5

Staggered solution strategy adopted for the proposed model

At each pseudo-time/loading step, we must solve the weak counterparts of the momentum equation (a) and evolution equation (g). Both equations involve the variables $\varvec{u},\, s$, as well as the internal plastic variables $\varvec{\varepsilon }^\mathrm{p},\, \alpha$ and the additional variable $p$. We group these variables in two sets, set A including $\varvec{u},\, \varvec{\varepsilon }^\mathrm{p}$ (from which $\varvec{\varepsilon }$ and $\varvec{\varepsilon }^\mathrm{e}$ can be computed) and $\alpha$, and set B including $s$ and $p$.

First, the momentum equation (a) is solved for frozen set B, to determine the new set A. Along with equation (a), the evolution equations (d) are also solved while ensuring conditions (c) and (e), using the return mapping algorithm presented in Sect. 4.2. Using the updated elastic and plastic strains, the variable $p$ is computed and the phase-field evolution equation (g) is solved for frozen A.

Note that there are different possible ways to group the governing variables in the two sets A and B. The chosen one, where $p$ and $\varvec{\varepsilon }^\mathrm{p}$ are included in different sets, might appear counter-intuitive but greatly simplifies the return mapping algorithm presented in Sect. 4.2. We use the same implementation strategy for the model in Table 2, with the only difference that, in this case, $p$ is not present as additional variable.

Finally, we comment on the convergence and the stopping criterion of the staggered iterative process in Fig. 5. We control the (monotonically decreasing) sequence of energies $\{E_{\ell ,i}\},\, i=1,2,...x$ and the iterative process is stopped when the user-prescribed tolerance for the quantity $\gamma (E_{\ell ,i}),\, i=1,2,...$ is achieved. Herein, $\gamma$ represents the normalized energy- and number-of-iterations-related scales. We refer to our recent paper [39] for further details.

4.2 Time integration

The time integration algorithm for the elasto-plastic constitutive equations for the models of Tables 1 and 2 is briefly presented as follows. The evolution equations of the plastic variables in Tables 1(d) and 2(d) can be integrated with the backward Euler scheme, obtaining

$$\begin{aligned} \varvec{\varepsilon } _{n + 1}^\mathrm{p} = \varvec{\varepsilon }_n^\mathrm{p} + \Delta \lambda \sqrt{\frac{3}{2}} \varvec{n}_{n + 1}, \qquad {\alpha _{n + 1}} = {\alpha _n} + \Delta \lambda , \end{aligned}$$

(29)

with $\varvec{n} = \frac{{\varvec{\sigma } _{\mathrm{dev},n + 1}}}{{\left\| {\varvec{\sigma } _{\mathrm{dev},n + 1}} \right\| }}$ and $\Delta \lambda >0$ as the incremental plastic multiplier. The subscripts $(\cdot )_{n}$ and $(\cdot )_{n+1}$ define the values of $(\cdot )$ at $t_n$ and $t_{n+1}$, respectively. The discrete versions of the yielding and of the Kuhn-Tucker conditions read

$$\begin{aligned} \begin{aligned} f({\varvec{\sigma }} _{n + 1},{\alpha _{n + 1}}) = \sqrt{3{J_2}\left( {{\varvec{\sigma }} _{\mathrm{dev},n + 1}} \right) } - ({\sigma _\mathrm{y}} + h{\alpha _{n + 1}})\le 0\\ \Delta \lambda \ge 0,\quad \mathrm{{ }} f({\varvec{\sigma }_{n + 1}},{\alpha _{n + 1}}) \le 0,\quad \mathrm{{ }}\Delta \lambda f({\varvec{\sigma }_{n + 1}},{\alpha _{n + 1}}) = 0. \end{aligned} \end{aligned}$$

(30)

In order to solve (29) while satisfying (30), we adopt the classical elastic predictor and plastic corrector (return-mapping) algorithm outlined in [52]. Given the elastic strain, plastic strain and internal variables $\varvec{\varepsilon }_n^\mathrm{e},\, \varvec{\varepsilon }_n^\mathrm{p}$ and $\alpha _n$ at the beginning of the pseudo-time interval $[t_n, t_{n+1}]$ and with the prescribed incremental strain $\Delta \varvec{\varepsilon }$ for this interval, we consider an elastic trial state obtained by freezing plastic flow ($\Delta \lambda =0$). For the $J_2$-plasticity model with linear isotropic hardening, the trial deviatoric stress and the trial yielding condition are given by

$$\begin{aligned} \varvec{\sigma } _{\mathrm{dev},n + 1}^\mathrm{tr}&= \hat{g} 2\mu \varvec{\varepsilon } _{\mathrm{dev},n + 1}^\mathrm{{e,tr}}\\ f_{n + 1}^\mathrm{{tr}}&= \sqrt{3{J_2}\left( {\varvec{\sigma }_{\mathrm{dev}, n + 1}^{\mathrm{tr}}} \right) } - ({\sigma _\mathrm{y}} + h{\alpha _{n}}) \le 0 \end{aligned}$$

where $(\cdot )^\mathrm{tr}$ denotes a trial quantity and $\hat{g}=g(\hat{s}, \hat{p})$ (model in Table 1) or $\hat{g}=g(\hat{s})$ (model in Table 2) with $\hat{s}$ and $\hat{p}$ as frozen variables of the current staggered iteration. If $f_{n + 1}^\mathrm{tr} \le 0$ then the process is purely elastic and the elastic trial state is the solution. If, on the other hand, $f_{n + 1}^\mathrm{tr} > 0$, the trial stress is not admissible, the process is elasto-plastic and a plastic corrector step is needed. For the present case, the incremental plastic multiplier can be obtained from the following scalar equation having $\Delta \lambda >0$ as the only unknown

$$\begin{aligned} \sqrt{3{J_2}\left( {\varvec{\sigma }_{\mathrm{dev},n + 1}^\mathrm{tr}} \right) } - ({\sigma _\mathrm{y}} + h{\alpha _n}) - h\Delta \lambda - {{\hat{g}}}3\mu \Delta \lambda = 0. \end{aligned}$$

With the solution $\Delta \lambda$ at hand, the state variables are updated as follows

$$\begin{aligned} \varvec{\varepsilon }_{n + 1}^\mathrm{p} = \varvec{\varepsilon }_n^\mathrm{p} + \Delta \lambda \sqrt{\frac{3}{2}} {\varvec{n}}_{n+1}^\mathrm{tr}, \qquad \alpha _{n + 1} = \alpha _n + \Delta \lambda , \end{aligned}$$

where

$$\begin{aligned} \varvec{n}_{n+1}^\mathrm{tr} = \frac{{{\varvec{\sigma }} _{\mathrm{dev},n + 1}^\mathrm{tr}}}{{\left\| {{\varvec{\sigma }}_{\mathrm{dev},n + 1}^\mathrm{tr}} \right\| }}, \end{aligned}$$

and the final stress state $\varvec{\sigma } _{\mathrm{dev},n + 1}$ is the projection of the trial stress onto the yield surface as

$$\begin{aligned} {\varvec{\sigma } _{\mathrm{dev},n + 1}} = {{\varvec{\sigma }}_{\mathrm{dev},n + 1}^\mathrm{tr} - \Delta \lambda \hat{g} 2\mu \sqrt{\frac{3}{2}} {\varvec{n}}_{n+1}^\mathrm{tr} }. \end{aligned}$$

The above return mapping closely resembles the standard return mapping of $J_2$-plasticity with linear isotropic hardening from which it only differs for the presence of $\hat{g}$ in some of the equations. The same equations are obtained for the models in Table 1 and Table 2, the only difference being in the definition of $\hat{g}$. However, for the model of Table 1, the above results are valid within a staggered implementation where $s$ and $p$ are frozen while solving the momentum equation. Should we let $p$ evolve with $\varvec{\varepsilon }^\mathrm{p}$ (i.e. should $p$ belong to group A in Figure 5), the return mapping would assume a more complicated non-linear form, for which a local numerical iterative solution would be needed.

5 Numerical examples

We now investigate through several examples the ability of the proposed approach to capture representative aspects of the fracture processes in ductile materials. In the first two examples (an I-shaped specimen and an asymmetrically notched specimen), we aim at illustrating the effect on the numerical predictions of the proposed coupling between the phase field and the equivalent plastic strain. Moreover, we also assess the role of the critical equivalent plastic strain. In the third example we investigate notched specimens with two different notch radii, and test the ability of the model to predict the experimentally observed influence of the notch radius on the fracture pattern. In the subsequent single edge tension/shear test we focus on the effect of the loading angle on results. Finally, we illustrate for completeness two additional problems, namely a double notched specimen and a compact tension specimen.

All numerical computations are performed within the finite element framework using fully integrated 4-node quadrilateral elements and assuming plain strain conditions, with the material properties shown in Table 3. Displacement controlled conditions are always assumed. We adopt the staggered solution strategy presented in Sect. 4.1.

Table 3 Material parameters used in the numerical simulations [20]

5.1 I-shaped specimen

To gain the first insight into the performance of the model, we analyze a tensile test on an I-shaped specimen, with the geometric properties and boundary conditions shown in Fig. 6. A vertical displacement is applied to the top edge, which is restrained horizontally, whereas the bottom edge is completely fixed. The material parameters are those of Material I in Table 3, moreover we assume $\ell$=0.2 mm and $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$=10 %. A uniform mesh with 8847 quadrilateral elements is first used in order to eliminate any mesh-related effects. For specimens in plane strain conditions, the experimental evidence shows that the crack forms in the middle of the specimen with an inclination of about $\pm 45^{0}$ with respect to the major principal stress direction [54].

Fig. 6

I-shaped specimen. Geometry and boundary conditions [31]. Dimensions in mm

First, we compare the predictions of the proposed model with those of its uncoupled counterpart. For both models, Fig. 7a shows the equivalent plastic strain field at incipient cracking, whereas Fig. 7b–e illustrate the evolution of the crack phase field from incipient cracking to complete failure. The stages indicated in the diagram correspond to the points labeled accordingly in the load–displacement curves of Fig. 8. With the uncoupled model, the first crack appears at one of the notches, i.e. at the location of the elastic stress concentration, and then gradually propagates towards the center. Conversely, according to the proposed model the evolution of the crack phase field is driven by the plastic strain localization which takes place in the middle of the specimen. Therefore, this is also the location of the first crack. As the localized damage band bifurcates into two inclined branches, the crack propagates by following one of the two directions with a consequent loss of symmetry. Failure occurs when the boundary of the specimen is reached. Unlike those of the uncoupled model, predictions of the proposed model correctly reproduce the experimental evidence described in [54].

Fig. 7

I-shaped specimen. a Equivalent plastic strain field at the onset of cracking and b–e crack phase field at various fracture stages (see labels in Fig. 8). Red corresponds to damaged and blue to undamaged material. (Color figure online)

Fig. 8

I-shaped specimen. Load–displacement curves

Next, we assess the effect of the critical equivalent plastic strain on the model predictions. Here we refine the mesh in the central region of the specimen where crack propagation is expected, so that the mesh now contains 10,499 quadrilateral elements. The effect of $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$ on the crack path and on the load–displacement curve is shown respectively in Figs. 9 and 10. It can be observed that a change in $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$ does not affect the fracture process in terms of crack path but influences the load bearing capacity. Finally, the influence of the length scale parameter $\ell$ on crack path and load–displacement behavior is shown respectively in Figs. 11 and 12 for $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$=10 %.

Fig. 9

I-shaped specimen. Effect of $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$ on the fracture process. a–d Crack phase field at various fracture stages (see labels in Fig. 10) and e equivalent plastic strain field at the final stage

Fig. 10

I-shaped specimen. Effect of $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$ on the load–displacement curve

Fig. 11

I-shaped specimen. Effect of $\ell$ (mm) on the fracture process. a1–c2 Crack phase field at the initial and final fracture stages and d equivalent plastic strain field at the final stage

Fig. 12

I-shaped specimen. Effect of $\ell$ (mm) on the load–displacement curve

5.2 Asymmetrically notched specimen

We now examine the asymmetrically notched specimen illustrated in Fig. 13. The top edge is restrained horizontally and displaced vertically, whereas the bottom edge is fixed. The material parameters are those of Material I in Table 3, in addition to $\ell$=0.08 mm and $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$=10 %. The spatial discretization of the model comprises 10,800 quadrilateral elements, with refinement in the central region between the notches where the crack is expected to form.

Fig. 13

Asymmetrically notched specimen. Geometry and boundary conditions. Dimensions in mm

The evolution of the equivalent plastic strain and crack phase fields is provided in Fig. 14 for both the uncoupled and the proposed models. As expected, the equivalent plastic strain is maximum at both notch roots and localization branches form between the notches at an angle of about $45^{\circ }$ dictated by the specific geometry. Both models are able to predict crack initiation at the notches. However, during the subsequent stages, the standard model predicts the initial cracks to propagate sub-horizontally towards the center of the specimen, leading to a final crack pattern which deviates from the region of plastic strain localization. Conversely, with the proposed model the initial cracks propagate within the plastic strain localization band and eventually merge leading to complete failure.

Fig. 14

Asymmetrically notched specimen. a1–c1 Equivalent plastic strain field and a2–c2 crack phase field at various fracture stages

The effect of the critical equivalent plastic strain on results in terms of crack path and load–displacement curve is evaluated respectively in Figs. 15 and 16. As for the previous example, the crack path is not appreciably influenced, whereas the fracture branch of the load–displacement curve corresponds to increasing values of displacement for increasing $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$. Additionally, the role played by the exponent $m$ in the coupling term $p^{m}$ is investigated in Figs. 17 and 18 with $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$=12 %. As the order $m$ increases, the inclination of the incipient crack pattern increasingly follows the direction of the plastic strain localization band, whereas the fracture branch of the load–displacement curve becomes more abrupt.

Fig. 15

Asymmetrically notched specimen. Effect of $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$ on the fracture process. a1–c1 Equivalent plastic strain field and a2–c2 crack phase field at various fracture stages (see labels in Fig. 16)

Fig. 16

Asymmetrically notched specimen. Effect of $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$ on the load–displacement curve

Fig. 17

Asymmetrically notched specimen. Effect of the order $m$ on the fracture process. a1–c1 Equivalent plastic strain field and a2–c2 crack phase field at various fracture stages (see labels in Fig. 18)

Fig. 18

Asymmetrically notched specimen. Effect of the order $m$ on the load–displacement curve

Results for $m=2$ and $m=3$ are however quite similar. Finally, Fig. 19 focuses on the effect of the mesh size on the fracture pattern, with the corresponding load–displacement curves reported in Fig. 20. For all discretizations the model delivers similar initial and final crack shapes, however the finest mesh resolves the crack profile most accurately. As visible in Fig. 20, the decreasing branch appears smoother for the finest discretizations. Convergence of the results as the mesh is refined is also evident.

Fig. 19

Asymmetrically notched specimen. Effect of the mesh size (5459, 10,800 and 15,394 elements) on the fracture process. (a-c)(1-2) Crack phase field at the initial and final fracture stages (see labels in Fig. 20)

Fig. 20

Asymmetrically notched specimen. Effect of the mesh size (5459, 10,800 and 15,394 elements) on the load–displacement curve

5.3 Notched specimens

In this example, we aim at reproducing the experimental evidence that, in tensile tests on notched specimens, the crack initiates at the notch root or in the middle of the specimen depending on the notch radius [56]. We thus examine two notched specimens with different notch radii and investigate the failure mechanisms predicted by the model. The geometry and boundary conditions of the problem are illustrated in Fig. 21, whereas the material parameters are those of Material I in Table 3, as well as $\ell$=0.08 mm and $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$=10 %. A discretization with 10,713 (specimen with notch radius of 5 mm) and 10,142 (specimen with notch radius of 2.5 mm) elements is used with local mesh refinement between the notches.

Fig. 21

Notched specimens. Dimensions in mm

Figure 22 reports the evolution of the equivalent plastic strain field and of the crack phase field at three loading stages whereas the load–deflection curves are given in Fig. 23. For a notch radius of 5 mm, the model predicts crack initiation at the center of the specimen, followed by formation of two shear bands at an angle of about $\pm 45^{\circ }$ to the loading direction and by crack propagation along one of the two directions. Conversely, for the specimen with the smallest notch radius the crack initiates at the notch roots, where the largest plastic strain occurs. Subsequently, we observe an unsymmetric crack propagation from the notches inward, and at the same time the initiation of an additional inclined crack slightly offset from the middle of the specimen. Merging of all these cracks leads to final failure. Interestingly, the different crack pattern for the two notch radii is associated to a significantly different load–displacement behavior, the specimen with the larger notch radius failing more abruptly than the other one.

Fig. 22

Notched specimens. Effect of the notch radius on the fracture process. a1–c1 Equivalent plastic strain field and a2–c2 crack phase field at various fracture stages (see labels in Fig. 23)

Fig. 23

Notched specimens. Effect of the notch radius on the load–displacement curves

5.4 Single-edge notched tension/shear test

In [20, 53, 57, 58] the single-edge notched test is investigated in detail, both experimentally and numerically, for different values of the loading angle $\beta$ (Fig. 24). Experiments [57] and numerical simulations [53] agree in predicting mode-I crack growth for $\beta = 30^{\circ }\le \beta \le 90^{\circ }$ and mode-II for $\beta = 15^{\circ }$ and $\beta = 0^{\circ }$.

Fig. 24

Single-edge notched tension/shear test. Geometry and boundary conditions [53]. Dimensions in mm

Here we perform the same investigation to compare predictions of the proposed phase-field model with the aforementioned results. The geometric properties and boundary conditions of the specimen are shown in Fig. 24. The material parameters are those of Material II in Table 3, moreover $\ell$=0.05 mm and $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$=10 %. Loading is applied at three different angles (namely, $90^{\circ },\, 0^{\circ }$ and $45^{\circ }$) to obtain different modes of fracture. The spatial discretization contains 10,600 ($\beta = 90^{\circ }$), 10,262 ($\beta$ = 0$^{\circ }$) and 19,256 ($\beta = 45^{\circ }$) quadrilateral elements with a refinement in the region where the crack is expected to form.

Figures 25, 26 and 27 depict the evolution of the equivalent plastic strain field and of the corresponding crack phase field at several stages of loading. In pure mode I ($\beta = 90^{\circ }$) as well as in mode-II ($\beta = 0^{\circ }$) the crack propagates horizontally. A bending upwards of the crack from the initial tip occurs for a loading angle $\beta =45^{0}$. A phenomenon that is observed in these simulations is that the plastic strain localization takes place mainly in front of the crack tip which results in a stable crack propagation. The load–displacement curves are given in Fig. 28 for all loading angles.

Fig. 25

Single-edge notched tension/shear test. $\beta$ = 90$^{0}$. a–c Equivalent plastic strain field and crack phase field at various fracture stages (see labels in Fig. 28)

Fig. 26

Single-edge notched tension/shear test. $\beta = 0^{0}$. a–c Equivalent plastic strain field and crack phase field at various fracture stages (see labels in Fig. 28)

Fig. 27

Single-edge notched tension/shear test. $\beta = 45^{0}$. a–c Equivalent plastic strain field and crack phase field at various fracture stages (see labels in Fig. 28)

Fig. 28

Single-edge notched tension/shear test. Effect of the loading angle on the load–displacement curve

5.5 Double notched specimen

In this example, we model a double notched specimen with a vertical displacement imposed to the top edge and left edge. These edges are both restrained horizontally, whereas the bottom and right edges are fixed, as illustrated in Fig. 29. In the context of ductile fracture, the same problem has been addressed in [20] using a non-local damage model for the initial continuum damage phase, followed by a discontinuous crack propagation phase predicted through a remeshing strategy. Results showed the development of a plastic shear band diagonally across the specimen, which in turn results in a curved crack trajectory which initiates at both the notches and propagates towards the center of the specimen where the two crack branches merge (Fig. 30).

Fig. 29

Double notched specimen. Geometry and boundary conditions [20]. Dimensions in mm

Fig. 30

Double notched specimen. a–d Equivalent plastic strain field and crack phase field at various fracture stages (see labels in Fig. 31)

Fig. 31

Double notched specimen. Effect of $p$ on the load–displacement curve

The material parameters are those of Material II in Table 3, also it is $\ell$=0.03 mm and $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$=25 %. The adopted discretization contains 10,300 quadrilateral elements with mesh refinement in the expected crack propagation region.

Figure 30 shows the evolution of equivalent plastic strain and the corresponding crack phase field at several stages of fracture process. The load-deflection curves are shown in Fig. 31. The obtained behavior is in very good agreement with the results in [20].

5.6 Compact tension (CT) specimen

Finally, we model crack initiation and propagation for a CT specimen. The geometry and boundary conditions are shown in Fig. 32. The specimen contains an horizontal notch at its mid-height, and load is applied by a top pin which is displaced vertically, whereas the lower pin is fixed. The material parameters are those of Material I in Table 3, additionally $\ell$=0.09 mm and $\varepsilon _\mathrm{eq,crit}^\mathrm{p}$=5 %. The mesh comprises 10,097 quadrilateral elements with refinement in the areas where the crack is expected to form.

Fig. 32

CT specimen. Geometry and loading conditions [55]. Dimensions in mm

The results are shown in Figs. 33 and 34. It can be observed as the plastic deformations concentrate ahead of the notch (and later of the crack) tip, forming what can be considered as a plastic hinge. Accordingly, an horizontal crack propagates inward from the notch tip and, at the last stage, a secondary crack starts from the left edge of the specimen until failure results.

Fig. 33

CT specimen. a–d Equivalent plastic strain field and crack phase-field at various fracture stages (see labels in Fig. 34)

Fig. 34

CT specimen. Load–displacement curve

6 Conclusions

In this paper, we proposed a new phase-field model for ductile fracture in elasto-plastic solids, within the quasi-static kinematically linear regime. The distinct feature of the model is that it couples the evolution of the crack phase field with the accumulation of the plastic strains in a thermodynamically consistent way. As demonstrated by several numerical examples, this coupling enables the formulation to predict the initiation of fracture in the regions of plastic strain localization, in agreement with the experimental evidence. As a result, the model is able to predict several features of the phenomenology of quasi-static ductile fracture, including the shape and location of the crack pattern in a tensile specimen, the role played by the notch radius in notched specimens, and the change in fracture mode with the inclination of the applied load. With respect to brittle phase-field models, the proposed ductile fracture model includes two additional parameters, a threshold equivalent plastic strain and an exponent in the coupling function, which can facilitate the quantitative prediction of test results. While requiring further investigations, including e.g. the extension to the three-dimensional large deformation framework, the study of volumetric locking effects and a thorough experimental validation, the proposed model appears a very promising tool for the investigation of ductile fracture within the phase-field framework. Overall, this framework seems to be the ideal candidate to unify the prediction of diffuse ductile damage and (within the diffusive approximation) of discrete crack propagation, thus overcoming the difficulties of many other approaches.

Appendix

1.1 Perturbation analysis for the $s$ and $p$ mutual interaction

One of the most important aspects in our phase-field model of elasto-plastic ductile fracture is the coupling function $g(s,p):=s^{2p}$. Introduction of the exponent $p$, which accounts for the accumulation and localization of plastic strains, into the classic brittle-case function $g(s)=s^{2}$ allows us to let $s$ explicitly depend also on the plastic energy density $\Psi _\mathrm{p}$, and not only on the elastic one, $\Psi _\mathrm{e}$. This can be formally seen from the corresponding evolution equation for $s$ (25). More importantly, we show below that the evolution of $s$ in this case will mainly be governed by $p\sim \Psi _\mathrm{p}$ rather than $\Psi _\mathrm{e}$, thus delaying the brittle-like fracture development and enabling the desired plastic-driven fracture mechanism.

Without loss of generality, we restrict ourselves to the pure tensile loading situation so that no split of the elastic energy density function $\Psi _\mathrm{e}$ is required and the evolution equation for $s$ is given by

$$\begin{aligned} -4\ell ^2\Delta s+s+\frac{4\ell }{G_c}\Psi _\mathrm{e}(\varvec{\varepsilon })p s^{2p-1}=1. \end{aligned}$$

(31)

Equation (31) is a non-linear partial differential equation whose explicit analytical solution for $s$ is out of reach: one can only conclude that with $p\equiv 0$ (zero plastic strains), a trivial solution is $s=1$ (no phase-field development occurs). With a suitable rescaling of variables (i.e. non-dimensionalization), one can obtain a dimensionless version of (31) containing a small (perturbation) parameter. An approximate analytical solution of such perturbed non-linear equation can then be constructed explicitly, establishing a relation between $s$ and $p$.

Let $L$ be the maximal macroscopic dimension of the considered body. We introduce the following non-dimensional quantities:

$$\begin{aligned} (\bar{x},\bar{y}):=\left( \frac{x}{L},\frac{y}{L}\right) , \quad \bar{\varvec{u}}:=\frac{\varvec{u}}{A}, \quad \bar{\mathbb C}:=\frac{\mathbb C}{E}, \quad \bar{\ell }:=\frac{\ell }{\frac{1}{2}L}, \end{aligned}$$

(32)

where $A>0$ is a constant whose particular choice will be motivated below. The scaled strain tensor $\bar{\varvec{\varepsilon }}=\frac{1}{2}(\bar{\nabla }\bar{\varvec{u}}+\bar{\nabla }\bar{\varvec{u}}^T)$, with $\bar{\nabla }$ denoting the gradient w.r.t. the non-dimensional variables $(\bar{x},\bar{y})$, relates to the actual strain tensor $\varvec{\varepsilon }$ as

$$\begin{aligned} \varvec{\varepsilon }(\varvec{u})=\frac{A}{L}\bar{\varvec{\varepsilon }}(\bar{\varvec{u}}), \end{aligned}$$

(33)

yielding for $\Psi _\mathrm{e}$ the relation

$$\begin{aligned} \Psi _\mathrm{e}(\varvec{\varepsilon }) =\frac{1}{2}\mathbb {C}\varvec{\varepsilon }^2 =\frac{1}{2} E \bar{\mathbb {C}} \left( \frac{A}{L} \right) ^2 \bar{\varvec{\varepsilon }}^2 =E\left( \frac{A}{L}\right) ^2 \bar{\Psi }_\mathrm{e}(\bar{\varvec{\varepsilon }}). \end{aligned}$$

(34)

Also, we set $\bar{s}:=s$ so that $\Delta s=\frac{1}{L^2}\bar{\Delta }\bar{s}$, with $\bar{\Delta }$ standing for the Laplace operator w.r.t. $(\bar{x},\bar{y})$. Finally, a non-dimensional plastic strain variable is defined as $\overline{\varvec{\varepsilon }^\mathrm{p}}:=\varvec{\varepsilon }^\mathrm{p}$ leading to the corresponding definition of $\bar{p}$:

$$\begin{aligned} \bar{p}:=\frac{ \overline{\varepsilon ^\mathrm{p}_\mathrm{eq}} }{\varepsilon ^\mathrm{p}_\mathrm{eq,crit}}, \quad \overline{\varepsilon ^\mathrm{p}_\mathrm{eq}}(t):= \sqrt{\frac{2}{3}}\int _{0}^t \sqrt{ \dot{\overline{\varvec{\varepsilon }^\mathrm{p}}}:\dot{\overline{\varvec{\varepsilon }^\mathrm{p}}} } \;d\tau . \end{aligned}$$

(35)

Note that the denominator remains the same as in the definition of $p$.

Using (32)–(35) we turn (31) into

$$\begin{aligned} -\bar{\ell }^2\bar{\Delta }\bar{s}+\bar{s} +\frac{2\bar{\ell } L}{G_c} E \left( \frac{A}{L} \right) ^2 \bar{\Psi }_\mathrm{e}(\bar{\varvec{\varepsilon }}) \bar{p} \bar{s}^{2\bar{p}-1}=1. \end{aligned}$$

In the above, the scaling constant $A$ can be chosen to provide $\frac{2L}{G_c} E \left( \frac{A}{L} \right) ^2=1$, that is, $A:=\sqrt{\frac{G_c L}{2E}}$, and the dimensionless counterpart of (31) we end up with reads as

$$\begin{aligned} -\bar{\ell }^2\bar{\Delta }\bar{s}+\bar{s} +\bar{\ell } \bar{\Psi }_\mathrm{e}(\bar{\varvec{\varepsilon }}) \bar{p} \bar{s}^{2\bar{p}-1}=1. \end{aligned}$$

(36)

In what follows, we set $\gamma :=\bar{\ell }$ and also drop the bars over all remaining variables in (36). This yields

$$\begin{aligned} -\gamma ^2\Delta s+s+\gamma \Psi _\mathrm{e}(\varvec{\varepsilon }) p s^{2p-1}=1, \end{aligned}$$

(37)

where, by definition, $\gamma$ is a small (perturbation) parameter, that is, $0<\gamma \ll 1$.

According to the perturbation analysis framework [59], an asymptotic expansion of $s$ is taken in a form of a power series in $\gamma$:

$$\begin{aligned} s=s_0+\gamma s_1+\gamma ^2 s_2+\cdots , \end{aligned}$$

(38)

what yields for $\Delta s$ and $s^{2p-1}$ the expansions

$$\begin{aligned} \Delta s=\Delta s_0+\gamma \Delta s_1+\gamma ^2 \Delta s_2+\cdots , \end{aligned}$$

(39)

and

$$\begin{aligned} s^{2p-1}&= s_0^{2p-1}+\gamma (2p-1)s_0^{2p-2}s_1 \nonumber \\&\quad \ + \gamma ^2(2p-1)s_0^{2p-3}\left( s_0s_2+s_1^2(p-1)\right) +\cdots , \end{aligned}$$

(40)

respectively. In (39) and (40), only the terms up to order $O(\gamma ^2)$ have been retained, consistently with the assumed expansion (38). We now substitute (38)–(40) into the governing equation (37) and collect the coefficients of like powers of $\gamma$ to obtain:

$$\begin{aligned}&s_0+\gamma \left( s_1+p\Psi _\mathrm{e}s_0^{2p-1} \right) \nonumber \\&\quad + \gamma ^2 \left( -\Delta s_0+s_2+p(2p-1)\Psi _\mathrm{e}s_0^{2p-2}s_1 \right) +\cdots =1. \end{aligned}$$

(41)

Equating the coefficients of each power of $\gamma$ to zero we ’extract’ the equations for $s_0,s_1$ and $s_2$. The corresponding solutions are

$$\begin{aligned} s_0=1, \quad s_1=-p\Psi _\mathrm{e}, \quad s_2=p^2(2p-1)\Psi _\mathrm{e}^2, \end{aligned}$$

(42)

and, due to (38), we finally obtain

$$\begin{aligned} s = 1-\gamma p\Psi _\mathrm{e} + \gamma ^2 p^2(2p-1)\Psi _\mathrm{e}^2+\cdots , \end{aligned}$$

(43)

to be treated as an approximate analytical solution of equation (37). Note that with $\gamma \rightarrow 0$, equation (37) reduces to $s=1$. Sending $\gamma$ to zero also in (43), we recover the same result, i.e. $s=1$, as expected. Recall also that setting $p=0$ in (37), the trivial solution of the reduced equation is $s=1$. Similar result is obtained while substituting $p=0$ in (43).

From (43) the influence of $p$ on the phase-field $s$ can be grasped. In the linear elastic regime (no plastic strains, $p=0$) and at the beginning of the plastic regime (plastic strains are still negligibly small, $0<p\ll 1$), the evolution of $s$ is minor even with a (possibly large) non-zero contribution of $\Psi _\mathrm{e}$. In other words, the presence of $p$ in $g(s,p)=s^{2p}$ delays the brittle-like fracture formation. This is in a contrast to the brittle phase-field formulation, when the use of $g(s)=s^2$ results in $s$ depending solely on $\Psi _\mathrm{e}$ (expansion (43) with $p\equiv 1$) meaning that the crack development occurs independently of the evolution of the plastic strains.

1.2 Proof of thermodynamic consistency

In this Appendix, the governing equations of the proposed model are rewritten in the framework of the principle of virtual power as developed by Gurtin, see [60, 61], and their thermodynamic consistency is investigated.

1.2.1 Kinematics

The kinematics is based on the decomposition of the displacement gradient into elastic and plastic components $\nabla \mathbf {u}=\mathbf {H}^\mathrm{e}+\mathbf {H}^\mathrm{p}$. Correspondingly, we define the elastic and plastic strain tensors as

$$\begin{aligned} {\varvec{\varepsilon }}^\mathrm{e}=\frac{1}{2}\left( \mathbf {H}^\mathrm{e}+\mathbf {H}^{\mathrm{e}T}\right) \quad {\varvec{\varepsilon }}^\mathrm{p}=\frac{1}{2}\left( \mathbf {H}^\mathrm{p}+\mathbf {H}^{\mathrm{p}T}\right) \end{aligned}$$

(44)

so that the total strain tensor is given by ${\varvec{\varepsilon }}={\varvec{\varepsilon }}^\mathrm{e}+{\varvec{\varepsilon }}^\mathrm{p}$. Finally, we assume that $\mathbf {H}^\mathrm{p}$ is purely deviatoric, i.e. $\mathrm{tr}\,\mathbf {H}^\mathrm{p}=\mathrm{tr}\,{\varvec{\varepsilon }}^\mathrm{p}=0$.

1.2.2 Balance equations

Let us introduce the internal power in the form

$$\begin{aligned} \mathcal {I}\left( P\right)= & {} \int _{P}{{\varvec{\sigma }}}^\mathrm{e}:\dot{\mathbf {H}}^\mathrm{e}\;dv+\int _{P}{\varvec{\sigma }}^\mathrm{p}:\dot{\mathbf {H}}^\mathrm{p}\;dv+\int _{P}{\varvec{\xi }}\cdot \nabla \dot{s}\;dv\nonumber \\&+ \int _{P}\zeta \cdot \dot{s}\;dv \end{aligned}$$

(45)

where ${{\varvec{\sigma }}}^\mathrm{e}$ and ${{\varvec{\sigma }}}^\mathrm{p}$ are respectively an elastic stress, power-conjugate to $\dot{\mathbf {H}}^\mathrm{e}$, and a plastic stress, power-conjugate to $\dot{\mathbf {H}}^\mathrm{p}$. Since $\mathbf {H}^\mathrm{p}$ is deviatoric, we may assume without loss of generality that ${{\varvec{\sigma }}}^\mathrm{p}$ is deviatoric, i.e. that $\mathrm{tr}{\varvec{\sigma }}^\mathrm{p}=0$. Moreover, ${\varvec{\xi }}$ is the microscopic stress power-conjugate to $\nabla \dot{s}$, and $\zeta$ is the microscopic internal body force power-conjugate to $\dot{s}$, where $s$ is the crack field parameter, $0\le s\le 1$. The integration domain is any subregion $P$ of the body under consideration. The external power is given by

$$\begin{aligned} \mathcal {W}\left( P\right)= & {} \int _{\partial P}\varvec{t}\left( \varvec{n}\right) \cdot \dot{\varvec{u}}\;da+\int _{P}\varvec{b}\cdot \dot{\varvec{u}}\;dv\nonumber \\&+\int _{\partial P}\chi \left( \varvec{n}\right) \dot{s}\;da+\int _{P}\gamma \dot{s}\;dv \end{aligned}$$

(46)

where $\varvec{t}$ is the traction vector on the elementary area $da$ of the surface of $P,\, \partial P$, with outward unit normal $\varvec{n},\, \varvec{b}$ is the body force, $\chi$ and $\gamma$ are respectively the microscopic external traction and the microscopic external body force, both power-conjugate to $\dot{s}$. Considering a generalized virtual velocity

$$\begin{aligned} \mathcal {V}=\left( \tilde{\varvec{u}},\tilde{\mathbf {H}}^\mathrm{e},\tilde{\mathbf {H}}^\mathrm{p},\tilde{s}\right) \end{aligned}$$

(47)

satisfying the kinematical constraints above, the principle of virtual power reads

$$\begin{aligned}&\int _{P}{{\varvec{\sigma }}}^\mathrm{e}:\tilde{\mathbf {H}}^\mathrm{e}\;dv\!+\!\int _{P}{{\varvec{\sigma }}}^\mathrm{p}:\tilde{\mathbf {H}}^\mathrm{p}\;dv\!+\!\int _{P}{\varvec{\xi }}\cdot \nabla \tilde{s}\;dv\!+\!\int _{P}\zeta \cdot \tilde{s}\;dv\nonumber \\&=\int _{\partial P}\varvec{t}\left( \varvec{n}\right) \cdot \varvec{\tilde{u}}\;da\!+\!\int _{P}\varvec{b}\cdot \varvec{\tilde{u}}\;dv\!+\!\int _{\partial P}\chi \left( \varvec{n}\right) \tilde{s}\;da\!+\!\int _{P}\gamma \tilde{s}\;dv\nonumber \\ \end{aligned}$$

(48)

for any subregion $P$ of the body and any $\mathcal {V}$. Frame invariance implies that ${\varvec{\sigma }}^\mathrm{e}$ is symmetric, therefore ${\varvec{\sigma }}^\mathrm{e}:\tilde{\mathbf {H}}^\mathrm{e}={\varvec{\sigma }}^\mathrm{e}:\tilde{{{\varvec{\varepsilon }}}}^\mathrm{e}$. Applying Eq. (48) with $\mathcal {V}=\left( \tilde{\varvec{u}},\nabla \tilde{\varvec{u}}, \mathbf {0},0\right)$ leads to the macroscopic force balance $\mathrm{div}\varvec{\sigma }+\varvec{b}=\mathbf {0}$ and to the expression of the macroscopic traction $\varvec{t}\left( \varvec{n}\right) ={\varvec{\sigma }}\cdot \varvec{n}$, where we have introduced ${\varvec{\sigma }}:={\varvec{\sigma }}^\mathrm{e}$ as the (standard) Cauchy stress. Considering next a virtual velocity $\mathcal {V}=\left( \mathbf {0},-\tilde{\mathbf {H}}^\mathrm{p},{\tilde{\mathbf {H}}}^\mathrm{p},0\right)$ delivers the plastic microscopic force balance [61], ${\varvec{\sigma }}_{dev}={\varvec{\sigma }}^\mathrm{p}$, where ${\varvec{\sigma }}_{dev}$ is the deviatoric component of the stress tensor. Note that thus also ${\varvec{\sigma }}^\mathrm{p}$ is symmetric, therefore ${\varvec{\sigma }}^\mathrm{p}:\tilde{\mathbf {H}}^\mathrm{p}={\varvec{\sigma }}^\mathrm{p}:\tilde{{{\varvec{\varepsilon }}}}^\mathrm{p}$. Finally, insertion in Eq. (48) of a virtual velocity $\mathcal {V}=\left( \mathbf {0},\mathbf {0},\mathbf {0},\tilde{s}\right)$ yields

$$\begin{aligned} \int _{P}{\varvec{\xi }}\cdot \nabla \tilde{s}\;dv+\int _{P}\zeta \cdot \tilde{s}\;dv=\int _{\partial P}\chi \left( \varvec{n}\right) \tilde{s}\;da+\int _{P}\gamma \tilde{s}\;dv. \end{aligned}$$

(49)

Through the divergence theorem, Eq. (49) leads to the phase-field microscopic force balance

$$\begin{aligned} \mathrm{div}{\varvec{\xi }}-\zeta +\gamma =0 \end{aligned}$$

(50)

and to the expression of the phase-field microscopic traction $\chi \left( \varvec{n}\right) ={{\varvec{\xi }}}\cdot \varvec{n}$.

As a consequence of the above, and if we further introduce the codirectionality constraint valid for $J_{2}$ plasticity, $\frac{\dot{{\varvec{\varepsilon }}}^\mathrm{p}}{\left\| \dot{{\varvec{\varepsilon }}}^\mathrm{p}\right\| }=\varvec{n}^\mathrm{p}$ with $\varvec{n}^\mathrm{p}=\frac{{\varvec{\sigma }}_{dev}}{\left\| {\varvec{\sigma }}_{dev}\right\| }$, the power balance takes the final form

$$\begin{aligned}&\int _{P}{{\varvec{\sigma }}}:\dot{{\varvec{\varepsilon }}}^\mathrm{e}\;dv+\int _{P}\tau ^\mathrm{p}\dot{e}^\mathrm{p}\;dv+\int _{P}{\varvec{\xi }}\cdot \nabla \dot{s}\;dv+\int _{P}\zeta \cdot \dot{s}\;dv\\&= \int _{\partial P}\varvec{t}\left( \varvec{n}\right) \cdot \dot{\varvec{u}}\;da+\int _{P}\varvec{b}\cdot \dot{\varvec{u}}\;dv\!+\!\int _{\partial P}\chi \left( \varvec{n}\right) \dot{s}\;da\!+\!\int _{P}\!\gamma \dot{s}\;dv, \end{aligned}$$

where

$$\begin{aligned} \tau ^\mathrm{p}:=\left\| {\varvec{\sigma }}_{dev}\right\| , \quad \dot{e}^\mathrm{p}:=\left\| \dot{{\varvec{\varepsilon }}}^\mathrm{p}\right\| \ge 0, \quad e^\mathrm{p}\left( t\right) =\int _{0}^{t}\left\| \dot{{\varvec{\varepsilon }}}^\mathrm{p}\right\| \;d\tau \end{aligned}$$

(51)

1.2.3 Dissipation inequality and constitutive laws

Based on the formulation in Sect. 1, the dissipation inequality can be written (in local form) as

$$\begin{aligned} \dot{E}_\ell -{\varvec{\sigma }}:\dot{{\varvec{\varepsilon }}}^\mathrm{e}-\tau ^\mathrm{p}\dot{e}^\mathrm{p}-{\varvec{\xi }}\cdot \nabla \dot{s}-\zeta \cdot \dot{s}=-D\le 0 \end{aligned}$$

(52)

with $E_\ell$ as the free energy and $D$ as the dissipation rate, both per unit volume. Let us consider the following form of the free energy

$$\begin{aligned} E_\ell =E_\ell \left( {\varvec{\varepsilon }}^\mathrm{e},e^\mathrm{p},\alpha ,s,\nabla s\right) . \end{aligned}$$

(53)

This postulated form contains the “standard” dependencies on the elastic strain ${\varvec{\varepsilon }}^\mathrm{e}$ and on the hardening variable $\alpha$, plus further dependencies on the phase field and on its gradient, as well as on $e^\mathrm{p}$. The latter is a scalar measure of plastic strain accumulation defined in Eq. (51). The dependency of the free energy on $e^\mathrm{p}$ is needed to realize a coupling between the evolution of the phase-field parameter and the accumulation of plastic strains, and is an essential ingredient of the proposed model. Substitution of Eq. (53) in the dissipation inequality (52) leads to

$$\begin{aligned}&\left( \frac{\partial E_\ell }{\partial {\varvec{\varepsilon }}^\mathrm{e}}-{\varvec{\sigma }}\right) :\dot{{\varvec{\varepsilon }}}^\mathrm{e}+\left( \frac{\partial E_\ell }{\partial e^\mathrm{p}}-\tau ^\mathrm{p}\right) \dot{e}^\mathrm{p}+\frac{\partial E_\ell }{\partial \alpha }\dot{\alpha }\nonumber \\&+\left( \frac{\partial E_\ell }{\partial s}-\zeta \right) \dot{s}+\left( \frac{\partial E_\ell }{\partial \nabla s}-{\varvec{\xi }}\right) \cdot \nabla \dot{s}=-D\le 0. \end{aligned}$$

(54)

Well-known arguments lead immediately to the elastic stress-strain relationship

$$\begin{aligned} {\varvec{\sigma }}=\frac{\partial E_\ell }{\partial {\varvec{\varepsilon }}^{e}}. \end{aligned}$$

(55)

Additional consequences can be driven by applying the inequality individually to the group of terms related to the phase field

$$\begin{aligned} \left( \frac{\partial E_\ell }{\partial s}-\zeta \right) \dot{s}+\left( \frac{\partial E_\ell }{\partial \nabla s}-{\varvec{\xi }}\right) \cdot \nabla \dot{s}\le 0. \end{aligned}$$

(56)

From (56) follow the phase-field microscopic constitutive equations

$$\begin{aligned} {\varvec{\xi }}=\frac{\partial E_\ell }{\partial \nabla s}, \qquad \zeta =\frac{\partial E_\ell }{\partial s}. \end{aligned}$$

(57)

Substituting eqs. (57) into (50) leads to the phase-field evolution equation

$$\begin{aligned} \mathrm{div}\left( \frac{\partial E_\ell }{\partial \nabla s}\right) -\frac{\partial E_\ell }{\partial s}=0, \end{aligned}$$

(58)

where we have further assumed $\gamma =0$.

As a result of Eq. (55) and inequality (56), and introducing the thermodynamic force power-conjugate to $\dot{\alpha }$,

$$\begin{aligned} t_{\alpha }:=-\frac{\partial E_\ell }{\partial \alpha }, \end{aligned}$$

(59)

the following reduced dissipation inequality is obtained from (54)

$$\begin{aligned} D:=\tau ^\mathrm{p}\dot{e}^\mathrm{p}+t_{\alpha }\dot{\alpha }-\frac{\partial E_\ell }{\partial e^\mathrm{p}}\dot{e}^\mathrm{p}\ge 0. \end{aligned}$$

(60)

Note that, being $\dot{e}^\mathrm{p}\ge 0$, inequality (60) can be further reduced to its “classical” version

$$\begin{aligned} \tau ^\mathrm{p}\dot{e}^\mathrm{p}+t_{\alpha }\dot{\alpha }\ge 0, \end{aligned}$$

(61)

(whose satisfaction is ensured by the “classical” flow rule and hardening evolution equation of $J_{2}$-plasticity used in this work) provided that the following inequality holds

$$\begin{aligned} \frac{\partial E_\ell }{\partial e^\mathrm{p}}\le 0. \end{aligned}$$

(62)

From the specific choice of the free energy in Eq. (16) follows $\frac{\partial E_\ell }{\partial e^\mathrm{p}}=\frac{\partial g}{\partial e^\mathrm{p}}\Psi _\mathrm{e}^{+}({\varvec{\varepsilon }}^\mathrm{e})$ and therefore inequality (62) holds [and the reduced dissipation inequality takes the form (61)] provided that

$$\begin{aligned} \frac{\partial g}{\partial e^\mathrm{p}}\le 0. \end{aligned}$$

(63)

A possible specific choice of degradation function $g$ complying with (63) is the following

$$\begin{aligned} g\left( s,e^\mathrm{p}\right) =s^{2e^\mathrm{p}/e_\mathrm{crit}^\mathrm{p}}+\eta \end{aligned}$$

(64)

with coincides with the one in Eq. (17) by taking

$$\begin{aligned} e_\mathrm{crit}^\mathrm{p}=\sqrt{\frac{3}{2}}\varepsilon _\mathrm{eq,crit}^\mathrm{p} \end{aligned}$$

(65)

This proves the thermodynamic consistency of the proposed model.