Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Simulations in linear elastic fracture mechanics pose a challenging task for numerical methods, as they deal with discontinuities and singularities in solids. For such simulations the efficiency of the standard finite element method (FEM) and boundary element method (BEM) is limited by the \(\sqrt{r}\) behaviour of the displacements in the vicinity of the crack tip/front. Special elements at the crack tip/front, like ‘quarter-point’ elements [13, 20, 21], improve the approach. However, a suitable mesh has to be provided for each crack geometry during propagation which frequently requires a remeshing. The extended finite element method (XFEM) [17, 24] treats these discontinuities and singularities within the elements by additional enrichment functions, wherefore a simple, often structured background mesh is possible with a completely decoupled description of the crack.

In the XFEM, cracks may be defined in different ways. An implicit crack description by means of level-set functions, where the crack geometry is described by the zero level-sets of scalar functions [7, 23]. This description is a standard in the XFEM, however it has the disadvantage that, in general, the update of level-set functions after a propagation step can be cumbersome [7, 12, 22]. A hybrid explicit-implicit crack description [10] combines the advantages of an implicitly defined crack with those of an explicit representation, e.g. by means of straight line segments in two dimensions or flat triangles in three dimensions. An explicit crack description allows a simple update of the crack geometry during the crack propagation as the update of the crack geometry is achieved by adding new segments. This hybrid explicit-implicit description is based on three level-set functions ϕ j which are derived from the explicitly defined master configuration, see Sect. 2.1. In this work, this second representation of the crack geometry is used.

The behaviour of the fracture including the propagation may be based on stress intensity factors (SIFs). A linear combination of three independent crack modes which are scaled by the SIFs uniquely describes the situation at the crack front. A challenging task is the computation of these scaling factors for non-planar crack geometries with stress-free or loaded crack surfaces. One of the most important technique is based on the interaction integral [6, 18, 26], which is based on the energy release rate G. SIFs are then computed by means of auxiliary fields and the relation of the energy release rate and SIFs. However, for complex three-dimensional crack geometries the evaluation of this integral can be computationally expensive and unstable. In this paper, a more intuitive and computationally cheap method is introduced which allows a straightforward extension to three dimensions also considering mode I​I​I. This is achieved by observing the displacements, particularly the crack opening displacements (CODs), in the vicinity of the crack tip/front and their comparison with the expected openings for a pure mode I, I​I and I​I​I crack. The fitting of CODs has frequently been done in classical FEM simulations with conforming meshes [5, 20], however, not in an XFEM context.

The paper is organized as follows: Sect. 2 recalls the XFEM approach in linear elastic fracture mechanics and a hybrid explicit-implicit crack description. In Sect. 3, the computation of stress intensity factors (SIFs) by crack opening displacements (CODs) is discussed. Special attention is also given to the location of the fitting approach and the consideration of the crack front. Numerical results in two and three dimensions are presented in Sect. 4. Finally, Sect. 5 concludes this paper with a brief summary.

2 XFEM with a Hybrid Explicit-Implicit Crack Description

In this section, the XFEM approach in linear elastic fracture mechanics with a hybrid explicit-implicit crack description is shortly discussed. Beside of phase-field- or thick level-set-models [4, 15, 19], the XFEM offers a popular approach for linear elastic fracture problems as it allows the approximation of inner-element discontinuities, singularities, kinks and other non-smooth features within elements with optimal accuracy. Therefore, a priori knowledge about the solution characteristics is introduced to the problem using enrichment functions.

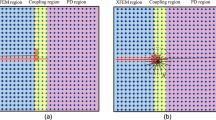
Starting point is a domain Ω with the boundary Γ u where the displacements are prescribed, and the boundary Γ t where the tractions are prescribed. The domain is cracked by the (curved) crack path/surface Γ c which may be stress-free or loaded as in applications of hydraulic fracturing. A hybrid explicit-implicit description of the crack is used which is explained in more detail in Sect. 2.1. Cracks feature discontinuous displacements along Γ c and singular stresses at the crack tip/front. An illustration of the situation is given in Fig. 1 for a two-dimensional case.

Fig. 1
figure 1

Situation of a cracked domain in two dimensions

Full size image

Additional enrichment functions which extend the standard finite element approach incorporate the discontinuities and singularities in the displacement and stress fields. For linear elastic fracture problems, the enriched approximation of the XFEM [17] is given by

$$\displaystyle{ u^{h}(\mathbf{x}) =\sum _{ I}N_{i}(\mathbf{x})u_{i} +\sum _{I^{{\ast}}}N_{i}(\mathbf{x})\psi _{step}(\mathbf{x})a_{i} +\sum _{ j=1}^{4}\sum _{ J^{{\ast}}}N_{i}(\mathbf{x})\psi _{tip}^{\,j}(r,\theta )b_{ i}^{\,j}. }$$
(1)

The first term of the right side represents the standard finite element approach, where N i are the finite element shape functions. The discontinuities in the displacement field are considered by the additional enrichment function ψ step and the singular stresses at the crack tip/front are considered by the four enrichment functions ψ tip  j. Additional degrees of freedom (a i , b i  j) are introduced at the enriched nodes I ∗ and J ∗ [17]. In linear elastic fracture mechanics it is standard to use the Heaviside function for the step enrichment ψ step [17] and

$$\displaystyle{ \psi _{tip}^{\,j}(r,\theta ) = \left [\sqrt{r}sin \frac{\theta } {2},\ \ \sqrt{r}cos \frac{\theta } {2},\ \ \sqrt{r}sin \frac{\theta } {2}sin\theta,\ \ \sqrt{r}cos \frac{\theta } {2}sin\theta \right ] }$$
(2)

for the crack tip/front enrichment. These enrichment functions are based on a polar coordinate system (r, θ) which is aligned with the tangent at the crack tip/front and has its origin at the crack tip/front. The definition of this coordinate system is based on three level-set functions which is discussed in Sect. 2.1.

2.1 Hybrid Explicit-Implicit Crack Description

The explicit-implicit crack description is recalled in this section. The aim is to combine an explicit crack description by means of straight line segments in two dimensions or flat triangles in three dimensions, which simplifies the crack update during propagation, and an implicitly defined crack by means of level-set functions. In Fig. 2a, an example for a three-dimensional explicitly defined crack is illustrated. Simulations with the XFEM typically use level-set functions to determine the enrichments. The definition of the enriched nodes (I ∗ and J ∗) is also based on level-set functions, wherefore they are derived from the explicitly defined master configuration. In [10], three level-set functions ϕ j are introduced which are the basis for the crack location and the enrichment functions in the XFEM. The three level-set functions are defined as follows:

  • ϕ 1(x) is the (unsigned) distance function to the crack path/surface.

  • ϕ 2(x) is the (unsigned) distance function to the crack tip/front.

  • ϕ 3(x) is a signed distance function to the extended crack path/surface.

Fig. 2
figure 2

(a ) Explicitly defined crack and level-sets: (b ) ϕ 1 = 1, (c ) ϕ 2 = 1, (d ) ϕ 3 = 0; 1; 2; 3 [10]

Full size image

An illustration of these functions is presented in Fig. 2b–d, where the corresponding level-sets for a three-dimensional crack geometry are illustrated. Furthermore, these functions imply two coordinate systems (r,θ) and (a,b), which are required for the enrichment functions (Sect. 2) and the reference state for the fitting (Sect. 3.2). These two coordinate systems are discussed in the following.

2.1.1 Coordinate System (a, b)

The (a,b)-coordinate system is defined by two scalar functions a(x) and b(x). The correlation of the level-set functions and the coordinates is given by

$$\displaystyle{ b(\mathbf{x}) =\phi _{3}(\mathbf{x}) }$$
(3)

and

$$\displaystyle{ a^{{\ast}}(\mathbf{x}) = \sqrt{\phi _{ 2}(\mathbf{x})^{2} -\phi _{3}(\mathbf{x})^{2}}. }$$
(4)

As a ∗(x) only describes an unsigned distance its sign has to be adapted for a(x), see [10] for further details. Figure 3a shows the (a,b)-coordinate system in two dimensions and (b) the zero level-sets of a(x) and b(x) in three dimensions. This coordinate system simplifies the localisation of the enriched nodes [10]. However, the enrichment functions themselves are based on the polar coordinate system (r, θ), wherefore the relation of these two coordinate systems is discussed in the following section.

Fig. 3
figure 3

(a ) Coordinate system (a, b) in two dimensions and (b ) zero level-sets of a(x) and b(x) implied by the three level-set functions [10]

Full size image

2.1.2 Coordinate System (r, θ)

The polar coordinate system (r, θ) can be expressed by the three level-set functions as shown in [10]. A similar setting is used, for example, in [23]. However, for the computation of the expected openings in the reference configuration (Sect. 3.2), it is preferred to express these coordinates by the two scalar functions a(x) and b(x). The radius r is given by

$$\displaystyle{ r(\mathbf{x}) = \sqrt{a(\mathbf{x} )^{2 } + b(\mathbf{x} )^{2}}. }$$
(5)

For the definition of θ, several cases must be considered. With the limitation that b(x) ≠ 0, the angle θ(x) is provided by

$$\displaystyle\begin{array}{rcl} \theta (\mathbf{x}) = \left \{\begin{array}{@{}l@{\quad }l@{}} tan^{-1}\left (\frac{b(\mathbf{x})} {a(\mathbf{x})}\right ) \quad &\text{for: }a > 0 \\ tan^{-1}\left (\frac{b(\mathbf{x})} {a(\mathbf{x})}\right )+\pi \quad &\text{for: }a < 0 \\ \frac{\pi }{2} \quad &\text{for: }a = 0;\ \ b > 0 \\ \frac{3\pi } {2} \quad &\text{for: }a = 0;\ \ b < 0.\\ \quad \end{array} \right.& &{}\end{array}$$
(6)

A graphical representation of the polar coordinate system (r, θ) in two dimensions is found in Fig. 4.

Fig. 4
figure 4

Coordinate system (r, θ) in 2D implied by the (a, b) coordinate system [10]

Full size image

3 Stress Intensity Factors Through Crack Opening Displacements

The proposed method shows the computation of SIFs by observing the displacement field in the vicinity of the crack tip/front. This method is intuitive and the extension from two to three dimensions is straightforward and treats mode I​I​I as the other modes. Furthermore, no modification is necessary for curved and loaded cracks. The approximated displacements, which are extracted from the XFEM simulation, are compared with the expected displacements for a pure mode I, I​I and I​I​I crack. That is, two different states are involved which are described in more detail in Sects. 3.1 and 3.2. It is noted that any displacements in the vicinity of the crack tip/front can be used for the computation of SIFs. However, translations by means of rigid body motions have to be extracted from these displacements which complicates the computation. Therefore, we prefer to use relative displacements Δ u, particularly the crack opening displacements (CODs), as shown in Fig. 5 which consider rigid body motions automatically.

Fig. 5
figure 5

Crack opening in two dimensions

Full size image

The relative displacement Δ u COD h contains the first two modes in two dimensions and all three modes in three dimensions, wherefore all modes can be extracted from this opening. Section 3.3 specifies selected directions where the best results can be expected. In the following sections, the computation of the approximated and expected CODs is discussed in more detail. Additionally, in Sect. 3.3 it is shown how to use these openings for the evaluation of SIFs.

3.1 Approximated State

This section shows the computation of the approximated crack opening \(\varDelta \mathbf{u}_{COD}^{h(S)}\) of a point S on the crack path/surface. Openings of the point S are computed after solving the linear elastic fracture problem based on Eq. (1) as a post-processing step. The difficulty here is that the enrichment and shape functions have to be evaluated in a special setting so that CODs are obtained. For that, in a first step a point has to be found on the implicitly described crack path/surface. It is hardly possible to do this in a global setting as the level-set functions are only given at the nodes and are interpolated within the two or three-dimensional elements by the corresponding shape functions [10].

$$\displaystyle{ \phi _{j}^{h} =\sum _{ i}N_{i}(\mathbf{x})\phi _{j}(\mathbf{x}_{i}),j = 1,2,3\,. }$$
(7)

This interpolation automatically leads to curved zero level-sets in general. However, the following section shows a simplified detection of the zero level-sets. Starting point is a reference quadrilateral or hexahedral element which is called ‘master element’. This is decomposed into simplex elements which are called ‘sub-elements’ and allow for a simple detection of a planar zero level-set. It is noted that a similar setting of the introduced technique is also used for the integration of the domain, see e.g. [9, 11].

3.1.1 Localisation of the Zero Level-Sets

Each potentially cut master element, identified by the condition

$$\displaystyle{ max[\phi _{3}(\mathbf{x}_{i})] \cdot min[\phi _{3}(\mathbf{x}_{i})] < 0, }$$
(8)

is subdivided into two linear triangular elements in two dimensions or into six linear tetrahedral elements in three dimensions to ensure that the zero level-set is piecewise straight/planar. Then the level-set functions are interpolated within the sub-elements by the standard simplex shape functions N i S(x). The intersections of the zero level-set with the element edges are marked with x Si , in three dimensions this is: x Si  = [x Si ,   y Si ,   z Si ]T. Based on the roots on the sub-element edges, the zero level-set is interpolated within the sub-element by the shape functions N i S(x). This leads to a straight or flat representation of the zero level-set in the sub-element, as illustrated in Fig. 6.

Fig. 6
figure 6

Zero level-set in reference (a ) triangular and (b ) tetrahedral element

Full size image

Only three different shapes of the zero level-set are possible: straight lines in two dimensions and flat triangles or quadrilaterals in three dimensions. These straight/flat elements represent the crack path/surface and are, hence, called ‘crack elements’. We associate standard finite element shape functions N i C(x) to them.

3.1.2 Computation of Approximated CODs

The crack elements are the basis for finding the points x S  j on the crack path/surface as all points within these elements can be mapped to the sub-element by

$$\displaystyle{ \mathbf{x}_{S}^{\,j} =\sum _{ i}N_{i}^{C}(\mathbf{x}_{ j})\mathbf{x}_{Si}. }$$
(9)

As the displacement field is discontinuous on the crack surface, the point x S  j has to be ‘splitted’ into the two opposite on the crack surface which are infinitesimally close. We call one point S + on the positive side and the other one S − on the negative side. The sign of the sub-domain is defined by the sign of the third level-set function ϕ 3(x). This splitting is done in the sub-element by the normalized normal vector n S  j as illustrated in Eq. (10).

$$\displaystyle{ \mathbf{x}_{S^{\pm }}^{\,j} = \mathbf{x}_{ S}^{\,j} \pm \varepsilon \mathbf{n}_{ S}^{\,j}\mathrm{with:}\vert \vert \mathbf{n}_{ S}^{\,j}\vert \vert = 1 }$$
(10)

Herein, ɛ defines the shifting magnitude of the point. It should be small enough so that the splitted points are as close as possible. The normalized normal vector n S  j is defined by the cross product of two tangential vectors t 1 and t 2,

$$\displaystyle{ \mathbf{n}_{S}^{\,j} = \frac{\mathbf{t}_{1} \times \mathbf{t}_{2}} {\vert \vert \mathbf{t}_{1} \times \mathbf{t}_{2}\vert \vert }, }$$
(11)

see Fig. 6. The sign of the normal vector is chosen such that it always points to the positive sub-domain, as shown in Fig. 7 for some example values of the level-set function ϕ 3(x) in the corner nodes.

Fig. 7
figure 7

Master and sub-elements in (a ) two dimensions and (b ) three dimensions and the identified straight zero level-set

Full size image

There, the master element is illustrated by the dashed line and the sub-element by the solid line. The green line/surface represents the crack element, i.e. the zero level-set within the sub-element. The blue point illustrates a point on the implicitly defined crack path/surface and the blue line its normal vector pointing towards the positive sub-domain.

If the level-set functions and local coordinates (a,b) are known in the two opposite but infinitesimally close points \(\mathbf{x}_{S^{\pm }}^{\,j}\) their polar coordinates \(r(\mathbf{x}_{S^{\pm }}^{\,j})\) and \(\theta (\mathbf{x}_{S^{\pm }}^{\,j})\) are determined with Eqs. (5) and (6). Then the approximated displacements \(\mathbf{u}_{COD}^{h(S^{+}) }\) and \(\mathbf{u}_{COD}^{h(S^{-}) }\) are evaluated by Eq. (1). The approximated crack opening Δ u COD h(S) is described in the global coordinate system (x, y, z) by the difference of both displacements.

$$\displaystyle{ \varDelta \mathbf{u}_{COD}^{h(S)}(\mathbf{x}_{ S}) = \mathbf{u}_{COD}^{h(S^{+}) }(\mathbf{x}_{S^{+}}^{\,j}) -\mathbf{u}_{ COD}^{h(S^{-}) }(\mathbf{x}_{S^{-}}^{\,j}) }$$
(12)

For the sake of clarity, the index COD is not written anymore, instead, the index is used to give information about the current coordinate system, where (x) describes the global coordinate system and (a) the coordinate system mentioned in Sect. 2.1. This information is used for the evaluation of SIFs in Sect. 3.3 to indicate the current coordinate system.

3.2 Reference State for Pure Mode I, I​I and I​I​I Cracks

In this section, the reference state is discussed which is needed for the evaluation of the expected CODs for a pure mode I, I​I and I​I​I crack, respectively. For straight or planar crack geometries, the definition of the reference configuration can be based on an orthonormal coordinate system which is aligned with the tangent at the crack tip/front. However, in practical applications, cracks are often curved, especially for propagating cracks where mode I​I is dominant. For such problems, the use of an orthonormal coordinate system is not easily justified. We propose the definition of a reference state based on the local coordinate system (a,b) which is also valid for curved cracks. The definition of this coordinate system has been discussed in Sect. 2.1.1. Figure 8a illustrates a two-dimensional curved crack (bold black line) in the (a,b)-coordinate system.

Fig. 8
figure 8

Curved crack in the (a,b)-coordinate system in a (a ) closed and (b ) open setting

Full size image

3.2.1 Stress Intensity Approach

A satisfactory description of the crack tip/front behaviour is given by a linear combination of three independent crack modes which are scaled by the SIFs k I , k I​I and k I​I​I . This approach completely describes the state of the displacements, stresses and strains in the vicinity of the crack tip/front. Under general mixed-mode loadings, the displacements are given in the (a,b,c)-coordinate system by Anderson [1]:

$$\displaystyle{ \left [\begin{array}{*{10}c} u_{a} \\ u_{b} \\ u_{c}\\ \end{array} \right ] = \left [\begin{array}{*\c@MaxMatrixCols l} \frac{k_{I}} {2\mu } \sqrt{\frac{r} {2\pi }}cos \frac{\theta } {2}\left (\kappa -1 + 2sin^{2} \frac{\theta } {2}\right ) + \frac{k_{I\!I}} {2\mu } \sqrt{\frac{r} {2\pi }}sin \frac{\theta } {2}\left (\kappa +1 + 2cos^{2} \frac{\theta } {2}\right ) \\ \frac{k_{I}} {2\mu } \sqrt{\frac{r} {2\pi }}sin \frac{\theta } {2}\left (\kappa +1 - 2cos^{2} \frac{\theta } {2}\right ) -\frac{k_{I\!I}} {2\mu } \sqrt{\frac{r} {2\pi }}cos \frac{\theta } {2}\left (\kappa -1 - 2sin^{2} \frac{\theta } {2}\right ) \\ \frac{2k_{I\!I\!I}} {\mu } \sqrt{\frac{r} {2\pi }}sin \frac{\theta } {2}\\ \end{array} \right ] }$$
(13)

with \(\;\quad \mu = \frac{E} {2(1+\nu )}\quad \;\) and \(\quad \;\kappa = \left \{\begin{array}{@{}l@{\quad }l@{}} \frac{3-\nu } {1+\nu } \quad &\text{for plane stress} \\ 3 - 4\nu \quad &\text{for plane strain.} \end{array} \right.\)

Herein, k I , k I​I and k I​I​I are the SIFs for mode I − I​I​I, μ the second Lamé-Constant and κ a material parameter. The parameters r and θ describe the polar coordinate system at the crack tip/front, which has been mentioned in Sect. 2.1.2. As Eq. (13) shows, displacements out of the plane only exist if mode I​I​I is non zero. However, displacements in direction of a and b consist of a combination of mode I and I​I for any 0 <  | θ |  < π. It is noted that in three dimensions, only plain strain conditions make sense and each point on the crack front has its own stress SIFs.

3.2.2 Computation of Expected CODs

Starting from the definition of the crack in the (a,b)-coordinate system, the expected CODs Δ u a m(S) of the point x S  j for a pure mode I, I​I and I​I​I are evaluated. The point x S  j and its splitting in two opposite points \(\mathbf{x}_{S^{+}}^{\,j}\) and \(\mathbf{x}_{S^{-}}^{\,j}\) is the same as in Sect. 3.1 for which the local coordinates \(a(\mathbf{x}_{S^{\pm }}^{\,j})\) and \(b(\mathbf{x}_{S^{\pm }}^{\,j})\) are already known. A representation of the undeformed situation is presented in Fig. 8a. By using the relation of the coordinates (a,b) and (r,θ) (Eqs. (5) and (6)) as well as the application of Eq. (13), the expected displacements \(\mathbf{u}_{\mathbf{a}}^{m(S^{\pm }) }\), with \(\mathbf{u}_{\mathbf{a}}^{m(S^{\pm }) } = [u_{a}^{m(S^{\pm }) },\ \ u_{b}^{m(S^{\pm }) },\ \ u_{c}^{m(S^{\pm }) }]^{T}\), of the points \(\mathbf{x}_{S^{+}}^{\,j}\) and \(\mathbf{x}_{S^{-}}^{\,j}\) are evaluated. Herein, m describes the current crack mode, wherefore, for the expected openings \(\mathbf{u}_{\mathbf{a}}^{m(S^{\pm }) }\), the stress intensity factor k m is set to 1 and the others to 0. The expected COD of mode m is then given by the difference of both points

$$\displaystyle{ \varDelta \mathbf{u}_{\mathbf{a}}^{m(S)} =\varDelta \mathbf{u}_{\mathbf{ a}}^{m(S^{+}) }(\mathbf{x}_{S^{+}}^{\,j}) -\varDelta \mathbf{u}_{\mathbf{ a}}^{m(S^{-}) }(\mathbf{x}_{S^{-}}^{\,j}). }$$
(14)

In Fig. 8b, the expected opening (red line) for a pure mode I is presented in the (a,b)-coordinate system. Furthermore, the expected COD of the point x S  j in direction of b (blue line) is illustrated. Note that the expected openings are given in the (a,b,c)-coordinate system. In the following section, the computation of SIFs based on the evaluated CODs in the approximated and reference state is discussed.

3.3 Computation of SIFs Using CODs

A comparison of the approximated and expected openings is only possible if both openings are described in the same coordinate system. Therefore, the approximated CODs, which are given in the global coordinate system (x,y,z), are transformed into the local coordinate system (a,b,c). In two dimensions, this is done based on the Jacobi-matrix J of the coordinate transformation, hence,

$$\displaystyle{ \varDelta \mathbf{u}_{\mathbf{a}}^{h} = \mathbf{J}\cdot \varDelta \mathbf{u}_{\mathbf{ x}}^{h}\qquad \mathrm{with}\,\,\,\,\mathbf{J} = \left [\begin{array}{*{10}c} \\ \\ a_{,x}&a_{,y}\\ \\ \\ b_{,x} & b_{,y}\\ \end{array} \right ],\quad i = 1,2. }$$
(15)

It is noted that ∇a and ∇b are only orthonormal for straight/planar cracks. In three dimensions there is no need to explicitly define a third function as ∇c is always normal to ∇a and ∇b. Therefore, ∇c can be computed by the cross-product of ∇a and ∇b.

$$\displaystyle{ \nabla c = \nabla a \times \nabla b }$$
(16)

With this information of the third direction, Eq. (15) is straightforwardly extended to the third dimension.

$$\displaystyle{ \varDelta \mathbf{u}_{\mathbf{a}}^{h} = \mathbf{J}\cdot \varDelta \mathbf{u}_{\mathbf{ x}}^{h}\qquad \mathrm{with}\,\,\,\,\mathbf{J} = \left [\begin{array}{*{10}c} \\ \\ a_{,x}&a_{,y}&a_{,z}\\ \\ \\ b_{,x} & b_{,y} & b_{,z}\\ \\ \\ c_{,x} & c_{,y} & c_{,z}\\ \end{array} \right ],\quad i = 1,2,3. }$$
(17)

Now that both CODs are available in the same coordinate system, the comparison of the approximated and expected CODs leads to the following system of equations:

$$\displaystyle{ \varDelta \mathbf{u}_{\mathbf{a}}^{h} = k_{ I} \cdot \varDelta \mathbf{u}_{\mathbf{a}}^{I} + k_{ I\!I} \cdot \varDelta \mathbf{u}_{\mathbf{a}}^{I\!I} + k_{ I\!I\!I} \cdot \varDelta \mathbf{u}_{\mathbf{a}}^{I\!I\!I}. }$$
(18)

However, the impact of the individual SIFs to the displacement components of a point which is ‘quasi’ on the crack surface with: θ = ±(π −ɛ), is quite different as Eq. (13) shows. Herein, k I mainly leads to displacements in direction of b, k I​I to displacements in direction of a and k I​I​I to displacements in direction of c. Therefore, SIFs can be directly computed by

$$\displaystyle{ k_{I} =\varDelta u_{b}^{h}/\varDelta u_{ b}^{I};\qquad k_{ I\!I} =\varDelta u_{a}^{h}/\varDelta u_{ a}^{I\!I};\qquad k_{ I\!I\!I} =\varDelta u_{c}^{h}/\varDelta u_{ c}^{I\!I\!I}. }$$
(19)

It remains to specify the location of the considered fitting points and the consideration of the crack front in the context of a numerical simulation.

3.4 Location of the Fitting Points

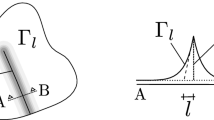
It is well known that the stress intensity approach is only valid in the vicinity of the crack tip/front, wherefore the maximum distance of the fitting points to the crack tip/front is limited. Numerical results indicate that in two dimensions 10 % of the crack length l c yield satisfactory results. However, in three dimensions there is no ‘classical’ crack length available, wherefore the maximum distance is limited by 10 % of an effective crack length l c eff. This effective crack length is described by the ratio of the area of the crack surface A c and the length of the crack front l cf :

$$\displaystyle{ l_{c}^{eff} = \frac{A_{c}} {l_{cf}}. }$$
(20)

The limitation of the maximum distance of the fitting point x S  j to the crack tip/front can then be expressed as follows:

$$\displaystyle\begin{array}{rcl} r(\mathbf{x}_{S}^{\,j}) \leq \left \{\begin{array}{@{}l@{\quad }l@{}} 0.1 \cdot l_{c} \quad &\text{in 2D} \\ 0.1 \cdot l_{c}^{eff}\quad &\text{in 3D.}\\ \quad \end{array} \right.& &{}\end{array}$$
(21)

For the evaluation of the partial derivatives of a(x) and b(x) it turned out that it is preferable to use points within sign enriched elements rather than crack-tip enriched elements. In coarse meshes or small crack geometries, it may happen that such points are hard to find. Then, the point x S  j is used where the distance r(x S  j) is a minimum. Additionally, there exists a wide range of different crack configurations, wherefore it is hardly possible to determine a fixed point on the crack path/surface where the best results are obtained. Therefore, it is proposed to use a number of points in this scope and compute averaged SIFs which also leads to an increased robustness.

In Sect. 3.2.1, it has been mentioned that each point of the crack front has its own SIFs to be determined by Eq. (19). However, for a numerical simulation it is not necessary to know the SIFs of the whole crack front. As [10] shows, it is often sufficient to know the behaviour at the explicitly defined nodes on the crack front. Therefore, the following section investigates the situation at the crack front.

3.5 Consideration of the Crack Front

Each point x S  j on the implicitly defined crack surface generally describes the behaviour of some related point on the crack front. The localisation of several points which are representative for one special point at the crack front is quite difficult. It is assumed that the point x S  j is valid for the point F j on the crack front where it has a minimum distance, see Fig. 9a. By using an explicit-implicit crack description, a propagation is considered by adding new segments. Therefore, SIFs are needed in the explicitly defined crack front nodes where the direction and distance of the propagation is determined. It can be assumed that the change of the SIFs along the crack front changes slowly for physically justified crack surfaces. Therefore, each evaluated point F j is assigned to the explicitly defined crack front node K n where the distance is a minimum, see Fig. 9b. It is noted that the distance of F j and K n is also limited by 10 % of the effective crack length, so that only SIFs are considered in the vicinity of the node. However, this limitation is only used for coarsely described crack geometries.

Fig. 9
figure 9

Three-dimensional crack front: (a ) Scope of computed SIFs and (b ) assignment to crack front node

Full size image

In Fig. 9, a three-dimensional crack front (bold black line) is presented with possible points x S  j on the crack surface (black stars). The assignment of these points to the crack front is illustrated by the blue dashed lines and the scope of the crack front node K n is illustrated by the red line. The SIFs \(k_{m}^{(K_{n})}\) of node K n related to mode m is obtained by the average of all SIFs of the points which are assigned to node K n . This can be expressed by

$$\displaystyle{ k_{m}^{(K_{n})} =\sum _{ j=1}^{N}\frac{k_{m}^{(F_{j})}} {N}. }$$
(22)

SIFs are now known for each node of the crack front in the explicit crack description.

4 Numerical Results

In this section, five test cases in linear elastic fracture mechanics are presented in two and three dimensions. The first four examples investigate the behaviour of static planar crack configurations with well known analytical or numerical solutions to show the validity of the proposed method. Herein, SIFs are computed on different meshes and are compared with the expected solutions. In the results, the ratio of the computed and the expected SIFs are plotted over the used number of elements. The first two examples are in two dimensions and refer to externally loaded domains with different boundary conditions and stress-free crack surfaces. Loaded crack surfaces are illustrated in examples three and four, where one is in two and the other in three dimensions. A quasi-static two-dimensional crack propagation is presented in the last example to show the accuracy of the proposed method also for curved cracks. Each mesh is based on bilinear 4-node quadrilateral or trilinear 8-node hexahedral elements. Furthermore, a brittle and isotropic material is used with a Young’s modulus E = 35 GPa and a Poisson’s ratio ν = 0. 3 . In two dimensions, plane stress conditions are assumed. The interest is only in the computation of SIFs in brittle materials under quasi-static mixed-mode loadings, wherefore no dynamic effects [14] or cohesive models [16] are considered herein.

4.1 Eccentric Three-Point Bending Test

This test case shows an edge cracked three-point bending test with an eccentric load, where F = 100 kN and the eccentricity d = 75 cm. The beam is 600 cm long (l) and 150 cm high (h) and exhibits an l c  = 75 cm long initial crack in the middle, see Fig. 10a. The expected SIFs are given [8] by

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{*{10}c} k_{I} \\ k_{I\!I}\\ \end{array} \right ] = \left [\begin{array}{*\c@MaxMatrixCols l} \frac{3Fl\sqrt{\pi l_{c}}} {h^{2}} \cdot \frac{F_{I}^{'}} {\left (1-\frac{l_{c}} {h} \right )^{\frac{3} {2} }} \\ \frac{3Fl\sqrt{\pi l_{c}}} {h^{2}} \cdot F_{I\!I}\\ \end{array} \right ].& &{}\end{array}$$
(23)

With F I ′ = 0. 4010 and F I​I  = 0. 0876 , Eq. (23) leads to the expected SIFs k I  = 69. 64 and k I​I  = 5. 38 . Starting with a coarse mesh and 390 elements as shown in Fig. 10b, SIFs are computed on seven different meshes, which are generated by a refinement until a fine mesh with 67.470 elements is obtained. A local refinement in the vicinity of the crack allows a limitation of the element number. Figure 10c shows the normalized results of the computed SIFs for mode I (red) and I​I (blue).

Fig. 10
figure 10

Eccentric three-point bending test in two dimensions (a ) geometry parameters, (b ) mesh and (c ) results

Full size image

In this test case, the proposed method provides results within 5 % for mode I on any of the meshes. The results of mode I​I are a little bit worse, however the achieved error is also limited to 10 % on the coarse mesh and improves upon refinement.

4.2 Shear Edge Crack

A shear loaded edge cracked rectangular plate is investigated next. The extent of the plate is given by: h = 7 m, l = 16 m and exhibits an initial crack with a length l c  = 3. 5 m, as shown in Fig. 11a. SIFs are computed on 12 different meshes. We start with a coarse mesh (77 elements), which is locally refined at the crack, as illustrated in Fig. 11b. This mesh is refined until 46.025 elements are obtained.

Fig. 11
figure 11

Edge cracked rectangular plate (a ) geometry parameters and (b ) mesh

Full size image

The plate is clamped on the bottom and loaded by a shear traction τ = 1 GPa on the top as Fig. 12a shows. This configuration leads to a mixed-mode loading, where the SIFs are given with k I  = 34 and k I​I  = 4. 55 , see e.g. [2]. The obtained results are illustrated in Fig. 12b, where the red line represents the normalized mode I and the blue line the normalized mode I​I SIF.

Fig. 12
figure 12

Edge cracked rectangular plate (a ) boundary and loading conditions and (b ) results

Full size image

This test case also achieves good results, where the error of k I is below 5 % for all used meshes and shows a clear convergence during the refinement. Mode I​I has again less accurate results, but also converges upon refinement.

In this two externally loaded test cases with stress-free crack paths, mode I SIFs were evaluated within an error of 5 % and mode I​I SIFs within 10 %. The next two cases investigate loaded crack surfaces which would lead to issues in the ‘classical’ interaction integral. A big advantage of the proposed method is that no modifications are necessary as the following examples show.

4.3 Loaded Crack in 2D

In this example, the accuracy of the proposed method for loaded crack surfaces is shown. Therefore, an edge cracked rectangular plate is loaded by a tension σ = 1 GPa and shear traction τ = 1 GPa within the crack. The load situation and boundary conditions are illustrated in Fig. 13a. This test case uses the same geometry parameters and meshes as in Sect. 4.2. Due to the large l∕h ratio it is assumed that the impact of the boundary conditions is relatively small compared to the behaviour of the crack. This assumption leads to following expected SIFs [25]:

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{*{10}c} k_{I} \\ k_{I\!I}\\ \end{array} \right ] = \left [\begin{array}{*\c@MaxMatrixCols l} \sigma \sqrt{\pi l_{c}}\left (1.122 - 0.231\frac{l_{c}} {h} + 10.550\frac{l_{c}^{2}} {h^{2}} - 21.710\frac{l_{c}^{3}} {h^{3}} + 30.382\frac{l_{c}^{4}} {h^{4}} \right ) \\ \tau \sqrt{ \frac{\pi l_{c } } {1-\frac{l_{c}} {h} }}\left (1.122 + 0.561\frac{l_{c}} {h} + 0.085\frac{l_{c}^{2}} {h^{2}} + 0.180\frac{l_{c}^{3}} {h^{3}} \right ) \\ \end{array} \right ].& &{}\end{array}$$
(24)

By inserting the given geometry parameters into Eq. (24), the SIFs are given by k I  = 9. 381 and k I​I  = 4. 151 . The ratio of the computed to the expected SIFs are shown in Fig. 13b, where the red line represents mode I and the blue line mode I​I.

Fig. 13
figure 13

Loaded crack in two dimensions (a ) boundary and loading conditions and (b ) results

Full size image

Figure 13b shows that the proposed method leads for most of the meshes to SIFs within an error of 5 %. That is, the proposed method allows the computation of SIFs also for loaded crack surfaces with a similar accuracy as for stress-free crack surfaces.

4.4 Penny-Shaped Crack

Another test case without crack propagation is considered in three dimensions. An embedded penny-shaped crack with tension and shear loaded crack surfaces is examined. The individual components of the loading are given in the global coordinate system (see Fig. 14b) by σ = 1 GPa, \(\tau _{x} =\tau _{y} = \frac{1} {\sqrt{2}}\,\mathrm{GPa}\). The crack surface has a diameter d = 2 m and is explicitly described by 1.536 flat triangles and the crack front by 64 line segments as shown in Fig. 14a. As shown in Fig. 14c, the crack is located within a cube-like domain with a side length of 4 m. Displacements are prescribed to zero at some corner nodes on the bottom. An illustration of the situation is presented in Fig. 14. For this test case, four different meshes with trilinear hexahedral elements are used. The number of elements along an edge varies between 13 and 25. Figure 14c shows an example mesh with 2.197 elements.

Fig. 14
figure 14

Penny shaped crack (a ) explicitly defined crack surface, (b ) situation and (c ) mesh

Full size image

In this general example, SIFs vary along the crack front. The expected SIFs for the whole front are given [25] by

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{*{10}c} k_{I} \\ k_{I\!I} \\ k_{I\!I\!I}\\ \end{array} \right ] = \left [\begin{array}{*\c@MaxMatrixCols l} \frac{2} {\pi } \sigma \sqrt{\pi \frac{d} {2}} \\ \frac{4} {\pi \left (2-\nu \right )}\left (\tau cos\omega \right )\sqrt{\pi \frac{d} {2}} \\ \frac{4\left (1-\nu \right )} {\pi \left (2-\nu \right )} \left (\tau sin\omega \right )\sqrt{\pi \frac{d} {2}} \end{array} \right ],& &{}\end{array}$$
(25)

where ω describes the angle between the direction of the resultant shear traction and the reviewed point. Here, the point A (see Fig. 15a) with an angle of \(\omega = \frac{\pi } {4}\) is observed and all three modes are present there. For that point, Eq. (25) leads to the following SIFs: k I  = 11. 28 , k I​I  = 9. 39 and k I​I​I  = 6. 57 . The normalized computed SIFs of point A are presented in Fig. 15b.

Fig. 15
figure 15

Penny shaped crack (a ) investigated point A and (b ) results

Full size image

In this example, mode I​I and mode I​I​I are computed with a similar accuracy as shown in Fig. 15b. Furthermore, the result shows that with only 173 elements, SIFs can be computed with an error of less than 10 % and 213 elements lead to results below 5 %. That is, SIFs are well obtained for a general three-dimensional crack configuration with stresses on the crack surface without any modifications.

4.5 Crack Propagation in Two Dimensions

Until now, only cases with straight or flat crack geometries have been investigated. To show the accuracy of the proposed method also for curved cracks, this final test case shows a mixed-mode crack propagation in a square specimen with the extent l = 1 m [3, 10], where curved cracks are generally expected. The displacements are prescribed on the upper and lower side of the domain with 1 mm in direction of the specified angle α, as illustrated in Fig. 16a. These boundary conditions produce an opening of the crack, wherefore no other loadings are needed. The domain is discretized by a structured mesh. It is noted that our interest is only in the computation of SIFs, wherefore no attention is given to the crack velocities. It is assumed that the crack always propagates by the crack increment da in direction of the maximum circumferential stresses. By using SIFs and the maximum circumferential stress criterion, the propagation angle θ c can be expressed as follows [17]

$$\displaystyle{ \theta _{c} = 2arctan\frac{1} {4}\left ( \frac{k_{I}} {k_{I\!I}} \pm \sqrt{\left ( \frac{k_{I } } {k_{I\!I}}\right )^{2} + 8}\right ), }$$
(26)

where the sign depends on the sign of k I​I .

Fig. 16
figure 16

Edge crack in a squared plate (a ) geometry parameters and supports and (b ) results of the crack propagation

Full size image

This test case starts with an initial crack of length l c  = 0. 5 m which is described by one straight line segment. Then, the boundary conditions are prescribed and the resulting SIFs are computed by the proposed method. With these SIFs the propagation angle θ c is evaluated and a new line segment of the length da = 5 cm in direction of θ c is added. This process is performed ten times. To keep the influence of the element size to a minimum, a fine setting with 101 × 101 elements is used. The prescribed direction of the boundary conditions is varied from 15 ≤ α ≤ 165. In Fig. 16b, the results of the computed crack paths are presented.

As expected, for α = 90 the crack propagates horizontally as for a pure tension loading where only mode I is relevant. The greater the boundary conditions deviate from a pure tension loading, the more dominant the impact of mode I​I is. The obtained crack paths for the different α are in good agreement to [3] so that it is concluded that the proposed technique is also working for curved cracks.

5 Conclusions

In the presented work, it is shown how crack opening displacements (CODs) are used for the computation of SIFs within the XFEM in two and three dimensions. The use of CODs for computing SIFs provides an intuitive, computationally cheap and robust method, which works in two and three dimensions in a consistent manner no matter whether the crack surfaces are stress-free or loaded. The aim is to use this approach also in simulations of hydraulic fracturing where stresses are exerted by a fluid on the crack surface.

Two coordinate systems are used to simplify the definition of the enrichment functions on the basis of level-set functions and describe a reference state, where pure mode I, I​I and I​I​I openings are evaluated. These coordinate systems consider curved cracks as well as planar ones. A comparison of the approximated states and the reference states leads to the SIFs. An assignment of the fitting points to the explicitly defined crack front nodes provides SIFs for each of those nodes. At the crack tip/front, it is recommended to have rather small elements which considerably improves the solutions in general. The accuracy and robustness of the proposed method has been shown by five examples in two and three dimensions. For each test case, results were achieved below 10 % error improving upon mesh refinement. All obtained results are in good agreement with the available analytical, numerical and experimental solutions so that it is concluded that the proposed method provides good results for any crack configurations.