Keywords

1 Introduction

Crack propagation phenomenon appears in various situations from tiny size to huge scale and often causes serious problems, for example, in tiny precision machine and its parts, the body of a car or a ship, a building, a large structure, the ground, or the crust of the earth. Since the propagation of a relatively small crack in such material may cause the collapse of the whole structure, to understand the behavior of the crack propagation is very important.

Among various crack propagation models in fracture mechanics, the phase field approximation [20] of the crack seems to be one of very interesting ideas. A number of engineering-oriented discrete models, such as extended finite element method (XFEM) [3, 21], rigid body spring model (RBSM) [16], discrete element method (DEM) [9, 22], or particle discretization scheme-FEM (PDS-FEM) [13, 14], etc., are widely used for fracture analysis in engineering simulations. On the other hand, such discrete models are dependent on the FEM mesh and other numerical parameters and algorithms. From the mathematical point of view, a mathematically closed continuous model is also preferable.

In [24, 25], the authors proposed a phase filed model for mode III crack propagation on a two dimensional plate and showed several numerical examples. In this paper, we consider some generalizations of our phase field model and discuss their properties based on the idea of [19].

In Sect. 2, we derive our phase field model with two-dimensional linear elasticity. The model is derived as the gradient flow of the Francfort-Marigo type energy [7, 10] with the Ambrosio-Tortorelli regularization [2]. We also introduce a non-repair condition of the crack without destructing the gradient flow structure.

In Sect. 3, we give some numerical examples of crack propagation for mode III case and modes I and II case. We also show how it works in the case that the fracture toughness is spatially variable. For the simulation, we use P2 adaptive mesh finite element method with FreeFEM++ software [12].

2 Derivation of Crack Propagation Models

We suppose that \(\Omega \subset \mathbb {R}^2\) is a bounded elastic body without crack. Let \(u(x)\in \mathbb {R}^2\) be an in-plane displacement field at \(x\in \Omega \). The strain tensor is denoted by \(e[u]=(e_{ij}[u](x))\), where

$$ e_{ij}[u](x):=\frac{1}{2} \left( \frac{\partial u_i}{\partial x_j}(x) +\frac{\partial u_j}{\partial x_i}(x) \right) \quad (i,j=1,2). $$

We use the Einstein summation convention for spatial indices \(i,j,k,l\in \{1,2\}\). We suppose that the elasticity tensor \(c_{ijkl}(x)\) satisfies the symmetries \(c_{ijkl}(x)=c_{klij}(x)=c_{jikl}(x)\) and the positivity condition \(c_{ijkl}(x)\, \xi _{ij}\,\xi _{kl}\, \ge \,c_*\,|\xi |^2\) for \(x\in \Omega ,~ \xi \in \mathbb {R}^{n\times n}_\mathrm{sym}\), where \(|\xi |:=\sqrt{\xi _{ij}\,\xi _{ij}}\). The stress tensor is denoted by \(\sigma [u]=(\sigma _{ij}[u](x))\) and is defined as

$$ \sigma _{ij}[u](x)=c_{ijkl}(x)e_{kl}[u](x). $$

Then the equilibrium equation is given by

$$\begin{aligned} -\text{ div }\sigma [u]=f(x) \quad x\in \Omega , \end{aligned}$$
(1)

where \(f(x)\in \mathbb {R}^2\) is a given body force at \(x\). It is known that the solution \(u\) is obtained as the minimizer of the following elastic energy including the body force under a suitable boundary condition:

$$ E_0(u)=\frac{1}{2} \int \limits _\Omega \sigma [u]:e[u]\,dx -\int \limits _\Omega f(x)\cdot u(x)\,dx, $$

where \(\sigma : e =\sigma _{ij}e_{ij}\).

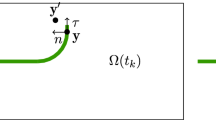
Let us assume that there is a crack \(\Sigma \) in \(\Omega \), where \(\Sigma \) is a smooth curve in \(\Omega \) with finite length and that \(\Omega \setminus \Sigma \) is open and connected. We have crack opening modes I and II with two-dimensional displacement. We derive a crack propagation model of modes I and II.

We introduce the following smooth function \(z(x)\) for \(x\in \Omega \) to represent the approximate profile of the crack. We assume that \(0\le z(x)\le 1\) and \(z(x)\approx 1\) for around the crack \(\Sigma \) and \(z(x)\approx 0\) for the other region. We call \(z(x)\) the phase field for the crack shape and derive a time evolution model of \(z\).

We suppose that the damaged stress tensor is defined as

$$\begin{aligned} \tilde{\sigma }[u]:=(1-z)^2\sigma [u]. \end{aligned}$$
(2)

The function \(z\) also can be considered as a damage variable which represents the damage ratio of the material in the sense of (2).

Then we have the modified elastic energy:

$$ E_1(u,z)=\frac{1}{2} \int \limits _\Omega (1-z)^2\sigma [u]:e[u]\,\mathrm{{d}}x -\int \limits _\Omega f(x)\cdot u(x)\,\mathrm{{d}}x. $$

The surface energy on the crack is approximated by

$$ E_2(z)=\frac{1}{2} \int \limits _\Omega \gamma (x) \left( \varepsilon |\nabla z|^2+ \frac{1}{\varepsilon }z^2 \right) \,\mathrm{{d}}x, $$

where the fracture toughness \(\gamma (x)>0\) is a given function and \(\varepsilon >0\) is a small regularization parameter. This is called the Ambrosio-Tortorelli regularization and they proved that the energy \(E_2(z)\) approximates the surface energy \(\int \limits _\Sigma \gamma (x) \mathrm{{d}}s\) in the sense of \(\Gamma \)-convergence for some special cases [2].

Following the derivation of the phase field model in [25], we consider a regularized Francfort-Marigo type energy [10]:

$$ E(u,z):=E_1(u,z)+E_2(z), $$

and derive our model as a gradient flow of \(E\). It is shown that this energy approach is compatible to the classical Griffith theory [7, 10, 11].

Let the boundary \(\Gamma =\partial \Omega \) be Lipschitz and piece-wise smooth, and the unit outward normal vector on \(\Gamma \) is denoted by \(n\). We suppose that \(\Gamma _D\) is a nonempty open piece-wise smooth portion of \(\Gamma \), and define \(\Gamma _N:=\Gamma \setminus \Gamma _D\). The displacement on \(\Gamma _D\) is given as \(u=g(x)\) and the traction free condition is assumed on \(\Gamma _N\). We consider the following boundary condition:

$$ u=g\quad \text{ on }\quad \Gamma _D, \qquad \sigma [u]n=0\quad \text{ on }\quad \Gamma _N, \qquad \frac{\partial z}{\partial n}=0 \quad \text{ on }\quad \Gamma . $$

If \(f\) and \(g\) do not depend on \(t\), the first variations of the energy \(E(u,z)\) with respect to \(u\) and \(z\) are formally derived as follows. For arbitrary \(v(x)\) with \(v=0\) on \(\Gamma _D\), we have

$$\begin{aligned} \left. \frac{\mathrm{{d}}}{\mathrm{{d}} \rho } E(u + \rho v, z) \right| _{\rho =0} = - \int \limits _\Omega \left\{ \text{ div }\left( (1-z)^2 \sigma [u]\right) + f \right\} v \, \mathrm{{d}}x \end{aligned}$$

Hence, the gradient flow equation of the displacement \(u(x,t)\) becomes

$$\begin{aligned} \alpha _1 \frac{\partial u}{\partial t} = \text{ div }\left( (1-z)^2 \sigma [u] \right) +f, \end{aligned}$$
(3)

where \(\alpha _1\ge 0\) is a small time constant. It must be remarked that the case \(\alpha _1=0\) corresponds to the equilibrium state of forces (1), however, for numerical simulation, we can set \(0< \alpha _1 <<1\) to stabilize the numerical solution even in the case of \(z=1\), where the ellipticity is broken.

For any \(\zeta (x)\), we derive the first variation of the energy \(E(u,z)\) with respect to \(z\) as

$$\begin{aligned} \left. \frac{\mathrm{{d}}}{\mathrm{{d}} \rho } E(u, z + \rho \zeta ) \right| _{\rho =0} = - \int \limits _\Omega \left\{ \varepsilon \; \text{ div }\left( \gamma (x) \nabla z \right) - \frac{\gamma (x)}{\varepsilon } z + \sigma [u]:e[u] (1-z) \right\} \zeta \, \mathrm{{d}}x . \end{aligned}$$
(4)

The gradient flow equation of the damage variable \(z(x,t)\) becomes

$$\begin{aligned} \alpha _2 \frac{\partial z}{\partial t} = \varepsilon \text{ div }\left( \gamma (x) \nabla z \right) - \frac{\gamma (x)}{\varepsilon } z + \sigma [u]:e[u] (1 - z), \end{aligned}$$

where \(\alpha _2 >0\) is a time constant.

The resulted phase field model is as follows:

$$\begin{aligned} \left\{ \begin{array}{rcll} {\displaystyle \alpha _1 \frac{\partial u}{\partial t}} &{} = &{} {\displaystyle \mathrm{div} \left( (1-z)^2 \sigma [u] \right) + f(x, t)} &{} x \in \Omega ,\, t > 0\\ {\displaystyle \alpha _2 \frac{\partial z}{\partial t}} &{} = &{} {\displaystyle \left( \varepsilon \; \mathrm{div} \left( \gamma (x) \nabla z \right) - \frac{\gamma (x)}{\varepsilon } z + \sigma [u]:e[u] (1 - z) \right) _+}\quad &{} x \in \Omega , \,t > 0\\ u &{} = &{} g(x, t) &{} x \in \Gamma _D, \,t > 0\\ {\displaystyle \sigma [u]n} &{} = &{} 0 &{} x \in \Gamma _N, \,t > 0\\ {\displaystyle \frac{\partial z}{\partial n}} &{} = &{} 0 &{} x \in \Gamma , \,t > 0\\ u(x,0) &{} = &{} u_0(x) &{} \begin{array}{l} x \in \Omega \\ \text{(omit } \text{ if } \alpha _1=0\text{) } \end{array}\\ z(x,0) &{} = &{} z_0(x)\in [0,1] &{} x\in \Omega \end{array} \right. \end{aligned}$$
(5)

Since a crack once generated can be no longer repaired, we put \((~)_+\) to the right-hand side of the second equation, where \((a)_+ = \max (a,0)\). It guarantees the non-repair condition for the crack: \(\frac{\partial z}{\partial t}\ge 0\). The second equation expresses the crack evolution due to the magnitude of the elastic energy density \(\sigma :e\). The fracture toughness \(\gamma (x) > 0\) prescribes the critical value of the energy release rate in the Griffith criterion. It is harder for the crack to grow, if the value of \(\gamma \) is larger.

We remark that the second equation is a fully nonlinear parabolic equation and it is called an irreversible system in the mathematical field of evolution equation. One of the authors recently established a global existence of a unique strong solution for the irreversible diffusion equation \(u_t=(\Delta u+f(x,t))_+\) in [1].

If \(f\) and \(g\) do not depend on \(t\), under suitable regularity assumptions, formally we have the following energy decay property:

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t}E(u(\cdot ,t),z(\cdot ,t))&=-\int \limits _\Omega \left\{ \mathrm{div}((1-z)^2\sigma [u])+f\right\} \frac{\partial u}{\partial t} \,\mathrm{{d}}x\\&\quad -\int \limits _\Omega \left\{ \varepsilon \text{ div }(\gamma \nabla z)-\frac{\gamma }{\varepsilon }z +\sigma [u]:e[u](1-z)\right\} \frac{\partial z}{\partial t} \,\mathrm{{d}}x\\&= -\alpha _1\int \limits _\Omega \left| \frac{\partial u}{\partial t} \right| ^2\,\mathrm{{d}}x -\alpha _2\int \limits _\Omega \left| \frac{\partial z}{\partial t} \right| ^2\,\mathrm{{d}}x \le 0. \end{aligned}$$

This stands for the gradient flow structure of our phase field model (5) even with the non-repair condition.

We remark that the phase field model (5) can be also considered in the three-dimensional case, \(u(x,t)\in \mathbb {R}^3\), \(x\in \Omega \subset \mathbb {R}^3\).

In [25], the authors studied our phase field model in two dimension with scalar anti-plane displacement \(u(x,t)\in \mathbb {R}\), \(x\in \Omega \subset \mathbb {R}^2\):

$$\begin{aligned} \left\{ \begin{array}{rcll} {\displaystyle \alpha _1 \frac{\partial u}{\partial t}} &{} = &{} {\displaystyle \mu \text{ div }\left( (1-z)^2 \nabla u \right) + f(x, t)} &{} x \in \Omega ,\, t > 0\\ {\displaystyle \alpha _2 \frac{\partial z}{\partial t}} &{} = &{} {\displaystyle \left( \varepsilon \; \mathrm{div} \left( \gamma (x) \nabla z \right) - \frac{\gamma (x)}{\varepsilon } z + \mu |\nabla u|^2 (1 - z) \right) _+}\quad &{} x \in \Omega , \,t > 0\\ u &{} = &{} g(x, t) &{} x \in \Gamma _D, \,t > 0\\ {\displaystyle \frac{\partial u}{\partial n}} &{} = &{} 0 &{} x \in \Gamma _N, \,t > 0\\ {\displaystyle \frac{\partial z}{\partial n}} &{} = &{} 0 &{} x \in \Gamma , \,t > 0\\ u(x,0) &{} = &{} u_0(x) &{} \displaystyle {\begin{array}{l} x \in \Omega \\ \text{(omit } \text{ if } \alpha _1=0\text{) } \end{array}}\\ z(x,0) &{} = &{} z_0(x)\in [0,1] &{} x\in \Omega , \end{array} \right. \end{aligned}$$
(6)

where \(\mu >0\) denotes the rigidity, one of the Lamé constant. This is a mode III crack propagation model. See [25] for detail of the derivation of our phase field models.

We cannot find any difficulty to compute crack growth numerically. This model equation makes possible to analyze the crack growth phenomena by well-known numerical method, only taking notice about the mesh size that you must choose carefully. In the next section, we show some numerical results of crack growth from this model equation.

Similar mathematical models for simulation based on the Fracfort-Marigo type energy are also found in [4–8, 15].

3 Numerical Results

We show some numerical results of our phase field models of crack growth derived in the previous section. We use a free software FreeFem++ [12] for our computation. It is a useful tool of finite element method for our purpose. Due to the small regularization parameter \(\varepsilon \) introduced in our model, the profiles of \(u\) and \(z\) have small spatial patterns of \(\varepsilon \)-scale. We, however, use an adaptive mesh finite element method with the help of FreeFEM++.

We fix \(\tau > 0\) as a constant time step, \(u^k(x)\) and \(z^k(x)\) are the approximated solution of \(u\) and \(z\), respectively, at \(t=k\tau \) \((k=0,1,2,\ldots )\).

First, we make two types of numerical simulation of the single-line crack growth of the mode III type (6). We set minimum mesh size more than \(2\times 10^{-3}\) and maximum number of the vertices of triangular mesh less than 5,000. The numerical solution \((u^{k}, z^{k})\) for mode III model (6) are computed from \((u^{k-1}, z^{k-1})\) with the semi-implicit scheme:

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \alpha _1 \frac{u^k-u^{k-1}}{\tau } &{} = &{} \displaystyle \mu \; \mathrm{div} \left( (1-z^{k-1})^2 \nabla u^k \right) \\ \displaystyle \alpha _2 \frac{\tilde{z}^k-z^{k-1}}{\tau } &{} = &{} \displaystyle \varepsilon \; \mathrm{div} \left( \gamma (x) \nabla \tilde{z}^k \right) - \frac{\gamma (x) }{\varepsilon } \tilde{z}^k + \mu |\nabla u^{k-1}|^2 (1 - \tilde{z}^k)\\ z^k&{}=&{}\min (1,~\max (\tilde{z}^k,\,z^{k-1})) \end{array} \right. \end{aligned}$$
(7)

We remark that \(0 \le z^k \le 1\) is guaranteed when \(z^0 \in [0,1]\) at \(t=0\). For spatial discretization, we use adaptive mesh P2 finite element method. The model of modes I and II (5) is similarly discretized. It is necessary to set the mesh of small size near crack region (\(z \sim 1\)), because the values of \(u\) and \(z\) change drastically around there. We solve (7) by FreeFem++ with adaptive P2-element, where \(z\) is evaluated for remeshing at each time step.

Fig. 1
figure 1

Domain of numerical simulation of mode III crack growth (a) and mode I+II crack growth (b)

Full size image

Initial crack is set as Fig. 1a, single-line from left hand side. Figure 2 shows that a crack propagates to the another side when fracture toughness \(\gamma \) is homogeneous. Adaptive mesh is effective to follow the crack path. As the crack grows, FreeFem++ adapts to set small size mesh near the crack, and the number of vertices becomes larger till it breaks down (Fig. 3).

Fig. 2
figure 2

An initial crack grows in isotropic media with given boundary displacement \({\varvec{g}}=(0,0,10) \times t\) (\(u\) (upper), \(z\) (middle), mesh (lower))

Full size image
Fig. 3
figure 3

Temporal evolution of a the minimum and maximum mesh size, (b) number of vertices

Full size image

When \(\gamma \) is inhomogeneous, the crack intends to follow the weak region. Figure 4 shows the crack growth when \(\gamma \) has the profile as stripe (\(\gamma (x,y)=0.5(1+0.2 \sin 20(x+y))\)). First crack grows following weak position, after that, sub-branch emerges repeatedly.

Fig. 4
figure 4

An initial crack grows in an anisotropic media (\(\gamma (x,y)=0.5*(1+0.2*sin(20*(x+y)))\)) with given boundary displacement \({\varvec{g}}=(0,0,10) \times t\) (\(u\) (upper), \(z\) (middle), mesh (lower))

Full size image

Finally, we show the numerical results of mode I+II crack growth. We use the phase field model (5) with isotropic elasticity tensor. Lamé constants are set as \(\lambda =26.76, \mu =19.38\), where Young’s modulus and Poisson’s ratio are set as \(E=50,\sigma =0.29\), respectively. Initial crack which is shaped as slit changes its direction to perpendicular to the displacement on \(\Gamma _D\) (Fig. 1b). It shows that crack kinks to annihilate mode II at the front (Fig. 5).

Fig. 5
figure 5

An initial crack grows in an isotropic media with given boundary displacement \({\varvec{g}}=(1,1,0) \times t\) (\(u\) (upper), \(z\) (middle), mesh (lower))

Full size image

From these results, using adaptive mesh method is effective to calculate the crack path. For the similar purpose, we use ALBERTA toolbox [23] in [24, 25]. Adaptive mesh method is also useful in other free boundary or pattern formation problem, such as reaction-diffusion model [17, 18].