1 Introduction

Sandwich structures are widely used in the aircraft, aerospace, flexible electronics and biomedical fields due to their many advantages, including as their light weight and excellent bending stiffness [1]. A typical sandwich structure consists of a homogeneous core sandwiched between two homogenous face sheets. Sandwich structures have recently become even more appealing as a result of the development of materials that are not homogeneous, functionally graded materials (FGMs) for example, Garg et al. [2]. FGMs improve sandwich structures' mechanical and thermal properties by reducing interlaminar stresses and thermal stresses as choices for the face sheets and/or the core [3,4,5,6,7,8,9,10,11]. Two forms of FG sandwich structures are primarily covered in the literature: Type-A sandwich structures have FGM face sheets and a homogeneous core [12,13,14,15,16], whereas type-B sandwich structures do the opposite [17,18,19]. FGM sandwich structures provide exceptional potential in many engineering domains, such as submarines, return capsules, planetary exploratory landers and so on [20, 21]. They combine the two benefits of sandwich structures and FGMs. Researchers have looked into the buckling behavior of FG sandwich constructions as one of the important failure types. However, the majority among them limited to FGM sandwich plates when subjected to thermal load or mechanical load [22,23,24,25,26,27,28,29,30,31,32,33,34,35]. There are not many publications that take mechanical and thermal load into account. For an accurate prediction of the buckling issue, it is crucial to take both into account because in actuality, sandwich plates made of FGMs are regularly subjected to simultaneous mechanical and thermal loads. In order to investigate the type-A FG sandwich plate's buckle under mechanical load and uniform temperature escalation, the Galerkin-differential quadrature method is used by Yang et al. [36] utilizing a high-order equivalent-single-layer (ESL) theory. Shen and his colleagues [37, 38] investigated the buckling and post-buckling of type-A FG sandwich plates under thermal and mechanical loads using a method called two-step perturbation. Yaghoobi and Yaghoobi [39] studied the effects of both thermal and mechanical buckling of type-A FG sandwich plates supported by an elastic base using a first-order ESL theory. Using a first-order ESL theory, Tung [40] performed a thermomechanical post-buckling analysis of FG sandwich plates under mechanical load and uniform temperature rise.

Inside the plate made of FGMs, micro-voids or porosities are created during the production. Different temperatures of solidification for the components that make up FGMs result in the creation of porosity or micro-voids inside the plate for the period of manufacturing. Porosities or micro-voids in the materials diminish the plate's mechanical rigidity, which could result in structural failure [41,42,43]. Investigating the structural response of porous FG plates requires taking into account the plate's porosity. To determine the structural response of porous FG sandwich models, a variety of even and uneven porosity models have been proposed and developed [44,45,46]. By taking into account in-surface curvilinear motions, Karami and Ghayesh [47] investigate the vibrations of sandwich micro-shells with functionally graded porous face sheets. Hadji et al. [48] have analyzed the naturel frequency of the natural frequency of the sandwich FG-plate comprised the micro-voids in the face sheets and reposed on Winkler–Pasternak foundation with the help of the kinematic of the third-order shear deformation theory. Ghazwani et al. [49] examined the impact of various distribution of the porosity on the vibrational response of the FG-nanobeams based on Hamilton’s principle and Eringen’s theory. The trigonometric shear deformation theory (TrSDT) is used by Avcar et al. [50] to examine the natural frequency of perfect/imperfect FG sandwich beam reposed on two-parameter elastic foundation. The analysis is performed for various edges boundary conditions. Avcar et al. [51] examined the flexural behaviors of FG sandwich beam with including the porosity effect by modifying the rule of mixtures of material. The analysis has performed via hyperbolic shear deformation theory. Also, the dynamic analysis of the FG- sandwich beams is investigated based on the trigonometric shear deformation theory by Avcar et al. [52]. The effect of the porosity volume fractions with different types of porosity distribution pattern is also discussed. The effects of the boundary conditions, porosity volume fraction, lay-up scheme and side-to-thickness ratio on the vibrational analysis of FG sandwich plates are studied analytical by Hadji and Avcar [53] by employing the hyperbolic shear displacement theory. Also, recent various works are published to investigate the impact of the geometric imperfection on the structures responses as [54,55,56,57].

The literature research revealed that the scant amount of information that is currently accessible is insufficient for supplying a thorough familiarity with the behavior that buckles FG sandwich plates when subjected to thermal and mechanical loads. There have not been any studies looking into the detrimental impact of voids on the buckling behavior of FG sandwich plates. Based on the four integral shear deformation theory, a methodical solution for the thermomechanical buckling analysis of imperfect FG sandwich plate has been performed in the current work. The current displacements field is simplified and contains only four unknowns compared to five or more in the similar models and ensures the zero shear stresses at the top and bottom surfaces of the FG sandwich plates based on the hyperbolic warping function in order to avoid the introduction of correction factors. The effect of the porosity in the materials properties is considered because of the possibility of the appearance of porosity in the micro-void form due to the difference of solidification temperature of the (ceramic/metal) constituents in the manufacturing phase. Even, uneven, logarithmic uneven and linear uneven porosity distributions are considered in order to include porosity in the sandwich plate's upper and lower FGM faces and core. This study also includes sandwich plates using type-A and type-B FGM. Considerations are made for both a graded and a uniform temperature rise. Here, power-law FGM is adopted. Temperature independence of the material characteristics is assumed [58, 59]. The Navier method is used to solve the governing equations, which are derived from the idea of minimum total potential energy. By contrasting computed results with those from the existing literature, the validity of the proposed theory was established. The thermomechanical buckling of FG sandwich plates was computed numerically while taking into account the effects of geometrical parameters, porosity coefficient and porosity distribution model.

2 Theoretical formulations

2.1 Geometry and concept of FG sandwich plate

2.1.1 Sandwich plate Type-A

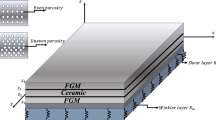
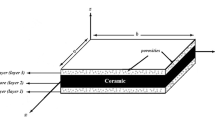
Figure 1 illustrates how the face sheets in type-A sandwich plates are functionally graded across thickness while the sandwich core is homogeneous. The type-A sandwich plate's ceramic volume fraction is provided by [24]:

$$ \begin{gathered} V^{\left( 1 \right)} = \left( {\frac{{z - h_{0} }}{{h_{1} - h_{0} }}} \right)^{p} \, z \in \left[ {h_{0} ,h_{1} } \right] \hfill \\ V^{\left( 2 \right)} = 1 \, z \in \left[ {h_{1} ,h_{2} } \right] \hfill \\ V^{\left( 3 \right)} = \left( {\frac{{z - h_{3} }}{{h_{2} - h_{3} }}} \right)^{p} \, z \in \left[ {h_{2} ,h_{3} } \right] \hfill \\ \end{gathered} $$
(1)
Fig. 1
figure 1

Sandwich plates with FGM come in two varieties a FG face sheets and a homogenous core characterize type A. b FG core and homogenous face-sheets for type-B

Full size image

2.1.2 Sandwich plate Type-B

As shown in Fig. 1, type-B sandwich plates have uniform face sheets but functionally graded core layers that vary in thickness. The following is the amount of ceramics of sandwich plate type-B [24]:

$$ \begin{gathered} V^{\left( 1 \right)} = 0 \, z \in \left[ {h_{0} ,h_{1} } \right] \hfill \\ V^{\left( 2 \right)} = \left( {\frac{{z - h_{1} }}{{h_{2} - h_{1} }}} \right)^{p} \, z \in \left[ {h_{1} ,h_{2} } \right] \hfill \\ V^{\left( 3 \right)} = 1 \, z \in \left[ {h_{2} ,h_{3} } \right] \hfill \\ \end{gathered} $$
(2)

2.2 Porosity distribution models

By employing Voigt's model and taking into account the power law, the effective material parameters of the FG sandwich plate are determined. Four even and uneven porosity models are taken into account in the current work to account for the porosity in FG faces or cores of FG sandwich plates. The materials that work best for porous FG sandwich plates are given below [60].

2.2.1 Even porosity (Imperfect I)

$$ {\text{ Type A Sandwich Plate}}\left\{ \begin{gathered} \Gamma_{1} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 1 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right) \hfill \\ \Gamma_{2} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 2 \right)} + \Gamma_{m} (T) \, \hfill \\ \Gamma_{3} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 3 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right) \hfill \\ \end{gathered} \right. $$
(3)
$$ {\text{Type B Sandwich Plate }}\left\{ \begin{gathered} \Gamma_{1} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 1 \right)} + \Gamma_{m} (T) \, \hfill \\ \Gamma_{2} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 2 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right) \, \hfill \\ \Gamma_{3} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 3 \right)} + \Gamma_{m} (T) \, \hfill \\ \end{gathered} \right. $$
(4)

2.2.2 Uneven porosity (Imperfect 2)

$$ {\text{Type A Sandwich Plate}}\left\{ \begin{gathered} \Gamma_{1} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 1 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{\left| {2z - \left( {z_{0} + z_{1} } \right)} \right|}}{{z_{1} - z_{0} }}} \right] \hfill \\ \Gamma_{2} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 2 \right)} + \Gamma_{m} (T) \, \hfill \\ \Gamma_{3} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 3 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{\left| {2z - \left( {z_{2} + z_{3} } \right)} \right|}}{{z_{3} - z_{2} }}} \right] \hfill \\ \end{gathered} \right. $$
(5)
$$ {\text{Type B Sandwich Plate }}\left\{ \begin{gathered} \, \Gamma_{1} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 1 \right)} + \Gamma_{m} (T) \, \hfill \\ \, \Gamma_{2} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 2 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{\left| {2z - \left( {z_{1} + z_{2} } \right)} \right|}}{{z_{2} - z_{1} }}} \right] \, \hfill \\ \, \Gamma_{3} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 3 \right)} + \Gamma_{m} (T) \, \hfill \\ \end{gathered} \right. $$
(6)

2.2.3 Uneven porosities (Imperfect 3)

$$ {\text{Type A Sandwich Plate }}\left\{ \begin{gathered} \, \Gamma_{1} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 1 \right)} + \Gamma_{m} (T) - \log \left( {1 + \frac{\xi }{2}} \right)\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{\left| {2z - \left( {z_{0} + z_{1} } \right)} \right|}}{{z_{1} - z_{0} }}} \right] \hfill \\ \, \Gamma_{2} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 2 \right)} + \Gamma_{m} (T) \, \hfill \\ \, \Gamma_{3} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 3 \right)} + \Gamma_{m} (T) - \log \left( {1 + \frac{\xi }{2}} \right)\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{\left| {2z - \left( {z_{2} + z_{3} } \right)} \right|}}{{z_{3} - z_{2} }}} \right] \hfill \\ \end{gathered} \right. $$
(7)
$$ {\text{Type B Sandwich Plate}}\left\{ \begin{gathered} \, \Gamma_{1} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 1 \right)} + \Gamma_{m} (T) \, \hfill \\ \, \Gamma_{2} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 2 \right)} + \Gamma_{m} (T) - \log \left( {1 + \frac{\xi }{2}} \right)\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{\left| {2z - \left( {z_{1} + z_{2} } \right)} \right|}}{{z_{2} - z_{1} }}} \right] \, \hfill \\ \, \Gamma_{3} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 3 \right)} + \Gamma_{m} (T) \, \hfill \\ \end{gathered} \right. $$
(8)

2.2.4 Linear uneven porosities (Imperfect 4)

$$ {\text{Type A Sandwich Plate }}\left\{ \begin{gathered} \, \Gamma_{1} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 1 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{z - z_{0} }}{{z_{0} - z_{1} }}} \right] \hfill \\ \, \Gamma_{2} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 2 \right)} + \Gamma_{m} (T) \, \hfill \\ \, \Gamma_{3} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 3 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{z - z_{3} }}{{z_{2} - z_{3} }}} \right] \hfill \\ \end{gathered} \right. $$
(9)
$$ {\text{Type B Sandwich Plate}}\left\{ \begin{gathered} \, \Gamma_{1} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 1 \right)} + \Gamma_{m} (T) \, \hfill \\ \, \Gamma_{2} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 2 \right)} + \Gamma_{m} (T) - \frac{\xi }{2}\left( {\Gamma_{c} + \Gamma_{m} } \right)\left[ {1 - \frac{{z - z_{1} }}{{z_{1} - z_{2} }}} \right] \hfill \\ \, \Gamma_{3} (z) = \left( {\Gamma_{c} - \Gamma_{m} } \right)V^{\left( 3 \right)} + \Gamma_{m} (T) \, \hfill \\ \end{gathered} \right. $$
(10)

2.3 Kinematics and strains

The indeterminate integrals are used to reconstruct the conventional five shear deformation theory, reducing the number of variables to just four. It is shown how the generalized displacement field looks like [24]:

$$ \begin{gathered} u(x,y,z,t) = u_{0} (x,y,t) - z\frac{{\partial w_{0} }}{\partial x} + f(z)\phi_{x} (x,y,t) \hfill \\ \hfill \\ v(x,y,z,t) = v_{0} (x,y,t) - z\frac{{\partial w_{0} }}{\partial y} + f(z)\phi_{y} (x,y,t) \hfill \\ \hfill \\ w(x,y,z,t) = w_{0} (x,y,t) \hfill \\ \end{gathered} $$
(11)

where \(u_{0}\); \(v_{0}\); \(w_{0}\), \(\phi_{x}\), \(\phi_{y}\) are five unknown displacements of the mid-plane of the plate, \(f(z)\) denotes shape function representing the variation of the transverse shear strains and stresses within the thickness. By considering that \(\phi_{x} = \int {\theta (x,y)dx}\) and \(\phi_{y} = \int {\theta (x,y)dy}\), the displacement field of the present model can be expressed in a simpler form as:

$$ \begin{gathered} u(x,y,z,t) = u_{0} (x,y,t) - z\frac{{\partial w_{0} }}{\partial x} + k_{1} \,f(z)\int {\theta \,(x,y,t)} \,dx \hfill \\ \hfill \\ v(x,y,z,t) = v_{0} (x,y,t) - z\frac{{\partial w_{0} }}{\partial y} + k_{2} \,f(z)\int {\theta \,(x,y,t)} \,dy \hfill \\ \hfill \\ w(x,y,z,t) = w_{0} (x,y,t) \hfill \\ \end{gathered} $$
(12)

The current higher-order shear deformation plate theory is obtained in this paper by setting [61]:

$$ f(z) = h\sinh \left( \frac{z}{h} \right) - z\cosh \left( \frac{1}{2} \right) $$
(13)

It can be seen that the displacement field in Eq. (12) introduces only four unknowns (\(u_{0}\),\(v_{0}\),\(w_{0}\) and \(\theta\)). The nonzero von Karman strains associated with the displacement field in Eq. (12) are:

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {k_{x}^{b} } \\ {k_{y}^{b} } \\ {k_{xy}^{b} } \\ \end{array} } \right\} + f(z)\left\{ {\begin{array}{*{20}c} {k_{x}^{s} } \\ {k_{y}^{s} } \\ {k_{xy}^{s} } \\ \end{array} } \right\},\quad \left\{ {\begin{array}{*{20}c} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = g(z)\left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\} $$
(14)

where

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \\ {\frac{{\partial v_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \\ {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x} + \left( {\frac{{\partial w_{0} }}{\partial x}} \right)\left( {\frac{{\partial w_{0} }}{\partial y}} \right)} \\ \end{array} } \right\},\quad \left\{ {\begin{array}{*{20}c} {k_{x}^{b} } \\ {k_{y}^{b} } \\ {k_{xy}^{b} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \\ { - \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \\ { - 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \\ \end{array} } \right\} $$
(15a)
$$ \left\{ {\begin{array}{*{20}c} {k_{x}^{s} } \\ {k_{y}^{s} } \\ {k_{xy}^{s} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {k_{1} \theta } \\ {k_{2} \theta } \\ {k_{1} \frac{\partial }{\partial y}\int {\theta \, dx} + k_{2} \frac{\partial }{\partial x}\int {\theta \, dy} } \\ \end{array} } \right\},\quad \left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {k_{2} \int {\theta \, dy} } \\ {k_{1} \int {\theta \, dx} } \\ \end{array} } \right\} $$
(15b)

and

$$ g(z) = \frac{df(z)}{{dz}} $$
(16)

The integrals defined in the above equations shall be resolved by a Navier type method and can be written as follows:

$$ \frac{\partial }{\partial y}\int {\theta \, dx} = A^{{\prime }} \frac{{\partial^{2} \theta }}{\partial x\partial y},\quad \frac{\partial }{\partial x}\int {\theta \, dy} = B^{{\prime }} \frac{{\partial^{2} \theta }}{\partial x\partial y},\quad \int {\theta \, dx} = A^{{\prime }} \frac{\partial \theta }{{\partial x}},\quad \int {\theta \, dy} = B^{{\prime }} \frac{\partial \theta }{{\partial y}} $$
(17)

where the coefficients \(A^{\prime}\) and \(B^{\prime}\) are expressed according to the type of solution used. In this case via Navier, therefore, \(A^{\prime}\), \(B^{\prime}\), \(k_{1}\) and \(k_{2}\) are expressed as follows:

$$ A^{{\prime }} = - \frac{1}{{\alpha^{2} }},\quad B^{{\prime }} = - \frac{1}{{\beta^{2} }},\quad k_{1} = \alpha^{2} ,\quad k_{2} = \beta^{2} $$
(18)

where \(\alpha\) and \(\beta\) are defined in expression (31).

For the n-th layer, the stress–strain relationships that take into account thermal effects can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\tau_{yz} } \\ {\tau_{xz} } \\ {\tau_{xy} } \\ \end{array} } \right\}^{(n)} = \left\{ {\begin{array}{*{20}c} {\sigma_{x}^{0} } \\ {\sigma_{y}^{0} } \\ {\tau_{yz}^{0} } \\ {\tau_{xz}^{0} } \\ {\tau_{xy}^{0} } \\ \end{array} } \right\}^{(n)} + \left\{ {\begin{array}{*{20}c} {\sigma_{x}^{T} } \\ {\sigma_{y}^{T} } \\ {\tau_{yz}^{T} } \\ {\tau_{xz}^{T} } \\ {\tau_{xy}^{T} } \\ \end{array} } \right\}^{(n)} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & 0 & 0 & 0 \\ 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]^{(n)} \left\{ {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ \end{array} } \right\}^{(n)} - \alpha \Delta T\left\{ \begin{gathered} 1 \hfill \\ 1 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right\}^{n} } \right\},\left( {n = 1,2,3} \right) $$
(19)

Stiffness coefficients, \(C_{ij}\), can be expressed as [22]:

$$ C_{11}^{\left( n \right)} = C_{22}^{{^{\left( n \right)} }} = \frac{{E^{{^{\left( n \right)} }} (z)}}{{1 - \nu^{2} }}, $$
(20.a)
$$ C_{12}^{{^{\left( n \right)} }} = \nu C_{11}^{{^{\left( n \right)} }} , $$
(20.b)
$$ C_{44}^{{^{\left( n \right)} }} = C_{55}^{{^{\left( n \right)} }} = C_{66}^{{^{\left( n \right)} }} = \frac{{E^{{^{\left( n \right)} }} (z)}}{{2\left( {1 + \nu } \right)}}, $$
(20.c)

2.4 Governing equations

The minimum total potential energy principle, which may be expressed as follows, is employed in this work [61].

$$ \delta \left( {U + U_{e} } \right) = 0 $$
(21)
$$ U = \frac{1}{2}\int\limits_V^{} {{\text{ }}\left[ {\sigma _x^0{\varepsilon _x} + \sigma _y^0{\text{ }}{\varepsilon _y} + \tau _{xy}^0\delta {\text{ }}{\gamma _{xy}} + \tau _{yz}^0\delta {\text{ }}{\gamma _{yz}} + \tau _{xz}^0\delta {\text{ }}{\gamma _{xz}}} \right]dV} + \frac{1}{2}\int\limits_V^{} {{\text{ }}\left[ {\sigma _x^T{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}^2} + \sigma _y^T{{\left( {\frac{{\partial w}}{{\partial y}}} \right)}^2}} \right]dV} $$
(22)

The calculation of the external force's potential energy uses [62]:

$$ U_{e} = \frac{1}{2}\int\limits_{V}^{{}} { \, \left[ {N_{x}^{0} \left( {\frac{\partial w}{{\partial x}}} \right)^{2} + N_{y}^{0} \left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right]dV} $$
(23)

where \(N_{x}^{0}\) and \(N_{y}^{0}\) depict dispersed, compressive, x- and y-directional forces (per unit length) in a plane.

By substituting Eqs. (14) and (19) into Eq. (21), the following can be derived:

$$ \begin{aligned} & \delta \, u_{0} : \, \frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = 0 \\ & \delta \, v_{0} : \, \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{y} }}{\partial y} = 0 \\ & \delta \, w_{0} : \, \frac{{\partial^{2} M_{x}^{b} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy}^{b} }}{\partial x\partial y} + \frac{{\partial^{2} M_{y}^{b} }}{{\partial y^{2} }} + \overline{N} + \overline{N}^{T} = 0\, \\ & \delta \, \theta : \, - {\text{k}}_{{1}} \,M_{x}^{s} - {\text{k}}_{{2}} \,M_{y}^{s} \, - \left( {k_{1} A^{\prime} + k_{2} \,B^{\prime}} \right)\frac{{\partial^{2} M_{xy}^{s} }}{\partial x\partial y} + k_{1} \,A^{\prime}\frac{{\partial S_{xz}^{s} }}{\partial x} + k_{2} \,B^{\prime}\frac{{\partial S_{yz}^{s} }}{\partial y} + \overline{N} + \overline{N}^{T} = \,\,\,0 \\ \end{aligned} $$
(24)

where the stress resultants \(N\), \(M\) and \(S\) are defined by

$$ \left( {N_{i} ,M_{i}^{b} ,M_{i}^{s} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {1,z,f} \right)\sigma_{i} dz} ,\quad \left( {i = x,y,xy} \right)\quad {\text{and}}\quad \left( {S_{xz}^{s} ,S_{yz}^{s} } \right) = \int\limits_{ - h/2}^{h/2} {g\left( {\tau_{xz} ,\tau_{yz} } \right)dz} $$
(25)

And

$$ \overline{N} = N_{x}^{0} \frac{{\partial^{2} \left( {w_{0} } \right)}}{{\partial x^{2} }} + N_{y}^{0} \frac{{\partial^{2} \left( {w_{0} } \right)}}{{\partial y^{2} }} $$
(26)
$$ \overline{N}^{T} = - N_{x}^{T} \frac{{\partial^{2} \left( {w_{0} } \right)}}{{\partial x^{2} }} - N_{y}^{T} \frac{{\partial^{2} \left( {w_{0} } \right)}}{{\partial y^{2} }} $$
(27)

In which [62]:

$$ \left\{ {\begin{array}{*{20}c} {N_{x}^{T} } \\ {N_{y}^{T} } \\ \end{array} } \right\} = \sum\limits_{n = 1}^{3} {\int\limits_{{h_{n - 1} }}^{{h_{n} }} {\left\{ {\begin{array}{*{20}c} {\left( {C_{11} + C_{12} } \right)\alpha T} \\ {\left( {C_{11} + C_{12} } \right)\alpha T} \\ \end{array} } \right\}} }^{\left( n \right)} dz $$
(28)

2.5 Temperature field

2.5.1 Temperature increase that is uniform

The temperature of the FG sandwich plate is uniformly raised from its initial temperature \(T_{i}\) to the desired temperature \(T_{f}\) in this scenario as the sandwich plate buckles. \(\Delta T = T_{f} - T_{i}\) is the temperature increment.

2.5.2 Temperature increase that is graded

The top surface temperature \(T_{t}\) differs from the bottom surface temperature \(T_{b}\), which varies depending on the plate thickness [35]:

$$ T(z) = \Delta T\left( {\frac{z}{h} + \frac{1}{2}} \right)^{n} + T_{t} $$
(29)

In which n is the temperature index (0 < n < ∞) and \(\Delta T = T_{t} - T_{b}\) is the buckling temperature difference.

3 Analytical solution

The displacement fields are expressed as a function of the boundary conditions using the Navier technique with simply supported boundaries [62].

$$ \left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{0} } \\ \theta \\ \end{array} } \right\} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left\{ {\begin{array}{*{20}c} {U_{mn} {\kern 1pt} \cos (\lambda \, x)\sin (\mu \, y)} \\ {V_{mn} {\kern 1pt} \sin (\lambda \, x)\cos (\mu \, y)} \\ {W_{0mn} {\kern 1pt} \sin (\lambda \, x)\sin (\mu \, y)} \\ {\theta_{mn} {\kern 1pt} \sin (\lambda \, x)\sin (\mu \, y)} \\ \end{array} } \right\}} } $$
(30)

where \(U_{mn}\), \(V_{mn}\), \(W_{bmn}\) and \(\theta_{mn}\) are arbitrary parameters to be determined.

$$ \lambda = m\pi /a\quad {\text{and}}\quad \mu = n\pi /b $$
(31)

A system of in-plane compressive stresses that are uniform. \(N_{x}^{0}\),\(N_{y}^{0}\) and \(N_{xy}^{0} = 0\) in a thermal environment can be used to calculate FGM sandwich plates' critical buckling loads and temperature increase.

Equation (30) can be substituted for Eq. (24), resulting in the following result: Assuming that \(N_{x}^{0}\) and \(N_{y}^{0}\) have a specific ratio so that \(N_{x}^{0} = - N_{{}}^{0}\) and \(N_{y}^{0} = - \gamma N_{{}}^{0}\), one can obtain:

$$ \begin{gathered} \left( {\left[ {\begin{array}{*{20}c} {S_{11} } & {S_{12} } & {S_{13} } & {S_{14} } \\ {S_{12} } & {S_{22} } & {S_{23} } & {S_{24} } \\ {S_{13} } & {S_{23} } & {S_{33} } & {S_{34} } \\ {S_{14} } & {S_{24} } & {S_{34} } & {S_{44} } \\ \end{array} } \right]} \right) - \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & P & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & l & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right] = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\} \hfill \\ \hfill \\ \end{gathered} $$
(32)

where:

$$ \begin{aligned} S_{11} = & (\alpha^{2} A_{11} + \beta^{2} A_{66} ) \\ S_{12} = & \alpha \beta (A_{12} + A_{66} ) \\ S_{13} = & - \alpha^{3} B_{11} - \alpha \beta^{2} (B_{12} + 2B_{66} ) \\ S_{14} = & \alpha ((k_{2} B^{\prime}B_{12}^{s} + (k_{1} A{\prime} + k_{2} B{\prime} )B_{66}^{s} )\beta^{2} + k_{1} A^{\prime}B_{11}^{s} \alpha^{2} ) \\ S_{22} = & (\alpha^{2} A_{66} + \beta^{2} A_{22} ) \\ S_{23} = & - \alpha^{2} \beta \,(B_{12} + 2B_{66} ) - \beta^{3} B_{22} \\ S_{24} = & \beta ((k_{1} A^{\prime}B_{12}^{s} + (k_{1} A{\prime} + k_{2} B{\prime} )B_{66}^{s} )\alpha^{2} + k_{2} B^{\prime}B_{22}^{s} \beta^{2} ) \\ S_{33} = & (\alpha^{4} D_{11} + \beta^{4} D_{22} + 2\alpha^{2} \beta^{2} (D_{12} + 2D_{66} )) + K_{w} + K_{s} (\alpha^{2} + \beta^{2} ) \\ S_{34} = & - (\alpha^{4} k_{1} A^{\prime}D_{11}^{s} + \beta^{4} k_{2} B^{\prime}D_{22}^{s} ) - \alpha^{2} \beta^{2} (k_{1} A{\prime} + k_{2} B{\prime} )(D_{12}^{s} + 2D_{66}^{s} ) \\ S_{44} = & \alpha^{4} \left( {k_{1} A^{\prime}} \right)^{2} H_{11}^{s} + \beta^{4} (k_{2} B^{\prime})^{2} H_{22}^{s} + (2k_{1} k_{2} A^{\prime}B^{\prime}H_{12}^{s} + (k_{1} A{\prime} + k_{2} B{\prime} )^{2} H_{66}^{s} )\alpha^{2} \beta^{2} \\ & + \alpha^{2} ((k_{1} A{\prime} )^{2} F_{55}^{s} + 2k_{1} A^{\prime}X_{55}^{s} + A_{55}^{s} ) + \beta^{2} ((k_{2} B{\prime} )^{2} F_{44}^{s} + A_{44}^{s} ) \\ P = & N_{0} \left( {\lambda^{2} + \gamma \mu^{2} } \right) \\ l = & \lambda^{2} N_{x}^{T} + \mu^{2} N_{y}^{T} \\ \end{aligned} $$
(33)

4 Numerical results

This section provides a comparative analysis to support the existing formulation. To adequately understand the thermomechanical buckling of FGM sandwich plates, many results are presented that take into account the effects of volume fraction distribution, geometric factors, mechanical and thermal loads. Table 1 lists the material characteristics for ceramics and metals utilized in the numerical illustrations. Assuming nothing else, Tt = 25 K, γ = 1 and a/h = 10.

Table 1 Material properties [62]
Full size table

4.1 Validation study

The following categories are used to conduct the verification investigation: mechanical buckling, thermal buckling and thermomechanical buckling of the two type of FG sandwich plates. The FG sandwich plates are constructed of zirconia (ZrO2) and titanium (Ti-6Al-4V) for thermal buckling and thermomechanical buckling and aluminum (Al) and alumina (Al2O3) for mechanical buckling.

The following relationships are used as comparisons and examples [62]:

$$ \overline{N}_{0} = \frac{{N_{0}^{cr} a^{2} }}{{100h^{3} E_{0} }};{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} T_{cr} = 10^{ - 3} \Delta T_{cr} $$

where \(E_{0} = 1\,{\text{GPa}}\).

Mechanical load and temperature rise are used as dimensionless parameters [62]:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{0} = \frac{{N_{0}^{T} a^{2} }}{{100h^{3} E_{0} }}, \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} = \frac{{10^{ - 3} \Delta T}}{{T_{0} }} $$

where \(T_{0} = 1K\).

Tables 2, 3, 4 and 5 display the two type sandwich plates' critical temperature rise and buckling load and for various layer thickness ratios and power indices. As benchmark results, further calculations made using different theories from the literature are also provided. As seen, a good agreement is established for every facet of the buckling problem. It is clear for the type-A, the critical buckling load is biggest one in the case of 1-2-1 because the ceramic layer is thick and has a higher young modulus. We can see also in the same type (A) that the critical buckling loads decrease with the increase of the face’s sheets power law because these layers become rich on metal.

Table 2 Dimensionless type-A square sandwich plate critical buckling load \(\overline{N}_{0}\)
Full size table
Table 3  Dimensionless type-B square sandwich plate critical buckling load \(\overline{N}_{0}\)
Full size table
Table 4 Type-A square sandwich plate's critical buckling temperature rises Tcr under uniform temperature rise
Full size table
Table 5  Type-B square sandwich plate's critical buckling temperature rises Tcr during nonlinear temperature rise
Full size table

Also, the critical buckling temperature is in inverse relation with the side-to-thickness ratio because the plate becomes thin and flexible and a small temperature leads to buckling of the structure. For the second type (B), we can observe for 1-0-1 plate, the power-law index has no influence because the structure does not contain a core, but in the others case (2-1-2 and 1-1-1) the critical buckling temperature rises Tcr are in inverse relation with the inhomogeneity index because the core becomes riche on metal and therefore less rigid.

4.2 Imperfect sandwich plate buckling analysis under mechanical and thermal loads

In this illustration, the impact of mechanical and thermal loads on a square, imperfect sandwich plate with simple support is taken into account. It is presummated that the plate buckles when it is subjected to a mechanical load \(N_{0}^{T}\) and a temperature increase \(\Delta T\) during both temperature rise (uniform/linear).

First, we determine the dimensionless critical buckling load and temperature increment for imperfect 1 type-A square sandwich plates for \(\xi\) = 0, 0.05, 0.1, 0.15 and 0.2 with a variety of 2-1-2, 1-0-1, 1-2-1 and 1-1-1layer thickness ratios under uniform/linear temperature rise using half of the uniform temperature rise critical buckling temperature increment, the mechanical load is then calculated. Additionally, the temperature increase is calculated under a linear and uniform temperature rise by applying half of the critical buckling stress. Table 6 lists these outcomes. The dimensionless critical temperature increase under uniform and linear temperature rise, respectively, are \(T_{cr}^{u}\) and \(T_{cr}^{l}\). The dimensionless mechanical load under uniform temperature rise is:\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0pt} 2}}}\) using half of the critical buckling temperature increment. Using half of the critical buckling load, the dimensionless temperature increments \(T_{N/2}^{l}\) and \(T_{N/2}^{u}\) are defined as the linear and uniform temperature rise. It has been found that \(N_{{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0pt} 2}}} = \frac{1}{2}N_{0}\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T}_{N/2}^{u} = \frac{1}{2}T_{cr}^{u}\), but that \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T}_{N/2}^{l} \prec \frac{1}{2}T_{cr}^{l}\). It is remarkable that the dimensionless critical mechanical load decrease with the increase of the porosity index because the structures become less rigid. But for critical temperature change, this conclusion is inversed. The same type of work was done for imperfect 1 type-B FGM (Ti-6Al-4V/ZrO2) sandwich plates under the effect of thermal loads and mechanical loads as observed in Table 7.

Table 6 Type-A square imperfect 1 sandwich plate’s dimensionless mechanical load and temperature change
Full size table
Table 7 Type-B imperfect 1 square sandwich plate’s dimensionless mechanical load and temperature change
Full size table

The relationship between temperature increment and mechanical load for the type-A sandwich plates (1-0-1), (2-1-2), (1-1-1) and (1-2-1) is shown in Figs. 2, 3 for \(\xi\) = 0.05, 0.15 and 0.2. Figures 2, 3 show that the connection is linear. The mechanical load diminishes as the temperature increment rises. Due to an increase in temperature, compressive internal forces produced, this is to be expected. In Fig. 2, the mechanical load value is zero when the temperature rise reaches its maximum, also the opposite. On the other hand, in Fig. 3, the value of temperature is negative when the mechanical load value reaches its maximum. We can conclude also that the mechanical buckling characteristics are biggest in the case of the 1-2-1 plate type-A, because the thicker layer (core layer) is entirely made of ceramic and therefore the most rigid layer which increases the rigidity of the entire structure.

Fig. 2
figure 2

Temperature increment under uniform temperature rise and the mechanical stress of an imperfect 1 type-A sandwich plate

Full size image
Fig. 3
figure 3

Temperature increment under linear temperature rise and the mechanical stress of an imperfect 1 type-A sandwich plate

Full size image

Analysis of various porosity distributions' effects on the buckling behavior of porous FG sandwich plates has been done in Figs. 4, 5.

Fig. 4
figure 4

Temperature increment under uniform temperature rise and the mechanical stress of an imperfect 1,2,3 and 4 type-A sandwich plate

Full size image
Fig. 5
figure 5

Temperature increment under uniform temperature rise and the mechanical stress of an imperfect 1, 2, 3 and 4 type-B sandwich plate

Full size image

The impact of porosity distribution on buckling analysis is examined using models for even, uneven, logarithmic uneven and linear uneven porosity. Porosity distributions' effects on the buckling behavior of porous FG sandwich plates are more prominent in the type-A sandwich plates.

5 Conclusion

The current study has produced an analytical solution for the thermomechanical buckling analysis of porous FG sandwich plates. Using a four-variable integral plate theory, buckling analysis of FG sandwich plates under thermomechanical load was performed. Sandwich plates with homogenous core and face sheets made of FGMs were included for type-A. Sandwich plates had the reverse, while type-B plates. On the basis of the minimal total potential energy concept, the governing equations were derived. The Navier method was used to provide the analytical answers for boundary conditions with simple support. To show the accuracy of the proposed theory, the critical buckling load and temperature increase under four temperature rise were computed as well as compared with the results reported in the researches. The thermomechanical buckling behavior of FG sandwich plates was studied while taking the effects of volume fraction distribution, geometrical parameters and porosity into consideration. To study the impact of porosity, four porosity distribution models even (Imperfect 1), uneven (Imperfect 2), logarithmic uneven (Imperfect 3) and linear uneven (Imperfect 4) have been taken into consideration. The obtained results from the present investigation demonstrated the following concluding remarks:

  • The critical buckling loads are in inverse relation with face’s sheets heterogeneity index because these layers become rich on metal.

  • The higher values of the critical buckling load are obtained for 1-2-1 plate (type-A) because the thicker layer (core) is entirely ceramic.

  • The increase in the values of the geometry ration leads to decrease the values of the critical buckling temperature.

  • The presence of the porosity in the structures has an effect on the critical mechanical and thermal load.

The current finding could serve as a reference point for additional research on FG sandwich plates. The proposed model can be used in the future to examine others type of structures and solve others structural problems [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85].