1 Introduction

Carbon nanotubes (CNT) were discovered by Sumio Iijima in 1991 [1] during a space research program. After the discovery, CNT has attracted various material as well as the structural research groups (biomedical engineering, aerospace, marine, and mechanical) due to their multi-functional properties [2] and the available unmatched features (excellent specific strength, the high aspect ratios, the extraordinary thermal and electrical properties). Besides these, CNT has proven to be a worthy reinforcement fiber for the preparation of hybrid composite because of the remarkable improvement in the physical and mechanical properties of the parent material. Moreover, a considerable improvement of the binding force between the fibers and the mortar phase can be observed. In this regard, several kinds of reported research articles are discussed relevant to the property evaluation of the CNT/CNT-reinforced composite [3,4,5]. In general, CNT fibers are classified primarily into two different types according to their number of walls, e.g., the single- and multi-walled nanotube (SWCNT and MWCNT). The elastic modulus data of CNTs may also vary as per the walls in between 5 and 6TPa (approximately) for the SWCNT, whereas 1-2TPa (approximately) for MWCNT fibers [6]. With subsequent development in the field of material modeling with the advent of applied mathematics, the concept of functionally grading between the metal and ceramic has been adopted [7] to obtain a functionally graded CNT-reinforced composite (FG-CNTRC) by varying the volume fractions, and the nonlinear bending responses are examined. Further, the modeling has been extended to explain the effect of variable grading patterns of CNT fractions and named as UD (CNT is uniformly distributed throughout the plate), FG-X (CNT concentration is zero at the mid-plane and gradually increases toward the top and bottom surface of the plate), FG-O (CNT concentration is maximum at the mid-plane and gradually decreases toward the top and bottom surface of the plate) and FG-V (CNT concentration is zero at the bottom surface and gradually increases toward the top surface of the plate). Reddy’s higher-order shear deformation theory (HSDT) with seven degrees of freedom (DOF) at each node [8] including von-Kármán type of strain is implemented to model the FG-CNTRC structure mathematically to investigate the large deformation behavior. Additionally, the effect of grading configurations on the nonlinear bending deflections of the FG-CNTRC plate has also been examined [9]. In addition, the post-buckling responses of the CNTRC structure were reported [10] by considering von-Kármán nonlinear strain and the HSDT displacement model. Similarly, von-Kármán strain–displacement relations are adopted [11] to investigate the nonlinear flexural responses of the CNTRC plate. The first-order shear deformation theory (FSDT) associated with von-Kármán nonlinear strain was utilized [12] for the evaluation of the large deformation deflection characteristics of the FG-CNTRC plate. Additionally, several motivational research works appeared in the past related to the modeling and analysis of the composite structure with and without CNT reinforcement for the evaluation of the frequency, deflection, transient response, and the buckling strength, etc. [13,14,15,16,17,18,19,20,21,22,23]. Recently, the nonlinear behavior (vibration and deflection) of the FG sandwich structure reinforced with SWCNT was reported by considering the large deformation via von-Kármán type of geometrical strain in the framework of Reddy’s HSDT kinematics model [24]. Further, the linear bending and vibration behavior of the FG sandwich plate structure was reported in [25] by considering several types of mid-plane kinematic theories and variable DOF at each node (FSDT with five DOF at each node, HSDT with seven DOF at each node, HSDT with nine DOF at each node, HSDT with eleven DOF at each node, and HSDT with thirteen DOF at each node). The published open research article indicates the importance of each kind of shear deformable kinematic theory for the evaluation of eigenfrequency and/or deflection responses. The reported study gives an exclusive understanding of the degree of differences between the outcomes (frequency and deflection) for different kinematic models and the total number of DOFs. Subsequently, the post-buckling strength of the FG-CNT-reinforced sandwich beam structure is investigated via the FSDT kinematics and von-Kármán nonlinear strains [26]. The nonlinear frequency of the layered micro-/nanoplate structural panel is examined [27] using the differential quadrature technique in association with Mindlin theory and von-Kármán strain. Later, the HSDT type of displacement model and von-Kármán strain [28] was adopted to examine the free vibration and the dynamic characteristics of the FG-CNTRC structure with the softcore. Similarly, the free vibration frequencies of the CNT-reinforced sandwich structure resting on the elastic foundation were examined using a refined shear deformation kinematic model [29] for the randomly oriented CNT-reinforced composite, whereas CNT is graded through the thickness of the composite. It is important to mention that the final elastic constants of the randomly oriented CNT-reinforced composite structures are generally evaluated using the most common type method, Mori-Tanaka scheme. Also, some of the new theoretical modeling approaches were reported in the open literature, e.g., a four-variable refined plate theory by improving the classical laminated plate theory for the computation of the frequency responses of the functionally graded sandwich plate [30]. In continuation of the CNT-reinforced composite structure, the buckling and the post-buckling behavior of the functionally graded structure have been reported [31]. Additionally, many other relevant research articles were already published to illustrate the mechanical responses of the sandwich structure [32,33,34,35,36,37,38] including the effect of kinematic theories and types of material.

The reviews related to the linear and nonlinear analysis of the structural components including the displacement field theories and the structural configurations (layered composite and sandwich) have been performed considering the large deformation strain kinematics of the CNT-reinforced composite. The relative assessment indicates the significant breaches within the available studies relevant to the nonlinear strain kinematics and the adopted displacement field for the mathematical formulation. It can be easily noted that the nonlinear deformations of the FG-CNTRC sandwich structure under the combined loading conditions are mainly utilizing the von-Kármán-type nonlinear strain theory in the framework of the FSDT/HSDT displacement field. Hence, the authors of the current article aim to evaluate the nonlinear transverse thermomechanical bending deflections of the FG-CNT-reinforced sandwich flat structural panel numerically with the help of the HSDT type of displacement field model including Green–Lagrange nonlinear strain including the elevated temperature of the environment. In this regard, the final nonlinear static equilibrium equation of the graded sandwich flat structure panel has been solved under the combined effect of thermomechanical loading iteratively with the help of the direct iterative method in conjunction with the finite element method (FEM). The final central deflection data of the FG-CNT-reinforced sandwich structure are obtained computationally with the help of an original MATLAB code utilizing the current higher-order numerical model. Further, the convergence and the validity of the numerical solutions are established by solving similar kinds of numerical examples available in the sources. Finally, the deflection parameters of the sandwich structure are obtained for the variable types of input data, and their subsequent influences due to the elevated temperature are provided in detail as per including the thermal environmental effect.

2 Theory and general formulation

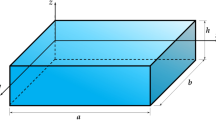
The rectangular sandwich plate model has been derived mathematically for the present analysis including the associated geometrical dimension (i.e., length, a; width, b; and thickness, h; along the X-, Y-, and Z-axes, respectively). In general, the sandwich construction consists of three different layers (i.e., a softcore layer of isotropic material bounded with two stiff face sheets made from the FG-CNTRC layer). Additionally, the face sheets are assumed to be graded functionally with four different types of CNT distribution patterns defined as UU (CNTs are UD for both top and bottom face sheets), FG-\(\Lambda \)V (top face sheet is graded with FG-V type, whereas the bottom face sheet is inverted type, i.e., FG-\(\Lambda \)), FG-OO (both face sheets are graded FG-O type of CNTs distribution) and FG-XX (both face sheets are FG-X type of CNT distribution). The total sandwich thickness is the sum of the individual layer thicknesses (i.e., the face sheets and the core layer defined as \(h_{f}\) and \(h_{c}\), respectively), as shown in Fig. 1. The face sheets are functionally graded due to different CNT grading patterns, and their effective volume fractions are evaluated using similar steps as in [33]:

Fig. 1
figure 1

FG-CNT-reinforced sandwich plate

Full size image

For an FG-UU-type distributed FG-CNT-reinforced sandwich plate:

$$\begin{aligned} \left. {\begin{array}{l} V_{CNT} =V_{CNT}^*\\ V_{CNT} =0 \\ \end{array}} \right\} {\begin{array}{l} {\hbox {for top and bottom face sheet}} \\ {\hbox {for core} }; \\ \end{array} } \end{aligned}$$
(1)

For an FG-\(\Lambda \)V-type distributed FG-CNT-reinforced sandwich plate:

$$\begin{aligned} \left. {\begin{array}{l} V_{CNT} =2\left( {\frac{z_1 -z}{z_1 -z_0 }} \right) V_{CNT}^*\\ V_{CNT} =0 \\ V_{CNT} =2\left( {\frac{z-z_2 }{z_3 -z_2 }} \right) V_{CNT}^*\\ \end{array}} \right\} \hbox { }{\begin{array}{l} {\hbox {for bottom face sheet}} \\ \\ {\hbox {for core} } \\ \\ {\hbox {for top face sheet}}; \\ \end{array} } \end{aligned}$$
(2)

For an FG-OO-type distributed FG-CNT-reinforced sandwich plate:

$$\begin{aligned} \left. {\begin{array}{l} V_{CNT} =2\left( {1-\left| {\frac{2z-z_1 -z_0 }{z_1 -z_0 }} \right| } \right) V_{CNT}^*\\ V_{CNT} =0 \\ V_{CNT} =2\left( {1-\left| {\frac{2z-z_3 -z_2 }{z_3 -z_2 }} \right| } \right) V_{CNT}^*\\ \end{array}} \right\} \hbox { }{\begin{array}{l} {\hbox {for bottom face sheet}} \\ \\ {\hbox {for core} } \\ \\ {\hbox {for top face sheet}}; \\ \end{array} } \end{aligned}$$
(3)

For an FG-XX-type distributed FG-CNT-reinforced sandwich plate:

$$\begin{aligned} \left. {\begin{array}{l} V_{CNT} =2\left( {\left| {\frac{2z-z_1 -z_0 }{z_1 -z_0 }} \right| } \right) V_{CNT}^*\\ V_{CNT} =0 \\ V_{CNT} =2\left( {\left| {\frac{2z-z_3 -z_2 }{z_3 -z_2 }} \right| } \right) V_{CNT}^*\\ \end{array}} \right\} \hbox { }{\begin{array}{l} {\hbox {for bottom face sheet}} \\ \\ {\hbox {for core} } \\ \\ {\hbox {for top face sheet }} \\ \end{array} } \end{aligned}$$
(4)

where \(V_{CNT}^*\) is the CNT volume fraction in each face sheet.

2.1 Effective material properties

Now, the extended rule of mixture [39] has been adopted to evaluate the effective elastic properties of FG-CNT sandwich face sheets and conceded as:

$$\begin{aligned} E_{11}= & {} \eta _1 V_{CNT} E_{11}^{CNT} +V_m E^{m}, \end{aligned}$$
(5)
$$\begin{aligned} \frac{\eta _2 }{E_{22} }= & {} \frac{V_{CNT} }{E_{22}^{CNT} }+\frac{V_m }{E^{m}}, \end{aligned}$$
(6)
$$\begin{aligned} \frac{\eta _3 }{G_{12} }= & {} \frac{V_{CNT} }{G_{12}^{CNT} }+\frac{V_m }{G^{m}} \end{aligned}$$
(7)

where \(E_{11}\), \(E_{22}\), and \(G_{12}\) are the effective elastic constants of the composite component (CNT/polymer) along the principal material direction. Similarly, \(E_{11}^{CNT} \), \(E_{22}^{CNT} \), and \(G_{12}^{CNT} \) are the longitudinal, transverse, and shear moduli of CNT, whereas \(E_{m}\) and \(G_{m}\) represent elastic moduli of the matrix material. Additionally, \(\eta _1 \), \(\eta _2 \), and \(\eta _3 \) are the effectiveness parameters of the CNT fiber taken from the source [40] for the current analysis.

In general, the total volume of the composite is considered to be one, and it includes the volume fractions of each part, i.e., fiber and the mortar phase. Hence, the effective volume fractions of the matrix can be evaluated by using the following formulae:

$$\begin{aligned} V_m = 1-V_{CNT}. \end{aligned}$$
(8)

Further, the rule of mixture formulae has been employed to compute Poisson’s ratio (\(v_{12} )\), density (\(\rho \)), and the thermal expansion coefficients (\(\alpha \)\(_{11}\) and \(\alpha \)\(_{22})\) of the CNT-reinforced sandwich structure, and the corresponding mathematical form is expressed as [39]:

$$\begin{aligned} v_{12}= & {} V_{CNT}{v_{11}}^{CNT} +V_m v^{m}, \end{aligned}$$
(9)
$$\begin{aligned} \rho= & {} V_{CNT}\rho ^{CNT}+V_m \rho ^{m}, \end{aligned}$$
(10)
$$\begin{aligned} \alpha _{11}= & {} \alpha _{11}^{CNT} V_{CNT} +\alpha ^{m}V_m, \end{aligned}$$
(11)
$$\begin{aligned} \alpha _{22}= & {} (1+\upsilon _{12}^{CNT} )V_{CNT} \alpha _{22}^{CNT} +(1+\upsilon ^{m})V_m \alpha ^{m}-\upsilon _{12} \alpha _{11}. \end{aligned}$$
(12)

2.2 Kinematic model

The displacement field components of any arbitrary point in the structural domain are expressed as u, v, and w along x-, y-, and z-axis, respectively. The field variables are expressed with the help of Taylor’s series expansion including the thickness coordinate as in [41]:

$$\begin{aligned} \left. {\begin{array}{l} u\left( {x,y,z} \right) = u_0 \left( {x,y} \right) +z\varphi _x \left( {x,y} \right) +z^{2}\psi _x (x,y)+z^{3}\theta _x \left( {x,y} \right) \\ v\left( {x,y,z} \right) = v_0 \left( {x,y} \right) +z\varphi _y \left( {x,y} \right) +z^{2}\psi _y (x,y)+z^{3}\theta _y \left( {x,y} \right) \\ w\left( {x,y,z} \right) = w_0 \left( {x,y} \right) \\ \end{array}} \right\} \end{aligned}$$
(13)

where \(u_{0}\), \(v_{0}\), and \(w_{0}\) are the extensional displacement components of any general point defined at the mid-plane of the plate geometry along x-, y-, and z-axes, respectively. Similarly, the rotation of the normal about the mid-plane is defined as \(\varphi _x \) and \(\varphi _y \) alternatively, for y- and x-axes, respectively. The higher-order terms \(\psi _x \), \(\psi _y \), \(\theta _x \), and \(\theta _y \) are introduced from Taylor series expansion in the displacement function to achieve the parabolic shear stress variation through the thickness of the CNT-reinforced sandwich and eliminate the use of the shear correction factor [8]. The current kinematic model is capable of expressing the small strain and moderate rotation problems correctly and employed here for the necessary analysis purpose.

Now the displacement field vector \(\left[ {\left\{ \lambda \right\} = \{u\, v\, w\}^{T}} \right] \) can be expressed in matrix form as:

$$\begin{aligned} \left\{ \lambda \right\} = \left[ H \right] \left\{ {\lambda _0 } \right\} \end{aligned}$$
(14)

where \(\left[ H \right] \) and \(\left\{ {\lambda _0 } \right\} \) are the thickness coordinate matrix and mid-plane displacement field vector, respectively. The coefficient matrices of Eq. (14) (i.e., \(\left[ H \right] \) and \(\left\{ {\lambda _0 } \right\} )\) are provided in “Appendix A.”

2.3 Strain–displacement relations

The sandwich structural distortion under the influence of the combined mechanical and thermal loading has been modeled including full geometrical nonlinearity via Green–Lagrange strain kinematics and expressed as in [8]:

$$\begin{aligned} \{\varepsilon _{ij} \}= & {} \left\{ {\begin{array}{l} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \gamma _{xy} \\ \gamma _{zx} \\ \gamma _{yz} \\ \end{array}} \right\} =\left\{ {\begin{array}{l} u_{,x} \\ v_{,y} \\ u_{,y} +v_{,x} \\ u_{,z} +w_{,x} \\ v_{,z} +w_{,y} \\ \end{array}} \right\} +\left\{ {{\begin{array}{l} {\frac{1}{2}\left[ {\left( {u_{,x} } \right) ^{2}+\left( {v_{,x} } \right) ^{2}+\left( {w_{,x} } \right) ^{2}} \right] } \\ {\frac{1}{2}\left[ {\left( {u_{,y} } \right) ^{2}+\left( {v_{,y} } \right) ^{2}+\left( {w_{,y} } \right) ^{2}} \right] } \\ {u_{,x} u_{,y} +v_{,x} v_{,y} +w_{,x} w_{,y} } \\ {u_{,z} u_{,x} +v_{,z} v_{,x} +w_{,z} w_{,x} } \\ {u_{,z} u_{,y} +v_{,z} v_{,y} +w_{,z} w_{,y} } \\ \end{array} }} \right\} \nonumber \\ \hbox { or } \left\{ {\varepsilon _{ij} } \right\}= & {} \left\{ {\varepsilon _L } \right\} _{ij} +\left\{ {\varepsilon _{NL} } \right\} _{ij}, \end{aligned}$$
(15)
$$\begin{aligned} \{\varepsilon _{ij} \}= & {} \left\{ {\begin{array}{l} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \gamma _{xy} \\ \gamma _{zx} \\ \gamma _{yz} \\ \end{array}} \right\} =\left\{ {\begin{array}{l} \varepsilon _x^0 \\ \varepsilon _y^0 \\ \varepsilon _{xy}^0 \\ \varepsilon _{zx}^0 \\ \varepsilon _{yz}^0 \\ \end{array}} \right\} +\left\{ {\begin{array}{l} \varepsilon _x^4 \\ \varepsilon _y^4 \\ \varepsilon _{xy}^4 \\ \varepsilon _{zx}^4 \\ \varepsilon _{yz}^4 \\ \end{array}} \right\} +z\left\{ {\left\{ {\begin{array}{l} k_x^1 \\ k_y^1 \\ k_{xy}^1 \\ k_{zx}^1 \\ k_{yz}^1 \\ \end{array}} \right\} +\left\{ {\begin{array}{l} k_x^5 \\ k_y^5 \\ k_{xy}^5 \\ k_{zx}^5 \\ k_{yz}^5 \\ \end{array}} \right\} } \right\} +z^{2}\left\{ {\left\{ {\begin{array}{l} k_x^2 \\ k_y^2 \\ k_{xy}^2 \\ k_{zx}^2 \\ k_{yz}^2 \\ \end{array}} \right\} +\left\{ {\begin{array}{l} k_x^6 \\ k_y^6 \\ k_{xy}^6 \\ k_{zx}^6 \\ k_{yz}^6 \\ \end{array}} \right\} } \right\} \nonumber \\&+z^{3}\left\{ {\left\{ {\begin{array}{l} k_x^3 \\ k_y^3 \\ k_{xy}^3 \\ k_{zx}^3 \\ k_{yz}^3 \\ \end{array}} \right\} +\left\{ {\begin{array}{l} k_x^7 \\ k_y^7 \\ k_{xy}^7 \\ k_{zx}^7 \\ k_{yz}^7 \\ \end{array}} \right\} } \right\} +z^{4}\left\{ {\begin{array}{l} k_x^8 \\ k_y^8 \\ k_{xy}^8 \\ k_{zx}^8 \\ k_{yz}^8 \\ \end{array}} \right\} +z^{5}\left\{ {\begin{array}{l} k_x^9 \\ k_y^9 \\ k_{xy}^9 \\ k_{zx}^9 \\ k_{yz}^9 \\ \end{array}} \right\} +z^{6}\left\{ {\begin{array}{l} k_x^{10} \\ k_y^{10} \\ k_{xy}^{10} \\ k_{zx}^{10} \\ k_{yz}^{10} \\ \end{array}} \right\} . \end{aligned}$$
(16)

Further, Eq. (16) is rearranged to be expressed in matrix form:

$$\begin{aligned} \left\{ {\varepsilon _{ij} } \right\} =\left[ {H_L } \right] \left\{ {\bar{{\varepsilon }}_L } \right\} +\left[ {H_{NL} } \right] \left\{ {\bar{{\varepsilon }}_{NL} } \right\} \end{aligned}$$
(17)

where \(\left\{ {\bar{{\varepsilon }}_L } \right\} =\left\{ {\varepsilon _x^0 \,\varepsilon _y^0 \,\varepsilon _{xy}^0 \,\varepsilon _{zx}^0 \,\varepsilon _{yz}^0 \, k_x^1 \, k_y^1 \, k_{xy}^1\, k_{zx}^1\, k_{yz}^1\, k_x^2\, k_y^2\, k_{xy}^2\, k_{zx}^2\, k_{yz}^2\, k_x^3\, k_y^3\, k_{xy}^3\, k_{zx}^3\, k_{yz}^3 } \right\} ^{T}\) and \(\left\{ {\bar{{\varepsilon }}_{NL} } \right\} = \left\{ {\begin{array}{l} \varepsilon _x^4 \,\varepsilon _y^4\, \varepsilon _{xy}^4\, \varepsilon _{zx}^4\, \varepsilon _{yz}^4\, k_x^5\, k_y^5\, k_{xy}^5\, k_{zx}^5\, k_{yz}^5\, k_x^6\, k_y^6\, k_{xy}^6 \,k_{zx}^6\, k_{yz}^6\, k_x^7\, k_y^7\, k_{xy}^7\, k_{zx}^7\, k_{yz}^7 \\ k_x^8\, k_y^8\, k_{xy}^8\, k_{zx}^8\, k_{yz}^8\, k_x^9\, k_y^9\, k_{xy}^9\, k_{zx}^9\, k_{yz}^9\, k_x^{10}\, k_y^{10}\, k_{xy}^{10}\, k_{zx}^{10}\, k_{yz}^{10} \\ \end{array}} \right\} ^{T}\) are the linear and the nonlinear strain vectors defined at the mid-plane, respectively, and the individual terms are explained in “Appendix B.” Similarly, the linear and the nonlinear thickness coordinate matrices are defined as [\(H_{L}\)] and [\(H_{NL}\)], respectively, and provided in “Appendix C” for the sake of clarity.

2.4 Constitutive relations

The generalized stress–strain behavior for any general layered material is adopted to model the constitutive relations of the current FG-CNT-reinforced sandwich structural component [8]:

$$\begin{aligned}&\left\{ {{\begin{array}{l} {\sigma _{xx} } \\ {\sigma _{yy} } \\ {\tau _{xy} } \\ {\tau _{zx} } \\ {\tau _{yz} } \\ \end{array} }} \right\} ^{k}=\left[ {{\begin{array}{lllll} {Q_{11} }&{}\quad {Q_{12} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ {Q_{21} }&{}\quad {Q_{22} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {Q_{66} }&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad {Q_{55} }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {Q_{44} } \\ \end{array} }} \right] ^{k}\left( {\left\{ {{\begin{array}{l} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ {\gamma _{xy} } \\ {\gamma _{zx} } \\ {\gamma _{yz} } \\ \end{array} }} \right\} -\left\{ {{\begin{array}{l} {\alpha _{11} } \\ {\alpha _{22} } \\ 0 \\ 0 \\ 0 \\ \end{array} }} \right\} \Delta T} \right) ^{k} \nonumber \\&\hbox {or }\left\{ \sigma \right\} ^{k}=\left[ Q \right] ^{k}\left\{ {\varepsilon -\alpha \Delta T} \right\} ^{k} \end{aligned}$$
(18)

where \(Q_{11} =E_{11} /(1-\nu _{12} \nu _{21} )\), \(Q_{12} =\nu _{12} E_{22} /(1-\nu _{12} \nu _{21} )\), \(Q_{22} =E_{22} /(1-\nu _{12} \nu _{21} )\), \(Q_{66} =G_{12} \), \(Q_{44} =G_{13} \), and \(Q_{55} =G_{23}\). Additionally, the shear modulus values (\(G_{13} =G_{12}\) and \(G_{23} =1.2G_{12} )\) were defined in [42] and are included for the current computation. Similarly, \(\Delta T\) represents the uniform temperature rise across the plate thickness. Moreover, the superscript “k” associated with the coefficients indicates the face and the core layers (i.e., \(k = 1, 2,\) and 3 defined as the bottom face sheet, the core layer, and the top face sheet, respectively).

2.5 Finite element formulation

FEM has already been proved to be a robust numerical tool and accurate enough to investigate the structural problem allied with the geometrical and material complexities. Based on the capabilities of FEM, the present governing equation of the functionally graded sandwich flat structural panel problem has been discretized via a nine-noded Lagrangian isoparametric element with nine degrees of freedom at each node. After the successful implementation of FEM, the new mid-plane displacement vector \(\left\{ {\lambda _0}\right\} \) of the sandwich structure has been expressed in the form of the nodal displacement vector \(\left\{ {\lambda _{0i}}\right\} \) and the shape functions (\(N_{\mathrm{i}})\) [43]:

$$\begin{aligned} \left\{ {\lambda _0 } \right\} =\sum _{i=1}^9 {N_i \left\{ {\lambda _{0i} } \right\} } \end{aligned}$$
(19)

where “i” is the node number and \(\left\{ {\lambda _{0i} } \right\} =\left[ {u_{0_i } \,v_{0_i } \,w_{0_i } \,\varphi _{x_i }\, \varphi _{y_i } \,\psi _{x_i } \,\psi _{y_i } \,\theta _{x_i }\, \theta _{y_i}}\right] ^{T}\).

The linear and nonlinear mid-plane strain vector in terms of nodal displacement vectors can be rewritten with the help of FEM as [43]

$$\begin{aligned} \left\{ {\bar{{\varepsilon }}_L } \right\} \hbox { }=\hbox { }\left[ B \right] \left\{ {\lambda _{0_i } } \right\} ,\quad \left\{ {\bar{{\varepsilon }}_G } \right\} \hbox { }=\hbox { }\left[ {B_G } \right] \left\{ {\lambda _{0_i } } \right\} \left\{ {\bar{{\varepsilon }}_{NL} } \right\} \hbox { }=\hbox { }\left[ A \right] \left[ G \right] \left\{ {\lambda _{0_i } } \right\} \end{aligned}$$
(20)

where [B], [\(B_{G}\)], and [G] are the linear strain–displacement matrices associated with the shape functions and the differential operators. Similarly, [A] is utilized to define the nonlinear strain and dependent on the linear displacement solution. The details of the individual matrices (e.g., [B], [\(B_{G}\)], [A], and [G]) can be seen in Ref. [44].

2.6 Strain energy

The strain energy functional of a CNT-reinforced functionally graded sandwich plate can be computed using the following formula:

$$\begin{aligned} U=\frac{1}{2}\int \int {\sum _{k=1}^3 {\left[ {\mathop {\int }\limits _{Z_{k-1} }^{Z_k } {\left\{ \varepsilon \right\} ^{T}\left\{ \sigma \right\} \text {d}z} } \right] } } \text {d}x\text {d}y. \end{aligned}$$
(21)

By substituting the values of strain and stress tensors, Eq. (21) can be updated as:

$$\begin{aligned} U=\frac{1}{2}\mathop {\int }\limits _A {\left( {\left\{ {\bar{{\varepsilon }}_l } \right\} ^{T}\left[ {D_1 } \right] \left\{ {\bar{{\varepsilon }}_L } \right\} +\left\{ {\bar{{\varepsilon }}_L } \right\} ^{T}\left[ {D_2 } \right] \left\{ {\bar{{\varepsilon }}_{NL} } \right\} +\left\{ {\bar{{\varepsilon }}_{NL} } \right\} ^{T}\left[ {D_3 } \right] \left\{ {\bar{{\varepsilon }}_L } \right\} +\left\{ {\bar{{\varepsilon }}_{NL} } \right\} ^{T}\left[ {D_4 } \right] \left\{ {\bar{{\varepsilon }}_{NL} } \right\} } \right) } \text {d}A \end{aligned}$$
(22)

where [\(D_{1}\)], [\(D_{2}\)], [\(D_{3}\)], and [\(D_{4}\)] are the material property matrices, and details can be seen in “Appendix D.”

2.7 External work done

The functionally graded sandwich plate is subjected to external mechanical and thermal loading due to the change in environmental temperature. Additionally, the current analysis is utilizing two different types of mechanical loading and denoted as UDL (uniformly distributed load) and SDL (sinusoidal distributed load) as follows:

  1. 1.

    UDL: When the externally applied load is uniformly distributed over the entire plate and evaluated using the loading function as \(q(x,y)=q_0\).

  2. 2.

    SDL: The external mechanical load over the plate is distributed as a sine function and expressed as \(q(x,y)=q_0 \sin (\pi x/a)\sin (\pi y/b)\). The numerical load intensity values will be maximum at the mid of the plate, whereas zero at the edges.

Therefore, the total work done due to the combination of the mechanical and elevated environmental temperature can be calculated using the following mathematical function:

$$\begin{aligned} W=\int \int {\left\{ {\lambda _0 } \right\} ^{T}\left\{ q \right\} \text {d}x\text {d}y} +\int \int {\left( {\left\{ \varepsilon \right\} ^{T}\left[ Q \right] \left\{ {\varepsilon _{th} } \right\} } \right) } \text {d}x\text {d}y. \end{aligned}$$
(23)

2.8 Final governing equation

The variational principle is adopted to obtain the final nonlinear equilibrium equations of the functionally graded sandwich plate under the combined thermomechanical loading. The variational form of the total potential energy functional is expressed as:

$$\begin{aligned} \delta \prod =\delta U-\delta W=0 \end{aligned}$$
(24)

where \(\delta \) is the variational symbol and \(\prod \) is a functional expression of the total potential energy. Now, the final governing equation is further derived by substituting the required values of the internal energy and the work done in Eq. (24). Subsequently, the governing equation is rearranged to the following form:

$$\begin{aligned} \left[ {K_s } \right] \left\{ {\lambda _s } \right\} =\left\{ {F_m } \right\} +\left\{ {F_{th} } \right\} \end{aligned}$$
(25)

where [Ks] and [\(\lambda s\)] are the global system stiffness matrix and the global displacement vector, respectively. Additionally, \(F_{m}\) and \(F_{th}\) signify the global mechanical and thermal load vectors, respectively.

2.9 Solution procedure

Now, Eq. (25) can be solved via the direct iterative method to compute the static central deflection values of the graded CNT-reinforced sandwich structure of various grading patterns. The detailed stepwise implementation of the direct iterative method is provided in the following [8]:

  1. 1.

    Initialization of the individual matrices and calculation of the elemental stiffness matrix and the force vectors by the finite element (FE) step.

  2. 2.

    Further, the FE assembling steps are followed to obtain the global stiffness and force vectors, respectively.

  3. 3.

    Firstly, the linear deflection values are computed without considering the nonlinear stiffness matrices.

  4. 4.

    Now, the final updated stiffness matrix for the deformed plate is constructed using the linear displacement values and proceeds further to obtain the nonlinear deflection values.

  5. 5.

    The above steps (i.e., 1 to 4) are carried out repetitively with the help of the iteration steps until the value reaches the defined convergence. In this present analysis, the convergence criteria are set as \(\left( {\sqrt{(\bar{{W}}_n -\bar{{W}}_{n-1} )^{2}/(\bar{{W}}_n )^{2}}\le \chi } \right) \) (“\(\bar{{W}}\)” is central point deflection, “\(\chi \) = 10\(^{-3}\)” is the convergence tolerance, and “n” is the number of iteration steps, respectively).

3 Results and discussion

The linear and the nonlinear central static deflection values of the graded sandwich CNT-reinforced structure are evaluated numerically with the derived higher-order nonlinear FE model. The nonlinear finite element solutions are computed iteratively via the customized computer code (MATLAB). In this analysis, the core layer of the sandwich structure is assumed to be an isotropic homogeneous material (polymer), and the corresponding temperature-dependent properties are taken the same as those of the source [10], (e.g., \(\rho = 1150\ \hbox {kg/m}^{3}\), \(E^{m} = (3.52 - 0.0034T)\) GPa, and \(\alpha = 45 (1+0.0005 {\Delta T}) \times 10^{-6}\)/K, where \(\Delta T = T- T_{0}\) and \(T_{0} = 300\) K). Similarly, the face sheets of the sandwich structure are made of the SWCNT-reinforced composite, and their temperature-dependent material properties are taken the same as the values of Ref. [16]. Now the elastic constants and the thermal expansion coefficients of the SWCNT are evaluated under the uniform temperature field using the following polynomial expressions:

$$\begin{aligned} \left. {\begin{array}{l} E_{11}^{CNT} (\hbox {TPa}) = 6.3998-4.338417\times 10^{-3}T + 7.43\times 10^{-6}T^{2} - 4.45833\times 10^{-9}T^{3} \\ E_{22}^{CNT} (\hbox {TPa}) = 8.02155-5.420375\times 10^{-3}T + 9.275\times 10^{-6}T^{2} - 5.5625\times 10^{-9}T^{3} \\ G_{12}^{CNT} (\hbox {TPa}) = 1.40755+ 3.476208\times 10^{-3}T - 6.965\times 10^{-6}T^{2} + 4.479167\times 10^{-9}T^{3} \\ \alpha _{11}^{CNT} (10^{-6}/\hbox {K}) = -1.12515+ 0.02291688T - 2.887\times 10^{-5}T^{2} + 1.13625\times 10^{-8}T^{3} \\ \alpha _{22}^{CNT} (10^{-6}/\hbox {K}) = 5.43715- 0.984625\times 10^{-4}T + 2.9\times 10^{-7}T^{2} + 1.25\times 10^{-11}T^{3} \\ \end{array}} \right\} . \end{aligned}$$
(26)

To provide the necessary constraint at the edges, the following type support conditions are utilized at the edges:

  1. (a)

    For simply support condition (S):

    $$\begin{aligned}&v = w = {\varphi }_{y} = {\psi }_{y } = { \theta }_{y} = 0\hbox { at }x = 0, a\hbox { and }\\&u = w = {\varphi }_{x} = {\psi }_{x } = { \theta }_{x} = 0\hbox { at }y = 0, b; \end{aligned}$$
  2. (b)

    For fixed condition (C):

    $$\begin{aligned} u = v = w = {\varphi }_{x} = {\varphi }_{y} = {\psi }_{x } = {\psi }_{y } = {\theta }_{x} = {\theta }_{y} = 0\hbox { for both }x = 0, a \hbox { and }y = 0, b; \end{aligned}$$
  3. (c)

    For free condition (F):

$$\begin{aligned} u \ne v \ne w \ne {\varphi }_{x}\ne {\varphi }_{y} \ne {\psi }_{x }\ne {\psi }_{y }\ne {\theta }_{x} \ne {\theta }_{y} \ne 0\hbox { for both }x = 0, a \hbox { and }y = 0, b. \end{aligned}$$

The linear and the nonlinear bending deflection values of the sandwich plate are normalized using the formula \(\bar{{W}}_c =W_c /h\), where \(W_{c}\) is the deflection of the central point of the plate, h is the total structural thickness, and \(\bar{{W}}_c \) is the normalized central deflection.

3.1 Convergence and validation study

In the finite element analysis, evaluation of the optimal number of mesh divisions for the generation of the desired output is an essential exercise to minimize the total computational cost without hampering the accuracy. In this regard, the convergence test of the derived higher-order numerical model has been carried out for five different core to face thickness ratios (\(h_{c}/h_{f} = 0, 1, 3, 5\), and 10) and four different CNT grading configurations (FG-UU, FG-AV, FG-OO, and FG-XX) and is shown in Fig. 2a, b. The convergence clearly indicates that a (\(6\times 6\)) mesh is adequate enough for the computation of the necessary results.

Fig. 2
figure 2

Results of the FE convergence study of the CNT-reinforced sandwich plate

Full size image

Further, the derived sandwich linear and nonlinear model validity has been established by solving different numerical examples. As a first step, the comparison between the available laminated sandwich plate (0/90/core/90/0) deflections is made with the results computed with the present higher-order model. For the current analysis, the results are calculated for the simply supported sandwich structure including the material and geometrical parameters, the same as the Ref. [45] data, and the sandwich properties are given in Table 1. The computed results are shown in Fig. 3 for the laminated sandwich structure and indicate the accuracy of the current higher-order nonlinear FE model while compared with the source values [45, 46]. The major differences are between the analysis are the kind of mid-plane kinematics and nonlinear strain–displacement relations. The references are adopting von-Kármán type of nonlinear strain without considering all of the higher-order strain terms in the framework of the combinations of mid-plane kinematics model of the face sheets and the core, i.e., classical and Reddy’s higher-order shear deformation theory [45], whereas the second one utilized the normal deformation theory. Moreover, both references solved the nonlinear equilibrium equation using Newton–Raphson’s technique to reduce the computational cost in terms of mid-plane kinematics and to obtain a robust nonlinear solution. The current study adopted the higher-order shear deformation theory in association with Green–Lagrange nonlinear strain, and the nonlinear central deflections are obtained via the direct iterative technique.

Table 1 Material properties of the laminated sandwich plate
Full size table
Fig. 3
figure 3

Comparison of the nonlinear bending behavior of a laminated sandwich plate

Full size image

After the check for laminated sandwich construction, the model is extended to compute the deflection values for the CNTRC structure. In this regard, the linear bending behavior of the square simply supported FG-CNTRC plate structure under the influence of the mechanical UDL is computed (\(h = 0.002\) m, \(a/b = 1\), \(T = 300\) K, \(V_{CNT}^*= 0.14\), and \(q_{0} = 0.1\) MPa) and reported in Table 2 including Ref. [39] data. It can be easily visualized that the present HSDT and the reference FSDT responses are showing good agreement including the simulation data obtained via ANSYS.

Further, the nonlinear transverse deflection values of the FG-CNTRC structural plate examples have been solved using the current higher-order model and compared with the previously published results. Currently, the central deflection values are obtained including reference data provided in Table 3. The required static deflection analysis is performed for two thickness ratios (\(a/h = 10\) and 20) by considering the associated geometrical (\(a/b = 1\)) and the material parameters (\(V_{CNT}^*= 0.17\)) as same as reference [7] under the mechanical UDL at ambient condition (\(T = 300\) K). The comparison study indicates the differences between the present deflection and the published data within an acceptable range (i.e., the deviations are below 4% for almost each case of loading except for the small loading amplitude). The current model is based on the HSDT kinematics with nine degrees of freedom at each node in association with the full geometrical nonlinearity (Green–Lagrange strain) for the large deformation part, whereas the reference utilized Reddy’s (seven degrees of freedom at each node by imposing the zero shear stress at top and bottom) displacement field model in conjunction with von-Kármán nonlinearity.

Table 2 Comparison of normalized central deflection of the FG-CNTRC plate
Full size table
Table 3 Comparison of nonlinear central point deflection of the FG-CNTRC plate
Full size table
Fig. 4
figure 4

Comparison of normalized in-plane stress \(\bar{{\sigma }}_{xx} =\sigma _{xx} h^{2}/\left( {\left| {q_0 } \right| a^{2}} \right) \) of the FG-CNTRC plate

Full size image

Based on the required comparison of the deflection (linear and nonlinear) values, the model has been extended to show the precision further by validating the results with available stress values. In this regard, the normalized in-plane stress \(\bar{{\sigma }}_{xx} =\sigma _{xx} h^{2}/\left( {\left| {q_0 } \right| a^{2}} \right) \) parameters are evaluated numerically for two grading configurations (FG-X and FG-O) of the sandwich structural plate configuration and compared with previously published results [39] using similar input parameters (i.e., \(h = 0.002\) m, \(a/h = 50\), \(a/b = 1\), \(T = 300\) K, \(V_{CNT}^*= 0.17\), and \(q_{0} = 0.1\) MPa) as in the Reference. The current and the reference values are plotted in Fig. 4, and the comparison indicates that the derived higher-order model is also suitable to provide the stresses including the deflection parameter.

3.2 Parametric study

The convergence study indicates the consistency of the developed nonlinear model, whereas the comparison shows the accuracy level. Further, the derived model is utilized to compute the deflection parameter via solving several numerical examples to explore either the individual or the combined effect on the deflection responses. For the computation of new results, the sandwich thickness is set to be 5 mm, if not stated otherwise.

Example 1

The effect of various grading configurations on the transverse flexural strength (linear and nonlinear) of the functionally graded sandwich plate is investigated in this example. Figure 5 shows the effect of four-type CNT grading pattern on the bending values of a simply supported square (\(a/b = 1\)) sandwich structure (\(a/h = 50\), \(V_{CNT}^*= 0.17\), \(h_{{c}}/h_{f} = 1\)) at ambient environmental (\(T = 300\) K) condition. The results indicate that the deflection values are following an increasing trend with respect to the load (mechanical UDL) values regardless of the grading pattern of the face sheets. Also, the figure indicates that FG-\(\Lambda \)V type of CNT grading configuration (face sheet) type of sandwich plate is the stiffest configuration while compared to the other three grading types.

Fig. 5
figure 5

Effect of CNT grading configurations on normalized central deflection of the FG-CNTRC plate

Full size image

Example 2

The fiber-reinforced composite structural strength and the stiffness values largely depend on the fiber fraction. Hence, to investigate the similar kind of behavior the current example reported the flexural strength of a CNT-reinforced sandwich structure under two types of mechanical loading (UDL and SDL) and is plotted in Fig. 6 a, b for three different volume fractions of CNT (\(V_{CNT}^*= 0.12\), 0.17, and 0.28). The linear and nonlinear normalized deflection values of the FG-\(\Lambda \)V type of graded sandwich plate are computed by considering the necessary geometrical parameters say, \(a/b=1\), \(a/h=50\), \(T=300\) K, and \(h_{c}/h_{f}=1\). The normalized values of the central deflection parameters follow an increasing slope with the increment of the load factor, whereas the deflection maintains all-time low for the higher CNT fractions (i.e., \(V_{CNT}^*=0.28\)). The deflection values are higher under the influence of the mechanical UDL while compared to the SDL-type loading. This is mainly because the UDL covers the total surface area in comparison with the SDL.

Fig. 6
figure 6

Effect of CNT volume fraction on normalized central deflection of the FG-CNTRC plate

Full size image

Example 3

In this example the effect of the core to face thickness ratios (\(h_{c}/h_{f})\) on the nonlinear transverse deflection values of the simply supported graded (FG-\(\Lambda \)V) sandwich plate are analyzed and presented in Fig. 7. The numerical results are evaluated for four different values of the core to face thickness ratios (\(h_{c}/h_{f}=0\), 1, 3, and 5) including the additional parameters as \(a/b=1\), \(a/h=50\), \(T=300\) K, and \(V_{CNT}^*=0.17\) under the UDL type of loading. Figure 7 illustrates that the linear and nonlinear central deflection values of the sandwich plate are increasing during the rise of \(h_{c}/h_{f}\). The well-known fact related to the sandwich structure is that the face sheets are stiffer in comparison with the core layer, and \(h_{c}/h_{f}\) increases (i.e., the face sheets become thin), while the structural stiffness reduces further.

Fig. 7
figure 7

Effect of core to face thickness ratio on normalized central deflection of the FG-CNTRC plate

Full size image

Example 4

The effect of variable thickness ratios (\(a/h = 10\), 20, 30, 40, 50, and 60) and the end support conditions (CCCC, CSCS, SSSS, and CCCF) on the deflection parameters of the graded sandwich construction (FG-\(\Lambda \)V) are examined in this example and plotted in Fig. 8. The numerical analysis has been performed by taking the simple or the combination of end constraints, including the mechanical load (UDL and SDL) of intensity \(q_{0}=0.1\) MPa and the associated geometrical parameters (\(a/b=1\), \(V_{CNT}^*=0.17\), \(h_{c}/h_{f}=1\)) under ambient condition (\(T=300\) K). The deflection values are higher for the CCCF support under the UDL whereas lower for the clamped (CCCC) sandwich panel under the SDL loading. Additionally, the flexural strength values are following an increasing trend, while the thickness ratio values increase as expected.

Fig. 8
figure 8

Effect of thickness ratio and support conditions on normalized central deflection of the FG-CNTRC plate

Full size image

Example 5

Figure 9 illustrates the linear and the nonlinear normalized central deflection parameter of the simply supported CNT-reinforced graded (FG-\(\Lambda \)V) thin (\(a/h=50\)) sandwich structure for variable aspect ratios (\(a/b=1\), 1.5, 2, and 2.5) under different mechanical loading intensities (\(q_{0}=0.1\), 0.2, 0.4, 0.6, 0.8, and 1 MPa). The results follow a descending trend, while the aspect ratio values increase and the deflection parameters are within the expected line for both the linear and nonlinear cases. It is important to discuss that the thickness of the sandwich construction is fixed throughout the analysis, and a / h also is fixed for the current example. Therefore, the aspect ratio increases which indicates that the structural width (b) decreases (i.e., the total area of load intensity decreases), and the results follow the desired path.

Fig. 9
figure 9

Effect of aspect ratio on normalized central deflection of the FG-CNTRC plate

Full size image

Example 6

In this example, the effect of temperature (\(T=300\) K, 500 K, and 700 K) distribution and variable mechanical UDL (\(q_{0 }= 0.1\), 0.2, 0.4, 0.6, 0.8, and 1.0 MPa) on the nonlinear deflection behavior of the simply supported FG-\(\Lambda \)V graded sandwich plate structure is explored. Additionally, the properties of individual material of the sandwich construction (i.e., CNT and polymer material) are taken to be temperature-dependent. The responses are obtained via the currently developed higher-order nonlinear numerical model using the associated input parameter as \(a/b=1\), \(a/h=50\), \(h_{c}/h_{f}=1\), and \(V_{CNT}^*=0.17\) and presented in Fig. 10. The Figure indicates that the linear and the nonlinear transverse deflection parameters are following an increasing path in a progressive manner, while the environmental temperature increases. This is because of the well-known reason that the structural stiffness degrades while exposed to an elevated environmental temperature.

Fig. 10
figure 10

Effect of thermomechanical loading on normalized central deflection of the FG-CNTRC plate

Full size image

Example 7

To evaluate the effect of temperature (\(T = 300\) K, 400 K and 500 K), temperature-dependent properties, and grading patterns (FG-UU and FG-\(\Lambda \)V) on the normalized thermomechanical bending stress values of the CNT-reinforced sandwich structure are computed in this example and plotted in Fig. 11. The stresses are computed for the clamped square sandwich structure (\(a/h = 50\)) under UDL type of mechanical loading (\(q_{0} = 0.1\) MPa) including the different temperature environments. From the pattern of stress distribution, it is clearly understood that the stress values of an FG-\(\Lambda \)V type of sandwich follow a smooth variation from the top to the bottom faces irrespective of the input parameter. However, a sharp jump of the stresses can be observed for FG-UU grading at the interface between the core and the face due to the CNT concentration. Hence, FG-\(\Lambda \)V type of graded sandwich structures is preferred over UD construction while exposed to high bending stress. Additionally, an interesting conclusion can be made that the stress values are not varying much for the different elevated thermal environments, although the constituent properties depend on temperature. This is because of the fact that the assumed constitutive relation is utilized in the current analysis.

Fig. 11
figure 11

Normalized in-plane stress (\(\bar{{\sigma }}_{xx} =\sigma _{xx} h^{2}/\left( {\left| {q_0 } \right| a^{2}} \right) )\) of the FG-CNTRC plate

Full size image

4 Conclusions

The current research reported the nonlinear FE solutions of the transverse flexural deflection and the stress values of the FG-CNT-reinforced sandwich plate structure under two types of mechanical loading (UDL and SDL) and uniform thermal environment. For the numerical analysis purpose, a nonlinear higher-order mathematical model is derived including the temperature-dependent properties of the sandwich constituents (i.e., CNT and polymer) and Green–Lagrange geometrical strain to include the large deformation characteristics. The mathematical model has been utilized to derive a suitable MATLAB code for the computation of the deflection values including the direct iterative method. Further, the linear and the nonlinear flexural responses are explored for the different design parameters and the ambient as well as the elevated environmental effect. Subsequently, the inferences related to the obtained deflection values are discussed in the following including the model accuracy:

  1. (a)

    The convergence characteristics and the validity study of the present higher-order nonlinear FE solutions are established via solving several numerical examples.

  2. (b)

    The normalized central deflection parameters follow an ascending path, while the thickness ratio, the core to face thickness ratio, and the temperature load are increasing. However, the bending deflection shows a decremental behavior for the higher aspect ratio and the volume fraction of CNT.

  3. (c)

    The computational deflection values clearly show that the FG-\(\Lambda \)V-type graded sandwich construction is the stiffest configuration when compared to three other configurations regardless of the loading type, the temperature effect, and variable geometrical parameter.

  4. (d)

    Similarly, the deflection values of the clamped sandwich structure are showing the minimum values due to the stiffer configuration, and the results follow the expected line.

  5. (e)

    The static deflections bending values under the mechanical UDL are higher than in the SDL case. It is because of the fact that UDL is distributed over the entire surface of the sandwich structure, whereas part loading is experienced by the structure under the SDL.

  6. (f)

    Also, the stress analysis indicates that the configurations consisting of higher fractions of CNT volume either at the top or at the bottom of the plate are capable of resisting the higher amount of the normal stresses.