Examination of the high-frequency behavior of functionally graded porous nanobeams using nonlocal simple higher-order shear deformation theory

Abstract

The primary objective of this paper is to examine the free vibration behaviors of functionally graded nanobeams with porosity while considering nonlocal parameters. The nanobeams are built of functionally graded materials, having material features that change smoothly over the beam’s thickness. To illustrate how porosity is distributed throughout the body of the beams, four different forms of porosity distribution are taken into consideration. Eringen’s nonlocal parameter elasticity theory and Hamilton’s principle are used to establish the governing equations of the motion of the functionally graded porous nanobeams. Then, the closed-form solution of Navier is used to solve the eigenvalue problems to find the frequencies of the functionally graded porous nanobeams. A comprehensive parametric study is also carried out to demonstrate the influence of geometric parameters, material gradient index, and nonlocal parameters on low- and high-frequency vibration behaviors of the functionally graded porous nanobeams. The results of the vibration of the functionally graded porous nanobeams undergoing the low- and high-frequency conditions can serve as benchmarks for applications of such structures in engineering and for future work.

1 Introduction

Functionally graded materials (FGMs) have drawn a lot of interest recently because of their numerous uses and distinctive mechanical characteristics [1,2,3]. FGMs exhibit a spatial variation in composition, resulting in tailored properties that can be manipulated to optimize performance across a range of engineering and scientific specialties. The study of FGMs has paved the way for innovative solutions in fields such as aerospace engineering, structural mechanics, biomechanics, and nanotechnology [4,5,6,7,8,9,10,11,12]. Particularly intriguing are functionally graded (FG) nanostructures, which extend these advantages to the nanoscale, enabling enhanced material functionality and novel applications.

The analysis of nanostructures, including nanoplates, nano-shells, and nanobeams, has been the subject of intensive research. Various theories have been employed to study their mechanical behavior, ranging from classical elasticity to more advanced approaches that account for size-dependent and nonlocal effects [13,14,15]. These theories have revealed a capital of insights into the mechanics of nanostructures, shedding light on phenomena such as size-dependent stiffness, surface effects, and nonlocal behavior [16,17,18]. Therefore, understanding the vibration characteristics of nanostructures has become essential for designing and optimizing nanoscale devices and systems.

In recent years, investigating the vibration problems in nanostructures has become particularly prominent. Nanobeams, which have become fundamental building blocks in many nanoscale applications, have been of particular interest. Notably, FG nanobeams exhibit distinct behavior because of the gradual variation of material features through the thickness. Eringen [19,20,21,22] provided the differential constitutive model and integral constitutive model of the nonlocal elasticity theory (NET), which has been applied by many scientists to analyze nanostructures. By using NET, the nonlocal bending, free vibration, and buckling behaviors of the isotropic and FG nanobeams have been investigated extensively by Eltaher et al. [23], Thai et al. [24], Rahmani et al. [25], Arefi et al. [26], Gholami et al. [27]. Ebrahimi et al. [28,29,30,31], and Karami et al. [32]. The effects of the hygrothermal, piezoelectricity, magneto-piezoelectricity, and flexoelectricity on the mechanical behaviors of the nanobeams were also investigated carefully. The results of these studies also show that the nonlocal parameters have significant effects on the behaviors of the nanostructures.

It is noticed that the integration of porosity into these structures leads to an additional level of complexity, affecting their mechanical response. Therefore, examining the mechanical behaviors of porous nanobeams has become the focus of researchers’ attention. Several studies on the effects of porosity were caried out, for example, Aria et al. [33], Ghobadi et al. [34], Ebrahimi et al. [35], Wang et al. [36, 37], Faghidian et al. [38], Civalek et al. [39], Rastehkenari et al. [40], Chandel et al. [41], Hadji et al. [42], and Akbas [43], and so on. More details on the analysis of the FG nanobeams with and without porosity are reported in the studies of Numanoğlu et al. [44], Şimşek [45], Barati et al. [46], and their references. In those studies, NET and nonlocal strain gradient theory were applied to consider for small-scale effects. The outcomes of these works also demonstrated that the distribution of porosity and coefficient of porosity plays a significant role in the behaviors of the nanostructures.

Consequently, the results of above-mentioned works showed that porosity has considerable influences on the dynamic responses of the FG porous nanobeams and should be investigated more. Additionally, in the above-mentioned studies, only some first modes of the nanobeams, especially the fundamental mode, were investigated. Therefore, despite the growing body of knowledge in this area, a comprehensive study of the vibration behavior of FG porous nanobeams, especially undergoing high-frequency conditions considering the influence of nonlocal parameters, remains an important research gap. Therefore, the present study aims to report this problem by analyzing the free vibration behaviors of FG nanobeams, including porosity, while considering the effects of nonlocal parameters. This investigation not only contributes to the understanding the vibration behavior of FG porous nanobeams but also provides insights into the influence of geometric parameters, material gradient index, and nonlocal parameters on their low- and high-frequency vibration characteristics. The obtained results offer valuable benchmarks for the engineering applications of such structures and guide future research endeavors. By exploring the effects of porosity and considering various material property gradients, this research advances the knowledge base in the field of nano-mechanics and offers practical insights for the design and optimization of nanoscale devices and systems.

2 Theoretical formulation of the problem

2.1 Functionally graded porous nanobeams

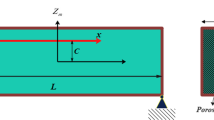
In this study, as presented in Fig. 1, an FG porous nanobeam is considered. The porosity distributes through the volume of the nanobeam, with uniform distribution through the longitudinal direction, and non-uniform through the thickness of the nanobeams. The beam’s height is $h$, and the beam’s length is $L$.

Fig. 1

The model of the FG nanobeams

The variation of the material characteristics along the thickness of the FG porous nanobeams can be estimated using the simple mixing rule. For the perfect FG nanobeams

$$\begin{gathered} E(z) = E_{{\text{m}}} + \left( {E_{{\text{c}}} - E_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} \hfill \\ \rho (z) = \rho_{{\text{m}}} + \left( {\rho_{{\text{c}}} - \rho_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} \hfill \\ \nu (z) = \nu_{{\text{m}}} + \left( {\nu_{{\text{c}}} - \nu_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} \hfill \\ \end{gathered}$$

(1)

where subscripts $c,\;m$ denote the ceramic and metal phases, respectively, $k$ is the material gradient index, and $E,\;\rho ,\;\nu$ represent the Young’s modulus, mass density, and Poisson’s ratio of material, respectively.

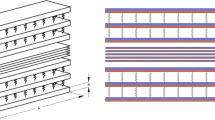
The manufacturing process of sintering, which is common in the production of FGMs, is responsible for the formation of voids or porosities within the materials. On the other hand, FGMs can be further improved in terms of weight reduction and energy absorption by introducing porosity while maintaining a significant amount of its strength. Besides, FG porous media can be utilized in several engineering applications, such as enhanced filtration, the automotive industry, and medical implants. Therefore, it is important to introduce the porosity effects at the analysis, testing, and design stage of the FG structures. The distribution of porosity in FG structures can be random or regular. In this study, four common types of distributions, called Type I, II, III, and IV, are utilized to consider the effects of the porosity on the change of the material properties of the FG nanobeams. These distributions are given by the following formulae [47].

$$\left\{ {\begin{array}{*{20}l} {{\text{Type}}\;{\text{I}}\;\;\;{:}} \hfill & {p(z) = P_{0} \cos \left[ {\frac{\pi }{2}\left( {\frac{z}{h} - 0.5} \right)} \right]} \hfill \\ {{\text{Type}}\;{\text{II}}\;\;{:}} \hfill & {p(z) = P_{0} \cos \left[ {\frac{\pi }{2}\left( {\frac{z}{h} + 0.5} \right)} \right]} \hfill \\ {{\text{Type}}\;{\text{III:}}} \hfill & {p(z) = P_{0} \cos \left[ {\pi \left( \frac{z}{h} \right)} \right]} \hfill \\ {{\text{Type}}\;{\text{IV:}}} \hfill & {p(z) = P_{0} - P_{0} \cos \left[ {\pi \left( \frac{z}{h} \right)} \right]} \hfill \\ \end{array} } \right.$$

(2)

where $p(z)$ is the function that demonstrates the porosity distribution throughout the thickness of the FG porous nanobeams, and $P_{0}$ is the maximum porosity coefficient. The illustration of the functions of the porosity distributions are presented in Fig. 2.

Fig. 2

The porosity distribution throughout the thickness of the FG porous nanobeams

The effective material characteristics of the FG porous nanobeams are computed as follows:

$$\begin{gathered} E(z) = \left[ {E_{{\text{m}}} + \left( {E_{{\text{c}}} - E_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} } \right]\left( {1 - p(z)} \right) \hfill \\ \rho (z) = \left[ {\rho_{{\text{m}}} + \left( {\rho_{{\text{c}}} - \rho_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} } \right]\left( {1 - p(z)} \right) \hfill \\ \end{gathered}$$

(3)

According to some published works, the effects of the Poisson’s ratio on the mechanical behaviors of the structures are small [48,49,50]; therefore, in this study, the Poisson’s ratio is assumed to be independent of porosity. Figure 3 shows the variation of the effective Young’s modulus, $E(z)$, through the thickness of the FG porous nanobeams with $E_{{\text{c}}} {/}E_{{\text{m}}} = 10$.

Fig. 3

The variation of effective Young’s modulus throughout the thickness of the FG porous nanobeams

2.2 The simple higher-order shear beam theory

To establish the equations of motion of the FG porous nanobeams, a simple higher-order shear deformation theory [51] is used; therefore, the displacement fields of the FG porous nanobeams are as follows:

$$\begin{gathered} u(x,z,t) = u(x,t) - z\frac{{\partial w_{b} (x,t)}}{\partial x} - f(z)\frac{{\partial w_{s} (x,t)}}{\partial x} \hfill \\ w(x,z,t) = w_{b} (x,t) + w_{s} (x,t) \hfill \\ \end{gathered}$$

(4)

where $u(x,t)$ denotes the axial displacement, $w_{{\text{b}}} (x,t)$ and $w_{{\text{s}}} (x,t)$ describe the bending and shear parts of the transverse displacement of a point at the midplane of the beams. The bending part $w_{{\text{b}}} (x,t)$ is assumed to be similar to the displacement of the classical beam theory; the shear part $w_{{\text{s}}} (x,t)$ gives rise to the nonlinear variation of the shear strain $\gamma_{xz}$ and hence to the shear stress $\tau_{xz}$ through the thickness of the beams in such a way that the shear stress $\tau_{xz}$ satisfies free condition at the top and bottom surfaces of the beams. The formulation of $f(z)$ is chosen to fulfill the free condition of the shear stress on the top and bottom surfaces of the FG porous nanobeams. In this study, the function $f(z)$ is chosen as follows [52]:

$$f(z) = \frac{{5z^{3} }}{{3h^{2} }} - \frac{z}{h}$$

(5)

The strain fields of the FG porous nanobeams can be expressed as follows:

$$\begin{gathered} \varepsilon_{x} = \frac{\partial u}{{\partial x}} - z\frac{{\partial^{2} w_{{\text{b}}} }}{{\partial x^{2} }} - f\frac{{\partial^{2} w_{{\text{s}}} }}{{\partial x^{2} }} \hfill \\ \gamma_{xz} = g\frac{{\partial w_{{\text{s}}} }}{\partial x} \hfill \\ \end{gathered}$$

(6)

where

$$g(z) = 1 - \frac{{{\text{d}}f(z)}}{{{\text{d}}z}}$$

(7)

It is evident that the simple higher-order shear deformation theory involves only three unknowns, similar to the conventional first-order shear deformation beam theory. In contrast, other higher-order shear deformation beam theories often employ four, five, or even more unknowns. The utilization of a polygonal function, denoted as $f(z)$, introduces nonlinearity in the distribution of transverse shear strain and stress throughout the thickness direction. This polygonal function effectively satisfies traction-free boundary conditions on the top and bottom surfaces of the beam, eliminating the need for a shear correction factor—a factor dependent on material gradient, as noted by Nguyen et al. [53] and Menaa et al. [54]. In comparison to other functions like hyperbolic, trigonometric, or exponential functions, the polygonal function stands out for its simplicity and ability to yield a high convergence rate during integration through the thickness of the beam.

2.3 Nonlocal constitutive relations

To consider the small-scale influences on the mechanical behaviors of the FG porous nanobeams, Eringen’s nonlocal theory [19,20,21,22] is adopted herein. According to Eringen’s nonlocal theory, the stress at a location is determined by the stresses at all of the body’s neighboring points; hence, the nonlocal stress tensor $\sigma_{ij}^{nl}$ at a point $x$ is obtained via the local stress tensor $\sigma_{ij}^{l}$ as the following formula

$$\sigma_{ij}^{nl} = \int\limits_{V} {\alpha \left( {\left| {{\mathbf{x}}^{{\mathbf{\prime }}} - {\mathbf{x}}} \right|,\tau } \right)\sigma_{ij}^{l} {\text{d}}V({\mathbf{x}}^{{\mathbf{\prime }}} )}$$

(8)

where $\alpha$ is the kernel function, which contains the small-scale effects incorporating into constitutive equations the nonlocal effects at the reference point ${\mathbf{x}}$ produced by local strain at the source ${\mathbf{x}}^{{\mathbf{\prime }}}$. This function depends on two variables $\left| {{\mathbf{x}}^{{\mathbf{\prime }}} - {\mathbf{x}}} \right|$ and $\tau$, where $\left| {{\mathbf{x}}^{{\mathbf{\prime }}} - {\mathbf{x}}} \right|$ is the distance in Euclidean form, $\tau = e_{0} a{/}L$ is a material constant that depends on internal and external characteristic length (such as the lattice spacing and wavelength). The parameter $e_{0}$ is vital for the validity of nonlocal models. This parameter is determined by matching the dispersion curves based on atomistic models. The classical stress tensor is defined as follows:

$$\sigma_{ij}^{l} = C_{ijkl} :\varepsilon_{kl}$$

(9)

where $C_{ijkl}$ denote the fourth order elasticity tensor. By choosing the appropriate kernel function, Eringen showed that the nonlocal constitutive equation in integral form can be represented in an equivalent differential form as

$$(1 - \mu \nabla^{2} )\sigma_{ij}^{nl} = \sigma_{ij}^{l}$$

(10)

where $\mu = (e_{0} a)^{2}$ is the nonlocal parameter, which includes the small-scale effect. The nonlocal constitutive relation for a nonlocal beam may be expressed as follows:

$$\left( {1 - \mu \nabla^{2} } \right)\left\{ \begin{gathered} \sigma_{x} \hfill \\ \tau_{xz} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {\Theta_{11} } & 0 \\ 0 & {\Theta_{55} } \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \gamma_{xz} \hfill \\ \end{gathered} \right\}$$

(11)

where

$$\Theta_{11} = E(z),\;\Theta_{55} = G(z) = \frac{E(z)}{{2(1 + \nu (z))}}$$

(12)

2.4 Equations of motion in terms of displacements

The following application of Hamilton’s principle is used to generate the equations of motion of the FG porous nanobeams:

$$0 = \int\limits_{0}^{T} {\left( {\delta \Pi - \delta T} \right){\text{d}}t}$$

(13)

where $\delta \Pi$ and $\delta T$ are the variations of the strain energy and the kinetic energy, respectively.

The variation of the strain energy can be obtained as the follow:

$$\delta \Pi = \int\limits_{0}^{L} {\int\limits_{A} {\left( {\sigma_{x} \delta \varepsilon_{x} + \tau_{xz} \delta \gamma_{xz} } \right){\text{d}}A{\text{d}}x} }$$

(14)

After some mathematical operations and simplifications, one gets the following equation:

$$\delta \Pi = \int\limits_{0}^{L} {\left( {N\frac{\partial \delta u}{{\partial x}} - M\frac{{\partial^{2} \delta w_{{\text{b}}} }}{{\partial x^{2} }} - P\frac{{\partial^{2} \delta w_{{\text{s}}} }}{{\partial x^{2} }} + Q\frac{{\partial \delta w_{{\text{s}}} }}{\partial x}} \right)} {\text{d}}x$$

(15)

where $N,\;M,\;P$ and $Q$ are the stress resultants which can be calculated by

$$\begin{gathered} N = \int\limits_{A} {\sigma_{x} {\text{d}}A} ;\;M = \int\limits_{A} {z\sigma_{x} {\text{d}}A} ; \hfill \\ P = \int\limits_{A} {(f)\sigma_{x} {\text{d}}A} ;\;Q = \int\limits_{A} {(g)\tau_{xz} {\text{d}}A} \hfill \\ \end{gathered}$$

(16)

The variation of the kinetic energy of the FG nanobeams can be expressed as follows:

$$\delta T = \int\limits_{0}^{L} {\int\limits_{A} {\left( {\dot{u}\delta \dot{u} + \dot{w}\delta \dot{w}} \right)\rho {\text{d}}A{\text{d}}x} }$$

(17)

$$\begin{gathered} \delta T = \int\limits_{0}^{L} {\int\limits_{A} {\left( {\dot{u} - z\frac{{\partial \dot{w}_{{\text{b}}} }}{\partial x} - f\frac{{\partial \dot{w}_{{\text{s}}} }}{\partial x}} \right)\rho (z)\left( {\delta \dot{u} - z\frac{{\partial \delta \dot{w}_{{\text{b}}} }}{\partial x} - f\frac{{\partial \delta \dot{w}_{{\text{s}}} }}{\partial x}} \right)} } \hfill \\ \quad \quad \quad + \left( {\dot{w}_{{\text{b}}} + \dot{w}_{{\text{s}}} } \right)\rho \left( {\delta \dot{w}_{{\text{b}}} + \delta \dot{w}_{{\text{s}}} } \right){\text{d}}A{\text{d}}x \hfill \\ \end{gathered}$$

(18)

After some mathematical operations and simplifications, one gets the following equation:

$$\begin{gathered} \delta T = \int\limits_{0}^{L} {\left[ {I_{0} \left( {\dot{u}\delta \dot{u} + (\dot{w}_{{\text{b}}} + \dot{w}_{{\text{s}}} )(\delta \dot{w}_{{\text{b}}} + \delta \dot{w}_{{\text{s}}} )} \right)} \right.} + I_{1} \left( {\dot{u}\frac{{\partial \delta \dot{w}_{{\text{b}}} }}{\partial x} + \frac{{\partial \dot{w}_{{\text{b}}} }}{\partial x}\delta \dot{u}} \right) + I_{2} \left( {\dot{u}\frac{{\partial \delta \dot{w}_{{\text{s}}} }}{\partial x} + \frac{{\partial \dot{w}_{{\text{s}}} }}{\partial x}\delta \dot{u}} \right) \hfill \\ \quad \quad \quad + I_{3} \left( {\frac{{\partial \dot{w}_{{\text{b}}} }}{\partial x}\frac{{\partial \delta \dot{w}_{{\text{b}}} }}{\partial x}} \right) + I_{4} \left( {\frac{{\partial \dot{w}_{{\text{b}}} }}{\partial x}\frac{{\partial \delta \dot{w}_{{\text{s}}} }}{\partial x} + \frac{{\partial \dot{w}_{{\text{s}}} }}{\partial x}\frac{{\partial \delta \dot{w}_{{\text{b}}} }}{\partial x}} \right)\left. { + I_{5} \left( {\frac{{\partial \dot{w}_{{\text{s}}} }}{\partial x}\frac{{\partial \delta \dot{w}_{{\text{s}}} }}{\partial x}} \right)} \right]{\text{d}}x \hfill \\ \end{gathered}$$

(19)

where

$$\begin{gathered} I_{0} = \int\limits_{A} {\rho (z){\text{d}}A} ;\;I_{1} = \int\limits_{A} {\rho (z)\left( { - z} \right){\text{d}}A} ;\;I_{2} = \int\limits_{A} {\rho (z)\left( { - f} \right){\text{d}}A} ; \hfill \\ I_{3} = \int\limits_{A} {\rho (z)\left( {z^{2} } \right){\text{d}}A} ;\;I_{4} = \int\limits_{A} {\rho (z)\left( {zf} \right){\text{d}}A} ;\;I_{5} = \int\limits_{A} {\rho (z)\left( {f^{2} } \right){\text{d}}A} \hfill \\ \end{gathered}$$

(20)

Substituting Eqs. (15) and (19) into Eq. (13) and integrating by parts, the equilibrium equations of the FG porous nanobeams are found as follows:

$$\begin{gathered} \delta u:\; - \frac{\partial N}{{\partial x}} = - I_{0} \ddot{u} - I_{1} \frac{{\partial \ddot{w}_{{\text{b}}} }}{\partial x} - I_{2} \frac{{\partial \ddot{w}_{{\text{s}}} }}{\partial x}; \hfill \\ \delta w_{{\text{b}}} : - \frac{{\partial^{2} M}}{{\partial x^{2} }} = - I_{0} (\ddot{w}_{{\text{b}}} + \ddot{w}_{{\text{s}}} ) + I_{1} \frac{{\partial \ddot{u}}}{\partial x} + I_{3} \frac{{\partial^{2} \ddot{w}_{{\text{b}}} }}{{\partial x^{2} }} + I_{4} \frac{{\partial^{2} \ddot{w}_{{\text{s}}} }}{{\partial x^{2} }}; \hfill \\ \delta w_{{\text{s}}} : - \frac{{\partial^{2} P}}{{\partial x^{2} }} - \frac{\partial Q}{{\partial x}} = - I_{0} \left( {\ddot{w}_{{\text{b}}} + \ddot{w}_{{\text{s}}} } \right) + I_{2} \frac{{\partial \ddot{u}}}{\partial x} + I_{4} \frac{{\partial^{2} \ddot{w}_{{\text{b}}} }}{{\partial x^{2} }} + I_{5} \frac{{\partial^{2} \ddot{w}_{{\text{s}}} }}{{\partial x^{2} }}. \hfill \\ \end{gathered}$$

(21)

The boundary conditions of the present theory are as follows:

$$\begin{array}{*{20}l} {{\text{Specify}}} \hfill & u \hfill & {{\text{or}}} \hfill & N \hfill \\ {{\text{Specify}}} \hfill & {w_{{\text{b}}} } \hfill & {{\text{or}}} \hfill & {V_{{\text{b}}} \equiv \frac{\partial M}{{\partial x}} + I_{3} \frac{{\partial \ddot{w}_{{\text{b}}} }}{\partial x}} \hfill \\ {{\text{Specify}}} \hfill & {w_{{\text{s}}} } \hfill & {{\text{or}}} \hfill & {V_{{\text{s}}} \equiv \frac{\partial P}{{\partial x}} + Q + I_{5} \frac{{\partial \ddot{w}_{{\text{s}}} }}{\partial x}} \hfill \\ {{\text{Specify}}} \hfill & {\frac{{\partial w_{{\text{b}}} }}{\partial x}} \hfill & {{\text{or}}} \hfill & M \hfill \\ {{\text{Specify}}} \hfill & {\frac{{\partial w_{{\text{s}}} }}{\partial x}} \hfill & {{\text{or}}} \hfill & P \hfill \\ \end{array}$$

(22)

By substituting Eq. (6) into Eq. (11) and the subsequent results into Eq. (16), the stress resultants of the FG porous nanobeams are obtained as follows

$$\left\{ \begin{gathered} N \hfill \\ M \hfill \\ P \hfill \\ \end{gathered} \right\} - \mu \nabla^{2} \left\{ \begin{gathered} N \hfill \\ M \hfill \\ P \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} A &\quad B &\quad C \\ B & D & E \\ C & E & F \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}}} \\ { - \frac{{\partial^{2} w_{{\text{b}}} }}{{\partial x^{2} }}} \\ { - \frac{{\partial^{2} w_{{\text{s}}} }}{{\partial x^{2} }}} \\ \end{array} } \right\}$$

(23)

$$Q - \mu \nabla^{2} Q = S\frac{{\partial w_{{\text{s}}} }}{\partial x}$$

(24)

where

$$\begin{gathered} A = \int\limits_{A} {\Theta_{11} {\text{d}}A} ;\;B = \int\limits_{A} {\Theta_{11} \left( z \right){\text{d}}A} ;\;D = \int\limits_{A} {\Theta_{11} \left( {z^{2} } \right){\text{d}}A} ; \hfill \\ C = \int\limits_{A} {\Theta_{11} \left( f \right){\text{d}}A} ;\;E = \int\limits_{A} {\Theta_{11} \left( {zf} \right){\text{d}}A} ;\;F = \int\limits_{A} {\Theta_{11} \left( {f^{2} } \right){\text{d}}A} \hfill \\ \end{gathered}$$

(25)

$$S = \int\limits_{A} {\Theta_{55} \left( g \right)^{2} {\text{d}}A}$$

(26)

Inserting Eqs. (23) and (24) into Eq. (21), the equations of motion of the FG porous nanobeams in terms of displacements are obtained as:

$$\begin{gathered} \delta u:\;A\frac{{\partial^{2} u}}{{\partial x^{2} }} - B\frac{{\partial^{3} w_{{\text{b}}} }}{{\partial x^{3} }} - C\frac{{\partial^{3} w_{{\text{s}}} }}{{\partial x^{3} }} \hfill \\ \, = \left( {1 - \mu \nabla^{2} } \right)\left( {I_{0} \ddot{u} + I_{1} \frac{{\partial \ddot{w}_{{\text{b}}} }}{\partial x} + I_{2} \frac{{\partial \ddot{w}_{{\text{s}}} }}{\partial x}} \right), \hfill \\ \delta w_{{\text{b}}} :B\frac{{\partial^{3} u}}{{\partial x^{3} }} - D\frac{{\partial^{4} w_{{\text{b}}} }}{{\partial x^{4} }} - E\frac{{\partial^{4} w_{{\text{s}}} }}{{\partial x^{4} }} \hfill \\ \, = \left( {1 - \mu \nabla^{2} } \right)\left( {I_{0} (\ddot{w}_{{\text{b}}} + \ddot{w}_{{\text{s}}} ) - I_{1} \frac{{\partial \ddot{u}}}{\partial x} - I_{3} \frac{{\partial^{2} \ddot{w}_{{\text{b}}} }}{{\partial x^{2} }} - I_{4} \frac{{\partial^{2} \ddot{w}_{{\text{s}}} }}{{\partial x^{2} }}} \right), \hfill \\ \delta w_{{\text{s}}} :C\frac{{\partial^{3} u}}{{\partial x^{3} }} - E\frac{{\partial^{4} w_{{\text{b}}} }}{{\partial x^{4} }} - F\frac{{\partial^{4} w_{{\text{s}}} }}{{\partial x^{4} }} + S\frac{{\partial^{2} w_{{\text{s}}} }}{{\partial x^{2} }} \hfill \\ \, = \left( {1 - \mu \nabla^{2} } \right)\left( {I_{0} \left( {\ddot{w}_{{\text{b}}} + \ddot{w}_{{\text{s}}} } \right) - I_{2} \frac{{\partial \ddot{u}}}{\partial x} - I_{4} \frac{{\partial^{2} \ddot{w}_{{\text{b}}} }}{{\partial x^{2} }} - I_{5} \frac{{\partial^{2} \ddot{w}_{{\text{s}}} }}{{\partial x^{2} }}} \right). \hfill \\ \end{gathered}$$

(27)

3 Analytical solution of the problem

Since this study considers a simply supported FG porous nanobeams, the Navier’s solution method is used to solve the equations of motion, and the following formulas are employed to represent the unknown displacement functions of the beams:

$$\begin{gathered} u(x,t) = \sum\limits_{m = 1}^{\infty } {U_{m} \cos \alpha_{m} x\sin \omega t} \hfill \\ w_{{\text{b}}} (x,t) = \sum\limits_{m = 1}^{\infty } {Wb_{m} \sin \alpha_{m} x\sin \omega t} \hfill \\ w_{{\text{s}}} (x,t) = \sum\limits_{m = 1}^{\infty } {Ws_{m} \sin \alpha_{m} x\sin \omega t} \hfill \\ \end{gathered}$$

(28)

where $\alpha_{m} = m\pi /L$, $\omega$ is the frequency of the nanobeams, $U_{m} ,\;Wb_{m} ,\;Ws_{m}$ are the unknown coefficients.

Substituting Eq. (28) into Eq. (27), the subsequent equation is gotten and the results for vibration behaviors of the FG porous nanobeams are found from the solution of it:

$$\left( {\left[ {\begin{array}{*{20}c} {k_{11} } &\quad {k_{12} } &\quad {k_{13} } \\ {k_{12} } & {k_{22} } & {k_{23} } \\ {k_{13} } & {k_{23} } & {k_{33} } \\ \end{array} } \right] - \omega^{2} \vartheta \left[ {\begin{array}{*{20}c} {m_{11} } &\quad {m_{12} } &\quad {m_{13} } \\ {m_{12} } & {m_{22} } & {m_{23} } \\ {m_{13} } & {m_{23} } & {m_{33} } \\ \end{array} } \right]} \right)\left\{ \begin{gathered} U_{m} \hfill \\ Wb_{m} \hfill \\ Ws_{m} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right\}$$

(29)

where

$$\begin{gathered} k_{11} = \alpha^{2} A;\;k_{12} = - \alpha^{3} B;\;k_{13} = - C\alpha^{3} ; \hfill \\ k_{22} = \alpha^{4} D;\;k_{23} = \alpha^{4} E;\;k_{33} = \alpha^{2} \left( {F\alpha^{2} + S} \right); \hfill \\ m_{11} = I_{0} ;\;m_{12} = I_{1} \alpha ;\;m_{13} = I_{2} \alpha ; \hfill \\ m_{22} = I_{3} \alpha^{2} + I_{0} ;\;m_{23} = I_{4} \alpha^{2} + I_{0} ;\;m_{33} = I_{5} \alpha^{2} + I_{0} ; \hfill \\ \vartheta = \left( {\alpha^{2} \mu + 1} \right). \hfill \\ \end{gathered}$$

(30)

4 Numerical results

In this section, at first illustrative examples regarding the free vibration behaviors of the FG porous beams and FG nanobeams are considered to verify the validity of the existing theory and formulations. Then, the proposed algorithm is applied to study the free vibration behaviors of the FG porous nanobeams, and the high-frequency and of low-frequency behaviors of the FG porous nanobeams are compared. By this way, some new important results are provided to help researchers and engineers understand more clearly the response of the FG porous nanobeams at high-frequency conditions.

4.1 Validations

Firstly, a simply supported FG porous beams made from ${\text{Al}}_{{2}} {\text{O}}_{{3}} {\text{/Al}}$ with the uniform distributed porosity is considered. The material features of the ceramic phase, ${\text{Al}}_{{2}} {\text{O}}_{{3}}$, are $E_{{\text{c}}} = 380\;{\text{GPa}}$, $\rho_{{\text{c}}} = 3960\;{\text{kg/m}}^{{3}}$, $\nu_{{\text{c}}} = 0.3$; for the metal phase, ${\text{Al}}$, are $E_{{\text{m}}} = 70\;{\text{GPa}}$, $\rho_{{\text{m}}} = 2702\;{\text{kg/m}}^{{3}}$, $\nu_{{\text{m}}} = 0.3$, and the length of the beam is $L = 10h$, the nonlocal parameter is given $\mu = 0$ (local beams). Two types of porosity distributions, even and uneven porosity distributions, are considered. The material properties of the FGP beam are expressed as follows:

For even porosity distribution [42]:

$$\begin{gathered} E(z) = \left[ {E_{{\text{m}}} + \left( {E_{{\text{c}}} - E_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} } \right] - \frac{1}{2}P_{0} \left( {E_{{\text{c}}} + E_{{\text{m}}} } \right) \hfill \\ \rho (z) = \left[ {\rho_{{\text{m}}} + \left( {\rho_{{\text{c}}} - \rho_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} } \right] - \frac{1}{2}P_{0} \left( {\rho_{{\text{c}}} + \rho_{{\text{m}}} } \right) \hfill \\ \end{gathered}$$

(31)

For uneven porosity distribution [42]:

$$\begin{gathered} E(z) = \left[ {E_{{\text{m}}} + \left( {E_{{\text{c}}} - E_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} } \right] - \frac{1}{2}P_{0} \left( {E_{{\text{c}}} + E_{{\text{m}}} } \right)\left( {1 - \frac{2|z|}{h}} \right) \hfill \\ \rho (z) = \left[ {\rho_{{\text{m}}} + \left( {\rho_{{\text{c}}} - \rho_{{\text{m}}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} } \right] - \frac{1}{2}P_{0} \left( {\rho_{{\text{c}}} + \rho_{{\text{m}}} } \right)\left( {1 - \frac{2|z|}{h}} \right) \hfill \\ \end{gathered}$$

(32)

The material gradient index is taken to be $k = 2$, and the non-dimensional frequency of the beam is expressed as follows:

$$\overline{\omega } = \omega \frac{{L^{2} }}{h}\sqrt {\frac{{\rho_{{\text{m}}} }}{{E_{{\text{m}}} }}}$$

(33)

Table 1 compares the numerical results from the current study with those of Hadji et al. [42] using two types of porosity distributions and $L{/}h$ ratios. It is noticed that the results of Hadji et al. [42] are found using NET and hyperbolic shear deformation theory, in which the hyperbolic function was used to describe the nonlinear variation of the transverse shear strain through the thickness of the nanobeam. The results of the current study and those of Hadji et al. [42] are in good agreement, as shown in Table 1.

Table 1 Comparison of the non-dimensional frequency of the FG porous beams versus different porosity distribution and L/h

Secondly, the free vibration of the simply supported FG nanobeams is considered. The beam is made from ${\text{Al}}_{{2}} {\text{O}}_{{3}}$ as ceramic phase and ${\text{Fe}}$ as metal phase. The material properties of the ceramic and metal phases are: $E_{{\text{c}}} = 390\;{\text{GPa}}$, $\rho_{{\text{c}}} = 3960\;{\text{kg/m}}^{{3}}$, $\nu_{{\text{c}}} = 0.24$; $E_{{\text{m}}} = 210\;{\text{GPa}}$, $\rho_{{\text{m}}} = 7800\;{\text{kg/m}}^{{3}}$, $\nu_{{\text{m}}} = 0.3$. The beam’s length is $L = 10,000\;{\text{nm}}$. The non-dimensional frequency of the FG nanobeams is found as:

$$\omega * = \omega L^{2} \sqrt {\frac{{\rho_{{\text{c}}} A}}{{E_{{\text{c}}} I}}} ,\;A = bh,\;I = \frac{{bh^{3} }}{12}$$

(34)

Table 2 compares the present results regarding the non-dimensional fundamental natural frequency of the FG nanobeams versus different $L{/}h$ ratios and nonlocal parameter with the results of Ahmadi [55]. From Table 2, it is observed that the present results are coincide with the results of Ahmadi [55]. It is noticed that there is a slight difference between the present results and Ahmadi’s results. Because the present results are obtained via higher-order shear deformation theory and analytical solution, while the results of Ahmadi are found using first-order shear deformation theory and meshless method.

Table 2 Comparison non-dimensional fundamental frequency of the FG nanobeams versus different L/h and μ

4.2 Parameter study

A simply supported FG porous nanobeams with the length of $L = 10\;{\text{nm}}$, the depth of $b = 1\;{\text{nm}}$, and the height of $h$ is considered in this parametric study. The FG porous nanobeams are made from ceramic phase and metal phase with the material properties of $E_{{\text{c}}} = 14.4 \times 10^{9} \;{\text{Pa}}$, $\rho_{{\text{c}}} = 12.2 \times 10^{3} \;{\text{kg/m}}^{{3}}$, $\nu_{{\text{c}}} = 0.38$, $E_{{\text{m}}} = 1.44 \times 10^{9} \;{\text{Pa}}$, $\rho_{{\text{m}}} = 1.22 \times 10^{3} \;{\text{kg/m}}^{{3}}$, $\nu_{{\text{m}}} = 0.38$. The subsequent non-dimensional quantities are considered for convenience:

$$\Omega = \omega L^{2} \sqrt {\frac{{\rho_{{\text{c}}} A}}{{E_{{\text{c}}} I}}} ;\;A = bh_{0} \;;I = \frac{{bh_{0}^{3} }}{12};\;h_{0} = \frac{L}{10}$$

(35)

Table 3 examines the effects of the nonlocal parameter on the low-frequency vibration of FG porous nanobeams for $L{/}h = 10$, $P_{0} = 0.5$. It is observed that when the nonlocal parameter is considered, the frequencies of the FG porous nanobeams are lower than the local beams ($\mu = 0$). As the nonlocal parameter increases, the non-dimensional frequency of the FG porous nanobeams decrease for all cases of porosity distributions and power-law indexes.

Table 3 The first six non-dimensional frequencies of the FG porous nanobeams against different nonlocal parameters and porosity distributions

Next, the four frequencies for 10th, 50th, 100th, and 200th modes of the FG porous nanobeams are presented in Table 4 with $L{/}h = 10$, $P_{0} = 0.5$. By comparing these two tables, the frequencies of the FG porous nanobeams increase rapidly when the mode number increases. Again, when the nonlocal parameter increases, the frequencies of the FG porous nanobeams decrease rapidly. It is noticed that the effects of the nonlocal parameter on the high-frequency vibration of the FG porous nanobeams are more significant than on the low frequency. For example, the non-dimensional frequency of the FG porous nanobeams of type I with $\mu = 0$, $k = 1$ is 18% greater than the those with $\mu = 4$, while the frequency of 100th mode of the FG porous nanobeams with $\mu = 0$, $k = 1$ is 6100% greater than those with $\mu = 4$, and the difference being 12,400% for the 200th mode.

Table 4 The high frequencies of the FG porous nanobeams against different nonlocal parameters and porosity distributions

Table 5 examines the effect of the ratio $L/h$ on the non-dimensional frequencies of the FG porous nanobeams for $k = 1$, $P_{0} = 0.5$, $\mu = 2$. According to this table, as the ratio $L/h$ rises, the non-dimensional frequencies of the FG porous nanobeams are reduced for all cases of porosity distribution, both low- and high-frequency vibration. The non-dimensional fundamental frequencies of the FG porous nanobeams with $L/h = 10$ are 9–10 times greater than those for FG porous nanobeams with $L/h = 100$. For 10th mode, the non-dimensional fundamental frequencies of the FG porous nanobeams with $L/h = 10$ is 4–6 times greater than that of such FG porous nanobeams with $L/h = 100$. For 100th and 200th modes, the frequency of the FG porous nanobeams with $L/h = 10$ is $1 - 2$ times greater than that of such FG porous nanobeams with $L/h = 100$.

Table 5 The variation of non-dimensional frequencies of FG porous nanobeams against ratio L/h

Figure 4 illustrates the variation of the non-dimensional frequencies of the FG porous nanobeams concerning to the mode numbers for different porosity distributions and nonlocal parameters. It is observed that the non-dimensional frequencies of the FG porous nanobeams increases rapidly with the increase of mode number, and the difference in the non-dimensional frequencies of the four types of porosity distribution is low. The non-dimensional frequencies of the FG porous nanobeams with type II porosity are the highest ones, while the non-dimensional frequencies of the FG porous nanobeams with type IV porosity are the lowest ones. On the other hand, it is concluded that the effects of the nonlocal parameters are significant on the vibration of the FG porous nanobeams. For local vibration ($\mu = 0$), the non-dimensional frequency of the FG porous increase more quickly than those for nonlocal vibration of the FG porous nanobeams ($\mu > 0$).

Fig. 4

The variation of the non-dimensional frequency of the FG porous nanobeams for $L/h = 10$, $k = 1$, $P_{0} = 0.5$ against different values of nonlocal parameters

More details on the effects of the nonlocal parameter on the high-frequency vibration of the FG porous nanobeams are illustrated in Fig. 5. Again, it is found that the influence of the type of the porosity distribution is low, while the effects of the nonlocal parameters on the vibration of the FG porous nanobeams are noteworthy, especially for high frequencies of the FG porous nanobeams. For example, the local frequencies ($\mu = 0$) of 200th modes are approximately 2000% greater than those of nonlocal frequencies with $\mu = 0.1$, and are approximately 16,000% greater than those of nonlocal frequencies with $\mu = 4$.

Fig. 5

The variation of the non-dimensional frequency of the FG porous nanobeams with $L/h = 10$, $k = 1$, $P_{0} = 0.5$ versus different types of porosity distributions

Continuously, the variation of the non-dimensional frequencies of the FG porous nanobeams with different values of the power-law index is demonstrated in Fig. 6. As shown in Fig. 6, the influence of the power-law index on the free vibration behaviors of FG porous nanobeams is dependent on the kind of porosity distribution. Because both porosity distribution and power-law index effect on the mass density and rigidity of the FG porous nanobeams. Therefore, it should be noticed this couple-effects between the power-law index and the type of the porosity distribution in design, testing and manufacture the FG porous nanodevices.

Fig. 6

The variation of the non-dimensional frequency of the FG porous nanobeams with $L/h = 10$, $P_{0} = 0.5$, $\mu = 2$ versus different values of power-law index

The influence of the porosity coefficient $P_{0}$ on the non-dimensional frequencies of the FG porous nanobeams with four types of porosity distribution are investigated in Fig. 7 for 1st, 10th, 20th, and 100th modes. It is obvious that the variation of the non-dimensional frequencies of the FG porous nanobeams not only depends on the variation of the porosity coefficient but also the mode of the vibration of the FG porous nanobeams. For the 1st mode, when the porosity coefficient increases, the non-dimensional frequencies of the FG porous nanobeams increase for type I and type III of the porosity distribution, while the non-dimensional frequencies of the FG porous nanobeams decrease for type II and type IV of the porosity distribution. For the 10th mode, when the porosity coefficient increases, the non-dimensional frequencies of the FG porous nanobeams of type I increase, while the frequencies of the FG porous nanobeams of types II, III, and IV decrease. In the case of the 20th mode, when the porosity coefficient increases, the non-dimensional frequencies of the FG porous nanobeams of type I increase, the non-dimensional frequencies of type II and III decrease, while the non-dimensional frequencies of type IV increase when the $P_{0}$ increases from 0 to 0.6, then the non-dimensional frequencies decrease as the increase of $P_{0}$ from 0.6 to 0.8. In the cases of the 100th mode, when the coefficient $P_{0}$ increase, the non-dimensional frequencies of types I and II increase, and the non-dimensional frequencies of type IV decrease, but the non-dimensional frequencies of type III increase when $P_{0}$ increase from 0 to 0.4, then the frequencies decrease as increase of $P_{0}$ from 0.4 to 0.8.

Fig. 7

The variation of the non-dimensional frequency of the FG porous nanobeams versus $P_{0}$ for $L/h = 10$, $k = 1$,$\mu = 2$

Figure 8 examines the influence of the power-law index $k$ on the vibration behaviors of the FG porous nanobeams. According to Fig. 8, it is found that the influences of the power-law index are complex, and it depends on the mode numbers. When the $k$ increases from 0 to 2, the non-dimensional fundamental frequencies of the FG porous nanobeams decrease rapidly, then the non-dimensional fundamental frequencies increase with the increase of the $k$ from 2 to 10. Besides, the effects of the power-law index on the fundamental frequencies of the FG porous nanobeams with four types of porosity distribution are approximated. For high-frequency vibration, when the $k$ increases, the non-dimensional frequencies of the FG porous nanobeams also decrease and then increase; however, some maximum and minimum values appear. Additionally, the effects of the power-law index on the high frequencies of the FG porous nanobeams depend significantly on the porosity distributions. The reason is that when the power-law index increases, both effective mass density and Young’s modulus decrease; therefore, the variation of the fundamental frequencies of the FG porous nanobeams is more complex. Consequently, the vibration behaviors of the FG porous nanobeams undergoing high-frequency conditions should be analyzed carefully. When $k = 0$, the FG porous nanobeams become the homogeneous isotropic ones, and the non-dimensional frequencies of such beams of type I and II are identical.

Fig. 8

The variation of the non-dimensional frequency of the FG porous nanobeams versus $k$ for $L/h = 10$, $P_{0} = 0.5$, $\mu = 2$

Lastly, the influence of the nonlocal parameter on the behaviors of the FG porous nanobeams is studied for some vibration modes and different types of porosity distribution in Fig. 9. For both low- and high-frequency vibration of the FG porous nanobeams, the nonlocal parameter reduces the non-dimensional frequencies of such beams. For low-frequency vibration, the non-dimensional frequencies of the FG porous nanobeams decrease linearly as the increase of the nonlocal parameter. For high-frequency vibration, the non-dimensional frequencies of the FG porous nanobeams decrease nonlinearly as the increase of the nonlocal parameter. When the nonlocal parameter increases from 0 to 0.5, the non-dimensional frequencies of the FG porous nanobeams decrease rapidly, and the speed of the decrease slowdown when the nonlocal parameter increase from 0.5 to 4.

Fig. 9

The variation of the non-dimensional frequency of the FG porous nanobeams against $\mu$ for $L/h = 10$, $P_{0} = 0.5$, $k = 1$

5 Conclusions

This work presented a thorough examination of the free vibration behavior of FG porous nanobeams in low- and high-frequency conditions. Higher-order shear deformation theory and nonlocal elasticity theory were used to develop the governing equations. To solve the system of equations of motion, the Navier closed-form solution was utilized, and the numerical results were compared to published data to check the correctness of the suggested approach. The computed program was then employed to generate the FG porous nanobeams’ low- and high-frequency vibration. Some major conclusions may be drawn from the numerical results, which are as follows:

• When the nonlocal parameter is included, the non-dimensional frequencies of the FG porous nanobeams are reduced, especially for high modes.

• The effects of the porosity depend on the type of the distribution and the power-law index, it can improve or reduce the non-dimensional frequencies of the FG porous nanobeams and should be considered carefully in practice.

• The effects of the power-law index on the high-frequency of the FG porous nanobeams are also more complex than on the low-frequency vibration of such beams.

The current finding can serve as a benchmark result for the design, testing, optimization, and use of the FG porous nanobeams as well as high-frequency behaviors of the structures with different geometries.