1 Introduction

Composite laminates are accepted as an ideal material for structural application in weight-sensitive modern industries such as civil, automobiles, marine, and space vehicles due to tailor-made properties (excellent specific strength, specific stiffness, low specific weight, corrosion registrant, chemically unreactive up to many extents, lower life-cycle cost, etc.). Depending on the type of application, various shapes of the cutout are produced in these composite components to meet the practical requirements. These cutouts disrupt the continuity of the material, causing stress concentration and reduced stiffness. Moreover, the structural components do not experience a constant load during the operational life, and the load may vary with time to some extent, including the environmental effects. Besides, high acceleration in a short period may lead to severe destruction to the structural mechanisms due to the different mounting. The combined effect of dynamic load and the presence of cutout in the laminate cause geometrical nonlinear large-amplitude deflection and show complex responses. In order to get a better insight into the structural responses under the time-dependent pulse loading, the literature reported in the past is reviewed and discussed in the following lines.

The first-order displacement theory (FDST)-based nonlinear theory was initially proposed [1] to examine the dynamic behavior of layered shells based on Sander-Koiter nonlinear terms. FSDT-based isoparametric finite element (FE) procedure was presented to predict the time-dependent deflection behavior of layered shell panel structures using Green–Lagrange strain [2, 3]. The composite beam’s energy release rate with mid-plane delamination was investigated using the Euler–Bernoulli beam theory [4]. The blast response of metal sandwich plate load was presented using the Galerkin procedure based on Reissner–Hellinger’s variational principle [5]. The dynamic deflection analysis of sandwich structure [6] based on the first- and higher-order displacement theory (HSDT) was investigated using the radial basis function in the pseudo-spectra framework. HSDT-based FE approach was developed [7] to analyze the nonlinear dynamic deflection of elastoplastic plates. The isogeometric approach (IGA) based on classical plate theory (CPT) was used [8] to obtain the transient behavior of the layered plates. The generalized differential quadrature method and Newmark integration technique were utilized to predict the transient behavior of the layered cylindrical panels [9]. A three-dimensional FE solution for the dynamic deflection of sandwich panels exposed to blast load was predicted using commercially available FE tools LS-DYNA and ANSYS [10]. The frequency and stability responses of laminated plates were studied [11] using the discrete singular convolution (DSC) method. Similar approaches were utilized to evaluate the geometrically nonlinear dynamic behavior of the laminate with the elastic foundation [12, 13]. The three-dimensional elasticity solution for the dynamic behavior of the laminate and sandwich beams, plates, and solids was presented and compared with the results obtained via layerwise theory-based FE solution in the framework of Reddy’s HSDT [14]. The layered flat/curved panels’ nonlinear transient behavior was studied using the shear deformation theory-based FE approach [15]. Using the Galerkin approach, Reddy’s HSDT was applied to investigate the transient behavior of thick FG shell structures [16, 17]. The dynamic behavior (natural frequency) of the graphene-reinforced composite and FG flat/shell panels was investigated using FSDT differential quadrature method (DQM) [16,17,18]. The static and dynamic buckling responses of FG and composite structures were examined via DQM, meshfree, and energy approaches [19,20,21,22,23].

The transient deflection responses of the various composite panels exposed to blast loading were presented experimentally and theoretically by a closed-form solution, FE approach, and differential quadrature method [24]. The geometrically nonlinear dynamic behavior of layered plates with the elastic foundation was investigated using the computational platform of MSC/Nastran [25]. The modified couple stress theory has been presented to examine the nonlinear dynamic characteristics of shear deformable microplates and shells [26, 27]. The HSDT was presented to examine layered shell panels’ nonlinear bending, vibration, and transient analysis [28]. The FSDT-based numerical and experimental investigation of the influences of cracked laminated beams has been reported using the FE approach [29]. The thermal buckling behavior of a stiffened laminated composite plate with a cutout was investigated using isogeometric finite element analysis based on FSDT and non-uniform rational B-splines (NURBS) [30, 31]. The influences of crack and delamination of the laminated static and dynamic behavior have been reported recently based on the HSDT-based FE approach [32]. In another work, the influences of low-velocity impact on the transient behavior of the cylindrical shell have been examined using Love’s thin shell theory [33].

The analytical solution for the dynamic behavior of the isotropic plates with elastic foundation exposed to thermomechanical load was investigated using FSDT using modal superposition and state variable approach [34]. Further, they extended the work to layered plates considering Reddy’s HSDT [35]. The cantilever curved laminates’ dynamic responses were examined using FSDT when subjected to time-dependent thermal load [36]. The third-order piston theory has been implemented to investigate the nonlinear dynamic behavior of functionally graded beams subjected to aerothermal loads [37]. The frequency and transient deflection behavior of the layered sandwich panels of variable thickness exposed to the thermal environment were investigated using FSDT and von Kármán geometrical nonlinear strains by following the Galerkin method [38]. Also, different analyses on the laminated structures were carried out to examine the influences of cutout [39,40,41,42]. In another work, the dynamic deflection of the layered plate structure was calculated using a central difference approximation [43]. Also, the geometrical nonlinear effect on the transient deflection of layered shell panels was examined via the von Kármán strain [44].

The comprehensive review of the research articles available in the published domain indicates that a large number of works analyzing laminated structures have been reported without considering the influences of the cutout. The cutout’s effect on the laminate’s dynamic responses is limited to linear analysis. Moreover, the work considers the influence of only one individual shape of the cutout (circular, square, rectangular, elliptical, or any regular/irregular shape). Most of the small strain and large-deformation problems utilize the von Kármán strain, and the utilization of the Green–Lagrange stain is limited in numbers. The well-known fact is that the von Kármán strain is inadequate to acquire the effect of the large deformation behavior of the flexible structures. The dynamic analysis of the laminated structure with cutout considering the impact of an elevated thermal environment with temperature-dependent composite elastic properties has not been studied extensively. In order to fill the gap, a general FE model is developed based on the HSDT along with Green–Lagrange and von Kármán geometrical nonlinear strain. Then, the stability and validity of the developed nonlinear FE models are verified by comparing the results with the published data and subsequent experimentation. Finally, the influences of the cutout on the nonlinear dynamic responses are studied, including the various geometrical parameters of the multilayered panels considering temperature-dependent elastic properties.

2 Theoretical formulation

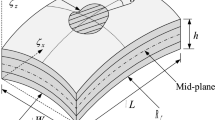
The laminated shell structure is defined in the curvilinear orthogonal coordinate system (x, y, z) with length ‘a’ and width ‘b’ in the x–y plane, as shown in Fig. 1. The total thickness ‘h’ of the laminate is considered in the z-direction. It is made up of ‘n’ number of orthotropic laminae that are arbitrarily oriented at an angle ‘Ɵ’ along the x-axis. The principal radii of curvature ‘Rx’ and ‘Ry’ are defined along x- and y-axes. The associated geometrical parameters to define the dimension of the layered shell panel are given in Table 1. The laminated shell panel of different geometrical contour is achieved based on the principal radii of curvature as: (i) plate (SP-I): Rx = ∞, Ry = ∞; cylindrical (SP-II): Rx = ∞, Ry = R; spherical (SP-III): Rx = R, Ry = R; hyperboloid (SP-IV): Rx = -R, Ry = R; and elliptical (SP-V): Rx = 2R, Ry = R.

Fig. 1
figure 1

Geometrical configuration of laminated shell panel structure

Full size image
Table 1 Geometrical parameters defining the dimension of the laminated shell panel
Full size table

2.1 Displacement field

The theoretical formulation of the laminated shell panel begins by considering a higher-order displacement field polynomial [45] \(^{\prime}\overline{u}^{\prime}\) with nine state-space variables for an arbitrary point at the mid-plane of laminate and expressed as is considered as:

$$ \overline{u}(x,y,z;t) = \left\{ {\begin{array}{*{20}c} {u(x,y,z;t)} & {v(x,y,z;t)} & {w(x,y,z;t)} \\ \end{array} } \right\} = \sum\limits_{i = 0}^{n} {\left\{ {\begin{array}{*{20}c} {u^{(i)} } & {v^{(i)} } & {w^{(i)} } \\ \end{array} } \right\}z^{(i)} } .$$
(1)

The displacement variables along x- and y-axes (\(u^{(i)}\) and \(v^{(i)}\)) are expanded up to i = 3. The transverse displacement along the z-axis (\(w^{(i)}\)) is considered only for i = 0. The terms corresponding to i = 0, (\(u^{(0)}\), \(v^{(0)}\), and \(w^{(0)}\)) denote the displacements along with respective directions. The rotation of the transverse normal at mid-plane about y- and x-axes is termed as \(u^{(1)}\) and \(v^{(1)}\) corresponding to i = 1, respectively. Similarly, the terms corresponding to i = 2 and 3 (\(u^{(2)} ,v^{(2)} ,u^{(3)},\) and \(v^{(3)}\)) are constants used to maintain the stress variation of through-thickness.

Further, Eq. (1) can be rearranged as:

$$ \left\{ {\overline{u}} \right\} = \left[ H \right]\left\{ {u_{0} } \right\} $$
(2)

where [H] is the thickness coordinate matrix, and \(\left\{ {u_{0} } \right\}\) are state-space variables.

2.2 Strain–displacement relations

The state of deformation in the laminated structure considering geometrical nonlinearity is introduced using two different geometrically nonlinear strain–displacement relations, (i) Green–Lagrange and (ii) von Kármán, which are used in this work. The Green–Lagrange nonlinear strain–displacement relation [46] is referred to as NLM-I and expressed in Eq. (3),

$$ \left\{ \varepsilon \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{xy} } \\ {\varepsilon_{xz} } \\ {\varepsilon_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{12} + \varepsilon_{21} } \\ {\varepsilon_{13} + \varepsilon_{31} } \\ {\varepsilon_{23} + \varepsilon_{32} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\frac{1}{2}\left( {\varepsilon_{11}^{2} + \varepsilon_{21}^{2} + \varepsilon_{31}^{2} } \right)} \\ {\frac{1}{2}\left( {\varepsilon_{22}^{2} + \varepsilon_{12}^{2} + \varepsilon_{32}^{2} } \right)} \\ {\varepsilon_{11} \varepsilon_{12} + \varepsilon_{22} \varepsilon_{21} + \varepsilon_{31} \varepsilon_{32} } \\ {\varepsilon_{11} \varepsilon_{13} + \varepsilon_{33} \varepsilon_{31} + \varepsilon_{21} \varepsilon_{23} } \\ {\varepsilon_{22} \varepsilon_{23} + \varepsilon_{33} \varepsilon_{32} + \varepsilon_{12} \varepsilon_{13} } \\ \end{array} } \right\}, $$
(3)

where

$$ \varepsilon_{11} = \frac{\partial u}{{\partial x}} + \frac{w}{{R_{x} }};\,\varepsilon_{22} = \frac{\partial v}{{\partial y}} + \frac{w}{{R_{y} }};\varepsilon_{12} = \frac{\partial u}{{\partial y}} + \frac{w}{{R_{xy} }};\varepsilon_{21} = \frac{\partial v}{{\partial x}} + \frac{w}{{R_{xy} }}; $$
$$ \varepsilon_{31} = \frac{\partial w}{{\partial x}} - \frac{u}{{R_{x} }};\varepsilon_{32} = \frac{\partial w}{{\partial y}} - \frac{v}{{R_{y} }};\varepsilon_{13} = \frac{\partial u}{{\partial z}};\varepsilon_{23} = \frac{\partial v}{{\partial z}};\varepsilon_{33} = \frac{\partial w}{{\partial z}} .$$

The small strain terms of Eq. (3) are neglected, and the von Kármán geometrical nonlinear strain–displacement relation [47] is obtained (referred to as NLM-II) and expressed in Eq. (4),

$$ \left\{ \varepsilon \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{xy} } \\ {\varepsilon_{xz} } \\ {\varepsilon_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{12} + \varepsilon_{21} } \\ {\varepsilon_{13} + \varepsilon_{31} } \\ {\varepsilon_{23} + \varepsilon_{32} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\frac{1}{2}\varepsilon_{31}^{2} } \\ {\frac{1}{2}\varepsilon_{32}^{2} } \\ {\varepsilon_{31} \varepsilon_{32} } \\ 0 \\ 0 \\ \end{array} } \right\}. $$
(4)

Further, the total strain \(\left\{ \varepsilon \right\}\) of Eq. (3) and (4) is written in generalized form by separating in the linear \(\left\{ {\varepsilon^{L} } \right\}\) and nonlinear \(\left\{ {\varepsilon^{NL} } \right\}\) strain terms as in Eq. (5),

$$ \left\{ \varepsilon \right\} = \left\{ {\varepsilon^{L} } \right\} + \left\{ {\varepsilon^{NL} } \right\} = \left[ {\overline{H}^{L} } \right]\left\{ {\overline{\varepsilon }^{L} } \right\} + \left[ {\overline{H}^{NL} } \right]\left\{ {\overline{\varepsilon }^{NL} } \right\}. $$
(5)

\(\left[ {\overline{H}^{L} } \right]\) and \(\left[ {\overline{H}^{NL} } \right]\) are the thickness coordinate matrices related to the linear \(\left\{ {\overline{\varepsilon }^{L} } \right\}\) and nonlinear \(\left\{ {\overline{\varepsilon }^{NL} } \right\}\) mid-plane strain vectors, respectively, and the details can be seen in [48].

2.3 Thermo-elastic stress–strain relation

The constitutive stress–strain relation [49] for the kth lamina of the laminated shell structure subjected to the thermal field is given by:

$$ \left\{ \sigma \right\}^{k} = \left[ Q \right]^{k} \left\{ \varepsilon \right\}^{k} - \left[ Q \right]^{k} \left\{ {\varepsilon_{TH} } \right\}^{k} = \left[ Q \right]^{k} \left\{ \varepsilon \right\}^{k} - \left[ Q \right]^{k} \left\{ \alpha \right\}^{k} \Delta T $$
(6)

or

$$ \left\{ \sigma \right\}^{k} = \left\{ {\sigma_{E} } \right\}^{k} - \left\{ {\sigma_{TH} } \right\}^{k} $$
(7)

where \(\left\{ \sigma \right\}\) is the stress tensor, ‘ΔT’ is the temperature rise across the thickness of the shell structure, and \(\left[ Q \right]\) is the reduced elastic stiffness matrix.

2.4 Strain energy

The strain energy of the laminated shell structure in terms of stress and strain is given by:

$$ U_{SE} = \frac{1}{2}\int_{A} {\left[ {\sum\limits_{k = 1}^{n} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \varepsilon \right\}^{T} \left[ {\overline{Q}} \right]\left\{ \varepsilon \right\}dz} } } \right]} \,dA. $$
(8)

The strain energy due to thermal load is calculated as:

$$ U_{TH} = \int_{A} {\left( {\sum\limits_{k = 1}^{n} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left\{ {\begin{array}{*{20}c} {1/2\left\{ {\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial v}{{\partial x}}} \right)^{2} + \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right\}N_{x} } \\ { + 1/2\left\{ {\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \left( {\frac{\partial v}{{\partial y}}} \right)^{2} + \left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right\}N_{y} } \\ { + \left\{ {\left( {\frac{\partial u}{{\partial x}}} \right)\left( {\frac{\partial u}{{\partial y}}} \right) + \left( {\frac{\partial v}{{\partial x}}} \right)\left( {\frac{\partial v}{{\partial y}}} \right) + \left( {\frac{\partial w}{{\partial x}}} \right)\left( {\frac{\partial w}{{\partial y}}} \right)} \right\}N_{xy} } \\ \end{array} } \right\}dz} } } \right)} dA $$
(9)

or

$$ U_{TH} = \int_{A} {\left\{ {\overline{\varepsilon }^{G} } \right\}^{T} \left[ {D^{G} } \right]\left\{ {\overline{\varepsilon }^{G} } \right\}} dA $$
(10)

where Nx and Ny are in-plane forces due to thermal load along x- and y-axes, respectively. The induced in-plane shear force due to a change in temperature is denoted by Nxy.

2.5 Kinetic energy

The kinetic energy (UKE) of the laminated shell structure is given by:

$$ U_{KE} = \frac{1}{2}\int_{A} {\left( {\sum\limits_{k = 1}^{n} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left\{ {\dot{u}} \right\}^{T} \rho \left\{ {\dot{u}} \right\}dz} } } \right)} dA $$
(11)

or

$$ U_{KE} = \frac{1}{2}\int\limits_{A} {\left( {\sum\limits_{k = 1}^{Nl} {\int_{{\zeta_{k - 1} }}^{{\zeta_{k} }} {\left\{ {\dot{u}_{0} } \right\}^{T} \left[ H \right]^{T} \rho \left[ H \right]\left\{ {\dot{u}_{0} } \right\}dz} } } \right)} \,dA\, = \frac{1}{2}\int\limits_{A} {\left\{ {\dot{u}_{0} } \right\}^{T} \left[ m \right]\left\{ {\dot{u}_{0} } \right\}} \,dA $$
(12)

where \(\rho\) is density, \(\left\{ {\dot{u}} \right\}\) is velocity vector, and \(\left[ m \right]\) is inertia matrix.

The mass matrix is expressed as:

$$ \left[ m \right] = \sum\limits_{k = 1}^{n} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left[ H \right]^{T} \rho \left[ H \right]dz} }. $$
(13)

2.6 Work done

The work done due to externally applied mechanical and thermal load is obtained as:

$$ W = \int\limits_{A} {\left\{ {u_{0} } \right\}^{T} \left\{ {f_{M} + f_{TH} } \right\}} dA $$
(14)

where {fM} is mechanical load and {fTH} is thermal load vector, respectively.

The mathematical form of the applied mechanical loading is as follows:

  1. (i)

    Uniformly distributed load (UDL): \(f_{M} (x,y) = q_{0},\)

  2. (ii)

    Point load (PL): \(f_{M} (x,y) = \left. {\begin{array}{*{20}c} {q_{0} } \\ 0 \\ \end{array} } \right\} \) at an arbitrary point (x1, y1),

  3. (iii)

    Sinusoidally distributed load (SDL): \(f_{M} (x,y) = q_{0} \sin (\pi x/a)\sin (\pi y/b)\)

where \(q_{0}\) is the maximum intensity of the applied mechanical load.

The induced in-plane thermal forces {fT} due to elevated thermal environment in laminated shell structure are obtained as:

$$ \left\{ {f_{TH} } \right\} = \left\{ {N_{x} \,\,N_{y} \,\,N_{xy} \,\,0\,\,0} \right\}^{T} = \sum\limits_{k = 1}^{3} {\int\limits_{{Z_{k - 1} }}^{{Z_{k} }} {\left( {\left[ Q \right]\left\{ {\alpha_{1} \,\,\alpha_{2} \,\,0\,\,0\,\,0} \right\}^{T} \Delta T} \right)\,\,dz} }. $$
(15)

3 Finite element formulation

It is difficult to obtain an analytical solution for practical engineering problems involving complex geometry, material properties, and boundary conditions. Hence, the FE approach is adopted to obtain the approximate nonlinear numerical solution. The layered shell structure with a cutout is discretized using a nine-noded isoparametric quadrilateral shell element having nine nodal degrees of freedom.

The elemental state-space variables at each node of the element is expressed as [50]:

$$ \left\{ {u_{0} } \right\}\, = \sum\limits_{i = 1}^{9} {\left[ {N_{i} } \right]} \left\{ {u_{0i} } \right\}\, $$
(16)

where \(\left\{ {u_{0} } \right\} = \left\{ {u^{(0)} \,v^{(0)} \,w^{(0)} \,u^{(1)} \,v^{(1)} \,u^{(2)} \,v^{(2)} \,u^{(3)} \,v^{(3)} \,} \right\}^{T}\) is elemental and \(\left\{ {u_{0i} } \right\}\, = \left\{ u_{0i}^{(0)} \,v_{0i}^{(0)} \,w_{0i}^{(0)} \,u_{0i}^{(1)}\right.\break\left. \,v_{0i}^{(1)} \,u_{0i}^{(2)} \,v_{0i}^{(2)} \,u_{0i}^{(3)} \,v_{0i}^{(3)} \right\}^{T}\) is the nodal displacement vector.

The linear and nonlinear mid-plane stain tensor from Eq. (4) and (10), in terms of nodal displacement, can be expressed as:

$$ \left\{ {\overline{\varepsilon }^{L} } \right\} = \left[ {\beta^{L} } \right]\left\{ {u_{0i} } \right\}, $$
(17)
$$ \left\{ {\overline{\varepsilon }^{NL} } \right\} = \left[ {\beta^{NL} } \right]\left\{ {u_{0i} } \right\} = \left[ \Lambda \right]\left[ G \right]\left\{ {u_{0i} } \right\}, $$
(18)
$$ \left\{ {\overline{\varepsilon }^{G} } \right\} = \left[ {\beta^{G} } \right]\left\{ {u_{0i} } \right\} $$
(19)

where \(\left[ {\beta^{L} } \right]\), \(\left[ {\beta^{G} } \right]\), and \(\left[ G \right]\) matrices are the product of shape functions and differential operators associated with the linear, nonlinear, and geometrical mid-plane strain, respectively. The matrix \(\left[ {\beta^{NL} } \right]\) is further subdivided in the product form of the matrices \(\left[ \Lambda \right]\) and \(\left[ G \right]\); the details can be seen in [48].

3.1 Governing equations

Using Hamilton’s principle, the governing equation for the laminate’s structural response is obtained and expressed as:

$$ \delta \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {U_{KE}^{{}} - \left( {U_{SE}^{{}} + U_{TH}^{{}} + W^{{}} } \right)} \right)dt = 0}.$$
(20)

From Eqs. (8), (10), (11), and (14), Eq. (20) is modified as:

$$ \left[ M \right]\left\{ {\ddot{u}} \right\} + \left( {\left[ {\kappa^{L} } \right] + \,\left[ {\kappa^{NL} } \right]} \right)\left\{ u \right\} + \left[ {\kappa^{G} } \right]\left\{ u \right\} = \left\{ {f_{M} } \right\} + \left\{ {f_{TH} } \right\} $$
(21)

where \(\left[ {\kappa^{L} } \right],\,\left[ {\kappa^{NL} } \right],\left[ {\kappa^{G} } \right],\left[ M \right]{, }\left\{ {f_{M} } \right\}, \,{\text{and}}\left\{ {f_{TH} } \right\}\,\,\) are the global matrices/vectors corresponding to elemental matrices/vectors. The terms \(\left\{ u \right\}\) and \(\left\{ {\ddot{u}} \right\}\) denote the displacement and acceleration vector, respectively.

3.2 Nonlinear transient analysis

The steady-state nonlinear time-dependent deflection of the laminate subjected to thermomechanical is obtained using Eq. (21) by dropping the inertia and geometrical stiffness matrix and written as:

$$ \left[ M \right]\left\{ {\ddot{u}} \right\} + \left( {\left[ {\kappa^{L} } \right] + \,\left[ {\kappa^{NL} } \right]} \right)\left\{ u \right\} = \left\{ {f_{M} } \right\} + \left\{ {f_{TH} } \right\} $$
(22)

or

$$ \left[ M \right]\left\{ {\ddot{u}} \right\} + \left[ \kappa \right]^{S} \left\{ u \right\} = \left\{ f \right\}^{S} $$
(23)

where \(\left[ \kappa \right]^{S} = \left[ {\kappa^{L} } \right] + \,\left[ {\kappa^{NL} } \right]\) and \(\left\{ f \right\}^{S} = \left\{ {f_{M} } \right\} + \left\{ {f_{TH} } \right\}\).

The matrices and the vectors presented in Eq. (23) are considered as functions of time. Newmark’s integration method [51] is used to calculate the dynamic deflection. In order to apply Newmark’s method, first of all, some integration constants such as \(\gamma = 0.25\), \(\lambda = 0.5\), and \(\left( {\ell_{0} ,\ell_{1} ,\ell_{2} ,...\ell_{7} } \right)\) are defined. The expansion of the \(\left( {\ell_{0} ,\ell_{1} ,\ell_{2} ,...\ell_{7} } \right)\) is as follows:

$$ \left. \begin{gathered} \ell_{0} = \frac{1}{{\gamma \Delta t^{2} }};\ell_{1} = \frac{\lambda }{{\gamma \Delta t^{2} }};\ell_{2} = \frac{1}{\gamma \Delta t};\ell_{3} = \frac{1}{2\gamma } - 1;\ell_{4} = \frac{\lambda }{\gamma } - 1; \hfill \\ \ell_{5} = \frac{\Delta t}{2}\left( {\frac{\lambda }{\gamma } - 2} \right);\ell_{6} = \Delta t\left( {1 - \lambda } \right);\ell_{7} = \lambda \Delta t \hfill \\ \end{gathered} \right\},$$
(24)

The effective stiffness matrix at a time instant \(^{\prime}t^{\prime}\) is calculated as:

$$ \left[ {\hat{\kappa }} \right]^{S} = \left[ \kappa \right]^{S} + \ell_{0} \left[ M \right]. $$
(25)

Similarly, the effective force vector at for time \(^{\prime}t + \Delta t^{\prime}\) is obtained as:

$$^{t + \Delta t} \left[ {\hat{f}} \right]^{S} =^{t + \Delta t} \left[ {\hat{f}} \right]^{S} + \left[ M \right]\left( {\ell_{0}^{t} u + \ell_{2}^{t} \dot{u} + \ell_{3}^{t} \ddot{u}} \right) .$$
(26)

Now, the displacement at a time \(^{\prime}t + \Delta t^{\prime}\) is obtained by solving the following relation:

$$ \left[ {\hat{K}} \right]^{S} \,^{t + \Delta t} \left\{ u \right\} = \,^{t + \Delta t} \left[ {\hat{f}} \right]^{S}.$$
(27)

The acceleration and the velocity at a time \(^{\prime}t + \Delta t^{\prime}\) is calculated as:

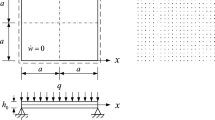
$$ \left. \begin{gathered}^{t + \Delta t} \ddot{u} = \ell_{0} \left( {{}^{t + \Delta t}u - {}^{t}u} \right) - \ell_{2} {}^{t}\dot{u} - \ell_{3} {}^{t}\ddot{u} \hfill \\^{t + \Delta t} \dot{u} = {}^{t}\dot{u} + \ell_{6} {}^{t}\ddot{u} + \ell_{7} {}^{t + \Delta t}\ddot{u} \hfill \\ \end{gathered} \right\}, $$
(28)

The transient responses are obtained using Eq. (23) by imposing the following end-support conditions:

  • All edge simply supported (Es-a):

    \(v^{(0)} = w^{(0)} = v^{(1)} = v^{(2)} = v^{(3)} = 0\) at \(x = 0\,{\text{and}}\,a\),

    \(u^{(0)} = w^{(0)} = u^{(1)} = u^{(2)} = u^{(3)} = 0\) at \(y = 0\,{\text{and}}\,b;\)

  • Cantilever support (Es-b):

\(u^{(0)} = v^{(0)} = w^{(0)} = u^{(1)} = v^{(1)} = u^{(2)} = v^{(2)} = u^{(3)} = v^{(3)} = 0,\) at \(x = 0.\)

3.3 Solution technique

Picard’s iterative method is used to solve the governing equation to obtain the nonlinear responses (transient) by following the steps below:

  1. (i)

    The elemental matrices are initially calculated and globalized by following the above finite element steps.

  2. (ii)

    The linear solutions are calculated by neglecting the nonlinear part of the governing equation.

  3. (iii)

    The nonlinear values are modified stepwise using the initial linear solution.

  4. (iv)

    Now, the convergence of the nonlinear solution is established using \(\sqrt {\left( {(\chi_{n} - \chi_{n - 1} )^{2} /(\chi_{n} )^{2} } \right)} \le 10^{ - 3}\) where \(\chi_{n}\) and \(\chi_{n - 1}\) are transient deflection values at nth and (n-1)th iteration, respectively.

  5. (v)

    After satisfying the convergence conditions, the procedure was stopped. If not, the steps are repeated from (iii) until the satisfying convergence criteria.

4 Cutout modeling

The layered panel with a cutout of various shapes at the center is built using the quarter shell model [52, 53]. Figure 2 depicts the plan view of the quarter shell model, which includes the discretized surface, and utilizing this model, the full panel geometry with different shapes of cutout is generated as shown in Fig. 3. The discretized laminated panel with different shapes of cutouts and the associated parameters are listed in Table 2.

Fig. 2
figure 2

Quarter panel model of the laminate shell structure

Full size image
Fig. 3
figure 3

Plan view of the entire panel obtained using quarter panel model

Full size image
Table 2 Parameters associated with various shapes of cutout
Full size table

5 Experimentation

In this work, composite laminates are fabricated using the wet layup process [54] using plain weaved E-glass fiber of 610 gsm and epoxy resin (Lapox L-12) with hardener (K-6). The tensile properties of the fabricated laminate are evaluated experimentally by following the ASTM D3039/3039 M test procedure. The Young’s modulus has been evaluated using UTM (INSTRON-5967) for the test specimen in three different fiber orientations, e.g., longitudinal (0°), transverse (90°), and 45° (named as E11, E22 and E45). Poisson’s (µ12) ratio is taken as 0.17 from Ref. [55]. The coefficient of thermal expansion is taken as \(\alpha_{1} = \alpha_{2}\) = \(5.5 \times 10^{ - 6} /^\circ {\text{C}}\). The average elastic properties of the laminate are considered for experimentation and listed in Table 3, in which the shear modulus (G12) is calculated as [56]:

$$ \left( {G_{12} = \frac{1}{{\frac{4}{{E_{45^\circ } }} - \frac{1}{{E_{11} }} - \frac{1}{{E_{22} }} - \frac{{2\mu_{12} }}{{E_{11} }}}}} \right),$$
(29)
Table 3 Experimentally evaluated composite elastic properties of the fabricated laminate
Full size table

The fabricated laminated flat panel’s dynamic deflection has been examined experimentally using the laboratory-scale experimental test setup shown in Fig. 4. The transient deflection is calculated for the cantilever support. Initially, the exciter gives a concentrated load (1 N) with sinusoidal excitation at a certain frequency (20 Hz) to the cantilever laminate at the center of the free edge, as shown in Fig. 4. The function generator (Scientech, 4060) generates the sinusoidal excitation load in association with the exciter. The acceleration of the laminated panel is recorded by the attached accelerometer (National Instruments, 352C03) just above the excitation point and fed to the DAQ system (National Instruments, 9178) for further processing. The acceleration signal is converted into a velocity and displacement signal with the help of the appropriate integration module in the LabView (2016) VI program (Fig. 5). Finally, the displacement response in the time domain is displayed on the monitor of a computer system.

Fig. 4
figure 4

Experimental arrangement for dynamic deflection a Graphical view, b Real-time view

Full size image
Fig. 5
figure 5

LabVIEW virtual program for transient analysis

Full size image

6 Results and discussion

The laminated panel structure’s nonlinear dynamic behavior is now examined in thermal environments using the derived higher-order nonlinear FE model (NLM-I and NLM-II). The nonlinear response is computed by considering all linear and nonlinear terms using an in-house developed computational code in MATLAB.

6.1 Convergence study

After developing the HSDT-based FE model, the element sensitivity test (convergence) is initially performed. The transient deflection values are calculated at the cutout edge on the longitudinal axis of the laminated panel (at point ‘O’ in Fig. 6) unless otherwise mentioned. The convergence of the solution is verified in two steps. Firstly, the convergence of the finite element solution for the transient responses is carried out for constant time sub-step (0.2 ms) and by changing the mesh density in half portion of the quarter panel model (Fig. 2) for the laminated panel with cutout, and the same is implemented for the entire structure (Fig. 3). The mesh density is varied along x- and y-axes, as given in Table 4. Then, utilizing the optimal mesh density, the optimal time sub-step is identified for transient analysis by varying the time sub-step.

Fig. 6
figure 6

Location of point ‘O’ at which transient deflection is measured

Full size image
Table 4 Mesh density in half of quarter panel model vs. total number of elements in the discretized laminated panel with or without cutout
Full size table

The convergence behavior of the developed FE model for the linear and nonlinear transient deflection of cutout abided laminated shell panels subjected to the thermomechanical load is examined. The convergence behavior of nonlinear responses is obtained using NLM-I and NLM-II. In this regard, an Es-a-supported four-layered antisymmetric eight-layered (45°/-45°/45°/-45°) square SP-III panel (SR = 1, ST = 50, SC = 10) having different shapes of cutout (CR = 0.25) is used for the analysis. The laminate is subjected to a stepped pulse of UDL (q0 = 10 kN/m2) and an elevated thermal environment. The analysis utilizes temperature-dependent composite elastic properties given below to compute the transient response, and the deflection values are normalized as \(\overline{w}^{L} = w^{L} /h\). The computed time-dependent deflection results using NLM-I are shown in Figs. 7 and 8, whereas the deflection data obtained via NLM-II are shown in Figs. 9 and 10. The result shows that the FE solution for the transient deflection converges for the mesh density of 3 × 3 and time sub-step of 0.2 ms and is thus taken for further analysis.

Fig. 7
figure 7

Convergence of normalized transient deflection (\(\overline{w}^{NL}\)) responses of SP-III laminated shell panels having cutouts of different shapes using NLM-I for different mesh densities at elevated temperature (T = 400 K)

Full size image
Fig. 8
figure 8

Convergence of normalized transient deflection (\(\overline{w}^{NL}\)) responses of SP-III laminated shell panels having cutouts of different shapes using NLM-I for different time steps at elevated temperature (T = 400 K)

Full size image
Fig. 9
figure 9

Convergence of normalized transient deflection (\(\overline{w}^{NL}\)) responses of SP-III laminated shell panels having cutouts of different shapes using NLM-II for different mesh densities at elevated temperature (T = 400 K)

Full size image
Fig. 10
figure 10

Convergence of normalized transient deflection (\(\overline{w}^{NL}\)) responses of SP-III laminated shell panels having cutouts of different shapes using NLM-II for different time steps at elevated temperature (T = 400 K)

Full size image

Temperature-dependent lamina properties are:

\(E_{11} = 150(1 - 0.5 \times 10^{ - 3} \Delta {\text{T}})\,{\text{GPa}}\), \(E_{22} = 9(1 - 0.2 \times 10^{ - 3} \Delta {\text{T}})\,{\text{GPa}}\), \(G_{12} = G_{13} = 7.1(1 - 0.2 \times 10^{ - 3} \Delta {\text{T}})\,{\text{GPa}}\), \(G_{23} = 2.5(1 - 0.2 \times 10^{ - 3} \Delta {\text{T}})\,{\text{GPa}}\), \(\mu_{12} = 0.3\), \(\rho = 1600\,{\text{kg/m}}^{3}\), \(\alpha_{11} = 1.1 \times 10^{ - 6} (1 + 0.5 \times 10^{ - 3} \Delta {\text{T}})\,{\text{K}}^{ - 1}\), \(\alpha_{22} = 25.2 \times 10^{ - 6} (1 + 0.5 \times 10^{ - 3} \Delta {\text{T}})\,{\text{K}}^{ - 1}\).

6.2 Validation

The accuracy of the currently derived higher-order FE model is verified after the appropriate convergence test by solving various numerical examples. The model’s validity has been discussed by comparing current numerical deflection and stress values with the published data. Furthermore, the responses are validated using the authors’ experimental deflection data to enhance the confidence in the current theoretical model. The validation study is divided into two major categories: theoretical and experimental verification, including various flat/curved laminated structures with and without cutout in ambient and elevated thermal environments.

6.2.1 Numerical validation

The nonlinear transient deflection values calculated for four-layered (0°/90°/0°90°) SP-II and SP-III laminate (SR = 1, ST = 20, SC = 10) with Es-a support are calculated considering temperature-dependent material properties [57]. The laminated panels are subjected to UDL (\(q_{0}\) = 0.1 MPa) and uniform temperature rise. The calculated results are compared in Fig. 11 with the FE solution [58]. The result agrees with the reference data and indicates the validity of the present HSDT-based nonlinear models.

Fig. 11
figure 11

Transient behavior four-layered (0°/90°/0°90°) panel exposed to UDL and uniform thermal field a SP-III b SP-II

Full size image

6.2.2 Experimental validation

Now, the investigation is extended to acquire the transient deflection data of the laminate with cutout experimentally, at the same point discussed earlier (Sect. 5), having cantilever support (Es-b) in the elevated thermal field (ΔT = 20 °C). The transient deflection of the laminate (a = b = 0.15 m) with the cutout is recorded experimentally for the square laminate with concentric CT-III cutout (c = 0.05 m) and compared with the nonlinear numerical results (NLM-I and II) in Fig. 12. Then, the laminates having CT-I cutout (r = 0.015 m) at different locations, i.e., at the center of the first and fourth quadrant, are considered to record the transient deflection values at the central point of the laminate. The comparative representation of the results is shown in Fig. 13. The comparison of the experimental and numerical results indicates the accuracy of the present nonlinear models and confirms that they can predict the transient deflection values considering the thermal effect.

Fig. 12
figure 12

Nonlinear transient deflection of laminate with concentric CT-III-type cutout at the elevated thermal environment (ΔT = 20 °C)

Full size image
Fig. 13
figure 13

Nonlinear transient deflection of the laminate with concentric CT-III-type cutout at the elevated thermal environment (ΔT = 20 °C)

Full size image

The comparative analysis of the present numerical results with published and experimental data shows that the dynamic deflection significantly increases with an increase in the temperature of the environment for the constant magnitude of the applied mechanical load. Additionally, the presence of the cutout also decreases the structural stiffness, i.e., the laminate with a cutout possesses higher deflection values than the intact laminate, while comparing the experimental deflection data with the numerical results from the developed computational models (linear, NLM-I, and NLM-II) indicates that the HSDT model considering Green–Lagrange strain (NLM-I) gives contiguous results with the experimental data.

6.3 Additional assessments

The developed FE model for the cutout-borne layered shell panel is extended to demonstrate the effect of different cutout and geometrical parameters on nonlinear thermomechanical transient deflection and stress responses. All the numerical assessments have been carried out for square laminates (SR = 1) using temperature lamina properties (Sect. 6.1) considering temperature T = 300 K as reference temperature, else stated otherwise. The transient deflection and stress values are calculated at point ‘O’ (Fig. 6) and normalized as:

Normalized transient deflection: \(\overline{w}^{NL} = w^{NL} /h\), Normalized stress: \(\overline{\sigma }_{ij}^{NL} = \sigma_{ij}^{NL} \times 10^{6} /E_{22}\).


The analysis is carried out for the laminates subjected to different types of pulse load, as shown in Fig. 14, and their mathematical expressions are as follows:

  • Stepped pulse: \(q(t) = q_{0}\),

  • Triangular pulse: \(q(t) = q_{0} (1 - t/T_{t} )\),

  • Sine pulse: \(q(t) = q_{0} \sin \left( {\pi t/T_{t} } \right)\),

  • Blast pulse: \(q(t) = q_{0} (1 - t/T_{t} )e^{{ - \vartheta t/T_{t} }}\), where \(\vartheta\) = -2.

Fig. 14
figure 14

Graphical representation of different time-dependent pulse loads

Full size image

Here, t is time instant, and Tt is total time.

6.3.1 Effect of load magnitude

The influence of the magnitude of applied mechanical load variation on the transient deflection is calculated using NLM-I and NLM-II. The analysis considers a four-layered (45°/-45°/45°/-45°) Es-a-supported SP-I laminate (ST = 50) with cutout (CR = 0.25) of different shapes and subjected to UDL stepped pulse load (\(q_{0}\) = 10 and 25 kN/m2). The deflection values are calculated and presented in Fig. 15 when the laminate is exposed to ambient (T = 300 K) and thermal field (T = 400 K). The result indicates that deflection increases with an increase in the magnitude of applied mechanical and thermal load. Also, it is observed that the NLM-II predicts lower deflection values than the NLM-I. The results show that the NLM-I and NLM-II have nearly identical deflection for the lower mechanical load (\(q_{0}\) = 10 kN/m2). However, a larger change in the results is detected for the higher mechanical load (\(q_{0}\) = 25 kN/m2). This validates the use of NLM-I for the nonlinear behavior of laminated panels; thus, NLM-I is used throughout the work.

Fig. 15
figure 15

Transient deflection of Es-a-supported SP-I laminate with different shapes of cutout subjected to UDL stepped pulse and thermal load

Full size image

6.3.2 Effect of pulse load

The laminated panel may be exposed to several types of time-dependent pulse loads during its service life. Therefore, the influences of different pulse loads (stepped, sine, triangular, and blast pulse) on the nonlinear transient responses are examined for the four-layered (45°/− 45°/45°/− 45°) Es-a-supported SP-III and SP-IV (SC = 10, ST = 50) laminate with CT-I cutout (CR = 0.25). The laminate is subjected to UDL (\(q_{0}\) = 10 kN/m2) and thermal field (T = 300 and 400 K). Figure 16 depicts the obtained nonlinear transient deflection values. The results show that for a stepped and sinusoidal pulse the maximum and minimum variation in time-dependent deflection for the laminate are observed, irrespective of shell geometry and thermal load. Also, deflection increases with an increase in the temperature of the environment.

Fig. 16
figure 16

Transient deflection of an Es-a-supported SP-III and SP-IV laminate with CT-I cutout under different types of UDL pulse load in the thermal field

Full size image

6.3.3 Effect of cutout shape and size

Now, the transient behavior is evaluated for the SP-III and SP-IV laminate panel (ST = 20 and SC = 10) with cutout (CT-I, CT-II, and CT-III) of the equal area (CR = 0.2) as shown in Fig. 17. The Es-a-supported laminate consists of four layers of the antisymmetric angle-ply lamina (45°/-45°/45°/-45°) and is subjected to the UDL (\(q_{0}\) = 10 kN/m2) stepped pulse load in the elevated thermal environment. The result shows that the laminate having elliptical cutout (CT-II) shows the lowest time-dependent deflection. Further, the influences of cutout size (CR = 0, 0.1, and 0.2) on the dynamic deflection of the SP-III laminate are calculated and shown in Fig. 18. The Figure shows that the deflection responses follow an inclination behavior for cutout size CR = 0.1 compared to the intact laminate (CR = 0). With a further increase in cutout size, the transient deflection decreases irrespective of shell geometry and cutout shape.

Fig. 17
figure 17

Comparison of the transient deflection of an Es-a-supported SP-III and SP-IV laminate having cutouts of different shapes subjected to UDL stepped pulse and thermal load

Full size image
Fig. 18
figure 18

Effect of cutout size on the transient deflection of an Es-a-supported SP-III laminate having different shapes of cutout

Full size image

6.3.4 Effect of shell configuration

The diverse configurations of shell geometries can be obtained by altering the curvature radii of the laminated shell panel. Thus, the relative analysis of dynamic deflection for different laminated shell configurations is carried out for the Es-a-supported four-layered (45°/ − 45°/45°/ − 45°) (ST = 50 and SC = 10) laminate with C-I-, CT-II-, and CT-III-type cutout (CR = 0.2) and presented in Fig. 19. The shells are subjected to the UDL (\(q_{0}\) = 10 kN/m2) in ambient and thermal conditions. The shell panel with the highest stiffness and lowest deflection has positive radii of curvature (spherical shell). However, when the curvature radii are opposite in direction but equal in magnitude (hyperboloid shell), it exhibits the highest deflection.

Fig. 19
figure 19

Influence of geometry on the transient behavior of a laminate with cutout subjected to UDL stepped pulse

Full size image

6.3.5 Effect of curvature ratio

Further, the influence of curvature (SC = 5, 10, 15, 20, 25, and 100) on the dynamic deflection of the Es-a-supported SP-III and SP-IV laminated shell structures (ST = 50) with CT-I-type cutout (CR = 0.25) subjected to UDL of intensity \(q_{0}\) = 10 kN/m2 in the thermal environment is examined and shown in Fig. 20. The results indicate that the deflection of the SP-III shell increases as the curvature ratio increases, but there is no significant variation in the transient deflection of the shell structure (SP-IV) with opposite curvature radii.

Fig. 20
figure 20

Effect of curvature ratio on the transient deflection of an Es-a-supported SP-III laminate having CT-I cutout

Full size image

6.3.6 Effect of lamination scheme

The SP-III and SP-IV laminated shell panel (ST = 20, SC = 10) with cutout (CR = 0.25) under different elevated temperatures (T = 300 and 500 K) subjected to UDL (\(q_{0}\) = 10 kN/m2) stepped pulse load is analyzed for nonlinear transverse deflection responses. The responses are calculated for a four-layered laminate with the laminae stacked in symmetric/antisymmetric cross-ply and angle-ply manner, as shown in Fig. 21. The Figure indicates that the nonlinear deflection response increases with an increase in temperature. Also, for the assumed geometrical parameters, an antisymmetric cross-ply laminate (45°/ −45°/45°/ –45°) gives the stiffest configuration, i.e., lower transverse deflection is observed irrespective of shell configuration.

Fig. 21
figure 21

Influence of layup scheme on the nonlinear transient deflection of Es-a-supported laminates with cutout subjected to UDL stepped pulse load

Full size image

6.3.7 Transient stress

Now, the time-dependent variation of stresses on the Es-a-supported symmetric angle-ply (45º/-45º/45º/-45º) SP-III laminate (ST = 20, SC = 10) having CT-I, CT-II, and CT-III cutouts is calculated and compared in Figs. 22. The nonlinear stress values are calculated using the constitutive relation (Eq. (3.9)) at the cutout edge on the x-direction (at point ‘O’ in Fig. 6) when subjected to UDL (\(q_{0}\) = 10 kN/m2) stepped pulse load at T = 300 K. The critical observation of the results indicates that the lowest and highest magnitude of normal stress (\(\overline{\sigma }_{xx}^{NL}\)) is observed for the square (CT-III) and elliptical cutout (CT-II) abided laminate. At the same time, the maximum normal stress (\(\overline{\sigma }_{yy}^{NL}\)) is observed for the laminate with a circular (CT-I) cutout. Further, the maximum variation in the in-plane stress (\(\overline{\tau }_{xy}^{NL}\)) is observed for the laminate with CT-III cutout.

Fig. 22
figure 22

Normal and in-plane transient stresses of an Es-a-supported SP-III laminate with cutout

Full size image

7 Conclusions

This work makes an effort to predict the geometrically nonlinear transient deflection of the laminated shell panel with the cutout of various shapes and sizes using the HSDT-based FE computational model. Also, a comparison in nonlinear dynamic responses is presented using Green–Lagrange and von Kármán strain. The uniform distribution of temperature in the thickness direction of the laminate is assumed, and the responses are calculated using temperature-dependent lamina properties. Initially, the necessary convergence and accuracy of the models were checked. The pertinency of the Green–Lagrange stain is determined by comparing with published and own experimental results. Based on the parametric study, the following conclusions are drawn:

  • The transient deflection and stress values obtained via the present computational model are aligned with the published and experimental results.

  • The NLM-II overpredicts the structural stiffness, i.e., lower deflection values are obtained compared to NLM-I.

  • The differences between the results obtained via NLM-I and NLM-II are more significant for the higher magnitude of the load and show the applicability of full geometrically nonlinear strain (Green–Lagrange) instead of von Kármán strain.

  • Comparative analysis of the transient deflection obtained by different pulse loads indicates that the maximum deflection is observed for the stepped pulse load.

  • The laminate with a square cutout (CT-III) shows the most flexible behavior compared to the laminate with other cutout shapes.

  • The spherical shell (SP-III) has the highest stiffness compared to other shell configurations, irrespective of cutout shapes.