1 Introduction

Herringbone gear is widely used in aviation, heavy machinery transmission and other fields, due to its small meshing impact, smooth transmission torque, high bearing capacity, and low axial force [1]. The dynamic characteristics of gear transmission directly affect the working performance of the whole equipment. With the development of mechanical equipment to large-scale, high reliability, high precision and long life, the requirements for the dynamic performance of gear transmission system are also increasing. It is becoming more and more important to accurately predict the dynamic performance of the system. In-depth dynamic research on the gear transmission system can lay a foundation for the safety, optimal design, and reliability evaluation of the mechanical equipment.

Extensive research works have been done on dynamic modeling and vibration analysis of gear transmission system [2, 3]. For the dynamics of herringbone gear transmission system, Choi et al. [4] used the finite element method to analyze the transverse, torsional and axial vibration characteristics of herringbone teeth. Sondkar and Kahraman [5] put forward a three-dimensional dynamic model of herringbone gear planetary system with gear meshing, bearing, and supporting accessories, and studied the effects of planetary phase angle, error and gear supporting conditions on the dynamic response of gear system. Chen et al. [6, 7] investigated the influence of runout and pitch error on the dynamic response of herringbone gear. Wang et al. [8] established a dynamic model of double helical gears considering axial vibration and side clearance. Dong et al. [9] built up a dynamic model of herringbone teeth based on Timoshenko beam and lumped parameter method, and verified it by experiments. Wang et al. [10] presented a model of double helical gears by taking the axial vibration and backlash into account. Liu et al. [11] developed an improved dynamic analysis model of double helical gear reducer using hybrid user-defined element method (HUELM). Yin et al. [12, 13] developed a bending–torsional–axial coupling model for dynamic analysis of double-helical gear system. They then carried out theoretical and experimental research on the dynamic characteristics of herringbone gear system by considering the oil film effect among meshing teeth.

However, most of the above researches on gear system dynamics are treated as deterministic problems. In practical engineering, uncertain factors widely exist in mechanical systems such as gear transmission [14,15,16,17], due to errors in manufacturing, processing, assembly, wear, lubrication and changes in operating environment. These uncertainties will affect the dynamic characteristics of the gear system. Guerine et al. [18] investigated the effects of random uncertainty of mass, damping coefficient, bending stiffness and torsion stiffness on the dynamic response of single-stage spur gear system. Yang et al. [19] studied the dynamic characteristics of gear transmission system under the combined action of deterministic and random excitations. Beyaoui et al. [20] explored the impact of random perturbation caused by aerodynamic torque excitation on the dynamic response of fan gear system. Mabrouk et al. [21] investigated the dynamic behavior of a bevel gear system with uncertainty associated to the performance coefficient of the input aerodynamic torque based on the projection on polynomial chaos. Fang et al. [22] proposed a dynamic model of spur gear pair and investigated the random effects of load and friction on its transient characteristics. Hajnayeb and Sun [23] studied the vibration caused by random machining error of gear tooth profile based on a simplified model of gear pair, and obtained the transfer function between manufacturing error and common measuring position. Wei et al. [24] provided a dynamic model of spur gear system with uncertain parameters, and studied the dynamic response of the system by using Chebyshev inclusion function. Fu et al. [25] explored the dynamic characteristics of wind turbines system under aleatory and epistemic uncertainties.

The above researches on the dynamic uncertainty of gear system are mainly focused on the spur gear system, while the research on the uncertainty of herringbone gear system is relatively less. In addition, most of the above studies are based on the pure torsion dynamic model of gear. In this paper, a dynamic model of herringbone gear-shaft-bearing system is established. The uncertainty of the system is modeled by PCE method, and the effects of gear meshing stiffness, bearing stiffness, and damping on the vibration response of the system are analyzed.

2 Dynamic model of gear transmission system

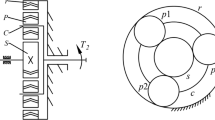
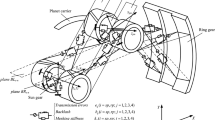
The herringbone gear transmission system investigated in this paper is shown in Fig. 1, which consists of a pair of herringbone gears, two gear shafts and two pairs of journal bearings. The design parameters of the system are listed in Table 1.

Fig. 1
figure 1

Schematic diagram of the herringbone system

Full size image
Table 1 Design parameters of the herringbone system
Full size table

2.1 Shaft model

As shown in Fig. 2, the shaft model is based on Timoshenko beam element by using the finite element method, which is divided into 41 nodes, each node has 6 degrees of freedom, including three translations and two rotations, expressed as x, y, z, θx, θy and θz. Using the Lagrange equation, the free vibration equation of the rotor can be expressed as

$${{\varvec{M}}}_{s}{\stackrel{..}{{\varvec{X}}}}_{s}+{{\varvec{C}}}_{s}{\stackrel{.}{{\varvec{X}}}}_{s}+{{\varvec{K}}}_{s}{{\varvec{X}}}_{s}=0,$$
(1)

where Ms, Cs and Ks are the mass matrix, damping matrix and stiffness matrix of shaft, respectively.

Fig. 2
figure 2

Typical rotor configuration and coordinate system

Full size image

The mass matrix of the shaft Ms can be written as:

$${{\varvec{M}}}_{{\text{s}}}={\text{diag}}\left\{{m}_{s1},{m}_{s1},{m}_{s1},{I}_{xs1},{I}_{ys1},{I}_{zs1},{m}_{s2},{m}_{s2},{m}_{s2},{I}_{xs2},{I}_{ys2},{I}_{zs2}\right\},$$

where msi and Iski are the mass and moment of inertia of the ith beam element, respectively, i = 1,2, k = x, y, z.

According to the theory of elasticity, the 12 × 12 stiffness matrix of Timoshenko beam element Ks can be obtained.

$${{\varvec{K}}}_{s}=\left[\begin{array}{cccccccccccc}\frac{AE}{L}& & & & & & & & & & & \\ 0& {a}_{x}& & & & & & & & & & \\ 0& 0& {a}_{y}& & & & & & & & & \\ 0& 0& 0& \frac{GJ}{L}& & & & & & {\text{Sym}}& & \\ 0& 0& -{c}_{y}& 0& {e}_{y}& & & & & & & \\ 0& {c}_{x}& 0& 0& 0& {e}_{x}& & & & & & \\ -\frac{AE}{L}& 0& 0& 0& 0& 0& \frac{AE}{L}& & & & & \\ 0& -{a}_{x}& 0& 0& 0& -{c}_{x}& 0& {a}_{x}& & & & \\ 0& 0& -{a}_{y}& 0& {c}_{y}& 0& 0& 0& {a}_{y}& & & \\ 0& 0& 0& \frac{GJ}{L}& 0& 0& 0& 0& 0& \frac{GJ}{L}& & \\ 0& 0& -{c}_{y}& 0& {f}_{y}& 0& 0& 0& {c}_{y}& 0& {e}_{y}& \\ 0& {c}_{x}& 0& 0& 0& {f}_{x}& 0& -{c}_{x}& 0& 0& 0& {e}_{x}\end{array}\right].$$
(2)
$$\left\{ {\begin{array}{*{20}c} {a_{x} = a_{y} = \frac{12EI}{{L^{3} \left( {1 + \varphi } \right)}},c_{x} = c_{y} = \frac{6EI}{{L^{2} \left( {1 + \varphi } \right)}}} \\ {e_{x} = e_{y} = \frac{{\left( {4 + \varphi } \right)EI}}{{L\left( {1 + \varphi } \right)}},f_{x} = f_{y} = \frac{{\left( {2 - \varphi } \right)EI}}{{L\left( {1 + \varphi } \right)}}} \\ \end{array} } \right.$$
(3)

where E is the Young’s modulus; μ is the Poisson’s ratio; A is the element cross-sectional area; L is the element length; G is the shear modulus; J is the torsional moment of inertia; I is the moment of inertia of diameter; φ is the shear influence factor, φ = 12EI/(GAKL2); K is the shearing coefficient, K = 6(1 + μ)/ (7 + 6μ).

The damping matrix of the shaft can be expressed as Cs = γKs, where γ is the proportional damping coefficient, where γ is 1 × 10–5 [26].

2.2 Gear model

2.2.1 Gear model

The gear mesh model is shown in Fig. 3, the gear consists of a pinion and a gear, which are represented by mesh stiffness kpg and meshing damping cpg along the mesh line. The rotation angular velocity of the pinion and gear are ω1 and ω2, respectively. The torque of the pinion and gear are T1 and T2, respectively. The static transmission error of gear epg(t) can be expressed as

$$e_{{{\text{pg}}}} \left( t \right) = e_{{{\text{pg}}}} \sin (\omega_{{\text{p}}} z_{{\text{p}}} t),$$
(4)
Fig. 3
figure 3

Gear mesh model

Full size image

The relative displacement of the gear pair along the line of action can be written as

$$\begin{aligned} {\varvec{V}} & = [\cos \beta_{{{\text{pg}}}} \sin \varphi_{{{\text{pg}}}} , \pm \cos \beta_{{{\text{pg}}}} \cos \varphi_{{{\text{pg}}}} ,\sin \beta_{{{\text{pg}}}} , \mp r_{{\text{p}}} \sin \beta_{{{\text{pg}}}} \sin \varphi_{{{\text{pg}}}} , \\ & \quad r_{{{\text{bp}}}} \sin \beta_{{{\text{pg}}}} \cos \varphi_{{{\text{pg}}}} , \pm r_{{{\text{bp}}}} \cos \beta_{{{\text{pg}}}} , - \cos \beta_{{{\text{pg}}}} \sin \varphi_{{{\text{pg}}}} , \mp \cos \beta_{{{\text{pg}}}} \cos \varphi_{{{\text{pg}}}} , \\ & \quad - \sin \beta_{{{\text{pg}}}} , \mp r_{{{\text{bg}}}} \sin \beta_{{{\text{pg}}}} \sin \varphi_{{{\text{pg}}}} , - r_{{{\text{bg}}}} \sin \beta_{{{\text{pg}}}} \cos \varphi_{{{\text{pg}}}} , \pm r_{{{\text{bg}}}} \cos \beta_{{{\text{pg}}}} ] \\ \end{aligned}$$
(5)

where rbp and rbg are the radius of the base circle of the pinon and the gear; β is the helix angle of the base circle; φpg is the angle between the end joint line and the y-axis, which varies with the rotation of the pinon

$$\varphi_{{{\text{pg}}}} = \left\{ {\begin{array}{*{20}l} {\varphi_{{{\text{pg}}}} - \alpha_{{{\text{pg}}}} } \hfill & {\quad {\text{counterclockwise}}} \hfill \\ { - \varphi_{{{\text{pg}}}} + \alpha_{{{\text{pg}}}} ,} \hfill & {\quad {\text{clockwise}}} \hfill \\ \end{array} ,} \right.$$
(6)

The motion coupling equation of gear pair can be expressed as

$${\varvec{M}}_{{{\text{pg}}}} \mathop {\varvec{X}}\limits^{..}_{{{\text{pg}}}} + \left( {{\varvec{C}}_{{{\text{pg}}}} + {\varvec{G}}_{{{\text{pg}}}} } \right)\dot{\user2{X}}_{{{\text{pg}}}} + {\varvec{K}}_{{{\text{pg}}}} {\varvec{X}}_{{{\text{pg}}}} = {\varvec{F}}_{{\text{m}}} ,$$
(7)

where Mpg is the gear mass matrix; Cpg is the gear mesh damping matrix; Gpg is the gyroscopic matrix; Kpg is the mesh stiffness matrix; Fm is the static transmission error excitation. They can be written as

$${\varvec{M}}_{{{\text{pg}}}} = {\text{diag}}\left\{ {m_{p} ,m_{p} ,m_{p} ,I_{xp} ,I_{yp} ,I_{zp} ,m_{g} ,m_{g} ,m_{g} ,I_{xg} ,I_{yg} ,I_{zg} } \right\},$$
(8)
$${\varvec{X}}_{{{\text{pg}}}} = \left\{ {x_{{\text{p}}} ,y_{{\text{p}}} ,z_{p} ,\theta_{xp} ,\theta_{yp} ,\theta_{zp} ,x_{g} ,y_{g} ,z_{g} ,\theta_{xg} ,\theta_{yg} ,\theta_{zg} } \right\}^{{\text{T}}} ,$$
(9)
$${\varvec{K}}_{{{\text{pg}}}} = k_{{{\text{pg}}}} .{\varvec{V}}^{T} .{\varvec{V}},$$
(10)
$${\varvec{C}}_{{{\text{pg}}}} = C_{{{\text{pg}}}} .{\varvec{V}}^{T} .{\varvec{V}},$$
(11)
$${\varvec{G}}_{{{\text{pg}}}} = \left[ {\begin{array}{*{20}c} {{\varvec{g}}_{{\text{p}}} } & 0 \\ 0 & {{\varvec{g}}_{{\text{g}}} } \\ \end{array} } \right],$$
(12)
$${\varvec{g}}_{p,g} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {I_{zp,g} \omega_{p,g} } & 0 & 0 \\ 0 & 0 & { - I_{zp,g} \omega_{p,g} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],$$
(13)
$${\varvec{F}}_{{\text{m}}} = k_{{{\text{pg}}}} {\varvec{V}}^{T} e_{{{\text{pg}}}} \left( t \right) + c_{{{\text{pg}}}} {\varvec{V}}^{T} \dot{e}_{{{\text{pg}}}} \left( t \right),$$
(14)
$${\varvec{F}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & {T_{{\text{p}}} } & 0 & 0 & 0 & 0 & 0 & {T_{{\text{g}}} } \\ \end{array} } \right],$$
(15)

2.2.2 Gear mesh stiffness

The main calculation methods for gear mesh stiffness include the potential energy method, the finite element method and the Ishikawa method [27]. Although the calculation cost of the finite element method is high, its calculation result is relatively more accurate. In this subsection, the gear mesh stiffness is obtained by using the finite element method. In order to reduce the calculation time, only the three-dimensional local mesh model of the gear is established, as shown in Fig. 4. Ignoring the influence of tooth profile error on contact analysis, the static transmission error during load is equal to the deformation of gear teeth, and the mesh stiffness Kn of gear can be expressed as the ratio of the load on the gear to the mesh deformation of gear teeth

$$K_{n} = \frac{{F_{n} }}{{\delta_{n} }},$$
(16)

where Fn is the normal load of the tooth surface; δn is the normal comprehensive elastic deformation of the tooth surface, which includes the contact elastic deformation caused by the local Hertz contact, the contact position deformation caused by the loaded bending of the gear teeth and the contact position displacement caused by the hub deformation [28].

Fig. 4
figure 4

Finite element model of the herringbone gear pair

Full size image

Consider a mesh cycle where the pinon from the mesh of one gear tooth to the mesh of the next tooth. In one circle, the rotation angle of the pinon is 7.826°. The angle is divided into 10 parts equally, and 11 discrete angle positions are obtained. Each angle position is loaded and solved, and the angular deformation is extracted. Then, the torsional mesh stiffness KT can be calculated

$$K_{{\text{T}}} = \frac{{T_{{\text{m}}} }}{\Delta \theta }.$$
(17)

where Tm is the drag torque; \(\Delta \theta\) is the angular deformation of gear mesh point.

The Fn and \(\Delta \theta\) can be calculated by the following equations

$$F_{{\text{n}}} = \frac{{T_{{\text{m}}} }}{{r_{{\text{p}}} \cos \alpha_{{\text{n}}} {\text{cos}}\beta_{{{\text{pg}}}} }} ,\quad \Delta_{\theta } = \frac{{\delta_{{\text{n}}} }}{{r_{{\text{p}}} }},$$
(18)

where r is the indexing circle radius of the pinon; \({\upalpha }_{n}\) is the normal pressure angle.

Substituting Eqs. (16) and (18) to Eq. (17), the mesh stiffness can be obtained

$$K_{n} = K_{T} .\frac{{4{\text{cos}}\beta_{{{\text{pg}}}} }}{{\left( {m_{n} z_{{\text{p}}} } \right)^{2} \cos \alpha_{n} }},$$
(19)

where mn the normal modulus; zp is the teeth number of the pinion.

With a drag torque of 26191 Nm, the equivalent meshing stiffness of three complete mesh cycles is obtained according to the above method, as shown in Fig. 5. For the convenience of modeling, the average mesh stiffness is Km = 2.28 × 107 N/mm. By substituting this stiffness value to Eq. (10), the gear meshing stiffness matrix can be obtained.

Fig. 5
figure 5

Mesh stiffness of the herringbone pair

Full size image

2.3 Bearing model

In this subsection, the DyRoBeS software is applied to calculate the stiffness and damping of the bearing. DyRoBeS is a commercial software for bearing and rotor dynamic characteristics analysis, which is widely used in rotor dynamic field.

The fluid film journal bearings are used in the investigated herringbone gear transmission system. For simplicity, the bearing is simplified to massless spring and damping. The stiffness and damping of the bearings can be obtained by using the DyRoBeS bearing module. The calculation results are shown in Fig. 6 and Table 2. According to the node position of the bearing in the actual transmission system, the stiffness and damping matrix of the bearings are then integrated to the system matrix.

Fig. 6
figure 6

Calculation results of the bearing stiffness and damping

Full size image
Table 2 Bearing stiffness and damping
Full size table

2.4 Gear-shaft-bearing model

The mass matrix, damping matrix, gyroscopic matrix, stiffness matrix and mesh effect of each shaft segment, as well as the stiffness and damping matrix of bearings are assembled according to the node position, and the dynamic equation of the system is obtained.

$${\varvec{M}}\mathop {\varvec{X}}\limits^{..} + \left( {{\varvec{C}} + \Omega {\varvec{G}}} \right)\dot{\user2{X}} + {\varvec{KX}} = {\varvec{q}},$$
(20)

where M, C, G, and K are the mass matrix, damping matrix, gyroscopic matrix and stiffness matrix of the system, respectively; q is the excitation includes static transmission error excitation and external torque excitation.

Equation (20) can be transformed into frequency domain analysis and expressed as

$${\varvec{A}}\left( \omega \right){\varvec{X}}\left( \omega \right) = {\varvec{Q}}\left( \omega \right),$$
(21)

where

$${\varvec{A}}\left( \omega \right) = - \omega^{2} {\varvec{M}} + i\omega \left( {{\varvec{C}} + {\varvec{G}}} \right) + \varvec{K},$$
(22)
$${\varvec{X}} = Xe^{i\omega t} ,{\varvec{Q}} = Qe^{i\omega t} ,$$
(23)

3 Uncertainty model

The model parameters such as mass, stiffness and damping in Eq. (20) are uncertain due to the influence of geometric factors or material parameters. These factors lead to the uncertainty of the response of the system. Therefore, in the dynamic analysis of gear-rotor system, the A, X, and Q should be regarded as a random process. If the uncertain parameters in the gear rotor system are represented as random variables, the stochastic dynamics equation of the system can be expressed as

$${\varvec{A}}\left( \tau \right){\varvec{X}}\left( \tau \right) = {\varvec{Q}}\left( \tau \right),$$
(24)

where

$${\varvec{A}}\left( \tau \right) = - \omega^{2} {\varvec{M}}\left( \tau \right) + i\omega \left( {{\varvec{C}}\left( \tau \right) + {\varvec{G}}\left( \tau \right)} \right) + {\varvec{K}}\left( \tau \right),$$
(25)

where τ is the random characteristic of the uncertain parameters.

There are many methods for uncertainty analysis of stochastic processes, the most common of which is Monte Carlo method. However, the MCS method has a large amount of calculation, thus it is usually used as a reference method for uncertainty analysis. PCE method is a relative novel method for uncertainty analysis. With its good mathematical basis and the ability to accurately describe the randomness of random variables with arbitrary distribution, PCE has been more and more widely used in the field of dynamic analysis in recent years [29]. PCE is an uncertainty propagation method based on polynomial chaotic theory. It possesses good mathematical basis and the ability to accurately describe the randomness of random variables with arbitrary distribution. In PCE, the sum of orthogonal polynomials corresponding to the distribution of input parameters is used to approximately represent a random output process. In this section, the PCE method is used to construct the uncertainty model of the gear system.

3.1 Model building

The Askey scheme is the foundation of PCE model construction [30]. It points out the optimal orthogonal polynomial basis function corresponding to different distribution types of random variables. The PCE model can be constructed by selecting the corresponding orthogonal basis function according to the distribution type of input variables. For a random variable Y, the Hermite polynomial can be expressed as

$$\begin{aligned} Y\left( \theta \right) & = c_{0} I_{0} + \mathop \sum \limits_{{i_{1} = 1}}^{\infty } c_{{i_{1} }} I_{1} \left( {\xi_{{i_{1} }} \left( \theta \right)} \right) + \mathop \sum \limits_{{i_{1} = 1}}^{\infty } \mathop \sum \limits_{{i_{2} = 1}}^{{i_{1} }} c_{{i_{1} i_{2} }} I_{2} \left( {\xi_{{i_{1} }} \left( \theta \right),\xi_{{i_{2} }} \left( \theta \right)} \right), \\ & \quad + \;\mathop \sum \limits_{{i_{1} = 1}}^{\infty } \mathop \sum \limits_{{i_{2} = 1}}^{{i_{1} }} \mathop \sum \limits_{{i_{3} = 1}}^{{i_{2} }} c_{{i_{1} i_{2} i_{3} }} I_{3} \left( {\xi_{{i_{1} }} \left( \theta \right),\xi_{{i_{2} }} \left( \theta \right),\xi_{{i_{3} }} \left( \theta \right)} \right) + \cdots \\ \end{aligned}$$
(26)

where \(\theta\) represents the random variable, which will be omitted in the following equations for simplicity; \(I_{n} \left( {\xi_{{i_{1} }} \left( \theta \right),\xi_{{i_{2} }} \left( \theta \right), \ldots ,\xi_{{i_{n} }} \left( \theta \right)} \right)\) denotes a mixed orthogonal polynomial of order n, which is a function of multidimensional standard random variables \(\xi_{{i_{1} }} ,\xi_{{i_{2} }} , \ldots ,\xi_{{i_{n} }}\).

In general, the dimension of \({ }\xi = [\xi_{{i_{1} }} ,\xi_{{i_{2} }} , \ldots ,\xi_{{i_{n} }} ]\) is the same as that of the random input variable \(X = [X_{1} ,X_{2}, \ldots ,X_{n} ]\) in the original random space. Therefore, Eq. (26) can be simplified as

$$Y = \mathop \sum \limits_{i = 0}^{\infty } c_{i} \psi_{i} \left( \xi \right).$$
(27)

where \(C_{i}\) and \(\psi_{i}\) correspond to \(\alpha_{{i_{1} i_{2} }} ..._{{i_{n} }}\) and \(I_{n} \left( {\xi_{{i_{1} }} ,\xi_{{i_{2} }} ,\xi_{{i_{3} }} , \ldots } \right)\) in Eq. (27), respectively; \(C_{i}\) is the chaotic polynomial coefficient to be solved, when it is calculated, MCS can be run on the chaotic polynomial model, and the random probability characteristic of the output response Y can be obtained.

The number of terms in Eq. (27) is infinite, in order to reduce the amount of calculation, it is usually truncated at a certain order p, and the corresponding model can be expressed as

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y} = \mathop \sum \limits_{i = 0}^{P} c_{i} \psi_{i} \left( \xi \right).$$
(28)

The number of coefficients in a truncated polynomial can be determined by the following equation

$$N = \frac{{\left( {d + p} \right)!}}{d!p!}.$$
(29)

where d is the dimension of the random variable.

The random parameters can be expanded by Karhunen–Loeve method, and the stochastic dynamic equation of gear-rotor system is obtained

$$\left( {\sum\limits_{i = 0}^{\infty } {\{ A\}_{i} } \psi_{i} \left( {\xi \left( \tau \right)} \right)} \right)\left( {\sum\limits_{j = 0}^{\infty } {\{ X\}_{j} } \psi_{j} \left( {\xi \left( \tau \right)} \right)} \right) = \left( {\sum\limits_{k = 0}^{\infty } {\{ Q\}_{k} } \psi_{k} \left( {\xi \left( \tau \right)} \right)} \right),$$
(30)

where \(\psi_{i} \left( {\xi \left( \tau \right)} \right)\) denotes the chaotic orthogonal polynomial of order p, which is composed of the product of 1-dimensional orthogonal polynomial corresponding to each dimensional random variable; \(\{ A\}_{nn}\) represents the coefficient of the nn’th orthogonal polynomial corresponding to \(\psi_{nn} \left( {\xi \left( \tau \right)} \right)\) and nn = i, j, k.

3.2 PCE coefficients calculation

In this subsection, the stochastic response surface method (SRSM) is used to calculate the PCE coefficients. The calculation process is mainly divided into three steps: the selection of sample points, the calculation of response value and the estimation of PCE coefficient.

The Latin hypercube design (LHD) approach is used to extract the sample points. The sampling points should be selected in the standard random space, which means that each dimension in the space is a standard random variable from the Askey scheme. Selecting N sample points in the standard random space can be expressed as

$${{\varvec{\upxi}}}^{s} = \left[ {\xi_{1}^{s} , \cdots ,\xi_{j}^{s} , \cdots ,\xi_{N}^{s} } \right]^{T} .$$
(31)

The original random variable is usually not a standard random variable. In order to obtain the real response value, the sampling point on the standard random space ξ should be transformed into its original random space X

$${\text{X}}^{s} = \left[ {X_{1}^{s} , \cdots ,X_{j}^{s} , \cdots ,X_{N}^{s} } \right]^{{\text{T}}} .$$
(32)

The transformed sample points are then brought into the original response function, and the response value at the sample is

$$F\left( X \right) = \left[ {F\left( {X_{1}^{s} } \right), \cdots ,F\left( {X_{j}^{s} } \right), \cdots ,F\left( {X_{N}^{s} } \right)} \right]^{T} .$$
(33)

The PCE coefficients can be estimated by least quadratic regression method. The sample points and function response values are substituted into (28), and the following equation can be obtained

$${\varvec{Ac}} = {\varvec{Y}}\user2{.}$$
(34)

where

$${\varvec{A}} = \left[ {\begin{array}{*{20}c} {\Phi_{0} \left( {\xi_{1}^{s} } \right)} & {\Phi_{1} \left( {\xi_{1}^{s} } \right)} & \cdots & {\Phi_{P} \left( {\xi_{1}^{s} } \right)} \\ {\Phi_{0} \left( {\xi_{2}^{s} } \right)} & {\Phi_{1} \left( {\xi_{2}^{s} } \right)} & \cdots & {\Phi_{P} \left( {\xi_{2}^{s} } \right)} \\ \vdots & \vdots & \cdots & \vdots \\ {\Phi_{0} \left( {\xi_{N}^{s} } \right)} & {\Phi_{1} \left( {\xi_{N}^{s} } \right)} & \cdots & {\Phi_{P} \left( {\xi_{3}^{s} } \right)} \\ \end{array} } \right].$$
(35)
$${\varvec{c}} = \left[ {\begin{array}{*{20}c} {c_{0} } \\ {c_{1} } \\ \vdots \\ {c_{N} } \\ \end{array} } \right].$$
(36)
$${\varvec{Y}} = \left[ {\begin{array}{*{20}c} {F\left( {X_{1}^{s} } \right)} \\ {F\left( {X_{2}^{s} } \right)} \\ \vdots \\ {F\left( {X_{N}^{s} } \right)} \\ \end{array} } \right].$$
(37)

According to the least square regression, the PCE coefficient can be calculated

$${\varvec{c}} = \left( {AA^{T} } \right)^{ - 1} A^{T} {\varvec{Y}}\user2{.}$$
(38)

4 Uncertainty analysis of vibration response

The mesh stiffness and bearing stiffness are important parameters that affect the dynamic characteristics of gear rotor system. In engineering, due to assembly error, bearing clearance tolerance, gear wear, operating conditions and other factors, the mesh stiffness and bearing stiffness and damping of gear system are actually uncertain parameters, which will lead to errors if deterministic parameters are used in dynamic modeling. In this section, the uncertainty of gear rotor vibration response is investigated by considering the uncertainty of meshing stiffness, bearing stiffness and damping.

The dynamic model of the herringbone gear rotor system with deterministic parameters in Table 1 is established and solved. The Campbell diagram of the system is then obtained and shown in Fig. 7. The first eight critical speeds of the system are 525 r/min, 5709 r/min, 5929 r/min, 7603 r/min, 9217 r/min, 116,190 r/min, 12135 r/min, respectively. It can be seen that the gear rotor system will experience many oscillations when increasing speed. The frequency response of each node of the system is shown in Fig. 8. In order to facilitate the analysis, the vibration response in the X direction of node 11 is selected to study. At the same time, the third critical speed 5929r/min and its nearby speed region [5600 6100] r/min are selected to study, and the corresponding vibration response is shown in Fig. 9. It should be pointed out that logarithmic coordinates are used here to better reflect the variation of amplitude with rotational speed.

Fig. 7
figure 7

Campbell diagram of the system

Full size image
Fig. 8
figure 8

Frequency response of the system

Full size image
Fig. 9
figure 9

Vibration amplitude of the system with deterministic parameters

Full size image

4.1 Mesh stiffness uncertainty

Considering the uncertainty of the meshing stiffness, it is expressed as interval parameters [km-ξkm km, km + ξkm km], km and ξkm are average meshing stiffness and deviation coefficient, respectively. The order p of PCE is set to 6 in this paper and the results are compared with those obtained with the Monte Carlo method (20,000 samplings). It can be seen from Fig. 10, when ξkm = 0.1, the PCE-mean curves are superposed almost perfectly with those of Monte Carlo. It should be noted that only ξkm = 0.1 is selected here for simplicity.

Fig. 10
figure 10

Amplitude–frequency response of the system with uncertain mesh stiffness when ξkm = 0.1

Full size image

When ξkm = 0.05, 0.1 and 0.15, the upper and lower boundaries of the amplitude–frequency response of the system are obtained as shown in Fig. 11. Note that the sampling points are encrypted here for better comparison. It can be seen that the interval value of the vibration amplitude increases with the increase of ξkm, especially near the resonance region of the system, which indicates that the dynamic characteristics of the system near the resonance region are more sensitive to the uncertainty of mesh stiffness. It can also be found that when ξkm increases, the upper boundary of the response region of the resonance region shifts to the right and the lower boundary of the region shifts to the left, compared with the system response results under deterministic parameters. This is mainly because the mesh stiffness leads to the change of the natural frequency, which has a direct impact on the resonance peak.

Fig. 11
figure 11

Amplitude–frequency response of the system with uncertain mesh stiffness

Full size image

4.2 Bearing stiffness uncertainty

Considering the uncertainty of the bearing stiffness, in order to simplify the analysis, the four stiffnesses of the bearing take the same deviation coefficient. The uncertainty of bearing stiffness can be expressed as [kb-ξkbkb, kb + ξkbkb], kb and ξkb are the average bearing stiffness and deviation coefficient, respectively. It can be seen from Fig. 12, when ξkb = 0.1, the PCE-mean curves are superposed almost perfectly with those of Monte Carlo method. When ξkb = 0.05, 0.1 and 0.15, the upper and lower boundaries of the amplitude–frequency response of the system are obtained as shown in Fig. 13. It can be seen that there is no obvious deviation between the upper and lower boundary values of the vibration amplitude of the system, indicating that the uncertainty of bearing stiffness has little influence on the frequency domain response of the gear system.

Fig. 12
figure 12

Amplitude–frequency response of the system with uncertain bearing stiffness when ξkb = 0.1

Full size image
Fig. 13
figure 13

Amplitude–frequency response of the system with uncertain bearing stiffness

Full size image

4.3 Bearing damping uncertainty

Considering the uncertainty of the bearing damping, the four dampings take the same deviation coefficient. The uncertainty of bearing damping can be expressed as [cb-ξcb cb, cb + ξcb cb], cb and ξcb are the average damping and deviation coefficient of bearing, respectively. It can be seen from Fig. 14, when ξcb = 0.1, the PCE-mean curves are superposed almost perfectly with those of Monte Carlo. When ξcb = 0.05, 0.1 and 0.15, the vibration response of the system is obtained as shown in Fig. 15. It can be seen that there is no obvious deviation between the upper and lower boundary values of the vibration amplitude of the system. In addition, the impact of the uncertainty of bearing damping on the frequency domain response of the system is mainly concentrated in the resonance region, but has no obvious effect on other speed regions. The reason for this difference is that changing the bearing damping will change the amplitude of the dynamic response, especially in the resonance region.

Fig. 14
figure 14

Amplitude–frequency response of the system with uncertain bearing damping when ξcb = 0.1

Full size image
Fig. 15
figure 15

Amplitude–frequency response of the system with uncertain bearing damping

Full size image

4.4 Hybrid uncertainty

Considering the uncertainty of gear meshing stiffness, bearing stiffness and damping, taking different deviation coefficients, the amplitude–frequency response of the system is obtained as shown in Fig. 16. It can be seen that the upper and lower boundary values of the vibration amplitude of the system are obviously offset under different deviation coefficients. In Fig. 16a, the deviation of the upper and lower boundary value of the system amplitude is the most obvious when ξkm changes, indicating that the uncertainty of mesh stiffness has a greater influence on the natural frequency of the system. The deviations of the upper and lower limits of the system amplitude in Fig. 16b and c are mainly due to the impact of ξkm. In addition, the amplitude variation in Fig. 16c is more obvious than that in Fig. 16b. This is mainly because the uncertainty of bearing damping has a greater influence on the amplitude of the dynamic response of the system.

Fig. 16
figure 16

Amplitude–frequency response of the system with hybrid uncertainty. a Amplitude–frequency response with ξkm = 0.05, 0.1, 0.15 and ξkb = ξcb = 0.05. b Amplitude–frequency response with ξkb = 0.05, 0.1, 0.15 and ξkm = ξcb = 0.05. c Amplitude–frequency response with ξcb = 0.05, 0.1, 0.15 and ξkm = ξkb = 0.05

Full size image

5 Conclusions

There are a large number of uncertainties in the gear transmission system, which makes the stiffness, damping and load parameters of the system have a certain degree of uncertainty. It is of great significance for gear system design and reliability analysis to correctly estimate the influence of these uncertain parameters on the dynamic characteristics of the system. In this paper, the dynamic models of gear, shaft and bearing aiming in a herringbone gear transmission system, are established, respectively, and the dynamic model of the system is obtained after integration. The uncertainty of the system is modeled by the PCE method, and the influence of the uncertain parameters on the vibration response of the system is analyzed. The main conclusions are as follows:

  1. 1.

    The influence level of the uncertainty of different parameters is different. With the increase of the uncertainty of mesh stiffness, the upper boundary of the vibration response region of the system resonance region shifts to the right and the lower boundary of the interval shifts to the left.

  2. 2.

    The influence of the uncertainty of bearing damping on the frequency domain response of the system is mainly concentrated in the resonance region, but has no obvious effect on other speed regions. The uncertainty of bearing stiffness has little influence on the system response.

  3. 3.

    The influence of mixed uncertainty on the vibration response of the system is comprehensive, and the greater the uncertainty deviation coefficient of a parameter, the greater the influence on the vibration response of the system.