1 Introduction

The herringbone planetary gear system has the advantages of a high contact ratio and high load-carrying capacity, which is widely used in high-speed and heavy-load fields such as aerospace, ships, and vehicles. However, the working environment of the herringbone gear is complex and affected by various nonlinear factors, the system is easy to enter an unstable motion state during meshing transmission, which causes premature failure of the gear. Further research on the nonlinear characteristics of herringbone planetary gears and the influence laws of various parameters on system stability is necessary.

Gears are widely used in various fields, and many scholars have conducted corresponding dynamic research in the gear transmission systems for different scenarios. Chen [1] et al. established a finite element model of a planetary gear system for wind turbines and studied the dynamic characteristics of the system under different loads. Yang [2] et al. studied the two-stage planetary gear reducer used in mining and analyzed the radiation noise of the system by deriving the dynamic meshing contact equation and transmission frequency response. Wang [3] et al. established a torsional nonlinear dynamic model of the aircraft engine transmission system and proved the gear system existence of different nonlinear dynamic characteristics by the bifurcation diagram, FFT spectrogram, etc. Xiang [4] et al. developed a nonlinear dynamic model of the multistage gear system to analyze the effect of tooth crack faults on the wind turbine gear system. The effect of different factors on the bifurcation characteristics of the system is analyzed by the bifurcation diagrams, phase diagrams, and frequency spectrogram. Fan [5] et al. take the helicopter planetary gear train as the research object and researched the impact of carrier plate crack on system dynamic characteristics considering damping, gear tooth backlash, and time-varying meshing stiffness. In order to improve the dynamic stability of the herringbone planetary gear transmission system, many scholars have made a series of research results in the field of gear dynamic characteristics, which has important reference significance for this paper. Wang [6] et al. study the load sharing performance of the herringbone planetary gear system, a dynamic model of the planetary gear system with flexible pins considering the effects of meshing stiffness and brace stiffness is established. The results showed that increasing input speed and reducing input power can decrease the load performance of the system. Li [7] et al. developed a herringbone planetary gear model to study the factors affecting gear efficiency, and the effects of installation error and torque on gear load coefficient are analyzed under multiple load cases. Guo [8] et al. developed a dynamic model of a herringbone planetary gear system considering the influence of eccentricity error, and the impact of operating frequency changes on the nonlinear characteristics of the system is analyzed by using bifurcation diagrams and phase diagrams. Mo [9] et al. established a dynamic model of a herringbone planetary gear system considering support stiffness, meshing error, and staggered angle. The dynamic characteristics of the system are analyzed under different factors. The results showed that the staggered angle and support stiffness have a significant impact on the dynamic characteristics of the system. Li [10] et al. study the effects of different factors on the dynamic characteristics of herringbone gear transmission systems by combining the bifurcation diagram, phase diagram, and Poincare diagram under three-dimensional modification and unmodified conditions. The gear system has the nonlinear dynamic characteristics of multiple variables. For the impact of different factors on the system, scholars have also made many research results. Wang [11] et al. analyzed the effect of meshing damping ratio on the nonlinear dynamics of the system under low and heavy load conditions by considering gear backlash, time-varying stiffness, and meshing error. The results show that the meshing damping ratio has a greater impact on the system under low load conditions and a smaller impact on the system under heavy load conditions. Dong [12] et al. developed the bending-torsion coupling model of planetary gear and analyzed the influence laws of input speed and gear backlash on the system dynamic characteristics by time course chart and phase chart, etc. Wang [13] et al. studied the influence of different excitation frequencies on the nonlinear characteristics of the single-stage spur gear system by considering gear backlash and time-varying stiffness. Hu [14] et al. established a dynamic model of the multistage planetary gear system considering tooth crack faults, and the nonlinear characteristics of the system at different speeds are analyzed under fault and no-fault conditions by combining with kinematic characteristic images such as bifurcation diagram and phase diagram. Liu [15] et al. introduce the effect of temperature change and study the temperature effect on the dynamic characteristics of the planetary gear system. The results show that high temperatures can make the displacement and load of the system stronger. Xiao [16] et al. considered the factors such as backlash and friction, and the dynamic behavior of the system is analyzed under different load conditions by bifurcation diagram, frequency spectra diagram, and phase diagram. Most of the existing studies ignore the effect of temperature on the gear transmission system. Wang [17] et al. considered the influence of temperature on the system, but only the nonlinear analysis have been done on a single degree of freedom spur cylindrical gear system. Ren [18] and Xu [19] et al. established a dynamic model of the herringbone planetary transmission system that includes multiple factors such as meshing stiffness and engagement error. However, they did not consider the influence of the temperature effect on the nonlinear characteristics of the herringbone planetary gear. Currently, studies on the nonlinear dynamic characteristics of herringbone planetary gear systems considering factors such as temperature effect, engagement damping, and time-varying stiffness simultaneously are lacking. With the increasing popularity of herringbone planetary gear train transmission systems in various fields, it is urgent to delve into the study of temperature effects on their influence law of nonlinear characteristics.

In this paper, a nonlinear dynamics model of herringbone planetary gear with multiple factor effects is developed based on the principle of thermal deformation introducing the effect of temperature on gear backlash, and taking into account the time-varying meshing stiffness, engagement damping, and engagement error, etc. The nonlinear dynamic characteristic of the system is studied by the bifurcation diagram, maximum Lyapunov index diagram, time domain diagram, spectrogram, phase diagram, and Poincare diagram to analyze the impact law of temperature and damping ratio changes on the bifurcation features of the gear system, which provide a theoretical basis for the optimal design of the dynamic structure stability of herringbone planetary gear.

2 Multiple factors herringbone planetary gear system nonlinear dynamics model considering temperature effect

2.1 Herringbone planetary gear model establishment

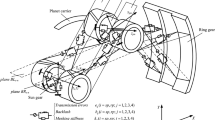
The composition and transmission principle of herringbone planetary gear are shown in Fig. 1. The model mainly consists of sun gear (s), planetary gear (pi), inner gear ring (r), and planetary carrier (c). The input torque T1 acts on the sun gear, and the output torque T2 acts on the planetary carrier output shaft. All gears are herringbone gears in the system, and each herringbone gear is regarded as two identical helical gears with opposite rotation directions.

Fig. 1
figure 1

Structural diagram of herringbone planetary gears

Full size image

The following assumptions are made for the drive train in establishing the nonlinear dynamic model:

  1. (1)

    Elastic deformation of support is neglected in the model. Assuming that the support stiffness between gears is very high, only the torsional displacement of meshing gears is studied.

  2. (2)

    Each rotating body is symmetric about its torsional center in the model, and the gears are considered rigid and have the same physical properties.

  3. (3)

    Friction caused by sliding of gear teeth is ignored.

  4. (4)

    The influence of bending, shearing, and torsional rigidity of intermediate chamfer of herringbone gear on its transmission is not considered.

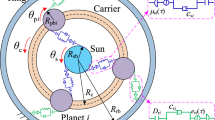
Based on the above assumptions, the nonlinear dynamic model of herringbone gear planetary gear system established by the lumped-parameter method is shown in Fig. 2. θm represents the torsional angular displacement of each component, β is the helix angle of the gear base circle. The superscript L, R represent the left and right sides of the herringbone gear, respectively. The subscript spi represents the meshing pair between the sun gear and the i-th planetary gear. The subscript rpi represents the meshing pair between the internal ring gear and the i-th planetary gear. espi, cspi, kspi, bspi represent the engagement error, engagement damping, engagement rigidity, and tooth side clearance between the sun wheel and the i-th planetary wheel, respectively. For the same reason, erpi, crpi, krpi, brpi represent the relevant parameters between the internal ring gear and the i-th planetary gear, respectively.

Fig. 2
figure 2

Dynamic model of herringbone planetary gear transmission system

Full size image

2.2 Temperature effect on the gear backlash

The gear system is designed and installed with reserve a small amount of clearance to avoid jamming of the teeth due to thermal expansion during meshing transmission, as shown in Fig. 3. In order to express the influence of backlash on system dynamics, the backlash is treated as symmetry as shown in Fig. 4. Then the gear backlash function f (x) of the system can be expressed as [4]:

$$f(x) = \begin{cases} x \,- b \, & x > b \hfill \\ 0\,& { | }x| \le b \hfill \\ x + b \, & x < - b \hfill \\ \end{cases}$$
(1)

where: x represents the relative displacement of the meshing gear pair on the meshing line. When x > b, the gear teeth engage forward. When -b < x < b, the gear teeth detach. When x < -b, the gear teeth engage in reverse.

Fig. 3
figure 3

Gear clearance diagram

Full size image
Fig. 4
figure 4

Nonlinear function of the gear clearance

Full size image

In the gear dynamics model, the backlash function describes the reflects the influence of the tiny backlash on the kinematic characteristics of the gear transmission system. Therefore, the backlash change has a significant impact on the nonlinear characteristics of the gear system. The gear has thermal deformation under the influence of temperature, which results in a smaller clearance between gear backlash and further affects the nonlinear dynamic characteristics of the gear system. For the herringbone planetary gears system, the reduction of the backlash Δb caused under the influence of temperature effect can be expressed as [17, 20]:

$$\left\{ \begin{gathered} \Delta b_{spi}^{u} = \Delta T\gamma (1 + \Delta T\gamma )m_{t} \pi + [m_{t} \Delta T\gamma (z_{s} + z_{p} )\sin a^{\prime}]/2 \hfill \\ \Delta b_{rpi}^{u} = \Delta T\gamma (1 + \Delta T\gamma )m_{t} \pi + [m_{t} \Delta T\gamma (z_{r} + z_{p} )\sin a^{\prime}]/2 \hfill \\ \end{gathered} \right.$$
(2)

where: zs, zp, and zr are the number of teeth of the sun wheel, planetary wheel, and internal ring gear, respectively; Symbols u = (L, R) represents the left and right sides of the herringbone gear; mt is the gear transverse module; ΔT is the gear temperature rise; γ is the gear's coefficient of linear expansion; αˊ is the angle of engagement after thermal deformation.

Consequently, the gear backlash is redefined under the impact of temperature effect as:

$$\left\{ \begin{gathered} b_{{spi}}^{{{u'}}} = b - \Delta b_{{spi}}^{u} /2 \hfill \\ b_{{rpi}}^{{u'}} = b - \Delta b_{{rpi}}^{u} /2 \hfill \\ \end{gathered} \right.$$
(3)

where: 2bˊ is the gear backlash by considering the temperature effect.

Then the clearance function f (x(t)) of internal and external engagement pairs influenced by the temperature effect as:

$$f(x_{j}^{u} (t)) = \begin{cases} x_{j}^{u} (t) - b_{j}^{{{u^{\prime}}}} & x_{j}^{u} (t) > b_{j}^{{{u^{\prime}}}} \, \hfill \\ 0 & { | }x_{j}^{u} (t)| \le b_{j}^{{{u^{\prime}}}} \, \hfill \\ x_{j}^{u} (t) + b_{j}^{{{u^{\prime}}}} & x_{j}^{u} (t) < - b_{j}^{{{u^{\prime}}}} \, \hfill \\ \end{cases} \, j = spi,rpi$$
(4)

2.3 Gear time-varying meshing stiffness

The meshing stiffness represents the ability of gear teeth to resist deformation, which is one of the excitations for studying the dynamic characteristics of gears. According to the knowledge of material mechanics and elastic mechanics, the total stiffness of a single-tooth meshing of the gear system is expressed as [21, 22]:

$$k_{e1} = \frac{1}{{\frac{1}{{k_{h} }} + \frac{1}{{k_{a1} }} + \frac{1}{{k_{b1} }} + \frac{1}{{k_{s1} }} + \frac{1}{{k_{f1} }} + \frac{1}{{k_{a2} }} + \frac{1}{{k_{b2} }} + \frac{1}{{k_{s2} }} + \frac{1}{{k_{f2} }}}}$$
(5)

where: kh is contact stiffness, ka is compression stiffness, kb is bending stiffness, ks is shear stiffness, kf is the flexible stiffness, and subscripts 1, 2 represent active and passive gears, respectively.

When there are two pairs of gear teeth for meshing, the total meshing stiffness of the gear system is expressed as follows.

$$k_{e} = k_{e1} + k_{e2} = \sum\limits_{i = 1}^{2} {\frac{1}{{\frac{1}{{k_{h,i} }} + \frac{1}{{k_{a1,i} }} + \frac{1}{{k_{b1,i} }} + \frac{1}{{k_{s1,i} }} + \frac{1}{{k_{f1,i} }} + \frac{1}{{k_{a2,i} }} + \frac{1}{{k_{b2,i} }} + \frac{1}{{k_{s2,i} }} + \frac{1}{{k_{f2,i} }}}}}$$
(6)

Under the influence of the system coincidence degree, the gear single and double pairs of teeth alternately intermesh in periodic transmission, which causes the gear meshing stiffness periodic time variation. It can be expressed as a computational formula for Fourier series expansion.

$$k(t) = k_{m} + \sum\limits_{j = 1}^{n} {k_{j} \cos (j\omega t + \varphi_{a} )}$$
(7)

where: km is the average engagement stiffness, kj is the j-order amplitude of stiffness fluctuations, ω is the meshing frequency, and φa is the initial phase angle of the meshing stiffness.

In the calculation process of this paper, which takes the first-order harmonic component of the time-varying meshing stiffness, the expression of the time-varying meshing stiffness of inner and outer engaging pairs of herringbone planetary gears is expressed as follows.

$$\left\{ \begin{gathered} k_{spi}^{L} (t) = k_{mspi}^{L} [1 + k\cos (\omega_{m} t + \varphi_{aspi}^{L} )] \hfill \\ k_{spi}^{R} (t) = k_{mspi}^{R} [1 + k\cos (\omega_{m} t + \varphi_{aspi}^{R} )] \hfill \\ k_{rpi}^{L} (t) = k_{mrpi}^{L} [1 + k\cos (\omega_{m} t + \varphi_{arpi}^{L} )] \hfill \\ k_{rpi}^{R} (t) = k_{mrpi}^{R} [1 + k\cos (\omega_{m} t + \varphi_{arpi}^{R} )] \hfill \\ \end{gathered} \right.$$
(8)

where: k is the stiffness coefficient. (Assuming that the stiffness coefficient of each engagement pair is the same).

2.4 Gear meshing error and engagement damping

The gear pair has transmission errors and eccentric errors by reason of Manufacturing and installation during the gear meshing process. Similar to the time-varying meshing stiffness, the meshing error can also be written as the Fourier series expansion [23]:

$$e(t) = e_{m} + \sum\limits_{i = 1}^{n} {e_{j} \sin (j\omega t + \varphi_{b} )}$$
(9)

where: em is the average meshing error, ej is the j-order fluctuation amplitude reflecting the change in meshing error, ω is the meshing frequency, and φb is the initial phase angle of the meshing error.

In the calculation process of this paper, which takes the first-order harmonic component of the meshing error, and the meshing error expression of the herringbone planetary gear internal and external engaging pair can be written as:

$$\left\{ \begin{gathered} e_{spi}^{L} (t) = e_{mspi}^{L} \sin (\omega_{m} t + \varphi_{bspi}^{L} ) \hfill \\ e_{spi}^{R} (t) = e_{mspi}^{R} \sin (\omega_{m} t + \varphi_{bspi}^{R} ) \hfill \\ e_{rpi}^{L} (t) = e_{mspi}^{L} \sin (\omega_{m} t + \varphi_{brpi}^{L} ) \hfill \\ e_{rpi}^{R} (t) = e_{mspi}^{R} \sin (\omega_{m} t + \varphi_{brpi}^{R} ) \hfill \\ \end{gathered} \right.$$
(10)

Damping plays a significant role in maintaining the transmission stability of the system. The damping ratio is an important parameter to measure the degree of vibration system damping, which can affect the dynamic response characteristics of the system. It is defined as the ratio of the actual viscous damping coefficient to the critical damping coefficient. There is no accurate formula to calculate the damping value at the moment, and the meshing damping of the gear pair is mainly calculated by the empirical formula [24].

$$\left\{ \begin{gathered} c_{spi}^{L} = 2\xi \sqrt {k_{mspi}^{L} /(1/M_{s}^{L} + 1/M_{p}^{L} )} \hfill \\ c_{spi}^{R} = 2\xi \sqrt {k_{mspi}^{R} /(1/M_{s}^{R} + 1/M_{p}^{R} )} \hfill \\ c_{rpi}^{L} = 2\xi \sqrt {k_{mrpi}^{L} /(1/M_{r}^{L} + 1/M_{p}^{L} )} \hfill \\ c_{rpi}^{R} = 2\xi \sqrt {k_{mrpi}^{R} /(1/M_{r}^{R} + 1/M_{p}^{R} )} \hfill \\ \end{gathered} \right. \,$$
(11)

where: \(M_{j} = I_{j} /r_{bj} \left( {j = s,r,p} \right)\) represents the equivalent mass of each component; ξ is the engagement damping ratio of the internal and external engagement pairs of the system (Assuming that the engagement damping ratio of each engagement pair is the same), and generally takes a value in the range of 0.03–0.17.

2.5 Gear system dynamics equation establishment and solution

Based on the gear dynamics theory and the dynamic model of the system in Fig. 2, the torsional vibration of the inner gear ring is not considered, and the dynamic equations of the system component are established by applying Newton's law. The nonlinear effects of the system can be captured through dynamic equations, which is crucial for understanding and predicting the motion and design of gear systems and ensure stability and reliability of the system.

The carrier’s motion equation can be expressed as:

$$I_{ce} \ddot{\theta }_{c} - \sum\limits_{i = 1}^{3} {\left[ \begin{gathered} k_{spi}^{L} f(x_{spi}^{L} ) + c_{spi}^{L} \dot{x}_{spi}^{L} + k_{rpi}^{L} f(x_{rpi}^{L} ) + c_{rpi}^{L} \dot{x}_{rpi}^{L} \hfill \\ + k_{spi}^{R} f(x_{spi}^{R} ) + c_{rpi}^{R} \dot{x}_{rpi}^{R} + k_{rpi}^{R} f(x_{rpi}^{R} ) + c_{rpi}^{R} \dot{x}_{rpi}^{R} \hfill \\ \end{gathered} \right]r_{bc} \cos \beta } = - T_{2}$$
(12)

The left and right sun gear’s motion equations can be expressed as:

$$\left\{ \begin{gathered} I_{s}^{L} \ddot{\theta }_{s}^{L} + \sum\limits_{i = 1}^{3} {\left[ {k_{spi}^{L} f(x_{spi}^{L} ) + c_{spi}^{L} \dot{x}_{spi}^{L} } \right]r_{bs} \cos \beta } = \frac{{T_{1} }}{2} \hfill \\ I_{s}^{R} \ddot{\theta }_{s}^{R} + \sum\limits_{i = 1}^{3} {\left[ {k_{spi}^{R} f(x_{spi}^{R} ) + c_{spi}^{R} \dot{x}_{spi}^{R} } \right]r_{bs} \cos \beta } = \frac{{T_{1} }}{2} \hfill \\ \end{gathered} \right.$$
(13)

The ith left and right planet–gear’s motion equations can be expressed as:

$$\left\{ \begin{gathered} I_{pi}^{L} \ddot{\theta }_{pi}^{L} - \left[ {k_{spi}^{L} f(x_{spi}^{L} ) + c_{spi}^{L} \dot{x}_{spi}^{L} - k_{rpi}^{L} f(x_{rpi}^{L} ) - c_{rpi}^{L} \dot{x}_{rpi}^{L} } \right]r_{bpi} \cos \beta { = }0 \hfill \\ I_{pi}^{R} \ddot{\theta }_{pi}^{R} - \left[ {k_{spi}^{R} f(x_{spi}^{R} ) + c_{spi}^{R} \dot{x}_{spi}^{R} - k_{rpi}^{R} f(x_{rpi}^{R} ) - c_{rpi}^{R} \dot{x}_{rpi}^{R} } \right]r_{bpi} \cos \beta { = 0} \hfill \\ \end{gathered} \right.$$
(14)

where: the equivalent moment of inertia for carrier \(I_{ce} = (I_{c} + \sum\limits_{i = 1}^{3} {m_{pi} r_{bc}^{2} } )\), θm (m = c, s, pi) represents the torsional angular displacement of each component, rbm represents the radius of the base circle of each component.

Considering the existence of rigid body displacement in the gear system, the equation will not converge if solved directly, which cause fails the solution. It is necessary to convert the rigid body displacement into relative displacement before solving. Therefore, the force analysis in the meshing line direction is studied in this paper, and the relative displacement in the direction of the meshing line of the meshing gear pair is considered. The specific formula as [25]:

The relative displacement between the ith left and right planet–gear and the sun gear:

$$\left\{ \begin{gathered} x_{spi}^{L} = (r_{bs}^{L} \theta_{s}^{L} - r_{bpi}^{L} \theta_{pi}^{L} - r_{bc}^{L} \theta_{c}^{L} )\cos \beta - e_{spi}^{L} \hfill \\ x_{spi}^{R} = (r_{bs}^{R} \theta_{s}^{R} - r_{bpi}^{R} \theta_{pi}^{R} - r_{bc}^{R} \theta_{c}^{R} )\cos \beta - e_{spi}^{R} \hfill \\ \end{gathered} \right.$$
(15)

The relative displacement between the ith left and right planet–gear and the ring gear:

$$\left\{ \begin{gathered} x_{rpi}^{L} = (r_{bpi}^{L} \theta_{pi}^{L} - r_{bc}^{L} \theta_{c}^{L} )\cos \beta - e_{rpi}^{L} \hfill \\ x_{rpi}^{R} = (r_{bpi}^{R} \theta_{pi}^{R} - r_{bc}^{R} \theta_{c}^{R} )\cos \beta - e_{rpi}^{R} \hfill \\ \end{gathered} \right.$$
(16)

Considering the large difference in magnitude between the excitation parameters, it is necessary to dimensionless the differential equations before further analysis during the solution of the gear system’s nonlinear differential equations.

The dimensional time variable is defined as \(\overline{t} = \omega_{n} t\), the natural frequency of the system as \(\omega_{n} = \sqrt {k_{m} /(1/M_{s} + 1/M_{p} )}\), introducing the displacement scale bc, define the dimensionless frequency as \(\Omega = \omega /\omega_{n}\), other non-dimensional physical quantities are represented as follows.

$$\overline{x} = x/b_{c} {, }\dot{\overline{x}} = \dot{x}/(b_{c} \omega_{n} {), }\ddot{\overline{x}} = \ddot{x}{/(}b_{c} \omega_{n}^{2} {), }\ddot{\overline{e}} = \ddot{e}/(b_{c} \omega_{n}^{2} )$$
(17)

The differential equations of the system after dimensionless treatment are expressed as:

$$\left\{ \begin{gathered} \ddot{\overline{x}}_{spi}^{L} + \frac{{\sum\limits_{i = 1}^{3} {\left[ {k_{spi}^{L} f(\overline{x}_{spi}^{L} ) + k_{rpi}^{L} f(\overline{x}_{rpi}^{L} ) + k_{spi}^{R} f(\overline{x}_{spi}^{R} ) + k_{rpi}^{R} f(\overline{x}_{rpi}^{R} )} \right]} \cos^{2} \beta }}{{M_{c} \omega_{n}^{2} }} + \frac{{\sum\limits_{i = 1}^{3} {\left[ {c_{spi}^{L} \dot{\overline{x}}_{spi}^{L} + c_{rpi}^{L} \dot{\overline{x}}_{rpi}^{L} + c_{spi}^{R} \dot{\overline{x}}_{spi}^{R} + c_{rpi}^{R} \dot{\overline{x}}_{rpi}^{R} } \right]} \cos^{2} \beta }}{{M_{c} \omega_{n} }} + \frac{{\sum\limits_{i = 1}^{3} {k_{spi}^{L} f(\overline{x}_{spi}^{L} )} \cos^{2} \beta }}{{M_{s}^{L} \omega_{n}^{2} }} \hfill \\ + \frac{{\sum\limits_{i = 1}^{3} {c_{spi}^{L} \dot{\overline{x}}_{spi}^{L} } \cos^{2} \beta }}{{M_{s}^{L} \omega_{n} }} + \frac{{k_{spi}^{L} f(\overline{x}_{spi}^{L} )\cos^{2} \beta }}{{M_{pi}^{L} \omega_{n}^{2} }} + \frac{{c_{spi}^{L} \dot{\overline{x}}_{spi}^{L} \cos^{2} \beta }}{{M_{pi}^{L} \omega_{n} }} - \frac{{k_{rpi}^{L} f(\overline{x}_{rpi}^{L} )\cos^{2} \beta }}{{M_{pi}^{L} \omega_{n}^{2} }} - \frac{{c_{rpi}^{L} \dot{\overline{x}}_{rpi}^{L} \cos^{2} \beta }}{{M_{pi}^{L} \omega_{n} }} = \frac{{T_{1} \cos \beta }}{{2r_{bs} M_{s}^{L} \omega_{n}^{2} b_{c} }} + \frac{{T_{2} \cos \beta }}{{r_{bc} M_{c} \omega_{n}^{2} b_{c} }} - \ddot{\overline{e}}_{spi}^{L} \hfill \\ \ddot{\overline{x}}_{spi}^{R} + \frac{{\sum\limits_{i = 1}^{3} {\left[ {k_{spi}^{L} f(\overline{x}_{spi}^{L} ) + k_{rpi}^{L} f(\overline{x}_{rpi}^{L} ) + k_{spi}^{R} f(\overline{x}_{spi}^{R} ) + k_{rpi}^{R} f(\overline{x}_{rpi}^{R} )} \right]} \cos^{2} \beta }}{{M_{c} \omega_{n}^{2} }} + \frac{{\sum\limits_{i = 1}^{3} {\left[ {c_{spi}^{L} \dot{\overline{x}}_{spi}^{L} + c_{rpi}^{L} \dot{\overline{x}}_{rpi}^{L} + c_{spi}^{R} \dot{\overline{x}}_{spi}^{R} + c_{rpi}^{R} \dot{\overline{x}}_{rpi}^{R} } \right]} \cos^{2} \beta }}{{M_{c} \omega_{n} }} + \frac{{\sum\limits_{i = 1}^{3} {k_{spi}^{R} f(\overline{x}_{spi}^{R} )} \cos^{2} \beta }}{{M_{s}^{R} \omega_{n}^{2} }} \hfill \\ + \frac{{\sum\limits_{i = 1}^{3} {c_{spi}^{R} \dot{\overline{x}}_{spi}^{R} } \cos^{2} \beta }}{{M_{s}^{R} \omega_{n} }} + \frac{{k_{spi}^{R} f(\overline{x}_{spi}^{R} )\cos^{2} \beta }}{{M_{pi}^{R} \omega_{n}^{2} }} + \frac{{c_{spi}^{R} \dot{\overline{x}}_{spi}^{R} \cos^{2} \beta }}{{M_{pi}^{R} \omega_{n} }} - \frac{{k_{rpi}^{R} f(\overline{x}_{rpi}^{R} )\cos^{2} \beta }}{{M_{pi}^{R} \omega_{n}^{2} }} - \frac{{c_{rpi}^{R} \dot{\overline{x}}_{rpi}^{R} \cos^{2} \beta }}{{M_{pi}^{R} \omega_{n} }} = \frac{{T_{1} \cos \beta }}{{2r_{bs} M_{s}^{R} \omega_{n}^{2} b_{c} }} + \frac{{T_{2} \cos \beta }}{{r_{bc} M_{c} \omega_{n}^{2} b_{c} }} - \ddot{\overline{e}}_{spi}^{R} \hfill \\ \ddot{\overline{x}}_{rpi}^{L} - \frac{{k_{spi}^{L} f(\overline{x}_{spi}^{L} )\cos^{2} \beta }}{{M_{pi}^{L} \omega_{n}^{2} }} - \frac{{c_{spi}^{L} \dot{\overline{x}}_{spi}^{L} \cos^{2} \beta }}{{M_{pi}^{L} \omega_{n} }} + \frac{{\sum\limits_{i = 1}^{3} {\left[ {k_{spi}^{L} f(\overline{x}_{spi}^{L} ) + k_{rpi}^{L} f(\overline{x}_{rpi}^{L} ) + k_{spi}^{R} f(\overline{x}_{spi}^{R} ) + k_{rpi}^{R} f(\overline{x}_{rpi}^{R} )} \right]} \cos^{2} \beta }}{{M_{c} \omega_{n}^{2} }} + \frac{{k_{rpi}^{L} f(\overline{x}_{rpi}^{L} )\cos^{2} \beta }}{{M_{pi}^{L} \omega_{n}^{2} }} + \frac{{c_{rpi}^{L} \dot{\overline{x}}_{rpi}^{L} \cos^{2} \beta }}{{M_{pi}^{L} \omega_{n} }} \hfill \\ + \frac{{\sum\limits_{i = 1}^{3} {\left[ {c_{spi}^{L} \dot{\overline{x}}_{spi}^{L} + c_{rpi}^{L} \dot{\overline{x}}_{rpi}^{L} + c_{spi}^{R} \dot{\overline{x}}_{spi}^{R} + c_{rpi}^{R} \dot{\overline{x}}_{rpi}^{R} } \right]} \cos^{2} \beta }}{{M_{c} \omega_{n} }} = \frac{{T_{2} \cos \beta }}{{r_{bc} M_{c} \omega_{n}^{2} b_{c} }} - \ddot{\overline{e}}_{rpi}^{L} \hfill \\ \ddot{\overline{x}}_{rpi}^{R} - \frac{{k_{spi}^{R} f(\overline{x}_{spi}^{R} )\cos^{2} \beta }}{{M_{pi}^{R} \omega_{n}^{2} }} - \frac{{c_{spi}^{R} \dot{\overline{x}}_{spi}^{R} \cos^{2} \beta }}{{M_{pi}^{R} \omega_{n} }} + \frac{{\sum\limits_{i = 1}^{3} {\left[ {k_{spi}^{L} f(\overline{x}_{spi}^{L} ) + k_{rpi}^{L} f(\overline{x}_{rpi}^{L} ) + k_{spi}^{R} f(\overline{x}_{spi}^{R} ) + k_{rpi}^{R} f(\overline{x}_{rpi}^{R} )} \right]} \cos^{2} \beta }}{{M_{c} \omega_{n}^{2} }} + \frac{{k_{rpi}^{R} f(\overline{x}_{rpi}^{R} )\cos^{2} \beta }}{{M_{pi}^{R} \omega_{n}^{2} }} + \frac{{c_{rpi}^{R} \dot{\overline{x}}_{rpi}^{R} \cos^{2} \beta }}{{M_{pi}^{R} \omega_{n} }} \hfill \\ + \frac{{\sum\limits_{i = 1}^{3} {\left[ {c_{spi}^{L} \dot{\overline{x}}_{spi}^{L} + c_{rpi}^{L} \dot{\overline{x}}_{rpi}^{L} + c_{spi}^{R} \dot{\overline{x}}_{spi}^{R} + c_{rpi}^{R} \dot{\overline{x}}_{rpi}^{R} } \right]} \cos^{2} \beta }}{{M_{c} \omega_{n} }} = \frac{{T_{2} \cos \beta }}{{r_{bc} M_{c} \omega_{n}^{2} b_{c} }} - \ddot{\overline{e}}_{rpi}^{R} \hfill \\ \end{gathered} \right.$$
(18)

3 Nonlinear dynamics analysis of herringbone planetary gear system

The herringbone planetary gear system has multivariable nonlinear dynamic characteristics. Dynamic response of the system will be generated under the combined action of these factors, which result in vibration and noise. It is necessary to analyze the influence of different factors on the nonlinear dynamics of the system. The kinematic characteristics of the internal and external meshing pairs are essentially the same in the herringbone planetary gear system, so only the internal meshing pair xspi is used as the analysis object. In this paper, the effects of the temperature and damping ratio changes on the nonlinear bifurcation characteristics of the system are studied by combining the bifurcation diagram, maximum Lyapunov exponents diagram, phase diagram, Poincare diagram, and other kinematic characteristics diagram.

The relevant parameters of the herringbone planetary gear are shown in Tables 1 and 2.

Table 1 Parameters of herringbone planetary gear system
Full size table
Table 2 Herringbone planetary gear system stiffness parameters
Full size table

The other parameters selected are as follows: input torque is T1 = 220 N m, the dimensionless excitation frequency is Ω = 1, the meshing damping ratio is ξ = 0.07, the dimensionless initial gear backlash is b = 0.6, and the dimensionless error amplitude is em = 0.35.

3.1 Analysis of temperature effect on nonlinear dynamics of the system

The thermal deformation induced by temperature changes can cause gear backlash change, and the backlash as one of the internal excitations also influences the nonlinear dynamic response of the gear. Figure 5 shows the bifurcation diagram of the system and its maximum Lyapunov exponent diagram when the temperature rises ∆T changes from 0 to 100 °C.

Fig. 5
figure 5

Bifurcation diagram a and maximum Lyapunov exponent diagram b of the system with temperature rise ∆T change

Full size image

As shown the bifurcation diagram in Fig. 5, with the increase in temperature rise, the system exhibits chaotic characteristics and abundant bifurcation characteristics. When the temperature rise ∆T increases from 0 to 64 °C, the system shows the dynamic characteristics of chaos, and the corresponding maximum Lyapunov index is greater than 0. As shown in Fig. 6, when ∆T = 20 °C, the time course diagram curve changes irregularly, the phase trajectory diagrams are intertwined and chaotic, the Poincare diagram is composed of dense points in sheets, and the spectrogram shows that there are spikes in fundamental frequency and fraction frequency, indicating that the system is chaotic motion. When ∆T = 64 °C, the system changes from chaotic to three-period motion, and its maximum Lyapunov index changes from positive to negative. As shown in Fig. 7, when ∆T = 65 °C, the time course diagram has periodicity, the phase diagram is a closed graph formed around three weeks of phase trajectory, the Poincare diagram shows three points, and the spectrogram is distributed on the discrete points of hΩa/3 (h is a positive integer and Ωa is a fundamental frequency), which indicates that the system is in three-period motion. When 67 °C < ∆T < 80 °C, the system enters a two-period motion. Figure 8 shows that when ∆T = 70 °C, the time course diagram has periodicity, the phase diagram is a closed graph formed around two weeks of phase trajectory, the Poincare diagram shows two points, and the frequency spectrum is distributed at the discrete points of hΩa/2, which indicates that the system is in two-period motion. When ∆T > 80 °C, the system changes from two-period motion to one-period motion, and the maximum Lyapunov exponent remains less than 0. As shown in Fig. 9, when ∆T = 85 °C, the time course diagram has periodicity, the phase diagram is a closed graph formed by the phase trajectory encircling one circle, and the Poincare diagram shows one point, the frequency spectrum is dominated by fundamental frequency, which indicates that the system is in single-period motion.

Fig. 6
figure 6

Chaotic kinematics characteristic diagram of the system at ΔT = 20 °C

Full size image
Fig. 7
figure 7

Three-period kinematics characteristic diagram of the system at ΔT = 65 °C

Full size image
Fig. 8
figure 8

Two-period kinematics characteristic diagram of the system at ΔT = 70 °C

Full size image
Fig. 9
figure 9

Single-period kinematics characteristic diagram of the system at ΔT = 85 °C

Full size image

From the above analysis can be seen that the temperature effect has a significant impact on the nonlinear characteristics of the herringbone planetary gear. With the increase in temperature rise, the system shows chaotic, three-period, two-period, and single-period motion. The gear is in an unstable state when the system enters chaotic motion, it is easy to produce vibration and noise, which reduce the gear life. For the gear dynamics model studied in this article, the system can enter periodic motion by increasing temperature rise, which reduces vibration and collision during the gear meshing transmission.

3.2 Analysis of engagement damping ratio on nonlinear dynamics of the system

The damping ratio is one of the dynamic characteristics affecting the gear amplitude, which is a term used to describe the energy dissipation in the gear vibration process. Taking the temperature rise ∆T = 50 °C and keeping the other parameters constant. Figure 10 shows the bifurcation diagram and the maximum Lyapunov exponent diagram of the system with the change of engagement damping ratio ξ from 0.02 to 0.18.

Fig. 10
figure 10

Bifurcation diagram a and maximum Lyapunov exponent diagram b of the system with engagement damping ratio ξ change

Full size image

As shown in Fig. 10, with the increase of engagement damping ratio, the gear system initially shows the dynamic characteristics of chaos, and the corresponding maximum Lyapunov index is greater than 0. Figure 11 shows that when ξ = 0.04, the time course diagram curve changes irregularly, and the phase trajectory is intertwined and disorderly. The Poincare section consists of dense points, and the spectrogram shows that there are spikes in fundamental frequency and fraction frequency, indicating that the system is in chaotic motion. When 0.122 < ξ < 0.144, the system enters a four-period motion, and its maximum Lyapunov exponent changes from positive to negative. As shown in Fig. 12, when ξ = 0.13, the time course diagram exhibits obvious periodicity, the phase diagram is a closed figure formed by the phase trajectory orbiting around four weeks, the Poincare diagram consists of four dense points, and the spectrum diagram is distributed on discrete points of hΩa/4, indicating that the system is in four-period motion. The system occurs inverse period doubling bifurcation at ξ = 0.145 and ξ = 0.163, which change from four-period motion to two-period motion, and two-period motion to single-period motion, respectively. The corresponding maximum Lyapunov index is less than 0. The motion characteristic diagrams of Figs. 13 and 14 show that the system is in two-period motion at ξ = 0.15, and in single-period motion at ξ = 0.17, respectively.

Fig. 11
figure 11

Chaotic kinematics characteristic diagram of the system at ξ = 0.04

Full size image
Fig. 12
figure 12

Four-period kinematics characteristic diagram of the system at ξ = 0.13

Full size image
Fig. 13
figure 13

Two-period kinematics characteristic diagram of the system at ξ = 0.15

Full size image
Fig. 14
figure 14

Single-period kinematics characteristic diagram of the system at ξ = 0.17

Full size image

It can be seen from the above analysis that the engagement damping ratio has a greater impact on the bifurcation characteristics of the system. With the change of engagement damping ratio, the system experiences the motion process of "chaotic—four period—two period—single period ". Under the premise of guaranteeing the gear transmission efficiency, the vibration amplitude of the system can be reduced by increasing the engagement damping ratio, which make the transmission smoother.

4 Chaos control of the herringbone planetary gear transmission system

From the above analysis, it can be seen that the gear system exhibits chaotic motion when the system selects some parameter values. Considering the adverse effects of chaotic motion on the nonlinear dynamic characteristics of the herringbone planetary gear system, the suppression and control of chaotic motion in gear systems under temperature effects must be studied.

There are many methods of chaos control, and the method of the external periodic signal is used to analyze and control the chaos phenomena in this paper. It is a non-feedback control method that does not need continuous observation and is unaffected by the control signal. Therefore, it is more convenient than traditional feedback control methods.

For n-dimensional systems:

$$\dot{X} = F(X(t),t), \, Y = MX$$
(19)

where: X represents system state variables, X = [X1, X2,Xn]T; F represents nonlinear vector function; M is a constants matrix of 1 × n; Y represents system output.

The external periodic signal function G is:

$$G = K\cos (\omega t)$$
(20)

where: K is the periodic feedback control parameter. It is a variable parameter that can suppress chaos or transfer it to other periodic orbits by selecting different K values.

The controlled n-dimensional system is:

$$\dot{X} = F(X(t),t) - G$$
(21)

Applying the periodic signal controller to the gear system, assuming K = [0, k, 0, k, 0, k, 0, k,]T, then the state equation of the controlled system is:

$$\left\{\begin{gathered} \dot{y}_{1} = y_{2} \hfill \\ \dot{y}_{2} = - \left(\frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }} + \frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{s}^{L} \omega _{n}^{2} }} + \frac{{k_{{spi}}^{L} \cos ^{2} \beta }}{{M_{{pi}}^{L} \omega _{n}^{2} }}\right)y_{1} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }} + \frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{s}^{L} \omega _{n} }} + \frac{{c_{{spi}}^{L} \cos ^{2} \beta }}{{M_{{pi}}^{L} \omega _{n} }}\right)y_{2} - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}y_{3} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}y_{4} \hfill \\ - \left(\frac{{\sum\limits_{{i = 1}}^{3} {k_{{rpi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }} - \frac{{k_{{rpi}}^{L} \cos ^{2} \beta }}{{M_{{pi}}^{L} \omega _{n}^{2} }}\right)y_{5} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {c_{{rpi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }} - \frac{{c_{{rpi}}^{L} \cos ^{2} \beta }}{{M_{{pi}}^{L} \omega _{n} }}\right)y_{6} - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{rpi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}y_{7} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{rpi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}y_{8} \hfill \\ + \frac{{T_{1} \cos \beta }}{{2r_{{bs}} M_{s}^{L} \omega _{n}^{2} b_{c} }} + \frac{{T_{2} \cos \beta }}{{r_{{bc}} M_{c} \omega _{n}^{2} b_{c} }} - \ddot{\bar{e}}_{{spi}}^{L} - Kcos\left( {\Omega t} \right) \hfill \\ \dot{y}_{3} = y_{4} \hfill \\ \dot{y}_{4} = - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}y_{1} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}y_{2} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }} + \frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{s}^{R} \omega _{n}^{2} }} + \frac{{k_{{spi}}^{R} \cos ^{2} \beta }}{{M_{{pi}}^{R} \omega _{n}^{2} }}\right)y_{3} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }} + \frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{s}^{R} \omega _{n} }} + \frac{{c_{{spi}}^{R} \cos ^{2} \beta }}{{M_{{pi}}^{R} \omega _{n} }}\right)y_{4} \hfill \\ - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{rpi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}y_{5} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{rpi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}y_{6} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {k_{{rpi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }} - \frac{{k_{{rpi}}^{R} \cos ^{2} \beta }}{{M_{{pi}}^{R} \omega _{n}^{2} }}\right)y_{7} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {c_{{rpi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }} - \frac{{c_{{rpi}}^{R} \cos ^{2} \beta }}{{M_{{pi}}^{R} \omega _{n} }}\right)y_{8} \hfill \\ + \frac{{T_{1} \cos \beta }}{{2r_{{bs}} M_{s}^{R} \omega _{n}^{2} b_{c} }} + \frac{{T_{2} \cos \beta }}{{r_{{bc}} M_{c} \omega _{n}^{2} b_{c} }} - \ddot{\bar{e}}_{{spi}}^{R} - Kcos\left( {\Omega t} \right) \hfill \\ \dot{y}_{5} = y_{6} \hfill \\ \dot{y}_{6} = \left(\frac{{k_{{spi}}^{L} \cos ^{2} \beta }}{{M_{{pi}}^{L} \omega _{n}^{2} }} - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}\right)y_{1} + \left(\frac{{c_{{spi}}^{L} \cos ^{2} \beta }}{{M_{{pi}}^{L} \omega _{n} }} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}\right)y_{2} - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}y_{3} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}y_{4} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {k_{{rpi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }} + \frac{{k_{{rpi}}^{L} \cos ^{2} \beta }}{{M_{{pi}}^{L} \omega _{n}^{2} }}\right)y_{5} \hfill \\ - \left(\frac{{\sum\limits_{{i = 1}}^{3} {c_{{rpi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }} + \frac{{c_{{rpi}}^{L} \cos ^{2} \beta }}{{M_{{pi}}^{L} \omega _{n} }}\right)y_{6} - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{rpi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}y_{7} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{rpi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}y_{8} + \frac{{T_{2} \cos \beta }}{{r_{{bc}} M_{c} \omega _{n}^{2} b_{c} }} - \ddot{\bar{e}}_{{rpi}}^{L} - Kcos\left( {\Omega t} \right) \hfill \\ \dot{y}_{7} = y_{8} \hfill \\ \dot{y}_{8} = - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}y_{1} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}y_{2} + \left(\frac{{k_{{spi}}^{R} \cos ^{2} \beta }}{{M_{{pi}}^{R} \omega _{n}^{2} }} - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}\right)y_{3} + \left(\frac{{c_{{spi}}^{R} \cos ^{2} \beta }}{{M_{{pi}}^{R} \omega _{n} }} - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{spi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}\right)y_{4} - \frac{{\sum\limits_{{i = 1}}^{3} {k_{{rpi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }}y_{5} \hfill \\ - \frac{{\sum\limits_{{i = 1}}^{3} {c_{{rpi}}^{L} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }}y_{6} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {k_{{rpi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n}^{2} }} - \frac{{k_{{rpi}}^{R} \cos ^{2} \beta }}{{M_{{pi}}^{R} \omega _{n}^{2} }}\right)y_{7} - \left(\frac{{\sum\limits_{{i = 1}}^{3} {c_{{rpi}}^{R} \cos ^{2} \beta } }}{{M_{c} \omega _{n} }} + \frac{{c_{{rpi}}^{R} \cos ^{2} \beta }}{{M_{{pi}}^{R} \omega _{n} }}\right)y_{8} + \frac{{T_{2} \cos \beta }}{{r_{{bc}} M_{c} \omega _{n}^{2} b_{c} }} - \ddot{\bar{e}}_{{rpi}}^{R} - Kcos\left( {\Omega t} \right) \hfill \\ \end{gathered} \right.$$
(22)

From the bifurcation diagram of the system in Fig. 5, it can be seen that the system exhibits chaotic motion in the range of 0 °C < ∆T < 64 °C. Taking ∆T = 50 °C, ξ = 0.10, and other parameters of the system as keep constant. Figure 15 shows the bifurcation diagram and the maximum Lyapunov exponent diagram of the controlled system of the herringbone planetary gear under the change of periodic feedback control parameter K.

Fig. 15
figure 15

Bifurcation diagram a and maximum Lyapunov exponent diagram b of the controlled system with feedback control parameter K change

Full size image

From the diagram can be seen that as K increases from 0 to 0.224, the controlled system exhibits chaotic dynamic characteristics, and the corresponding maximum Lyapunov exponent is greater than 0. Figure 16 shows that when K = 0.1, the time course diagram curve changes irregularly, and the phase trajectory is intertwined and disorderly. The Poincare section consists of dense points, and the spectrogram shows that there are spikes in fundamental frequency and fraction frequency, indicating that the controlled system is in chaotic motion. At K = 0.224, the controlled system is changed from chaotic to four-period motion, and its maximum Lyapunov exponent is changed from positive to negative. Figure 17 shows that when K = 0.23, the time course diagram exhibits obvious periodicity, the phase diagram is a closed figure formed by a phase trajectory orbiting around four weeks, the Poincare cross diagram consists of four dense points, and the spectrum diagram is distributed on discrete points of hΩa/4, indicating that the controlled system is in four-period motion. The controlled system enters a two-period motion when 0.242 < K < 0.33. As shown in Fig. 18, when K = 0.3, the time course diagram has periodicity, the phase diagram is a closed graph formed around two weeks of phase trajectory, the Poincare diagram shows two points, and the frequency spectrum is distributed at the discrete points of hΩa/2, which indicates that the system is in two-period motion. The controlled system changes from two-period motion to single-period motion when K > 0.33 and the corresponding maximum Lyapunov exponent remains in a state of less than 0. Figure 19 shows that when K = 0.5, the time course diagram has periodicity, the phase diagram is a closed graph formed around one week of phase trajectory, the Poincare diagram shows one point, and the frequency spectrum is dominated by fundamental frequency, indicating that the controlled system is in single-period motion.

Fig. 16
figure 16

Chaotic kinematics characteristic diagram of the controlled system at K = 0.1

Full size image
Fig. 17
figure 17

Four-period kinematics characteristic diagram of the controlled system at K = 0.23

Full size image
Fig. 18
figure 18

Two-period kinematics characteristic diagram of the controlled system at K = 0.3

Full size image
Fig. 19
figure 19

Single-period kinematics characteristic diagram of the controlled system at K = 0.5

Full size image

From the above analysis, it can be seen that the chaotic control method of the external periodic signal can control the system to multi-periodic orbits. To better illustrate the suppression effect of the system’s chaotic regions after introducing the controller, introducing controllers with K = 0.3 and K = 0.5, the bifurcation diagram of the system with temperature rise changes is obtained, as shown in Fig. 20.

Fig. 20
figure 20

Bifurcation diagram the controlled system with temperature rise ∆T change under different feedback control parameters K

Full size image

Comparing Figs. 5 and 20, it is evident that the chaotic region of the system is well suppressed after introducing the controller. When the controller with K = 0.3 is introduced, the chaotic motion state of the system is suppressed to a two-period motion state within the area of 43 °C < ∆T < 53 °C, and the chaotic motion state of the system is suppressed to a single-period motion state within the area of 53 °C < ∆T < 64 °C. When the controller with K = 0.5 is introduced, the chaotic motion of the system is suppressed to a two-period motion within the area of 9 °C < ∆T < 14 °C and the chaotic motion state of the system is suppressed to a single-period motion state within the area of 14 °C < ∆T < 64 °C.

Therefore, the chaotic motion can be controlled to other periodic motion orbit by applying a periodic signal controller to the system. In addition, although the feedback control parameter K is obtained by analyzing a certain temperature state, the resulting control excitation is also applicable to chaos control over the entire temperature range. In addition, the control effect achieved is basically the same. Therefore, the chaos control method has good applicability under temperature changes.

5 Conclusion

In this paper, a nonlinear dynamic model of the herringbone planetary gear system considering the temperature effect is established. The system is solved by using the Runge–Kutta method. The nonlinear dynamic characteristics of the system are studied by multiple nonlinear characteristic diagrams. And the chaotic region of the system is analyzed and controlled by using a non-feedback control method with the external periodic signal. The following conclusions are obtained:

  1. (1)

    With the increase of temperature rise, the gear system experiences the motion process of "chaos—three periodic—two periodic—single periodic," and the corresponding maximum Lyapunov index changes from positive to negative. It shows that the higher temperature rise can make the system enter stable periodic motion and reduce vibration noise during gear meshing transmission.

  2. (2)

    With the increase of engagement damping ratio, the system initially exhibits chaotic characteristics and then undergoes inverse period doubling bifurcation, the system changes from chaotic motion to periodic motion, and its maximum Lyapunov index changes from positive to negative. It shows that the larger engagement damping ratio can reduce the system’s vibration amplitude and make the transmission more stable.

  3. (3)

    For the chaos problem in gear systems, through the application of the chaos control method with external periodic signals, the chaos is effectively controlled to the periodic motion orbit, which makes the gear system more stable.