1 Introduction

Gear systems are widely used in the modern power transmission systems. Plenty of studies have been performed on dynamic modeling of spur gear transmission systems [1]. It is well known that the characteristics of a gear system are affected by internal and external excitations [2]. Internal excitations include backlash [3], time-varying mesh stiffness (TVMS) [4, 5], transmission error [6]. Many studies focused on the investigation of internal excitations, while only a few did investigation on external excitation (e.g., varying load [7]).

Gear dynamics under deterministic load has been explored for decades. Wang et al. [8] reviewed the models and approaches used in gear dynamics. Khabou et al. [9] investigated the dynamic behavior of a single-stage spur gear system under deterministic load and concluded that adequate external load should be chosen to reduce vibration. Shao and Chen [2] proposed an analytical model of a spur gear pair with tooth root crack under deterministic load. These existing models reveal the mechanism of gear systems and contribute to the understanding of gear dynamics. However, they restricted the gear dynamics problems in the deterministic domain, which reduces the difficulties in obtaining dynamic responses of a gear system.

A few studies investigated randomness of external load in gear system analysis. Utagawa and Harada [10] investigated the influence of randomness on dynamic loads for high-speed gears. Tobe et al. [11] investigated stochastic load, which was treated as Gaussian white noise. Their results were validated by comparing with the experiment results reported in [12]. Ref. [11] was one of the earliest reported studies in gear stochastic dynamics, and the randomness of external load was examined via laboratory experiments. Wang et al. [13] studied a wind turbine generator suffering from stochastic wind with varying directions and loads. The extensions of the models from deterministic domain to stochastic domain lead to more realistic representation of real gear systems.

Patil et al. [14] analyzed the effects of wind stochastic energy change on gear system’s steady and transient states. Drago [15] studied the influence of stochastic start-up load to the potential failure of gears. Gear vibrations and noises are mainly induced by load variation at gear transient state [9]. It is necessary to consider the stochastic external load in gear system modeling especially at transient state.

Researchers have made some improvements in modeling gear dynamics under stochastic load. Wang and Zhang [16] considered the speed-dependent stochastic errors in their one-dimensional spur gear pair model. Theodossiades and Natsiavas [17] introduced the gear systems with periodic stiffness and backlash, and they considered the transmission errors as static errors. Yang [18] investigated a gear multi-mesh dynamic model under Gaussian white noise and assumed constant mesh stiffness and damping coefficient. Recently, Wen and Yang [19] developed a gear pair’s dynamic model considering constant damping coefficient, backlash, and TVMS. It was solved by numerical and analytical methods.

Friction has been identified as a cause of vibration, noise and failure of a gear system [20]. Many researchers have reported the effects of friction on gear dynamics under deterministic excitation. A detailed review of friction prediction in gear teeth was conducted by Martin [21], which concluded that the values of coefficients of friction could be predicted reasonably according to various lubrication theories. Yang et al. [22] proposed a model of a spur gear pair considering friction, Hertzian damping, and bending under deterministic load. He et al. [23] investigated vibrational characteristics of a gear system affected by friction under deterministic load. Krupka et al. [24] studied the effect of surface lubrication film on vibrational characteristics under transient conditions. He et al. [25] reported several sliding friction models in spur gear dynamics to analyze friction forces.

Friction has not been considered for modeling a gear system with stochastic load. In this paper, friction is taken into consideration for a pair of spur gears under stochastic load. Transient characteristics of this gear system are studied. The influences of stochastic load and surface sliding friction on gear system stability are investigated.

The remaining part of this paper is organized as follows. In Sect. 2 the proposed stochastic dynamic model for a spur gear pair is described. Section 3 illustrates the effects of friction coefficient and stochastic load on gear transient characteristics. Section 4 draws the conclusion. A shorter version of this paper has been accepted in the conference IEEE SMC 2017 [26].

2 Nonlinear stochastic gear dynamic model considering friction

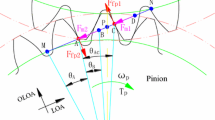
In this section, a single-degree-of-freedom (SDOF) nonlinear dynamic model of a spur gear pair is developed based on the model reported in [22]. TVMS, backlash, sliding friction, and stochastic load are considered in our model. Figure 1 shows the model of the geared system. Only rotation of the gear is considered in this model. Figure 2 shows the TVMS used in this study.

Fig. 1
figure 1

Model of a gear system [19]

Full size image
Fig. 2
figure 2

Time-varying mesh stiffness [19]

Full size image

The equations of motion for the system given in Fig. 1 can be expressed as

$$\begin{aligned} {{\mathrm{J}}_\mathrm{{1}}}{\ddot{\theta }_\mathrm{{1}}}= & {} {{\mathrm{T}}_\mathrm{{1}}}\mathrm{{ - }}(F + G){R_{\mathrm{b}1}} - {F_f}{X_1} \end{aligned}$$
(1)
$$\begin{aligned} {{\mathrm{J}}_\mathrm{{2}}}{\ddot{\theta }_\mathrm{{2}}}= & {} {{\mathrm{T}}_\mathrm{{2}}} + (F + G){R_{\mathrm{b}2}} + {F_f}({l_p} - {X_1}) \end{aligned}$$
(2)

where \({J_i}\), \({T_i}\), \({\ddot{\theta }_i}\), \({R_{\mathrm{b}i}}\) are the moment of inertia, external torque, angular acceleration, and base circle of gear i \((i = 1,2)\), respectively, F is the total elastic force between the contact teeth shown in Fig. 3, G is the damping force, \({F_f}\) is sliding friction, \({X_1}\) denotes the distance between the tangent point \({C_1}\) on the action line and the force contact point \({B_1}\), and \({l_p}\) means the length of the action line.

Multiply Eq. 1 by \({R_{\mathrm{b}1}}/{J_1}\) and Eq. 2 by \({R_{\mathrm{b}2}}/{J_2}\), and then subtract the second from the first one. We can get the expression shown in Eq. 3.

$$\begin{aligned} {R_{\mathrm{b}1}}{{\ddot{\theta }}_1} - {R_{\mathrm{b}2}}{{\ddot{\theta }}_2}= & {} \left( {\frac{{{T_1}{R_{\mathrm{b}1}}}}{{{J_1}}} - \frac{{{T_2}{R_{\mathrm{b}2}}}}{{{J_2}}}} \right) \nonumber \\&- \left( {F + G} \right) \left( \frac{{R_{\mathrm{b}1}^2}}{{{J_1}}} + \frac{R_{\mathrm{b}2}^2}{J_2}\right) \nonumber \\&- {F_f}\left[ \frac{{{X_1}R_{\mathrm{b}1}^{}}}{{{J_1}}} + \frac{({l_p} - {X_1})R_{\mathrm{b}2}^{}}{J_2}\right] \nonumber \\ \end{aligned}$$
(3)
Fig. 3
figure 3

Elastic force on the tooth of gear 1

Full size image

Let \(\delta ={R_{\mathrm{b}1}}{\theta _1} - {R_{\mathrm{b}2}}{\theta _2}\). The gear pair’s equation is reduced to a SDOF nonlinear system with TVMS, backlash, and friction.

$$\begin{aligned} \ddot{\delta }= \varPhi - \left( {K\delta + \alpha \delta \dot{\delta }} \right) {q_3} - \mu \left( {K\delta + \alpha \delta \dot{\delta }} \right) \left( {{q_1} + {\theta _1}{q_2}} \right) \end{aligned}$$
(4)

where

$$\begin{aligned}&{F_f} = \mu (F + G) \end{aligned}$$
(5)
$$\begin{aligned}&{l_p} = ({R_{\mathrm{b}1}} + {R_{\mathrm{b}2}})\sin {\alpha _0} \end{aligned}$$
(6)
$$\begin{aligned}&{X_1} = \left( {{a_0} + {\theta _1} + {\theta _{b1}}} \right) {R_{\mathrm{b}1}} \end{aligned}$$
(7)
$$\begin{aligned}&{\theta _{b1}} = \frac{\pi }{{2{Z_1}}} + \tan \alpha - \alpha \end{aligned}$$
(8)
$$\begin{aligned}&F = Kg(\delta ) \end{aligned}$$
(9)
$$\begin{aligned}&G = \alpha \delta \dot{\delta }\end{aligned}$$
(10)
$$\begin{aligned}&\varPhi = \frac{{{T_1}{R_{\mathrm{b}1}}}}{{{J_1}}} - \frac{{{T_2}{R_{\mathrm{b}2}}}}{{{J_2}}} \end{aligned}$$
(11)
$$\begin{aligned}&{q_1} = {\alpha _0}\left( {\frac{R_{\mathrm{b}1}^2}{{J_1}} + \frac{{R_{\mathrm{b}2}^2}}{J_2}} \right) + {\theta _{b1}}\left( {\frac{{R_{\mathrm{b}1}^2}}{{J_1}} - \frac{{{R_{\mathrm{b}1}}R_{\mathrm{b}2}^{}}}{{{J_2}}}} \right) \end{aligned}$$
(12)
$$\begin{aligned}&{q_2} = \frac{{R_{\mathrm{b}1}^2}}{{{J_1}}} - \frac{{{R_{\mathrm{b}1}}R_{\mathrm{b}2}^{}}}{{{J_2}}} \end{aligned}$$
(13)
$$\begin{aligned}&{q_3} = \frac{{R_{\mathrm{b}1}^2}}{{{J_1}}} + \frac{{R_{\mathrm{b}2}^2}}{{{J_2}}} \end{aligned}$$
(14)

In Eqs. 5–14, \({\theta _{b1}}\) is half of the tooth angle (see Fig. 3), \({\alpha _0}\) denotes the pressure angle, K is the effective mesh stiffness, \(\delta \) gives relative angular displacement of the gear pair, \(\alpha \) is the damping coefficient, \(\varPhi \) represents the equivalent external excitation, \(\mu \) is the friction coefficient, and \({q_1}\), \({q_2}\), and \({q_3}\) denote polynomials as shown in Eqs. 12–14.

Rewriting Eq. 4, a second-order ordinary differential equation (ODE) is obtained as

$$\begin{aligned} \ddot{\delta }+ Q({\theta _1})g(\delta )\alpha \dot{\delta }+ Q({\theta _1})K({\theta _1})g(\delta ) = \varPhi \end{aligned}$$
(15)

The expressions of \(Q\left( {{\theta _1}} \right) \), \(g(\delta )\), and \(K(\theta )\) are given below

$$\begin{aligned}&Q({\theta _1}) = {q_3} + \mu ({q_1} + {\theta _1}{q_2}) \end{aligned}$$
(16)
$$\begin{aligned}&g(\delta ) = \left\{ {\begin{array}{l} {\delta - b,}\\ {0,}\\ {\delta + b,} \end{array}} \right. \begin{array}{l} \quad {\delta > b}\\ \quad { - \,b \le \delta \le b}\\ \quad {\delta < -\, b} \end{array} \end{aligned}$$
(17)
$$\begin{aligned}&K(\theta ) = \left\{ {\begin{array}{l} {{k_1}}\\ {{k_2}} \end{array}} \right. \hbox {for}\begin{array}{l} \quad {(n - 1){\phi _{n}} \le \theta< (n-1){\phi _{n}} + {\phi _{m}}}\\ \quad {(n - 1){\phi _{n}} + {\phi _{m}} \le \theta < n{\phi _{n}}} \end{array}\nonumber \\ \end{aligned}$$
(18)

where \(Q({\theta _1})\) is a function of \({\theta _1}\), \(g\left( \delta \right) \) denotes the function of backlash, \({\phi _{n}}\) and \({\phi _{m}}\) represent gear rotation angles during a mesh circle and the single tooth pair mesh duration in a mesh circle, respectively.

A Gaussian diffusion process is used to simulate the equivalent external excitation \(\varPhi \). It is the integration of Gaussian white noise. It is assumed that \(\varPhi \) can be approximated by an Itô [27] stochastic differential equation (SDE) in the following form [28]:

$$\begin{aligned} \hbox {d}\varPhi (t) = \lambda \hbox {d}t + \sigma \hbox {d}W(t) \end{aligned}$$
(19)

where \(\lambda \) is the drift scalar, \(\sigma \) is the diffusion scalar, and W(t) is a standard Wiener process.

Recently, a stochastic dynamic model was investigated in [19]. They considered the excitation as a combination of constant deterministic part \({f_0}\), a deterministic periodically changing part \({f_1}\cos ({\varOmega _{m}}t)\) and Gaussian white noise \(\xi (t)\). Their nonlinear system equation is given as follows:

$$\begin{aligned} \ddot{\delta }+ \alpha \dot{\delta }+ K({\theta _1})g(\delta )={f_0} + {f_1}\cos ({\varOmega _{m}}t) + \xi (t)\nonumber \\ \end{aligned}$$
(20)

In the above equation, \({f_0}\), \({f_1}\), and \({\varOmega _{m}}\) are constant. Comparing Eq. 15 with Eq. 20, the damping coefficient in [19] is a constant \(\alpha \), while the \(Q({\theta _1})g(\delta )\alpha \) in our model is dependent on \(\delta \). Expand \(Q({\theta _1})g(\delta )\alpha \) and all relevant parameters are shown:

$$\begin{aligned} Q({\theta _1})g(\delta )\alpha = \left[ {{q_3} + \mu ({q_1} + {\theta _1}{q_2})} \right] g(\delta )\alpha \end{aligned}$$
(21)

where \({q_1}\), \({q_2}\), \({q_3}\), \(g(\delta )\) and \(\alpha \) are deterministic. Due to stochastic external load, \({\theta _1}\) is a stochastic variable. Since \(g(\delta )\) is nonlinear and \(Q({\theta _1})\) is stochastic, there is no doubt that our proposed model reflects more nonlinearity than the existing model and is more difficult to solve.

3 Dynamic characteristics of a gear pair considering friction

To analyze the dynamic characteristics of the proposed model, this section gives the numerical simulation results. The main objective of this section is to investigate the friction and stochastic load effects on system’s transient characteristics. Section 3.1 will give the validation of the proposed model. The results will be compared with [3]. Section 3.2 will study the stochastic load effects on transient characteristics, such as periodicity, chaos, and stability. Section 3.3 will study the friction coefficient effects on transient characteristics, namely stability and dispersion.

3.1 Validation of the proposed model

The validation is done by comparing with the result reported in [3], which proposed a model of a spur gear pair under deterministic load considering TVMS and backlash. TVMS was modeled the same way as shown in Fig. 2. The gear pair parameters used in [3] will be also used in our proposed model (see Table 1).

Table 1 Gear pair parameters
Full size table

If we assume that the friction coefficient equals to zero, Eq. 15 is the same as the model in [3]. Angular displacements of two gears during free vibration are solved. Ref. [3]’s results and our results are given in Fig. 4. Compared to [3], our results (angular displacements) are almost the same in both magnitude and tendency. Although this validation is conducted under deterministic load, it still supports the correctness of our model to some degree. And the model can be extended to stochastic external excitation to explore the characteristics in stochastic gear dynamics.

Fig. 4
figure 4

Angular displacement comparison

Full size image

3.2 Load effect on dynamic characteristics

This section shows the effects of stochastic and deterministic loads on a gear system’s dynamic characteristics. All the simulations in this section are under a constant load or a certain Gaussian diffusion process modeled as given in Table 2.

Table 2 The scenario of Gaussian diffusion process
Full size table

This scenario given in Table 2 is used for all stochastic loads simulated in this paper. Figure 5 shows three loading processes: \({S_1}\) is a constant loading process. \({S_2}\) and \({S_3}\) are two realizations of the Gaussian diffusion process.

Fig. 5
figure 5

External load processes

Full size image

The external load is assumed to be a summation of a deterministic load component and Gaussian white noise [11, 12, 19]. Compared with Gaussian white noise, Gaussian diffusion process has fluctuating mean values, which is more appropriate in our model to study the transient characteristics caused by the randomness of load. The assumption of Gaussian diffusion process may be better on some occasions, for example, wind turbine suffering from time-varying load [14].

The friction coefficient usually varies with load and speed in real applications. Under stochastic loading, it is not easy to precisely analyze the friction mechanism as many factors are involved (e.g., lubrication, surface roughness, load, sliding velocity, and temperature) [23, 29]. According to the research results from [23, 29], the friction coefficient has a small variation when the load and relative velocity vary in a small range. Ref. [25] compared the influence of five different friction coefficient models on gear dynamic responses under constant load. One model used constant friction coefficient, while others adopted time-varying friction coefficients. According to their results, gearbox systems behave similarly in many aspects even though the friction models are different. They concluded that the simplified assumption of constant friction coefficient is still adoptable to some extent compared to those time-varying friction coefficient models. The purpose of this paper is not to analyze the friction mechanism but to investigate the transient characteristics affected by friction under stochastic load. Even though a constant friction model is used in this study, the proposed model can still generate reasonable results especially when the variation of load and relative velocity is small. If the variations of load and velocity are large, further research is needed.

According to [21], the friction coefficient in a gear system may vary from 0.01 to 0.08. In this section, we fix the friction coefficient at 0.04 to illustrate the load effect on gear dynamic characteristics.

3.2.1 Duration in transient state

Numerical solutions to the equations of motion are obtained by MATLAB. Figure 6 presents the relative angular displacement \(\delta \) of the gear pair under stochastic and deterministic loads.

Fig. 6
figure 6

Relative angular displacement under three load processes

Full size image

As time goes, when the relative angular displacement does not change very much anymore, the system is considered to be in the steady state. Figure 6 shows that the system used about 0.35 s to reach the steady state under the deterministic load (\({S_1}\)). Under the stochastic load (\({S_2}\) and \({S_3}\)), the system has not reached the steady state before 0.4 s. Therefore, the system with stochastic load uses much longer time to reach steady state than that with deterministic load.

3.2.2 Periodicity and chaos

In this section, the dynamic characteristics including periodicity and chaos are studied.

The chaotic oscillation cannot be intuitively observed in \({S_2}\) or \({S_3}\) compared to that in \({S_1}\). There are two possible reasons: (1) The chaos of responses under this scenario of Gaussian diffusion process is not strong enough to appear in this scale. (2) The coupling of the friction, and the randomness weakens the chaotic oscillation. The chaotic oscillation of the system could be addressed using secondary Poincaré map [30] in future work.

The periodic and quasiperiodic dynamical oscillations can exist simultaneously [30, 31]. Most periodic behaviors are not perfect periodic and neither quasiperiodic nor chaotic as well [30]. From Fig. 7, phase diagram of \({S_1}\) shows overlapped loops while phase diagrams of \({S_2}\) and \({S_3}\) give independent loops. Thus, the gear system under deterministic load holds the properties of periodic and quasiperiodic oscillations simultaneously. Under stochastic load, gear system shows quasiperiodic oscillation.

Fig. 7
figure 7

Phase diagrams of relative angular displacement and relative angular velocity in the time interval [0.35, 0.4]s under three loading scenarios, \({S_1}\), \({S_2}\), and \({S_3}\)

Full size image

3.2.3 Transient asymptotic stability

To investigate the performance of a gear system in the transient state, one of the most important aspects is the transient stability [14]. According to [14], the responses of gear system will converge to a certain orbit. In our case, the convergency of responses under stochastic load can be visualized as shown in Fig. 6, while the convergence orbit is not clear to identify. However, we can utilize the convergence orbit obtained under deterministic load in [22] for reference, which \(\delta \) has a small perturbation near 0.05 (value of backlash) and \(\dot{\delta }\) has a small perturbation near 0. The gear system is approaching to a stable state with the relative motion decreasing and transmission ratio approaching to a constant. This phenomenon is asymptotically stable [32]. We apply an indicator to quantify such transient asymptotic stability. Choose a certain time interval and define center distance as

$$\begin{aligned} d= & {} {\left[ {\left( {\max (\delta ) - 0.05} \right) - \left( {\min (\delta ) - 0.05} \right) } \right] ^{\frac{1}{2}}}\nonumber \\&\times \,{\left[ {\left( {\max (\dot{\delta }) - 0} \right) - \left( {\min (\dot{\delta }) - 0} \right) } \right] ^{\frac{1}{2}}}\nonumber \\= & {} {\left[ {\max (\delta ) - \min (\delta )} \right] ^{\frac{1}{2}}}{\left[ {\max (\dot{\delta }) - \min (\dot{\delta })} \right] ^{\frac{1}{2}}} \end{aligned}$$
(22)

The center distance indicates the range of vibration response in a certain time interval. The transient state is more stable with a lower center distance.

When \(t \in \left[ {0.35,0.4} \right] \) and \(\mu =0.04\), we found \(d = 0.34\,\mathrm{mm/{s^{\textstyle {1 \over 2}}}}\) for \({S_1}\), \(d = 0.44\,\mathrm{mm/\mathrm{{s^{{\textstyle {1 \over 2}}}}}}\) for \({S_2}\) and \(d = 0.59\,\mathrm{mm/\mathrm{{s^{{\textstyle {1 \over 2}}}}}}\) for \({S_3}\). Even if \({S_2}\) and \({S_3}\) follow the same scenario, they show quite some differences in center distance from each other.

Since the responses (\(\delta \) and \(\dot{\delta }\)) of the gear pair under Gaussian diffusion process are random variables, it is necessary to give statistical information of transient stability under stochastic load. In dealing with random variable, the probabilistic method is a classical approach for uncertainty modeling based on the well-developed probability theory [33].

To obtain statistical results, we adopt direct Monte Carlo (MC) method instead of path integration method [34,35,36,37] or the stochastic perturbation method [38, 39]. Although MC takes more calculation time, we can achieve the desired accuracy by increasing simulation time. In this simulation, each realization follows the same scenario in Table 2.

When \(t \in \left[ {0.35,0.4} \right] \) and \(\mu =0.04\), we simulated 100 realizations and obtained corresponding center distances. There are 93 center distances greater than that obtained under deterministic load. We conclude that the center distance under stochastic load had \(93\% \) possibility greater than that under deterministic load. Therefore, it can be concluded that there is lower transient stability under the stochastic load.

3.3 Friction effects on dynamic characteristics

This section evaluates the influence of different friction coefficient values on the dynamic characteristics of the gear system under a certain stochastic load with the same scenario in Table 2. Six cases of the friction coefficient values (\(\mu =\left\{ {0,\,0.01,\,0.02,\,0.03,0.04,0.05} \right\} \)) are used, and responses are compared with one another. The friction coefficient effect on the transient stability will be studied in Sect. 3.3.1. Section 3.3.2 will investigate the friction coefficients’ influence on the dispersion of responses.

Fig. 8
figure 8

Comparison of center distance with each friction coefficient

Full size image
Fig. 9
figure 9

Boxplot of center distance with each friction coefficient

Full size image
Fig. 10
figure 10

PDF evolution plot depicts the change of the PDF distribution within 0.1s. a 0.3 s, b 0.33 s, c 0.36 s, d 0.4 s

Full size image

3.3.1 Transient asymptotic stability

This section shows the effects of different friction coefficient values on the transient stability. Firstly, the center distances under three loadings (\({S_1},{S_2},{S_3}\)) are shown in Fig. 8. Then, the statistical analysis of the center distance under stochastic load is shown in Fig. 9.

Figure 8 shows the comparison of center distances between the three loading realizations. From Fig. 8, the trend of the center distance of \({S_2}\) shared similarity with that of \({S_1}\). However, the trend of \({S_3}\) was different from \({S_1}\) and \({S_2}\). Even \({S_2}\) and \({S_3}\) followed the same scenario, they showed great differences from each other in amplitude. It should be noticed that the change of center distance with the increasing of friction coefficient is not monotonous. A small friction coefficient does not guarantee a better transient stability from the observation in Fig. 8.

Figure 9 is a boxplot that denotes the statistical properties of center distances under each friction coefficient value. The dot in a circle is the median, the block with solid line is the interquartile range, and the dash line is the range of the minimum and maximum. From Fig. 9, the range of center distance with the friction coefficient being 0 is smaller than most of the cases with positive friction coefficient. Thus, friction causes more instability in transient state. But there is no obvious trend between center distance and friction coefficients. In those cases with positive friction coefficient values, the minimum range of center distance is found at \(\mu =0.02\), and the maximum range of center distance is found at \(\mu =0.01\) or \(\mu =0.03\).

Hence, gear system has worst transient stability with \(\mu =\{ 0.01,0.03\} \) and best transient stability with \(\mu =\{ 0,0.02\} \). According to this result, we should find out and avoid the friction coefficient which will worsen transient stability in the gear design phase. At the same time, the friction coefficient should be adjusted to a suitable value in gear system to increase transient stability.

3.3.2 Dispersion of responses

The descriptions of responses in the gear system under stochastic load are analyzed with probability density functions (PDFs) [40]. Figure 10 describes the PDF evolution during the time range [0.3, 0.4]s with \(\mu =0.04\). With increase of time, the joint PDFs between relative angular displacement and relative angular velocity become more concentrated. It indicates that the system approaches a stable state. Hence, in this simulation, \(t=0.4\) s is the most stable state for a gear system under stochastic load. If a rule of this evolution can be found, the PDF prediction can be done with an initial PDF.

Since \(t=0.4\) s is considered as the most stable state, the following discussion is limited to that time point. Figures 11 and 12 show the instantaneous PDFs of relative displacement and relative velocity, respectively, at \(t=0.4\) s. The corresponding solutions of the deterministic case at the same time point are shown in Table 3. Due to the calculation difficulty, deterministic responses are easier to obtain than stochastic responses. If the responses under stochastic load fall in the center region of the responses under deterministic load, we can predict the stochastic responses corresponding to the deterministic responses. Compare Figs. 11, 12 and Table 3, the results of relative angular displacement in Fig. 11 falls in the center regions around the results of deterministic load. But the mean of relative angular velocity did not fall in the center regions around the result of deterministic load.

Fig. 11
figure 11

PDF of relative angular displacement in different friction coefficient at \(t=0.4\) s

Full size image
Fig. 12
figure 12

PDF of relative angular velocity in different friction coefficient at \(t=0.4\) s

Full size image

For a gear pair with fault, the PDFs of relative displacement and relative velocity are definitely different from those in the perfect gear case (without fault). According to the dispersion property investigated in the previous paragraph, relative displacement is more appropriate to be an indicator of fault diagnoses for further study. Thus, these PDFs of relative angular displacement obtained by our study for perfect gear system may be used as references in gear health monitoring.

Table 3 Responses under deterministic load
Full size table

On the other hand, according to Figs. 11 and 12, the difference in the PDFs of different coefficient is obvious. This also proves that the friction cannot be ignored in dealing with gear stochastic dynamics. However, the relationship between friction, stochastic load, and time is not given. This will be further explored in our future work.

Probabilities of gear system responses (relative angular displacement and relative angular velocity) in a safety interval are given in Table 4. Safety interval means that the gear system responses have a high possibility of occurring in this interval. If the responses exceed the safety interval, there is higher possibility that the gear system has failure [41]. We can select a proper safety interval based on accuracy demand. In Table 4, the safety intervals are chosen based on the rule that there are at least \(75\% \) data falling in the safety intervals. According to our model, we choose \(\delta \in \left[ {0.04,0.055} \right] \) and \(\dot{\delta }\in [ - 16,16]\) for analysis. When \(\delta \in \left[ {0.04,0.055} \right] \), we noticed that the probability of \(\delta \) was the lowest (equal to 76%, as indicated by the boldface 76 in Table 4) when friction coefficient \(\mu =0.03\). When \(\dot{\delta }\in [ - 16,16]\), the probability of \(\dot{\delta }\) was the lowest (equal to 79%, as indicated by the boldface 79 in Table 4) with \(\mu =0.01\). The lower interval probability indicates higher data dispersion. The higher dispersion of the values always reflects higher uncertainty in the data [40]. It is concluded that gear responses have a higher proportion exceeding a certain safety interval and have a higher potential failure probability with \(\mu =0.01\) or 0.03.

Table 4 The probabilities of a safety interval under each friction coefficient value (\(\% \))
Full size table

4 Conclusion

In this study, a gear stochastic dynamic model for a spur gear pair considering TVMS, gear mesh damping, backlash, friction, and stochastic load is established. The dynamic responses of this model are investigated using numerical simulation and compared with previous work. The analysis results demonstrate that (a) the established SDOF gear dynamic model is more realistic than reported models which did not consider friction, (b) under the same friction coefficient value (\(\mu =0.04\)), the stochastic load generates longer duration and more quasi-periodicity in the transient state than the constant load. Stochastic load causes lower transient stability than deterministic load, (c) under stochastic load, the gear system has the worst transient stability with \(\mu =0.01\) or 0.03 and best transient stability with \(\mu =0\) or 0.02. Friction generates higher dispersion of relative angular displacement with \(\mu =0.01\) or 0.03 in the transient state.

This analysis gives us better understanding on stochastic load and friction effects on the gear dynamic characteristics. The proposed gear dynamic model and numerical results can be used as a reliable tool to investigate the gear random dynamics. Future work will design corresponding experiments to validate our numerical findings. Moreover, we will further extend our gear model by incorporating varying friction coefficient and analyzing the effects of different friction models on gearbox dynamics under stochastic load in our future work.