Introduction

The herringbone gear is composed of a pair of symmetrical helical gears and an intermediate shaft segment. It can eliminate the additional axial load during the meshing process of helical gears, increase the contact ratio, and make the meshing more stable. Therefore, it is widely used in gear transmission systems. The nonlinear characteristics of the gear system are analyzed, the influence of various factors on nonlinear behavior is explored, and the stable operation interval is found, this will be beneficial to the design work.

Research of the system’s nonlinear characters has been conducted deeply by Substantial scholars. They [1,2,3,4,5,6,7,8,9,10,11] established and solved the nonlinear dynamic model of the system considering the influence of time-varying meshing stiffness, pitch deviation, backlash, and tooth center deviation. The double planetary gear sets (DPGSs) have excellent performance and is widely used in the transmission system. In previous studies, the time-varying gear excitation is often ignored, which makes the vibration characteristic analysis results inaccurate. Liu [12, 13] establishes the dynamic model of the flexible shaft gear transmission system (FGDS) and the dynamic model of the double planetary gear set (DPGS). The theoretical analysis and experimental verification are combined to study the nonlinear dynamic characteristics of the time-varying excitation force of the system through the acceleration map, spectrum map and other images. Xu [14] takes the tooth surface friction into account, to study the system dynamic response, propose a dynamic model of new HPGS coupling. Mo [15,16,17,18,19] established a face gear model, in which the axis of the gear is not perpendicular to each other, and studied its nonlinear dynamic response by cell mapping method. Wang [20, 21] established the improved GTF aero-engine gear–rotor coupling transmission system nonlinear dynamic model considering multiple nonlinear parameters and studied the influence of bifurcation parameters, such as damping ratio and comprehensive meshing error on the dynamic response of the system. Tian [22] considered the time-varying contact stiffness, clearance of bearing and backlash, establish the motion model of coupling. The complex nonlinear behaviors of the system were revealed by the bifurcation diagram, time domain diagram, Poincare section diagram and phase plane diagram.

The multi-scale method includes analysis methods, such as primary resonance analysis, super-harmonic analysis, and sub-harmonic analysis. It usually decomposes the differential equation solution into multiple time-scale functions, which can effectively improve the calculation accuracy and has broad applications in various research fields. Wang et al. [23] derived the displacement and voltage frequency response functions of the monostable energy harvester based on the harmonic balance expansion method and the multi-scale method, respectively. Jian [24] established an active control system model with time delay feedback, analyzed the stability of the system by an effective method. Huang [25] and other scholars established the dynamic model of a high-speed train gear transmission system under stick–slip oscillation, listed the super-harmonic resonance frequency response equation of the system by multi-scale method, and analyzed the stability of the system by perturbation theory. Many scholars [26,27,28,29,30,31,32] consider plurality system nonlinear factors that exist in engineering practice and introduce them, then system nonlinear dynamic model can be established, and carried out a multi-scale analysis of the main resonance characteristics of the system to determine the stable operation region of the system.

The nonlinear vibration and primary resonance response of herringbone gear transmission systems considering time-varying meshing stiffness, clearance of tooth side, error of transmission, clearance of bearing, and other factors is what this paper mainly focuses on. The main content of the article can be divided into the following parts: in the first part, to analyze the nonlinear meshing force on the gear, the error of meshing and the backlash are selected to introduce in the actual existence of many nonlinear factors. In the actual production, bearing will have clearance, which should be introduced to establish the nonlinear vibration dynamic model of bearing and calculate the force in the bearing. The system components dynamic analysis is carried out, and the calculation method and numerical images at different times of the system time-varying stiffness of gears meshing is given. Second, the second part establishes the system dynamics model, lists the vibration differential equations, and performs dimensionless processing. Subsequently, the third part solves an example and studies the influence of excitation frequency on the nonlinear behavior of the system through a time domain diagram, frequency domain diagram, phase diagram, Poincare section, and bifurcation diagram. In the fourth part, using the multi-scale method, one of the characteristics of the herringbone gear transmission system-stability conditions has been derived. Using the numerical method, how will the changing of meshing damping and load excitation influence the amplitude–frequency characteristics of the system have been simulated, this is beneficial to establish the stable operation interval of the system. Finally, the conclusion is drawn in the fifth part. The workflow of the research is shown in Fig. 1.

Fig. 1
figure 1

Structure flow chart of nonlinear dynamic analysis

Full size image

Dynamics Analysis of System Components

Meshing Line Displacement and Meshing Force

Taking the right helical gear pair as an example, the meshing line displacement is calculated by the following equation:

$$\begin{aligned} x_{n1} & = (x_{1} - x_{2} )\sin \alpha_{n} + (y_{1} - y_{2} )\cos \alpha_{n} \cos \beta + (z_{1} - z_{2} )\cos \alpha_{n} \sin \beta \\ & \quad + (R_{b1} \theta_{1} - R_{b2} \theta_{2} )\cos \alpha_{n} \cos \beta - e(t). \\ \end{aligned}$$
(1)

In the formula, x1, y1, z1, θ1 is The vibration displacement and torsional displacement of the right active helical gear; x2, y2, z2, θ2 is The vibration displacement and torsional displacement of the right driven helical gear in each direction; αn, β are the normal pressure angle and spiral angle, respectively. e(t) is the static transfer error, calculated by the following equation:

$$e(t) = e\sin \omega_{m} t.$$
(2)

In the formula, e is the mean value of static transmission error, and ωm is the meshing frequency of the helical gear pair, which is equal to the product of helical gear rotation frequency and tooth number.

Express the backlash nonlinear function in the following equation:

$$f(x_{n1} ) = \left\{ {\begin{array}{*{20}c} {x_{n1} - b_{m} ,} & {x_{n1} > b_{m} } \\ {0,} & {\left| {x_{n1} } \right| < b_{m} } \\ {x_{n1} + b_{m} ,} & {x_{n1} < - b_{m} } \\ \end{array} } \right..$$
(3)

In the formula, bm is half of the tooth side clearance value.

The calculation formula of meshing force is shown in the following formula:

$$F_{m1} = K_{m} (t)f(x_{n1} ) + C_{m} \dot{x}_{n1} .$$
(4)

In the formula, Km(t) is the time-varying meshing stiffness of the helical gear pair, and Cm is the meshing damping. The force of the gear meshing process is shown in Fig. 2.

Fig. 2
figure 2

Meshing force of herringbone gear

Full size image

According to the above relationship, the calculation formula of meshing force is obtained, as shown in the following formula:

$$\left\{ \begin{gathered} F_{mx1} = F_{m1} \sin \alpha_{n} \hfill \\ F_{my1} = F_{m1} \cos \alpha_{n} \cos \beta \hfill \\ F_{mz1} = F_{m1} \cos \alpha_{n} \sin \beta \hfill \\ \end{gathered} \right..$$
(5)

The calculation method of the meshing force of the left helical gear pair is the same.

Time-Varying Meshing Stiffness and Damping

Approximating the meshing stiffness of the gear pair as a rectangular wave. The calculation method is as follows:

According to ISO6336-2006, the calculation formula of single tooth meshing stiffness is:

$${C^{\prime}} = c_{{{\text{th}}}}{\prime} C_{M} C_{R} C_{B} B\cos \beta$$
(6)

In the formula, β is the helix angle, B is the tooth width, \(c_{{{\text{th}}}}{\prime}\) can be calculated by the following formula:

$$\left\{ \begin{gathered} c^{\prime}_{th} = \frac{1}{{q^{\prime}}} \hfill \\ q^{\prime} = C_{1} + \frac{{C_{2} }}{{z_{n1} }} + \frac{{C_{3} }}{{z_{n2} }} + C_{4} x_{1}^{*} + \frac{{C_{5} x_{1} }}{{z_{n1} }} + C_{6} x_{2}^{*} + \frac{{C_{7} x_{2} }}{{z_{n2} }} \hfill \\ \end{gathered} \right..$$
(7)

In Eq. (2), the values of each coefficient are shown in Table 1. Because the helical gear has no displacement, so x1 = x2 = 0.

Table 1 Coefficients of polynomials
Full size table

CM is an experimental correction coefficient to measure the difference between the measured value and the theory, usually 0.8. CR reflects the flexibility of the rim and web, generally 1.0. CB is the basic rack correction coefficient, Cγα is double tooth meshing stiffness, and εα is gear contact ratio, the calculation method are shown in the following equation:

$$\left\{ \begin{gathered} C_{B} = [1 + 0.5(1.25 - h_{fp} /m_{n} )][1 - 0.02(20^\circ - \alpha_{n} )] \hfill \\ C_{\gamma \alpha } = C^{\prime}(0.75\varepsilon_{\alpha } + 0.25) \hfill \\ \varepsilon_{\alpha } = [z_{n1} (\tan \alpha_{a1} - \tan \alpha_{n} ) + z_{n2} (\tan \alpha_{a2} - \tan \alpha_{n} )]/2\pi \hfill \\ \end{gathered} \right..$$
(8)

In the formula, hfp is tooth dedendum, mn is normal-mode propagation module, and αn is normal pressure angle. αa1, αa2 is the Tooth tip circular pressure angle.

The calculation formula of Kmi(t) (i = 1, 2) is

$$K_{mi} (t) = \left\{ {\begin{array}{*{20}c} {C_{\gamma \alpha } } & {0 \le t \le (\varepsilon_{\alpha } - 1)T} \\ {C^{\prime} } & {(\varepsilon_{\alpha } - 1)T \le t \le T} \\ \end{array} } \right..$$
(9)

In the formula, T is the meshing stiffness variation period. To make the curve of meshing stiffness who has time-varying characteristic more accurate, expand the wave by the Fourier series. Δksn is the stiffness variation, ωl is the meshing frequency, \(a_{sn}^{l}\) and \(b_{sn}^{l}\) are the Fourier coefficient, γsn is the Axis intersection angle, εα is the Coincidence degree, Fourier series Order is represented by l, and The 5th order accuracy is enough. The stiffness calculation method is shown in Formulas (10) and (11):

$$\left\{ \begin{gathered} K_{mi} (t) = k + \Delta k_{sn} (t) \hfill \\ k = C_{\gamma \alpha } (\varepsilon_{\alpha } - 1) + {C^{\prime}} (2 - \varepsilon_{\alpha } ) \hfill \\ \Delta k_{sn} (t) = \sum\limits_{l = 1}^{\infty } {(a_{sn}^{l} \cos l\omega_{l} t + b_{sn}^{l} \sin l\omega_{l} t)} \hfill \\ \end{gathered} \right.$$
(10)
$$\left\{ \begin{gathered} b_{sn}^{l} = k^{*} \{ 2\sin \pi l(2\gamma_{sn} + \varepsilon_{\alpha } - 1)\sin \pi l(\varepsilon_{\alpha } - 1) + (1 - \varepsilon_{\alpha } )[\cos 2\pi l(2 - \gamma_{sn} - \varepsilon_{\alpha } ) - 1]\} \hfill \\ a_{sn}^{l} = k^{*} [2\cos \pi l(2\gamma_{sn} + \varepsilon_{\alpha } - 1)\sin \pi l(\varepsilon_{\alpha } - 1) + (1 - \varepsilon_{\alpha } )[\sin 2\pi l(2 - \gamma_{sn} - \varepsilon_{\alpha } )] \hfill \\ k^{*} = \frac{{c_{\gamma \alpha } - c^{\prime}}}{1.6l\pi }. \hfill \\ \end{gathered} \right.$$
(11)

The time-varying meshing stiffness curves of meshing line 1 and meshing line 2 are shown in Fig. 3.

Fig. 3
figure 3

Time-varying meshing stiffness of each meshing line

Full size image

The meshing damping cm is calculated as follows:

$$c_{m} = 2\xi \sqrt {\frac{{K_{m} R_{{\text{p}}}^{2} R_{{\text{g}}}^{2} J_{{\text{P}}} J_{{\text{g}}} }}{{R^{2} J_{{\text{p}}} + R_{{\text{g}}}^{2} J_{{\text{g}}} }}} .$$
(12)

In the formula, ξ is the damping coefficient, usually 0.03–0.17, Jp and Jg are the rotational inertia of the driving gear and the driven gear, respectively, and Rp and Rg are the radius of the dividing circle of the driving gear and the driven gear, respectively.

Bearing Force Calculation

In the process of establishing the herringbone gears system, the bearings being used are deep groove ball bearings. The structure and coordinate system establishment method are shown in Fig. 4.

Fig. 4
figure 4

Bearing model of the herringbone gears system

Full size image

What the rotating shaft connects to is the inner ring of the bearing, and the bearing seat is what the outer ring is fixed to. The bearing coordinate system has its own origin, the center of curvature of the inner ring is where it is located. The rotating shaft has its own axis, which is coincides with Z axis.

In the raceway, the rolling elements is assumed that being arranged equidistantly and do not have relative sliding. There are contact points between rolling element and rings, whose linear velocity can be calculated by the following formula:

$$\left\{ \begin{gathered} v_{bi} = \omega_{bi} \cdot r_{bi} \hfill \\ v_{bo} = \omega_{bo} \cdot r_{bo} \hfill \\ \end{gathered} \right..$$
(13)

In the formula, ωbi and ωbo are the angular velocities of the inner and outer rings, and rbi and rbo are the radii of the inner and outer rings of the bearing, respectively. What the bearing seats connect to is the outer rings, so ωbo = 0, that is, vbo = 0.

The revolution angular velocity of the rolling element around the axis of the rotating shaft is calculated by the following formula:

$$\omega_{bn} = \frac{{v_{bi} + v_{bo} }}{{r_{bi} + r_{bo} }} = \frac{{\omega_{bi} \cdot r_{bi} }}{{r_{bi} + r_{bo} }}.$$
(14)

The position angle of the rolling element changes with time, and its calculation method is given by the following equation:

$$\theta_{i} (t) = \frac{2\pi (i - 1)}{{Z_{b} }} + \omega_{bn} t\quad (i = 1,2, \ldots Z_{b} ).$$
(15)

In the formula, Zb is the number of rolling elements in the bearing.

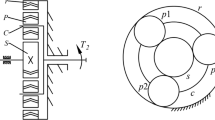
The deformation of the bearing rolling element is shown in Fig. 5. When not deformed, Obo, Obi represent outer and inner raceway curvature center of the bearing, respectively, rbo and rbi represent the radius of curvature, respectively. γi represents the contact angle between the rolling element and the outer raceway and the inner raceway when the rolling element is not deformed, and \(\gamma^{\prime}_{i}\) represents the contact angle between the deformed rolling element and the outer raceway and the inner raceway. As shown in Fig. 6, because the seat of bearing is connected with the outer ring, it is considered that the center of curvature does not change after the outer ring is stressed. that is, Obo and \(O^{\prime}_{bo}\) are in the same position, and inner ring also changes its curvature center from Obi to \(O^{\prime}_{bi}\).

Fig. 5
figure 5

Rolling deformation diagram

Full size image
Fig. 6
figure 6

Geometric relationship diagram

Full size image

Along the coordinate axis, there are displacement of the bearing, which is the factor that should be considered to calculated center distance of the curvature center of both rings after deformation, after deforming, there will be deformation angle in the rolling element, it can be calculated by the following formula:

$$\left\{ \begin{gathered} l^{\prime} = \sqrt {(l\sin \gamma_{i} + z + r_{bo} \delta_{\theta } \cos \theta_{i} )^{2} + \left( {y\sin \theta_{i} + l\cos \gamma_{i} + x\cos \theta_{i} } \right)^{2} } \hfill \\ \tan \gamma^{\prime}_{i} = \frac{{l\sin \gamma_{i} + z + r_{bo} \delta_{\theta } \cos \theta_{i} }}{{y\sin \theta_{i} + l\cos \gamma_{i} + x\cos \theta }} \hfill \\ \end{gathered} \right..$$
(16)

In the formula, x, y, and z is the vibration displacement of the bearing along the corresponding direction of the coordinate axis.

Taking c as the radial clearance of the bearing, the deformation of the rolling element is calculated by the following formula:

$$\delta = l^{\prime} - l - c.$$
(17)

When the rolling element deformation δ > 0, the bearing force will exist, so the Heaviside function is introduced, as shown in Eq. (19):

$$H(\delta ) = \left\{ {\begin{array}{*{20}c} {1,} & {\delta > 0} \\ {0,} & {\delta < 0} \\ \end{array} } \right..$$
(18)

The force calculation method of a single rolling element is shown in formula (20), where Fab is the axial force of the rolling element, Frb is the radial force of the rolling element, and Kb is the contact stiffness between the rolling element and the raceway, the calculation method is as follows:

$$\left\{ \begin{gathered} K_{b} = 3.217 \times 10^{5} (\delta^{*} )^{ - 3/2} \delta_{c}^{1/2} \left( {\sum \rho } \right)^{ - 1/2} \hfill \\ \delta^{*} = \frac{2\Gamma (e)}{\pi }\left( {\frac{{\pi (1 - e^{2} )}}{2\prod (e)}} \right)^{1/3} \hfill \\ \end{gathered} \right..$$
(19)

In the formula, \(\delta_{c}\) is the juxtaposition metamorphosis, \(\sum \rho\) is the auxiliary function of raceway contact point. When the bearing is a ball bearing, take n = 2/3, when the bearing is a roller bearing, take n = 9/10:

$$\left\{ \begin{gathered} F_{ab} = K_{b} \delta^{n} \sin \gamma^{\prime}_{i} \cdot H\left( \delta \right) \hfill \\ F_{rb} = K_{b} \delta^{n} \cos \gamma^{\prime}_{i} \cdot H\left( \delta \right) \hfill \\ \end{gathered} \right..$$
(20)

The force of a single bearing is expressed as

$$F_{bx} = \sum\limits_{i = 1}^{{Z_{b} }} {F_{rb} \cos \theta_{i} } , \, F_{by} = \sum\limits_{i = 1}^{{Z_{b} }} {F_{rb} \sin \theta_{i} } , \, F_{bz} = \sum\limits_{i = 1}^{{Z_{b} }} {F_{ab} } .$$
(21)

Dynamic Model of Herringbone Gear

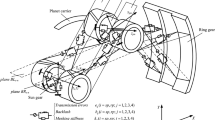
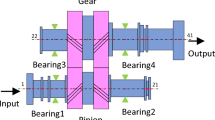
Herringbone gears system is composed of an input shaft, an output shaft, four bearings of input and output shaft, respectively, and a pair of herringbone gears. Its three-dimensional model is shown in Fig. 7.

Fig. 7
figure 7

Three-dimensional model of herringbone gears

Full size image

To study the nonlinear behavior of herringbone gears system under certain conditions, the initial parameters of the system are defined, as shown in Table 2, 3, and 4.

Table 2 Basic parameters of the whole system
Full size table
Table 3 Basic parameters of herringbone gears
Full size table
Table 4 Basic parameters of bearings
Full size table

The multi-degree-of-freedom coupling vibration model of the single-stage herringbone gear transmission system shown in Fig. 8 is constructed. The herringbone gears are regarded as combinations of four helical gears and two intermediate shaft segments. Herringbone gears system vibration model takes backlash, the error of transmission, nonlinear vibration of bearing, input torque fluctuation, time-varying stiffness of meshing gears into account while being established. In the diagram, m1, m3, I1, I3 is the active helical gear mass and moment of inertia on the right and left sides, respectively, and m2, m4, I2, I4 are the driven helical gear mass and moment of inertia on the right and left sides, respectively. mA1 and mA2 are the bearing mass on the right and left sides of the input shaft, respectively, and mB1 and mB2 are the bearing mass on the right and left sides of the output shaft, respectively. kA1i, kA2i, kB1i, kB2i, cA1i, cA2i, cB1i, cB2i (i = x, y) are the stiffness and damping of each bearing inner ring. k1i, k2i, k3i, k4i, c1i, c2i, c3i, c4i (i = x, y, z, θ) are the stiffness and damping of gear and bearing connecting shaft. k13i, k24i, c13i, c24i (i = x, y, z, θ) are the stiffness and damping of the intermediate shaft.

Fig. 8
figure 8

Vibration model of herringbone gear transmission system

Full size image

The gears are regarded as mass points, their mass is concentrated at the centric. The bearing and the rotating shaft are rigidly connected, so the bearing and the rotating shaft on the same side are regarded as the mass concentrated at the centric. The force on the bearing raceway and the gear meshing force can be decomposed in x, y and z directions. The system considers 24 degrees of freedom:

$$\{ x_{1} ,y_{1} ,z_{1} ,\theta_{1} ,x_{2} ,y_{2} ,z_{2} ,\theta_{2} ,x_{3} ,y_{3} ,z_{3} ,\theta_{3} ,x_{4} ,y_{4} ,z_{4} ,\theta_{4} ,x_{A1} ,y_{A1} ,x_{A2} ,y_{A2} ,x_{B1} ,y_{B1} ,x_{B2} ,y_{B2} \} .$$

Among them, xi, yi, zi, θi (i = 1, 2, 3, 4) are the vibration and torsional displacement of each helical gear, xvj, yvj (v = A, B; j = 1, 2) are the radial and tangential displacements of each bearing.

The system vibration differential equation is as follows:

$$\left\{ \begin{aligned} & m_{1} \ddot{x}_{1} + c_{x1} (\dot{x}_{1} - \dot{x}_{A1} ) + c_{x13} (\dot{x}_{1} - \dot{x}_{3} ) + k_{x1} (x_{1} - x_{A1} ) + k_{x13} (x_{1} - x_{A1} ) = - F_{mx1} \\ & m_{1} \ddot{y}_{1} + c_{y1} (\dot{y}_{1} - \dot{y}_{A1} ) + c_{y13} (\dot{y}_{1} - \dot{y}_{3} ) + k_{y1} (y_{1} - x_{A1} ) + k_{y13} (y_{1} - y_{A1} ) = - F_{my1} - m_{A1} g + F_{1} \\ & m_{1} \ddot{z}_{1} + c_{z1} (\dot{z}_{1} - \dot{z}_{A1} ) + c_{z13} (\dot{z}_{1} - \dot{z}_{3} ) + k_{z1} (z_{1} - z_{A1} ) + k_{z13} (z_{1} - z_{A1} ) = F_{mz1} \\ & I_{1} \ddot{\theta }_{1} + c_{t13} (\dot{\theta }_{1} - \dot{\theta }_{3} ) + c_{t1} \dot{\theta }_{1} + k_{t13} (\theta_{1} - \theta_{3} ) + k_{t1} \theta_{1} = T_{1} - F_{my1} R_{b1} - m_{A1} gR_{b1} + F_{1} R_{b1} \\ \end{aligned} \right.$$
(22)
$$\left\{ \begin{aligned} & m_{3} \ddot{x}_{3} + c_{x3} (\dot{x}_{3} - \dot{x}_{A2} ) + c_{x13} (\dot{x}_{3} - \dot{x}_{1} ) + k_{x3} (x_{3} - x_{A2} ) + k_{x13} (x_{3} - x_{A2} ) = - F_{mx2} \\ & & m_{3} \ddot{y}_{3} + c_{y3} (\dot{y}_{3} - \dot{y}_{A2} ) + c_{y13} (\dot{y}_{3} - \dot{y}_{1} ) + k_{y3} (y_{3} - x_{A2} ) + k_{y13} (y_{3} - y_{A2} ) = - F_{my2} - m_{A2} g + F_{3} \\ & m_{3} \ddot{z}_{3} + c_{z3} (\dot{z}_{3} - \dot{z}_{A2} ) + c_{z13} (\dot{z}_{3} - \dot{z}_{1} ) + k_{z3} (z_{3} - z_{A2} ) + k_{z13} (z_{3} - z_{A2} ) = - F_{mz2} \\ & I_{3} \ddot{\theta }_{3} + c_{t13} (\dot{\theta }_{3} - \dot{\theta }_{1} ) + c_{t3} \dot{\theta }_{3} + k_{t13} (\theta_{3} - \theta_{1} ) + k_{t3} \theta_{3} = T_{3} - F_{my2} R_{b3} - m_{A2} gR_{b3} + F_{3} R_{b3} \\ \end{aligned} \right.$$
(23)
$$\left\{ \begin{aligned} & m_{2} \ddot{x}_{2} + c_{x2} (\dot{x}_{2} - \dot{x}_{B1} ) + c_{x24} (\dot{x}_{2} - \dot{x}_{4} ) + k_{x2} (x_{2} - x_{B1} ) + k_{x24} (x_{2} - x_{B1} ) = F_{mx1} \\ & m_{2} \ddot{y}_{2} + c_{y2} (\dot{y}_{2} - \dot{y}_{B1} ) + c_{y24} (\dot{y}_{2} - \dot{y}_{4} ) + k_{y2} (y_{2} - x_{B1} ) + k_{y24} (y_{2} - y_{B1} ) = F_{my1} - m_{B1} g - F_{2} \\ & m_{2} \ddot{z}_{2} + c_{z2} (\dot{z}_{2} - \dot{z}_{B1} ) + c_{z24} (\dot{z}_{2} - \dot{z}_{4} ) + k_{z2} (z_{2} - z_{B1} ) + k_{z24} (z_{2} - z_{B1} ) = F_{mz1} \\ & I_{2} \ddot{\theta }_{2} + c_{t24} (\dot{\theta }_{2} - \dot{\theta }_{4} ) + c_{t2} \dot{\theta }_{2} + k_{t24} (\theta_{2} - \theta_{4} ) + k_{t2} \theta_{2} = - T_{2} - F_{my1} R_{b2} - m_{B1} gR_{b2} + F_{2} R_{b2} \\ \end{aligned} \right.$$
(24)
$$\left\{ \begin{aligned} & m_{4} \ddot{x}_{4} + c_{x4} (\dot{x}_{4} - \dot{x}_{B2} ) + c_{x24} (\dot{x}_{4} - \dot{x}_{2} ) + k_{x4} (x_{4} - x_{B2} ) + k_{x24} (x_{4} - x_{B2} ) = F_{mx2} \\ & m_{4} \ddot{y}_{4} + c_{y4} (\dot{y}_{4} - \dot{y}_{B2} ) + c_{y24} (\dot{y}_{4} - \dot{y}_{2} ) + k_{y4} (y_{4} - x_{B2} ) + k_{y24} (y_{4} - y_{B2} ) = F_{my2} - m_{B2} g - F_{4} \\ & m_{4} \ddot{z}_{4} + c_{z4} (\dot{z}_{4} - \dot{z}_{B2} ) + c_{z24} (\dot{z}_{4} - \dot{z}_{2} ) + k_{z4} (z_{4} - z_{B2} ) + k_{z24} (z_{4} - z_{B2} ) = F_{mz2} \\ & I_{4} \ddot{\theta }_{4} + c_{t24} (\dot{\theta }_{4} - \dot{\theta }_{2} ) + c_{t4} \dot{\theta }_{4} + k_{t24} (\theta_{4} - \theta_{2} ) + k_{t4} \theta_{4} = - T_{4} - F_{my2} R_{b4} - m_{B2} gR_{b4} + F_{4} R_{b4} \\ \end{aligned} \right.$$
(25)
$$\left\{ \begin{gathered} m_{A1} \ddot{x}_{A1} + c_{x1} (\dot{x}_{A1} - \dot{x}_{1} ) + c_{xA1} \dot{x}_{A1} + k_{x1} (x_{A1} - x_{1} ) = - F_{bxA1} \hfill \\ m_{A1} \ddot{y}_{A1} + c_{y1} (\dot{y}_{A1} - \dot{y}_{1} ) + c_{yA1} \dot{y}_{A1} + k_{y1} (y_{A1} - y_{1} ) = - F_{byA1} - m_{A} g \hfill \\ \end{gathered} \right.$$
(26)
$$\left\{ \begin{gathered} m_{A2} \ddot{x}_{A2} + c_{x3} (\dot{x}_{A2} - \dot{x}_{3} ) + c_{xA2} \dot{x}_{A2} + k_{x3} (x_{A2} - x_{3} ) = - F_{bxA2} \hfill \\ m_{A2} \ddot{y}_{A2} + c_{y3} (\dot{y}_{A2} - \dot{y}_{3} ) + c_{yA2} \dot{y}_{A2} + k_{y3} (y_{A2} - y_{3} ) = - F_{byA2} - m_{A2} g \hfill \\ \end{gathered} \right.$$
(27)
$$\left\{ \begin{gathered} m_{B1} \ddot{x}_{B1} + c_{x2} (\dot{x}_{A1} - \dot{x}_{2} ) + c_{xB1} \dot{x}_{B1} + k_{x2} (x_{B1} - x_{2} ) = - F_{bxB1} \hfill \\ m_{B1} \ddot{y}_{B1} + c_{y2} (\dot{y}_{B1} - \dot{y}_{2} ) + c_{yB1} \dot{y}_{B1} + k_{y2} (y_{B1} - y_{2} ) = - F_{byB1} - m_{B1} g \hfill \\ \end{gathered} \right.$$
(28)
$$\left\{ \begin{gathered} m_{B2} \ddot{x}_{B2} + c_{x4} (\dot{x}_{B2} - \dot{x}_{4} ) + c_{xB2} \dot{x}_{B2} + k_{x4} (x_{B2} - x_{4} ) = - F_{bxB2} \hfill \\ m_{B2} \ddot{y}_{B2} + c_{y4} (\dot{y}_{B2} - \dot{y}_{4} ) + c_{yB2} \dot{y}_{B2} + k_{y4} (y_{B2} - y_{4} ) = - F_{byB2} - m_{B2} g \hfill \\ \end{gathered} \right.,$$
(29)

where g is the acceleration of gravity, Fmij (i = x, y, z; j = 1, 2, 3, 4) is the meshing force of helical gear pair; Fbij (i = x, y; j = A1, A2, B1, B2) is the bearing force of each bearing.

To improve the calculation speed and accuracy, it is necessary to conduct dimensionless treatment to the system vibration differential equation. Replace the torsional displacement of (22), (23), (24) and (25) with the meshing line displacement:

$$\left\{ \begin{gathered} m_{e1} \ddot{x}_{n1} = m_{e1} (\ddot{x}_{1} - \ddot{x}_{2} )\sin \alpha_{n} + m_{e1} (\ddot{y}_{1} - \ddot{y}_{2} )\cos \alpha_{n} \cos \beta + m_{e1} (\ddot{z}_{1} - \ddot{z}_{2} )\cos \alpha_{n} \sin \beta \hfill \\ - k_{m1} f(x_{n1} ) - c_{m1} \dot{x}_{n1} + F_{1} + e_{1} \omega_{m1}^{2} \sin \omega_{m1}^{2} t \hfill \\ m_{e2} \ddot{x}_{n2} = m_{e2} (\ddot{x}_{3} - \ddot{x}_{4} )\sin \alpha_{n} + m_{e2} (\ddot{y}_{3} - \ddot{y}_{4} )\cos \alpha_{n} \cos \beta + m_{e2} (\ddot{z}_{3} - \ddot{z}_{4} )\cos \alpha_{n} \sin \beta \hfill \\ - k_{m2} f(x_{n2} ) - c_{m2} \dot{x}_{n2} + F_{2} + e_{2} \omega_{m2}^{2} \sin \omega_{m2}^{2} t \hfill \\ \end{gathered} \right..$$
(30)

Among them, meshing line 1 is the meshing line of the right helical gear pair, and meshing line 2 is the meshing line of the left helical gear pair. mei (i = 1, 2) is the equivalent mass, Fi (i = 1, 2) is the external load, and the calculation method is shown by the following equation:

$$\left\{ \begin{gathered} m_{e1} = \frac{{J_{1} J_{2} }}{{J_{1} r_{2}^{2} + J_{2} r_{1}^{2} }} \hfill \\ m_{e2} = \frac{{J_{3} J_{4} }}{{J_{3} r_{4}^{2} + J_{4} r_{3}^{2} }} \hfill \\ F_{i} = \frac{{T_{j} (t)}}{{r_{j} }}(i = 1,2;j = 1,3) \hfill \\ \end{gathered} \right..$$
(31)

Among them, Ji (i = 1, 2, 3, 4) is the rotational inertia of each gear, and ri (i = 1, 2, 3, 4) is the radius of each gear dividing circle. The tooth side clearance bm is taken for dimensionless processing of the dynamic differential equation. The results are as follows:

$$\left\{ \begin{aligned} & \ddot{\overline{x}}_{n1} = (\ddot{\overline{x}}_{1} - \ddot{\overline{x}}_{2} )\sin \alpha_{n} + (\ddot{\overline{y}}_{1} - \ddot{\overline{y}}_{2} )\cos \alpha_{n} \cos \beta + (\ddot{\overline{z}}_{1} - \ddot{\overline{z}}_{2} )\cos \alpha_{n} \sin \beta \\ & - \kappa_{m1} f(\overline{x}_{n1} ) - \xi_{m1} \dot{\overline{x}}_{n1} + f_{1} + f_{e1} \\ & \ddot{\overline{x}}_{n2} = (\ddot{\overline{x}}_{3} - \ddot{\overline{x}}_{4} )\sin \alpha_{n} + (\ddot{\overline{y}}_{3} - \ddot{\overline{y}}_{4} )\cos \alpha_{n} \cos \beta + (\ddot{\overline{z}}_{3} - \ddot{\overline{z}}_{4} )\cos \alpha_{n} \sin \beta \\ & - \kappa_{m2} f(\overline{x}_{n2} ) - \xi_{m2} \dot{\overline{x}}_{n2} + f_{1} + f_{e2} \\ \end{aligned} \right.$$
(32)
$$\left\{ \begin{aligned} & \ddot{\overline{x}}_{1} + \xi_{x1} (\dot{\overline{x}}_{1} - \dot{\overline{x}}_{A1} ) + \xi_{x13} (\dot{\overline{x}}_{1} - \dot{\overline{x}}_{3} ) + \xi_{x1} (\overline{x}_{1} - \overline{x}_{A1} ) + \xi_{x13} (\overline{x}_{1} - \overline{x}_{A1} ) = ( - \kappa_{m1} f(\overline{x}_{n1} ) - \xi_{m1} \dot{\overline{x}}_{n1} )\sin \alpha_{n} \\ & & \ddot{\overline{y}}_{1} + \xi_{y1} (\dot{\overline{y}}_{1} - \dot{\overline{y}}_{A1} ) + \xi_{y13} (\dot{\overline{y}}_{1} - \dot{\overline{y}}_{3} ) + \kappa_{y1} (\overline{y}_{1} - \overline{x}_{A1} ) + \kappa_{y13} (\overline{y}_{1} - \overline{y}_{A1} ) \\ & = ( - \kappa_{m1} f(\overline{x}_{n1} ) - \xi_{m1} \dot{\overline{x}}_{n1} )\cos \alpha_{n} \cos \beta - f_{g} \\ & \ddot{\overline{z}}_{1} + \xi_{z1} (\dot{\overline{z}}_{1} - \dot{\overline{z}}_{A1} ) + \xi_{z13} (\dot{\overline{z}}_{1} - \dot{\overline{z}}_{3} ) + \kappa_{z1} (\overline{z}_{1} - \overline{z}_{A1} ) + \kappa_{z13} (\overline{z}_{1} - \overline{z}_{A1} ) = ( - \kappa_{m1} f(\overline{x}_{n1} ) - \xi_{m1} \dot{\overline{x}}_{n1} )\cos \alpha_{n} \sin \beta \\ \end{aligned} \right.$$
(33)
$$\left\{ \begin{aligned} & \ddot{\overline{x}}_{2} + \xi_{x2} (\dot{\overline{x}}_{2} - \dot{\overline{x}}_{B1} ) + \xi_{x24} (\dot{\overline{x}}_{2} - \dot{\overline{x}}_{4} ) + \kappa_{x2} (\overline{x}_{2} - \overline{x}_{B1} ) + \kappa_{x24} (\overline{x}_{2} - \overline{x}_{B1} ) = ( - \kappa_{m1} f(\overline{x}_{n1} ) - \xi_{m1} \dot{\overline{x}}_{n1} )\sin \alpha_{n} \\ & & \ddot{\overline{y}}_{2} + \xi_{y2} (\dot{\overline{y}}_{2} - \dot{\overline{y}}_{B1} ) + \xi_{y24} (\dot{\overline{y}}_{2} - \dot{\overline{y}}_{4} ) + \kappa_{y2} (\overline{y}_{2} - \overline{x}_{B1} ) + \kappa_{y24} (\overline{y}_{2} - \overline{y}_{B1} ) \\ & = ( - \kappa_{m1} f(\overline{x}_{n1} ) - \xi_{m1} \dot{\overline{x}}_{n1} )\cos \alpha_{n} \cos \beta - f_{g} \\ & \ddot{\overline{z}}_{2} + \xi_{z2} (\dot{\overline{z}}_{2} - \dot{\overline{z}}_{B1} ) + \xi_{z24} (\dot{\overline{z}}_{2} - \dot{\overline{z}}_{4} ) + \kappa_{z2} (\overline{z}_{2} - \overline{z}_{B1} ) + \kappa_{z24} (\overline{z}_{2} - \overline{z}_{B1} ) = ( - \kappa_{m1} f(\overline{x}_{n1} ) - \xi_{m1} \dot{\overline{x}}_{n1} )\cos \alpha_{n} \sin \beta \\ \end{aligned} \right.$$
(34)
$$\left\{ \begin{aligned} & \ddot{\overline{x}}_{3} + \xi_{x3} (\dot{\overline{x}}_{3} - \dot{\overline{x}}_{A2} ) + \xi_{x13} (\dot{\overline{x}}_{3} - \dot{\overline{x}}_{1} ) + \kappa_{x3} (\overline{x}_{3} - \overline{x}_{A2} ) + \kappa_{x13} (\overline{x}_{3} - \overline{x}_{A2} ) = ( - \kappa_{m2} f(\overline{x}_{n2} ) - \xi_{m2} \dot{\overline{x}}_{n2} )\sin \alpha_{n} \\ & & \ddot{\overline{y}}_{3} + \xi_{y3} (\dot{\overline{y}}_{3} - \dot{\overline{y}}_{A2} ) + \xi_{y13} (\dot{\overline{y}}_{3} - \dot{\overline{y}}_{1} ) + \kappa_{y3} (\overline{y}_{3} - \overline{x}_{A2} ) + \kappa_{y13} (\overline{y}_{3} - \overline{y}_{A2} ) \\ & = ( - \kappa_{m2} f(\overline{x}_{n2} ) - \xi_{m2} \dot{\overline{x}}_{n2} )\cos \alpha_{n} \cos \beta - f_{g} \\ & \ddot{\overline{z}}_{3} + \xi_{z3} (\dot{\overline{z}}_{3} - \dot{\overline{z}}_{A2} ) + \xi_{z13} (\dot{\overline{z}}_{3} - \dot{\overline{z}}_{1} ) + \kappa_{z3} (\overline{z}_{3} - \overline{z}_{A2} ) + \kappa_{z13} (\overline{z}_{3} - \overline{z}_{A2} ) = ( - \kappa_{m2} f(\overline{x}_{n2} ) - \xi_{m2} \dot{\overline{x}}_{n2} )\cos \alpha_{n} \sin \beta \\ \end{aligned} \right.$$
(35)
$$\left\{ \begin{aligned} & \ddot{\overline{x}}_{4} + \xi_{x4} (\dot{\overline{x}}_{4} - \dot{\overline{x}}_{B2} ) + \xi_{x24} (\dot{\overline{x}}_{4} - \dot{\overline{x}}_{2} ) + \kappa_{x4} (\overline{x}_{4} - \overline{x}_{B2} ) + \kappa_{x24} (\overline{x}_{4} - \overline{x}_{B2} ) = ( - \kappa_{m2} f(\overline{x}_{n2} ) - \xi_{m2} \dot{\overline{x}}_{n2} )\sin \alpha_{n} \\ & & \ddot{\overline{y}}_{4} + \xi_{y4} (\dot{\overline{y}}_{4} - \dot{\overline{y}}_{B2} ) + \xi_{y24} (\dot{\overline{y}}_{4} - \dot{\overline{y}}_{2} ) + \kappa_{y4} (\overline{y}_{4} - \overline{x}_{B2} ) + \kappa_{y24} (\overline{y}_{4} - \overline{y}_{B2} ) \\ & = ( - \kappa_{m2} f(\overline{x}_{n2} ) - \xi_{m2} \dot{\overline{x}}_{n2} )\cos \alpha_{n} \cos \beta - f_{g} \\ & \ddot{\overline{z}}_{4} + \xi_{z4} (\dot{\overline{z}}_{4} - \dot{\overline{z}}_{B2} ) + \xi_{z24} (\dot{\overline{z}}_{4} - \dot{\overline{z}}_{2} ) + \kappa_{z4} (\overline{z}_{4} - \overline{z}_{B2} ) + \kappa_{z24} (\overline{z}_{4} - \overline{z}_{B2} ) = ( - \kappa_{m2} f(\overline{x}_{n2} ) - \xi_{m2} \dot{\overline{x}}_{n2} )\cos \alpha_{n} \sin \beta \\ \end{aligned} \right..$$
(36)

In the formula

$$\begin{aligned} \overline{x}_{i} & = x_{i} /b_{m} , \, \overline{y}_{i} = y_{i} /b_{m} , \, \overline{z}_{i} = z_{i} /b_{m} , \, f\left( {\overline{x}_{ni} } \right) = f(\overline{x}_{ni} )/b_{m} = \left\{ \begin{gathered} \overline{x}_{ni} - 1, \, \overline{x}_{ni} > 1 \hfill \\ 0, \, \left| {\overline{x}_{ni} } \right| < 1 \hfill \\ \overline{x}_{ni} + 1, \, \overline{x}_{ni} < - 1 \hfill \\ \end{gathered} \right., \, \tau = \omega_{n} t,\omega_{n} = \sqrt {\frac{{K_{a} }}{{m_{e} }}} , \, \\ \omega_{ji} & = \sqrt {\frac{{K_{ji} }}{{m_{ji} }}} , \, \kappa_{ji} = \frac{{\omega_{ij}^{2} }}{{\omega_{n}^{2} }}, \, \kappa_{mi} = \frac{{\omega_{ji}^{2} }}{{\omega_{n}^{2} }}\kappa (\tau ), \, \kappa (\tau ) = \frac{{K_{mv} (t)}}{{K_{a} }}, \, \xi_{ji} = \frac{{C_{ji} }}{{2m_{i} \omega_{n} }}, \, \xi_{mv} = \frac{{C_{mv} }}{{2m_{ev} \omega_{n} }}, \, f = \frac{{F\cos \alpha_{n} }}{{m_{ev} b_{m} \omega_{n}^{2} }}, \, \\ f_{g} & = \frac{g}{{b_{m} \omega_{n}^{2} }},f_{ev} = \frac{{{\text{d}}^{2} e_{v} (\tau )/{\text{d}}\tau^{2} }}{{b_{m} }}(i = 1,2,3,4;v = 1,2;j = x,y,z). \\ \end{aligned}$$

System Dynamic Response

System Response Under Different Torques

This part explores the nonlinear response of the herringbone gear system under different input torque Tp. The value of Tp is equal to the sum of the value of T1 and T3. Keep the other system parameters unchanged, change Tp value, and observe the nonlinear response of displacement of meshing line 1 and meshing line 2, respectively. It can be seen from Fig. 9a, b that changing the value of Tp does not change the trajectory trend of the vibration displacement curve, so the changing trend of speed is also unchanged, as shown in Fig. 9c, d. When Tp increases slowly, the average vibration displacement of the meshing line increases, and the amplitude increases slowly. When the input torque changes from 100 to 250 N m, the vibration displacement peaks of meshing line 1 are 1.13 μm, 1.2 μm, 1.3 μm and 1.4 μm, respectively, and the vibration displacement peaks of meshing line 2 are 1.1 μm, 1.28 μm, 1.37 μm and 1.44 μm, respectively. From the velocity–displacement image, it can be seen that meshing line 1 and meshing line 2 have almost the same movement trend under different torques, so the peak of acceleration is almost the same, about 2.5 μm/s.

Fig. 9
figure 9

System response under different torques

Full size image

System Response Under Different Meshing Damping

This part explores the nonlinear response of the herringbone gear system under different meshing damping coefficients ξm. Keep other system parameters unchanged, change ξm value, and observe the meshing line 1 nonlinear displacement and meshing line 2 nonlinear displacement, respectively. By analyzing Fig. 10a, b, it can be seen that changing the value of ξm will change the trajectory trend of the vibration displacement curve. As shown in Fig. 10a, b, slowly increasing ξm, the vibration displacement of the meshing line gradually changes from stable single-period motion to double-period motion and multi-period motion, and the vibration amplitude gradually increases. When the meshing damping ratio changes from 0.15 to 0.3, the peak of vibration velocity of meshing line 1 is 8 μm/s, 6 μm/s, 4.4 μm/s and 4.3 μm/s, respectively, and the peak of vibration velocity of meshing line 2 is 7 μm/s, 4.7 μm/s, 4.5 μm/s and 3.8 μm/s, respectively.

Fig. 10
figure 10

System response under different meshing damping

Full size image

System Response Under Different Backlashes

This part explores how will the nonlinear dynamical behavior of the herringbone gear system change while changing tooth side backlash bm. Keep other system parameters unchanged, change bm value, and observe the nonlinear response of the displacement of meshing line 1 and meshing line 2, respectively. It can be seen from Fig. 11a, b that changing the value of bm will change the trajectory trend of the vibration displacement curve. When bm increases slowly, the meshing line vibration displacement gradually changes from a stable single-period motion to a double-period motion and a multi-period motion, and the fluctuation amplitude gradually increases. As shown in Fig. 11c, d, when the backlash changes from 1 to 4 μm, the peak value of stable single-period vibration velocity of meshing line 1 is 2.3 μm/s, and the peak value of stable single-period vibration velocity of meshing line 2 is 2.5 μm/s, respectively.

Fig. 11
figure 11

System response under different backlashes

Full size image

System Response Under Different Meshing Stiffness

This part explores how will the nonlinear dynamical behavior of the herringbone gear system change while changing the mean values of meshing stiffness Km. Keep the other system parameters unchanged, change the Km value, and observe the nonlinear response of displacement of meshing line 1 and meshing line 2, respectively. By analyzing Fig. 12a, b, it can be seen that changing the value of Km will change the trajectory trend of the vibration displacement curve. The vibration displacement of the meshing line is in the chaotic motion state primarily, when Km increases slowly, it gradually changes to multi-period motion and double-period motion, and finally to stable single-period motion. In this process, the amplitude of velocity fluctuation decreases gradually. As shown in Fig. 12c, d, the peak of vibration velocity of meshing line 1 is 0.43 μm/s and the peak of vibration velocity of meshing line 2 is 0.45 μm/s in the stable motion state.

Fig. 12
figure 12

System response under different meshing stiffness

Full size image

System Response Under Different Bearing Damping

This part explores how will the nonlinear dynamical behavior of the herringbone gear system change while changing the mean values of bearing damping, The damping of each bearing along the x and y directions is represented by ξb. Keep the other system parameters unchanged, change the ξb value, and observe the nonlinear response of displacement of meshing line 1 and meshing line 2, respectively. By analyzing Fig. 13a, b, it can be seen that changing the value of ξb will change the trajectory trend of the vibration displacement curve. The image is analyzed, and the vibration displacement curve and the vibration velocity curve show that when the bearing damping is low, the system will be in a multi-period motion state and a quasi-periodic motion state, and the stability is low. Gradually increasing the bearing damping, the system motion state changes to a stable single-period motion, which indicates that appropriately increasing the bearing damping is beneficial to the system to maintain stability.

Fig. 13
figure 13

System response under different meshing stiffness

Full size image

System Response Under Different Excitation Frequencies

This part explores how will the nonlinear dynamical behavior of the herringbone gear system change while changing the external load excitation frequency. Taking equivalent displacement as the research object, Fig. 14 shows when the excitation frequency ωe is 1, 1.55 and 2.2, respectively, What the variation trend of it of meshing line 1 be like. When ωe = 1, the phase plane is a multi-turn winding trajectory, the points on the Poincaré map are concentrated near two regions, there are two main resonance peaks in the spectrum, and the frequency is between 0.1 and 0.2, it shows that the system is in double periodic motion state. It indicates that the system transits from a stable state to an unstable state. When ωe = 1.55, the equivalent displacement frequency domain signal on the meshing line has a certain width discrete spectrum, the chaotic frequency is between 0 and 0.4, and its phase plane contains chaotic attractors. The system is doing chaotic motion, which can be shown by the Poincaré map—there are disordered points on the Poincaré map. When ωe = 2.2, the equivalent displacement phase plane of the meshing line is a orbit, the system is doing Regular periodic motion, which can be shown by the Poincaré map—the Poincaré map only exists one point.

Fig. 14
figure 14

Changing trend of dynamic response of meshing line 1 under the different excitation frequency

Full size image

The vibration displacement on the meshing line is analyzed by the wavelet transform method, and the time–frequency diagram at each frequency is shown in Fig. 15. According to the diagram, when ωe = 1, the main vibration frequency of the meshing displacement is 0.8ωe and the component is 1.6ωe, and the amplitude is about 0.15 and 0.25, respectively. When ωe = 1.55, in addition to the frequency of 0.25ωe, there are more chaotic frequencies, and the amplitude is concentrated at about 0.05, which is consistent with the chaotic motion state of the time history.

Fig. 15
figure 15

Meshing line 1 time–frequency diagram of wavelet transform

Full size image

The spectrum of the motion space of the system is shown in Fig. 16a. It can be seen that when the excitation frequency is about 1.25 and 1.68, Chaotic motion is what the system is doing. That moment, when system excitation frequency is about 1, the vibration frequency shows a double peak, showing that multi-period motion is the motion that the system is doing. In that case, the system transits from a stable state to an unstable state. In addition, Fig. 16b draws the phase plane and Poincaré image in the spatial state. It can be seen that the system first undergoes multi-period motion, then gradually transitions to chaotic motion, and finally enters a single-period motion. The motion state changes from intermediate to completely unstable, and finally to stable. In Fig. 16, all coordinate values are dimensionless.

Fig. 16
figure 16

Spectrum characteristic of meshing line 1

Full size image

While changing the external load excitation frequency ωe. The data in the diagram shows that when ωe < 0.7, the system is in a stable one-cycle motion state; when ωe is between 0.7 and 1.25, the multi-periodic motion is what the system is doing. When ωe is between 1.25 and 1.72, the system is in a chaotic state; when ωe is between 1.72 and 1.88, the system is in double-periodic motion. When ωe is greater than 1.88, the system enters a stable periodic motion again (Fig. 17).

Fig. 17
figure 17

Bifurcation diagram of meshing line 1

Full size image

Similar methods can also be used to study the influence of external load excitation frequency on meshing line 2. Taking equivalent displacement as the research object, Fig. 18 shows when the excitation frequency ωe is 0.9, 1.45 and 2.1, respectively, what the variation trend of it of meshing line 2 be like. When ωe = 0.9, the phase diagram is a multi-turn winding closed trajectory, and the points on the Poincaré section are concentrated near two regions, It shows that the system is in double periodic motion state. It indicates that the system transits from a stable state to an unstable state. When ωe = 1.45, the equivalent displacement frequency domain signal on the meshing line has a certain width discrete spectrum, and its phase plane contains chaotic attractors. The system is doing chaotic motion, which can be shown by the Poincaré map—there are disordered points on the Poincaré map.

Fig. 18
figure 18

Changing trend of dynamic response of meshing line 2 under the different excitation frequency

Full size image

The vibration displacement on the meshing line is analyzed by the wavelet transform method, and the time–frequency images at each frequency are shown in Fig. 19. According to the FFT image, when ωe = 0.9, the main vibration frequency of the meshing displacement is 0.7ωe and the component is 1.5ωe, and the amplitude is about 0.1 and 0.2, respectively. When ωe = 1.45, in addition to the frequency of 0.23ωe, there are more chaotic frequencies, and the amplitude is concentrated around 0.13, which is consistent with the chaotic motion state of the time history. When ωe = 2.1, the meshing displacement is mainly composed of 0.35ωe, and the amplitude is about 0.12.

Fig. 19
figure 19

Meshing line 2 time–frequency diagram of wavelet transform

Full size image

The spectrum of the motion space of the system is shown in Fig. 20a. It can be seen that when the excitation frequency is about 1.25 and 1.68, the vibration frequency of the system appears multi-value phenomenon, showing that chaotic motion is what the system is doing. In that case, when the excitation frequency is about 1, the vibration frequency shows a double peak, showing that multi-period motion is what Herringbone gears system is doing. In addition, from Fig. 20b, it can be seen that the system generally undergoes a state of motion from multi-cycle to chaos to single cycle. In Fig. 20, all coordinate values are dimensionless, the specific dimensionless way is given in the second chapter.

Fig. 20
figure 20

Spatial spectrum and spatial phase diagram

Full size image

To further study how will the nonlinear dynamical behavior of the herringbone gear system change while changing the external load excitation frequency ωe, the bifurcation diagram drawing has been drawn, as shown in Fig. 21. The data in the diagram shows that when ωe < 0.63, the system is in a stable one-cycle motion state; when ωe is between 0.63 and 1.21, the multi-periodic motion is what the system is doing. When ωe is between 1.21 and 1.75, the system is in a chaotic state; when ωe is between 1.75 and 1.9, the system is in double-periodic motion. When ωe is greater than 1.9, the system enters a stable periodic motion again.

Fig. 21
figure 21

Bifurcation diagram of meshing line 2

Full size image

System Main Resonance Analysis

Primary Resonance Used in Analysis of Stability

The characteristics of primary resonance of helical gear pair torsional vibration split by herringbone gear pair are analyzed by multi-scale method. How can excitation load, time-varying meshing stiffness and meshing damping influence the dynamic behavior of herringbone gear system have been studied.

Simplifying Eq. (31), in this case, only taking torsional vibration into account:

$$\ddot{\overline{x}}_{n} + 2\xi_{m} \dot{\overline{x}}_{n} \cos \alpha_{t} + \kappa (\tau )f(\overline{x}_{n} )\cos \alpha_{t} = f_{0} - f\cos \omega \tau .$$
(37)

In the formula, f0 represents the dimensionless equivalent static load, and f represents the dimensionless load fluctuation range.

The high-order polynomial fitting of the backlash function, the third-order polynomial accuracy is sufficient:

$$f(\overline{x}_{n} ) = \delta_{1} \overline{x}_{n} + \delta_{2} \overline{x}_{n}^{3} = \delta_{1} (\overline{x}_{n} + \delta_{0} \overline{x}_{n}^{3} ).$$
(38)

The high-order small quantity ε is introduced to represent the variables of time in various scales, as shown in formula (39):

$$T_{i} = \varepsilon_{i} \tau \, (i = 0,1,...).$$
(39)

In different scales, expressing the nonlinear vibration as a time variable function:

$$\overline{x}_{n} (\tau ,\varepsilon ) = \sum\limits_{i = 1}^{m} {\varepsilon^{i} x_{n} } (T_{0} ,T_{1} ,...,T_{m} ).$$
(40)

In the formula, the highest rank of small parameters has been represented by m, the higher the calculation accuracy, the greater the m value.

Define the partial derivative operator:

$$\frac{{\text{d}}}{{{\text{d}}\tau }} = \sum\limits_{n = 1}^{m} {\varepsilon^{n} \frac{\partial }{{\partial T_{n} }} = D_{0} + \varepsilon D_{1} + \cdots + } \varepsilon^{m} D_{m}$$
(41)
$$\frac{{{\text{d}}^{2} }}{{{\text{d}}\tau^{2} }} = \frac{{\text{d}}}{{{\text{d}}\tau }}\left( {\sum\limits_{n = 1}^{m} {\varepsilon^{n} \frac{\partial }{{\partial T_{n} }}} } \right) = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \varepsilon^{2} (D_{1}^{2} + 2D_{0} D_{1} ) + \cdots$$
(42)

The gear meshing frequency ω = ω0 + ω1ε + ω2ε2 + … is defined, system natural frequency has been represented by ω0. Other parameters of the system can take effective approximate solutions according to the same method. The system parameters 2ξm = 2εξm, κ = εκ, δ0 = εδ0, f = εf are redefined.

The mathematical model (43) is re-expressed as

$$\ddot{\overline{x}}_{n} + 2\varepsilon \xi_{m} \dot{\overline{x}}_{n} \cos \alpha_{t} + (1 + \varepsilon \kappa \cos \omega \tau )\delta_{1} (\overline{x}_{n} + \varepsilon \delta_{0} \overline{x}_{n}^{3} )\cos \alpha_{t} = f_{0} - \varepsilon f\cos \omega \tau .$$
(43)

The partial derivative operator and the approximate solution are brought into Eq. (44). After the expansion, ε is taken to the quadratic term. List the differential equations shown in Eqs. (43) and (44):

$$\varepsilon^{0} :D_{0}^{2} x_{0} + \omega_{0}^{2} x_{0} = f_{0}$$
(44)
$$\begin{aligned} \varepsilon^{1} :D_{0}^{2} x_{1} + \omega_{0}^{2} x_{1} & = f\cos \omega \tau - 2D_{0} D_{1} x_{0} - 2\xi_{m} D_{0} x_{0} \cos \alpha_{t} - \delta_{2} x_{0}^{3} \cos \alpha_{t} \\ & - \omega_{0}^{2} \kappa x_{0} \cos \alpha_{n} \cos \omega \tau . \\ \end{aligned}$$
(45)

Assume that the solution of the 0-order coefficient Eq. (46) is

$$x_{0} = A(T_{1} )e^{{i\omega_{0} T_{0} }} + f + \overline{A}(T_{1} )e^{{ - i\omega_{0} T_{0} }} .$$
(46)

The excitation frequency offset parameter σ is introduced. Let ω = ω0 + εσ, and rewrite the cosine function with excitation frequency:

$$\cos \omega \tau = \cos (\omega_{0} \tau + \varepsilon \sigma \tau ) = \cos (\omega_{0} T_{0} + \sigma T_{1} ) = \frac{1}{2}e^{{i\sigma T_{1} }} e^{{i\omega_{0} T_{0} }} + cc,$$
(47)

where cc denotes the conjugate plural of its preceding term.

Replace expressions (46) and (47) with ε1:

$$\begin{aligned} D_{0}^{2} x_{1} + \omega_{0}^{2} x_{1} & = \frac{f}{2}e^{{i\sigma T_{1} }} e^{{i\omega_{0} T_{0} }} - 2iD_{1} A\omega_{0} e^{{i\omega_{0} T_{0} }} - 2i\xi_{m} A\omega_{0} e^{{i\omega_{0} T_{0} }} \cos \alpha_{t} \\ & \quad - \delta_{2} \left( {\frac{{6A\overline{A}f_{0} + f_{0}^{3} }}{2} + A^{3} e^{{3i\omega_{0} T_{0} }} + 3A^{2} e^{{2i\omega_{0} T_{0} }} + 3A^{2} \overline{A}e^{{i\omega_{0} T_{0} }} + 3Af_{0}^{2} e^{{i\omega_{0} T_{0} }} } \right)\cos \alpha_{t} \\ & \quad - \frac{1}{2}\kappa \omega_{0}^{2} (Ae^{{i\sigma T_{1} }} e^{{i\omega_{0} T_{0} }} + f_{0} e^{{i\sigma T_{1} }} e^{{i\omega_{0} T_{0} }} + Ae^{{ - i\sigma T_{1} }} )\cos \alpha_{t} + cc. \\ \end{aligned}$$
(48)

To avoid perpetual projects, should meet

$$\frac{f}{2}e^{{i\sigma T_{1} }} - 2iD_{1} A\omega_{0} - 3\delta_{2} A^{2} \overline{A}\cos \alpha_{t} - 3\delta_{2} Af_{0}^{2} \cos \alpha_{t} - \frac{1}{2}\kappa \omega_{0}^{2} f_{0} e^{{i\sigma T_{1} }} \cos \alpha_{t} = 0.$$
(49)

Rewrite equation A, as shown in the following equation:

$$A(T_{1} ) = \frac{1}{2}\alpha (T_{1} )e^{{i\beta (T_{1} )}} .$$
(50)

α(T1) denotes the slow change of system amplitude and β(T1) denotes the slow change of system frequency. Eliminating \(e^{{i\beta (T_{1} )}}\) on both sides simultaneously and separating the real and imaginary parts:

$$D_{1} \alpha = - \xi_{m} \alpha \cos \alpha_{t} + \frac{1}{{2\omega_{0} }}(f - \omega_{0}^{2} \kappa f_{0} \cos \alpha_{n} )\sin \varphi$$
(51)
$$\alpha D_{1} \varphi = \alpha \sigma - \frac{{3\delta_{2} \alpha^{3} \cos \alpha_{t} + 12\delta_{2} \alpha f_{0}^{2} \cos \alpha_{t} }}{{8\omega_{0} }} + \frac{1}{{2\omega_{0} }}(f - \omega_{0}^{2} \kappa f_{0} \cos \alpha_{t} )\cos \varphi$$
(52)

φ = β(T1)–σT1 describes the real phase of the system.

Let \(\frac{{{\text{d}}\alpha }}{{{\text{d}}\tau }} = \alpha \frac{{{\text{d}}\varphi }}{{{\text{d}}\tau }} = 0\), the amplitude and phase satisfy the algebraic equation:

$$\left\{ \begin{gathered} \overline{\alpha }\xi_{m} \cos \alpha_{t} = \frac{1}{{2\omega_{0} }}(f - \omega_{0}^{2} \kappa f_{0} \cos \alpha_{t} )\sin \overline{\varphi } \hfill \\ \overline{\alpha }\sigma - \frac{{3\delta_{2} \overline{\alpha }^{3} \cos \alpha_{t} + 12\delta_{2} \overline{\alpha }f_{0}^{2} \cos \alpha_{t} }}{{8\omega_{0} }} = - \frac{1}{{2\omega_{0} }}(f - \omega_{0}^{2} \kappa f_{0} \cos \alpha_{t} )\cos \overline{\varphi } \hfill \\ \end{gathered} \right..$$
(53)

The amplitude–frequency response equation is shown in Eq. (53):

$$(\xi_{m} \overline{\alpha }\cos \alpha_{n} )^{2} + \left( {\overline{\alpha }\sigma - \frac{{3\delta_{2} \overline{\alpha }^{3} \cos \alpha_{n} + 12\delta_{2} \overline{\alpha }f_{0}^{2} \cos \alpha_{n} }}{{8\omega_{0} }}} \right)^{2} = \left( {\frac{{f - \omega_{0}^{2} \kappa f_{0} \cos \alpha_{t} }}{{2\omega_{0} }}} \right)^{2}$$
(54)
$$\overline{\varphi } = \arctan \left( {\frac{{\overline{\alpha }\xi_{m} \cos \alpha_{t} }}{{\frac{{3\delta_{2} \overline{\alpha }^{3} \cos \alpha_{t} + 12\delta_{2} \overline{\alpha }f_{0}^{2} \cos \alpha_{t} }}{{8\omega_{0} }} - \overline{\alpha }\sigma }}} \right).$$
(55)

Equations (51) and (52) are linearized to form a differential equation related to the amplitude disturbance Δα and the phase disturbance Δφ:

$$\left\{ \begin{gathered} D_{1} \Delta \alpha = - \Delta \alpha \xi_{m} \cos \alpha_{t} + \Delta \varphi \frac{1}{{2\omega_{0} }}(f - \omega_{0}^{2} \kappa f_{0} \cos \alpha_{t} )\cos \overline{\varphi } \hfill \\ D_{1} \Delta \varphi = - \Delta \alpha \left( {\frac{{3\delta_{2} \overline{\alpha }\cos \alpha_{t} }}{{4\omega_{0} }} + \frac{{f - \omega_{0}^{2} \kappa f_{0} \cos \alpha_{t} }}{{2\omega_{0} \overline{\alpha }^{2} }}\cos \overline{\varphi }} \right) - \Delta \varphi \frac{{f - \omega_{0}^{2} \kappa f_{0} \cos \alpha_{t} }}{{2\omega_{0} \overline{\alpha }^{2} }}\sin \overline{\varphi } \hfill \\ \end{gathered} \right..$$
(56)

Eliminate \(\overline{\varphi }\), system equilibrium equation is shown as follows:

$$\det \left[ \begin{gathered} - \lambda - \xi_{m} \cos \alpha_{t} - \overline{\alpha }\left( {\frac{{3\delta_{2} \overline{\alpha }^{3} \cos \alpha_{t} + 12\delta_{2} f_{0}^{2} \cos \alpha_{t} }}{{8\omega_{0} }}} \right) \hfill \\ \, \frac{1}{{\overline{\alpha }}}\left( {\sigma - \frac{{3\delta_{2} \overline{\alpha }^{2} \cos \alpha_{t} + 12\delta_{2} f_{0}^{2} \cos \alpha_{t} }}{{8\omega_{0} }}} \right) - \lambda - \xi_{m} \cos \alpha_{t} \hfill \\ \end{gathered} \right].$$
(57)

In summary, when ξm > 0, the system stability condition is

$$(\xi_{m} \cos \alpha_{t} )^{2} + \left( {\sigma - \frac{{3\delta_{2} \overline{\alpha }^{2} \cos \alpha_{t} + 12\delta_{2} f_{0}^{2} \cos \alpha_{t} }}{{8\omega_{0} }}} \right)\left( {\sigma - \frac{{9\delta_{2} \overline{\alpha }^{2} \cos \alpha_{t} + 12\delta_{2} f_{0}^{2} \cos \alpha_{t} }}{{8\omega_{0} }}} \right) > 0.$$
(58)

Numerical Analysis of Primary Resonance

Discuss how will system primary resonance response change while meshing damping is changing. Define the initial parameters in Eq. (53), meshing damping ξm = 0.05, dimensionless static load f = 0.3, dynamic load fluctuation amplitude f = 0.3.

Change the parameter ξm and draw the amplitude–frequency diagram, as shown in Fig. 22. When ξm is 0.05, 0.07 and 0.09, There are unstable fragments in the curve in the diagram. Increase ξm, system main resonance amplitude α decreases, and the unstable fragments gradually shrinks. When ξm is 0.12, the curve in the figure is a solid line, indicating that the system is stable. This indicates that when the damping increases, it will help the system to maintain stability. When ω takes different values, changing ξm, α will also change. In this case, the curve is drawn to show the trend of α, as shown in Fig. 22b. When ω is 0.4 and 0.75, increase ξm will lead to the decrease of the system main resonance amplitude. When ω is 1.25, the amplitude of the system is in the transition stage between stable and unstable, and there is a trend of multi-value jump. When ω is 1.55, the main amplitude of the system is in the unstable stage, and there will be a multi-value jump phenomenon in the shadow part of the graph. At this time, increase ξm slowly from 0.2, α will first change from single value to multi-value, and then change back from multi-value to single value. A1, A2, A3, A4 are the critical points of single-value region and multi-value region, respectively.

Fig. 22
figure 22

Main resonance response of meshing damping

Full size image

Discuss how will system primary resonance response change, while external load is changing. Define the initial parameters in Eq. (53), meshing damping ξm = 0.05, dimensionless static load f = 0.3, dynamic load fluctuation amplitude f = 0.3.

Change the parameter external load f and draw the amplitude–frequency diagram, as shown in Fig. 23. When f is 0.4 and 0.9, There are unstable fragments in the curve in the diagram, Represented by dotted line. Decrease f, system main resonance amplitude α decreases, and the unstable fragments gradually shrinks. When f is 0.1 and 0, the curve in the figure are solid lines, indicating that the system is stable. When f is 0.4 and 0.9, the curve in the figure are solid lines, indicating that the system is unstable. This indicates that when the external load decreases, it will help the system to maintain stability. When ω takes different values, changing f, α will also change. In this case, the curve is drawn to show the trend of α, as shown in Fig. 23b. When ω is 0.75, decrease f will lead to the decrease of the system main resonance amplitude. When ω is 1.05, the amplitude of the system is in the transition stage between stable and unstable, and there is a trend of multi-value jump. When ω is 1.25, the main amplitude of the system is in the unstable stage, and there will be a multi-value jump phenomenon in the shadow part of the graph. At this time, increase f slowly from 0.08, α will first change from single value to multi-value.

Fig. 23
figure 23

Primary resonance response of load fluctuation

Full size image

Discuss how will system primary resonance response change, while meshing stiffness is changing. Define the initial parameters in Eq. (53), meshing damping ξm = 0.05, dimensionless static load f = 0.3, dynamic load fluctuation amplitude f = 0.3.

Change the parameter meshing stiffness κ and draw the amplitude–frequency diagram, as shown in Fig. 24. When κ is 0.4 and 0.6. There are unstable fragments in the curve in the diagram, the unstable segment is represented by a dotted line in the figure. Increase κ, system main resonance amplitude α decreases, and the unstable fragments gradually shrinks. When κ is 0.8 and 1, the curve in the figure are solid lines, indicating that the system is stable. This indicates that keep other parameters of the system, such as ω unchanged, when the meshing stiffness increases, it will help the system to maintain stability. When ω takes different values, changing κ, α will also change. In this case, the curve is drawn to show the trend of α, as shown in Fig. 24b. When ω is 0.5, increase κ will lead to the decrease of the system main resonance amplitude, at this time, the stability of nonlinear periodic vibration of the system increases. When ω is 0.75 and 1, the amplitude of the system is in the transition stage between stable and unstable, and there is a trend of multi-value jump. When ω is 1.25, the main amplitude of the system is in the unstable stage, and there will be a multi-value jump phenomenon in the shadow part of the graph. At this time, increase κ slowly from 0.6, α will first change from single value to multi-value, and then change back from multi-value to single value. A1, A2, A3, A4 are the critical points of single-value region and multi-value region, respectively.

Fig. 24
figure 24

Primary resonance response of stiffness fluctuation

Full size image

Conclusion

  1. 1.

    The nonlinear dynamic model of herringbone gear is established and its vibration characteristics are analyzed. The results show that the bending-torsion coupled herringbone gear system has rich nonlinear behavior. Keeping other parameters of the system unchanged, changing the excitation frequency, meshing stiffness, backlash, input torque, meshing damping and bearing damping, respectively, the system will experience periodic motion, quasi-periodic motion, multi-periodic motion, chaos and other motion states. When these parameters are not within a reasonable range, the system will fall into chaos and the motion state is unpredictable. This indicates that the system parameters should be reasonably selected, so that it can run stably.

  2. 2.

    The main resonance characteristics of the system are analyzed by the multi-scale method. The results show that increasing the meshing damping ratio is beneficial to suppress the excessive amplitude, which is helpful to reduce the unstable branch and prevent amplitude mutation. One of the factors causing instability of the system is excessive load fluctuation, and the system amplitude is positively correlated with the load amplitude. The system stability is negatively correlated with the external excitation frequency and positively correlated with the meshing stiffness amplitude. Increase the meshing stiffness will reduce the amplitude jump probability and interval of the system and improve its stability.