Vibration of rotating porous nanocomposite eccentric semi-annular and annular plates in uniform thermal environment using TDQM

Abstract

In this paper, free vibration of rotating functionally graded (FG) porous eccentric semi-annular (ESA) and eccentric annular (EA) plates reinforced with graphene nanoplatelets (GPLs) in a thermal environment is solved with the help of transformed differential quadrature method (TDQM). Symmetrical and asymmetrical distributions are considered for both the porosity and the graphene nanoplatelets; the estimation of the Young’s modulus is conducted by the model of Halpin–Tsai. A higher-order shear deformation theory is considered as the basis for the employment of the Hamilton’s principle for the derivation of both the initial equations of the plates-up to the dynamic equilibrium point and the oscillation phenomena afterward. The method of TDQ utilizes a conformal mapping in order to obtain the DQ weighting coefficients and then discretizes the partial differential equations of the motion, as well as the boundary conditions; this discretization takes place in the physical domain directly. The results indicate that the employed numerical approach is advantageous in high solution accuracy in addition to fast convergence rate. Furthermore, the variation of the natural frequencies of the FG plates with different boundary conditions is investigated by taking into account the influences of several parameters: the geometry, such as eccentricity, thickness ratio, radius ratio; the material, such as the type of porosity and GPLs, the porosity parameter and the weight fraction of GPLs, and other parameters, such as temperature difference and rotating speed.

1 Introduction

During the past decades, carbon-based reinforcements, such as 1-dimensional nanotubes and 2-demensional graphene, have been employed for enhancing the mechanical and electrical properties of composite materials. According to the development of manufacturing methods in terms of reducing the cost of raw materials, nanocomposites have been highly used in flexible batteries, manufacturing alternative bone structures in the body, structural engineering (such as aerospace, automotive and civil engineering) and lightweight sensors. Therefore, the importance of such potential and the vast application of these composite structures have raised the attention of researchers toward them. Reports of experiments demonstrate a significant increase in mechanical, thermal and physical properties of polymers, when additives such as carbon nanotubes are introduced into the polymer matrix [1, 2]. Hence, industrial societies have taken great interest in carrying out studies on the mechanical behavior of porous graphene-reinforced nanocomposites. Studies showed a better performance of graphene platelets in comparison with the carbon nanotube additives when it comes to mechanical properties epoxy nanocomposites; part of the results indicated that the Young’s modulus of the graphene nanocomposite, at a nanofiller weight fraction of 0.1 ± 0.002%, increased by 31%, whereas a rise by 3% was recorded for single-walled carbon nanotubes [2]. The stiffening effect of functionally graded graphene composite plates was compared with those reinforced with carbon nanotubes [3]. The researchers took into account the agglomeration effects as well as restacking of graphene sheets and realized a better load bearing capacity of graphene nanotubes (GNTs) compared to carbon nanotubes (CNTs).

Regarding the nonlinear behavior of composite structures, multiscale doubly curved nanocomposites nanoshells made of CNT/GPL-fiber are studied in [4]. Also, nonlinear vibration and bending characteristic of multilayered composite beams reinforced with uniform distribution and uniform dusting of graphene fibers under Timoshenko’s theory were investigated by Feng et al. [5, 6]. Studying the buckling and free vibration of the same structure, Kitipornchai et al. [7] discovered that more concentration of graphene toward the outer surfaces of a composite beam rose its stiffness significantly, which led to the growth in natural frequency and the buckling load. Further studies on functionally graded graphene platelets reinforced composite (FG-GRC) structures with more complex geometries, such as toroidal panels [8] and conical shells [9], are carried out in terms of oscillatory behavior and post-buckling analysis, respectively.

A new class of lightweight materials which have internal porosity are known as metal foams. The engineering applications of such materials are restricted due to their low strength. In order to surmount this obstacle, however, carbon nanostructures are exploited which have the ability to forge a bond with the matrix, in contrast to carbon nanotubes. Consequently, the load is uniformly transferred and an increase in strength is obtained [10,11,12,13]. Materials such as these are not only able to keep the properties of porous structures [14,15,16,17] (light weight, low density and high energy absorption) but also able to gain nanocomposite characteristics (high elastic modulus, high fracture strength and high thermal conductivity). A reinforced porous nanocomposite beam constructed with functionally graded graphene was studied in terms of free vibration, nonlinear vibration, elastic buckling and post-buckling [7, 18]. The imperfection geometry was taken into account when analyzing the post-buckling of a porous beam with GPLs reinforcements mounted on a nonlinear elastic foundation [19]. The study found that the post-buckling load reached its peak when a symmetrical dispersion was considered for the porosity and the GPLs, while the minimum load was recorded for the structure with uniform porosity. In addition, better mechanical performance was obtained when the GPLs were distributed uniformly, rather than symmetrically. Similarly, investigating the impact of using GPLs on the buckling pressure of a functionally graded porous cylinder [20] showed that a non-uniform but symmetrical distribution for GPLs and porosity led to the highest pressure capacity.

For the past few years, scientists—in the fields of aeronautic, automotive industries or many others—have become more attracted to study the characteristics of the structures with round shapes [21]. Żur [22] studied the free vibration of axisymmetric and non-axisymmetric oscillation of an elastically supported FG annular plate with variety of inner boundary conditions, whereas Allahkarami [23] surveyed the impact of a periodic radial compressive load on the dynamic stability of the same structure—but reinforced with GPLs. Many articles considered the variable thickness of annular plates not only as a highly influential factor to attain economical usage of material but also as a practical mean to stiffen the structure having less weight; the thickness can change either abruptly [24] or gradually [25], along the radial direction.

One type of geometry imperfection is when the structure, especially a plate, contains one [26] or multiple [27] perforations with diverse shapes and sizes. Having these internal cutouts relocated to a further distance from the center of symmetry, one encounters even more complex mathematical formulations [28]. These eccentric cutouts can have significant effect on the vibrating behavior of EA plates [29,30,31]. Askari et al. [32] dealt with the partial differential equation of free and coupled-fluid vibration of these EA plates based on the separation of variables [33]. On the other hand, a systematic approach for solving FG-GRC-EA plates with integrated piezo layers is presented in [34].

Thermal environment, similar to the eccentricity, can make a noticeable difference when involved in the overall assumptions of a mechanical problem. This can be exemplified by undesired buckling or dynamic responses [35]. Since these environments with high temperatures are inevitable in many industrial procedures, structures with FG properties have become introduced by many scientists [36, 37]. Malekzadeh et al. [38] believed that the FGMs outperform those traditional composite laminates by reducing thermal stresses or stress concentrations. Recently, Lal and Saini [39] investigated the effects of thermal environments on an annular plate; in their work, in contrast to [38], the thickness of the plate is considered to be variable.

Rotating machineries are widely employed throughout industrial processes. The rotating system models can be introduced as a shaft, a shell [40] and a disk or a blade attached to the axis of rotation; in [41], the Rayleigh beam theory and Euler‐Bernoulli beam theory are used to present the free vibration of a pre‐twisted blade‐shaft assembly; in the similar work, done by Zhao et al. [42], the natural frequencies of a disk-shaft rotor system are computed analytically and the model is built based on Kirchhoff plate theory and Timoshenko beam theory; in another model, a setting angle is considered for a pre-twisted blade, which is mounted on a rotating disk with a centric hole [43]. In another contribution [44], a plate is attached to a rotating hub modeled as an elastic cylindrical shell. For investigation of the free vibration, the dynamical model is constructed based on the Donnell shell theory and the Kirchhoff plate theory and the coupled vibration.

Another type of rotating systems is circular plate without a centric hole [45], which is among the critical components of industry, whose vibration and stability should be studied carefully [46,47,48]. Bagheri and Jahangiri [49] investigated the free vibration of rotating disks with FG properties. Yang and Kang [50], as well as Younesian et al. [51], published papers regarding the analysis of annular plates subjected to compressive centrifugal body force and peripheral transverse loads, respectively. The assumptions for the circular plates with off-center hole in thermal environment, in company with the rotating phenomenon, will result in enormous equations of motion. So, Transformed Differential Quadrature method (TDQM) is a powerful numerical tool for solving difficult equations of motion (especially those structures with complex shape). In this method, the discretization of the governing equations is directly conducted in the physical domain for determining the weighting coefficients [52,53,54].

The presented article exploits the TDQM in investigating the free vibration of a rotating FG-GRC porous semi-annular plates with an off-centered semicircle cut-out in thermal environment. To the best of the authors’ knowledge acquired from the latest contributions, the TDQM has not been utilized as a numerical tool for tackling the eigenvalue problem of such ESA plates (with the proposed characteristics) yet. Two different types of porosity are considered in the analysis: the symmetrical and the asymmetrical distributions. Also, the dispersion of graphene platelets is categorized into three types: symmetrical (non-uniform), asymmetrical (non-uniform) and uniform. The Halpin–Tsai micromechanics model is proposed in order to determine the elastic modulus of graphene nanoplatelets; other mechanical properties, such as the density, Poisson’s ratio and thermal expansion coefficients, are obtained using the rule of mixture.

Once the mechanical properties of the structure are defined completely, two consecutive phases are introduced, based on which the governing equations of motion are presented: the first stage—which involves in-plane deformations due to the rotation and a steady change in temperature—lasts until the dynamic equilibrium is reached; the second stage, however, is the out-of-plane oscillation phenomenon, which is then handled using a higher-order shear theory (with 7 degrees of freedom). By applying the TDQM, the obtained equations from the first and second phases are discretized directly in the physical domain using an appropriate conformal mapping. Finally, the first four natural frequencies are numerically illustrated and how variations in different parameters, such as geometry, material, boundary conditions, rotational speed and temperature would manipulate these results, are meticulously investigated for both the annular and semi-annular FG-GRC plates. Using the TDQM for tackling the governing equations of an eccentric semi-annular vibrating plate can be considered as the starting point for putting a systematic solution forward to the analysis of sector-plates with more complex structures; this, consequently, inclines the authors to put forth the presented technique for handling eccentric sector-plates in future studies.

The following section describes the geometry of the proposed structure and its mechanical properties. Then, the governing equations and the use of discretization technique in TDQM are presented. Section 3 is dedicated to the numerical results and the comprehensive parameter study. In the end, Sect. 4 summarizes the overall methodology and discusses the conclusions thoroughly.

2 Mathematical model

2.1 The geometry of the FG-GRC plates

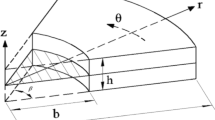
Two eccentric plates are proposed as the mechanical structures, each of which is provided with the cylindrical coordinate system $(r,\theta ,z)$ labeling the points of the structure when no deformation is occurred. These two models are defined as eccentric annular (EA) plate $(\theta = 2\pi )$ and eccentric semi-annular (ESA) plate $(\theta = \pi )$, having circular and semi-circular cutouts (Fig. 1), respectively. The eccentricity is denoted by $\overline{e}$. The thickness of the plates, the inner radius and the outer radius are $h$, $b$ and $a$, respectively. Functionally graded distribution for porosity and graphene platelets includes diverse models along the thickness of the plates. In Fig. 2, it can be seen that the GPLs are distributed based on three different patterns: Type-A, non-uniform and symmetrical; Type-B, non-uniform and asymmetrical; Type-C, uniform. Moreover, the pattern of porosity is categorized into two types: Type-I, symmetrical; Type-II, asymmetrical.

Fig. 1

The geometry of the FG-GRC-ESA plate

Fig. 2

Various dispersion patterns considered for the porosity and the graphene platelets

2.2 Material properties

The mechanical properties of the FG-GRC model with porosity, such as Young’s modulus $E$, shear modulus $G$, density $\rho$ and thermal expansion coefficient $\alpha$, are defined as functions of $z$ [55]. We have:

$$ \begin{gathered} E\left( z \right) = E^{*} \left( {1 - e_{0} \lambda (z)} \right) \hfill \\ G\left( z \right) = G^{*} \left( {1 - e_{0} \lambda (z)} \right) \hfill \\ \rho \left( z \right) = \rho^{*} \left( {1 - e_{m} \lambda (z)} \right) \hfill \\ \alpha \left( z \right) = \alpha^{*} \left( {1 - e_{m} \lambda (z)} \right) \hfill \\ \end{gathered} $$

(1)

$$ \lambda (z) = \left\{ {\begin{array}{*{20}c} {\cos \left( {{{\pi z} \mathord{\left/ {\vphantom {{\pi z} h}} \right. \kern-\nulldelimiterspace} h}} \right){\text{ Type - I}}} \\ {\cos \left( {{{\pi z} \mathord{\left/ {\vphantom {{\pi z} {2h + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}}}} \right. \kern-\nulldelimiterspace} {2h + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}}}} \right){\text{ Type - II}}} \\ \end{array} } \right. $$

(2)

In Eq. 1, $E^{ * } , \, G^{ * } , \, \rho^{ * } {\text{ and }}\alpha^{ * }$ are the corresponding mechanical properties of the nonporous FG-GRC. $\lambda (z)$ demonstrates two types of porosity distribution in the $z$ direction, given in Eq. 2. Accordingly, Type-I is related to the symmetrical distribution, where the maximum and minimum values of porosity are at $z = 0$ and $z = \pm {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}$, respectively. In Type-II, porosity is asymmetrically distributed—the maximum/minimum value are located at the bottom/top surface, respectively. The following relation expresses the connection between parameter $e_{m}$ (mass density coefficient) and $e_{0}$ (porosity coefficient).

$$ e_{m} = \frac{{1 - \sqrt {1 - e_{0} \lambda \left( z \right)} }}{\lambda \left( z \right)} $$

(3)

In order to obtain the modulus of elasticity for the nonporous graphene-reinforced composites, Halpin–Tsai micro mechanical model [56] is employed, and hence we have:

$$ E^{*} = \frac{3}{8}\left( {\frac{{1 + \xi_{GPL}^{L} \eta_{GPL}^{L} V_{GPL} }}{{1 - \eta_{GPL}^{L} V_{GPL} }}} \right)E_{m} + \frac{5}{8}\left( {\frac{{1 + \xi_{GPL}^{W} \eta_{GPL}^{W} V_{GPL} }}{{1 - \eta_{GPL}^{W} V_{GPL} }}} \right)E_{m} $$

(4)

where

$$ \begin{aligned} & \xi_{GPL}^{L} = \frac{{2l_{GPL} }}{{h_{GPL} }}, \, \xi_{GPL}^{W} = \frac{{2w_{GPL} }}{{h_{GPL} }} \\ & \eta_{GPL}^{L} = \frac{{E_{GPL} - E_{m} }}{{E_{GPL} + \xi_{GPL}^{L} E_{m} }}, \, \eta_{GPL}^{W} = \frac{{E_{GPL} - E_{m} }}{{E_{GPL} + \xi_{GPL}^{W} E_{m} }} \\ \end{aligned} $$

(5)

In Eq. 4, the polymer matrix contains $E_{m}$ as the Young’s modulus. Other dimensionless parameters labeled with ${\text{GPL}}$ are the properties of GPLs introduced in Eq. 5. The volume fraction in the direction of $z$ is named $V_{GPL}$. In Eq. 5,$E_{GPL} , \, l_{GPL} , \, w_{GPL} ,$ and $h_{GPL}$ are the elastic modulus, length, width, and thickness of GPLs, respectively.

Following the rule of mixture [57], one is able to express density $\rho^{*}$, Poisson’s ratio $\nu^{*}$ and the thermal expansion coefficient $\alpha^{*}$ of the GPLs reinforced nanocomposite without porosity, with the formulations below:

$$ \begin{gathered} \rho^{*} = \rho_{GPL} V_{GPL} + \rho_{m} V_{m} \hfill \\ \nu^{*} = \nu_{GPL} V_{GPL} + \nu_{m} V_{m} \hfill \\ \alpha^{*} = \alpha_{GPL} V_{GPL} + \alpha_{m} V_{m} \hfill \\ \end{gathered} $$

(6)

where $\rho_{GPL} , \, \nu_{GPL} {\text{ and }}\alpha_{GPL}$ are density, Poisson’s ratio and the thermal expansion coefficients of GPLs, and their isotropic matrix counterparts are $\rho_{m} , \, \nu_{m} {\text{ and }}\alpha_{m}$. $V_{m}$ indicates the volume fraction of the matrix. The relationship of shear modulus and the elasticity modulus for the nonporous GPLs reinforced nanocomposite is obtained as follow:

$$ G^{*} = \frac{{E^{*} }}{{2\left( {1 + \nu^{*} } \right)}} $$

(7)

Regarding the volume fraction, three different patterns (in the direction of $z$) are investigated [20]. Although Type-A and Type-B illustrate the symmetrical and asymmetrical distribution of graphene, they are both considered non-uniform. In the third pattern, on the other hand, the volume fraction is assumed to be uniform.

$$ V_{GPL} \left( z \right) = \left\{ {\begin{array}{*{20}c} {s_{1} \left( {1 - \cos \left( {{{\pi z} \mathord{\left/ {\vphantom {{\pi z} h}} \right. \kern-\nulldelimiterspace} h}} \right)} \right)} & {\text{Type - A}} \\ {s_{2} \left( {1 - \cos \left( {{{\pi z} \mathord{\left/ {\vphantom {{\pi z} {2h + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}}}} \right. \kern-\nulldelimiterspace} {2h + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}}}} \right)} \right)} & {\text{Type - B}} \\ {s_{3} } & {\text{Type - C}} \\ \end{array} } \right. $$

(8)

In order to obtain the constant parameters $s_{i} {\text{ for }}i = 1,2,3$, each pattern in Eq. 8 needs to be substituted into the following relation [58]:

$$ \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\frac{{V_{GPL} }}{{V_{GPL}^{0} }}} \left( {1 - e_{m} \lambda \left( z \right)} \right)dz - \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left( {1 - e_{m} \lambda \left( z \right)} \right)dz = 0} $$

(9)

where

$$ V_{GPL}^{0} = \frac{{\Lambda_{GPL} \rho_{m} }}{{\Lambda_{GPL} \rho_{m} + \rho_{GPL} (1 - \Lambda_{GPL} )}} $$

(10)

In Eq. 10, $\Lambda_{GPL}$ is the weight fraction of GPLs.

2.3 Dynamic Equations and boundary conditions

When the free vibration of a rotating model in a thermal environment is under investigation, one is able to express the initial displacements $(u_{r0} ,u_{\theta 0} ,u_{z0} )$ as follows:

$$ \begin{gathered} u_{r0} = \overline{u}\left( {r,\theta } \right), \hfill \\ u_{\theta 0} = \overline{v}\left( {r,\theta } \right), \hfill \\ u_{z0} = 0. \hfill \\ \end{gathered} $$

(11)

where the displacement components $(\overline{u},\overline{v})$ originate from both a steady change in the model’s temperature (no thermal gradient is taken into account) and a dynamical rotation. These thermal and rotating characteristics only affect the in-plane displacements along the radial $(r)$ and azimuth $(\theta )$ coordinates. Therefore, in-plane strain–displacement relations are formulated as follows [59]:

$$ \begin{aligned} & \varepsilon_{rr0} = \frac{{\partial \overline{u}}}{\partial r}, \\ & \varepsilon_{\theta \theta 0} = \frac{{\overline{u}}}{r} + \frac{1}{r}\frac{{\partial \overline{v}}}{\partial \theta }, \\ & \varepsilon_{r\theta 0} = \frac{1}{r}\frac{{\partial \overline{u}}}{\partial \theta } - \frac{{\overline{v}}}{r} + \frac{{\partial \overline{v}}}{\partial r}. \\ \end{aligned} $$

(12)

The Hamilton’s principle, for the time interval $t_{1}$ to $t_{2}$ [60], suggests that:

$$ \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta T_{0} - \delta U_{0} } \right){\text{d}}t} = 0 $$

(13)

in which the kinetic energy $T_{0}$ and the potential $U_{0}$ (in their initial states) are introduced. Parameter $t$ is time. The variations of the aforementioned energies are expressed as follows [45]:

$$ \delta T_{0} = \int\limits_{\Lambda } {\rho \,} \Omega^{2} \left[ {\left( {r + \overline{u}} \right)\delta \overline{u} - \overline{v}\delta \overline{v}} \right]\;d\Lambda $$

(14)

$$ \delta U_{0} = \int\limits_{\Lambda } {\left( {\sigma_{rr0} - \sigma_{Tr0} } \right)\delta \varepsilon_{rr0} } + \left( {\sigma_{\theta \theta 0} - \sigma_{T\theta 0} } \right)\delta \varepsilon_{\theta \theta 0} + \left( {\sigma_{r\theta 0} } \right)\delta \varepsilon_{r\theta 0} \;d\Lambda $$

(15)

In Eq. 14, $\rho$ and $\Lambda$ are known as the mass density and the volume of the circular plate, respectively. Additionally, the plate rotates at the speed $\Omega$. In Eq. 15, the corresponding stresses are obtained on the basis of the former in-plane strains and $Q_{ij}$ introduced as the elements of the reduced stiffness matrix (see Appendix A). We have:

$$ \sigma_{rr0} = Q_{11} \varepsilon_{rr0} + Q_{12} \varepsilon_{\theta \theta 0} ,\sigma_{\theta \theta 0} = Q_{12} \varepsilon_{rr0} + Q_{22} \varepsilon_{\theta \theta 0} ,\sigma_{r\theta 0} = Q_{66} \varepsilon_{r\theta 0} $$

(16)

On the other side, the initial thermal stresses along the radial direction and the circumferential direction are also expressed as follows:

$$ \sigma_{Tr0} = \left( {Q_{11} + Q_{12} } \right)\alpha (z)\Delta T,\sigma_{T\theta 0} = \left( {Q_{12} + Q_{22} } \right)\alpha (z)\Delta T $$

(17)

in which $\Delta T$ shows the temperature difference between two time-intervals. It should be mentioned that the temperature is uniformly distributed throughout the whole plate in each time-interval.

By using Eqs. 14, 15, 16 and 17, as well as 12, the governing equations can be extracted from Eq. 13 as follows:

$$ \begin{aligned} & H_{11} \frac{{\partial^{2} \overline{u}}}{{\partial r^{2} }} + \frac{{H_{66} }}{{r^{2} }}\frac{{\partial^{2} \overline{u}}}{{\partial \theta^{2} }} + \frac{{H_{11} }}{r}\frac{{\partial \overline{u}}}{\partial r} - \frac{{H_{22} \overline{u}}}{{r^{2} }} - \left( {\frac{{H_{22} }}{{r^{2} }} + \frac{{H_{66} }}{{r^{2} }}} \right)\frac{{\partial \overline{v}}}{\partial \theta } + \left( {\frac{{H_{12} }}{r} + \frac{{H_{66} }}{r}} \right)\frac{{\partial^{2} \overline{v}}}{\partial r\,\partial \theta } + \frac{{N_{T\theta 0} }}{r} - \frac{{N_{Tr0} }}{r} \\ & = - m_{1} \Omega^{2} \left( {r + \overline{u}} \right) \\ \end{aligned} $$

(18)

$$ \left( {\frac{{H_{22} }}{{r^{2} }} + \frac{{H_{66} }}{{r^{2} }}} \right)\frac{{\partial \overline{u}}}{\partial \theta } + \left( {\frac{{H_{12} }}{r} + \frac{{H_{66} }}{r}} \right)\frac{{\partial^{2} \overline{u}}}{\partial r\,\partial \theta } + H_{66} \frac{{\partial^{2} \overline{v}}}{{\partial r^{2} }} + \frac{{H_{66} }}{r}\frac{{\partial \overline{v}}}{\partial r} + \frac{{H_{22} }}{{r^{2} }}\frac{{\partial^{2} \overline{v}}}{{\partial \theta^{2} }} - \frac{{H_{66} \overline{v}}}{{r^{2} }} = - m_{1} \Omega^{2} \overline{v} $$

(19)

in which $H_{ij}^{\chi \kappa }$ and $m_{\chi \kappa }$ are obtained using the following relations:

$$ \begin{aligned} & H_{ij}^{\chi \kappa } = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {Q_{ij} \chi (z)\kappa (z)dz} \\ & {\text{for }}\left( {\chi ,\kappa = \{ \} ,f,g,f^{\prime } ,g^{\prime } } \right){\text{ and }}\left( {i,j = 1,2,4,5,6} \right) \\ \end{aligned} $$

(20)

$$ \begin{aligned} & m_{\chi \kappa } = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\rho {\kern 1pt} \chi (z)\kappa (z)dz} \\ & {\text{for (}}\chi = 1,f,g{),(}\kappa = \{ \} ,f,g{) } \\ \end{aligned} $$

(21)

Also, for $N_{Tr0}$ and $N_{T\theta 0}$, we have:

$$ \left[ {\begin{array}{*{20}c} {N_{Tr0} } \\ {N_{T\theta 0} } \\ \end{array} } \right] = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {\begin{array}{*{20}c} {\sigma_{Tr0} } \\ {\sigma_{T\theta 0} } \\ \end{array} } \right\}} dz $$

(22)

Other notations of $\chi$ and $\kappa$ (rather than 1) will be used in handling the free vibration of the model; also, $\chi ,\kappa = \{ \}$ means that there is no notation and the parameter is left blank.

The essential and natural boundary conditions are applied on the proposed structure (see Fig. 3). We have:

$$ {\text{Either }}n_{r} \overline{u}\; + n_{\theta } \overline{v} = 0\;{\text{ or }}n_{r}^{2} N_{rr0} + 2n_{r} n_{\theta } N_{r\theta 0} + n_{\theta }^{2} N_{\theta \theta 0} = 0 $$

(23)

$$ {\text{Either }} - n_{\theta } \overline{u}\; + n_{r} \overline{v} = 0\;{\text{ or }}n_{r} n_{\theta } (N_{\theta \theta 0} - N_{rr0} ) + (n_{r}^{2} - n_{\theta }^{2} )N_{r\theta 0} = 0 $$

(24)

where $(n_{r} ,n_{\theta } )$ are the radial and circumferential components of the unit normal to the boundaries of the EA/ESA plate, respectively. Also, $N_{rr0}$, $N_{\theta \theta 0}$ and $N_{r\theta 0}$ are defined as

$$ \left[ {\begin{array}{*{20}c} {N_{rr0} } \\ {N_{\theta \theta 0} } \\ {N_{r\theta 0} } \\ \end{array} } \right] = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {\begin{array}{*{20}c} {\sigma_{rr0} + \sigma_{Tr0} } \\ {\sigma_{\theta \theta 0} + \sigma_{T\theta 0} } \\ {\sigma_{r\theta 0} } \\ \end{array} } \right\}} dz $$

(25)

Fig. 3

The geometry of transformation for an ESA plate, a the physical domain, b computational domain

When the free vibration of the structure (with initial displacements) is to be investigated, the following formulations for the displacement field are suggested.

$$ \begin{aligned} & u_{r} = \overline{u}\left( {r,\theta } \right) + \hat{u}\left( {r,\theta ,z,t} \right), \\ & u_{\theta } = \overline{v}\left( {r,\theta } \right) + \hat{v}\left( {r,\theta ,z,t} \right), \\ & u_{z} = \hat{w}\left( {r,\theta ,t} \right). \\ \end{aligned} $$

(26)

in which $(\overline{u},\overline{v})$ are already defined from Eqs. 18 and 19. However, according to the higher-order shear theory, $(\hat{u},\hat{v},\hat{w})$ can be expressed such that [61]:

$$ \begin{aligned} \hat{u} & = u\left( {r,\theta ,t} \right) + f\left( z \right)\varphi^{r} \left( {r,\theta ,t} \right) + g\left( z \right)\psi^{r} \left( {r,\theta ,t} \right), \\ \hat{v} & = v\left( {r,\theta ,t} \right) + f\left( z \right)\varphi^{\theta } \left( {r,\theta ,t} \right) + g\left( z \right)\psi^{\theta } \left( {r,\theta ,t} \right), \\ \hat{w} & = w\left( {r,\theta ,t} \right). \\ \end{aligned} $$

(27)

In Eq. 27, $(u,v,w)$ are the displacement components in the direction of $(r,\theta )$ for the material point on the mid-surface of the EA/ESA plate where $z = 0$. $(\varphi^{r} ,\varphi^{\theta } )$ are the rotations of transverse normal around the $(\theta ,r)$. Considering the warping of the plate, two other degrees of freedom are introduced as $(\psi^{r} ,\psi^{\theta } )$. Functions $(f,g)$ are formulated based on the third-order shear deformation theory given as follows:

$$ f(z) = z - \frac{{4z^{3} }}{{3h^{2} }}, \, g(z) = - \frac{{4z^{3} }}{{3h^{2} }} $$

(28)

According to the cylindrical coordinate system, the strain–displacement elements (upon which the out-of-plane oscillation phenomenon is to be investigated) with nonzero values can be expressed as [59]:

$$ \begin{aligned} & \varepsilon_{rr} = \frac{{\partial \hat{u}}}{\partial r},\varepsilon_{rrn} = \frac{1}{2}\left( {\frac{{\partial \hat{w}}}{\partial r}} \right)^{2} , \, \varepsilon_{\theta \theta } = \frac{{\hat{u}}}{r} + \frac{1}{r}\frac{{\partial \hat{v}}}{\partial \theta },\varepsilon_{\theta \theta n} = \frac{1}{{2r^{2} }}\left( {\frac{{\partial \hat{w}}}{\partial \theta }} \right)^{2} , \\ & \gamma_{r\theta } = \frac{1}{r}\frac{{\partial \hat{u}}}{\partial \theta } - \frac{{\hat{v}}}{r} + \frac{{\partial \hat{v}}}{\partial r},\gamma_{r\theta n} = \frac{1}{r}\frac{{\partial \hat{w}}}{\partial r}\frac{{\partial \hat{w}}}{\partial \theta }, \, \gamma_{rz} = \frac{{\partial \hat{u}}}{\partial z} + \frac{{\partial \hat{w}}}{\partial r}, \, \gamma_{\theta z} = \frac{{\partial \hat{v}}}{\partial z} + \frac{1}{r}\frac{{\partial \hat{w}}}{\partial \theta }. \\ \end{aligned} $$

(29)

Notations without subscript n are connected to the linear strain components, whereas the other notations with n are the nonlinear ones.

Once again, the Hamilton’s principle is applied so that:

$$ \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta T - \delta U} \right)dt} = 0 $$

(30)

In Eq. 30, $\delta T$ and $\delta U$ are, respectively, the variations of kinetic and potential energy [45], written as:

$$ \delta T = \int\limits_{\Lambda } {\rho \left\{ {\left( {\frac{{\partial u_{r} }}{\partial t} - \Omega u_{\theta } } \right)\left( {\frac{{\partial \delta \hat{u}}}{\partial t} - \Omega \delta \hat{v}} \right) + \left[ {\Omega \left( {r + u_{r} } \right) + \frac{{\partial u_{\theta } }}{\partial t}} \right]} \right.} \left( {\Omega \delta \hat{u}_{r} + \frac{{\partial \delta \hat{v}}}{\partial t}} \right)\left. { + \frac{{\partial \hat{w}}}{\partial t}\frac{{\partial \delta \hat{w}}}{\partial t}} \right\}d\Lambda $$

(31)

And

$$ \delta U = \int\limits_{\Lambda } {\left( {\sigma_{rr} \delta \varepsilon_{rr} } \right. + \sigma_{rr0} \delta \varepsilon_{rrn} } + \sigma_{\theta \theta } \delta \varepsilon_{\theta \theta } + \sigma_{\theta \theta 0} \delta \varepsilon_{\theta \theta n} + \sigma_{r\theta } \delta \gamma_{r\theta } + \sigma_{r\theta 0} \delta \gamma_{r\theta n} + \sigma_{rz} \delta \gamma_{rz} + \;\left. {\sigma_{\theta z} \delta \gamma_{\theta z} } \right)d\Lambda $$

(32)

where

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{rr} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{r\theta } } \\ {\sigma_{rz} } \\ {\sigma_{\theta z} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11}^{{}} } & {Q_{12}^{{}} } & 0 & 0 & 0 \\ {Q_{12}^{{}} } & {Q_{22}^{{}} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66}^{{}} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44}^{{}} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{55}^{{}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{rr} } \\ {\varepsilon_{\theta \theta } } \\ {\gamma_{r\theta } } \\ {\gamma_{rz} } \\ {\gamma_{\theta z} } \\ \end{array} } \right\} $$

(33)

Introducing (31, 32 and 33) and (29) in (30), along with the integration by parts, results in the following equations for the translational, rotational and warping degrees of freedom.

$$ \begin{gathered} \delta u: \hfill \\ \frac{{N_{rr} }}{r} + \frac{{\partial N_{rr} }}{\partial r} - \frac{{N_{\theta \theta } }}{r} + \frac{1}{r}\frac{{\partial N_{r\theta } }}{\partial \theta } + m_{1} \Omega^{2} u + m_{f} \Omega^{2} \varphi^{r} + m_{g} \Omega^{2} \psi^{r} = m_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - 2m_{1} \Omega \frac{\partial v}{{\partial t}} - 2m_{f} \Omega \frac{{\partial \varphi^{\theta } }}{\partial t} \hfill \\ - 2m_{g} \Omega \frac{{\partial \psi^{\theta } }}{\partial t} + m_{f} \frac{{\partial^{2} \varphi^{r} }}{{\partial t^{2} }} + m_{g} \frac{{\partial^{2} \psi^{r} }}{{\partial t^{2} }} \hfill \\ \end{gathered} $$

(34)

$$ \begin{gathered} \delta v: \hfill \\ \frac{{2N_{r\theta } }}{r} + \frac{{\partial N_{r\theta } }}{\partial r} + \frac{1}{r}\frac{{\partial N_{\theta \theta } }}{\partial \theta } + m_{1} \Omega^{2} v + m_{f} \Omega^{2} \varphi^{\theta } + m_{g} \Omega^{2} \psi^{\theta } = m_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} + 2m_{1} \Omega \frac{\partial u}{{\partial t}} - 2m_{f} \Omega \frac{{\partial \varphi^{r} }}{\partial t} \hfill \\ - 2m_{g} \Omega \frac{{\partial \psi^{r} }}{\partial t} + m_{f} \frac{{\partial^{2} \varphi^{\theta } }}{{\partial t^{2} }} + m_{g} \frac{{\partial^{2} \psi^{\theta } }}{{\partial t^{2} }} \hfill \\ \end{gathered} $$

(35)

$$ \begin{aligned} & \delta w: \\ & N_{rr0} \frac{{\partial^{2} w}}{{\partial r^{2} }} + \left( {\frac{{N_{rr0} }}{r} + \frac{{\partial N_{rr0} }}{\partial r} + \frac{1}{r}\frac{{\partial N_{r\theta 0} }}{\partial \theta }} \right)\frac{\partial w}{{\partial r}} + \frac{{N_{\theta \theta 0} }}{{r^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + \left( {\frac{1}{r}\frac{{\partial N_{r\theta 0} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial N_{\theta \theta 0} }}{\partial \theta }} \right)\frac{\partial w}{{\partial \theta }} \\ & + \frac{{2N_{r\theta 0} }}{r}\frac{{\partial^{2} w}}{\partial r\,\partial \theta } + \frac{{\partial Q_{rz} }}{\partial r} + \frac{1}{r}\frac{{\partial Q_{\theta z} }}{\partial \theta } + \frac{{Q_{rz} }}{r} = m_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} \\ \end{aligned} $$

(36)

$$ \begin{aligned} & \delta \varphi^{r} : \\ & \frac{{\partial M_{rr} }}{\partial r} + \frac{{M_{rr} }}{r} + \frac{1}{r}\frac{{\partial M_{r\theta } }}{\partial \theta } - \frac{{M_{\theta \theta } }}{r} - R_{rz} + m_{f} \Omega^{2} u + m_{ff} \Omega^{2} \varphi^{r} + m_{fg} \Omega^{2} \psi^{r} = m_{f} \frac{{\partial^{2} u}}{{\partial t^{2} }} + m_{ff} \frac{{\partial^{2} \varphi^{r} }}{{\partial t^{2} }} + m_{fg} \frac{{\partial^{2} \psi^{r} }}{{\partial t^{2} }} \\ & - 2m_{f} \Omega \frac{\partial v}{{\partial t}} - 2m_{ff} \Omega \frac{{\partial \varphi^{\theta } }}{\partial t} - 2m_{fg} \Omega \frac{{\partial \psi^{\theta } }}{\partial t} \\ \end{aligned} $$

(37)

$$ \begin{aligned} & \delta \psi^{r} : \\ & \frac{{\partial P_{rr} }}{\partial r} + \frac{{P_{rr} }}{r} + \frac{1}{r}\frac{{\partial P_{r\theta } }}{\partial \theta } - \frac{{P_{\theta \theta } }}{r} - T_{rz} + m_{g} \Omega^{2} u + m_{fg} \Omega^{2} \varphi^{r} + m_{gg} \Omega^{2} \psi^{r} = m_{g} \frac{{\partial^{2} u}}{{\partial t^{2} }} + m_{fg} \frac{{\partial^{2} \varphi^{r} }}{{\partial t^{2} }} + m_{gg} \frac{{\partial^{2} \psi^{r} }}{{\partial t^{2} }} \\ & - 2m_{g} \Omega \frac{\partial v}{{\partial t}} - 2m_{fg} \Omega \frac{{\partial \varphi^{\theta } }}{\partial t} - 2m_{gg} \Omega \frac{{\partial \psi^{\theta } }}{\partial t} \\ \end{aligned} $$

(38)

$$ \begin{aligned} & \delta \varphi^{\theta } : \\ & \frac{{\partial M_{r\theta } }}{\partial r} + \frac{{2M_{r\theta } }}{r} + \frac{1}{r}\frac{{\partial M_{\theta \theta } }}{\partial \theta } - R_{\theta z} + m_{f} \Omega^{2} v + m_{ff} \Omega^{2} \varphi^{\theta } + m_{fg} \Omega^{2} \psi^{\theta } = m_{f} \frac{{\partial^{2} v}}{{\partial t^{2} }} + m_{ff} \frac{{\partial^{2} \varphi^{\theta } }}{{\partial t^{2} }} + m_{fg} \frac{{\partial^{2} \psi^{\theta } }}{{\partial t^{2} }} \\ & + 2m_{f} \Omega \frac{\partial u}{{\partial t}} + 2m_{ff} \Omega \frac{{\partial \varphi^{r} }}{\partial t} + 2m_{fg} \Omega \frac{{\partial \psi^{r} }}{\partial t} \\ \end{aligned} $$

(39)

$$ \begin{aligned} & \delta \psi^{\theta } : \\ & \frac{{\partial P_{r\theta } }}{\partial r} + \frac{{2P_{r\theta } }}{r} + \frac{1}{r}\frac{{\partial P_{\theta \theta } }}{\partial \theta } - T_{\theta z} + m_{g} \Omega^{2} v + m_{fg} \Omega^{2} \varphi^{\theta } + m_{gg} \Omega^{2} \psi^{\theta } = m_{g} \frac{{\partial^{2} v}}{{\partial t^{2} }} + m_{fg} \frac{{\partial^{2} \varphi^{\theta } }}{{\partial t^{2} }} + m_{gg} \frac{{\partial^{2} \psi^{\theta } }}{{\partial t^{2} }} \\ & + 2m_{g} \Omega \frac{\partial u}{{\partial t}} + 2m_{fg} \Omega \frac{{\partial \varphi^{r} }}{\partial t} + 2m_{gg} \Omega \frac{{\partial \psi^{r} }}{\partial t} \\ \end{aligned} $$

(40)

Corresponding natural and essential boundary conditions for the obtained equations of motion are:

$$ \begin{aligned} & {\text{Either }}u_{n} = n_{r} u + n_{\theta } v = 0\quad \quad \;\;{\text{or}}\quad N_{nn} = n_{r}^{2} N_{rr} + 2n_{r} n_{\theta } N_{r\theta } + n_{\theta }^{2} N_{\theta \theta } = 0 \\ & {\text{Either }}u_{s} = - n_{\theta } u + n_{r} v = 0\quad \quad {\text{or}}\quad N_{ns} = (n_{r}^{2} - n_{\theta }^{2} )N_{r\theta } + n_{r} n_{\theta } (N_{rr} - N_{\theta \theta } ) = 0 \\ & {\text{Either }}w = 0\quad \quad \quad \quad \quad \quad \quad \,\,{\text{or}}\quad Q_{nz} = n_{r} Q_{rz} + n_{\theta } Q_{\theta z} = 0 \\ & {\text{Either }}\varphi_{n} = n_{r} \varphi^{r} + n_{\theta } \varphi^{\theta } = 0\quad \;\,{\text{or}}\quad M_{nn} = n_{r}^{2} M_{rr} + 2n_{r} n_{\theta } M_{r\theta } + n_{\theta }^{2} M_{\theta \theta } = 0 \\ & {\text{Either }}\varphi_{s} = - n_{\theta } \varphi^{r} + n_{r} \varphi^{\theta } = 0\quad {\text{or}}\quad M_{ns} = (n_{r}^{2} - n_{\theta }^{2} )M_{r\theta } + n_{r} n_{\theta } (M_{rr} - M_{\theta \theta } ) = 0 \\ & {\text{Either }}\psi_{n} = n_{r} \psi^{r} + n_{\theta } \psi^{\theta } = 0\;\;\,\;\,{\text{or}}\quad P_{nn} = n_{r}^{2} P_{rr} + 2n_{r} n_{\theta } P_{r\theta } + n_{\theta }^{2} P_{\theta \theta } = 0 \\ & {\text{Either }}\psi_{s} = - n_{\theta } \psi^{r} + n_{r} \psi^{\theta } = 0\;\;\,{\text{or}}\quad P_{ns} = (n_{r}^{2} - n_{\theta }^{2} )P_{r\theta } + n_{r} n_{\theta } (P_{rr} - P_{\theta \theta } ) = 0 \\ \end{aligned} $$

(41)

where

$$ \left[ {\begin{array}{*{20}c} {N_{rr} } & {M_{rr} } & {P_{rr} } \\ {N_{\theta \theta } } & {M_{\theta \theta } } & {P_{\theta \theta } } \\ {N_{r\theta } } & {M_{r\theta } } & {P_{r\theta } } \\ \end{array} } \right] = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {\begin{array}{*{20}c} {\sigma_{rr} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{r\theta } } \\ \end{array} } \right\}} \left[ {\begin{array}{*{20}c} 1 & f & g \\ \end{array} } \right]dz $$

(42)

$$ \left[ {\begin{array}{*{20}c} {Q_{rz} } & {R_{rz} } & {T_{rz} } \\ {Q_{\theta z} } & {R_{\theta z} } & {T_{\theta z} } \\ \end{array} } \right] = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {\begin{array}{*{20}c} {\sigma_{rz} } \\ {\sigma_{\theta z} } \\ \end{array} } \right\}} \left[ {\begin{array}{*{20}c} 1 & f & g \\ \end{array} } \right]dz $$

(43)

The compatibility conditions for the annular plate whose coupling sector exists at $\theta = (0, \, 2\pi )$ can be defined such that:

$$ \begin{aligned} & \mu (r,0,t) = \mu (r,2\pi ,t)\quad {\text{for}}\quad \mu = \left( {u,v,w,\varphi^{r} ,\varphi^{\theta } ,\psi^{r} ,\psi^{\theta } } \right) \\ & Q_{nz} (r,0,t) = Q_{nz} (r,2\pi ,t), \\ & \mu_{nn} (r,0,t) = \mu_{nn} (r,2\pi ,t), \, \mu_{ns} (r,0,t) = \mu_{ns} (r,2\pi ,t)\quad {\text{for}}\quad \mu = \left( {N,M,P} \right) \\ \end{aligned} $$

(44)

Also, for the boundary conditions we have:

Clamped,

$$ u_{n} = 0, \, u_{s} = 0, \, w = 0, \, \varphi_{n} = 0, \, \varphi_{s} = 0, \, \psi_{n} = 0, \, \psi_{s} = 0 $$

(45)

Simple supported,

$$ u_{n} = 0, \, u_{s} = 0, \, w = 0, \, M_{nn} = 0, \, \varphi_{s} = 0, \, P_{nn} = 0, \, \psi_{s} = 0 $$

(46)

and free,

$$ N_{nn} = 0, \, N_{ns} = 0, \, Q_{nz} = 0, \, M_{nn} = 0, \, M_{ns} = 0, \, P_{nn} = 0, \, P_{ns} = 0. $$

(47)

2.4 The TDQ algorithm for discretization

Recently, variety of numerical techniques are employed for mechanical structures with complex motion formulations. These methods, which can be used for solving differential equations, are available mostly by the name of generalized differential quadrature [62], harmonic differential quadrature [63], or mixed finite element-differential quadrature method. Thus, Differential Quadrature (DQ) is a numerical tool which is highly applicable in discretizing linear governing equations or nonlinear ones, accompanied by the corresponding boundary conditions. However, the need for a more systematic procedure in solving equations for structures—with variety of shapes, led to an extended version of DQ method called TDQM, which is capable of determining DQ weighting coefficients in such way that the discretization of both the governing equations and the corresponding boundary conditions happens in the physical domain directly.

In order to achieve this, a suitable conformal mapping is employed as follows, which is capable of analytically transforming the proposed plates (both annular and semi-annular) with eccentricity into the new geometry without eccentricity. This transformation is geometrically depicted in Fig. 3.

$$ L = \frac{{\hat{Z}}}{{c \, \hat{Z} + 1}} + d $$

(48)

in which $L = r + {\overline{\text{j}}}\theta {\text{ (where }}\overline{{\text{j}}} = \sqrt { - 1} )$ is the complex variable of the physical domain and $\hat{Z} = \xi + {\overline{\text{j}}}\eta$ is taken as the complex variable of the computational domain in which the weighting coefficients are to be obtained. In Eq. 48:

$$ c = \frac{{\overline{e}}}{{\sqrt {\overline{e}^{4} - 2\overline{e}^{2} \left( {a^{2} + b^{2} } \right) + \left( {b^{2} - a^{2} } \right)^{2} } }}, \, d = \frac{{c\hat{b}^{2} }}{{1 - \left( {c\hat{b}} \right)^{2} }} $$

(49)

The transferred domain has the inner and outer radius $\hat{b}$ and $\hat{a}$, respectively; these two notations are dependent on the in-plane geometrical characteristics of the main annular model.

$$ \hat{a} = \frac{{\sqrt {4c^{2} b^{2} + 1} - 1}}{{2c^{2} b}}, \, \hat{b} = \frac{{\sqrt {4c^{2} a^{2} + 1} - 1}}{{2c^{2} a}} $$

(50)

By inserting $L = r + {\overline{\text{j}}}\theta \,$ and $\hat{Z} = \xi + {\overline{\text{j}}}\eta$ in Eq. 48, the real and imaginary parts can be separated as follows:

$$ r = \frac{{\sqrt {\left[ {c\xi^{2} (cd + 1) + \xi (2cd + 1)\cos \eta + d} \right]^{2} + \xi^{2} \sin^{2} \eta } }}{{c^{2} \xi^{2} + 2c\xi \cos \eta + 1}} $$

(51)

$$ \theta = \tan^{ - 1} \left[ {\frac{\xi \sin \eta }{{c\xi^{2} (cd + 1) + \xi (2cd + 1)\cos \eta + d}}} \right] $$

(52)

The chain rule of derivative gives the following relations of transformation, which relate physical coordinates $(r,\theta )$ to the computational coordinates $(\xi ,\eta )$.

$$ \left\{ {\begin{array}{*{20}c} {\frac{\partial \mu }{{\partial r}}} \\ {\frac{\partial \mu }{{\partial \theta }}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ {T_{21} } & {T_{22} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\frac{\partial \mu }{{\partial \xi }}} \\ {\frac{\partial \mu }{{\partial \eta }}} \\ \end{array} } \right\} $$

(53)

in which $\mu$ is an arbitrary function; T_ij (for i,j = 1, 2) are obtained as follows:

$$ \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ {T_{21} } & {T_{22} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{\partial r}{{\partial \xi }}} & {\frac{\partial \theta }{{\partial \xi }}} \\ {\frac{\partial r}{{\partial \eta }}} & {\frac{\partial \theta }{{\partial \eta }}} \\ \end{array} } \right]^{ - 1} $$

(54)

Regarding the DQM, the number of radial and circumferential grid points (in the computational domain) are taken as $N_{\xi }$ and $N_{\eta }$, respectively. The grids are generated based on the Gauss Lobatto Chebyshev; thus we have:

$$ \begin{gathered} \, \xi_{i} = \hat{b} + \frac{{(\hat{a} - \hat{b})}}{2}\left\{ {1 - \cos \left[ {\frac{(i - 1)\pi }{{N_{\xi } - 1}}} \right]} \right\}, \, \eta_{j} = \frac{\pi }{k}\left\{ {1 - \cos \left[ {\frac{(j - 1)\pi }{{N_{\eta } - 1}}} \right]} \right\}{\text{ for }}k = \left\{ {\begin{array}{*{20}c} 1 & {{\text{EA}}} \\ 2 & {{\text{ESA}}} \\ \end{array} ,} \right. \hfill \\ \, i = 1,2,...,N_{\xi } {, }j = 1,2,...,N_{\eta } . \hfill \\ \end{gathered} $$

(55)

The first-order derivatives of $\mu = (u,v,w,\phi^{r} ,\phi^{\theta } ,\psi^{r} ,\psi^{\theta } )$ at the point $(r_{i} ,\theta_{j} )$ are derived based on DQM in the physical domain. So, we have:

$$ \left( {\frac{\partial \mu }{{\partial r}}} \right)_{ij} = \sum\limits_{p = 1}^{{N_{r} = N_{\xi } }} {\sum\limits_{q = 1}^{{N_{\theta } = N_{\eta } }} {\tilde{A}_{ijpq}^{r} } } \mu_{pq} , \, \left( {\frac{\partial \mu }{{\partial \theta }}} \right)_{ij} = \sum\limits_{p = 1}^{{N_{r} = N_{\xi } }} {\sum\limits_{q = 1}^{{N_{\theta } = N_{\eta } }} {\tilde{A}_{ijpq}^{\theta } } } \mu_{pq} $$

(56)

in which

$$ \begin{gathered} \tilde{A}_{ipjq}^{r} = \left( {T_{11} } \right)_{ij} A_{ip}^{\xi } \delta_{jq}^{{}} + \left( {T_{12} } \right)_{ij} \delta_{ip}^{{}} A_{jq}^{\eta } , \hfill \\ \tilde{A}_{ipjq}^{\theta } = \left( {T_{21} } \right)_{ij} A_{ip}^{\xi } \delta_{jq}^{{}} + \left( {T_{22} } \right)_{ij} \delta_{ip}^{{}} A_{jq}^{\eta } \hfill \\ \end{gathered} $$

(57)

In Eq. 57, the transformed weighting coefficients $\tilde{A}_{ipjq}^{r}$ and $\tilde{A}_{ipjq}^{\theta }$ are introduced, in which $A_{ij}^{\gamma } (\gamma = \xi ,\eta )$ illustrate the first-order weighting coefficients along the direction of $\gamma = (\xi ,\eta )$; also, $\delta_{ij}$ is Kronecker delta.

The discretization of the second-order derivatives (in the physical domain at the point $(r_{i} ,\theta_{j} )$) is formulated using the similar procedure, as follows:

$$ \begin{aligned} & \left( {\frac{{\partial^{2} \mu }}{{\partial r^{2} }}} \right)_{ij} = \sum\limits_{p = 1}^{{N_{r} = N_{\xi } }} {\sum\limits_{q = 1}^{{N_{\theta } = N_{\eta } }} {\tilde{B}_{ijpq}^{r} } } \mu_{pq} , \, \left( {\frac{{\partial^{2} \mu }}{{\partial \theta^{2} }}} \right)_{ij} = \sum\limits_{p = 1}^{{N_{r} = N_{\xi } }} {\sum\limits_{q = 1}^{{N_{\theta } = N_{\eta } }} {\tilde{B}_{ijpq}^{\theta } } } \mu_{pq} , \\ & \left( {\frac{{\partial^{2} \mu }}{\partial r\partial \theta }} \right)_{ij} = \sum\limits_{p = 1}^{{N_{r} = N_{\xi } }} {\sum\limits_{q = 1}^{{N_{\theta } = N_{\eta } }} {\tilde{B}_{ijpq}^{r\theta } } } \mu_{pq} \\ \end{aligned} $$

(58)

Including the coefficients from Eq. 57, the transformed coefficients related to the second-order derivatives are expressed such that:

$$ \begin{aligned} & \tilde{B}_{ipjq}^{r} = \sum\limits_{k = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{N_{\theta } }} {\tilde{A}_{ikjl}^{r} \tilde{A}_{kplq}^{r} } } , \, \tilde{B}_{ipjq}^{r\theta } = \sum\limits_{k = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{N_{\theta } }} {\tilde{A}_{ikjl}^{r} \tilde{A}_{kplq}^{\theta } } } , \\ & \tilde{B}_{ipjq}^{\theta } = \sum\limits_{k = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{N_{\theta } }} {\tilde{A}_{ikjl}^{\theta } \tilde{A}_{kplq}^{\theta } } } \\ \end{aligned} $$

(59)

Now, the initial displacements $(\overline{u},\overline{v})$ can be discretized based on the mentioned rules of TDQM. So, we have:

$$ \begin{aligned} & \delta \overline{u}: \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {\left( {\frac{{H_{11} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + \frac{{H_{66} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{11} \tilde{B}_{ipjq}^{{r_{ij} }} - \frac{{H_{22} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\overline{u}_{pq} } \right.} } \\ & + \left. {\left[ { - \left( {\frac{{H_{22} }}{{r_{ij}^{2} }} + \frac{{H_{66} }}{{r_{ij}^{2} }}} \right)\tilde{A}_{ipjq}^{\theta } + \frac{{H_{12} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }}} \right]\overline{v}_{pq} } \right\} = \\ & - \frac{{N_{T\theta 0} }}{{r_{ij} }} + \frac{{N_{Tr0} }}{{r_{ij} }} - m_{1} \Omega^{2} (r_{ij} + \overline{u}_{ij} ) \\ \end{aligned} $$

(60)

$$ \begin{aligned} & \delta \overline{v}: \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {\left[ {\left( {\frac{{H_{22} }}{{r_{ij}^{2} }} + \frac{{H_{66} }}{{r_{ij}^{2} }}} \right)\tilde{A}_{ipjq}^{\theta } + \frac{{H_{12} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }}} \right]\overline{u}_{pq} } \right.} } \\ & \quad \left. { + \left( {\frac{{H_{66} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + \frac{{H_{22} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{66} \tilde{B}_{ipjq}^{{r_{ij} }} - \frac{{H_{66} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\overline{v}_{pq} } \right\} = - m_{1} \Omega^{2} \overline{v}_{ij} \\ \end{aligned} $$

(61)

in which $r_{ij} = {{\sqrt {\left[ {c\xi_{i}^{2} (cd + 1) + \xi_{i} (2cd + 1)\cos \eta_{j} + d} \right]^{2} + \xi_{i}^{2} \sin^{2} \eta_{j} } } \mathord{\left/ {\vphantom {{\sqrt {\left[ {c\xi_{i}^{2} (cd + 1) + \xi_{i} (2cd + 1)\cos \eta_{j} + d} \right]^{2} + \xi_{i}^{2} \sin^{2} \eta_{j} } } {(c^{2} \xi_{i}^{2} + 2c\xi_{i} \cos \eta_{j} + 1)}}} \right. \kern-\nulldelimiterspace} {(c^{2} \xi_{i}^{2} + 2c\xi_{i} \cos \eta_{j} + 1)}}.$ With the similar manner, the discretized form for Eqs. 34, 35, 36, 37, 38, 39 and 40 is presented as follows:

$$ \begin{aligned} & \delta u: \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {\left( {\frac{{H_{66} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{11} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{11} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + m_{1} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)u_{pq} } \right.} } \\ & + \left( {\frac{{H_{12} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)v_{pq} \\ & + \left( {\frac{{H_{11}^{f} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + H_{11}^{f} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66}^{f} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + m_{f} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22}^{f} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\varphi^{r}_{pq} + \\ & \left( {\frac{{H_{11}^{g} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + H_{11}^{g} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66}^{g} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + m_{g} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22}^{g} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\psi^{r}_{pq} + \\ & \left( {\frac{{H_{12}^{f} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{f} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22}^{f} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66}^{f} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\varphi^{\theta }_{pq} + \left. {\left( {\frac{{H_{12}^{g} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{g} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22}^{g} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66}^{g} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\psi^{\theta }_{pq} } \right\} \\ & = m_{1} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)_{ij} - 2m_{1} \Omega \left( {\frac{\partial v}{{\partial t}}} \right)_{ij} - 2m_{f} \Omega \left( {\frac{{\partial \varphi^{\theta } }}{\partial t}} \right)_{ij} - 2m_{g} \Omega \left( {\frac{{\partial \psi^{\theta } }}{\partial t}} \right)_{ij} + m_{f} \left( {\frac{{\partial^{2} \varphi^{r} }}{{\partial t^{2} }}} \right)_{ij} + m_{g} \left( {\frac{{\partial^{2} \psi^{r} }}{{\partial t^{2} }}} \right)_{ij} \\ \end{aligned} $$

(62)

Note that only $\delta u$ is shown above; the rest of the discretized equations can be pursued in Appendix B.

One is able to compress the motion equations and the boundary conditions into a matrix. Hence, for the initial displacements Eq. 60 and 61, we have:

$$ \left[ {\begin{array}{*{20}c} {K_{{\overline{u}\overline{u}}} } & {K_{{\overline{u}\overline{v}}} } \\ {K_{{\overline{v}\overline{u}}} } & {K_{{\overline{v}\overline{v}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\overline{u}} \\ {\overline{v}} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {F_{{\overline{u}}} } \\ {F_{{\overline{v}}} } \\ \end{array} } \right\} $$

(63)

where $(K_{{\overline{u}\overline{u}}} ,K_{{\overline{u}\overline{v}}} ,K_{{\overline{v}\overline{u}}} ,K_{{\overline{v}\overline{v}}} )$ are the initial stiffness elements and $(F_{{\overline{u}}} ,F_{{\overline{v}}} )$ are the body forces. In addition, the equations of motion in Eqs. 62, 68, 69, 70, 71, 72 and 73 are presented as follows:

$$ \left[ {K_{db}^{{}} } \right]\left\{ {U_{b} } \right\} + \left[ {K_{dd}^{{}} } \right]\left\{ {U_{d} } \right\} + \left[ M \right]\left\{ {\frac{{d^{2} U_{d} }}{{dt^{2} }}} \right\} = 0 $$

(64)

where $\left\{ {U_{i} } \right\} = \left[ {\begin{array}{*{20}c} {\left\{ {u_{i} } \right\}^{T} } & {\left\{ {v_{i} } \right\}^{T} } & {\left\{ {w_{i} } \right\}^{T} } & {\left\{ {\varphi_{i}^{r} } \right\}^{T} } & {\left\{ {\varphi_{i}^{\theta } } \right\}^{T} \quad \left\{ {\psi_{i}^{r} } \right\}^{T} \quad \left\{ {\psi_{i}^{\theta } } \right\}^{T} } \\ \end{array} } \right]^{ \, T}$ with i = b and d. Also, $\left[ {K_{ij}^{{}} } \right]$ and $\left[ M \right]$ with $(i,j = b,d)$ are the stiffness and mass matrices, respectively. Above, the subscripts b and d are short forms for the boundary and the domain, respectively. Also, for the boundary conditions we have:

$$ \left[ {K_{bb} } \right]\left\{ {U_{b} } \right\} + \left[ {K_{bd} } \right]\left\{ {U_{d} } \right\} = 0 $$

(65)

By replacing Eq. 65 into 64, it is possible to omit $U_{b}$, so that the following algebraic eigenvalue problem emerges from which the natural frequencies of the FG-GRC eccentric annular or semi-annular plate, as well as its mode shapes, can be obtained.

$$ \left( {\left[ K \right] - \omega_{i}^{2} \left[ M \right]} \right)\left\{ {\hat{U}_{d} } \right\} = 0,{\text{ for }}i = 1,2,3,... $$

(66)

In Eq. 66, $\left[ K \right] = \left[ {K_{dd}^{{}} } \right] - \left[ {K_{db} } \right]\left[ {K_{bb} } \right]^{ - 1} \left[ {K_{bd} } \right]$. Additionally, it is important to mention that Eq. 66 is derived based on the harmonic essence of the motion and as a result, $\omega_{i}$ for i = 1,2,3, … is the ith natural frequency of the plate and $\left\{ {\hat{U}_{d} } \right\}$ are the corresponding mode shape of the proposed oscillating model, respectively.

3 Numerical results

In this section, the information regarding the free vibration of the FG-GRC plate, along with a complete parameter study, is provided in diverse ways. To apply the numerical approach, the following values are assumed for both the geometric parameters and material properties of the graphene platelets (according to Yas and Rahimi [64]).

$$ GPLs \, \left\{ {\begin{array}{*{20}c} {l_{GPL} = 2.5\,{\mu m},} & {w_{GPL} = 1.5\,{\mu m},} & {t_{GPL} = 1.5\,{\text{nm}},} & {} \\ {\rho_{GPL} = 1062.5\;{\text{Kg}}\,{\text{m}}^{ - 3} ,} & {E_{GPL} = 1.01\,{\text{TPa}},} & {\nu_{GPL} = 0.186,} & {\alpha_{GPL} = - 3.75 \times 10^{ - 6} K^{ - 1} } \\ \end{array} } \right. $$

In addition, the polymer matrix is made of copper with the following material properties in the room temperature [64].

$$ {\text{Matrix }}\left\{ {\begin{array}{*{20}c} {\rho_{m} = 8960{\text{ Kg m}}^{ - 3} ,} & {E_{m} = 130{\text{ GPa}},} & {\nu_{m} = 0.34,} & {\alpha_{m} = 17 \times 10^{ - 6} {\text{K}}^{ - 1} } \\ \end{array} } \right. $$

In the presented study, a complete eccentric annular and half-circle eccentric sector plate (semi-annular) are discussed. The boundary condition of the annular plate is identified using the two initials of the inner and outer boundary (arc) conditions; for example, the boundary condition for an EA plate with clamped inner arc and free outer arc is noted as ${\text{C - F}}$. The first two letter of the boundary condition for the ESA plate can also be noted with the similar manner; in addition, the notation is followed by the initials related to the conditions at $\theta \;{ = }\;{0}$ and $\theta \;{ = }\;\pi$, respectively. Only then the ESA plate’s boundary condition is fully identified. By means of example, for an ESA plate with clamped inner semicircle, free outer semicircle, simple boundary at $\theta \;{ = }\;{0}$ and free boundary at $\theta \;{ = }\;\pi$, the boundary condition is noted as C-F-S-F.

In Table 1, the convergence of the natural frequencies (Hz) of an ESA plate is investigated. The authenticity of the results is established using the numerical software suite called ABAQUS, whose computational analysis is performed based on finite element methods. The convergent simulation’s results are conducted using 1564 elements whose type is chosen to be ‘S4RT’. The simulation has been carried out to verify the accuracy of the problem in a limited case (uniform distribution of GPLs) with the presence of thermal environment. Only the temperature difference is considered, and the rotating is assumed to be zero. For this purpose, the solver “coupled temp-displacement (steady-state)” is used. After applying each of this effect, a frequency analysis is performed on the ESA plate to calculate the frequencies of the system under the applied conditions. The model is considered neither porous nor revolving. However, the graphene is distributed uniformly based on Type-C (Eq. 8) and the boundary condition is introduced as C-C-F-F. Table 1 contains the data for the first four natural frequencies, which are in good agreement with those obtained from ABAQUS—either with $(\overline{e}/a = 0.2)$ or without $(\overline{e}/a = 0)$ eccentricity; this is also applied to those results when $\Delta T$ varies from 0 to 15, and then 30 degrees. The rate of convergence is considered to be good—based on the given number of node—although for higher frequencies the rate of convergence seems to decrease slightly when the eccentricity appears $(\overline{e}/a = 0.2)$. Overall, the natural frequencies, especially the fundamental frequencies, decline when the eccentricity or the temperature difference increases.

Table 1 Comparing the convergence rate of a C–C–F–F nonrotating and nonporous FG-GRC-ESA plate with uniform distribution of graphene platelets at various temperature difference; $({{a = 1{\text{ m}}, \, h} \mathord{\left/ {\vphantom {{a = 1{\text{ m}}, \, h} a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3,$$\Lambda_{GPL} = 0.01)$. The frequencies $\omega_{i}$ for i = 1,2,3 and 4 are in Hz, and the temperature difference $\Delta T$ is in Celsius

Table 2 shows the convergence of the natural frequencies (Hz) of an annular plate with rising rotating speed when the temperature difference $\Delta T$, and the eccentricity $\overline{e}$, are assumed zero. This rise in rotating speed causes the natural frequencies to increase. What is more, the given results are in good agreement with those obtained from ABAQUS—using the element type ‘S4R’; nonetheless, the total number of elements for the annular plate to have yielded convergent results is 4564. Another simulation has been conducted to verify the accuracy of the problem in which the rotating speed is taken into account, while the temperature difference is zero. In the loading part of the software, a distributed uniform centrifugal force is defined as rotational body force to evaluate the rotating effect on the annular plate. Next, a further frequency analysis is simulated on the annular plate.

Table 2 Comparing the convergence rate of a C-F nonporous FG-GRC annular plate with uniform distribution of graphene platelets at various rotating speed $\Omega$ (rad/s); $(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, \Delta T = 0, \, \Lambda_{GPL} = 0.01)$. The frequencies $\omega_{i}$ for i = 1,2,3 and 4 are in Hz, and the temperature difference $\Delta T$ is in Celsius

Regarding the validation of the proposed method, the results of the non-dimensional fundamental frequency are compared with two sets of data from the literature [34, 65], and those obtained from simulation using ABAQUS (with the prescribed number and type of elements), are presented in Table 3. The comparison is performed for two different boundary conditions, along with various values for eccentricity parameter. Eventually, it is obviously confirmed that results of the current study are in close agreement with the other approaches.

Table 3 Comparison study of the fundamental dimensionless frequency $\overline{\omega } = \sqrt[4]{{\omega^{2} \frac{{12m_{1} a^{4} (1 - \upsilon^{2} )}}{{Eh^{3} }}}}$$[4]$${{\omega^{2} \frac{{12m_{1} a^{4} (1 - \upsilon^{2} )}}{{Eh^{3} }}}}$ for the EA plates in terms of various boundary conditions and eccentricity parameter; ${{(b} \mathord{\left/ {\vphantom {{(b} a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, \Lambda_{GPL} = 0,{\text{ e}}_{0} { = 0, }\upsilon = 0.3 \, \Delta {\rm T} = 0,$$\, \Omega = 0)$

In Table 4, the fundamental frequency (Hz) of a rotating ESA plate in variety of circumstances under two different boundary conditions is investigated. It is deduced from Table 4 that for both of the presented boundary conditions, the increase in the eccentricity parameter $\overline{e}$ has led to the drop in frequency regardless of the graphene distribution. This is also true when the porosity is included in the investigations. Additionally, significant reduction in the fundamental frequency is observed when the distribution of the porosity varies from the symmetrical pattern (Type-I) to the asymmetrical one (Type-II). The role of graphene distribution is also crucial when identifying the natural frequencies. It can be seen that the lowest value and the highest in each set of data belong to the Type-B (whose pattern is considered non-uniform and asymmetrical) and Type-A (with non-uniform, yet symmetrical distribution), respectively.

Table 4 Fundamental frequency (Hz) of an FG-GRC-ESA plate;$(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, \Omega = 100 \, {{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}},$$\Lambda_{GPL} = 0.01)$

In Table 5, the fundamental frequency (Hz) of the EA plate with porosity Type-I and graphene Type-A is presented. It is inferred from Table 5 that by increasing the volume fraction $\Lambda_{GPL}$, the frequency for the corresponding rotating speed adds up. On the other side, the rise in $\Delta T$ mostly affects the boundary conditions C-C and C-S, whereas its influence on C-F is subtle. In contrast, the rise in $\Omega$ appears to have the major effect on the boundary condition C-F, rather than the other two. In Table 6, changes in fundamental frequency (Hz) of a clamped-simple rotating EA plate in terms of the various geometrical parameters are presented. The porosity and the graphene dispersion are considered asymmetrical and symmetrical, respectively. Accordingly, it is clear that the growth in plate’s thickness $h$ causes the natural frequency to rise; similarly, the same phenomenon happens when the volume fraction $\Lambda_{GPL}$ changes from 0.5 to 2 percent. On the other hand, Table 6 displays a vivid decline of the natural frequency when either the inner radius shrinks, or the outer radius enlarges. Moreover, when the off-center hole is relocated to a farther distance from the center, the frequency drops.

Table 5 Fundamental frequency (Hz) of an FG-GRC-EA plate (Type-A) with the porosity being symmetrically distributed at various rotating speed $\Omega$ (rad/s); $(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, {{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.2, \, e_{0} = 0.5)$. The temperature difference $\Delta T$ is in Celsius

Table 6 Fundamental frequency (Hz) of a rotating FG-GRC-EA plate (Type-A) with the porosity being asymmetrically distributed; $(a = 1{\text{ m}},\Omega = 100 \, {{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}},\Delta {\rm T} = 10^{ \circ } ,e_{0} = 0.5)$

The first four mode shapes of a porous FG-GRC-EA plate are displayed in Figs. 4 and 5. The model in Figs. 4 and 5 has symmetrical dispersion of graphene and porosity. The boundary conditions vary from Fig. 4 (C–C) to Fig. 5 (C–F). Similar assumptions are made in order to, graphically, express the first four mode shapes of a porous FG-GRC-ESA plate (Figs. 6 and 7). The applied boundary conditions are C-C-C-C for Fig. 6 and C-F-C-C for Fig. 7. In Fig. 8, the variation of the fundamental natural frequency (Hz) versus temperature difference $\Delta T$ is presented for a rotating FG-GRC-EA plate, which has C–C boundary condition and Type-I porosity. As we can see in Fig. 8, the growth in temperature difference causes the fundamental frequency to drop, regardless of the change in the distribution of graphene platelets. Furthermore, increasing the eccentricity reduces the fundamental frequency. When it comes to the influence of graphene platelets, one is able to see that distribution Type-A marks higher range of fundamental frequencies in comparison with Type-B and Type-C.

Fig. 4

Mode shapes of a ${\text{C - C}}$ porous FG-GRC-EA plate, with symmetrical dispersion of graphene platelets (Type-A) and porosity (Type-I);$(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, {{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.2, \, \Omega = 0, \, \Delta T = 0, \, e_{0} = 0.5, \, \Lambda_{GPL} = 0.01, \, N_{r} = N_{\theta } = 43)$; a first mode, b second mode, c third mode and d forth mode

Fig. 5

Mode shapes of a ${\text{C - F}}$ porous FG-GRC-EA plate, with symmetrical dispersion of graphene platelets (Type-A) and porosity (Type-I); $(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, {{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.2, \, \Omega = 0, \, \Delta T = 0, \, e_{0} = 0.5, \, \Lambda_{GPL} = 0.01, \, N_{r} = N_{\theta } = 43)$; a first mode, b second mode, c third mode and d forth mode

Fig. 6

Mode shapes of a ${\text{C - C - C - C}}$ porous FG-GRC-ESA plate, with symmetrical dispersion of graphene platelets (Type-A) and porosity (Type-I); $(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, {{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.2, \, \Omega = 0, \, \Delta T = 0, \, e_{0} = 0.5, \, \Lambda_{GPL} = 0.01, \, N_{r} = N_{\theta } = 43)$; a first mode, b second mode, c third mode and d forth mode

Fig. 7

Mode shapes of a ${\text{C - F - C - C}}$ porous FG-GRC-ESA plate, with symmetrical dispersion of graphene platelets (Type-A) and porosity (Type-I); $(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, {{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.2, \, \Omega = 0, \, \Delta T = 0, \, e_{0} = 0.5, \, \Lambda_{GPL} = 0.01, \, N_{r} = N_{\theta } = 43)$; a first mode, b second mode, c third mode and d forth mode

Fig. 8

The influence of temperature difference and eccentricity on the fundamental natural frequency of a rotating FG-GRC-EA plate with symmetrical porosity (Type-I) and C–C boundary conditions; the temperature difference $\Delta T$ is in Celsius.$(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, \Omega = 100{\text{ rad/s}}, \, e_{0} = 0.5, \, \Lambda_{GPL} = 0.01)$; a Type-A, b Type-B and c Type-C

In Fig. 9, the effect of the rotating speed on the first four natural frequencies of an FG-GRC-EA plate is investigated. For the given C-F boundary condition, the rise in rotating speed $\Omega {\text{ (rad/s)}}$ appears to have increased all the four natural frequencies. Another major point is that the third and fourth natural frequencies experience a significant drop when the eccentric parameter varies from zero to a small amount ${{(\overline{e}} \mathord{\left/ {\vphantom {{(\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.05)$; however, once the eccentricity continues to grow, the third and fourth natural frequencies tend to increase. Nevertheless, this is not the case for the first and second frequencies since gradual decrease is recorded for both when the eccentricity increases.

Fig. 9

The influence of rotating speed ${\text{(rad/s)}}$ on the first four natural frequencies of an FG-GRC-EA plate with C-F boundary condition and symmetrical dispersion of porosity (Type-I) and graphene platelets (Type-A); $(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, \Delta T = 0, \, e_{0} = 0.2, \, \Lambda_{GPL} = 0.01)$; a ${{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0$, b ${{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.05$, c ${{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.15$ and d ${{\overline{e}} \mathord{\left/ {\vphantom {{\overline{e}} a}} \right. \kern-\nulldelimiterspace} a} = 0.2$

Figure 10 illustrates the variation of the fundamental natural frequency for a nonrotating ESA plate versus the radius ratio ${{(b} \mathord{\left/ {\vphantom {{(b} a}} \right. \kern-\nulldelimiterspace} a})$—which is ratio of the inner radius to the outer radius—for two different boundary conditions. The fundamental natural frequency rises as the consequence of increasing the size of the clamped inner semicircle. In addition, steady rise in eccentricity results in the decline of fundamental frequency. This decline is shown to be more noticeable for bigger radius ratios.

Fig. 10

The influence of the geometry on the fundamental natural frequency of a nonrotating FG-GRC-ESA plate with symmetrical dispersion of porosity (Type-I) and graphene platelets (Type-A); the temperature difference $\Delta T$ is in Celsius.$(a = 1{\text{ m}}, \, {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.01, \, \Delta T = 0, \, \Omega = 0, \, e_{0} = 0.5, \, \Lambda_{GPL} = 0.01)$; a C–C–F–F and b C–F–F–F

In Fig. 11, the four natural frequencies for a nonrotating FG-GRC-ESA plate are presented. These frequencies vary due to the change in thickness ratio $({h \mathord{\left/ {\vphantom {h {a)}}} \right. \kern-\nulldelimiterspace} {a)}}$, as well as the temperature difference $\Delta T$. Although increasing the temperature was known to decrease the natural frequencies, this effect is reduced at larger thickness ratios; that is, the effect of temperature on the natural frequencies is more substantial when the thickness ratio is small, especially for the first mode. However, as the modes get higher, the impact of temperature diminishes even for small thickness ratios.

Fig. 11

The first four natural frequencies versus the thickness ratio $({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a})$ for a nonrotating FG-GRC-ESA plate with boundary conditions C–C–C–C, porosity Type-I and graphene platelets Type-A;$(a = 1{\text{ m}}, \, {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} = 0.3, \, \Omega = 0, \, e_{0} = 0.5, \, \Lambda_{GPL} = 0.01)$; a 1st, b 2nd, c 3rd and d 4th natural frequency

4 Conclusion

The current paper analyzed the free oscillation of rotating FG annular and semi-annular plates with off-centered circular cut-outs and various boundary conditions in a thermal environment. Porosity is included in the model with symmetrical and asymmetrical dispersions along the thickness of the plate; the structure is reinforced with GPLs based on three different types, including non-uniform (symmetrical and asymmetrical) and uniform. These assumptions lead to complex equations derived using Hamilton’s principles, and then tackled utilizing the systematic and efficient transformed differential quadrature method (TDQM). Diverse numerical results certified that the developed method has fast convergence rate and is highly accuracy.

Many parameters have shown to have impact on the final results. In the realm of geometry, as the eccentricity shifts further from the center of the plate, the fundamental frequency tends to decrease. Moreover, the oscillating plate with bigger inner radius is stiffer, and thus its natural frequencies rise. In the realm of material properties, the results recorded the highest natural frequencies for graphene distribution Type-A and the lowest ones for Type-B. The rotational speed and temperature exert arguable influences on the natural frequencies. As an example, the rotational speed has significant impact on those FG-GRC plates whose boundary conditions include a free one. Accordingly, by increasing the rotational speed the natural frequencies tend to grow. On the other hand, the rise in temperature reduces the natural frequencies; however, for a structure with free boundaries (except the inner one), the effect of temperature seems to somewhat diminish for higher modes or greater thickness ratios. The presented technique is anticipated to be recognized as a highly applicable approach for solving oscillatory phenomenon of the eccentric sector-plates in the future.

Appendices

Appendix A

The elements of the reduced stiffness matrix are as follows:

$$ Q_{11} = Q_{22} = \frac{E(z)}{{1 - \upsilon (z)^{2} }},Q_{12} = \frac{\upsilon (z)E(z)}{{1 - \upsilon (z)^{2} }},Q_{44} = Q_{55} = Q_{66} = \frac{E(z)}{{2\left( {1 + \upsilon (z)} \right)}} $$

(67)

Appendix B

$$ \begin{aligned} & \delta v: \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {\left( {\frac{{H_{12} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)u_{pq} } \right.} } + \\ & \left( {\frac{{H_{22} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{66} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + m_{1} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{66} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)v_{pq} \\ & + \left( {\frac{{H_{12}^{f} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{f} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22}^{f} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{f} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\varphi^{r}_{pq} + \left( {\frac{{H_{12}^{g} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{g} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22}^{g} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{g} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\psi^{r}_{pq} \\ & + \left( {\frac{{H_{22}^{f} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{f} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + H_{66}^{f} \tilde{B}_{ipjq}^{{r_{ij} }} + m_{f} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{66}^{f} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\varphi^{\theta }_{pq} \\ & + \left. {\left( {\frac{{H_{22}^{g} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{g} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + H_{66}^{g} \tilde{B}_{ipjq}^{{r_{ij} }} + m_{g} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{66}^{g} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\psi^{\theta }_{pq} } \right\} = m_{1} \left( {\frac{{\partial^{2} v}}{{\partial t^{2} }}} \right)_{ij} + 2m_{1} \Omega \left( {\frac{\partial u}{{\partial t}}} \right)_{ij} \\ & - 2m_{f} \Omega \left( {\frac{{\partial \varphi^{r} }}{\partial t}} \right)_{ij} - 2m_{g} \Omega \left( {\frac{{\partial \psi^{r} }}{\partial t}} \right)_{ij} + m_{f} \left( {\frac{{\partial^{2} \varphi^{\theta } }}{{\partial t^{2} }}} \right)_{ij} + m_{g} \left( {\frac{{\partial^{2} \psi^{\theta } }}{{\partial t^{2} }}} \right)_{ij} \\ \end{aligned} $$

(68)

$$ \begin{aligned} & \delta w: \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {w_{pq} \left( {\frac{{2N_{r\theta 0} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{44} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{N_{\theta \theta 0} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{55} \tilde{B}_{ipjq}^{{r_{ij} }} + N_{rr0} \tilde{B}_{ipjq}^{{r_{ij} }} } \right.} \right.} } + \frac{{\partial N_{r\theta 0} }}{\partial r}\frac{{\tilde{A}_{ipjq}^{\theta } }}{{r_{ij} }} + \frac{{\partial N_{\theta \theta 0} }}{\partial \theta }\frac{{\tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{\partial N_{rr0} }}{\partial r}\tilde{A}_{ipjq}^{{r_{ij} }} \\ & \quad \left. { + \frac{{\partial N_{r\theta 0} }}{\partial \theta }\frac{{\tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + \frac{{H_{55} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + \frac{{N_{rr0} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }}} \right) + \left( {H_{55}^{{f^{\prime } }} \tilde{A}_{ipjq}^{{r_{ij} }} + \frac{{H_{55}^{{f^{\prime } }} \tilde{\delta }_{ipjq} }}{{r_{ij} }}} \right)\varphi^{r}_{pq} + \left( {H_{55}^{{g^{\prime } }} \tilde{A}_{ipjq}^{{r_{ij} }} + \frac{{H_{55}^{{g^{\prime } }} \tilde{\delta }_{ipjq} }}{{r_{ij} }}} \right)\psi^{r}_{pq} \\ & \quad \left. { + \frac{{H_{44}^{{f^{\prime } }} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij} }}\varphi^{\theta }_{pq} + \frac{{H_{44}^{{g^{\prime } }} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij} }}\psi^{\theta }_{pq} } \right\} = m_{1} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)_{ij} \\ \end{aligned} $$

(69)

$$ \begin{aligned} & \delta \varphi^{r} : \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {\left( {\frac{{H_{11}^{f} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + H_{11}^{f} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66}^{f} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + m_{f} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22}^{f} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)u_{pq} } \right.} } \\ & \quad + \left( {\frac{{H_{12}^{f} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{f} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22}^{f} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66}^{f} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)v_{pq} \\ & \quad - H_{55}^{{f^{\prime}}} \tilde{A}_{ipjq}^{{r_{ij} }} w_{pq} + \left( {\frac{{H_{66}^{ff} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{11}^{ff} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{11}^{ff} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} - H_{55}^{{f^{\prime}f^{\prime}}} \tilde{\delta }_{ipjq} + m_{ff} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22}^{ff} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\varphi^{r}_{pq} + \\ & \left( {\frac{{H_{66}^{fg} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{11}^{fg} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{11}^{fg} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} - H_{55}^{{f^{\prime}g^{\prime}}} \tilde{\delta }_{ipjq} + m_{fg} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22}^{fg} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\psi^{r}_{pq} \\ & \quad + \left( {\frac{{H_{12}^{ff} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{ff} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22}^{ff} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66}^{ff} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\varphi^{\theta }_{pq} + \left. {\left( {\frac{{H_{12}^{fg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{fg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22}^{fg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66}^{fg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\psi^{\theta }_{pq} } \right\} \\ & = m_{f} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)_{ij} + m_{ff} \left( {\frac{{\partial^{2} \varphi^{r} }}{{\partial t^{2} }}} \right)_{ij} + m_{fg} \left( {\frac{{\partial^{2} \psi^{r} }}{{\partial t^{2} }}} \right)_{ij} - 2m_{f} \Omega \left( {\frac{\partial v}{{\partial t}}} \right)_{ij} - 2m_{ff} \Omega \left( {\frac{{\partial \varphi^{\theta } }}{\partial t}} \right)_{ij} - 2m_{fg} \Omega \left( {\frac{{\partial \psi^{\theta } }}{\partial t}} \right)_{ij} \\ \end{aligned} $$

(70)

$$ \begin{aligned} & \delta \varphi^{\theta } : \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {\left( {\frac{{H_{12}^{f} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{f} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22}^{f} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{f} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)u_{pq} } \right.} } \\ & \quad + \left( {\frac{{H_{22}^{f} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{f} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + H_{66}^{f} \tilde{B}_{ipjq}^{{r_{ij} }} + m_{f} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{66}^{f} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)v_{pq} \\ & \quad - \frac{{H_{44}^{{f^{\prime } }} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij} }}w_{pq} + \left( {\frac{{H_{12}^{ff} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{ff} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22}^{ff} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{ff} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\varphi^{r}_{pq} \\ & \quad + \left( {\frac{{H_{12}^{fg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{fg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22}^{fg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{fg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\psi^{r}_{pq} + \\ & \left( {\frac{{H_{22}^{ff} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{66}^{ff} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66}^{ff} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} - H_{44}^{{f^{\prime } f^{\prime } }} \tilde{\delta }_{ipjq} + m_{ff} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{66}^{ff} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\varphi^{\theta }_{pq} + \\ & \left. {\left( {\frac{{H_{22}^{fg} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{66}^{fg} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66}^{fg} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} - H_{44}^{{f^{\prime}g^{\prime}}} \tilde{\delta }_{ipjq} + m_{fg} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{66}^{fg} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\psi^{\theta }_{pq} } \right\} \\ & = m_{f} \left( {\frac{{\partial^{2} v}}{{\partial t^{2} }}} \right)_{ij} + m_{ff} \left( {\frac{{\partial^{2} \varphi^{\theta } }}{{\partial t^{2} }}} \right)_{ij} + m_{fg} \left( {\frac{{\partial^{2} \psi^{\theta } }}{{\partial t^{2} }}} \right)_{ij} + 2m_{f} \Omega \left( {\frac{\partial u}{{\partial t}}} \right)_{ij} + 2m_{ff} \Omega \left( {\frac{{\partial \varphi^{r} }}{\partial t}} \right)_{ij} + 2m_{fg} \Omega \left( {\frac{{\partial \psi^{r} }}{\partial t}} \right)_{ij} \\ \end{aligned} $$

(71)

$$ \begin{aligned} & \delta \psi^{r} : \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {\left( {\frac{{H_{11}^{g} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + H_{11}^{g} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66}^{g} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + m_{g} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22}^{g} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)u_{pq} } \right.} } \\ & \quad + \left( {\frac{{H_{12}^{g} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{g} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22}^{g} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66}^{g} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)v_{pq} + \\ & \left( {\frac{{H_{12}^{fg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{fg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22}^{fg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66}^{fg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\varphi^{\theta }_{pq} + \left( {\frac{{H_{12}^{gg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{gg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} - \frac{{H_{22}^{gg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} - \frac{{H_{66}^{gg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\psi^{\theta }_{pq} + \\ & \left( {\frac{{H_{66}^{fg} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{11}^{fg} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{11}^{fg} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} - H_{55}^{{f^{\prime } g^{\prime } }} \tilde{\delta }_{ipjq} + m_{fg} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22}^{fg} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\varphi^{r}_{pq} + \\ & \left. {\left( {\frac{{H_{66}^{gg} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{11}^{gg} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{11}^{gg} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} - H_{55}^{{g^{\prime } g^{\prime } }} \tilde{\delta }_{ipjq} + m_{gg} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{22}^{gg} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\psi^{r}_{pq} } \right\} \\ & = m_{g} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)_{ij} + m_{fg} \left( {\frac{{\partial^{2} \varphi^{r} }}{{\partial t^{2} }}} \right)_{ij} + m_{gg} \left( {\frac{{\partial^{2} \psi^{r} }}{{\partial t^{2} }}} \right)_{ij} - 2m_{g} \Omega \left( {\frac{\partial v}{{\partial t}}} \right)_{ij} - 2m_{fg} \Omega \left( {\frac{{\partial \varphi^{\theta } }}{\partial t}} \right)_{ij} - 2m_{gg} \Omega \left( {\frac{{\partial \psi^{\theta } }}{\partial t}} \right)_{ij} \\ \end{aligned} $$

(72)

$$ \begin{aligned} & \delta \psi^{\theta } : \\ & \sum\limits_{p = 1}^{{N_{r} }} {\sum\limits_{q = 1}^{{N_{\theta } }} {\left\{ {\left( {\frac{{H_{12}^{g} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{g} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22}^{g} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{g} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)u_{pq} } \right.} } \\ & \quad + \left( {\frac{{\tilde{B}_{ipjq}^{\theta } H_{22}^{g} }}{{r_{ij}^{2} }} + \frac{{H_{66}^{g} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} + H_{66}^{g} \tilde{B}_{ipjq}^{{r_{ij} }} + \Omega^{2} m_{g} \tilde{\delta }_{ipjq} - \frac{{H_{66}^{g} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)v_{pq} \\ & \quad - \frac{{H_{44}^{{g^{\prime}}} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij} }}w_{pq} + \left( {\frac{{H_{12}^{fg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{fg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22}^{fg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{fg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\varphi^{r}_{pq} + \\ & \left( {\frac{{H_{12}^{gg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{66}^{gg} \tilde{B}_{ipjq}^{r\theta } }}{{r_{ij} }} + \frac{{H_{22}^{gg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + \frac{{H_{66}^{gg} \tilde{A}_{ipjq}^{\theta } }}{{r_{ij}^{2} }}} \right)\psi^{r}_{pq} + \\ & \left( {\frac{{H_{22}^{fg} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{66}^{fg} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66}^{fg} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} - H_{44}^{{f^{\prime } g^{\prime } }} \tilde{\delta }_{ipjq} + m_{fg} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{66}^{fg} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\varphi^{\theta }_{pq} + \\ & \left. {\left( {\frac{{H_{22}^{gg} \tilde{B}_{ipjq}^{\theta } }}{{r_{ij}^{2} }} + H_{66}^{gg} \tilde{B}_{ipjq}^{{r_{ij} }} + \frac{{H_{66}^{gg} \tilde{A}_{ipjq}^{{r_{ij} }} }}{{r_{ij} }} - H_{44}^{{g^{\prime } g^{\prime } }} \tilde{\delta }_{ipjq} + m_{gg} \Omega^{2} \tilde{\delta }_{ipjq} - \frac{{H_{66}^{gg} \tilde{\delta }_{ipjq} }}{{r_{ij}^{2} }}} \right)\psi^{\theta }_{pq} } \right\} \\ & = m_{g} \left( {\frac{{\partial^{2} v}}{{\partial t^{2} }}} \right)_{ij} + m_{fg} \left( {\frac{{\partial^{2} \varphi^{\theta } }}{{\partial t^{2} }}} \right)_{ij} + m_{gg} \left( {\frac{{\partial^{2} \psi^{\theta } }}{{\partial t^{2} }}} \right)_{ij} + 2m_{g} \Omega \left( {\frac{\partial u}{{\partial t}}} \right)_{ij} + 2m_{fg} \Omega \left( {\frac{{\partial \varphi^{r} }}{\partial t}} \right)_{ij} + 2m_{gg} \Omega \left( {\frac{{\partial \psi^{r} }}{\partial t}} \right)_{ij} \\ \end{aligned} $$

(73)