1 Introduction

Functionally graded materials (FGMs) are advanced composite materials with numerous applications in various fields, such as aircraft, aerospace, and computer circuit industries due to their adequate thermo-mechanical properties. The concept of FGM is to make a composite material by changing the microstructure from a material (like metal) to another (like ceramic) with a specific gradient. The transition between the phases of FGMs can be estimated utilizing a power series. The feature of varying the microstructure makes this class of composite an improved material that possesses the best of both constituents. For example, in aerospace structures, which must withstand very high thermal gradients, FGMs can be utilized by using a ceramic layer connected with a metallic layer. Biomedical, electromagnetic and optical fields are FGMs’ other fields of applications [1,2,3,4,5,6]. Owing to these widespread applications, the mechanical behaviors of structural elements made of FGMs, including buckling, bending, and vibrations of plates/beams/shells have been studied by several researchers hitherto. The reader is referred to [7,8,9] as three review papers for the mentioned studies.

During the manufacturing process, FGMs could be produced with porosities. Therefore, the effect of porosity must be considered in the analysis to achieve accurate results. The distribution of porosities within the structure may be considered even or uneven. Herein, some of the works presented on the structures made of porous FGMs are cited. Mirjavadi et al. [10] studied the thermal vibrations of microbeams made of porous FGMs based on the Timoshenko beam theory. They incorporated the size effects into the formulation using the couple stress theory (CST), and the generalized differential quadrature (GDQ) method was used in the solution procedure. Babaei and Eslami [11] addressed the nonlinear vibrations and snap-through stability problems of porous FG curved micro-tubes by means of the two-step perturbation method. They also presented the thermally-induced nonlinear stability and imperfection sensitivity analyses of FG porous micro-tubes [12]. Recently, Yang et al. [13] investigated the forced vibrations and dynamic buckling of fixed FGM graphene platelet-reinforced composite (GPLRC) porous arches under impulsive loading. They concluded that vibrational and buckling behaviors are quite sensitive to impulsive load duration. Hidayat [14] proposed a meshless thermal model for the analysis of FG porous materials subjected to temperature-dependent heat sources. Arshid et al. [15] studied the vibration behavior of a 3-layered sandwich microplate, including an FG porous core, and piezoelectric carbon nanotube (CNT)-reinforced face sheets under an electric field in a hygro-thermal environment in the context of modified CST. Moreover, Gao et al. [16] analyzed wave propagation in GPLRC FG metal foam porous plates based on various plate theories.

Hygroscopic and thermal stresses (hygrothermal stresses) generated as a result of a difference in moisture concentration and temperature throughout the structural elements can significantly affect their mechanical behaviors. Hygrothermal stresses become important when engineering structures are subjected to high temperatures and increased moisture levels. They are generated due to the combined impact of thermal expansion, which causes the material to expand or contract, and moisture-induced swelling or shrinkage, leading to changes in material's deformation. Consequently, these factors result in mechanical deformation and generate stress within the structure. FGMs can be employed in the construction of gas turbine components such as blades, vanes and combustor liners. Gas turbines are widely used in power generation, aviation and other industries. These turbines operate at high temperatures and are exposed to varying levels of humidity. FGMs with tailored composition and microstructure can be employed to optimize the thermal and mechanical properties of the turbine components. For instance, near the hot combustion gases, where temperatures are highest, the material composition can be designed to have a higher thermal resistance. As one moves away from the hot region towards the cooler parts, the composition can gradually change to a material with better resistance to moisture-induced degradation. This gradient in material properties helps mitigate the detrimental effects of thermal expansion and hygroscopic forces.

Several research works can be found in which the hygro-thermal influences have been studied. Mashat and Zenkour [17] investigated the hygrothermal bending behavior of a sector annular plate with variable radial thickness based on the classical plate theory. The bending response of FG nanoscopic beams with internal porosity under hygro-thermo-mechanical loading was investigated by Jouneghani et al. [18] based on the nonlocal elasticity theory. Zenkour and El-Shahrany [19] used the analytical Navier-type solution method for the vibration problem of sandwich plates with viscoelastic layers in the core and faces including magnetostrictive actuating layers resting on a three-parameter viscoelastic medium subjected to hygrothermal loading. Nguyen et al. [20] investigated the effects of hygrothermal stress resultants on the vibrations and thermal buckling of beams made of FGMs. Hygrothermally-induced vibrations of bidirectional FG porous Timoshenko beams were analyzed by Ansari et al. [21] using a numerical approach. The nonlinear vibrations of FG porous circular plates under hygrothermal loading were also investigated in [22]. Wang et al. [23] studied the hygrothermal effects on the buckling of porous bi-directional FG small-scale beams based on two-phase local/nonlocal strain gradient theory. The dynamic snap-through of perfect [24] and imperfect [25] arches were studied under instantaneous thermal shock. Recently, Salmanizade et al. [26] studied the vibrations of FG conical panels under instantaneous thermal shock, employing the Chebyshev-Ritz method. They concluded that for thick shells, the thermally-induced vibrations diminish, and the dynamic and quasi-static responses become identical. Esmaeili and Kiani [27] conducted the same analysis on GPLRC plates. Also, Vu et al. [28] investigated bending, buckling and free vibration of FG plates based on a new quasi-3D logarithmic shear deformation theory embedded in an elastic foundation.

In recent years, the utilization of deep neural network (DNN) methods has gained popularity in solving partial differential equations within computational mechanics which involve minimizing a loss function by training a neural network. Notably, Samaniego et al. [29] investigated the implementation of DNNs in solving various benchmark engineering problems. They employed different linear and nonlinear activation functions during the network training process, achieving successful results. Furthermore, another work introduces the deep autoencoder based energy method (DAEM) for analysing bending, buckling and vibration in the Kirchhoff plates. By combining a deep autoencoder with the minimum total potential principle, the DAEM enables unsupervised feature learning. The method accurately determines field variables, natural frequencies and critical buckling loads, providing valuable insights into plate’s behavior [30]. Similarly, the deep collocation method (DCM) was employed to investigate plate bending [31]. Specifically, they studied the bending of clamped circular plates, simply-supported and clamped square plates, as well as simply-supported square plates resting on Winkler foundations. DCM utilizes a feed-forward deep neural network with three hidden layers, each comprising 50 neurons, to predict maximum deflections. This approach overcomes the challenges posed by the C1 continuity requirements in traditional mesh-based methods. The results demonstrate the accuracy of the proposed method even with a limited number of hidden layers and neurons.

In the present contribution, the variational differential quadrature (VDQ) method is applied to the thermally-induced large-amplitude vibration analysis of FG porous circular plates under the action of hygrothermal loads. The formulation is developed in a novel vector–matrix form, and the VDQ method is directly applied to the weak form of equations, so that the derivation process of the strong form of the equations is bypassed. This method does not require the local interpolation and the assemblage emerging in similar methodologies applied on the weak form of equations. Two types of porosity distributions, hygroscopic stresses generated due to the nonlinear rise in moisture concentration, two-parameter elastic foundation, temperature-dependent nature of material properties and both simply-supported and clamped boundary conditions are considered herein. The modified Voigt's rule of mixture and Touloukian formula are used to compute the temperature-dependent properties of considered FG porous material. Even (FGM-I) and uneven (FGM-II) distributions of porosities are considered. The equations of motion are obtained within the frameworks of first-order shear deformation plate theory and von Kármán assumptions through Hamilton’s principle. The temperature equation is also solved using the GDQ method [32] in conjunction with the Newmark integration algorithm. Moreover, the equations of motion are solved using the VDQ method [33]. Selected numerical results are given to investigate the effects of temperature distribution, porosity volume fraction, moisture concentration, elastic foundation parameters, and FG index on the nonlinear vibration behavior of clamped and simply-supported plates.

2 Theory and formulation

2.1 Porous functionally graded material

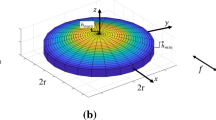
A porous circular plate with radius \(a\) and thickness \(h\) is considered as illustrated in Fig. 1. The modified Voigt's rule of mixture for even (FGM-I) and uneven (FGM-II) distributions of porosities takes the following form [34]

$$P\left(z,T\right)={P}_{m}\left(T\right)\left({V}_{m}\left(z\right)-\frac{\xi }{2}\right)+{P}_{c}\left(T\right)\left({V}_{c}\left(z\right)-\frac{\xi }{2}\right)$$
(1a)
$$P\left(z,T\right)={P}_{m}\left(T\right)\left({V}_{m}\left(z\right)-\frac{\xi }{2}\left(1-\frac{2\left|z\right|}{h}\right)\right)+{P}_{c}\left(T\right)\left({V}_{c}\left(z\right)-\frac{\xi }{2}\left(1-\frac{2\left|z\right|}{h}\right)\right)$$
(1b)

where \(P\left(z,T\right)\) is a material property such as Young’s modulus or thermal expansion coefficient as a function of temperature (\(T\)) and position in the thickness direction (\(z\)). Also, \(V\) denotes the volume fraction of each constituent, in which, \(m\) and \(c\) subscripts denote metal and ceramic phases, respectively. Furthermore, \(\xi\) stands for the porosity volume fraction. The volume fractions of metal and ceramic are formulated as

$${V}_{c}\left(z\right)={\left(\frac{1}{2}+\frac{z}{h}\right)}^{\zeta }$$
(2a)
$${V}_{m}\left(z\right)=1-{V}_{c}\left(z\right)$$
(2b)

in which \(\zeta\) is a non-negative number indicating the FG index along the thickness direction (the metal volume fraction gets larger as this parameter increases). Also, \({V}_{c}+{V}_{m}=1\). Substituting Eq. (2) in (1a) for even distribution results in

Fig. 1
figure 1

Geometry and coordinates system of FG porous circular plate, a cross-sectional view, b top view [22]

Full size image
$$P\left(z,T\right)={P}_{m}+\left({P}_{c}-{P}_{m}\right){\left(\frac{1}{2}+\frac{z}{h}\right)}^{\zeta }-\frac{\xi }{2}\left({P}_{c}+{P}_{m}\right)$$
(3)

Also, by inserting in Eq. (1b) for uneven porosities, one has

$$P\left(z,T\right)={P}_{m}+\left({P}_{c}-{P}_{m}\right){\left(\frac{1}{2}+\frac{z}{h}\right)}^{\zeta }-\frac{\xi }{2}\left(1-\frac{2\left|z\right|}{h}\right)\left({P}_{c}+{P}_{m}\right)$$
(4)

The effective material properties of constituents are considered temperature-dependent using the Touloukian experiments according to the following formula [35, 36]

$$P\left(T\right)={P}_{0}({P}_{-1}{T}^{-1}+1+{P}_{1}T+{P}_{2}{T}^{2}+{P}_{3}{T}^{3})$$
(5)

where \({P}_{0}\), \({P}_{-1}\), \({P}_{1}\), \({P}_{2}\) and \({P}_{3}\) are coefficients for both metal and ceramic phases, and \(T\) is the temperature in Kelvin.

2.2 Formulation of motion

Based on the first-order shear deformation plate theory, the displacement field in the circular plate is given by

$${u}_{r}\left(r,z,t\right)=u\left(r,t\right)+z\psi (r,t)$$
(6a)
$${u}_{\theta }\left(r,z,t\right)=0$$
(6b)
$${u}_{z}\left(r,z,t\right)=w(r,t)$$
(6c)

where \({u}_{r}\), \({u}_{\theta }\) and \({u}_{z}\) are displacements of the mid-plane points in \(r, \theta ,\) and \(z\) directions, respectively, and \(t\) denotes time. With the von-Kármán geometrical nonlinearity assumption and considering hygrothermal effects, the strain field is [37]

$$\left\{{\varvec{\varepsilon}}\right\}=\left\{{{\varvec{\varepsilon}}}^{0}\right\}+z\left\{{{\varvec{\varepsilon}}}^{1}\right\}=\left[\begin{array}{c}{\varepsilon }_{rr}\\ {\varepsilon }_{\theta \theta }\\ 2{\varepsilon }_{rz}={\gamma }_{rz}\end{array}\right]$$
(7a)
$$\left[\begin{array}{c}{\varepsilon }_{rr}^{0}\\ {\varepsilon }_{\theta \theta }^{0}\\ {\gamma }_{rz}^{0}\end{array}\right]=\left[\begin{array}{c}{u}_{,r}+\frac{1}{2}{w}_{,r}^{2}\\ \frac{u}{r}\\ \psi +{w}_{,r}\end{array}\right], \left[\begin{array}{c}{\varepsilon }_{rr}^{1}\\ {\varepsilon }_{\theta \theta }^{1}\\ {\gamma }_{rz}^{1}\end{array}\right]=\left[\begin{array}{c}{\psi }_{,r}\\ \frac{\psi }{r}\\ 0\end{array}\right]$$
(7b)
$${\varvec{\varepsilon}}={\mathbf{P}}_{0}\mathbf{E}\mathbf{U}+\frac{1}{2}{\mathbf{P}}_{1}{\mathbf{E}}_{\mathbf{n}}\mathbf{U}$$
(7c)

where the tensors introduced in Eq. (7c) are defined as

$${\mathbf{P}}_{0}=\left[\begin{array}{ccccc}1&\,\, 0&\,\, 0&\,\, z&\,\, 0\\ 0&\,\, 1&\,\, 0&\,\, 0&\,\, z\\ 0&\,\, 0&\,\, 1&\,\, 0&\,\, 0\end{array}\right],\boldsymbol{ }\boldsymbol{ }\mathbf{E}=\left[\begin{array}{ccc}{\partial }_{r}& 0&\,\, 0\\ \frac{1}{r}&\,\, 0&\,\, 0\\ 0&\,\, {\partial }_{r}&\,\, 1\\ 0&\,\, 0&\,\, {\partial }_{r}\\ 0&\,\, 0&\,\, \frac{1}{r}\end{array}\right]\boldsymbol{ },\boldsymbol{ }\boldsymbol{ }\mathbf{U}=\left[\begin{array}{c}u\\ w\\ \psi \end{array}\right]$$
(7d)
$${\mathbf{P}}_{1}=\left[\begin{array}{ccc}0&\,\, 1&\,\, 0\\ 0&\,\, 0&\,\, 0\\ 0&\,\, 0& 0\end{array}\right],\boldsymbol{ }\boldsymbol{ }{\mathbf{E}}_{\mathbf{n}}=\langle \mathbf{G}\mathbf{U}\rangle \mathbf{G},\mathbf{G}=\left[\begin{array}{ccc}0&\,\, 0&\,\, 0\\ 0& {\partial }_{r}&\,\, 0\\ 0&\,\, 0&\,\, 0\end{array}\right]$$
(7e)

Also, the stress field is expressed as

$${\varvec{\sigma}}=\left[\begin{array}{c}{\sigma }_{rr}\\ {\sigma }_{\theta \theta }\\ {\tau }_{rz}\end{array}\right]=\mathbf{C}\left({\varvec{\varepsilon}}-\Delta T\left[\begin{array}{c}\alpha \\ \alpha \\ 0\end{array}\right]-\Delta C\left[\begin{array}{c}\beta \\ \beta \\ 0\end{array}\right]\right)$$
(8a)
$$\mathbf{C}=\left[\begin{array}{ccc}{C}_{11}& {C}_{12}& 0\\ {C}_{12}& {C}_{22}& 0\\ 0& 0& {C}_{55}\end{array}\right]$$
(8b)
$$C_{11} = C_{22} = \frac{E}{{1 - \upsilon^{2} }} , \quad C_{12} = \frac{\upsilon E}{{1 - \upsilon^{2} }} , \quad C_{55} = \frac{E}{{2\left( {1 + \upsilon } \right)}}$$
(8c)

where \(\alpha\) and \(\beta\) are the thermal and moisture expansion coefficients, respectively. Moreover, \(C\), \(T\), \({C}_{0}\), and \({T}_{0}\) are the moisture concentration, temperature distribution, reference moisture concentration and reference temperature distribution of the plate, respectively. Elastic modulus and Poisson’s ratio are also shown by \(E\) and \(\upsilon\). To derive the equations of motion, Hamilton’s principle is used, which states that

$$\underset{{t}_{1}}{\overset{{t}_{2}}{\int }}\left(\delta T-\delta {U}^{int}+\delta {W}^{ext}\right)dt=0$$
(9a)

where \(\delta T\), \(\delta {U}^{int}\), and \(\delta {W}^{ext}\) are variations of kinetic energy, elastic energy and work done by external loads, respectively. Also,

$$\delta {U}^{int}={\int }_{\vartheta }\delta \widehat{u}d\vartheta ={\int }_{\vartheta }{\sigma }_{ij}\delta {\varepsilon }_{ij}d\vartheta =2\pi \underset{0}{\overset{a}{\int }}\underset{-0.5h}{\overset{0.5h}{\int }}\delta {{\varvec{\varepsilon}}}^{\mathrm{T}}{\varvec{\sigma}}\boldsymbol{ }rdzdr$$
(9b)
$$\begin{aligned} \delta U^{int} & = 2\pi \mathop \int \limits_{0}^{a} \mathop \int \limits_{ - 0.5h}^{0.5h} \delta \left( {{\mathbf{U}}^{{\text{T}}} {\mathbf{E}}^{{\text{T}}} {\mathbf{P}}_{0}^{{\text{T}}} + \frac{1}{2}{\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} {\mathbf{P}}_{1}^{{\text{T}}} } \right)\left[ {{\mathbf{C}}\left( {{\mathbf{P}}_{0} {\mathbf{EU}} + \frac{1}{2}{\mathbf{P}}_{1} {\mathbf{E}}_{{\mathbf{n}}} {\mathbf{U}}} \right)} \right.\user2{ } \\ & \quad \left. { - {\mathbf{C}}\left[ {\begin{array}{*{20}c} {\alpha {\Delta }T + \beta {\Delta }C} \\ {\alpha {\Delta }T + \beta {\Delta }C} \\ 0 \\ \end{array} } \right]} \right]rdzdr \\ \end{aligned}$$
(9c)

Considering \(\mathrm{X}\circ \mathrm{Y}=\langle \mathrm{X}\rangle \mathrm{Y}=\langle \mathrm{Y}\rangle \mathrm{X}\), where a \(\langle \mathbf{V}\rangle\) operator forms a diagonal matrix from vector \(\mathbf{V}\), and \(\circ\) represents the Hadamard product, one can prove that

$$\begin{aligned} \delta \left( {{\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} } \right) & = \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} + {\mathbf{U}}^{{\text{T}}} \delta {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} = \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} + {\mathbf{U}}^{{\text{T}}} \delta \left( {{\mathbf{G}}^{{\mathbf{T}}} {\mathbf{U}}^{{\text{T}}} {\mathbf{G}}^{{\text{T}}} } \right) \\ & = \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} + {\mathbf{U}}^{{\text{T}}} {\mathbf{G}}^{{\mathbf{T}}} \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{G}}^{{\text{T}}} = \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} + \delta {\mathbf{U}}^{{\text{T}}} \left( {{\mathbf{G}}^{{\mathbf{T}}} {\mathbf{U}}^{{\text{T}}} {\mathbf{G}}^{{\text{T}}} } \right) = 2\delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} \\ \end{aligned}$$
(10)

Taking the variation in Eq. (9) and utilizing Eq. (10), one can write

$$\begin{aligned} \delta U^{int} & = 2\pi \mathop \int \limits_{0}^{a} \mathop \int \limits_{ - 0.5h}^{0.5h} \left( {\delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}^{{\text{T}}} {\mathbf{P}}_{0}^{{\text{T}}} + \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} {\mathbf{P}}_{1}^{{\text{T}}} } \right)\left[ {{\mathbf{C}}\left( {{\mathbf{P}}_{0} {\mathbf{EU}} + \frac{1}{2}{\mathbf{P}}_{1} {\mathbf{E}}_{{\mathbf{n}}} {\mathbf{U}}} \right)} \right.\user2{ } \\ & \quad \left. { - {\mathbf{C}}\left[ {\begin{array}{*{20}c} {\alpha {\Delta }T + \beta {\Delta }C} \\ {\alpha {\Delta }T + \beta {\Delta }C} \\ 0 \\ \end{array} } \right]} \right]rdzdr \\ \end{aligned}$$
(11)

By multiplying, Eq. (11) takes the following form

$$\begin{aligned} \delta U^{int} & = 2\pi \mathop \int \limits_{0}^{a} \mathop \int \limits_{ - 0.5h}^{0.5h} \left[ {\delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}^{{\text{T}}} {\mathbf{P}}_{0}^{{\text{T}}} {\mathbf{CP}}_{0} {\mathbf{EU}} + \frac{1}{2}} \right.\delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}^{{\text{T}}} {\mathbf{P}}_{0}^{{\text{T}}} {\mathbf{CP}}_{1} {\mathbf{E}}_{{\mathbf{n}}} {\mathbf{U}} \\ & \quad + \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} {\mathbf{P}}_{1}^{{\text{T}}} {\mathbf{CP}}_{0} {\mathbf{EU}} + \frac{1}{2}\delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} {\mathbf{P}}_{1}^{{\text{T}}} {\mathbf{CP}}_{1} {\mathbf{E}}_{{\mathbf{n}}} {\mathbf{U}} - \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}^{{\text{T}}} {\mathbf{P}}_{0}^{{\text{T}}} {\mathbf{C}}\left[ {\begin{array}{*{20}c} {\alpha {\Delta }T + \beta {\Delta }C} \\ {\alpha {\Delta }T + \beta {\Delta }C} \\ 0 \\ \end{array} } \right] \\ & \quad \left. { - \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} {\mathbf{P}}_{1}^{{\text{T}}} {\mathbf{C}}\left[ {\begin{array}{*{20}c} {\alpha {\Delta }T + \beta {\Delta }C} \\ {\alpha {\Delta }T + \beta {\Delta }C} \\ 0 \\ \end{array} } \right]} \right]rdzdr \\ \end{aligned}$$
(12)

Now, the following matrix is defined

$${{\varvec{\Lambda}}}_{1}=\underset{-0.5h}{\overset{0.5h}{\int }}{\mathbf{P}}_{0}^{\mathrm{T}}\mathbf{C}{\mathbf{P}}_{0}dz=\left[\begin{array}{ccccc}{A}_{11}&\,\, {A}_{12}&\,\, 0&\,\, {B}_{11}&\,\, {B}_{12}\\ {A}_{12}&\,\, {A}_{22}&\,\, 0&\,\, {B}_{12}&\,\, {B}_{22}\\ 0&\,\, 0&\,\, {A}_{55}&\,\, 0&\,\, 0\\ {B}_{11}&\,\, {B}_{12}&\,\, 0&\,\, {D}_{11}&\,\, {D}_{12}\\ {B}_{12}&\,\, {B}_{22}&\,\, 0&\,\, {D}_{12}&\,\, {D}_{22}\end{array}\right]$$
(13a)

where \({A}_{ij}\), \({B}_{ij}\), and \({D}_{ij}\) are stiffness components that are computed as

$$\left({A}_{ij},{B}_{ij},{D}_{ij}\right)={\int }_{A}\left({C}_{ij},z{C}_{ij},{z}^{2}{C}_{ij}\right)dA$$
(13b)

In addition,

$${{\varvec{\Lambda}}}_{2}=\underset{-0.5h}{\overset{0.5h}{\int }}{\mathbf{P}}_{0}^{\mathrm{T}}\mathbf{C}{\mathbf{P}}_{1}dz=\left[\begin{array}{ccccc}0&\,\, 0&\,\, {A}_{11}&\,\, 0&\,\, 0\\ 0&\,\, 0&\,\, {A}_{12}&\,\, 0&\,\, 0\\ 0&\,\, 0&\,\, 0&\,\, 0&\,\, 0\\ 0&\,\, 0&\,\, {B}_{11}&\,\, 0&\,\, 0\\ 0&\,\, 0& {B}_{12}&\,\, 0&\,\, 0\end{array}\right]$$
(14a)
$${{\varvec{\Lambda}}}_{3}=\underset{-0.5h}{\overset{0.5h}{\int }}{\mathbf{P}}_{0}^{\mathrm{T}}\mathbf{C}{\mathbf{P}}_{1}dz=\left[\begin{array}{ccccc}0&\,\, 0& \,\,0&\,\, 0&\,\, 0\\ {A}_{11}&\,\, {A}_{12}&\,\, 0&\,\, {B}_{11}&\,\, {B}_{12}\\ 0&\,\, 0&\,\, 0&\,\, 0&\,\, 0\end{array}\right]$$
(14b)
$${{\varvec{\Lambda}}}_{4}=\underset{-0.5h}{\overset{0.5h}{\int }}{\mathbf{P}}_{1}^{\mathrm{T}}\mathbf{C}{\mathbf{P}}_{1}dz=\left[\begin{array}{lll}0&\; 0&\; 0\\ 0&\; {A}_{11}&\; 0\\ 0&\; 0&\; 0\end{array}\right]$$
(14c)

Also,

$${\mathbf{F}}_{1}=\underset{-0.5h}{\overset{0.5h}{\int }}{\mathbf{P}}_{0}^{\mathrm{T}}\mathbf{C}\left[\begin{array}{c}\alpha\Delta T+\beta\Delta C\\ \alpha\Delta T+\beta\Delta C\\ 0\end{array}\right]dz=\left[\begin{array}{c}{N}^{TC}\\ {N}^{TC}\\ 0\\ {M}^{TC}\\ {M}^{TC}\end{array}\right]$$
(15a)

and

$${\mathbf{F}}_{2}=\underset{-0.5h}{\overset{0.5h}{\int }}{\mathbf{P}}_{1}^{\mathrm{T}}\mathbf{C}\left[\begin{array}{c}\alpha\Delta T+\beta\Delta C\\ \alpha\Delta T+\beta\Delta C\\ 0\end{array}\right]dz=\left[\begin{array}{c}0\\ {N}^{TC}\\ 0\end{array}\right]$$
(15b)

\({N}^{TC}\) and \({M}^{TC}\) are hygrothermal force and moment resultants, respectively, given by

$${N}^{TC}={N}^{T}+{N}^{C}$$
(16a)
$${M}^{TC}={M}^{T}+{M}^{C}$$
(16b)

where \({N}^{T}\), \({M}^{T}\), \({N}^{C}\), and \({M}^{C}\) are thermal force, thermal moment, hygroscopic force and hygroscopic moment resultants, respectively, expressed as

$$\left({N}^{T},{M}^{T}\right)=\int_{A}\frac{E\alpha (T-{T}_{0})}{1-\nu }\left(1,z\right)dA$$
(17a)
$$\left({N}^{C},{M}^{C}\right)={\int }_{A}\frac{E\beta (C-{C}_{0})}{1-\nu }\left(1,z\right)dA$$
(17b)

Now, resulting from Eq. (12), one can write

$$\begin{aligned} \delta U^{int} & = 2\pi \mathop \int \limits_{0}^{a} \left[ {\delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}^{{\text{T}}} {{\varvec{\Lambda}}}_{1} {\mathbf{EU}} + \frac{1}{2}} \right.\delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}^{{\text{T}}} {{\varvec{\Lambda}}}_{2} {\mathbf{E}}_{{\mathbf{n}}} {\mathbf{U}} \\ & \qquad \left. { + \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} {{\varvec{\Lambda}}}_{3} {\mathbf{EU}} + \frac{1}{2}\delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} {{\varvec{\Lambda}}}_{4} {\mathbf{E}}_{{\mathbf{n}}} {\mathbf{U}} - \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}^{{\text{T}}} {\mathbf{F}}_{1} - \delta {\mathbf{U}}^{{\text{T}}} {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} {\mathbf{F}}_{2} } \right]rdr \\ \end{aligned}$$
(18)

For the variation of kinetic energy, one has

$$dT=\frac{1}{2}dm{V}^{2}=\frac{1}{2}\rho {V}^{2}rdrdzd\theta$$
(19)

Considering the following equation for the velocity vector

$$\mathbf{V}={\dot{u}}_{r}\overrightarrow{{e}_{r}}+{\dot{u}}_{z}\overrightarrow{{e}_{z}}=(\dot{u}+z\dot{\psi })\overrightarrow{{e}_{r}}+\dot{w}\overrightarrow{{e}_{z}}$$
(20)

and taking variation of Eq. (19), employing Eq. (20) results in

$$\delta dT=\frac{\rho }{2}\left[2\dot{u}\delta \dot{u}+2{z}^{2}\dot{\psi }\delta \dot{\varphi }+2z\dot{\psi }\delta \dot{u}+2z\dot{u}\delta \dot{\psi }+2\dot{w}\delta \dot{w}\right]rdrdzd\theta$$
(21)

Consequently, \(\delta T\) is given as

$$\begin{aligned} \delta T & = \mathop \int \limits_{\vartheta } \delta dTd\vartheta = 2\pi \mathop \int \limits_{0}^{a} \mathop \int \limits_{ - 0.5h}^{0.5h} \rho \left[ {\dot{u}\delta \dot{u} + z^{2} \dot{\psi }\delta \dot{\varphi } + z\dot{\psi }\delta \dot{u}} \right. \\ & \quad \left. { + z\dot{u}\delta \dot{\psi } + \dot{w}\delta \dot{w}} \right] rdzdr \\ \end{aligned}$$
(22)

Defining

$$({I}_{1},{I}_{2},{I}_{3})={\int }_{z}\left(1,z ,{z}^{2}\right){\rho }_{\left(z,T\right)}dz$$
(23)

and taking a time integral, performing integration by parts one can arrive at

$$\underset{{t}_{1}}{\overset{{t}_{2}}{\int }}\delta Tdt=-2\pi \underset{{t}_{1}}{\overset{{t}_{2}}{\int }}\underset{0}{\overset{a}{\int }}\left[{I}_{1}\ddot{u}\delta u+{I}_{3}\ddot{\psi }\delta \psi +{I}_{2}\ddot{\psi }\delta u+{I}_{2}\ddot{u}\delta \psi +{I}_{1}\ddot{w}\delta w\right]rdrdt$$
(24)

Finally, considering the Winkler-Pasternak foundation, the variation of work done by external loads takes the following form

$$\delta {W}^{ext}=-2\pi \underset{0}{\overset{a}{\int }}\left({k}_{w}w\delta w+{k}_{g}{w}_{,r}\delta {w}_{,r}\right)rdr$$
(25)

where \({{k}}_{\mathrm{w}}\) and \({{k}}_{\mathrm{g}}\) are the elastic foundation parameters.

2.3 Temperature and moisture distribution

The heat transfer differential equation is written as [38]

$$\nabla \cdot \left[ {K\nabla T\left( {r,t} \right)} \right] + g\left( {r,t} \right) = \rho C_{v} \frac{{\partial T\left( {r,t} \right)}}{\partial t}$$
(26)

For the present problem, since the circular plate is thin, it is reasonable to assume that the one-dimensional heat conduction occurs only in the thickness direction. In addition, following that there is no heat generation, Eq. (26) is reduced to

$$\frac{\partial }{\partial z}\left(K(z,T)\frac{\partial T}{\partial z}\right)=\rho {(z,T)C}_{v}(z,T)\frac{\partial T}{\partial t}$$
(27)

with the following thermal boundary and initial conditions

$$Boundary \,condition : T\left(+0.5h,t\right)={T}_{T} , T\left(-0.5h,t\right)={T}_{B}$$
(28a)
$$Initial \,condition : {T}_{(z,0)}={T}_{0}$$
(28b)

Besides, the nonlinear moisture distribution is considered as [39, 40]

$$C\left(z\right)=\left({C}_{T}-{C}_{B}\right){\left[\frac{1}{2}+\frac{z}{h} \right]}^{{\gamma }_{H}}+{C}_{B}$$
(29)

where \({C}_{T}\) and \({C}_{B}\) are the top and bottom surface moisture concentrations of the plate, and \({\gamma }_{H}\) is the hygroscopic exponent.

3 Solution methodology

3.1 Temperature equation

Applying the GDQ method to the temperature equation yields

$${\mathbf{C}}_{\mathrm{T}}\dot{\mathbf{T}}+{\mathbf{K}}_{\mathrm{T}}\mathbf{T}={\mathbf{F}}_{\mathrm{T}}$$
(30a)

where

$$\mathbf{T}={\left[{T}_{1},{T}_{2},\dots ,{T}_{{N}_{z}}\right]}^{\mathrm{T}}$$
(30b)
$${\mathbf{K}}_{\mathrm{T}}=-\left(\langle \mathbf{k}\rangle {\mathbf{D}}_{z}^{\left(2\right)}+\langle {\mathbf{D}}_{z}^{\left(1\right)}\mathbf{k}\rangle {\mathbf{D}}_{z}^{\left(1\right)}\right)$$
(30c)
$${\mathbf{C}}_{\mathrm{T}}=\langle {\varvec{\uprho}}\circ {\mathbf{C}}_{v}\rangle$$
(30d)
$${\mathbf{F}}_{\mathrm{T}}={0}_{{N}_{z}\times 1}$$
(30e)

Also, \(\mathbf{I}\) is the identity matrix. Moreover,

$$\mathbf{k}={\left[{k}_{1},{k}_{2},\dots ,{k}_{{N}_{z}}\right]}^{\mathrm{T}}$$
(31a)
$${\varvec{\uprho}}={\left[{\rho }_{1},{\rho }_{2},{\rho }_{{N}_{z}}\right]}^{\mathrm{T}}$$
(31b)
$${\mathbf{C}}_{v}={\left[{{C}_{v}}_{1},{{C}_{v}}_{2},\dots ,{{C}_{v}}_{{N}_{z}}\right]}^{\mathrm{T}}$$
(31c)

The Newmark-beta integration method based on the average constant acceleration scheme [41] is used on the temperature equation, which leads to

$$\widehat{\mathbf{K}}{\mathbf{T}}_{n+1}=\widehat{\mathbf{F}}$$
(32a)

where \({\mathbf{T}}_{n+1}\) is the next time step unknown temperature vector. Furthermore

$$\widehat{\mathbf{K}}={\mathbf{K}}_{\mathrm{T}}+{a}_{3}{\mathbf{M}}_{\mathrm{T}}+{a}_{6}{\mathbf{C}}_{\mathrm{T}}$$
(32b)
$$\widehat{\mathbf{F}}={\mathbf{F}}_{\mathrm{T}}+{\mathbf{M}}_{\mathrm{T}}\left({a}_{3}{\mathbf{T}}_{\mathrm{n}}+{a}_{4}{\dot{\mathbf{T}}}_{\mathbf{n}}+{a}_{5}{\ddot{\mathbf{T}}}_{\mathrm{n}}\right)+{\mathbf{C}}_{\mathbf{T}}({a}_{6}{\mathbf{T}}_{\mathrm{n}}+{a}_{7}{\dot{\mathbf{T}}}_{\mathrm{n}}+{a}_{8}{\ddot{\mathbf{T}}}_{\mathrm{n}})$$
(32c)

where

$${a}_{1}=\alpha \Delta t , {a}_{2}=\left(1-\alpha \right)\Delta t , {a}_{3}=\frac{1}{\beta \Delta {t}^{2}} , {a}_{4}=\frac{1}{\beta \Delta t} , {a}_{5}=\frac{1-2\beta }{2\beta }$$
(32d)
$${a}_{6}=\frac{\alpha }{\beta \Delta t} , {a}_{7}=\frac{\alpha -\beta }{\beta } , {a}_{8}=\frac{\left(\alpha -2\beta \right)\Delta t}{2\beta }$$
(32e)
$${\ddot{\mathbf{T}}}_{n+1}={a}_{3}\left({\mathbf{T}}_{n+1}-{\mathbf{T}}_{n}\right)-{a}_{4}{\dot{\mathbf{T}}}_{n}-{a}_{5}{\ddot{\mathbf{T}}}_{n}$$
(32f)
$${\dot{\mathbf{T}}}_{n+1}={\dot{\mathbf{T}}}_{n}+{a}_{2}{\ddot{\mathbf{T}}}_{n}+{a}_{1}{\ddot{\mathbf{T}}}_{n+1}$$
(32g)

3.2 Equation of motion

The VDQ method is used to discretize the equations of motion. Using this technique, Eq. (24) is discretized as follows

$$\underset{{t}_{1}}{\overset{{t}_{2}}{\int }}\delta Tdt=-2\pi \underset{{t}_{1}}{\overset{{t}_{2}}{\int }}\underset{0}{\overset{a}{\int }}\delta {\mathbf{U}}^{\mathrm{T}}{\mathbf{I}}_{\mathrm{K}}\ddot{\mathbf{U}}rdrdt$$
(33a)

where

$${\mathbf{I}}_{\mathrm{K}}=\left[\begin{array}{ccc}{\mathrm{I}}_{1}&\; 0&\; {\mathrm{I}}_{2}\\ 0&\; {\mathrm{I}}_{1}&\; 0\\ {\mathrm{I}}_{2}&\; 0&\; {\mathrm{I}}_{3}\end{array}\right]$$
(33b)

Equation (25) is also discretized as

$$\delta {W}^{ext}=-2\pi \underset{0}{\overset{a}{\int }}\delta {\mathbf{U}}^{\mathrm{T}}{\mathbf{L}}^{\mathrm{T}}\mathbf{H}\mathbf{L}\mathbf{U}rdr$$
(34a)

in which

$$\mathbf{L}=\left[\begin{array}{ccc}0&\; 1&\; 0\\ 0&\; {\partial }_{r}&\; 0\end{array}\right],\boldsymbol{ }\boldsymbol{ }\mathbf{H}=\left[\begin{array}{cc}{k}_{w}&\; 0\\ 0&\; {k}_{g}\end{array}\right]$$
(34b)

The variation of strain energy is similarly discretized. Substituting the discretized energy terms into Hamilton’s principle leads to

$$\begin{aligned} & \mathop \int \limits_{{t_{1} }}^{{t_{2} }} 2\pi \delta {\mathbf{U}}^{{\text{T}}} \left[ {{\mathbf{E}}^{{\text{T}}} \left( {{\mathbf{I}}_{5} { \circledast }r \circ s} \right){{\varvec{\Lambda}}}_{1} {\mathbf{EU}} + \frac{1}{2}} \right.{\mathbf{E}}^{{\text{T}}} \left( {{\mathbf{I}}_{5} { \circledast }r \circ s} \right){{\varvec{\Lambda}}}_{2} {\mathbf{E}}_{{\mathbf{n}}} {\mathbf{U}} \\ & \quad + {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} \left( {{\mathbf{I}}_{3} { \circledast }r \circ s} \right){{\varvec{\Lambda}}}_{3} {\mathbf{EU}} + \frac{1}{2}{\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} \left( {{\mathbf{I}}_{3} { \circledast }r \circ s} \right){{\varvec{\Lambda}}}_{4} {\mathbf{E}}_{{\mathbf{n}}} {\mathbf{U}} \\ & \quad - {\mathbf{E}}^{{\text{T}}} \left( {{\mathbf{I}}_{5} { \circledast }r \circ s} \right){\mathbf{F}}_{1} - {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} \left( {{\mathbf{I}}_{3} { \circledast }r \circ s} \right){\mathbf{F}}_{2} + \left( {{\mathbf{I}}_{3} { \circledast }r \circ s} \right){\mathbf{I}}_{{\text{K}}} {\ddot{\mathbf U}} \\ & \quad \left. { + {\mathbf{L}}^{{\text{T}}} \left( {{\mathbf{I}}_{2} { \circledast }r \circ s} \right){\mathbf{HLU}}} \right]dt = 0 \\ \end{aligned}$$
(35)

where \({ \circledast }\) symbol is used to represent the Kronecker product. Finally, using the fundamental lemma of the calculus of variations, one can get

$${\mathbb{M}}\ddot{\mathbb{U}}+{\Bbbk }{\mathbb{U}}={\mathbb{F}}$$
(36a)

where

$$\begin{aligned} {\Bbbk } & = {\mathbf{E}}^{{\text{T}}} \left( {{\mathbf{I}}_{5} { \circledast }r \circ s} \right){{\varvec{\Lambda}}}_{1} {\mathbf{E}} + \frac{1}{2}{\mathbf{E}}^{{\text{T}}} \left( {{\mathbf{I}}_{5} { \circledast }r \circ s} \right){{\varvec{\Lambda}}}_{2} {\mathbf{E}}_{{\mathbf{n}}} \\ & \quad + {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} \left( {{\mathbf{I}}_{3} { \circledast }r \circ s} \right){{\varvec{\Lambda}}}_{3} {\mathbf{E}} + \frac{1}{2}{\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} \left( {{\mathbf{I}}_{3} { \circledast }r \circ s} \right){{\varvec{\Lambda}}}_{4} {\mathbf{E}}_{{\mathbf{n}}} \\ \end{aligned}$$
(36b)
$${\mathbb{F}} = {\mathbf{E}}^{{\text{T}}} \left( {{\mathbf{I}}_{5} { \circledast }r \circ s} \right){\mathbf{F}}_{1} + {\mathbf{E}}_{{\mathbf{n}}}^{{\text{T}}} \left( {{\mathbf{I}}_{3} { \circledast }r \circ s} \right){\mathbf{F}}_{2}$$
(36c)
$${\mathbb{M}} = \left( {{\mathbf{I}}_{3} { \circledast }r \circ s} \right){\mathbf{I}}_{{\text{K}}}$$
(36d)

4 Results and discussion

In this section, comprehensive studies are presented to investigate the nonlinear large-amplitude hygrothermally induced vibrations of FG porous circular thin plates under simply-supported and clamped boundary conditions. The metal constituent is considered as stainless steel (\(\mathrm{SUS}304\)), and the ceramic constituent is chosen as Silicon Nitride (\({\mathrm{Si}}_{3}{\mathrm{N}}_{4}\)). The temperature-dependent properties, as formerly introduced in Eq. (5), are given in Table 1. In this scrutiny, the maximum dimensionless lateral deflection of the thin circular plate is denoted by \(W\). Furthermore, the instantaneous hygrothermal shock is applied to the fully ceramic surface while the metal-rich surface is kept at the reference temperature \({T}_{0}=300 K\), unless otherwise stated.

Table 1 Temperature-dependent coefficients for metal \((\mathrm{SUS}304)\) and ceramic \(({\mathrm{Si}}_{3}{\mathrm{N}}_{4})\) [20]
Full size table

4.1 Convergence study

First, the convergence of the developed numerical approach is shown in Table 2. In this table, the maximum dimensionless lateral deflection of a simply-supported circular plate made of FGM-I with \(a=80\mathrm{ mm}\), \(h=1\mathrm{ mm}\), \({k}_{w}={k}_{g}=\Delta C=0\), \(\xi =0.2\), \(\zeta =1\) and \({T}_{T}=310 K\) is computed for various values of \({N}_{r}\). The converging trend of results with increasing \({N}_{r}\) is seen in the table. According to Table 2, \({N}_{r}=19\) is selected for generating the rest of the results.

Table 2 Convergence study
Full size table

4.2 Validation study

For validation, Fig. 2 is given in which the maximum dimensionless lateral deflection is plotted versus time for a simply-supported FGM circular plate considering \(a=80\mathrm{ mm}\), \(h=1\mathrm{ mm}\), \({k}_{w}={k}_{g}=\Delta C= \xi =0\), \(\zeta =1\), \({T}_{T}=310\mathrm{ K}\), and the present results are compared with those reported by Kiani and Eslami [42] which were obtained using the conventional multi-term Ritz method. The effects of porosity, moisture and elastic foundation are neglected in producing the results of Fig. 2. One can find excellent agreement between two sets of results which shows the validity of the developed numerical approach.

Fig. 2
figure 2

Temporal evolution of dimensionless maximum lateral deflection of a simply-supported FGM circular plate predicted based on the present approach and obtained in [42]

Full size image

4.3 Parametric studies

In Fig. 3, the temporal evolution of \(W/h\) of a clamped FGM-I (First type of porosity) circular plate is indicated for \(\zeta =\mathrm{0,1},3\) to illustrate the effect of the FG index on the vibrational behavior. In this case, \(a=80\mathrm{ mm}\), \(h=1\mathrm{ mm}\), \({k}_{w}={k}_{g}=\Delta C= 0\), \(\xi =0.2\), \({T}_{T}=350 K\), \({T}_{B}=320 K\) are considered. The results reveal that the maximum dimensionless deflection of the circular plate increases as the FG index enlarges. It can be explained by the fact that increasing \(\zeta\) results in increasing the volume fraction of the metal phase in the FGM. It is also concluded that in the case of a circular plate with a high FG index, the edge support cannot handle the induced external moment, and consequently, the vibrations start earlier than the plate with a low FG index. Similar results are presented in Fig. 4 for simply-supported boundary conditions and \(a=100\mathrm{ mm}\), \(h=1\mathrm{ mm}\), \(\Delta C= 0\), \({k}_{w}=5\times {10}^{4}\), \({k}_{g}=5\times {10}^{3}\), \(\xi =0.2\), \({T}_{T}=310 K\). Also, both distribution types for porosity (FGM-I: even distribution and FGM-II: uneven distribution) are considered in Fig. 4.

Fig. 3
figure 3

Temporal evolution of dimensionless maximum lateral deflection of a clamped FGM-I circular plate for various values of FG index

Full size image
Fig. 4
figure 4

Temporal evolution of dimensionless maximum lateral deflection of a simply-supported circular plate for various values of FG index according to both types of porosity distributions

Full size image

The influence of porosity volume fraction (\(\xi\)) on the thermally-induced nonlinear vibration response of a simply-supported circular plate with \(a=100\mathrm{ mm}\), \(h=1\mathrm{ mm}\), \(\zeta =2\), \(\Delta C={k}_{w}={k}_{g}= 0\), \({T}_{T}=310 K\) is highlighted in Fig. 5. The results of this figure are obtained for both types of porosity distribution. It is seen that increasing the porosity volume fraction has a decreasing effect on the deflection of the plate. Furthermore, the frequency of vibrations decreases as the porosities are considered within the structure.

Fig. 5
figure 5

Temporal evolution of dimensionless maximum lateral deflection of a simply-supported circular plate for various values of porosity volume fraction according to both types of porosity distributions

Full size image

In order to investigate the effect of hygroscopic force on the hygrothermally-induced vibrations of the plate, the temporal evolution of dimensionless maximum lateral deflection of a simply-supported circular plate considering \(a=100\mathrm{ mm}\), \(h=1\mathrm{ mm}\), \(\zeta =1\), \(\xi =0.1\), \({k}_{w}=5\times {10}^{4}, {k}_{g}=5\times {10}^{3}\), \({\gamma }_{H}=2\), \({T}_{T}=310 K\) is represented in Fig. 6 for various values of difference in moisture concentration between the top and bottom surfaces \((\Delta C)\). It is seen that, at a given value time, increasing the difference in moisture concentration leads to increasing the amplitude of vibration.

Fig. 6
figure 6

Temporal evolution of dimensionless maximum lateral deflection of a simply-supported circular plate for various values of moisture concentration difference according to both types of porosity distributions

Full size image

Finally, the effect of the elastic foundation is shown in Fig. 7, in which the temporal evolution of \(W/h\) is given for different values of \({k}_{g}\) and \({k}_{w}\) according to FGM-I and FGM-II. In this case, \(a=100\mathrm{ mm}\), \(h=1\mathrm{ mm}\), \(\zeta =2\), \(\xi =0.1\), \({T}_{T}=320 K\). As expected, the maximum lateral deflection decreases with increasing the parameters of the Winkler-Pasternak model.

Fig. 7
figure 7

Temporal evolution of dimensionless maximum lateral deflection of a simply-supported circular plate for various values of elastic foundation parameters according to both types of porosity distributions

Full size image

5 Conclusion

In this article, the hygrothermally-induced vibration of FG porous circular plates was investigated by applying the VDQ method. The temperature-dependence of material properties, Winkler-Pasternak foundation, hygroscopic stresses, geometrical nonlinearity and the porosities scattered over the structure’s thickness were all taken into account. The heat conduction equation was established through the thickness direction of the thin plate and solved numerically using the GDQ and beta-Newmark methods to obtain the temperature history. In addition, considering the first-order shear deformation theory and the von-Kármán geometrical nonlinearity assumption, the equations of motion were obtained by applying Hamilton’s principle, and, solved numerically using the VDQ method in conjunction with the beta-Newmark time integration scheme and an iterative algorithm, afterward. The convergence of the results was examined, and a validation study was conducted to ensure the validity of the present approach. The effects of porosity distribution, FG index, moisture concentration, Winkler-Pasternak parameters and temperature elevation were investigated on the maximum lateral deflection of the thin plate. The main conclusions of the present work are.

  • The VDQ method, which is applied to the weak form of the equations, yields accurate results for the hygrothermally-induced vibrations phenomena considering compact vector–matrix formulation which could be easily employed in the coding process. In addition, this method can be extended and effectively employed in order to directly discretize the energy functional in mechanical systems where the derivation of the strong form of equations is challenging.

  • Increasing FG index causes higher lateral deflection for the circular plate, and in the case of clamped boundary conditions, an earlier excitation additionally.

  • The increase in the porosity index decreases lateral deflection for both types of porosity distributions, but the drop is more prominent for even porosities.

  • The FG circular plates resting on an elastic foundation exhibit slighter lateral deflections under the same circumstances compared to not embedding the plate in the foundation.

  • By applying the additional hygroscopic load, the amplitude of the vibrations will increase, consequently.