1 Introduction

Vibrations of plates or panels with geometric discontinuities such as internal cutouts are widely encountered problems in various fields of engineering and technology. Cutouts of various shapes are often created in structural components due to many practical requirements such as lightening the structure, venting, changing the structural resonant frequency, and inspection/access ports. Vibration analysis of such structures can form the basis for damage detection, structural parameter identification, and vibration control. Most research works performed over the past few decades have focused on vibrations of circular plates with centrally or eccentrically located internal cutouts of various shapes. Analytical solutions can readily be attained only when the outer and inner boundaries are concentric circles or confocal ellipses [1–3]. When the boundaries are eccentric or of some other shape, a wide range of approximate methods such as the perturbation techniques, finite difference method, the Rayleigh–Ritz method, the finite element method, the boundary element method, the boundary integral equation method, the differential quadrature method, as well as experimental techniques, have been employed by numerous researchers to treat the problem. For example, Nayfeh et al. [4] presented an approximate perturbation procedure (i.e., the method of strained parameters) to determine the natural frequencies and mode shapes of nearly annular and circular plates clamped on both the inner and outer boundaries. Nagaya [5] developed an analytical solution for computation of the natural frequencies of an eccentric annulus having a clamped inner edge and a free outer edge, and made validations against experimental results. Rajamani and Prabakaran [6, 7] analyzed the free and forced dynamic response of simply-supported generally orthotropic square plates with centrally located square cut-outs. Eastep and Hemmig [8] adopted an approximate perturbation method for estimating the natural frequencies of slightly non-circular (elliptic) plates with free-edge circular cutouts. Khurasia and Rawtani [9] used the finite-element method to examine the effect of variation in circular cutout eccentricity on the natural frequencies and vibration modes of annular-like plates. Lin [10] presented an exact analytical methodology, based on the transformation of cylindrical Bessel functions, for calculating the free transverse vibrations of uniform thin circular plates with eccentric holes. Huang and Wang [11] applied the finite strip and receptance methods to investigate the modal characteristics of an elliptical or a square plate with a central elliptical hole or a symmetrically located slit. Ramakrishna et al. [12] used the hybrid stress finite elements to perform free vibration analysis of laminates with elliptical cutouts. The effects of parameters like fibre orientation, width to thickness ratio, hole size and major to minor axis ratio were studied. Chen and Zhou [13] used the boundary element approach to illustrate the low-frequency mode shapes of a small disc with eccentric holes. The effect of splitting of doublet frequencies on the vibration modes of the eccentric structure was investigated. Parker and Mote Jr. [14] presented a perturbation solution for analytical determination of the eigensolutions of nearly annular or circular plates. The eigensolutions of an elliptical plate were calculated and compared against finite element analysis. Also, splitting of degenerate eigenvalues of the unperturbed problem, due to geometric asymmetry in the perturbed problem, was identified. Chakraverty et al. [15] used boundary characteristic orthogonal polynomials (BCOPs) as trial functions in the Rayleigh–Ritz method to investigate free vibration of isotropic annular elliptical plates for various combinations of edge conditions. Laura et al. [16, 17] applied the Rayleigh–Ritz variational method for free vibration analysis of an elliptical plate with a central circular hole as well as a circular plate with an eccentric circular hole. Cheng et al. [18] employed numerical (FEM-Nastran) and experimental (modal testing) approaches for free vibration analysis of an annular plate with a slightly eccentric hole. Zhong and Yu [19] used a variational-based differential quadrature method to study the free flexural vibrations of an eccentric annular Mindlin plate with typical combinations of inner and outer boundary conditions. Laura and Avalos [20] applied the Rayleigh–Ritz method to calculate the first four frequency coefficients for free transverse vibrations of circular plates with an eccentric rectangular perforation that is elastically restrained against rotation and translation. Nallim and Grossi [21] used Rayleigh–Ritz method to present a free vibration analysis of symmetrically laminated cross-ply and angle-ply annular elliptic plates for different aspect ratios and boundary conditions. Houmat [22] employed a new polynomially enriched sector elliptic p-element to investigate the nonlinear free vibration of a thick laminated composite annular elliptical plate with elliptically orthotropic plies. Recently, in a series of papers, Lee and coworkers [23–26] adopted semi-analytical approaches based on the indirect boundary integral equation (BIEM), the null field integral equation, and the multipole Trefftz methods, in conjunction with the addition theorem for cylindrical Bessel functions and complex Fourier series, to investigate the free vibrations of circular plates with multiple circular holes.

The above review clearly indicates that, while there exists a notable body of literature investigating the free vibrational characteristics of elastic circular plates with concentric/eccentric circular cutouts, there appears to be no rigorous analysis on the vibrations of elliptical plates with single or multiple eccentric circular or elliptical cutouts of arbitrary location/orientation. The primary purpose of the current work is to take advantage of the powerful collocation multipole method to fill this important gap. Excellent accuracy, fast rate of convergence, and high computational efficiency are the key features of the adopted method [27]. Also, fictitious or spurious eigensolutions, which normally stem from non-uniqueness of solutions when using the classical boundary element, boundary integral equation, or boundary collocation methods (BEM, BIEM, BCM) for solving structural dynamic problems in multiply-connected domains [23, 26, 28, 29], are well known not to be generated in the presently adopted “collocation multipole” method [27]. In particular, numerous recent numerical experiments [25, 27, 30, 31] demonstrate the lack of spurious eigen-values essentially due to the completeness and uniqueness of adopted solution representations in the latter approach. This task is achieved by application of the classical method of separation of variables and utilization of a complete basis in terms of products of the radial and angular Mathieu functions in the present multiply-connected domain problem. The proposed semi-analytic model is of both academic and technical interest basically due to its inherent value as a canonical problem in structural dynamics. It can also be valuable for general dynamic analysis of perforated elliptical panels in a wide variety of engineering applications [32–37]. Furthermore, the presented set of highly accurate converged solutions can provide useful information for structural designers and engineers, serving as a benchmark for verification of solutions obtained by other numerical or asymptotic approaches [38–40].

2 Basic equations and the general solutions

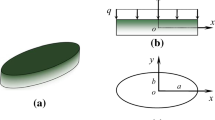
The basic elliptical coordinate system used is depicted in Fig. 1a. The foci of the ellipse are located at (x=±c, y=0), where the foci ±c are given by c 2=a 2−b 2. The elliptic coordinates (ξ,η) are defined according to the transformation x+iy=ccosh(ξ+iη) such that x=ccoshξcosη, y=csinhξsinη, z=z, and \(\mathrm{i} = \sqrt{-1}\), where ξ≥0 works as a radial coordinate, the coordinate 0≤η<2π is an angular coordinate, and the orthogonally intersecting confocal ellipses “ξ=constant” and hyperbolas “η=constant” are illustrated in Fig. 1a. In addition, the boundary of the elliptic plate can be initially represented by ξ=ξ 0 with the semi-major axis, a=ccoshξ 0 and the semi-minor axis, b=csinhξ 0. Here, we note that as ξ 0→0, the elliptical boundary degenerates to a strip of length “2c” joining the two foci, which is henceforth referred to as the “inter-focal distance.” Also, if “c” tends to zero, assuming \(r= \sqrt{x ^{2} + y ^{2}}\) to remain constant, then ξ tends to infinity, the foci coalesce at the origin, and the transition to the circular case of radius r occurs.

Fig. 1a
figure 1

Basic elliptical coordinate system

Full size image

According to the classical small-deflection theory, the differential equation of motion governing the transverse displacement response of a thin elastic elliptical plate of mass density ρ, thickness h, Young’s modulus E, and Poisson’s ratio υ, subjected to an arbitrarily distributed time-dependent transverse external force per unit area f(ξ,η,t), is written as [41]:

$$ \begin{array}{l} D \nabla ^{4} w +\rho h \displaystyle\frac{\partial ^{2} w}{\partial t ^{2}} =f ( \xi, \eta,t ),\\ w ( \xi, \eta,0 ) = w _{0} ( \xi, \eta ),\\ \partial w ( \xi, \eta,0 ) / \partial t= v _{0} ( \xi, \eta ), \end{array} $$
(1)

where ∇4 is the classical biharmonic operator, w is the flexural displacement, t is the time, D=Eh 3/12(1−υ 2) is the flexural rigidity of the plate, and (w 0,v 0) are the problem initial conditions. Considering the free vibration problem, one generally assumes time harmonic displacement variations, w(ξ,η,t)=W(ξ,η,ω)sinωt, and in the absence of the forcing function (f=0), Eq. (1) becomes [41]:

$$ \nabla ^{4} W- k ^{4} W=0, $$
(2)

where k 4=ρhω 2/D. The above equation can favorably be factored in the form

$$ \bigl(\nabla ^{2} + k ^{2} \bigr) \bigl(\nabla^{2} - k ^{2} \bigr)W=0. $$
(3)

The general solution of (3) may be written as W=W 1+W 2, where W 1 and W 2 satisfy

$$\begin{aligned} &{\nabla ^{2} W _{1} + k ^{2} W _{1} =0,} \end{aligned}$$
(4a)
$$\begin{aligned} &{\nabla ^{2} W _{2} - k ^{2} W _{2} =0,} \end{aligned}$$
(4b)

which are explicitly expanded in the elliptical coordinates as [42].

$$\begin{aligned} &{\biggl( \frac{\partial ^{2} W _{i}}{\partial\xi ^{2}} + \frac{\partial ^{2} W _{i}}{\partial\eta ^{2}} \biggr) + 2 q _{i} ( \cosh 2 \xi- \cos 2\eta ) W _{i} =0,} \\ \end{aligned}$$
(5)

where i=1,2 and \(q _{1} = \frac{c ^{2}}{4} \sqrt{\rho h \omega ^{2} /D}\), \(q _{2} = - \frac{c ^{2}}{ 4} \sqrt{\rho h \omega ^{2} /D}\). By using separation of variables, W i (ξ,η)=R i (ξ)Θ i (η), in Eq. (5) one obtains the following radial and angular Mathieu equations

$$ \begin{array}{l} \displaystyle\frac{\mathrm{d} ^{2} R _{i} ( \xi )}{\mathrm{d} \xi ^{2}} - ( \lambda _{i} -2 q _{i} \cosh 2\xi ) R _{i} ( \xi ) =0,\\ \displaystyle\frac{\mathrm{d} ^{2} \varTheta _{i} ( \eta )}{\mathrm{d} \eta ^{2}} + ( \lambda _{i} -2 q _{i} \cos 2\eta ) \varTheta _{i} ( \eta ) =0, \end{array} $$
(6)

where i=1,2; and λ i are separation constants. Thus, the solutions of the Helmholtz Eqs. (5) in the elliptical coordinates can be written in the separated form [43]

$$\begin{aligned} &{R _{m} ^{(i)} ( \xi ) \varTheta _{m} ^{(i)} ( \eta )} \\&{\quad = \left \{ \begin{array}{l@{\quad}l} Mc _{m} ^{(j)} ( \xi, q _{i} ) ce _{m} ( \eta, q _{i} ), & m=0,1,2,\dots,\\ Ms _{m} ^{(j)} ( \xi, q _{i} ) se _{m} ( \eta, q _{i} ), & m=1,2,3,\dots, \end{array} \right .} \end{aligned}$$
(7)

where i,j=1,2.

Now, as the products \(Ms _{m} ^{(2)} ( \xi, q _{i} ) se _{m} ( \eta, q _{i} )\) (i=1,2) do not satisfy the function continuity, and the products \(Mc _{m} ^{(2)} ( \xi, q _{i} ) ce _{m} ( \eta, q _{i} )\) do not satisfy the continuity in gradient across the inter-focal line [27, 44], the permissible general solutions of Eq. (2) in the interior and exterior domains of the elliptical boundary are respectively written as

$$\begin{aligned} \begin{array}{l} W ^{\mathrm{in}} ( \xi,\eta ) = \displaystyle\sum_{m=0}^{\infty} \bigl[ a _{m} Mc _{m} ^{ ( 1 )} ( \xi, q _{1} ) ce _{m} ( \eta, q _{1} )\\ \hphantom{W ^{\mathrm{in}} ( \xi,\eta ) =} {} + b _{m} Mc _{m} ^{ ( 1 )} ( \xi, q _{2} ) ce _{m} ( \eta, q _{2} ) \bigr]\\ \hphantom{W ^{\mathrm{in}} ( \xi,\eta ) =} {}+ \displaystyle\sum_{m=1}^{\infty} \bigl[ c _{m} M s _{m} ^{ ( 1 )}(\xi, q _{1}) se _{m} ( \eta, q _{1} )\\ \hphantom{W ^{\mathrm{in}} ( \xi,\eta ) =} {} + d _{m} M s _{m}^{(1)}(\xi,q_{2})se_{m}(\eta,q_{2})\bigr], \\ W ^{\mathrm{ex}} ( \xi,\eta ) = \displaystyle\sum_{m=0} ^{\infty} \bigl[ a _{m} Mc _{m} ^{ ( 2 )} ( \xi, q _{1} ) ce _{m} ( \eta, q _{1} )\\ \hphantom{W ^{\mathrm{ex}} ( \xi,\eta ) =} {} + b _{m} Mc _{m} ^{ ( 2 )} ( \xi, q _{2} ) ce _{m} ( \eta, q _{2} ) \bigr]\\ \hphantom{W ^{\mathrm{ex}} ( \xi,\eta ) =} {}+ \displaystyle\sum_{m=1} ^{\infty} \bigl[ c _{m} M s _{m} ^{ ( 2 )} ( \xi, q _{1} ) se _{m} ( \eta, q _{1} )\\ \hphantom{W ^{\mathrm{ex}} ( \xi,\eta ) =} {} + d _{m} M s _{m} ^{ ( 2 )} ( \xi, q _{2} ) se _{m} ( \eta, q _{2} ) \bigr]. \end{array} \end{aligned}$$
(8)

3 The collocation multipole method

At this point we consider a two-dimensional domain Ω of the elliptical plate which is enclosed with the boundary, \(B= \bigcup _{j=1} ^{L} B _{j}\), (j=1,2,…,L), including L−1 non overlapping elliptical cut-outs, as shown in Fig. 1b, where O j and B j (j=2,…,L) denote the center of the j-th elliptical cutout and its boundary, and O 1 is the center of the elliptical plate (outer ellipse). Here, we shall employ L+1 observer coordinate systems: where (z 1,z 2) is a global Cartesian coordinate system positioned at point O, and (ξ j , η j ) is the j-th (j=1,2,…,L) local elliptical coordinate system centered at O j with global Cartesian coordinates (\(z _{1} ^{j},\ z _{2} ^{j}\)). Also, a j and b j are the major and minor semi axes of j-th ellipse, respectively, where its associated local coordinate system makes an angle θ j with respect to the global coordinate system. Moreover, the multiply connected elliptical plate problem can be decomposed into one interior domain problem and L−1 exterior domain problems. Thus, utilizing the general solutions (8), the displacement function satisfying Eq. (2) can be explicitly expressed as an infinite sum of multipoles at the center of each ellipse in the form [27]

$$\begin{aligned} &{W ( \xi _{1}, \eta _{1}, \xi _{2}, \eta _{2},\dots, \xi _{L}, \eta _{L} )} \\&{\quad = a _{0} ^{1} Mc _{0} ^{(1)} ( \xi _{1}, q _{1} ) ce _{0} ( \eta _{1}, q _{1} )} \\&{\qquad{} {} + b _{0} ^{1} Mc _{0} ^{(1)} ( \xi _{1}, q _{2} ) ce _{0} ( \eta _{1}, q _{2} )} \\&{\qquad {} + \sum_{m=1} ^{\infty} \bigl[ a _{m} ^{1} Mc _{m} ^{ ( 1 )} ( \xi _{1}, q _{1} ) ce _{m} ( \eta _{1}, q _{1} )} \\&{\qquad {} + b _{m} ^{1} Mc _{m} ^{ ( 1 )} ( \xi _{1}, q _{2} ) ce _{m} ( \eta _{1}, q _{2} )} \\&{\qquad {} + c _{m} ^{1} Ms _{m} ^{ ( 1 )} ( \xi _{1}, q _{1} ) se _{m} ( \eta _{1}, q _{1} )} \\&{\qquad {}+ d _{m} ^{1} Ms _{m} ^{ ( 1 )} ( \xi _{1}, q _{2} ) se _{m} ( \eta _{1}, q _{2} ) \bigr]} \\&{\qquad {} + \sum_{j=2} ^{L} \Biggl\{ a _{0} ^{j} Mc _{0} ^{(2)} ( \xi _{j}, q _{1} ) ce _{0} ( \eta _{j}, q _{1} )} \\&{\qquad{} + b _{0} ^{j} Mc _{0} ^{(2)} ( \xi _{j}, q _{2} ) ce _{0} ( \eta _{j}, q _{2} )} \\&{\qquad {} + \sum_{m=1} ^{\infty} \bigl[ a _{m} ^{j} Mc _{m} ^{ ( 2 )} ( \xi _{j}, q _{1} ) ce _{m} ( \eta _{j}, q _{1} )} \\&{\qquad{} + b _{m} ^{j} Mc _{m} ^{ ( 2 )} ( \xi _{j}, q _{2} ) ce _{m} ( \eta _{j}, q _{2} )} \\&{\qquad {} + c _{m} ^{j} Ms _{m} ^{ ( 2 )} ( \xi _{j}, q _{1} ) se _{m} ( \eta _{j}, q _{1} )} \\&{\qquad {}+ d _{m} ^{j} Ms _{m} ^{ ( 2 )} ( \xi _{j}, q _{2} ) se _{m} ( \eta _{j}, q _{2} ) \bigr] \Biggr\}.} \end{aligned}$$
(9)

The coefficients \(a _{m} ^{j}\) through \(d _{m} ^{j}\) (j=1,2,…,L) can be determined by matching the boundary conditions on each elliptical boundary as follows. Assuming clamped boundary conditions on the g-th elliptical boundary require the corresponding displacements and slopes to vanish, i.e.,

$$\begin{aligned} &{W ( \xi _{g}, \eta _{g} ) =0,\qquad \frac{\partial W}{\partial n} ( \xi _{g}, \eta _{g} ) =0,} \\&{\quad (g=1,\dots, L).} \end{aligned}$$
(10)

In this work, in order to avoid the complications of the classical addition theorem approach, we shall adopt the collocation method to calculate Eq. (9) directly in each local elliptical coordinate system. This will involve determination of elliptical coordinates and evaluation of the normal derivative of Mathieu functions with respect to different local coordinate systems. By uniformly collocating N=(2M+1) points on each elliptical boundary and truncating the infinite series of Eq. (9), one obtains

$$\begin{aligned} &{W \bigl( \xi _{1} ^{gn}, \eta _{1} ^{gn}, \xi _{2} ^{gn}, \eta _{2} ^{gn},\dots, \xi _{L} ^{gn}, \eta _{L} ^{gn} \bigr)} \\&{\quad = a _{0} ^{1} Mc _{0} ^{(1)} \bigl( \xi _{1} ^{gn}, q _{1} \bigr) ce _{0} \bigl( \eta _{1} ^{gn}, q _{1} \bigr)} \\&{\qquad{} {} + b _{0} ^{1} Mc _{0} ^{(1)} \bigl( \xi _{1} ^{gn}, q _{2} \bigr) ce _{0} \bigl( \eta _{1} ^{gn}, q _{2} \bigr)} \\&{\qquad {} + \sum_{m=1} ^{M} \bigl[ a _{m} ^{1} Mc _{m} ^{ ( 1 )} \bigl( \xi _{1} ^{gn}, q _{1} \bigr) ce _{m} ( \eta _{1}, q _{1} )} \\&{\qquad {} + b _{m} ^{1} Mc _{m} ^{ ( 1 )} \bigl( \xi _{1} ^{gn}, q _{2} \bigr) ce _{m} \bigl( \eta _{1} ^{gn}, q _{2} \bigr)} \\&{\qquad{} + c _{m} ^{1} Ms _{m} ^{ ( 1 )} \bigl( \xi _{1} ^{gn}, q _{1} \bigr) se _{m} \bigl( \eta _{1} ^{gn}, q _{1} \bigr)} \\&{\qquad {} + d _{m} ^{1} Ms _{m} ^{ ( 1 )} \bigl( \xi _{1} ^{gn}, q _{2} \bigr) se _{m} \bigl( \eta _{1} ^{gn}, q _{2} \bigr) \bigr]} \\&{\qquad{} {} + \sum _{j=2} ^{L} \Biggl\{ a _{0} ^{j} Mc _{0} ^{(2)} \bigl( \xi _{j} ^{gn}, q _{1} \bigr) ce _{0} \bigl( \eta _{j} ^{gn}, q _{1} \bigr)} \\&{\qquad{} {} + b _{0} ^{j} Mc _{0} ^{(2)} \bigl( \xi _{j} ^{gn}, q _{2} \bigr) ce _{0} \bigl( \eta _{j} ^{gn}, q _{2} \bigr)} \\&{\qquad{} {} + \sum _{m=1} ^{M} \bigl[ a _{m} ^{j} Mc _{m} ^{ ( 2 )} \bigl( \xi _{j} ^{gn}, q _{1} \bigr) ce _{m} \bigl( \eta _{j} ^{gn}, q _{1} \bigr)} \\&{\qquad{} {} + b _{m} ^{j} Mc _{m} ^{ ( 2 )} \bigl( \xi _{j} ^{gn}, q _{2} \bigr) ce _{m} \bigl( \eta _{j} ^{gn}, q _{2} \bigr)} \\&{\qquad{} {} + c _{m} ^{j} Ms _{m} ^{ ( 2 )} \bigl( \xi _{j} ^{gn}, q _{1} \bigr) se _{m} \bigl( \eta _{j} ^{gn}, q _{1} \bigr)} \\&{\qquad{} {} + d _{m} ^{j} Ms _{m} ^{ ( 2 )} \bigl( \xi _{j} ^{gn}, q _{2} \bigr) se _{m} \bigl( \eta _{j} ^{gn}, q _{2} \bigr) \bigr] \Biggr\}} \end{aligned}$$
(11)

for g=1,2,3,…,L and n=1,2,3,…,N, where (\(\xi _{j} ^{gn}\), \(\eta _{j} ^{gn}\)), as depicted in Fig. 1c, refers to the elliptical coordinates of the n-th collocation point on the g-th elliptical boundary with respect to the j-th local elliptical coordinate system. Consequently, one arrives at a linear algebraic system of 2LN equation which can advantageously be written in the general Ab=0 matrix form:

$$ \left [ \begin{array}{c@{\quad}c@{\quad}c} \begin{array}{c@{\quad}c} \mathbf{A} ^{11} & \mathbf{A} ^{12}\\\mathbf{A} ^{21} & \mathbf{A} ^{22} \end{array} & \cdots & \begin{array}{c} \mathbf{A} ^{1L}\\\mathbf{A} ^{2L} \end{array} \\\vdots & \ddots & \vdots \\\begin{array}{c@{\quad}c} \mathbf{A} ^{L1} & \mathbf{A} ^{L2} \end{array} & \cdots & \mathbf{A} ^{LL} \end{array} \right ] \left \{ \begin{array}{c} \begin{array}{c} \mathbf{b} ^{1}\\\mathbf{b} ^{2} \end{array} \\\begin{array}{c} \vdots\\\mathbf{b} ^{L} \end{array} \end{array} \right \} = \left \{ \begin{array}{c} 0\\\begin{array}{c} 0\\\begin{array}{c} \vdots\\0 \end{array} \end{array} \end{array} \right \}, $$
(12)

where \(\mathbf{b} ^{j} = \{ \begin{array}{c@{\ }c@{\ }c} a _{0} ^{j} & b _{0} ^{j} & \begin{array}{c@{\ }c@{\ }c} a _{1} ^{j} & b _{1} ^{j} & \begin{array}{c@{\ }c@{\ }c} c _{1} ^{j} & d _{1} ^{j} & \begin{array}{c@{\ }c@{\ }c} \dots & a _{M} ^{j} & \begin{array}{c@{\ }c@{\ }c} b _{M} ^{j} & c _{M} ^{j} & d _{M} ^{j} \end{array} \end{array} \end{array} \end{array} \end{array} \!\!\!\!\}^{T}\) is the unknown coefficient vector, and the explicit expression for the A gj sub-matrices are provided in the Appendix.

Fig. 1b
figure 2

General problem geometry

Full size image
Fig. 1c
figure 3

Coordinate transformation and the collocation points

Full size image

In order to calculate the submatrices A gj in Eq. (12), one should first determine the elliptical coordinates (\(\xi _{j} ^{gn}\), \(\eta _{j} ^{gn}\)), n=1,2,…,N, of the collocation point with respect to each local elliptical coordinate system. When g=j, elliptical coordinates, (\(\xi _{g} ^{gn}\), \(\eta _{g} ^{gn}\)), can be easily determined, being uniformly distributed along the elliptical boundary. On the other hand, when g≠j, elliptical coordinates (\(\xi _{j} ^{gn}\), \(\eta _{j} ^{gn}\)) can be determined from (\(\xi _{g} ^{gn}\), \(\eta _{g} ^{gn}\)) through the transformation between two local elliptical systems. Accordingly, the rectangular coordinates in the g-th coordinate system are first determined from the elliptical coordinates in the form \(x _{g} ^{gn} + \mathrm{i} y _{g} ^{gn} =c \cosh ( \xi _{g} ^{gn} + \mathrm{i} \eta _{g} ^{gn} )\) (see Fig. 1c). Subsequently, the rectangular coordinates in the j-th local system can be transformed from the g-th local rectangular coordinate system by

$$\begin{aligned} &{\left \{ \begin{array}{l} x _{j} ^{gn}\\ y _{j} ^{gn} \end{array} \right \} = \mathbf{R} ( -\theta _{j} ) \left \{ \left\{ \begin{array}{l} z _{1} ^{g}\\ z _{2} ^{g} \end{array} \right\} - \left\{ \begin{array}{l} z _{1} ^{j}\\ z _{2} ^{j} \end{array} \right\} + \mathbf{R} ( \theta _{g} ) \left\{ \begin{array}{l} x _{g} ^{gn}\\ y _{g} ^{gn} \end{array} \right\} \right \},} \\ \end{aligned}$$
(13)

where \(\mathbf{ R}( \theta ) = \big[ \begin{array}{c@{\ }c} \scriptstyle \cos \theta & \scriptstyle \sin \theta\\ \scriptstyle -\sin \theta & \scriptstyle \cos \theta \end{array} \big]\). Lastly, the elliptical coordinates with respect to the j-th elliptical coordinate system are determined through the simple relation \(\xi _{j} ^{gn} + \mathrm{i} \eta _{j} ^{gn} = \cosh ^{-1} [ ( x _{j} ^{gn} + \mathrm{i} y _{j} ^{gn} ) /c ]\). This way, one can readily resolve the elliptical coordinates of collocation points with respect to any local elliptical coordinate system. Also, one needs to evaluate the terms which involve the gradient operator in the sub-matrice A gj (g,j=1,2,3,…,L). In particular, when g=j, the field point on the boundary of an ellipse can be described by its local elliptical coordinate system, and the normal derivative can be simply expressed by ∂/∂ξ. Consequently, the gradient terms at the n-th collocation point on the g-th boundary \(( \xi _{g} ^{gn}, \eta _{g} ^{gn} )\) are written as

$$ \begin{array}{l} \displaystyle\frac{\partial}{\partial n} \bigl[ Mc _{m} ^{(j)} ( \xi, q _{i} ) ce _{m} ( \eta, q _{i} ) \bigr]\\ \quad = ce _{m} ( \eta, q _{i} ) \displaystyle\frac{\partial Mc _{m} ^{(j)} ( \xi, q _{i} )}{h _{\xi} \partial\xi}\bigg|_{\xi= \xi_g ^{gn},\eta= \eta_g ^{gn}},\\ \displaystyle\frac{\partial}{\partial n} \bigl[ Ms _{m} ^{(j)} ( \xi, q _{i} ) se _{m} ( \eta, q _{i} ) \bigr]\\ \quad = se _{m} ( \eta, q _{i} ) \displaystyle\frac{\partial Ms _{m} ^{(j)} ( \xi, q _{i} )}{h _{\xi} \partial\xi}\bigg|_{\xi= \xi_g ^{gn},\eta= \eta_g ^{gn}}, \end{array} $$
(14)

where i,j=1,2, and \(h _{\xi} =\mathrm{c}\ \sqrt{(\cosh 2 \xi- \cos 2\eta)/2}\). On the other hand, when g≠j, the gradient term can be obtained by utilization of the definition of a directional derivative. Accordingly, the derivative normal to the g-th boundary with respect to the j-th local elliptical coordinate system can be found as described below. First, one should consider the mathematical relationship [45]

$$\begin{aligned} \frac{\partial S}{\partial n} =& \boldsymbol{\nabla} S\boldsymbol{\cdot} \boldsymbol{n} = \left [ \begin{array}{c@{\quad}c} \displaystyle\frac{\partial S}{h _{\xi} \partial\xi} & \displaystyle\frac{\partial S}{h _{\eta} \partial\eta} \end{array} \right ] \left [ \begin{array}{l} \cos \delta\\\sin \delta \end{array} \right ] \\=& \biggl( \frac{\partial S}{h _{\xi} \partial\xi} \biggr) \cos \delta + \biggl( \frac{\partial S}{h _{\eta} \partial\eta} \biggr) \sin \delta, \end{aligned}$$
(15)

where S may be any of the Mathieu product functions \(Mc _{m} ^{ ( j )} ( \xi, q _{i} ) ce _{m} ( \eta, q _{i} )\), \(Ms _{m} ^{ ( j )} ( \xi, q _{i} ) se _{m} ( \eta, q _{i} )\), \(h _{\xi} = h _{\eta} =c \sqrt{ ( \cosh 2 \xi- \cos 2\eta ) /2}\), and \(\delta= \varphi _{j} ^{gn} - \psi _{j} ^{gn}\), in which \(\psi _{j} ^{gn} = \tan ^{-1} ( \tan \eta _{j} ^{gn} / \tanh \xi _{j} ^{gn} )\) is the angle of the unit vector normal to the “ξ=constant” curves, \(\boldsymbol{u} _{\xi_{j}}\), as depicted in Fig. 1c, \(\varphi _{j} ^{gn} = \varphi _{g} ^{gn} + \theta _{g} - \theta _{j}\), in which \(\varphi _{g} ^{gn} = \tan ^{-1} ( \tan \eta _{g} ^{gn} / \tanh \xi _{g} ^{gn} )\), and θ g and θ j are orientation angles of the g-th and the j-th local coordinate system, respectively. Thus, by using (15), one can write the general expressions for the gradient terms at the n-th collocation point on the g-th boundary \(( \xi _{j} ^{gn}, \eta _{j} ^{gn} )\) as

$$ \begin{array}{l} \displaystyle\frac{\partial}{\partial n} \bigl[ Mc _{m} ^{ ( j )} ( \xi, q _{i} ) ce _{m} ( \eta, q _{i} ) \bigr]\\ \quad = ce _{m} ( \eta, q _{i} ) \displaystyle\frac{\partial Mc _{m} ^{ ( j )} ( \xi, q _{i} )}{h _{\xi} \partial\xi} \cos \delta \bigg|_{\xi= \xi_j ^{gn}, \eta= \eta_j ^{gn}}\\ \qquad{}+ Mc _{m} ^{(j)} ( \xi, q _{i} ) \displaystyle\frac{\partial ce _{m} ( \eta, q _{i} )}{h _{\eta} \partial\eta} \sin \delta \bigg|_{\xi= \xi_j ^{gn},\eta= \eta_j ^{gn}}\\ \displaystyle\frac{\partial}{\partial n} \bigl[ Ms _{m} ^{ ( j )} ( \xi, q _{i} ) se _{m} ( \eta, q _{i} ) \bigr]\\ \quad = se _{m} ( \eta, q _{i} ) \displaystyle\frac{\partial Ms _{m} ^{ ( j )} ( \xi, q _{i} )}{h _{\xi} \partial\xi} \cos \delta \bigg|_{\xi= \xi_j ^{gn},\eta= \eta_j ^{gn}}\\ \qquad {} + Ms _{m} ^{(j)} ( \xi, q _{i} ) \displaystyle\frac{\partial se _{m} ( \eta, q _{i} )}{h _{\eta} \partial\eta} \sin \delta \bigg|_{\xi= \xi_j ^{gn},\eta= \eta_j^{gn},} \end{array} $$
(16)

where i,j=1,2. Finally, the coupled algebraic linear system of Eqs. (12) can be solved for the nontrivial eigensolutions and the multipole expansion coefficients (eigenvectors). Once the eigenvalues are obtained, the associated mode shapes can be readily found by substituting the eigenvectors into the corresponding multipole expansion (9). This completes the necessary background required for the analysis of the problem. Next we consider some numerical examples.

4 Numerical examples

In order to illustrate the nature and general behavior of the solution, we consider some numerical examples in this section. Realizing the wide range of geometric parameters such as the plate/cutout aspect ratios (1≤a 1/b 1,…,a j /b j <∞), cutout orientation/location (e j ,α j ,θ j ;j=2,3,…,L) (see Fig. 1b), and number of cutouts (L−1), while keeping in mind the intense computations involved here, we shall not attempt an exhaustive presentation of numerical results and will therefore confine our attention to some particular examples. Accordingly, thin elliptical aluminum plates (ν=0.3, ρ=2700 kg/m3, E=7×1010 N/m2, h=0.005 m) with single or double elliptical cutouts (L=2,3) of selected geometric parameters (a 1/b 1, a 2/b 2, a 3/b 3=1,2; b 1=1 m; b 2,b 3=0.25 m) are considered. The cutout position is assumed to vary from the plate center along the positive x-axis (α 2,α 3=0∘), y-axis (α 2,α 3=90∘), or along the x/y-plane bisector (α 2,α 3=45∘). In particular, three different cutout orientations (θ 2,θ 3=0,45,90∘) at three distinct locations (\(\overline{e} _{2}\), \(\overline{e} _{3} = e _{2} / e _{\max }\), e 3/e max=0,0.5,0.9), where e max is the maximum possible eccentricity parameter for the internal cutout, are considered. A general Maple code was constructed for numerical treatment of the linear system of Eqs. (12), i.e., to calculate the resonance frequencies and to determine the unknown mode shapes as functions of panel/cutout aspect ratios as well as cutout orientation/location parameters. The computations were performed on a network of core i7-based desktop computers. Also, a simple and very efficient direct root finding scheme based on the classical bisection method [46] was employed to determine the roots of the characteristic equation |A|=0, by performing tedious frequency sweepings with extremely small frequency steps for detection of the values of the frequency parameters that cause the determinant to change sign. This procedure was repeated for all selected cutout orientation/location parameters. Furthermore, after finding the roots of the characteristic equation by the above mentioned procedure, each root is substituted back into the coefficient matrix A in Eq. (12), and the corresponding eigenvector (mode shape) is obtained by using the powerful Maple built-in function “nullspace(A).” The convergence of numerical solutions was systematically checked in a simple trial and error manner, by increasing the number of modes, while looking for steadiness or stability in the numerical value of the solutions. Using a truncation constant of M=14 in the series solution (11), with N=(2M+1)=29 collocation points on each elliptical boundary, were found to yield satisfactory results for the selected geometric parameters. Table 1 shows the trend of convergence of calculated dimensionless fundamental frequency of an elliptical plate with an elliptical cutout with the following geometric parameters (a 1/b 1,a 2/b 2=2; b 1=1 m, b 2=0.25 m; α 2,θ 2=0,45,90∘; \(\overline{e} _{2} = e _{2} / e _{\max } =0,0.5,0.9\)). It is clear that adequate convergence can be obtained by using a truncation constant of M=14. Also, as the cutout becomes more eccentric (and/or more elliptic), the rate of convergence deteriorates. Lastly, it should be noted that, since the largest dimensions of cut-outs (a 2,a 3=0.25 m) are much larger than the panel thickness (h=0.005 m), three dimensional behavior in the vicinity of the cut-out is not expected.

Table 1 Convergence of calculated dimensionless fundamental frequency of an elliptical plate with an elliptical cutout for selected geometric parameters
Full size table

Figures 2a, 2b, 2c, 2d and 2f display the first three calculated dimensionless natural frequencies, \(\omega _{i} b _{1} ^{2} \sqrt{\rho h/D} \ (i=1,2,3)\), along with the associated deformation mode shapes of the panel with a single cutout (L=2; a 1/b 1, a 2/b 2=1,2; b 1=1 m, b 2=0.25 m) for selected cutout orientations and positions (α 2,θ 2=0,45,90∘; \(\overline{e} _{2} = e _{2} / e _{\max } =0,0.5,0.9\)). Also, tabulated in bold numerics, are the natural frequencies computed using the commercial package ABAQUS [47]. Nearly regardless of the input geometric parameters, excellent agreements are obtained (under 1 %), as displayed in the figure. The most important observations are as follows. Regardless of cutout shape, increasing cutout eccentricity along the major or minor plate axis leads to a general decrease in the system natural frequencies, while no common remarks can be made about increasing the cutout eccentricity along the x–y bisector axis. Also, when an elliptic cutout is located along the major axis of the elliptic plate (α 2=0∘), increasing the cutout orientation,θ 2, leads to a general decrease in the natural frequencies. On the other hand, when the elliptic cutout is located off-center (\(\overline{e} _{2} \neq0\)) along the minor axis of the elliptic plate (α 2=90∘), increasing the cutout orientation causes a general increase in the natural frequencies. Furthermore, the natural frequencies for an elliptic plate with an elliptic cutout is generally higher than those for an elliptic plate with a circular cutout, which may directly be linked to the increase in the structural stiffness due to the presence of a longer constraining boundary in the former (elliptical cutout) configuration. Moreover, the natural frequencies for a circular plate with an elliptic cutout is in general remarkably higher than those for an elliptic plate with the same elliptical perforation, which may be related to the increase in the structural stiffness due to the decrease of plate area in the circular plate configuration. Besides, almost regardless of cutout eccentricity, the natural frequencies of a circular plate with an elliptical cutout is in general higher than those of a circular plate with a circular cutout, which may be also linked to the increase in the constraining boundary length in the former situation. Lastly, Figs. 3a, 3b, 3c display some representative calculated dimensionless fundamental natural frequencies, \(\omega _{1} b _{1} ^{2} \sqrt{\rho h/D}\), along with the associated deformation mode shapes of the panel with two cutouts (L=3; a 1/b 1, a 2/b 2, a 3/b 3=1,2; b 1=1 m; b 2, b 3=0.25 m) for selected cutouts orientations and positions (α 2,θ 2,θ 3=0,45,90∘; α 3=180,225,270∘; \(\overline{e} _{2}, \overline{e} _{3} =0.5,0.9\)). Also, tabulated in bold numerics, are the natural frequencies computed using the commercial package ABAQUS [47]. Comments very similar to those made for Figs. 2a through 2f can readily be made. Also, excellent agreements are obtained, further demonstrating the accuracy of the adopted method.

Fig. 2a
figure 4

Effects of changing the elliptical cutout position (eccentricity) and orientation along the plate major axis on the first three calculated dimensionless natural frequencies and the associated mode shapes of the elliptic panel

Full size image
Fig. 2b
figure 5

Effects of changing the elliptical cutout position (eccentricity) and orientation along the plate bisector axis on the first three calculated dimensionless natural frequencies and the associated mode shapes of the elliptic panel

Full size image
Fig. 2c
figure 6

Effects of changing the elliptical cutout position (eccentricity) and orientation along the plate minor axis on the first three calculated dimensionless natural frequencies and the associated mode shapes of the elliptic panel

Full size image
Fig. 2d
figure 7

Effects of changing the circular cutout position (eccentricity) along the plate major, bisector, and minor axes on the first three calculated dimensionless natural frequencies and the associated mode shapes of the elliptic panel

Full size image
Fig. 2e
figure 8

Effects of changing the elliptical cutout position (eccentricity) and orientation on the first three calculated dimensionless natural frequencies and the associated mode shapes of the circular panel

Full size image
Fig. 2f
figure 9

Effects of changing the circular cutout position (eccentricity) on the first three calculated dimensionless natural frequencies and the associated mode shapes of the circular panel

Full size image
Fig. 3a
figure 10

Some representative calculated dimensionless fundamental natural frequencies and the associated deformation mode shapes of elliptical panels with two elliptical cutouts

Full size image
Fig. 3b
figure 11

Some representative calculated dimensionless fundamental natural frequencies and the associated deformation mode shapes of elliptical panels with two circular cutouts

Full size image
Fig. 3c
figure 12

Some representative calculated dimensionless fundamental natural frequencies and the associated deformation mode shapes of circular panels with two elliptical cutouts

Full size image

Finally, as a further check on the overall validity of the work, we used our general Maple code to compute the first five dimensionless natural frequencies, \(\omega _{i} b _{1} ^{2} \sqrt{\rho h/D} \ (i=1,2,\dots,5)\), of a thin annular elliptic plate (ν=0.333), clamped at the outer/inner edges for selected cutout dimensions (a 1/b 1=a 2/b 2=2; b 2/b 1=0, 0.2, 0.4, 0.6). The outcome, as presented in Table 2 exhibits fair agreements with the data presented in Table 2 of Ref. [15], where authors employed the boundary characteristic orthogonal polynomials as shape functions in the classical Rayleigh–Ritz method to compute the natural frequencies. Also demonstrated in Table 2 are the excellent agreements obtained by the present authors through use of the FEM package ABAQUS.

Table 2 Comparison of the first five calculated dimensionless natural frequencies of a thin annular clamped elliptic plate with the data available in the literature and FEM
Full size table

5 Conclusions

A general semi-analytic solution involving products of radial and angular Mathieu functions and based on the elaborated collocation multipole method is presented for the free flexural vibration analysis of a fully clamped elliptical plate with multiple internal elliptical cutouts of arbitrary size, location and orientation. Lack of spurious eigensolutions, excellent accuracy, fast rate of convergence, and high computational efficiency are the key features of the adopted method. Extensive numerical data are presented for the first three natural frequencies and the associated deformed mode shapes of an elliptical plate with an elliptical cutout of about ¼ dimension, for a wide range of plate/cutout aspect ratios and cutout location/orientation parameters. The presented results confirm that the dynamic plate characteristics are significantly influenced by the plate/cutout geometric parameters. In particular, it is observed that almost regardless of cutout shape (i.e., circular or elliptic), increasing cutout eccentricity along the major or minor plate axis leads to an overall decrease in the system natural frequencies. Also, when an eccentric elliptic cutout is located anywhere along the major (minor) axis of the elliptic plate, increasing the cutout orientation leads to a general decrease (increase) in the natural frequencies. Furthermore, the natural frequencies for an elliptic (a circular) plate with an elliptical cutout is in general found to be moderately (remarkably) higher than those of an elliptic plate with a circular (an elliptical) cutout. Lastly, nearly regardless of cutout eccentricity, the natural frequencies of a circular plate with an elliptical cutout is normally higher than those of a circular plate with a circular cutout, which is linked to the increase in the constraining boundary length in the former situation.