Thermal vibration of thick FGM spherical shells by using TSDT

Abstract

The effects of TSDT on the thermal vibration of thick FGM spherical shells are investigated by using the GDQ numerical method. The c₁ term of nonlinear coefficient in TSDT displacement is included to obtain the dynamic GDQ discrete equations. Parametric variables for environment temperature, FGM power law index and calculated shear coefficient are used to study the main effects on the stress and center deflection. The calculated thermal deflection and stress data of time response and transient response are presented for the thick FGM spherical shells.

1 Introduction

Analytical and numerical studies in many kinds of spherical shells have been already presented. Venås and Jenserud (2019) presented the exact results of acoustic scattering by using the separation of variables for the spherical symmetric scatters with fluid and solid layers. Kareem and Majeed (2019) presented the transient response results by using the higher order shear deformation theory for the laminated shallow spherical shell subjected to low-velocity impact. Huang et al. (2019) presented the numerical fluid–structure interaction vibration results by using the wave superposition method for the elastic spherical shells. Sayyad and Ghugal (2019) presented the free vibration results for the laminated spherical shells by using a generalized higher-order shell theory. Stampouloglou and Theotokoglou (2018) presented the elastic-static results for the inhomogeneous equal thickness spherical shells by using an exact analytical method. Duc et al. (2017) presented the numerical nonlinear dynamic and vibration results by using the classical shell theory and Pasternak's two parameters elastic foundations (EF) for the Sigmoid power law distribution functionally graded material (S-FGM) shallow spherical shells. Sahan (2016) presented the numerical dynamic response results for the viscoelastic cross-ply laminated shallow spherical shells. Fu and Hu (2013) presented the numerical nonlinear transient response results by using the higher order shear deformation theory for the fibre metal laminated (FML) shallow spherical shells under one-dimensional unsteady temperature fields. Sepiani et al. (2010) presented the numerical free vibration and buckling results by using the first-order shear deformation theory (FSDT) formulation for the functionally graded material (FGM) shells without considering the thermal effect. The motivation of the paper is to obtain the calculated thermal deflection and stress data of time response and transient response for the thick FGM spherical shells by considering the nonlinear TSDT and the fully homogeneous equation.

The author has presented some papers of thermal vibration for the generalized differential quadrature (GDQ) numerical method applied in the composited FGM shells. Hong (2016) presented the thermal vibration of Terfenol-D and FGM circular cylindrical shells mainly by using FSDT model. Hong (2014) presented the thermal vibration of Terfenol-D and FGM cylindrical shells mainly by using varied shear coefficient. It is interesting to investigate the GDQ solution of thermal stresses and center displacement mainly by considering the effects of third-order shear deformation theory (TSDT) and vibration frequency of fully homogeneous equation on the thermal vibration of thick FGM spherical shells under four edges simply support. Parametric variables of environment temperature, FGM power law index and calculated shear coefficient are used to study the main affects on the stress and center deflection for the thick FGM spherical shells.

2 Procedures of formulation

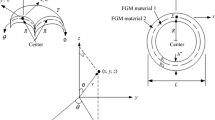
For a two-material e.g. stainless steel and silicon nitride FGM spherical shell under temperature difference $\Delta T$ is shown in Fig. 1 with thickness h₁ of inner constituent layer FGM material 1 and thickness h₂ of outer constituent layer FGM material 2, L is the axial length of FGM spherical shells, h^* is the total thickness of FGM spherical shells. A point in the coordinates $\left( {r, \theta , \emptyset } \right)$ of spherical axes can be corresponded to the coordinates $\left( {x, y, z} \right)$ of the Cartesian axes, in which r is the radius of FGM shells with x = r sin$\emptyset$ cos$\theta$ and y = r sin$\emptyset$ sin$\theta$. The angle $\theta$ denotes in the circumferential direction of the shells. The angle $\emptyset$ denotes in the direction of z axis and the direction of radius in the spherical shells. The properties P_i of individual constituent material of FGM spherical shells are in functions of environment temperature T and temperature coefficients $P_{0} ,P_{ - 1} ,P_{1} ,P_{2}$ and P₃ (Hong 2016). The material of power-law function of FGM spherical shells are assumed by Young’s modulus E_fgm of FGM represented in standard variation form of power law index R_n, the other properties e.g. Poisson’s ratios are simply assumed in the average form (Hong 2014).

Fig. 1

Two-material thick FGM spherical shell under $\Delta T$

The nonlinear displacements u, v and w in time dependent of thick FGM spherical shells are assumed in the nonlinear coefficient c₁ term of TSDT equations (Lee et al. 2004) as follows,

$$\begin{aligned} u & = u_{0} \left( {x,\theta ,t} \right) + z\phi_{x} \left( {x,\theta ,t} \right) - c_{1} z^{3} \left( {\phi_{x} + \frac{\partial w}{{\partial x}}} \right), \\ v & = v_{0} \left( {x,\theta ,t} \right) + z\phi_{\theta } \left( {x,\theta ,t} \right) - c_{1} z^{3} \left( {\phi_{\theta } + \frac{\partial w}{{R\partial \theta }}} \right), \\ w & = w\left( {x,\theta ,t} \right) \\ \end{aligned}$$

(1)

where u₀ and v₀ are tangential displacements in the in-surface coordinates x and $\theta$ axes direction, respectively. w is transverse displacement in the out of surface coordinates z axis thickness direction of the middle-plane of shells. $\phi_{x}$ and $\phi_{\theta }$ are the shear rotations. R is the middle-surface radius of FGM spherical shells. t is time. Coefficient of $c_{1} = 4/\left[ {3(h^{*} )^{2} } \right]$ is assumed in TSDT approach.

For the normal stresses ($\sigma_{x}$ and $\sigma_{\theta }$) and the shear stresses ($\sigma_{x\theta }$, $\sigma_{\theta z}$ and$\sigma_{xz}$) in the thick FGM spherical shells under $\Delta T$ for the subscript kth constituent layer are assumed in terms of the stiffness $\overline{Q}_{ij}$, in-plane strains $\varepsilon_{x}$, $\varepsilon_{\theta }$ and $\varepsilon_{x\theta }$, not negligible shear strains $\varepsilon_{\theta z}$ and $\varepsilon_{xz}$ as follows (Lee and Reddy 2005; Whitney 1987),

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}_{\left( k \right)} & = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{16} } \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & {\overline{Q}_{26} } \\ {\overline{Q}_{16} } & {\overline{Q}_{26} } & {\overline{Q}_{66} } \\ \end{array} } \right]_{\left( k \right)} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} - \alpha_{x} \Delta T} \\ {\varepsilon_{\theta } - \alpha_{\theta } \Delta T} \\ {\varepsilon_{x\theta } - \alpha_{x\theta } \Delta T} \\ \end{array} } \right\}_{\left( k \right)} , \\ \left\{ {\begin{array}{*{20}c} {\sigma_{\theta z} } \\ {\sigma_{xz} } \\ \end{array} } \right\}_{\left( k \right)} & = \left[ {\begin{array}{*{20}c} {\overline{Q}_{44} } & {\overline{Q}_{45} } \\ {\overline{Q}_{45} } & {\overline{Q}_{55} } \\ \end{array} } \right]_{\left( k \right)} \left\{ {\begin{array}{*{20}c} {\varepsilon_{\theta z} } \\ {\varepsilon_{xz} } \\ \end{array} } \right\}_{\left( k \right)} , \\ \end{aligned}$$

(2)

where $\alpha_{x}$ and $\alpha_{\theta }$ are the coefficients of thermal expansion, $\alpha_{x\theta }$ is the coefficient of thermal shear in the in-surface coordinates x and $\theta$ axes direction, respectively.

Simply, the heat conduction equation for the FGM shell in the spherical coordinates is assumed as follows (Hong 2016),

$$K\left( {\frac{{\partial^{2} \Delta T}}{{\partial x^{2} }} + \frac{{\partial^{2} \Delta T}}{{R^{2} \partial \theta^{2} }} + \frac{{\partial^{2} \Delta T}}{{(R\sin \emptyset )^{2} \partial \emptyset^{2} }}} \right) = \frac{\partial \Delta T}{{\partial t}},$$

(3)

where $K = \kappa_{fgm} /\left( {\rho_{fgm} C_{vfgm} } \right)$, in which $\kappa_{fgm}$ is thermal conductivity of FGM spherical shells, ρ_fgm is density of FGM spherical shells, $C_{vfgm}$ is specific heat of FGM spherical shells. $\Delta T = T_{0} \left( {x,\theta ,t} \right) + \frac{z}{{h^{*} }}T_{1} \left( {x,\theta ,t} \right)$ is the temperature difference between the FGM spherical shells and curing area, it is assumed in linear with variable z, in which T₀ and T₁ are temperature parameters in functions of coordinates x, $\theta$ and t. The frequency of heat flux for the thermal loads on the spherical FGM shells would be given from the Eq. (3) with the simplified sinusoidal temperature loading $\Delta T = \frac{z}{{h^{*} }}\overline{T}_{1} \sin \left( {\pi x/L} \right)\sin \left( {\pi \theta } \right)\sin \left( {\gamma t} \right)$ and$z = R\cos \emptyset$, in which $\gamma$ is the frequency of heat flux, $\overline{T}_{1}$ is the amplitude of temperature, thus the frequency of heat flux equation is obtained as follows by applying the heat conduction equation in the cylindrical shells (Hong 2016),

$$\frac{{L^{2} }}{{K\pi^{2} [1 + \left( \frac{L}{R} \right)^{2} + \left( {\frac{L}{\pi R\sin \emptyset })^{2} } \right]}}\gamma \cos \left( {\gamma t} \right) + \sin \left( {\gamma t} \right) = 0$$

(4)

The novelty presented in the paper is to assume the dynamic equations of motion with TSDT in the FGM cylindrical shells can be applied further into the FGM spherical shells for a small element on a given $\theta$ angle. The dynamic equations of motion with TSDT for a small element on a given ∅ angle in the FGM spherical shells are assumed as follows (Sayyad and Ghugal 2019; Reddy 2002),

$$\frac{{\partial N_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial N_{x\theta } }}{\partial \theta } = I_{0} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + J_{1} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - c_{1} I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{\partial w}{{\partial x}}} \right),$$

$$\frac{{\partial N_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial N_{\theta \theta } }}{\partial \theta } = I_{0} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + J_{1} \frac{{\partial^{2} \phi_{\theta } }}{{\partial t^{2} }} - c_{1} I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{\partial w}{{R\partial \theta }}} \right),$$

$$\begin{aligned} \frac{{\partial \overline{Q}_{x} }}{\partial x} + & \frac{1}{R}\frac{{\partial \overline{Q}_{\theta } }}{\partial \theta } + c_{1} \left( {\frac{{\partial^{2} P_{xx} }}{{\partial x^{2} }} + \frac{2}{R}\frac{{\partial^{2} P_{x\theta } }}{\partial x\partial \theta } + \frac{1}{{R^{2} }}\frac{{\partial^{2} P_{\theta \theta } }}{{\partial \theta^{2} }}} \right) + q = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - c_{1}^{2} I_{6} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) \\ & + c_{1} \left[ {I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{R}\frac{{\partial v_{0} }}{\partial \theta }} \right) + J_{4} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{1}{R}\frac{{\partial \phi_{\theta } }}{\partial \theta }} \right)} \right], \\ \end{aligned}$$

$$\left( {\frac{{\partial \overline{M}_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial \overline{M}_{x\theta } }}{\partial \theta } - \overline{Q}_{x} } \right) = \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {J_{1} u_{0} + K_{2} \phi_{x} - c_{1} J_{4} \frac{\partial w}{{\partial x}}} \right),$$

$$\left( {\frac{{\partial \overline{M}_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial \overline{M}_{\theta \theta } }}{\partial \theta } - \overline{Q}_{\theta } } \right) = \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {J_{1} v_{0} + K_{2} \phi_{\theta } - c_{1} J_{4} \frac{1}{R}\frac{\partial w}{{\partial \theta }}} \right),$$

(5)

where $\overline{M}_{\alpha \beta } = M_{\alpha \beta } - c_{1} P_{\alpha \beta }$, $\overline{Q}_{\alpha } = Q_{\alpha } - 3c_{1} R_{\alpha }$, $\alpha ,\beta = x,\theta$. q is the external pressure load.

$$\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{\theta \theta } } \\ {N_{x\theta } } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}dz,\left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{\theta \theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}zdz,\left\{ {\begin{array}{*{20}c} {P_{xx} } \\ {P_{\theta \theta } } \\ {P_{x\theta } } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}z^{3} dz,$$

$$\left\{ {\begin{array}{*{20}c} {R_{\theta } } \\ {R_{x} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{\theta z} } \\ {\sigma_{xz} } \\ \end{array} } \right\}z^{2} dz, \left\{ {\begin{array}{*{20}c} {Q_{\theta } } \\ {Q_{x} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{\theta z} } \\ {\sigma_{xz} } \\ \end{array} } \right\}dz, I_{i} = \mathop \sum \limits_{k = 1}^{{N^{*} }} \mathop \int \limits_{k}^{k + 1} \rho^{\left( k \right)} z^{i} dz,\left( {i = 0,{1},{2}, \ldots ,{6}} \right),$$

in which N^* is total number of constituent layers, $\rho^{\left( k \right)}$ is the density of kth constituent ply.$J_{i} = I_{i} - c_{1} I_{i + 2}$, (i = 1,4), $K_{2} = I_{2} - 2c_{1} I_{4} + c_{1}^{2} I_{6}$.

The Von Karman type of strain–displacement relations with $\frac{{\partial v_{0} }}{\partial z} = \frac{{ - v_{0} }}{R\sin \emptyset }$, $\frac{{\partial u_{0} }}{\partial z} = \frac{{ - u_{0} }}{R\sin \emptyset }$ are assumed in the spherical shell and $\frac{\partial w}{{\partial z}} = \frac{{\partial \phi_{x} }}{\partial z} = \frac{{\partial \phi_{\theta } }}{\partial z} = 0$ are used as follows,

$$\varepsilon_{x} = \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} = \frac{{\partial u_{0} }}{\partial x} + z\frac{{\partial \phi_{x} }}{\partial x} - c_{1} z^{3} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} ,$$

$$\varepsilon_{\theta } = \frac{1}{R}\frac{\partial v}{{\partial \theta }} + \frac{1}{2}\left( {\frac{1}{R}\frac{\partial w}{{\partial \theta }}} \right)^{2} = \frac{1}{R}\frac{{\partial v_{0} }}{\partial \theta } + z\frac{1}{R}\frac{{\partial \phi_{\theta } }}{\partial \theta } - c_{1} z^{3} \left( {\frac{1}{R}\frac{{\partial \phi_{\theta } }}{\partial \theta } + \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) + \frac{1}{2}\frac{1}{{R^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} ,$$

$$\varepsilon_{zz} = 0,$$

$$\varepsilon_{x\theta } = \frac{1}{R}\frac{\partial u}{{\partial \theta }} + \frac{\partial v}{{\partial x}} + \left( {\frac{\partial w}{{\partial x}}} \right)\left( {\frac{1}{R}\frac{\partial w}{{\partial \theta }}} \right) = \frac{1}{R}\left[ {\frac{{\partial u_{0} }}{\partial \theta } + z\frac{{\partial \phi_{x} }}{\partial \theta } - c_{1} z^{3} \left( {\frac{{\partial \phi_{x} }}{\partial \theta } + \frac{{\partial^{2} w}}{\partial x\partial \theta }} \right)} \right] + \frac{{\partial v_{0} }}{\partial x} + z\frac{{\partial \phi_{\theta } }}{\partial x} - c_{1} z^{3} \left( {\frac{{\partial \phi_{\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial^{2} w}}{\partial x\partial \theta }} \right) + \left( {\frac{\partial w}{{\partial x}}} \right)\left( {\frac{1}{R}\frac{\partial w}{{\partial \theta }}} \right),$$

$$\varepsilon_{\theta z} = \frac{\partial v}{{\partial z}} + \frac{1}{R}\frac{\partial w}{{\partial \theta }} = \frac{{ - v_{0} }}{R\sin \emptyset } + \phi_{\theta } - 3c_{1} z^{2} \left( {\phi_{\theta } + \frac{1}{R}\frac{\partial w}{{\partial \theta }}} \right) + \frac{1}{R}\frac{\partial w}{{\partial \theta }},$$

$$\varepsilon_{xz} = \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}} = \frac{{ - u_{0} }}{R\sin \emptyset } + \phi_{x} - 3c_{1} z^{2} \left( {\phi_{x} + \frac{\partial w}{{\partial x}}} \right) + \frac{\partial w}{{\partial x}}.$$

(6)

After substituting Eqs. (2) and (6) into Eq. (5), the dynamic equilibrium differential equations with nonlinear TSDT of FGM spherical shells can be derived in matrix forms and similar to the published paper contained the following stiffness coefficients in the 5 by 5 matrix (Hong 2019),

$$\left( {A_{{i^{s} j^{s} }} ,B_{{i^{s} j^{s} }} ,D_{{i^{s} j^{s} }} ,E_{{i^{s} j^{s} }} ,F_{{i^{s} j^{s} }} ,H_{{i^{s} j^{s} }} } \right) = \mathop \int \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \overline{Q}_{{i^{s} j^{s} }} \left( {1,z,z^{2} ,z^{3} ,z^{4} ,z^{6} } \right)dz,\left( {i^{s} ,j^{s} = 1,2,6} \right),$$

$$\left( {A_{{i^{*} j^{*} }} ,B_{{i^{*} j^{*} }} ,D_{{i^{*} j^{*} }} ,E_{{i^{*} j^{*} }} ,F_{{i^{*} j^{*} }} ,H_{{i^{*} j^{*} }} } \right) = \mathop \int \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} k_{\alpha } \overline{Q}_{{i^{*} j^{*} }} \left( {1,z,z^{2} ,z^{3} ,z^{4} ,z^{5} } \right)dz,(i^{*} ,j^{*} = 4,5),$$

(7)

in which $k_{\alpha }$ is the shear coefficient. The $\overline{Q}_{{i^{s} j^{s} }}$ and $\overline{Q}_{{i^{*} j^{*} }}$ for thick FGM spherical shells containing with not neglect terms $z/(R\sin \emptyset )$ can be assumed in the simple forms as follows,

$$\overline{Q}_{11} = \overline{Q}_{22} = \frac{{E_{fgm} }}{{1 - \nu_{fgm}^{2} }},$$

$$\overline{Q}_{12} = \overline{Q}_{21} = \frac{{\nu_{fgm} E_{fgm} }}{{\left( {1 + \frac{z}{R\sin \emptyset }} \right)\left( {1 - \nu_{fgm}^{2} } \right)}},$$

$$\overline{Q}_{44} = \frac{{E_{fgm} }}{{2(1 + \nu_{fgm} )}},$$

$$\overline{Q}_{55} = \overline{Q}_{66} = \frac{{E_{fgm} }}{{2\left( {1 + \frac{z}{R\sin \emptyset }} \right)\left( {1 + \nu_{fgm} } \right)}},$$

$$\overline{Q}_{16} = \overline{Q}_{26} = \overline{Q}_{45} = 0,$$

(8)

in which $\nu_{fgm} = \left( {\nu_{1} + \nu_{2} } \right)/2$ is the Poisson’s ratios of the FGM spherical shells simply expressed in average form, $E_{fgm} = (E_{2} - E_{1} )\left( {\frac{{z + h^{*} /2}}{{h^{*} }}} \right)^{{R_{n} }} + E_{1}$ is the Young’s modulus of the FGM spherical shells expressed in standard form of power-law function, E₁ and E₂ are the Young’s modulus, $\nu_{1}$ and $\nu_{2}$ are the Poisson’s ratios of the two-material constituent FGM, respectively.

The time sinusoidal displacement and shear rotations of thermal vibrations in a typical nonlinear time response analysis, they can be assumed and used as follows (Hong 2016),

$$\begin{aligned} & u_{0} \left( {x,\theta ,t} \right) = u_{0} \left( {x,\theta } \right)\sin (\omega_{mn} t), \\ & v_{0} \left( {x,\theta ,t} \right) = v_{0} \left( {x,\theta } \right)\sin (\omega_{mn} t), \\ & w\left( {x,\theta ,t} \right) = w\left( {x,\theta } \right)\sin (\omega_{mn} t), \\ & \phi_{x} \left( {x,\theta ,t} \right) = \phi_{x} \left( {x,\theta } \right)\sin (\omega_{mn} t), \\ & \phi_{\theta } \left( {x,\theta ,t} \right) = \phi_{\theta } \left( {x,\theta } \right)\sin (\omega_{mn} t), \\ \end{aligned}$$

(9)

in which $\omega_{mn}$ is the natural frequency in two directional mode shape subscript numbers m and n of the shells. Also the simple vibration of sinusoidal temperature parameter for the thermal loads are assumed as follows for the GDQ computation,

$$\Delta T = \left[ {T_{0} \left( {x,\theta } \right) + \frac{z}{{h^{*} }}T_{1} \left( {x,\theta } \right)} \right]\sin \left( {\gamma t} \right),$$

$$T_{0} \left( {x,\theta } \right) = 0,$$

$$T_{1} \left( {x,\theta } \right) = \overline{T}_{1} \sin \left( {\pi x/L} \right)\sin \left( {\pi \theta /R} \right)$$

(10)

3 Some numerical results and discussions

The GDQ method is presented by Shu and Richards in 1990 (Bert et al. 1989; Shu and Du 1997). The boundary conditions in dynamic GDQ discrete equations approach can be considered for four sides simply supported, not symmetric, orthotropic of laminated thick FGM spherical shells. Thus the dynamic GDQ discrete equations can be rewritten into the following matrix form for a given typical grid point (i, j),

$$\left[ A \right]\left\{ {W^{*} } \right\} = \left\{ B \right\},$$

(11)

where {B} is a N^**th order row external loads vector. [A] is a dimension of N^** by N^** coefficient matrix with $N^{**} = \left( {N - 2} \right) \times \left( {M - 2} \right) \times 5$ containing the stiffness coefficients and GDQ weighting parameters. And {W^*} is a N^**th order unknown column vector to be found and can be expressed as $\{ W^{*} \} = \{ U_{2,2} , \ldots , U_{2,M - 1} ,U_{3,2} , \ldots , U_{3,M - 1} , \ldots ,U_{N - 1,2} , \ldots , U_{N - 1,M - 1}$, $V_{2,2} , \ldots , V_{2,M - 1} ,V_{3,2} , \ldots , V_{3,M - 1} , \ldots ,V_{N - 1,2} , \ldots , V_{N - 1,M - 1}$, $W_{2,2} , \ldots , W_{2,M - 1} ,W_{3,2} , \ldots , W_{3,M - 1} , \ldots ,W_{N - 1,2} , \ldots , W_{N - 1,M - 1}$, $\phi_{x2,2} ,\phi_{x2,3} \ldots,\phi_{x2,M - 1} ,\phi_{x3,2} ,\phi_{x3,3} ,\ldots,\phi_{x3,M - 1} ,\ldots,\phi_{xN - 1,2} ,\phi_{xN - 1,3} ,\ldots,\phi_{xN - 1,M - 1}$, $\phi_{\theta 2,2} ,\phi_{\theta 2,3} ,\ldots,\phi_{\theta 2,M - 1} ,\phi_{\theta 3,2} ,\phi_{\theta 3,3} ,\ldots,\phi_{\theta 3,M - 1} ,\ldots,\phi_{\theta N - 1,2} ,\phi_{\theta N - 1,3} ,\ldots,\phi_{\theta N - 1,M - 1} \}^{t}$, in which the subscript numbers are represented as the corresponding interior grid point for the non-dimensional unknown variables $U = u_{0} /L$, $V = v_{0} /R$, $W = w/h^{*}$, $\phi_{x}$ and $\phi_{\theta }$.

For the constituent layers of spherical FGM shells are in the same stacking, without in-plane forces and external pressure $(q = 0)$. The coordinates x_i and $\theta_{j}$ for the grid points numbers N and M of thick FGM shells are used as follows,

$$x_{i} = 0.5\left[ {1 - \cos \left( {\frac{i - 1}{{N - 1}}\pi } \right)} \right]L,i = 1,2, \ldots ,N,$$

$$\theta_{j} = 0.5\left[ {1 - \cos \left( {\frac{j - 1}{{M - 1}}\pi } \right)} \right]R,j = 1,2, \ldots ,M$$

(12)

Also the computed values of inter-laminar stresses $\sigma_{x}$, $\sigma_{\theta }$, $\sigma_{x\theta }$, $\sigma_{\theta z}$ and $\sigma_{xz}$ in the kth constituent layer can be obtained after the values of non-dimensional variables U, V, W, $\phi_{x}$ and $\phi_{\theta }$ are found. Before the process of thermal vibrations of spherical FGM shell, it is needed to obtain the calculation values of frequency $\omega_{mn}$, in which two directional subscript m is the number of axial half-waves, n is the number of circumferential waves. It is reasonable to assumed that u₀, v₀, w, $\phi_{x}$ and $\phi_{\theta}$ are expressed in the time sinusoidal form of free vibration for spherical FGM shell under four sides simply supported (Hong 2016). After substituting sinusoidal displacement equations into dynamic equilibrium differential equations and including the nonlinear effects of c₁ terms in the elements of homogeneous matrix, thus the fully homogeneous equation can be obtained and contained with $\lambda_{mn} = I_{0}\omega_{mn}^{2}$. The zero value of determinant for the coefficient matrix in fully equation, the polynomial equation in fifth-order of $\lambda_{mn}$ can be obtained, thus the $\omega_{mn}$ can be computed.

The transverse shear locking issue did not occur in the GDQ numerical method. It is very interesting to study the thick nonlinear TSDT FGM spherical shells with L/R = 1, h^* = 1.2 mm, h₁ = h₂ = 0.6 mm, m = n = 1 and q = 0. The FGM material 1 is SUS304 (stainless steel) at inner position, the FGM material 2 is Si₃N₄ (silicon nitride) at outer position used for the numerical GDQ computations. Firstly, the dynamic convergence study of center deflection amplitude w(L/2, 2π/2) (unit mm) in the thermal vibration of nonlinear TSDT is obtained. The investigation cases are under the values of c₁ = 0.925925 and c₁ = 0 for thick L/h^* = 10 with $\gamma$ = 0.2618004/s and for L/h^* = 5 with $\gamma$ = 0.261802/s, respectively. The GDQ convergence results of deflection versus grid points number at t = 6 s, T = 100 K, $\bar{T}_{1}$ = 100 K calculated on $\emptyset = 10^{\circ}, 45^{\circ}$ and 90° are presented in Tables 1, 2, 3. In the nonlinear L/h^* = 5 case of c₁ = 0.925925/mm²: (a) for value of R_n = 0.5, $k_{\alpha}$ = 0.111874 and $\omega_{11}$ = 0.003031/s, 0.000554/s and 0.000241/s respectively on $\emptyset = 10^{\circ}, 45^{\circ}$ and 90° are obtained. (b) for value of R_n = 1, $k_{\alpha}$ = 0.149001 and $\omega_{11}$ = 0.002490/s, 0.002063/s and 0.000238/s respectively on $\emptyset = 10^{\circ}, 45^{\circ}$ and 90° are obtained. (c) for value of R_n = 2, $k_{\alpha}$ = 0.231364 and $\omega_{11}$ = 0.001923/s, 0.002056/s and 0.000230/s respectively on $\emptyset = 10^{\circ}, 45^{\circ}$ and 90° are obtained. In the linear L/h^* = 5 case of c₁ = 0/mm²: (d) for value of R_n = 0.5, $k_{\alpha}$ = 0.111874 and $\omega_{11}$ = 0.011064/s, 0.003546/s and 0.001583/s respectively on $\emptyset = 10^{\circ}, 45^{\circ}$ and 90° are obtained. (e) for value of R_n = 1, $k_{\alpha}$ = 0.149001 and $\omega_{11}$ = 0.040200/s, 0.002699/s and 0.001335/s respectively on $\emptyset = 10^{\circ}, 45^{\circ}$ and 90° are obtained. (f) for value of R_n = 2, $k_{\alpha}$ = 0.231364 and $\omega_{11}$ = 0.029226/s, 0.001404/s and 0.000490/s respectively on $\emptyset = 10^{\circ}, 45^{\circ}$ and 90° are obtained. The error accuracy of convergence study for the $w(L/2, 2\pi/2)$ is 1.6e−05 on $\emptyset = 45^{\circ}$, R_n = 1 and L/h^* = 10 case. Thus grid points $N{\times} M$ = 13 × 13 can be accepted in very good convergence condition, and used well in the GDQ computations of nonlinear TSDT time responses and stresses.

Table 1 Convergence of TSDT FGM spherical shells on $\emptyset = 10^\circ$ at t = 6 s

Table 2 Convergence of TSDT FGM spherical shells on $\emptyset = 45^\circ$ at t = 6 s

Table 3 Convergence of TSDT FGM spherical shells on $\emptyset = 90^\circ$ at t = 6 s

Secondly, the values of $w(L/2, 2\pi/2)$ (unit mm) for the thermal vibration of nonlinear TSDT are calculated. The $\gamma$ values are decreasing from $\gamma$ = 15.707966/s at t = 0.1 s to $\gamma$ = 0.523602/s at t = 3.0 s used for L/h^* = 5, from $\gamma$ = 15.707964/s at t = 0.1 s to $\gamma$ = 0.523599/s at t = 3.0 s used for L/h^* = 10 when $\gamma$. Figure 2 shows the response values of $w(L/2, 2\pi/2)$ (unit mm) versus time t of nonlinear TSDT and linear under the values of c₁ = 0.925925/mm² and c₁ = 0 in FGM spherical shells on $\emptyset = 10^{\circ}$ for thick L/h^* = 5 and 10, respectively, $R_{n}=1$, $k_{\alpha}$ = 0.120708, T = 600 K, $\bar{T}_{1}$ = 100 K and t = 0.1–3.0 s with time step is 0.1 s. The maximum value of $w(L/2, 2\pi/2)$ is − 14.930645 mm occurs at t = 0.5 s for thick L/h^* = 5 with c₁ = 0.925925/mm² and $\gamma$ = 3.141596/s. The maximum value of $w(L/2, 2\pi/2)$ is 16.736791 mm occurs at t = 0.5 s for thick L/h^* = 10 with c₁ = 0/mm² and almost same frequency of applied heat flux $\gamma$ = 3.141593/s. The values of $w(L/2, 2\pi/2)$ are underestimated with time in the case c₁ = 0/mm² for L/h^* = 5. But they are overestimated with time in the case c₁ = 0/mm² for L/h^* = 10 when $\emptyset = 10^{\circ}$.

Fig. 2

$w(L/2, 2\pi/2)$ versus t on $\emptyset = 10^{\circ}$

Figure 3 shows the response values of $w(L/2, 2\pi/2)$ (unit mm) versus time t of nonlinear TSDT and linear under the values of c₁ = 0.925925/mm² and c₁ = 0 in FGM spherical shells on $\emptyset = 10^{\circ}$ for thick L/h^* = 5 and 10, respectively, $R_{n}=1$, $k_{\alpha}$ = 0.120708, T = 600 K, $\bar{T}_{1}$ = 100 K and t = 0.1–3.0 s with time step is 0.1 s. The maximum value of $w(L/2, 2\pi/2)$ is 5.043568 mm occurs at t = 0.1 s for thick L/h^* = 5 with c₁ = 0.925925/mm² and higher frequency of applied heat flux $\gamma$ = 15.707964/s. The maximum value of $w(L/2, 2\pi/2)$ is 722.487366 mm occurs at t = 0.1 s for thick L/h^* = 10 with c₁ = 0/mm² and higher frequency of applied heat flux $\gamma$ = 15.707963/s. The values of $w(L/2, 2\pi/2)$ are underestimated with time in the case c₁ = 0/mm² for L/h^* = 5. Also they are overestimated with time in the case c₁ = 0/mm² for L/h^* = 10 when $\emptyset = 45^{\circ}$. The values of $w(L/2, 2\pi/2)$ are converging with time in the cases c₁ = 0.925925/mm² and c₁ = 0/mm² for thick L/h^* = 5 and 10 respectively, except that a small jump near around t = 1.2 s and L/h^* = 5 when $\emptyset = 45^{\circ}$.

Fig. 3

$w(L/2, 2\pi/2)$ versus t on $\emptyset = 45^{\circ}$

Figure 4 shows the response values of $w(L/2, 2\pi/2)$ (unit mm) versus time t of nonlinear TSDT and linear under the values of c₁ = 0.925925/mm² and c₁ = 0 in FGM spherical shells on ${{\emptyset }=90}^{^\circ }$ for thick L/h^* = 5 and 10, respectively, $R_{n=1}$, $k_{\alpha}$ = 0.120708, T = 600 K, $\bar{T}_{1}$ = 100 K and t = 0.1–3.0 s with time step is 0.1 s. The maximum value of $w(L/2, 2\pi/2)$ is − 33.955257 mm occurs at t = 0.1 s for thick L/h^* = 5 with c₁ = 0.925925/mm² and higher frequency of $\gamma$ = 15.707964/s. The maximum value of $w(L/2, 2\pi/2)$ is 1837.97571 mm occurs at t = 0.1 s for thick L/h^* = 10 with c₁ = 0/mm² and higher frequency of $\gamma$ = 15.707963/s. The values of $w(L/2, 2\pi/2)$ are underestimated with time in the case c₁ = 0/mm² for L/h^* = 5. But they are overestimated with time in the case c₁ = 0/mm² for L/h^* = 10 when ${\emptyset}=45^{^\circ }$. The values of $w(L/2, 2\pi/2)$ are converging with time in the cases c₁ = 0.925925/mm² and c₁ = 0/mm² for thick L/h^* = 5 and L/h^* = 10 when ${\emptyset}=45^{^\circ }$, respectively. The values of $w(L/2, 2\pi/2)$ of thick FGM spherical shells need to be modified and reduced to smaller values by using the nonlinear coefficient c₁ term of displacement field of TSDT e.g. with c₁ = 0.925925/mm².

Fig. 4

$w(L/2, 2\pi/2)$ versus t on ${\emptyset}=90^{^\circ }$

The advantages of TSDT (with c₁ = 0.925925/mm²) compared to the FSDT (with c₁ = 0/mm²) in the Figs. 2, 3, 4 and Tables 1, 2, 3 can be explained in more detail as follows. The time response values of center deflection are underestimated in the linear FSDT case c₁ = 0/mm² for more thick L/h^* = 5, but they are overestimated in the linear FSDT case c₁ = 0/mm² for less thick L/h^* = 10, respectively when comparison with the data of nonlinear TSDT case c₁ = 0.925925/mm² when ${\emptyset}=10^{^\circ }$. It can be shown that the advantage of TSDT model is to provide the more accurate data in the studies of thick FGM spherical shells.

Figure 5a shows the ${\sigma }_{x}$ (unit GP_a) versus z/h^* and Fig. 5b shows the ${\sigma }_{x\theta }$ (unit GP_a) versus z/h^* at center position (x = L/2, $w(L/2, 2\pi/2)$) of FGM spherical shells on ${\emptyset}=45^{^\circ }$, respectively at t = 3.0 s for thick a/h^* =  10 with c₁ = 0.925925/mm² and R_n = 1. The value (1.7311E-03 GP_a) of ${\sigma }_{x}$ at z =  − 0.5h^* is found in the greater value than the value (2.6456E-04 GP_a) of ${\sigma }_{x\theta }$ at z = 0.5h^*, thus the normal stress ${\sigma }_{x}$ can be treated as the dominated stress. Figure 5c, d shows the time responses of the dominated stresses ${\sigma }_{x}$ (unit GP_a) at center position of inner surface z =  − 0.5h^* as the analyses of deflection case of FGM spherical shells on ${\emptyset}=45^{^\circ }$ in Fig. 3 for R_n = 1, thick L/h^* = 5 and 10 with c₁ = 0.925925/mm², respectively. The maximum value of stresses ${\sigma }_{x}$ is 1.9684E-03 GP_a occurs at t = 0.1 s in the periods t = 0.1–3 s for thick L/h^* = 5. The values of dominated stresses ${\sigma }_{x}$ are all decreasing with time in the case c₁ = 0.925925/mm² for thick L/h^* = 5 and 10 of FGM spherical shells when ${\emptyset}=45^{^\circ }$, respectively.

Fig. 5

Stresses versus z/h^* and t on ${\emptyset}=45^{^\circ }$

Figure 6 shows the response values of $w(L/2, 2\pi/2)$ (unit mm) versus T (100 K, 600 K and 1000 K) and R_n = 0.1–10 of nonlinear TSDT under the values of c₁ = 0.925925/mm² for thick L/h^* = 5 and 10 of FGM spherical shells when $\emptyset = 10^{\circ}$, 45° and 90°, respectively with the vibration frequency approach of fully homogeneous equation in ${\bar{T}}_{1}$=100 K, $\gamma$ values of applied heat flux, calculated and varied values of $k_{\alpha}$ at t = 0.1 s. Figure 6a shows the curves of $w(L/2, 2\pi/2)$ versus T and R_n for the L/h^* = 5 on ${{\emptyset }=10}^{^\circ }$ case, the maximum value of $w(L/2, 2\pi/2)$ is 129.502029 mm occurs at T = 600 K for R_n = 0.5. The $w(L/2, 2\pi/2)$ values are all increasing versus T from T = 100 K to T = 600 K then decreasing versus T from T = 600 K to T = 1000 K for R_n = 0.5. The amplitude $w(L/2, 2\pi/2)$ of the L/h^* = 5 can withstand for higher environment temperature (T = 1000 K) for R_n = 0.5 on ${{\emptyset }=10}^{^\circ }$. Figure 6b shows the curves of $w(L/2, 2\pi/2)$ versus T and R_n for the L/h^* = 10 on ${{\emptyset }=10}^{^\circ }$ case, the maximum value of $w(L/2, 2\pi/2)$ is 74.199798 mm occurs at T = 1000 K for R_n = 0.2. The $w(L/2, 2\pi/2)$ values are all decreasing versus T from T = 600 K to T = 1000 K for R_n = 2. The amplitude $w(L/2, 2\pi/2)$ of the L/h^* = 10 can withstand for higher environment temperature (T = 1000 K) for R_n = 2 on ${{\emptyset }=10}^{^\circ }$. Figure 6c shows the curves of $w(L/2, 2\pi/2)$ versus T and R_n for the L/h^* = 5 on ${\emptyset}=45^{^\circ }$ case, the maximum value of $w(L/2, 2\pi/2)$ is 10801.9971 mm occurs at T = 100 K for R_n = 0.5. The $w(L/2, 2\pi/2)$ values are all increasing versus T from T = 600 K to T = 1000 K for values of R_n = 0.5, 1 and 2. The $w(L/2, 2\pi/2)$ values are almost constant versus T from T = 600 K to T = 1000 K for values of R_n = 0.1, 0.2, 5 and 10. The amplitude $w(L/2, 2\pi/2)$ of the L/h^* = 5 cannot withstand for higher environment temperature (T = 1000 K) on ${\emptyset}=45^{^\circ }$. Figure 6d shows the curves of $w(L/2, 2\pi/2)$ versus T and R_n for the L/h^* = 10 on ${\emptyset}=45^{^\circ }$ case, the maximum value of $w(L/2, 2\pi/2)$ is 2.440104 mm occurs at T = 1000 K for value of R_n = 0.1. The $w(L/2, 2\pi/2)$ values are all increasing versus T for all value of R_n, the $w(L/2, 2\pi/2)$ values of the L/h^* = 10 also cannot withstand for higher environment temperature (T = 1000 K) at t = 0.1 s of FGM spherical shells when ${\emptyset}=45^{^\circ }$. Figure 6e shows the curves of $w(L/2, 2\pi/2)$ versus T and R_n for the L/h^* = 5 on ${\emptyset}=90^{^\circ }$ case, the maximum value of $w(L/2, 2\pi/2)$ is − 50.971008 mm occurs at T = 1000 K for R_n = 2. The $w(L/2, 2\pi/2)$ values are all increasing versus T from T = 600 K to T = 1000 K for value of R_n except that R_n = 5. The amplitude $w(L/2, 2\pi/2)$ of the L/h^* = 5 cannot withstand for higher environment temperature (T = 1000 K) except that R_n = 5 on ${\emptyset}=90^{^\circ }$. Figure 6f shows the curves of $w(L/2, 2\pi/2)$ versus T and R_n for the L/h^* = 10 on ${\emptyset}=90^{^\circ }$ case, the maximum value of $w(L/2, 2\pi/2)$ is 7.039263 mm occurs at T = 1000 K for R_n = 0.1. The $w(L/2, 2\pi/2)$ values are all increasing versus T from T = 600 K to T = 1000 K for all value of R_n. The amplitude $w(L/2, 2\pi/2)$ of the L/h^* = 10 cannot withstand for higher environment temperature (T = 1000 K) on ${\emptyset}=90^{\circ}$.

Fig. 6

$w(L/2, 2\pi/2)$ versus T and R_n for L/h^* = 5 and 10 when $\emptyset = 10^{\circ}$, 45° and 90°

Figure 7 shows the ${\sigma }_{x}$ (unit GP_a) at center position of inner surface z =  − 0.5h^* versus T and all different values R_n for the thermal vibration of nonlinear TSDT of FGM spherical shells when $\emptyset = 45^{\circ}$, thick L/h^* = 5 and 10 as the analyses of deflection case in Fig. 6. Figure 7a shows the curves of ${\sigma }_{x}$ versus T and R_n for the L/h^* = 5, the values of ${\sigma }_{x}$ versus T are all increasing (from T = 100 K to T = 600 K) and then all decreasing (from T = 600 K to T = 1000 K) for value of R_n except that R_n = 0.5, 1 and 2. The maximum value of ${\sigma }_{x}$ is − 0.116254GP_a occurs at T = 100 K for R_n = 0.5. The dominated stress ${\sigma }_{x}$ of the L/h^* = 5 can withstand for higher environment temperature (T = 1000 K) for value of R_n except that R_n = 0.5. Figure 7b shows the curves of ${\sigma }_{x}$ versus T and R_n for the L/h^* = 10 case, the values of ${\sigma }_{x}$ versus T are all increasing (from T = 100 K to T = 600 K) and then all decreasing (from T = 600 K to T = 1000 K) for all value of R_n. The maximum value of ${\sigma }_{x}$ is 0.001954GP_a occurs at T = 600 K, for R_n = 10. The dominated stress ${\sigma }_{x}$ of the L/h^* = 10 for all value of R_n can withstand for higher environment temperature (T = 1000 K) at t = 0.1 s of FGM spherical shells when $\emptyset = 45^{\circ}$.

Fig. 7

${\sigma }_{x}$ versus T on $\emptyset = 45^{\circ}$

Finally, the transient responses of $w(L/2, 2\pi/2)$ (unit mm) are presented with $c_{1}$ = 0.925925/mm² for the thermal vibration of nonlinear TSDT of FGM spherical shells when $\emptyset = 45^{\circ}$. Figure 8a shows the transient values of $w(L/2, 2\pi/2)$ in the thermal vibration of nonlinear TSDT FGM spherical shells for thick L/h^* = 5 with fixed $\omega_{11}$ = 0.005154/s and L/h^* = 10 with fixed $\omega_{11}$ = 0.000220/s, respectively. Also used the fixed value $\gamma$ = 296880.5/s of applied heat flux to calculate the transient response of super high frequency, $R_{n} = 1$, $k_{\alpha}$ = 0.120708, T = 600 K, $\bar{T}_{1}$ = 100 K for t = 0.01–0.2 s and time step is 0.001 s. The maximum value of $w(L/2, 2\pi/2)$ is 4543.42627 mm occurs at t = 0.011 s for thick L/h^* = 10. Figure 8b shows the enlargements of the transient response $w(L/2, 2\pi/2)$ for thick L/h^* = 5 and 10, during t = 0.01–0.03 s and time step is 0.001 s. The amplitude value of $w(L/2, 2\pi/2)$ of the thermal nonlinear TSDT thick FGM spherical shells at t = 0.011 s is 4543.42627 mm for L/h^* = 10 and is greater than that − 409.009521 mm for L/h^* = 5. It is very interesting to make the comparison with published work and verify the present work. There was a published similarly work by Mao et al. (2011) that is shown in the reprint Fig. 8c for transient responses of deflection in the FGM shallow spherical shell. The responses of deflections are oscillating and decreasing with time under temperature difference. Figure 8d shows the comparisons of the transient response $w(L/2, 2\pi/2)$ for thick L/h^* = 10, during t = 0.05–0.2 s and time step is 0.001 s with low $\gamma$ = 785.3982/s, $\omega_{11}$ = 0.001497/s and super high $\gamma$ = 296880.5/s, $\omega_{11}$ = 0.000220/s, respectively. The more high frequency of applied heat flux gets more high amplitude of deflection. The transient values of center deflection amplitudes versus $\gamma$ are all decreasing for thick L/h^* = 10.

Fig. 8

Transient responses of $w(L/2, 2\pi/2)$ and comparison for L/h^* = 5 and 10 on $\emptyset = 45^{\circ}$

4 Conclusions

The GDQ numerical solutions are obtained for the deflections and stresses in the thermal vibration of thick FGM spherical shells by considering the nonlinear coefficient c₁ term of TSDT. The values of center deflection amplitudes are underestimated with time in the linear case c₁ = 0/mm² for L/h^* = 5, but they are overestimated with time in the linear case c₁ = 0/mm² for L/h^* = 10, respectively by comparison with the data of nonlinear case c₁ = 0.925925/mm² when $\emptyset = 10^{\circ}$. The values of dominated stresses $\sigma_{x}$ are all decreasing with time in the case c₁ = 0.925925/mm² for thick L/h^* = 5 and 10, respectively. The amplitude $w(L/2, 2\pi/2)$ on $\emptyset = 10^{\circ}$ can withstand for higher temperature (T = 1000 K) of environment in the cases of L/h^* = 5, R_n = 0.5 and L/h^* = 10, R_n = 2. Also the dominated stress $\sigma_{x}$ in the cases of L/h^* = 5, R_n = 0.5 and L/h^* = 10 for all value of R_n can withstand for higher temperature (T = 1000 K) of environment at t = 0.1 s.