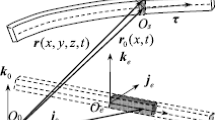Dynamic modeling and simulation of a rotating flexible hub-beam based on different discretization methods of deformation fields

Abstract

The dynamic modeling and simulation of a rotating flexible hub-beam based on different discretization methods of the deformation fields are studied. For a rotating flexible cantilever beam, assumed mode method, finite element method (FEM), Bezier interpolation method (BIM), and B-spline interpolation method (BSIM) are adopted to describe the deformation field of flexible beam and to construct unified. By means of Lagrange’s equation of the second kind, taking into account both longitudinal and transverse deformations, as well as longitudinal shortening in the longitudinal deformation caused by transverse bending deformation, dynamic simulation software based on four different discretization methods is prepared, and simulation examples are given for dynamic problems of the hub-beam. The simulation results show that FEM has a low computing efficiency, and the deformation of a flexible beam discretized by FEM cannot be guaranteed second derivative continuous at the element nodes. BIM and BSIM can be used as new discretization methods to effectively describe the deformation fields of flexible beams and have high computing efficiencies, perfectly meeting the needs of actual projects. Therefore, BIM and BSIM have good performance and application value in multi-flexible-body system dynamics.

1 Introduction

The discretization of deformation fields of flexible beams is a fundamental issue of multi-body system dynamics as well as one of the difficulties in the current research stage in this regard. Early research work in linkage elastodynamics was summarized in Refs. [1, 2], and the flexibility of mechanisms was introduced into the research of multi-body systems. The AMM and FEM are the most widely used discretization methods. Originating from the natural vibration mode of the middle of a beam in structural mechanics, the AMM is characterized by fewer modals, better approximation results and higher computing efficiency [3]. However, AMM’s applicability in solving large deformation problems is still to be verified since it derives from small deformation assumptions. FEM is a popular discretization method for deformation fields, but it requires complicated preprocessing and significant time for meshing. Besides, high-order continuous functions are not easily constructed via the FEM, which generally symbolizes continuity of displacement but not continuity of stress–strain. Moreover, since the system’s generalized coordinates are finite element nodes, there are a great number of generalized coordinates for the resulting dynamic equations [4,5,6], leading to a low real-time computing efficiency for large structures. As a result, efficient and accurate discretization methods have become a difficult key research point for rapid real-time computation of complex and flexible multi-body dynamics.

The BIM has been widely used for constructing curves and surfaces [7, 8]. Geometric construction via Bezier curves was studied in Ref. [9], and stretching, deformation, and perturbation energy of Bezier curves were analyzed. Reference [10] proposed adopting cubic spline functions to describe the deformation of flexible beams and dissected the dynamic behavior of the flexible stepped beam model for controlling its vibration. The B-spline method was used in two-dimensional elastic mechanics to solve statics problems of beams and plane plates [11]. References [12, 13] presented a theoretical derivation of the relationships among BIM, BSIM, and FEM under the absolute nodal coordinate formulation (ANCF), achieving the unification of geometric modeling in computer-aided design (CAD) and deformation fields description in computer-aided analysis (CAA). The conversion between geometric computation methods (mainly BIM and BSIM) and FEM under ANCF was studied in Refs. [14, 15], and simulation examples were given, showing that these unifications would help to achieve isogeometric analysis [16] between CAD and CAA. Later, dynamic problems of rotating flexible cantilever and tapered beams discretized by BIM and BSIM were studied [17,18,19]. Li et al. [20] presented dynamic analysis of an axially rotating FG tapered beams based on a new rigid–flexible coupled dynamic model using the B-spline method. Smoothed-point interpolation method and radial-point interpolation method were applied to the discretization of the deformation fields of flexible beams [21, 22], and the dynamic issues of a rotating flexible beam were investigated, thus enriching theories for the deformation fields description of flexible beams.

In this study, BIM and BSIM are adopted as new discretization methods to explore their performance in the dynamic modeling and analysis of flexible hub-beams. In addition, their formats are unified with those of AMM and FEM to facilitate the derivation of dynamic equations and the preparation of dynamic simulation software. In the proposed dynamic model, the transverse bending deformation and longitudinal deformation of the flexible beam are considered, and the longitudinal shortening caused by transverse bending deformation is also taken into account. C++ is used to prepare the dynamic simulation software of a flexible hub-beam based on four different discretization methods (AMM, FEM, BIM, and BSIM). The simulation results calculated by BIM and BSIM are compared with those calculated by AMM and FEM in Sect. 5; the response amplitudes and frequencies based on FEM, AMM, BIM, and BSIM are basically the same. Comparison of the advantages and disadvantages of FEM, AMM, BIM, and BSIM is studied in Sect. 6; in the case that an external torque is applied on the hub, and the rotational motion of the system is unknown. The simulation results show that the FEM has a low computing efficiency, and the deformation of a flexible beam discretized by the FEM cannot be guaranteed second derivative continuous at the element nodes. BIM and BSIM can be used as new discretization methods to effectively describe the deformation fields of flexible beams and provide high computing efficiencies. BIM and BSIM have good performance and application value in multi-flexible-body system dynamics.

2 Physical model of rotating flexible beam

Several simplifying assumptions are made to limit the range of applications of the planar rotating hub-beam system model to be derived.

• 1. The rotating beam is a uniform, homogeneous Euler–Bernoulli beam. A cross section of the beam is perpendicular to the centroid line of the beam and remains in a plane after deformation.

• 2. While stretch along the centroid line of the beam is considered, the area of any cross section of the beam remains the same after deformation.

• 3. The beam moves in a horizontal plane, and gravity is not considered.

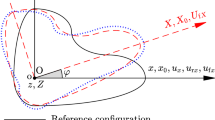
As shown in Fig. 1, the flexible hub-beam moves within the horizontal plane. To be specific, the hub rotates around a fixed axis, and its upper part is fixed by a flexible cantilever beam. An inertial coordinate system oij is established through the center of rotation of the hub. A floating coordinate system ${o}'{i}'{j}'$ is built on the flexible beam. The rotational inertia of the hub around the rotational center o is $J_{oh}$; the rotating angle of the hub is $\theta$ measured counterclockwise with respect to the ${i}'$-axis of the floating coordinate system ${o}'{i}'{j}'$. The radius of the hub is a; the length of flexible beam is L; the density, cross-sectional area, and second moment of area are $\rho$, S, and I, respectively; the bending stiffness and compressive stiffness of the beam are EI and ES, respectively.

Fig. 1

Physical model of the rotating flexible beam

It is shown in Fig. 1 that the radius vector based on the floating coordinate system from the origin o to a certain point P on the flexible beam after the deformation can be written as

$$\begin{aligned} \mathbf{r}=\mathbf{r}_{\mathrm{A}} +\mathbf{r}_0 +\mathbf{u} \end{aligned}$$

(1)

where $\mathbf{r}_{\mathrm{A}}$ is the radius vector from the center o of the hub to the base point ${o}'$ of the floating coordinate system, and $\mathbf{r}_0$ is the radius vector of point P under the floating coordinate system before the deformation. The deformation vector of point P is $\mathbf{u}=[u_x ,u_y ]^{\mathrm{T}}$, which can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} u_x =u_{x1} +u_{x2} \\ u_y =u_y \\ \end{array}} \right. \end{aligned}$$

(2)

where $u_{x1}$ is the longitudinal deformation, $u_y$ is the transverse bending deformation, and $u_{x2}$ is the longitudinal shortening caused by transverse bending. This nonlinear coupling term can be expressed as

$$\begin{aligned} u_{x2} =-\frac{1}{2}\int _0^x \left( \frac{\partial u_y}{\partial \xi }\right) ^{2} \hbox {d}\xi \end{aligned}$$

(3)

Assuming that ${\varvec{\Theta }}$ is the direction cosine matrix of the floating coordinate system compared to the inertial coordinate system, the coordinate matrices of the radius vector $\mathbf{r}$ under the inertial coordinate system are written as

$$\begin{aligned} \mathbf{r}={\varvec{\Theta }}(\mathbf{r}_{\mathrm{A}} +\mathbf{r}_0 +\mathbf{u}) \end{aligned}$$

(4)

where $\mathbf{r}_{\mathrm{A}} =(a,0)^{\mathrm{T}}$, $\mathbf{r}_0 =(x,0)^{\mathrm{T}}$, $\mathbf{u}=[u_x ,u_y ]^{\mathrm{T}}$, and ${\varvec{\Theta }}=\left( {\begin{array}{cc} \cos \theta &{}-\sin \theta \\ \sin \theta &{}\cos \theta \\ \end{array}} \right)$. The velocity vector can be determined as

$$\begin{aligned} \dot{\mathbf{r}}=\dot{{\varvec{\Theta }}}(\mathbf{r}_{\mathrm{A}} +\mathbf{r}_0 +\mathbf{u})+{\varvec{\Theta }}\dot{\mathbf{u}} \end{aligned}$$

(5)

The kinetic energy of the system can be written as

$$\begin{aligned} T=\frac{1}{2}\int _V {\rho S(\dot{\mathbf{r}}^{\mathrm{T}}\dot{\mathbf{r}})} \hbox {d}V+\frac{1}{2}J_{oh} \dot{\theta }^{2} \end{aligned}$$

(6)

where $J_{oh}$ is the rotary inertia of hub; $\dot{\theta }$ is the rotational angular velocity of hub.

The potential energy of the system can be written as

$$\begin{aligned} U=\frac{1}{2}\int _0^L \left[ ES\left( \frac{\partial u_{x1} }{\partial x}\right) ^{2} +\frac{1}{2}EI\left( \frac{\partial ^{2}u_y }{\partial x^{2}}\right) ^{2}\right] dx \end{aligned}$$

(7)

3 Description of deformation fields

3.1 Assumed mode method (AMM)

Based on the AMM, the longitudinal deformation and transverse bending deformation of a flexible beam can be written as [23]

$$\begin{aligned} \left\{ {\begin{array}{l} u_{x1} =\varvec{\Phi }_x (x)\mathbf{A}(t) \\ u_y =\varvec{\Phi }_y (x)\mathbf{B}(t) \\ \end{array}} \right. \end{aligned}$$

(8)

where $\varvec{\Phi }_x (x)\in \mathbf{R}^{1\times Nx}$ and $\varvec{\Phi }_y (x)\in \mathbf{R}^{1\times Ny}$ are the modal function row vectors of longitudinal and transverse vibrations of the flexible beam, respectively; $\mathbf{A}(t)\in \mathbf{R}^{Nx}$ and $\mathbf{B}(t)=\mathbf{R}^{Ny}\in$ are the modal coordinate column vectors of longitudinal and transverse vibrations of flexible beam, respectively. These can additionally be written as

$$\begin{aligned} \left\{ {\begin{array}{ll} \varvec{\Phi }_x (x)=[\phi _{x1} (x),\phi _{x2} (x),\cdots \phi _{xNx} (x)]&{}\mathbf{A}(t)=[A_1 (t),A_2 (t),\cdots A_{Nx} (t)]^{\mathrm{T}} \\ \varvec{\Phi }_y (x)=[\phi _{y1} (x),\phi _{y2} (x),\cdots \phi _{yNy} (x)]&{}\mathbf{B}(t)=[B_1 (t),B_2 (t),\cdots B_{Ny} (t)]^{\mathrm{T}} \\ \end{array}} \right. \end{aligned}$$

(9)

where the modal functions $\phi _{xi} (x)$ and $\phi _{yi} (x)$ of a cantilever beam are written as

$$\begin{aligned} \begin{aligned} \phi _{xi} (x)&=\sin \frac{(2i-1)\pi }{2L}x,\quad i=1,2,\ldots ,Nx \\ \phi _{yi} (x)&=\cos (\beta _i x)-\cosh (\beta _i x)+\gamma _i \left[ {\sin (\beta _i x)-\sinh (\beta _i x)} \right] ,\quad i=1,2,\ldots ,Ny \\ \end{aligned} \end{aligned}$$

(10)

where

$$\begin{aligned} \beta _1 L= & {} 1.875,\quad \beta _2 L=4.694 \nonumber \\ \beta _i L= & {} (i-0.5)\pi ,\quad i\ge 3 \end{aligned}$$

(11)

$$\begin{aligned} \gamma _i= & {} -\frac{\cos (\beta _i L)+\cosh (\beta _i L)}{\sin (\beta _i L)+\sinh (\beta _i L)} \end{aligned}$$

(12)

Substituting Eq. (8) into Eq. (2) yields the deformation displacement of point P

$$\begin{aligned} \left\{ {\begin{array}{l} u_x =\varvec{\Phi }_x (x)\mathbf{A}(t)-\frac{1}{2}{} \mathbf{B}^{\mathrm{T}}(t)\mathbf{H}(x)\mathbf{B}(t) \\ u_y =\varvec{\Phi }_y (x)\mathbf{B}(t) \\ \end{array}} \right. \end{aligned}$$

(13)

where $\mathbf{H}(x)=\mathbf{R}^{Ny\times Ny}$ is the coupling shape function

$$\begin{aligned} \mathbf{H}(x)=\int _0^x \left( \frac{\partial \varvec{\Phi }_y^{\mathrm{T}} (\xi )}{\partial \xi }\right) \left( \frac{\partial \varvec{\Phi }_y (\xi )}{\partial \xi }\right) \hbox {d}\xi \end{aligned}$$

(14)

3.2 Finite element method (FEM)

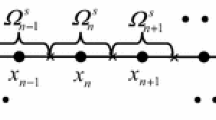
As shown in Fig. 2, the FEM is adopted to discretize the deformation fields of a flexible beam. The beam is divided into n elements, and $u_{x1}$ and $u_y$ of any point P within element $j(j=1,2\ldots n)$ are written as the linear interpolation of the deformation of the element node

$$\begin{aligned} u_{x1} =\mathbf{N}_{j,1} (\bar{{x}})\mathbf{E}_j \quad u_y =\mathbf{N}_{j,2} (\bar{{x}})\mathbf{F}_j \end{aligned}$$

(15)

Fig. 2

Finite element model of the flexible beam

where $\bar{{x}}$ is P’s Y-coordinate in the element coordinate system $O_j -X_j Y_j$. It is assumed that the element j has a length of $l_j$ and that $\hat{{x}}=\frac{\bar{{x}}}{l_j}$, so that the shape function matrix can be written as

$$\begin{aligned} \begin{aligned}&\mathbf{N}_{j,1} (\bar{{x}})=[\begin{array}{cc} N_{11}&N_{12} \end{array}] \\&\mathbf{N}_{j,2} (\bar{{x}})=[ \begin{array}{cccc} N_{21}&N_{31}&N_{22}&N_{32} \end{array}] \end{aligned} \end{aligned}$$

(16)

where

$$\begin{aligned} \begin{aligned}&N_{11} =1-\hat{{x}}\quad N_{12} =\hat{{x}} \\&N_{21} =1-3\hat{{x}}^{2}+2\hat{{x}}^{3}\quad N_{31} =l_j (\hat{{x}}-2\hat{{x}}^{2}+\hat{{x}}^{3}) \\&N_{22} =3\hat{{x}}^{2}-2\hat{{x}}^{3}\quad N_{31} =l_j (-\hat{{x}}^{2}+\hat{{x}}^{3}) \end{aligned} \end{aligned}$$

(17)

The deformation array of the element node is shown as:

$$\begin{aligned} \mathbf{E}_j =[\begin{array}{cc} u_{x1}^m&u_{x1}^k \end{array}]^{\mathrm{T}}\quad \mathbf{F}_j =[\begin{array}{cccc} u_y^m&\theta _m&u_k^m&\theta _k \end{array}]^{\mathrm{T}} \end{aligned}$$

(18)

where

$$\begin{aligned} \theta _m =\left. {\frac{\partial u_y }{\partial \bar{{x}}}} \right| _{\bar{{x}}=0} \quad \theta _m =\left. {\frac{\partial u_y }{\partial \bar{{x}}}} \right| _{\bar{{x}}=l_j } \end{aligned}$$

(19)

It is assumed that $\mathbf{C}_{xj}$, $\mathbf{C}_{yj}$ are the positional matrices decided by the element number and that $\mathbf{E}$ and $\mathbf{F}$ are the overall longitudinal and transverse deformation arrays. Then, they can be written as

$$\begin{aligned} \mathbf{E}_j =\mathbf{C}_{xj} \mathbf{E}\quad \mathbf{F}_j =\mathbf{C}_{yj} \mathbf{F} \end{aligned}$$

(20)

where

$$\begin{aligned} \begin{aligned} \mathrm{node}\,\mathrm{number}.&1\quad 2\,\cdots \cdots \,m\,k\cdots \cdots n+1 \\&\mathbf{E}=\,[u_{x1}^1 \,u_{x1}^2 \cdots \cdots u_{x1}^m \,u_{x1}^k \cdots \cdots u_{x1}^{n+1} ]^{\mathrm{T}} \\&\mathbf{C}_{xj} =\left[ {\begin{array}{l} 0\,0\,\cdots \cdots \,1\,0\,\cdots \cdots \,0 \\ 0\,0\,\cdots \cdots \,0\,1\,\cdots \cdots \,0\, \\ \end{array}} \right] \, \\ \mathrm{node}\,\mathrm{number}.&1\quad 2\,\cdots \cdots \,m\,k\,\cdots \cdots \,n+1 \\&\mathbf{E}=\,[u_y^1 \,\theta _1 \,u_y^2 \,\theta _2 \,\cdots u_y^m \,\theta _m \,u_y^k \,\theta _k \cdots u_y^{n+1} \,\theta _{n+1} ]^{\mathrm{T}} \\&\mathbf{C}_{xj} =\left[ {\begin{array}{l} 0_{2\times 2} \,0_{2\times 2} \,\cdots \,I_{2\times 2} \,0_{2\times 2} \,\cdots \,0_{2\times 2} \\ 0_{2\times 2} \,0_{2\times 2} \,\cdots \,0_{2\times 2} \,I_{2\times 2} \,\cdots \,0_{2\times 2} \, \\ \end{array}} \right] \\ \end{aligned} \end{aligned}$$

(21)

Based on the boundary conditions of the beam, $\mathbf{E}$, $\mathbf{F}$ can be written as

$$\begin{aligned} \mathbf{E}=\mathbf{R}_x \mathbf{A}\quad \mathbf{F}=\mathbf{R}_y \mathbf{B} \end{aligned}$$

(22)

where $\mathbf{A}$, $\mathbf{B}$ are the overall independent longitudinal and transverse deformation matrices and $\mathbf{R}_x$, $\mathbf{R}_y$ are the transformed matrices. For example, for a cantilever beam constrained by a fixed end, $u_{x1}^1 =0$, $u_y^1 =0$, $\theta _1=0$, $\mathbf{R}_x$, $\mathbf{R}_y$, and $\mathbf{A}$, $\mathbf{B}$ can be written as

$$\begin{aligned} \begin{aligned}&\mathbf{R}_x =\left[ {\begin{array}{l} \mathbf{0}_{1\times n} \\ I_{n\times n} \\ \end{array}} \right] _{(n+1)\times n} \quad \mathbf{A}=[u_{x1}^2 \,u_{x1}^3 \,\cdots \cdots u_{x1}^{n+1} ]^{\mathrm{T}} \\&\mathbf{R}_y =\left[ {\begin{array}{l} \mathbf{0}_{2\times 2n} \\ I_{2n\times 2n} \\ \end{array}} \right] _{2(n+1)\times 2n} \quad \mathbf{B}=[u_y^2 \,\theta _2 \,\cdots \cdots u_y^{n+1} \theta _{n+1} ]^{\mathrm{T}} \\ \end{aligned} \end{aligned}$$

(23)

Thus,

$$\begin{aligned} u_{x1}= & {} \mathbf{N}_1 \mathbf{A},u_y =\mathbf{N}_2 \mathbf{B} \end{aligned}$$

(24)

$$\begin{aligned} \mathbf{N}_1= & {} \mathbf{N}_{j,1} \mathbf{C}_{xj} \mathbf{R}_x\quad \mathbf{N}_2 =\mathbf{N}_{j,2} \mathbf{C}_{yj} \mathbf{R}_y \end{aligned}$$

(25)

The longitudinal shortening deformation caused by transverse bending deformation is written as

$$\begin{aligned} u_{x2} =-\frac{1}{2}{} \mathbf{B}^{\mathrm{T}}(t)\mathbf{H}(x)\mathbf{B}(t) \end{aligned}$$

(26)

where

$$\begin{aligned} \mathbf{H}(x)=\mathbf{R}_y^{\mathrm{T}} \mathbf{C}_{yj}^\mathbf{T} \int _0^{\bar{{x}}} \left( \frac{\partial \mathbf{N}_{j,2}^T }{\partial \bar{{x}}}\cdot \frac{\partial \mathbf{N}_{j,2} }{\partial \bar{{x}}}\right) \hbox {d} \bar{{x}}{} \mathbf{C}_{yj} \mathbf{R}_y +\sum _{i=1}^{j-1} {\mathbf{R}_y^{\mathrm{T}} \mathbf{C}_{yi}^\mathbf{T} \int _0^{l_i } \left( \frac{\partial \mathbf{N}_{i,2}^T }{\partial \bar{{x}}}\cdot \frac{\partial \mathbf{N}_{i,2} }{\partial \bar{{x}}}\right) } \hbox {d}\bar{{x}}{} \mathbf{C}_{yi} \mathbf{R}_y \end{aligned}$$

(27)

3.3 Bezier interpolation method (BIM)

Bezier adopted the deformation of vertices of characteristic polygons and linear combinations of Bernstein bases to express the deformation

$$\begin{aligned} r(\varepsilon )=\sum _{i=0}^m {J_{m,i} (\varepsilon )} V_i \end{aligned}$$

(28)

where m is the number of Bezier curves; $V_i$ is the deformation of a vertex of a characteristic polygon, and the Bernstein functions $J_{m,i} (\varepsilon )$ are written as

$$\begin{aligned} J_{m,i} (\varepsilon )= & {} C_m^i \varepsilon ^{i}(1-\varepsilon )^{m-i} \end{aligned}$$

(29)

$$\begin{aligned} C_m^i= & {} \frac{m!}{i!(m-i)!} \end{aligned}$$

(30)

Then, the longitudinal and transverse deformations of the beam can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} w_1 =\mathbf{Ja } \\ w_2 =\mathbf{Jb } \\ \end{array}} \right. \end{aligned}$$

(31)

where

$$\begin{aligned} \begin{aligned} \mathbf{J }&=\left[ J_{m,0} \left( \frac{x}{L}\right) ,J_{m,1} \left( \frac{x}{L}\right) \cdots \cdots J_{m,m} \left( \frac{x}{L}\right) \right] \\ \mathbf{a }&=[a_0 ,a_1 ,\cdots \cdots a_m ]^{\mathrm{T}} \\ \mathbf{b }&=[b_0 ,b_1 ,\cdots \cdots b_m ]^{\mathrm{T}} \\ \end{aligned} \end{aligned}$$

(32)

where $a_i ,b_i$ are the deformation time variables of a vertex of a characteristic polygon along the longitudinal and transverse directions of the beam. Based on the BIM, the longitudinal deformation and transverse bending deformation of any point on the cantilever beam can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} u_{x1} =\varvec{\Phi }_x (x)\mathbf{A}(t) \\ u_y =\varvec{\Phi }_y (x)\mathbf{B}(t) \\ \end{array}} \right. \end{aligned}$$

(33)

where $\varvec{\Phi }_x (x)\in \mathbf{R}^{1\times Nx}$ and $\varvec{\Phi }_y (x)\in \mathbf{R}^{1\times Ny}$ are the row vectors of the Bernstein functions of the longitudinal and transverse vibrations of the beam, respectively; $\mathbf{A}(t)\in \mathbf{R}^{Nx}$ and $\mathbf{B}(t)\in \mathbf{R}^{Ny}$ are the column vectors of Bezier interpolation controlled-vertex deformations of longitudinal and transverse vibrations, which can be written as

$$\begin{aligned}&\left\{ {\begin{array}{l} \varvec{\Phi }_x (x)=[J_{Nx,1} (x),J_{Nx,1} (x),\cdots J_{Nx,Nx} (x)] \\ \mathbf{A}(t)=[a_1 ,a_2 ,\cdots a_{Nx} ]^{\mathrm{T}} \\ \end{array}} \right. \end{aligned}$$

(34)

$$\begin{aligned}&\left\{ {\begin{array}{l} \varvec{\Phi }_y (x)=[J_{Ny+1,2} (x),J_{Ny+1,3} (x),\cdots J_{Ny+1,Ny+1} (x)]\\ \mathbf{B}(t)=[b_2 ,b_3 ,\cdots b_{Ny+1} ]^{\mathrm{T}}\\ \end{array}} \right. \end{aligned}$$

(35)

The longitudinal shortening caused by transverse bending deformation is written as

$$\begin{aligned} u_{x2} =-\frac{1}{2}{} \mathbf{B}^{\mathrm{T}}(t)\mathbf{H}(x)\mathbf{B}(t) \end{aligned}$$

(36)

where $\mathbf{H}(x)=\mathbf{R}^{Ny\times Ny}$ is a coupling shape function

$$\begin{aligned} \mathbf{H}(x)=\int _0^x \left( \frac{\partial \varvec{\Phi }_y^{\mathrm{T}} (\xi )}{\partial \xi }\right) \left( \frac{\partial \varvec{\Phi }_y (\xi )}{\partial \xi }\right) \hbox {d}\xi \end{aligned}$$

(37)

3.4 B-spline interpolation method (BSIM)

Spline partition is conducted on the beam axis along the x direction

$$\begin{aligned} \begin{aligned}&0=x_0<x_1<x_2<\cdots <x_n =l \\&x_i =x_0 +ih\quad h=x_{i+1} -x_i =l/n \end{aligned} \end{aligned}$$

(38)

The beam axis within the interval [0, l] is divided into n parts, and the longitudinal and transverse deformation functions of the beam are written as

$$\begin{aligned} \left\{ {\begin{array}{l} w_1 ={\varvec{\varphi }} \mathbf{a } \\ w_2 ={\varvec{\varphi }} \mathbf{b } \\ \end{array}} \right. \end{aligned}$$

(39)

where

$$\begin{aligned} \begin{aligned} \mathbf{a }&=[u_0 \,{u}'_0 \,a_1 ,\cdots \cdots a_{n-1} \,u_n \,{u}'_n \,]^{\mathrm{T}} \\ \mathbf{b }&=[w_0 \,{w}'_0 \,b_1 ,\cdots \cdots b_{n-1} \,w_n \,{w}'_n \,]^{\mathrm{T}} \\ {\varvec{\upvarphi }}&=[\phi _{-1} \,\phi _0 \,\phi _1 \,\cdots \,\phi _{n-1} \,\phi _n \,\phi _{n-1} ] \end{aligned} \end{aligned}$$

(40)

where $u_0 \,,w_0 ,\,{u}'_0 ,{w}'_0$ are the longitudinal and transverse deformations of the left end ($x=0$) of the beam and their angles of rotation, respectively; $u_n \,,w_n ,\,{u}'_n ,{w}'_n$ are the longitudinal and transverse deformations of the right end ($x=l)$ of the beam and their angles of rotation, respectively; and $a_1 ,\cdots \cdots a_{n-1}$ and $\,b_1 ,\cdots \cdots b_{n-1}$ are the deformation time variables of the vertex of a characteristic polygon. Cubic B-spline functions $\varphi _3 (\eta )$ are employed to construct the basis function $\phi _i (x)$:

$$\begin{aligned} \left\{ {\begin{array}{l} \phi _{-1} =\frac{3}{2}\varphi _3 \left( \frac{x}{h}\right) \,\phi _0 =\frac{h}{2}\varphi _3 \left( \frac{x}{h}\right) -2h\varphi _3 \left( \frac{x}{h}+1\right) \, \\ \phi _1 =\varphi _3 \left( \frac{x}{h}-1\right) -\frac{1}{2}\varphi _3 \left( \frac{x}{h}\right) +\varphi _3 \left( \frac{x}{h}+1\right) \\ \phi _i =\varphi _3 \left( \frac{x}{h}-i\right) \,i=2,3,\cdots n-2 \\ \phi _{n-1} =\varphi _3 \left( \frac{x}{h}-n+1\right) -\frac{1}{2}\varphi _3 \left( \frac{x}{h}-n\right) +\varphi _3 \left( \frac{x}{h}-n-1\right) \\ \phi _n =\frac{3}{2}\varphi _3 \left( \frac{x}{h}-n\right) \\ \phi _{n+1} =2h\varphi _3 \left( \frac{x}{h}-n-1\right) -\frac{h}{2}\varphi _3 \left( \frac{x}{h}-n\right) \\ \end{array}} \right. \end{aligned}$$

(41)

where

$$\begin{aligned} \varphi _3 (\eta )=\frac{1}{6}\left\{ {\begin{array}{ll} (\eta +2)^{3}&{}\quad \eta \in [-2,-1] \\ (\eta +2)^{3}-4(1+\eta )^{3}&{}\quad \eta \in [-1,0] \\ (2-\eta )^{3}-4(1-\eta )^{3}&{}\quad \eta \in [0,1] \\ (2-\eta )^{3}&{}\quad \eta \in [1,2] \\ 0&{}\quad \left| \eta \right| \ge 2 \\ \end{array}} \right. \end{aligned}$$

(42)

The spline function in Eq. (41) has the following characteristics:

$$\begin{aligned} \left\{ {\begin{array}{ll} \phi _i (0)=0\,(i\ne -1)&{}\quad \phi _{-1} (0)=1 \\ {\phi }'_i (0)=0\,(i\ne 0)&{}\quad \phi _0 (0)=1 \\ \phi _i (l)=0\,(i\ne n)&{}\quad \phi _n (l)=1 \\ {\phi }'_i (l)=0\,(i\ne n+1)&{}\quad {\phi }'_{n+1} (l)=1 \\ \end{array}} \right. \end{aligned}$$

(43)

Benefiting from the characteristics of spline function in Eq. (43), the boundary conditions of flexible beam can be effectively processed. Based on the BSIM, the longitudinal and transverse deformations of the cantilever beam can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} w_1 =\varvec{\Phi }_x (x)\mathbf{A}(t) \\ w_2 =\varvec{\Phi }_y (x)\mathbf{B}(t) \\ \end{array}} \right. \end{aligned}$$

(44)

where

$$\begin{aligned} \left\{ {\begin{array}{l} \varvec{\Phi }_x (x)=[\phi _1 \,\phi _2 \,\cdots \,\phi _n \,\phi _{n+1} ]\, \\ \mathbf{A}(t)=[a_1 \,a_2 \,\cdots \,u_n \,u_{n+1} ]^{\mathrm{T}} \\ \varvec{\Phi }_y (x)=[\phi _1 \,\phi _2 \,\cdots \,\phi _n \,\phi _{n+1} ]\, \\ \mathbf{B}(t)=[b_1 \,b_2 \,\cdots \,w_n \,w_{n+1} ]^{\mathrm{T}} \\ \end{array}} \right. \end{aligned}$$

(45)

Substituting Eq. (44) into Eq. (2) gives the deformation of Point P as

$$\begin{aligned} \left\{ {\begin{array}{l} u_x =\varvec{\Phi }_x (x)\mathbf{A}(t)-\frac{1}{2}{} \mathbf{B}^{\mathrm{T}}(t)\mathbf{H}(x)\mathbf{B}(t) \\ u_y =\varvec{\Phi }_y (x)\mathbf{B}(t) \\ \end{array}} \right. \end{aligned}$$

(46)

where $\mathbf{H}(x)$ is a coupling shape function, which can be written as:

$$\begin{aligned} \mathbf{H}(x)=\int _0^x \left( \frac{\partial \varvec{\Phi }_y^{\mathrm{T}} (\xi )}{\partial \xi }\right) \left( \frac{\partial \varvec{\Phi }_y (\xi )}{\partial \xi }\right) \hbox {d}\xi \end{aligned}$$

(47)

4 Dynamic modeling of rotating flexible beam

The longitudinal and transverse deformations of the beam based on the four discretization methods are substituted into the expressions (Eqs. 6, 7) for kinetic energy and potential energy of the beam. The generalized coordinates and generalized external force are taken as $\mathbf{q}=(\theta ,\mathbf{A}^{\mathrm{T}},\mathbf{B}^{\mathrm{T}})$ and $\mathbf{F}_q =(\tau ,\mathbf{0},\mathbf{0})^{\mathrm{T}}$. The Lagrange’s dynamic equation of the second kind is adopted. Thus, the dynamic equation can be derived as

$$\begin{aligned} \left[ {\begin{array}{ccc} M_{11} &{}\mathbf{M}_{12} &{}\mathbf{M}_{13} \\ M_{21} &{}\mathbf{M}_{22} &{}\mathbf{0} \\ M_{31} &{}\mathbf{0}&{}\mathbf{M}_{33} \\ \end{array}} \right] \left[ {\begin{array}{c} \ddot{\theta } \\ \ddot{\mathbf{A}} \\ \ddot{\mathbf{B}} \\ \end{array}} \right] =\left[ {\begin{array}{c} Q_\theta \\ \mathbf{Q}_A \\ \mathbf{Q}_B \\ \end{array}} \right] \end{aligned}$$

(48)

where

$$\begin{aligned} M_{11}= & {} J_{oh} +J_{ob} +2\mathbf{S}_x \mathbf{A}+\mathbf{A}^{\mathrm{T}}\mathbf{M}_1 \mathbf{A}+\mathbf{B}^{\mathrm{T}}{} \mathbf{M}_2 \mathbf{B}-\mathbf{B}^{\mathrm{T}}(a\mathbf{C}+\mathbf{D})\mathbf{B} \end{aligned}$$

(49)

$$\begin{aligned} M_{21}= & {} M_{12}^{\mathrm{T}} =-\mathbf{M}_3 \mathbf{B} \end{aligned}$$

(50)

$$\begin{aligned} \mathbf{M}_{13}= & {} \mathbf{M}_{31}^{\mathrm{T}} =\mathbf{S}_y^{\mathrm{T}} +\mathbf{M}_3^\mathbf{T} \mathbf{A} \end{aligned}$$

(51)

$$\begin{aligned} \mathbf{M}_{22}= & {} \mathbf{M}_1 =\int _0^L {\rho S\varvec{\Phi }_x^{\mathrm{T}} \varvec{\Phi }_x \hbox {d}x} \end{aligned}$$

(52)

$$\begin{aligned} \mathbf{M}_{33}= & {} \mathbf{M}_2 =\int _0^L {\rho S\varvec{\Phi }_y^{\mathrm{T}} \varvec{\Phi }_y \hbox {d}x} \end{aligned}$$

(53)

$$\begin{aligned} Q_\theta= & {} \tau -2\dot{\theta }[\mathbf{S}_x \dot{\mathbf{A}}+\mathbf{A}^{\mathrm{T}}{} \mathbf{M}_1 \dot{\mathbf{A}}+\mathbf{B}^{\mathrm{T}}{} \mathbf{M}_2 \dot{\mathbf{B}}-\mathbf{B}^{\mathrm{T}}(a\mathbf{C}+\mathbf{D})\dot{\mathbf{B}}] \end{aligned}$$

(54)

$$\begin{aligned} Q_A= & {} \dot{\theta }^{2}{} \mathbf{S}_x^\mathbf{T} +2\dot{\theta }{} \mathbf{M}_3 \dot{\mathbf{B}}+(\dot{\theta }^{2}{} \mathbf{M}_1 -\mathbf{K}_1 )\mathbf{A}] \end{aligned}$$

(55)

$$\begin{aligned} Q_B= & {} \dot{\theta }^{2}(\mathbf{M}_2 -a\mathbf{C}-\mathbf{D})\mathbf{B}-2\dot{\theta }{} \mathbf{M}_3 \dot{\mathbf{A}}+\mathbf{K}_2 \mathbf{B}] \end{aligned}$$

(56)

In Eqs. (49–56), $\mathbf{S}_x$, $\mathbf{S}_y$, $\mathbf{M}_3$, $\mathbf{C}$, $\mathbf{D}$, $\mathbf{K}_1$, and $\mathbf{K}_2$ are constant coefficient matrices which are shown by Refs. [17, 18].

5 Interpolation method validation

In this section, the results calculated by BIM and BSIM are compared with those calculated by AMM and FEM. Adams’ predictor–corrector method was used to solve the system’s equations. The parameters of the rotating hub-beam [23] are $a=0\,\hbox {m}$, $L=8\,\hbox {m}$, $S=7.2968\times 10^{-5}\,\hbox {m}^{\mathrm{2}}$, $I=8.2189\times 10^{-9}\,\hbox {m}^{\mathrm{4}}$, $\rho =2.7667\times 10^{3}\,\hbox {Kg/m}^{\mathrm{3}}$, and $E=6.8952\times 10^{10}\,\hbox {N/m}^{\mathrm{2}}$. Four degrees of freedom for the transverse bending direction are chosen by AMM, FEM, BIM, and BSIM, shown in figures as AMM4, FEM4, BIM4, and BSIM4.

5.1 Dynamic of the rotating hub-beam system when the angular velocity of the hub is given

When the angular velocity of the hub is given, Eq. (48) can be written as

$$\begin{aligned} \left[ {\begin{array}{cc} \mathbf{M}_{22} &{}\mathbf{0} \\ \mathbf{0}&{}\mathbf{M}_{33} \\ \end{array}} \right] \left[ {\begin{array}{c} \ddot{\mathbf{A}} \\ \ddot{\mathbf{B}} \\ \end{array}} \right] =\left[ {\begin{array}{cc} \mathbf{Q}_A&{} -M_{21} \ddot{\theta } \\ \mathbf{Q}_B&{} -M_{31} \ddot{\theta } \\ \end{array}} \right] \end{aligned}$$

(57)

where $M_{21}$, $M_{31}$, $\mathbf{M}_{22}$, $\mathbf{M}_{33}$, $\mathbf{Q}_A$, and $\mathbf{Q}_B$ are shown in Eqs. (50),(51),(52),(53),(55), and (56). The spin-up maneuver of the flexible beam is prescribed by the angular rate of the hub:

$$\begin{aligned} \dot{\theta }=\left\{ {\begin{array}{ll} \frac{\Omega _{\mathrm{0}} }{\hbox {T}}t-\frac{\Omega _{\mathrm{0}} }{2\uppi }\sin \left( \frac{2\uppi }{\hbox {T}}t\right) ,&{}0\le t\le \hbox {T} \\ \Omega _{\mathrm{0}} &{}t>\hbox {T} \\ \end{array}} \right. \end{aligned}$$

(58)

This function can guarantee that angular speed increases very smoothly (when $t\le \hbox {15\,s}$). Then, the beam can rotate at the constant angular speed after reaching a steady-state angular speed ($t>\hbox {15\,s}$). For these examples, $\Omega _{\mathrm{0}} =4\,\hbox {rad}/\hbox {s}$ and $\Omega _{\mathrm{0}} =10\,\hbox {rad}/\hbox {s}$.

Fig. 3

Tip transverse bending deformation of the beam when $\Omega _{\mathrm{0}} =4\,\hbox {rad}/\hbox {s}$

Fig. 4

Tip transverse bending deformation of the beam when $\Omega _{\mathrm{0}} =10\,\hbox {rad}/\hbox {s}$

Figure 3 presents the tip transverse deformation of the beam when $\Omega _{\mathrm{0}} =4\,\hbox {rad}/\hbox {s}$.The response amplitudes and response frequencies based on FEM, AMM, BIM, and BSIM are basically the same, consistent with the simulation results in Refs. [17,18,19, 21, 23]. Figure 4 presents the tip transverse bending deformation of the beam when $\Omega _{\mathrm{0}} =10\,\hbox {rad}/\hbox {s}$; the simulation results based on FEM, BIM, BSIM and AMM again show no difference. Figure 5 shows the tip longitudinal deformation $u_{x1}$ of the beam without the longitudinal shortening $u_{x2}$. Figure 6 shows the tip longitudinal deformation $u_x =u_{x1} +u_{x2}$ (the longitudinal shortening caused by transverse bending deformation is considered) of the beam. The results in Figs. 5 and 6 show that the longitudinal deformation compared with the longitudinal shortening caused by transverse bending deformation is very small; thus, longitudinal deformation will not greatly influence transverse deformation and the longitudinal shortening caused by transverse bending cannot be neglected. The computing efficiencies, errors, response frequencies, and response amplitudes for the flexible beam when the angular velocity of the hub is $\Omega _{\mathrm{0}} =4\,\hbox {rad}/\hbox {s}$ based on FEM, BIM, BSIM, and AMM are presented in Table 1; From this table, it is seen that the response frequencies and amplitudes for the beam are basically the same across all methods. It can be found from the computation errors in the FEM that AMM, BIM, and BSIM all meet the needs of projects, while BIM and BSIM have higher high-speed simulation precision. In terms of computing efficiency, the FEM has the lowest efficiency; BIM has the highest efficiency, followed by the BSIM.

Fig. 5

Tip longitudinal deformation of the beam when $\Omega _{\mathrm{0}} =4\,\hbox {rad}/\hbox {s}$ (the longitudinal shortening caused by transverse bending deformation is not considered)

Fig. 6

Tip longitudinal deformation of the beam when $\Omega _{\mathrm{0}} =10\,\hbox {rad}/\hbox {s}$ (the longitudinal shortening caused by transverse bending deformation is considered)

Table 1 Computation time, errors, response frequencies, and response amplitudes for the beam based on four discretization methods of FEM, BIM, BSIM, and AMM ($\Omega _{\mathrm{0}} =4\,\hbox {rad}/\hbox {s})$

5.2 Dynamic of the rotating hub-beam system when an external torque is applied on the hub

As shown by Refs. [18, 23], a rotating torque on the hub is given by:

$$\begin{aligned} \tau (t)=\left\{ {\begin{array}{ll} \tau _0 \sin \left( \frac{2\uppi }{\hbox {T}}t\right) ,&{}\quad 0\le t\le T \\ 0&{}\quad t>T \\ \end{array}} \right. \end{aligned}$$

(59)

where $T=\hbox {10s}$, $\tau _0 =\hbox {1N}\, \hbox {m}$, and $\tau _0 =\hbox {10N}\, \hbox {m}$.

Figures 7 and 8 present the tip transverse deformation of the beam when $\tau _0 =\hbox {1N}\, \hbox {m}$ and $\tau _0 =\hbox {10N}\, \hbox {m}$. Again the results for four different discretization methods are basically the same; as shown in partially enlarged graph, their response frequencies show no difference.

Fig. 7

Tip transverse bending deformation of flexible beam when $\tau _0 =\hbox {1N}\, \hbox {m}$

Fig. 8

Tip transverse bending deformation of flexible beam when $\tau _0 =\hbox {10N}\, \hbox {m}$

6 Comparison of four discretization methods

In this section, the advantages and disadvantages of FEM, AMM, BIM, and BSIM are studied when an external torque is applied to the hub. The parameters of the rotating beam and the rotating torque on the hub are the same as in Sect. 5. As shown by Sect. 5 and Refs. [18, 23], the longitudinal deformation is very small compared to the longitudinal shortening caused by transverse bending. So the longitudinal deformation can be neglected in this section.

Fig. 9

Tip transverse bending deformation of flexible beam by using the FEM a when $\tau _0 =\hbox {1N}\, \hbox {m}$ and b when $\tau _0 =\hbox {10N}\, \hbox {m}$

Fig. 10

Tip transverse bending deformation of flexible beam using the AMM a when $\tau _0 =\hbox {1N}\, \hbox {m}$ and b when $\tau _0 =\hbox {10N}\, \hbox {m}$

Fig. 11

Tip transverse bending deformation of flexible beam using the BIM a when $\tau _0 =\hbox {1N}\, \hbox {m}$ and b when $\tau _0 =\hbox {10N}\, \hbox {m}$

Figures 9, 10, 11, and 12 show tip transverse bending deformation of a flexible beam using different discretization methods when $\tau _0$ is chosen to be 1 and 10 Nm. The simulation results are compared by changing degrees of freedom for the transverse bending direction. Figure 9 shows that the tip transverse bending deformation of the flexible beam discretized by the FEM are not the same when $\tau _0$ is chosen to be 1 and 10 Nm. Shape functions for the FEM are derived from Hermite interpolation, which is not guaranteed second derivative continuous at the element nodes. As shown in Fig. 10, the tip transverse bending deformations of the flexible beam discretized by the AMM are the same. Shape functions of the AMM are represented by trigonometric functions, which are guaranteed unlimited number of derivative continuous. The simulation result discretized by the AMM is more correct as the modal order increases. As shown in Fig. 11, the tip transverse bending deformations of the flexible beam discretized by the BIM are the same. Shape functions of the BIM are derived from Bernstein functions, which are guaranteed m-order derivative continuous. As shown in Fig. 12, the tip transverse bending deformations of the flexible beam discretized by the BSIM are the same. Shape functions of the BSIM are derived from cubic spline function, which is guaranteed second derivative continuous. In terms of computing efficiency, the FEM has a low real-time computing efficiency because it needs to deal with the subsection integral. The BIM has the highest efficiency, followed by AMM and BSIM.

Fig. 12

Tip transverse bending deformation of flexible beam using the BSIM: a when $\tau _0 =\hbox {1N}\, \hbox {m}$ and b when $\tau _0 =\hbox {10N}\, \hbox {m}$

7 Conclusions

• (1) For dynamic problems with flexible beams in rotation, under small deformation, AMM, BIM, and BSIM all have high computing efficiencies and precisions, while FEM has a relatively low computing efficiency.

• (2) In the dynamic analysis of rotating cantilever beams, the neglect of longitudinal deformation will not have a great influence on the dynamic behavior of the transverse vibration, but longitudinal shortening caused by transverse bending deformation should not be neglected.

• (3) The deformation of flexible beams discretized by the FEM cannot be guaranteed second derivative continuous at the element nodes; therefore, the stress–strain of the system is not necessarily continuous. AMM, BIM, and BSIM do not have this problem.