Experimental validation of rigid-flexible coupling dynamic formulation for hub–beam system

Abstract

The aim of this paper is to compare the accuracy of the absolute nodal coordinate formulation and the floating frame of reference formulation for the rigid-flexible coupling dynamics of a three-dimensional Euler–Bernoulli beam by numerical and experimental validation. In the absolute nodal coordinate formulation, based on geometrically exact beam theory and considering the torsion effect, the material curvature of the beam is derived, and then variational equations of motion of a three-dimensional beam are obtained, which consist of three position coordinates, two slope coordinates, and one rotational coordinate. In the floating frame of reference formulation, the displacement of an arbitrary point on the beam is described by the rigid-body motion and a small superimposed deformation displacement. Based on linear elastic theory, the quadratic terms of the axial strain are neglected, and the curvatures are simplified to the first order. Considering both the linear damping and the quadratic air resistance damping, the equations of motion of the multibody system composed of air-bearing test bed and a cantilevered three-dimensional beam are derived based on the principle of virtual work. In order to verify the results of the computer simulation, two experiments are carried out: an experiment of hub–beam system with large deformation and a dynamic stiffening experiment. The comparison of the simulation and experiment results shows that in case of large deformation, the frequency result obtained by the floating frame of reference formulation is lower than that obtained by the experiment. On the contrary, the result obtained by the absolute nodal coordinate formulation agrees well with that obtained by the experiment. It is also shown that the floating frame of reference formulation based on linear elastic theory cannot reveal the dynamic stiffening effect. Finally, the applicability of the floating frame of reference formulation is clarified.

1 Introduction

In multibody system simulation, the appearance of light weight structures has increased the need to account for the flexibility of structural components. Due to practical applications, such as helicopter rotor blades, turbine machine rotor blades, flexible robot arms, and spacecrafts with flexible appendages, the rigid-flexible coupling effect has been paid attention to in case of large deformation.

The floating frame of reference formulation has been applied for simulation of flexible multibody system for a long time. The advantage of such a formulation is that in case of small deformation, the stiffness matrix of the elastic body is linear and that the modal reduction approaches can be used for reducing the degrees of freedom of the system. In the linear hybrid coordinate formulation of flexible multibody system, with the assumption of small deformation, the quadratic terms in strain are not taken into account. Based on the linear model, coupling between rigid-body motion and elastic deformations was taken into account in [1]. It was found that such a linear approximated formulation fails to explain the stiffening effect for a high-speed rotating elastic beam [2], and then, considering centrifugal stiffening effect, dynamic performance of a rotating hub–beam system was investigated using the stress stiffening method in [3, 4]. The stress stiffness matrix was derived from the internal virtual work that includes nonlinear terms of strain-displacement relationship and the reference stresses induced by existing loads before deformation. Another nonlinear formulation for dynamic stiffening analysis was proposed, in which the longitudinal deformation was expressed using an axial stretch coordinate along the deformed axis [2, 5]. The advantage of such a method is that by using a stretch variable, a linear expression of strain energy can be obtained, so that it has been efficiently used for investigating dynamic stiffening problems. This formulation was extended to investigate a hub–beam system with a tip mass considering both viscous damping and air drag force [6], and then a criterion was proposed to clarify the application range of the linear model in which the stiffening effect can be neglected [7]. However, it was found that in case of large deformation, the high-order deformation terms cannot be neglect, nor can the modal reduction technique be used, and therefore the use of the floating frame of reference formulation may significantly increase the time cost because the generalized mass matrices, the stiffness matrices, and the generalized force matrices are highly nonlinear [8, 9].

Absolute nodal coordinate formulation is now widely used for simulation of flexible multibody system with large deformation. The investigation of beam finite elements of absolute nodal coordinate formulation can be divided into two main research directions: the gradient deficient beam elements and the cross-section deformable elements considering shear effect. In the direction of the gradient deficient beam elements, the transverse shear deformation is not taken into account. The position vector of an arbitrary point on the centerline can be described by employing absolute position coordinates and the slope coordinates in the axial direction of the element. The gradient deficient beam elements lack slope vectors in the transverse direction. In early investigations of ANCF, two-dimensional gradient deficient beam elements were employed under the Euler–Bernoulli beam assumption by employing a local coordinate system to evaluate the elastic forces based on nonlinear strain-displacement relationship [10], in which the generalized axial strain and spatial measure of curvature for bending were used. The description of elastic forces was enhanced by using the material measure of curvature [11]. It was also demonstrated that the planar ANCF elements can include the geometrical stiffening effect correctly [12]. The investigation of ANCF was then extended to three-dimensional beams. Neglecting the torsion deformation, a three-dimensional ANCF beam element using the Euler–Bernoulli theory was developed [13]. In order to consider the torsion deformation, two slope coordinates and one rotational coordinate were used to represent the attitude motion of the cross-section [14]. In the investigation, the geometrical curvature was used to describe the bending and torsion deformation of the beam. It has been shown, with simple planar analysis, that the material measure of curvature should be used for a description of large bending deformation instead of the geometrical curvature. Furthermore, it has been observed that the use of rotational parameters in the ANCF can lead to a numerical singularity problem, which can be solved with the director update method [15]. In the second direction of investigation based on ANCF, shear and cross-section deformable elements were developed [16]. By introducing the additional slopes in the transverse directions of the element, transverse shear deformation can be described. In such a formulation, the vector of elastic forces was derived based on the second Piola–Kirchhoff stress and the Green–Lagrange strain. In addition, the deformation of the cross-section can be allowed by relaxing some of the assumptions used in the Euler–Bernoulli and Timoshenko beam theories. Using a continuum mechanics approach, the elastic forces were defined straightforwardly by the use of the slopes in the element transverse directions. In the three-dimensional beam, the elastic forces were defined by introducing the Serret–Frenet frame and the Gram–Schmidt orthogonalization [17]. However, it was found that the use of a continuum mechanics approach may lead to the results that do not converge to the correct solutions in case the Poisson ratio is not equal to zero [18], which is called the Poisson locking problem. The approach to prevent Poisson locking was to remove the Poisson effect [19] or to set the Poisson ratio equal to zero [20]. In addition to Poisson locking, it was also shown that the ANCF beam elements suffered from shear locking [21]. It was found that the application of the Hellinge–Reissner principle, together with an elastic line approach, may lead to an improved convergence of bending dominated problems. The definition of elastic forces was improved by use of the Hellinger–Reissner principle [22, 23]. Furthermore, it was shown that the selective reduced integration alleviates the shear locking [24]. A further optimized reduced integration scheme can improve the convergence, especially for thin elements.

A comparison of the floating frame of reference and the absolute nodal coordinate formulation was performed for static and dynamic problems, both in the small and large deformation regimes [25]. It was concluded that for both static and dynamic problems, the ANCF method is faster with an increasing number of finite elements in case of large deformation. However, the accuracy of the floating frame of reference and the absolute nodal coordinate formulation have not been validated through comparison with the experiment results.

In order to verify the effectiveness of the absolute nodal coordinate formulation, large oscillations of a thin cantilever beam are studied in this paper to numerically model the beam, which also accounts for the effects of an attached end-point weight and damping forces [26]. The experiments were carried out using a high-speed camera and a data acquisition system. In this investigation, only proportional damping was considered. To consider the external damping that includes aerodynamic and hydrodynamic drag, two types of damping models, proportional damping and quadratic damping, were investigated [27]. A new experimental modal testing method was presented using a high-speed camera, and the parameter identification method of each damping model is explained. Recently, the accuracies of the geometrically exact beam and absolute nodal coordinate formulations are studied by comparing their predictions against an experimental data set referred to as the “Princeton beam experiment” [28]. The experiment deals with a cantilevered beam experiencing coupled flap, lag, and twist deformations. This study demonstrates the crucial need for thorough validation of the beam elements used for the simulation of flexible multibody systems before they are used to solve practical problems. Moreover, some flexible multibody dynamics beam formulations are validated using benchmark problems [29].

In most of the previous experimental investigations, the beams are cantilevered without large overall motion, and therefore the coupling effect of the rigid-body motion and the elastic deformation has not been paid attention to. The aim of this paper is to compare the accuracy of the absolute nodal coordinate formulation and the floating frame of reference formulation for a three-dimensional Euler–Bernoulli beam by numerical and experimental validation, in which the coupling effect of the rigid-body motion and the elastic deformation is taken into account. Firstly, based on the Euler–Bernoulli assumption and geometric exact beam theory, the material curvature of the beam is derived, and then the variational equations of motion of a three-dimensional Euler-Bernoulli beam is derived by using absolute nodal coordinate formulation, in which the torsion deformation is taken into account and the singularity problem due to the use of the rotation variable can be solved. Secondly, based on the assumption of small deformation, the variational equations of motion of a three-dimensional Euler–Bernoulli beam is derived using floating frame of reference formulation. In such a formulation, the dynamic stiffening terms are not included based on the linear elastic theory, and the curvature is simplified to the first order. The numerical results obtained by the absolute nodal coordinate formulation and the floating frame of reference formulation considering both the linear damping and the quadratic air resistance damping are compared with the results obtained by experiment to verify the accuracy and applicability of different formulations. A single-axis air-bearing apparatus is made up of an air-lubricated thrust bearing, a hub with a gyroscopic instrument, a strain measurement instrument, and a data acquisition system. The axis of the beam is in the horizontal plane perpendicular to the axis of rotation of the hub. The beam is slender and very thin (i.e., the height-to-length ratio and thickness-to-height ratio are small). The beam is cantilevered into the hub that allows rotation of the beam about its reference axis by an angle. An experiment of a hub–beam system with large deformation is carried out to compare the results obtained by different formulations. A gyroscopic instrument is used to measure the angular velocity of the hub, and a strain measurement instrument is used to measure the axial strain of a special point on the upper surface of the beam. For further investigation, in case of different thickness of the beam, the simulation results obtained by the absolute nodal coordinate formulation and the floating frame of reference formulation are compared in detail to clarify the applicability of the floating frame of reference formulation. Finally, a dynamic stiffening experiment is carried out to reveal the dynamic stiffening effect.

2 The absolute nodal coordinate formulation

2.1 Kinematics description

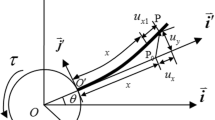
A three-dimensional beam undergoing large overall motion is shown in Fig. 1. The absolute nodal coordinate formulation is used for modeling the spatial beam with large deformation. In the large rotation vector formulation, it is assumed that the cross-section remains plane and maintains its area and shape in case of deformation. Based on the Euler–Bernoulli assumption, the neutral axis is assumed to be normal to the cross-section of the beam. The beam has homogeneous and isotropic material properties, and the elastic and centroidal axes in the cross section of a beam coincide so that the effects due to eccentricity are not taken in account.

Fig. 1

An elastic spatial beam before and after deformation

Using the finite element method, the beam is divided into $n$ elements. As shown in Fig. 1, $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$ represents the inertial frame, $O_{e} - \boldsymbol{i}_{e}\boldsymbol{j}_{e}\boldsymbol{k}_{e}$ represents the element coordinate system, and $O_{s} - \boldsymbol{\tau mn}$ represents the cross-section coordinate system after deformation. The absolute position vector of the point $k$ on the cross-section takes the form

$$ \boldsymbol{r} ( x,y,z,t ) = \boldsymbol{r}_{0} ( x,t ) + \boldsymbol{R} ( x,t ) \begin{bmatrix} 0 & y & z \end{bmatrix} ^{\mathrm{T}}, $$

(1)

where $( x,y,z )$ represents the coordinate of point $k$ defined in $O_{e} - \boldsymbol{i}_{e}\boldsymbol{j}_{e}\boldsymbol{k}_{e}$ before deformation, and $\boldsymbol{r}_{0} ( x,t )$ represents the absolute position vector of the corresponding point on the neutral axis of the beam defined in $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$, which can be written as

$$ \boldsymbol{r}_{0} ( x,t ) = \begin{bmatrix} r_{1} ( x,t ) & r_{2} ( x,t ) & r_{3} ( x,t ) \end{bmatrix} ^{\mathrm{T}}. $$

(2)

Defining $\boldsymbol{\theta} = \left ( \begin{array}{ccc} \theta_{1} & \theta_{2} & \theta_{3} \end{array} \right )^{\mathrm{T}}$ as the rotational coordinate vector, and $C_{i} = \cos \theta_{i}$, $S_{i} = \sin \theta_{i}$, the transformation matrix from $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$ to the cross-section coordinate system $O_{s} - \boldsymbol{\tau mn}$ is given by $\boldsymbol{R} = {}^{3}\boldsymbol{R}(\theta_{3}){}^{2}\boldsymbol{R}(\theta_{2}){}^{1}\boldsymbol{R}(\theta_{1})$, which yields

$$ \boldsymbol{R} = \begin{bmatrix} \boldsymbol{\tau} & \boldsymbol{m} & \boldsymbol{n} \end{bmatrix} = \begin{pmatrix} C_{2}C_{3} & - C_{1}S_{3} + S_{1}S_{2}C_{3} & S_{1}S_{3} + C_{1}S_{2}C_{3} \\ C_{2}S_{3} & C_{1}C_{3} + S_{1}S_{2}S_{3} & - S_{1}C_{3} + C_{1}S_{2}S_{3} \\ - S_{2} & S_{1}C_{2} & C_{1}C_{2} \end{pmatrix} . $$

(3)

Defining $( \cdot )'$ and $( \cdot )''$ as the first and second derivatives with respect to $x$, based on the geometric nonlinear theory, the section strain component vector defined in $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$ is given by [28]

$$ \boldsymbol{\varGamma} = \boldsymbol{r}'_{0} - \boldsymbol{R} \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} ^{\mathrm{T}}. $$

(4)

The curvature component vector defined in $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$ is given by $\boldsymbol{\varLambda} = \mathrm{axial} ( \boldsymbol{R}'\boldsymbol{R}^{\mathrm{T}} )$, and the skew-symmetric matrix corresponding to $\boldsymbol{\varLambda}$ can be written as

$$ \tilde{\boldsymbol{\varLambda}} = \frac{1}{2} \bigl[ \boldsymbol{R}' \boldsymbol{R}^{\mathrm{T}} - \bigl( \boldsymbol{R}' \boldsymbol{R}^{\mathrm{T}} \bigr)^{\mathrm{T}} \bigr]. $$

(5)

Since $\boldsymbol{R}$ is an orthogonal matrix, $\boldsymbol{RR}^{\mathrm{T}}$ is equal to the identity matrix; therefore, $\boldsymbol{R'R}^{\mathrm{T}} + \boldsymbol{RR}^{\prime\,\mathrm{T}} = \mathbf{0}$, and Eq. (5) can be rewritten as

$$ \tilde{\boldsymbol{\varLambda}} = \boldsymbol{R}'\boldsymbol{R}^{\mathrm{T}}. $$

(6)

Substituting Eq. (3) into (4), the section strain component vector defined in $O_{s} - \boldsymbol{\tau mn}$ is given by

$$ \boldsymbol{\varGamma}^{ *} = \begin{bmatrix} \varepsilon_{0} \\ \gamma_{xy} \\ \gamma_{xz} \end{bmatrix} = \boldsymbol{R}^{\mathrm{T}} \boldsymbol{\varGamma} = \begin{bmatrix} \boldsymbol{\tau}^{\mathrm{T}}\boldsymbol{r}'_{0} - 1 \\ \boldsymbol{m}^{\mathrm{T}}\boldsymbol{r}'_{0} \\ \boldsymbol{n}^{\mathrm{T}}\boldsymbol{r}'_{0} \end{bmatrix} $$

(7)

where $\varepsilon_{0}$ represents the axial strain, and $\gamma_{xy}$ and $\gamma_{xz}$ represent the transverse shear strains of an arbitrary point on the neutral axis of the beam.

Defining $\boldsymbol{\varLambda}^{ *} = \begin{bmatrix} \kappa_{1} & \kappa_{2} & \kappa_{3} \end{bmatrix} ^{\mathrm{T}}$ as the curvature component vector defined in $O_{s} - \boldsymbol{\tau mn}$ and $\tilde{\boldsymbol{\varLambda}}^{ *}$ as the corresponding skew-symmetric matrix, by using Eq. (6), $\tilde{\boldsymbol{\varLambda}}^{ *}$ can be written as

$$ \tilde{\boldsymbol{\varLambda}}^{ *} = \boldsymbol{R}^{\mathrm{T}} \tilde{\boldsymbol{\varLambda}} \boldsymbol{R} = \boldsymbol{R}^{\mathrm{T}} \boldsymbol{R}'. $$

(8)

Based on the Euler–Bernoulli assumption, $\boldsymbol{\tau}$ is in the same direction as $\boldsymbol{r}'_{0}$; therefore, $\boldsymbol{m}^{\mathrm{T}}\boldsymbol{r}'_{0} = 0$, $\boldsymbol{n}^{\mathrm{T}}\boldsymbol{r}'_{0} = 0$, and Eq. (7) shows that $\gamma_{xy} = 0$, $\gamma_{xz} = 0$. In addition, the relation between $\boldsymbol{\tau}$ and $\boldsymbol{r}'_{0}$ is given by

$$ \boldsymbol{\tau} = \frac{\boldsymbol{r}'_{0}}{\vert \boldsymbol{r}'_{0} \vert }. $$

(9)

Substituting Eqs. (9) into Eq. (7), the axial strain of an arbitrary point on the neutral axis of the beam is given by

$$ \varepsilon_{0} = \bigl\vert \boldsymbol{r}'_{0} \bigr\vert - 1 = \sqrt{\boldsymbol{r}_{0}^{\prime\,\mathrm{T}} \boldsymbol{r}'_{0}} - 1. $$

(10)

Substituting Eq. (3) into Eq. (8), the curvature components are given by

$$ \begin{aligned}[c] & \kappa_{1} = \boldsymbol{n}^{\mathrm{T}} \boldsymbol{m}' = \theta '_{1} - \sin \theta_{2}\theta '_{3}, \\ &\kappa_{2} = \boldsymbol{\tau}^{\mathrm{T}}\boldsymbol{n}' = \cos \theta_{1}\theta '_{2} + \sin \theta_{1}\cos \theta_{2}\theta '_{3}, \\ &\kappa_{3} = - \boldsymbol{\tau}^{\mathrm{T}}\boldsymbol{m}' = - \sin \theta_{1}\theta '_{2} + \cos \theta_{1}\cos \theta_{2}\theta '_{3}. \end{aligned} $$

(11)

For rotation 3-2-1, substituting Eqs. (2) and (3) into (9) and considering $- \pi /2 < \theta_{2} < \pi /2$, we obtain that

$$ \begin{aligned}[c] &\sin \theta_{2} = - \frac{r'_{3}}{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2} + r_{3}^{\prime\,2}}},\qquad \cos \theta_{2} = \frac{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2}}}{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2} + r_{3}^{\prime\,2}}}, \\ &\sin \theta_{3} = \frac{r'_{2}}{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2}}}, \qquad \cos \theta_{3} = \frac{r'_{1}}{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2}}}. \end{aligned} $$

(12)

Substituting Eq. (12) into Eq. (11), the curvature components can be expressed as

$$\begin{aligned} & \kappa_{1} = \theta '_{1} + \frac{ ( r''_{2}r'_{1} - r'_{2}r''_{2} ) r'_{3}}{ ( r_{1}^{\prime\,2} + r_{2}^{\prime\,2} )\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2} + r_{3}^{\prime\,2}}}, \\ &\kappa_{2} = \frac{\cos \theta_{1} ( r'_{1}r''_{1}r'_{3} + r'_{2}r''_{2}r'_{3} - r_{1}^{\prime\,2}r''_{3} - r_{2}^{\prime\,2}r''_{3} )}{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2}} ( r_{1}^{\prime\,2} + r_{2}^{\prime\,2} + r_{3}^{\prime\,2} )} + \frac{\sin \theta_{1} ( r'_{1}r''_{2} - r''_{1}r'_{2} )}{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2}} \sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2} + r_{3}^{\prime\,2}}}, \\ &\kappa_{3} = - \frac{\sin \theta_{1} ( r'_{1}r''_{1}r'_{3} + r'_{2}r''_{2}r'_{3} - r_{1}^{\prime\,2}r''_{3} - r_{2}^{\prime\,2}r''_{3} )}{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2}} ( r_{1}^{\prime\,2} + r_{2}^{\prime\,2} + r_{3}^{\prime\,2} )} + \frac{\cos \theta_{1} ( r'_{1}r''_{2} - r''_{1}r'_{2} )}{\sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2}} \sqrt{r_{1}^{\prime\,2} + r_{2}^{\prime\,2} + r_{3}^{\prime\,2}}}. \end{aligned}$$

(13)

Note that for $r'_{1} = r'_{2} = 0$, the singularity problem may occur. In order to solve such a problem, rotation 2-3-1 is employed to replace rotation 3-2-1, in which the transformation matrix is replaced by $\boldsymbol{A} = \boldsymbol{A}_{2}\boldsymbol{A}_{3}\boldsymbol{A}_{1}$.

2.2 Equations of motion

Using the finite element method for discretization of the beam, the absolute position vector of the corresponding point on the neutral axis of the beam $\boldsymbol{r}_{0}$ and the rotational angle $\theta_{1}$ are represented by using the shape function matrices as

$$ \boldsymbol{r}_{0} = \boldsymbol{S}_{1} \boldsymbol{q}_{e},\qquad \theta_{1} = \boldsymbol{S}_{2} \boldsymbol{q}_{e}, $$

(14)

where $\boldsymbol{q}_{e} = [ \boldsymbol{r}_{01}^{\mathrm{T}} \ \boldsymbol{r}_{01}^{\prime\,\mathrm{T}} \ \theta_{11} \ \theta '_{11} \ \boldsymbol{r}_{02}^{\mathrm{T}} \ \boldsymbol{r}_{02}^{\prime\,\mathrm{T}}\ \theta_{12} \ \theta '_{12} ]^{\mathrm{T}}$ is the vector of absolute position coordinates and gradient of the absolute position coordinates of an element. The expressions of $\boldsymbol{S}_{1}$ and $\boldsymbol{S}_{2}$ are given by

$$\begin{aligned} &\boldsymbol{S}_{1} = \begin{bmatrix} s_{1}(\xi )\boldsymbol{I}_{3 \times 3} & s_{2}(\xi )\boldsymbol{I}_{3 \times 3} & \mathbf{0}_{3 \times 1} & \mathbf{0}_{3 \times 1} & s_{3}(\xi )\boldsymbol{I}_{3 \times 3} & s_{4}(\xi )\boldsymbol{I}_{3 \times 3} & \mathbf{0}_{3 \times 1} & \mathbf{0}_{3 \times 1} \end{bmatrix} , \end{aligned}$$

(15)

$$\begin{aligned} &\boldsymbol{S}_{2} = \begin{bmatrix} \mathbf{0}_{1 \times 3} & \mathbf{0}_{1 \times 3} & s_{1}(\xi ) & s_{2}(\xi ) & \mathbf{0}_{1 \times 3} & \mathbf{0}_{1 \times 3} & s_{3}(\xi ) & s_{4}(\xi ) \end{bmatrix}, \end{aligned}$$

(16)

where $\xi = x/l$, $s_{1}(\xi ) = 1 - 3\xi^{2} + 2\xi^{3}$, $s_{2}(\xi ) = l(\xi - 2\xi^{2} + \xi^{3})$, $s_{3}(\xi ) = 3\xi^{2} - 2\xi^{3}$, $s_{4}(\xi ) = l( - \xi^{2} + \xi^{3})$, and $l$ is the length of the beam element.

Since $\boldsymbol{\tau}$, $\boldsymbol{m}$, and $\boldsymbol{n}$ are all functions of $r'_{1}, r'_{2}, r'_{3}, \theta_{1}$, define

$$ \boldsymbol{s} = \begin{bmatrix} \boldsymbol{r}'_{0} \\ \theta_{1} \end{bmatrix},\qquad \bar{\boldsymbol{S}} = \begin{bmatrix} \boldsymbol{S}'_{1} \\ \boldsymbol{S}_{2} \end{bmatrix} . $$

(17)

Then $\boldsymbol{s}$ can be written as

$$ \boldsymbol{s} = \bar{\boldsymbol{S}q}_{e}. $$

(18)

The strain energy of the beam takes the form

$$ U = \sum_{e = 1}^{n} \frac{1}{2} \int_{0}^{l} \bigl( EA\varepsilon_{0}^{2} + GJ\kappa_{1}^{2} + EI_{z}\kappa_{3}^{2} + EI_{y}\kappa_{2}^{2} \bigr) \,dx, $$

(19)

where $J = \int_{A} ( y^{2} + z^{2} ) \,dA$, $I_{z} = \int_{A} y^{2}\,dA$, $I_{y} = \int_{A} z^{2}\,dA$, and $E$ and $G$ represent the elastic modulus and shear modulus, respectively, and $n$ is the element number.

The variation of $\varepsilon_{x}$ and $\kappa_{i}\ (i = 1,2,3)$ are given by

$$\begin{aligned} &\delta \varepsilon_{0} = \frac{\boldsymbol{r}_{0}^{\prime\,\mathrm{T}}\delta \boldsymbol{r}'_{0}}{\sqrt{\boldsymbol{r}_{0}^{\prime\,\mathrm{T}}\boldsymbol{r}'_{0}}} = \frac{\boldsymbol{r}_{0}^{\prime\,\mathrm{T}}\boldsymbol{S}'_{1}}{\vert \boldsymbol{r}'_{0} \vert } \delta \boldsymbol{q}_{e}, \end{aligned}$$

(20)

$$\delta {\kappa }_i=\frac{\partial {\kappa }_i}{\partial \mathit{s}}\delta \mathit{s}+{\frac{\partial {\kappa }_i}{\partial \mathit{s}}}^{\prime }\delta {\mathit{s}}^{\prime }={\mathit{D}}_i\delta {\mathit{q}}_e(i=1,2,3),$$

(21)

where

$$ \boldsymbol{D}_{i} = \frac{\partial \kappa_{i}}{\partial \boldsymbol{s}}\bar{\boldsymbol{S}} + \frac{\partial \kappa_{i}}{\partial \boldsymbol{s}'}\bar{\boldsymbol{S}'}\quad ( i = 1,2,3 ). $$

(22)

Defining $\boldsymbol{a}_{\boldsymbol{s}} = \partial \boldsymbol{a}/\partial \boldsymbol{s}$, differentiation of Eq. (1) with respect to time leads to

$$\begin{aligned} &\dot{\boldsymbol{r}} = \dot{\boldsymbol{r}}_{0} + y \dot{\boldsymbol{m}} + z\dot{\boldsymbol{n}}, \end{aligned}$$

(23)

$$\begin{aligned} &\ddot{\boldsymbol{r}} = \ddot{\boldsymbol{r}}_{0} + y \ddot{\boldsymbol{m}} + z\ddot{\boldsymbol{n}}, \end{aligned}$$

(24)

where

$$\begin{aligned} &\dot{\boldsymbol{m}} = \boldsymbol{m}_{\boldsymbol{s}}\dot{\boldsymbol{s}},\qquad \dot{\boldsymbol{n}} = \boldsymbol{n}_{\boldsymbol{s}}\dot{\boldsymbol{s}}, \end{aligned}$$

(25)

$$\begin{aligned} &\ddot{\boldsymbol{m}} = ( \boldsymbol{m}_{\boldsymbol{s}}\dot{\boldsymbol{s}} )_{\boldsymbol{s}}\dot{\boldsymbol{s}} + \boldsymbol{m}_{\boldsymbol{s}} \ddot{\boldsymbol{s}}, \end{aligned}$$

(26)

$$\begin{aligned} &\ddot{\boldsymbol{n}} = ( \boldsymbol{n}_{\boldsymbol{s}}\dot{\boldsymbol{s}} )_{\boldsymbol{s}}\dot{\boldsymbol{s}} + \boldsymbol{n}_{\boldsymbol{s}} \ddot{\boldsymbol{s}}, \end{aligned}$$

(27)

and the variation of $\boldsymbol{r}$ is given by

$$ \delta \boldsymbol{r} = \delta \boldsymbol{r}_{0} + y\delta \boldsymbol{m} + z\delta \boldsymbol{n}, $$

(28)

where

$$ \delta \boldsymbol{m} = \boldsymbol{m}_{\boldsymbol{s}} \delta \boldsymbol{s}, \qquad \delta \boldsymbol{n} = \boldsymbol{n}_{\boldsymbol{s}} \delta \boldsymbol{s}. $$

(29)

The virtual work of the inertial force takes the form

$$\begin{aligned} \delta W_{i}&=-\sum_{e=1}^{n} \int_{V}\rho\delta \boldsymbol{r}^{\mathrm{T}}\ddot{ \boldsymbol{r}}\,dV =-\sum_{e=1}^{n} \int_{0}^{l}\bigl(\rho A\delta \boldsymbol{r}_{0}^{\mathrm{T}} \ddot{\boldsymbol{r}}+ \rho I_{z}\delta \boldsymbol{m} ^{\mathrm{T}}\ddot{ \boldsymbol{m}} +\rho I_{y}\delta \boldsymbol{n}^{\mathrm{T}}\ddot{\boldsymbol{n}}\bigr)\, dx. \end{aligned}$$

(30)

The virtual work of the gravitational force takes the form

$$ \delta W_{g} = \sum_{e = 1}^{n} \int_{V} \delta \boldsymbol{r}^{\mathrm{T}}\rho \boldsymbol{g} \,dV, $$

(31)

where $\boldsymbol{g}$ is the vector of the gravitational acceleration.

Substituting Eq. (1) into (31) and considering $\int_{A} y\,dA = 0$, $\int_{A} z\,dA = 0$, we obtain that

$$ \delta W_{g} = \sum_{e = 1}^{n} \int_{V} \delta \boldsymbol{r}_{0}^{\mathrm{T}} \rho \boldsymbol{g} \,dV. $$

(32)

Application of the virtual work principle leads to

$$ \delta W_{i} + \delta W_{d} + \delta W_{g} - \delta U = 0, $$

(33)

where $\delta W_{d}$ is the virtual work of the damping force.

Defining $\boldsymbol{q}$ as the generalized coordinate vector of the beam, the relation between $\boldsymbol{q}_{e}$ and $\boldsymbol{q}$ is given by $\boldsymbol{q}_{e} = \boldsymbol{B}_{e}\boldsymbol{q}$. Substituting Eqs. (14)–(32) into (33), the variational equations of motion read

$$ \delta \boldsymbol{q}^{\mathrm{T}} ( \boldsymbol{Q}_{g} + \boldsymbol{Q}_{f} + \boldsymbol{Q}_{v} - \boldsymbol{M}\ddot{\boldsymbol{q}} ) + \delta W_{d} = 0, $$

(34)

where $\boldsymbol{M} = \sum_{e = 1}^{n} \boldsymbol{B}_{e}^{\mathrm{T}}\boldsymbol{M}_{e}\boldsymbol{B}_{e}$, $\boldsymbol{Q}_{g} = \sum_{e = 1}^{n} \boldsymbol{B}_{e}^{\mathrm{T}}\boldsymbol{Q}_{ge}$, $\boldsymbol{Q}_{f} = \sum_{e = 1}^{n} \boldsymbol{B}_{e}^{\mathrm{T}}\boldsymbol{Q}_{f e}$, $\boldsymbol{Q}_{v} = \sum_{e = 1}^{n} \boldsymbol{B}_{e}^{\mathrm{T}}\boldsymbol{Q}_{v e}$, and the element matrices are given by

$$\begin{aligned} & \boldsymbol{M}_{e} = \int_{0}^{l} \rho A \boldsymbol{S}_{1}^{\mathrm{T}} \boldsymbol{S}_{1} \,dx + \int_{0}^{l} \rho I_{z} ( \boldsymbol{m}_{\boldsymbol{s}}\bar{\boldsymbol{S}} )^{\mathrm{T}} ( \boldsymbol{m}_{\boldsymbol{s}}\bar{\boldsymbol{S}} ) \,dx + \int_{0}^{l} \rho I_{y} ( \boldsymbol{n}_{\boldsymbol{s}}\bar{\boldsymbol{S}} )^{\mathrm{T}} ( \boldsymbol{n}_{\boldsymbol{s}}\bar{\boldsymbol{S}} ) \,dx, \end{aligned}$$

(35)

$$\begin{aligned} &\boldsymbol{Q}_{g e} = \int_{0}^{l} \rho A \boldsymbol{S}_{1}^{\mathrm{T}} \boldsymbol{g} \,dx, \\ &\boldsymbol{Q}_{f e} = - \int_{0}^{l} EA \boldsymbol{S}_{1}^{\prime\,\mathrm{T}} \frac{\boldsymbol{r}'_{0}}{\vert \boldsymbol{r}'_{0} \vert }\varepsilon_{0} \,dx - \int_{0}^{l} GJ \boldsymbol{D}_{1}^{\mathrm{T}} \kappa_{1}\,dx - \int_{0}^{l} EI_{y} \boldsymbol{D}_{2}^{\mathrm{T}}\kappa_{2} \,dx - \int_{0}^{l} EI_{z}\boldsymbol{D}_{3}^{\mathrm{T}} \kappa_{3}\,dx, \\ &\boldsymbol{Q}_{v e} = - \biggl( \int_{0}^{l} \rho I_{z} ( \boldsymbol{m}_{\boldsymbol{s}}\bar{\boldsymbol{S}} )^{\mathrm{T}} ( \boldsymbol{m}_{\boldsymbol{s}}\dot{\boldsymbol{s}} )_{\boldsymbol{s}} \bar{\boldsymbol{S}} \,dx \biggr)\dot{\boldsymbol{q}}_{e} - \biggl( \int_{0}^{l} \rho I_{y} ( \boldsymbol{n}_{\boldsymbol{s}}\bar{\boldsymbol{S}} )^{\mathrm{T}} ( \boldsymbol{n}_{\boldsymbol{s}}\dot{\boldsymbol{s}} )_{\boldsymbol{s}} \bar{\boldsymbol{S}} \,dx \biggr)\dot{\boldsymbol{q}}_{e}. \end{aligned}$$

(36)

For arbitrary $\dot{\boldsymbol{q}}_{e} \ne \boldsymbol{0}$, there exists some special points on the beam whose velocities are nonzero, and the kinetic energy of the beam element $T_{e} = \frac{1}{2}\int_{V} \rho \dot{\boldsymbol{r}}^{\mathrm{T}}\dot{\boldsymbol{r}} \,dV = \frac{1}{2}\dot{\boldsymbol{q}}_{e}^{\mathrm{T}}\boldsymbol{M}_{e}\dot{\boldsymbol{q}}_{e} > 0$; therefore, $\boldsymbol{M}_{e}$ is positive definite. The Gaussian integral is used for integration of the mass and force matrices.

The damping force includes the proportional damping force and the wind resistance force. For slender beam, the damping force can be approximated as [27]

$$ \boldsymbol{f}_{d} = - \varsigma_{1}\dot{\boldsymbol{r}}_{0} - \varsigma_{2}\dot{\boldsymbol{r}}_{0} \vert \dot{\boldsymbol{r}}_{0} \vert , $$

(37)

where $\varsigma_{1}$ and $\varsigma_{2}$ represent the coefficients of the proportional damping force and the wind resistance force, which are identified by experiment data. The virtual work of the damping force is given by

$$ \delta W_{d} = \sum_{e = 1}^{n} \int_{A_{w}} \delta \boldsymbol{r}_{0}^{\mathrm{T}} \boldsymbol{f}_{d}dA_{w}, $$

(38)

where $A_{w}$ is the frontal area of the beam element.

Substitute Eq. (37) into (38), we obtain that

$$ \delta W_{d} = - \sum_{e = 1}^{n} \int_{A_{w}} \delta \boldsymbol{r}_{0}^{\mathrm{T}} \bigl( \varsigma_{1}\dot{\boldsymbol{r}}_{0} + \varsigma_{2}\dot{\boldsymbol{r}}_{0}\vert \dot{\boldsymbol{r}}_{0} \vert \bigr)dA_{w}. $$

(39)

Substitute Eq. (14) into (39), the virtual work of the damping force is given by $\delta W_{d} = \delta \boldsymbol{q}^{\mathrm{T}}\boldsymbol{Q}_{d}$, and the generalized damping force takes the form $\boldsymbol{Q}_{d} = \sum_{e = 1}^{n} \boldsymbol{B}_{e}^{\mathrm{T}}\boldsymbol{Q}_{d e}$, where the element damping force is given by

$$ \boldsymbol{Q}_{d e} = - \biggl( \int_{A_{w}} \boldsymbol{S}_{1}^{\mathrm{T}} \bigl( \varsigma_{1} + \varsigma_{2}\vert \boldsymbol{S}_{1} \dot{\boldsymbol{q}}_{e} \vert \bigr)\boldsymbol{S}_{1}dA_{w} \biggr) \dot{\boldsymbol{q}}_{e}. $$

(40)

The variational equations of motion take the form

$$ \delta \boldsymbol{q}^{\mathrm{T}} ( \boldsymbol{M}\ddot{\boldsymbol{q}} - \boldsymbol{Q} ) = 0, $$

(41)

where $\boldsymbol{Q} = \boldsymbol{Q}_{v} + \boldsymbol{Q}_{g} + \boldsymbol{Q}_{f} + \boldsymbol{Q}_{d}$.

3 The floating frame of reference formulation

3.1 Kinematics of beam undergoing large spatial motion

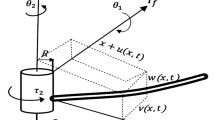
In this section, the floating frame of reference formulation of a three-dimensional Euler–Bernoulli beam undergoing large overall motion is established. Small deformation is assumed for the application of the floating frame of reference formulation.

A three-dimensional beam is shown in Fig. 2. Two following coordinate systems are introduced to describe the motion of the beam: The global coordinate system $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$ and the body-fixed coordinate system $O_{b} - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$.

Fig. 2

A spatial beam undergoing large overall motion

The coordinate matrix of the position vector of point $k$ with respect to the $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$ can be written as

$$ \boldsymbol{r} = \boldsymbol{r}_{C} + \boldsymbol{A}_{0} \bigl( \boldsymbol{\rho}_{0}^{b} + \boldsymbol{u}^{b} \bigr), $$

(42)

where, as shown in Fig. 2, $\boldsymbol{r}_{C}$ is the position vector of the reference point $O_{ b}$ defined in $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$, $\boldsymbol{\rho}_{0}^{b} = [ x \ y \ z ]^{\mathrm{T}}$ is the position vector of $k$ with respect to $O_{b} - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$ in the undeformed state defined in $O_{b} - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$, $\boldsymbol{u}^{b} = [ u \ v \ w ]^{\mathrm{T}}$ is the deformation displacement vector defined in $O_{b} - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$, and $\boldsymbol{A}_{0}$ is the transformation matrix that defines the orientation of the body-fixed frame.

Based on the Euler–Bernoulli assumption and small deformation, the deformation displacement vector of the point $k$ defined in $O_{b} - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$ can be expressed as

$$ \boldsymbol{u}^{b} = \begin{bmatrix} u \\ v \\ w \end{bmatrix} = \begin{bmatrix} u_{0} - y\frac{\partial v_{0}}{\partial x} - z\frac{\partial w_{0}}{\partial x} \\ v_{0} - z\theta_{\tau} \\ w_{0} + y\theta_{\tau} \end{bmatrix} , $$

(43)

where $\boldsymbol{u}_{0}^{b} = [ u_{0}\ v_{0} \ w_{0} ]^{\mathrm{T}}$ represents the deformation displacement vector of the corresponding point on the neutral axis of the beam defined in $O_{b} - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$, and $\theta_{\tau}$ represents the torsion angle of the cross-section of the beam.

Defining $\boldsymbol{\omega}^{b} = [ \omega_{1} \ \omega_{2} \ \omega_{3} ]^{\mathrm{T}}$ to be the coordinate vector of the angular velocity of the body-fixed frame defined in $O_{b} - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$, by differentiating Eq. (42) the expression for the inertial velocity of point $k$ can be obtained as

$$ \dot{\boldsymbol{r}} = \dot{\boldsymbol{r}}_{C} - \boldsymbol{A}_{0}\bigl(\tilde{\boldsymbol{\rho}}_{0}^{b} + \tilde{\boldsymbol{u}}^{b}\bigr)\boldsymbol{\omega}^{b} + \boldsymbol{A}_{0}\dot{\boldsymbol{u}}^{b}, $$

(44)

where $\tilde{\boldsymbol{\rho}}_{\boldsymbol{0}}^{\boldsymbol{b}}$ and $\tilde{\boldsymbol{u}}^{b}$ are the corresponding skew matrices of $\boldsymbol{\rho}_{0}^{b}$ and $\boldsymbol{u}^{b}$, respectively.

The inertial acceleration can be obtained by differentiation of Eq. (44) as

$$ \ddot{\boldsymbol{r}} = \ddot{\boldsymbol{r}}_{C} - \boldsymbol{A}_{0}\bigl(\tilde{\boldsymbol{\rho}}_{0}^{b} + \tilde{\boldsymbol{u}}^{b}\bigr)\dot{\boldsymbol{\omega}}^{b} + \boldsymbol{A}_{0}\ddot{\boldsymbol{u}}^{b} + \boldsymbol{A}_{0}\tilde{\boldsymbol{\omega}}^{b}\tilde{\boldsymbol{\omega}}^{b}\bigl( \boldsymbol{\rho}_{0}^{b} + \boldsymbol{u}^{b} \bigr) + 2\boldsymbol{A}_{0}\tilde{\boldsymbol{\omega}}^{b} \dot{\boldsymbol{u}}^{b}, $$

(45)

where $\tilde{\boldsymbol{\omega}}^{b}$ is the corresponding skew matrix of $\boldsymbol{\omega}^{b}$.

3.2 Equations of motion

The strain energy can be expressed as

$$ U = \sum_{e = 1}^{n} \frac{1}{2} \int_{ 0}^{ l} \bigl( EA\varepsilon_{0}^{2} + GJ\theta _{\tau}^{\prime\,2} + EI_{y}w^{\prime\prime\,2} + EI_{z}v^{\prime\prime\,2} \bigr)\,dx, $$

(46)

where $\varepsilon_{0}$ is the axial normal strain of an arbitrary point on the neutral axis of the beam. The virtual power of the elastic force can be written as

$$ \delta P_{f} = - \sum_{e = 1}^{n} \int_{ 0}^{ l} \bigl( EA\delta \dot{ \varepsilon}_{0}\varepsilon_{0} + GJ\delta \dot{\theta }'_{\tau} \theta '_{\tau} + EI_{y}\delta \dot{w}''w'' + EI_{z}\delta \dot{v}''v'' \bigr)\,dx. $$

(47)

For the floating frame of reference formulation without considering the dynamic stiffening effect, the axial strain can be simplified as

$$ \varepsilon_{0} = u'_{0}. $$

(48)

Based on the virtual power principle, the variational equations of motion of the beam take the form

$$ \sum_{e = 1}^{n} \int_{ V} \bigl( \delta \dot{\boldsymbol{r}}^{\mathrm{T}} \boldsymbol{g} - \rho \delta \dot{\boldsymbol{r}}^{\mathrm{T}} \ddot{\boldsymbol{r}} \bigr) \,dV + \delta P_{f} + \delta P_{d} = 0, $$

(49)

where $\boldsymbol{g}$ is the coordinate matrix of the gravitational acceleration defined in $O_{0} - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$, and $\delta P_{d}$ is the virtual power of the damping force.

Using the finite element method, the longitudinal, lateral and torsion deformations of the neutral axis can be represented by the shape function matrices as

$$ u_{0} = \boldsymbol{N}_{1}\boldsymbol{p}_{e},\qquad v_{0} = \boldsymbol{N}_{2}\boldsymbol{p}_{e},\qquad w_{0} = \boldsymbol{N}_{3}\boldsymbol{p}_{e}, \qquad \theta_{\tau} = \boldsymbol{N}_{4} \boldsymbol{p}_{e}, $$

(50)

where $\boldsymbol{p}_{e} = [ u_{01} \ v_{1}\ v'_{1} \ w_{1} \ w'_{1} \ \theta_{1} \ u_{02} \ v_{2} \ v'_{2} \ w_{2}\ w'_{2} \ \theta_{2} ]^{\mathrm{T}}$ is the vector of deformation displacement coordinates, and the expressions of $\boldsymbol{N}_{i}\ ( i = 1, \ldots,4 )$ are given by

$$\begin{aligned} &\boldsymbol{N}_{1} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} g_{1} & 0 & 0 & 0 & 0 & 0 & g_{4} & 0 & 0 & 0 & 0 & 0 \end{array}\displaystyle \right ], \end{aligned}$$

(51)

$$\begin{aligned} &\boldsymbol{N}_{2} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & g_{2} & g_{3} & 0 & 0 & 0 & 0 & g_{5} & g_{6} & 0 & 0 & 0 \end{array}\displaystyle \right ], \end{aligned}$$

(52)

$$\begin{aligned} &\boldsymbol{N}_{3} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 0 & g_{2} & g_{3} & 0 & 0 & 0 & 0 & g_{5} & g_{6} & 0 \end{array}\displaystyle \right ], \end{aligned}$$

(53)

$$\begin{aligned} &\boldsymbol{N}_{4} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 0 & 0 & 0 & g_{1} & 0 & 0 & 0 & 0 & 0 & g_{4} \end{array}\displaystyle \right ], \end{aligned}$$

(54)

where $g_{1}(\xi ) = 1 - \xi$, $g_{2}(\xi ) = 1 - 3\xi^{2} + 2\xi^{3}$, $g_{3}(\xi ) = l(\xi - 2\xi^{2} + \xi^{3})$, $g_{4}(\xi ) = \xi$, $g_{5}(\xi ) = 3\xi^{2} - 2\xi^{3}$, $g_{6}(\xi ) = l( - \xi^{2} + \xi^{3})$, and $\xi = x/l$.

Defining $\boldsymbol{p}$ as the generalized coordinate vector of the beam, the relation between $\boldsymbol{p}_{e}$ and $\boldsymbol{p}$ is given by $\boldsymbol{p}_{e} = \boldsymbol{B}_{e}\boldsymbol{p}$. Substituting Eq. (50) into Eqs. (44) and (45), the inertial velocity and acceleration read

$$ \dot{\boldsymbol{r}} = \boldsymbol{Sv},\qquad \ddot{\boldsymbol{r}} = \boldsymbol{S}\dot{\boldsymbol{v}} + \boldsymbol{s}, $$

(55)

where

$$\begin{aligned} &\begin{aligned}[c] & \boldsymbol{S} = \begin{bmatrix} \boldsymbol{I} & - \boldsymbol{A}_{0}\bigl(\tilde{\boldsymbol{\rho}}_{0}^{b} + \tilde{\boldsymbol{u}}^{b}\bigr) & \boldsymbol{A}_{0}\boldsymbol{NB}_{e} \end{bmatrix}, \\ &\boldsymbol{s} = \boldsymbol{A}_{0}\tilde{\boldsymbol{ \omega}}^{b}\tilde{\boldsymbol{\omega}}^{b}\bigl( \boldsymbol{\rho}_{0}^{b} + \boldsymbol{NB}_{e} \boldsymbol{p}\bigr) + 2\boldsymbol{A}_{0}\tilde{\boldsymbol{ \omega}}^{b}\boldsymbol{NB}_{e}\dot{\boldsymbol{p}}, \end{aligned} \end{aligned}$$

(56)

$$\begin{aligned} &\boldsymbol{N} = \begin{bmatrix} \boldsymbol{N}_{1} - y\boldsymbol{N}'_{2} - z\boldsymbol{N}'_{3} \\ \boldsymbol{N}_{2} - z\boldsymbol{N}_{4} \\ \boldsymbol{N}_{3} + y\boldsymbol{N}_{4} \end{bmatrix} , \end{aligned}$$

(57)

$$\begin{aligned} &\boldsymbol{v} = \begin{bmatrix} \dot{\boldsymbol{r}}_{C}^{\mathrm{T}} & \boldsymbol{\omega}^{b\,\mathrm{T}} & \dot{\boldsymbol{p}}^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}. \end{aligned}$$

(58)

Substituting Eq. (50) into Eqs. (47) and (48), the virtual power of the elastic force reads

$$ \delta P_{f} = \delta \boldsymbol{v}^{\mathrm{T}} \boldsymbol{Q}_{f}, $$

(59)

where

$$ \boldsymbol{Q}_{f} = \begin{bmatrix} \boldsymbol{0}^{\mathrm{T}} & \boldsymbol{0}^{\mathrm{T}} & ( - \boldsymbol{K} \boldsymbol{p} )^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}, $$

(60)

and $\boldsymbol{K}$ represents the stiffness matrix, which can be written as $\boldsymbol{K} = \sum_{e = 1}^{n} \boldsymbol{B}_{e}^{\mathrm{T}}\boldsymbol{K}_{e}\boldsymbol{B}_{e}$, where the element stiffness matrix takes the form

$$ \boldsymbol{K}_{e} = \int_{ 0}^{ l} EA \boldsymbol{N}_{1}^{\prime\,\mathrm{T}} \boldsymbol{N}'_{1}\,dx + \int_{ 0}^{ l} EI_{z}\boldsymbol{N}_{2}^{\prime\prime\,\mathrm{T}} \boldsymbol{N}''_{2}\,dx + \int_{ 0}^{ l} EI_{y}\boldsymbol{N}_{3}^{\prime\prime\,\mathrm{T}} \boldsymbol{N}''_{3}\,dx + \int_{ 0}^{ l} GJ \boldsymbol{N}_{4}^{\prime\,\mathrm{T}} \boldsymbol{N}'_{4}\,dx. $$

(61)

The damping force includes proportional damping force and the wind resistance force, which has the same expression as Eq. (37). The virtual power of the damping force is given by

$$ \delta P_{d} = \sum_{e = 1}^{n} \int_{A_{w}} \delta \dot{\boldsymbol{r}}_{0}^{\mathrm{T}} \boldsymbol{f}_{d}dA_{w} = - \sum _{e = 1}^{n} \int_{A_{w}} \delta \dot{\boldsymbol{r}}_{0}^{\mathrm{T}} \bigl( \varsigma_{1}\dot{\boldsymbol{r}}_{0} + \varsigma_{2}\dot{\boldsymbol{r}}_{0}\vert \dot{\boldsymbol{r}}_{0} \vert \bigr)dA_{w}, $$

(62)

where $\dot{\boldsymbol{r}}_{0} = \dot{\boldsymbol{r}}(x,0,0)$, and $A_{w}$ is the frontal area of the beam element.

Defining $\boldsymbol{S}_{0} = \boldsymbol{S}(x,0,0)$ and substituting Eq. (55) into (62), we obtain that

$$ \delta P_{d} = \delta \boldsymbol{v}^{\mathrm{T}} \boldsymbol{Q}_{d}, $$

(63)

where the generalized damping force takes the form

$$ \boldsymbol{Q}_{d} = - \sum_{e = 1}^{n} \biggl( \int_{A_{w}} \boldsymbol{S}_{0}^{\mathrm{T}} \bigl( \varsigma_{1} + \varsigma_{2}\vert \boldsymbol{S}_{0} \boldsymbol{v} \vert \bigr)\boldsymbol{S}_{0}dA_{w} \biggr) \boldsymbol{v}. $$

(64)

Substituting Eqs. (55), (59), and (63) into (49), we obtain that

$$ \delta \boldsymbol{v}^{\mathrm{T}} ( \boldsymbol{Q}_{g} + \boldsymbol{Q}_{f} + \boldsymbol{Q}_{d} + \boldsymbol{Q}_{v} - \boldsymbol{M}_{v}\dot{\boldsymbol{v}} ) = 0, $$

(65)

where

$$\begin{aligned} &\boldsymbol{M}_{v} = \sum_{e = 1}^{n} \int_{ V} \rho \boldsymbol{S}^{\mathrm{T}}\boldsymbol{S} \,dV, \end{aligned}$$

(66)

$$\begin{aligned} &\boldsymbol{Q}_{g} = \sum_{e = 1}^{n} \int_{ V} \boldsymbol{S}^{\mathrm{T}}\boldsymbol{g} \,dV,\qquad \boldsymbol{Q}_{v} = - \sum_{e = 1}^{n} \int_{ V} \rho \boldsymbol{S}^{\mathrm{T}}\boldsymbol{s} \,dV. \end{aligned}$$

(67)

Considering the relations [30]

$$ \boldsymbol{\omega}^{b} = \boldsymbol{D}\dot{\boldsymbol{\varTheta}},\qquad \dot{\boldsymbol{\omega}}^{b} = \boldsymbol{D}\ddot{\boldsymbol{\varTheta}} + \dot{\boldsymbol{D}}\dot{\boldsymbol{\varTheta}}, $$

(68)

where $\boldsymbol{\varTheta}$ represents the vector of the Cardan angle of the body-fixed frame, and defining $\boldsymbol{q} = [ \boldsymbol{r}_{c}^{\mathrm{T}} \ \boldsymbol{\varTheta}^{\mathrm{T}} \ \boldsymbol{p}^{\mathrm{T}} ]^{ \mathrm{T}}$, we obtain that

$$ \boldsymbol{v} = \boldsymbol{H}\dot{\boldsymbol{q}},\qquad \dot{\boldsymbol{v}} = \boldsymbol{H}\ddot{\boldsymbol{q}} + \boldsymbol{h}, $$

(69)

where

$$ \boldsymbol{H} = \begin{bmatrix} \boldsymbol{I} & \boldsymbol{0} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{D} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{I} \end{bmatrix},\qquad \boldsymbol{h} = \begin{bmatrix} \boldsymbol{0} \\ \dot{\boldsymbol{D}}\dot{\boldsymbol{\varTheta}} \\ \boldsymbol{0} \end{bmatrix}. $$

(70)

In case that singularity occurs, the Cardan angle can be replaced by the Euler angle.

The variational equations are given by

$$ \delta \dot{\boldsymbol{q}}^{\mathrm{T}} ( \boldsymbol{Q} - \boldsymbol{M}\ddot{\boldsymbol{q}} ) = 0, $$

(71)

where

$$ \begin{aligned}[c] & \boldsymbol{M} = \boldsymbol{H}^{\mathrm{T}} \boldsymbol{M}_{v}\boldsymbol{H}, \\ &\boldsymbol{Q} = \boldsymbol{H}^{\mathrm{T}} ( \boldsymbol{Q}_{g} + \boldsymbol{Q}_{f} + \boldsymbol{Q}_{d} + \boldsymbol{Q}_{v} ) - \boldsymbol{H}^{\mathrm{T}} \boldsymbol{M}_{v}\boldsymbol{h}. \end{aligned} $$

(72)

4 Rigid-flexible coupling equations of the hub–beam system

As can be seen in Fig. 3, the hub can rotate along the $\boldsymbol{j}$ axis, and a thin rectangular beam is connected to the hub with a fixed joint at point $A$. Three coordinate systems are introduced: global frame $O - \boldsymbol{i}_{0}\boldsymbol{j}_{0}\boldsymbol{k}_{0}$, body-fixed frame of the hub $O - \boldsymbol{i}_{h}\boldsymbol{j}_{h}\boldsymbol{k}_{h}$, and the body-fixed frame of the spatial beam $A - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$. Defining $\theta$ as the rotational angle of the hub, $\beta$ as the constant angle between $\boldsymbol{j}_{h}$ and $\boldsymbol{j}_{b}$, and $J$ as the rotary inertia of the hub, the kinematics constraint equations are given by

$$ \boldsymbol{\varPhi}^{K} = \begin{bmatrix} \boldsymbol{r}_{A} - \boldsymbol{A}_{h} ( \theta ) [ R \ 0 \ 0 ]^{\mathrm{T}} \\ \boldsymbol{k}_{h}^{\mathrm{T}}\boldsymbol{i}_{b} \\ \boldsymbol{j}_{h}^{\mathrm{T}}\boldsymbol{i}_{b} \\ \boldsymbol{j}_{h}^{\mathrm{T}}\boldsymbol{j}_{b} - \cos\beta \end{bmatrix} = \boldsymbol{0}, $$

(73)

where $R$ is the distance from point $O$ to point $A$, $\boldsymbol{A}_{h} ( \theta )$ is the transformation matrix of $O - \boldsymbol{i}_{h}\boldsymbol{j}_{h}\boldsymbol{k}_{h}$, and $\boldsymbol{j}_{h}$, $\boldsymbol{k}_{h}$ are given by

$$\begin{aligned} &\begin{aligned}[c] & \boldsymbol{A}_{h} ( \theta ) = \begin{bmatrix} \cos\theta & 0 & - \sin\theta \\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \end{bmatrix} , \\ &\boldsymbol{j}_{h} = \begin{bmatrix} 0 & 1 & 0 \end{bmatrix} ^{\mathrm{T}},\quad \boldsymbol{k}_{h} = \boldsymbol{A}_{h} ( \theta ) \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} ^{\mathrm{T}}. \end{aligned} \end{aligned}$$

(74)

Fig. 3

Hub and spatial beam system

For absolute nodal coordinate formulation, $\boldsymbol{i}_{b}$ and $\boldsymbol{j}_{b}$ are given by

$$ \begin{aligned}[c] & \boldsymbol{i}_{b} = \boldsymbol{r}'_{0}(0,t)/ \bigl\Vert \boldsymbol{r}'_{0}(0,t) \bigr\Vert , \\ &\boldsymbol{j}_{b} = \boldsymbol{m}(0,t), \end{aligned} $$

(75)

and the deformation displacement vector $\boldsymbol{u}^{b}$ can be calculated according to Eq. (42), in which the transformation matrix of $O - \boldsymbol{i}_{b}\boldsymbol{j}_{b}\boldsymbol{k}_{b}$ is given by $\boldsymbol{A}_{0} = \left [ \begin{array}{ccc} \boldsymbol{i}_{b} & \boldsymbol{j}_{b} & \boldsymbol{k}_{b} \end{array} \right ]$, where $\boldsymbol{k}_{b} = \boldsymbol{n}(0,t)$.

For the floating frame of reference formulation, $\boldsymbol{q} = \left [ \begin{array}{ccc} \boldsymbol{r}_{c}^{\mathrm{T}} & \boldsymbol{\varTheta}^{\mathrm{T}} & \boldsymbol{p}^{\mathrm{T}} \end{array} \right ]^{ \mathrm{T}}$, $\boldsymbol{i}_{b}$ and $\boldsymbol{j}_{b}$ are given by

$$ \begin{aligned}[c] &\boldsymbol{i}_{b} = \boldsymbol{A}_{0} \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} ^{\mathrm{T}}, \\ &\boldsymbol{j}_{b} = \boldsymbol{A}_{0} \begin{bmatrix} 0 & 1 & 0 \end{bmatrix} ^{\mathrm{T}}. \end{aligned} $$

(76)

If the driving constraint equations are given by $\boldsymbol{\varPhi}^{D} = \boldsymbol{0}$, then the system constraint equations can be written as $\boldsymbol{\varPhi} = [ \boldsymbol{\varPhi}^{K T} \ \boldsymbol{\varPhi}^{D T} ]^{\mathrm{T}} = \boldsymbol{0}$.

The Lagrange equation of the first kind is given by

$$ \begin{bmatrix} \bar{\boldsymbol{M}} \ddot{\bar{\boldsymbol{q}}} + \boldsymbol{\varPhi}_{\bar{\boldsymbol{q}}}^{\mathrm{T}}\boldsymbol{\lambda} - \bar{\boldsymbol{Q}} \\ \boldsymbol{\varPhi} \end{bmatrix} = \boldsymbol{0}, $$

(77)

where the generalized mass matrix, force matrix, and the generalized coordinate vector take the form

$$ \bar{\boldsymbol{M}} = \begin{bmatrix} J & \boldsymbol{0}^{\mathrm{T}} \\ \boldsymbol{0} & \boldsymbol{M} \end{bmatrix} ,\qquad \bar{\boldsymbol{Q}} = \begin{bmatrix} T - T_{d} \\ \boldsymbol{Q} \end{bmatrix} ,\qquad \bar{\boldsymbol{q}} = \begin{bmatrix} \theta \\ \boldsymbol{q} \end{bmatrix} , $$

(78)

and $T$ and $T_{d}$ represent the external torque and damping torque applied on the hub, respectively, and $\boldsymbol{\varPhi}_{\bar{\boldsymbol{q}}}$ and $\boldsymbol{\lambda}$ represent the Jacobian matrix and vector of the Lagrange multiplier, respectively. A generalized-$\alpha$ method is used for integration of differential-algebraic equations [31, 32].

5 Experiment of hub–beam system with large deformation

An air-floating platform is used in the experiment as the hub, as shown in Fig. 4. The air-floating platform can be adopted to simulate frictionless mechanical environment by suspending the platform in air. The prototype of the air-floating platform experiment equipment is the hub–beam dynamics system, in which the air-floating platform is used to replace the hub, whereas the designed aluminum plate is used to replace the flexible beam. The hub–beam system is a typical rigid-flexible coupling system, which has a strong engineering background in the fields of spacecrafts, space robot arms, and so on. There are theoretical and experimental studies of many scholars, especially in the United States National Aeronautics and Space Administration (NASA). Japanese NASDA Tsukuba Research Center also had studied the rigid-flexible coupling problem of the solar wings and a central rigid attitude control system for the technology experimental satellite (ETS-V1); therefore, the hub–beam system has not only wide engineering application background, but also important theoretical value for the study of rigid-flexible coupling dynamics of multibody systems. This is why we design and develop the air-floating platform. The experimental platform has the capacity of multichannel data acquisition and real-time monitoring with high precision, low damping, and easy to operate.

Fig. 4

Air-floating platform

The platform can rotate along the vertical axis, and the frictional torque of the platform can be neglected. Since the damping torque applied on the hub is very small, it is assumed that $T_{d} = 0$. The external torque applied on the hub is $T = 0$. The rotary inertia of the hub is $J = 9.557\ \mbox{kg} {\cdot} \mbox{m}^{2}$, and the distance from point $O$ to point $A$ is $R = 0.35\ \mbox{m}$. The constant angle between $\boldsymbol{j}_{h}$ and $\boldsymbol{j}_{b}$ is $\beta = \pi / 4$.

Initially, the axis $\boldsymbol{i}_{b}$ of the beam is in horizontal position without elastic deformation, and $\dot{\bar{\boldsymbol{q}}}(0) = \boldsymbol{0}$. For absolute nodal coordinate formulation, the initial generalized coordinates of the system are given by

$$\begin{aligned} & \begin{aligned}[c] & \bar{\boldsymbol{q}}(0) = \begin{bmatrix} \theta (0) & \boldsymbol{q}(0)^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}},\qquad \boldsymbol{q}(0) = \begin{bmatrix} \boldsymbol{q}_{1}(0)^{\mathrm{T}} & \cdots & \boldsymbol{q}_{i}(0)^{\mathrm{T}} & \cdots & \boldsymbol{q}_{n + 1}(0)^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}, \\ &\theta (0) = 0,\qquad \boldsymbol{q}_{i}(0) = \begin{bmatrix} \boldsymbol{r}_{0i}(0)^{\mathrm{T}} & \boldsymbol{r}'_{0i}(0)^{\mathrm{T}} & \theta_{1i}(0)^{\mathrm{T}} & \theta '_{1i}(0)^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}, \\ &\boldsymbol{r}_{0i}(0) = \begin{bmatrix} R + ( i - 1 ) l & 0 & 0 \end{bmatrix} ^{\mathrm{T}},\qquad \boldsymbol{r}'_{0i}(0) = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} ^{\mathrm{T}}, \\ & \theta_{1i}(0) = - \pi /4,\qquad \theta '_{1i}(0) = 0, \end{aligned} \end{aligned}$$

(79)

where $i$ represents the node number.

For floating frame of reference formulation, the initial generalized coordinates of the system are given by

$$ \begin{aligned}[c] & \bar{\boldsymbol{q}}(0) = \begin{bmatrix} \theta (0) & \boldsymbol{\varTheta} (0)^{\mathrm{T}}\quad \boldsymbol{p}(0)^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}, \\ &\theta (0) = 0,\quad \boldsymbol{\varTheta} (0) = \begin{bmatrix} - \pi /4 & 0 & 0 \end{bmatrix} ^{\mathrm{T}},\quad \boldsymbol{p}(0) = \boldsymbol{0}. \end{aligned} $$

(80)

Applied with gravitational force, the beam has bending and torsion deformation, which leads to the rotational motion of the hub. A gyroscopic instrument is used to measure the angular velocity of the hub. Two strain gauges are attached on the upper surface of points $P_{1}$ and $P_{2}$, and the distances from point $A$ to $P_{1}$ and $P_{2}$ are 0.3 m and 1.2 m, respectively. The material and geometric properties of the beam are given in Table 1.

Table 1 Material and geometric properties of the beam

The linear and quadratic proportional damping coefficients $\varsigma_{1}$ and $\varsigma_{2}$ are obtained by measurement and are given by $\varsigma_{1} = 1.73$, $\varsigma_{2} = 1.4$.

Figure 5(a) and 5(b) show the comparison of the simulation and experiment results of the axial strain on the upper surface of $P_{1}$ and $P_{2}$, respectively. Figure 6 shows the comparison of the simulation and experiment results of the angular velocity of the hub. As can be seen in the figure, the frequency result of the axial strain obtained by the absolute nodal coordinate formulation agrees well with the experiment result. However, the frequency of the axial strain obtained by the floating frame of reference formulation based on small deformation is lower than the experiment result. In order to show the convergence property, FFT analysis is carried out to obtain the vibration frequencies. Table 2 shows comparison of the first vibration frequencies of different formulations. It is indicated that with the increase of the DOF of the beam, the relative error of the first vibration frequency obtained by the absolute nodal coordinate formulation decreases significantly. However, the relative error of the first vibration frequency obtained by the floating frame of reference formulation does not change.

Fig. 5

(a) Axial strain of the upper surface of point $\mathrm{P}_{1}$. (b) Axial strain of the upper surface of point $\mathrm{P}_{2}$

Fig. 6

Angular velocity of the hub

Table 2 Convergence of the first vibration frequency obtained by different formulations

Figure 7 and Fig. 8 show the comparison of the simulation results of the axial strain on the upper surface of $P_{1}$ and the angular velocity of the hub, respectively, in case the thickness of the plate is increased to 0.004 m. As can be seen in the figures, with the increase of the thickness and the decrease of the deflection, the frequency result obtained by the absolute nodal coordinate formulation agrees well with the results obtained by the floating frame of the reference formulation.

Fig. 7

Axial strain of the upper surface of point $P_{1}$ for $h = 0.004\ \mbox{m}$

Fig. 8

Angular velocity of the hub for $h = 0.004\ \mbox{m}$

Figure 9 and Fig. 10 show the comparison of the simulation results of the axial strain on the upper surface of $P_{1}$ and the angular velocity of the hub, respectively, in case the thickness of the plate is reduced to 0.001 m. It is shown that with the decrease of the thickness, the elastic deformation significantly increases. The frequency obtained by the floating frame of the reference formulation based on the assumption of small deformation is much lower than that obtained by the absolute nodal coordinate formulation, and the vibration amplitude is much larger. Table 3 shows the comparison of the first vibration frequency obtained by different formulations. Defining $w_{m}$ as the peak deformation displacement in the $\boldsymbol{k}_{b}$ direction, it is indicated that when $w_{m}$ is larger than 0.55 m (38 % of the beam length), the error of the vibration frequency obtained by the floating frame of reference formulation based on small deformation increases significantly, which should be paid attention to.

Fig. 9

Axial strain of the upper surface of point $P_{1}$ for $h = 0.001\ \mbox{m}$

Fig. 10

Angular velocity of the hub for $h = 0.001\ \mbox{m}$

Table 3 Comparison of the first vibration frequency for different thickness

6 Experiment of hub–beam system with prescribed angular velocity

The second experiment investigates the centrifugal stiffening effect of a hub–beam system undergoing prescribed rotational motion as shown in Fig. 11. The rotary inertia of the hub is $J = 11.8\ \mbox{kg} {\cdot} \mbox{m}^{2}$, and the distance from point $O$ to point $A$ is $R = 0.55\ \mathrm{m}$. The constant angle between $\boldsymbol{j}_{h}$ and $\boldsymbol{j}_{b}$ is $\beta = 0$. The material and geometric properties of the beam are given in Table 4.

Fig. 11

Air floating platform undergoing rotational motion

Table 4 Material and geometric properties of the beam

In this experiment, the external torque applied on the hub is $T = 0$, and the damping torque $T_{ d}$ is not taken into account. The linear and quadratic proportional damping coefficients $\varsigma_{1}$ and $\varsigma_{2}$ are the same as in the previous experiment.

Actuated by an electric motor, the hub undergoes rotational motion. The driving angular velocity obtained using PID control law is given as follows:

$$ \omega (t) = \textstyle\begin{cases} \omega_{s}(1 - e^{ - 5t/T}) &0 \le t < t_{1} \\ \omega_{s} &t \ge t_{1} \end{cases} $$

(81)

where $\omega_{s} =3.05\ \mbox{rad/s}$, $T=100\ \mathrm{s}$, $t_{1} =80\ \mathrm{s}$. The angular velocity of the hub is measured by a gyroscopic instrument. The fitted curve of the angular velocity of the hub is given in Fig. 12. The driving constraint equation is given by

$$ \varPhi^{D} = \theta - \theta (t) = 0, $$

(82)

where

$$ \theta (t) = \textstyle\begin{cases} \omega_{s}(t + \frac{1}{5}Te^{ - 5t/T} - \frac{1}{5}T) &0 \le t < t_{1} \\ \omega_{s}(t_{1} + \frac{1}{5}Te^{ - 5t_{1}/T} - \frac{1}{5}T) + \omega_{s} ( t - t_{1} )& t \ge t_{1}. \end{cases} $$

(83)

Fig. 12

The prescribed angular velocity of the hub

Initially, the axis $\boldsymbol{i}_{b}$ of the beam is in horizontal position without elastic deformation, and $\dot{\bar{\boldsymbol{q}}}(0) = \boldsymbol{0}$. For absolute nodal coordinate formulation, the initial generalized coordinates of the system are given by

$$\begin{aligned} & \begin{aligned}[c] & \bar{\boldsymbol{q}}(0) = \begin{bmatrix} \theta (0) & \boldsymbol{q}(0)^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}},\qquad \boldsymbol{q}(0) = \begin{bmatrix} \boldsymbol{q}_{1}(0)^{\mathrm{T}} & \cdots & \boldsymbol{q}_{i}(0)^{\mathrm{T}} & \cdots & \boldsymbol{q}_{n + 1}(0)^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}, \\ &\theta (0) = 0,\qquad \boldsymbol{q}_{i}(0) = \begin{bmatrix} \boldsymbol{r}_{0i}(0)^{\mathrm{T}} & \boldsymbol{r}'_{0i}(0)^{\mathrm{T}} & \theta_{1i}(0)^{\mathrm{T}} & \theta '_{1i}(0)^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}, \\ &\boldsymbol{r}_{0i}(0) = \begin{bmatrix} R + ( i - 1 ) l & 0 & 0 \end{bmatrix} ^{\mathrm{T}},\qquad \boldsymbol{r}'_{0i}(0) = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} ^{\mathrm{T}},\\ & \theta_{1i}(0) = 0,\qquad \theta '_{1i}(0) = 0, \end{aligned} \end{aligned}$$

(84)

where $i$ represents the node number.

For the floating frame of reference formulation, the initial generalized coordinates of the system are given by

$$ \begin{aligned}[c] & \bar{\boldsymbol{q}}(0) = \begin{bmatrix} \theta (0) & \boldsymbol{\varTheta} (0)^{\mathrm{T}}\quad \boldsymbol{p}(0)^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}, \\ &\theta (0) = 0,\qquad \boldsymbol{\varTheta} (0) = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix} ^{\mathrm{T}},\qquad \boldsymbol{p}(0) = \boldsymbol{0}. \end{aligned} $$

(85)

The calculated time history of the tip deflection of the beam is shown in Fig. 13. As can be seen in the figure, the result obtained by the absolute nodal coordinate formulation agrees well with the experiment. However, the error of the result obtained by the floating frame of reference formulation is significant due to the neglect of the dynamic stiffening effect.

Fig. 13

The tip deflection of the beam

Table 5 shows the comparison of the tip deflection of the beam for $t = 80\ \mathrm{s}$ obtained by different formulations. It is indicated that with the increase of the DOF of the beam, the relative error of the tip deflection obtained by the absolute nodal coordinate formulation can be reduced significantly, whereas the relative error of the tip deflection obtained by the floating frame of reference formulation still increases. Defining $\omega_{m}$ as the angular velocity of the hub for $t = 80\ \mathrm{s}$, Table 6 shows the comparison of the tip deflection ($t = 80\ \mbox{s}$) for different angular velocities. It can be seen that with the increase of $\omega_{m}$, the simulation error of the floating frame of reference formulation increases significantly, although the deflection is small. According to the measurement, the first natural frequency of the beam is 0.9766 Hz. It can be seen that for $\omega_{m} \ge 2\ \mbox{rad/s}$ (33 % of the first natural frequency of the beam), the difference of the result obtained by two formulations should be paid attention to.

Table 5 Convergence of the tip deflection ($t = 80\ \mbox{s}$) obtained by different formulations

Table 6 Comparison of the tip deflection ($t = 80\ \mbox{s}$) for different angular velocities

7 Conclusions

Considering the proportional damping and quadratic air resistance damping force, equations of motion of flexible multibody system composed of a rotational hub and a three-dimensional beam are derived. The comparison of the simulation results obtained by the floating frame of reference formulation, the absolute nodal coordinate formulation, and the experiment results shows that in case of large deformation, the frequency of the axial strain and the angular velocity of the hub obtained by the floating frame of reference formulation based on the linear elastic theory is lower than the experiment result. On the contrary, the results obtained by the absolute nodal coordinate formulation agree well with the experiment. In addition, it is shown that with the increase of the rotating speed of the hub, the tip deflection of the beam obtained by the floating frame of reference formulation is much larger than the experiment result, whereas the results obtained by the absolute nodal coordinate formulation still agree well with the experiment due to the inclusion of the consideration of geometric nonlinear effect.

It is concluded that with the increase of the thickness and the decrease of the deflection, the frequency result obtained by the absolute nodal coordinate formulation agrees well with the results obtained by the floating frame of the reference formulation. It is also concluded that with the decrease of the thickness and the increase of the deflection, the use of the floating frame of reference formulation based on the linear elastic theory may lead to a low vibration frequency and large vibration amplitude. In case the peak deflection $w_{m}$ is larger than 38 % of the beam length, the error of the vibration frequency obtained by the floating frame of reference formulation based on the linear elastic theory increases significantly, which should be paid attention to. Furthermore, it is concluded that when the rotating speed of the hub is larger than 33 % of the first natural frequency of the beam, the dynamic stiffening effect should be taken into account.