1 Introduction

Discretization of the deformation field of a flexible body in rigid-flexible coupled systems requires careful consideration to accurately model the dynamical behavior of the systems. Currently, the discrete methods including the assumed mode method (AMM) [1,2,3] and the finite element method (FEM) [4,5,6,7] are widely used. The AMM is originated from the method of using natural modes of vibration. The advantage is that a good approximate result can be achieved by using few modes, and hence the computation efficiency is often very high. However, how to find the natural modes can be difficult when the flexible body has an irregular shape. The FEM on the other hand is versatile for complex geometry. It is a robust and thoroughly developed discrete method that is widely used to solve many types of linear and non-linear engineering problems. Most practical engineering problems related to solids and structures are currently solved by using FEM packages that are commercially available. However, the FEM has also inherent shortcomings. It uses the Galerkin weak form and the essential formulations are confined with elements, which leads to discontinuous of derivatives for the displacement functions arose the interface of the elements, so that the stress solutions is low accuracy [8]. Therefore, researchers have begun to look for new theory and discrete method for effective modeling the rigid-flexible coupled systems dynamics, such as the absolute nodal coordinate formulation [9, 10] and the B-spline interpolation method [11, 12].

Recently, mesh-free methods have been proposed and applied to solve complex problems in engineering and sciences. Mesh-free methods use shape functions created using nodes, including the smoothed particle hydrodynamic method (SPH) [13,14,15], the element-free Galerkin method (EFG) [16], the reproducing kernel particle methods (RKPM) [17], the meshless local Petrov–Galerkin method (MLPG) [18], the point interpolation method (PIM) [19, 20], and the radial point interpolation method (RPIM) [21, 22]. The node-based smoothed PIM (NS-PIM or LC-PIM termed originally [23]) has been recently developed and found very stable, is free from volumetric locking, and capable of producing upper bound solutions for force driving static problems [24,25,26]. The discretized system equations in an NS-PIM are established using weakened weak (W2) forms based on a set of background cells, and the numerical operations are not confined within the cells, but across the neighboring cells. The W2 form introduces the so-called softening effects to the discretized system equation, and hence can effectively overcome the disadvantage of the FEM [27]. This work aims to extend the mesh-free NS-PIM to solve problems of rigid-flexible coupled systems dynamics.

The behavior of beams based on the Euler–Bernoulli theory are governed by a typical 4th order differential equation with respect to coordinates. In the early work of solving 4th order boundary value problems, both displacement and slope (derivative of the displacement) are treated as independent variables. In this paper, due to the use of W2 concept, we solve the 4th order boundary value problems considering only displacement as the unknown variable, and its approximation is performed using the simple linear point interpolation method [28]. In other words, we solve 4th order differential equations using only 1st order approximation. In our examination for static problems, the beams with three types of boundary conditions are analyzed, and the results are compared with the analytic solution, which shows the effectiveness of this method. The NS-PIM is then further extended for solving a rigid-flexible coupled system dynamics problem, considering a rotating flexible cantilever beam. In this case, we consider not only the transverse deformations of the rotating flexible cantilever beam, but also the longitudinal deformations. The rigid-flexible coupled dynamic equations of the system are derived via employing Lagrange’s equations of the second kind. Simulation results of the NS-PIM are compared with those obtained using FEM and AMM. It is found that compared with FEM, the NS-PIM makes the system soften and has anti-ill solving ability under the same calculation conditions.

2 Static analysis

2.1 Brief on the weak form for the Euler–Bernoulli beam

Considering the small deformation situation, for a giving bending stiffness EI, the strong form of governing equation of an Euler–Bernoulli beam is expressed by the well-known fourth-order differential equation [27]

$$\begin{aligned} EI\frac{\hbox {d}^{4}v}{\hbox {d}x^{4}}=b_y,\quad \hbox {in domain}\,\varOmega , \end{aligned}$$
(1)

where v is transverse deflection, and \(b_{y}\) is the distributed load in the transverse direction along the beam. Depending on the problem, the boundary conditions can be given using a complementary pair of equations listed as follows

$$\begin{aligned}&v(x_0 )=v_\varGamma ,\quad \hbox {on}\,\,\,\varGamma _v, \end{aligned}$$
(2)
$$\begin{aligned}&-\frac{\hbox {d}v(x_0 )}{\hbox {d}x}=\theta _\varGamma ,\quad \hbox {on}\,\,\,\varGamma _\theta , \end{aligned}$$
(3)
$$\begin{aligned}&M(x_0 )=EI\frac{\hbox {d}^{2}v}{\hbox {d}x^{2}}=M_\varGamma ,\quad \hbox {on}\,\,\,\varGamma _M, \end{aligned}$$
(4)
$$\begin{aligned}&Q(x_0 )=-EI\frac{\hbox {d}^{3}v}{\hbox {d}x^{3}}=Q_\varGamma ,\quad \hbox {on}\,\,\,\varGamma _Q, \end{aligned}$$
(5)

where M and Q denote the bending moment and shear force acting at the cross-section of the beam, respectively. \(\varGamma _v\) and \(\varGamma _\theta \) are essential boundaries where deflection and slope are specified; \(\varGamma _M\) and \(\varGamma _Q\) are natural boundaries where bending moment and shear force are specified, respectively. The complementary condition requires that when the deflection (or slope) is specified at an end of the beam, the shear force (or moment) cannot be specified. This is to avoid the possibility of the Cauchy boundary value problem not being well posed [29]. For example, Eq. (2) may pair with Eq. (3) (for fully clamped), Eq. (2) with Eq. (4) (simply support), Eq. (3) with Eq. (5) (sliding), and Eq. (4) with Eq. (5) (free).

The standard Galerkin weak form used in the FEM formulation can be rewritten as

$$\begin{aligned} \mathop {\int }\limits _\varOmega EI\frac{\hbox {d}^{2}(\delta v)}{\hbox {d}x^{2}}\frac{\hbox {d}^{2}v}{\hbox {d}x^{2}}\hbox {d}x= & {} \mathop {\int }\limits _\varOmega {\delta vb_y \hbox {d}x} +\left. {Q_\varGamma \delta v} \right| _{\varGamma _Q } \nonumber \\&\;\;-\,\left. {M_\varGamma \frac{\hbox {d}(\delta v)}{\hbox {d}x}} \right| _{\varGamma _M }, \end{aligned}$$
(6)

in which we may note that the assumed deflection function v must be of at least 2nd order consistency. It is weaker compared to the strong form give in Eq. (1) which requires the assumed deflection function is at least 4th order consistency. The “weaker” here means that the assumed deflection function has lower consistency.

2.2 Formulation of NS-PIM for Euler–Bernoulli beam

2.2.1 Smoothed Galerkin weak form: a typical W2

In a W2 formulation, we consider a beam discretized with \(N_{n}\) nodes, as shown in Fig. 1. Every two neighboring nodes form a cell known as background cell. For each node, a smoothing domain is formed that consists of the nearer halves of the two neighboring cells, and hence there are a total of \(N_{s}\) smoothing domains: \( N_{s} =N_{n}\). We require the smoothing domain “seamless”: \(\varOmega =\cup _{i=1}^{N_s } \varOmega _i^s\) and \(\varOmega _i^s \cap \varOmega _j^{s} =0\), \(\forall i\ne j\). The smoothing domains for the two boundary nodes are formed only with half a cell on the boundary. In the present NS-PIM formulation, the displacement interpolation is based on cells, but the integration/assembling is based on the smoothing domains. Therefore, the cell functions quite differently as the element in FEM. The smoothing domain \(\varOmega _n^s \) is influenced by n nodes that are the nodes of the cells having a contribution to \(\varOmega _n^s\). For the smoothing domain for a boundary node, \(n=2\) and for all the smoothing domain of an interior node, \(n=3\). For example, nodes 1 and 2 influence \(\varOmega _1^s\), nodes \(n-1\), n, and \(n+1\) influence \(\varOmega _n^s\).

Fig. 1
figure 1

Discretization of the problem domain with nodes and the node-based smoothing domains

Full size image

Using the gradient smoothing operations [30], the smoothed first derivative of v can be expressed as

$$\begin{aligned} \frac{\overline{\hbox {d}v} }{\hbox {d}x}=\int _{\varGamma _i^s } {n(x)v(\xi )} \bar{{W}}(x-\xi )\hbox {d}\xi -\int _{\varOmega _i^s } {v(\xi )} \frac{\partial \bar{{W}}(x-\xi )}{\partial x}\hbox {d}\xi , \end{aligned}$$
(7)

where n(x) is the unit outward normal to domain \(\varOmega _i^s \) (which is either 1 or −1 for beams), \(\varGamma _i^s \) is the boundary (point) of the domain \(\varOmega _i^s \) and \(\bar{{W}}\) is the smoothing function, which is continuously differentiable in \(\varOmega _i^s \). For simplicity, the smoothing function is a local constant

$$\begin{aligned} \bar{{W}}(x-\xi )=\left\{ \begin{array}{ll} 1/A_i^s, &{}\quad \xi \in \varOmega _i^s, \\ 0,&{}\quad \xi \notin \varOmega _i^s, \\ \end{array} \right. \end{aligned}$$
(8)

where \(A_i^s\) is the area of smoothing domain at point x. So the second derivative (the curvature) of the deflection function for the smoothing domain \(\varOmega _i^s\) can now be approximated using

$$\begin{aligned} \frac{\overline{\hbox {d}^{2}v} }{\hbox {d}x^{2}}=\frac{1}{l_i^s }\int _{\varGamma _i^s } {\left( {n(x)\frac{\hbox {d}v}{\hbox {d}x}} \right) } \hbox {d}x, \end{aligned}$$
(9)

where \(l_i^s\) and is the length of the smoothing domain \(\varOmega _i^s \). Using Eqs. (9) and (6) can be written as the following smoothed Galerkin weak form.

$$\begin{aligned}&\sum _{i=1}^{N_n } {\frac{1}{l_i^s }} \left[ {\int _{\Gamma _i^s } {\left( {n(x)\frac{\hbox {d}\delta v}{\hbox {d}x}} \right) } \hbox {d}x} \right] \left[ {EI\int _{\varGamma _i^s } {\left( {n(x)\frac{\hbox {d}v}{\hbox {d}x}} \right) } \hbox {d}x} \right] \nonumber \\&\qquad =\,\int _\varOmega {\delta vb_y } \hbox {d}x+\left. {Q_\varGamma \delta v} \right| _{\varGamma _Q } -M_\varGamma \left. {\frac{\hbox {d}\delta v}{\hbox {d}x}} \right| _{\varGamma _M }, \end{aligned}$$
(10)

in which we may note: (1) the deflection function v can now only be of the first order consistency (a weakened weak form); (2) the domain integration on the left hand side is now converted to a simple summation (for better computational efficiency).

2.2.2 NS-PIM equations for Euler–Bernoulli beams

Because of the W2 formulation, in our NS-PIM, each node has only one degree of freedom (DOF) which is the deflection. We now use a linear interpolation of the deflection v in each cell (cell \(\varOmega _n^c \) in Fig. 1) to approximate the deflection, which can be expressed as

$$\begin{aligned} v(x)=\left\{ \begin{array}{ll} {\phi _n (x)}&{} {\phi _{n+1} (x)} \\ \end{array} \right\} \left\{ \begin{array}{l} {v_n } \\ {v_{n+1} } \\ \end{array} \right\} ,\quad x\in \varOmega _n^c, \end{aligned}$$
(11)

where the linear shape function can be simply given as

$$\begin{aligned} \begin{array}{l} {\phi _1 (x)=1-(x-x_n )/l_n^c}, \\ {\phi _2 (x)=(x-x_n )/l_n^c }, \\ \end{array}\quad x\in \varOmega _n^c, \end{aligned}$$
(12)

where \(l_n^c =x_{n+1} -x_n \) is the length of the cell \(\varOmega _n^c,v_n \), and \(v_{n+1} \) denote the nodal values of the deflection at nodes n and \(n+1\). Substituting Eq. (11) into Eq. (9), the smoothed curvature for the smoothing domain \(\varOmega _n^s\) with interior nodes can be given as

$$\begin{aligned}&\frac{1}{l_i^s }\int _{\varGamma _i^s } {\left( {n(x)\frac{\hbox {d}v}{\hbox {d}x}} \right) } \hbox {d}x\nonumber \\&\quad ={\underbrace{\frac{1}{l_i^s}\left\{ {{\begin{array}{c} {-\phi _{1,x} } \\ {\phi _{1,x} -\phi _{2,x} } \\ {\phi _{2,x} } \\ \end{array} }} \right\} }_{{\varvec{B}}_{\varvec{n}}}}^{{\mathrm{T}}}\underbrace{\left\{ {{\begin{array}{l} {v_{n-1} } \\ {v_n } \\ {v_{n+1} } \\ \end{array} }} \right\} }_{{\varvec{d}}_{\varvec{n}}} ={\varvec{B}}_{\varvec{n}} {\varvec{d}}_{\varvec{n}} , \end{aligned}$$
(13)

where \(n=2,3,\ldots ,N_n -1\).

Fig. 2
figure 2

Three types of boundary conditions of beams with distributed load: cantilever beam, simply–simply supported beam, and clamped-simply supported beam, respectively

Full size image

For simply supported boundary conditions, the zero deflection is set at the corresponding boundary point, just like in the FEM. For clamped boundary conditions, however, the following treatment is needed to impose the zero-slope conditions. The reason is the formulation of NS-PIM does not have rotation as a DOF. For the clamped boundary on the left end (\(n=1\)), we used the smoothed gradient that can be given by

$$\begin{aligned} \frac{1}{l_1^s }\int _{\varGamma _1^s } {\left( {n(x)\frac{\hbox {d}v}{\hbox {d}x}} \right) } \hbox {d}x={\underbrace{\frac{1}{l_1^s }\left\{ \begin{array}{l} {\phi _{1,x} } \\ {\phi _{2,x} } \\ \end{array} \right\} }_{{\varvec{B}}_1^{C}}}^{\mathrm{T}}\underbrace{\left\{ \begin{array}{l} {v_1 } \\ {v_2 } \\ \end{array} \right\} }_{{\varvec{d}}_1 }={\varvec{B}}_1^{C}{\varvec{d}}_1 . \end{aligned}$$
(14)

Similarly, for the clamped boundary on the right end (\(n=N_{n})\), the smoothed gradient is given by

$$\begin{aligned}&\frac{1}{l_{N_n }^s }\int _{\varGamma _{N_n }^s } {\left( {n(x)\frac{\hbox {d}v}{\hbox {d}x}} \right) } \hbox {d}x\nonumber \\&\quad ={\underbrace{\frac{1}{l_{N_n }^s }\left\{ \begin{array}{l} {-\phi _{1,x} } \\ {-\phi _{2,x} } \\ \end{array}\right\} }_{{{\varvec{B}}_{Nn}^{C}}}}^{\mathrm{T}}\underbrace{\left\{ \begin{array}{l} {v_{N_n -1} } \\ {v_{N_n } } \\ \end{array} \right\} }_{{\varvec{d}}_{N_n }}={\varvec{B}}_{N_n }^{^{C}} {\varvec{d}}_{N_n}. \end{aligned}$$
(15)

It is clear that the zero-slope condition is imposed using the relation of two nodes on the boundary, which can be conveniently done without using two DOFs at a node.

Next, substituting Eq. (13) into Eq. (10), a set of discretized algebraic system equations can be obtained in the following matrix form

$$\begin{aligned} {\varvec{KU}}={\varvec{F}}, \end{aligned}$$
(16)

where \({\varvec{U}}=\left\{ \begin{array}{llll} {v_1 }&{} {v_2 }&{} \cdots &{} {v_{Nn}} \\ \end{array}\right\} ^{\mathrm{T}}\) is the vector of the nodal deflections, and \({\varvec{F}}\) is the force vector defined as

$$\begin{aligned} {\varvec{F}}= & {} \int _\varOmega {{\varvec{\varPhi }}^{\mathrm{T}}} (x)b_y \hbox {d}x+\int _{\varGamma _Q } {{\varvec{\varPhi }}^{\mathrm{T}}} (x)Q_\varGamma \hbox {d}\varGamma \nonumber \\&-\int _{\varGamma _M } {{\varvec{\varPhi }}_{,x}^{\mathrm{T}} (x)} M_\varGamma \hbox {d}\varGamma , \end{aligned}$$
(17)

where \({\varvec{\varPhi }} (x)\) is the global matrix of all these nodal shape functions. The global smoothed stiffness matrix is assembled in the form of

$$\begin{aligned} {\varvec{K}}=\sum _{n=1}^{N_n } {{\varvec{K}}_n }, \end{aligned}$$
(18)

where \({\varvec{K}}_n \) which is the stiffness matrix associated with \(\varOmega _n^s \) is computed using

$$\begin{aligned} {\varvec{K}}_n =EI({\varvec{B}}_n )^{\mathrm{T}}{\varvec{B}}_n l_n. \end{aligned}$$
(19)

The summation in Eq. (18) means an assembly (node marched summary). The assembling process is similar as that in the FEM, but must be based on the smoothing domains.

We may note that in the FEM for beam, there are two DOFs (deflection and rotation) at each node, which is double of that in NS-PIM when the same number of nodes is used.

2.3 Numerical examination of NS-PIM for static problems

The NS-PIM is coded and examination has been performed to verify the formulation for static problems. Figure 2 shows three types of boundary conditions with distributed load that are considered in this examination. The parameters are taken as \(L=1\, \hbox {m},\, EI=1\, \hbox {N}\cdot \hbox {m}^{2}\), and \(q=1\, \hbox {N/m}\). Figure 3a–c shows the results of deflection under three types of boundary conditions using NS-PIM, FEM, AMM, together with the exact solution. The NS-PIM uses 22 DOFs, the FEM also uses 22 DOFs, and the AMM uses the first three modes. It is shown that these numerical results agree very well, and the differences are not distinguishable. These examples indicate that the NS-PIM has high accuracy even if using linear interpolation.

The results of deflection are computed and listed in Tables 1–3. It can be seen that the NS-PIM provides an upper bound solution for the deflection. This demonstrates that the NS-PIM makes the system soften.

Fig. 3
figure 3

The deflection under different boundary conditions: a cantilever beam; b simply–simply supported beam; c clamped-simply supported beam

Full size image

Figure 4 shows a cantilever beam subjected to pure bending moment at free end. The bending moment \(M_\mathrm{e}=1\, \hbox {N}\cdot \hbox {m}\). Figure 5 shows the results of deflection. The NS-PIM uses 22 DOFs. It is shown that the numerical results agree very well with the exact solution, and the differences are not distinguishable. It also indicates that the pure bending boundary condition is able to be addressed by NS-PIM even if there is no rotation as the degree of freedom.

3 NS-PIM of rigid-flexible coupled system dynamics

3.1 NS-PIM for rotating flexible beams

For rotating flexible beams, we assume that for the bending deformations, the rotating flexible beam obeys the Euler–Bernoulli beam theory. This means that the cross-section of the beam is perpendicular to the central axis of the beam and remains in a plane after deformation.

Table 1 The deflection of cantilever beam
Full size table
Table 2 The deflection of simply–simply supported beam
Full size table
Table 3 The deflection of clamped-simply supported beam
Full size table

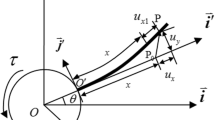
Consider a flexible beam attached to a rigid hub of radius a, and rotating about the Z axis, following the right-hand rule convention in the inertial coordinate system OXYZ, as shown in Fig. 6. A planar floating coordinate system, which rotates with the beam is denoted by \(O^{{\prime }}xyz\). The rotary inertia of the hub is \(J_{h}\). Physical parameters of the beam are as follows: length L, cross-section area S, Young’s modulus E, area moment of inertia I,  and mass density \(\rho \). The position vector of arbitrary point P on the flexible beam in the inertial frame OXYZ after deformation can be given by

$$\begin{aligned} {\varvec{r}}={\varvec{\varTheta }} \left( {\varvec{r}}_\mathrm{A} +{\varvec{\rho }} _0 +{\varvec{u}}\right) , \end{aligned}$$
(20)

where

$$\begin{aligned}&{\varvec{r}}_\mathrm{A} =(a,0)^{\mathrm{T}}, {\varvec{\rho }}_0 =(x,0)^{\mathrm{T}}, {\varvec{u}}=(u_x ,u_y )^{\mathrm{T}},\nonumber \\&{\varvec{\varTheta }} =\left( \begin{array}{ll} {\cos \theta }&{}\qquad {-\sin \theta } \\ {\sin \theta }&{}\qquad {\cos \theta } \\ \end{array}\right) . \end{aligned}$$
(21)
Fig. 4
figure 4

A cantilever beam subjected to pure bending moment at free end

Full size image
Fig. 5
figure 5

The deflection with pure bending moment at free end

Full size image
Fig. 6
figure 6

The deformation of rotating flexible beam

Full size image

In Eq. (21), \({\varvec{\varTheta }}\) is the direction cosine matrix of floating coordinate system relative to the inertial coordinate system. The deformation vector \({\varvec{u}}\) in the floating coordinate system \(O^{{\prime }}xyz\) can be expressed by

$$\begin{aligned} {\varvec{u}}=\left[ \begin{array}{l} u_x \\ u_y \\ \end{array}\right] =\left[ \begin{array}{c} w_1 +w_c \\ w_2 \\ \end{array}\right] , \end{aligned}$$
(22)

where \(w_1\) is the axial stretch deformation and \(w_2\) is the transverse deformations of the flexible beam. \(w_c\) is the coupling term of the deformation which is caused by the transverse deformation. It can be given by

$$\begin{aligned} w_c =-\frac{1}{2}\int _0^x {\left( {\frac{\partial w_2 }{\partial \zeta }} \right) }^{2}\hbox {d}\zeta . \end{aligned}$$
(23)

The velocity vector of arbitrary point P in the inertial coordinate system can be obtained through the first derivative of Eq. (20) versus time. It can be given by

$$\begin{aligned} \dot{{\varvec{r}}}=\dot{{\varvec{\varTheta }}}({\varvec{r}}_\mathrm{A} +{\varvec{\rho }}_0 +{\varvec{u}})+{\varvec{\varTheta }} \dot{{\varvec{u}}}. \end{aligned}$$
(24)

Then the kinetic energy of the system is

$$\begin{aligned} T=\frac{1}{2}J_{oh} \dot{\theta }^{2}+\frac{1}{2}\int _V {\rho \dot{{\varvec{r}}}^{\mathrm{T}}} \dot{{\varvec{r}}}\hbox {d}V. \end{aligned}$$
(25)

The elastic potential energy of the system is

$$\begin{aligned} U=\frac{1}{2}\int _0^L {ES\left( {\frac{\partial w_1 }{\partial x}} \right) }^{2}\hbox {d}x+\frac{1}{2}\int _0^L {EI\left( {\frac{\partial ^{2}w_2 }{\partial x^{2}}} \right) }^{2}\hbox {d}x.\nonumber \\ \end{aligned}$$
(26)

3.2 Dynamic equations of the rotating flexible beam system

The flexible beam is divided into \(N_{c}\) cells shown in Fig. 1. As discussed in Sect. 2.3, using Eqs. (11) and (12), the axial stretch deformation \(w_1\) and the transverse deformations \(w_2\) in ith cell can be expressed

$$\begin{aligned} {{\begin{array}{ll} {w_1 =\left\{ {{\begin{array}{ll} {\phi _i (x)}&{} {\phi _{i+1} (x)} \\ \end{array} }} \right\} \left\{ {{\begin{array}{c} {u_{xi} } \\ {u_{x(i+1)} } \\ \end{array} }} \right\} ={\varvec{\varPhi }}^{i}(x){\varvec{A}}^{i}(t)}, \\ {w_2 =\left\{ {{\begin{array}{ll} {\phi _i (x)}&{} {\phi _{i+1} (x)} \\ \end{array} }} \right\} \left\{ {{\begin{array}{c} {u_{yi} } \\ {u_{y(i+1)} } \\ \end{array} }} \right\} ={\varvec{\varPhi }}^{i}(x){\varvec{B}}^{i}(t)}, \\ \end{array} }} \quad x\in \varOmega _i^c \end{aligned}$$
(27)

where \({\varvec{A}}^{\varvec{i}}(t)\) and \({\varvec{B}}^{i}(t)\) are the axial stretch deformation vector and the transverse deformations vector of nodes i and \(i+1\) with the change of time, respectively. The generalized coordinates of the beam are

$$\begin{aligned} {\varvec{A}}= & {} \left\{ \begin{array}{llll} {u_{x1} }&{} {u_{x2} }&{} \cdots &{} {u_{xN_n } } \\ \end{array} \right\} ^{\mathrm{T}},\nonumber \\ {\varvec{B}}= & {} \left\{ \begin{array}{llll} {u_{y1} }&{} {u_{y2} }&{} \cdots &{} {u_{yN_n } } \\ \end{array}\right\} ^{\mathrm{T}}. \end{aligned}$$
(28)

So the nodal coordinate vector can be written as

$$\begin{aligned} {\varvec{A}}^{i}= & {} {\varvec{R}}^{i}{\varvec{A}}, \nonumber \\ {\varvec{B}}^{i}= & {} {\varvec{R}}^{i}{\varvec{B}}, \end{aligned}$$
(29)

where \({\varvec{R}}^{i}\) is a Boolean matrix given by

$$\begin{aligned} \hbox {Node number}:\begin{array}{ccccccc} 1&2&\cdots&i&i+1&\cdots&N_{n} \end{array}\nonumber \\ {\varvec{R}}^{i}=\left[ \begin{array}{ccccccc} 0 &{}\quad 0 &{}\quad \cdots &{}\quad 1 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ \end{array}\right] . \end{aligned}$$
(30)

Substituting Eq. (29) into Eq. (27) yields

$$\begin{aligned} \begin{array}{l} {w_1 ={\varvec{\varPhi }} (x){\varvec{A}}(t)}, \\ {w_2 ={\varvec{\varPhi }} (x){\varvec{B}}(t)}, \\ \end{array}\quad x\in \varOmega _i^c, \end{aligned}$$
(31)

where \({\varvec{\varPhi }} (x)={\varvec{\varPhi }}^{i}(x){\varvec{R}}^{i}\).

Substituting Eq. (31) into Eq. (22), the deformation matrix of arbitrary point P on the flexible beam can be expressed by

$$\begin{aligned} {\varvec{u}}=\left[ {\begin{array}{l} u_x \\ u_y \\ \end{array}} \right] =\left[ {\begin{array}{l} {\varvec{\varPhi }} (x){\varvec{A}}(t)-\frac{1}{2}{\varvec{B}}^{\mathrm{T}}(t){\varvec{H}}(x){\varvec{B}}(t) \\ {\varvec{\varPhi }} (x){\varvec{B}}(t) \\ \end{array}} \right] , \end{aligned}$$
(32)

where \({\varvec{H}}(x)\) is the coupling shape functions, it can be given by

$$\begin{aligned} {\varvec{H}}(x)={\varvec{R}}^{i\mathrm{T}}\int _0^x {{\varvec{\varPhi }}^{i{'}\mathrm{T}}(\zeta ){\varvec{\varPhi }}^{i{'}}(\zeta )} \hbox {d}\zeta {\varvec{R}}^{i}, \end{aligned}$$
(33)

where \({\varvec{\varPhi }}^{{\prime }}(\zeta )\) means the first derivative of \({\varvec{\varPhi }}(\zeta )\) versus \(\zeta \).

Let \({\varvec{q}}=\left( \begin{array}{lll} \theta &{}\, {{\varvec{A}}^{\mathrm{T}}}&{} \,{{\varvec{B}}^{\mathrm{T}}} \\ \end{array}\right) ^{\mathrm{T}}\) be the generalized coordinate vector. Substituting Eqs. (25) and (26) into Lagrange’s equations of the second kind

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial T}{\partial \dot{{\varvec{q}}}}} \right) -\frac{\partial T}{\partial {\varvec{q}}}=-\frac{\partial U}{\partial {\varvec{q}}}+{\varvec{F}}_q, \end{aligned}$$
(34)

where \({\varvec{F}}_q =\left( \begin{array}{lll} \tau &{}\, \mathbf{0}&{}\, \mathbf{0} \\ \end{array}\right) ^{\mathrm{T}}\) is the generalized force vector. \(\tau \) is an external torque applied on the rigid hub. Then the dynamic equations can be given by

$$\begin{aligned} \left( \begin{array}{ccc} {M_{11} }&{}\quad {{\varvec{M}}_{12} }&{}\quad {{\varvec{M}}_{13} } \\ {{\varvec{M}}_{21} }&{}\quad {{\varvec{M}}_{22} }&{}\quad \mathbf{0} \\ {{\varvec{M}}_{31} }&{}\quad \mathbf{0}&{}\quad {{\varvec{M}}_{33} } \\ \end{array}\right) \left( \begin{array}{l} {\ddot{\theta }} \\ {\ddot{{\varvec{A}}}} \\ {\ddot{{\varvec{B}}}} \\ \end{array}\right) =\left( \begin{array}{l} {Q_\theta } \\ {{\varvec{Q}}_A } \\ {{\varvec{Q}}_B } \\ \end{array}\right) , \end{aligned}$$
(35)

where

$$\begin{aligned}&M_{11} =J_{oh} +J_{ob} +2{\varvec{SA}}+{\varvec{A}}^{\mathrm{T}}{\varvec{MA}}\nonumber \\&+\,{\varvec{B}}^{\mathrm{T}}{\varvec{MB}}-\underline{{\varvec{B}}^{\mathrm{T}}(a{\varvec{C+D)B}}}, \end{aligned}$$
(36)
$$\begin{aligned}&{\varvec{M}}_{21} ={\varvec{M}}_{12}^{\mathrm{T}}=-{\varvec{MB}}, \end{aligned}$$
(37)
$$\begin{aligned}&{\varvec{M}}_{31} ={\varvec{M}}_{13}^{\mathrm{T}}=-{\varvec{S}}^{\mathrm{T}}+{\varvec{M}}^{\mathrm{T}}{\varvec{A}}, \end{aligned}$$
(38)
$$\begin{aligned}&{\varvec{M}}_{22} ={\varvec{M}}_{33} ={\varvec{M}}, \end{aligned}$$
(39)
$$\begin{aligned}&Q_\theta =\tau -2\dot{\theta }[{\varvec{S}}\dot{{\varvec{A}}}+{\varvec{A}}^{\mathrm{T}}{\varvec{M}}\dot{{\varvec{A}}}+{\varvec{B}}^{\mathrm{T}}{\varvec{M}}\dot{{\varvec{B}}} \nonumber \\&-\,\underline{{\varvec{B}}^{\mathrm{T}}(a{\varvec{C+D)}}\dot{{\varvec{B}}}}], \end{aligned}$$
(40)
$$\begin{aligned}&{\varvec{Q}}_A =\dot{\theta }^{2}{\varvec{S}}^{\mathrm{T}}+2\dot{\theta }{\varvec{M}}\dot{{\varvec{B}}}+(\dot{\theta }^{2}{\varvec{M}}-{\varvec{K}}_1 ){\varvec{A}}, \end{aligned}$$
(41)
$$\begin{aligned}&{\varvec{Q}}_B =\dot{\theta }^{2}({\varvec{M}}-\underline{a{\varvec{C-D}}})B-2\dot{\theta }{\varvec{M}}\dot{{\varvec{A}}}-{\varvec{K}}_2 {\varvec{B}}, \end{aligned}$$
(42)
$$\begin{aligned}&K_1 =ES\int _0^L {{\varvec{\varPhi }}^{{'}\mathrm{T}}{\varvec{\varPhi }}^{'}\hbox {d}x} , \end{aligned}$$
(43)
$$\begin{aligned}&{\varvec{K}}_2 =EI\int _0^L {{\varvec{\varPhi }}^{\mathrm{{''}T}}{\varvec{\varPhi }}^{{''}}\hbox {d}x}, \end{aligned}$$
(44)

where \(J_{oh} \) and \(J_{ob} \) are constant; \({{\varvec{S, M, C}}}\), and \({\varvec{D}}\) are constant matrixes. The underlined term is additional coupling term which caused by transverse bending deformation and it makes the longitudinal deformation shorten. This term appears in the generalized mass matrix and the generalized force matrix.

With the discussion of Sect. 2.3, using the smoothing operations, the stiffness matrix \({\varvec{K}}_2 \) can be expressed by

$$\begin{aligned} {\varvec{K}}_2 =\sum _{i=1}^{N_n } {\frac{1}{l_i^s }} \left[ {\int _{\varGamma _i^s } {\left( {n(x)\frac{\hbox {d}v}{\hbox {d}x}} \right) } \hbox {d}x} \right] \left[ {EI\int _{\varGamma _i^s } {\left( {n(x)\frac{\hbox {d}v}{\hbox {d}x}} \right) } \hbox {d}x} \right] . \end{aligned}$$
(45)

Using Eqs. (18) and (19), the global smoothed stiffness matrix can be obtained.

3.3 Transient dynamic simulation

When the angular velocity of the hub is given, the dynamic equations of the system can be expressed by

$$\begin{aligned} \left( \begin{array}{cc} {{\varvec{M}}_{22} }&{}\quad \mathbf{0} \\ \mathbf{0}&{}\quad {{\varvec{M}}_{33} } \\ \end{array}\right) \left( \begin{array}{l} {\ddot{{\varvec{A}}}} \\ {\ddot{{\varvec{B}}}} \\ \end{array}\right) =\left( \begin{array}{ll} {{\varvec{Q}}_A -{\varvec{M}}_{21} \ddot{\theta }} \\ {{\varvec{Q}}_B -{\varvec{M}}_{31} \ddot{\theta }} \\ \end{array}\right) . \end{aligned}$$
(46)

Assuming the angular velocity of the hub is given by

$$\begin{aligned} \dot{\theta }=\left( \begin{array}{ll} \frac{\varOmega _0 }{T}t-\frac{\varOmega _0 }{2\uppi }\sin \left( \frac{2\uppi }{T}t \right) , &{} {0\le t\le T} \\ \varOmega _0 ,&{} {t>T} \\ \end{array}\right) , \end{aligned}$$
(47)

where \(T=15\, \hbox {s}\). The angular velocity of the hub reaches \(\varOmega _0\) at time T. The hub radius \(a=0\). Parameters of the rotating beam are [31]: \(L=8\,\hbox {m}\), \(S=7.2968\times 10^{-5}\,\hbox {m}^{2}\), \(I=8.2189\times 10^{-9}\,\hbox {m}^{4},\rho =2766.7\,\hbox {kg/m}^{\mathrm{3}}\), and \(E=68.952\,\hbox {GPa}\).

Fig. 7
figure 7

Tip responses of the rotating beam for slow rotation (\(\varOmega _0 =4\,\hbox {rad/s}\)): a The longitudinal deformation at the tip of the beam; b the transverse deformation at the tip of the beam; c the transverse deformation at the tip of the beam after 15 s

Full size image
Fig. 8
figure 8

Tip transverse deformation rate of the beam for slow rotation (\(\varOmega _0 =4\,\hbox {rad/s})\): a tip transverse deformation rate from 0 to 20 s; b tip transverse deformation rate after 15 s

Full size image
Fig. 9
figure 9

Tip responses of the rotating beam for fast rotation (\(\varOmega _0 =20\,\hbox {rad/s})\): a the longitudinal deformation at the tip of the beam; b the transverse deformation at the tip of the beam; c the transverse deformation at the tip of the beam after 15 s

Full size image
Fig. 10
figure 10

Tip transverse deformation rate of the beam for fast rotation (\(\varOmega _0 =20\,\hbox {rad/s})\): a tip transverse deformation rate from 0 to 20 s; b tip transverse deformation rate after 15 s

Full size image

The tip responses of the rotating beam with different \(\varOmega _0 \) are shown in Figs. 7–10. The simulation results of AMM, FEM, and NS-PIM are compared. AMM uses three to seven modes, FEM uses ten elements and NS-PIM uses 21 nodes. Figure 7a shows the longitudinal deformation at the tip of the beam when \(\varOmega _0 =4\,\hbox {rad/s}\). It is seen that these three discrete methods almost overlap with each other. The longitudinal deformation \(u_x \) contains two parts: the axial stretch deformation \(w_1\) and the coupling term of the deformation \(w_c\), which is caused by the transverse deformation. It is negative meaning that the longitudinal deformation is mainly caused by the coupling term \(w_c\). Figures 7b–c and 8 show the tip transverse bending deformation and its deformation rate which is the first derivative of deformation versus time, respectively. As shown in these figures, the results of these three discrete methods almost overlap with each other. Figure 9a shows the longitudinal deformation at the tip of the beam when \(\varOmega _0 =20\,\hbox {rad/s}\). In order to illustrate the less accuracy of AMM when the deformation is large, the elasticity modulus reduces to 50  GPa. It is seen that the results of NS-PIM and FEM are almost overlap, but AMM is quite different. Figures 9b–c and 10 show the tip transverse bending deformation and its deformation velocity, respectively. It is seen that the results of AMM is quite different from the other two methods. That means AMM is not applicable when the deformation is large, it is applicable in the case of small deformation. Compared with FEM, NS-PIM is a little different. Figures 9c and 10c show that the amplitude of AMM is much smaller than FEM, the amplitude of NS-PIM is nearly the same as FEM. However, the vibration phase of NS-PIM is different from FEM. This is because of the soft characteristic of NS-PIM. In order to illustrate that AMM is not applicable in the case of large deformation, Fig. 11 shows the tip transverse bending deformation when \(\varOmega _0 =20\,\hbox {rad/s}\) and \(E=20\,\hbox {GPa}\). It is seen that the largest deformation is over 5 m, belong to large deformation problem. AMM is divergent, that means AMM is not applicable in the large deformation problem. NS-PIM and FEM are convergent. But there are a little difference between NS-PIM and FEM. Still, this is because of the soft characteristic of NS-PIM.

Fig. 11
figure 11

Large deformation situation

Full size image
Table 4 The relative time, the relative error and the amplitude of these three discrete methods (\(\varOmega _0 =4\,\hbox {rad/s}\))
Full size table
Table 5 The relative time, the relative error and the amplitude of these three discrete methods (\(\varOmega _0 =20\,\hbox {rad/s}\))
Full size table

Tables 4 and 5 show the relative time, the relative error and the amplitude of these three discrete methods when \(\varOmega _0 =4\,\hbox {rad/s}\) and \(\varOmega _0 =20\,\hbox {rad/s}\), respectively. AMM uses the first three to seven modes, and the relative time is compared with three modes AMM. The relative error is compared with ten elements FEM. NS-PIM uses 21 nodes. It is seen that three modes AMM computes the fastest, and NS-PIM is faster than FEM. When \(\varOmega _0 =4\,\hbox {rad/s}\), the deformation is small so AMM is applicable. For AMM, the error of the amplitude is small and the accuracy is not improved even if increasing the modes. Instead, the computational efficiency reduces significantly. When \(\varOmega _0 =20\,\hbox {rad/s}\), the deformation is large so AMM is not applicable and the error is big to 45.45%. Regardless of the deformation is small or large, the FEM and NS-PIM are applicable. But the amplitude of NS-PIM is larger than FEM, this is also because of the soft characteristic of NS-PIM, and its accuracy is very high even if using the linear shape function.

When there is an external torque acting on the hub, the large overall motion of the system is unknown. The dynamic responses of the beam can be calculated from Eq. (35). The parameters of the beam are the same as the situation when the angular velocity of the hub is given. Assuming the external torque of the hub is given by

$$\begin{aligned} \tau =\left\{ \begin{array}{ll} \tau _0 \sin \left( {\frac{2{\uppi }}{T}t} \right) ,&{} 0\le t\le T, \\ 0,&{} t>T, \\ \end{array}\right. \end{aligned}$$
(48)

where \(T=10\, \hbox {s}\), and \(\tau _0 \) is the amplitude of the external torque.

The rotation angle and the tip responses of the rotating beam are shown in Fig. 12 when \(\tau _0\) equals \(10\, \hbox {N}\cdot \hbox {m}\). It is seen that these three discrete methods almost overlap with each other. When the external torque is removed, the flexible beam swings back and forth in which the rotation angle is equal to 4.5 rad. From Fig. 12c, one can observe that the amplitude of NS-PIM is lager and the vibrational frequency is smaller than the other two methods. This phenomenon demonstrates again that the NS-PIM makes the system soften. Figure 13 shows the tip transverse deformation of FEM and NS-PIM when \(\tau _0\) equals \(50\, \hbox {N}\cdot \hbox {m}\) under the same calculation conditions. It is seen that the result of FEM is divergent quickly. This is because the dynamic equations of FEM are ill-conditioned. However, the result of NS-PIM is still convergent. One can conclude that the dynamic equations of NS-PIM have anti-ill solving ability compared with FEM under the same calculation conditions.

Fig. 12
figure 12

The rotation angle and the tip responses of the rotating beam (\(\tau _0 =10\,\hbox {N}\cdot \hbox {m})\): a the rotation angle; b tip transverse deformation from 0 to 15 s; c tip transverse deformation after 10 s

Full size image
Fig. 13
figure 13

The tip responses of the rotating beam (\(\tau _0 =50\,\hbox {N}\cdot \hbox {m})\)

Full size image

4 Conclusion

In this paper, a mesh-free method which is called NS-PIM is formulated for rigid-flexible coupled dynamic analysis of beams. We conclude the paper with the following points.

  1. (1)

    Through the smoothing operation based on nodes, the requirements on the consistence of the displacement functions are further weakened. The solutions of fourth-order boundary value and initial value problems can now be approximated using linear shape functions in NS-PIM.

  2. (2)

    For static problems, NS-PIM has high accuracy even if using linear interpolation. It provides a unique upper bound solution for the deflection.

  3. (3)

    For the problem of rotating flexible beam, when the deformation is small, the results of AMM, FEM, and NS-PIM are close. Even if increasing the number of modes, the accuracy is not improved for AMM, but the computational efficiency reduces significantly. When the deformation is large, AMM is not applicable, but FEM and NS-PIM is still applicable. The soft characteristic of NS-PIM is more obvious than the situation of small deformation. What’s more, the dynamic equations of NS-PIM have anti-ill solving ability compared with FEM under the same calculation conditions. In other words, the NS-PIM is more stable than FEM.

  4. (4)

    Because of only displacement as independent variable at per node, NS-PIM the total DOFs is half of that of FEM model using the same number of nodes, and hence NS-PIM computes faster than FEM.