Abstract
Dynamic analysis of flexible body under large rotation becomes increasingly important in many engineering applications. This work takes rotating flexible beam as numerical example under assumptions of straight beam, small deformation and fixed axis rotation. Results of six finite element methods are compared: floating frame of reference formulation (FFRF), generalized component mode synthesis (GCMS), total Lagrangian formulation (TLF), linear Euler–Bernoulli beam (LEBB), nonlinear Euler–Bernoulli beam (NEBB) and absolute nodal coordinate formulation (ANCF). Due to the effect of geometric nonlinearity or centrifugal stiffening, the results of linear methods FFRF, GCMS and LEBB are different to geometrically nonlinear methods TLF, NEBB and ANCF. Three points of view are obtained through numerical result analysis. Firstly, based on the equivalence between FFRF and GCMS, a special type of parametrically excited nonlinear system is equivalent to linear system, so as to analyze the Lyapunov stability of its solution. Secondly, for the ANCF, the system invariant matrix is presented to calculate elastic force, which avoids element integration or assembling in each time step, and then the computational efficiency is improved by at least an order of magnitude when compared to adopting element invariant matrix. Thirdly, for GCMS, TLF and ANCF, the velocity of relative coordinate for deformation is adopted to calculate linear internal damping force, which gets different deflection result in comparison with adopting velocity of absolute coordinate for deformation, under large rotational speed.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The finite element method [1,2,3,4,5,6] is widely applied for accurate dynamic analysis of flexible body under large rotation [7]. These finite element methods are usually categorized according to kinematic analysis approach: the FFRF [7], GCMS [2], LEBB [4] and NEBB [5] separate flexible deformation from rigid rotation, whereas the TLF [8] and ANCF [7] do not. The former categorized method is also known as hybrid coordinate method [9] or common flexible multibody dynamic method. According to deformation measurement approach, the four hybrid coordinate methods can be further categorized: the FFRF, LEBB and NEBB measure deformation by relative coordinate, whereas the GCMS by absolute coordinate [10]. Even under the same kinematic analysis approach and the same deformation measurement approach, there are more detailed categories; for example, the common FFRF interpolates deformation based on solid element, whereas the LEBB and NEBB base on beam element. Up to now, the comparison of these different finite element methods is necessary but still rare.
As an efficient flexible multibody dynamic method, the FFRF is already widely used in commercial softwares [11] and its performance is continuously enhanced by various new approaches. In order to avoid costly integral updates at each time step, the inertia and quadratic velocity force of FFRF are presented as a function of inertia shape integrals [7, 12]. Based on the Sherman-Morrison-Woodbury formula, the iterative equation of FFRF is solved with infinite penalty factor of joint constraint, and the factorization of unchanged mass and stiffness matrices part is reused [13]. To avoid using Lagrange multiplier of kinematic constraints, the absolute floating frame coordinates and local interface coordinates are transformed into absolute interface coordinate, and the tangent stiffness matrix is derived by variation of equilibrium equation [14]. By numerical examples, it is verified that three component mode synthesis methods both lead to correct numerical results: Guyan-Iron condensation method, modal truncation technique, Craig-Bampton synthesis approach [15]. After effect analysis of reference condition, it is proved there is no single set of reference conditions suited for all applications [16]. Through nodal-based treatment of FFRF, a concise equation of motion is derived without using inertia shape integrals or lumped mass approximation [11]. With the aid of inertia shape integrals method, component mode synthesis method and employment of reference condition, the method of FFRF is implemented in this work.
The GCMS is a promising alternative to flexible multibody dynamic analysis. The GCMS is based on absolute coordinate formulation, which measures deformation by absolute coordinate and partially linearizes the Green strain tensor with respect to co-rotated frame; the resulting mass and stiffness matrices are constant apart from a transformation based on rotation matrix [17]. For planar example, the component mode synthesis is applied to absolute coordinate formulation; although the number of deformation modes increases, the computational complexity for the system Jacobian factorization reduces from cubic to quadratic [18]. Through direct approximation of total displacements by global mode shapes, the total displacements are linearly dependent on reduced generalized coordinates, and the resulting equation of motion also preserves constant mass matrix, co-rotated stiffness matrix and avoids quadratic velocity vector [10]. For the flexible bodies with large rotations about one axis, the GCMS is formulated by reducing the number of flexible shape functions to three times the number of component mode synthesis shape functions [19]. To avoid the matrix ill condition which is caused by linear dependence and different Euclidean norm magnitude orders of generalized component modes, a “shortened” version of the classical Gram-Schmidt process is adopted to obtain desired independent set of generalized component modes [2]. In this work, the absolute coordinate formulation is organized in a comparative way to FFRF, and the global mode shapes are not given since they are already involved by previous work [20].
The TLF [8] is also called as a reference configuration formulation [21], which solves geometrically nonlinear problems with finite deformation. Except for problems with large mesh distortion, the TLF is widely applied in geometrically nonlinear problems of continua and structures, such as gear dynamics [3], rotating blade [22], car crash [23] and metal forming [24]. Via highly parallel graphics processing unit, the efficiency of biomechanical simulation based on TLF is increased by 16.8 times [25] and 20 times [26], respectively, in comparison with CPU implementations. The TLF is also the basis of constitutive equation for many complex nonlinear materials, such as silica-filled rubber material [27], viscoelastic plane structures [28], incompressible finite strain solid [29] and fiber composites [30]. For the TLF implementation in this work, the parallel computation [31] is regretfully not employed, the internal nodal force computation is less efficient than the procedure in section 4.9 of [8], and these two weaknesses restrict our result validity and our TLF implementation in this work only provides reference of numerical accuracy but not numerical efficiency.
The LEBB is based on Euler–Bernoulli beam assumption and linear elasticity assumption. A linear state-space model of flexible beam is established for single-link flexible manipulator simulation, it is shown the dominant parts of transient responses are characterized by only two flexible modes [4]. Through experiment and simulation comparisons, it is shown the LEBB based on linear elastic theory leads to a low vibration frequency and large vibration amplitude, along with the decrease of beam thickness and the increase of deflection [32]. Through separating the element motion into local system movement and elastic deflection, the dynamic equation of 3D beam element is formulated with lumped mass matrix, where the beam element is denoted by three lumped mass points [33]. Besides finite element method, the Euler–Bernoulli beam assumption and linear elasticity assumption are also used in analytical or semi-analytical method, such as inverse dynamics solution of slewing beam [34], dynamic analysis of single-link manipulator arm [35]. In this work, the inertia shape integrals are explicitly given for mass matrix calculation of LEBB.
The main difference between NEBB and LEBB is that NEBB adopts von Kármán strain–displacement relationship [36]. Through writing the equations of motion in terms of axial coordinate along the deformed axis, a constant stiffness matrix is obtained even if higher-order terms are retained in strain–displacement relationship [37]. A second-order approximation for the displacement field of flexible beam is proposed to account for dynamic stiffening, and the effects of tip mass and damping on dynamic behavior of the hub-beam system are analyzed on the basis of a finite element model [5]. Based on geometric nonlinear elastic theory and finite element method, the dynamic equations of elastic beams under large overall rotation are derived, and the effect of coupling deformation on system dynamic behavior is analyzed [38]. Using the fully nonlinear Green strain–displacement relationships, the coupling equation of motion for a rotating three-dimensional cantilever beam is established, and the effect of steady-state axial deformation and Coriolis term on coupling vibration is analyzed [39]. Besides finite element method, the Euler–Bernoulli beam assumption and von Kármán strain–displacement relationship are also used in analytical or semi-analytical method, such as parametric resonance of double-clamped micro-beams by electro-thermal heating [40], nonlinear resonant response of cable-stayed beam [41]. In pursuit of a uniform expression for geometrically nonlinear methods, the elastic force of NEBB is also calculated by system invariant matrix in this work.
As the same as TLF, the ANCF solves geometrically nonlinear problems with finite deformation; as the same as LEBB and NEBB, the ANCF attains finite element model with small degrees of freedom (DOF) [7]. The ANCF is proposed for large rotation and deformation analysis of shearable beam element with deformable cross section, it leads to constant mass matrix, zero centrifugal forces and zero Coriolis forces as the same as GCMS [42, 43]. In order to alleviate the Poisson locking caused by coupling between axial and transverse stress, the enhanced continuum method divides the elasticity matrix into two parts and only considers the Poisson effect at beam axis [44]; the enhanced assumed strain method enriches the displacement-dependent compatible strain by a set of additional independent enhanced strain [45]; the strain split method divides the Green-Lagrange strain into two parts and does not introduce additional variables [46]; the higher-order beam method enriches the interpolation polynomial basis to allow correct coupling between axial and transverse strain [47]. Different Poisson locking alleviation methods are compared and none of them are suitable for all ANCF element types [45, 46]. As for the alleviation of curvature thickness locking and shear locking, a new ANCF element with redefined interpolation polynomial expansion and reduced integration procedure is proposed [48]. In this work, the higher-order beam method [47] is adopted, and the computational efficiency of ANCF which adopts system invariant matrix is compared with ANCF which adopts element invariant matrix [49].
The above parts give separate illustrations for each single method. Because of the importance, the comparison of these different finite element methods is already concerned by many researches [5, 7, 10, 18, 19, 32, 43, 50]. Based on existing researches, this work tries to make a more comprehensive comparison of abovementioned six finite element methods. Some views are obtained after comparison; for example, the parametrically excited nonlinear system in GCMS can be transformed to linear system in FFRF. Besides advantages, simultaneous accommodation of six methods also brings weaknesses: only a rotating flexible beam example under centerline transverse load is considered; the narrations and notations may look weird due to the fact that they are different to classical researches and conventions; plenty of existing researches are not adopted to improve a single method to its extreme. This work attempts to deal with the conflict between these advantages and weaknesses.
The arrangement of this work is as follows. In Sect. 2, the three finite element methods FFRF, GCMS and TLF which base on solid element are introduced. In Sect. 3, the three finite element methods LEBB, NEBB and ANCF which base on beam element are introduced. In Sect. 4, numerical results of the six finite element methods under different rotational speeds are compared; the computational efficiencies of the six finite element methods are compared; the influence of system invariant matrix on computational efficiency is analyzed for TLF, NEBB and ANCF; the influence of damping on numerical results of GCMS, TLF and ANCF is analyzed. In Sect. 5, summaries and conclusions are given.
2 Methods based on solid element
2.1 The method of FFRF
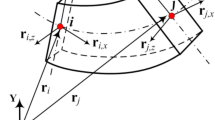
In order to describe the configuration of flexible body under large rotation, the FFRF establishes two reference frames: inertial frame \(o-xyz\) and floating frame \(O-XYZ\) as shown in Fig. 1. The inertial frame is fixed and the floating frame is rotating along with the body, and the motion of the flexible body point is then separated into two parts: rigid rotation and elastic deformation. The rigid rotation part can be represented by the motion of floating frame and measured in \(o-xyz\) as vector \(\varvec{u}_\mathrm{{r}} = {\left[ {\begin{array}{ccc} {{u_{\mathrm{{r}}x}}}&{{u_{\mathrm{{r}}y}}}&{{u_{\mathrm{{r}}z}}} \end{array}} \right] ^\mathrm{{T}}}\). The elastic deformation part can be measured in \(o-xyz\) as absolute coordinate vector \(\varvec{u}_\mathrm{{f}} = {\left[ {\begin{array}{ccc} {{u_{\mathrm{{f}}x}}}&{{u_{\mathrm{{f}}y}}}&{{u_{\mathrm{{f}}z}}} \end{array}} \right] ^\mathrm{{T}}}\) or measured in \(O-XYZ\) as relative coordinate vector \(\varvec{U}_\mathrm{{f}} = {\left[ {\begin{array}{ccc} {{U_{\mathrm{{f}}X}}}&{{U_{\mathrm{{f}}Y}}}&{{U_{\mathrm{{f}}Z}}} \end{array}} \right] ^\mathrm{{T}}}\) [10]. Measure the Cartesian coordinate of undeformed body point in frame \(O-XYZ\) as vector \({\varvec{X}_0} = {\left[ {\begin{array}{ccc} {{X_0}}&{{Y_0}}&{{Z_0}} \end{array}} \right] ^\mathrm{{T}}}\), vector \(\varvec{X}_0\) is constant and adopted to specify different body points. The total displacement vector \(\varvec{u} = {\left[ {\begin{array}{ccc} {{u_x}}&{{u_y}}&{{u_z}} \end{array}} \right] ^\mathrm{{T}}}\) of point \(\varvec{X}_0\) is measured in \(o-xyz\) as follows:
Different parameters are proposed to represent the rigid rotation of floating frame, such as Rodriguez parameters, Euler angles and direction cosines [7]. The direction cosines lead to linear dependence between reference coordinates and rigid rotation displacement, while additional constraints about reference coordinates are added [10]. This work only considers the fixed axis rotation case where rotational axis is z axis or Z axis, and rotational angle is \(\varphi \). Correspondingly, the rigid rotation displacement \(\varvec{u}_\mathrm{{r}}\) of point \(\varvec{X}_0\) and the reference coordinate constraint are given by
where matrix \({\varvec{N}_\mathrm{{r}}}({\varvec{X}_0}) = \left[ {\begin{array}{cc} {{\mathbf{{G}}_1} \cdot {\varvec{X}_0}{}}&{{\mathbf{{G}}_2} \cdot {\varvec{X}_0}} \end{array}} \right] \), \(\mathbf{{G}_1} = \left[ {\begin{array}{ccc} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}0 \end{array}} \right] \), \({\mathbf{{G}}_2} = \left[ {\begin{array}{ccc} 0&{}{ - 1}&{}0\\ 1&{}0&{}0\\ 0&{}0&{}0 \end{array}} \right] \), reference coordinate vector \({\varvec{q}_\mathrm{{r}}} = {\left[ {\begin{array}{ccc} {\cos \varphi {\quad }}&{\sin \varphi } \end{array}} \right] ^\mathrm{{T}}}\) and vector \(\varvec{q}_{\mathrm{{r}}0}\) is the initial value of \(\varvec{q}_\mathrm{{r}}\).
The two measurements \(\varvec{u}_\mathrm{{f}}\) and \(\varvec{U}_\mathrm{{f}}\) of elastic deformation are correlated by the rotation matrix \(\varvec{A}\) as follows
When it is difficult to find analytical solution of governing equations for three-dimensional continuum elasticity problem, the integral or weak form equivalent to the governing differential equations is usually adopted to find approximate solution [21]. The finite element method subdivides the continuum domain as a finite number of elements, and the deformation vector \(\varvec{U}_\mathrm{{f}}\) of point \(\varvec{X}_0\) in the e-th element is approximated by interpolation of node deformation as follows
where \(\varvec{N}({\varvec{X}_0})\) is the shape function, element elastic coordinate vector \({\varvec{U}_{\mathrm{{f}}e}} = {\left[ {\begin{array}{cccc} {\varvec{U}_{\mathrm{{f}}e1}^\mathrm{{T}}}&{\varvec{U}_{\mathrm{{f}}e2}^\mathrm{{T}}}&{ \cdots }&{\varvec{U}_{\mathrm{{f}}em}^\mathrm{{T}}} \end{array}} \right] ^\mathrm{{T}}}\), \(\varvec{U}_{\mathrm{{f}}ei}\) is the deformation vector of the i-th node for the e-th element, m is the number of nodes for the e-th element.
To facilitate numerical integration, the Cartesian coordinate \(\varvec{X}_0\) is one-to-one mapped to local coordinate \(\varvec{\xi } = {\left[ {\begin{array}{ccc} {\xi {}}&{\eta {}}&\zeta \end{array}} \right] ^\mathrm{{T}}}, - 1 \le \xi ,\eta ,\zeta \le 1\), on the basis of shape function \(\varvec{N}(\varvec{\xi } )\) as follows
where \({\varvec{X}_{0e}} = {\left[ {\begin{array}{cccc} {\varvec{X}_{0e1}^\mathrm{{T}}}&{\varvec{X}_{0e2}^\mathrm{{T}}}&{\cdots }&{\varvec{X}_{0em}^\mathrm{{T}}} \end{array}} \right] ^\mathrm{{T}}}\) is the element Cartesian coordinate vector.
The 8-node brick isoparametric element is adopted in this work, and the shape functions \(\varvec{N}({\varvec{X}_0})\) and \(\varvec{N}(\varvec{\xi } )\) are the same and given by
where \({N_i} = \frac{{(1 + {\xi _i}\xi ) \cdot (1 + {\eta _i}\eta ) \cdot (1 + {\zeta _i}\zeta )}}{8}\), \(\mathbf{{I}}_3\) is \(3 \times 3\) identity matrix, \(\xi _i, \eta _i, \zeta _i\) are the local coordinate of the i-th node.
The derivative of displacement relative to time is velocity as follows
Due to the fact that components in matrix \(\dot{\varvec{A}}\) are identical with the components in vector \(\dot{\varvec{q}}_\mathrm{{r}}\), above velocity formula is transformed as
where matrix \({\varvec{N}_\mathrm{{r}}}({\varvec{X}}) = {\varvec{N}_{\mathrm{{r}}}}({\varvec{X}_0}) + \left[ {\begin{array}{cc} {\mathbf{{G}_1} \cdot {{\varvec{U}}_\mathrm{{f}}}{}}&{\mathbf{{G}_2} \cdot {{\varvec{U}}_\mathrm{{f}}}} \end{array}} \right] \), \(\varvec{X} = {\left[ {\begin{array}{ccc} {X {}}&{Y {}}&{Z} \end{array}} \right] ^\mathrm{{T}}}\) is the Cartesian coordinate of point \(\varvec{X}_0\) after deformation and it is also measured in frame \(O-XYZ\).
According to the velocity, the element kinetic energy \(T_e\) can be calculated through integration over element volume v as follows
where \(\rho \) is material density, element coordinate \({\varvec{q}_e} = {\left[ {\begin{array}{cc} {{\varvec{q}_\mathrm{{r}}}{}}&{{{\varvec{U}}_{\mathrm{{f}}e}}} \end{array}} \right] ^\mathrm{{T}}}\), the element mass matrix \({\varvec{M}_e} = \left[ {\begin{array}{cc} {{\varvec{M}_{\mathrm{{rr}}e}}}&{}{{\varvec{M}_{\mathrm{{rf}}e}}}\\ {\varvec{M}_{\mathrm{{rf}}e}^\mathrm{{T}}}&{}{{\varvec{M}_{\mathrm{{ff}}e}}} \end{array}} \right] \), \({\varvec{M}_{\mathrm{{rr}}e}} = \int _v {\rho \cdot \varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}}) \cdot {\varvec{N}_\mathrm{{r}}}(\varvec{X} )\mathrm{{d}}v}\), \({\varvec{M}_{\mathrm{{rf}}e}} = \int _v {\rho \cdot \varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}}) \cdot \varvec{A} \cdot \varvec{N}(\varvec{\xi } )\mathrm{{d}}v}\), \({\varvec{M}_{\mathrm{{ff}}e}} = \int _v \rho \cdot {\varvec{N}^\mathrm{{T}}}(\varvec{\xi } ) \cdot \varvec{N}(\varvec{\xi } )\mathrm{{d}}v\).
Under the assumption of small deformation, the strain vector \(\varvec{\varepsilon } = {\left[ {\begin{array}{cccccc} {{\varepsilon _X}{}}&{{\varepsilon _Y}{}}&{{\varepsilon _Z}{}}&{{\gamma _{XY}}{}}&{{\gamma _{YZ}}{}}&{{\gamma _{ZX}}} \end{array}} \right] } ^ \mathrm{{T}}\) of point \(\varvec{X}_0\) is linearly related to element elastic coordinate vector as follows [21]
where differential operator \(\varvec{L} = {\left[ {\begin{array}{cccccc} {\frac{\partial }{{\partial X}}}&{}0&{}0&{}{\frac{\partial }{{\partial Y}}}&{}0&{}{\frac{\partial }{{\partial Z}}}\\ 0&{}{\frac{\partial }{{\partial Y}}}&{}0&{}{\frac{\partial }{{\partial X}}}&{}{\frac{\partial }{{\partial Z}}}&{}0\\ 0&{}0&{}{\frac{\partial }{{\partial Z}}}&{}0&{}{\frac{\partial }{{\partial Y}}}&{}{\frac{\partial }{{\partial X}}} \end{array}} \right] ^\mathrm{{T}}}\), \(\varvec{B}_\mathrm{{L}}\) is linear strain matrix.
On account of small deformation assumption, the deformed coordinates X, Y, Z in operator \(\varvec{L}\) can also be replaced by undeformed coordinates \(X_0,Y_0,Z_0\). Then the components in strain matrix \(\varvec{B}_\mathrm{{L}}\) are calculated as follows
where vector \(\varvec{n} = {\left[ {\begin{array}{cccc} {{N_1}{}}&{{N_2}{}}&{\cdots {}}&{{N_m}} \end{array}} \right] ^\mathrm{{T}}}\).
According to the strain, the elastic potential energy \(V_e\) is calculated as follows
where \(\textbf{E}\) is elasticity matrix of moduli, element stiffness matrix \({\varvec{K}_{\mathrm{{L}}e}} = \int _v {\varvec{B}_\mathrm{{L}}^\mathrm{{T}} \cdot \mathbf{{E}} \cdot {\varvec{B}_\mathrm{{L}}}\mathrm{{d}}v}\).
As for the linear internal damping, it is assumed that the damping force is proportional to deformation velocity and its direction is opposite to deformation velocity [51]. Measure the damping force intensity of point \({\varvec{X}}_0\) in frame \(O-XYZ\) as \({\varvec{F}_\mathrm{{d}}}\); then \({\varvec{F}_\mathrm{{d}}}\) is proportional to the velocity of relative coordinate for deformation as follows
where c is damping coefficient.
Measure the damping force in frame \(o-xyz\) as \(\varvec{A} \cdot {\varvec{F}_\mathrm{{d}}}\); then the virtual work \(\delta {W_e}\) of damping force for the e-th element is as follows
where element damping matrix \({\varvec{D}_e} = \left[ {\begin{array}{c} {\tilde{\varvec{A}} \cdot {\varvec{D}_{\mathrm{{rf}}1e}} + {\varvec{D}_{\mathrm{{rf}}2e}}}\\ {{\varvec{D}_{\mathrm{{ff}}e}}} \end{array}} \right] \), \(\tilde{\varvec{A}} = \left[ {\begin{array}{cc} {\cos \varphi }&{}{ - \sin \varphi }\\ {\sin \varphi }&{}{\cos \varphi } \end{array}} \right] \), \({\varvec{D}_{\mathrm{{rf}}1e}} = c \cdot \int _v {\varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}_0}) \cdot \varvec{N}(\varvec{\xi } )\mathrm{{d}}v}\), \({\varvec{D}_{\mathrm{{rf}}2e}} = c \cdot \left[ {\begin{array}{c} {\varvec{U}_{\mathrm{{f}}e}^\mathrm{{T}} \cdot {\varvec{D}_{\mathrm{{ff}}e}} \cdot \mathbf{{G}}_{1\textrm{d}}^\mathrm{{T}} \cdot {\varvec{A}_\mathrm{{d}}}}\\ {\varvec{U}_{\mathrm{{f}}e}^\mathrm{{T}} \cdot {\varvec{D}_{\mathrm{{ff}}e}} \cdot \mathbf{{G}}_{2\textrm{d}}^\mathrm{{T}} \cdot {\varvec{A}_\mathrm{{d}}}} \end{array}} \right] \), \(\varvec{D}_{\mathrm{{ff}}e} = c / \rho \cdot {\varvec{M}_{\mathrm{{ff}}e}}\), matrix \(\varvec{A}_\mathrm{{d}}\) is block-diagonal with each diagonal block equal to \(\varvec{A}\), \(\mathbf{{G}}_{1\textrm{d}}\) is block-diagonal with each diagonal block equal to \(\mathbf{{G}}_1\), \(\mathbf{{G}}_{2\textrm{d}}\) is block-diagonal with each diagonal block equal to \(\mathbf{{G}}_2\), and the dimensions of matrices \(\varvec{A}_\mathrm{{d}}\), \(\mathbf{{G}}_{1\textrm{d}}\) and \(\mathbf{{G}}_{2\textrm{d}}\) are dependent on the context.
The element damping matrix is composed of coupling part \(\tilde{\varvec{A}} \cdot {\varvec{D}_{\mathrm{{rf}}1e}} + {\varvec{D}_{\mathrm{{rf}}2e}}\) and elastic part \(\varvec{D}_{\mathrm{{ff}}e}\). The elastic part is proportional to elastic mass matrix \(\varvec{M}_{\mathrm{{ff}}e}\) as general Rayleigh proportional damping [52], and the coupling part emerges because the assumption of Eq. (15) means the deformation velocity of one point does not lead to dissipative force on another point [51]. In order to get an element damping matrix without coupling part, the internal damping model based on viscoelasticity [51] may be adopted.
According to the kinetic energy, elastic potential energy and damping virtual work, the generalized inertia force, generalized elastic force and generalized damping force can be obtained. Substituting them in the fundamental nonholonomic form of Lagrange’s equation [53], the following system dynamic equation is then obtained
where \(\varvec{M}\) is system mass matrix, system coordinate \(\varvec{q} = {\left[ {\begin{array}{cc} {\varvec{q}_\mathrm{{r}}^\mathrm{{T}}{}}&{\varvec{U}_{\mathrm{{fs}}}^\mathrm{{T}}} \end{array}} \right] ^\mathrm{{T}}}\), \(\varvec{U}_{\mathrm{{fs}}}\) is system elastic coordinate vector, \({\frac{{\partial \varvec{C}}}{{\partial \varvec{q}}}}\) is the Jacobian matrix of constraint vector \(\varvec{C}\), \(\varvec{\lambda }\) is the Lagrange multiplier vector of constraint, \(\varvec{Q}_\mathrm{{e}}\) is external force vector, quadratic velocity vector \({\varvec{Q}_v} = - \dot{\varvec{M}} \cdot \dot{\varvec{q}} + {\left( {\frac{{\partial T}}{{\partial \varvec{q}}}} \right) ^\mathrm{{T}}}\), T is system kinetic energy, damping force vector \({\varvec{Q}_\mathrm{{d}}} = \varvec{D} \cdot {\dot{\varvec{U}}_\mathrm{{fs}}}\), \(\varvec{D}\) is system damping matrix, system elastic force vector \({\varvec{Q}_k} = {\varvec{K}_\mathrm{{L}}} \cdot {\varvec{U}_\mathrm{{fs}}}\), \(\varvec{K}_\mathrm{{L}}\) is system stiffness matrix.
The quadratic velocity vector [7] is resulted from the differentiation of kinetic energy with respect to time and with respect to system coordinates. The gyroscopic and Coriolis force components are contained in this quadratic velocity vector. This term is also utilized by following researches [2, 10, 12, 18].
In combination with constraint equation, the above system dynamic equation composes a differential algebraic equation, which can be transformed into an ordinary differential equation [20]. There are different numerical methods to solve the ordinary differential equation, such as Runge–Kutta method and Adams method. Besides, the component mode synthesis method [15] is adopted to improve solution efficiency, and the eigenmode is calculated under reference condition [16]. Due to the order of matrix \(\varvec{D}_{\mathrm{{rf}}2e}\) cannot be reduced by component mode synthesis method, in order to improve calculation efficiency, this matrix is ignored on the basis of small deformation assumption, which means terms related to \(\delta \varvec{A}\) are ignored in virtual work calculation of damping force. Numerical result shows the influence of this ignorance on calculation accuracy is quite small.
2.2 The method of GCMS
Similar to FFRF, the GCMS establishes inertial frame \(o-xyz\) and floating frame \(O-XYZ\), and the total motion of flexible body point is separated into rigid motion part and elastic deformation part. However, different to FFRF, the GCMS adopts absolute coordinate vector \(\varvec{u}_\mathrm{{f}}\) rather than relative coordinate vector \(\varvec{U}_\mathrm{{f}}\) to measure the elastic deformation [10]. The elastic deformation \(\varvec{u}_\mathrm{{f}}\) of point \(\varvec{X}_\mathrm{{0}}\) in the e-th element is approximated by interpolation of node deformation as follows
where \({\varvec{u}_{\mathrm{{f}}e}} = {\left[ {\begin{array}{cccc} {\varvec{u}_{\mathrm{{f}}e1}^\mathrm{{T}}}&{\varvec{u}_{\mathrm{{f}}e2}^\mathrm{{T}}}&{ \cdots }&{\varvec{u}_{\mathrm{{f}}em}^\mathrm{{T}}} \end{array}} \right] ^\mathrm{{T}}}\) is element elastic coordinate vector.
In this case, the total velocity \(\dot{\varvec{u}}\) of point \(\varvec{X}_0\) is given by
The element kinetic energy \(T_e\) is correspondingly calculated by
where element coordinate \({\varvec{q}_e} = {\left[ {\begin{array}{cc} {{\varvec{q}_\mathrm{{r}}}{}}&{{{\varvec{u}}_{\mathrm{{f}}e}}} \end{array}} \right] ^\mathrm{{T}}}\), the element mass matrix \({\varvec{M}_e} = \left[ {\begin{array}{cc} {{\varvec{M}_{\mathrm{{rr}}e}}}&{}{{\varvec{M}_{\mathrm{{rf}}e}}}\\ {\varvec{M}_{\mathrm{{rf}}e}^\mathrm{{T}}}&{}{{\varvec{M}_{\mathrm{{ff}}e}}} \end{array}} \right] \), mass submatrices \({\varvec{M}_{\mathrm{{rr}}e}} = \int _v {\rho \cdot \varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}}_0) \cdot {\varvec{N}_\mathrm{{r}}}(\varvec{X}_0 )\mathrm{{d}}v}\), \({\varvec{M}_{\mathrm{{rf}}e}} = \int _v {\rho \cdot \varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}_0}) \cdot \varvec{N}(\varvec{\xi } )\mathrm{{d}}v}\), \({\varvec{M}_{\mathrm{{ff}}e}} = \int _v \rho \cdot {\varvec{N}^\mathrm{{T}}}(\varvec{\xi } ) \cdot \varvec{N}(\varvec{\xi } )\mathrm{{d}}v\).
Above equation shows the mass matrix of GCMS is constant which differs from FFRF. This means the quadratic velocity vector is avoided for calculation of generalized inertia force [10] and it usually improves calculation efficiency. Apologetically, the same notations \(\varvec{q}_e\), \(\varvec{M}_e\), \(\varvec{M}_{\mathrm{{rr}}e}\) and \(\varvec{M}_{\mathrm{{rf}}e}\) are used for both GCMS and FFRF, while their specific composition or calculation is different. In consideration of their same physical meaning, this kind of notation usage may be tolerable.
As for the element elastic potential energy \(V_e\), it is given by
Different to FFRF, the damping force intensity \(\varvec{F}_\mathrm{{d}}\) measured in \(O-XYZ\) for GCMS is expressed as follows
Virtual work \(\delta {W_e}\) of damping force for the e-th element is as follows
where element damping matrix \({\varvec{D}_e} = \left[ {\begin{array}{c} {{\varvec{D}_{\mathrm{{rf}}e}}}\\ {{\varvec{D}_{\mathrm{{ff}}e}}} \end{array}} \right] \), \({\varvec{D}_{\mathrm{{rf}}e}} = c / \rho \cdot {\varvec{M}_{\mathrm{{rf}}e}}\), \({\varvec{D}_{\mathrm{{ff}}e}} = c / \rho \cdot {\varvec{M}_{\mathrm{{ff}}e}}\).
According to the energy and virtual work, the generalized force can be obtained. Substituting them in the fundamental nonholonomic form of Lagrange’s equation, the following system dynamic equation is then obtained
where system coordinate \(\varvec{q} = {\left[ {\begin{array}{cc} {{\varvec{q}_\mathrm{{r}}}}&{{{\varvec{u}}_\mathrm{{fs}}}} \end{array}} \right] ^\mathrm{{T}}}\), \({\varvec{u}}_\mathrm{{fs}}\) is system elastic coordinate vector, damping force vector \({\varvec{Q}_\mathrm{{d}}} = \varvec{D} \cdot ({\varvec{A}_\mathrm{{d}}} \cdot \dot{\varvec{A}}_\mathrm{{d}}^\mathrm{{T}} \cdot {\varvec{u}_{\mathrm{{fs}}}} + {{\dot{\varvec{u}}}_{\mathrm{{fs}}}})\), system elastic force vector \({\varvec{Q}_k} = \left[ {\begin{array}{c} {\varvec{u}_{\mathrm{{fs}}}^\mathrm{{T}} \cdot {\mathbf{{G}}_{1\textrm{d}}} \cdot {\varvec{K}_\mathrm{{L}}} \cdot \varvec{A}_\mathrm{{d}}^\mathrm{{T}} \cdot {\varvec{u}_{\mathrm{{fs}}}}}\\ {\varvec{u}_{\mathrm{{fs}}}^\mathrm{{T}} \cdot {\mathbf{{G}}_{2\textrm{d}}} \cdot {\varvec{K}_\mathrm{{L}}} \cdot \varvec{A}_\mathrm{{d}}^\mathrm{{T}} \cdot {\varvec{u}_{\mathrm{{fs}}}}}\\ {{\varvec{A}_\mathrm{{d}}} \cdot {\varvec{K}_\mathrm{{L}}} \cdot \varvec{A}_\mathrm{{d}}^\mathrm{{T}} \cdot {\varvec{u}_{\mathrm{{fs}}}}} \end{array}} \right] \).
The solution method of above system dynamic equation is similar to FFRF, where component mode synthesis method is also adopted. As for the eigenmode of GCMS, it is transformed from the eigenmode of FFRF [10, 20].
2.3 The method of TLF
Different to the above two methods, the TLF only establishes inertial frame and the total motion of flexible body point is not separated. Before rigid rotation and elastic deformation, the configuration of flexible body is called the reference configuration; after rigid rotation and elastic deformation, the configuration of flexible body is called the current configuration [21]. The inertial frame is expressed by \(o-xyz\): the Cartesian coordinate for point of reference configuration is measured in inertial frame as vector \(\varvec{x}_0 = \left[ {\begin{array}{ccc} x_0&y_0&z_0 \end{array}} \right] ^\mathrm{{T}}\), the Cartesian coordinate for point of current configuration is measured in inertial frame as vector \(\varvec{x} = \left[ {\begin{array}{ccc} x&y&z \end{array}} \right] ^\mathrm{{T}}\). The vector \(\varvec{x}_0\) is constant and adopted to specify different body point, and the total displacement vector \(\varvec{u} = \left[ {\begin{array}{ccc} {u_x}&{u_y}&{u_z} \end{array}} \right] ^\mathrm{{T}}\) of point \(\varvec{x}_0\) is measured in inertial frame as
where t is time.
In finite element discretization, the Cartesian coordinate \(\varvec{x}\) is one-to-one mapped to local coordinate \(\varvec{\xi } = {\left[ {\begin{array}{ccc} \xi&\eta&\zeta \end{array}} \right] ^\mathrm{{T}}}, - 1 \le \xi ,\eta ,\zeta \le 1\) as follows
where \(\varvec{N}(\varvec{\xi } )\) is shape function and keeps the same as Eq. (8), \(\varvec{x}_{e}={\left[ {\begin{array}{cccc} {\varvec{x}_{e1}^\mathrm{{T}}}&{\varvec{x}_{e2}^\mathrm{{T}}}&\cdots&{\varvec{x}_{em}^\mathrm{{T}}} \end{array}} \right] ^\mathrm{{T}}}\) is element Cartesian coordinate vector.
The total displacement vector \(\varvec{u}\) of point \(\varvec{x}_0\) in the e-th element is approximated by interpolation of node displacement as
where \(\varvec{u}_e={\left[ {\begin{array}{cccc} {\varvec{u}_{e1}^\mathrm{{T}}}&{\varvec{u}_{e2}^\mathrm{{T}}}&\cdots&{\varvec{u}_{em}^\mathrm{{T}}} \end{array}} \right] ^\mathrm{{T}}}\) is element displacement vector.
The second derivative of displacement relative to time is acceleration as follows
According to the acceleration, the virtual work \(\delta T_e\) of inertia force for the e-th element is as follows
where \(\rho \) is material density under current configuration, v is element volume under current configuration, element mass matrix \({\varvec{M}_e} = \int _{v_0} {\rho _0 \cdot {\varvec{N}^\mathrm{{T}}}(\varvec{\xi } ) \cdot \varvec{N}(\varvec{\xi } )\mathrm{{d}}{v_0}}\), \(\rho _0\) is material density under reference configuration, \(v_0\) is element volume under reference configuration.
The TLF adopts Green-Lagrange strain to measure deformation [21, 54], which is invariant under rigid motion. The strain vector \(\varvec{\varepsilon } = \left[ {\begin{array}{cccccc} {{\varepsilon _x}}&{{\varepsilon _y}}&{{\varepsilon _z}}&{{\gamma _{xy}}}&{{\gamma _{yz}}}&{{\gamma _{zx}}} \end{array}} \right] ^\mathrm{{T}}\) of point \(\varvec{x}_0\) is nonlinearly related to element displacement vector as follows
where linear strain matrix \(\varvec{B}_\mathrm{{L}} = \varvec{L} \cdot \varvec{N}(\varvec{\xi })\) and \(\varvec{L} = {\left[ {\begin{array}{cccccc} {\frac{\partial }{{\partial x_0}}}&{}0&{}0&{}{\frac{\partial }{{\partial y_0}}}&{}0&{}{\frac{\partial }{{\partial z_0}}}\\ 0&{}{\frac{\partial }{{\partial y_0}}}&{}0&{}{\frac{\partial }{{\partial x_0}}}&{}{\frac{\partial }{{\partial z_0}}}&{}0\\ 0&{}0&{}{\frac{\partial }{{\partial z_0}}}&{}0&{}{\frac{\partial }{{\partial y_0}}}&{}{\frac{\partial }{{\partial x_0}}} \end{array}} \right] ^\mathrm{{T}}}\), the components of \(\varvec{B}_\mathrm{{L}}\) are calculated by \({\left( {\frac{{\partial \varvec{n}}}{{\partial \varvec{x}_0}}} \right) ^\mathrm{{T}}} = {\left[ {{{\left( {\frac{{\partial {\varvec{x}_0}}}{{\partial \varvec{\xi } }}} \right) }^\mathrm{{T}}}} \right] ^{ - 1}} \cdot {\left( {\frac{{\partial \varvec{n}}}{{\partial \varvec{\xi } }}} \right) ^\mathrm{{T}}}\), vector \(\varvec{n} = {\left[ {\begin{array}{cccc} {{N_1}}&{{N_2}}&\cdots&{{N_m}} \end{array}} \right] ^\mathrm{{T}}}\), nonlinear strain matrix \({\varvec{B}_\mathrm{{N}}} = {\varvec{B}_\mathrm{{N}1}} \cdot {\varvec{B}_\mathrm{{N}2}}\), \({\varvec{B}_\mathrm{{N}1}} = \left[ {\begin{array}{ccc} {{{\left( {\frac{{\partial \varvec{N}}}{{\partial x_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}}&{}\varvec{0}&{}\varvec{0}\\ \varvec{0}&{}{{{\left( {\frac{{\partial \varvec{N}}}{{\partial y_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}{{{\left( {\frac{{\partial \varvec{N}}}{{\partial z_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}}\\ {{{\left( {\frac{{\partial \varvec{N}}}{{\partial y_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}}&{}{{{\left( {\frac{{\partial \varvec{N}}}{{\partial x_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}}&{}\varvec{0}\\ \varvec{0}&{}{{{\left( {\frac{{\partial \varvec{N}}}{{\partial z_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}}&{}{{{\left( {\frac{{\partial \varvec{N}}}{{\partial y_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}}\\ {{{\left( {\frac{{\partial \varvec{N}}}{{\partial z_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}}&{}\varvec{0}&{}{{{\left( {\frac{{\partial \varvec{N}}}{{\partial x_0}} \cdot {\varvec{u}_e}} \right) }^\mathrm{{T}}}} \end{array}} \right] \), \({\varvec{B}_\mathrm{{N}2}} = \left[ {\begin{array}{cccc} {\frac{{\partial {N_1}}}{{\partial x_0}} \cdot {\mathbf{{I}}_3} \quad }&{}{\frac{{\partial {N_2}}}{{\partial x_0}} \cdot {\mathbf{{I}}_3} \quad }&{} {\cdots \quad } &{}{\frac{{\partial {N_m}}}{{\partial x_0}} \cdot {\mathbf{{I}}_3}}\\ {\frac{{\partial {N_1}}}{{\partial y_0}} \cdot {\mathbf{{I}}_3} \quad }&{}{\frac{{\partial {N_2}}}{{\partial y_0}} \cdot {\mathbf{{I}}_3} \quad }&{} {\cdots \quad } &{}{\frac{{\partial {N_m}}}{{\partial y_0}} \cdot {\mathbf{{I}}_3}}\\ {\frac{{\partial {N_1}}}{{\partial z_0}} \cdot {\mathbf{{I}}_3} \quad }&{}{\frac{{\partial {N_2}}}{{\partial z_0}} \cdot {\mathbf{{I}}_3} \quad }&{} {\cdots \quad } &{}{\frac{{\partial {N_m}}}{{\partial z_0}} \cdot {\mathbf{{I}}_3}} \end{array}} \right] \).
Above displacement and strain are expressed as function of the Lagrange coordinate \(\varvec{x}_0\) rather than the Euler coordinate \(\varvec{x}\), and this is the difference between TLF and updated Lagrangian formulation [8, 55].
Through matrix transformation, the nonlinear strain matrix \(\varvec{B}_\mathrm{{N}}\) is transformed as
where \(\varvec{B}_{\mathrm{{N}}5} = {\varvec{B}_{\mathrm{{N}}3}} \cdot {\varvec{B}_{\mathrm{{N}}4}}\), \({\varvec{B}_{\mathrm{{N}}3}} = \left[ {\begin{array}{ccc} {\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial x_0}}}&{}\varvec{0}&{}\varvec{0}\\ \varvec{0}&{}{\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial y_0}}}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}{\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial z_0}}}\\ {\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial y_0}}}&{}{\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial x_0}}}&{}\varvec{0}\\ \varvec{0}&{}{\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial z_0}}}&{}{\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial y_0}}}\\ {\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial z_0}}}&{}\varvec{0}&{}{\frac{{\partial {\varvec{n}^\mathrm{{T}}}}}{{\partial x_0}}} \end{array}} \right] \), \({\varvec{B}_{\mathrm{{N}}4}} = \left[ {\begin{array}{cccc} {\frac{{\partial {N_1}}}{{\partial x_0}} \cdot {\mathbf{{I}}_m}{}}&{}{\frac{{\partial {N_2}}}{{\partial x_0}} \cdot {\mathbf{{I}}_m}{}}&{} {\cdots {}} &{}{\frac{{\partial {N_m}}}{{\partial x_0}} \cdot {\mathbf{{I}}_m}}\\ {\frac{{\partial {N_1}}}{{\partial y_0}} \cdot {\mathbf{{I}}_m}{}}&{}{\frac{{\partial {N_2}}}{{\partial y_0}} \cdot {\mathbf{{I}}_m}{}}&{} {\cdots {}} &{}{\frac{{\partial {N_m}}}{{\partial y_0}} \cdot {\mathbf{{I}}_m}}\\ {\frac{{\partial {N_1}}}{{\partial z_0}} \cdot {\mathbf{{I}}_m}{}}&{}{\frac{{\partial {N_2}}}{{\partial z_0}} \cdot {\mathbf{{I}}_m}{}}&{} {\cdots {}} &{}{\frac{{\partial {N_m}}}{{\partial z_0}} \cdot {\mathbf{{I}}_m}} \end{array}} \right] \), \(\mathbf{{I}}_m\) is \(m \times m\) identity matrix, \(\varvec{u}_{\mathrm{{d}}e}\) is block-diagonal with each diagonal block equal to \({\varvec{u}_{\mathrm{{B}}e}} = \left[ {\begin{array}{ccc} {{u_{xe1}}}&{}{{u_{ye1}}}&{}{{u_{ze1}}}\\ {{u_{xe2}}}&{}{{u_{ye2}}}&{}{{u_{ze2}}}\\ \vdots &{} \vdots &{} \vdots \\ {{u_{xem}}}&{}{{u_{yem}}}&{}{{u_{zem}}} \end{array}} \right] \).
The variation of Green-Lagrange strain \(\delta \varvec{\varepsilon }\) is as follows [21]
According to the Greed-Lagrange strain, the second Piola-Kirchhoff stress is calculated. The virtual work \(\delta V_e\) of elastic force for the e-th element is as follows [54]
where linear element stiffness matrix \({\varvec{K}_{\mathrm{{L}}e}} = \int _{v_0} \varvec{B}_\mathrm{{L}}^\mathrm{{T}} \cdot \mathbf{{E}} \cdot {\varvec{B}_\mathrm{{L}}}\mathrm{{d}}{v_0}\), nonlinear element stiffness matrix \({\varvec{K}_{\mathrm{{N}}e}} = {\varvec{K}_{\mathrm{{N}}1e}} \cdot {\varvec{u}_{\mathrm{{d}}e}} + \varvec{u}_{\mathrm{{d}}e}^\mathrm{{T}} \cdot {\varvec{K}_{\mathrm{{N}}2e}} + \varvec{u}_{\mathrm{{d}}e}^\mathrm{{T}} \cdot {\varvec{K}_{\mathrm{{N}}3e}} \cdot {\varvec{u}_{\mathrm{{d}}e}}\), matrices \(\varvec{K}_{\mathrm{{N}}1e}\), \(\varvec{K}_{\mathrm{{N}}2e}\) and \(\varvec{K}_{\mathrm{{N}}3e}\) are time-invariant, \({\varvec{K}_{\mathrm{{N}}1e}} = \frac{1}{2} \cdot \int _{v_0} {\varvec{B}_\mathrm{{L}}^\mathrm{{T}} \cdot \mathbf{{E}} \cdot {\varvec{B}_{\mathrm{{N}}5}}{\mathrm{{d}}{v_0}}}\), \({\varvec{K}_{\mathrm{{N}}2e}} = \int _{v_0} {\varvec{B}_{\mathrm{{N}}5}^\mathrm{{T}} \cdot \mathbf{{E}} \cdot {\varvec{B}_\mathrm{{L}}}\mathrm{{d}}{v_0}}\), \({\varvec{K}_{\mathrm{{N}}3e}} = \frac{1}{2} \cdot \int _{v_0} {\varvec{B}_{\mathrm{{N}}5}^\mathrm{{T}} \cdot \mathbf{{E}} \cdot {\varvec{B}_{\mathrm{{N}}5}}\mathrm{{d}}{v_0}}\).
The above equation provides a procedure to compute elastic force of element as \({{\varvec{Q}}_{ke}} = ({\varvec{K}_\mathrm{{L}e}} + {\varvec{K}_\mathrm{{N}e}}) \cdot {\varvec{u}_e}\). This procedure is different to the procedure in section 4.9 of [8]. While full quadrature is adopted, the number of arithmetic operations including addition and multiplication is analyzed for these two procedures. For the procedure based on above equation, the matrix multiplication order is implemented from right to left, and then the number of arithmetic operations is \(2 \cdot m^4 + 12 \cdot m^3 + 38 \cdot m^2 - 12 \cdot m\). For the procedure in section 4.9 of [8], the number of arithmetic operations is obtained as \(n_\mathrm{{m}} \cdot (39 \cdot m+174)\), where \(n_\mathrm{{m}}\) is the number of quadrature points. Under \(m = 8\) and \(n_\mathrm{{m}} = 3^3\), the numbers of arithmetic operations are, respectively, 16672 and 13122 for the two procedures. The presented procedure is less efficient but still adopted, and two reasons are: the element assembly in advance of solving system dynamic equation compensates efficiency; the time-invariant features of \(\varvec{K}_{\mathrm{{N}}1e}\), \(\varvec{K}_{\mathrm{{N}}2e}\) and \(\varvec{K}_{\mathrm{{N}}3e}\) reflect systemic inherent characteristics; for example, these three matrices are potential to provide possibly more accurate and efficient calculation of reduced quadratic and cubic stiffness coefficients in nonlinear reduced order model [56].
In order to not to damp rigid motion [51] or eliminate the influence of external damping [57], the total displacement is subtracted by rigid rotation displacement as deformation. The virtual work \(\delta W_e\) of damping force for the e-th element in TLF is similar to GCMS and given by
where element damping matrix \({\varvec{D}_e} = c / \rho \cdot {\varvec{M}_e}\), \(\varvec{u}_\mathrm{{r}e}\) is element displacement vector under only rigid rotation.
According to the virtual work statement [21], the following system dynamic equation is then obtained
where \(\varvec{u}_\mathrm{{s}}\) is system displacement vector, damping force vector \({\varvec{Q}_\mathrm{{d}}} = \varvec{D} \cdot \left[ {{\varvec{A}_\mathrm{{d}}} \cdot {\dot{\varvec{A}}}_\mathrm{{d}}^\mathrm{{T}} \cdot ({\varvec{u}_\mathrm{{s}}} - {\varvec{u}_{\mathrm{{rs}}}}) + ({{\dot{\varvec{u}}}_\mathrm{{s}}} - {{\dot{\varvec{u}}}_{\mathrm{{rs}}}})} \right] \), \(\varvec{u}_{\mathrm{{rs}}}\) is system displacement vector under only rigid rotation, system elastic force vector \({\varvec{Q}_k} = ({\varvec{K}_\mathrm{{L}}} + {\varvec{K}_\mathrm{{N}}}) \cdot {\varvec{u}_\mathrm{{s}}}\), nonlinear system stiffness matrix \({\varvec{K}_\mathrm{{N}}} = {\varvec{K}_{\mathrm{{N}}1}} \cdot {\varvec{u}_{\mathrm{{ds}}}} + \varvec{u}_{\mathrm{{ds}}}^\mathrm{{T}} \cdot {\varvec{K}_{\mathrm{{N}}2}} + \varvec{u}_{\mathrm{{ds}}}^\mathrm{{T}} \cdot {\varvec{K}_{\mathrm{{N}}3}} \cdot {\varvec{u}_{\mathrm{{ds}}}}\), matrices \(\varvec{K}_{\mathrm{{N}}1}\), \(\varvec{K}_{\mathrm{{N}}2}\), \(\varvec{K}_{\mathrm{{N}}3}\) and \(\varvec{u}_{\mathrm{{ds}}}\) are obtained by assembling \(\varvec{K}_{\mathrm{{N}}1e}\), \(\varvec{K}_{\mathrm{{N}}2e}\), \(\varvec{K}_{\mathrm{{N}}3e}\) and \(\varvec{u}_{\mathrm{{d}}e}\).
In the above equation, matrices \(\varvec{K}_{\mathrm{{N}}1}\), \(\varvec{K}_{\mathrm{{N}}2}\) and \(\varvec{K}_{\mathrm{{N}}3}\) are time-invariant, so they are called system invariant matrix. Once these matrices are obtained by element integration and assembly before solving system dynamic equation, they can be reused in every time step, which means there is no need of element integration and assembly in each time step. The similar method is also used by the inertia shape integrals method [7, 12] and the element invariant matrix method [49]: The former calculates system mass matrix for FFRF and the latter calculates components of element stiffness matrix for ANCF.
3 Methods based on beam element
3.1 The method of LEBB
Similar to FFRF, the LEBB also establishes inertial frame \(o-xyz\) and floating frame \(O-XYZ\), and the total motion of flexible body point is separated into rigid motion part and elastic deformation part. However, different from FFRF, the LEBB adopts deformation on one-dimensional centerline to determine deformation of three-dimensional beam. This work only considers the straight beam case, the X axis coincides with the undeformed straight beam centerline, and rotational axis is still z axis or Z axis. Measure the Cartesian coordinate of undeformed body point in frame \(O-XYZ\) as vector \(\varvec{X}_0 = \left[ {\begin{array}{ccc} X_0&Y_0&Z_0 \end{array}} \right] ^\mathrm{{T}}\); vector \(\varvec{X}_0\) is constant and adopted to specify different body points. For the point \(\varvec{X}_0\) of the three-dimensional beam, its deformation is measured in \(O-XYZ\) as relative coordinate vector \({\varvec{U}_\mathrm{{f}}}({\varvec{X}_0}) = {\left[ {\begin{array}{ccc} {{U_{\mathrm{{f}}X}}}&{{U_{\mathrm{{f}}Y}}}&{{U_{\mathrm{{f}}Z}}} \end{array}} \right] ^\mathrm{{T}}}\). For the cross section at \(X_0\), its configuration is measured in \(O-XYZ\) as relative coordinate vector \({\varvec{W}_\mathrm{{f}}}(X_0) = {\left[ {\begin{array}{cccccc} {{W_X}}&{{W_Y}}&{{W_Z}}&{{\theta _X}}&{{\theta _Y}}&{{\theta _Z}} \end{array}} \right] ^\mathrm{{T}}}\), where \(W_X\), \(W_Y\) and \(W_Z\) are translational displacement component, \(\theta _X\), \(\theta _Y\) and \(\theta _Z\) are rotational angle component. For most beam theories, the plane cross-section assumption [21] is adopted that a cross-section orthogonal to the centerline remains plane and keeps its shape throughout deformation process. In additional consideration of the small deformation assumption, the deformation \({\varvec{U}_\mathrm{{f}}}(\varvec{X}_0)\) of three-dimensional beam is then determined by deformation \({\varvec{W}_\mathrm{{f}}}(X_0)\) on one-dimensional centerline as follows
where matrix \({\varvec{N}_\mathrm{{c}}}(\varvec{X}_0) = \left[ {\begin{array}{cccccc} 1&{}0&{}0&{}0&{}Z_0&{}{ - Y_0}\\ 0&{}1&{}0&{}{ - Z_0}&{}0&{}0\\ 0&{}0&{}1&{}Y_0&{}0&{}0 \end{array}} \right] \).
When the ratio of length to cross-section dimension is not very high, the Euler–Bernoulli beam theory permits accurate solution [21]. The Euler–Bernoulli beam assumes that the rotated cross section keeps orthogonal to the deformed centerline throughout deformation process. In this case, the rotational angle \(\theta _Y(X_0)\) and \(\theta _Z(X_0)\) can be calculated by derivatives of deflection \(W_Y(X_0)\) and \(W_Z(X_0)\), the interpolations for deflection \(W_Y(X_0)\) and \(W_Z(X_0)\) should have \(C^1\) continuity, whereas interpolations for deformation \(W_X(X_0)\) and angle \(\theta _X(X_0)\) still use \(C^0\) interpolation. Then the deformation \({\varvec{W}_\mathrm{{f}}}(X_0)\) of cross section at \(X_0\) is approximated by interpolation of node deformation as
where shape function \({\varvec{N}_\mathrm{{E}} }(\xi ) = \left[ {\begin{array}{cc} {{\varvec{N}_{\mathrm{{E}} i}}(\xi )}&{{\varvec{N}_{\mathrm{{E}} j}}(\xi )} \end{array}} \right] \), \({\varvec{N}_{\mathrm{{E}} i}}(\xi ) = \left[ {\begin{array}{cccccc} {{N_{1\mathrm{{E}} i}}}&{}0&{}0&{}0&{}0&{}0\\ 0&{}{{N_{2\mathrm{{E}} i}}}&{}0&{}0&{}0&{}{{N_{3\mathrm{{E}} i}}}\\ 0&{}0&{}{{N_{2\mathrm{{E}} i}}}&{}0&{}{ - {N_{3\mathrm{{E}} i}}}&{}0\\ 0&{}0&{}0&{}{{N_{1\mathrm{{E}} i}}}&{}0&{}0\\ 0&{}0&{}{ - {N_{4\mathrm{{E}} i}}}&{}0&{}{{N_{5\mathrm{{E}} i}}}&{}0\\ 0&{}{{N_{4\mathrm{{E}} i}}}&{}0&{}0&{}0&{}{{N_{5\mathrm{{E}} i}}} \end{array}} \right] \), \({\varvec{N}_{\mathrm{{E}} j}}(\xi ) = \left[ {\begin{array}{cccccc} {{N_{1\mathrm{{E}} j}}}&{}0&{}0&{}0&{}0&{}0\\ 0&{}{{N_{2\mathrm{{E}} j}}}&{}0&{}0&{}0&{}{{N_{3\mathrm{{E}} j}}}\\ 0&{}0&{}{{N_{2\mathrm{{E}} j}}}&{}0&{}{ - {N_{3\mathrm{{E}} j}}}&{}0\\ 0&{}0&{}0&{}{{N_{1\mathrm{{E}} j}}}&{}0&{}0\\ 0&{}0&{}{ - {N_{4\mathrm{{E}} j}}}&{}0&{}{{N_{5\mathrm{{E}} j}}}&{}0\\ 0&{}{{N_{4\mathrm{{E}} j}}}&{}0&{}0&{}0&{}{{N_{5\mathrm{{E}} j}}} \end{array}} \right] \), \({N_{1\mathrm{{E}} i}} = 1 - \xi \), \({N_{1\mathrm{{E}} j}} = \xi \), \({N_{2\mathrm{{E}} i}} = 1 - 3{\xi ^2} + 2{\xi ^3}\), \({N_{2\mathrm{{E}} j}} = 3{\xi ^2} - 2{\xi ^3}\), \({N_{3\mathrm{{E}} i}} = {l_e} \cdot (\xi - 2{\xi ^2} + {\xi ^3})\), \({N_{3\mathrm{{E}} j}} = {l_e} \cdot ({\xi ^3} - {\xi ^2})\), \({N_{4\mathrm{{E}} i}} = ( - 6\xi + 6{\xi ^2})/{l_e}\), \({N_{4\mathrm{{E}} j}} = (6\xi - 6{\xi ^2})/{l_e}\), \({N_{5\mathrm{{E}} i}} = 1 - 4\xi + 3{\xi ^2}\), \({N_{5\mathrm{{E}} j}} = 3{\xi ^2} - 2\xi \), \(0\le \xi \le 1\), \(l_e\) is element length, element elastic coordinate vector \({\varvec{W}_{\mathrm{{f}}e}} = {\left[ {\begin{array}{cc} {{\varvec{W}_{\mathrm{{f}}ei}}}&{{\varvec{W}_{\mathrm{{f}}ej}}} \end{array}} \right] ^\mathrm{{T}}}\), \(\varvec{W}_{\mathrm{{f}}ei}\) and \(\varvec{W}_{\mathrm{{f}}ej}\) are the relative coordinate vector of the deformation for the two nodes i and j.
According to above deformation expression, the total displacement vector \(\varvec{u}\) of point \(\varvec{X}_0\) is measured in \(o-xyz\) and calculated similar to FFRF, and the corresponding velocity is given by
where matrix \({\varvec{N}_\mathrm{{r}}}({\varvec{X}})\) is the same as Eq. (10), matrix \({\varvec{N}_\mathrm{{f}}}({\varvec{X}_0}) = {\varvec{N}_\mathrm{{c}}}({\varvec{X}_0}) \cdot {\varvec{N}_\mathrm{{E}} }(\xi )\).
According to the velocity, the element kinetic energy \(T_e\) is calculated by
where element coordinate \({\varvec{q}_e} = {\left[ {\begin{array}{cc} {{\varvec{q}_\mathrm{{r}}}{}}&{{\varvec{W}_{\mathrm{{f}}e}}} \end{array}} \right] ^\mathrm{{T}}}\), the element mass matrix \({\varvec{M}_e} = \left[ {\begin{array}{cc} {{\varvec{M}_{\mathrm{{rr}}e}}}&{}{{\varvec{M}_{\mathrm{{rf}}e}}}\\ {\varvec{M}_{\mathrm{{rf}}e}^\mathrm{{T}}}&{}{{\varvec{M}_{\mathrm{{ff}}e}}} \end{array}} \right] \), \({\varvec{M}_{\mathrm{{rr}}e}} = \int _v {\rho \cdot \varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}}) \cdot {\varvec{N}_\mathrm{{r}}}(\varvec{X} )\mathrm{{d}}v}\), \({\varvec{M}_{\mathrm{{rf}}e}} = \int _v \rho \cdot \varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}}) \cdot \varvec{A} \cdot \varvec{N}_\mathrm{{f}}(\varvec{X}_0 )\mathrm{{d}}v\), \({\varvec{M}_{\mathrm{{ff}}e}} = \int _v {\rho \cdot {\varvec{N}_\mathrm{{f}}^\mathrm{{T}}}(\varvec{X}_0 ) \cdot \varvec{N}_\mathrm{{f}}(\varvec{X}_0 )\mathrm{{d}}v}\).
Mass matrices \(\varvec{M}_{\mathrm{{rr}}e}\) and \(\varvec{M}_{\mathrm{{rf}}e}\) can also be calculated by inertia shape integrals method [7, 12], and the relevant formulas are shown in “Appendix.”
The deformation in Eq. (36) is also adopted to calculate linear strain of three-dimensional beam. There are three nonzero strains \(\varepsilon _{X}\), \(\gamma _{XY}\) and \(\gamma _{XZ}\), and the strain vector \(\varvec{\varepsilon } = {\left[ {\begin{array}{ccc} {{\varepsilon _X}}&{{\gamma _{XY}}}&{{\gamma _{XZ}}} \end{array}} \right] ^\mathrm{{T}}}\) of point \(\varvec{X}_0\) is linearly related to element elastic coordinate as follows [21]
where matrix \({\varvec{L}_1} = \left[ {\begin{array}{cccc} 1&{}{ - {Z_0}}&{}{ - {Y_0}}&{}0\\ 0&{}0&{}0&{}{ - {Z_0}}\\ 0&{}0&{}0&{}{{Y_0}} \end{array}} \right] \), differential operator \({\varvec{L}_2} = \left[ {\begin{array}{cccccc} {\frac{\mathrm{{d}}}{{\mathrm{{d}}X}}}&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}{\frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{X^2}}}}&{}0&{}0&{}0\\ 0&{}{\frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{X^2}}}}&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}{\frac{\mathrm{{d}}}{{\mathrm{{d}}X}}}&{}0&{}0 \end{array}} \right] \), \(\varvec{B}_\mathrm{{L}}\) is linear strain matrix.
With the above nonzero strains, the beam is treated as orthotropic linear elastic material to calculate stress \({\sigma _X}\), \({\tau _{XY}}\) and \({\tau _{XZ}}\) [21]. The element elastic potential energy \(V_e\) is calculated as
where \(\textrm{E}\) is elastic modulus, \(\textrm{G}\) is shear moduli, element stiffness matrix \({\varvec{K}_{\mathrm{{L}}e}} = {l_e} \cdot \int _0^1 \varvec{N}_\mathrm{{E}}^\mathrm{{T}}(\xi ) \cdot \varvec{L}_2^\mathrm{{T}} \cdot \mathbf{{E}} \cdot {\varvec{L}_2} \cdot {\varvec{N}_\mathrm{{E}}}(\xi )\mathrm{{d}}\xi \), cross-section stiffness \(\mathbf{{E}} = \left[ {\begin{array}{cccc} {\mathrm{{E}} \cdot A}&{}{ - \mathrm{{E}} \cdot {S_Y}}&{}{ - \mathrm{{E}} \cdot {S_Z}}&{}0\\ { - \mathrm{{E}} \cdot {S_Y}}&{}{\mathrm{{E}} \cdot {I_Y}}&{}{\mathrm{{E}} \cdot {I_{YZ}}}&{}0\\ { - \mathrm{{E}} \cdot {S_Z}}&{}{\mathrm{{E}} \cdot {I_{YZ}}}&{}{\mathrm{{E}} \cdot {I_Z}}&{}0\\ 0&{}0&{}0&{}{\mathrm{{G}} \cdot J_X} \end{array}} \right] \), A is the area of cross section, \({S_Y} = \int _A {{Z_0}\mathrm{{d}}A}\) and \({S_Z} = \int _A {{Y_0}\mathrm{{d}}A}\) are the first-order moments of cross section, \({I_Y} = \int _A {Z_0^2\mathrm{{d}}A}\) and \({I_Z} = \int _A {Y_0^2\mathrm{{d}}A}\) are the inertia moment of cross section, \({I_{YZ}} = \int _A {{Y_0} \cdot {Z_0}\mathrm{{d}}A}\) is the inertia product of cross section, \(J_X=I_Y+I_Z\) is the polar inertia moment of cross section.
As the same as in FFRF, the virtual work \(\delta W_e\) of damping force for the e-th element is calculated by
where terms related to \(\delta \varvec{A}\) are ignored, element damping matrix \({\varvec{D}_e} = \left[ {\begin{array}{c} {{\tilde{\varvec{A}}} \cdot {\varvec{D}_{\mathrm{{rf}}e}}}\\ {{\varvec{D}_{\mathrm{{ff}}e}}} \end{array}} \right] \), \({\varvec{D}_{\mathrm{{rf}}e}} = c \cdot \int _v \varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}_0}) \cdot {\varvec{N}_\mathrm{{f}}}({\varvec{X}_0})\mathrm{{d}}v\), \({\varvec{D}_{\mathrm{{ff}}e}} = c / \rho \cdot {\varvec{M}_{\mathrm{{ff}}e}}\).
As for the virtual work \(\delta W_e\) of load intensity \(\varvec{F}_\mathrm{{e}} = {\left[ {\begin{array}{cccccc} {F_{\mathrm{{e}}X}}&{F_{\mathrm{{e}}Y}}&{F_{\mathrm{{e}}Z}}&{T_{\mathrm{{e}}X}}&{T_{\mathrm{{e}}Y}}&{T_{\mathrm{{e}}z}} \end{array}} \right] ^\mathrm{{T}}}\) on beam centerline, it is calculated on the basis of small deformation assumption and given by
where terms related to \(\delta \varvec{A}\) are ignored, \(\varvec{\varphi } = {\left[ {\begin{array}{ccc} 0&0&\varphi \end{array}} \right] ^\mathrm{{T}}}\), \(\varvec{\theta } = {\left[ {\begin{array}{ccc} {{\theta _X}}&{{\theta _Y}}&{{\theta _Z}} \end{array}} \right] ^\mathrm{{T}}}\), \({\varvec{R}_e} = \left[ {\begin{array}{c} {\begin{array}{cc} {\varvec{N}_\mathrm{{r}}^\mathrm{{T}}({\varvec{X}_0}) \cdot \varvec{A} \quad }&{}{{\varvec{R}_{e1}}} \end{array}}\\ {\varvec{N}_\mathrm{{E}}^\mathrm{{T}}(\xi )} \end{array}} \right] \), \({\varvec{R}_{e1}} = \left[ {\begin{array}{ccc} 0&{}0&{}{ - \sin \varphi }\\ 0&{}0&{}{\cos \varphi } \end{array}} \right] \),
According to the energy and virtual work, the generalized force can be obtained. Substituting them in the fundamental nonholonomic form of Lagrange’s equation, the system dynamic equation is given by
where system coordinate \(\varvec{q} = {\left[ {\begin{array}{cc} {\varvec{q}_\mathrm{{r}}^\mathrm{{T}}{}}&{\varvec{W}_{\mathrm{{fs}}}^\mathrm{{T}}} \end{array}} \right] ^\mathrm{{T}}}\), \(\varvec{W}_{\mathrm{{fs}}}\) is system elastic coordinate vector, derivative \(\dot{\varvec{M}}\) and partial derivative \(\frac{{\partial {T}}}{{\partial \varvec{q}}}\) for calculation of \(\varvec{Q}_v\) are shown in “Appendix,” damping force vector \({\varvec{Q}_\mathrm{{d}}} = \varvec{D} \cdot {\dot{\varvec{W}}_\mathrm{{fs}}}\), system elastic force vector \({\varvec{Q}_k} = {\varvec{K}_\mathrm{{L}}} \cdot {\varvec{W}_\mathrm{{fs}}}\).
3.2 The method of NEBB
The kinematic analysis approach of NEBB is the same as LEBB, and then the calculations for kinetic energy and damping force virtual work in NEBB are also the same as in LEBB. Difference between NEBB and LEBB lies in the calculation of strain, and then their calculation for elastic potential energy is also different. In NEBB, the nonzero strain vector \(\varvec{\varepsilon } = {\left[ {\begin{array}{ccc} {{\varepsilon _X}}&{{\gamma _{XY}}}&{{\gamma _{XZ}}} \end{array}} \right] ^\mathrm{{T}}}\) of point \(\varvec{X}_0\) is nonlinearly related to element elastic coordinate as follows
where linear strain matrix \(\varvec{B}_\mathrm{{L}}\) is the same as in Eq. (40), nonlinear strain matrix \({\varvec{B}_\mathrm{{N}}} = \left[ {\begin{array}{c} {\varvec{W}_{\mathrm{{f}}e}^\mathrm{{T}}}\\ \varvec{0} \end{array}} \right] \cdot \varvec{N}_\mathrm{{E}}^\mathrm{{T}}(\xi ) \cdot \varvec{L}_3^\mathrm{{T}}\cdot {\varvec{L}_3}\cdot {\varvec{N}_\mathrm{{E}}}(\xi )\), differential operator \({\varvec{L}_3} = \left[ {\begin{array}{cccccc} 0&{}{\frac{\mathrm{{d}}}{{\mathrm{{d}}X}}}&{}0&{}0&{}0&{}0\\ 0&{}0&{}{\frac{\mathrm{{d}}}{{\mathrm{{d}}X}}}&{}0&{}0&{}0 \end{array}} \right] \).
Through matrix transformation, the nonlinear strain matrix \(\varvec{B}_\mathrm{{N}}\) is transformed as
where \({\varvec{B}_{\mathrm{{N}}3}} = \left[ {\begin{array}{c} {{\varvec{B}_{\mathrm{{N}}1}}}\\ \varvec{0} \end{array}} \right] \cdot {\varvec{B}_{\mathrm{{N}}2}}\), \({\varvec{B}_{\mathrm{{N}}1}} = \left[ {\begin{array}{cccccccc} {\frac{{\partial {N_{2\mathrm{{E}}i}}}}{{\partial X}}}&{\frac{{\partial {N_{3\mathrm{{E}}i}}}}{{\partial X}}}&{\frac{{\partial {N_{2\mathrm{{E}}j}}}}{{\partial X}}}&{\frac{{\partial {N_{3\mathrm{{E}}j}}}}{{\partial X}}}&{\frac{{\partial {N_{2\mathrm{{E}}i}}}}{{\partial X}}}&{\frac{{\partial {N_{3\mathrm{{E}}i}}}}{{\partial X}}}&{\frac{{\partial {N_{2\mathrm{{E}}j}}}}{{\partial X}}}&{\frac{{\partial {N_{3\mathrm{{E}}j}}}}{{\partial X}}} \end{array}} \right] \), \({\varvec{B}_{\mathrm{{N}}2}} = \mathrm{{diag}}({\varvec{B}_{\mathrm{{N}}2i}},{\varvec{B}_{\mathrm{{N}}2i}},{\varvec{B}_{\mathrm{{N}}2j}},{\varvec{B}_{\mathrm{{N}}2j}})\), \({\varvec{B}_{\mathrm{{N}}2i}} = \left[ {\begin{array}{cccccc} {\frac{{\partial {N_{2\mathrm{{E}}i}}}}{{\partial X}}}&{}0&{}0&{}{ - \frac{{\partial {N_{3\mathrm{{E}}i}}}}{{\partial X}}}&{}{\frac{{\partial {N_{3\mathrm{{E}}i}}}}{{\partial X}}}&{}0\\ 0&{}{\frac{{\partial {N_{2\mathrm{{E}}i}}}}{{\partial X}}}&{}{ - \frac{{\partial {N_{2\mathrm{{E}}i}}}}{{\partial X}}}&{}0&{}0&{}{\frac{{\partial {N_{3\mathrm{{E}}i}}}}{{\partial X}}} \end{array}} \right] \), \({\varvec{B}_{\mathrm{{N}}2j}} = \left[ {\begin{array}{cccccc} {\frac{{\partial {N_{2\mathrm{{E}}j}}}}{{\partial X}}}&{}0&{}0&{}{ - \frac{{\partial {N_{3\mathrm{{E}}j}}}}{{\partial X}}}&{}{\frac{{\partial {N_{3\mathrm{{E}}j}}}}{{\partial X}}}&{}0\\ 0&{}{\frac{{\partial {N_{2\mathrm{{E}}j}}}}{{\partial X}}}&{}{ - \frac{{\partial {N_{2\mathrm{{E}}j}}}}{{\partial X}}}&{}0&{}0&{}{\frac{{\partial {N_{3\mathrm{{E}}j}}}}{{\partial X}}} \end{array}} \right] \), \(\varvec{W}_{\mathrm{{d}}e}\) is block-diagonal with each diagonal block equal to \({\varvec{W}_{\mathrm{{B}}e}} = \left[ {\begin{array}{c} {{\varvec{W}_{\mathrm{{B}}ei}}}\\ {{\varvec{W}_{\mathrm{{B}}ej}}} \end{array}} \right] \), \({\varvec{W}_{\mathrm{{B}}ei}} = \left[ {\begin{array}{cccccc} 0&{}{{W_{Yi}}}&{}{{W_{Zi}}}&{}0&{}0&{}0\\ 0&{}{{\theta _{Zi}}}&{}0&{}0&{}0&{}0\\ 0&{}0&{}{{\theta _{Yi}}}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}{{W_{Zi}}}&{}0\\ 0&{}0&{}0&{}0&{}0&{}{{W_{Yi}}}\\ 0&{}0&{}0&{}0&{}{{\theta _{Yi}}}&{}{{\theta _{Zi}}} \end{array}} \right] \), \({\varvec{W}_{\mathrm{{B}}ej}} = \left[ {\begin{array}{cccccc} 0&{}{{W_{Yj}}}&{}{{W_{Zj}}}&{}0&{}0&{}0\\ 0&{}{{\theta _{Zj}}}&{}0&{}0&{}0&{}0\\ 0&{}0&{}{{\theta _{Yj}}}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}{{W_{Zj}}}&{}0\\ 0&{}0&{}0&{}0&{}0&{}{{W_{Yj}}}\\ 0&{}0&{}0&{}0&{}{{\theta _{Yj}}}&{}{{\theta _{Zj}}} \end{array}} \right] \).
The variation of nonlinear strain \(\delta \varvec{\varepsilon }\) is as follows
According to the nonlinear strain, stresses \({\sigma _X}\), \({\tau _{XY}}\) and \({\tau _{XZ}}\) are calculated as the same as LEBB. The virtual work \(\delta V_e\) of elastic force for the e-th element is as follows
where nonlinear element stiffness matrix \({\varvec{K}_{\mathrm{{N}}e}} = {\varvec{K}_{\mathrm{{N}}1e}} \cdot {\varvec{W}_{\mathrm{{d}}e}} + \varvec{W}_{\mathrm{{d}}e}^\mathrm{{T}} \cdot {\varvec{K}_{\mathrm{{N}}2e}} + \varvec{W}_{\mathrm{{d}}e}^\mathrm{{T}} \cdot {\varvec{K}_{\mathrm{{N}}3e}} \cdot {\varvec{W}_{\mathrm{{d}}e}}\), matrices \(\varvec{K}_{\mathrm{{N}}1e}\), \(\varvec{K}_{\mathrm{{N}}2e}\) and \(\varvec{K}_{\mathrm{{N}}3e}\) are time-invariant, \({\varvec{K}_{\mathrm{{N}}1e}} = \frac{1}{2} \cdot {l_e} \cdot \int _0^1 { {\varvec{N}_\mathrm{{E}}^\mathrm{{T}}(\xi ) \cdot \varvec{L}_2^\mathrm{{T}} \cdot {\mathbf{{E}}_1} \cdot {\varvec{B}_{\mathrm{{N}}3}}} \mathrm{{d}}\xi }\), \({\mathbf{{E}}_1} = \left[ {\begin{array}{ccc} {\mathrm{{E}}A}&{}0&{}0\\ { - \mathrm{{E}}{S_Y}}&{}0&{}0\\ { - \mathrm{{E}}{S_Z}}&{}0&{}0\\ 0&{}{ - \mathrm{{G}}{S_Y}}&{}{\mathrm{{G}}{S_Z}} \end{array}} \right] \), \({\varvec{K}_{\mathrm{{N}}2e}} = {l_e} \cdot \int _0^1 \varvec{B}_{\mathrm{{N}}3}^\mathrm{{T}} \cdot \mathbf{{E}}_1^\mathrm{{T}} \cdot {\varvec{L}_2} \cdot {\varvec{N}_\mathrm{{E}}}(\xi ) \mathrm{{d}}\xi \), \({\varvec{K}_{\mathrm{{N}}3e}} = \frac{1}{2} \cdot {l_e} \cdot \int _0^1 {\varvec{B}_{\mathrm{{N}}3}^\mathrm{{T}} \cdot {\mathbf{{E}}_3} \cdot {\varvec{B}_{\mathrm{{N}}3}}} \mathrm{{d}}\xi \), \({\mathbf{{E}}_3} = \left[ {\begin{array}{ccc} {\mathrm{{E}}A}&{}0&{}0\\ 0&{}{\mathrm{{G}}A}&{}0\\ 0&{}0&{}{\mathrm{{G}}A} \end{array}} \right] \).
The system dynamic equation of NEBB is similar to LEBB, and the only difference is that system elastic force vector \({\varvec{Q}_k} = ({\varvec{K}_\mathrm{{L}}} + {\varvec{K}_\mathrm{{N}}}) \cdot {\varvec{W}_\mathrm{{fs}}}\) in NEBB.
3.3 The method of ANCF
Similar to TLF, the ANCF only establishes inertial frame which is expressed by \(o-xyz\): The Cartesian coordinate for point of reference configuration is measured in inertial frame as vector \(\varvec{x}_0 = \left[ {\begin{array}{ccc} x_0&y_0&z_0 \end{array}} \right] ^\mathrm{{T}}\), and the Cartesian coordinate for point of current configuration is measured in inertial frame as vector \(\varvec{x} = \left[ {\begin{array}{ccc} x&y&z \end{array}} \right] ^\mathrm{{T}}\).
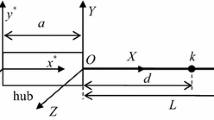
The main difference between ANCF and TLF lies in the displacement interpolation approach: Their element type, nodal coordinate and shape function are different. As shown in Fig. 2, coordinate \(\varvec{x}\) is one-to-one mapped to local coordinate \({\tilde{\varvec{X}}} = {\left[ {\begin{array}{ccc} {\tilde{X}}&{{\tilde{Y}}}&{{\tilde{Z}}} \end{array}} \right] ^\mathrm{{T}}}\), where \(\tilde{\varvec{X}}\) is local coordinate of a straight beam. Longitudinal coordinate \(\tilde{X}\) specifies different cross sections, and transverse coordinates \(\tilde{Y}\) and \(\tilde{Z}\) specify different points on cross section. The mapping from \(\varvec{x}\) to \({\tilde{\varvec{X}}}\) is given by
where \(\varvec{N}({\tilde{\varvec{X}}})\) is shape function, element coordinate vector \(\varvec{e} = {\left[ {\begin{array}{cc} {\varvec{e}_i^\mathrm{{T}}{}}&{\varvec{e}_j^\mathrm{{T}}} \end{array}} \right] ^\mathrm{{T}}}\), \(\varvec{e}_i\) and \(\varvec{e}_j\) are the nodal coordinate vector of nodes i and j.
The nodal coordinate vector simultaneously includes global position and gradient as follows
where \(g_{i,\alpha }\) is Pascal triangle polynomial about \(\tilde{Y}\) and \(\tilde{Z}\) [47], \(1 \le i \le (n + 1) \cdot (n + 2)/2\), the order \(\alpha \) of Pascal triangle satisfies \(0 \le \alpha \le n\), n is the order of the beam model and the beam model is called higher-order beam model if \(n>1\).
In order to prevent Poisson locking and hold high efficiency, the second order beam model of which \(n = 2\) is adopted [47]. Corresponding Pascal triangle polynomial is as follows
For positions and gradients only related to centerline, the interpolation polynomial is cubic in \(\tilde{X}\) direction; for gradients related to cross section, the interpolation polynomial is linear in \(\tilde{X}\) direction. Corresponding shape function \(\varvec{N}({\tilde{\varvec{X}}})\) is given by
where \({N_{1i}} = 1 - 3{\xi ^2} + 2{\xi ^3}\), \({N_{2i}} = {l_e} \cdot (\xi - 2{\xi ^2} + {\xi ^3})\), \({N_{3i}} = 1 - \xi \), \({N_{1j}} = 3{\xi ^2} - 2{\xi ^3}\), \({N_{2j}} = {l_e} \cdot ( - {\xi ^2} + {\xi ^3})\), \({N_{3j}} = \xi \), \(\xi = \tilde{X} / l_e\) and \(\xi \) linearly changes from 0 to 1 when centerline point moves from node i to j.
The total displacement vector \(\varvec{u} = \left[ {\begin{array}{ccc} {u_x}&{u_y}&{u_z} \end{array}} \right] ^\mathrm{{T}}\) of point \(\tilde{\varvec{X}}\) is then given by
where \(\varvec{e}_0\) is the initial value of \(\varvec{e}\).
According to total displacement in above equation, the virtual works of inertia force, elastic force and damping force are, respectively, calculated, in a similar way in Sect. 2.3. The resultant virtual work \(\delta T_e\) of inertia force for the e-th element is
where \({\varvec{M}_e} = \int _{v_0} {\rho _0 \cdot {\varvec{N}^\mathrm{{T}}}({\tilde{\varvec{X}}}) \cdot \varvec{N}({\tilde{\varvec{X}}})\mathrm{{d}}{v_0}}\).
The resultant virtual work \(\delta V_e\) of elastic force for the e-th element is
where \({\varvec{K}_{\mathrm{{L}}e}} = \int _{v_0} {\varvec{B}_\mathrm{{L}}^\mathrm{{T}} \cdot \mathbf{{E}} \cdot {\varvec{B}_\mathrm{{L}}}\mathrm{{d}}{v_0}}\), \({\varvec{K}_{\mathrm{{N}}e}} = {\varvec{K}_{\mathrm{{N}}1e}} \cdot {({\varvec{e}_\mathrm{{d}}} - {\varvec{e}_{\mathrm{{d}}0}})} + {({\varvec{e}_\mathrm{{d}}} - {\varvec{e}_{\mathrm{{d}}0}})^\mathrm{{T}}} \cdot {\varvec{K}_{\mathrm{{N}}2e}} + {({\varvec{e}_\mathrm{{d}}} - {\varvec{e}_{\mathrm{{d}}0}})^\mathrm{{T}}} \cdot {\varvec{K}_{\mathrm{{N}}3e}} \cdot {({\varvec{e}_\mathrm{{d}}} - {\varvec{e}_{\mathrm{{d}}0}})}\), \(\varvec{B}_\mathrm{{L}}\) is linear strain matrix as the same as Eq. (30), matrices \(\varvec{K}_{\mathrm{{N}}1e}\), \(\varvec{K}_{\mathrm{{N}}2e}\) and \(\varvec{K}_{\mathrm{{N}}3e}\) are time-invariant and the same as Eq. (33), matrix \(\varvec{B}_{\mathrm{{N}}5}\) for calculating \(\varvec{K}_{\mathrm{{N}}1e}\), \(\varvec{K}_{\mathrm{{N}}2e}\) and \(\varvec{K}_{\mathrm{{N}}3e}\) is the same as Eq. (31) where \(m = 2 + (n + 1) \cdot (n + 2)\), \(\varvec{e}_\mathrm{{d}}\) is block-diagonal with each diagonal block equal to \({\varvec{e}_\mathrm{{B}}} = \left[ {\begin{array}{ccc} {{e_1}}&{}{{e_2}}&{}{{e_3}}\\ {{e_4}}&{}{{e_5}}&{}{{e_6}}\\ \vdots &{} \vdots &{} \vdots \\ {{e_{3m-2}}}&{}{{e_{3m-1}}}&{}{{e_{3m}}} \end{array}} \right] \), \(e_k\) is the component in the k-th row of vector \(\varvec{e}\), \(\varvec{e}_{\mathrm{{d}}0}\) is the initial value of \(\varvec{e}_\mathrm{{d}}\).
In a similar way to TLF, the above equation provides a procedure to compute elastic force of element. Under \(m=14\) and \(n_\mathrm{{m}} = 5 \cdot 3 \cdot 3\), the numbers of arithmetic operations are, respectively, 117040 and 32400 for the presented procedure and the procedure in section 4.9 of [8]. The reason for adopting the presented procedure is the same as TLF.
The resultant virtual work \(\delta V_e\) of damping force for the e-th element is
where element damping matrix \({\varvec{D}_e} = c / \rho \cdot {\varvec{M}_e}\), \(\varvec{e}_\mathrm{{r}}\) is element coordinate vector under only rigid rotation.
According to the virtual work statement, the system dynamic equation of ANCF is given by
where \(\varvec{e}_\mathrm{{s}}\) is system coordinate vector, damping force vector \({\varvec{Q}_\mathrm{{d}}} = \varvec{D} \cdot \left[ {{\varvec{A}_\mathrm{{d}}} \cdot {\dot{\varvec{A}}}_\mathrm{{d}}^\mathrm{{T}} \cdot ({\varvec{e}_\mathrm{{s}}} - {\varvec{e}_{\mathrm{{rs}}}}) + ({{\dot{\varvec{e}}}_\mathrm{{s}}} - {{\dot{\varvec{e}}}_{\mathrm{{rs}}}})} \right] \), \(\varvec{e}_{\mathrm{{rs}}}\) is system coordinate vector under only rigid rotation, system elastic force vector \({\varvec{Q}_k} = ({\varvec{K}_\mathrm{{L}}} + {\varvec{K}_\mathrm{{N}}}) \cdot ({\varvec{e}_\mathrm{{s}}} - {\varvec{e}_{\mathrm{{s}}0}})\), nonlinear system stiffness matrix \({\varvec{K}_\mathrm{{N}}} = {\varvec{K}_{\mathrm{{N}}1}} \cdot {({\varvec{e}_\mathrm{{ds}}} - {\varvec{e}_{\mathrm{{ds}}0}})} + {({\varvec{e}_\mathrm{{ds}}} - {\varvec{e}_{\mathrm{{ds}}0}})^\mathrm{{T}}} \cdot {\varvec{K}_{\mathrm{{N}}2}} + {({\varvec{e}_\mathrm{{ds}}} - {\varvec{e}_{\mathrm{{ds}}0}})^\mathrm{{T}}} \cdot {\varvec{K}_{\mathrm{{N}}3}} \cdot {({\varvec{e}_\mathrm{{ds}}} - {\varvec{e}_{\mathrm{{ds}}0}})}\), \(\varvec{K}_{\mathrm{{N}}1}\), \(\varvec{K}_{\mathrm{{N}}2}\), \(\varvec{K}_{\mathrm{{N}}3}\), \(\varvec{e}_{\mathrm{{ds}}}\) and \(\varvec{e}_{\mathrm{{ds}}0}\) are obtained by element assembly.
In the above equation, matrices \(\varvec{K}_{\mathrm{{N}}1}\), \(\varvec{K}_{\mathrm{{N}}2}\) and \(\varvec{K}_{\mathrm{{N}}3}\) are time-invariant, so they are also called system invariant matrix. Once these matrices are obtained by element integration and assembly before solving system dynamic equation, they can be reused in every time step. Theoretically, system invariant matrix holds higher efficiency in comparison with element invariant matrix [49]. In every time step, the element invariant matrix method needs to calculate every component of element stiffness matrix at first; assembly from element to system is needed at next.
4 Numerical examples
This section takes a variable cross-section beam as numerical example, and its geometry is shown in Fig. 3a. The length of the beam is \(l=1\textrm{m}\), and the rectangular cross section linearly shrinks and rotates from left end to right end. The width and height of left end rectangle are \(l_\mathrm{{W}1}=0.06\textrm{m}\) and \(l_\mathrm{{H}1}=0.12\textrm{m}\), the width and height of right end rectangle are \(l_\mathrm{{W}2}=0.04\textrm{m}\) and \(l_\mathrm{{H}2}=0.08\textrm{m}\), and the rotation angle of right end rectangle relative to left end rectangle is \(\gamma =45^\circ \). The frame origin O locates at the center of the left end rectangle and the left end rectangle keeps rigid during rotation. As for material parameter, the elastic modulus is \(210\textrm{GPa}\), the Poisson’s ratio is 0.28, and the density is \(7.85 \times 10^3 \textrm{kg}\cdot \mathrm{{m}}^{-3}\). As for load, the centerline load intensity along z direction is \(-8\textrm{kN} \cdot \mathrm {m^{-1}}\); in order to avoid impact, the load intensity is linearly increased from \(0\textrm{kN} \cdot \mathrm {m^{-1}}\) to \(-8\textrm{kN} \cdot \mathrm {m^{-1}}\) by \(300{\upmu \textrm{s}}\). As for component mode synthesis, the number of eigenmodes for FFRF is 30, and the number of global eigenmodes for GCMS is 90. In all the following numerical calculations, these geometric, material, load and mode parameters keep unchanged.
There are three values for rotational speed: \({\dot{\varphi }}_1 = 1.0 \times 10^3 \textrm{rpm}\), \({\dot{\varphi }}_2 = 5.0 \times 10^3 \textrm{rpm}\), \({\dot{\varphi }}_3 = 1.0 \times 10^4 \textrm{rpm}\). There are three values for damping coefficient: \(c_1 = 1.0 \times 10^2 \textrm{kg}\cdot \textrm{s}^{-1}\cdot \textrm{m}^{-3}\), \(c_2 = 5.0 \times 10^2 \textrm{kg}\cdot \textrm{s}^{-1}\cdot \textrm{m}^{-3}\), \(c_3 = 1.0 \times 10^3 \textrm{kg}\cdot \textrm{s}^{-1}\cdot \textrm{m}^{-3}\). In the following calculations, these two parameters are changeable and only their symbols are used to refer to them.
For FFRF, GCMS and TLF, the number of solid elements is \(100 \times 6 \times 12\) as shown in Fig. 3b; for LEBB, NEBB and ANCF, the number of beam elements is 10. Numerical result shows these selected grid sizes are feasible for accuracy and efficiency. As for the solver of system dynamics differential equation, two solvers are adopted: Adams-Bashforth two-step method (AB) [58] for FFRF, GCMS, LEBB and NEBB, central difference method (CD) [59] for TLF and ANCF. These two solvers are explicit and convenient to implement, the AB is strongly stable [58], and the CD is conditionally stable [8, 31]. The time step sizes are \(0.5{\upmu \textrm{s}}\), \(0.3{\upmu \textrm{s}}\), \(0.5{\upmu \textrm{s}}\), \(0.4{\upmu \textrm{s}}\), \(0.4{\upmu \textrm{s}}\) and \(1.7{\upmu \textrm{s}}\) for FFRF-AB, GCMS-AB, TLF-CD, LEBB-AB, NEBB-AB and ANCF-CD, respectively. To confirm availability of the selected time step sizes, the following gives numerical result comparison under different time step sizes. Without clear indication, the collocations of grid size, solver and time step size are adopted for following calculations by default.
4.1 Results under different rotational speeds
This section compares the numerical results under different finite element methods and rotational speeds. Because the solver and time step size are different for different finite element methods, this section will not compare the efficiency of different methods. Under rotational speed \({\dot{\varphi }}_1\) and damping coefficient \(c_3\), the free end deflections obtained by different finite element methods are shown in Fig. 4. The longitudinal deflection means deflection along undeformed centerline direction, and the orthogonal transverse deflection means deflection orthogonal to both centerline and load direction. For all finite element methods, the value of deflection gradually goes convergent along with the increase of time. Before convergence, the oscillation of longitudinal deflection is much obvious than the other two deflections, and the reason is that larger tension stiffness requires larger critical damping than smaller bending stiffness. Although there is no load along the direction orthogonal to both centerline and load direction, the orthogonal transverse deflection is not zero, the reason is that nonzero cross-section rotation angle \(\gamma \) causes nonzero inertia product \(I_{YZ}\).
The FFRF-AB, GCMS-AB and LEBB-AB are linear method which holds linear form of strain–displacement equation, the TLF-CD, NEBB-AB and ANCF-CD are nonlinear method which holds nonlinear form of strain–displacement equation. From Fig. 4, the results of linear methods are close to each other, the results of nonlinear methods are close to each other, whereas the results of linear methods are different from nonlinear methods. Convergent deflections of the six methods are shown in Table 1. From the table, the results of FFRF-AB and GCMS-AB are almost the same, and the result difference rate of LEBB-AB relative to FFRF-AB is less than \(1.5\%\). The result difference rate of NEBB-AB relative to TLF-CD is less than \(1.3\%\), and the three result difference rates of ANCF-CD relative to TLF-CD are \(1.7\%\), \(4.0\%\) and \(1.5\%\). The difference rate for orthogonal transverse deflection of ANCF-CD relative to TLF-CD is a little large; however, when the number of beam elements for ANCF-CD increases to 20, this difference rate does not decrease. Due to the influence of geometric nonlinearity or dynamic stiffening, the three deflections of nonlinear methods are all smaller than corresponding deflections of linear methods; for example, the orthogonal transverse deflection of TLF-CD is \(12.7\%\) smaller than FFRF-AB, and the transverse deflection along z axis of TLF-CD is \(8.9\%\) smaller than FFRF-AB.
To confirm the availability of selected time step sizes, the orthogonal transverse deflections under different time step sizes are shown in Fig. 5, with rotational speed \({\dot{\varphi }}_1\) and damping coefficient \(c_3\). In the figure, the time step size equal to half of selected value is adopted, the time step size slightly larger than selected value is also adopted. From the figure, when the time step size reduces by half, the numerical result is still close to that under selected value; when the time step size is unsuitably large, the numerical result becomes infinite or apparently different from that under selected value. For example, the numerical results of FFRF-AB under \(0.5{\upmu \textrm{s}}\) and \(0.25{\upmu \textrm{s}}\) are close to each other, whereas the numerical result of FFRF-AB under \(0.6{\upmu \textrm{s}}\) goes numerically infinite. For calculations in this work, the selected time step size \(\mathrm{{\Delta }} t\) satisfies: if the numerical result is convergent under time step size \(\mathrm{{\Delta }} t\), then the result under \(\mathrm{{\Delta }} t / 2\) is also convergent and close to result under \(\mathrm{{\Delta }} t\); if the numerical result is divergent under time step size \(\mathrm{{\Delta }} t\), then the result under \(\mathrm{{\Delta }} t / 10\) is also divergent. Comparing the six methods, the selected time step size of ANCF-CD is the largest. Mathematically, the optimal time step size is subject to eigenvalues of the generalized amplification matrix [8].
When the rotational speed changes to \({\dot{\varphi }}_2\), the free end deflections obtained by different methods are shown in Fig. 6. As the same as under \({\dot{\varphi }}_1\), the value of deflection gradually goes convergent along with the increase of time; for all finite element methods, the results of linear methods are close to each other, the results of nonlinear methods are close to each other, whereas the results of linear methods are different to nonlinear methods. Different from \({\dot{\varphi }}_1\), the two transverse deflections of nonlinear method are much smaller than linear method; for example, the orthogonal transverse deflection of TLF-CD is \(91.8\%\) smaller than FFRF-AB, the transverse deflection along z axis of TLF-CD is \(72.9\%\) smaller than FFRF-AB. Comparing results under \({\dot{\varphi }}_2\) with \({\dot{\varphi }}_1\), the two transverse deflections, respectively, increase by \(118.7\%\) and \(8.28\%\) for FFRF-AB, the two transverse deflections, respectively, decrease by \(79.6\%\) and \(67.8\%\) for TLF-CD. This means the transverses stiffness decreases for linear methods and increases for nonlinear methods, when speed increases from \({\dot{\varphi }}_1\) to \({\dot{\varphi }}_2\).
When the rotational speed changes to \({\dot{\varphi }}_3\), the free end deflections obtained by different methods are shown in Fig. 7. As the same as under \({\dot{\varphi }}_1\) and \({\dot{\varphi }}_2\), the results of linear methods are close to each other, the results of nonlinear methods are close to each other, whereas the results of linear methods are different to nonlinear methods. Different from \({\dot{\varphi }}_1\) and \({\dot{\varphi }}_2\), the value of deflection only goes convergent for nonlinear methods, the value of deflection goes divergent for linear methods. The Table 2 shows convergent deflections of TLF-CD under three different rotational speeds: longitudinal deflection increases and transverse deflection decreases, along with increase of rotational speed. Due to the centrifugal force is proportional to square of rotational speed, the longitudinal deflection of TLF-CD under \({\dot{\varphi }}_2\) and \({\dot{\varphi }}_3\) are, respectively, approximately 25 times and 100 times that under \({\dot{\varphi }}_1\). In comparison with \({\dot{\varphi }}_2\), the two transverse deflections of nonlinear methods under \({\dot{\varphi }}_3\) further decrease and it means the transverse stiffness further increases for nonlinear methods.
The reasons of deflection divergence for FFRF-AB and GCMS-AB are explained separately. As the kinematic and strain analysis approaches of LEBB-AB are the same as FFRF-AB, the explanations of deflection divergence are the same for LEBB-AB and FFRF-AB. For these two methods, the reference coordinate vector \(\varvec{q}_\mathrm{{r}}\) is well constrained according to constant rotational speed, then the deflection divergence is explained by only elastic vibration equations in system dynamic equation. Taking LEBB-AB for example, the corresponding elastic vibration equations are given by
According to formulas in “Appendix,” the above equations are simplified as
where \({\dot{\varphi }}\) is constant rotational speed, \(\varvec{M}_{\mathrm{{rr}}6}\) is obtained by assembling \(\varvec{M}_{\mathrm{{rr}}6e}\), \(\varvec{M}_{\mathrm{{rf}}3}\) is obtained by assembling \(\varvec{M}_{\mathrm{{rf}}3e}\), \(\varvec{M}_{\mathrm{{rr}}2(,1)}\) is the first column of \(\varvec{M}_{\mathrm{{rr}}2}\).
The matrix \({\varvec{M}_{\mathrm{{rf}}3}}\) is skew symmetric, so the damping matrix \(- 2 \cdot \dot{\varphi }\cdot {\varvec{M}_{\mathrm{{rf}}3}}\) is also skew symmetric; numerical result shows matrix \({\varvec{M}_{\mathrm{{rr}}6}}\) is positive definite, so the stiffness matrix \(- {{\dot{\varphi }}^2} \cdot {\varvec{M}_{\mathrm{{rr}}6}}\) is negative definite; the load vector \({\varvec{Q}_\mathrm{{e}}}\) becomes constant after incremental phase and the load vector \({{\dot{\varphi }} ^2} \cdot {\varvec{M}_{\mathrm{{rr}}2(,1)}}\) is constant, so the solution of above linear system mainly depends on its free-vibration response. Along with the increase of rotational speed \(\dot{\varphi }\), the total damping matrix \({\varvec{D}_{\mathrm{{ff}}}} - 2 \cdot \dot{\varphi }\cdot {\varvec{M}_{\mathrm{{rf}}3}}\) and the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\varvec{M}_{\mathrm{{rr}}6}}}\) change, the roots of the characteristic equation [60] of above linear system also change. Once there emerges at least one root with positive real part or at least one multiple purely imaginary root in the characteristic equation, the solution of linear system in Eq. (59) goes divergent. This explains the deflection divergence for LEBB-AB as well as FFRF-AB; also it can be used to explain the decrease of transverses stiffness for LEBB-AB and FFRF-AB, when speed increases from \({\dot{\varphi }}_1\) to \({\dot{\varphi }}_2\).
As for GCMS-AB, the corresponding elastic vibration equations are given by
Due to the rotational speed is constant, the acceleration of reference coordinate vector \({\ddot{\varvec{q}}}_\mathrm{{r}}\) is periodic, and the matrix \({\varvec{A}_\mathrm{{d}}} \cdot \dot{\varvec{A}}_\mathrm{{d}}^\mathrm{{T}}\) is constant. Besides, after incremental phase, the external force vector \(\varvec{Q}_\mathrm{{e}}\) of centerline load along z direction is constant. So, different to the linear system in Eq. (59), the above equation forms a parametrically excited nonlinear system with finite DOF [61], of which the time-varying part of stiffness matrix has periodic form \({\varvec{A}_\mathrm{{d}}} \cdot {\varvec{K}_\mathrm{{L}}} \cdot \varvec{A}_\mathrm{{d}}^\mathrm{{T}}\). In view of the equivalence between GCMS and FFRF, this type of parametrically excited nonlinear system can be equivalent to linear system, so as to analyze the convergence and Lyapunov stability of its solution. Take the following nonlinear system with two DOFs as an example
where \({\varvec{u}_{\mathrm{{fs}}}} = {\left[ {\begin{array}{cc} {{u_{\mathrm{{fs}}1}}}&{{u_{\mathrm{{fs}}2}}} \end{array}} \right] ^\mathrm{{T}}}\), \({\varvec{K}_\mathrm{{L}}} = \mathrm{{diag}}({K_{\mathrm{{L}}1}},{K_{\mathrm{{L}}2}})\), \({K_{\mathrm{{L}}1}}> {K_{\mathrm{{L}}2}} > 0\), matrix \(\tilde{\varvec{A}}\) is periodic and \(\dot{\varphi }\) is constant.
With variable replacement \({\varvec{U}_{\mathrm{{fs}}}} = {{\tilde{\varvec{A}}}^\mathrm{{T}}} \cdot {\varvec{u}_{\mathrm{{fs}}}}\), the above nonlinear system is equivalent to following linear system
where \({\mathbf{{G}}_3} = \left[ {\begin{array}{cc} {0{}}&{}{1}\\ { - 1{}}&{}{0} \end{array}} \right] \), \(\mathbf{{I}}_2\) is \(2 \times 2\) identity matrix.
The root \(\iota \) of the characteristic equation for above linear system is given by
Once the damping matrix \(- 2 \cdot \dot{\varphi }\cdot {\mathbf{{G}}_3}\) and the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) are given, the root obtained by above equation is constant, the stability for all solutions of Eq. (62) keeps the same. The following only considers the stability of zero equilibrium position:
-
1.
\({{\dot{\varphi }}^2} > {K_{\mathrm{{L}}1}}\). In this case, the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is negative definite, all the four roots of \(\iota \) are purely imaginary, and there is no multiple root. Consequently, there is only oscillation function in the solution of Eq. (62), and the zero equilibrium position of Eq. (61) is stable.
-
2.
\({K_{\mathrm{{L}}2}}< {{\dot{\varphi }}^2} < {K_{\mathrm{{L}}1}}\). In this case, the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is indefinite, two roots of \(\iota \) are purely imaginary and two roots of \(\iota \) are purely real, and one of the purely real root is positive. Consequently, there emerges exponentially increasing function in the solution of Eq. (62), the zero equilibrium position of Eq. (61) is unstable.
-
3.
\({{\dot{\varphi }}^2} < {K_{\mathrm{{L}}2}}\). In this case, the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is positive definite, all the four roots of \(\iota \) are purely imaginary, there is no multiple root. Consequently, there is only oscillation function in the solution of Eq. (62), the zero equilibrium position of Eq. (61) is stable.
-
4.
\({{\dot{\varphi }}^2} = {K_{\mathrm{{L}}1}}\). In this case, the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is positive semi-definite, all the four roots of \(\iota \) are purely imaginary, two of them are equal to zero and are multiple purely imaginary root. Consequently, there emerges polynomially increasing function in the solution of Eq. (62), the zero equilibrium position of Eq. (61) is unstable.
-
5.
\({{\dot{\varphi }}^2} = {K_{\mathrm{{L}}2}}\). For the similar reason in case 4, the zero equilibrium position of Eq. (61) is unstable.
In summary, the necessary and sufficient condition of zero equilibrium position stability for Eq. (61) is \({{\dot{\varphi }}^2} < {K_{\mathrm{{L}}2}}\) or \({{\dot{\varphi }}^2} > {K_{\mathrm{{L}}1}}\); the necessary and sufficient condition of zero equilibrium position instability for Eq. (61) is \({K_{\mathrm{{L}}2}} \le {{\dot{\varphi }}^2} \le {K_{\mathrm{{L}}1}}\). In other words, the zero equilibrium position of Eq. (61) or Eq. (62) is stable if the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is positive definite or negative definite; the zero equilibrium position of Eq. (61) or Eq. (62) is unstable if the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is positive semi-definite or indefinite.
For comparison, the stability condition of zero equilibrium position for following undamped linear system is derived
The zero equilibrium position of above equation is stable if the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is positive definite; the zero equilibrium position of above equation is unstable if the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is positive semi-definite, indefinite or negative definite. This means although the damping dissipation rate \(- 2 \cdot \dot{\varphi }\cdot {{\dot{\varvec{U}}}^\mathrm{{T}}_{\mathrm{{fs}}}} \cdot {\mathbf{{G}}_3} \cdot {{\dot{\varvec{U}}}_{\mathrm{{fs}}}}\) is always equal to zero, the skew symmetric damping matrix \(- 2 \cdot \dot{\varphi }\cdot {\mathbf{{G}}_3}\) can change the solution stability when the total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot {\mathbf{{I}}_2}}\) is negative definite.
4.2 Comparison of computational efficiency
For all the calculations in this section, the rotational speed is \({\dot{\varphi }}_1\), the damping coefficient is \(c_3\) and the time step size is \(0.02{\upmu \textrm{s}}\). At first, the efficiencies of different finite element methods are compared; next, the influence of system invariant matrix on computational efficiency is analyzed.
In order to compare the efficiency of different methods, the solver of system dynamic equation is selected as AB for all the six finite element methods. Although the time step size and solver may be different from Sect. 4.1, the deflection result of each finite element method is close to that in Sect. 4.1 and not repeated in this section. Table 3 compares the preprocessing time and the solving time for different finite element methods, where the solving time just means the time cost of \(1 \times 10^4\) time step iterations. This table also shows the DOF of different finite element methods, where the DOF of FFRF-AB and GCMS-AB is the DOF after modal order reduction. The computer running the code is a PC with AMD Ryzen 5 4500U and 16 G RAM.
For FFRF-AB, the preprocessing includes: mesh generation, calculation of elastic mass matrix and stiffness matrix, calculation of inertia shape integrals, calculation of eigenmode, modal order reduction, initialization. In comparison with FFRF-AB, the preprocessing of GCMS-AB does not include calculation of inertia shape integrals. For TLF-AB and ANCF-AB, the preprocessing includes: mesh generation, calculation of mass matrix and linear stiffness matrix, calculation of system invariant matrix, initialization. For LEBB-AB, the preprocessing includes: mesh generation, calculation of elastic mass matrix and stiffness matrix, calculation of inertia shape integrals, initialization. In comparison with LEBB-AB, the preprocessing of NEBB-AB additionally includes calculation of system invariant matrix.
In all the six finite element methods, the GCMS-AB holds the minimum solving time cost, although it holds the second largest preprocessing time cost; the LEBB-AB holds the minimum preprocessing time cost and its solving time cost is also not very large. This means: In the case that geometric nonlinearity is not obvious, the GCMS-AB is the best choice for long time simulation, the LEBB-AB is the best choice for short time simulation. The TLF-AB holds the maximum solving time cost, and this is because the TLF-AB holds the largest DOF and our code implementation is serial but not parallel [31]. In all the three geometrically nonlinear methods, the NEBB-AB simultaneously holds the minimum preprocessing time and the minimum solving time. This means: In the case of both small deformation and obvious geometric nonlinearity, the NEBB-AB is the best choice for simulation.
Subsequently, the influence of system invariant matrix on the three geometrically nonlinear methods is analyzed, where the solver of system dynamic equation is CD for TLF and ANCF, AB for NEBB. When the system invariant matrix is not used for TLF-CD, the nonlinear element stiffness matrix in Eq. (33) is calculated as follows
Because matrix \(\varvec{K}_{\mathrm{{N}}e}\) is time-varying, in each time step, it is firstly necessary to calculate \(\varvec{K}_{\mathrm{{N}}e}\) by integration over element volume, and secondly, assembling from \(\varvec{K}_{\mathrm{{N}}e}\) to \(\varvec{K}_\mathrm{{N}}\) is needed. The corresponding time costs with and without using system invariant matrix under different element number are shown in Table 4. From the table, under different number of elements, the solving time of using system invariant matrix is smaller than not using, by at least an order of magnitude; the preprocessing time of using system invariant matrix is larger than not using, due to the extra calculation of system invariant matrix. There are more efficient implementations of TLF in [8] and [62] which are regretfully not adopted in this work, so our efficiency comparison conclusion about TLF is restricted as mentioned in the introduction.
For NEBB-AB, when the system invariant matrix is not used, the nonlinear element stiffness matrix in Eq. (48) is calculated as follows
where \(\varvec{B}_\mathrm{{N}}\) is calculated according to Eq. (45) but not Eq. (46).
As the same as TLF-CD, in each time step, the element integration and assembly are needed for NEBB-AB, when system invariant matrix is not used. The corresponding time costs with and without using system invariant matrix under different element number are shown in Table 5. From the table, under different number of elements, the solving time of using system invariant matrix is just a little smaller than not using. This is because the time cost for calculation of inertia force is much higher than that of elastic force in NEBB-AB, and the system invariant matrix method can just reduce time cost for calculation of elastic force and then only influence computational efficiency slightly.
For ANCF-CD, the preprocessing time and solving time are compared between system invariant matrix method and element invariant matrix method. The corresponding time costs under different number of elements are shown in Table 6. From the table, the adoption of system invariant matrix improves the calculation efficiency by at least an order of magnitude, under different number of elements. In comparison with the last row of Table 3, the solving time at the fourth row of Table 6 is obviously smaller, and this is caused by the difference between AB and CD.
On the whole, the efficiency comparison conclusion in this section is only valid for our implementation of different finite element methods, under the rotating flexible beam example. Making absolute conclusion of computational efficiency comparison is difficult, the three main reasons are: different methods have different advantages and applicabilities, the code implementation is limited, the DOFs of different methods are not equal. Taking the first reason for example, there is no need to select the same solver and the same time step size for all finite element methods. If the ANCF-AB in Table 3 is replaced by ANCF-CD in Table 6, the most efficient geometrically nonlinear method changes to ANCF-CD but not NEBB-AB. Meanwhile, the ANCF-CD holds the largest time step size \(1.7{\upmu \textrm{s}}\) as shown in Sect. 4.1, and this further enhances efficiency advantages of ANCF-CD. Actually, the ANCF-CD holds the highest computational efficiency for calculations in Sect. 4.1.
As for the reason about code implementation limitation, there exist plenty of unused theories and techniques to further improve efficiency, such as parallel computation for multilevel decomposition approach [63], preconditioning of generalized component modes [2], nodal-based treatment of FFRF [11], nonlinear reduced order model [56], implicit solver of system dynamic equation by analytical calculation of Jacobian matrix [47]. The efficiency comparison conclusion may be different, if these theories and techniques are implemented in code.
4.3 Results under different dampings
This section analyzes the influence of linear internal damping on numerical result. For the six finite element methods, the adopted damping model calculates internal damping force by velocity of relative coordinate for deformation. Due to the deformation is also measured by relative coordinate for FFRF, LEBB and NEBB, the adoption of this damping model is spontaneous [5, 64]. However, due to the relative coordinate is not employed for GCMS, TLF and ANCF, the adoption of this damping model is not as previously spontaneous. This section only focuses on the damping influence analysis for GCMS, TLF and ANCF. In all the calculations of this section, the time step sizes are, respectively, 0.1 µs, 0.5 µs, 1.7 µs for GCMS-AB, TLF-CD and ANCF-CD.
At first, the influence of damping coefficient is analyzed. Under rotational speed \({\dot{\varphi }}_1\) and different damping coefficients, the orthogonal transverse deflections obtained by GCMS-AB, TLF-CD and ANCF-CD are shown in Fig. 8. The longitudinal deflection and transverse deflection along z axis are not shown for narrative conciseness. By comparison, two conclusions are obtained for all the three finite element methods: deflection oscillation is more obvious under smaller damping coefficient; the convergent value of deflection keeps the same under different damping coefficients. Under rotational speed \({\dot{\varphi }}_3\) and different damping coefficients, the orthogonal transverse deflections obtained by GCMS-AB, TLF-CD and ANCF-CD are shown in Fig. 9. As the same as under rotational speed \({\dot{\varphi }}_1\), two same conclusions are obtained for TLF-CD and ANCF-CD. From Fig. 9a, the larger damping coefficient decelerates the deflection divergence for GCMS-AB. The deceleration of deflection divergence partly relies on the smaller Coriolis force: There is no initial deformation, and then the centrifugal force will cause longitudinal deformation and the velocity of longitudinal deformation is smaller under larger damping coefficient; because the rotational speed is unchanged, the smaller Coriolis force occurs under larger damping coefficient and causes smaller absolute value of orthogonal transverse deflection.
For GCMS, TLF and ANCF, although it is more spontaneous to calculate internal damping force by velocity of absolute coordinate for deformation, the following numerical result shows this will cause different deflection result in comparison with velocity of relative coordinate. If the internal damping force is calculated by velocity of absolute coordinate for deformation, then the damping force vector of GCMS becomes
where \(\varvec{D}\) is obtained by assembling \(\varvec{D}_e\), \(\varvec{D}_e\) is the same as Eq. (23).
The damping force vector of TLF becomes
where \(\varvec{D}\) is obtained by assembling \(\varvec{D}_e\), \(\varvec{D}_e\) is the same as Eq. (34).
The damping force vector of ANCF becomes
where \(\varvec{D}\) is obtained by assembling \(\varvec{D}_e\), \(\varvec{D}_e\) is the same as Eq. (56).
By above three equations, the deflection of the rotating flexible beam is calculated. Under rotational speed \({\dot{\varphi }}_1\) and different damping coefficients, the orthogonal transverse deflections obtained by GCMS-AB, TLF-CD and ANCF-CD are shown in Fig. 10. By comparison, for all the three finite element methods, the convergent value of deflection slightly decreases along with the increase of damping coefficients. Under the rotational speed \({\dot{\varphi }}_3\) and different damping coefficients, the orthogonal transverse deflections obtained by GCMS-AB, TLF-CD and ANCF-CD are shown in Fig. 11. By comparison, the absolute value of convergent deflection increases along with the increase of damping coefficients, for TLF-CD and ANCF-CD; the larger damping coefficient decelerates the deflection divergence for GCMS-AB.
In Figs. 10 and 11, the convergent value of deflection changes under different damping coefficients, and this means external damping is caused if damping force is calculated by velocity of absolute coordinate for deformation. In order to eliminate the influence of external damping, it is necessary to calculate damping force according to velocity of relative coordinate for deformation, rather than velocity of absolute coordinate for deformation.
5 Conclusions
Taking a rotating flexible beam as example, the numerical results of six different finite element methods are compared, under assumptions of straight beam, small deformation and fixed axis rotation. When the rotational speed becomes very large, the deflection results of FFRF-AB, GCMS-AB and LEBB-AB become divergent due to ignorance of geometric nonlinearity effect, the transverse stiffnesses of TLF-CD, NEBB-AB and ANCF-CD become higher due to geometric nonlinearity effect.
For a special type of nonlinear system, of which the time-varying part of stiffness matrix has periodic form \({\varvec{A}_\mathrm{{d}}} \cdot {\varvec{K}_\mathrm{{L}}} \cdot \varvec{A}_\mathrm{{d}}^\mathrm{{T}}\), it is equivalent to linear system to analyze the Lyapunov stability of its solution. With regard to the nonlinear system example with two DOFs, the stability of its zero equilibrium position is dependent on the definiteness of total stiffness matrix \({{\varvec{K}_\mathrm{{L}}} - {{\dot{\varphi }}^2} \cdot \mathbf{{I}_2}}\). The nonlinear system example also shows the damping may still change the solution stability, although the damping dissipation rate is equal to zero.
With the same solver of system dynamic equation, the GCMS-AB holds the minimum solving time cost of \(1 \times 10^4\) time step iterations. For NEBB-AB, the efficiency improvement by adoption of system invariant matrix is slight, due to the proportion of elastic force calculation in total time cost of NEBB-AB is very small. For ANCF-CD, the adoption of system invariant matrix improves the computational efficiency by at least an order of magnitude, in comparison with adoption of element invariant matrix. Among six finite element methods, the ANCF-CD is optimal for the authors because of its highest efficiency in the rotating flexible beam example.
For GCMS-AB, TLF-CD and ANCF-CD, the convergent value of deflection keeps the same under different damping coefficients. Although the deformation is measured by absolute coordinate for GCMS-AB, TLF-CD and ANCF-CD, it is not suitable to calculate internal damping force by velocity of absolute coordinate for deformation. The reason is that external damping will be caused if velocity of absolute coordinate for deformation is adopted to calculate damping force.
Data availability
The presented methods are implemented in C++, and the results of numerical examples can be replicated on the basis of supplementary material.
References
Ziegler, P., Eberhard, P.: Simulative and experimental investigation of impacts on gear wheels. Comput. Methods Appl. Mech. Eng. 197, 4653–4662 (2008)
Zwölfer, A., Gerstmayr, J.: Preconditioning strategies for linear dependent generalized component modes in 3D flexible multibody dynamics. Multibody Syst. Dyn. 47, 65–93 (2019)
Thube, S.V., Bobak, T.R.: Dynamic Analysis of a Cycloidal Gearbox Using Finite Element Method. AGMA Technical Paper, Virginia (2012)
Hastings, G.G., Book, W.J.: A linear dynamic model for flexible robotic manipulators. IEEE Contr. Syst. Mag. 7, 61–64 (1987)
Yang, H., Hong, J., Yu, Z.: Dynamics modelling of a flexible hub-beam system with a tip mass. J. Sound Vib. 266, 759–774 (2003)
Bayoumy, A.H., Nada, A.A., Megahed, S.M.: A continuum based three-dimensional modeling of wind turbine blades. J. Comput. Nonlinear Dyn. 8, 031004 (2013)
Shabana, A.A.: Dynamics of Multibody Systems. Cambridge University Press, Cambridge (2005)
Belytschko, T., Liu, W.K., Moran, B., Elkhodary, K.I.: Nonlinear Finite Elements for Continua and Structures. Wiley, Chiechester (2014)
Likins, P.W.: Finite element appendage equations for hybrid coordinate dynamic analysis. Int. J. Solids Struct. 8, 709–731 (1972)
Pechstein, A., Reischl, D., Gerstmayr, J.: A generalized component mode synthesis approach for flexible multibody systems with a constant mass matrix. J. Comput. Nonlinear Dyn. 8, 011019 (2013)
Zwölfer, A., Gerstmayr, J.: The nodal-based floating frame of reference formulation with modal reduction. Acta. Mech. 232, 835–851 (2021)
Orzechowski, G., Matikainen, M.K., Mikkola, A.M.: Inertia forces and shape integrals in the floating frame of reference formulation. Nonlinear Dyn. 88, 1953–1968 (2017)
Huang, G., Zhu, W., Yang, Z., Feng, C., Chen, X.: Reanalysis-based fast solution algorithm for flexible multi-body system dynamic analysis with floating frame of reference formulation. Multibody Syst. Dyn. 49, 271–289 (2020)
Schilder, J., Dwarshuis, K., Ellenbroek, M., de Boer, A.: The tangent stiffness matrix for an absolute interface coordinates floating frame of reference formulation. Multibody Syst. Dyn. 47, 243–263 (2019)
Cammarata, A., Pappalardo, C.M.: On the use of component mode synthesis methods for the model reduction of flexible multibody systems within the floating frame of reference formulation. Mech. Syst. Signal Process. 142, 106745 (2020)
Shabana, A.A., Wang, G.: Durability analysis and implementation of the floating frame of reference formulation. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 232, 295–313 (2018)
Gerstmayr, J., Schöberl, J.: A 3D finite element method for flexible multibody systems. Multibdody Syst. Dyn. 15, 309–324 (2006)
Gerstmayr, J., Ambrósio, J.A.C.: Component mode synthesis with constant mass and stiffness matrices applied to flexible multibody systems. Int. J. Numer. Methods Eng. 73, 1518–1546 (2008)
Ziegler, P., Humer, A., Pechstein, A., Gerstmayr, J.: Generalized component mode synthesis for the spatial motion of flexible bodies with larger rotations about one axis. J. Comput. Nonlinear Dyn. 11, 041018 (2016)
Lin, T., Peng, Q., Liu, W., Chen, B.: Centrifugal stiffening analysis of gear pair with generalized component mode synthesis and semi-analytic contact technique. Meccanica 55, 567–579 (2020)
Zienkiewicz, O.C., Taylor, R.L.: The Finite Element Method. Elsevier Butterworth-Heinemann, Oxford (2005)
Kee, Y.J., Shin, S.J.: Structural dynamic modeling for rotating blades using three dimensional finite elements. J. Mech. Sci. Technol. 29, 1607–1618 (2015)
Kim, Y.S., Cho, J.R.: Numerical analysis of rollover and head-on crash response of non-step bus. Int. J. Mod. Phy. B 22, 1736–1741 (2008)
Tang, S.C., Pan, J.: Mechanics Modeling of Sheet Metal Forming. SAE International, Warrendale (2007)
Taylor, Z.A., Cheng, M., Ourselin, S.: High-speed nonlinear finite element analysis for surgical simulation using graphics processing units. IEEE Trans. Med. Imaging 27, 650–663 (2008)
Joldes, G.R., Wittek, A., Miller, K.: Real-time nonlinear finite element computations on GPU - Application to neurosurgical simulation. Comput. Methods Appl. Mech. Eng. 199, 3305–3314 (2010)
Laiarinandrasana, L., Piques, R., Robisson, A.: Visco-hyperelastic model with internal state variable coupled with discontinuous damage concept under total Lagrangian formulation. Int. J. Plasticity 19, 977–1000 (2003)
Siqueira, T.M., Coda, H.B.: Total Lagrangian FEM formulation for nonlinear dynamics of sliding connections in viscoelastic plane structures and mechanisms. Finite Elem. Anal. Des. 129, 63–77 (2017)
Castañar, I., Baiges, J., Codina, R.: A stabilized mixed finite element approximation for incompressible finite strain solid dynamics using a total Lagrangian formulation. Comput. Methods Appl. Mech. Eng. 368, 113164 (2020)
Tojaga, V., Hazar, S., Östlund, S.: Compressive failure of fiber composites containing stress concentration: homogenization with fiber-matrix interfacial decohesion based on a total Lagragian formulation. Compos. Sci. Technol. 182, 107758 (2019)
Zhang, X., Wang, T., Liu, Y.: Computational Dynamics. Tsinghua University Press, Beijing (2015)
Liu, Z., Liu, J.: Experimental validation of rigid-flexible coupling dynamic formulation for hub-beam system. Multibody Syst. Dyn. 40, 303–326 (2017)
Wang, G., Qi, Z., Xu, J.: A high-precision co-rotational formulation of 3D beam elements for dynamic analysis of flexible multibody systems. Comput. Methods Appl. Mech. Eng. 360, 112701 (2020)
Sun, Q.: An existence condition for the inverse dynamics solution of a slewing Euler-Bernoulli beam. Mech. Mach. Theory 46, 845–860 (2011)
Lu, J., Sun, X., Vakakis, A.F., Bergman, L.A.: Influence of backlash in gear reducer on dynamic of single-link manipulator arm. Robotica 33, 1671–1685 (2015)
Kim, K., Ri, K., Yun, C., Pak, C., Han, P.: Nonlinear forced vibration analysis of composite beam considering internal damping. Nonlinear Dyn. 107, 3407–3423 (2022)
Mayo, J., Dominguez, J., Shabana, A.A.: Geometrically nonlinear formulations of beams in flexible multibody dynamics. J. Vib. Acoust. 117, 501–509 (1995)
Liu, Z., Hong, J., Liu, J.: Finite element formulation for dynamics of planar flexible multi-beam system. Multibody Syst. Dyn. 22, 1–26 (2009)
Zhao, G., Wu, Z.: Coupling vibration analysis of rotating three-dimensional cantilever beam. Comput. Struct. 179, 64–74 (2017)
Torteman, B., Kessler, Y., Liberzon, A., Krylov, S.: Micro-beam resonator parametrically excited by electro-thermal Joule’s heating and its use as a flow sensor. Nonlinear Dyn. 98, 3051–3065 (2019)
Wang, L., Peng, J., Zhang, X., Qiao, W., He, K.: Nonlinear resonant response of the cable-stayed beam with one-to-one internal resonance in veering and crossover regions. Nonlinear Dyn. 103, 115–135 (2021)
Shabana, A.A., Yakoub, R.Y.: Three dimensional absolute nodal coordinate formulation for beam elements: Theory. J. Mech. Des. 123, 606–613 (2001)
Yakoub, R.Y., Shabana, A.A.: Three dimensional absolute nodal coordinate formulation for beam elements: implementation and applications. J. Mech. Des. 123, 614–621 (2001)
Gerstmayr, J., Matikainen, M.K., Mikkola, A.M.: A geometrically exact beam element based on the absolute nodal coordinate formulation. Multibody Syst. Dyn. 20, 359–384 (2008)
Obrezkov, L.P., Mikkola, A., Matikainen, M.K.: Performance review of locking alleviation methods for continuum ANCF beam elements. Nonlinear Dyn. 109, 531–546 (2022)
Patel, M., Shabana, A.A.: Locking alleviation in the large displacement analysis of beam elements: the strain split method. Acta. Mech. 229, 2923–2946 (2018)
Shen, Z., Li, P., Liu, C.: A finite element beam model including cross-section distortion in the absolute nodal coordinate formulation. Nonlinear Dyn. 77, 1019–1033 (2014)
Vallejo, D.G., Mikkola, A.M., Escalona, J.L.: A new locking-free shear deformable finite element based on absolute nodal coordinates. Nonlinear Dyn. 50, 249–264 (2007)
Vallejo, D.G., Mayo, J., Escalona, J.L., Domínguez, J.: Efficient evaluation of the elastic forces and the Jocobian in the absolute nodal coordinate formulation. Nonlinear Dyn. 35, 313–329 (2004)
Dibold, M., Gerstmayr, J., Irschik, H.: A detailed comparison of the absolute nodal coordinate and the floating frame of reference formulation in deformable multibody systems. J. Comput. Nonlinear Dyn. 4, 021006 (2009)
Vallejo, D.G., Valverde, J., Domínguez, J.: An internal damping model for the absolute nodal coordinate formulation. Nonlinear Dyn. 42, 347–369 (2005)
Inman, D.J.: Engineering Vibration. Pearson, Essex (2014)
Greenwood, D.T.: Advanced Dynamics. Cambridge University Press, Cambridge (2003)
Wriggers, P.: Computational Contact Mechanics. Springer, Berlin (2006)
Wang, X.: Finite Element Method. Tsinghua University Press, Beijing (2003)
Mahdiabadi, M.K., Tiso, P., Brandt, A., Rixen, D.J.: A non-intrusive model-order reduction of geometrically nonlinear structural dynamics using modal derivatives. Mech. Syst. Signal Process. 147, 107126 (2021)
Lee, J.W., Kim, H.W., Ku, H.C., Yoo, W.S.: Comparison of external damping models in a large deformation problem. J. Sound Vib. 325, 722–741 (2009)
Sauer, T.: Numerical Analysis. Pearson, Boston (2012)
LSTC: LS-DYNA Theory Manual. LSTC, Livermore (2014)
Rao, S.S.: Mechanical Vibrations. Pearson, Harlow (2018)
Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley, Weinheim (2004)
Zhang, J.: A direct Jacobian total Lagrangian explicit dynamics finite element algorithm for real-time simulation of hyperelastic materials. Int. J. Numer. Methods Eng. 122, 5744–5772 (2021)
Li, P., Liu, C., Tian, Q., Hu, H., Song, Y.: Dynamics of a deployable mesh reflector of satellite antenna: parallel computation and deployment simulation. J. Comput. Nonlinear Dyn. 11, 061005 (2016)
Liu, J., Pan, K.: Rigid-flexible-thermal coupling dynamic formulation for satellite and plate multibody system. Aerosp. Sci. Technol. 52, 102–114 (2016)
Acknowledgements
The authors gratefully acknowledge the open-source library Eigen (http://eigen.tuxfamily.org/index.php?title=Main_Page) from eigenproject team and the open source library Spectra (http://spectralib.org/index.html) from Yixuan Qiu.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. The first draft of the manuscript was written by Quancheng Peng, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix
Appendix
where \(q_{ei}\) is the i-th component of vector \(\varvec{q}_e\).
where \(W_{\mathrm{{f}}ei}\) is the i-th component of vector \(\varvec{W}_{\mathrm{{f}}e}\), \({\varvec{H}_{\mathrm{{f}}ei}} = \frac{{\partial {\varvec{W}_{\mathrm{{f}}e}}}}{{\partial {W_{\mathrm{{f}}ei}}}}\).
where \(q_{\mathrm{{r}}i}\) is the i-th component of vector \(\varvec{q}_\mathrm{{r}}\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Peng, Q., Li, M. Comparison of finite element methods for dynamic analysis about rotating flexible beam. Nonlinear Dyn 111, 13753–13779 (2023). https://doi.org/10.1007/s11071-023-08568-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-023-08568-7