Abstract
Since its original introduction in structural design, density-based topology optimization has been applied to a number of other fields such as microelectromechanical systems, photonics, acoustics and fluid mechanics. The methodology has been well accepted in industrial design processes where it can provide competitive designs in terms of cost, materials and functionality under a wide set of constraints. However, the optimized topologies are often considered as conceptual due to loosely defined topologies and the need of postprocessing. Subsequent amendments can affect the optimized design performance and in many cases can completely destroy the optimality of the solution. Therefore, the goal of this paper is to review recent advancements in obtaining manufacturable topology-optimized designs. The focus is on methods for imposing minimum and maximum length scales, and ensuring manufacturable, well-defined designs with robust performances. The overview discusses the limitations, the advantages and the associated computational costs. The review is completed with optimized designs for minimum compliance, mechanism design and heat transfer.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction to topology optimization
The topology optimization process aims at distributing a specified amount of material in a given design domain by minimizing an objective function and fulfilling a set of constraints. Here the focus is on density-based formulations which in general can be written as
where \(J\left( \rho , u\right) \) is an objective function (weight, material volume, mechanical compliance, displacements or velocities at a subdomain of the design domain), \(r\left( \rho ,u\right) =0\) represents the residual of the equations modeling the physical system with solution \(u\in {\mathcal {U}}_{\text {ad}}\), and \(\left\{ g_i\left( \cdot \right) \le 0, i=1,\dots , N_g\right\} \) is a set of constraints. The design domain is an open bounded domain in \({\mathbb {R}}^d\) with Lipschitz boundary \(\varGamma =\partial \varOmega \). The material density field is represented by a bounded function \(\rho \in L^\infty \left( \varOmega \right) \) and \(\rho _{\min } \le \rho \left( {\mathbf {x}}\right) \le \rho _{\max }, {\mathbf {x}}\in \varOmega \), i.e., \({\mathcal {D}}_{\text {ad}} =\left\{ \rho \in L^\infty \left( \varOmega \right) : \rho _{\min } \le \rho \left( {\mathbf {x}}\right) \le \rho _{\max }, {\mathbf {x}}\in \varOmega \right\} \). Usually, the upper bound is set to one and the lower bound to zero.
If the material density field is equal to one at a point in the design domain, the point is occupied with material. The material density field is equal to zero at the void regions. The discrete 0/1 problem is relaxed in order to utilize gradient-based optimization techniques, and the material density is allowed to take intermediate values. Such a relaxation requires some interpretation of the gray transition regions. Removing them in a postprocessing step might affect the optimality of the solution and might violate the design constraints. Hence, reviewing the techniques for avoiding the post processing step while obtaining well-performing and manufacturable designs close to 0/1 is the main goal of this article. The focus is on the so-called three-field density representation where the density field representing the design is obtained by a series of transformations in order to restrict the design space and ensure manufacturability of the design.
1.1 Interpolation schemes in topology optimization
The most popular problem in topology optimization is minimum compliance design originally formulated by Bendsøe and Kikuchi in [18]. The idea is to distribute material in a design domain in order to minimize the compliance of a mechanical system, and the material properties are obtained using a homogenization approach. Later, the so-called Simplified Isotropic Material with Penalization (SIMP) [17] approach has been introduced in order to reduce the complexity of the original homogenization formulation. The SIMP formulation has been utilized in many following papers to improve convergence to 0/1 solution, e.g., Zhou and Rozvany [167] and Mlejnek [106], and physical justification is presented later in [19]. For linear elasticity, SIMP relates the modulus of elasticity \(E\left( {\mathbf {x}}\right) , {\mathbf {x}}\in \varOmega \) and the material density field by the power law given as
where \(E_{\min }\) is taken to be a small value larger than zero in order to ensure existence of the solution of the linear elastic problem, \(E_0\) is the modulus of elasticity for the solid material, and p is a penalization parameter. For \(p=1\), the minimum compliance problem is convex and possesses a unique solution with large gray regions. Increasing the penalty parameter improves the contrast, and a value of \(p=3\) usually ensures good convergence to 0/1 designs. It should be pointed out that the penalization works only for problems with constraints which directly or indirectly limit the material volume.
The SIMP interpolation scheme results in zero gradients for all regions with zero density \(\rho =0\). An alternative scheme, the so-called Rational Approximation of Material Properties (RAMP) interpolation is proposed in the literature [129] and can be utilized for problems where SIMP is undesirable. For general discussion and comparison, the readers are referred to [130] and the recent review papers on topology optimization [37, 125]. Designs close to 0/1 can be obtained by tuning the parameters for the selected material optimization scheme. Recently, an interpolation scheme for nonlinear materials was proposed in [148] where the interpolation is performed between two material potentials rather than between two material properties. Such an interpolation avoids the numerical instabilities observed for optimization problems with large deformations.
Another alternative to the implicit penalization provided by SIMP or RAMP is to utilize explicit penalization of the intermediate values by adding the following term to the objective function, e.g., Allaire and Francfort [5] and Allaire and Kohn [9].
Explicit penalization is often utilized for wave propagation optimization problems [144] where the traditional interpolation schemes cannot penalize the intermediate values, e.g., Lazarov et al. [85]. The main difficulty consists in determining the penalization parameter \(\alpha \). The explicit penalization can be introduced to the optimization problem as a constraint. However, in this case, the difficulty for selecting \(\alpha \) is transferred to the selection of the constraint value. A variation of the explicit penalization is proposed in [22] where the density \(\rho \) in Eq. 6 is replaced with a density average which imposes a length scale on the design, however, with the same challenges in selecting \(\alpha \) as for the expression given by Eq. 6.
1.2 Discretization schemes
The optimization is performed iteratively using the so-called nested formulation, where at each optimization step the state problem is solved, the objective and the constraints are computed from the obtained state solution, the gradients of the objective and the constraints with respect to the parametrization of the design field are computed using adjoint analysis, and the design field is updated based on the gradients. The areas of applicability include problems in linear elasticity, heat transfer, fluid mechanics, vibrations, acoustics, electromagnetics and nanomechanics. The state problem can be discretized and solved using almost any of the available numerical methods for solving partial differential equations such as finite element method (FEM), finite volume (FV), finite difference (FD) and discontinuous Galerkin (DG-FEM).
The material density field usually follows the discretization of the state solvers. For a FEM discretization, the density field is mostly represented using constant values within each finite element. For a FD discretization, a constant value is associated with the cell surrounding each node. For FV and DG-FEM a constant value is often utilized for each control volume. The density field discretization can be decoupled from the discretization of the state problem [65] which might result in reduction of the optimization time.
1.3 Regularization in topology optimization
Minimizing the compliance of a structure using material density associated with each finite element results in two major issues: (1) mesh dependency and (2) checkerboard patterns. Mesh dependency can be observed by refining the design domain for a design obtained with a coarse mesh and running the optimization on the refined mesh. The optimization might converge to a completely different and more complex topology than the one obtained using the coarse mesh. Such problems are referred to as ill-posed in the mathematical literature since they do not posses a solution. Checkerboard patterns appear due to bad numerical properties of the discretization, and they do not represent optimal solutions [38, 76].
Existence of the solution is provided by regularizing the optimization problem, i.e., by restricting the solution space. A number of regularization schemes have been proposed in the literature: perimeter control [69], sensitivity filtering [122] and mesh-independent density filtering [23, 27]. Here the focus is on density filtering combined with subsequent transformations. For discussion of the other regularization techniques, the reader is referred to [125].
1.4 Alternative density-based approaches
Number of alternatives to the density-based approaches have been proposed in the research literature. The most popular of them is the level- set method, which utilizes a level-set function to represent the shape of the design [7, 8, 151]. Recent overview of different level-set methods can be found in [141] and comparison to density-based approaches in [125]. As outlined several times in [125], the projection-based three-field formulation which is in focus in this article becomes more and more similar to the level-set methods. Hence, many techniques developed for one of the approaches can often be easily transferred to the other one. Other alternatives include the topological derivative method [126], the phase field method [24] and evolutionary approaches [156].
2 Density filters
Density filtering in topology optimization can be written in the form of a convolution integral [23] given as

where \(\widetilde{\rho }\) is the filtered density field, \(\rho \) is the original design field and \( w\left( \cdot \right) \) is a weighting function. The different density filters differ mainly in their weighting functions. The weighting function for the classical density filter [23] is the Hat function given by
where the normalization factor \(w_w\) is obtained from the condition \(\int w\left( {\mathbf {x}}\right) \text {d}{\mathbf {x}}=1\). The support domain of the filter function \(B={\mathop {\mathrm{supp}}}\left( w\right) \) is circular in 2D and spherical in 3D with radius \(R_f\). The integral condition for determining the normalization factor ensures that the filter preserves as the total volume.
In general, the support domain can take any shape which will determine the properties of the projections discussed in the following section. For density filters with finite support domain, the design domain is extended by dilating it with the filter support, i.e., \(\varOmega ^*=\left\{ {\mathbf {x}}: {\mathbf {y}}\in \varOmega \wedge w\left( {\mathbf {x}}-{\mathbf {y}} \right) \ne 0\right\} \), where \(\varOmega ^*\) is the extended design domain. The values of the design field outside the design domain \(\rho \left( {\mathbf {x}}\right) , {\mathbf {x}}\in \varOmega ^* \setminus \varOmega \) can be either prescribed in order to ensure a particular behavior of the filtered field around the boundaries of \(\varOmega \), or they can be included in the optimization problem. Often the design domain is not extended, and in this case, the filter behavior around \(\partial \varOmega \) differs from the filter behavior in the interior of the design domain.
In [27], an exponential filter function is proposed which does not posses finite support. In this case, the function support can be truncated. Alternatively, some assumptions about the input design field outside the design domain have to be provided in advance. The convolution integral Eq. 8 is extended over \({\mathbb {R}}^d\), where \(d=2,3\) is the dimensionality of the problem.
An alternative to the convolution integral formulation, based on the solution of a partial differential equation (PDE), has been proposed first for sensitivity filtering in [86] and later extended to density filtering in [78, 92]. The idea is to obtain the filtered field as the solution of a PDE given as
The parameter \(r_f\left( {\mathbf {x}}\right) \) controls the effective width of the filter. It can be fixed or allowed to vary along the design domain. Larger \(r_f\) results in larger gray transition regions, and smaller \(r_f\) results in sharper transition between void and solid. The filter is volume-preserving for Neumann boundary conditions, \(\partial {\widetilde{\rho }}/{\partial {\mathbf {n}}}=0\) on \(\partial \varOmega \), where \({\mathbf {n}}\) is the outward normal to the design domain boundary. The main advantages compared to classical filters are the lower computational cost [2], the re-utilization of solvers developed for the state problems [92], relatively easy parallelization for large-scale problems [1], utilization of different filter parameters in different parts of the design domain, and the possibility of controlling the behavior of the filtered field without extending the design domain. The Neumann boundary conditions can be replaced with Dirichlet boundary conditions which prescribe exact boundary values for the filtered field [89]. The solution of the PDE can be expressed as the convolution of the input design field \(\rho \left( {\mathbf {x}}\right) \) and the Green’s functions [159] of the boundary value problem given by Eq. 9. The filter support domain coincides with the design domain. The computational cost of the PDE filter using multigrid solvers is \({\mathcal {O}}\left( n\right) \) [142].
A relation between the length parameter \(r_f\) in Eq. 9 and the filter radius \(R_f\) in Eq. 8 can be obtained by matching the second central moments of the Hat function and the Green’s function for the PDE filter on unbounded domain [92]. The condition leads to similar filter fields and gray levels. The length parameter \(r_f\) can be related to \(R_f\) as follows
Following the idea of state solver re-utilization in the filtering process, the implementation of topology optimization problems with transient behavior, e.g., Nomura et al. [109] would benefit from transient PDE filtering schemes. Based on regularization strategies utilized in image processing [16] a time-dependent nonlinear diffusion regularization scheme in topology optimization is proposed in [150] where the focus is mainly on reducing the gray transition regions by tuning the diffusion coefficient along the design edges. In [77], a time-dependent diffusion is utilized for regularizing a level-set like topology optimization formulation. State solver re-utilization and the parallelization benefits for density-based topology optimization of time-dependent problems in photonics are demonstrated in [44]. The filtered field is obtained as the solution \(\widetilde{\rho }\left( {\mathbf {x}},t\right) \) of the following diffusion equation
with prescribed boundary conditions and initial condition \(\widetilde{\rho }\left( t=0, {\mathbf {x}}\right) = \rho \left( {\mathbf {x}}\right) , {\mathbf {x}}\in \varOmega \). The solution can be represented in the form of Eq. 7, where the filter function is a Gaussian kernel [16]
with filter parameter \(\sigma \) which scales with time as \(\sigma =\sqrt{2 t}\).
The time-dependent heat equation as well as the PDE filter discussed above diffuses the design field in an isotropic manner. Anisotropic filters which favor a particular direction and stops information propagation in others can be obtained by replacing the scalar coefficients with tensor quantities. Anisotropic filtering can be achieved in the classical filter given by Eq. 7 by selecting weighting function with support different than circular.
In all cases, the filter acts as a low-pass filter to the original design field \(\rho \). For regular rectangular domains low-pass filtering can effectively be constructed by Fourier transform, e.g., Solomon and Breckon [127]. The idea is applied in density-based topology optimization in [87]. The design field \(\rho \left( {\mathbf {x}}\right) \) is transformed in the frequency domain using 1D, 2D or 3D discrete Fourier transform and then convoluted with a filter function. The filter function in this case is defined entirely in the frequency domain. The filter is given by the following three steps
where \({\mathcal {F}}\) denotes the Fourier transform and \({\mathcal {F}}_i\) its inverse. Practical realizations of the above filter benefit significantly from the tuned fast numerical implementations based on the fast Fourier transform (FFT). The appearance of artifacts around the boundaries of the design domain can be decreased by padding (extending) the domain with zeros. Extending the domain with patterns different than zero can control design field values around the borders of the design domain. Any postprocessing of the filtered design, e.g., finding derivatives of any order, can be easily performed in the frequency domain [139]. The larger freedom in constructing the filter weighting function in the frequency domain can be utilized for controlling the maximum length scale as well as the spacing between the solid and the void regions [87]. These aspects are discussed in Sect. 8.2.
The main limitation in utilizing FFT filters in topology optimization is the requirement for rectangular shape of the design domain. Irregular domains can be padded with zeros or prescribed patterns. Alternatively, an effective algorithm for calculating the convolution integral given by Eq. 7 can be based on the fast multipole method (FMM) [56]. Such a possibility remains to be investigated.
3 Projections
Gray regions always exist in the solution due to the relaxation of the original 0/1 problem. Penalization schemes can decrease their appearance to some extend; however, some postprocessing of the design might be necessary if the final goal of the optimization process is pure black and white design. Aiming at reducing the intermediate transition regions between solid and void, various alternative filtering schemes based on projections [60], on morphological operators [123] and more recently on Pythagorean means [134] have been proposed in the literature.
The projection scheme proposed in [60] can impose length scale either on the solid phase or on the void phase [123]. The idea is to filter the design field using filter with finite support and project all values of \(\widetilde{\rho }\) above 0–1. Such a projection step ensures that the smallest solid feature in the design will be equal or larger than the filter support, i.e., the solid design can be painted with a circle in 2D or a sphere in 3D with radius \(R_f\). The projection step is given as
where \(H\left( \cdot \right) \) is the Heaviside function. The Heaviside function is not differentiable; therefore, for gradient-based optimization, it is replaced with a parameter dependent expression
The above expression approaches the Heaviside function for \(\beta \rightarrow \infty \). Length scale on the void phase can be obtained by applying the Heaviside projection to \(1-\widetilde{\rho }\), i.e., the projected field is obtained as
In [123], so-called morphological operators [108] are applied as filters in topology optimization. The two basic morphological operators, erode and dilate, are defined originally for black and white images. The erode operator sets a point to zero if any point in the neighborhood covered by the filter support has zero value and one otherwise. The dilate operator sets a point to one if any point in the neighborhood covered by the filter support has value one and zero otherwise, i.e., the dilate operator deposits material along the perimeter of the design. For gray-scale images, the erode operator sets the value of a point to the maximal value in the neighborhood covered by the filter support and the dilate operator sets it to the minimum. The dilate operator is given as
and the erode operator is defined as
Both operators utilize Kreisselmeier–Steinhauser [83] approximation to the \(\min /\max \) operator.
Recently, an alternative definition of erode/dilate filters based on Pythagorean means has been proposed in [134]. The erode/dilate filters based on harmonic mean can be written in integral form as
where the parameter \(\beta \) controls the sharpness of the projection.
The above projections rely on the finite filter support to impose length scale on the optimized designs. The original Heaviside projection [60] projects the transition region to 0 and 1; however, due to the continuity of the projected field \(\widehat{\widetilde{\rho }}\), the transition from void to solid passes always through intermediate values. In [134], the Hat filter is replaced with uniform weights (constant value) inside the filter support. This provides sharper transition due to the allowance of discontinuities in the final design \(\widehat{\widetilde{\rho }}\). For well-penalized optimization problems, a constant filter results in sharp black and white designs; however, for problems where the objective benefits from the appearance of intermediate design values, the above projection techniques will result in gray in the final design. The projections do not penalize the designs. They only allow for sharper transition. These effects can be clearly observed on designs shown in Tables 3 and 4. Another important observation for the morphological filters is that they project to the min/max value within the filter support which is different than 0 or 1 in the relaxed optimization problem.
Any of the above projection techniques for PDE/FFT/FMM filters, with support coinciding with the design domain, will result in design domain occupied entirely by one of the phases. Such behavior can be alleviated by thresholding the design or the filtered field with threshold between 0 and 1 [158]. It should be pointed out that in this case the length scale (mesh independence) imposed on the design is lost. These effects are discussed in detail in [147] where the expression for the intermediate threshold Heaviside projection, which is utilized here, is proposed in the form
with parameter \(\beta \) playing the same role as in Eq. 16 and \(\eta \) denoting the threshold level.
4 Three-field density representation
As discussed in the previous sections, the final density field \(\widehat{\widetilde{\rho }}\) is obtained by series of transformations applied on the original design field \(\rho \). The basic transformations are filtering and projection, and the chain of transformations can be written as \(\rho \leadsto \widetilde{\rho } \leadsto \widehat{\widetilde{\rho }}\) which will be referred to as the three-field density representation. The concept provides a powerful tool for controlling the final topology and acts as a basic building block for more complex control strategies summarized in Table 1.
In [61], length scales on both phases are obtained by the utilization of two design fields. The first one \(\overline{\rho }_1\) represents the void, and the second one \(\overline{\rho }_2\) represents the solid. They are obtained by using the three-field representation from two design fields \(\rho _1\) and \(\rho _2\), respectively. The final design field is obtained as average of the two fields, which produces gray transition regions. Various extensions are presented in [62, 63, 68] where combinations of multiple phases and Heaviside projection with fixed support shape are utilized to control particle topologies, positions and distances between them in the design of structures and materials. In [163], the theoretical development is demonstrated in the design of 3D woven lattices.
In [120], the void phase is represented as a union of discrete shape projections. The idea is extended in [146] for the design of photonic crystal wave guides, and recently, it is applied in [110] to density-based topology-optimized designs consisting of a union of elements with prescribed pattern. In general, several strategies are applicable to density-based formulations: (1) The design can be obtained by a union of prescribed number of discrete shapes; (2) the original design field can be represented as a union of discrete shapes, and the final one is obtained using the three-field representation; and (3) the original design field is filtered or projected using filters with compact support defined by the desired shape. The first case might result in a nondifferentiable formulation, e.g., Zhang et al. [160]. The second provides limits on the optimization space as each shape is defined by a few parameters and the total number of shapes is fixed. This can result in faster convergence; however, the design might be poorly performing compared to designs obtained with larger number of parameters. The third approach keeps the complete freedom of the topology optimization, and the only limit is imposed by the discretization process.
Another recent extension [34] of the three-field representation utilizes the gradient of the projected density field \(\overline{\rho }\) for optimizing structures with a coating layer. The boundary of the solid phase can be identified by using the gradients of the density. As the transition from solid to void can become very sharp and is mesh dependent, the density field is filtered first and then differentiated. Inside solid or void regions, the norm of the gradient vector field \(\left| \nabla \widetilde{\overline{\rho }} \right| \) is zero or close to zero. Close to the transition regions, the norm is different than zero, which is utilized for defining a coating layer around the solid region. Then, Heaviside projection of \(\left| \nabla \widetilde{\overline{\rho }} \right| \) combined with control on the magnitude of the gradient norm provides density interpolation for the coating material. A similar extension is utilized in the design of piezo modal transducers with prescribed electrode gaps in [40].
As discussed in detail in [147] and demonstrated in Table 4, a density field based on Heaviside projection combined with filtering with finite support provides length scale on either the void or the solid phase, i.e., designs with length scale imposed on the solid can posses extremely small features in the void regions, and vice verse. These small features might be mesh dependent and observable by refining the mesh. This often results in lack of manufacturability, extremely sensitive performance due to manufacturing and exploitation uncertainties, stress concentration, etc. The projection does not provide penalization to the optimization problem, and it cannot avoid the appearance of intermediate densities. This effect is pronounced especially well in the design of heat sink Table 3. Hence, in general, topology-optimized designs based solely on Heaviside projection requires postprocessing which might destroy completely the effect of the optimization. More complex extensions, which avoid the postprocessing, are discussed in Sects. 7 and 8. They are built on the three-field formulation or additional constraints and provide length scale on both phases [166] and robust designs performance [89, 121, 147].
5 Numerical examples
In order to demonstrate the effect of the different projection and filtering strategies a set of selected topology optimization problems are shown in Fig. 1 and described below. The set consists of: (1) L-bracket optimization [93], (2) compliant mechanism design [122] and (3) heat sink optimization problem [20]. The same or similar examples have been considered in [147] and subsequent papers. The design domains are discretized using first-order finite elements [171]. The design field \(\rho \), the filtered field \(\widetilde{\rho }\) and the projected field \(\overline{\rho }\) are discretized using constant values within each finite element. The collected values are stored in vectors denoted as \({\varvec{\rho }}\), \(\widetilde{{\varvec{\rho }}}\) and \(\overline{{\varvec{\rho }}}\), respectively.
The L-bracket optimization problem can be written in discrete form as
where \({\mathbf {K}}\) is the stiffness matrix obtained using finite element discretization, \({\mathbf {f}}\) is a vector consisting of the input supplied to the system, \(V^*\) denotes the material volume, and the vector \({\mathbf {v}}\) consists of the volumes of all elements. The gradients with respect to the projected densities are obtained using adjoint analysis and are given as
The gradients with respect to the original design field are obtained using the chain rule
The compliant mechanism optimization problem is defined as
where \({\mathbf {l}}\) is a vector with zeros and value one and minus one at the positions corresponding to the vertical displacement at the jaw corners. In order to save computational time, only half of the design domain with symmetry boundary conditions is utilized in the computations. The gradients with respect to the projected densities are obtained using adjoint analysis and are given as
where \({\varvec{\lambda }}\) is obtained as a solution to the following adjoint problem
The gradients with respect to the design field are obtained by using the chain rule. The heat sink problem is defined in the same way as the minimum compliance problem with unit heat input uniformly distributed over the design domain.
The results for L-bracket optimization for the standard density- based filter without Heaviside projection, and with Heaviside projections given by Eqs. 17, 23 and 21 are shown in Table 2. The modulus of elasticity for the solid material is taken to be one, and the applied force is set to one as well. The density filter radius is \(R_f=5.6L/200\). The volume fraction is 50 %. The discreteness of the obtained designs is represented with the following gray indicator [123]
As expected, the design obtained with density filter without any projection possesses large gray regions and actual realization would require postprocessing, i.e., removing the gray transition regions. The designs with Heaviside projections are with similar levels of intermediate design elements. Length scale on the solid regions for the designs obtained with Eqs. 17 and 21 can be clearly identified. All solid features are larger than a dot with radius equal to the radius of the filter. On the other hand, the void regions do not possess length scale, which is evident either from the sharp internal bracket corner or the sharp corners in the elements connections. Such sharp corners lead to stress concentration and are undesirable mechanical designs. The design obtained with the \(\tanh \) projection does not have sharp internal bracket corner due to the extension of the design domain and the intermediate threshold \(\eta =0.5\).
Heat sink designs are shown in Table 3. The volume fraction is 50 %, and filter parameters are the same as for the L-bracket optimization problem. It can be observed that all designs posses large gray regions with gray index in the same order as the gray index for the unprojected design. The projections cannot suppress the appearance of intermediate densities. Hence, the heat sink example is probably the simplest problem where new techniques for imposing length scale on black and white designs can be tested.
Results for compliant mechanism design are shown in Table 4. Only the upper half of the design domain shown in the table is utilized in the computations. The volume fraction is 30 %. The ratio of the output springs stiffness to the input spring stiffness is 0.005. The output springs are vertical and are positioned at the output points shown with bold black dots in Fig. 1. The thickness of the jaws is 0.05L. Similar to the L-bracket, the projections decrease the gray level in the obtained designs. Length scale is clearly imposed on the solid regions for the design obtained with the Dilate and the Harmonic filters; however, some of the elements are with intermediate densities, which again indicates that the projection alone cannot ensure 0/1 designs. The void regions do not posses length scale, which leads to the appearance of hinges in the connecting regions.
In general, the three-field formulation can in some cases improve the discreteness of the obtained designs; however, for problems where the optimization can benefit from the appearance of gray regions, 0/1 design cannot be guaranteed. Heaviside projection with threshold projection \(\eta =0\) or \(\eta =1\) and filtered field obtained using filter function with finite support can ensure length scale on either the solid or the void regions in the design. However, the projections alone cannot provide length scale on both phases; therefore, they cannot prevent the appearance of sharp inter-element connections which lead to stress concentration. Furthermore, the appearance of sharp features in either solid or the void regions might lead to lack of manufacturability in some production processes due to lack of resolution. This is especially evident in compliant mechanism designs where small imperfections around the mechanism hinges can lead to completely disintegrated mechanisms. Manufacturability can be ensured either by taking into account the production uncertainties in the optimization process, or in some cases by imposing length scale on both phases.
6 On the similarities between three-field representation and micro- and nanoscale production processes
The three-field representation provides the basic building block for controlling geometrical details of optimized designs. Two of the the three fields (\(\rho \) and \(\widetilde{\rho }\)) are seemingly pure mathematical entities. They are utilized in restricting the design space and removing the necessity of imposing additional constraints on the optimization problem. The original intent for introducing them in topology optimization was to ensure mesh-independent solutions. However, due to the complex chain of transformations, often the link to the real physics of the problem is lost. Once the final design is obtained from the topology optimization process, it sends for manufacturing. The designer usually postprocesses the optimized topology and sends it to the manufacturer who is responsible for transforming the design to a set of parameters for controlling the production machines. This transformation is based on purely geometric properties, i.e., the manufacturer minimizes the difference between the optimized topology and the one obtained by the manufacturing process by tuning the production parameters, e.g., Poonawala and Milanfar [112]. The design information which is lost during this transformation process may reduce the performance of the manufactured designs. Hence, avoiding or reducing the number of transformations will bring the performance of the realizations and the optimized design closer.
A striking similarity between micro- and nanolithography production processes and the three-field representation is demonstrated in [72]. The article presents in detail the link between electron beam lithography (EBL) and projection schemes in topology optimization and provides a direct map between the production parameters and the optimized topology. Later, a similar link is demonstrated to optical projection lithography in [165]. The two processes and possible extensions to other micro- and nanoscale production technologies are presented in detail in the following.
6.1 Electron beam lithography
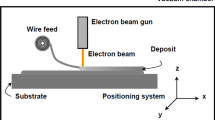
Electron beam lithography [36] is a nanofabrication process usually applied in small volume production. It allows direct writing of 2D design patterns down to sub-10nm dimensions. The goal is to transfer a pattern to a thin layer of material referred to as resist in the literature. A typical setup, shown in Fig. 2, consists of an electron beam which exposes the resist material laid on a substrate. The resist consists of a polymer which is sensitive to electron beam exposure [107].
The EBL process consists of two main phases. First, the resist is bombarded with electrons originating from the electron gun. The exposure causes local changes in the properties of the polymeric material. As a second step, a solvent is added to the process in order to develop the exposed pattern on the resist. Two kinds of resists, negative and positive, are utilized in practice. Negative resist forms new bounds during the exposure, while for positive resist bounds are broken. The solvent removes molecules with smaller molecular weight which results in removing the exposed areas for positive resist and the unexposed for negative resits. The setup on Fig. 2 demonstrates positive resist exposure and development. The process can be combined with other nanoproduction technologies for printing multimaterial or 3D layered designs [84], e.g., material deposition and subsequent etching. The focus here is only on demonstrating the link between the first two steps and the three-field representation in topology optimization; hence, for more details, the interested readers are referred to the existing literature on the subject, e.g., Landis [84] and Cui [36].
In the exposure step, the electron gun emits electrons which are directed by a magnetic and electrostatic field to a prescribed location on the resist [131]. The charge density directed to the resist is given as
where \(T\left( {\mathbf {x}}\right) \) denotes the time period for pointing the electron beam at position \({\mathbf {x}}\) and I is the beam current. The exposure time can be specified for every point and is modeled as continuous variable. When an electron beam hits the resist, the electrons interact with the material which results in scattering of the electrons. Part of electrons reaching the substrate layer is reflected back causing a secondary backscattering to the resist. The forward and the backward scattering increases the width of the electron beam which is characterized by the so-called point spread function \(F\left( {\mathbf {x}}\right) \), which expresses the energy distribution of an incident point source due to scattering effects. The point spread function \(D\left( {\mathbf {x}}\right) \) is approximated by a sum of two Gaussians [29]. The final energy exposure \(E\left( {\mathbf {x}}\right) \) of the resists at point \({\mathbf {x}}\) is determined by a convolution integral
which resembles closely the density filtering process in topology optimization Eq. 7.
The development phase consists of several steps and can be modeled with different levels of complexity [39]. The simplest model assumes constant threshold [26], i.e., for positive resist the material exposed to a level above a certain level \(E_\mathrm{cl}\) is etched away. The level is controllable and depends on the process temperature, the solvent concentration, resist material, etc. The final resulting pattern written on the resist can be expressed as a Heaviside projection of the energy exposure
which coincides with the projection step in the three-field density formulation. Hence, for EBL, the three fields can be associated directly with real physical fields and the chain of transformation represents the different steps in the production process. The design field \(\rho \) matches the exposure time, the filtered field \(\widetilde{\rho }\) matches the energy exposure, and the density field \(\widehat{\widetilde{\rho }}\) matches the final developed pattern. Such a map allows for direct transfer of the physical parameters to the manufactures, which ensures manufacturability of the design and removes the postprocessing step. Furthermore, in addition to the optimization of the design performance, the map allows for optimization of the production parameters such as total exposure time and exposure patterns [73].
6.2 Optical lithography
Optical lithography similar to the EBL process aims at transferring a 2D pattern onto a thin layer of material. A typical production process consists of multiple steps [98], and here it is exemplified in Fig. 3. A pattern is transferred onto a thin film layer deposited on a substrate. In a preparatory phase, a thin layer of material is deposited on a wafer and then coated with light-sensitive polymer called a photoresist. As a following step, a mask (a pattern) is projected onto the photoresist with the help of an optical system. The projected image is developed, and the exposed areas of the photoresist are removed. In the following steps, the developed image is transferred to the film by an etching process, and the photoresist is removed from the design.
The mask pattern can be represented using a binary image \(I_\mathrm{M}\left( {\mathbf {x}}\right) \) defined on a finite domain in \({\mathbb {R}}^2\). The intensity of the projected aerial image onto the photoresist is given as
where \(*\) denotes the convolution operator and \(H_\beta \) is the point spread function of the optical projection system. The etching phase is modeled with the help of the Heaviside projection and is given as
where \(I_P\) is the final developed pattern and \(\eta \) represents an intensity threshold above which the material is etched away for positive photoresist. For a so-called negative photoresist, the areas with intensity smaller than the threshold are etched away.
Similar to the EBL process presented in Sect. 6.1 the three fields representation in topology optimization can be directly matched to the physical fields in photolitography [165]. The original design field \(\rho \) can be utilized for representing the image mask \(I_M\), the intermediate filtered field can represent the projected image and the developed design \(I_P\) is represented by the projected field \(\widehat{\widetilde{\rho }}\). The differences compared to the standard transformation chain \(\rho \leadsto \widetilde{\rho } \leadsto \widehat{\widetilde{\rho }}\) are: (1) The filtered field is pointwise squared, and (2) the mask \(I_M\) is required to be a 0/1 image. Detailed discussions and demonstration of the similarities can be found in [165].
6.3 Other micro- and nanoproduction processes
One of the main limitations of the EBL and photolitography production processes is the lack of capability for arbitrary three-dimensional geometries. Three-dimensional designs can be manufactured layer by layer by stacking several 2D projection-etching-deposition cycles on top of each other; however, the resulting process is still incapable of producing arbitrary 3D shapes. This limitation has stimulated research in mask less direct writing techniques [36] using focused optical beams. The light diffraction provides a limit on the resolution for direct writing, and an alternative based on nonlinear interaction processes, the so-called two photon polymerization, has been proposed in [100]. The technology has been developed further to produce features down to a few nanometers [50]. The process utilizes ultrashort laser pulses focused into the volume of a photoresistive material. A polymerization of the photoresist is initiated in the vicinity of the focal point, and after illumination of the 3D structure and subsequent etching, the polymerized regions will remain in the printed form, which allows fabrication of almost any complicated 3D pattern [28, 79]. Due to the threshold behavior and the nonlinear nature of the process, a resolution beyond the diffraction limit can be realized [152]. The three-field representation model can be mapped directly to physical parameters by representing the focal point and the laser intensity with the design field, the exposed pattern with the filtered field and the final developed pattern with the projected field.
The research in nanofabrication constantly provides new production processes capable of manufacturing devices with finer and finer resolution. The smallest features which can be produced are always limited by the available fabrication tools. On the other hand, there are a large number of examples of extremely complex structures assembled on molecular level with subnanometer scale features. Such patterns in nature are realized by self-assembly, which provides one of the most promising mechanism for producing devices in the subnanometer range [84]. The process can be modeled numerically, and optimized template patterns have been demonstrated in [70]. Similarities with the three-field representation can be easily identified; however, topology optimization of a full device still remains to be demonstrated.
The above examples demonstrate the flexibility of the three-field model to represent real physical fields in standard macro- and nanomanufacturing processes. Topology optimization based on this model controls directly the input production parameters and results in designs which incorporate the physical limitations in the design process. Optimization driven directly with the physical parameters avoids the postprocessing steps known as proximity effect correction in electron beam lithography and optical proximity correction in photolithography, and results in manufacturable topologies.
7 Topology optimization under geometrical uncertainties
Uncertainties in the production parameters are inevitable parts of every manufacturing process. Therefore, their inclusion in the optimization is necessary in order to ensure manufacturable designs with robust performance. The three-field representation provides a excellent base for integrating the uncertainties in the topology optimization process, and this application has been demonstrated in a number of problems.
Replacing the threshold parameter \(\eta \) in the projection step with a random variable \(\eta \in {\mathcal {P}}\), where \({\mathcal {P}}\) is a selected random distribution, can be utilized for modeling uniform erosion and dilation along the design perimeter [89]. The projection step represents the etching process in lithography; therefore, the above modification can represent uncertainties in the temperature or the chemical concentration which leads to different threshold values. The deterministic objective function in Eq. 1 can be replaced with a combination of the mean deterministic objective function and its standard deviation \({\text{ E }}\left( J\right) +\kappa \text {STD}\left( J\right) \) [99], where \(\kappa \) is free parameter selected by the designer. The above modification tries to improve the average performance and at the same time to reduce its variability. The main difficulties with such a reformulation is the selection of the parameter \(\kappa \) and the fact that such an objective is not a coherent risk measure [119], i.e., if a design \(\rho _1\) is outperforming design \(\rho _2\) for almost all possible realizations, the above objective might not reflect this property. Nevertheless, the above reformulation has been demonstrated to produce robust designs for a number of problems in mechanics [114] and electromagnetics [43].
The constant threshold model can model only uniform erosion and dilation along the design perimeter. An extension has been proposed in [121], where the random variable has been replaced with a random field defined over the design domain. In this way, spatially varying geometric imperfections can be easily represented. Similar models for level-set approaches have been proposed in [30, 31]. An additional study including spatially varying uncertainties in the material parameters is presented in [90]. One of the main conclusions is that spatially varying geometric uncertainties have very little effect on the topology of the optimized designs and often neglecting the spatial variability and considering constant threshold along the design domain produced results with similar performance, especially for mechanical design problems such as minimum compliance and compliant mechanisms. Recently, it has been demonstrated in [32] that spatial variations can affect severely the topology for wave propagation problems. An alternative model has been proposed in [73] where the manufacturing uncertainties have been modeled as misplacement of material. Such a model can be utilized in the 3D printing processes where material is deposited by the printer head layer by layer.
The computational cost in the case of stochastic variations increases significantly and depends on the dimensionality of the stochastic space. In [121] Monte Carlo (MC) sampling has been utilized for obtaining the mean and the standard deviation of the system response. Even though MC possesses dimension independent convergence, its convergence speed is relatively slow [157]. An alternative stochastic collocation sampling approach has been investigated in [43, 89, 90]. The main advantage is that the already developed deterministic solvers are utilized without any modifications in the optimization process. However, for fast oscillatory uncertainties and small number of sampling points without any error control, the optimization process often tunes the design for the sampling points and any intermediate realizations may possess responses which are not robust with respect to the true nondiscrete realizations [43]. A topology optimization formulation with error control on the mean and the standard deviation remains to be demonstrated.
In attempt to decrease the computational cost, perturbation-based stochastic solvers have been utilized in [91]. It has been clearly demonstrated that in general the Taylor expansion of the response around a single point in the stochastic space cannot capture the overall behavior and might lead to the same effects observed in [43], i.e., tuning the design performance for the expansion point. However, for relatively smooth problems, it has been demonstrated in [74] that the perturbation approach can represent the response of the system due to stochastic imperfections and can lead to significant reduction in the computation time for geometrically nonlinear optimization problems.
Another way to account for the manufacturing and exploitation uncertainties is to utilize the so-called reliability-based design optimization (RBDO) [101]. For general discussion, overview and comparison between the different approaches, the reader is referred to [21, 45, 49, 101]. In RBDO, the objective is either to minimize the probability of failure subjected to a set of additional constraints or the probability of failure is set as a constraint to the optimization problem. The probability of failure is often estimated approximately using the so-called first-order reliability method (FORM) or second-order reliability method (SORM). Such approaches rely on the stochastic behavior around a single point in the stochastic space (most probable failure point MPP) and suffer from the same disadvantages in optimization as the perturbation approaches, i.e., the design is optimized for a particular point (set of parameters) in the stochastic space and some of the more important regions might be omitted by the optimizer. Reliability-based topology optimization has been demonstrated for compliant mechanisms in [102] and for minimum compliance in [80].
The above approaches are nonintrusive, i.e., one can utilize standard deterministic solvers for evaluating the moments of the response. For stochastic perturbation approaches, only slight modifications are necessary. Another alternative for estimating the stochastic response is the stochastic Galerkin approach [54]. The method requires development of new solvers and for large dimensionality in the stochastic space might result in extremely large systems of equations. In topology optimization the method has been utilized in minimum compliance optimization under material uncertainties [137].
A large number of research papers are devoted to the exploitation of uncertainties like random inputs or imperfections in boundary conditions, e.g., Kogiso et al. [82], Lógó et al. [97], Dunning and Kim [42] and Zhao and Wang [162]. It should be emphasized that the focus here is on manufacturability and length scale of the optimized designs; therefore, a detailed review on topology optimization under other types of uncertainties is omitted here.
Often the exact distribution of the random variables is unknown, and it is desirable to account only for the worst-case scenario from all possible design realizations. Such an approach leads to the so-called min/max formulation which in the case of minimum compliance optimization and compliant mechanism designs is given as
where \({\varvec{\eta }}\) is a vector with all random parameters and \({\varvec{\eta }}^*= \arg \max _{\eta } {J\left( {\varvec{\rho }}, {\mathbf {u}}, {\varvec{\eta }} \right) }\). The volume constraint \(\max _{\eta }{V\left( {\varvec{\rho }},{\varvec{\eta }}\right) }\le V^*\) can also be replaced with a fixed point in the random space. Such a formulation is demonstrated in [147] where the volume constraint is applied on the most dilated design which actually coincides with the \(\arg \max _{\eta } {V\left( {\varvec{\rho }},{\varvec{\eta }}\right) }\). Alternatively, the volume constraint can be applied on the mean volume [121].
For compliant mechanism design and threshold projection \(\eta \in \left[ \eta _d, \eta _e\right] \), which is constant in the design domain, it has been observed that the worst performing design is either the most eroded or the most dilated design [124]. This has been utilized in [114, 147] for simplifying the formulation given by Eq. 45 to
where \(\{ J_e, J_d\}\) are standard deterministic objectives for thresholds \(\eta _e\) and \(\eta _d\) , respectively. As the worst performing case is for either threshold \(\eta _e\), or threshold \(\eta _d\), the case for \(\eta _i\) corresponding to the blueprint design supplied to the manufacturer can be omitted in the optimization formulation which can save around a third of the computational time compared to the formulation in [147]. In contrast to the deterministic case, the robust formulation requires one or more systems solutions corresponding to each realization which significantly increases the computational load.
In the general case, the worst case is not known in advance and a large number of samples in the stochastic space is utilized in order to approximate the random response and to find the worst-case scenario. The optimization formulation for such a case becomes
where \(N_s\) is the number of samples and \({\varvec{\eta }}_i\) is a point in the random space. The above formulation has been utilized for photonic crystal design [145, 146], for topology optimization in acoustics [32], and for material design in [149]. Without any constraints, min/max formulations have been demonstrated for topology optimization in photonics in [115, 116] where a cheap surrogate model has been utilized for reduction in the computational cost. Another demonstration in photonic crystal design considering manufacturing uncertainties based on robust regularization of a function is shown in [104]. In compliant mechanism design and minimum compliance problems a multiple load case scenario with localized damage has been demonstrated to limit the maximum member size in [75].
The \(\max \) function is not differentiable and the optimization problem given by Eq. 38 is usually reformulated using the so-called bound formulation as
The above formulation can be naturally implemented using any MMA implementation [132].
Replacing the deterministic optimization formulation with a formulation which accounts for uncertainties in the production process removes the human factor in the optimization process. First, the three-field model ensures that the design is manufacturable, and second requiring robustness of the response ensures that the obtained designs will posses robust behavior for a wide range of variations in production parameters. It has been observed in [92, 121, 147] that requiring robustness of the performance with respect to uniform erosion and dilation for compliant mechanism design removes the single-node hinge problem, demonstrated in Table 7, and results in black and white designs with minimum length scale on the obtained topology. It should be stressed that the length scale is guaranteed only if the designed topology does not change for all possible realizations. Such changes in topology have been demonstrated for photonic crystals in [145], for optimization in acoustics in [32] and for compliant mechanisms in [87]. Nevertheless, the designs obtained by requiring robustness of the performance can be sent to manufacturing without any postprocessing and human interventions. The full cycle has been demonstrated in the design of auxetic materials in [14].
Examples of designs with robust performance with respect to uniform erosion/dilation \(\eta \in \left[ 0.35,0.65\right] \) for the L-bracket, the Heat sink and the compliant gripper optimization problems are shown in Tables 5, 6 and 7, respectively. In the first row of each table, the most eroded and the most dilated designs are obtained using the Harmonic mean filter given by Eqs. 21 and 22, respectively. The filter radius for the Harmonic filter is set to 2.17 L / 200. As it can be observed, such a model does not impose length scale, cannot ensure black and white designs, and cannot prevent hinges in compliant mechanism designs. This is due to the fact that the Harmonic erode and dilate operations can produce projected fields with equal values, and hence, they cannot model erosion/dilation imperfections. In contrast, the tanh projection given by Eq. 23 always produces different projected field values for different thresholds. This property results in length scale on both the solid and void regions and in designs close to black and white.
7.1 Minimum compliance design with random projection threshold
The main reason that the robust formulation has not yet been adopted by the industry is the additional computational cost associated with solving the multiple design realizations and the large number of optimization iterations due to the continuation strategy. The most popular topology optimization problem is minimum compliance design. By careful analysis, the computational cost for the robust formulation presented above can be reduced to be equal to the cost associated with solving a single-case deterministic problem.
The threshold projection is assumed to be uniform, and the threshold is modeled as a random variable \(\eta \in {\mathcal {P}}\left( \eta _d,\eta _e\right) \), where \({\mathcal {P}}\) is an unspecified random distribution with support \([\eta _d,\eta _e]\). The compliance is given as

where \({\mathbf {u}}\) depends on the physical density and on the threshold \(\eta \) though the state equation. The compliance is positive, and for \(E_j\left( {\mathbf {x}}\right) \ge E_i\left( {\mathbf {x}}\right) , \forall {\mathbf {x}}\in \varOmega \), the compliance \(J_j\) is always smaller or equal to the compliance \(J_i\), i.e. \(J_j\le J_i\). Using the SIMP model given by Eq. 5 with a physical density field obtained by projecting filtered density field \(\widetilde{\rho }\) with thresholds \(\eta _i\) and \(\eta _j\), the following relation can be identified
where \(\overline{\rho }_k= {\text{ H }}_{\eta _k}\left( \widetilde{\rho }\right) , k=i,j\). Therefore, the maximum compliance for any filtered density distribution \(\widetilde{\rho }\) is obtained for the most eroded realization \(\eta _e\), i.e.
Using similar argumentation, the maximum material volume \(\max _{\eta \in {\mathcal {P}}\left( \eta _d,\eta _e\right) } \left\{ V\left( \rho ,\eta \right) \right\} \) can be obtained for the most dilated design, i.e.
where the material volume is computed as

Therefore, the optimization formulation given by Eq. 45 can be replaced with an equivalent one given as
In contrast to the general case, the reduced formulation requires only a single-state solution. Furthermore, as the volume constraint is always active and \({\varvec{\rho }}_d > {\varvec{\rho }}_e\), the problem is self-penalizing and the penalty parameter in the SIMP interpolation can be set to 1, i.e, the interpolation between void and solid is linear. The above formulation leads to black and white designs with response robust with respect to uniform erosion and dilation along the design perimeter. Due to the lack of local minima and maxima between the most eroded and the most dilated cases, it results in clearly defined minimum length scale on both the solid and the void regions for a blueprint design obtained for an intermediate \(\eta \). The same reduction can be applied to any spatially varying projection threshold which is bounded between two constant values, \(\eta _d\le \eta \left( {\mathbf {x}}\right) \le \eta _e\). Hence, the worst-case formulation in minimum compliance topology optimization leads to a problem with computation cost similar to the computational cost for the deterministic minimum compliance optimization problem.
The methodology is demonstrated in Tables 8 and 9 for L-bracket and heat sink designs. The boundary conditions, the filter radius and the input to the system are the same as for the robust optimization case. The formulation results in black and white designs with minimum length scale imposed on both the solid and the void regions. The objective for penalization parameter \(p=1\) is slightly better for both of the considered cases. Using linear interpolation decreases the number of local minima and maxima for the optimization problem. Based on the authors experience, linear interpolation improves the convergence speed. Different length scales can be imposed on the void and the solid regions by selecting thresholds which are not symmetric with respect to the intermediate threshold \(\eta =0.5\) [147]. Using such an approach, the designers can control the rounding radius and hence the stress concentration in the final designs without explicitly accounting for stress concentration in the optimization problem.
8 Length scale in macroscale production processes
Manufacturing is the technological process which utilizes different physical processes to modify the geometry and properties of a given amount of material in order to create parts of products as well as to assemble these parts in a final product [57]. The process consists of a sequence of operations, which brings an initial block of material closer to the desired final detail. The set of possible operations can include wide ranges of subprocesses such as casting and molding, material forming, material removal processes (turning, drilling, milling, grinding) and material deposition processes. Each one of these technological operations imposes some restrictions on the parts under production. Therefore, in order to ensure manufacturability of designs obtained using topology optimization, these restrictions need to be imposed during the optimization process.
Several articles have presented such methodologies in topology optimization. In casting, one of the important requirements is that the casting molds should be removable without damaging the cast part and the mold tools [154], i.e., the mold parts should not have concave geometry and any interior voids. The first mathematical formulation of casting constraints was proposed in [164]. Topology optimization using the constraints has been demonstrated in [71]. Transformation of the constraints making them applicable to level-set-based approaches is demonstrated in [154, 155]. For the density-based formulation, [53] has proposed an explicit parametrization for casting constraints based on a Heaviside projection which recently has been extended in [96]. An alternative is proposed in [66] where projection-based algorithms have been utilized for imposing casting as well as milling constraints on topology-optimized designs. A general overview for applications in the aerospace industry can be found in [170] where the main focus is on the design of thin-walled structures with stiffeners [169]. For laminated composites, an optimization formulation can be found in [128]. A machining feature-based level-set optimization approach is presented in [95]. Most of the casting and machining manufacturing constraints do not affect explicitly the length scale imposed on the solid regions of the design. They are related mainly to the convexity of the design envelope and the length scale imposed on the void regions. Therefore, the minimum length scale on the solid is governed by the manufacturing uncertainties, i.e., the same considerations applied to micro- and nanoscale production processes are applicable to the manufacturing processes mentioned above.
Often a number of features with explicit shape are required to be embedded in the optimized design due to esthetic considerations in architecture, manufacturing restrictions, or holes and components passing through the design [33]. Most of the publications presenting such optimization formulations utilize level- set approaches, e.g., Mei et al. [103] and Zhou and Wang [168]. A general review can be found in [160] where a large number of density-based examples are presented. Requiring embedded design features does not affect the length scale on the actual free design domain and additional constraints based on either the requirement for robustness or explicit length scale are discussed later in this section.
Additive manufacturing (AM), also known as 3D printing, is a relatively new production technology. In contrast to traditional machining where the manufacturing relies on material removal, AM is based on adding material layer by layer, thus, avoiding large part of the manufacturing constraints imposed by other production techniques. Often a design obtained by a CAD system can be directly fabricated without the need of process planning [55]. Different 3D printing processes have been developed for different materials. Modern devices can utilize polymers, metals, ceramic and even bio-materials for printing human tissues, e.g., Tumbleston et al. [140], Travitzky et al. [138] and Doyle [41]. Due to the fast development of the technology, cheap desktop 3D printers are widely available for both prototyping, as well as mass production. However, even though AM has received big impulse from both industrial manufacturers and hobby enthusiasts many challenges still exist and are subject to active research. Several of them outlined in [111] and related to the current review paper are the lack of computationally efficient 3D topology optimization software, the lack of robust modeling and optimization tools utilizing material microstructures, and the need for postprocessing of optimized designs.
Topology optimization as a design process is the perfect supplement to the additive manufacturing as it can completely utilize the manufacturing freedom. Topology optimization for additive manufacturing has been demonstrated in a large number of articles [25, 136] and recently for multi material designs in [51, 135]. One of the issues is the postprocessing step for designs obtained using pure SIMP approach, i.e., the physical density is modeled using the filtered design field and posses gray regions. Such a postprocessing step can be removed ether by requiring robustness of the design performance with respect to variations in the geometry or by obtaining black and white designs with clearly defined minimum length scale. The first approach relies on the theory presented in Sect. 7 and is demonstrated for auxetic material microstructure design in [14]. The second will be discussed in detail later in this section.
Even though additive manufacturing avoids most of the design constraints, the process requires that the manufactured structures are self-supported. This requirement can be fulfilled by constraining the size of the overhanging part. The approach presented in [94] is essentially a postprocessing step and as discussed earlier might destroy the optimality of the solution. A solution based on projections without additional constraints is presented in [52].
In order to save material and increase the production speed in 3D printing, the production details are printed using thin walls for the surface and internal porous filling material. Such a process imposes several challenges for topology optimization. The first one is resolving the thin wall and the internal porous structure, and the second is parametrization of the different parts of detail during the optimization process. A parametrization based on the standard three-field representation combined with an additional field utilizing the gradient of the physical density is presented in [34]. In such a parametrization, the filling material can be realized using uniform material microstructure, thus avoiding the requirement for detailed modeling inside the design. This microstructure can be designed using topology optimization applied for material design where additional local constraints can be easily imposed [64]. Uniform material microstructure does not utilize the additional freedom provided by the technology, i.e., the material properties can vary spatially within the manufacturing domain. A nonuniform microstructure can be designed using hierarchical homogenization [35, 117]. The varying microstructural cells lack connectivity which requires modification of the design for connecting the different microstructures. Furthermore, the homogenization theory does not account for the boundary conditions and local effects (concentrated loading, loss of local stability). An alternative which provides spatially varying manufacturable microstructures without any postprocessing is presented in [3, 4]. The presented methodology resolves all microstructural details and accounts for boundary conditions and localized effects.
8.1 Minimum length scale
With the exception of compliance like optimization problems, the robust topology optimization formulation requires the solution of several state problems. The number of state problems depends on the ratio of the characteristic length of the design domain and the correlation length of the stochastic uncertainties. It can vary from several [89, 147] to several hundred and thousand solves [43, 75]. The increased computational cost is often unacceptable especially for problems where the solution of a single-state problem is expensive. Therefore, an alternative solution is to impose a minimum length scale with the assumption that such an additional constraint will provide at least to some extend robustness of the performance with respect to uncertainties in the production process.
The first article [60] to propose an approach for imposing length scale on the solid regions in the design domain utilizes the three-field design representation with density field obtained using filtering with finite support. The filter support provides the smallest building block for the phase which can be viewed as a union of an infinite number of filter support shapes. The projection threshold is set to \(\eta =0\) for imposing length scale on the solid phase and \(\eta =1\) for imposing length scale on the void phase.
Imposing length scale only on one of the phases does not always guarantees manufacturability [147], e.g., hinges cannot be avoided in mechanism design Table 4 and the appearance of gray transition regions cannot be avoided Table 3. Therefore, an explicit length scale control on both phases is necessary. Such a mathematically rigorous approach has been proposed recently for density-based topology optimization in [166].
For density-based topology optimization, the minimum length scale on both phases is imposed with the help of an additional constraints [166]. The idea is based on the observation in [147], i.e., a length scale can be guaranteed on both phases for the intermediate design if the topology does not change for all possible design realizations. It should be pointed out that in case of standard robust topology optimization formulation this feature is a result from the optimization and is not guaranteed for all optimized designs. In the methodology proposed in [166], it is explicitly required; hence, it is guaranteed that the final design will posses minimum length scale.
A topology described by a continuous density field does not change if the following two conditions are satisfied
The above conditions utilize the three-field formulation. The first condition ensures minimum length scale on the solid phase, and the second condition ensures minimum length scale on the void phase. The numerical implementation is discussed in detail in [166], and an example for heat sink design with imposed minimum length scale on both phases is shown in Table 10. An approach which also is based on an additional constraint is proposed in [113]. This alternative requires more complex implementation however.
For level-set approaches, mathematically rigorous formulations for imposing minimum length scale have been proposed in [6, 105]. Attempting to provide simpler formulations, several other papers [67, 153, 161] propose a skeleton- based idea to control the minimum length scale. The idea is to extract the medial zone of a structure and to constrain the corresponding density values. A shortcoming of the presented formulations is that the gradients of the medial zone are neglected. The same is valid for the extension to density-based topology optimization proposed in [161]. The possible shortcomings for these approaches are discussed in [6].
As stated in [6], so far the perfect formulation for imposing minimum length scale remains to be discovered. Several critical cases for the level-set formulation are discussed in [6]. For the density-based formulation presented in [166], the requirement is that the constraints are applied on some initial topology. As demonstrated in [166], the topology can be changed by the optimization process. A comparison [166] to compliant mechanisms optimized using the robust formulation shows that for the intermediate blueprint design the performance is slightly better than the robust design; however, for different realizations, the variations in the performance are significantly larger for the mechanism optimized only for minimum length scale. The same effect is observed for photonic crystals in [166].
8.2 Maximum length scale
Imposing restrictions on the maximum length scale of the void phase, the solid phase, or of both phases result in the appearance of redundant members which provide diversification of the load path [58]. This effect can be clearly observed in [75] where maximum length scale on the design members appears as a result of the required robustness with respect to localized damage. Maximum length scale on optimized designs can be required due to technological limitations, e.g., for high-rise buildings, the size of the bottom columns is limited due to difficulties with transportation and lifting, or due to limitations in the maximal size of the available steel sheets. Other maximum length scale requirements may be imposed due to desired properties which cannot be included in the optimization process. An example is requiring a specific porosity in scaffold designs which can be indirectly imposed by setting constraints on the maximum length scale.
In [58] maximum length scale is enforced on topology- optimized designs by restricting the amount of material in the neighborhood of each point in the design domain. This approach leads to a large number of constraints (one constraint for each design variable). Two alternatives are proposed in [87]. The first one is based on the design of band- pass filters and is an extension of the idea presented in [81]. Band-pass filters can be designed directly in the frequency domain, and the filtering can be realized using FFT/iFFT transformations. An alternative is to present the filtered field as the difference of two filtered fields obtained from the same density field \(\rho \), i.e., one obtained with larger filter radius, and the other obtained with smaller filter radius [87]. The Fourier transform of the resulting field does not posses any values around the zero frequency which results in suppression of the appearance of large void or solid areas in the filtered design. The proposed technique restricts the design space and therefore does not require any additional constraints. The main limitation is that the maximum length scale is defined only loosely in the frequency domain.
The second alternative proposed in [87] is based on morphological operators [108]. A figure of a house together with two images obtained by dilation and erosion operations are shown in Fig. 4. The erosion and the dilation operations are applied with a rectangular box with dimensions \(5\times 5\) pixels. As demonstrated all solid(black) elements with dimensions smaller than the structural element (\(5\times 5\) box) are erased in the erosion operation and all void elements with dimensions smaller than the structural element are erased in the dilation operation. Hence, this behavior can be utilized in defining maximum length scale in topology optimization. The maximum length scale is defined with the help of a structural element which can take any shape, i.e., maximum length scale on a phase is defined by the parameter/parameters necessary to define the smallest structural element with specified shape for which the eroded/dilated design coincides with the design domain filled entirely with the other phase. If an erosion operation with a specified structural element is applied on a design and the result is a design domain filled with void phase, the maximal feature in the solid phase is smaller than the specified structural element. If a dilation operation is applied on a design and the result is that a solid phase is distributed everywhere in the design domain, the maximal feature in the void regions is smaller than the specified structural element.
The erosion and the dilation can be modeled using Heaviside projections with thresholds \(\eta =0\) and \(\eta =1\) and filter with finite support coinciding with the desired structural element. The eroded design will be denoted with \(\overline{\rho }_e={\text{ H }}\left( \widetilde{\overline{\rho }},\eta =1\right) \) and the dilated with \(\overline{\rho }_d={\text{ H }}\left( \widetilde{\overline{\rho }},\eta =0\right) \). It should be noted that the erosion and the dilation operations are applied on the filtered field \(\widetilde{\overline{\rho }}\) obtained by filtering the physical design \(\overline{\rho }\). The conditions for ensuring maximum length scale on the solid can be written as

and the condition for ensuring maximum length scale on the void is given as

Taking into account the two additional constraints leads to the following modified minimum compliance optimization problem
where \(\varepsilon _s\) and \(\varepsilon _v\) are small positive parameters used for relaxing slightly the problem. The two constraints can be combined with any of the approaches for imposing minimum length scale or with the robust formulation. An example for topology-optimized design with maximum length scale on the solid region and minimum length scale on both phases is shown in Fig. 5.
For level-set approaches, maximum length scale control is proposed in [6, 105]. Another attempt based on skeleton extraction is shown in [67]. The idea is further developed in the following two papers [153, 161]. The main weakness in the latter formulations is that all of them disregard the gradients of the skeleton in the sensitivity analysis.
9 Computational cost
One of the main issues in density-based topology optimization is the large number of optimization iterations. Each of them requires a system solve, which for large-scale problems can be time-consuming. This is unacceptable, and a large number of solutions have been proposed in the literature. As the state solvers can take more than 99 % of the total computational time [2], the main focus has been in speeding up their solution time. The computational time can be decreased by improving the state solver’s complexity, by parallelization of the algorithms, by reformulation of the optimization problems or decreasing the number of optimization steps, or by combination of any of the previous approaches.
Traditionally, the solution of the system of equations obtained by discretization of the state problem is obtained by direct solvers due to their robustness. Their main limitations are the large amount of memory required during the factorization phase, the large computational complexity, and the lack of parallel scalability. Iterative solvers provide a solution to the above limitations; however, they lack the robustness of the direct solvers. They rely on preconditioners in order to ensure convergence. Therefore, the weight in iterative solver development is on the construction of effective preconditioners. For elliptic problems, the most effective preconditioners, as well as solvers, are based on multigrid techniques [142]. Multigrid solvers are very effective for problems with smooth solutions and material properties, and one of the main arguments against their use in topology optimization has been the high contrast in the material properties of the optimized designs. It should be pointed out that standard geometric multigrid methods are convergent [142] even though the convergence rate is affected by the high contrast in the material parameters. Their effectiveness is demonstrated in [1, 11]. Other alternatives which have been demonstrated to be very effective not only for elliptic but also for wave propagation problems are domain decomposition techniques [48]. Recently, contrast-independent preconditioners utilizing ideas from both domain decomposition and multigrid have been presented in [88]. The preconditioners have been applied in the design of robust manufacturable design with full resolution of the microstructural details [3, 4]. The solvers have provided an optimized solution overnight on a single CPU for several million degrees of freedom. This is achieved by reusing the preconditioners between the different realizations in the robust formulation [13] and during the optimization between the different optimization steps. Another example for effective recycling of preconditioners is shown recently in [10].
The possibility of re-utilizing preconditioners between the different optimization steps [12] is based on the fact that the design changes slowly between updates. Furthermore, the solution tolerance can often be reduced for intermediate optimization steps [11], which is a still widely unexplored area. From a SAND (Simultaneous Analysis and Design [15]) formulation point of view, the reduced tolerance for the intermediate solves can be seen as an inexact solves to the saddle point system arising from the formulation. It has been demonstrated in [118] that the SAND formulation leads to a very robust optimization process; however, an effective preconditioners for the saddle point system is necessary to be developed. Other computationally effective optimization formulations have been demonstrated in [46, 47]. They are applicable only for specific problems and are difficult to generalize. However, the examples demonstrate clearly the potential gains from reformulating the optimization problems.
An optimization based on the three-field representation requires specification of the Heaviside projection relaxation parameter \(\beta \). The optimization usually starts with small \(\beta \) close to zero, and after convergence for the selected value, the relaxation parameter \(\beta \) is increased. Such a continuation strategy may result in a divergence of the optimization process for large increments. For small increments, the number of optimization iterations might be unnecessarily increased. Selecting close to optimal continuation strategy is an open question. A formulation which avoids the continuation and utilizes fixed \(\beta \) is proposed in [59].
The widely utilized MMA optimizer [132] is a first- order optimization method which in general leads to large number of optimization steps resulting in larger number of system solves. A number of alternatives have been compared in [118], and the conclusion is that general nonlinear optimization solvers, such as IPOPT [143], often outperform MMA and its globally convergent counterpart GCMMA [133]. Hence, the best optimization solver for density- based topology optimization problems is still to be developed and is subject to active research.
10 Summary
The article aggregates the available techniques for obtaining manufacturable designs from density-based topology optimization processes. The recent developments remove the postprocessing steps, thus shortening the link between the design phase and the manufacturing phase. Incorporating the manufacturing process in the optimization formulation in some cases provides physical meaning for the originally pure mathematical entities utilized in the parametrization of the designs. Such an extension ensures manufacturability of the obtained designs and defines the design in terms of control parameters supplied to the manufacturer rather than a pure geometrical description. Furthermore, it removes not only the postprocessing step applied on the designer side but also the preprocessing manufacturing step, e.g., optical proximity correction in photolithography and proximity effect correction in EBL. In addition to the manufacturability, incorporating the control parameters in the optimization provides better management of the production cost and time. The similarities between the parametrization in density-based topology optimization and nano- and microscale fabrication processes have been discussed for several of them. Further extensions and modifications remain to be seen for others.
Ensuring manufacturability does not guarantee well-performing designs due to inevitable uncertainties in manufacturing. Hence, the optimization process needs to account for these uncertainties in order to reduce the waste products. The theoretical progress in this direction has been significant with a verification example in material design which demonstrates the removal of the postprocessing phases between topology optimization and manufacturing. Other verification examples will further strengthen the theoretical bases and will provide new development directions. Wider acceptance in industrial settings will be ensured by solving the high computational cost issues. A step in this direction is demonstrated here for minimum compliance optimal designs.
Often, due to lack of information, knowledge and experience, production and exploitation uncertainties cannot be supplied to the designer. In such cases, rough manufacturing constraints, such as minimum or maximum length scale, entirely based on engineering intuition, can be applied in the optimization process. Most of the constraints can be formulated as a single additional constraint to the topology optimization problem, thus providing relatively cheap solutions from a computational point of view. For compliance design, the minimum length scale constraint provides some robustness for the design performance; however, for wave propagation and compliant mechanism optimization problems, such behavior is not guaranteed. On the other hand, restricting the design space, by enforcing minimum length scale on the design, speeds up the optimization process significantly and can be utilized to ensure existence of solutions. The broad range of other manufacturing constraints makes the development, implementation and coordination with already developed techniques difficult. Their unification and the expansion of the already relatively wide set of constraints will be a subject of future research.
References
Aage, N., Andreassen, E., Lazarov, B.: Topology optimization using petsc: an easy-to-use, fully parallel, open source topology optimization framework. Struct. Multidiscip. Optim. 51(3), 565–572 (2015). doi:10.1007/s00158-014-1157-0
Aage, N., Lazarov, B.: Parallel framework for topology optimization using the method of moving asymptotes. Struct. Multidiscip. Optim. 47(4), 493–505 (2013). doi:10.1007/s00158-012-0869-2
Alexandersen, J., Lazarov, B.: Tailoring macroscale response of mechanical and heat transfer systems by topology optimization of microstructural details. In: Lagaros, N.D., Papadrakakis, M. (eds.) Engineering and Applied Sciences Optimization, Computational Methods in Applied Sciences, vol. 38, pp. 267–288. Springer, Berlin (2015). doi:10.1007/978-3-319-18320-6_15
Alexandersen, J., Lazarov, B.S.: Topology optimisation of manufacturable microstructural details without length scale separation using a spectral coarse basis preconditioner. Comput. Methods Appl. Mech. Eng. 290, 156–182 (2015). doi:10.1016/j.cma.2015.02.028
Allaire, G., Francfort, G.: A numerical algorithm for topology and shape optimization. In: Bendse, M., Soares, C. (eds.) Topology Design of Structures, NATO ASI Series, vol. 227, pp. 239–248. Springer, Netherlands (1993). doi:10.1007/978-94-011-1804-0_16
Allaire, G., Jouve, F., Michailidis, G.: Thickness control in structural optimization via a level set method (2014). https://hal.archives-ouvertes.fr/hal-00985000
Allaire, G., Jouve, F., Toader, A.M.: A level-set method for shape optimization. Comptes Rendus Mathematique 334(12), 1125–1130 (2002). doi:10.1016/S1631-073X(02)02412-3
Allaire, G., Jouve, F., Toader, A.M.: Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 194(1), 363–393 (2004). doi:10.1016/j.jcp.2003.09.032
Allaire, G., Kohn, R.: Topology optimization and optimal shape design using homogenization. In: Bendse, M., Soares, C. (eds.) Topology Design of Structures, NATO ASI Series, vol. 227, pp. 207–218. Springer, Netherlands (1993). doi:10.1007/978-94-011-1804-0_14
Amir, O.: Revisiting approximate reanalysis in topology optimization: on the advantages of recycled preconditioning in a minimum weight procedure. Struct. Multidiscip. Optim. 51(1), 41–57 (2015). doi:10.1007/s00158-014-1098-7
Amir, O., Aage, N., Lazarov, B.: On multigrid-CG for efficient topology optimization. Struct. Multidiscip. Optim. 49(5), 815–829 (2014). doi:10.1007/s00158-013-1015-5
Amir, O., Sigmund, O.: On reducing computational effort in topology optimization: how far can we go? Struct. Multidiscip. Optim. 44(1), 25–29 (2011). doi:10.1007/s00158-010-0586-7
Amir, O., Sigmund, O., Lazarov, B.S., Schevenels, M.: Efficient reanalysis techniques for robust topology optimization. Comput. Methods Appl. Mech. Eng. 245246, 217–231 (2012). doi:10.1016/j.cma.2012.07.008
Andreassen, E., Lazarov, B.S., Sigmund, O.: Design of manufacturable 3D extremal elastic microstructure. Mech. Mater. 69(1), 1–10 (2014). doi:10.1016/j.mechmat.2013.09.018
Arora, J., Wang, Q.: Review of formulations for structural and mechanical system optimization. Struct. Multidiscip. Optim. 30(4), 251–272 (2005). doi:10.1007/s00158-004-0509-6
Aubert, G., Kornprobst, P.: Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations, 2nd edn. Springer, Berlin (2006)
Bendsøe, M.P.: Optimal shape design as a material distribution problem. Struct. Optim. 1(4), 193–202 (1989). doi:10.1007/BF01650949
Bendsøe, M.P., Kikuchi, N.: Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 71(2), 197–224 (1988). doi:10.1016/0045-7825(88)90086-2, http://www.sciencedirect.com/science/article/pii/0045782588900862
Bendsøe, M.P., Sigmund, O.: Material interpolation schemes in topology optimization. Arch. Appl. Mech. 69, 635–654 (1999)
Bendsøe, M.P., Sigmund, O.: Topology Optimization—Theory, Methods and Applications. Springer, Berlin (2003)
Beyer, H.G., Sendhoff, B.: Robust optimization—a comprehensive survey. Comput. Methods Appl. Mech. Eng. 196(33–34), 3190–3218 (2007). doi:10.1016/j.cma.2007.03.003
Borrvall, T., Petersson, J.: Topology optimization using regularized intermediate density control. Comput. Methods Appl. Mech. Eng. 190(37–38), 4911–4928 (2001)
Bourdin, B.: Filters in topology optimization. Int. J. Numer. Methods Eng. 50, 2143–2158 (2001)
Bourdin, B., Chambolle, A.: Design-dependent loads in topology optimization. ESAIM: Control Optim. Calc. Var. 9, 19–48 (2003). doi:10.1051/cocv:2002070
Brackett, D., Ashcroft, I., Hague, R.: Topology optimization for additive manufacturing. In: Proceedings of the 22nd Annual International Solid Freeform Fabrication Symposium (2011)
Brunner, T.A., Ferguson, R.A.: Approximate models for resist processing effects. Proc. SPIE 2726, 198–207 (1996). doi:10.1117/12.240906
Bruns, T.E., Tortorelli, D.A.: Topology optimization of non-linear elastic structures and compliant mechanisms. Comput. Methods Appl. Mech. Eng. 190, 3443–3459 (2001)
Bückmann, T., Stenger, N., Kadic, M., Kaschke, J., Frölich, A., Kennerknecht, T., Eberl, C., Thiel, M., Wegener, M.: Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography. Adv. Mater. 24(20), 2710–2714 (2012). doi:10.1002/adma.201200584
Chang, T.H.P.: Proximity effect in electronbeam lithography. J. Vac. Sci. Technol. 12(6), 1271–1275 (1975). doi:10.1116/1.568515, http://scitation.aip.org/content/avs/journal/jvst/12/6/10.1116/1.568515
Chen, S., Chen, W.: A new level-set based approach to shape and topology optimization under geometric uncertainty. Struct. Multidiscip. Optim. 44(1), 1–18 (2011). doi:10.1007/s00158-011-0660-9
Chen, S., Chen, W., Lee, S.: Level set based robust shape and topology optimization under random field uncertainties. Struct. Multidiscip. Optim. 41, 507–524 (2010). doi:10.1007/s00158-009-0449-2
Christiansen, R.E., Lazarov, B.S., Jensen, J.S., Sigmund, O.: Creating geometrically robust designs for highly sensitive problems using topology optimization. Struct. Multidiscipl. Optim. 1–18 (2015). doi:10.1007/s00158-015-1265-5
Clausen, A., Aage, N., Sigmund, O.: Topology optimization with flexible void area. Struct. Multidiscip. Optim. 50(6), 927–943 (2014). doi:10.1007/s00158-014-1109-8
Clausen, A., Aage, N., Sigmund, O.: Topology optimization of coated structures and material interface problems. Comput. Methods Appl. Mech. Eng. 290, 524–541 (2015). doi:10.1016/j.cma.2015.02.011
Coelho, P., Fernandes, P., Rodrigues, H., Cardoso, J., Guedes, J.: Numerical modeling of bone tissue adaptational hierarchical approach for bone apparent density and trabecular structure. J. Biomech. 42(7), 830–837 (2009). doi:10.1016/j.jbiomech.2009.01.020
Cui, Z.: Nanofabrication: Principles, Capabilities and Limits. Springer, US (2008). doi:10.1007/978-0-387-75577-9_2
Deaton, J.D., Grandhi, R.V.: A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct. Multidiscip. Optim. 49(1), 1–38 (2014). doi:10.1007/s00158-013-0956-z
Diaz, A., Sigmund, O.: Checkerboard patterns in layout optimization. Struct. Multidiscip. Optim. 10, 40–45 (1995)
Dill, F., Neureuther, A.R., Tuttle, J., Walker, E.: Modeling projection printing of positive photoresists. IEEE Trans. Electron Devices 22(7), 456–464 (1975). doi:10.1109/T-ED.1975.18161
Donoso, A., Sigmund, O.: Topology optimization of piezo modal transducers with null-polarity phases. Struct. Multidiscip. Optim. (2015). doi:10.1007/s00158-015-1330-0
Doyle, K.: Bioprinting: from patches to parts. Genet. Eng. Biotechnol. News 34, 34–35 (2014). doi:10.1089/gen.34.10.02
Dunning, P.D., Kim, H.A.: Robust topology optimization: minimization of expected and variance of compliance. AIAA J. 51(11), 2656–2664 (2013). doi:10.2514/1.J052183
Elesin, Y., Lazarov, B., Jensen, J., Sigmund, O.: Design of robust and efficient photonic switches using topology optimization. Photonics Nanostruct. Fundam. Appl. 10(1), 153–165 (2012). doi:10.1016/j.photonics.2011.10.003
Elesin, Y., Lazarov, B., Jensen, J., Sigmund, O.: Time domain topology optimization of 3D nanophotonic devices. Photonics Nanostruct. Fundam. Appl. 12(1), 23–33 (2014). doi:10.1016/j.photonics.2013.07.008
Elishakoff, I., Ohsaki, M.: Optimization and Anti-optimization of Structures Under Uncertainty. Imperial College Press, London (2010)
Evgrafov, A.: State space newton’s method for topology optimization. Comput. Methods Appl. Mech. Eng. 278, 272–290 (2014). doi:10.1016/j.cma.2014.06.005
Evgrafov, A.: On chebyshevs method for topology optimization of stokes flows. Struct. Multidiscip. Optim. 1–11 (2015). doi:10.1007/s00158-014-1176-x
Evgrafov, A., Rupp, C., Maute, K., Dunn, M.: Large-scale parallel topology optimization using a dual-primal substructuring solver. Struct. Multidiscip. Optim. 36(4), 329–345 (2008). doi:10.1007/s00158-007-0190-7
Frangopol, D.M., Maute, K.: Life-cycle reliability-based optimization of civil and aerospace structures. Comput. Struct. 81(7), 397–410 (2003). doi:10.1016/S0045-7949(03)00020-8
Gan, Z., Cao, Y., Evans, R.A., Gu, M.: Three-dimensional deep sub-diffraction optical beam lithography with 9nm feature size. Nat. Commun. 4 (2013). doi:10.1038/ncomms3061
Gaynor, A.T., Meisel, N.A., Williams, C.B., Guest, J.K.: Multiple-material topology optimization of compliant mechanisms created via polyjet three-dimensional printing. J. Manuf. Sci. Eng. 136, 061015 (2014). doi:10.1115/1.4028439
Gaynor, A.T., Meisel, N.A., Williams, C.B., Guest, J.K.: Topology optimization for additive manufacturing: Considering maximum overhang constraint. In: AIAA Aviation, pp. –. American Institute of Aeronautics and Astronautics (2014). doi:10.2514/6.2014-2036
Gersborg, A.R., Andreasen, C.S.: An explicit parameterization for casting constraints in gradient driven topology optimization. Struct. Multidiscip. Optim. 44(6), 875–881 (2011). doi:10.1007/s00158-011-0632-0
Ghanem, R., Spanos, P.: Stochastic Finite Elements—A Spectral Approach. Dover Publications Inc, Mineola (2003)
Gibson, I., Rosen, D.W., Stucker, B.: Additive Manufacturing Technologies. Springer, Berlin (2010)
Greengard, L., Rokhlin, V.: A fast algorithm for particle simulations. J. Comput. Phys. 73(2), 325–348 (1987). doi:10.1016/0021-9991(87)90140-9
Groover, M.P.: Fundamentals of Modern Manufacturing: Materials, Processes, and Systems. Wiley, New York (2010)
Guest, J.: Imposing maximum length scale in topology optimization. Struct. Multidiscip. Optim. 37, 463–473 (2009). doi:10.1007/s00158-008-0250-7
Guest, J., Asadpoure, A., Ha, S.H.: Eliminating beta-continuation from heaviside projection and density filter algorithms. Struct. Multidiscip. Optim. 44(4), 443–453 (2011). doi:10.1007/s00158-011-0676-1
Guest, J., Prevost, J., Belytschko, T.: Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Methods Eng. 61(2), 238–254 (2004)
Guest, J.K.: Topology optimization with multiple phase projection. Comput. Methods Appl. Mech. Eng. 199(1–4), 123–135 (2009)
Guest, J.K.: Optimizing the layout of discrete objects in structures and materials: a projection-based topology optimization approach. Comput. Methods Appl. Mech. Eng. 283, 330–351 (2015). doi:10.1016/j.cma.2014.09.006
Guest, J.K., Ha, S.H.: Design of Multifunctional Material Structures Using Topology Optimization with Feature Control, pp. 129–134. Wiley, New York (2011). doi:10.1002/9781118147726.ch17
Guest, J.K., Prvost, J.H.: Optimizing multifunctional materials: design of microstructures for maximized stiffness and fluid permeability. Int. J. Solids Struct. 43(2223), 7028–7047 (2006). doi:10.1016/j.ijsolstr.2006.03.001
Guest, J.K., Smith Genut, L.C.: Reducing dimensionality in topology optimization using adaptive design variable fields. Int. J. Numer. Methods Eng. 81(8), 1019–1045 (2010). doi:10.1002/nme.2724
Guest, J.K., Zhu, M.: Casting and milling restrictions in topology optimization via projection-based algorithms. In: ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference Volume 3: 38th Design Automation Conference, Parts A and B Chicago, Illinois, USA, August, p. 1215 (2012)
Guo, X., Zhang, W., Zhong, W.: Explicit feature control in structural topology optimization via level set method. Comput. Methods Appl. Mech. Eng. 272, 354–378 (2014). doi:10.1016/j.cma.2014.01.010
Ha, S.H., Guest, J.: Optimizing inclusion shapes and patterns in periodic materials using discrete object projection. Struct. Multidiscip. Optim. 50(1), 65–80 (2014). doi:10.1007/s00158-013-1026-2
Haber, R., Jog, C., Bendsoe, M.: A new approach to variable-topology shape design using a constraint on perimeter. Struct. Optim. 11(1), 1–12 (1996)
Hannon, A.F., Ding, Y., Bai, W., Ross, C.A., Alexander-Katz, A.: Optimizing topographical templates for directed self-assembly of block copolymers via inverse design simulations. Nano Lett. 14(1), 318–325 (2014). doi:10.1021/nl404067s
Harzheim, L., Graf, G.: A review of optimization of cast parts using topology optimization. Struct. Multidiscip. Optim. 31(5), 388–399 (2006). doi:10.1007/s00158-005-0554-9
Jansen, M., Lazarov, B.S., Schevenels, M., Sigmund, O.: On the similarities between micro/nano lithography and topology optimization projection methods. Struct. Multidiscip. Optim. 48(4), 717–730 (2013). doi:10.1007/s00158-013-0941-6
Jansen, M., Lombaert, G., Diehl, M., Lazarov, B.S., Sigmund, O., Schevenels, M.: Robust topology optimization accounting for misplacement of material. Struct. Multidiscip. Optim. 47, 317–333 (2013). doi:10.1007/s00158-012-0835-z
Jansen, M., Lombaert, G., Schevenels, M.: Robust topology optimization of structures with imperfect geometry based on geometric nonlinear analysis. Comput. Methods Appl. Mech. Eng. 285, 452–467 (2015). doi:10.1016/j.cma.2014.11.028
Jansen, M., Lombaert, G., Schevenels, M., Sigmund, O.: Topology optimization of fail-safe structures using a simplified local damage model. Struct. Multidiscip. Optim. 49(4), 657–666 (2014). doi:10.1007/s00158-013-1001-y
Jog, C.S., Haber, R.B.: Stability of finite element models for distributed-parameter optimization and topology design. Comput. Methods Appl. Mech. Eng. 130(3–4), 203–226 (1996)
Kawamoto, A., Matsumori, T., Kondoh, T., Nomura, T., Yamasaki, S., Nishiwaki, S.: Topology optimization by using a time-dependent diffusion equation. In: Proceedings of 9th World Congress on Structural and Multidisciplinary Optimization, Shizuoka, Japan (2011)
Kawamoto, A., Matsumori, T., Yamasaki, S., Nomura, T., Kondoh, T., Nishiwaki, S.: Heaviside projection based topology optimization by a PDE-filtered scalar function. Struct. Multidiscip. Optim. 44, 19–24 (2011). doi:10.1007/s00158-010-0562-2
Kawata, S., Sun, H.B., Tanaka, T., Takada, K.: Finer features for functional microdevices. Nature 412, 697–698 (2001)
Kharmanda, G., Olhoff, N., Mohamed, A., Lemaire, M.: Reliability-based topology optimization. Struct. Multidiscip. Optim. 26, 295–307 (2004)
Kim, T.S., Kim, J.E., Jeong, J.H., Kim, Y.Y.: Filtering technique to control member size in topology design optimization. KSME Int. J. 18(2), 253–261 (2004). doi:10.1007/BF03184735
Kogiso, N., Ahn, W., Nishiwaki, S., Izui, K., Yoshimura, M.: Robust topology optimization for compliant mechanisms considering uncertainty of applied loads. J. Adv. Mech. Des. Syst. Manif. 2(1), 96–107 (2008). doi:10.1299/jamdsm.2.96
Kreisselmeier, G., Steinhauser, R.: Application of vector performance optimization to a robust control loop design for a fighter aircraft. Int. J. Control 37(2), 251–284 (1983). doi:10.1080/00207179.1983.9753066
Landis, S. (ed.): Nano-Lithography. Wiley, New York (2013)
Lazarov, B., Matzen, R., Elesin, Y.: Topology optimization of pulse shaping filters using the hilbert transform envelope extraction. Struct. Multidiscip. Optim. 44, 409–419 (2011). doi:10.1007/s00158-011-0642-y
Lazarov, B., Sigmund, O.: Sensitivity filters in topology optimisation as a solution to Helmholtz type differential equation. In: Proceedings of the 8th World Congress on Structural and Multidisciplinary Optimization (2009)
Lazarov, B., Wang, F.: Maximum length scale in density based topology optimization (2015) (in review)
Lazarov, B.S.: Topology optimization using multiscale finite element method for high-contrast media. In: Lirkov, I., Margenov, S., Waniewski, J. (eds.) Large-Scale Scientific Computing, Lecture Notes in Computer Science, pp. 339–346. Springer, Berlin (2014). doi:10.1007/978-3-662-43880-0_38
Lazarov, B.S., Schevenels, M., Sigmund, O.: Robust design of large-displacement compliant mechanisms. Mech. Sci. 2(2), 175–182 (2011). doi:10.5194/ms-2-175-2011
Lazarov, B.S., Schevenels, M., Sigmund, O.: Topology optimization considering material and geometric uncertainties using stochastic collocation methods. Struct. Multidiscip. Optim. 46, 597–612 (2012). doi:10.1007/s00158-012-0791-7
Lazarov, B.S., Schevenels, M., Sigmund, O.: Topology optimization with geometric uncertainties by perturbation techniques. Int. J. Numer. Methods Eng. 90(11), 1321–1336 (2012). doi:10.1002/nme.3361
Lazarov, B.S., Sigmund, O.: Filters in topology optimization based on Helmholtz-type differential equations. Int. J. Numer. Methods Eng. 86(6), 765–781 (2011). doi:10.1002/nme.3072
Le, C., Norato, J., Bruns, T., Ha, C., Tortorelli, D.: Stress-based topology optimization for continua. Struct. Multidiscip. Optim. 41(4), 605–620 (2010). doi:10.1007/s00158-009-0440-y
Leary, M., Merli, L., Torti, F., Mazur, M., Brandt, M.: Optimal topology for additive manufacture: a method for enabling additive manufacture of support-free optimal structures. Mater. Des. 63, 678–690 (2014). doi:10.1016/j.matdes.2014.06.015
Liu, J., Ma, Y.S.: 3d level-set topology optimization: a machining feature-based approach. Struct. Multidiscip. Optim. 1–20 (2015). doi:10.1007/s00158-015-1263-7
Liu, S., Li, Q., Chen, W., Hu, R., Tong, L.: H-DGTP-a heaviside-function based directional growth topology parameterization for design optimization of stiffener layout and height of thin-walled structures. Struct. Multidiscip. Optim. 1–11 (2015). doi:10.1007/s00158-015-1281-5
Lógó, J., Ghaemi, M., Rad, M.: Optimal topologies in case of probabilistic loading: the influence of load correlation. Mech. Based Des. Struct. Mach. 37(3), 327–348 (2009)
Mack, C.: Fundamental Principles of Optical Lithography: The Science of Microfabrication. Wiley, New York (2007)
Markowitz, H.: Portfolio selection. J. Finance 7(1), 77–91 (1952). doi:10.1111/j.1540-6261.1952.tb01525.x
Maruo, S., Nakamura, O., Kawata, S.: Three-dimensional microfabrication with two-photon-absorbed photopolymerization. Opt. Lett. 22(2), 132–134 (1997). doi:10.1364/OL.22.000132
Maute, K.: Topology optimization under uncertainty. In: Rozvany, G., Lewiski, T. (eds.) Topology Optimization in Structural and Continuum Mechanics, CISM International Centre for Mechanical Sciences, vol. 549, pp. 457–471. Springer, Vienna (2014). doi:10.1007/978-3-7091-1643-2_20
Maute, K., Frangopol, D.: Reliability-based design of mems mechanisms by topology optimization. Comput. Struct. 81, 813–824 (2003)
Mei, Y., Wang, X., Cheng, G.: A feature-based topological optimization for structure design. Adv. Eng. Softw. 39(2), 71–87 (2008). doi:10.1016/j.advengsoft.2007.01.023
Men, H., Freund, R.M., Nguyen, N.C., Saa-Seoane, J., Peraire, J.: Fabrication-adaptive optimization with an application to photonic crystal design. Oper. Res. 62(2), 418–434 (2014). doi:10.1287/opre.2013.1252
Michailidis, G.: Manufacturing constraints and multi-phase shape and topology optimization via a level-set method. Ph.D. thesis, Ecole Polytechnique (2014). https://pastel.archives-ouvertes.fr/pastel-00937306
Mlejnek, H.: Some aspects of the genesis of structures. Struct. Optim. 5(1–2), 64–69 (1992). doi:10.1007/BF01744697
Mohammad, M., Muhammad, M., Dew, S.K., Stepanova, M.: Fundamentals of electron beam exposure and development. In: Stepanova, M., Dew, S. (eds.) Nanofabrication, pp. 11–41. Springer, Vienna (2012). doi:10.1007/978-3-7091-0424-8_2
Najman, L., Talbot, H.: Mathematical Morphology: From Theory to Applications. Wiley, New York (2013). doi:10.1002/9781118600788
Nomura, T., Sato, K., Taguchi, K., Kashiwa, T., Nishiwaki, S.: Structural topology optimization for the design of broadband dielectric resonator antennas using the finite difference time domain technique. Int. J. Numer. Methods Eng. 71(11), 1261–1296 (2007). doi:10.1002/nme.1974
Norato, J., Bell, B., Tortorelli, D.: A geometry projection method for continuum-based topology optimization with discrete elements. Comput. Methods Appl. Mech. Eng. (2015). doi:10.1016/j.cma.2015.05.005, http://www.sciencedirect.com/science/article/pii/S0045782515001711
Oropallo, W., Piegl, L.: Ten challenges in 3D printing. Eng. Comput. 1–14 (2015). doi:10.1007/s00366-015-0407-0
Poonawala, A., Milanfar, P.: Mask design for optical microlithography—an inverse imaging problem. IEEE Trans. Image Process. 16(3), 774–788 (2007). doi:10.1109/TIP.2006.891332
Poulsen, T.A.: A new scheme for imposing a minimum length scale in topology optimization. Int. J. Numer. Methods Eng. 57, 741–760 (2003)
Qian, X., Sigmund, O.: Topological design of electromechanical actuators with robustness toward over- and under-etching. Comput. Methods Appl. Mech. Eng. 253, 237–251 (2013). doi:10.1016/j.cma.2012.08.020
Rehman, S., Langelaar, M., van Keulen, F.: Robust optimization of 2x2 multimode interference couplers with fabrication uncertainties. Proc. SPIE 8627, 862713 (2013). doi:10.1117/12.2000647
Rehman, S., Langelaar, M., van Keulen, F.: Efficient kriging-based robust optimization of unconstrained problems. J. Comput. Sci. 5(6), 872–881 (2014). doi:10.1016/j.jocs.2014.04.005, http://www.sciencedirect.com/science/article/pii/S1877750314000477
Rodrigues, H., Guedes, J., Bendsoe, M.: Hierarchical optimization of material and structure. Struct. Multidiscip. Optim. 24(1), 1–10 (2002). doi:10.1007/s00158-002-0209-z
Rojas-Labanda, S., Stolpe, M.: Benchmarking optimization solvers for structural topology optimization. Struct. Multidiscip. Optim. 1–21 (2015). doi:10.1007/s00158-015-1250-z
Ruszczynski, A., Shapiro, A.: Optimization of convex risk functions. Mathe. Oper. Res. 31(3), 433–452 (2006). doi:10.1287/moor.1050.0186
Saxena, A.: Topology design with negative masks using gradient search. Struct. Multidiscip. Optim. 44(5), 629–649 (2011). doi:10.1007/s00158-011-0649-4
Schevenels, M., Lazarov, B., Sigmund, O.: Robust topology optimization accounting for spatially varying manufacturing errors. Comput. Methods Appl. Mech. Eng. 200(49–52), 3613–3627 (2011). doi:10.1016/j.cma.2011.08.006
Sigmund, O.: On the design of compliant mechanisms using topology optimization. Mech. Struct. Mach. 25, 493–524 (1997)
Sigmund, O.: Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 33, 401–424 (2007). doi:10.1007/s00158-006-0087-x
Sigmund, O.: Manufacturing tolerant topology optimization. Acta Mech. Sin. 25, 227–239 (2009)
Sigmund, O., Maute, K.: Topology optimization approaches. Struct. Multidiscip. Optim. 48(6), 1031–1055 (2013). doi:10.1007/s00158-013-0978-6
Sokolowski, J., Zochowski, A.: On the topological derivative in shape optimization. SIAM J. Control Optim. 37(4), 1251–1272 (1999). doi:10.1137/S0363012997323230
Solomon, C., Breckon, T.: Fundamentals of Digital Image Processing: A Practical Approach with Examples in Matlab. Wiley, New York (2010)
Sørensen, R., Lund, E.: Thickness filters for gradient based multi-material and thickness optimization of laminated composite structures. Struct. Multidiscip. Optim. 1–24 (2015). doi:10.1007/s00158-015-1230-3
Stolpe, M., Svanberg, K.: An alternative interpolation scheme for minimum compliance topology optimization. Struct. Multidiscip. Optim. 22(2), 116–124 (2001). doi:10.1007/s001580100129
Stolpe, M., Svanberg, K.: On the trajectories of penalization methods for topology optimization. Struct. Multidiscip. Optim. 21(2), 128–139 (2001). doi:10.1007/s001580050177
Suzuki, K.: Electron beam lithography systems. In: Microlithography, pp. 329–360. CRC Press (2007). doi:10.1201/9781420051537.ch6
Svanberg, K.: The method of moving asymptotes—a new method for structural optimization. Int. J. Numer. Methods Eng. 24, 359–373 (1987)
Svanberg, K.: A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J. Optim. 12, 555–573 (2002)
Svanberg, K., Svärd, H.: Density filters for topology optimization based on the pythagorean means. Struct. Multidiscip. Optim. 48(5), 859–875 (2013). doi:10.1007/s00158-013-0938-1
Takezawa, A., Kobashi, M., Kitamura, M.: Porous composite with negative thermal expansion obtained by photopolymer additive manufacturing (2015). http://arxiv.org/abs/1504.07724v1
Tomlin, M., Meyer, J.: Topology optimization of an additive layer manufactured (ALM) aerospace part. In: The 7th Altair CAE Technology Conference (2011)
Tootkaboni, M., Asadpoure, A., Guest, J.K.: Topology optimization of continuum structures under uncertainty a polynomial chaos approach. Comput. Methods Appl. Mech. Eng. 201–204, 263–275 (2012). doi:10.1016/j.cma.2011.09.009
Travitzky, N., Bonet, A., Dermeik, B., Fey, T., Filbert-Demut, I., Schlier, L., Schlordt, T., Greil, P.: Additive manufacturing of ceramic-based materials. Adv. Eng. Mater. 16(6), 729–754 (2014). doi:10.1002/adem.201400097
Trefethen, L.N.: Spectral Methods in MATLAB. SIAM, Philadelphia (2000)
Tumbleston, J.R., Shirvanyants, D., Ermoshkin, N., Janusziewicz, R., Johnson, A.R., Kelly, D., Chen, K., Pinschmidt, R., Rolland, J.P., Ermoshkin, A., Samulski, E.T., DeSimone, J.M.: Continuous liquid interface production of 3D objects. Science 347(6228), 1349–1352 (2015). doi:10.1126/science.aaa2397
van Dijk, N., Maute, K., Langelaar, M., van Keulen, F.: Level-set methods for structural topology optimization: a review. Struct. Multidiscip. Optim. 48(3), 437–472 (2013). doi:10.1007/s00158-013-0912-y
Vassilevski, P.S.: Multilevel Block Factorization Preconditioners: Matrix-based Analysis and Algorithms for Solving Finite Element Equations. Springer, New York (2008)
Wächter, A., Biegler, L.T.: On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 106(1), 25–57 (2006). doi:10.1007/s10107-004-0559-y
Wadbro, E., Udawalpola, R., Berggren, M.: Shape and topology optimization of an acoustic horn–lens combination. J. Comput. Appl. Math. 234(6), 1781–1787 (2010). doi:10.1016/j.cam.2009.08.028
Wang, F., Jensen, J.S., Sigmund, O.: Robust topology optimization of photonic crystal waveguides with tailored dispersion properties. J. Opt. Soc. Am. B 28(3), 387–397 (2011). doi:10.1364/JOSAB.28.000387
Wang, F., Jensen, J.S., Sigmund, O.: High-performance slow light photonic crystal waveguides with topology optimized or circular-hole based material layouts. Photonics Nanostruct. Fundam. Appl. 10(4), 378–388 (2012). doi:10.1016/j.photonics.2012.04.004 (TaCoNa-Photonics 2011)
Wang, F., Lazarov, B., Sigmund, O.: On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 43(6), 767–784 (2011). doi:10.1007/s00158-010-0602-y
Wang, F., Lazarov, B.S., Sigmund, O., Jensen, J.S.: Interpolation scheme for fictitious domain techniques and topology optimization of finite strain elastic problems. Comput. Methods Appl. Mech. Eng. 276, 453–472 (2014). doi:10.1016/j.cma.2014.03.021
Wang, F., Sigmund, O., Jensen, J.S.: Design of materials with prescribed nonlinear properties. J. Mech. Phys. Solids 69(1), 156–174 (2014). doi:10.1016/j.jmps.2014.05.003
Wang, M., Zhou, S., Ding, H.: Nonlinear diffusions in topology optimization. Struct. Multidiscip. Optim. 28, 262–276 (2004)
Wang, M.Y., Wang, X., Guo, D.: A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 192(12), 227–246 (2003). doi:10.1016/S0045-7825(02)00559-5
Wu, S., Serbin, J., Gu, M.: Two-photon polymerisation for three-dimensional micro-fabrication. J. Photochem. Photobiol. A Chem. 181(1), 1–11 (2006). doi:10.1016/j.jphotochem.2006.03.004
Xia, Q., Shi, T.: Constraints of distance from boundary to skeleton: for the control of length scale in level set based structural topology optimization. Comput. Methods Appl. Mech. Eng. 295, 525–542 (2015). doi:10.1016/j.cma.2015.07.015
Xia, Q., Shi, T., Wang, M., Liu, S.: A level set based method for the optimization of cast part. Struct. Multidiscip. Optim. 41(5), 735–747 (2010). doi:10.1007/s00158-009-0444-7
Xia, Q., Shi, T., Wang, M., Liu, S.: Simultaneous optimization of cast part and parting direction using level set method. Struct. Multidiscip. Optim. 44(6), 751–759 (2011). doi:10.1007/s00158-011-0690-3
Xie, Y., Steven, G.: A simple evolutionary procedure for structural optimization. Comput. Struct. 49(5), 885–896 (1993). doi:10.1016/0045-7949(93)90035-C
Xiu, D.: Numerical Methods for Stochastic Computations: A Spectral Method Approach. Princeton University Press, Princeton (2010)
Xu, S., Cai, Y., Cheng, G.: Volume preserving nonlinear density filter based on heaviside functions. Struct. Multidiscip. Optim. 41, 495–505 (2010)
Zauderer, E.: Partial Differential Equations of Applied Mathematics, 2 edn. Wiley, New York (1998)
Zhang, W., Xia, L., Zhu, J., Zhang, Q.: Some recent advances in the integrated layout design of multicomponent systems. J. Mech. Des. 133, 15 (2011)
Zhang, W., Zhong, W., Guo, X.: An explicit length scale control approach in SIMP-based topology optimization. Comput. Methods Appl. Mech. Eng. 282, 71–86 (2014). doi:10.1016/j.cma.2014.08.027
Zhao, J., Wang, C.: Robust topology optimization under loading uncertainty based on linear elastic theory and orthogonal diagonalization of symmetric matrices. Comput. Methods Appl. Mech. Eng. 273, 204–218 (2014). doi:10.1016/j.cma.2014.01.018
Zhao, L., Ha, S., Sharp, K.W., Geltmacher, A.B., Fonda, R.W., Kinsey, A.H., Zhang, Y., Ryan, S.M., Erdeniz, D., Dunand, D.C., Hemker, K.J., Guest, J.K., Weihs, T.P.: Permeability measurements and modeling of topology-optimized metallic 3-D woven lattices. Acta Mater. 81, 326–336 (2014). doi:10.1016/j.actamat.2014.08.037
Zhou, M., Fleury, R., Shyy, Y.K., Thomas, H., Brennan, J.: Progress in topology optimization with manufacturing constraints. In: 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization (2002). doi:10.2514/6.2002-5614
Zhou, M., Lazarov, B.S., Sigmund, O.: Topology optimization for optical projection lithography with manufacturing uncertainties. Appl. Opt. 53(12), 2720–2729 (2014). doi:10.1364/AO.53.002720
Zhou, M., Lazarov, B.S., Wang, F., Sigmund, O.: Minimum length scale in topology optimization by geometric constraints. Comput. Methods Appl. Mech. Eng. 293, 266–282 (2015). doi:10.1016/j.cma.2015.05.003
Zhou, M., Rozvany, G.: The COC algorithm, part II: topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 89(13), 309–336 (1991). doi:10.1016/0045-7825(91)90046-9
Zhou, M., Wang, M.Y.: Engineering feature design for level set based structural optimization. Comput. Aided Des. 45(12), 1524–1537 (2013). doi:10.1016/j.cad.2013.06.016
Zhu, J.H., Gu, X.J., Zhang, W.H., Beckers, P.: Structural design of aircraft skin stretch-forming die using topology optimization. J. Comput. Appl. Math. 246, 278–288 (2013). doi:10.1016/j.cam.2012.09.001
Zhu, J.H., Zhang, W.H., Xia, L.: Topology optimization in aircraft and aerospace structures design. Arch. Comput. Methods Eng. 1–28 (2015). doi:10.1007/s11831-015-9151-2
Zienkiewicz, O.C., Taylor, R.L., Zhu, J.: The Finite Element Method. Elsevier, Amsterdam (2005)
Acknowledgments
The authors acknowledge the financial support received from the NextTop project, sponsored by the Villum foundation and the Hypercool project J. Nr. 117-2014-1 sponsored by the Innovation Fund Denmark.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lazarov, B.S., Wang, F. & Sigmund, O. Length scale and manufacturability in density-based topology optimization. Arch Appl Mech 86, 189–218 (2016). https://doi.org/10.1007/s00419-015-1106-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-015-1106-4