Topology optimization with flexible void area

Abstract

This paper presents a methodology for including fixed-area flexible void domains into the minimum compliance topology optimization problem. As opposed to the standard passive elements approach of rigidly specifying void areas within the design domain, the suggested approach allows these areas to be flexibly reshaped and repositioned subject to penalization on their moments of inertia, the positions of their centers of mass, and their shapes. The flexible void areas are introduced through a second, discrete design variable field, using the same discretization as the standard field of continuous density variables. The formulation is based on a combined approach: The primary sub-problem is to minimize compliance, subject to a volume constraint, with a secondary sub-problem of minimizing the disturbance from the flexible void areas. The design update is performed iteratively between the two sub-problems based on an optimality criterion and a discrete update scheme, respectively. The method is characterized by a high flexibility, while keeping the formulation very simple. The robustness and applicability of the method are demonstrated through a range of numerical examples. The flexibility of the method is demonstrated through several extensions, including a shape measure requiring the flexible void area to fit a given reference geometry.

1 Introduction

Structural engineering design problems are generally associated with geometrical restrictions. A common restriction is that void space should be reserved for functional or manufacturing specific reasons. Functional restrictions include e.g. other components passing through the structure or prescribed objects to be embedded. Holes for components passing through may or may not have a rigidly prescribed geometry and position, whereas embedded objects usually have a prescribed geometry. Manufacturing restrictions include reserving space for the assembly process or maintenance. The exact position and shape of the corresponding holes are usually not strictly defined.

Another area where structural optimization is increasingly being used is architecture (see e.g. (Stromberg et al. 2012)). Here geometrical restrictions are usually tightly connected to aesthetic considerations, meaning that prescribed holes may be attributed a considerable flexibility in terms of shape and position.

This paper considers design problems which are approached as a minimum compliance problem solved using topology optimization with the standard density approach (Bendsøe and Sigmund 2003). Holes or objects of a fixed shape and position are usually included by defining passive areas in the design domain, i.e. areas with a prescribed density. The corresponding elements are excluded from the set of design variables, but included in the evaluation of the structural response.

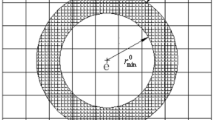
The passive elements method is easy to implement, but has certain drawbacks. As an example, consider the cantilever beam problem with a circular void inclusion shown in Fig. 1. Unless the shape of the hole is carefully defined, the resulting optimized structure may contain irregular beams (see Fig. 2), possibly with unwanted singularities. Furthermore, the position of the hole strongly impacts the compliance of the optimized structure (see Fig. 3). Problems also arise when structural optimization is used very early in the design phase. The method of defining fixed, passive areas requires a clear specification of the design space. Design choices made very early in the process will generally be based on experience rather than optimization, with the risk of choosing sub-optimal configurations which cannot be changed later. For holes where the shape and position are less strictly defined, the standard approach is therefore undesirable.

Fig. 1

Design domain for cantilever beam with void inclusion denoted by the dashed circle. The circle has radius l y/3 and the center is located at (2l x/3,l y/2)

Fig. 2

Optimized structure (160 by 100 elements) for problem defined in Fig. 1, using the passive elements method. Parameter data provided in Section 4. Compliance ϕ = 80.67

Fig. 3

Changing the position of the fixed circular void inclusion for the problem illustrated in Fig. 1 has a major impact on the compliance of the optimized structure. The figure shows how the compliance varies with varying position of the x-coordinate for the center of the circular void inclusion (the y-coordinate is fixed at l y/2). The compliance is normalized with respect to the optimized structure shown in Fig. 2

Different alternatives to the passive elements approach have been explored, in which the shape and position of embedded holes or objects are attributed a certain amount of freedom. (Qian and Ananthasuresh 2004) present a methodology for solving “the embedding problem” of optimally embedding predesigned objects of fixed geometry and stiffness into a design region, and simultaneously designing the topology of the connecting structure to optimize a characteristic of the overall assembly. The method is demonstrated with multiple objects, each determined by three design variables (in 2D): Centroid coordinates and part orientation. (Zhu et al. 2009) present a similar methodology for integrated layout design of multi-component systems, including a non-overlap constraint by means of the finite circle method and several other constraints, including a constraint of the gravity center position of the total structure (supporting structure and embedded objects together). The field of integrated layout design of multicomponent systems, also encompassing topology optimization with moveable components, is treated in an overview paper by (Zhang et al. 2011). Within the same area, (Xia et al. 2012) suggest a material perturbation model for the sensitivity analysis, as opposed to a usual geometric perturbation model. The authors’ attention have been drawn to the fact that the problem of embedding objects of fixed shape has earlier been approached with a combination of the density approach and the level set method, incl. a nonoverlap constraint. The work has appeared in Chinese language only.¹

(Kang Z and Wang Y 2012) present an approach for topology optimization with embedded, moveable holes (void areas) of fixed geometry. The method combines the density approach with the level-set method (for hole shape description). Like the above mentioned “embedding problem”, the position and rotation of each embedded object are determined by three design variables (2D), referred to as pseudo-velocities (two variables for the translational motion of the centroid, and one for the rotational motion). A non-overlap constraint based on a single integral-type constraint is included.

(Mei et al. 2008) present a method for constructing a topology optimized design from geometric primitives, such as circles, triangles, etc. The Constructive Solid Geometry (CSG) method is employed to gradually insert the primitives based on topological derivative analysis. In a recent paper, (Zhou M and Wang MY 2013) propose a method for combining feature design and topology optimization, more specifically combining CSG modeling and level set based shape and topology optimization. Each geometric feature is represented by a sub-level set half-space model, which is individually updated. On top of the three design variables used in the above papers, a fourth variable, a homogeneous scaling coefficient, is introduced for each sub-level set model. Thereby the method can represent shapes which may be obtained from affine transformations of the sub-level set models.

This paper presents a new method for including a flexible void area (hole) into a minimum compliance optimization problem. The main difference from the approaches in the above mentioned papers is in the void definition, allowing for full flexibility of the void space: Rather than using a level set function, the void is defined by means of a second design field. This field describes the flexible void area by means of discrete variables, and uses the same discretization as for the usual density variables. The discrete formulation allows the void region to take any shape and position, satisfying a connectivity and constant area requirement.

The paper is organized as follows. Section 2 presents the problem formulation, where the flexible void definition is presented, including the definition of two flexibility penalization measures (Section 2.1-2.2). The same Section presents a formal definition of the optimization problem, sensitivity analysis, and considerations related to the use of a sensitivity filter (Sections 2.3-2.5). In Section 3 the design update scheme is presented, with focus on the discrete update of the flexible void field. Section 4 presents a range of numerical results, followed by two examples of extensions to the method in Section 5. The method and the presented results are discussed in Section 6. Section 7 concludes the work.

2 Problem formulation

The introduction of a flexible void area through a second design field requires a formulation that allows for sensitivity calculation as the basis for design updates. Such a formulation is presented in the following subsection. Derived challenges such as properly defining penalization measures on the void shape and position, and formally including the flexibility into the optimization problem are treated in the following subsections.

2.1 Flexible void formulation

For a standard minimum compliance problem, the element densities, ρ _e , of the FE discretization are used as (continuous) design variables. As described in Section 1, the passive elements method copes with fixed objects by defining passive elements with a prescribed density. If the set of passive elements should be allowed to change during the optimization, a different formulation is required. For this end a second design variable, μ _e , is introduced for each element, defining whether the element is within the flexible void region or not. This variable may be interpreted as defining a second design field discretized the same way as the density variables. The flexible void variables are chosen to be discrete, as this allows for a convient design update scheme (see Section 3). The variables are allowed to take the value of either 1 (within flexible void) or 0 (outside flexible void). This way, by letting Ω refer to the entire, discretized design domain, the void area, B, may be formally defined as

$$ B = \left\{ e \in \varOmega \, | \, \mu_{e} = 1 \right\} $$

(1)

and the physical element density as

$$ \hat{\rho}_{e} = \rho_{e} (1-\mu_{e}) $$

(2)

The two fields are shown in Fig. 4. The flexible void should stay connected and with constant area throughout the optimization. Only changes in μ fulfilling these requirements are allowed.

Fig. 4

Arbitrary design domain, Ω. a Physical field described by $\boldsymbol {\widehat {\rho }}$. Standard passive elements are indicated by black (solid) and white (void), whereas the flexible void is indicated by white with a dashed interface. b Corresponding flexible void field described by μ. Void is defined by μ _e = 1 (black area). μ _e = 0 everywhere else

2.2 Void flexibility measures

A convenient way to interpret the flexible void region is as a geometrical entity, having a mass (area), a center of mass, and a moment of inertia. For some applications, the void area may be allowed to deform or move freely during the optimization, but for many applications the degree of flexibility is constrained by practical limitations. For this reason two different penalization measures are introduced: A deformation measure and a location measure. These may be included either individually or combined.

2.2.1 Deformation measure

The degree of deformation of the void is controlled using its moment of inertia, I(μ), normalized by a reference value, I ₀. Thus, the deformation measure, g ₁(μ), may be defined in the following way:

$$ g_1 (\boldsymbol{\mu}) = \frac{I(\boldsymbol{\mu})}{I_{0}} $$

(3)

where

$$ I(\boldsymbol{\mu})= {\displaystyle\sum\limits_{i=1}^{n}} \mu_{i} v_i r_{i}^{2} $$

(4)

Here, v _i is the element volume and r _i is the distance from the center of element i to the center of mass of the void area (the field μ). As the lowest possible moment of inertia for an object of a given area occurs when it is shaped as a circle, this value is chosen as the reference, I ₀. With this choice g ₁(μ) ≥ 1 for any μ satisfying the void volume constraint. Fig. 5 provides a few example values of the deformation measure.

Fig. 5

Example values of the deformation measure, g ₁(μ), for different shapes of a void region of constant area

2.2.2 Location measure

The freedom of translational motion is controlled using the void region’s center of mass. The location measure, g ₂(μ), is chosen as the (squared) radial distance, r _{c m} , from a given reference point, p ₀ = (x ₀,y ₀), to the void region’s center of mass, (x _{c m} ,y _{c m} ), normalized by a reference distance, r ₀:

$$ g_2 (\boldsymbol{\mu}) = \frac{ r_{cm}^{2}}{r_{0}^{2}} $$

(5)

with

$$ r_{cm}^{2}= {\displaystyle\sum\limits_{j=1}^{2}} (x_{cm}^{j}-x_{0}^{j})^{2}= {\displaystyle\sum\limits_{j=1}^{2}} \left(\frac{ {\displaystyle\sum\limits_{i=1}^{n}} \mu_{i} v_i x_{i}^{j}}{M}-x_{0}^{j}\right) ^{2} $$

(6)

The summation over j refers to the two coordinates (x, y), and M is the total mass of the void area, defined by

$$ M= {\displaystyle\sum\limits_{i=1}^{n}} \mu_{i} v_i $$

(7)

The reference distance used for normalization, r ₀, is chosen as the radius of a circle having the same area as the void.

It should be noted that the element volume, v _e , is part of the expressions for the deformation measure and the shape measure. However, as long as the analysis is performed on a uniform mesh the element volume may be ignored in these expressions.

2.3 Optimization problem

The inclusion of a flexible void area, as defined in the previous subsections, leads to a combined minimization problem. The primary problem is to minimize compliance, subject to a volume constraint. A sub-problem is to minimize the disturbance from the void, subject to restrictions on the shape and location. By including the void flexibility measures by means of the penalty method, the optimization problem may be defined in the following way:

$$ \min\limits_{\boldsymbol{\rho}, \boldsymbol{\mu}}: f(\boldsymbol{\rho}, \boldsymbol{\mu}) = \alpha_0 \phi(\boldsymbol{\rho}, \boldsymbol{\mu}) + {\displaystyle\sum\limits_{k}}{\alpha_k g_k (\boldsymbol{\mu}) } $$

$$\begin{array}{@{}rcl@{}} subject to: & \mathbf{KU=F} \\ & g_0(\boldsymbol{\rho}, \boldsymbol{\mu}) = V(\boldsymbol{\hat{\rho}})/V^{*} - 1 \leq 0 \\ \\ & \mathbf{0}\leq\boldsymbol{\rho} \leq \mathbf{1} \\ & \mu_{e}\in \{0,1\}\\ \\ &\widetilde{V}(\boldsymbol{\mu}) = \widetilde{V}^{*} \\ &\text{\textit{B} simply connected} \end{array} $$

(8)

Here f(ρ, μ) is the objective function expressed in terms of the two vectors of design variables, ρ and μ, ϕ(ρ, μ) is the compliance, α ₀ is a normalization factor for the compliance function, α _k is the weight of the penalization measure g _k (μ), K is the global stiffness matrix, U and F are the global displacement and force vectors, respectively, g ₀(ρ, μ) is the volume constraint, $V(\boldsymbol {\hat {\rho }}) = \sum {v_i \widehat {\rho }_{i}}$ and V ^∗ are the material volume and maximum allowed volume, respectively, and $\widetilde {V}(\boldsymbol {\mu })$ and $\widetilde {V}^{*}$ are the actual and required flexible void volume, respectively. The requirement that B be simply connected implies that this domain cannot contain holes. The compliance normalization factor, α ₀, is chosen as 1/4 of the the compliance of the case where the total material volume, V ^∗, is distributed equally over all non-void elements.

Using the modified SIMP approach, the Young’s modulus of an element is a function of the design variable, $\widehat {\rho _e}$:

$$ E(\widehat{\rho}_{e}) = E_{\min} + \widehat{\rho}_{e}^p (E_{0}-E_{\min}) $$

(9)

The global stiffness matrix, K, is defined as:

$$ \mathbf{K} = \sum\limits_e \mathbf{k}_e (\widehat{\rho_e}) = \sum\limits_e E(\widehat{\rho_e})\mathbf{k}_e^0 $$

(10)

where k _e is the element stiffness matrix, dependent on the element design variable, and $\mathbf {k}_e^0$ is the element stiffness matrix for an element with unit Young’s modulus. In this paper, the values E ₀ = 1 and $E_{\min } = 10^{-9}$ are used.

2.4 Sensitivity analysis

The formulation in which both ρ and μ are design variables, means that sensitivities must be calculated with respect to both ρ _e and μ _e . Differentiation with respect to ρ _e gives:

$$ \frac{\partial\phi}{\partial\rho_{e}}=\frac{\partial\phi}{\partial \widehat{\rho}_{e}}\frac{\partial\widehat{\rho}_{e}}{\partial\rho_e}=-p\left(E_{0}-E_{\min}\right) \widehat{\rho}_{e}^{p-1} \mathbf{u}_{e}^{T}\mathbf{k}_e^0\mathbf{u}_{e}\left(1-\mu_e\right) $$

(11)

$$ \frac{\partial g_{0}}{\partial\rho_{e}}=\frac{v_e}{V^{\ast}}\left(1-\mu_{e}\right) $$

(12)

$$ \frac{\partial g_{1}}{\partial\rho_{e}}=\frac{\partial g_{2}}{\partial \rho_{e}}=0 $$

(13)

Differentiation with respect to μ _e gives:

$$ \frac{\partial\phi}{\partial\mu_{e}}=\frac{\partial\phi}{\partial \widehat{\rho}_{e}}\frac{\partial\widehat{\rho}_{e}}{\partial\mu_{e}}=p\left(E_{0}-E_{\min}\right) \widehat{\rho}_{e}^{p-1}\mathbf{u}_{e}^{T}\mathbf{k}_e^0\mathbf{u}_{e} \rho _{e} $$

(14)

$$ \frac{\partial g_{1}}{\partial\mu_{e}}=\frac{v_e r_{e}^{2} }{I_{0}} $$

(15)

$$ \frac{\partial g_{2}}{\partial\mu_{e}}=\frac{2 v_e}{M r_{0}^{2}} {\displaystyle\sum\limits_{j=1}^{2}} (x_{cm}^{j}-x_{0}^{j}) (x_{e}^{j}-x_{cm}^{j}) $$

(16)

The positive sign in (14) (opposite compared to density variable sensitivities, (11)) is due to the choice of representing void elements with μ _e = 1 and non-void with μ _e = 0, meaning that an increase in a void variable implies a larger void and thereby a larger compliance.

The sensitivity of the volume constraint, g ₀, with respect to μ _e is not used, as the update scheme for μ does not require this constraint to be satisfied (see Section 3.1).

2.5 Sensitivity filtering

Topology optimization algorithms usually employ some sort of filtering to prevent numerical instabilities, such as checkerboards and mesh-dependency. A popular choice is the sensitivity filter (Sigmund 1994, 1997). The method was originally implemented as a heuristic modification of strain energy densities, but in a recent paper it was demonstrated that the filtering corresponds to optimizing for a nonlocal elasticity formulation (Sigmund and Maute 2012) and thereby is physically well-founded. The filtering is given by the expression:

$$ \widetilde{ \displaystyle \frac{\partial\phi}{\partial\rho_{e}}}=\frac{\sum\limits_{i\in N_{e}}w(\mathbf{c}_{i}) \rho_{i} \frac{\partial\phi}{\partial\rho_{i}} / v_{i}} {\rho_{e} / v_{e} \sum\limits_{i\in N_{e}}w(\mathbf{c}_{i})} $$

(17)

where

$$ w(\mathbf{c}_{i})=R-\left\Vert \mathbf{c}_{i}\mathbf{-c}_{e}\right\Vert $$

(18)

is a linearly decaying weight function, R is the filter radius, N _e is a list of elements for which the centers lie inside the filter radius, and c _j is the spatial location of the center of element j. In order to assure a non-zero denominator the density weight is defined as $\max (\rho _{e}, 10^{-3})$. The filtering is performed similarly for the sensitivities with respect to the discrete variable, μ, except that the density weight is defined as $\max (1-\mu _{e}, 10^{-3})$.

For consistency, the interface of the flexible void area and the domain border should influence neighboring elements in the same way. If elements outside the domain are attributed zero sensitivity, this simply corresponds to using the same normalization factor, $\sum _{i\in N_{e}}w(\mathbf {c}_{i})$, for all elements in the entire domain, i.e. assuming N _e being of full size.

3 Design update scheme

As described in Section 2, the overall optimization problem may be interpreted as two sub-problems, formulated in the two different variables ρ and μ. These two sub-problems are strongly coupled, as may be seen from the sensitivity expressions in  (11) and (14). The chosen discrete representation of μ allows to conveniently assure that the two geometrical requirements on the flexible void area, the connectivity requirement and the constant area requirement, be satisfied. The connectivity requirement is satisfied by only letting elements along the interface of the void area change during an update, and the constant area requirement is satisfied by swapping an equal number of elements between the interior and the exterior of the void area (see Section 3.1 for details).

The discrete nature of μ implies that the design variables ρ and μ should be updated separately. The design update is performed in an iterative manner, including the following two steps:

• With a fixed void area (fixed μ), perform a certain number of design updates for the minimum compliance sub-problem in the design variable ρ, using a standard optimality criterion method (see e.g. (Bendsøe M 1995))

• Perform a discrete update of the void variable, μ, satisfying the connectivity and constant area requirements

The flow chart for the entire optimization algorithm is shown in Fig. 6.

Fig. 6

Flowchart for optimizing with flexible void area

For the test problems it has shown appropriate with 3 iterations of the continuous field, ρ, before updating the flexible void area, μ. The overall optimization problem is considered converged, when the two sub-problems simultaneously attain convergence. The sub-problem in ρ is considered converged when the maximum (absolute) element density change is below the convergence criterion (=0.01). Convergence of the sub-problem in μ is discussed in the following section.

3.1 Update of flexible void area

As mentioned above, the update scheme for the flexible void area, μ, must comply with both the connectivity requirement (safisfied by only changing elements along the interface of the flexible void during an update) and the constant area requirement (satisfied by swapping an equal number of elements between the interior and the exterior of the void area).

The interface elements can be identified by applying a density filter (Bruns and Tortorelli 2001; Bourdin 2001) to the flexible void field, μ. Thereby interface elements get intermediate density, which may then be identified. The radius of the filter, r _i , determines the width of the interface, and thereby which elements are allowed to change. If only elements right at the interface should be allowed to change, this radius should take a value in the interval $1 < r_{i} < \sqrt {2}$ (for a mesh with square unit length elements). For many problems, a larger radius will lead to similar results, and may therefore be chosen to accelerate the optimization. However, if the radius is too high, the flexible void area may split into two different regions, e.g. by “jumping” over a thin bar. A simple way to assure connectivity of the void area is to keep r _i within the aforementioned interval.

The method requires a maximum for the number of flexible void elements allowed to change per iteration. Otherwise, elements at the interior and exterior of the same interface point might change simultaneously, implying non-connectivity. On the other hand, if too few void elements are changed the algorithm risks getting stuck in a local minimum. For the examples shown in this paper, the initial maximum value was chosen as 20% of the number of interface elements on a reference circle with the same area as the flexible void. Numerical experiments have shown that this approach is robust and independent of the test problem. It should be noted that when one or both penalization functions are applied (α ₁ > 0 or α ₂ > 0), the sensitivities are less homogeneous, as the contributions from the compliance expression and the penalization measures may be conflicting. In this case it might be necessary to choose a lower initial maximum number, e.g. 10-15 %.

The constant area requirement for the flexible void means that any design update corresponds to swapping an equal number of elements from within the void (interior) with elements outside the area (exterior). The discrete design update is based on ranking the sensitivities of the interface elements, quite similar to the approach employed in the BESO method (for a review, see e.g. (Huang and Xie 2010)). Interior and exterior elements are ranked separately. The interior elements with highest sensitivity are swapped with an equal number of exterior elements with the lowest sensitivities. The material volume constraint, g ₀(ρ, μ), is not taken into account in this scheme, as a minor violation is quickly counteracted by the subsequent update of the continuous field, ρ.

In order to prevent oscillating updates of the flexible void area, a move limit scheme is introduced, based on the last two updates of μ. If the compliance has not developed monotonously, the maximum number of elements allowed to change per iteration is decreased by a factor of 0.95. Inversely, if the compliance develops monotonously, the maximum number is increased by a factor of 1.03, though never above the initial limit of 20 %. The sub-problem is considered converged when the maximum number reaches 0.

4 Results

The following section presents a range of numerical examples to demonstrate the robustness and wide applicability of the presented method.

Where nothing else is mentioned, the problems are solved using unit length square elements, sensitivity filter radius R = 6, density filter radius r _i = 1.2 (for identification of void interface), and a volume constraint, V ^∗, of 40 % of the total volume. The optimization shown in Fig. 2 is likewise performed using these parameter values.

4.1 Progression of flexible void area

In order to demonstrate the optimization process, the design problem shown at the beginning of the paper, in Fig. 1, is used as an example.

The development is shown without applying the flexibility measures, i.e. α ₁ = α ₂ = 0. Snapshots from the iteration history are shown in Fig. 7. The flexible void area develops from being a circle placed at a sub-optimal location into a relocated (rounded) triangle, allowing the surrounding structure to assume an optimized shape, almost undisturbed by the void inclusion. It may be noticed that the method, in line with the passive elements method, leads to a sharp solid/void interface between the flexible void area and solid parts of the continuous field. As mentioned in Section 2.5, the interface is treated the same way as the outer domain border in terms of filtering.

Fig. 7

Iteration history for optimization of the problem shown in Fig. 1. The flexible void area is updated for every third iteration of the continuous problem, or when the continuous problem has converged

The compliance of the optimized structure (ϕ = 59.25) is 27% lower than for the fixed circle case (ϕ = 80.67). The compliance convergence is shown in Fig. 8. The compliance is seen to decrease stably, despite the discrete updates (seen as small bumps in the graph, see also detail). The topological change occuring around iteration 150 (a bar is eliminated, see Fig. 7) translates to a rapid decrease in compliance.

Fig. 8

Compliance development for optimization of the problem shown in Fig. 1. The compliance is normalized with respect to the optimized structure obtained using the passive elements method (see Fig. 2). The black dots refer to the iteration snapshots shown in Fig. 7

4.2 Size of flexible void area

The algorithm is able to handle flexible void areas of considerable size. To illustrate this, the problem from Fig. 1 (optimized structure shown in Fig. 7) is investigated using a larger void area. The radius of the initial void circle is increased by 25 %, from l y/3 to 5l y/12, corresponding to an area increase of 56 %. The optimized structure is compared to the original result in Fig. 9. The compliance has obviously increased due to the larger void area, but the geometry is very similar, except that the structure with the larger void area has been forced to fix the left diagonal cross bar at a higher point of the supported edge. The number of iterations has increased from 365 to 507.

Fig. 9

Influence of varying the size of the void area. In both cases the design domain from Fig. 1 is used, except that the radius of the initial void circle is increased for the structure shown in Fig. 9b

4.3 Validation of flexibility measures

In order to visualize the influence of the void flexibility measures, g ₁ and g ₂, the initial design in Fig. 10 is used. The figure refers to the flexible void variable μ. For the validation, the structural part is eliminated such that only penalization terms are active (α ₀ in (8) is set equal to 0), meaning that loads and supports are of no importance. The entire domain outside the flexible void area is allowed to be filled with material, meaning that the volume constraint is not active. The reference point, p ₀, for the location measure, g ₂, is indicated by a ×. In Fig. 11 the resulting “optimized” flexible void areas are shown. Application of the deformation measure alone (α ₁ = 1, α ₂ = 0) leads to a perfect circle with an unchanged center. Application of the location measure and deformation measure simultaneously (α ₁ = 1, α ₂ = 1) leads to a perfect circle centered at the reference point.

Fig. 10

Flexible void field, μ, used for verification of the two penalization terms. The center of the initial square void is located at (2l x/3,l y/2). The reference point, p ₀ (shown as a ×), is located at (l x/3,l y/2)

Fig. 11

Validation of penalization with flexibility measures, using the domain defined in Fig. 10 with α ₀ = 0. a Deformation measure alone (α ₁ = 1, α ₂ = 0). b Location measure and deformation measure applied simultaneously (α ₁ = 1, α ₂ = 1)

Application of the location measure alone, without an underlying compliance optimization, is numerically unstable. The reason is that the sensitivities for the location measure always constitutes monotonically changing isolines perpendicular to the vector from the void region center of mass to the reference point, p ₀, with the zero line passing through the center of mass. If the reference point is located outside the void region, this means that small bars perpendicular to the isolines will evolve in the flexible void region, and eventually violate the connectivity requirement. If a minimum compliance problem is solved simultaneously, this effect is counteracted by the compliance sensitivities, however the problem may still arise if the penalization weight, α ₂, is too high. The effect may to some extent be remedied by simultaneously applying the deformation measure, g ₁, as demonstrated in Fig. 11b. Issues with the connectivity requirement related to application of the location measure are further discussed in Section 6.

4.4 Effect of the flexibility penalization measures

The effect of the two flexibility penalization measures may be investigated by optimizing an identical problem with and without applying the penalization measures. The results are shown in Fig. 12. In Fig. 12a the optimization is run without applying the penalization measures, leading to the result which is already shown in Fig. 7. The same topology is obtained when the deformation measure, g ₁, is applied alone (see Fig. 12c) with α ₁ = 1. However, the void area is forced to assume a more rounded shape, leading to a higher disturbance of the structure and thereby a slightly higher compliance. When applying the location measure, g ₂, alone (see Fig. 12b) with α ₂ = 10 and the reference point, p ₀, at the center of the initial void area, a different topology is obtained. Due to the forced location of the void area, the compliance is significantly higher, but the void area smoothly follows the structure, thereby avoiding dents in the surrounding bars. When the two measures are applied simultaneously (see Fig. 12d), the same topology is obtained as when applying the location measure alone, however, in line with the result from Fig. 12c the presence of the deformation measure forces the void area into a more rounded shape. The void interface no longer “sticks” to the structure in the corners, leading to a higher compliance.

Fig. 12

Effect of the flexibility penalization measures on a minimum compliance problem, using the domain defined in Fig. 1. The reference point is equal to the center of the initial void area, p ₀ = (2l x/3,l y/2). a No flexibility measure applied. b Location measure alone. c & e Deformation measure alone. d & f Location measure and deformation measure applied simultaneously

In Fig. 12e and 12f, the optimizations from Fig. 12c and 12d, respectively, are repeated with a higher weight on the deformation measure (α ₁ = 10). This implies that the final shape of the flexible void area becomes close to circular. The limited flexibility of the void area also means, however, that the algorithm is not able to break down the slender bars. Therefore, the optimization shown in Fig. 12e, with the deformation measure applied alone but with a high weight, ends with the same topology as when the location measure is applied.

4.5 Mesh-independency

The method described in this paper leads to similar designs when using various discretizations for the same problem. This is illustrated in Fig. 13, where the optimized structure from Fig. 7 is compared with the very similar geometry obtained with a higher discretization (twice as many elements in both the x− and y−direction and a sensitivity filter radius, R, extending over twice as many elements). The difference in compliance is 2.4 %. This number is equal to the difference obtained when running the two problems without a void area, meaning that the difference is not due to variations in the final design, but inherent for the refined discretization.

Fig. 13

Influence of refining the discretization. Similar structures are obtained

The interface width of the flexible void area is determined using the same density filter radius, expressed in number of elements. This means that the void area will progress more slowly in the fine discretization case, as it will need twice as many steps to progress the same distance in the domain. The iteration number is therefore larger for the fine discretization (542 iterations) compared to the base case (365 iterations).

4.6 Moving circle

The flexible void method is an efficient way to reduce the disturbance from void inclusions. This is already illustrated in Section 4.1, Figs. 7-8, where the compliance is reduced by more than 25% by letting the void inclusion take a flexible shape and position. Also in the case where the position is restricted, the method may increase the performance of the optimized structure. This is illustrated in Fig. 14. In line with Fig. 3, the figure describes the variation in compliance with varying position of the void inclusion, but in this case, a position measure penalization is applied, with the reference point, p ₀, equal to the center point of the initial circle. For the solid line, the compliance is normalized with respect to the optimized structure shown in Fig. 2. The dotted line compares the passive and flexible void cases directly: The compliance for the flexible void optimization is normalized with respect to the corresponding passive element void inclusion (with same initial center). As expected, the flexible void method provides a lower compliance for all positions of the reference point. Comparison with the solid line shows, that the gain increases with increasing compliance for the test case, i.e. for more challenging positions of the inclusion.

Fig. 14

Variation of compliance with varying position of the x-coordinate for the center of the (initially circular) flexible void inclusion (y = l y/2), see reference domain in Fig. 1. Location penalization applied with p ₀ equal to the initial center, and α ₂ = 10. For the solid line, the compliance is normalized with respect to the optimized structure shown in Fig. 2. For the dashed line, the compliance is normalized with respect to the corresponding passive element void inclusion, i.e. the values of the graph in Fig. 3

4.7 Facade optimization in architecture

As briefly mentioned in the introduction, topology optimization is being increasingly used in architectural contexts. An example design problem is a concrete facade with a single, large window of fixed size, which may take any shape. The design domain, starting from a standard design, is shown in Fig. 15 (the × indicates the center of mass of the initial window). The facade should mainly be supporting a beam at the center, as indicated by the load case. The entire domain outside the flexible void area is allowed to be filled with material, meaning that the volume constraint is not active.

Fig. 15

Design domain for the facade optimization problem. The initial window is a square with side length l y/2, and the upper right corner placed at (l x/2,l y/4). The maximum material volume, V ^∗, is chosen such that all non-void elements are allowed to have maximum density (=1)

This constrained shape optimization problem may be solved using the flexible void method. Two optimized designs are shown in Fig. 16. In Fig. 16a, there are no restrictions on the position of the window, and the symmetric, (rounded) triangular shape of the flexible void is obtained. The design in Fig. 16b is obtained by applying the location measure penalization with α ₂ = 10. The design still follows the triangular shape at the left part, where it disturbs the load path least possible. The effect of varying the value of α ₂ is shown in Fig. 17. When increasing α ₂, the center of mass of the flexible void in the optimized design approaches the reference point (the center of mass of the initial window). With α ₂ = 100, the distance is below 1/10 of an element.

Fig. 16

Optimized designs for the facade optimization problem shown in Fig. 15. Only the flexible void field, μ, is shown, as the volume constraint is not active in the problem. a Optimization with no flexibility measures applied (α ₁ = 0, α ₂ = 0). b Optimization with location measure penalization (α ₁ = 0, α ₂ = 10)

Fig. 17

Influence of the weight, α ₂, of the location penalization measure, g ₂, demonstrated for the facade optimization problem defined in Fig. 15. The center of mass of the flexible void area (marked by a solid circle) is seen to approach the reference point (marked by a ×) as α ₂ increases

4.8 Design domain flexibility

Instead of representing a void inclusion, the flexible void formulation may alternatively be used to define a certain flexibility in the design domain. In this case the flexible void should initially be placed along the border of the domain. As opposed to the general case, where the flexible void area should be able to progress across potential bars (as in Fig. 7), the flexible void is in this case only supposed to reshape along the edge of the structure. For this reason, the filter radius R of the sensitivity filter has less influence of the ability of the flexible void to develop, meaning that a small filter radius will be sufficient.

An example of a flexible domain is the L-shape domain shown in Fig. 18. The standard passive elements method leads to the design shown in Fig. 19, using filter radius R = 2.1 and a volume constraint of 25 %. It is well-known that this design suffers from a singulariy at the corner of the passive void area. The same problem is optimized using the flexible void method, see Fig. 20a (α ₁ = 0) and Fig. 20b (α ₁ = 10), again with R = 2.1. In both cases the optimized designs exploit the opportunity of cutting the edge, while restricted from extending too far into the flexible void area. In the case where the deformation measure is applied (α ₁ = 10), the structure is extending less into the initial void area.

Fig. 18

Design domain for optimization of L-shape domain combined with a flexible void

Fig. 19

Optimization of the problem described in Fig. 18, using the passive elements method

Fig. 20

Optimization of the problem described in Fig. 18, using the flexible void method. The initial void area is indicated by the dashed square. a Optimization with no flexibility measure applied (α ₁ = α ₂ = 0). b Optimization with deformation measure (α ₁ = 10, α ₂ = 0)

4.9 Bridge

In order to illustrate the flexible void method on a larger example, the bridge problem shown in Fig. 21 is considered. The problem involves an initially rectangular void area placed at the bottom center of the domain (see Fig. 21a), with the dimensions (l x/2)×(2l y/3). The optimization is performed with a 800×200 elements discretization, 25 % volume fraction, sensitivity filter radius R = 8, and density filter radius for interface identification r _i = 1.2. The equally distributed load sums up to 1.

Fig. 21

Optimization of the bridge problem. Comparison of results obtained without void area (b), with the passive elements method (c), and with the flexible void method (d). The distributed load sums up to 1. The dimensions of the initial void rectangle placed at the bottom center of the domain is (l x/2)×(2l y/3)

For reference, the problem is first optimized without a void area, see Fig. 21b. However, if space is required under the bridge, e.g. for a train passing through, the void area should be included in the optimization. The results using the passive elements method and the flexible void method are shown in Fig. 21c and 21d, respectively. The compliance obtained using the flexible void method is strongly decreased, from 5.03 to 2.16 (57 %), and the design does not contain singularities. The possibility for rounding the corners of the void area allows to distribute the load much more evenly in the structure. Obviously, further design steps would be required to assure the right dimensions of the passage under the bridge, but the example illustrates the usefulness of the method in the early design phase.

5 Extensions

This section shows how the flexible void method may immediately be extended to include multiple void areas. Furthermore, a shape measure is introduced, requiring the flexible void area to fit a given reference geometry with a certain accuracy.

5.1 Multiple void areas

The method may easily be extended to include multiple flexible void areas, simply by defining multiple void fields, μ ¹, μ ², ..., μ ⁿ. Only minor modifications to the design update scheme described in Section 3 are required. Several approaches are possible. For the present implementation it has been chosen to update each flexible void area individually, without recomputing sensitivities (or the structural response) between the updates of individual void areas. When updating a void area, only interface elements which do not coincide with another flexible void area are allowed to change. This assures non-overlap of void areas, and thereby that the total flexible void area remains constant. The various penalization measures may be applied simply by adding the average across void areas to the compliance value in the objective function.

Figure 22 compares two examples of optimizing with two flexible void areas of equal size (and equal size across the two examples). For the first example (Fig. 22, left), the two void areas are initially further separated than in the second example (Fig. 22, right). The first example shows a standard situation where the two void areas remain separated throughout the optimization. In this case the behavior of each void area is highly similar to the corresponding single void area case.

Fig. 22

Optimization using multiple flexible void areas. In both examples the two void areas have size (2l y/3×l y/3). a Example 1: Centers of void areas placed in (l x/2,l y/4) and (l x/2,3l y/4). b) Example 2: Centers moved l y/10 towards each other. c Optimized structure from (a), c = 61.62. d Optimized structure from (b), c = 62.59

The second example illustrates the situation where two void areas merge from an initially divided state. Ideally, a merged area would behave similar to a single void area of the same size. However, since the update of elements is performed indidually for each void area, low sensitivity elements from one void area interface are not allowed to swap with high sensitivity elements from the other void area interface, thereby slowing down motion perpendicular to the interface between the two void areas. Another particular issue should be noticed. Since one void area is always updated before the other, low sensitivity elements at the interface between the two void areas will always be occupied by the first updated area. This possibly implies that the first void area slowly “floats” around the other area, until this latter area is completely absorbed in the first. This is partially occuring at the “tip” of the merged void areas in Fig. 22f. Another effect impeding motion perpendicular to the interface between the two void areas is that once the two areas are merged, the sensitivities along the interface of the two areas will remain zero, as all elements within the sensitivity filter radius have minimum density. This heavily impedes the flexible void areas to subdivide again, once they are merged. These effects combined imply that a merged flexible void area will have a tendency of moving in a direction parallel to the interface between the two areas, even though this direction would not necessarily be optimal. If the merged case arises it is recommended to substitute the merged areas with a single void area.

The two design problems presented in Fig. 22 only differ by the initial position of the flexible void areas. In the second example, where the space between the areas is smaller, the areas merge. More generally speaking, two void areas will have a tendency to merge if the sensitivities of elements between the void areas are smaller (absolute value) than sensitivities of elements at the remaining interface elements for at least one of the void areas. As in the second example, this will happen when the space between the areas is so small that no initial structural member passing through the areas will be formed. In this case the sensitivities will remain low. Simultaneously, structural members are enhanced around the flexible void area to compensate for the low stiffness in and between the void areas. Thus, sensitivities in these enhanced areas will be higher. The combined effect of these circumstances will imply a tendency of the void areas to merge.

5.2 Shape measure

The combined approach adopted in this paper introduces a high degree of flexibility for including geometrical constraints. The alternation between continuous and discrete updates makes it possible to use various heuristic design update schemes in the discrete field.

In line with the two flexibility measures introduced in Section 2.2, a shape measure, g ₃(μ), may be introduced. This measure controls the degree to which the void area is allowed to deviate from a given reference shape, B _{r e f} . The idea is illustrated in Fig. 23. B _{r e f} is defined in a new domain with same discretization as the design domain. This way, any geometry may easily be used as a reference without needing to parametrize the shape. B _{r e f} is (optionally) allowed to rotate freely around its center of mass. The rotation is defined by the angle 𝜃 as illustrated in Fig. 23b. The rotation is performed on a fixed mesh. For this reason the operation should always be applied to the original reference shape, as successive rotations will accumulate approximation errors and eventually, in the general case, modify the shape.

Fig. 23

Definition of the reference shape and signed distance function in a domain of same discretization as the design domain. In (c) and (d) the interface of the reference shape is indicated by black elements

The shape measure is based on the signed distance function, h. The value h _e is calculated for each element as the shortest distance from the center of element e to the interface of B _{r e f} (see Fig. 23c). The value is chosen to be negative in the interior of the flexible void area, B. The interface of B _{r e f} is defined by element interfaces. It is therefore possible to calculate the signed distance function based on information about the mesh. A drawback of this reference shape definition is that the interface becomes non-smooth at element corners. However, as the flexible void area is already defined on a fixed mesh, the shape measure cannot be smooth. It should be noted that the reference shape is translated to a position defined by the update scheme (see Section 5.2.1) before the signed distance function is computed.

The shape measure is defined as the sum of the value of the signed distance function for elements contained in the flexible void area, B:

$$ g_{3} (\boldsymbol{\mu}) = \frac{\sum{\mu_{i} v_{i} h_{i} }}{H_{0}} $$

(19)

H ₀ is a normalization factor. The calculation is illustrated in Fig. 23d, for the example flexible void area, B, from Fig. 23a and reference shape, B _{r e f} , from Fig. 23b. The figure shows element values of the signed distance function based on B _{r e f} for elements contained in B. It should be noted that the reference shape initially should be scaled to have the same area as the flexible void area.

The normalization factor, H ₀, is defined as the sum $\sum {\mu _{i} v_{i} h_{i}}$ for a circular flexible void region of same area as B, having itself as a reference shape (i.e. B = B _{r e f} ). This value may be analytically calculated as the surface integral (absolute value) of the signed distance function over the circle:

$$ H_{0} = \left| \int_{B}{h dA} \right| = \frac{\pi {r_{0}^{3}}}{3} $$

(20)

With this definition, the shape measure may immediately be included into the optimization problem as defined in (8), by penalizing with a factor α ₃, and taking the sum over three flexibility measures in the objective function.

The sensitivity of the shape measure with respect to the flexible void variable, μ _e , of element e is

$$ \frac{\partial g_{3}(\boldsymbol{\mu})}{\partial \mu_{e}} = \frac{v_{e} h_{e}}{H_{0}} $$

(21)

5.2.1 Continuation and design update for shape measure

In order to enforce the flexible void variables into a particular shape, a high penalization factor, α ₃, is required. However, a well-known issue in relation to high penalization is the increased risk of getting stuck in local minima. An often used remedy is some sort of continuation strategy, which is also applied here. Another modification to take into account is that the reference shape needs to be updated during the optimization.

The above considerations lead to the continuation scheme presented in Fig. 24. The optimization is initially run as a standard flexible void problem (i.e. α ₃ = 0) until convergence. Then the reference shape, B _{r e f} , is initialized by aligning its center of mass with the center of mass of the flexible void area, B, and rotating it the angle 𝜃 leading to the minimum value of the shape measure, g ₃(μ). The optimization is then continued with α ₃>0. When B converges, B _{r e f} should be updated. B _{r e f} is updated to the position and rotation for which the average compliance sensitivity (with respect to the flexible void variables) of elements contained in B _{r e f} is minimized. This happens at the step represented by the left-most box in Fig. 24. In order to smooth the iterative optimization problem the motion of B _{r e f} is restricted for this step: B _{r e f} is only allowed to rotate ±4^o per update and may only be translated up to m elements either diagonally or in an axial direction, where m is a number proportional to the sensitivity filter radius of the problem (here m = 2R/3). B _{r e f} is considered converged when no combination of the allowed translation and rotation leads to a smaller average sensitivity.

Fig. 24

Flowchart for continuation strategy when optimizing with shape measure

When B _{r e f} converges, the value of α ₃ is increased to its maximum value whereupon B and B _{r e f} are alternatingly updated until convergence. The problem is considered converged when B, B _{r e f} and ρ are simultaneously converged.

5.2.2 Shape measure results

A first example of optimization using the shape measure is shown in Fig. 25. The reference shape (an L-shape) is shown in the top row, the final flexible void geometry is shown at the bottom, and the middle figure shows the optimized structure. The initial guess for the flexible void area was a circle of same size as the reference shape, positioned as in the problem from Fig. 1. The penalization factor α ₃ was first increased from 0 to 10, then to the maximum value, 100. The example is run using the same parameters as in Section 4, with a discretization of 160 by 100 elements.

Fig. 25

Optimization with shape measure. a L-shaped reference shape with side lengths l x/8 and 3l x/8. b Optimized structure, c = 60.75. c Final void area

The example demonstrates the ability of the method to translate and rotate the reference shape into an optimized position for minimizing the disturbance on the compliance problem. Except for slightly rounded corners the final flexible void area is shaped like the reference. The area is placed with a certain overlap with the grayscale regions of the structure, whereas the solid edges are only touched.

Two other test examples, with a square of varying area as reference shape, are shown in Fig. 26. For both cases the initial guess for the void area and the continuation of α ₃ are defined as in the L-shape example, and the same discretization and optimization parameters are applied. For the small square the optimization algorithm exploits the opportunity of rotating the reference shape to make it fit with the triangle-shaped hole in the structure, similar to the optimization for the L-shape test case. However, when the size of the reference shape becomes larger compared to the size of the domain, as is the case for the large square, there is no longer an obvious way for the square to fit into the structure. Also for this case the algorithm moves the void area to minimize the disturbance on the structure. However, due to the size of the void area and the requirement to fit a square shape with sharp edges, the optimized structure is characterized by irregularities similar to those obtained when using standard passive elements.

Fig. 26

Optimization including shape measure. a Example 1: Square reference shape with side length l x/4. b Example 2: Square reference shape with side length l x/3. c Optimized structure from (a), c = 61.18. d Optimized structure from (b), c = 66.87. e-f) Corresponding final void areas

As illustrated by the test cases the shape measure extends the flexible void method to solve design problems with holes of a fixed shape. However, the method has certain drawbacks. First, as illustrated by the examples in Fig. 26, the method reaches its limitations when the reference shape area is large compared to the total domain area. Second, the iteration number becomes high due to continuation of the penalization parameter. The L-shaped test case converged in 722 iterations, whereas the square cases converged in 470 and 655 iterations, respectively. One way to decrease the iteration number would be to relax the convergence criterion determining when to update the reference shape. Another option is to modify the move limit scheme for the flexible void area to faster decrease the number of elements allowed to swap per update of the void area.

6 Discussion

One of the strengths of this new method is the ability to enforce a connected void area, while keeping the void definition simple and defining the design variables at an individual element level. Alternative approaches include implementation of a “casting constraint”, where element densities are required to change monotonously along a given casting direction (see e.g. (Gersborg and Andreasen 2011)), or a 2D level set definition (without topological derivatives), where only existing interfaces are changed, meaning that no new holes are introduced.

Cases may arise, however, where the connectivity is challenged. As mentioned in Section 4.3 this includes cases where the location measure is applied with a high weight. One remedy is, as already suggested, to simultaneously apply the deformation measure, which forces the flexible void elements towards its center of mass. Another approach is to implement a heuristic connectivity scheme, checking whether a given design update of μ implies non-connected areas, and if necessary removing elements leading to this situation from the update list.

The designs obtained with the flexible void method are obviously highly dependent on the initial location of the void area. An example is the cantilever beam problem with a flexible void circle from Fig. 1, with the final design shown as the last iteration in Fig. 7. If the initial circle is instead placed with its center point in (l x/3,l y/2), the flexible void area moves towards the left, ending up in a different local minimum as a triangle at the left edge (at the low density area in Fig. 7).

Put more generally, the efficiency and applicability of the method depends on characteristic parameters such as filter radii, the maximum number of elements allowed to change per iteration, and the weight of the penalization measures. If the filter radius, R, of the sensitivity filter is too small (e.g. R = r _i = 1.2), the flexible void area develops very slowly and tends to get stuck in a local minimum. As described in Section 3, an increased interface width (increased radius, r _i , on the density filter) decreases the number of iterations required for the flexible void area to move large “distances”. This is, however, with the risk of violating the connectivity. A necessary condition is r _i ≤R.

With the presented implementation, the flexible void area impacts surrounding elements in the same way as the domain border, as the unfiltered sensitivities inside the void are zero and the filtering weight factor is equal for all elements. When the volume constraint is defined on the physical densities, $\boldsymbol {\hat {\rho }}$, only, this has the implication that the interface between the structure and the flexible void becomes a sharp 0/1 edge. An alternative would be to apply the volume constraint to the continuous design variables, ρ. With this choice, however, the physical meaning of the constraint value is lost. The method leads to a grayscale interface, but the edge is still sharper than for interfaces between maximum and minimum densities in the remainder of the domain.

7 Conclusions

This paper presents a new method for including a flexible void area into a minimum compliance topology optimization problem. The void area is introduced as a second, discrete design variable field with the same discretization as the standard, continuous density field. This way, the method allows to define a void inclusion of fixed area, which may be flexibly reshaped and repositioned in order to disturb the structure least possible. The freedom of motion of the flexible void area may be restricted by penalizing its moment of inertia and the position of its center of mass. By formulating the problem as two strongly coupled sub-problems, the design update is performed in an iterative manner, alternating between updates of the continuous and discrete fields. This alternation allows to introduce various heuristic modifications to the design update scheme in the discrete field, as illustrated with the shape measure, forcing the void area to assume a predefined shape.

The robustness and applicability of the method is demonstrated through a range of numerical examples. The paper has focused on demonstrating the fundamental properties of the method. The method may easily be combined with the passive elements method for fixed solid or void inclusions, simply by excluding the passive elements from the set of design variables also in the discrete field, μ. Extension to 3D is straightforward.

The nature of the method furthermore makes it very suitable for interactive topology optimization applications, e.g. on handheld devices, as presented in (Aage et al. 2013). A challenge for this end is to handle the potential numerical instabilities described in Section 4.3, arising when the location constraint is applied with α ₂ too high. However, the interactive definition of characteristic parameters, such as penalization weights, α _k , and the interface width, r _i , allows to achieve maximum gain from the flexibility of the method.