Topology optimization of uniform thickness structures using discrete object projection

Abstract

Topology optimization (TO) is well suited to exploit the geometric freedom provided by additive manufacturing (AM), but only when the two technologies are properly integrated. Failure to account for the manufacturing process in the execution of the optimization formulation can lead to performance loss and increased production time and/or cost. This paper discusses a TO methodology motivated by the unique features of wire and filament based AM processes with high deposition rates where a constant thickness of deposited features is desired to manage heat flow and path planning during fabrication. In addition to typical manufacturing constraints such as minimum feature size and feature separation, the proposed approach utilizes discrete object projection to impose a constant thickness requirement on all structural features, including structural members and connection points (joints). The mathematical consistency of the developed framework enables the use of gradient-based optimizers, and tradeoffs between design freedom and computational cost are discussed. Although the technique was developed with a specific electron beam fabrication process in mind, it is readily extendable to other AM technologies with similar requirements as well as to create lattice-like designs. The approach is demonstrated on benchmark minimum compliance problems and is shown to successfully design structural components that are directly manufacturable.

1 Introduction

Topology optimization (TO) provides a framework for optimizing the distribution of a material within a domain by utilizing modern computational tools to improve performance over empirical design. As additive manufacturing (AM) offers unprecedented geometric freedom over conventional manufacturing processes, it is well-suited to harness the potential of TO, but only when the two technologies are properly coupled. Tailoring the design process to the specific capabilities and limitations of the manufacturing process produces useful results and reduces the need for post-processing. The incorporation of manufacturing constraints into topology optimization has been an active area of research, particularly for AM constraints related to (for example) unsupported overhangs (Gaynor et al. 2014b; Gaynor and Guest 2016; Langelaar 2016, 2017; Mass and Amir 2017; Gaynor and Johnson 2018) and consideration of build orientation (Langelaar 2018; Wang and Qian 2020).

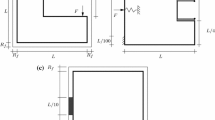
Electron Beam Freeform Fabrication (EBF3) is a wire-fed layer-additive metal AM process developed at NASA Langley Research Center (LaRC) with Sciaky technology. It fuses weldable wire onto an existing part or substrate using a focused electron beam (see Fig. 1). The wire and portion of the substrate directly underneath the electron beam’s focal point undergo a temperature increase of $O(10^3)$ K/s (Wȩglowski et al. 2016) to form a melt pool and then rapidly solidify with minimal heat distortion once the beam has passed. Adequate heat management measures such as cooling breaks, maximum feature widths, or heat monitoring with closed loop control are required to prevent features from melting if the e-beam must travel near previous deposits. The process is performed in a vacuum ($1.3\times 10^{-2}$ Pa or lower) to prevent dissipation of the electron beam, achieving approximately 95% energy efficiency (Taminger and Hafley 2003). The wire gauge and e-beam raster size determine the deposition width. Depending on the wire stock and the size of the vacuum chamber, this process can build parts on the centimeter to meter scale at deposition rates of 330 to 2500 $\hbox {cm}^3$/hr (Taminger and Hafley 2003), making it particularly suitable for large scale components. For most applications, it is considered a near net shape technique, as the large feature resolution typically necessitates some surface finishing.

Fig. 1

Electron beam freeform fabrication schematic. Reprinted from (Taminger and Hafley 2006)

While all manufacturing processes have a minimum feature size (the size of the smallest feature that can accurately be built), wire and filament based AM processes further require that structures be composed of integer multiples of the characteristic machine feature width. As the bead width increases with respect to the structure size, it becomes increasingly advantageous to design components comprised of features of uniform width. For EBF3, varying width throughout a component can be achieved by using multiple passes or changing the e-beam raster size, but local changes in width are generally undesirable. Designing structures with only single-pass features facilitates toolpath planning and helps to manage heat flow during fabrication, particularly considering the extreme heat fluxes developed in EBF3. Also, the beginning and end of any deposition path provide the least geometric precision, so continuous connectivity of components is advantageous. Crossing over previously deposited material leads to a buildup of material at the joint; this effect can be mitigated, however, with temporary manipulation of the deposition parameters. Considering these manufacturing challenges, a TO methodology capable of creating features of constant width is needed. This work seeks to address the need through a projection-based TO framework.

Length scale control was one of the earliest manufacturing constraints to be addressed in the field of topology optimization. The myriad methods can be roughly categorized into two approaches: filtering/projection and constraint-based, with many researchers employing a hybrid of these strategies. Filters based on relative densities (Bruns and Tortorelli 2001), Heaviside projection (Guest et al. 2004; Guest 2009b; Carstensen and Guest 2018), morphology (Sigmund 2007), and robustness (Wang et al. 2011) perform various operations on the independent design variables to generate the elemental relative densities that are used in finite element computations. While the functional forms vary, the constraint-based methods all rely on penalizing features that violate the desired length scale. Some methods use an indirect approach (Petersson and Sigmund 1998), while others impose an explicit characteristic length (Poulsen 2003; Guest 2009a; Allaire et al. 2016; Fernandez et al. 2019, 2021). These methods limit minimum length scale, maximum length scale, or both; however, all existing methods face numerical challenges such as failure to converge or the need for extensive parameter tuning when the minimum and maximum length scales are close in magnitude, as would be required for a uniform feature thickness constraint.

An additional approach to address these concerns involves the optimization of discrete objects. Discrete object projection (Guest 2011; Ha and Guest 2014; Guest 2015) maps features of a fixed size and/or shape onto a continuous design domain through the definition of neighborhood sets that use distinct material phases. As originally proposed, this formulation does not allow for the connectivity of the discrete objects. This was extended by (Koh and Guest 2017) to consider three material phases and by (Koh 2017) to consider reinforcing fibers in TO of composites. More recently, the approach was adapted to address the discrete nozzle size restriction of extrusion type AM processes (Carstensen 2020) by modifying the shape of the material mapping neighborhoods. This allows for full connectivity of the discrete objects along the print direction, while requiring that adjacent objects remain separate or tangent, but do not overlap. The work in (Carstensen 2020) was limited to only horizontal and vertical print directions, leading the algorithm to struggle with connectivity of oblique features. Geometry projection (Norato et al. 2015) can also be used to map parameterized discrete objects onto a continuous domain with consistent sensitivity analysis. Each feature can be defined with a fixed width, but as presented the method does not include a way to prevent in-plane overlapping of adjacent objects, which would increase the overall feature width. The technique is elegant and efficient with minimal parameter tuning, but is reported to be subject to numerical instabilities such as ground structure dependence, increased gray regions, and lack of symmetry (Norato et al. 2015). The method of moving morphable components (MMC) has similar functionalities (Guo et al. 2014), as discussed in a recent review paper (Wein et al. 2020); (Niu and Wadbro 2019) used penalization within the context of MMC to pursue uniform width features. Additional approaches have been developed using the level set method (Liu et al. 2018; Jang et al. 2019)

The approach presented in this paper uses a discrete object projection methodology with a novel mapping scheme that allows for long continuous features of uniform thickness while prohibiting the overlapping of adjacent features. The technique includes a user-specified discretization of print directions for increased design freedom, while offering computational tools to address the corresponding increase in dimensionality. This paper is organized as follows: Sect. 2 provides an overview of pertinent computational TO tools. The proposed method of addressing wire-fed AM design considerations is detailed in Sect. 3, followed by the problem formulation and sensitivity analysis in Sect. 4. Design examples and discussion are presented in Sect. 5, and conclusions in Sect. 6.

2 Background

The ultimate goal of density-based topology optimization is to select which material is present in each finite element. In traditional solid-void topology optimization, this is captured by an elemental volume fraction of $\rho ^e = 0$ (void) or $\rho ^e = 1$ (solid), relative to the baseline properties of a fully dense element. These elemental variables, however, are rarely used as the independent optimization variable as some form of geometric restriction, such as through projection methods, is typically required.

2.1 Multiphase heaviside projection method

The Heaviside Projection Method (HPM) (Guest et al. 2004; Guest 2009b) establishes a field of independent design variables $\varvec{\phi }$ that are mapped onto finite elements $\varvec{\rho }^e$ for analysis. The fundamental idea behind HPM is that a single independent design variable $\phi _{ij}$ has the ability to deposit a feature of material i into the design domain at location j when its magnitude is nonzero (i.e., $\phi _{ij}$$> 0$). The design variables, $\varvec{\phi }$, are filtered onto each element, e, using linear or uniform weighting, $w_{ij}^e$, to generate an elemental projection value for each material phase, $\mu _i^e$, as shown in Eq. (1) (Bruns and Tortorelli 2001; Bourdin 2001).

$$\begin{aligned} \mu _i^e = \dfrac{\displaystyle \sum\nolimits_j \phi _{ij} w_{ij}^e}{\displaystyle \sum\nolimits_j w_{ij}^e} \end{aligned}$$

(1)

These values then undergo a regularized Heaviside step [Eq. (2)] to determine a phase-specific elemental volume fraction, $\rho _i^e$, in the physical domain. We note that this property is typically tied to deposition of material, but can also be applied to machining and removal of material, often called void projection (Guest 2009b; Guest and Zhu 2012).

$$\begin{aligned}&\text {Void:}&\rho _0^e = e^{-\beta _0\mu _0^e} - \frac{\mu _0^e}{\phi _{max}} e^{-\beta _0\phi _{max}} \end{aligned}$$

(2a)

$$\begin{aligned}&\text {Solid:}&\rho _1^e = 1 - e^{-\beta _1\mu _1^e} + \frac{\mu _1^e}{\phi _{max}} e^{-\beta _1\phi _{max}} \end{aligned}$$

(2b)

where $\phi _{max}$ is the maximum allowable magnitude of the design variable (Guest et al. 2011). For sufficiently large values of the projection parameter $\beta _i$, any non-zero $\mu ^e$ produces a 0/1 (void/solid) elemental volume fraction. The authors have opted to use the original projection formulation rather than the thresholding projection formulation (Wang et al. 2011) for computational efficiency in the context of discrete object projection. The interested reader is referred to (Carstensen and Guest 2018) for a more detailed discussion.

Single-phase projection controls only the length scale of the active phase (e.g., void or solid), possibly resulting in unacceptable passive phase (e.g., solid or void, respectively) features. This is mitigated by combining the results of projecting both phases. Many problems use independent design variables for each phase, such that $\rho _0^e$ is a function of $\phi _{0j}$ and $\rho _1^e$ is a function of $\phi _{1j}$ (Guest 2009b; Gaynor et al. 2014a); other problems use a combined design variable such that both $\rho _0^e$ and $\rho _1^e$ are functions of the same $\phi _j$ (Ha and Guest 2014; Guest 2015; Carstensen 2020; Carstensen and Guest 2018). In either case, the two phase-specific volume fractions are then assembled to arrive at a final elemental volume fraction, $\rho ^e$, to be used in finite element analysis. Figure 2 shows a schematic representation of independent and combined multiphase projection. This work will utilize combined projection as discussed in Sect. 3.1, and $\phi _{ij}$ will herein be replaced by $\phi _j$ in all subsequent equations. The symbol $\phi _{(i)j}$ refers to both $\phi _{ij}$ and $\phi _j$.

Fig. 2

Independent and combined multiphase projection

To obtain the final elemental volume fraction, the multi-phase components, $\rho _0$ and $\rho _1$, can simply be averaged (Guest 2009b). This means both passive regions (no projection) and phase mixing (conflicting projection) achieve an intermediate volume fraction, which can be mitigated by existing methods for gray region penalization such as Solid Isotropic Material with Penalization (SIMP) (Bendsøe 1989; Zhou and Rozvany 1991) or Rational Approximation of Material Properties (RAMP) (Stolpe and Svanberg 2001). This provides mathematical motivation for the optimizer to drive toward a clean 0/1 (void/material) solution. Combining the independent projections in a slightly different manner penalizes phase mixing while allowing for passive regions by assigning a default phase (e.g., no active projection results in a void element) (Guest 2015). Other functional forms can be used to incentivize problem-specific desired behavior (Carstensen and Guest 2018; Carstensen 2020).

2.2 Manufacturing primitives

Topology optimization is most effective when the manufacturing process is incorporated into the design algorithm. This prevents designing components that are difficult or impossible to produce and greatly reduces the need for post-processing. By tying the feature deposited by an independent design variable in HPM to the fundamental building block of a manufacturing process, referred to as a manufacturing primitive, we can control component geometry and improve manufacturability. Conventional HPM (Guest et al. 2004; Guest 2009b) uses a circular manufacturing primitive as shown in Fig. 3a. If a design variable takes on a value greater than zero, any element whose centroid is within a user-specified radius of that design variable becomes solid, mimicking deposition of a circle and ensuring minimum feature size. This is readily extended to a rectangular primitive (Fig. 3b: any element whose centroid is within the bounding box would become solid. Note that any non-circular manufacturing primitive must incorporate a way to specify the orientation (shown here at 45$^\circ$). In this work, design variables are placed at the nodes of the finite element mesh for simplicity and to emphasize the distinction between the elements and the primitives, but one can choose other locations (Guest and Smith Genut 2010).

Fig. 3

Heaviside projection with manufacturing primitives: every design variable has the ability to create a manufacturing primitive in the design domain

Manufacturing primitives, similar to structuring elements in morphology, may consist of a shape adapted for a material or manufacturing process (Guest 2009b; Guest and Zhu 2012; Ha and Guest 2014; Guest 2015; Vatanabe et al. 2016; Ha et al. 2019), a morphable shape in which one or more parameter is variable (Ha and Guest 2014; Norato et al. 2015; Guo et al. 2017), or a surrogate representation of a manufacturing constraint (Gaynor and Guest 2016; Vatanabe et al. 2016). The primitive presented in (Carstensen 2020), for example, is aimed at nozzle-type AM and consists of an immutable core flanked by an adaptable bonding layer, resulting in features which are integer multiples of the nozzle diameter.

3 Design for uniform feature width

Characterizing the geometry of a manufacturing process is necessary in order to tailor the topology optimization approach. The wire-fed nature of the EBF3 process naturally creates oblong features in which the arclength is much larger than the width. The continuous nature of the wire can be exploited to create arbitrary shapes, but requires an increase in scale, e.g., a perimeter which is at least one wire wide plus infill. To minimize the need for process parameter manipulation and to simplify heat management in the extreme thermal environment of EBF3, we herein propose a topology optimization scheme to design components of uniform single wire bead width features. The projection-based approach consists of a tailored manufacturing primitive and a corresponding computational tool to improve convergence.

3.1 Manufacturing primitive for wire-fed AM

While a rectangular manufacturing primitive is a natural choice to represent a wire segment, this shape facilitates, but does not necessitate, the creation of oblong features of uniform width. To ensure the optimizer only places primitives end to end, we wrap the long edges of the rectangle in another primitive which deposits void onto the physical domain. Seen in Fig. 4, any element whose centroid is located within the red bounding box becomes solid when the design variable magnitude is greater than zero, while any element located within either of the blue bounding boxes becomes void (the definitive absence of material). This is an extension of discrete object HPM (Ha and Guest 2014; Guest 2015): one design variable is projecting two phases onto the physical domain. We will refer to the physical shape created by this combined phase projection as a bead primitive (shown here at an orientation of 45$^\circ$).

Fig. 4

Heaviside projection with EBF3 bead primitive. One design variable creates a wire segment and parallel void spaces to ensure features of fixed width without imposing limitations on feature length

The width of the solid phase rectangle, $d_{\text {min}}^\text {solid}$, is the required bead width dictated by the process parameters (wire diameter, raster size, etc.), while the length is chosen by the user (specified as an aspect ratio with respect to width). The width of the void rectangles, $d_{\text {min}}^\text {void}$, is the minimum separation required to keep adjacent beads from wicking together. Preliminary tests of the EBF3 process by the authors suggest a gap of approximately 60–70% of the bead width is sufficient. The length of the void rectangles, shown in Eq. (3), is determined by the length of the solid rectangle, but may not be less than the minimum void feature size.

$$\begin{aligned} L_{\text {void}} = \min \{d_{\text {min}}^\text {void},(\alpha -1)d_{\text {min}}^\text {solid}\} \end{aligned}$$

(3)

where $\alpha$ is a user-specified aspect ratio for the solid portion of the bead primitive. The void phase is slightly shorter than the solid phase to allow gradual changes in orientation along a structural ligament (feature comprised of multiple bead primitives laid end to end) and also to allow perpendicular and near perpendicular joints with other ligaments. Figure 5 shows several possible joints and curves that can be created using the bead primitive. This ability to construct curved features provides an advantage over a ground structure approach, which is limited to rectilinear features.

Fig. 5

Possible geometric features created by combining bead primitives. Passive white space will also become void when using “Default Void” phase assembly. All features have a uniform width but are free to vary in length

The user specifies a discrete set of candidate angles at which to orient the primitive, using one independent design variable for each orientation at each location, noting the trade-off between design freedom and computational cost. Selection of more than one orientation at a location (Fig. 6) or incompatible neighboring orientations results in phase mixing; this can be penalized through conventional methods or by the method described in Sect. 3.2.

Fig. 6

Combinations of design variable magnitudes at location j: a Projection of horizontal primitive only, b Projection of vertical primitive only, c Phase mixing due to simultaneous projection of horizontal and vertical bead primitives

Continuity is possible using this bead primitive and is incentivized through the sensitivities because it is mechanically advantageous. In order to avoid including independent void phase design variables, the authors recommend using combined projection with a “Default Void” option for phase assembly, in which the lack of any active projection results in a void phase elemental volume fraction (Guest 2015).

$$\begin{aligned} \rho ^e = \dfrac{\rho _1^e(1+\rho _0^e)}{2} \end{aligned}$$

(4)

Using this formulation, in the absence of any projection, the white space between primitives shown in Fig. 5 would become void elements, rather than the gray regions which would result from the averaging method of (Guest 2009b). We note this formulation is identical to (Guest 2015), which was modified by (Carstensen 2020) to allow objects to be placed tangent. These works demonstrate that by changing the functional relations of the projections, as well as shapes, length scales, and material composition of the primitives, researchers can achieve different topological controls.

The proposed approach can be used either in planar applications, or within each build layer of a 3D component. As sacrificial support structures would be difficult to remove in a process such as EBF3, the authors recommend the use of overhang constraint [e.g., (Gaynor and Guest 2016; Langelaar 2016)] when extending this method to 3D to ensure that material is present in the layer below a new deposition.

3.2 Phase mixing penalization

Conventional penalizations of intermediate volume fractions (e.g., SIMP, RAMP) incentivize 0/1 volume fractions through their effect on the physics and material cost. These methods are often sufficient to prevent phase mixing; however, the efficacy of the proposed bead projection to ensure minimum separation of adjacent features relies entirely on the penalization of phase mixing that occurs when one primitive’s solid region overlaps another primitive’s void region (see Fig. 6). Furthermore, adequate refinement of the finite element mesh typically results in an average element size that is considerably smaller than the proposed bead primitive and adequate discretization of the bead primitive orientation angle leads to multiple design variables capturing many of the same elements within their projection zones (e.g., if four orientation angles are considered, an element located at the center of a bead primitive will be within the projection zone of all four candidate primitives). From the element’s perspective, these two numerical scaling effects cause a marked increase in the number of design variables wielding influence over the element, exacerbating some of the known numerical challenges of multiphase projection. Combining the numerical difficulties with the heavy reliance on phase mixing penalization, the authors have found it beneficial to employ a more targeted approach when working with bead projection. In addition to a dramatic increase in the HPM regularization parameter (e.g., $\beta$ can be greater than 1000), we modify the volume computation to place a higher “cost” on phase mixing than on other instances of intermediate volume fractions, similar to volume constraint implemented in (Carstensen 2020).

Total material volume (in the objective function of a minimum volume problem or in a volume constraint) is computed as

$$\begin{aligned} V_{\text {tot}} = \sum _e \rho ^e v^e \end{aligned}$$

(5)

where e represents the element number and $v^e$ represents the elemental volume. Replacing the volume fraction, $\rho ^e$, (in volumetric computations only) with the effective volume fraction, $\rho _{\text {eff}_v}^e$, shown in Eq. (6) imposes a steep penalty on phase mixing while capturing a reasonably accurate measure of volume for single phase results. Note that this formulation is tailored for use with a phase assembly method that defaults to void projection [Eq. (4)].

$$\begin{aligned} \rho _{\text {eff}_v}^e = \rho _1^e(2-\rho _0^e) \end{aligned}$$

(6)

Whether computed directly, or with a penalization scheme such as SIMP or RAMP, elemental volume fractions typically range from 0 to 1; the proposed volume computation, herein referred to as an overlap volume penalty, ranges from 0 to 2. When a conventional approach is used for finite element analysis in conjunction with this approach for a volume constraint or minimum volume objective function, we maintain fidelity in the physics while also discouraging intermediate volume fractions, with an especially aggressive penalization of phase mixing. Table 1 aligns the conventional volume computation (using a “Default Void” phase assembly) to be further penalized with SIMP in stiffness calculations with the corresponding proposed volume computation under the possible phase projection combinations. When no phase or a single phase is projected, the volume computations are equal and representative; when both phases are actively projected, we penalize the FEA volume through reduced stiffness and inflate the volumetric cost with the overlap penalty. Figure 7 demonstrates this effect on the phase mixing example shown in Fig 6c, visualizing each phase-specific volume fraction, the reduced volume fraction used to compute stiffness, and the inflated volume fraction used to compute volume.

Table 1 Comparison of volume computations. Projection of zero or exactly one phase results in equal stiffness and volumetric relative densities

Fig. 7

Comparison of elemental volume computations in the presence of phase mixing: a $\rho _0^e$: Projection of void phase, b $\rho _1^e$: projection of solid phase, c $\rho ^e$: “Default Void” elemental volume fraction used for FEA, d $\rho _{\text {eff}_v}^e$: effective elemental volume fraction used for volume computations

4 Problem formulation and sensitivity analysis

Gradient-based optimization requires a sensitivity analysis. The sensitivity of functions that contain metrics of mechanical performance is typically solved using the adjoint method. Herein we consider classical minimum compliance problems, expressed as

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{{\varvec{\phi }}} &{} \mathbf{F }^T\mathbf{d }\\ s.t. &{} \mathbf{K }({\varvec{\phi }})\mathbf{d } = \mathbf{F }\\ &{} \displaystyle \sum _e \rho _{\text {eff}_v}v^e \le V_{\text {max}}\\ &{} 0 \le \phi _j \le \phi _{\text {max}} \quad \forall \;j \end{array} \end{aligned}$$

(7)

where F is the global force vector, d is the global displacement vector, $\mathbf{K }(\varvec{\phi })$ is the global stiffness matrix assembled from elemental stiffness matrices, $\mathbf{K }^e$, as:

$$\begin{aligned} \mathbf{K }^e(\varvec{\phi }) = \Big (\rho ^e_{\text {min}} + \big (\rho ^e(\varvec{\phi })\big )^\eta \Big ) \mathbf{K }^e_0 \end{aligned}$$

(8)

where $\rho ^e_{\text {min}}$ is a small positive number employed to ensure positive definiteness of the stiffness matrix, $\rho ^e$ is computed using Eq. (4), $\eta$ is the SIMP penalty, and $\mathbf{K }^e_0$ is the stiffness matrix of a fully dense element.

For a given objective or constraint function f, sensitivities are

$$\begin{aligned} \displaystyle \frac{\partial f}{\partial \phi _{(i)j}} = \sum _e \left[ \frac{\partial f}{\partial \rho ^e} \cdot \frac{\partial \rho ^e}{\partial \phi _{(i)j}} \right] \end{aligned}$$

(9)

where $\frac{\partial f}{\partial \rho ^e}$ for a compliance problem problem is given by the adjoint method as

$$\begin{aligned} \frac{\partial \,\mathbf{F }^T\mathbf{d }}{\partial \rho ^e} = -\eta \big (\rho ^e(\varvec{\phi })\big )^{\eta -1} {\mathbf{d }^e}^T \mathbf{K }^e_0 \mathbf{d }^e \end{aligned}$$

(10)

where $\mathbf{d }^e$ is the nodal displacement vector for element e and $\frac{\partial \rho ^e}{\partial \phi _{(i)j}}$ is given in the following sections.

4.1 Proposed bead projection

Our proposed manufacturing primitive constitutes a specific mapping scheme relating the design domain to the physical domain; this step is then situated in the standard workflow of multi-phase projection. Our approach relies on combined projection (Fig. 2) (Guest 2015), i.e., one design variable projects both void and solid phases. The distinction between independent and combined projection affects the sensitivity analysis as follows:

$$\begin{aligned} \begin{array}{ll} {\text{Independent}}: &{} \displaystyle \frac{\partial \rho ^e}{\partial \phi _{ij}} = \frac{\partial \rho ^e}{\partial \rho _i^e} \cdot \frac{\partial \rho _i^e}{\partial \mu _i^e} \cdot \frac{\partial \mu _i^e}{\partial \phi _{ij}} \\ {\text{Combined}}: &{} \displaystyle \frac{\partial \rho ^e}{\partial \phi _{j}} = \sum _i \left[ \frac{\partial \rho ^e}{\partial \rho _i^e} \cdot \frac{\partial \rho _i^e}{\partial \mu _i^e} \cdot \frac{\partial \mu _i^e}{\partial \phi _{j}} \right] \end{array} \end{aligned}$$

(11)

where i represents the material phase (0 for void, 1 for solid) and j represents design variable location. The reader is referred to (Guest 2009b) for details regarding the sensitivity of the phase-specific relative densities with respect to the design variable, $\frac{\partial \rho _i^e}{\partial \phi _j}$; the regularization of an otherwise non-differentiable Heaviside step function is an important property of HPM. The selection of the “Default Void” phase assembly formulation as given in Eq. (4) gives the following sensitivity components:

$$\begin{aligned}&\dfrac{\partial \rho ^e}{\partial \rho _0^e} = \dfrac{\rho _1^e}{2}\nonumber \\&\dfrac{\partial \rho ^e}{\partial \rho _1^e} = \dfrac{1+\rho _0^e}{2} \end{aligned}$$

(12)

Combining Eqs. (9)–(12) gives

$$\begin{aligned} \displaystyle \frac{\partial \,\mathbf{F }^T\mathbf{d }}{\partial \phi _j} = \sum _e \Bigg [\bigg (\!\!-\eta \big (\rho ^e\big )^{\eta -1} {\mathbf{d }^e}^T \mathbf{K }^e_0 \mathbf{d }^e\bigg )\nonumber \\ \bigg (\dfrac{\rho _1^e}{2} \cdot \frac{\partial \rho _0^e}{\partial \phi _{j}} + \dfrac{1+\rho _0^e}{2} \cdot \frac{\partial \rho _1^e}{\partial \phi _{j}} \bigg )\Bigg ] \end{aligned}$$

(13)

4.2 Phase mixing penalization

Whether used in an objective function or a constraint, the total volume is computed as shown in Eq. (5), replacing $\rho ^e$ with $\rho _{\text {eff}_v}^e$ [Eq. (6)]. Note that the fully dense volume of each element, $v^e$, is a constant (not necessarily uniform across all elements), and that the sensitivity with respect to each design variable has contributions from multiple elements:

$$\begin{aligned} \displaystyle \frac{\partial V_{\text {tot}}}{\partial \phi _j} \;=\; \sum _e \left[ \frac{\partial \rho _{\text {eff}_v}^e}{\partial \phi _j} v^e\right] \end{aligned}$$

(14)

From the definition of the effective volume fraction, we get the following sensitivities with respect to each phase-specific volume fraction:

$$\begin{aligned} {\, \dfrac{\partial \rho _{\text {eff}_v}^e}{\partial \rho _0^e} = \,-\,\rho _1^e} \nonumber \\ {\, \dfrac{\partial \rho _{\text {eff}_v}^e}{\partial \rho _1^e} = \,2 - \rho _0^e} \end{aligned}$$

(15)

Under combined multi-phase projection, the sensitivities with respect to each design variable are a summation of the sensitivities with respect to each phase. The sensitivities are summarized in Eq. (16).

$$\begin{aligned} \frac{\partial V_{\text {tot}}}{\partial \phi _j} = \sum _e \left[ \left( -\rho _1^e \cdot \frac{\partial \rho _0^e}{\partial \phi _j} \,+\, (2-\rho _0^e) \cdot \frac{\partial \rho _1^e}{\partial \phi _j} \right) v^e\right] \end{aligned}$$

(16)

5 Design examples and discussion

The proposed bead projection approach is demonstrated on two classical linear elastic minimum compliance problems: the Michell beam is used to illustrate the achievement of a uniform width design, and a simply supported beam highlights the effect of primitive orientation discretization. An additional example is presented to explore the performance of the proposed approach under multiple load cases. All examples employ SIMP penalization of intermediate volume fractions, multi-phase Heaviside Projection Method with “Default Void” phase assembly, the overlap penalty for the volume constraint, and are solved using the Method of Moving Asymptotes (MMA) (Svanberg 1987). Continuation is applied to increase the SIMP parameter, $\eta$, from 2 to 10, and the Heaviside parameters, $\beta _0$ and $\beta _1$, starting at 0 and following the Fibonacci sequence. Each continuation step is limited to 200 iterations and optimization progresses until the change in objective function is less than 0.5% coupled with a measure of non-discreteness (Sigmund 2007) of less than 5% for three consecutive continuation steps, or a maximum value of $\beta$ is reached (55 for the void phase and 1597 for the solid phase).

The structures are designed using material properties of Ti-6Al-4V; when processed with the EBF3, this alloy has been shown to exhibit material properties consistent with standard properties in the annealed wrought condition (Taminger and Hafley 2006). The 2D examples presented herein are designed within the build plane using isotropic material properties. Note that these examples were limited to bead primitives precisely one bead wide; however, the proposed framework allows for the inclusion of multiple bead widths.

The optimization is initialized with a uniform distribution of all possible orientations of all primitives, i.e., all design variables are equal at the start; a linesearch is executed at each continuation step to ensure feasibility. We note that alternative initial configurations were explored (e.g., a uniform distribution of only horizontal primitives). These solutions often suffered a loss of symmetry and had much worse performance; however, they occasionally outperformed the uniform initial guess. As no discernible pattern was observed, we recommend using a uniform distribution of initial design variables to prevent bias in the absence of a priori knowledge of a desired configuration. We also suggest using continuation on optimization parameters to minimize the dependence on the initial guess and to promote convergence to high quality local minima. As with all nonconvex problems, we cannot guarantee global optimality of the solutions.

5.1 Michell beam design

The design domain, $\Omega$, (Fig. 8) is subjected to a unit tip load and a minimum feature size of $d_{\text {min}} =$ $\frac{H}{12}$. A mesh of 192 $\times$ 144 finite elements was used. The MMA asymptote increase parameter was reduced to 1.1, and the initial asymptote was tightened to $\frac{0.1}{\beta +1}$ (Guest et al. 2011). Twelve possible orientations (15$^\circ$ increments) of each bead primitive were considered and the upper bound on the independent design variable was raised to $\phi _{\text {max}} = 10$ (Guest et al. 2011). The optimization process was performed at two maximum allowable global volume fractions.

Fig. 8

Michell beam design domain and boundary conditions

For each maximum volume, a conventional design using classical radial projection (circular primitives) (Guest et al. 2004) is used as a baseline for comparison. The results, as visualized through the elemental volume fraction, $\rho ^e$ [Eq. (4)], are shown in Figs. 9 and 10, where red indicates solid, blue indicates void, yellow/green indicates intermediate densities, C is the final compliance, V is the final global volume fraction, and $M_{nd}$ is the measure of non-discreteness (Sigmund 2007). For the low volume fraction case, most features located away from the support when using radial projection (Fig. 9a) have an approximate width of $d_{\text {min}}$, naturally approaching the uniform feature width condition. There is still, however, a 29% performance difference between this solution and the solution using bead projection (Fig. 9b). Given the qualitative similarities between the two designs, we initially suspected that the difference in performance was due to some minor defects in the bead projection design, namely pinholes and single-element ligaments. To examine the impact of these unexpected features, we performed a manual repair and found only a 1% improvement in the compliance. This leads us to conclude that the slightly thinner, branching features at the root of the constant thickness structure, which is where strain energies are largest, lead to a significant loss in stiffness when compared to the radial projection solution.

Fig. 9

Michell beam for 15% allowable volume using a classical radial projection and b single bead thickness projection

Fig. 10

Michell beam for 25% allowable volume using a classical radial projection and b single bead thickness projection

The effect of the bead projection is more pronounced as the maximum allowable volume increases. Figure 10a shows a conventional design with several internal struts at the minimum feature size, a thicker outer shell, and a large contiguous stem near the supports of the structure. All of these features pose manufacturing challenges for the EBF3 process, both in toolpath planning and in heat management. The design using the proposed bead projection approach (Fig. 10b) eliminates all of these variations in feature thickness by expanding vertically to use more of the design domain, leaving enough space to replace the large stem with a lattice composed of features of width $d_{\text {min}}$. The addition of this manufacturing constraint results in a 38% increase in the compliance; there is a larger trade-off between performance and manufacturability at the higher volume fraction because the baseline topology is further from meeting the uniform feature thickness condition, requiring more extensive design changes.

Due to the discretization of the angles available for primitive orientation, some slight curvature and waviness can be observed in the bead projection solutions (Figs. 9b and 10b), possibly contributing to the difference in compliance as straight and/or smoothed structural features would likely improve the performance of the designs. The authors believe that the bending introduced by these presumed imperfections is minor in the context of the available design alternatives. Under the current orientation discretization scheme, when the desired orientation of a feature does not align with the available options, the optimizer must decide between a change in global topology and approximating the desired angle with near matches of primitives offset by slight translations. Utilizing a finer discretization of angles may alleviate this challenge, but the benefits of such an approach must be weighed against the increased computational cost and decreased numerical conditioning. This trade-off is investigated further in Sect. 5.2.

Interestingly, we also note an increase in the measure of non-discreteness in the bead projection solution. This measure is larger throughout the optimization process, as can be seen in the convergence plots of Fig. 11, which compares the convergence of the radial projection and bead projection schemes used to produce the solutions in Fig. 9. The jumps in these plots are associated with continuation steps where the SIMP penalty is increased. As the non-discreteness measure is larger during intermediate iterations for the bead primitive case, increasing the SIMP penalty has a larger effect on the compliance, making these jumps more pronounced; nevertheless, the optimizer is able to locate and refine a high quality solution. Note that these curves are generally representative of the examples considered herein. The convergence behavior could perhaps be mitigated with additional parameter tuning; however, it is interesting to note that if we threshold all of the gray elements in this design, we achieve a final volume fraction of 22.6%, indicating an inactive volume constraint. It is difficult for the optimizer to make incremental changes to the volume, as primitives must be added in a series to create an entire structural feature and avoid phase mixing. This suggests that a minimum mass formulation may be more appropriate than a minimum compliance formulation when the volume is arbitrary, as the optimizer may grow new structural features without violating (for example) a compliance constraint.

Fig. 11

Convergence of the iterates in the Michell beam example (see Sect. 5.1) at 15% volume fraction when using a Radial Projection and b Bead Projection. $f^{(k)}$ and $M_{nd}^{(k)}$ are the values of the objective function (compliance) and non-discreteness metric, respectively, at iteration k

The larger number of iterations to convergence also necessarily means the computational cost of solving the beam primitive example is larger here than when using radial projection. More design iterations means more finite element analyses, which are the dominant cost in typical topology optimization problems. The larger number of design variables also leads to computational cost increases in the projection operations and the solution of the MMA subproblem, with the cost of these iterations scaling roughly linearly with the number of design variables. The increased number of iterations, however, is by far the most influential property in the computational cost.

To examine the convergence more closely, we have plotted in Fig. 12 the design evolution corresponding to the beam primitive convergence plot (Fig. 11). All major changes to the topology have been completed by approximately 450 iterations, with the remaining refinements to nearly 0-1 distribution comprising another 350 iterations, reflecting that large magnitudes of SIMP and beta may be required to drive the solution to 0-1. This again could likely be made more efficient with parameter tuning. Perhaps more importantly, the optimizer identifies an asymmetric solution fairly early in the evolution. This may extend the convergence process as the optimizer must adjust the beam design after the primary asymmetric feature is removed. It also introduces asymmetries in the final design, which was surprising to the authors. In contrast to typical topology optimization, the comparatively large size of the EBF3 bead manufacturing primitive compared to the size of the design domain, coupled with the discretization of the primitive orientation, limits the optimizer’s ability to make fine adjustments to the topology. This effect can give rise to asymmetry in the solution to an otherwise symmetric problem, as seen in Figs 9b and 10b. A solution which is symmetric about a horizontal line at mid-height is expected; however, as discussed in (Stolpe 2010), the presence of symmetry in the domain and boundary conditions of a topology optimization problem does not guarantee symmetry in the solution, especially when discrete geometric conditions (such as fixed member size) are required.

Fig. 12

Selected intermediate results of the optimized design shown in Fig. 9b

To investigate this aspect of the Michell beam problem (see Fig 8), we compare the solution found at the low volume fraction (Fig 9b) to one obtained using bead projection with forced symmetry. The top half of the domain was modeled and symmetric boundary conditions applied. The results are presented in Fig. 13b. The symmetric solution has weaker performance than the asymmetric solution in both compliance and the measure of non-discreteness. If the symmetric solution is post-processed to threshold all intermediate density elements, the compliance naturally decreases but the volume constraint is violated ($C = 2.63$ and $V = 15.68\%$, respectively). In this instance, the solution which does not impose symmetry outperforms the symmetric solution, though this relationship cannot be generalized as neither solution can be shown to be globally optimal.

Fig. 13

Comparison of bead projection a without and b with symmetry enforced

5.2 Effect of orientation discretization

The orientation of each instance of the bead primitive is chosen from a user-specified discrete set of angles, using one independent design variable for each angle at each location. This allows the user partial control over the complexity of the design. For example, selecting two candidate orientations allows the user to produce a design consisting of only horizontal and vertical members. A large number of candidate orientations improves design freedom and smoothness, but also increases computational cost. Furthermore, when a large number of candidate orientations is combined with a small finite element size, achieving convergence can prove difficult due to numerical conditioning. This effect is most noticeable when the size of the bead primitive is large with respect to the size of the design domain.

The level of coarseness in this discretization process can have a pronounced effect on the resulting design, as demonstrated on the simply supported beam problem. The design domain, $\Omega$, (Fig. 14) is subjected to a unit midspan load and a minimum feature size of $d_{\text {min}} = 0.1H$. One half of the domain was modeled using a mesh of 180 $\times$ 60 finite elements and symmetric boundary conditions were applied. The strategy to achieve convergence varies considerably with the number of candidate primitive orientations. When 2 or 3 orientations are considered, the design space is well conditioned but the number of feasible high performing solutions is fundamentally limited. The first two continuation steps for the Heaviside parameter were able to be skipped, and the value of $\beta _{\text {max}}$ was reduced to 610 for the solid phase. The MMA asymptote increase parameter was reduced to 1.1, and the initial asymptote followed (Guest et al. 2011). When 4 or more primitive orientations are considered, the design space is dramatically expanded, but it is more challenging for the optimizer to find a high performance solution due to numerical conditioning. These scenarios require a gradual start to allow sufficient time to thoroughly navigate the design space; they cannot accommodate skipping the initial $\beta$ values of 0 and 1 as used in the previous case. The initial asymptote was tightened to $\frac{0.1}{\beta +1}$. The maximum allowable volume fraction is 40% and the upper bound on the design variable (Guest et al. 2011) is set equal to the number of candidate orientations (but not more than 10) for all scenarios.

Fig. 14

Simply supported beam design domain and boundary conditions

Figure 15 compares the results of five primitive orientation scenarios, where C, $M_{nd}$, and the colors are as defined in Sect. 5.1. Under coarse angle discretization, the resulting designs are jagged and, for this particular example, roughly truss-like. As the number of orientation candidates increases, the design becomes smoother and trends toward a more classical solution. The waviness of structural features discussed in the previous example is more pronounced herein as the minimum feature size is large compared to the domain size, exacerbating any misalignment between the desired and available topologies. As expected, the compliance performance improves with each refinement of the discretization scheme, as the design freedom increases.

Fig. 15

Simply supported beam: bead primitive orientation angle discretization schemes. An increase in the number of orientation candidates is correlated with smoother topologies and improved performance

This exercise has been completed by simply dividing 180$^\circ$ into equal increments; however, this procedure is readily extended to include user-selected candidate orientations. This could be useful to represent possible moves of a specific manufacturing process, or perhaps to prevent unsupported overhangs by only allowing features oriented above the critical overhang angle. For problems without such orientation constraints, the authors have found that 15$^\circ$ increments (12 candidate orientations) are adequate to replicate the unconstrained condition for most applications, provided the ratio of domain size to primitive size is sufficiently high.

5.3 Multiple load case example

Fig. 16

Carrier plate design domain and boundary conditions

A carrier plate is subjected to independent shear and tensile loads. The optimizer must balance the needs of the differing stress flows, as the orientation of the primitives can no longer follow the orientations of the principal stresses. For this example, a square design domain, $\Omega$, (Fig. 16) is subjected to two unit distributed loads ($q_1 = q_2 = 1$) and a minimum feature size of $d_{\text {min}} = \frac{H}{30}$, using a mesh of 180 $\times$ 180 finite elements. The top of the domain where the loads are applied is prescribed to be solid, while the rest of the domain is to be designed by the optimizer. We use a modification of the minimum compliance problem to minimize the summation of two compliances, as seen in Eq. (17). Volume is limited to 30%. All other optimization parameters are consistent with the example in Sect. 5.1.

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{\varvec{\phi }} &{} \mathbf{F }_1^{\;T}\mathbf{d }_1 + \mathbf{F }_2^{\;T}\mathbf{d }_2\\ s.t. &{} \mathbf{K }_i({\varvec{\phi }})\mathbf{d }_i = \mathbf{F }_i \quad i \in \{1,2\}\\ &{} \displaystyle \sum _e \rho _{\text {eff}_v}v^e \le V_{\text {max}}\\ &{} 0 \le \phi _j \le \phi _{\text {max}} \quad \forall \;j \end{array} \end{aligned}$$

(17)

where i refers to load cases 1 and 2 as shown in Fig 16 and all other variables are as described in Sect. 4.

The results of the optimization are shown in Fig. 17. The final compliance was 0.212 units and the non-discreteness measure was 4.8%. It is interesting to note that this example required care to be taken in the relationship between the design and non-design domains. No design variable may be located within a distance $r_{\text {min}}^{\text {solid}}$ of the domain edges to prevent deposition of partial-width features (Guest and Smith Genut 2010); however, because the loading edge was designated as solid (see Fig 16), this distance must be increased to $3\,r_{\text {min}}^{\text {solid}}$ along the top edge. As phase mixing penalization has no effect on the non-design domain, it cannot be used to engender length scale control near the non-design domain.

Fig. 17

Carrier plate optimized for minimum compliance, subject to 30% volume fraction. $C = 0.212,\, M_{nd} = 4.8\%$

6 Conclusion

Herein we present a method to design structures composed of uniform thickness features. This is motivated by the ease of manufacture of such structures with wire/filament or nozzle-fed processes, especially for thermally intense processes such as EBF3, but has relations to the creation of lattice-like structures using local volume constraints (Guest 2009a; Wu et al. 2017, 2018; Tromme et al. 2020). It must be clearly stated that this is not a strict manufacturing requirement for EBF3, as processing parameters can be adjusted on the fly to achieve variable feature thickness, but rather a simplification to aid in the EBF3 deposition process.

The proposed method improves manufacturability of the resulting component by ensuring a uniform width of long continuous features, thereby minimizing the need for costly and time-consuming post-processing of the design and manipulation of the deposition parameters. A novel technique for penalizing phase mixing is also presented to ease the computational burden of the increased dimensionality. The proposed approach is specifically crafted to apply geometric control over the optimization process and the sensitivity analysis is mathematically consistent, allowing it to be readily extended to other wire-fed or extrusion type AM methods which have similar geometric considerations. Another advantage of this method is the explicit inclusion of feature orientation as a design component. This not only allows the user control over the angles featured in the design (e.g., for eliminating unsupported overhangs), but also allows the optimizer to export this information to a post-processor which can generate a toolpath and subsequent G-code.

The approach is currently limited to straight, single bead primitives which exclude wider features and sometimes result in small pores. The primary numerical challenge of this method arises from the large number of independent design variables and subsequent conditioning of the design space, requiring the user to seek a balance between design freedom and tractability/navigability. The highly nonlinear nature of the formulation also necessitates parameter tuning. Future work will explore the inclusion of multiple primitive types (e.g., double- and triple-wide bead primitives, predefined joints), consider reduced design variable fields (Guest and Smith Genut 2010), and focus on improving the computational efficiency of the method, thereby allowing for finer discretization of the primitive orientation, facilitating the extension to 3D applications, and mitigating the sensitivity to algorithm parameters. Alternative optimization formulations (e.g., mass minimization, stress constraints) will also be explored.