Optimizing inclusion shapes and patterns in periodic materials using Discrete Object Projection

Abstract

Current topology optimization methodologies assume a monolithic, free form approach to design. Many engineered materials and structures, however, are composed of discrete, non-overlapping objects such as fiber or particle-based materials. Application of the topology optimization methodology to these types of materials therefore requires controlling the shape and interaction of designed features to ensure solutions are meaningful and physically realizable. Achieving such control on continuum domains is challenging as features form via the union of elements of like phase. A topology optimization approach is proposed herein for optimizing the size, shape, and layout of inclusion-like features in a continuum domain. The technique is based on the Heaviside Projection Method and uses multiple regularized Heaviside functions whose interaction is tailored so that the designer may restrict the minimum and maximum length scale of inclusions, and minimum spacing between inclusions. The technique is demonstrated on the design of material microstructures with enhanced elastic stiffness.

1 Introduction

Continuum topology optimization algorithms are built around the assumption that the structure to be designed is monolithic. That is, the structure is characterized by a material distribution with a continuous connectivity of a phase. A beam with holes, for example, features a continuous load path from the applied load to the support boundary conditions. Many engineered structures and materials, however, gain functionality or are specifically manufactured from discrete objects. For example, fiber-reinforced composites where the objects (inclusions) are cylindrical and are not permitted to overlap. Current topology optimization methods are incapable of tackling such design problems.

Guest (2011) proposed a means of optimizing the patterning of such discrete objects at the 9^th World Congress on Structural and Multidisciplinary Optimization (WCSMO9). The approach was based upon the Heaviside Projection Method (HPM) for topology optimization (Guest et al. 2004) and achieved stiff discrete objects by giving each design variable the ability to simultaneously project stiff material locally over a radius of r _min and a compliant matrix material in the region enclosing this stiff inclusion. Each design variable thus had two projection domains characterized as concentric circles. The primary limitation of the approach was that the inclusions were fixed size and fixed shape (e.g., radial).

In this work we extend this so-called Discrete Object Projection approach to cases where the inclusions (or holes) are permitted to be variable in size and shape. The designer may prescribe a minimum and maximum length scale of the inclusions as well as the minimum spacing between inclusions, as may be required to guarantee sufficient matrix-inclusion bonding. The location, size, and shape of inclusions are then optimized. Unlike shape optimization, a key advantage of the Discrete Feature Projection approach is that inclusions may appear or disappear from any location in the domain, or translate across the domain (Guest 2011). This is more in the spirit of free-form topology optimization and, perhaps most importantly, means that the number of discrete inclusions need not be selected a priori.

The proposed algorithm will be demonstrated on the design of periodic materials with maximized elastic stiffness. The problem is posed as an inverse homogenization problem, where the goal is to identify unit cell topologies that offer optimized effective material properties at the bulk scale. The inverse homogenization design problem was first solved using topology optimization by Sigmund (1994a, b) using truss and frame representations of microstructures to design minimum weight materials with prescribed elastic properties, including negative Poisson’s ratio. This was later extended to continuum representations, including materials with optimized elastic and thermal expansion properties (Sigmund and Torquato 1997), fluid permeability (Guest and Prévost 2006), and multifunctional materials governed by multiple physics, including elastic stiffness and fluid permeability (Guest and Prévost 2006; Challis et al. 2012) and elastic stiffness and thermal conductivity (Challis et al. 2008; de Kruijf et al. 2007). Topology optimization has also been applied (for example) to the design of piezocomposites (Sigmund et al. 1998), phononic band-gap materials (Sigmund and Jensen 2003), photonic crystal structures (Jensen and Sigmund 2004), and most recently negative permeability metamaterials (Diaz and Sigmund 2010; Zhou et al. 2011). With the exception of the truss and frame representations (Sigmund 1994a, b), topologies in these works are assumed to be monolithic and may take on complex topologies.

The work here focuses on engineered materials that are fabricated by embedding discrete inclusions in a matrix material. These objects may be fibers or particles that enhance strength or multifunctionality of the material, or hollow particles to reduce material weight. Such inclusions are discrete objects, are not permitted to overlap, and are restricted to a fixed range of length scales. Both stiff and compliant inclusions are considered. Of course, the elastic properties of materials with stiff inclusions have been studied extensively in literature. Eshelby (1951, 1957, 1975), for example, has studied the mechanical properties of composites with circular and ellipsoid inclusions, and effect of inhomogeneities. This has subsequently facilitated shape optimization of such inclusions (e.g., Kolling et al. 2003). A key difference in this work is that shape, size, layout, and number of inclusions are simultaneously optimized.

2 Variable shape Discrete Feature Projection

Following the conventional radial projection-based methodology (Guest et al. 2004), each design variable ϕ _i has the potential to project a material phase onto the finite element space to create a topological feature. This projection is performed over a physical length scale and can be for the solid phase, creating solid elements ( ρ ^e = 1), or for the void phase, creating void elements ( ρ ^e = 0). Essentially the phase that is ‘actively’ projected is the phase whose length scale is controlled, as may be required by the governing manufacturing process. Examples of this include controlling minimum length scale of the solid phase (Guest et al. 2004), void phase (Sigmund 2007; Guest 2009a), or both phases (Sigmund 2007; Guest 2009a), or preventing solutions that are susceptible to over- and under-etching (Sigmund 2009; Wang et al. 2011). In these standard radial projection schemes, the projected features are permitted to overlap, creating a monolithic structure.

2.1 Review of discrete objects of fixed size and shape

In the Discrete Feature Projection approach (Guest 2011), a discrete object is created by projecting one phase onto the local radial domain ($\Omega _{L}^{n}$) and the alternate phase onto the so-called enclosure domain $\Omega _{E}^{n}$. In the case of a stiff inclusion, for example, the domain defaults to compliant matrix material and, when a design variable n achieves ϕ _n > 0, stiff material is projected over a radius r _min (diameter d _min ) and is then enclosed in compliant matrix material, as shown in Fig. 1. In the case where ϕ _n = 0, no projection occurs, and thus no inclusion is centered at design variable n.

Fig. 1

Discrete object projection from design variable n (indicated by pentagram). A discrete stiff object is created by projecting the stiff phase onto the local domain $\Omega _{L}^{n}$ and the compliant phase onto the enclosure domain $\Omega _{E}^{n}$. The upward and downward pointing triangles indicate elements becoming stiff and compliant, respectively, and the empty circles indicate elements that are not affected by the projection from n

The length scale of the enclosure space, denoted as t _E , is the minimum allowable distance between discrete objects, or equivalently the minimum length scale (diameter) of the second phase. It is user-defined and can be selected based on manufacturing or design specifications. For example, composite structures and materials typically require a minimum bonding distance.

As both the stiff and compliant phases are projected from each design variable, the projection functions were constructed to penalize phase mixing (Guest 2009a), a situation when elements receive both stiff and compliant material through the projection (Fig. 2a). Figure 2b shows the case where projecting design variables are spaced a distance 2 ∗ r _min + t _E apart, illustrating that the minimum length scale of the enclosure phase is in fact t _E . These projection functions will be presented in modified form in the following section.

Fig. 2

Discrete object projections from design variables n ₁ and n ₂ (ϕ _n1 gt; 0, ϕ _n2 > 0, all other ϕ = 0). a Hexagrams indicate elements receiving projection of both phases (phase mixing), which must be prevented. b Binary solutions may result when projecting design variables are at least a distance 2*r _min + t _E apart, also illustrating that the minimum length scale of the enclosure phase is t $_{E}$

2.2 Concept: discrete objects of variable size and shape

The idea now is to allow the designer to prescribe the minimum allowable length scale of objects (r _min ), maximum allowable length scale of objects (r _max ), and minimum allowable spacing between objects (s _min ), and have the optimizer design each object’s location, shape, and size respecting these restrictions. This enhanced capability is achieved by simply introducing a passive free zone of length scale t _F between the local and enclosure domains as shown in Fig. 3. A design variable does not directly influence elements located within this free zone. This means that a limited number of neighboring design variables may also project objects onto these elements, creating overlapping objects and thus new ‘shapes’, provided the projected local material does not mix with an actively projected enclosure phase.

Fig. 3

Variable radius discrete object projection from design variable n (indicated by pentagram) shown for stiff object projection. Stiff phase is projected onto the local domain $\Omega _{L}^{n}$, compliant phase is projected onto the enclosure domain $\Omega _{E}^{n}$, and no projection occurs within the free zone, leaving the compliant phase by default

Figure 4 illustrates these properties for an object of stiff phase enclosed in a compliant matrix material. A single projecting design variable creates a circular feature of radius r _min (diameter d _min ). A circular object of radius r _max (diameter d _max ) is achieved by the design variable distribution in Fig. 4a. A large free region provides more design freedom for the shape of the discrete object, allowing (for example) the creation of a line object or ellipse (Fig. 4b), or even ‘T-shape’ (Fig. 4c). Note that element-wise volume fractions are used herein, meaning stiff or compliant materials are projected onto element centroids. Figure 4c is thus free from phase mixing despite the minor overlap of stiff and compliant domains at the edges of the “T”.

Fig. 4

Candidate stiff phase objects for projection domains of Fig. 3 (r $_{min} =$ 2h, t $_{F} =$ 2h, and t $_{E} =$ 1h, where h is the element size). Design variable nodes marked with a pentagram have magnitude greater than zero and elements with circles at centroids are the compliant (blue) phase by default. Attainable features include a circle of diameter 2*r $_{min}$ (Fig. 3), a a circle of diameter d $_{max} =$ 2*r $_{min} +$ t $_{F}$, b an elipse of height 2*r $_{min}$ and length 2*r $_{min} +$ t $_{F}$, and c a “T-shape” of length and height 2*r $_{min} +$ t $_{F}$ (with other possible variations including L-shape)

Regardless of shape, the maximum diameter length scale of the discrete object is r _max = r _min + t _F / 2. As Fig. 5 illustrates, objects having length scale greater than this r _max along any axis incur phase mixing. We note the restricted maximum length scale here is different than that described and used in Guest (2009b) for controlling member sizes. Herein r _max is enforced in all directions leading to isolated objects. In the previous work, the constraint on r _max had to be satisfied in any single direction, thus allowing (for example) long beams of maximum width r _max .

Fig. 5

Objects of length scale greater than 2*r $_{min} +$ t $_{F}$ lead to phase mixing, which is prevented through penalization. Length scale annotations are associated with nodes n $_{1}$ and n $_{2}$

Using the free zone approach, discrete objects will be enclosed by the second phase with length scale of at least t _E + t _F . This length scale is thus the minimum spacing between objects and is denoted as s $_{min}$. Noting that the example projection domains in Fig. 3 have t _E = 2 elements and t _F = 1 element, this minimum spacing is clearly seen in Fig. 4 where all stiff objects are surrounded by 3 compliant elements.

Although the length scale variables t _E and t _F are needed to clearly explain the numerics of the algorithm in the following section, the variables r _max and s _min are more useful in terms of engineering design. Given these variables and r _min , one can simply use the following relations to determine the projection domain length scales t _E and t _F :

$$ {\begin{array}{ll} {t_{F} =2( {r_{\max } -r_{\min } } )} \\ {t_{E} =s_{\min } -t_{F} =S_{\min } -2( {r_{\max } -r_{\min } } )} \\ \end{array} } $$

(1)

As length scales must be positive, we note that the proposed framework requires s _min > 2(r _max − r _min ). This requirement is discussed further in Section 4.3. We also note that setting t _F = 0 yields r _min = r _max and thus the fixed size and shape case described in Guest (2011).

2.3 Numerical implementation

The following equations are developed for the projection domains shown in Section 2.2 for the case of a stiff object enclosed in compliant matrix material.

2.3.1 Neighborhood sets

As suggested by the preceding figures, a single design variable influences several elements. It follows that several design variables influence the phase distribution within each element. This mapping is stored in neighborhood sets for each element. The local ( $N_{L}^{e}$), free ($N_{F}^{e}$), and enclosure neighborhood sets ($N_{E}^{e}$) for element e contain the design variables for which the element is located in the local, free, and enclosure zones. More rigorously:

$$ {\begin{array}{lll} {i \in N_{L}^{e} } & {\text{if}\quad\left\| {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} \right\|\le r_{min } } \\ {i \in N_{F}^{e} } & {\text{if}\quad r_{min } < \left\| {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} \right\|\le r_{min } +t_{F} }\\ {i \in N_{E}^{e} } & {\text{if}\quad r_{min } +t_{F} < \left\| {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} \right\|\le r_{min } +t_{F} +t_{E} } \\ \end{array} } $$

(2)

where x _i is the location of design variable i, and x¯^e is the location of the centroid of element e. As design variables do not project either phase into the free region, the neighborhood set $N_{F}^{e}$ is not used in the equations below and need not be stored. It is simply identified for completeness.

2.3.2 Heaviside projection

The proposed technique projects design variables onto the local space and the extended space independently. Projection intensity in elemental neighborhood sets $N_{L}^{e}$ and $N_{E}^{e}$ are denoted as $\mu _{L}^{e}$ and $\mu _{E}^{e}$, respectively, and are computed using standard proximity-based filtering as

$$ \mu_{L}^{e} =\frac{\sum\limits_{i\in N_{L}^{e} } {\phi_{i} w_{L} ( {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} )} }{\sum\limits_{i\in N_{L}^{e} } {w_{L} ( {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} )} },\mu_{E}^{e} =\frac{\sum\limits_{i\in N_{E}^{e} } {\phi_{i} w_{E} ( {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} )} }{\sum\limits_{i\in N_{E}^{e} } {w_{E} ( {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} )} } $$

(3)

where the w _L and w _E are the local and extended region weighting functions, respectively, shown in Fig. 6 and given as

$$ {\begin{array}{ll} {w_{L} ( {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} )=\left\{ {{\begin{array}{cc} {\frac{r_{\min } -r_{i} }{r_{\min } }} & {if \mathbf{x}_{i} \in \boldsymbol{\Omega}_{L}^{e} }\\ 0 & {otherwise}\\ \end{array} }} \right\}} \\ {w_{E} ( {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} )=\left\{ {{\begin{array}{cc} {\frac{( {r_{\min } +t_{F} +t_{E} } )-r_{i} }{t_{E} }} & {if \mathbf{x}_{i} \in \boldsymbol{\Omega}_{E}^{e} }\\ 0 & {otherwise}\\ \end{array} }} \right\}} \\ \end{array} } $$

(4)

and r _i is simply the distance between design variable and element centroid.

$$ r_{i} \equiv \left\| {\mathbf{x}_{i} -\overline{\mathbf{x}}^{e}} \right\| $$

(5)

The variables $\mu _{L}^{e}$ and $\mu _{E}^{e}$ are then separately converted to binary pseudo-volume fractions $\rho _{L}^{e}$ and $\rho _{E}^{e}$ by passing them through the Heaviside projection operator as follows

$$ \begin{array}{l} \rho_{L}^{e} =H( {\mu_{L}^{e} } )=\left\{ {{\begin{array}{ll} {1~\mathit{if}~\mu_{L}^{e} > 0} \\ {0~\mathit{if}~\mu_{L}^{e} =0} \\ \end{array}}} \right\},\\ \rho_{E}^{e} =H( {\mu_{E}^{e} } )=\left\{ {{\begin{array}{ll} {1~\mathit{if}~\mu_{E}^{e} > 0} \\ {0~\mathit{if}~\mu_{E}^{e} =0} \\ \end{array} }} \right\}. \end{array} $$

(6)

For the use with gradient-based optimizers, the Heaviside operators are regularized as

$$ \begin{array}{l} \rho_{L}^{e} =1-e^{-\beta_{L} \mu_{L}^{e} (\boldsymbol{\upphi})}+\frac{\boldsymbol{\mu}_{L}^{e} (\boldsymbol{\upphi})}{\boldsymbol{\mu}_{\max } }e^{-\beta_{L} \mu_{\max } }, \\ \rho_{E}^{e} =1-e^{-\beta_{E} \mu_{E}^{e} (\boldsymbol{\upphi})}+\frac{\boldsymbol{\mu}_{E}^{e} (\boldsymbol{\upphi})}{\boldsymbol{\mu}_{\max } }e^{-\beta_{E} \mu_{\max }} \end{array} $$

(7)

where β _R indicates the curvature of the regularization in region R, and μ _max is simply the maximum possible projection intensity which is usually μ _max = ϕ _max. The operator is linear when β _R = 0, and converges to the discrete Heaviside function as β _R approaches infinity.

Fig. 6

Weighting functions w $_{L}$ and w $_{E}$ as a function of distance from design variable location to element centroid

The pseudo-volume fractions for local and enclosure domains are combined to yield physically meaningful element volume fraction ρ ^e using following expression as

$$ \rho^e=\frac{\rho_{L}^{e} \left( {2-\rho_{E}^{e} }\right )}{2} $$

(8)

Element e becomes a stiff element (ρ ^e = 1) only when $\rho _{L}^{e} =1$ and $\rho _{E}^{e} =0$, meaning element e is receiving material projected from a local domain only. When $\rho _{L}^{e}$ is equal to 0, the element is a compliant, regardless of $\rho _{E}^{e}$. In the case that an element is receiving both stiff and compliant material from projections $\left (\rho _{L}^{e} =1 and \rho _{E}^{e} =1\right )$, $\rho ^{e}$ becomes 0.5. This is referred to as phase mixing and will be prevented through standard intermediate volume fraction penalization techniques.

For the case of designing compliant features (e.g., holes) in a stiff domain, we project the compliant phase in the local domain and stiff phase in the enclosure domain. This is achieved by simply subtracting (8) from unity:

$$ \rho^e=1-\frac{\rho_{L}^{e} \left( {2-\rho_{E}^{e} } \right)}{2} $$

(9)

Finally, we note that expressions (8–9) are continuous when using the regularized functions (7). Derivatives $\frac {\partial \rho ^{e}}{\partial \phi _{i} }$ are thus straightforward and readily computed via the chain rule.

3 Problem formulation and algorithm

The new topology optimization algorithm is applied herein to design the unit cell microstructure of periodic materials. Homogenization theory is used to estimate the material’s effective stiffness tensor at the macro (bulk) scale given the micro (unit cell) topology. An inverse homogenization problem is then formulated to design the material distribution in the unit cell such that desired optimal properties at the macroscale are achieved, such as optimized elastic moduli with prescribed elastic symmetries. In this paper we consider maximization of bulk modulus under conditions of isotropic symmetry.

3.1 Elastic homogenization and inverse homogenization

Elastic homogenization theory (Bensoussan et al. 1978; Sanchez-Palencia 1980) and their finite element-based implementations (Guedes and Kikuchi 1990; Hassani and Hinton 1998) are well-known. We therefore present only the relevant finite element equations here. In short, the goal of elastic homogenization is to determine the effective stiffness tensor C ^H in the macroscale constitutive relation

$$ \boldsymbol{\upsigma} =\mathbf{C}^{\mathbf{H}}\boldsymbol{\upvarepsilon} $$

(10)

where σ and ε are the macroscopic stress and strain fields, respectively. In two-dimensions, the effective stiffness tensor is given in engineering notation as

$$ \mathbf{C}^{\mathbf{H}}=\left[ {{\begin{array}{lll} {C_{11}^{H} } & {C_{12}^{H} } & {C_{13}^{H} } \\ {C_{12}^{H} } & {C_{22}^{H} } & {C_{23}^{H} } \\ {C_{13}^{H} } & {C_{23}^{H} } & {C_{33}^{H} } \\ \end{array} }} \right] $$

(11)

and is computed via finite element analysis as

$$ C_{ij}^{H} =\frac{1}{|\boldsymbol{\Omega}|}\sum\limits_{e\in \Omega } {\left( {\mathbf{d}_{o}^{e(i)} -\mathbf{d}^{e( i )}} \right)^{T}\mathbf{k}^{e}( {\rho^{e}} )\left( {\mathbf{d}_{o}^{e(j)} -\mathbf{d}^{e(j)}}\right)} $$

(12)

where k ^e(ϕ) is the element stiffness matrix as a function of the design variables ϕ, and $\mathbf {d}_{o}^{e( i )}$ are the elemental nodal displacement vectors associated with the unit test strain fields for homogenization analysis. The nodal displacement vectors d ^e(i) are the elemental components of d ⁽ⁱ⁾, the nodal displacement vectors associated with the fluctuation strain fields due to heterogeneity of the unit cell. These are found by solving the finite element problem

$$ {\begin{array}{*{20}c} {\mathbf{K}( \boldsymbol{\upphi} )\mathbf{d}^{(i)}=\mathbf{f}^{(i)}( \boldsymbol{\upphi} )} \\ {\mathbf{d}^{( i )} ~is~ \boldsymbol{\Omega} -periodic} \\ \end{array}} $$

(13)

where the nodal forces f ⁽ⁱ⁾ result from the unit test strain field (i) and are computed by

$$ \mathbf{f}^{(i)}=\mathbf{K}( \boldsymbol{\upphi} )\mathbf{d}_{o}^{( i )} $$

(14)

The inverse homogenization problem can now be defined as

$${\begin{array}{*{20}c} {\max\limits_{\boldsymbol{\upphi}} } & & {f=f_{property} ( {\mathbf{C}^{H}( \boldsymbol{\upphi} )} )-f_{error} ( {\mathbf{C}^{H}(\boldsymbol{\upphi})})} \\ \end{array}} $$

$$ {\begin{array}{*{20}c} \text{subject\;to}&\mathbf{K}(\boldsymbol{\upphi})\mathbf{d}^{(i)}=\mathbf{f}^{(i)}\\ &\sum\limits_{e\in \Omega } {\rho^{e}(\boldsymbol{\upphi})v^e-V\le 0} \\ &0\le \phi_{i} \le \phi_{\max } \forall i\in \boldsymbol{\Omega} \\ \end{array} } $$

(15)

where v ^e are the elemental volumes and V the allowable volume of the stiff material phase. For the case of isotropic materials, the stiffness tensor (11) must take the following form:

$$ \mathbf{C}_{isotropic} =\left[ {{\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{11} } & 0 \\ 0 & 0 & {0.5( {C_{11} -C_{12} } )} \\ \end{array} }} \right] $$

(16)

This is imposed using the f _error penalty function, which quantifies anisotropy of the effective stiffness tensor. Comparing (11) and (16), this function may be defined as

$$\begin{array}{@{}rcl@{}} f_{error} &=&\left({C_{11}^{H} -C_{22}^{H} }\right)^2+\left({C_{11}^{H} -C_{12}^{H} -2C_{33}^{H} }\right)^{2} \notag\\ &&+\left({C_{13}^{H} }\right)^2+\left({C_{23}^{H} }\right)^2 \end{array} $$

(17)

This work considers maximizing the effective bulk modulus B ^H of the material, which may be expressed as

$$ f_{property} =B^H=\frac{1}{4}\left( {C_{11}^{H} +C_{22}^{H} +2C_{12}^{H} } \right) $$

(18)

The reader is referred to Guest and Prévost (2006) for a detail discussion of these and alternate formulations, including the sensitivity analysis.

3.2 Preventing intermediate volume fractions

In order to obtain 0–1 designs, intermediate volume fractions created by phase mixing must be prevented. In this paper we consider both the Solid Isotropic Material with Penalization (SIMP) method (Bendsøe 1989; Zhou and Rozvany 1991) and the Rational Approximation of Material Properties (RAMP) method (Stolpe and Svanberg 2001). SIMP models elemental Young’s modulus as

$$ E^{e}( \boldsymbol{\phi} )=E_{0} +\rho^{e}( \boldsymbol{\phi} )^{p}( {E_{1} -E_{0} } ) $$

(19)

where p ≥ 1 is the SIMP exponential penalty term, and E ₀ and E ₁ are Young’s moduli of the compliant and stiff phases, respectively. We have found that this method shows better performance for compliant feature inclusions such as holes. RAMP expresses elemental Young’s modulus as

$$ E^{e}( \boldsymbol{\phi} )=E_{0} +\frac{\rho^{e}( \boldsymbol{\phi} )}{1+\eta ( {1-\rho^{e}(\boldsymbol{\phi})})}({E_1-E_{0}}) $$

(20)

where $\eta$ $\ge$ 0 is the RAMP penalty term. We have found RAMP more effective for stiff feature inclusions (see Guest (2011) for additional details).

3.3 Optimization algorithm and parameters

All examples are solved using the Method of Moving Asymptotes (MMA) (Svanberg 1987). MMA is well-known to be very efficient for problems with a large number of design variables provided the number of active constraints is small. In this paper, we use constant projection parameters $\beta =$ 50 and $\phi _{max} =$ 3 with tightened MMA asymptotes as described in Guest et al. (2011), and constant penalization parameters p $=$ 5 for SIMP and $\eta =$ 10 for RAMP. The initial material distribution in all examples is selected as linear distribution that increases with the distance from the base cell centroid (Guest and Prévost 2007).

3.4 Reported metrics

Reported quantitative metrics will include the discreteness metric M proposed by Sigmund (2007):

$$ M=\left( {\frac{4}{n}} \right)\sum\limits_{e=1,n} {\rho^{e}( {1-\rho^{e}} )} $$

(21)

where n is the number of finite elements. This metric is zero for a fully binary solution and 100 % for a solution with all $\rho ^{e} =$ 0.5.

We will also report the effective bulk modulus B $^{H}$ for all optimized topologies. It must be emphasized, however, that this magnitude is only accurate when the topology achieves M $= 0$ (is a binary design). In the case of $M > 0$, one can use the RAMP or SIMP penalized stiffness in the calculation of B $^{H}$, or the unpenalized stiffness. The former underestimates the “actual” B $^{H}$ of the material while the latter overestimates it. This makes it difficult to compare to solutions to the theoretical Hashin-Shtrikman bounds on bulk modulus, as these do not apply for $M > 0$. In fact, and in some cases we see penalized B $^{H}$ below the Hashin-Shtrikman lower bound and unpenalized B $^{H}$ above the Hashin-Shtrikman upper bound. Due to this inconsistency, we chose to present the B $^{H}$ used in the objective function, which is the penalized B $^{H}$ evaluated with RAMP parameter $\eta = 10$ for stiff inclusion examples and SIMP exponent of p $= 5$ for soft inclusion examples. This enables a clear relative comparison between optimized topologies. Finally, we note that all results were isotropic with an error function magnitude f $_{error}$ of less than 10$^{-6}$. The magnitude of this function is thus not reported for each example.

4 Periodic material design examples

The variable shape, discrete object algorithm is now applied to design periodic microstructures with maximized effective bulk modulus and isotropic elastic symmetries. The design domain is the unit cell of the periodic material, defined here as a unit square meshed using 160 by 160 elements. The two material phases composing the microstructure are assumed isotropic with Poisson’s ratio of 0.3. Young’s moduli of these phases will be varied.

4.1 Optimizing size, shape, and layout of stiff inclusions in a compliant matrix material

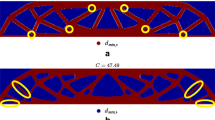
We begin with case of embedding a stiff phase of Young’s modulus E $_{1} =$ 1.0 into a compliant matrix material of Young’s modulus E $_{0} =$ 0.2. Figure 7 displays the isotropic, maximal bulk modulus solution for the case of a monolithic, single-scale topology with stiff phase volume fraction of 10 %. This topology is representative of what free-form (monolithic) topology optimization produces and exhibits a bulk modulus of 0.171, nearly achieving the Hashin-Shtrikman bound of 0.172 for this volume fraction.

Fig. 7

Maximum bulk modulus solution using monolithic topology optimization with 10 % volume constraint: unit cell (left) and periodic structure (right)

Using the discrete object projection concept, the stiff phase is now restricted to be circular inclusions of fixed diameter d $_{min} =$ d $_{max} =$ 0.06 units, spaced at a minimum distance of s $_{min} =$ 0.03 units. This is essentially the algorithm of Guest (2011) (Fig. 1) and is achieved herein using r $_{min} =$ 0.03, t $_{F} =$ 0, and t $_{E} =$ 0.03 units. The resulting topology is shown in Fig. 8a and, not surprisingly, it is seen that the inclusions are largely aligned with the load path of the monolithic solution. Increasing the required minimum spacing to s $_{min} =$ 0.06 units leads to the topologies in Fig. 8b. It is seen that all inclusions are the same size and shape, and spaced at the required minimum distance. Table 1 summarizes the bulk moduli for these (and the following) optimized topologies. It is clear from these results that the requirement to use discrete objects leads to a significant drop in bulk modulus over the free-form, monolithic solution (row 1).

Fig. 8

Maximum bulk modulus solutions for 10 % volume fraction of the stiff phase using Discrete Object Projection for circular inclusions of fixed size (d $_{min} =$ d $_{max} =$ 0.06 units) and minimum allowable spacing of a s $_{min} =$ 0.03 and b 0.06 units. Unit cells are shown in the left column and periodic structures in the right column. The red and blue length scale bars indicate the required circular object diameter and minimum spacing, respectively

Table 1 Comparison of bulk modulus for the monolithic topology (Fig. 7) and topologies found using Discrete Object Projection using objects of fixed size and shape (Fig. 8) and variable size and shape (Fig. 9)

Object design freedom is now enhanced using the new variable size and shape algorithm. Figure 9 shows a number of solutions found by imposing a minimum object diameter of d $_{min} =$ 0.06 units and various combinations of length scale restrictions on the maximum object diameter d $_{max}$ and minimum object spacing s $_{min}$. The solutions contain a variety of inclusion sizes and shapes, including circles, ellipses (Fig. 9b), heart-like shapes (see Fig. 9e), and even “bow-tie” shapes (see midpoints of unit cell boundaries in Fig. 9f). Before performing a detailed comparison of these topologies, we first illustrate that the prescribed length scales are indeed satisfied. As discussed in Section 2, the projection naturally imposes minimum and maximum length scales of d $_{min} =$ 2 r $_{min}$ and d $_{max} =$ 2r $_{max} =$ 2r $_{min} +$ t $_{F}$, respectively, and a minimum length scale for spacing of s $_{min} =$ t $_{F} +$ t $_{E}$. These length scale restrictions are illustrated with circles in Fig. 10, which contains an enlarged version of Fig. 9(d). It is clearly seen that all inclusions are between the minimum and maximum allowable length scales, and that all inclusions are spaced at least as far apart as the minimum allowable distance s $_{min}$. The designer may specify these three length scales according to the range of desirable (or available) inclusion sizes and minimum required bonding distances, and the projection algorithm naturally creates topologies under this restriction without the need for explicit constraints.

Fig. 9

Maximum bulk modulus solutions using Discrete Object Projection with variable size and shape inclusions having minimum diameter d _min = 0.06 and a d _max = 0.09, s _min = 0.06; b d _max = 0.09, s _min = 0.09; c d _max = 0.09, s _min = 0.12; d d _max = 0.12, s _min = 0.09; e d _max = 0.12, s _min = .12; and f d _max = 0.15, s _min = 0.12. Unit cells are shown in the left column and periodic structures in the right column. The two red length scale bars in each figure indicate the minimum and maximum allowable inclusion length scale in diameter, and the blue bar represents the minimum allowable spacing between inclusions

Fig. 10

An enlarged version of the periodic material in Fig. 9d annotated with length scales d $_{min} =$ 0.06, d $_{max} =$ 0.12, and s $_{min} =$ 0.09, the minimum and maximum allowable inclusion diameters and minimum allowable distance between inclusions, respectively

Figures 9a, b and c illustrate the effect of increasing s _min when using a constant d $_{min}$ and d $_{max}$. It is clear from these topologies that the inclusions move farther apart as s $_{min}$ increases. This also reduces stiffness of the design: Table 1 shows this quantitatively while visually we see inclusions pushed from the edges of the unit cell towards its interior. This has a very interesting effect on the designed shape of inclusions located at the midpoints of the unit cell boundaries. Examining closely these locations in Fig. 9b, we see these inclusions have been squeezed into ellipses, and that adjacent inclusions on the interior of the unit cell feature a flat exterior edge. This effectively keeps as much stiff phase as possible along the primary load path, the edge of the unit cell. In other words, if either the edge or interior inclusions were circular, the centroid of the interior inclusion would need to move further towards the centroid of the unit cell to respect the minimum spacing requirement.

Figures 9c, e, and f illustrate the effect of increasing shape freedom by increasing d $_{max}$ for constant d $_{min}$ (and s $_{min})$. Moving from Fig. 9c–e, we see the larger d $_{max}$ enables design of larger inclusions, and these inclusions have straight edges to enable tight packing along the unit cell boundary – no inclusions are found on the interior. This trend continues in Fig. 9f, where the algorithm has managed to pack all inclusions in line, away from the interior of the unit cell, including at the corners. Table 1 confirms that these topological changes improve the objective function, as B $^{H}$ increases from topology 9c to 9e to 9f.

Finally, it is worth noting that the algorithm is quite successful at creating near 0–1 solutions. The discreteness measure M is approximately 4 % or less for all of the topologies in Fig. 9.

Figure 11 shows an additional set of solutions using a larger minimum length scale diameter of d $_{min} =$ 0.12 units. The same trends are observed as in the previous example. As the minimum allowable spacing is increased, comparing Fig. 11a, b and c, inclusions move farther apart and are pushed into the interior of the cell. This is a less efficient region of the unit cell causing a corresponding decrease in bulk modulus (Table 2). Increasing d $_{max}$ provides more design freedom to the optimizer, reflected in the more complex shapes and an improved bulk modulus (Table 2) moving from Fig. 11d, b and e.

Fig. 11

Maximum bulk modulus solutions using Discrete Object Projection with variable size and shape inclusions having minimum diameter d _min = 0.12 and a d _min = 0.18, s _min = 0.09; b d _min = 0.18, s _min = 0.12; c d _min = 0.18, s _min = 0.15; d d $_{max} =$ 0.15, s $_{min} =$ 0.12; and e d $_{max} =$ 0.21, s $_{min} =$ 0.12. Stiff phase volume fraction is 15 %. Unit cells are shown in the left column and periodic structures in the right column

Table 2 Comparison of bulk modulus for variable size and shape discrete object topologies of Fig. 11

4.2 Optimizing size, shape, and layout of compliant inclusions in a stiff material

We now use the algorithm to optimize the shape, size, and layout of compliant inclusions in a stiff substrate. The compliant and stiff phases are assumed to have Young’s moduli of 0.33 and 1.0, respectively, and we consider a stiff phase volume fraction of 85 %. The monolithic solution, found using free form topology optimization, is shown in Fig. 12. This topology offers a bulk modulus of 0.598, again approaching the Hashin-Shtrickman bound of 0.601.

Fig. 12

Maximum bulk modulus solution found using monolithic topology optimization with a stiff phase volume fraction constraint of 85 %. Unit cell is shown in the left column and periodic structure in the right column

Figure 13 displays solutions using the variable size and shape discrete object projection algorithm with minimum length scale d $_{min} =$ 0.12 units and various magnitudes of the maximum and minimum spacing length scales. Quantitative metrics for these topologies are contained in Table 3. The solutions follow the expected trends: (1) as s $_{min}$ increases inclusions are pushed farther apart and the optimized bulk modulus decreases (compare Fig. 13a–b), and (2) as d $_{max}$ increases, more diverse inclusion shapes are seen and bulk modulus increases (compare Fig. 13c, b and d).

Fig. 13

Maximum bulk modulus solutions using Discrete Object Projection with variable shape compliant inclusions having minimum diameter d $_{min} =$ 0.12 and a d $_{max} =$ 0.18, s $_{min} =$ 0.09; b d $_{max} =$ 0.18, s $_{min} =$ 0.12; c d $_{max} =$ 0.15, s $_{min} =$ 0.12; d d $_{max} =$ 0.21, s $_{min} =$ 0.12. Unit cells are shown in the left column and periodic structures in the right column. The two blue length scale bars in each figure indicate the minimum and maximum allowable inclusion length scale in diameter, and the red bar represents the minimum allowable spacing between inclusions

Table 3 Comparison of bulk modulus for the monolithic topology (Fig. 12) and topologies found using Discrete Object Projection with variable size and shape objects (Fig. 13)

An interesting observation is that the layouts of the soft inclusions here strongly resemble the layouts of the stiff inclusions in the preceding examples. Figure 13d and 11e, for example, are essentially the inverse of each other. One explanation for this is that the inclusions introduce fluctuation strains in the microstructure and the optimizer orients these fluctuation strains in a ring-like pattern so as to maintain isotropic symmetry.

4.3 Topological limitations of the proposed algorithm

As demonstrated, the proposed algorithm allows the designer to prescribe the minimum allowable length scale diameter (d $_{min})$ and maximum allowable length scale diameter (d $_{max})$ of designed objects, as well as the minimum allowable spacing between objects (s $_{min})$. The larger the difference between d $_{max}$ and d $_{min}$, the larger the length scale of the free zone projection domain t $_{F}$, and thus the more design freedom in optimizing the shape of the inclusion.

The primary drawback of the algorithm as proposed is that increasing t $_{F}$ also increases the minimum allowable spacing between objects (s $_{min} =$ t $_{F} +$ t $_{E})$. Although one can reduce the enclosure zone length scale t $_{E}$ to mitigate this effect, it must remain a positive number and thus we are limited to cases where s $_{min} >$ 2(r $_{max} -$ r $_{min})$. This essentially means that the algorithm as presented is not capable of providing significantly large design freedom in size and shape while also allowing the inclusions to be tightly packed. This is one of the reasons the algorithm seems to prefer larger inclusions as t $_{F}$ increases in the preceding examples. This limitation becomes more restrictive as the allowable volume of material increases, as eventually the maximum stiffness problem will begin to resemble the packing problem (Guest 2011), and the algorithm will prefer all inclusions achieve the maximum length scale so as to maximize material volume. Ideally the minimum spacing s $_{min}$ would be a function of only the enclosure length scale t $_{E}$. Removing this dependency is the subject of future work.

5 Concluding remarks

A topology optimization method is presented for optimizing the size, shape, and layout of discrete non-overlapping objects, such as inclusions, in periodic materials. In contrast to traditional monolithic topology optimization, the designer may specify the minimum and maximum allowable object size as well as the minimum allowable spacing between discrete objects. These size and shape restrictions are satisfied naturally, without additional constraints, using the projection-based methodology. Specifically, each independent design variable is capable of actively projecting multiple material phases onto different regions of the finite element space and the interaction of these projections is tailored to yield near binary topologies.

As in the original Discrete Object Projection approach for features of fixed size and shape (Guest 2011, the variable size and shape scheme presented here progresses in the spirit of free-form topology optimization. That is, objects may appear, disappear, or translate across the design domain. This means the number of objects need not be defined a priori, which is particularly important in the design of multifunctional materials where the optimal number of inclusions may not be known. The scheme was demonstrated in the context of maximum stiffness materials for cases of stiff inclusions in a compliant matrix and compliant inclusions in a stiff substrate. Extension to 3d is straightforward with the circles in Figs. 1 and 3 simply becoming spheres.