Density filters for topology optimization based on the Pythagorean means

Abstract

In topology optimization, restriction methods are needed to prohibit mesh dependent solutions and enforce length scale on the optimized structure. This paper presents new restriction methods in the form of density filters. The proposed filters are based on the geometric and harmonic means, respectively, and possess properties that could be of interest in topology optimization, for example the possibility to obtain solutions which are almost completely black and white. The article presents the new filters in detail, and several numerical test examples are used to investigate the properties of the new filters compared to filters existing in the literature. The results show that the new filters in several cases provide solutions with competitive objective function values using few iterations, but also, and perhaps more importantly, in many cases, different filters make the optimization converge to different solutions with close to equal value. A variety of filters to choose from will hence provide the user with several suggested optimized structures, and the new filters proposed in this work may certainly provide interesting alternatives.

1 Introduction

In topology optimization, it is well known that to ensure mesh independence of solutions and prohibit modelling problems such as checkerboards, measures have to be taken. A method used in many applications is the sensitivity filter (Sigmund 1997), wherein a smoothing filter is applied to the derivatives of the objective function. This method has proven to work well in practice, making solutions mesh-independent and free from checkerboards. Another way of dealing with the problem is to use a density filter. Density filters restrict the possible solutions by separating the design variables, controlled by the optimizer, from the actual density variables. The filter is a function that, for given values on the design variables, gives a density distribution. By choosing the filter function in an appropriate way, unwanted features, for example checkerboards, can be eliminated from the solution. The filter also introduces a length scale to the problem, which can make the solution mesh independent. The linear density filter (Bruns and Tortorelli 2001; Bourdin 2001), is an example of such a filter, and while it does give good convergence properties, it produces solutions with large gray areas. In some cases, this can be a problem, and several other filtering techniques have been suggested to give more black and white solutions, for example using continuous forms of max or min operators. One example which has proved successful in producing discrete solutions is the Heaviside filter (Guest et al. 2004), which works by first applying the linear density filter, and then projecting the resulting density according to a continuous approximation of a Heaviside function. Sigmund proposes a new family of “morphological filters (Sigmund 2007), and compares them to a number of other density filters, concluding that an issue with both the morphological and the Heaviside filters is the need for a careful continuation of a filter parameter, successively altering the behaviour of the filter from linear to nonlinear, making the number of iterations quite large. Recent developments by (Guest et al. 2011) suggest solver parameters that reduce the need for continuation; since the proposed filters allow large changes of the density distribution as a result of small changes in design variables, the length of the steps taken by the solver should be restricted.

Using the linear density filter, the filtered density of an element can be regarded as a weighted arithmetic mean of the design variables in its neighbourhood. In this paper, we explore the idea of instead using the geometric mean or the harmonic mean, which have some properties that could be beneficial for topology optimization. The new filters are compared to some previously presented filtering techniques using three examples, and some differences are pointed out.

2 Background

There are already several filters suggested in the literature, see Section 3 below, why consider some more? In an attempt to answer this question, a short background on filters and topology optimization is first repeated.

2.1 The relaxation and penalization (RP) approachfor topology optimization

A commonly used solution approach for topology optimization problems with binary design variables is the relaxation/penalization (RP) approach in which first the binary constraints on the variables are relaxed and then variables which are strictly between zero and one are penalized in an attempt to drive them (almost) binary. The most well-known method based on this approach is SIMP, (Bendsøe and Sigmund 1999), in which “gray” elements, corresponding to design variables strictly between zero and one, are penalized by decreasing their stiffness-to-weight ratio. Related RP approaches are suggested in, e.g., (Stolpe and Svanberg 2001a) and (Borrvall and Petersson 2001).

The main advantage of an RP approach is that some gradient-based nonlinear programming (NLP) method can be used for solving the corresponding optimization problem with continuous design variables. An inevitable drawback, however, is the fact that the penalization of gray elements makes the optimization problem intrinsically nonconvex, with possibly a large number of different locally optimal solutions. Since no NLP method, or optimality critera (OC) method, is able to find anything better than a locally optimal solution to a nonconvex problem of realistic size, the user must accept that RP approaches are in this sense heuristics.

Consequently, there are no theoretical results of how “well” a certain RP approach solves various topology optimization problems, simply because it is virtually impossible to control which local optimum the underlying NLP method will converge to. It is not very difficult to find test examples where a small change of the move limiting parameter in the underlying NLP or OC method, or a small change of the starting point, results in a different final structure with even a different number of holes. Attempts have been made to gradually and slowly increase the penalty, but this does not help in general since the trajectory of globally optimal solutions when (e.g.) the SIMP penalty parameter increases may be discontinuous with large jumps, see (Stolpe and Svanberg 2001b). Nevertheless, the success of SIMP is indisputable, with repeated good experiences by numerous users over the years.

2.2 The role of the filter in RP approaches

Without filter, the NLP method typically ends up in a solution to the RP problem which is more or less worthless from a practical point of view since it corresponds to a scattered structure with too thin structural parts and/or too many small holes, e.g. checkerboards. The purpose of the filter is to modify the RP problem (by restricting the set of feasible solutions) in such a way that the NLP method, when applied to this modified problem, tends to find a solution corresponding to a useful structure. Ideally, the filter should also help the underlying NLP method to end up in a local optimum with low objective value! But since there are no scientific results on how a filter should accomplish such a task, the value of a new filter must be judged on experience, i.e. how it seems to work in practice. A natural first test is to apply new filters on various academic problems.

2.3 Why suggest new filters?

There are two main reasons for suggesting certain new filters in this study.

First reason

There are some natural filters missing in the topology optimization literature, namely filters based on the second and third Pythagorean means (geometric mean and harmonic mean). Since, so far, only the first Pythagorean mean (arithmetic mean) has been considered, it seems inevitable to investigate the missing Pythagorean filters, in particular since they possess some theoretical properties which might be advantageous for topology optimization.

Second reason

It may be argued that an extensive “filter tool box” is in practice better than a small one. Then main argument goes as follows: When topology optimization is applied in practice for designing a new structure, the most demanding task for the user is to formulate the problem in a correct and well-defined way. This includes setting up a reasonable FE-model, and specifying relevant load cases, boundary conditions, objective function, and constraint functions. When this has been done, a topology optimization software can be applied to calculate an “optimal” solution. But then, if a filter tool box is available, it takes just a small additional effort to solve the considered problem several times with alternative filters. Since the penalized problem is nonconvex, and since different filters restrict the set of feasible solutions in different ways, this repetition will typically provide the user with several different “optimal solutions”, each corresponding to a (hopefully clever) suggestion of how the structure should be designed. Since there are almost always some aspects which are not properly considered by the optimization model, like manufacturing aspects, it should be valuable for the user to have more than one suggestion to choose between before further post processing. This does not mean that any filter should be included in the tool box, but if a new filter is able to, on at least some nontrivial test problems, obtain relevant topologies and/or geometries not obtained by other filters, then this new filter should be a candidate for inclusion. In fact, the different filters considered in this study do indeed produce different solutions on the considered test problems. In particular, this holds for the suggested “Pythagorean” filters.

3 Some existing filters

In standard topology optimization, there is a density variable $\rho _{j}$ associated with each element j in the finite element model of the design space. The physical properties of the element, that is, the mass density and the stiffness, are then controlled by this density variable via some interpolation scheme, e.g. SIMP(Simplified Isotropic Material with Penalization) (Bendsøe and Sigmund 1999). When using a filter, variables called $\tilde {\rho }_{j}$ are introduced, related to the variables $\rho _{j}$ through a function called a filter as $\tilde {\boldsymbol {\rho }} = \text {F}(\boldsymbol {\rho })$, where $\boldsymbol {\rho }$ and $\tilde {\boldsymbol {\rho }}$ are vectors containing the respective variables $\rho _{j}$ and $\tilde {\rho }_{j}$ for all elements. The quantity $\tilde {\rho }_{j}$, identified as the physical density of element j, is then used to interpolate material properties, while the $\rho _{j}$, now denoted design variables, are to be interpreted as non-physical variables controlling the structure indirectly. All evaluations of structural behaviour are performed using the physical densities $\tilde {\rho }_{j}$. The optimizer is controlling the structure indirectly via the design variables $\rho _{j}$, and all derivatives are therefore calculated through the chain rule.

3.1 Linear density filter

The linear density filter (Bruns and Tortorelli 2001; Bourdin 2001) can be described by:

$$ \tilde{\rho}_{i} = \sum\limits_{j} w_{ij}\rho_{j}, $$

(1)

where $w_{ij}$ are weighting factors based on the distance between element i and element j. A reasonable requirement is that if all of the design variables are equal to a certain value, then the filtered density should also obtain this value. This motivates the condition:

$$ \sum\limits_{j} w_{ij} =1\quad,\forall{i}, $$

(2)

which will be used throughout this article. The weighting factors are normally taken $\neq 0$ in some neighbourhood $N_{i}$ of element i, and equal to zero outside the neighbourhood. The neighbourhood is usually taken circular (although this does not necessarily have to be the case), and its radius is commonly known as the filter radius, or simply R, in which case $N_{i} = \{j: d(i,j) \leq R\}$, where $d(i,j)$ is the distance between the centroids of element i and j. Two choices of weight factors are studied in this work, constant weights, where all weight factors in the neighbourhood are taken equal, and conic weights, taken as linearly decaying outwards from the neighbourhood center. Constant weights are defined by:

$$ w_{ij}= \begin{cases} \frac{1}{|N_{i}|} &\quad j\in N_{i} \\ \quad 0 &\quad j \notin N_{i} \\ \end{cases}, $$

(3)

where $|N_{i}|$ is the number of elements in the set $N_{i}$. Conic weights are defined by:

$$ w_{ij} = \begin{cases} \frac{R-d(i,j)}{\sum_{k \in N_{i}} (R - d(i,k))}&\quad j\in N_{i} \\ \quad 0 &\quad j \notin N_{i} \\ \end{cases} $$

(4)

3.2 Sensitivity filter

The original sensitivity filter (Sigmund 1997), is not a density filter in the sense indicated above. No filtering is conducted regarding the density itself, hence $\tilde {\boldsymbol {\rho }} = \boldsymbol {\rho }$. However, the sensitivities (derivatives) of an objective function $\phi$, are filtered, using:

$$ \widetilde{\frac{\partial\phi}{\partial\rho_i}} = \frac {\sum_{j \in N_{i}}\frac{{\partial\phi}}{\partial\rho_{j}}w_{ij}\rho_{j}} {\rho_{i}}. $$

(5)

This modification of the derivatives has proven to be effective in producing mesh-independent solutions.

3.3 Morphology-based filters

Sigmund proposes two morphology-based filters called Dilate and Erode (Sigmund 2007), both using continuous approximations of, respectively, the max and min operator. The Dilate filter is formulated as:

$$ \tilde{{\rho}_{i}} =\text{log}\left(\frac{{\sum_{j \in N_{i}} \text{e}^{\beta\rho_{j}}}} {|N_{i}|}\right)/\beta=\text{log}\left(\sum_{j} w_{ij}\text{e}^{\beta\rho_{j}}\right)/\beta, $$

(6)

where the weights used by Sigmund are constant, but could well be of for example cone type. The filter could also be stated as:

$$ \text{e}^{\beta \tilde{\rho}_{i}} = \sum\limits_{j} w_{ij} \text{e}^{\beta \rho_{j}}. $$

(7)

The erode filter is the opposite of the dilate filter, switching white to black by replacing $\rho$ with $1\,-\,\rho$, and $\tilde {\rho }$ with $1\,-\,\tilde {\rho }$:

$$ 1-\tilde{{\rho}_{i}} =\text{log}\left(\sum_{j} w_{ij}\text{e}^{\beta(1-\rho_{j})}\right)/\beta. $$

(8)

In the limit where $\beta$ gets large, the dilate/erode filters turn to max/min operators. For $\beta$ approaching zero on the other hand, the filters converge to the linear density filter.

3.4 Heaviside filters

Guest et al. (2004) propose a filter for obtaining 0/1 solutions, based on a continuous approximation of a Heaviside step. The design variables, $\rho$, are first filtered using the linear density filter (1), and the result is then mapped to a physical density by a Heaviside approximation:

$$ \tilde{\rho}_{i} = 1-\text{e}^{-\beta \sum_{j} w_{ij} \rho_{j}}+\text{e}^{-\beta}\sum\limits_{j} w_{ij} \rho_{j}, $$

(9)

where $\beta$ is a parameter controlling the approximation of the Heaviside step. For $\beta$ equal to zero, the filter turns into the linear density filter, whereas for $\beta$ approaching infinity, the mapping turns into a Heaviside step, meaning that if any design variable in the neighbourhood is larger than zero, the physical density is equal to one. This behaviour resembles that of the Dilate filter, which suggests that this filter could be named the “Heaviside Dilate”. Note that instead of the nodal design variables used by Guest et al, in this work, as done by Sigmund (2007), elemental design variables are used to make comparisons between the filters fair.

Switching $\rho$ with $(1-\rho )$, and $\tilde {\rho }$ with $(1-\tilde {\rho })$, we get the ”modified Heaviside filter”, as proposed by Sigmund (2007):

$$ 1\,-\,\tilde{\rho}_{i} = 1\,-\,\text{e}^{-\beta(1-\sum_{j} w_{ij} \rho_{j})}\,+\,\text{e}^{-\beta}\left(1\,-\,\sum\limits_{j} w_{ij} \rho_{j}\right). $$

(10)

This filter is the opposite of the Heaviside filter, still converging to the linear density filter as $\beta$ goes to zero, but having the property that for beta tending to infinity, the physical density is set to zero unless every design variable in the neighbourhood has value 1.

Since the behaviour for large $\beta$ and binary design variable distributions is similar to the morphological Erode filter, which is approximating the min operator in each neighbourhood, we will refer to this filter as the “Heaviside Erode”. To avoid confusion, the morphological filters suggested by Sigmund will hereby be denoted “Exponential Dilate” and “Exponential Erode”, respectively.

4 Two filters based on the geometric mean

Using the linear density filter, the density of an element is defined as a weighted arithmetic mean of the design variables in the neighborhood. It it natural to consider other means, for example the geometric mean. A filter based on the geometric mean can be formulated as:

$$ \tilde{{\rho}_{i}} = \prod\limits_{j \in N_{i}}\rho_{j}^{w_{ij}}. $$

(11)

It is clear from the definition that if any design variable in the neighborhood is equal to zero, the filtered density will be zero. This suggests that this filter will be able to create more black and white structures than the linear density filter. The filter can be rewritten as:

$$\log(\tilde{{\rho}_{i}}) =\sum\limits_{j} w_{ij} \log(\rho_{j}). $$

(12)

Since taking the logarithm of zero is not defined, we introduce a positive parameter, $\alpha$:

$$ \log(\tilde{{\rho}_{i}}+\alpha) =\sum\limits_{j} w_{ij} \log(\rho_{j}+\alpha). $$

(13)

For $\alpha$ approaching infinity, it can be shown that the filter is equivalent to the linear density filter, with smooth transitions between black and white. Since the behaviour for small $\alpha$ is similar to the Exponential erode filter, we will refer to this filter as the “Geometric Erode”. Note however, that the geometric erode filter is not in general an approximation of a min operator, the behaviour is only similar to that of the Exponential erode filter for binary design variable distributions.

When $\alpha = 0$, the derivative of an objective function $\phi$ with respect to the design variables using the new filter is, by the chain rule:

$$ \frac{\partial\phi}{\partial{\rho}_{i}}= \frac{\sum_{j}\frac{\partial\phi}{\partial\tilde{\rho}_{j}}w_{ji}\tilde{\rho}_{j}}{\rho_{i}}. $$

(14)

Recalling (5), we see that (14) is almost the derivatives obtained by using the sensitivity filter:

$$ \widetilde{\frac{\partial\phi}{\partial\rho_{i}} } = \frac {\sum_{j}\frac{{\partial\phi}}{\partial\rho_{j}}w_{ij}\rho_{j}} {\rho_{i}}. (5) $$

Thus, the sensitivity filter gives “almost” the derivatives of the objective function obtained by applying the geometric erode filter.

By switching $\rho$ and $\tilde {\rho }$ with $1\,-\,\rho$ and $1\,-\,\tilde {\rho }$ in (13), a second geometric filter is obtained:

$$ \log(1-\tilde{{\rho}_{i}}+\alpha) = \sum\limits_{j} w_{ij}\log(1-\rho_{j}+\alpha). $$

(15)

This filter does the opposite, that is, for $\alpha = 0$, any black pixel will be filtered to a black circle with radius equal to the filter radius. This behaviour resembles that of the Exponential dilate filter, which suggests that this filter could be named the “Geometric Dilate”. The behaviour of the geometric filters can be studied in a one-dimensional example in Fig. 1, where the geometric filters have been applied to a one dimensional example with 100 elements. Elements 1–50 have $\rho _{i} = 1$, while elements 51–100 have $\rho _{i} = 0$. The filter radius is 30 elements, and constant weights are used.

Fig. 1

An illustration of the behaviour of the geometric filters in one dimension

5 Two filters based on the harmonic mean

Another possible filter can be defined by the weighted harmonic mean:

$$ \frac{1}{\tilde{{\rho}_{i}}} = \sum\limits_{j} \frac{w_{ij}}{\rho_{j}}. $$

(16)

This filter also has the property that one design parameter equal to zero in the neighbourhood of an element gives that element zero density, which leads us to name this filter the “Harmonic Erode”.

To avoid division by zero, again, we introduce the parameter $\alpha$:

$$ \frac{1}{\tilde{{\rho}_{i}}+\alpha} = \sum\limits_{j} \frac{w_{ij}}{\rho_{j}+\alpha}. $$

(17)

As above, we also define the reverse filter, “Harmonic Dilate”, filtering a black pixel to a black circle, according to:

$$ \frac{1}{1-\tilde{\rho}_{i}+\alpha} =\sum\limits_{j} \frac{w_{ij}}{1-\rho_{j}+\alpha}. $$

(18)

The behaviour of the harmonic filters is shown in Fig. 2, where the setting is the same as in Fig. 1.

Fig. 2

An illustration of the behaviour of the harmonic filter in one dimension

It holds generally that the harmonic mean is smaller than the geometric mean, which in turn is smaller than the arithmetic mean, which would imply that this filter will give even more discrete solutions than the geometric filters. This is illustrated in Fig. 3, where the same one-dimensional example as in Figs. 1 and 2 is studied for different values of $\alpha$. The Measure of Discreteness ($M_{nd}$), defined as in (Sigmund 2007): $M_{nd} = \frac {\sum _{j=1}^{n} 4 \tilde {\rho }_{j} (1 - \tilde {\rho }_{j})}{n} \times 100~\%$, is shown for different values of $\alpha$. For large values of $\alpha$, the two filters converge to the linear density filter, with a quite substantial amount of gray in the filtered density. For $\alpha$ approaching zero, the filters both should be completely discrete, however, the harmonic filter approaches this limit more rapidly than the geometric filter. It should also be pointed out that for both filters, as $\alpha$ approaches zero, the usage of constant weights $w_{ij}$ reduces the amount of gray in the solution, opposite to the effect observed with the linear density filter, where constant weights lead to a less discrete solution. For comparison, the same measure is shown in Fig. 4 for the Exponential and Heaviside erode filters. The same conclusions apply: for low $\beta$ values, the filters converge to the linear density filter, and conic weights give the more discrete solution, while for high $\beta$ values, constant weights give more discrete results. To complete the investigation of the properties of the new filters, a study of the mesh independence obtained using the new filters is reported in Appendix A.4.

Fig. 3

The discreteness of the new filters in a one-dimensional example, as a function of the parameter $\alpha$

Fig. 4

The discreteness of the Exponential and Heaviside Erode filters in a one-dimensional example, as a function of the parameter $\beta$

5.1 Derivatives

Since we ultimately aim to solve the topology optimization problem using numerical methods, it of interest that the problem formulation is chosen in such a way that the numerical solver works in an efficient manner. For example, if the derivatives of the objective function or constraints take on very large values, this could cause numerical problems. Also, very large derivatives indicate the problem is very sensitive, and step length constraints or other measures may have to be taken in order to ensure convergence. It may therefore be assumed, that it is beneficial for the filter operator chosen to have bounded derivatives.

When using the sensitivity filtering proposed by Sigmund, the calculation of the filtered sensitivities involves dividing by the density, which creates problems when considering elements with density equal to zero. When using the modified SIMP method, the density variable is allowed to take on the value zero, making it necessary to replace the density in the denominator by the expression $\max (\rho _{j},\epsilon )$, which causes a non-smoothness of the derivative. For the geometric and harmonic filters, when the derivatives are calculated, division is made with $(\alpha + \rho _{j})$, which for small $\alpha$ could be a problem. One would suspect that derivatives tending towards infinity would be a problem for the optimizer, and therefore, the value of the largest filter derivative, $\max _{i,j}\frac {\delta \tilde {\rho _{i}}}{\delta \rho _{j}}$ has been studied in the one-dimensional setting used above, see Fig. 5. As can be seen, for small $\alpha$ the derivatives of the geometric erode filter become very large, while the derivatives of the harmonic erode filter stay bounded as $\alpha$ tends to zero. This fact can also be shown algebraically: the harmonic filter is described by:

$$ \frac{1}{\tilde{{\rho}_{i}}+\alpha} = \sum\limits_{j}\frac{w_{ij}}{\rho_{j}+\alpha}. $$

(19)

Multiplication on both sides with $\rho _{k}+\alpha$ gives:

$$\frac{\rho_{k}+\alpha}{\tilde{{\rho}_{i}}+\alpha} = w_{ik}+\sum\limits_{j\neq k}w_{ij}\frac{\rho_{k}+\alpha}{\rho_{j}+\alpha}>w_{ik}. $$

(20)

But the derivative of the filter, $\frac {\partial \tilde {\rho }_{i}}{\partial \rho _{k}}$, is $w_{ik}(\frac {\tilde {\rho }_{i}+\alpha }{\rho _{k}+\alpha })^{2}$. Using (20), we get that

$$ \frac{\partial\tilde{\rho}_{i}}{\partial\rho_{k}}=w_{ik}\left(\frac{\tilde{\rho}_{i}+\alpha}{\rho_{k}+\alpha}\right)^{2}<w_{ik}\left(\frac{1}{w_{ik}}\right)^{2}=\frac{1}{w_{ik}}. $$

(21)

Hence, the largest derivative of the filter is bounded by the inverse of the smallest (non-zero) weight factor, and the bound is independent of $\alpha$. A consequence of this is that for the same filter radius, constant weights should provide for smaller derivatives, as opposed to conic weights.

Fig. 5

The value of the largest filter derivative as a function of $\alpha$

It should be noted that the exponential filters also possess the property of having bounded derivatives as $\beta$ grows large, but the geometric filters do not in general have this property when $\alpha$ goes to zero, and the Heaviside filters do not have this property as $\beta$ grows large.

6 Convexity and concavity properties of the filters

The filter (1) above is called linear since each density $\tilde {\rho }_{i}$ is a linear function of the variable vector ${\rho }$. The eight dilate/erode filters described above are clearly nonlinear in this respect, but a closer examination reveals that the three dilate filters (6), (15), (18) and the Heaviside erode filter (10) are in fact convex density filters (each $\tilde {\rho }_{i}$ is a convex function of ${\rho }$), while the three erode filters (8), (13), (17) and the Heaviside dilate filter (9) are concave density filters (each $\tilde {\rho }_{i}$ is a concave function of ${\rho }$).

These properties can be proven by showing (analytically) that the Hessian matrix $\nabla ^{2}\tilde {\rho }_{i}({\rho })$ is always positive semidefinite for the four convex filters, and always negative semidefinite for the four concave filters.

More precisely, if $\tilde {\rho }_{i}({\rho })$ is given by (6), (10), (15) or (18), then

$$ \begin{array}{l}\mathbf{y}^{\mathsf{T}} \nabla^{2} \tilde{\rho}_{i}(\boldsymbol{\rho}) \mathbf{y} = \sum\limits_{j} \sum\limits_{k} \frac{\partial^{2} \tilde{\rho}_{i}}{\partial \rho_{j} \partial \rho_{k}} \,y_{j} y_{k} \geq 0, \\ \mbox{for all}\ \mathbf{y} \in \Re^{n} \ \mbox{and} \ {\rho} \in [0,1]^{n}, \end{array} $$

(22)

while if $\tilde {\rho }_i({\rho })$ is given by (8), (9), (13) or (17), then

$$ \begin{array}{l} \mathbf{y}^{\mathsf{T}} \nabla^{2} \tilde{\rho}_{i}(\boldsymbol{\rho}) \mathbf{y} =\sum\limits_{j} \sum\limits_{k}\frac{\partial^{2} \tilde{\rho}_{i}}{\partial \rho_{j} \partial \rho_{k}}\,y_{j} y_{k} \leq 0,\\ \mbox{for all}\ \mathbf{y} \in \Re^{n}\ \mbox{and} \ {\rho} \in [0,1]^{n}.\end{array} $$

(23)

The proofs of (22) and (23) are left to an appendix.

Three implications of these properties are the following:

• 1. For each of the convex filters, the volume $\sum _{i} \tilde {\rho }_{i}({\rho })$ is a convex function of ${\rho }$, so that the feasible region induced by a volume constraint is a convex set.

• 2. For each of the concave filters, the compliance without penalization ($p \,=\, 1$ in SIMP) is a convex function of ${\rho }$. This follows since the stiffness of each element is concave in ${\rho }$, see proposition 1 in (Stolpe and Svanberg 2001a).

• 3. For each of the four concave filters, the volume $\sum _{i} \tilde {\rho }_{i}({\rho })$ is a concave function of ${\rho }$. This implies that the MMA approximation of the volume will always be “conservative”, so that the optimal solution of the MMA subproblem will always satisfy the original volume constraint.

  Although the authors have not been able to explicitly utilize these convexity/concavity properties further in this study, they are still presented since they might cast some light on the nature of the considered filters.

7 Test examples

The new filters have been tested on three different test examples, and their performance has been compared to the original sensitivity filter, the linear density filter, the two morphological filters “Exponential Dilate” and “Exponential Erode” and the two Heaviside filters. The chosen test examples are a compliance minimization problem, a mechanism synthesis problem chosen similar to that in (Sigmund 2007), and a stress minimization problem chosen similar to that solved in (Le et al. 2010).

As indicated in Section 2, there is no way of proving that one filter compared to another will always give better solutions. The intent of the examples is rather to show that for some problems, the new filters obtain solutions which are in some way better than the ones obtained with other filters. Also, in several of the test problems, the different filters end up in rather different local optima, although they do not differ much in objective function value. This may in fact be beneficial: If the solution obtained using one filter is not satisfying, one may simply switch to a different filter and possibly obtain a more useful solution.

The standard density based approach for topology optimization has been used, with element-wise constant densities. The modulus of elasticity for each element is interpolated using the modified simplified isotropic material with penalization (SIMP) scheme:

$$ E_{i}=E(\tilde{\rho}_{i})=E_{\min}+\tilde{\rho}_{i}^{\,p}(E_{0}-E_{\min}), $$

(24)

with $E_{\min } = 10^{-9}$ and $E_{0} = 1$. The discretization is made using four node finite elements, and the implementation is done in MATLAB, using the “88-line code” of Andreassen et al. (2011). The optimizer used is the MATLAB version of the method of moving asymptotes, MMA (Svanberg 1987), with default values on all parameters, except for the addition of a move limit 0.2 on each variable in each iteration, implemented through the parameters alfa and beta in the subroutine mmasub.m. (The same move limit as used in the OC method of the “88-line code” of Andreassen et al. (2011)).

7.1 Test problem 1: Compliance minimization

In the first test problem, the sum of the compliances corresponding to four different load cases is minimized subject to a volume constraint. Three different weightings of the four load cases are studied, leading to test problems 1a, 1b and 1c.

The design domain consists of $140 \times 140 = 19600$ square finite elements and $141 \times 141 = 19881$ nodes with coordinates $(x,y)$, where $x \in \{-70,-69,\ldots ,69,70\}$ and $y \in \{-70,-69,\ldots ,69,70\}$. There are 18 degrees of freedom which are fixed to zero, namely the degrees of freedom corresponding to the nine nodes with coordinates $(x,y)$, where $x \in \{-1,0,1\}$ and $y \in \{-1,0,1\}$. In each of the four load cases, there are applied forces at each of the twelve nodes with coordinates $(x_i,y_i)$ according to Table 1. Note that $\displaystyle (30,52) \approx 60\cdot (1/2,\sqrt {3}/2)$, which means that the twelve nodes are located approximately on the boundary of a circle with radius 60 (with one “hour” between each node). The force $(F_{xi},F_{yi})$ applied at $(x_i,y_i)$ for the different load cases is defined in Table 2 and shown in Fig. 6, and the load coefficients in Table 2 are chosen according to Table 3.

Table 1 Coordinates for applied forces

Table 2 Load definitions

Table 3 Load coefficients

Fig. 6

The four load cases

The optimization problem can be formulated as:

$$ \min_{\rho}\quad \sum\limits_{\ell=1}^{4}\mathbf{f}_{\ell}^{\mathsf{T}}\mathbf{u}_{\ell}(\boldsymbol{\rho}) $$

(25)

$$ \text{s.t.} \left\{ \begin{array}{l l} \sum_{i=1}^{n} \tilde{\rho}_{i}(\boldsymbol{\rho}) \leq V^* \\ \boldsymbol{\rho} \in [0,1]^{n} \\ \end{array} \right. $$

(26)

where, for a given $\boldsymbol {\rho } \in [0,1]^{n}$, $\mathbf {u}_{\ell }(\boldsymbol {\rho })$ is obtained as the solution to:

$$\left(\sum\limits_{j=1}^{n}(E(\tilde{\rho}_{j}(\boldsymbol\rho{})) \mathbf{K}_{j}\right)\mathbf{u}_{\ell} = \mathbf{f}_{\ell},$$

(27)

where $\mathbf {u}_{\ell }$ and $\mathbf {f}_{\ell }$ are the displacement and force vectors corresponding to load case i, and $\mathbf {K}_{j}$ is the stiffness matrix of element j. The physical densities $\tilde {\rho _{j}}$ are obtained from one of the (1), (6), (8), (9), (10), (13), (15), (17), (18) or, if using the Sensitivity filter, $\tilde {\rho }_{j} = \rho _{j}$.

In this test problem, the chosen value of the penalty parameter in SIMP is $p\,=\,4$. Moreover, all the ten considered filters use conic weights with filter radius 2.4 elements (= 4 % of the radius of the “circle of loads”). Concerning the convergence criterion, the iterations are stopped when no variable has changed by more than 0.001 since the previous iteration, which is somewhat harder than the more commonly used 0.01.

When minimizing compliance, the objective value of an obtained solution is very sensitive to the amount of gray structure, which in turn is sensitive to the values of the parameters $\alpha$ (in the harmonic and geometry filters) and $\beta$ (in the exponential and Heaviside filters). Moreover, the linear density filter almost always comes out as a loser when comparing objective value, even though the generated topology and geometry may be very good, simply because the amount of (heavily penalized) gray structure is larger than for the other filters. Since it may be more interesting to compare the quality of different topologies and geometries rather than the amount of gray, the obtained final solutions for the different filters have also been rounded to pure black and white solutions as follows:

The right hand side of the volume constraint in the SIMP problem is set to 0.333 times the total number of elements, i.e., $0.333 \cdot 19600 = 6526.8$. When the convergence criterion has been fulfilled and the iterations stopped, the obtained (slightly gray) solution is rounded to a completely black and white solution by letting the 6528 elements with largest values on their physical design variable (“density”) be black, and the other 13072 elements white. This means that $6528/19600 \approx 0.33306$ of the total design domain becomes black.

With this rounding procedure, it is no longer important to choose $\alpha$ very small and $\beta$ very large. Instead, for test problem 1, we have chosen values on these parameters such that if all ρ _j are binary and $\sum _{j} w_{ij} \rho _{j} = \textstyle \frac {1}{2}$ then $\tilde {\rho }_{i}$ becomes roughly 0.1 for the erode filters and 0.9 for the dilate filters. More precisely, the following values have been used:

$$\begin{array}{lll}\alpha =0.1 &&for the harmonic filters,\\ \alpha =0.01 &&for the geometric filters, \\ \beta =6 &&for the exponential filters, \\ \beta =4 &&for the Heaviside filters.\end{array}$$

When using these values, reasonably black and white structures are obtained without any continuation procedure for gradually decreasing $\alpha$ or increasing $\beta$. The topology and geometry turns out to be essentially unaltered by the final rounding, but the boundaries become much sharper (of course) and the compliances decrease.

Finally, it should noted that symmetry of the structure is not enforced.

7.2 Test problem 2: The force inverter

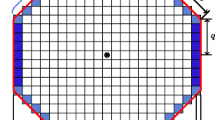
The second test example is a mechanism synthesis problem, namely that of a force inverter. A very similar problem has previously been used as a benchmark (Sigmund 1997). The design domain is rectangular, with aspect ratio width: height = 3:4, and displacements are fixed in two points, see Fig. 7. Between these, a force is applied, and the output displacement at the opposite side of the domain is minimized. Due to symmetry, only half of the domain is modelled, using 180 by 120 finite elements. Springs are attached to the input and output node, being of stiffness $k_{in}=1$ and $k_{out}=0.001$. The filter radius used for this problem is $R=2.5$, and the volume constraint $V^*$ is set to 33 % of the design volume.

Fig. 7

The force inverter

The optimization problem can be formulated as:

$$\min_{\rho} \quad \mathbf{e}_{l}^{T}\mathbf{u}(\boldsymbol{\rho})$$

(28)

$$ s.t. \left\{ \begin{array}{l l} \sum_{i=1}^{n} \tilde{\rho}_i(\boldsymbol{\rho}) \leq V^* \\ \boldsymbol{\rho} \in [0,1]^n\\ \end{array}\right. $$

(29)

where $\mathbf {e}_{l}$ is a vector which is zero at every position except that representing the out force, where it is equal to one, and $\mathbf {u}(\boldsymbol {\rho })$ is obtained as in test problem 1. The penalization parameter $p=3$ was used in SIMP.

7.3 Test problem 3: The L-bracket

The third test example is that of minimizing the p-norm of von Mises stress in a L-bracket. This example has been studied earlier, for example by Le et al. (2010). A vertical distributed load is applied to ten nodes at the tip of an L-shaped domain, fixed at the upper end, see Fig. 8.

Fig. 8

The L-bracket

The objective function to be minimized is:

$$ ||\sigma||_{p} = \left(\sum\limits_{i=1}^{n}\sigma_{j}(\boldsymbol{\rho})^{p}\right)^{1/p}, $$

(30)

where $\sigma _{j}$ is the von Mises stress at the centroid of element j. As in (Le et al. 2010), to penalize intermediate densities, the stress is calculated using a modified elasticity tensor, according to:

$$ \mathbb{C}(\tilde{\rho}_{i}) = \mathbb{C}_{0}\left( E_{min}+\tilde{\rho}_{i}^{1/3}(E_{0}-E_{min})\right), $$

(31)

where $\mathbb {C}_{0}$ is the elasticity tensor for material with unit modulus elasticity.

The enforcement of the L-shaped domain was carried out in a slightly different manner than usual. The “natural” way of doing this would be to discretize only the L-domain, making it impossible for the optimization to put material outside the domain. However, a drawback of this approach is that boundaries of the optimized structure, because of the use of a density filter, will look different depending on if they are inner or outer. In the interior of the domain, the structural edges are not sharp, instead there is a transition from material to void, whereas at the boundary of the finite element mesh, the transition is sharp. This difference could potentially make the optimization favour one type of boundary over another, which of course should not be the case. To avoid this phenomenon, a larger domain, embedding the L-domain, was modelled with finite elements, and a constraint in the optimization was added, restricting the total volume of elements outside the L-domain to be smaller than some small value. The extended domain is shown in Fig. 9. This has the effect of making all edges inner. The authors have experienced that this modelling technique yields better designs, and reduces the tendency to get stuck in local optima.

Fig. 9

The L-bracket, with extended domain

A constraint on the total volume of the structure was also included, which makes the optimization problem to be as follows:

$$\min_{\rho}\quad \left(\sum\limits_{i=1}^{n}\sigma_{j}(\boldsymbol{\rho})^{p}\right)^{1/p} $$

(32)

$$ \text{s.t.} \left\{ \begin{array}{l l} \sum_{i=1}^{n} \tilde{\rho}_{i}(\boldsymbol{\rho}) \leq V^* \\ \sum_{i \in \Omega_{void}} \tilde{\rho}_{i}(\boldsymbol{\rho}) \leq V_{void}^* \\ \boldsymbol{\rho} \in [0,1]^{n} \end{array} \right. $$

(33)

The elemental stresses $\sigma _{j}$ are calculated from the displacements $\mathbf {u}(\boldsymbol {\rho })$, which are obtained as in the first two test problems. The penalization parameter $p=3$ was used in SIMP. The filter radius used for this problem is $R=3.5$, the volume constraint $V^*$ is set to 50 % of the L-shaped design volume, the allowed volume outside the L-domain $V_{void}^*$ is 0.5 elements, and p in the p-norm is set equal to 6. The discretization of the design volume is made with 170 by 160 finite elements, and the width of the $\Omega _ {void}$ domain was 10 elements, making the actual design space 150 by 150 elements in size.

7.4 Optimization

The optimization problems are solved using MMA, increasing $\beta$ and decreasing $\alpha$ according to a simple scheme. Convergence is considered to occur when the maximum change in any design variable between two consecutive iterations is smaller than some tolerance. Although it might be argued that some other convergence criterion, e.g. norm of KKT residual, is a more appropriate indicator of optimality, our choice is common in literature and therefore used also in this work. The scheme used for the optimization is described by:

• 1:   initialize $\alpha =\alpha _0$, $\beta =\beta _0$

• 2:   while $change > changetol$ and $iter < N_{max}$ do

• 3:         if $\mod (iter,50)=0$ or $change < 0.01$ then

• 4:             $\alpha \leftarrow \text {max}(0.1\alpha ,\alpha _{min})$

• 5:             $\beta \leftarrow \text {min}(2\beta ,\beta _{max})$

• 6:         end if

• 7:         compute filtered densities $\tilde {\boldsymbol {\rho }}$

• 8:         assemble stiffness matrix and solve system

• 9:         calculate derivatives of the objective and constraint functions

• 10:         call MMA subroutine, get back new design variables $\boldsymbol {\rho }_{new}$

• 11:         calculate $change =||\boldsymbol {\rho }_{new}-\boldsymbol {\rho }||_{\infty }$

• 12:   end while

For the first test problem, $changetol\,=\,0.001$, $N_{max}\,=\,2000$, $\alpha _0 = \alpha _{min}$ and $\beta _0 = \beta _{max}$, i.e. no continuation of the filter parameters is carried out. For the other two problems, $changetol = 0.01$, $N_{max} =1000$, $\alpha _0 = 100$, $\alpha _{min} = 0.0005$, $\beta _0 = 0.2$ and $\beta _{max} = 200$. In the first test problem, conic weights have been used for all filters. In the second and third examples, for the sensitivity filter and the linear density filter, conic weights have been used, while constant weights have been used for all other filters. For the linear density filter, as can be seen in Fig. 3, conic weights give a more discrete solution, which is the reason for this choice. The opposite holds for the geometric, harmonic, exponential and Heaviside filters at low values of $\alpha$/high values of $\beta$, motivating the choice of constant weights for these filters. As suggested by (Guest et al. 2011), for the Heaviside filters, the MMA asymptotes were forced together at each continuation step, by using the proposed value of the variable asyinit. This has the effect, at high beta values, of making the steps taken by the optimization very small directly after an increase of $\beta$, reducing divergence tendencies. Otherwise, all parameters were kept standard.

8 Results

8.1 Obtained results for test problem 1

The obtained results on test problem 1 are presented in Tables 4, 5 and 6 and Figs. 10, 11 and 12 where the physical densities $\tilde {\rho }_{i}$ are plotted. Each table contains the following information:

• Column 1:   Number of MMA iterations for obtaining the gray solution.

• Column 2:   Penalized objective value for the obtained gray structure divided by objective value for the completely black structure (19600 black elements).

• Column 3:   Objective value for the rounded solution (6528 black elements) divided by objective value for the completely black structure (19600 black elements).

• Column 4:   Number of holes in the rounded solution.

Table 4 Results for test problem 1a

Table 5 Results for test problem 1b

Table 6 Results for test problem 1c

Fig. 10

Resulting density distributions for example 1a

Fig. 11

Resulting density distributions for example 1b

Fig. 12

Resulting density distributions for example 1c

A striking observation is that although the different filters produce quite different topologies, with quite different objective values of the gray solutions, the objective values of the corresponding rounded solutions are often very close. This makes it possible for the user to consider also other aspects than objective value when deciding which solution to recommend. A comment is in order regarding the result of the sensitivity filter on example 1b. While providing excellent solutions for the examples 1a and 1c, the sensitivity filter converges to a very gray solution with significantly larger compliance than all other filters for this weighting of the loads. Actually, this solution appears to be a KKT point with respect to the filtered derivatives. It is not, however, a local optimum to the optimization problem. In fact, looking at the iteration history for the sensitivity filter on example 1b, there are feasible solutions with lower objective values than the final objective value among the earlier iterates. It is not known to the authors exactly what features of this particular problem which causes this behaviour, but it shows that even established filters may sometimes encounter difficulties not encountered by other filters. Again, this is an argument for a filter tool box.

8.2 Obtained results for test problem 2

The results of the optimization for the force inverter are summarized in Table 7, and the density distributions are shown in Fig. 13. The table contains number of iterations, displacement of output node for gray structure, displacement of output node for rounded black and white structure, and measure of non discreteness for gray structure defined as in Section 5. Three different topologies are obtained as solutions, with the sensitivity filter and the Heaviside filters converging to one, the linear density filter and the exponential filters to another, and the geometric and harmonic filters converging to a third. The correlation between objective function value and discreteness is much weaker than for compliance optimization, with the sensitivity filter obtaining a solution that has a very large output displacement, despite having a quite large amount of gray elements. After rounding to a completely black and white solution, the difference between the best and worst solution is less than 6 %. As in the compliance example, this indicates that aspects other than objective may be of interest when choosing final design, and the existence of several filters giving different topologies is therefore beneficial.

Table 7 Results for the force inverter

Fig. 13

Resulting density distributions for the force inverter

8.3 Obtained results for test problem 3

The results of the optimization for the L bracket is summarized in Table 8, and the density distributions are shown in Fig. 14. For the Heaviside erode filter, the optimization diverged for high beta values. Because of this, results using a lower final beta value of $\beta _{max}=15$ is reported. One may note that for this objective function, a discrete solution is not always beneficial for the objective function value. For example, one of the best solutions, achieved by the sensitivity filter, is also one of the most non-discrete ones.

Table 8 Results for the L bracket

Fig. 14

Resulting density distributions for the L bracket

9 Conclusions

In this paper, four new density filters for topology optimization have been presented, and tested on three different types of optimization problems.

From the compliance minimization example, two perhaps surprising conclusions can be drawn. First, different local optima are reached for almost every filter, highlighting the nonconvexity of the problem solved. The solutions differ in objective function value, mostly due to different amounts of gray elements in the solution. However, the next surprising find is that when rounded to pure 0/1 structures, the structures perform almost identically to each other. As a user, there may be clear benefits of obtaining many of these similarly performing optimization results, before making the final design decision. Consider for example the results of example 1c displayed in Fig. 12. The results of the geometric dilate filter and the Heaviside erode filter are very similar in terms of stiffness, however, from a manufacturing point of view, the second structure is probably vastly more expensive than the first. This is not an attempt to claim that the geometric filter is always better than the Heaviside filter in this aspect, but rather that for this specific load case, it happens to be, and there is no obvious way of obtaining this structure but to try several filters for the same problem.

In the mechanism example, the conclusions from the compliance example hold: since the variations in objective function value are so small, it should be of interest to obtain several design suggestions before making a final decision.

The stress minimization example is clearly the most challenging optimization problem solved in this article, and the scatter in result is by far the greatest. Still, the conclusions from above hold, as a designer, one would likely prefer some of the obtained structures compared to the others. For example, the experienced engineer would know that even though the sensitivity filter result obtains a remarkably low objective function value, the re-entrant corner will lead to high stresses in the structure, and rather choose for example the result from the linear density filter, which rounds the corner in a smooth way.

So far, the arguments have been that having many filters in the tool box is advantageous. However, as mentioned above, one should not use this argument in favour of any filter, only filters which are “good” in some general sense, and produce results not obtained using other methods should be considered. Sigmund (2007) lists a number of properties that a “good” filter should possess:

• 1. Mesh-independent and checkerboard-free solutions

• 2. Black and white (0/1) solutions

• 3. Manufacturability

• 4. No extra constraints

• 5. Not too many tuning parameters

• 6. Stable and fast convergence

• 7. General applicability

• 8. Simple implementation

• 9. Low CPU-time

Regarding the first five items, the proposed new filters are equal to existing filters in the literature. Solutions exhibit no checkerboards or similar disturbances, very sharp black and white structures may be obtained, the manufacturability interpretations are the same as other erode and dilate filters, no extra constraints are introduced, and the amount of tuning parameters is equal to that of other filters. As for the point “Stable and fast convergence”, it may be noted that in all but one of the presented five optimization problems, one of the new filters meets the convergence criterion the fastest. While this is certainly not a proof for their superior convergence, it shows that the new filters are certainly competitive in this aspect. With regards to the remaining points, again, the proposed filters are similar to existing filters.

To summarize, the authors believe that the presented geometric and harmonic filters clearly qualify to be included in any filter tool box for topology optimization.

Appendices

Appendix: Proof of the convexity/concavity properties

In this appendix we prove the statements in Section 6, namely that for the exponential, harmonic and geometric dilate filters, and the Heaviside erode filter, each $\tilde {\rho }_i$ is a convex function of ${\rho }$, while for the exponential, harmonic and geometric erode filters, and the Heaviside dilate filter, each $\tilde {\rho }_i$ is a concave function of ${\rho }$.

First we note the it is sufficient to prove four of these eight statements. If a dilate filter is written $\tilde {\rho }_{i} = f_{i}({\rho })$ then the corresponding erode filter becomes $\tilde {\rho }_{i} = g_{i}({\rho }) = 1- f_{i}(\mathbf {1} - {\rho })$, where $\mathbf {1} = (1,\ldots ,1)^{\mathsf {T}}$. From this it immediately follows that $\nabla ^{2} f({\rho })$ is positive semidefinite for all ${\rho } \in [0,1]^{n}$ if and only if $\nabla ^{2} g({\rho })$ is negative semidefinite for all ${\rho } \in [0,1]^{n}$. Thus the considered dilate filter is convex if and only if the corresponding erode filter is concave.

We will show below that the Harmonic erode filter is concave, the Geometric erode filter is concave, the Exponential dilate filter is convex, and the Heaviside dilate filter is concave.

It then also follows that the Harmonic dilate filter is convex, the Geometric dilate filter is convex, the Exponential erode filter is concave, and the Heaviside erode filter is convex.

In the formulas below, $\delta _{jk} \,=\, 1$ if $j\,=\,k$ and $\delta _{jk} \,=\, 0$ if $j \neq k$.

1.1 A.1 The Harmonic erode filter

For the Harmonic erode filter,

$$\begin{array}{rll}\frac{1}{\tilde{\rho}_i + \alpha} &=&\sum\limits_j \frac{ w_{ij} }{\rho_j + \alpha}\,,\ \ \frac{\partial \tilde{\rho}_i}{\partial \rho_j} =\frac{w_{ij} (\tilde{\rho}_i + \alpha)^2}{(\rho_j + \alpha)^2}\,,\\ \frac{\partial^2 \tilde{\rho}_i}{\partial \rho_j \partial \rho_k} &=&\frac{2 w_{ij} w_{ik} (\tilde{\rho}_i + \alpha)^3}{(\rho_j + \alpha)^2 (\rho_k + \alpha)^2}\ -\ \delta_{jk}\, \frac{2 w_{ij} (\tilde{\rho}_i + \alpha)^2}{(\rho_j + \alpha)^3}\,.\end{array}$$

$$ \begin{array}{l}\mbox{Then}\ \ \frac{1}{2(\tilde{\rho}_i + \alpha)^3}\sum\limits_j \sum\limits_k \frac{\partial^2 \tilde{\rho}_i}{\partial \rho_j \partial \rho_k} \,y_j y_k \\ \quad = \sum\limits_j \sum\limits_k\frac{ w_{ij} w_{ik} y_j y_k }{(\rho_j \!+\! \alpha)^2 (\rho_k \!+\! \alpha)^2} \!-\!\frac{1}{\tilde{\rho}_i \!+\! \alpha}\sum\limits_j\frac{ w_{ij} y_j^2}{(\rho_j + \alpha)^3}\\ \quad=\left(\sum\limits_j\frac{ w_{ij} y_j }{(\rho_j \!+\! \alpha)^2}\right)^2 \!-\!\left(\sum\limits_j\frac{ w_{ij} }{\rho_j \!+\! \alpha}\right)\left(\ \sum\limits_j\frac{ w_{ij} y_j^2}{(\rho_j + \alpha)^3}\right)\\ \quad = \left(\sum\limits_j u_j v_j\right)^2 \ - \ \left(\sum\limits_j u_j^2\right)\left(\sum\limits_j v_j^2\right)\\ \quad = (\mathbf{u}^{\mathsf{T}}\mathbf{v})^2 -(\mathbf{u}^{\mathsf{T}}\mathbf{u})(\mathbf{v}^{\mathsf{T}}\mathbf{v}) \leq 0,\end{array} $$

$$\displaystyle\mbox{where}\ \ u_j = \frac{w_{ij}^{1/2}}{(\rho_j + \alpha)^{1/2}}\ \ \mbox{and}\ \ v_j = \frac{w_{ij}^{1/2}y_j}{(\rho_j + \alpha)^{3/2}}. $$

1.2 A.2 The Geometric erode filter

For the Geometric erode filter,

$$ \begin{array}{rll}\log(\tilde{\rho}_i + \alpha) &=&\sum\limits_j w_{ij} \log(\rho_j + \alpha),\ \ \frac{\partial \tilde{\rho}_i}{\partial \rho_j} = \frac{w_{ij} (\tilde{\rho}_i + \alpha)}{\rho_j + \alpha}\,,\\ \frac{\partial^2 \tilde{\rho}_i}{\partial \rho_j \partial \rho_k} &=&\frac{ w_{ij} w_{ik} (\tilde{\rho}_i + \alpha)}{(\rho_j + \alpha) (\rho_k + \alpha)}\ -\ \delta_{jk}\,\frac{ w_{ij} (\tilde{\rho}_i + \alpha)}{(\rho_j + \alpha)^2}\,.\end{array} $$

$$ \begin{array}{l}\mbox{Then}\ \ \frac{1}{\tilde{\rho}_i + \alpha}\sum\limits_j \sum\limits_k \frac{\partial^2 \tilde{\rho}_i}{\partial \rho_j \partial \rho_k} \,y_j y_k \\ \quad = \sum\limits_j \sum\limits_k\frac{ w_{ij} w_{ik} y_j y_k }{(\rho_j + \alpha) (\rho_k + \alpha)} \ - \ \sum\limits_j\frac{ w_{ij} y_j^2}{(\rho_j + \alpha)^2} \\ \quad= \left(\sum\limits_j\frac{ w_{ij} y_j }{\rho_j + \alpha}\right)^2 \ - \ \left(\sum\limits_j w_{ij}\right)\left(\sum\limits_j\frac{ w_{ij} y_j^2}{(\rho_j + \alpha)^2}\right)\\ \quad= \left(\sum\limits_j u_j v_j\right)^2 \ - \ \left(\sum\limits_j u_j^2\right)\left(\sum\limits_j v_j^2\right) \\ \quad=(\mathbf{u}^{\mathsf{T}}\mathbf{v})^2 -(\mathbf{u}^{\mathsf{T}}\mathbf{u})(\mathbf{v}^{\mathsf{T}}\mathbf{v}) \leq 0,\end{array} $$

$$\displaystyle \mbox{where}\ \ u_j = w_{ij}^{1/2} \ \ \mbox{and}\ \ v_j = \frac{w_{ij}^{1/2}y_j}{\rho_j + \alpha}. $$

1.3 A.3 The Exponential dilate filter

For the Exponential dilate filter,

$$ \begin{array}{rll} e^{\beta \tilde{\rho}_i} &=& \sum\limits_j w_{ij} e^{\beta \rho_j}\,,\ \ \frac{\partial \tilde{\rho}_i}{\partial \rho_j} =\frac{w_{ij} e^{\beta \rho_j}}{e^{\beta \tilde{\rho}_i}},\\ \frac{\partial^2 \tilde{\rho}_i}{\partial \rho_j \partial \rho_k} &=&-\, \frac{ \beta w_{ij} w_{ik} e^{\beta \rho_j} e^{\beta \rho_k}}{(e^{\beta \tilde{\rho}_i})^2}\ +\ \delta_{jk}\,\frac{ \beta w_{ij} e^{\beta \rho_j} e^{\beta \tilde{\rho}_i}}{(e^{\beta \tilde{\rho}_i})^2}\,.\end{array} $$

$$ \begin{array}{l}\mbox{Then}\ \ \frac{(e^{\beta \tilde{\rho}_i})^2}{\beta}\sum\limits_j \sum\limits_k \frac{\partial^2 \tilde{\rho}_i}{\partial \rho_j \partial \rho_k} \,y_j y_k \\ \quad = \ - \ \left(\sum\limits_j w_{ij} e^{\beta \rho_j} y_j \right)^2 \!+\!\left(\sum\limits_j w_{ij} e^{\beta \rho_j} \right)\left(\sum\limits_j w_{ij} e^{\beta \rho_j} y_j^2 \right) \\ \quad = \left(\sum\limits_j u_j^2\right)\left(\sum\limits_j v_j^2\right) \ - \ \left(\sum_j u_j v_j\right)^2 \\ \quad = (\mathbf{u}^{\mathsf{T}}\mathbf{u})(\mathbf{v}^{\mathsf{T}}\mathbf{v})- (\mathbf{u}^{\mathsf{T}}\mathbf{v})^2 \geq 0,\end{array} $$

where $u_j = (w_{ij} e^{\beta \rho _j})^{1/2} \ \ \mbox {and}\ \ v_j = y_j (w_{ij} e^{\beta \rho _j})^{1/2}.$

1.4 A.4 The Heaviside dilate filter

For the Heaviside dilate filter,

$$ \begin{array}{rll}\tilde{\rho}_i &=& 1 - e^{-\beta \sum_j\! w_{ij} \rho_j} + e^{-\beta} \sum\limits_j w_{ij} \rho_j,\\ \ \ \frac{\partial \tilde{\rho}_i}{\partial \rho_j} &=&\beta w_{ij} e^{-\beta \sum_j\! w_{ij} \rho_j} + w_{ij} e^{-\beta},\\ \frac{\partial^2 \tilde{\rho}_i}{\partial \rho_j \partial \rho_k} &=&- \beta^2 w_{ij} w_{ik} e^{-\beta \sum_j\! w_{ij} \rho_j}\,.\end{array} $$

$$ \begin{array}{l}\mbox{Then} \ \ \frac{e^{\beta \sum_j\! w_{ij} \rho_j}}{\beta^2}\sum\limits_j \sum\limits_k \frac{\partial^2 \tilde{\rho}_i}{\partial \rho_j \partial \rho_k} \,y_j y_k\\ \quad= - \sum\limits_j \sum\limits_k w_{ij} w_{ik} y_j y_k \;= \;- \left(\;\sum\limits_j w_{ij} y_j\,\right)^2 \leq 0.\end{array} $$

Appendix: Mesh independence study for the new filters

In this appendix, the results of a small mesh independence study of the new filters are reported. The classic MBB-beam has been used as a test example (see for example (Sigmund 2007)), and the mesh has been refined in three steps. 300 iterations were made with a fixed value of $\alpha = 0.1$. The results, displayed in Table 9, show that problems such as checkerboards are removed from the solutions, and that a length scale has been introduced, indicating that the problem of existence of solutions is remedied.

Table 9 Results of the mesh convergence study