A novel single-loop simulation algorithm combined with adaptive Kriging model for estimating the system failure probability function with multi-dimensional distribution parameter

Abstract

For the multi-failure-mode system with multi-dimensional distribution parameter, estimating system failure probability function (SFPF) is essential to grasp the influence of the distribution parameter on system failure probability and decouple the reliability-based design optimization model constrained by system failure probability. However, there is still a significant challenge in efficiently estimating the SFPF at present. Therefore, an efficient and universal algorithm is proposed in this paper for estimating the SFPF. In the proposed algorithm, a unified sampling probability density function, which is independent with the distribution parameter, is originally constructed by the integration operation over the concerned design domain of the distribution parameter, on which a single-loop numerical simulation can be formulated to simultaneously estimate the SFPF at arbitrary realization of multi-dimensional distribution parameter. Since the single-loop method is used to replace the direct double-loop one in the proposed algorithm, the computational efficiency is greatly improved in estimating the SFPF. Additionally, the proposed algorithm has no restriction on the dimensionality and the concerned design domain of the distribution parameter, and an adaptive Kriging model of the system performance function is embedded to help the proposed algorithm further improve the computational efficiency. A new adaptive learning strategy, which considers the possible correlations among the multi-failure-mode Kriging models, is presented using the probability of the multi-failure-mode Kriging model misjudging the candidate sample state. The superiority of the proposed algorithm in terms of single-loop numerical simulation and the new learning strategy over the existing methods is fully demonstrated by numerical and engineering examples.

1 Introduction

Random uncertainties (Xu et al. 2018; Vishwanathan and Vio 2019) are prevalent in practical engineering structural systems. Due to some uncontrolled incidental factors during processing and manufacturing, structure sizes and material properties possess uncertainty. Similarly, the working environment and the loads applied on the structure may be also random, since they cannot be strictly controlled. Under the condition of these random input factors (denoted by vector ${\varvec{X}}$), the performance function of the structure is also random and its safety degree can be characterized by failure probability. In the reliability-based design optimization (RBDO) (Enevoldsen and Sorensen 1994; Ghazaan and Saadatmand 2022) constrained by failure probability, the distribution parameter vector ${{\varvec{\theta}}}$ of the random input vector ${\varvec{X}}$ may be designed in the concerned design domain $\left[ {\varvec{\theta}}^{L} ,{\varvec{\theta}^{U} } \right]$, where ${\varvec{\theta}}^{L}$ and ${\varvec{\theta}}^{U}$ are, respectively, the concerned lower and upper bound vector of the distribution parameter vector ${\varvec{\theta}}$. In this case, the failure probability is a function of ${{\varvec{\theta}}}$, and it is defined as the failure probability function (FPF) and denoted as $P_{f} \left( {{\varvec{\theta}}} \right)$ (Feng et al. 2019; Zhang et al. 2022). The corresponding mathematical model of RBDO is generally formulated as follows:

$$\begin{gathered} {\text{Find }}{{\varvec{\theta}}} \hfill \\ \mathop {{\text{min}}}\limits_{{{\varvec{\theta}}}} \, W\left( {{\varvec{\theta}}} \right) \hfill \\ {\text{s}}{\text{.t}}{.}\left\{ \begin{gathered} P_{f} \left( {{\varvec{\theta}}} \right) \le P_{f}^{*} \hfill \\ {{\varvec{\theta}}}^{L} \le {{\varvec{\theta}}} \le {{\varvec{\theta}}}^{U} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(1)

where $W\left( {{\varvec{\theta}}} \right)$ is the generalized cost function and $P_{f}^{*}$ is the required target failure probability. In the model of the RBDO with the failure probability constraint of $P_{f} \left( {{\varvec{\theta}}} \right) \le P_{f}^{*}$, if the FPF $P_{f} \left( {{\varvec{\theta}}} \right)$ is obtained before executing RBDO, the coupling between the search of the optimal distribution parameters and the estimation of failure probability constraint can be directly removed, and the RBDO is spontaneously decoupled into an ordinary deterministic design optimization. What’s more, estimating the FPF is essential for understanding the effect of ${{\varvec{\theta}}}$ on the failure probability $P_{f}$ (Yuan et al. 2021). Currently, the algorithms for estimating the FPF of the single-failure-mode structure were well investigated, but there still lacks efficient algorithm for estimating the multi-failure-mode system FPF (SFPF) with multi-dimensional distribution parameter. The existing algorithms mainly focus on estimating the system failure probability, and the SFPF requires obtaining the failure probabilities corresponding to some discrete realizations of distribution parameter vector. If these algorithms for estimating the system failure probability are simply applied to estimate the SFPF, the efficiency of the algorithm may be very low due to the repeated system failure probability analysis at different realizations of ${{\varvec{\theta}}}$. In practical engineering, the multi-failure-mode system is commoner than the single-failure-mode one. Therefore, this paper devotes to the efficient algorithm for estimating the SFPF with multi-dimensional distribution parameter.

At present, the methods for estimating the FPF of a single-failure-mode structure can be classified into two categories, i.e., the distribution parameter discretization-based double-loop method and the Bayes formula-based single-loop method. The distribution parameter discretization-based double-loop method requires estimating the failure probabilities corresponding to some discrete realizations of distribution parameter, on which different interpolation techniques are used to obtain the FPF. Jensen (2005) and Gasser and Schuëller (1997) used linear and quadratic functions of the distribution parameter vector ${{\varvec{\theta}}}$, respectively, to locally approximate the logarithmic function $\ln \left[ {P_{f} \left( {{\varvec{\theta}}} \right)} \right]$ of $P_{f} \left( {{\varvec{\theta}}} \right)$, but both methods require numerous reliability analysis in different realizations of ${{\varvec{\theta}}}$, which may result in unaffordable computational cost for complicated engineering problems. Hence, to reduce the computational burden of estimating the FPF, Au (2004) proposed a single-loop method to estimate the FPF based on Bayes inference. In this method, the distribution parameter vector ${{\varvec{\theta}}}$ is extended into random variable vector in the concerned design domain $\left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$ and then the Bayes formula is used to convert the FPF into the estimation of two parts, i.e., the augmented failure probability and the conditional probability density function (PDF) of the distribution parameter on the failure domain. Based on the conversion, the failure probability at arbitrary realizations of the distribution parameter vector can be obtained by once augmented failure probability analysis. On basis of the failure sample information produced in estimating the augmented failure probability, the conditional PDF of the distribution parameter vector can be obtained by means of histogram approach (Au 2004) or the first-order maximum entropy method (Ching and Hsieh 2007). Usually, the existing PDF fitting methods are mainly applicable to the one-dimensional or two-dimensional variables, but the precision of the methods to fit the PDF of multi-dimensional variables needs to be improved. To avoid estimating the conditional PDF of the Bayes formula-based method for the FPF, Feng et al. (2019) introduced the differential region to approximate the realization of the distribution parameter vector and replaced the conditional PDF estimation with the conditional probability one. Yuan et al. (2021) derived the conditional PDF into the conditional expectation on the failure domain with the PDF of random input vector as the weight. Yuan et al. (2023) introduced a new sample regeneration algorithm to generate the required failure samples of distribution parameter vector without extra performance function evaluations.

The efficient and direct algorithm for estimating the SFPF of multi-failure-mode structure system is seldom studied in the literature, but the multi-failure-mode structure system is very common, thus it is highly desirable to investigate efficient method for estimating the SFPF. Although the Bayes formula-based single-loop method for estimating the FPF of a single-failure-mode structure can be extended to estimate the SFPF, there exist some difficulties for accurately fitting the conditional PDF of multi-dimensional distribution parameter. In this paper, an efficient algorithm for estimating the SFPF is proposed from the perspective of the single-loop numerical simulation. The basic idea of the proposed algorithm is to construct a unified sampling PDF independent of distribution parameter vector. Then by extracting one group sample of the unified sampling PDF, the system failure probability can be simultaneously estimated corresponding to arbitrary realizations of the multi-dimensional distribution parameter in the concerned design domain. In the proposed single-loop numerical simulation, the first issue to be solved is constructing the unified sampling PDF and extracting its samples. About the unified sampling PDF, this paper constructs it by integrating the PDF $f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}} \right)$ of ${\varvec{X}}$ at ${{\varvec{\theta}}}$ with an assigned prior PDF of ${{\varvec{\theta}}}$ over its concerned design domain $\left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$ as weight. About the samples of the unified sampling PDF, they are extracted by the combination sampling method (Butler 1956; Au 2004; Sheldon 2007). After the proposed algorithm solves the construction of the unified sampling PDF and the extraction of its samples, the next issue is how to efficiently identify the system states of the extracted samples to estimate the SFPF (the safe state of a sample corresponds to the system performance function is greater than zero, while the failure state of a sample corresponds to the system performance function is less than or equal to zero). Obviously, it is inefficient to identify the state of the samples by directly evaluating the multi-failure-mode system performance function, while replacing the system performance function with an adaptive Kriging model is a popular way to efficiently identify the system state of the extracted samples and estimate the SFPF.

As a typical continuous interpolation iteration method, the Kriging model (Echard et al. 2011; Yuan et al. 2020; Ma et al. 2022) has been widely used in estimating the failure probability of the single-failure-mode and the multi-failure-mode structure with the complex implicit performance functions. Among them, the efficient global reliability analysis (abbreviated as EGRA) (Bichon et al. 2008) and the adaptive Kriging model combined with Monte Carlo simulation (abbreviated as AK-MCS) (Echard et al. 2011) are two representative Kriging model-based methods in estimating component reliability analysis. The basic idea of EGRA and AK-MCS can be described as follows: the Kriging model of the performance function is constructed and adaptively updated in the candidate sample pool of the numerical simulation until the Kriging model is convergent. The convergent Kriging model can replace the real performance function to identify the state of the samples in the candidate sample pool and further estimate the failure probability. Therefore, both of them are able to estimate the failure probability with high efficiency and accuracy.

For system reliability analysis, EGRA-SYS (Bichon et al. 2011) and AK-SYS (Fauriat and Gayton 2014), which are modified versions of EGRA and AK-MCS, are two mature methods. The EGRA-SYS and AK-SYS method update the Kriging model by three strategies, where the third strategy of EGRA-SYS and AK-SYS (denoted as EGRA-SYS₃ and AK-SYS₃, respectively) may be most efficient. However, the study by (Yun et al. 2019) shows that EGRA-SYS₃ and AK-SYS₃ are less fault tolerant and the low prediction accuracy of the Kriging model in the previous step is possible to lead to the wrong system failure probability estimation in AK-SYS₃. To address the shortcoming of the EGRA-SYS₃ and AK-SYS₃, Yun et al. (2019) referred to the concept of the single-loop Kriging model method for time-dependent reliability analysis and proposed a new AK-SYSi learning strategy for multi-failure-mode system reliability analysis. AK-SYSi establishes the most easily identifiable model criterion to select the training point. Compared with AK-SYS₃, AK-SYSi has high fault tolerance, and the accuracy of AK-SYSi is not affected by the accuracy of the initial and pre-convergent Kriging model of single-failure-mode performance function. It is worth pointing out that both AK-SYS₃ and AK-SYSi do not take into account the correlations of individual mode when selecting training points. And they do not accurately analyze the system state misclassification probability resulted from the Gaussian distribution property of the Kriging model, which may lead to a negative effect on the computational efficiency for analyzing the multi-failure-mode system reliability.

Therefore, Jiang et al. (2020) derived the system state misclassification probability of each sample by multiplication operations based on probability of wrong sign prediction of each Kriging model. Yang et al. (2022) also derived the system state misclassification probability accurately and chose the ratio between system reliability and predicted system failure probability as the convergence criterion. Both of these are based on the assumption that the Kriging models of the multi-failure-mode performance functions are mutually independent. However, it is worth pointing out that the multi-failure-mode Kriging models are often correlated due to the identical inputs or training points, thus the computational efficiency may be affected by the assumption of the independent Kriging models of the multi-failure-mode performance functions. In order to improve the computational efficiency of the misclassification probability-guided training point selection strategy as much as possible, this paper tries to derive the misclassification probability by taking the correlations of the multi-failure-mode Kriging models into consideration. In view of the difficulty to quantify correlations among the multi-failure-mode Kriging models, this paper considers two extreme cases, i.e., mutually independent and perfectly correlated cases, of the correlations among the multi-failure-mode Kriging models, on which the cumulative distribution function (CDF) of the system Kriging model, and the system state misclassification probability can be accurately derived corresponding to these two extreme cases. Since the actual correlations of the multi-failure-mode Kriging models are unknown quantitatively, the average system state misclassification probability of two extreme cases is employed to guide the selection of the training point. Based on the derived system state misclassification probability-guided training point selection strategy, this paper also establishes the selection strategy of updating mode and corresponding convergence criterion for adaptive learning.

In summary, the motivation of the paper includes three aspects shown as follows:

• (1) For common structure system with multi-failure-mode, estimating the SFPF is important for grasping the effect of distribution parameter vector on system safety and decoupling the RBDO constrained by system failure probability. Therefore, it is necessary to research the efficient algorithm for estimating the SFPF.

• (2) At present, direct algorithm based on double-loop numerical simulation is general for estimating the SFPF. In this double-loop structure algorithm for estimating the SFPF, the system failure probability needs to be repeatedly estimated at different realizations of distribution parameter vector. Obviously, this repeated estimation may lead to loss of the efficiency for estimating the SFPF.

• (3) The effective way of improving efficiency of estimating the SFPF is designing a single-loop numerical simulation to replace the double-loop one for estimating the SFPF. Therefore, this paper devotes to the single-loop algorithm for estimating the SFPF. In the proposed single-loop algorithm, not only the unified sampling PDF is constructed to eliminate the double-loop structure, but also an adaptive learning strategy of Kriging model is researched to further improve the efficiency of estimating the SFPF.

The rest of the paper is organized as follows. Section 2 briefly describes the definition of the SFPF and presents the basic principle of the single-loop numerical simulation method as well as its basic implementation steps for estimating the SFPF. Section 3 combines AK-SYS₃ and AK-SYSi with the single-loop numerical simulation to form the single-loop-AK-SYS₃ (abbreviated as SL-AK-SYS₃) and single-loop-AK-SYSi (abbreviated as SL-AK-SYSi) algorithms for estimating the SFPF. By taking the correlations of the multi-failure-mode Kriging models into consideration, Sect. 4 establishes a novel adaptive Kriging model-based system reliability method denoted as AK-SYS_c, on which AK-SYS_c is combined with the single-loop numerical simulation to form the single-loop-AK-SYS_c (abbreviated as SL-AK-SYS_c) algorithm for estimating the SFPF. In Sect. 4, the CDF of the system Kriging model is accurately derived corresponding to two cases, i.e., the mutually independent and perfectly correlated multi-failure-mode Kriging models. The system state misclassification probability is represented by the average of those corresponding to two extreme cases of the correlations, and it is used to guide the selection of the training point in SL-AK-SYS_c for estimating the SFPF. Section 4 also gives the selection strategy of the updating mode and corresponding convergence criterion in SL-AK-SYS_c for estimating the SFPF. Section 5 presents the example validation, and Sect. 6 concludes the whole paper.

2 Single-loop numerical simulation algorithm

2.1 The concept of the SFPF

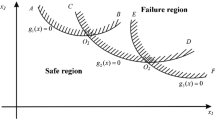
For a system with $m$ failure modes, the performance function of each mode is denoted by $Y_{j} = g_{j} \left( {\varvec{X}} \right)\left( {j = 1,2, \ldots ,m} \right)$, where ${\varvec{X}} = \left( {X_{1} ,X_{2} , \ldots ,X_{n} } \right)$ is an n-dimensional random input vector. The failure domain $F_{j} = \left\{ {{\varvec{x}}|g_{j} \left( {\varvec{x}} \right) \le 0} \right\}$ of j-th failure mode is defined by $g_{j} \left( {\varvec{x}} \right)$. The most basic connection of multi-failure-mode system includes series and parallel. Accordingly, the SFPF $P_{f}^{s} \left( {{\varvec{\theta}}} \right)$ of a multi-failure-mode system can be defined as follows:

$$P_{f}^{s} \left( {{\varvec{\theta}}} \right) = \int_{{F_{s} }} {f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}} \right){\text{d}}{\varvec{x}}} = \int {I_{{F_{s} }} } \left( {\varvec{x}} \right)f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}} \right){\text{d}}{\varvec{x}}$$

(2)

where $f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}} \right)$ is the PDF of ${\varvec{X}}$ given ${{\varvec{\theta}}}$ and $I_{{F_{s} }} \left( {\varvec{x}} \right)$ is the indicator function of the system failure domain $F_{s} = \left\{ {{\varvec{x}}|g_{s} \left( {\varvec{x}} \right) \le 0} \right\}$ defined by the system performance function $g_{s} \left( {\varvec{x}} \right)$,

$$I_{{F_{s} }} \left( {\varvec{x}} \right) = \left\{ {\begin{array}{*{20}c} 0 & {{\varvec{x}} \notin F_{s} } \\ 1 & {{\varvec{x}} \in F_{s} } \\ \end{array} } \right.$$

(3)

where $F_{s} = \left\{ {{\varvec{x}}|\mathop {\min }\limits_{j = 1}^{m} g_{j} \left( {\varvec{x}} \right) \le 0} \right\}$ for series system and $F_{s} = \left\{ {{\varvec{x}}|\mathop {\max }\limits_{j = 1}^{m} g_{j} \left( {\varvec{x}} \right) \le 0} \right\}$ for parallel system.

2.2 Fundamentals of the single-loop numerical simulation algorithm

In the direct double-loop numerical simulation for estimating the SFPF $P_{f}^{s} \left( {{\varvec{\theta}}} \right)$ with ${{\varvec{\theta}}} \in \left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$, the concerned design domain $\left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$ is firstly discretized as a set of fixed realizations ${{\varvec{\theta}}}_{i} \left( {i = 1,2, \ldots ,N} \right)$. For each realization ${{\varvec{\theta}}}_{i} \left( {i = 1,2, \ldots ,N} \right)$, generate the $N_{1}$-size sample pool ${\mathbf{S}}_{{\varvec{x}}}^{\left( i \right)} = \left\{ {{\varvec{x}}_{1}^{\left( i \right)} ,{\varvec{x}}_{2}^{\left( i \right)} , \ldots ,{\varvec{x}}_{{N_{1} }}^{\left( i \right)} } \right\}^{{\text{T}}}$ according to $f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}_{i} } \right)$. Then, the system failure probability $P_{f}^{s} \left( {{{\varvec{\theta}}}_{i} } \right)$ at each realization ${{\varvec{\theta}}}_{i}$ should be estimated one by one, on which the whole SFPF $P_{f}^{s} \left( {{\varvec{\theta}}} \right)$ under $\left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$ can be obtained by interpolating the sample pairs $\left( {{{\varvec{\theta}}}_{i} ,P_{f}^{s} \left( {{{\varvec{\theta}}}_{i} } \right)} \right)\left( {i = 1,2, \ldots ,N} \right)$. Then the number of the total performance function evaluations is $N_{T}^{DL} = N*N_{1}$.

Different from the double-loop numerical simulation, where $N$ repeated numerical simulations are needed to estimate $P_{f}^{s} \left( {{{\varvec{\theta}}}_{i} } \right)$ at ${{\varvec{\theta}}}_{i} \left( {i = 1,2, \ldots ,N} \right)$, the single-loop numerical simulation needs only once numerical simulation to estimate $P_{f}^{s} \left( {{{\varvec{\theta}}}_{i} } \right)$ at arbitrary realizations ${{\varvec{\theta}}}_{i} \in \left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$. Using integral operation over the concerned design domain $\left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$ of the distribution parameter vector ${{\varvec{\theta}}}$, the single-loop numerical simulation method firstly constructs a unified sampling PDF $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ as shown in Eq. (4),

$$\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right) = \int_{{{{\varvec{\theta}}}^{L} }}^{{{{\varvec{\theta}}}^{U} }} {f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}} \right)\varphi_{{{\varvec{\theta}}}} \left( {{\varvec{\theta}}} \right){\text{d}}{{\varvec{\theta}}}}$$

(4)

where $\varphi_{{{\varvec{\theta}}}} \left( {{\varvec{\theta}}} \right)$ is the assigned prior PDF of the distribution parameter vector ${{\varvec{\theta}}}$ in the concerned design domain $\left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$.

From Eq. (4), it can be seen that $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ is independent of ${{\varvec{\theta}}}$, and the samples of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ can be extracted by the combination sampling method (Butler 1956; Au 2004; Sheldon 2007). The advantage of constructing $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ is that the samples of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ can be shared simultaneously to estimate the failure probabilities of distribution parameter vector at its arbitrary realizations in the concerned design domain.

By substituting the unified sampling PDF $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ in Eq. (4) into Eq. (2), the SFPF $P_{f}^{s} \left( {{\varvec{\theta}}} \right)$ can be converted into the mathematical expectation in Eq. (5) with PDF $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ as the weight, and the mathematical expectation in Eq. (5) can be estimated by the sample mean denoted as $\hat{P}_{f}^{s} \left( {{\varvec{\theta}}} \right)$ in Eq. (6) after the samples of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ are extracted.

$$\begin{gathered} P_{f}^{s} \left( {{\varvec{\theta}}} \right) = \int {I_{{F_{s} }} \left( {\varvec{x}} \right)} f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}} \right){\text{d}}{\varvec{x}} = \int {\frac{{I_{{F_{s} }} \left( {\varvec{x}} \right)f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}} \right)}}{{\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)}}} \tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right){\text{d}}{\varvec{x}} \\ = E\left[ {\frac{{I_{{F_{s} }} \left( {\varvec{x}} \right)f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}} \right)}}{{\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)}}} \right] \\ \end{gathered}$$

(5)

where $E\left[ \bullet \right]$ is the expectation operator.

$$\hat{P}_{f}^{s} \left( {{\varvec{\theta}}} \right) = \frac{1}{N}\sum\limits_{i = 1}^{N} {\frac{{I_{{F_{s} }} \left( {{\varvec{x}}_{i} } \right)f_{{\varvec{X}}} \left( {{\varvec{x}}_{i} |{{\varvec{\theta}}}} \right)}}{{\tilde{f}_{{\varvec{X}}} \left( {{\varvec{x}}_{i} } \right)}}}$$

(6)

In Eq. (6), $\left\{ {{\varvec{x}}_{1} ,{\varvec{x}}_{2} , \ldots ,{\varvec{x}}_{N} } \right\}^{{\text{T}}}$ is an N-size candidate sample pool of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$. After an $N_{{{\varvec{\theta}}}}$-size candidate sample pool ${\mathbf{S}}_{{{\varvec{\theta}}}}^{{\tilde{f}}} = \left\{ {{{\varvec{\theta}}}_{1} ,{{\varvec{\theta}}}_{2} , \ldots ,{{\varvec{\theta}}}_{{N_{{{\varvec{\theta}}}} }} } \right\}^{{\text{T}}}$ of $\varphi_{{{\varvec{\theta}}}} \left( {{\varvec{\theta}}} \right)$ is extracted, $\tilde{f}_{{\varvec{X}}} \left( {{\varvec{x}}_{i} } \right)$ at ${\varvec{x}}_{i}$ in Eq. (6) can be estimated by Eq. (7) based on Eq. (4).

$$\tilde{f}_{{\varvec{X}}} \left( {{\varvec{x}}_{i} } \right) = \frac{1}{{N_{{{\varvec{\theta}}}} }}\sum\limits_{k = 1}^{{N_{{{\varvec{\theta}}}} }} {f_{{\varvec{X}}} \left( {{\varvec{x}}_{i} |{{\varvec{\theta}}}_{k} } \right)}$$

(7)

Obviously, the estimation of Eq. (7) does not involve the system performance function evaluation. And the proposed single-loop numerical simulation algorithm has no restriction on the dimensionality of the distribution parameter vector ${{\varvec{\theta}}}$, and it is suitable for the SFPF estimation for the system with multi-dimensional distribution parameter.

2.3 The detailed steps of the single-loop numerical simulation algorithm

Based on the basic principles of the above subsection, the detailed steps of the single-loop numerical simulation algorithm for estimating the SFPF can be listed as follows.

Step 1: Generate an $N$-size candidate sample pool ${\mathbf{S}}_{{\varvec{x}}} = \left\{ {{\varvec{x}}_{1} ,{\varvec{x}}_{2} , \ldots ,{\varvec{x}}_{N} } \right\}^{{\text{T}}}$ of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$. The samples of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ in Eq. (4) can be obtained by the combination sampling method (Butler 1956; Au 2004; Sheldon 2007). In the combination sampling method, an $N$-size candidate sample pool ${\mathbf{S}}_{{{\varvec{\theta}}}} = \left\{ {{{\varvec{\theta}}}_{1} ,{{\varvec{\theta}}}_{2} , \ldots ,{{\varvec{\theta}}}_{N} } \right\}^{{\text{T}}}$ of ${{\varvec{\theta}}}$ is firstly extracted by the prior PDF $\varphi_{{{\varvec{\theta}}}} \left( {{\varvec{\theta}}} \right)$ in the concerned design domain $\left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$. Generally, since $\varphi_{{{\varvec{\theta}}}} \left( {{\varvec{\theta}}} \right)$ is assigned as the uniform PDF in $\left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$, extracting sample of $\varphi_{{{\varvec{\theta}}}} \left( {{\varvec{\theta}}} \right)$ is very easy. For each ${{\varvec{\theta}}}_{i} \in {\mathbf{S}}_{{{\varvec{\theta}}}} \left( {i = 1,2, \ldots ,N} \right)$, a sample ${\varvec{x}}_{i} \left( {i = 1,2, \ldots ,N} \right)$ is extracted from $f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}_{i} } \right)$ and then the $N$-size candidate sample pool ${\mathbf{S}}_{{\varvec{x}}} = \left\{ {{\varvec{x}}_{1} ,{\varvec{x}}_{2} , \ldots ,{\varvec{x}}_{N} } \right\}^{{\text{T}}}$ of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ can be obtained.

Step 2: Estimate the SFPF by Eq. (6) and the extracted ${\mathbf{S}}_{{\varvec{x}}}$ of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ in Step 1. In Eq. (6), the system failure domain indicator function $I_{{F_{s} }} \left( {{\varvec{x}}_{i} } \right)$ defined in Eq. (3) can be estimated by evaluating the performance function $g_{j} \left( {{\varvec{x}}_{i} } \right)\left( {j = 1,2, \ldots ,m} \right)$ at ${\varvec{x}}_{i} \left( {i = 1,2, \ldots ,N} \right)$ and $\tilde{f}_{{\varvec{X}}} \left( {{\varvec{x}}_{i} } \right)$ can be estimated by Eq. (7) through ${\mathbf{S}}_{{{\varvec{\theta}}}}^{{\tilde{f}}}$.

From the above detailed steps for estimating the SFPF, it can be seen that the candidate sample pool ${\mathbf{S}}_{{\varvec{x}}}$ extracted from $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ can be shared to estimate the system failure probability at the arbitrary realizations of the distribution parameter vector and the strategy of sharing sample information avoids the huge computational cost of the direct double-loop analysis, where the distribution parameters need to be scattered and the system failure probability need to be estimated repeatedly at each scattered distribution parameter realization and the number of the total performance function evaluations is $N_{T}^{SL} = N$ in the single-loop numerical simulation. The main computational cost for estimating $\hat{P}_{f}^{s} \left( {{\varvec{\theta}}} \right)$ by Eq. (6) is in evaluating the multi-failure-mode performance functions to estimate the system failure domain indicator function $I_{{F_{s} }} \left( {{\varvec{x}}_{i} } \right)\left( {{\varvec{x}}_{i} \in {\mathbf{S}}_{{\varvec{x}}} } \right)$. In case of small SFPF $\hat{P}_{f}^{s} \left( {{\varvec{\theta}}} \right)$ of the engineering application with implicit performance function, it still requires a large candidate sample pool to obtain a convergent $\hat{P}_{f}^{s} \left( {{\varvec{\theta}}} \right)$, and this computational cost is usually unaffordable. For solving this issue, the Kriging models of the multi-failure-mode performance functions are embedded into the single-loop numerical simulation, so as to reduce the required computational cost of estimating the SFPF $\hat{P}_{f}^{s} \left( {{\varvec{\theta}}} \right)$ with ${{\varvec{\theta}}} \in \left[ {{{\varvec{\theta}}}^{L} ,{{\varvec{\theta}}}^{U} } \right]$.

3 Single-loop numerical simulation algorithm combined with AK-SYS₃ and AK-SYSi

In the single-loop numerical simulation algorithm for estimating the SFPF, the most time-consuming part is to estimate the system failure domain indicator function $I_{{F_{s} }} \left( {{\varvec{x}}_{i} } \right)$ at ${\varvec{x}}_{i} \in {\mathbf{S}}_{{\varvec{x}}} \left( {i = 1,2, \ldots ,N} \right)$. A more efficient way to address the time-consuming issue is to initially construct and adaptively update the Kriging models of the multi-failure-mode performance functions in ${\mathbf{S}}_{{\varvec{x}}}$ and then the convergent Kriging models are used to replace the performance functions to accurately and efficiently estimate $I_{{F_{s} }} \left( {{\varvec{x}}_{i} } \right)$ at ${\varvec{x}}_{i} \in {\mathbf{S}}_{{\varvec{x}}}$. Since the number of training points to obtain the convergent Kriging models is usually much smaller than that of candidate samples, combining the Kriging model with the single-loop numerical simulation method can significantly improve the efficiency of estimating the SFPF. In the following part, the existing AK-SYS₃ and AK-SYSi, two Kriging model-based system reliability analysis methods for the multi-failure-mode structure, are combined with the single-loop numerical simulation to form the SL-AK-SYS₃ and SL-AK-SYSi, respectively, for estimating the SFPF, in which the Kriging models are trained in ${\mathbf{S}}_{{\varvec{x}}}$ extracted from $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ in Eq. (4).

3.1 SL-AK-SYS₃

SL-AK-SYS₃ is the abbreviation of the algorithm combining the single-loop numerical simulation method with the AK-SYS₃ for estimating the SFPF. In the first step of SL-AK-SYS₃, the initial training point set is first selected in ${\mathbf{S}}_{{\varvec{x}}}$ for constructing the Kriging model $\hat{g}_{j} \left( {\varvec{x}} \right)$ of multi-failure-mode performance function $g_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$. Then Eq. (8) is used to identify the extreme value mode indicator $p\left( {\varvec{x}} \right)$ corresponding to ${\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}}$ by the mean $\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)$ of Kriging prediction $\hat{g}_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$.

$$p\left( {\varvec{x}} \right) = \left\{ \begin{gathered} \begin{array}{*{20}c} {\arg \mathop {\min }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)} & {\text{for series system}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\arg \mathop {\max }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)} & {\text{for parallel system}} \\ \end{array} \hfill \\ \end{gathered} \right.$$

(8)

Based on $p\left( {\varvec{x}} \right)$ in Eq. (8), the representative $U$ learning function $U_{{{\text{AK - SYS}}_{{3}} }} \left( {\varvec{x}} \right)$ for ${\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}}$ can be given as follows:

$$U_{{{\text{AK - SYS}}_{{3}} }} \left( {\varvec{x}} \right) = \frac{{\left| {\mu_{{\hat{g}_{{p\left( {\varvec{x}} \right)}} }} \left( {\varvec{x}} \right)} \right|}}{{\sigma_{{\hat{g}_{{p\left( {\varvec{x}} \right)}} }} \left( {\varvec{x}} \right)}}$$

(9)

In the second step of SL-AK-SYS₃ updating the Kriging model, the new training point ${\varvec{x}}^{u}$ is selected by Eq. (10) based on the $U$ learning function $U_{{{\text{AK - SYS}}_{{3}} }} \left( {\varvec{x}} \right)$ in Eq. (9),

$${\varvec{x}}^{u} = \arg \mathop {\min }\limits_{{{\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}} }} U_{{{\text{AK - SYS}}_{{3}} }} \left( {\varvec{x}} \right)$$

(10)

and the mode indicator $p^{u}$ that needs to be updated corresponding to ${\varvec{x}}^{u}$ is identified by Eq. (11),

$$p^{u} = p\left( {{\varvec{x}}^{u} } \right)$$

(11)

where $p\left( {{\varvec{x}}^{u} } \right)$ is determined by Eq. (8).

The SL-AK-SYS₃ algorithm only adds ${\varvec{x}}^{u}$ to the training set of the $p^{u}$-th mode at each updating from the second step onward and this updating of the Kriging model $\hat{g}_{{p^{u} }} \left( {\varvec{x}} \right)$ for the $p^{u}$-th mode continues until $U_{{{\text{AK - SYS}}_{{3}} }} \left( {{\varvec{x}}^{u} } \right) \ge 2$.

3.2 SL-AK-SYSi

Due to the possible convergence error problem of AK-SYS₃, Yun et al. (2019) proposed an AK-SYSi learning strategy for the multi-failure-mode system reliability analysis. In this paper, AK-SYSi is combined with the single-loop numerical simulation method to form the SL-AK-SYSi algorithm for efficiently estimating the SFPF. SL-AK-SYSi iteratively updates the Kriging model in a similar way as SL-AK-SYS₃, except that it uses the representative $U$ learning function $U_{{\text{AK - SYSi}}} \left( {\varvec{x}} \right)$ in Eq. (12) for selecting new training points ${\varvec{x}}^{u}$,

$$U_{{\text{AK - SYSi}}} \left( {\varvec{x}} \right) = \left\{ {\begin{array}{*{20}c} {\mathop {\min }\limits_{{j \in {\mathbf{w}}}} \frac{{\left| {\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)} \right|}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} & {{\mathbf{w}}^{*} = \emptyset } \\ {\mathop {\max }\limits_{{j \in {\mathbf{w}}^{*} }} \frac{{\left| {\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)} \right|}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} & {{\mathbf{w}}^{*} \ne \emptyset } \\ \end{array} } \right.$$

(12)

where ${\mathbf{w}} = \left\{ {1,2, \ldots ,m} \right\}$ is the indicator set of all modes and ${\mathbf{w}}^{*}$ is the mode indicator set in which Kriging prediction mean can identify the state of the multi-failure-mode system at ${\varvec{x}}$, for both series and parallel systems, ${\mathbf{w}}^{*}$ is shown as follows,

$${\mathbf{w}}^{*} = \left\{ \begin{gathered} \begin{array}{*{20}c} {\left\{ {j|\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) < 0,j \in {\mathbf{w}}} \right\}} & {\text{for series system}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\left\{ {j|\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) > 0,j \in {\mathbf{w}}} \right\}} & {\text{for parallel system}} \\ \end{array} \hfill \\ \end{gathered} \right.$$

(13)

SL-AK-SYSi uses $U_{{\text{AK - SYSi}}} \left( {\varvec{x}} \right)$ to select the new training point ${\varvec{x}}^{u}$ by Eq. (14), and the mode indicator $p^{u}$ to be updated is selected by Eq. (15).

$${\varvec{x}}^{u} = \arg \mathop {\min }\limits_{{{\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}} }} U_{{\text{AK - SYSi}}} \left( {\varvec{x}} \right)$$

(14)

$$p^{u} = \left\{ {\begin{array}{*{20}c} {\arg \mathop {\min }\limits_{{j \in {\mathbf{w}}}} U_{{\text{AK - SYSi}}} \left( {{\varvec{x}}^{u} } \right)} & {{\mathbf{w}}^{*} = \emptyset } \\ {\arg \mathop {\max }\limits_{{j \in {\mathbf{w}}^{*} }} U_{{\text{AK - SYSi}}} \left( {{\varvec{x}}^{u} } \right)} & {{\mathbf{w}}^{*} \ne \emptyset } \\ \end{array} } \right.$$

(15)

The convergence criterion of the SL-AK-SYSi learning strategy is $U_{{\text{AK - SYSi}}} \left( {{\varvec{x}}^{u} } \right) \ge 2$, which is also similar to that of the SL-AK-SYS₃. In Ref. (Yun et al. 2019), compared with SL-AK-SYS₃, SL-AK-SYSi is more fault tolerant. However, both methods do not consider the effect of the correlations among the Kriging models of the multi-failure-mode performance functions when constructing the learning function for selecting the new training points, which may potentially lose the efficiency of the algorithm. Therefore, the next section proposes a more efficient learning strategy and convergence criterion for estimating the SFPF, in which the correlations of the multi-failure-mode Kriging models are considered.

4 The proposed SL-AK-SYS_c algorithm

Since the correlations of the Kriging models for all failure modes are difficult to quantify, both AK-SYS₃ and AK-SYSi learning strategies select the new training points from the perspective of the extreme value, which may lead to a conservative selection of the new training points and a possible loss of the algorithm efficiency. For this reason, this paper defines system misclassification event, and this event means that the system Kriging prediction sign is different from the system Kriging prediction mean sign. Then, the probability of the system state misclassification is derived to guide updating the Kriging models, which is similar to the principle of the single-failure-mode $U$ learning function. To analytically derive the system state misclassification probability, the CDFs of the system Kriging prediction are firstly derived using the distribution characteristic of the multi-failure-mode Kriging models in two cases of mutual independence and perfect correlation, on which it can analytically derive the system state misclassification probabilities, respectively, corresponding to two cases. From the perspective of the average value of the misclassification probabilities corresponding to the mutual independence and perfect correlation, the training point selection strategy is constructed, and the corresponding adaptive learning convergence criterion is also given.

In the following, in order to obtain the system state misclassification probability, the CDFs of the system Kriging prediction are firstly derived in the cases of mutual independence and perfect correlation for series and parallel system. After the strategy of selecting the new training point and updating mode is established, this paper derives an upper bound on the expected relative error of the representative failure probability obtained by the system Kriging prediction and that by the system Kriging prediction mean, and this upper bound is employed to construct the corresponding convergence criterion for adaptive learning. Finally, the specific steps are given for the implementation of the SL-AK-SYS_c algorithm in the section.

4.1 Training point selection strategy

For series and parallel systems, the system Kriging prediction $\hat{g}_{s} \left( {\varvec{x}} \right)$ is related to the single-failure-mode Kriging prediction $\hat{g}_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$ as follows:

$$\hat{g}_{s} \left( {\varvec{x}} \right) = \left\{ {\begin{array}{*{20}c} {\mathop {\min }\limits_{j = 1}^{m} \hat{g}_{j} \left( {\varvec{x}} \right)} & {\text{for series system}} \\ {\mathop {\max }\limits_{j = 1}^{m} \hat{g}_{j} \left( {\varvec{x}} \right)} & {\text{ for parallel system}} \\ \end{array} } \right.$$

(16)

Since $\hat{g}_{j} \left( {\varvec{x}} \right)$ follows the Gaussian distribution with mean $\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)$ and variance $\sigma_{{\hat{g}_{j} }}^{2} \left( {\varvec{x}} \right)$, i.e., $\hat{g}_{j} \left( {\varvec{x}} \right)\sim N\left( {\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right),\sigma_{{\hat{g}_{j} }}^{2} \left( {\varvec{x}} \right)} \right)$, the CDF $F_{{\hat{g}_{s} }} \left( {{\varvec{x}},t} \right)$ of the system Kriging prediction $\hat{g}_{s} \left( {\varvec{x}} \right)$ can be derived as follows:

$$F_{{\hat{g}_{s} }} \left( {{\varvec{x}},t} \right) = {\text{Prob}}\left\{ {\hat{g}_{s} \left( {\varvec{x}} \right) \le t} \right\} = \left\{ {\begin{array}{*{20}c} {{\text{Prob}}\left\{ {\mathop {\min }\limits_{j = 1}^{m} \hat{g}_{j} \left( {\varvec{x}} \right) \le t} \right\}} & {\text{for series system}} \\ {{\text{Prob}}\left\{ {\mathop {\max }\limits_{j = 1}^{m} \hat{g}_{j} \left( {\varvec{x}} \right) \le t} \right\}} & {\text{ for parallel system}} \\ \end{array} } \right.$$

(17)

where ${\text{Prob}}\left\{ \bullet \right\}$ is the probability operator.

For the series system with $m$ Kriging models $\hat{g}_{j} \left( {\varvec{x}} \right)$ of the multi-failure-mode performance functions $g_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$, the CDF $F_{{\hat{g}_{s} }}^{I} \left( {{\varvec{x}},t} \right)$ of $\hat{g}_{s} \left( {\varvec{x}} \right)$ in case of mutually independent $\hat{g}_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$ and the CDF $F_{{\hat{g}_{s} }}^{C} \left( {{\varvec{x}},t} \right)$ of $\hat{g}_{s} \left( {\varvec{x}} \right)$ in case of fully correlated $\hat{g}_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$ can be derived, respectively, as follows according to the first-order bound theory (Ditlevsen 1979; Deb et al. 2009).

$$\begin{gathered} F_{{\hat{g}_{s} }}^{I} \left( {{\varvec{x}},t} \right) = {\text{Prob}}\left\{ {\hat{g}_{s} \left( {\varvec{x}} \right) \le t} \right\} = {\text{Prob}}\left\{ {\mathop {\min }\limits_{j = 1}^{m} \hat{g}_{j} \left( {\varvec{x}} \right) \le t} \right\} = 1 - {\text{Prob}}\left\{ {\mathop {\min }\limits_{j = 1}^{m} \hat{g}_{j} \left( {\varvec{x}} \right) > t} \right\} \\ = 1 - \prod\limits_{j = 1}^{m} {{\text{Prob}}\left\{ {\hat{g}_{j} \left( {\varvec{x}} \right) > t} \right\}} \\ = 1 - \prod\limits_{j = 1}^{m} {\Phi \left( {\frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) - t}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} \\ \end{gathered}$$

(18)

$$F_{{\hat{g}_{s} }}^{C} \left( {{\varvec{x}},t} \right) = \mathop {\max }\limits_{j = 1}^{m} {\text{Prob}}\left\{ {\hat{g}_{j} \left( {\varvec{x}} \right) \le t} \right\} = \mathop {\max }\limits_{j = 1}^{m} \Phi \left( {\frac{{t - \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)$$

(19)

where $\Phi \left( \bullet \right)$ denotes the standard normal CDF.

Similarly, for the parallel system with $m$ Kriging models $\hat{g}_{j} \left( {\varvec{x}} \right)$ of the multi-failure-mode performance functions $g_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$, the CDF $F_{{\hat{g}_{s} }}^{I} \left( {{\varvec{x}},t} \right)$ of $\hat{g}_{s} \left( {\varvec{x}} \right)$ in case of mutually independent $\hat{g}_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$ and the CDF $F_{{\hat{g}_{s} }}^{C} \left( {{\varvec{x}},t} \right)$ of $\hat{g}_{s} \left( {\varvec{x}} \right)$ in case of fully correlated $\hat{g}_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$ can be, respectively, derived as follows:

$$\begin{gathered} F_{{\hat{g}_{s} }}^{I} \left( {{\varvec{x}},t} \right) = {\text{Prob}}\left\{ {\hat{g}_{s} \left( {\varvec{x}} \right) \le t} \right\} = {\text{Prob}}\left\{ {\mathop {\max }\limits_{j = 1}^{m} \hat{g}_{j} \left( {\varvec{x}} \right) \le t} \right\} \\ = \prod\limits_{j = 1}^{m} {\Phi \left( {\frac{{t - \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} \\ \end{gathered}$$

(20)

$$F_{{\hat{g}_{s} }}^{C} \left( {{\varvec{x}},t} \right) = \mathop {\min }\limits_{j = 1}^{m} {\text{Prob}}\left\{ {\hat{g}_{j} \left( {\varvec{x}} \right) \le t} \right\} = \mathop {\min }\limits_{j = 1}^{m} \Phi \left( {\frac{{t - \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)$$

(21)

Due to the randomness of the system Kriging prediction $\hat{g}_{s} \left( {\varvec{x}} \right)$, the misclassification event may occur, and the misclassification event is denoted as $\left\{ E \right\} = \left\{ {{\text{sign}}\left( {\hat{g}_{s} \left( {\varvec{x}} \right)} \right) \ne {\text{sign}}\left( {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right)} \right)} \right\}$ with the sign denoted by ${\text{sign}}\left( {\hat{g}_{s} \left( {\varvec{x}} \right)} \right)$ of $\hat{g}_{s} \left( {\varvec{x}} \right)$ different from ${\text{sign}}\left( {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right)} \right)$ of the system Kriging prediction mean $\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right)$. Record the probability of $E$ as $P_{e} \left( {\varvec{x}} \right) = {\text{Prob}}\left\{ E \right\}$, and $P_{e} \left( {\varvec{x}} \right)$ can be referred to as the misclassification probability of the system Kriging prediction. Since the Kriging model-based reliability analysis uses the Kriging prediction mean replacing the performance function, the larger $P_{e} \left( {\varvec{x}} \right)$ means a higher probability of $\hat{g}_{s} \left( {\varvec{x}} \right)$ misclassifying the system state at ${\varvec{x}}$. Thus, $P_{e} \left( {\varvec{x}} \right)$ can be used to select the new training point for maximally improving the accuracy of $\hat{g}_{s} \left( {\varvec{x}} \right)$ predicting the system state. From the CDFs of $\hat{g}_{s} \left( {\varvec{x}} \right)$ derived above in two cases of the mutual independence and full correlation, the misclassification probability denoted as $P_{e}^{I} \left( {\varvec{x}} \right)$ in case of the mutual independence and that denoted as $P_{e}^{C} \left( {\varvec{x}} \right)$ in case of the full correlation can be derived, respectively, as follows:

$$P_{e}^{I} \left( {\varvec{x}} \right) = \left\{ {\begin{array}{*{20}l} \begin{gathered} \begin{array}{*{20}c} {1 - F_{{\hat{g}_{s} }}^{I} \left( {{\varvec{x}},t} \right) = \prod\limits_{j = 1}^{m} {\Phi \left( {\frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right) \, } } & { \, \mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\min }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) \le 0} \\ \end{array} \\ \begin{array}{*{20}c} {F_{{\hat{g}_{s} }}^{I} \left( {{\varvec{x}},t} \right) = 1 - \prod\limits_{j = 1}^{m} {\Phi \left( {\frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right) \, } } & { \, \mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\min }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) > 0} \\ \end{array} \\ \begin{array}{*{20}c} {1 - F_{{\hat{g}_{s} }}^{I} \left( {{\varvec{x}},t} \right) = 1 - \prod\limits_{j = 1}^{m} {\Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} } & { \, \mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\max }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) \le 0} \\ \end{array} \\ \begin{array}{*{20}c} {F_{{\hat{g}_{s} }}^{I} \left( {{\varvec{x}},t} \right) = \prod\limits_{j = 1}^{m} {\Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} } & { \, \mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\max }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) > 0} \\ \end{array} \\ \end{gathered} \hfill & \begin{gathered} {\text{for series system}} \hfill \\ \hfill \\ \hfill \\ \hfill \\ \hfill \\ {\text{for parallel system}} \hfill \\ \end{gathered} \hfill \\ \end{array} } \right.$$

(22)

$$P_{e}^{C} \left( {\varvec{x}} \right) = \left\{ {\begin{array}{*{20}l} \begin{gathered} \begin{array}{*{20}c} {1 - F_{{\hat{g}_{s} }}^{C} \left( {{\varvec{x}},t} \right) = 1 - \mathop {\max }\limits_{j = 1}^{m} \Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} & {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\min }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) \le 0} \\ \end{array} \\ \begin{array}{*{20}c} {F_{{\hat{g}_{s} }}^{C} \left( {{\varvec{x}},t} \right) = \mathop {\max }\limits_{j = 1}^{m} \Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} & { \, \mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\min }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) > 0} \\ \end{array} \\ \begin{array}{*{20}c} {1 - F_{{\hat{g}_{s} }}^{C} \left( {{\varvec{x}},t} \right) = 1 - \mathop {\min }\limits_{j = 1}^{m} \Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} & { \, \mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\max }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) \le 0} \\ \end{array} \\ \begin{array}{*{20}c} {F_{{\hat{g}_{s} }}^{C} \left( {{\varvec{x}},t} \right) = \mathop {\min }\limits_{j = 1}^{m} \Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} & { \, \mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\max }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) > 0} \\ \end{array} \\ \end{gathered} \hfill & \begin{gathered} {\text{for series system}} \hfill \\ \hfill \\ \hfill \\ \hfill \\ \hfill \\ {\text{for parallel system}} \hfill \\ \end{gathered} \hfill \\ \end{array} } \right.$$

(23)

In this paper, the average system state misclassification probability in two cases at ${\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}}$ is taken as the representative misclassification probability $P_{e} \left( {\varvec{x}} \right)$, i.e.,

$$P_{e} \left( {\varvec{x}} \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}l} {\begin{array}{*{20}c} {\frac{1}{2} - \frac{1}{2}\mathop {\max }\limits_{j = 1}^{m} \Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right) + \frac{1}{2}\prod\limits_{j = 1}^{m} {\Phi \left( {\frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} } & {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\min }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) \le 0} \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} {\frac{1}{2} - \frac{1}{2}\prod\limits_{j = 1}^{m} {\Phi \left( {\frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right) + \frac{1}{2}\mathop {\max }\limits_{j = 1}^{m} \Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} } & {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\min }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) > 0} \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} {1 - \frac{1}{2}\prod\limits_{j = 1}^{m} {\Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right) - \frac{1}{2}\mathop {\min }\limits_{j = 1}^{m} \Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} } & {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\max }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) \le 0} \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} {\frac{1}{2}\mathop {\min }\limits_{j = 1}^{m} \Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right) + \frac{1}{2}\prod\limits_{j = 1}^{m} {\Phi \left( { - \frac{{\mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}{{\sigma_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)}}} \right)} } & {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) = \mathop {\max }\limits_{j = 1}^{m} \mu_{{\hat{g}_{j} }} \left( {\varvec{x}} \right) > 0} \\ \end{array} } \hfill \\ \end{array} } & {\begin{array}{*{20}l} {\text{for series system}} \hfill \\ {} \hfill \\ {} \hfill \\ {} \hfill \\ {} \hfill \\ {\text{for parallel system}} \hfill \\ \end{array} } \\ \end{array} } \right.$$

(24)

Obviously, the candidate sample ${\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}}$ with the largest $P_{e} \left( {\varvec{x}} \right)$ should be added to the training set to minimize the system state misclassification probability of $\hat{g}_{s} \left( {\varvec{x}} \right)$. Simultaneously considering the PDF $f_{{\varvec{X}}} \left( {\varvec{x}} \right)$ of the candidate sample, the training point ${\varvec{x}}^{u}$ is selected by the following Eq. (25) in the proposed SL-AK-SYS_c,

$${\varvec{x}}^{u} = \arg \mathop {\max }\limits_{{{\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}} }} P_{e} \left( {\varvec{x}} \right)f_{{\varvec{X}}} \left( {\varvec{x}} \right)$$

(25)

and the updating mode indicator $p^{u}$ is selected by the least easily recognizable mode for the corresponding ${\varvec{x}}^{u}$, i.e.,

$$p^{u} = \arg \mathop {\min }\limits_{j = 1}^{m} U_{{\hat{g}_{j} }} \left( {{\varvec{x}}^{u} } \right) = \arg \mathop {\min }\limits_{j = 1}^{m} \frac{{\left| {\mu_{{\hat{g}_{j} }} \left( {{\varvec{x}}^{u} } \right)} \right|}}{{\sigma_{{\hat{g}_{j} }} \left( {{\varvec{x}}^{u} } \right)}}$$

(26)

4.2 Convergence criterion for adaptive learning

It can employ the maximum misclassification probability $\mathop {\max }\limits_{{{\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}} }} P_{e} \left( {\varvec{x}} \right)$ of ${\varvec{x}} \in {\mathbf{S}}_{{\varvec{x}}}$ less than a given threshold as the convergence criterion, but it may be conservative and computationally expensive as the traditional $U$ learning strategy. To avoid this conservation, the convergence of the SL-AK-SYS_c algorithm is evaluated by the relative error $\varepsilon = \left| {\hat{P}_{f}^{s} - \overline{P}_{f}^{s} } \right|/\overline{P}_{f}^{s}$, where $\hat{P}_{f}^{s}$ means the representative system failure probability estimated by the system Kriging prediction $\hat{g}_{s} \left( {\varvec{x}} \right)$ and $\overline{P}_{f}^{s}$ means the representative system failure probability estimated by the system Kriging prediction mean $\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right)$. $\hat{P}_{f}^{s}$ and $\overline{P}_{f}^{s}$ are named as the representative failure probabilities as the PDF for estimating $\hat{P}_{f}^{s}$ and $\overline{P}_{f}^{s}$ is the constructed $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$. Since $\hat{P}_{f}^{s}$ is a function of the random variable $\hat{g}_{s} \left( {\varvec{x}} \right)$, $\hat{P}_{f}^{s}$ and $\varepsilon$ are both random variables. Convergence can be assessed by the expectation $E\left( \varepsilon \right)$ of $\varepsilon$, and $E\left( \varepsilon \right)$ can be derived as follows:

$$E\left( \varepsilon \right) = E\left| {\left( {\hat{P}_{f}^{s} - \overline{P}_{f}^{s} } \right)/\overline{P}_{f}^{s} } \right| = \frac{1}{{\overline{P}_{f}^{s} }}E\left| {\int {\left[ {\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) - \overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)} \right]} \tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right){\text{d}}{\varvec{x}}} \right| \le \frac{1}{{\overline{P}_{f}^{s} }}\int {E\left| {\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) - \overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)} \right|} \tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right){\text{d}}{\varvec{x}}$$

(27)

where $\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right)$ and $\overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)$ are the system failure domain indicator functions estimated by $\hat{g}_{s} \left( {\varvec{x}} \right)$ and $\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right)$, respectively, i.e.,

$$\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) = \left\{ {\begin{array}{*{20}c} 1 & {\hat{g}_{s} \left( {\varvec{x}} \right) \le 0} \\ 0 & {\hat{g}_{s} \left( {\varvec{x}} \right) > 0} \\ \end{array} } \right.$$

(28)

$$\overline{I}_{{F_{s} }} \left( {\varvec{x}} \right) = \left\{ {\begin{array}{*{20}c} 1 & {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) \le 0} \\ 0 & {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right) > 0} \\ \end{array} } \right.$$

(29)

In order to obtain $E\left| {\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) - \overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)} \right|$ in Eq. (27), the statistical law of $\left| {\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) - \overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)} \right|$ needs to be analyzed. From Eq. (28) and Eq. (29), it is known that $\left| {\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) - \overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)} \right|$ is a discrete random variable with two values shown in Eq. (30).

$$\left| {\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) - \overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)} \right| = \left\{ {\begin{array}{*{20}c} 0 & {{\text{sign}}\left( {\hat{g}_{s} \left( {\varvec{x}} \right)} \right) = {\text{sign}}\left( {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right)} \right)} \\ 1 & {{\text{sign}}\left( {\hat{g}_{s} \left( {\varvec{x}} \right)} \right) \ne {\text{sign}}\left( {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right)} \right)} \\ \end{array} } \right.$$

(30)

Due to ${\text{Prob}}\left\{ {{\text{sign}}\left( {\hat{g}_{s} \left( {\varvec{x}} \right)} \right) \ne {\text{sign}}\left( {\mu_{{\hat{g}_{s} }} \left( {\varvec{x}} \right)} \right)} \right\} = P_{e} \left( {\varvec{x}} \right)$, $E\left| {\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) - \overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)} \right|$ can be obtained as follows:

$$E\left| {\hat{I}_{{F_{s} }} \left( {\varvec{x}} \right) - \overline{I}_{{F_{s} }} \left( {\varvec{x}} \right)} \right| = 1 \times P_{e} \left( {\varvec{x}} \right) + 0 \times \left[ {1 - P_{e} \left( {\varvec{x}} \right)} \right] = P_{e} \left( {\varvec{x}} \right)$$

(31)

Substituting Eq. (31) into Eq. (27), Eq. (32) can be obtained

$$E\left( \varepsilon \right) \le \frac{1}{{\overline{P}_{f}^{s} }}\int {P_{e} \left( {\varvec{x}} \right)} f_{{\varvec{X}}} \left( {\varvec{x}} \right){\text{d}}{\varvec{x}} = E^{u} \left( \varepsilon \right)$$

(32)

where $E^{u} \left( \varepsilon \right)$ represents the upper bound of the expected relative error between $\hat{P}_{f}^{s}$ and $\overline{P}_{f}^{s}$. If $E^{u} \left( \varepsilon \right)$ is less than a given threshold $\xi^{*}$, i.e.,$E^{u} \left( \varepsilon \right) \le \xi^{*}$, it can end the adaptive updating, and the SL-AK-SYS_c is converged.

4.3 The detailed steps of SL-AK-SYS_c algorithm

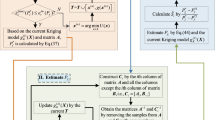
According to the basic principle demonstrated in subSects. 4.1 and 4.2, the detailed steps of the proposed SL-AK-SYS_c algorithm can be listed as follows, and the flowchart and the Pseudo-code of the SL-AK-SYS_c are shown in Fig. 1 and Table 1, respectively.

Fig. 1

The flowchart of the proposed SL-AK-SYS_c

Table 1 The Pseudo-code of the proposed SL-AK-SYS_c for estimating the SFPF

Step 1: Generate an $N$-size candidate sample pool ${\mathbf{S}}_{{\varvec{x}}} = \left\{ {{\varvec{x}}_{1} ,{\varvec{x}}_{2} , \ldots ,{\varvec{x}}_{N} } \right\}^{{\text{T}}}$ from $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$. The samples of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$ in Eq. (4) can be extracted by the combination sampling method, in which an $N$-size candidate sample pool ${\mathbf{S}}_{{{\varvec{\theta}}}} = \left\{ {{{\varvec{\theta}}}_{1} ,{{\varvec{\theta}}}_{2} , \ldots ,{{\varvec{\theta}}}_{N} } \right\}^{{\text{T}}}$ is firstly extracted from the assigned prior PDF $\varphi_{{{\varvec{\theta}}}} \left( {{\varvec{\theta}}} \right)$ of ${{\varvec{\theta}}}$ and for each ${{\varvec{\theta}}}_{i} \in {\mathbf{S}}_{{{\varvec{\theta}}}}$, one sample ${\varvec{x}}_{i}$ with respect to ${{\varvec{\theta}}}_{i}$ is generated by $f_{{\varvec{X}}} \left( {{\varvec{x}}|{{\varvec{\theta}}}_{i} } \right)$. Finally, ${\varvec{x}}_{i} \left( {i = 1,2, \ldots ,N} \right)$ corresponding to ${{\varvec{\theta}}}_{i} \left( {i = 1,2, \ldots ,N} \right)$ forms the candidate sample pool ${\mathbf{S}}_{{\varvec{x}}}$ of $\tilde{f}_{{\varvec{X}}} \left( {\varvec{x}} \right)$.

Step 2: Construct the initial Kriging models $\hat{g}_{j} \left( {\varvec{x}} \right)$ for all multi-failure-mode performance functions $g_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$. Randomly select an $N_{1}$-size sample from ${\mathbf{S}}_{{\varvec{x}}}$ to form an initial training sample set ${\varvec{X}}_{j}^{t} = \left\{ {{\varvec{x}}_{1}^{t} ,{\varvec{x}}_{2}^{t} , \ldots ,{\varvec{x}}_{{N_{1} }}^{t} } \right\}^{{\text{T}}}$ with $N_{1} \ll N$, and evaluate $g_{j} \left( {{\varvec{x}}_{k}^{t} } \right)\left( {j = 1,2, \ldots ,m;k = 1,2, \ldots ,N_{1} } \right)$ to form ${\mathbf{g}}_{j}^{t} = \left\{ {g_{j} \left( {{\varvec{x}}_{1}^{t} } \right),g_{j} \left( {{\varvec{x}}_{2}^{t} } \right), \ldots ,g_{j} \left( {{\varvec{x}}_{{N_{1} }}^{t} } \right)} \right\}^{{\text{T}}}$. By using of ${\varvec{X}}_{j}^{t}$ and ${\mathbf{g}}_{j}^{t}$, the initial Kriging models $\hat{g}_{j} \left( {\varvec{x}} \right)\left( {j = 1,2, \ldots ,m} \right)$ can be constructed for all multi-failure-mode performance functions.

Step 3: Estimate the $U$ learning function $U_{{\hat{g}_{j} }} \left( {\varvec{x}} \right)$ shown in Eq. (33), the system state misclassification probability $P_{e} \left( {\varvec{x}} \right)$ in Eq. (24), and the representative failure probability $\overline{P}_{f}^{s}$ in Eq. (34).

$$U_{{\hat{g}_{j} }} \left( {{\varvec{x}}_{i} } \right) = \frac{{\left| {\mu_{{\hat{g}_{j} }} \left( {{\varvec{x}}_{i} } \right)} \right|}}{{\sigma_{{\hat{g}_{j} }} \left( {{\varvec{x}}_{i} } \right)}}\left( {j = 1,2, \ldots ,m;i = 1,2, \ldots ,N} \right)$$

(33)

$$\overline{P}_{f}^{s} = \frac{{N_{{\mu_{{\hat{g}_{s} }} \le 0}} }}{N}$$

(34)

where $N_{{\mu_{{\hat{g}_{s} }} \le 0}}$ indicates the number of samples falling in the system failure domain $\left\{ {\mu_{{g_{s} }} \left( {\varvec{x}} \right) \le 0} \right\}$ based on the current system Kriging prediction mean $\mu_{{g_{s} }} \left( {\varvec{x}} \right)$.

Step 4: Judge the convergence of the algorithm. If $\frac{1}{N}\sum\limits_{i = 1}^{N} {P_{e} \left( {{\varvec{x}}_{i} } \right)} /\overline{P}_{f}^{s} \le \xi^{*}$ ($\xi^{*} = 0.01$ is the threshold value chosen in this paper) holds, turn to Step 6. If $\frac{1}{N}\sum\limits_{i = 1}^{N} {P_{e} \left( {{\varvec{x}}_{i} } \right)} /\overline{P}_{f}^{s} > \xi^{*}$, select the new training point ${\varvec{x}}^{u}$ by Eq. (35) and the updated mode indicator $p^{u}$ by Eq. (36), respectively.

$${\varvec{x}}^{u} = \arg \mathop {\max }\limits_{{{\varvec{x}}_{i} \in {\mathbf{S}}_{{\varvec{x}}} }} P_{e} \left( {{\varvec{x}}_{i} } \right)\tilde{f}_{{\varvec{X}}} \left( {{\varvec{x}}_{i} } \right)$$

(35)

$$p^{u} = \arg \mathop {\min }\limits_{j = 1}^{m} U_{{\hat{g}_{j} }} \left( {{\varvec{x}}^{u} } \right)$$

(36)

Step 5: Update the Kriging model $\hat{g}_{{p^{u} }} \left( {\varvec{x}} \right)$ of the $p^{u}$-th mode. Update ${\varvec{X}}_{{p^{u} }}^{t} = {\varvec{X}}_{{p^{u} }}^{t} \cup {\varvec{x}}^{u}$ and ${\mathbf{g}}_{{p^{u} }}^{t} = {\mathbf{g}}_{{p^{u} }}^{t} \cup g_{{p^{u} }} \left( {{\varvec{x}}^{u} } \right)$. After reconstructing $\hat{g}_{{p^{u} }} \left( {\varvec{x}} \right)$ by the updated ${\varvec{X}}_{{p^{u} }}^{t}$ and ${\mathbf{g}}_{{p^{u} }}^{t}$, return to Step 3.

Step 6: Estimate the SFPF $\hat{P}_{f}^{s} \left( {{\varvec{\theta}}} \right)$ by Eq. (6).

5 Examples

In this section, the SFPF of different multi-failure-mode systems is estimated to verify the efficiency, accuracy, and applicability of the proposed algorithms. The results of the Double Loop Monte Carlo Simulation (abbreviated as DLMCS) are used as the reference solution, while the accuracy of SLMCS, SL-AK-SYS₃, SL-AK-SYSi, and SL-AK-SYS_c are compared based on the reference solution obtained by DLMCS. The first example is a three-failure-mode parallel system (Yun et al. 2019) with two-dimensional random input vector. This example is used to verify the accuracy and efficiency of the algorithm in the simple numerical example with two cases, i.e., the distribution other than normal distribution and the correlation between the random input variables. The second example is a vehicle side impact problem (Youn et al. 2004; Yang et al. 2022), which is a series system with eleven-dimensional random input vector and ten failure modes. This example illustrates the applicability of the proposed algorithm to estimate the SFPF of the multi-failure-mode system with multi-dimensional distribution parameter. The third one is a single-beam wing structure model (Ajanas et al. 2021) with seven-dimensional random input vector and two failure modes, which aims at verifying the applicability of the proposed algorithm to practical engineering problems with implicit performance functions. To avoid the effect of randomness in the results of single run and to ensure fairness in the comparison of the various algorithms, the results of three compared methods are the average value of 20 runs.

5.1 Example 1 A three-failure-mode parallel system

A parallel system has three failure modes, and this example is used to verify the accuracy and efficiency of the algorithm in the simple numerical example with two cases. The corresponding performance functions and the system failure domain $F_{s}$ are, respectively, listed as follows,

$$g_{1} \left( {\varvec{X}} \right) = \left( {4 - 2.1X_{1}^{2} + X_{1}^{4} /3} \right)X_{1}^{2} + X_{1} X_{2} + \left( { - 4 + 4X_{2}^{2} } \right)X_{2}^{2} + 0.8$$

(37)

$$g_{2} \left( {\varvec{X}} \right) = 100\left( {4 - 2.1X_{1}^{2} + X_{1}^{4} /3} \right)X_{1}^{2} + 100X_{1} X_{2} + 100\left( { - 4 + 4X_{2}^{2} } \right)X_{2}^{2} + 60$$

(38)

$$g_{3} \left( {\varvec{X}} \right) = 500\left( {4 - 2.1X_{1}^{2} + X_{1}^{4} /3} \right)X_{1}^{2} + 500X_{1} X_{2} + 500\left( { - 4 + 4X_{2}^{2} } \right)X_{2}^{2} + 60$$

(39)

$$F_{s} = \left\{ {g_{1} \left( {\varvec{x}} \right) \le 0 \cap g_{2} \left( {\varvec{x}} \right) \le 0 \cap g_{3} \left( {\varvec{x}} \right) \le 0} \right\}$$

(40)

The Weibull distribution is considered in case (1) where $X_{1}$ and $X_{2}$ are mutually independent variables. The distribution parameters of $X_{1}$ and $X_{2}$ in case (1) of example 5.1 are listed in Table 2.

Table 2 The distribution parameters of the input variables in case (1) of example 5.1

Case (1) supposes the scale parameter of $X_{1}$ as the concerned distribution parameter, i.e., $\theta_{1} = \lambda_{{X_{1} }} \in \left[ {0.5,1.5} \right]$. The design domain of the concerned distribution parameter is uniformly scattered into 10 discrete points. The two-dimensional curves of the SFPF $P_{f}^{s} \left( {\theta_{1} } \right)$ obtained by the various methods are shown in Fig. 2. The size of candidate sample pool and the number of the performance function evaluations for each method in case (1) are shown in Table 3, where $N_{call}$ represents the number of the performance function evaluations.

Fig. 2

The two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} } \right)$ varying with $\theta_{1}$ of example 5.1

Table 3 The size of candidate sample pool and $N_{call}$ in case (1) of example 5.1

The correlation between the random input variables is considered in case (2) of example 5.1, where $X_{1}$ and $X_{2}$ are correlated. The correlation coefficient $\rho_{{X_{1} X_{2} }}$ between $X_{1}$ and $X_{2}$ is 0.4. The distribution parameters of $X_{1}$ and $X_{2}$ in case (2) of example 5.1 are listed in Table 4.

Table 4 The distribution parameters of the input variables in case (2) of example 5.1

Case (2) supposes the mean $\mu_{{X_{1} }}$ of $X_{1}$ and the standard deviation $\sigma_{{X_{2} }}$ of $X_{2}$ as the concerned parameters, i.e., ${{\varvec{\theta}}} = \left\{ {\theta_{1} ,\theta_{2} } \right\}^{{\text{T}}} = \left\{ {\mu_{{X_{1} }} ,\mu_{{X_{2} }} } \right\}^{{\text{T}}}$, where $\theta_{1} = \mu_{{X_{1} }} \in \left[ {0.5,0.7} \right]$, $\theta_{2} = \sigma_{{X_{2} }} \in \left[ { - 0.4,0} \right]$. The design domains of the concerned distribution parameters are uniformly scattered into 10 discrete points, respectively. The three-dimensional curves of the SFPF $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\left( {\theta_{1} ,\theta_{2} } \right)$ are shown in Fig. 3. However, as the three-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\left( {\theta_{1} ,\theta_{2} } \right)$ do not facilitate comparison of the accuracy, the two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} = \theta_{2}^{*} } \right)$ and $P_{f}^{s} \left( {\theta_{2} ,\theta_{1} = \theta_{1}^{*} } \right)$ are shown in Fig. 4. The size of candidate sample pool and $N_{call}$ of the parallel system for each method in case (2) of example 5.1 are shown in Table 5.

Fig. 3

The three-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\theta_{1}$ and $\theta_{2}$ of example 5.1

Fig. 4

The two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\theta_{1}$ or $\theta_{2}$ of example 5.1

Table 5 The size of candidate sample pool and $N_{call}$ in case (2) of example 5.1

From the curves of the SFPF of the three-failure-mode parallel system in example 5.1, it can be seen that the SFPF obtained by the SL-AK-SYS_c method has a very tiny error compared with that obtained by the DLMCS. From the number of the performance function evaluations, SL-AK-SYS_c method is significantly less than SL-AK-SYS₃ and SL-AK-SYSi under the acceptable accuracy. The result of this example shows that adaptive learning strategy with considering the possible correlations of the multi-failure-mode Kriging models is more efficient than that without considering the correlations, which indicates that the proposed algorithm is suitable for the cases of the distribution other than normal distribution and the correlation between the random input variables.

5.2 Example 2 A vehicle side impact problem

The vehicle side impact model in Fig. 5 is adapted from Refs. (Youn et al. 2004; Yang et al. 2022) and it is a series system with eleven-dimensional input vector and ten failure modes. Three cases are considered in this example to verify the efficiency and accuracy of the proposed algorithm for a large number of failure modes, input variables, and distribution parameters. In this problem, failure modes based on the safety regulation of the vehicle side impact are considered: the abdomen load ($AL$); the pubic symphysis force ($F$); the rib deflections at upper, middle, and lower locations ($RB_{u}$, $RB_{m}$, $RB_{l}$); the viscous criteria at upper, middle, and lower locations ($VC_{u}$, $VC_{m}$, $VC_{l}$); and the velocities at the B-pillar ($V_{B}$) and door ($V_{D}$).

Fig. 5

The illustration of the vehicle side impact model (Youn et al. 2004)

The failure domain $F_{s}$ of the vehicle side impact problem is formulated as

$$\begin{gathered} F_{s} = \left\{ {\left( {AL\left( {\varvec{x}} \right) > 1.0{\text{kN}}} \right) \cup \left( {F\left( {\varvec{x}} \right) > 4.2{\text{kN}}} \right) \cup \left( {RB_{u} \left( {\varvec{x}} \right) > 32.0{\text{mm}}} \right) \cup \left( {RB_{m} \left( {\varvec{x}} \right) > 32.0{\text{mm}}} \right) \cup } \right. \\ \left( {RB_{l} \left( {\varvec{x}} \right) > 32.0{\text{mm}}} \right) \cup \left( {VC_{u} \left( {\varvec{x}} \right) > 0.32{\text{m/s}}} \right) \cup \left( {VC_{m} \left( {\varvec{x}} \right) > 0.32{\text{m/s}}} \right) \cup \\ \left( {VC_{l} \left( {\varvec{x}} \right) > 0.32{\text{m/s}}} \right) \cup \left( {V_{B} \left( {\varvec{x}} \right) > 9.9{\text{m/s}}} \right) \cup \\ \left. {\left( {V_{D} \left( {\varvec{x}} \right) > 16.69{\text{m/s}}} \right)} \right\} \\ \end{gathered}$$

(41)

The ten performance functions are defined as follows:

$$AL\left( {\varvec{X}} \right) = 1.16 - 0.3717X_{2} X_{4} - 0.00931X_{2} X_{10} - 0.484X_{3} X_{9} + 0.01343X_{6} X_{10}$$

(42)

$$F\left( {\varvec{X}} \right) = 4.72 - 0.5X_{4} - 0.19X_{2} X_{3} - 0.0122X_{4} X_{10} + 0.009325X_{6} X_{10} + 0.000191X_{11}^{2}$$

(43)

$$RB_{u} \left( {\varvec{X}} \right) = 28.98 + 3.818X_{3} - 4.2X_{1} X_{2} + 0.0207X_{5} X_{10} + 6.63X_{6} X_{9} - 7.7X_{7} X_{8} + 0.32X_{9} X_{10}$$

(44)

$$RB_{m} \left( {\varvec{X}} \right) = 33.86 + 2.95X_{3} + 0.1792X_{10} - 5.057X_{1} X_{2} - 11X_{2} X_{8} - 0.0215X_{5} X_{10} - 9.98X_{7} X_{8} + 22X_{8} X_{9}$$

(45)

$$RB_{l} \left( {\varvec{X}} \right) = 46.36 - 9.9X_{2} - 12.9X_{1} X_{8} + 0.1107X_{3} X_{10}$$

(46)

$$VC_{u} \left( {\varvec{X}} \right) = 0.261 - 0.0159X_{1} X_{2} - 0.188X_{1} X_{8} - 0.019X_{2} X_{7} + 0.0144X_{3} X_{5} + 0.0008757X_{5} X_{10}$$

(47)

$$\begin{gathered} VC_{m} \left( {\varvec{X}} \right) = 0.214 + 0.00817X_{5} - 0.131X_{1} X_{8} - 0.0704X_{1} X_{9} + 0.03099X_{2} X_{6} - 0.018X_{2} X_{7} \\ + 0.0208X_{3} X_{8} + 0.121X_{3} X_{9} - 0.00364X_{5} X_{6} + 0.0007715X_{5} X_{10} \\ - 0.0005354X_{6} X_{10} + 0.00121X_{8} X_{11} \\ \end{gathered}$$

(48)

$$VC_{l} \left( {\varvec{X}} \right) = 0.74 - 0.61X_{2} - 0.163X_{3} X_{8} + 0.001232X_{3} X_{10} - 0.166X_{7} X_{9} + 0.227X_{2}^{2}$$

(49)

$$V_{B} \left( {\varvec{X}} \right) = 10.58 - 0.674X_{1} X_{2} - 1.95X_{2} X_{8} + 0.02054X_{3} X_{10} - 0.0198X_{4} X_{10} + 0.028X_{6} X_{10}$$

(50)

$$V_{D} \left( {\varvec{X}} \right) = 16.45 - 0.489X_{3} X_{7} - 0.843X_{5} X_{6} + 0.0432X_{9} X_{10} - 0.0556X_{9} X_{11} - 0.000786X_{11}^{2}$$

(51)

where the eleven-dimensional input vector ${\varvec{X}} = \left\{ {X_{1} ,X_{2} , \ldots ,X_{11} } \right\}$ is mutually independent. The description, distribution, mean, and standard deviation of the eleven-dimensional input vector ${\varvec{X}}$ are listed in Table 6.

Table 6 The distribution parameters of the input variables in example 5.2

Case (1) supposes the mean $\mu_{{X_{1} }}$ of $X_{1}$ as the concerned distribution parameter, i.e., $\theta_{1} = \mu_{{X_{1} }} \in \left[ {0.6,1.2} \right]$. The design domain of the concerned distribution parameter is uniformly scattered into 10 discrete points. The two-dimensional curves of the SFPF $P_{f}^{s} \left( {\theta_{1} } \right)$ obtained by the various methods are shown in Fig. 6. The size of candidate sample pool and the number of the performance function evaluation for each method in case (1) are shown in Table 7.

Fig. 6

The two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} } \right)$ varying with $\theta_{1}$ of example 5.2

Table 7 The size of candidate sample pool and $N_{call}$ in case (1) of example 5.2

Case (2) supposes the mean $\mu_{{X_{1} }}$ of $X_{1}$ and the standard deviation $\sigma_{{X_{2} }}$ of $X_{2}$ as the concerned distribution parameters, i.e., ${{\varvec{\theta}}} = \left\{ {\theta_{1} ,\theta_{2} } \right\}^{{\text{T}}} = \left\{ {\mu_{{X_{1} }} ,\sigma_{{X_{2} }} } \right\}^{{\text{T}}}$, where $\theta_{1} = \mu_{{X_{1} }} \in \left[ {0.6,1.2} \right]$,$\theta_{2} = \sigma_{{X_{2} }} \in \left[ {0.02,0.04} \right]$. The design domains of the concerned distribution parameters are uniformly scattered into 10 discrete points, respectively. The three-dimensional curves of the SFPF $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\left( {\theta_{1} ,\theta_{2} } \right)$ are shown in Fig. 7. Since the three-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\left( {\theta_{1} ,\theta_{2} } \right)$ do not facilitate comparison of the accuracy, the two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} = \theta_{2}^{*} } \right)$ and $P_{f}^{s} \left( {\theta_{2} ,\theta_{1} = \theta_{1}^{*} } \right)$ are shown in Fig. 8.

Fig. 7

The three-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\theta_{1}$ and $\theta_{2}$ of example 5.2

Fig. 8

The two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\theta_{1}$ or $\theta_{2}$ of example 5.2

The size of candidate sample pool and $N_{call}$ of each method in case (2) are shown in Table 8.

Table 8 The size of candidate sample pool and $N_{{{\text{call}}}}$ in case (2) of example 5.2

Case (3) supposes the mean vector $\left\{ {\mu_{{X_{1} }} ,\mu_{{X_{7} }} ,\mu_{{X_{8} }} } \right\}$ of $\left\{ {X_{1} ,X_{7} ,X_{8} } \right\}$ and the standard deviation vector $\left\{ {\sigma_{{X_{2} }} ,\sigma_{{X_{10} }} } \right\}$ of $\left\{ {X_{2} ,X_{10} } \right\}$ as the concerned distribution parameters, i.e., ${{\varvec{\theta}}} = \left\{ {\theta_{1} ,\theta_{2} ,\theta_{3} ,\theta_{4} ,\theta_{5} } \right\}^{{\text{T}}} = \left\{ {\mu_{{X_{1} }} ,\sigma_{{X_{2} }} ,\mu_{{X_{7} }} ,\mu_{{X_{8} }} ,\sigma_{{X_{10} }} } \right\}^{{\text{T}}}$, where $\theta_{1} = \mu_{{X_{1} }} \in \left[ {0.6,1.2} \right]$, $\theta_{2} = \sigma_{{X_{2} }} \in \left[ {0.02,0.04} \right]$, $\theta_{3} = \mu_{{X_{7} }} \in \left[ {0.35,0.65} \right]$, $\theta_{4} = \mu_{{X_{8} }} \in \left[ {0.30,0.39} \right]$, and $\theta_{5} = \sigma_{{X_{10} }} \in \left[ {8,12} \right]$. The design domains of the concerned distribution parameters are uniformly scattered into 10 discrete points, respectively. Whereas, it is not possible to visualize the six-dimensional curves of $P_{f}^{s} \left( {{\varvec{\theta}}} \right)$ varying with ${{\varvec{\theta}}} = \left\{ {\theta_{1} ,\theta_{2} , \ldots ,\theta_{5} } \right\}^{{\text{T}}}$. In order to visually compare the accuracy of each method, the two-dimensional curves of the SFPF $P_{f}^{s} \left( {\theta_{i} ,{{\varvec{\theta}}}_{ - i}^{*} } \right)$ varying with $\theta_{i}$ are shown in Fig. 9, where ${{\varvec{\theta}}}_{ - i}^{*}$ is the fixed value of the remaining four-dimensional distribution parameters after removing the $i$-th distribution parameter, i.e., ${{\varvec{\theta}}}_{ - i}^{*} = \left\{ {\theta_{1}^{*} , \ldots ,\theta_{i - 1}^{*} ,\theta_{i + 1}^{*} , \ldots ,\theta_{5}^{*} } \right\}^{{\text{T}}}$. The fixed value of the distribution parameters ${{\varvec{\theta}}}^{*}$ in Fig. 9 is taken as the median of its concerned domain, i.e., ${{\varvec{\theta}}}^{*} = \left\{ {0.9,0.03,0.5,0.345,10} \right\}^{{\text{T}}}$. The size of candidate sample pool and the number of the performance function evaluation for each method in case (3) are shown in Table 9.

Fig. 9

The two-dimensional curves of $P_{f}^{s} \left( {{\varvec{\theta}}} \right)$ varying with $\theta_{i}$ of example 5.2

Table 9 The size of candidate sample pool and $N_{{{\text{call}}}}$ in case (3) of example 5.2

From the curves of the SFPF of the vehicle side impact system in example 5.2, it can be concluded that the proposed algorithm is suitable for universal situation, which can include multi-failure-mode, multi-input dimension, and multi-distribution parameter. The Kriging model-based methods require far fewer performance function evaluations than those of double-loop numerical simulation and single-loop numerical simulation methods. In contrast to SL-AK-SYS₃ and SL-AK-SYSi, the SL-AK-SYS_c method has the fewest performance function evaluations under the acceptable accuracy, which indicates that considering the possible correlation among the multi-failure-mode Kriging models is effective in improving computational efficiency.

5.3 Example 3 A single-beam wing structure

The wing structure, one of the important components of the aircraft structure, is the main provider of the lift during the flight mission, and it is also the main bearer of the bending moment. Therefore, it is essential to analyze the reliability of the wing structure. The single-beam wing structure (Ajanas et al. 2021), a relatively common wing structure, is a series system with seven-dimensional input vector and two failure modes. This example is aimed at verifying the applicability of the proposed algorithm to the practical engineering problems with the implicit performance functions. The wing structure model is simplified to facilitate the calculation. The single-beam wing structure has 17 ribs, 3 sets of spars, and 1 wing beam. The main load-bearing structures in the wing are the wing beam, the wing ribs, the spars, and the skin. The wing span is 4.02 m and the wing chord length is 1.00 m. In the finite element model of the wing structure, the wing ribs are made of 2A12 Aluminum Alloy, the wing beams and spars are made of 2A16 Aluminum Alloy, and the skin is made of 7075 Aluminum Alloy. The components of the single-beam wing structure are shown in Fig. 10, and the distribution parameters of the input variables are shown in Table 10.

Fig. 10

The components of the single-beam wing structure

Table 10 The distribution parameters of the input variables in example 5.3

During the flight status, the boundary condition of the wing structure is set as the fixed support of the wing root and the applied load is simplified to the pressure difference between upper and lower wing surfaces shown in Fig. 11. The finite element calculation results are shown in Fig. 12 and Fig. 13, respectively, when all the input variables take their means.

Fig. 11

The applied load and the boundary condition of the single-beam wing structure

Fig. 12

The stress cloud result of the single-beam wing structure

Fig. 13

The displacement cloud result of the single-beam wing structure

Two main failure modes of the wing structure are considered in this example. The first one is that the stress at arbitrary position in the wing ribs exceeds the maximum permissible stress $\sigma^{*}$. Therefore, the performance function $g_{1} \left( {\varvec{X}} \right)$ of the first failure mode is constructed by the maximum permissible stress $\sigma^{*}$ and the actual maximum stress $\sigma_{\max } \left( {\varvec{X}} \right)$ as shown in the following equation.

$$g_{1} \left( {\varvec{X}} \right) = \sigma^{*} - \sigma_{\max } \left( {X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} ,X_{6} ,X_{7} } \right)$$

(52)

where the maximum permissible stress $\sigma^{*}$ is $380{\text{MPa}}$.

The second one is that the maximum node displacement in the wing structure exceeds the permissible value $\Delta^{*}$. The performance function $g_{2} \left( {\varvec{X}} \right)$ of the second failure mode is constructed by the permissible displacement value $\Delta^{*}$ and the actual maximum displacement $\Delta_{\max } \left( {\varvec{X}} \right)$ as shown in the following equation.

$$g_{2} \left( {\varvec{X}} \right) = \Delta^{*} - \Delta_{\max } \left( {X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} ,X_{6} ,X_{7} } \right)$$

(53)

where the permissible displacement value $\Delta^{*}$ is $280{\text{mm}}$.

Two cases of the single-beam wing structure are used to verify the applicability of the proposed algorithm to the engineering problems of the implicit performance functions.

Case (1) supposes the mean of $X_{7}$ as the concerned distribution parameter, i.e., $\theta_{1} = \mu_{{X_{7} }} \in \left[ {3100,3300} \right]$ Pa. The variation domain of the concerned distribution parameter is uniformly scattered into 10 discrete points. The two-dimensional curves of the SFPF $P_{f}^{s} \left( {\theta_{1} } \right)$ obtained by the various methods are shown in Fig. 14. The size of candidate sample pool and $N_{call}$ of each method is shown in Table 11.

Fig. 14

The two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} } \right)$ varying with $\theta_{1}$ of example 5.3

Table 11 The size of candidate sample pool and $N_{{{\text{call}}}}$ in case (1) of example 5.3

Case (2) supposes the mean vector $\left\{ {\mu_{{X_{1} }} ,\mu_{{X_{7} }} } \right\}$ of $X_{1}$ and $X_{7}$ as the concerned distribution parameters, i.e., ${{\varvec{\theta}}} = \left\{ {\theta_{1} ,\theta_{2} } \right\}^{{\text{T}}} = \left\{ {\mu_{{X_{1} }} ,\mu_{{X_{7} }} } \right\}^{{\text{T}}}$, where $\theta_{1} = \mu_{{X_{1} }} \in \left[ {68000,72000} \right]$ MPa and $\theta_{2} = \mu_{{X_{7} }} \in \left[ {3100,3300} \right]$ Pa. The variation domains of the concerned distribution parameters are uniformly scattered into 10 discrete points, respectively. The three-dimensional curves of the SFPF $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\left( {\theta_{1} ,\theta_{2} } \right)$ are shown in Fig. 15.

Fig. 15

The three-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\theta_{1}$ and $\theta_{2}$ of example 5.3

Since the three-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\left( {\theta_{1} ,\theta_{2} } \right)$ do not facilitate comparison of the accuracy, the two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} = \theta_{2}^{*} } \right)$ and $P_{f}^{s} \left( {\theta_{2} ,\theta_{1} = \theta_{1}^{*} } \right)$ are shown in Fig. 16. The size of candidate sample pool and $N_{call}$ of each method in case (2) are shown in Table 12.

Fig. 16

The two-dimensional curves of $P_{f}^{s} \left( {\theta_{1} ,\theta_{2} } \right)$ varying with $\theta_{1}$ or $\theta_{2}$ of example 5.3

Table 12 The size of candidate sample pool and $N_{{{\text{call}}}}$ in case (2) of example 5.3

From the curves of the SFPF of the single-beam wing structure in example 5.3, it can be seen that the system failure probability increases with the mean of the applied load $F$ and decreases with the mean of the elasticity modulus $E_{1}$ of the wing ribs. This is due to the fact that the stress and node displacement at the wing ribs increase with the mean of the applied load $F$, and the system failure probability increases with the increase of the stress and displacement. The stress and node displacement at the wing ribs decrease with the mean of the elasticity modulus $E_{1}$ of the wing ribs, and the system failure probability decreases with the decrease in stress and displacement. The relationship between material elasticity modulus mean $\mu_{{X_{1} }}$ and system failure probability $P_{f}^{s}$ can not only show the effect of $\mu_{{X_{1} }}$ on the system failure probability $P_{f}^{s}$ but also help decoupling the RBDO of the wing structure, while the relationship between the applied load mean $\mu_{{X_{7} }}$ and system failure probability $P_{f}^{s}$ indicates the safety level of the wing structure under given $\mu_{{X_{7} }}$.

According to the number of the performance function evaluations, it is obvious that the SL-AK-SYS_c method has significantly fewer performance function evaluations than those of the SL-AK-SYS₃ and the SL-AK-SYSi with acceptable accuracy. Thus, it can be concluded that the SL-AK-SYS_c algorithm can effectively improve the computational efficiency of estimating the SFPF, especially for the engineering problem of the implicit performance functions.

6 Conclusion

In order to accurately and efficiently estimate the system failure probability function (SFPF) of the multi-failure-mode system with multi-dimensional distribution parameter, this paper first constructs a single-loop numerical simulation method (SL) for estimating the SFPF and then the adaptive Kriging model is embedded into the single-loop numerical simulation method for SFPF. In the proposed SL combining with the AK-based method for SFPF, an innovative approach for selecting new training points and updating mode indicator are proposed by considering the possible correlation among the multi-failure-mode Kriging models, and the corresponding adaptive learning convergence criterion is also established. The following conclusions are drawn from the principles of the proposed algorithms and the analysis of three presented examples.

• (1) The samples extracted by the single-loop numerical simulation method can be shared simultaneously to estimate the system failure probability at the arbitrary realizations of all distribution parameters in their concerned design domains. Comparing with the double-loop numerical simulation method, the proposed single-loop numerical simulation method can significantly reduce the computational cost of estimating the SFPF due to the sample information sharing strategy.

• (2) Compared with the SL-AK-SYS₃ and SL-AK-SYSi, the SL-AK-SYS_c algorithm, which considers the possible correlations among multi-failure-mode Kriging models, is more efficient for estimating the SFPF.

• (3) For small failure probabilities ($10^{ - 4}$ or even smaller) in practical engineering problems, the proposed SL-AK-SYS_c algorithm still requires a large number of samples to obtain the convergent results, and the large candidate sample pool will directly lead to slow updating of the adaptive Kriging model, which affects the computational efficiency. In future research, we will consider reducing the size of the candidate sample pool to further improve the efficiency of estimating the SFPF.