An innovative adaptive Kriging-based parallel system reliability method under error stopping criterion for efficiently analyzing the global reliability sensitivity index

Abstract

Global reliability sensitivity index measures the effect of uncertainty of model input on model failure probability, which is critical for simplifying analysis model and the reliability-based design optimization model. For efficiently estimating the global reliability sensitivity index of each model input, this paper transforms it into estimating an unconditional failure probability and a two failure modes-based parallel system failure probability from the perspective of single-loop estimation method. Furthermore, the relationship of computational accuracy among the global reliability sensitivity index, the unconditional failure probability, and the two failure modes-based system failure probability is constructed, on which the error stopping criterion-based sequentially adaptive Kriging model approach is developed to significantly decrease the number of calls to the actual limit state functions and the corresponding computational time under the sufficient accuracy. Results of three case studies covering explicit and implicit limit state functions demonstrate the accuracy and efficiency of the proposed method.

1 Introduction

Reliability measures the ability of structures or systems fulfilling their functions under the required conditions. Due to the uncertainties of geometry, material and loads are considered in reliability analysis, a large number of calls to the limit state function are required to analyze the failure probability. In general, the limit state function is implicit in engineering problems such as the finite element model (FEM)-based limit state function. Once FEM analysis may require a lot of CPU time especially for the giant structures, and thus, a large number of FEM analyses are difficult to meet the requirements of rapid reliability analysis in engineering. For this reason, researchers have investigated the various efficient algorithms from different perspectives, including the approximately analytical algorithms (Keshtegar and Meng 2017; Rosario et al. 2019), numerical simulation algorithms (Liu 2001; Xiang et al. 2023; Hristov and Diazdelao 2023), moment-based algorithms (Zhang and Pandey 2013; Lu et al. 2017; Li et al. 2019a), and the adaptive surrogate model-based algorithms (Bichon et al. 2008; Echard et al. 2011). The adaptive surrogate model-based algorithms not only inherent the universality of numerical simulation methods but also avoid a large number of calls to limit state function by using the surrogate to substitute the actual limit state function, which have been extensively investigated in the past decade. The surrogate model combined Monte Carlo simulation (MCS) algorithm (Bichon et al. 2008; Echard et al. 2011) was one of the prior adaptive surrogate model-based algorithms to be investigated, where MCS samples construct the candidate sampling pool (CSP) for selecting the potential training samples and adaptively updating the surrogate model in order to ensure that the positive or negative limit state signs of MCS samples can be accurately recognized by the surrogate model. To decrease the size of CSP for enhancing the efficiency of selecting the potential training samples, importance sampling technique combined surrogate model method (Echard et al. 2013), subset simulation technique combined surrogate model method (Zhang and Quek 2022), and line sampling technique combined surrogate model method are researched (Wang et al. 2023).

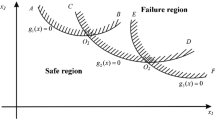
Based on reliability analysis, it is necessary to explore the influence of each input variable on reliability, i.e., reliability sensitivity analysis. Ref. (Li et al. 2012) defined the global reliability sensitivity index aims at quantifying the sensitivity information of each model input to the model failure probability by fixing the input over its whole distribution range. Suppose the limit state function is $Y{ = }g({\varvec{X}})$ where ${\varvec{X}} = [X_{1} ,...,X_{n} ]$ is the $n$-dimensional input variables. $g({\varvec{X}}) > 0$ denotes the safety state, $g({\varvec{X}}) < 0$ denotes the failure state, and $g({\varvec{X}}){ = }0$ denotes the limit state. The failure domain is usually defined as $F{ = [}{\varvec{x}}:g({\varvec{x}}) < 0]$ and the corresponding failure probability is defined as follows,

$$P_{f} = \Pr {[}g({\varvec{X}}) < 0] = \int_{{g({\varvec{x}}) < 0}} {f_{{\varvec{X}}} ({\varvec{x}})d{\varvec{x}}} ,$$

(1)

where $f_{{\varvec{X}}} ({\varvec{x}})$ is the joint probability density function (PDF) of variables ${\varvec{X}}$ and $\Pr {[} \cdot ]$ is the probability operation.

The form of the global reliability sensitivity index (Li et al. 2012) is

$$\delta_{i}^{P} = E(P_{f} - P_{{f|X_{i} }} )^{2} = V(E(I_{F} |X_{i} ))$$

(2)

where $P_{{f|X_{i} }} { = }E(I_{F} |X_{i} )$ is the conditional failure probability, $E( \cdot )$ is the expectation operator, $V( \cdot )$ is the variance operator, and $I_{F} ( \cdot )$ is the indicator function of the failure domain defined as $I_{F} ({\varvec{x}}) = \left\{ \begin{gathered} 0 g({\varvec{x}}) \ge 0 \hfill \\ 1 g({\varvec{x}}) < 0 \hfill \\ \end{gathered} \right.$.

Wei et al. (2012) standardized it through dividing Eq. (2) by the variance of the indicator function of the failure domain, i.e.,

$$S_{i} = \frac{{\delta_{i}^{P} }}{{V(I_{F} )}} = \frac{{V(E(I_{F} |X_{i} ))}}{{V(I_{F} )}}$$

(3)

From Eq. (3), it can be seen that traditional MCS is a nested double-loop process to estimate the item $V(E(I_{F} |X_{i} ))$ where the outer loop is to estimate the variance of the conditional failure probability $P_{{f|X_{i} }}$ and the inner loop is to estimate the conditional failure probability $P_{{f|X_{i} }}$ at each realization of $X_{i}$. To efficiently estimate the global reliability sensitivity indices, single-loop estimation method (Wei et al. 2012), maximum entropy-based method (Yun et al. 2019a) and Bayes formula-based method (Wang et al. 2018, 2019; Li et al. 2019b) have been investigated. Wei et al. 2012 constructed the single-loop estimation method by introducing the corresponding independent identically distributed variables and the corresponding number of calls to the limit state function is linearly dependent on the dimensionality of model inputs. Yun et al. 2019a proposed the maximum entropy-based method where the number of calls to the limit state function only relies on the analysis of unconditional fractional moments but the accuracy depends on the estimation accuracy of unconditional fractional moments and optimization process for finding the fitting parameters of unconditional and conditional PDFs of model output in the maximum entropy method. To overcome the dependence of number of limit state function evaluations on the dimensionality of model inputs, Wang et al. 2018 investigated the Bayes formula-based method in which the estimation of global reliability sensitivity indices is transformed into identifying the unconditional failure domain and estimating the failure-conditional PDFs. Estimating the failure-conditional PDFs does not require any extra calls to limit state function after estimating the unconditional failure probability but the estimation accuracy of global reliability sensitivity index relies on the estimation accuracy of failure-conditional PDF. For discounted failure domain, failure-conditional PDF is difficult to be accurately estimated by the present methods such as the maximum entropy method (Bierig and Chernov 2016), the kernel density method (Barabesi and Fattorini 2002), the Edgeworth expansion method (Assaf and Zirkle 1976), etc. To avoid estimating the failure-conditional PDF, He et al. 2019 used the conditional probability theorem to transform the estimating failure-conditional PDF into a series of interval probabilities while how to determine the interval influences the accuracy of approximation.

In this paper, based on the single-loop estimation method, an efficient algorithm is investigated in order to avoid the direct simulation process and inherent the accuracy of the single-loop estimation method. Firstly, based on the introduced independent identically distributed variables, the estimation of global reliability sensitivity index is equivalently transformed into estimating the unconditional failure probability and a two failure modes-based parallel system failure probability with the same form of the two failure modes’ limit state functions and different distributions of the corresponding model inputs where the two failure modes-based parallel system failure probability is an equivalent derivation to estimate the denominator of Eq. (3). Secondly, to efficiently estimate the unconditional failure probability and the two failure modes-based parallel system failure probability, the sequentially adaptive Kriging model of the limit state function is constructed to recognize the states (failure or safety) of the used random samples. Thirdly, to balance the accuracy and efficiency, error stopping criterion is constructed by propagating the estimation errors of the unconditional failure probability and the two failure modes-based parallel system failure probability. The innovations of the proposed method are summarized as follows.

• 1. Compared to directly applying the adaptive Kriging (AK) to recognizing the states (failure or safety) of random samples used in the single-loop estimation method, the proposed method transforms the directly recognizing states of all used samples into estimating the unconditional failure probability and the equivalently derived two failure modes-based parallel system failure probability. By virtue of the learning function in the system failure probability analysis, the states of all conditional samples do not require to be identified compared to directly applying the AK model into the single-loop method, which can reduce the number of calls to limit state function in adaptively updating the Kriging model.

• 2. By sequentially and adaptively updating Kriging model, the size of CSP in estimating the equivalently derived two failure modes-based parallel system failure probability can be reduced since the samples with safe states in the unconditional failure probability analysis can be removed from the CSP in estimating the derived system failure probability, which will accelerate the adaptively updating process of Kriging model for estimating the equivalently derived two failure modes-based parallel system failure probability.

• 3. Based on propagation of error, the relationship among the estimate error of global reliability sensitivity index, the estimate error of unconditional failure probability, and the estimate error of the two failure modes-based parallel system failure probability is established and then the corresponding error stopping criterion-based adaptive Kriging is constructed which can balance the accuracy and efficiency.

The rest of this paper is organized as follows. Section 2 briefly reviews the single-loop estimation method for estimating the global reliability sensitivity index. Section 3 elaborately introduces the proposed adaptive Kriging-based parallel system reliability method under error stopping criterion for estimating the global reliability sensitivity index. Section 4 analyzes the global reliability sensitivity index of a roof truss structure, an aero-engine turbine disk structure, and a wing structure with composite shin to verify the accuracy and efficiency of the proposed method. Section 5 summarizes the conclusions.

2 The brief review of the single-loop simulation method for estimating the global reliability sensitivity index

To construct the single-loop estimation process of $V(E(I_{F} |X_{i} ))$, the relationship between the variance and expectation as well as the total expectation law are used to establish the following formula,

$$S_{i} = \frac{{V(E(I_{F} |X_{i} ))}}{{V(I_{F} )}}{ = }\frac{{E(E^{2} (I_{F} |X_{i} )) - E^{2} (I_{F} )}}{{E(I_{F}^{2} ) - E^{2} (I_{F} )}}$$

(4)

where $E(I_{F}^{{}} ){ = }E(I_{F}^{2} )$ and $P_{f} { = }E(I_{F}^{{}} )$. Then, Eq. (4) is rewritten as

$$S_{i} = \frac{{V(E(I_{F} |X_{i} ))}}{{V(I_{F} )}}{ = }\frac{{E(E^{2} (I_{F} |X_{i} )) - P_{f}^{2} }}{{P_{f}^{{}} - P_{f}^{2} }}$$

(5)

The single-loop estimation formula of $E(E^{2} (I_{F} |X_{i} ))$ is constructed by introducing the corresponding independent identically distributed variables, i.e.,

$$\begin{gathered} E(E^{2} (I_{F} |X_{i} )){ = }\int_{{X_{i} }} {\left( {\int_{{{\varvec{X}}_{ - i} }} {I_{F} ({\varvec{x}}_{ - i} ,x_{i} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} )} d{\varvec{x}}_{ - i} } \right)}^{2} f_{{X_{i} }} (x_{i} )dx_{i} \hfill \\ { = }\int_{{X_{i} }} {\int_{{{\varvec{X}}_{ - i} }} {\int_{{\tilde{\user2{X}}_{ - i} }} {I_{F} } } } ({\varvec{x}}_{ - i} ,x_{i} )I_{F} (\tilde{\user2{x}}_{ - i} ,x_{i} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} )f_{{\tilde{\user2{X}}_{ - i} }} (\tilde{\user2{x}}_{ - i} )f_{{X_{i} }} (x_{i} )d{\varvec{x}}_{ - i} d\tilde{\user2{x}}_{ - i} dx_{i} \hfill \\ \end{gathered}$$

(6)

where $\tilde{\user2{X}}_{ - i}$ is the independent identically distributed variables of ${\varvec{X}}_{ - i}$, and by introducing $\tilde{\user2{X}}_{ - i}$ the double-loop nested integration is transformed into a $2n - 1$ dimensional single-loop integration.

The MCS processes for estimating $E(E^{2} (I_{F} |X_{i} ))$ by Eq. (6) and the global reliability sensitivity index $S_{i}$ are summarized as follows.

Step 1: Generate two $N \times n$-size sample matrices of ${\varvec{X}}$ by $f_{{\varvec{X}}} ({\varvec{x}})$, i.e.,

$${\varvec{A}}\,{ = }\,\left[ {\begin{array}{*{20}c} {x_{1}^{(1)} } {x_{2}^{(1)} } \cdots {x_{n}^{(1)} } \\ {x_{1}^{(2)} } {x_{2}^{(2)} } \cdots {x_{n}^{(2)} } \\ \vdots \vdots \ddots \vdots \\ {x_{1}^{(N)} } {x_{2}^{(N)} } \cdots {x_{n}^{(N)} } \\ \end{array} } \right]$$

(7)

$${\varvec{B}}\,{ = }\,\left[ {\begin{array}{*{20}c} {x_{1}^{{(N{ + }1)}} } {x_{2}^{{(N{ + }1)}} } \cdots {x_{n}^{{(N{ + }1)}} } \\ {x_{1}^{{(N{ + }2)}} } {x_{2}^{{(N{ + }2)}} } \cdots {x_{n}^{{(N{ + }2)}} } \\ \vdots \vdots \ddots \vdots \\ {x_{1}^{(2N)} } {x_{2}^{(2N)} } \cdots {x_{n}^{(2N)} } \\ \end{array} } \right]$$

(8)

Step 2: Generate another sample matrix ${\varvec{C}}_{i}$ by combining the $i$ th column of matrix ${\varvec{A}}$ and all the columns except the $i$ th of matrix ${\varvec{B}}$, i.e.,

$${\varvec{C}}_{i}\, { = [}\,{\varvec{A}}_{i} {,}{\varvec{B}}_{ - i} {] = }\left[ {\begin{array}{*{20}c} {x_{1}^{(N + 1)} } \cdots {x_{i}^{(1)} } \cdots {x_{n}^{(N + 1)} } \\ {x_{1}^{(N + 2)} } \cdots {x_{i}^{(2)} } \cdots {x_{n}^{(N + 2)} } \\ \vdots \ddots \vdots \ddots \vdots \\ {x_{1}^{(2N)} } \cdots {x_{i}^{(N)} } \cdots {x_{n}^{(2N)} } \\ \end{array} } \right]$$

(9)

Step 3: Compute the values of indicator function of the failure domain for each sample in matrices ${\varvec{A}}$ and ${\varvec{C}}_{i}$, then two $N$-dimensional vectors are obtained, i.e.,

$${\varvec{I}}_{{\varvec{A}}} \,{ = }\,I_{F} ({\varvec{A}}), {\varvec{I}}_{{{\varvec{C}}_{i} }} { = }I_{F} ({\varvec{C}}_{i} )$$

(10)

Step 4: Compute the global reliability sensitivity index $S_{i}$ by Eq. (11),

$$S_{i} \approx \frac{{D_{i}^{*} - P_{f}^{*2} }}{{D^{*} }}$$

(11)

where $D_{i}^{*}$, $P_{f}^{*}$, and $D^{*}$ are estimated by using the information in vectors ${\varvec{I}}_{{\varvec{A}}}$ and ${\varvec{I}}_{{{\varvec{C}}_{i} }}$, i.e.,

$$D_{i}^{*}\, { = }\,\frac{1}{N}\sum\limits_{j = 1}^{N} {I_{{\varvec{A}}}^{(j)} I_{{{\varvec{C}}_{i} }}^{(j)} }$$

(12)

$$P_{f}^{*}\, { = }\,\frac{1}{N}\sum\limits_{j = 1}^{N} {I_{{\varvec{A}}}^{(j)} }$$

(13)

$$D^{*} { = }P_{f}^{*} - P_{f}^{{*2}}$$

(14)

where $I_{{\varvec{A}}}^{(j)}$ and $I_{{{\varvec{C}}_{i} }}^{(j)}$ are the $j$ th elements of vectors ${\varvec{I}}_{{\varvec{A}}}$ and ${\varvec{I}}_{{{\varvec{C}}_{i} }}$ respectively.

From the aforementioned steps, it can be seen that $(n + 1)N$ samples are used to estimate all inputs’ global reliability sensitivity indices, which means that $(n + 1)N$ samples’ indicator function values of failure domain require to be identified. If the adaptive Kriging coupled with MCS technique (abbreviated as AK-MCS) is directly employed, $(n + 1)N$ candidate samples are involved in the process of adaptively constructing the Kriging model. To reduce the size of candidate samples and accelerate the adaptively learning process of Kriging model in order to efficiently and accurately estimate the global reliability sensitivity indices, an efficient adaptive Kriging-based parallel system reliability method under error stopping criterion is constructed in Sect. 3.

3 The proposed adaptive Kriging-based parallel system reliability method under error stopping criterion for estimating the global reliability sensitivity index

To directly apply AK-MCS to the single-loop method, all samples in matrices ${\varvec{A}}$ and ${\varvec{C}}_{i} (i = 1,...,n)$, i.e., $(n + 1)N$ candidate samples are used to adaptively training the Kriging model and U learning function-based stopping criterion is utilized. From Eq. (12), it can be seen that if $I_{{\varvec{A}}}^{(j)}$ equals to zero, the item $I_{{\varvec{A}}}^{(j)} I_{{{\varvec{C}}_{i} }}^{(j)}$ equals to zero too, and the value of $I_{{{\varvec{C}}_{i} }}^{(j)}$ is unimportant. Therefore, to estimate the global reliability sensitivity index, Kriging model does not require to accurately estimate every sample’s indicator function value of failure domain in the $(n + 1)N$ candidate samples. Furthermore, $E(E^{2} (I_{F} |X_{i} ))$ also can be derived as a two failure modes-based system failure probability, and then the system U learning function can be employed to accelerate convergence of updating Kriging model. Besides, error stopping criterion (ESC) is investigated in Refs. (Hu and Mahadevan 2016; Wang and Shafieezadeh 2019) and the relevant results demonstrate the efficiency of ESC compared to the direct U learning function-based stopping criterion. Thus, how to establish the estimation accuracy of global reliability sensitivity index with the adaptively training process of Kriging model is investigated in this Section. Section 3.1 briefly reviews the AK-MCS method, Sect. 3.2 elaborately introduces the proposed adaptive Kriging-based parallel system reliability method for estimating the item $E(E^{2} (I_{F} |X_{i} ))$, Sect. 3.3 detailedly illustrates the constructed error propagation process and the corresponding error stopping criterion in global reliability sensitivity analysis and Sect. 3.4 summarizes the concrete steps of the proposed method.

3.1 Brief review of AK-MCS method

Kriging model is a semi-parametric interpolation technique based on the statistical theory and consists of the parametric linear regression part and the nonparametric stochastic process (Gao et al. 2020). The Kriging model of the limit state function $g({\varvec{X}})$ can be denoted as $g_{K} ({\varvec{X}})$ which follows the normal distribution at each prediction, i.e., $g_{K} \left( {\varvec{X}} \right) \sim N\left( {\mu_{{g_{K} }} \left( {\varvec{X}} \right),\sigma_{{g_{K} }}^{2} \left( {\varvec{X}} \right)} \right)$ and can provide the prediction mean $\mu_{{g_{K} }} ({\varvec{X}})$ and prediction standard deviation $\sigma_{{g_{K} }}^{{}} ({\varvec{X}})$. Based on the property of Kriging model, Ref. (Echard et al. 2011) derived the U learning function which form is

$$U\left( {\varvec{X}} \right) = \frac{{\left| {\mu_{{g_{K} }} } \left( {\varvec{X}} \right) \right|}}{{\sigma_{{g_{K} }} \left( {\varvec{X}} \right)}}$$

(15)

where $\Phi ( - U({\varvec{x}}))$ measures the probability of making a mistake by using the Kriging model to identify the sign of limit state function at the sample ${\varvec{x}}$, and the larger the U value is, the more accurate the state of the corresponding sample is identified.

Suppose the states (failure or safety) of samples in matrix ${\varvec{S}}$ are required to be identified. The basic steps to identify the signs of limit state function of all samples in matrix ${\varvec{S}}$ by adaptive Kriging model are divided into the following four steps.

Step 1: Randomly select a few of samples $N_{0}$ in matrix ${\varvec{S}}$ and estimate the limit state function values of these samples. Then, the training sample set ${\varvec{T}}$ is firstly constructed by these $N_{0}$ samples, i.e., ${\varvec{T}}{ = }\bigcup\nolimits_{i = 1}^{{N_{0} }} {[{\varvec{x}}^{(i)} ,g(} {\varvec{x}}^{(i)} )]$. The initial Kriging model $g_{K} ({\varvec{X}})$ is constructed by using the MATLAB Dace toolbox based on the training sample set ${\varvec{T}}$.

Step 2: Judge whether the current Kriging model is convergent. Calculate the U values of all sample in matrix ${\varvec{S}}$ by Eq. (15). If the minimum value of U, i.e., $\mathop {\min }\limits_{{{\varvec{x}} \in {\varvec{S}}}} U({\varvec{x}})$ is larger or equal to 2 which implies that the confidence of correct sign prediction of the limit state function at every sample in matrix ${\varvec{S}}$ is larger than or equal to $1 - \Phi ( - 2) = 97.7\%$, the current Kriging model is regarded as a convergent and highly accurate one (Echard et al. 2011). Otherwise, the current Kriging model should be updated.

Step 3: Update the current Kriging model. The next best training sample is selected by the minimum value of U, i.e., ${\varvec{x}}^{(u)} = \mathop {\min }\limits_{{{\varvec{x}} \in {\varvec{S}}}} U({\varvec{x}})$ and the training sample set is updated, i.e., ${\varvec{T}}{ = }{\varvec{T}} \cup [{\varvec{x}}^{(u)} ,g({\varvec{x}}^{(u)} )]$. Then, the Kriging model $g_{K} ({\varvec{X}})$ is accordingly updated by taking the updated training sample set ${\varvec{T}}$ into the MATLAB Dace toolbox. Then, turn to Step 2 to further judge whether the Kriging model is convergent. If not, continuously execute Step 3 until the Kriging model is convergent.

Step 4: Use the convergent Kriging model $g_{K} ({\varvec{X}})$ to identify the states (failure or safety) of all samples in matrix ${\varvec{S}}$, i.e., if $\mu_{{g_{K} }} ({\varvec{x}}) > 0$, the sample ${\varvec{x}}$ is identified as failure sample, otherwise, the sample ${\varvec{x}}$ is regarded as safety sample.

3.2 The basic theory of the proposed adaptive Kriging-based parallel system reliability method to estimate $E(E^{2} (I_{F} |X_{i} ))$

Introducing$I_{{\tilde{F}}} ({\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} )$ where $I_{{\tilde{F}}} ({\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} ) = I_{F} ({\varvec{x}}_{ - i} ,x_{i} )I_{F} (\tilde{\user2{x}}_{ - i} ,x_{i} )$ and $I_{{\tilde{F}}} ({\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} ){ = }0$ if $I_{F} ({\varvec{x}}_{ - i} ,x_{i} )I_{F} (\tilde{\user2{x}}_{ - i} ,x_{i} ){ = }0$ otherwise $I_{{\tilde{F}}} ({\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} ){ = 1}$, Eq. (6) can be equivalently expressed as.

$$E\left( {E^{2} \left( {I_{F} |X_{i} } \right)} \right) = \int_{{X_{i} }} {\int_{{X_{{ - i}} }} {\int_{{\widetilde{X}_{{ - i}} }} {I_{{\tilde{F}}} } } } (\varvec{x}_{{ - i}} ,\widetilde{\varvec{x}}_{{ - i}} ,x_{i} )f_{{X_{{ - i}} }} (\varvec{x}_{{ - i}} )f_{{\widetilde{{X}}_{{ - i}} }} (\widetilde{\varvec{x}}_{{ - i}} )f_{{X_{i} }} (x_{i} )d{\varvec{x}}_{{ - i}} d\widetilde{\varvec{x}}_{{ - i}} dx_{i} ,$$

(16)

where $I_{{\tilde{F}}} ({\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} )$ also can be regarded as an indicator function of failure domain and the failure domain is defined as $\tilde{F}{ = [(}{\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} ):I_{F} ({\varvec{x}}_{ - i} ,x_{i} )I_{F} (\tilde{\user2{x}}_{ - i} ,x_{i} ){ = }0]$.

Thus, $E(E^{2} (I_{F} |X_{i} ))$ also can be regarded as a failure probability with $\tilde{F}$ failure domain and $2n - 1$ dimensional input variables $({\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} )$. Except using the indicator function of failure domain $I_{F} ( \cdot )$ to define the $I_{{\tilde{F}}} ( \cdot )$, the limit state function $g({\varvec{X}})$ also can be used to define $I_{{\tilde{F}}} ( \cdot )$, i.e.,

$$I_{{\tilde{F}}} \left( {\varvec{x}_{{ - i}} ,\tilde{\varvec{x}}_{{ - i}} ,x_{i} } \right) = \left\{ {\begin{array}{*{20}c} 0 & \quad {g\left( {\varvec{x}_{{ - i}} ,x_{i} } \right) \ge 0 \cup g\left( {\tilde{\varvec{x}}_{{ - i}} ,x_{i} } \right) \ge 0} \\ 1 & \quad {g\left( {\varvec{x}_{{ - i}} ,x_{i} } \right) < 0 \cap g\left( {\tilde{\varvec{x}}_{{ - i}} ,x_{i} } \right) < 0} \\ \end{array} } \right.$$

(17)

From Eq. (17), it can be seen that $E(E^{2} (I_{F} |X_{i} ))$ is equal to a two failure modes-based parallel system failure probability with the limit state functions being $g({\varvec{x}}_{ - i} ,x_{i} )$ and $g(\tilde{\user2{x}}_{ - i} ,x_{i} )$ where the form of limit state functions are the same but ${\varvec{x}}_{ - i}$ and $\tilde{\user2{x}}_{ - i}$ are independent identical distribution which leads to different random samples of ${\varvec{x}}_{ - i}$ and $\tilde{\user2{x}}_{ - i}$. Thus, the learning function of Kriging model in the two failure modes-based parallel system failure probability analysis (Yun et al. 2019b) can be used to adaptively train Kriging model of $g({\varvec{X}})$ to efficiently estimate the $E(E^{2} (I_{F} |X_{i} ))$, i.e.,

$$\tilde{U}\left( {\varvec{x}_{ - i} ,\tilde{\varvec{x}}_{ - i} ,x_{i} } \right) = \left\{ {\begin{array}{*{20}c} {\max \left[ {U\left( {\varvec{x}_{ - i} ,x_{i} } \right),U\left( {\tilde{\varvec{x}}_{ - i} ,x_{i} } \right)} \right]} &\quad {{\text{if }}\mu_{{g_{K} }} \left( {\varvec{x}_{ - i} ,x_{i} } \right) \ge 0 \cup \mu_{{g_{K} }} \left( {\tilde{\varvec{x}}_{ - i} ,x_{i} } \right) \ge 0} \\ \!\!\!{\min \left[ {U(\varvec{x}_{ - i} ,x_{i} ),U(\tilde{\varvec{x}}_{ - i} ,x_{i} )} \right]} & {{\text{if}} \mu_{{g_{K} }} (\varvec{x}_{ - i} ,x_{i} ) < 0 \cap \mu_{{g_{K} }} (\tilde{\varvec{x}}_{ - i} ,x_{i} ) < 0} \\ \end{array} } \right.$$

(18)

where $U({\varvec{x}}_{ - i} ,x_{i} )$ and $U(\tilde{\user2{x}}_{ - i} ,x_{i} )$ are the classical U learning function (Echard et al. 2011) defined as

$$U({\varvec{x}}_{ - i} ,x_{i} ){ = }\frac{{{|}\mu_{{g_{K} }} ({\varvec{x}}_{ - i} ,x_{i} ){|}}}{{\sigma_{{g_{K} }} ({\varvec{x}}_{ - i} ,x_{i} )}}$$

(19)

$$U(\tilde{\user2{x}}_{ - i} ,x_{i} ){ = }\frac{{{|}\mu_{{g_{K} }} (\tilde{\user2{x}}_{ - i} ,x_{i} ){|}}}{{\sigma_{{g_{K} }} (\tilde{\user2{x}}_{ - i} ,x_{i} )}}$$

(20)

The potential best training sample in the current iteration of learning Kriging model can be selected by

$${[}{\varvec{x}}_{ - i}^{(u)} ,\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} {] = }\arg \mathop {\min }\limits_{{({\varvec{x}}_{ - i} ,x_{i} ) \in {\varvec{A}},(\tilde{\user2{x}}_{ - i} ,x_{i} ) \in {\varvec{C}}_{i} }} U({\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} )$$

(21)

If $\mu_{{g_{K} }} ({\varvec{x}}_{ - i}^{(u)} ,x_{i} ) \ge 0 \cup \mu_{{g_{K} }} (\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} ) \ge 0$ satisfies, $[({\varvec{x}}_{ - i}^{(u)} ,x_{i} ),g({\varvec{x}}_{ - i}^{(u)} ,x_{i} )]$ is added into the current training sample set if $U({\varvec{x}}_{ - i}^{(u)} ,x_{i} ) > U(\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} )$ or $[(\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} ),g(\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} )]$ is added into the current training sample set if $U({\varvec{x}}_{ - i}^{(u)} ,x_{i} ) \le U(\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} )$. If $\mu_{{g_{K} }} ({\varvec{x}}_{ - i} ,x_{i} ) < 0 \cap \mu_{{g_{K} }} (\tilde{\user2{x}}_{ - i} ,x_{i} ) < 0$ satisfies, $[({\varvec{x}}_{ - i}^{(u)} ,x_{i} ),g({\varvec{x}}_{ - i}^{(u)} ,x_{i} )]$ is added into the current training sample set if $U({\varvec{x}}_{ - i}^{(u)} ,x_{i} ) \le U(\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} )$ or $[(\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} ),g(\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} )]$ is added into the current training sample set if $U({\varvec{x}}_{ - i}^{(u)} ,x_{i} ) > U(\tilde{\user2{x}}_{ - i}^{(u)} ,x_{i} )$.

The basic stopping criterion of adaptively learning Kriging model is $\mathop {\min }\limits_{{({\varvec{x}}_{ - i} ,x_{i} ) \in {\varvec{A}},(\tilde{\user2{x}}_{ - i} ,x_{i} ) \in {\varvec{C}}_{i} }} U({\varvec{x}}_{ - i} ,\tilde{\user2{x}}_{ - i} ,x_{i} ) \ge 2$ which means that every value of $I_{{\tilde{F}}} ( \cdot )$ in the $N$ samples is correctly estimated with a probability of $\Phi (2) = 97.7\%$ at least by the current training Kriging model. Besides using the direct U learning function-based training stopping criterion, Ref. (Hu and Mahadevan 2016; Wang and Shafieezadeh 2019) proposed the U learning function-based ESC which can sufficiently balance the accuracy and efficiency. Thus, in the estimation processes of $E(I_{F} )$ and $E(E^{2} (I_{F} |X_{i} ))$, ESC can be embedded. Nevertheless, the estimation error of $S_{i}$ cannot be directly reflected from the estimation errors of $E(I_{F} )$ and $E(E^{2} (I_{F} |X_{i} ))$. Section 3.3 will establish the estimation accuracy of $S_{i}$ with the accuracy of $E(I_{F} )$ and $E(E^{2} (I_{F} |X_{i} ))$ to guarantee the estimation accuracy of $S_{i}$ under the ESC in estimating the $E(I_{F} )$ and $E(E^{2} (I_{F} |X_{i} ))$.

3.3 Error propagation analysis and the corresponding error stopping criterion of updating Kriging model in global reliability sensitivity analysis

Let $P_{{f_{i} }}$ denote $E(E^{2} (I_{F} |X_{i} ))$, $S_{i}$ can be equivalently expressed as

$$S_{i} \,{ = }\,\frac{{P_{{f_{i} }} - P_{f}^{2} }}{{P_{f} - P_{f}^{2} }}$$

(22)

where $S_{i}$ is a function of $P_{{f_{i} }}$ and $P_{f}$.

Further denoting $P_{{f_{i} }}$ and $P_{f}$ by $x_{1}$ and $x_{2}$, respectively, $S_{i}$ can be further equivalently expressed as

$$S_{i} {(}x_{1} ,x_{2} {) = }\frac{{x_{1} - x_{2}^{2} }}{{x_{2} - x_{2}^{2} }}$$

(23)

Using $x_{1}^{*}$ and $x_{2}^{*}$ denote the approximate values of $x_{1}^{{}}$ and $x_{2}^{{}}$, the approximate value of $S_{i}$ can be obtained as $S_{i}^{*} { = }S_{i}^{*} {(}x_{1}^{*} ,x_{2}^{*} {)}$. Apply Taylor expansion series at the value $(x_{1}^{*} ,x_{2}^{*} )$ of $(x_{1}^{{}} ,x_{2}^{{}} )$, $S_{i} {(}x_{1} ,x_{2} {)}$ can be expressed as

$$\begin{gathered} S_{i} (x_{1} ,x_{2} ) = S_{i} (x_{1}^{*} ,x_{2}^{*} ) + \left[ {\left( {\frac{{\partial S_{i} }}{{\partial x_{1} }}} \right)^{*} (x_{1} - x_{1}^{*} ) + \left( {\frac{{\partial S_{i} }}{{\partial x_{2} }}} \right)^{*} (x_{2} - x_{2}^{*} )} \right] + \hfill \\ \frac{1}{2!}\left[ {\left( {\frac{{\partial^{2} S_{i} }}{{\partial x_{1}^{2} }}} \right)^{*} (x_{1} - x_{1}^{*} )^{2} + 2\left( {\frac{{\partial^{2} S_{i} }}{{\partial x_{1} \partial x_{2} }}} \right)(x_{1} - x_{1}^{*} )(x_{2} - x_{2}^{*} ) + \left( {\frac{{\partial^{2} S_{i} }}{{\partial x_{2}^{2} }}} \right)^{*} (x_{2} - x_{2}^{*} )^{2} } \right] + ... \hfill \\ \end{gathered}$$

(24)

where $x_{1} - x_{1}^{*} = \varepsilon (x_{1}^{*} )$ and $x_{2} - x_{2}^{*} = \varepsilon (x_{2}^{*} )$ denote the error between the estimates and the accurate values of $x_{1}$ and $x_{2}$, respectively.

Generally, $\varepsilon (x_{1}^{*} )$ and $\varepsilon (x_{2}^{*} )$ are small values, and by neglecting the higher-order small terms, $S_{i} (x_{1} ,x_{2} )$ can be approximately rewritten as

$$S_{i} (x_{1} ,x_{2} ) \approx S_{i} (x_{1}^{*} ,x_{2}^{*} ) + \left[ {\left( {\frac{{\partial S_{i} }}{{\partial x_{1} }}} \right)^{*} (x_{1} - x_{1}^{*} ) + \left( {\frac{{\partial S_{i} }}{{\partial x_{2} }}} \right)^{*} (x_{2} - x_{2}^{*} )} \right]$$

(25)

Based on Eq. (25), the absolute error between $S_{i} (x_{1} ,x_{2} )$ and $S_{i} (x_{1}^{*} ,x_{2}^{*} )$ is derived as

$$\varepsilon (S_{i}^{*} ) = S_{i} (x_{1} ,x_{2} ) - S_{i} (x_{1}^{*} ,x_{2}^{*} ) = \left[ {\left( {\frac{{\partial S_{i} }}{{\partial x_{1} }}} \right)^{*} (x_{1} - x_{1}^{*} ) + \left( {\frac{{\partial S_{i} }}{{\partial x_{2} }}} \right)^{*} (x_{2} - x_{2}^{*} )} \right]$$

(26)

Then, the relative error between $S_{i} (x_{1} ,x_{2} )$ and $S_{i} (x_{1}^{*} ,x_{2}^{*} )$ is derived based on Eq. (26) as

$$\varepsilon_{r} \left( {S_{i}^{*} } \right) = \frac{{\varepsilon \left( {S_{i}^{*} } \right)}}{{S_{i}^{*} }} = \frac{{x_{1}^{*} }}{{S_{i}^{*} }}\left( {\frac{{\partial S_{i} }}{{\partial x_{1} }}} \right)^{*} \frac{{\varepsilon \left( {x_{1}^{*} } \right)}}{{x_{1}^{*} }} + \frac{{x_{2}^{*} }}{{S_{i}^{*} }}\left( {\frac{{\partial S_{i} }}{{\partial x_{2} }}} \right)^{*} \frac{{\varepsilon \left( {x_{2}^{*} } \right)}}{{x_{2}^{*} }} = \frac{{x_{1}^{*} }}{{S_{i}^{*} }}\left( {\frac{{\partial S_{i} }}{{\partial x_{2} }}} \right)^{*} \cdot \varepsilon_{r} \left( {x_{1}^{*} } \right) + \frac{{x_{2}^{*} }}{{S_{i}^{*} }}\left( {\frac{{\partial S_{i} }}{{\partial x_{2} }}} \right)^{*} \cdot \varepsilon_{r} \left( {x_{2}^{*} } \right)$$

(27)

where $\varepsilon (x_{1}^{*} )$ and $\varepsilon (x_{2}^{*} )$ denote the relative error of the estimate $x_{1}^{*}$ and $x_{2}^{*}$, respectively, and

$$\frac{{\partial S_{i} }}{{\partial x_{1} }} = \frac{{2x_{1} x_{2} - x_{2} - x_{1}^{2} }}{{(x_{1} - x_{1}^{2} )^{2} }}$$

(28)

$$\frac{{\partial S_{i} }}{{\partial x_{2} }} = \frac{1}{{x_{1} - x_{1}^{2} }}$$

(29)

Then, by taking the estimates $P_{{f_{i} }}^{*}$ and $P_{f}^{*}$ into Eq. (27), the relationship among $\varepsilon_{r} (S_{i}^{*} )$, $\varepsilon_{r} (P_{{f_{i} }}^{*} )$, and $\varepsilon_{r} (P_{f}^{*} )$ is constructed, i.e.,

$$\varepsilon_{r} \left( {S_{i}^{*} } \right) = \frac{{P_{f}^{*} }}{{S_{i}^{*} }}\left( {\frac{{2P_{f}^{*} P_{{f_{i} }}^{*} - P_{{f_{i} }}^{*} - P_{f}^{*2} }}{{\left( {P_{f}^{*} - P_{f}^{*2} } \right)^{2} }}} \right)\varepsilon_{r} \left( {P_{f}^{*} } \right) + \frac{{P_{{f_{i} }}^{*} }}{{S_{i}^{*} }}\left( {\frac{1}{{P_{f}^{*} - P_{f}^{*2} }}} \right)\varepsilon_{r} \left( {P_{{f_{i} }}^{*} } \right)$$

(30)

where $P_{f}^{*}$ is the estimate of $P_{f}^{{}}$, $P_{{f_{i} }}^{*}$ is the estimate of $P_{{f_{i} }}^{{}}$, $S_{i}^{*}$ is the estimate of $S_{i}^{{}}$ calculated by $P_{f}^{*}$ and $P_{{f_{i} }}^{*}$.

To calculate $\varepsilon_{r} (P_{f}^{*} )$ and $\varepsilon_{r} (P_{{f_{i} }}^{*} )$, the actual values of $P_{f}^{{}}$ and $P_{{f_{i} }}^{{}}$ should be known in advance but $P_{f}^{{}}$ and $P_{{f_{i} }}^{{}}$ are the target estimates which cannot be known before estimation. Thus, $\varepsilon_{r} (S_{i}^{*} )$ cannot be calculated before obtaining the actual $S_{i}^{{}}$. Fortunately, the maximum values of $\varepsilon_{r} (P_{f}^{*} )$ and $\varepsilon_{r} (P_{{f_{i} }}^{*} )$ can be estimated in the processes of estimating $P_{f}^{*}$ and $P_{{f_{i} }}^{*}$ by Kriging model. Then, the following inequality can be obtained, i.e.,

$$\varepsilon_{r} \left( {S_{i}^{*} } \right) \le \left| {\frac{{P_{f}^{*} }}{{S_{i}^{*} }}\left( {\frac{{2P_{f}^{*} P_{{f_{i} }}^{*} - P_{{f_{i} }}^{*} - P_{f}^{*2} }}{{\left( {P_{f}^{*} - P_{f}^{*2} } \right)^{2} }}} \right)} \right|\varepsilon_{r}^{\max } \left( {P_{f}^{*} } \right) + \left| {\frac{{P_{{f_{i} }}^{*} }}{{S_{i}^{*} }}\left( {\frac{1}{{P_{f}^{*} - P_{f}^{*2} }}} \right)} \right|\varepsilon_{r}^{\max } \left( {P_{{f_{i} }}^{*} } \right)$$

(31)

where $\varepsilon_{r}^{\max } (P_{f}^{*} )$ is the maximum relative error between $P_{f}^{*}$ and $P_{f}^{{}}$, and $\varepsilon_{r}^{\max } (P_{{f_{i} }}^{*} )$ is the maximum relative error between $P_{{f_{i} }}^{*}$ and $P_{{f_{i} }}^{{}}$.

Therefore, the maximum value of $\varepsilon_{r} (S_{i}^{{}} )$ is accordingly obtained, i.e.,

$$\varepsilon_{r}^{\max } \left( {S_{i}^{*} } \right) = \left| {\frac{{P_{f}^{*} }}{{S_{i}^{*} }}\left( {\frac{{2P_{f}^{*} P_{{f_{i} }}^{*} - P_{{f_{i} }}^{*} - P_{f}^{*2} }}{{\left( {P_{f}^{*} - P_{f}^{*2} } \right)^{2} }}} \right)} \right|\varepsilon_{r}^{\max } \left( {P_{f}^{*} } \right) + \left| {\frac{{P_{{f_{i} }}^{*} }}{{S_{i}^{*} }}\left( {\frac{1}{{P_{f}^{*} - P_{f}^{*2} }}} \right)} \right|\varepsilon_{r}^{\max } \left( {P_{{f_{i} }}^{*} } \right)$$

(32)

Let $g_{K}^{(1)} ({\varvec{X}})$ denote the updated Kriging model of $g({\varvec{X}})$ with $\varepsilon_{r}^{\max } (P_{f}^{*} ) \le \varepsilon_{r}^{thr} (P_{f}^{{}} )$ and $g_{K}^{(2)} ({\varvec{X}})$ denote the updated Kriging model of $g({\varvec{X}})$ with $\varepsilon_{r}^{\max } (P_{{f_{i} }}^{*} ) \le \varepsilon_{r}^{thr} (P_{{f_{i} }}^{{}} )$ where $g_{K}^{(2)} ({\varvec{X}})$ is adaptively updated based on the final $g_{K}^{(1)} ({\varvec{X}})$. $\varepsilon_{r}^{thr} (P_{f}^{{}} )$ and $\varepsilon_{r}^{thr} (P_{{f_{i} }}^{{}} )$ denote the predefined accuracy of the estimate $P_{f}^{*}$ and $P_{{f_{i} }}^{*}$, respectively. $P_{f}^{*}$ is estimated by using $g_{K}^{(1)} ({\varvec{X}})$, $P_{{f_{i} }}^{*}$ is estimated by using $g_{K}^{(2)} ({\varvec{X}})$, and $S_{i}^{*}$ is estimated by taking $P_{f}^{*}$ and $P_{{f_{i} }}^{*}$ into Eq. (22). Then, the maximum value of $\varepsilon_{r} (S_{i}^{{}} )$ is estimated by taking $\varepsilon_{r}^{\max } (P_{f}^{*} )$, $\varepsilon_{r}^{\max } (P_{{f_{i} }}^{*} )$, $P_{f}^{*}$, $P_{{f_{i} }}^{*}$, and $S_{i}^{*}$ into Eq. (32). If $\varepsilon_{r}^{\max } (S_{i}^{*} ) \le \varepsilon_{r}^{thr} (S_{i}^{{}} )$, $\varepsilon_{r} (S_{i}^{*} ) \le \varepsilon_{r}^{thr} (S_{i}^{{}} )$ holds where $\varepsilon_{r}^{thr} (S_{i}^{{}} )$ is the predefined accuracy of the estimate $S_{i}^{*}$. Therefore, we can use $\varepsilon_{r}^{\max } (S_{i}^{*} ) \le \varepsilon_{r}^{thr} (S_{i}^{{}} )$ as a criterion to judge whether the $\varepsilon_{r}^{thr} (P_{f}^{{}} )$ and $\varepsilon_{r}^{thr} (P_{{f_{i} }}^{{}} )$ are set properly. If $\varepsilon_{r}^{\max } (S_{i}^{*} ) \le \varepsilon_{r}^{thr} (S_{i}^{{}} )$ are not satisfied, $\varepsilon_{r}^{thr} (P_{f}^{{}} )$ and $\varepsilon_{r}^{thr} (P_{{f_{i} }}^{{}} )$ can be decreased to reupdate the Kriging model $g_{K}^{(1)} ({\varvec{X}})$ and $g_{K}^{(2)} ({\varvec{X}})$ until the accuracy of the estimate $S_{i}^{*}$ is sufficient.

Based on the constructed adaptive Kriging-based parallel system reliability method for estimating the item $E(E^{2} (I_{F} |X_{i} ))$ and the derived estimate error of the global reliability sensitivity index $S_{i}$ related to the estimate error of the item $E(E^{2} (I_{F} |X_{i} ))$ and $E(I_{F} )$, the concrete steps of the proposed method are summarized in Sect. 3.4.

3.4 The concrete steps of the proposed method

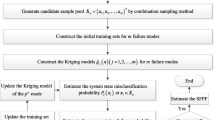
Based on Eq. (22), it can be seen that the key to estimating $S_{i}$ is to estimate the failure probabilities $P_{f}$ and $P_{{f_{i} }}$. The estimate of $P_{f}$ only depends on the information in vector ${\varvec{I}}_{A}$ in Eq. (10) and the estimate of $P_{{f_{i} }}$ not only relies on vector ${\varvec{I}}_{A}$ but also relies on vector ${\varvec{I}}_{{C^{(i)} }}$. Thus, we first adaptively construct the Kriging model $g_{K}^{(1)} ({\varvec{X}})$ to estimate $P_{f}$ with the learning stopping criterion $\varepsilon_{r}^{\max } (P_{f}^{*} ) \le \varepsilon_{r}^{thr} (P_{f}^{{}} )$ and then accordingly update the constructed $g_{K}^{(1)} ({\varvec{X}})$ to estimate $P_{{f_{i} }}$ with the learning stopping criterion $\varepsilon_{r}^{\max } (P_{{f_{i} }}^{*} ) \le \varepsilon_{r}^{thr} (P_{{f_{i} }}^{{}} )$. Besides, due to the Kriging model $g_{K}^{(1)} ({\varvec{X}})$ can accurately identify the limit states (failure or safety) of the samples in matrix ${\varvec{A}}$ and if the limit states of the samples in matrix ${\varvec{A}}$ are safe the corresponding limit states of the samples used to estimate the parallel system failure probability $E(E^{2} (I_{F} |X_{i} ))$ are safe, the samples in matrix ${\varvec{A}}$ with limit states judged by Kriging model $g_{K}^{(1)} ({\varvec{X}})$ are safe and the U learning function values are larger or equal to 2 and the corresponding samples in matrix ${\varvec{C}}_{i}$ can be simultaneously removed from the CSP used to adaptively construct the Kriging model $g_{K}^{(2)} ({\varvec{X}})$ to estimate $E(E^{2} (I_{F} |X_{i} ))$. Based on the above theory, the flowchart of the proposed method is shown in Fig. 1 and the concrete steps of the proposed method are summarized as follows.

Fig. 1

The flowchart of the proposed method

Step 1: Generate random samples. By $f_{{\varvec{X}}} ({\varvec{x}})$, two $N \times n$-size sample matrices of ${\varvec{X}}$ are generated, i.e.,

$${\varvec{A}}\,{ = }\,\left[ {\begin{array}{*{20}c} {x_{1}^{(1)} } & {x_{2}^{(1)} } & \cdots & {x_{n}^{(1)} } \\ {x_{1}^{(2)} } & {x_{2}^{(2)} } & \cdots & {x_{n}^{(2)} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{1}^{(N)} } & {x_{2}^{(N)} } & \cdots & {x_{n}^{(N)} } \\ \end{array} } \right]$$

(33)

$${\varvec{B}}\,{ = }\,\left[ {\begin{array}{*{20}c} {x_{1}^{{(N{ + }1)}} } & {x_{2}^{{(N{ + }1)}} } & \cdots & {x_{n}^{{(N{ + }1)}} } \\ {x_{1}^{{(N{ + }2)}} } & {x_{2}^{{(N{ + }2)}} } & \cdots & {x_{n}^{{(N{ + }2)}} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{1}^{(2N)} } & {x_{2}^{(2N)} } & \cdots & {x_{n}^{(2N)} } \\ \end{array} } \right]$$

(34)

Step 2: Construct the initial Kriging model $g_{K}^{(1)} ({\varvec{X}})$. Randomly select $N_{0} \ll N$ samples from matrix ${\varvec{A}}$ and estimate the corresponding limit state function values of the $N_{0}$ samples by the actual limit state function $g({\varvec{X}})$ to construct the initial training sample set ${\varvec{T}}{ = }\left\{ {[{\varvec{x}}_{1} ,g({\varvec{x}}_{1} )],[{\varvec{x}}_{2} ,g({\varvec{x}}_{2} )],...,[{\varvec{x}}_{{N_{0} }} ,g({\varvec{x}}_{{N_{0} }} )]} \right\}$. Then, the initial Kriging model $g_{K}^{(1)} ({\varvec{X}})$ can be constructed by using the MATLAB Dace toolbox based on the training sample set ${\varvec{T}}$, i.e., $g_{K}^{\left( 1 \right)} \left( {\varvec{X}} \right) \sim N\left( {\mu_{{g_{K}^{\left( 1 \right)} }} \left( {\varvec{X}} \right),\sigma_{{g_{K}^{\left( 1 \right)} }}^{2} \left( {\varvec{X}} \right)} \right)$.

Step 3: Update the Kriging model $g_{K}^{(1)} ({\varvec{X}})$. Judge whether the Kriging model $g_{K}^{(1)} ({\varvec{X}})$ has the sufficient accuracy to estimate the failure probability $P_{f}$ by using the maximum relative error of the failure probability estimated by the current Kriging model $g_{K}^{(1)} ({\varvec{X}})$. To estimate the maximum relative error of $P_{f}^{*}$, the samples in matrix ${\varvec{A}}$ are divided into two groups according to the U learning function values, i.e., the first group samples ${\varvec{x}}_{group1}^{(k)} (k = 1,...,N_{1} )$ with $U({\varvec{x}}_{group1}^{(k)} ) \ge 2$ and the second group samples ${\varvec{x}}_{group2}^{(k)} (k = 1,...,N_{2} )$ with $U({\varvec{x}}_{group2}^{(k)} ) < 2$ where $N_{1}$ is the number of samples in group one and $N_{2}$ is the number of samples in group two. Use the Kriging model $g_{K}^{(1)} ({\varvec{X}})$ to identify the failure samples in group one and group two, then denote the failure samples in group one recognized by $g_{K}^{(1)} ({\varvec{X}})$ as $N_{f1}$ and failure samples in group two recognized by $g_{K}^{(1)} ({\varvec{X}})$ as $N_{f2}$. The maximum relative error of the failure probability estimated by the current Kriging model $g_{K}^{(1)} ({\varvec{X}})$ is estimated as (Hu and Mahadevan 2016)

$$\varepsilon_{r}^{\max } (P_{f}^{*} ){ = }\mathop {\max }\limits_{{N_{f2}^{*} \in [0,N_{2} ]}} \left\{ {\frac{{|N_{f2} - N_{f2}^{*} |}}{{N_{f1} + N_{f2}^{*} }}} \right\}$$

(35)

If $\varepsilon_{r}^{\max } (P_{f}^{*} ) \le \varepsilon_{r}^{thr} (P_{f}^{{}} )$, the updating process of Kriging model $g_{K}^{(1)} ({\varvec{X}})$ can be stopped and turn to step 4 to estimate the failure probability $P_{f}^{{}}$ as well as continuously execute the rest of steps. Otherwise, continuously update the Kriging model $g_{K}^{(1)} ({\varvec{X}})$ by adding the following selected training samples into the training sample set ${\varvec{T}}$, i.e.,

$${\varvec{x}}^{(u)} = \arg \mathop {\min }\limits_{{{\varvec{x}} \in {\varvec{A}}}} U({\varvec{x}})$$

(36)

Then, the training sample set ${\varvec{T}}$ is updated, i.e., ${\varvec{T}}{ = }{\varvec{T}} \cup \left[ {{\varvec{x}}^{(u)} ,g({\varvec{x}}^{(u)} )} \right]$. By taking the current training sample set ${\varvec{T}}$ into the MATLAB Dace toolbox, the Kriging model $g_{K}^{(1)} ({\varvec{X}})$ is accordingly updated and then turn to the beginning of step 3.

Step 4: Estimate the failure probability $P_{f}^{{}}$ by using the finished updated Kriging model $g_{K}^{(1)} ({\varvec{X}})$, i.e.,

$$P_{f}^{*} { = }\frac{{N_{{\mu_{{g_{K}^{(1)} }} ({\varvec{x}}) < 0}} }}{N}$$

(37)

where $N_{{\mu_{{g_{K}^{(1)} }} ({\varvec{x}}) < 0}}$ denotes the number of failure samples in matrix ${\varvec{A}}$ judged by the current Kriging model $g_{K}^{(1)} ({\varvec{X}})$.

Step 5: Reduce CSP to prepare for constructing $g_{K}^{(2)} ({\varvec{X}})$. Pick out the samples in matrix ${\varvec{A}}$ with $\mu_{{g_{K}^{(1)} }} ({\varvec{x}}) \ge 0$ and $U({\varvec{x}}) \ge 2$, and put the corresponding row number of these satisfied samples into vector ${\varvec{I}}$. Then, a new sample matrix ${\varvec{A}}^{{ - {\varvec{I}}}}$ is constructed by removing the samples in matrix ${\varvec{A}}$ with row numbers belonging to the vector ${\varvec{I}}$.

Step 6: Obtain the initial Kriging model $g_{K}^{(2)} ({\varvec{X}})$ by using the finial updated Kriging model $g_{K}^{(1)} ({\varvec{X}})$, i.e., $g_{K}^{(2)} ({\varvec{X}}){ = }g_{K}^{(1)} ({\varvec{X}})$.

Step 7: Set $i = 1$.

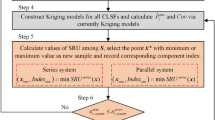
Step 8: Construct the CSP used in adaptively updating $g_{K}^{(2)} ({\varvec{X}})$ to estimate $P_{{f_{i} }}^{{}}$. Generate another sample matrix ${\varvec{C}}_{i}$ by the $i$ th column of matrix ${\varvec{A}}$ and all the columns except the $i$ th of matrix ${\varvec{B}}$, i.e.,

$${\varvec{C}}_{i} { = [}{\varvec{A}}_{i} {,}{\varvec{B}}_{ - i} {] = }\left[ {\begin{array}{*{20}c} {x_{1}^{(N + 1)} } & \cdots & {x_{i}^{(1)} } & \cdots & {x_{n}^{(N + 1)} } \\ {x_{1}^{(N + 2)} } & \cdots & {x_{i}^{(2)} } & \cdots & {x_{n}^{(N + 2)} } \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {x_{1}^{(2N)} } & \cdots & {x_{i}^{(N)} } & \cdots & {x_{n}^{(2N)} } \\ \end{array} } \right]$$

(38)

Then, the sample matrix ${\varvec{C}}_{i}^{{ - {\varvec{I}}}}$ is constructed by removing the samples in matrix ${\varvec{C}}_{i}$ with row numbers belonging to the vector ${\varvec{I}}$. Combining the matrices ${\varvec{A}}^{{ - {\varvec{I}}}}$ and ${\varvec{C}}_{i}^{{ - {\varvec{I}}}}$, matrix ${\varvec{D}}_{i}$ is obtained, i.e.,${\varvec{D}}_{i} { = [}{\varvec{A}}^{{ - {\varvec{I}}}} {,}{\varvec{C}}_{i}^{{ - {\varvec{I}}}} {]}$.

Step 9: Update the Kriging model $g_{K}^{(2)} ({\varvec{X}})$. Calculate the U learning function values of samples in matrices ${\varvec{A}}^{{ - {\varvec{I}}}}$ and ${\varvec{C}}_{i}^{{ - {\varvec{I}}}}$ by Eq. (18), i.e.,

$$\tilde{U}({\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ,{\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} ){ = }\left\{ \begin{gathered} \max \left[ {U({\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ),U({\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} )} \right] {\text{if}} \mu_{{g_{K} }} ({\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ) \ge 0 \cup \mu_{{g_{K} }} ({\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} ) \ge 0 \hfill \\ \min \left[ {U({\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ),U({\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} )} \right] {\text{if}} \mu_{{g_{K} }} ({\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ) < 0 \cap \mu_{{g_{K} }} ({\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} ) < 0 \hfill \\ \end{gathered} \right.$$

(39)

where ${\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)}$ is the $k$ th sample in matrix ${\varvec{A}}^{{ - {\varvec{I}}}}$ and ${\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)}$ is the $k$ th sample in matrix ${\varvec{C}}_{i}^{{ - {\varvec{I}}}}$.

Calculate the maximum relative error of the failure probability $P_{{f_{i} }}^{{}}$ estimated by the current Kriging model $g_{K}^{(2)} ({\varvec{X}})$. The samples in matrix ${\varvec{D}}_{i}$ are divided into two groups according to the $\tilde{U}$ learning function values, i.e., the first group samples $[{\varvec{x}}_{{group1\_{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ,{\varvec{x}}_{{group1\_{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} ](k = 1,...,\tilde{N}_{1} )$ with $\tilde{U}({\varvec{x}}_{{group1\_{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ,{\varvec{x}}_{{group1\_{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} ) \ge 2$ and the second group samples $[{\varvec{x}}_{{group2\_{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ,{\varvec{x}}_{{group2\_{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} ](k = 1,...,\tilde{N}_{2} )$ with $U({\varvec{x}}_{{group2\_{\varvec{A}}^{{ - {\varvec{I}}}} }}^{(k)} ,{\varvec{x}}_{{group2\_{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }}^{(k)} ) < 2$ where $\tilde{N}_{1}$ is the number of samples in group one and $\tilde{N}_{2}$ is the number of samples in group two. The maximum relative error of the failure probability $P_{{f_{i} }}^{{}}$ estimated by the current Kriging model $g_{K}^{(2)} ({\varvec{X}})$ is estimated as

$$\varepsilon_{r}^{\max } (P_{{f_{i} }}^{*} ){ = }\mathop {\max }\limits_{{N_{f2}^{*} \in [0,\tilde{N}_{2} ]}} \left\{ {\frac{{|\tilde{N}_{f2} - N_{f2}^{*} |}}{{\tilde{N}_{f1} + N_{f2}^{*} }}} \right\}$$

(40)

where $\tilde{N}_{f1}$ and $\tilde{N}_{f2}$ are the failure samples in group one and group two, respectively, recognized by $g_{K}^{(2)} ({\varvec{X}})$ based on Eq. (17).

If $\varepsilon_{r}^{\max } (P_{{f_{i} }}^{*} ) \le \varepsilon_{r}^{thr} (P_{{f_{i} }}^{{}} )$, the updating process of Kriging model $g_{K}^{(2)} ({\varvec{X}})$ can be stopped and turn to step 10 to estimate the failure probability $P_{{f_{i} }}^{{}}$ as well as continuously execute the rest of steps. Otherwise, continuously update the Kriging model $g_{K}^{(2)} ({\varvec{X}})$ by adding the following selected potential training sample into the training sample set ${\varvec{T}}$, i.e.,

$$\left[ {{\varvec{x}}^{{\left( {u_{1} } \right)}} ,{\varvec{x}}^{{\left( {u_{2} } \right)}} } \right] = \arg \mathop {\min }\limits_{{{\varvec{x}}_{{{\varvec{A}}^{ - I} }} \in {\varvec{A}}^{{ - {\varvec{I}}}} ,{\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }} \in {\varvec{C}}_{i}^{{ - {\varvec{I}}}} }} \tilde{U}\left( {{\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }} ,{\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }} } \right)$$

(41)

If $\mu_{{g_{K}^{(2)} }} ({\varvec{x}}^{{(u_{1} )}} ) > 0$ or $\mu_{{g_{K}^{(2)} }} ({\varvec{x}}^{{(u_{2} )}} ) > 0$, the added training sample is selected as

$${\varvec{x}}^{(u)} { = }\left\{ \begin{gathered} {\varvec{x}}^{{(u_{1} )}} {\text{if}} U({\varvec{x}}^{{(u_{1} )}} ) \ge U({\varvec{x}}^{{(u_{2} )}} ) \hfill \\ {\varvec{x}}^{{(u_{2} )}} {\text{if}} U({\varvec{x}}^{{(u_{1} )}} ) < U({\varvec{x}}^{{(u_{2} )}} ) \hfill \\ \end{gathered} \right.$$

(42)

If $\mu_{{g_{K}^{(2)} }} ({\varvec{x}}^{{(u_{1} )}} ) \le 0$ and $\mu_{{g_{K}^{(2)} }} ({\varvec{x}}^{{(u_{2} )}} ) \le 0$, the added training sample is selected as

$${\varvec{x}}^{(u)} { = }\left\{ \begin{gathered} {\varvec{x}}^{{(u_{1} )}} {\text{if}} U({\varvec{x}}^{{(u_{1} )}} ) < U({\varvec{x}}^{{(u_{2} )}} ) \hfill \\ {\varvec{x}}^{{(u_{2} )}} {\text{if}} U({\varvec{x}}^{{(u_{1} )}} ) \ge U({\varvec{x}}^{{(u_{2} )}} ) \hfill \\ \end{gathered} \right.$$

(43)

Then, the training sample set ${\varvec{T}}$ is updated, i.e., ${\varvec{T}}{ = }{\varvec{T}} \cup \left[ {{\varvec{x}}^{(u)} ,g({\varvec{x}}^{(u)} )} \right]$. By taking the current training sample set ${\varvec{T}}$ into the MATLAB Dace toolbox, the Kriging model $g_{K}^{(2)} ({\varvec{X}})$ is updated and then turn to the beginning of step 9.

Step 10: Estimate the failure probability $P_{{f_{i} }}^{{}}$ by using the current Kriging model $g_{K}^{(2)} ({\varvec{X}})$, i.e.,

$$P_{{f_{i} }}^{*} { = }\frac{{N_{{\mu_{{g_{K}^{(2)} }} ({\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }} ) < 0 \cap \mu_{{g_{K}^{(2)} }} ({\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }} ) < 0}} }}{N}$$

(44)

where $N_{{\mu_{{g_{K}^{(2)} }} ({\varvec{x}}_{{{\varvec{A}}^{{ - {\varvec{I}}}} }} ) < 0 \cap \mu_{{g_{K}^{(2)} }} ({\varvec{x}}_{{{\varvec{C}}_{i}^{{ - {\varvec{I}}}} }} ) < 0}}$ denotes the number of failure samples in matrices ${\varvec{A}}^{{ - {\varvec{I}}}}$ and ${\varvec{C}}_{i}^{{ - {\varvec{I}}}}$ simultaneously.

Step 11: Estimate the global reliability sensitivity index $S_{i}$ by the following equation, i.e.,

$$S_{i}^{*} { = }\frac{{P_{{f_{i} }}^{*} - P_{f}^{*2} }}{{P_{f}^{*} - P_{f}^{*2} }}$$

(45)

Step 12: Estimate the maximum relative error of the estimate $S_{i}^{*}$, i.e., $\varepsilon_{r}^{\max } (S_{i}^{*} )$ by taking the final $\varepsilon_{r}^{\max } (P_{f}^{*} )$, $P_{f}^{*}$, $P_{{f_{i} }}^{*}$, $\varepsilon_{r}^{\max } (P_{{f_{i} }}^{*} )$, and $S_{i}^{*}$ calculated by Eqs. (35), (37), (40), (44), and (45) into Eq. (32).

Step 13: Judge whether all inputs’ global reliability sensitivity indices are completely estimated. If $i = n$, turn to Step 14. Otherwise set $i = i + 1$ and turn to step 8.

Step 14: Judge whether the estimates satisfy the predefined accuracy. If not, decrease $\varepsilon_{r}^{thr} (P_{f}^{*} )$ and $\varepsilon_{r}^{thr} (P_{{f_{i} }}^{*} )$, and then turn to Step 3. Otherwise, end the analyses and output the global reliability sensitivity indices.

4 Case studies

In the following case studies, Sobol’s sequence (Sobol 1998) is chosen to generate the random samples for its high convergence rate. Sobol’s sequence is the best choice and performs optimal when the sample size $N$ equals to a power of 2, i.e., $N{ = }2^{m}$ ($m \in Z^{ + }$) where $m$ is a non-negative integer. Furthermore, all analyses are carried out in this paper by using the same computer with Inter (R) Core (TM) i7-10700CPU@2.90GHZ.

The sequential CSPs in Tables 3, 7, and 10 are the sample matrices used in the proposed method where the samples in matrix ${\varvec{A}}$ are used to estimate $P_{f}$ and the samples in matrix ${\varvec{E}}_{i} (i = 1,2,...,n)$ and ${\varvec{A}}$ are jointly used to estimate $P_{{f_{i} }} (i = 1,2,...,n)$. The sample states (failure or safety) in matrices ${\varvec{A}}$ and ${\varvec{E}}_{i} (i = 1,2,...,n)$ are identified by the proposed sequentially updated Kriging model-based method.

4.1 Case study I: a roof truss structure

A roof truss is shown in Fig. 2. The top boom and the compression bars are reinforced by concrete. The bottom boom and the tension bars are steel. The uniformly distributed load $q$ is applied on the roof truss, which can be transformed into the nodal load $P = ql/4$. The perpendicular deflection $\Delta_{C}$ of the node $C$ can be obtained by the mechanical analysis, which is the function of the input variables, i.e.,

$$\Delta_{C} = \frac{{ql^{2} }}{2}\left( {\frac{3.81}{{A_{c} E_{c} }} + \frac{1.13}{{A_{s} E_{s} }}} \right)$$

(46)

where $A_{c}$ and $A_{s}$ are the sectional area variables denoting the sectional area of each steel bar, $E_{c}$ and $E_{s}$ denote the elastic modulus, and $l$ denotes the length of each steel bar.

Fig. 2

The schematic diagram of roof truss structure

The limit state function is established as follows,

$$g({\varvec{x}}) = 0.025 - \Delta_{C} ,$$

(47)

where 0.025 m is the failure threshold. The six inputs $q$, $l$, $A_{s}$, $A_{c}$, $E_{s}$, and $E_{c}$ are regarded as random variables in this case study for some machining tolerances and environmental uncertainties. The six input random variables are assumed as the mutually independent normal variables, and the distribution parameters are shown in Table 1.

Table 1 The distribution parameter of the input variables of the roof truss structure

To guarantee the robustness of each estimate measured by the coefficient of variation (COV) of the estimate less than 0.1, $N$ in the $N \times 6$ matrices ${\varvec{A}}$ and ${\varvec{E}}_{i} (i = 1,2,...,n)$ is set as $2^{23}$ in this case study. Table 2 shows the results of global reliability sensitivity indices of the six input variables by using the single-loop coupled with direct AK-MCS method and the proposed single-loop coupled with ESC-based adaptive Kriging coupled with parallel system reliability (abbreviated as AK-PSR) method. Table 3 shows the corresponding number of calls to the limit state function and the CPU time of each method by setting the threshold of relative error of failure probabilities in each method as 0.01. The predefined accuracy of the estimated global reliability sensitivity indices is that the maximum error of each estimate is not larger than 10%. It can be seen from Tables 2 and 3 that the estimation accuracy of the proposed method is consistent with both the single-loop MCS method and the single-loop coupled with direct AK-MCS method, while the proposed method only uses 240 limit state function evaluations which are the smallest among the three methods and the corresponding results also demonstrate that the proposed method can reduce 87.25% CPU time compared to directly applying the AK-MCS to the single-loop estimation method.

Table 2 The results of global reliability sensitivity indices for the roof truss structure estimated by the single-loop MCS method, the proposed single-loop coupled with ESC-based AK-PSR method, and the single-loop coupled with direct AK-MCS method

Table 3 The number of training samples and CPU time in the proposed single-loop coupled with ESC-based AK-PSR method and the single-loop coupled with direct AK-MCS method in the roof truss structure

4.2 Case study II: an aero-engine turbine disk structure

An aero-engine turbine disk shown in Fig. 3 is a key component to aero-engine rotating structure which endures the centrifugal force and the thermal stress in the processes of starting and accelerating. Combined with the complex shape, the stress concentration position may appear in the pin hole and the bottom of tongue-and-groove during the process of work. After working for a period of time, cracks may appear in these positions. The load applied on the aero-engine turbine disk is.

$$F{ = }\frac{{C\omega^{2} }}{2\pi }{ + }2\rho \omega^{2} J$$

(48)

where $\rho$, $C$, $\omega$, and $J$ are mass density, coefficient, rotational speed, and cross-sectional moment of inertia, respectively. $\omega { = }2\pi n$ where $n$ is the rotational frequency.

Fig. 3

Diagram of crack of an aero-engine turbine disk

The angular velocity $\omega$ is changed under different flight conditions. In this case, two task profiles are considered, i.e., “start-maximum-start” and “cruise-maximum-cruise.” The corresponding load spectrum is shown in Table 4.

Table 4 The load spectrum of the aero-engine turbine disk within 900 h

Under the state of “start-maximum-start,” the fatigue life is estimated by the modified Manson-Coffin equation. The temperature considered in this case is $450^\circ {\text{C}}$, and the corresponding Manson–Coffin equation is

$$\frac{{\Delta \varepsilon_{t} }}{2} = 0.0063(1 - \frac{{\sigma_{m} }}{1127})(2N_{f} )^{ - 0.045} + 0.303(2N_{f} )^{ - 0.705}$$

(49)

According to the data in material manual (China Aeronautical Materials Handbook 2001), we use the dual-stage linear model to reflect the relationship between the stress and strain and the corresponding figure is shown in Fig. 4, i.e.,

$$\varepsilon = \left\{ {\begin{array}{*{20}c} {\frac{\sigma }{{1.6304 \times 10^{5} }}} & {\sigma < 750{\text{MPa}}} \\ {\left( {\sigma - 970} \right)/\left( {4.07407 \times 10^{4} } \right) + 0.01} & {\sigma \ge 750{\text{MPa}}} \\ \end{array} } \right.$$

(50)

Fig. 4

The relationship between the strain and stress of material GH4169 under $450\;^\circ {\text{C}}$

The inverse strain range-based limit state function is constructed as follows (Yun et al. 2019b),

$$G(\Delta \varepsilon_{t}^{(1)} ,\sigma^{(2)} ,\sigma^{(1)} ,\sigma_{m}^{(1)} ) = 0.0063(1 - \frac{{\sigma_{m}^{(1)} }}{1127})(\frac{{2N^{*} }}{{(1 + n)(\frac{1}{n})^{{\gamma^{{\sigma^{(2)} /\sigma^{(1)} }} }} }})^{ - 0.045} + 0.303(\frac{{2N^{*} }}{{(1 + n)(\frac{1}{n})^{{\gamma^{{\sigma^{(2)} /\sigma^{(1)} }} }} }})^{ - 0.705} - \frac{{\Delta \varepsilon_{t} }}{2}$$

(51)

where the total strain range in the main cycle, the stress range $\sigma^{(1)}$ in the main cycle, the stress range $\sigma^{(2)}$ in the secondary cycle, and the average stress of the main cycle are obtained by the following equations,

$$\Delta \varepsilon_{t}^{\left( 1 \right)} = \left\{ {\begin{array}{*{20}c} {\frac{{\sigma_{\omega = 13000} }}{{1.6304 \times 10^{5} }} - 0} & {\sigma_{\omega = 13000} < 750{\text{MPa}}} \\ {\left( {\sigma_{\omega = 13000} - 970} \right)/\left( {4.07407 \times 10^{4} } \right) + 0.01 - 0} & {\sigma_{\omega = 13000} \ge 750{\text{MPa}}} \\ \end{array} } \right.$$

(52)

$$\sigma^{(1)} { = }\sigma_{\omega = 13000} - 0 = {{\left( {\frac{{C\omega_{13000}^{2} }}{2\pi }{ + }2\rho \omega_{13000}^{2} J} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{C\omega_{13000}^{2} }}{2\pi }{ + }2\rho \omega_{13000}^{2} J} \right)} A}} \right. \kern-0pt} A}$$

(53)

$$\sigma^{(2)} { = }\sigma_{\omega = 13000} - \sigma_{\omega = 12000} = {{\left( {\frac{{C\omega_{13000}^{2} }}{2\pi }{ + }2\rho \omega_{13000}^{2} J - \frac{{C\omega_{12000}^{2} }}{2\pi }{ - }2\rho \omega_{12000}^{2} J} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{C\omega_{13000}^{2} }}{2\pi }{ + }2\rho \omega_{13000}^{2} J - \frac{{C\omega_{12000}^{2} }}{2\pi }{ + }2\rho \omega_{12000}^{2} J} \right)} A}} \right. \kern-0pt} A}$$

(54)

$$\sigma_{m} = \sigma_{\omega = 13000} /2 = \sigma_{LCF} /2$$

(55)

where the detailed distribution types and distribution parameters of the basic input variables $\rho$, $C$, $A$, $J$, $\omega_{{{13000}}}$, and $\omega_{{{12000}}}$ are listed in Table 5. The threshold of combined fatigue life $N^{*}$ is set as 10,000 cycles.

Table 5 The distribution types and distribution parameters of variables

To guarantee the robustness of the estimate measured by the COV of the estimate less than 0.1, $N$ in the $N \times 6$ matrices ${\varvec{A}}$ and ${\varvec{E}}_{i} (i = 1,2,...,n)$ is set as $2^{19}$ in this case study. Figure 5 shows the results of global reliability sensitivity indices obtained by the single-loop MCS, the single-loop coupled with direct AK-MCS method, and the proposed single-loop coupled with ESC-based AK-PSR method, from which it can be seen that the variables $C$ and $\omega_{12000}$ almost have no influence on failure probability and Table 6 only compares the results of the rest variables. By setting the threshold of relative error of failure probabilities in each method as 0.01, the accurate results in the single-loop coupled with direct AK-MCS method and the single-loop coupled with ESC-based AK-PSR method are obtained and the maximum relative errors of the estimates are less than 10%. Table 7 shows the number of training samples and the corresponding CPU time used in the single-loop coupled with direct AK-MCS method and the proposed single-loop coupled with ESC-based AK-PSR method, which demonstrates that compared to directly applying AK-MCS method the investigated method saves 35% training samples and 65.85% CPU time under the same accuracy and robustness. Results of this case study demonstrate that the proposed method can well suited to the case that the input variables have hybrid distribution types.

Fig. 5

The global reliability sensitivity indices of all input variables of the turbine blade structure

Table 6 The results of global reliability sensitivity indices for the turbine blade structure estimated by the single-loop MCS method, the proposed single-loop coupled with ESC-based AK-PSR method, and the single-loop coupled with direct AK-MCS method

Table 7 The number of training samples and CPU time in the proposed single-loop coupled with ESC-based AK-PSR method and the single-loop coupled with direct AK-MCS method in the aero-engine turbine disk

4.3 Case study III: a wing structure with composite shin

The NACA0012 airfoil wing (Saludheen et al. 2021; Feng et al. 2023) shown in Fig. 6 is analyzed in this example. The wing structure mainly consists of three components, i.e., stringers, ribs, and skin. The material of stringers and ribs is aluminum, and that of the skin is T-300 3 K/916. The isotropic material is employed to define the section of stringers and ribs of the wing structure, while the lamina material is used for the skin. The external load $F$ is applied and the finite element model constructed and analyzed by ABAQUS 6.14 is shown in Fig. 7. The maximum displacement $d_{\max }$ of the wing structure is deemed as the model response and the limit state function is defined in Eq. (56).

$$g({\varvec{X}}) = 95 - d_{\max } ({\varvec{X}}),$$

(56)

where the unit of displacement is mm, and the distribution parameters of input variables are shown in Table 8.

Fig. 6

The wing structure and its composition

Fig. 7

The FEM of the wing structure

Table 8 The distribution parameters of input variables for the wing structure

To guarantee the robustness of the estimate measured by the COV of the estimate less than 0.1, $N$ in the $N \times 9$ matrices ${\varvec{A}}$ and ${\varvec{E}}_{i} (i = 1,2,...,n)$ is set as $2^{17}$ in this case study. Figure 8 shows the global reliability sensitivity indices of the random input variables estimated by the single-loop coupled with direct AK-MCS method and the proposed single-loop coupled with ESC-based AK-PSR method, it can be seen from Fig. 8 that with the exception of $E_{11}$, $G_{12} /G_{13}$, and $F$, the global reliability sensitivity indices are all close to zero and thus the attention is fixed on the estimation accuracy of the variables $E_{11}$, $G_{12} /G_{13}$, and $F$. Table 9 gives the global reliability sensitivity results of the variables $E_{11}$, $G_{12} /G_{13}$, and $F$ by setting the threshold of relative error of failure probabilities in each method as 0.01, from which the accuracy and robustness are demonstrated. Furthermore, the number of calls to limit state function is used in each method and the corresponding CPU time are shown in Table 10, and results in Table 10 demonstrate that compared to directly introducing AK-MCS method into the single-loop method, the proposed single-loop coupled with ESC-based AK-PSR method can save 108 FEM analyses and 35.63% CPU time. The results of global reliability sensitivity indices demonstrate that the uncertainties of variables $E_{Al}$, $\nu_{Al}$, $E_{22} /E_{33}$, $\nu_{23}$, $G_{23}$, and $\theta$ can be neglected in reliability analysis to simplify uncertainty analysis model, and $F$ can be chosen firstly to decrease the failure probability by decreasing its uncertainty.

Fig. 8

The global reliability sensitivity indices of all input variables of the wing structure

Table 9 The results of global reliability sensitivity indices for the wing structure estimated by the single-loop MCS method, the proposed single-loop coupled with ESC-based AK-PSR method, and the single-loop coupled with direct AK-MCS method

Table 10 The number of training samples and CPU time in the proposed single-loop coupled with ESC-based AK-PSR method and the single-loop coupled with direct AK-MCS method in the wing structure

5 Conclusions

Global reliability sensitivity analysis is a key preprocessing for simplifying reliability-based design optimization model, and its efficient algorithm has drawn widely attention. In this paper, an innovative efficient algorithm is proposed by transforming the estimation of global reliability sensitivity index into the estimations of two failure probabilities based on the single-loop method, i.e., the unconditional failure probability and a two failure modes-based parallel system failure probability which can be estimated by the limit state function. To avoid large number of calls to the actual limit state function, adaptive Kriging (AK) model can be embedded. Then, the dual-stage sequential AK model of the limit state function is constructed to estimate the unconditional failure probability and the derived two failure modes-based parallel system failure probability accordingly, in which the learning function of system failure probability analysis can be used to accelerate the convergence of Kriging model. By error propagation analysis, the relationship among the estimation errors of the global reliability sensitivity index, the unconditional failure probability, and the two failure modes-based parallel system failure probability is constructed. Hence, the error stopping criterion can be employed in adaptively updating the Kriging model, and the estimate error of the global reliability sensitivity index can be controlled by adjusting the predefined limits of the estimate errors used in adaptive Kriging model-based processes for estimating the unconditional failure probability and the two failure modes-based parallel system failure probability. Through the learning function in system reliability analysis and the error stopping criterion, the Kriging model can be fast convergent while ensuring estimation accuracy. Results of a roof truss structure, an aero-engine turbine disk structure and a wing structure with composite shin demonstrate the superiority of the proposed method compared to directly inducting AK model into the single-loop method.

Due to the Kriging model can provide the prediction mean and prediction variance, efficient learning function can be constructed for adaptively updating Kriging model to accurately and efficiently recognize the states (failure or safety) of random samples which are used in reliability analysis, in this paper, the adaptive Kriging model is employed to substitute the actual limit state function to classify the used samples in the proposed algorithm for estimating the global reliability sensitivity indices. However, the derived two failure modes-based parallel failure probability-based global reliability sensitivity analysis formula has no limitation on the types of surrogate models. Other surrogate models which can efficiently and accurately classify the used samples also can be employed in the proposed algorithm to estimate the global reliability sensitivity indices.