1 Introduction

Nano-structured materials, like carbon nanotubes (CNTs), have found various conceivable applications in the ground-breaking fields of nano-engineering in consequence of the significant material properties at micro- and nano-scales [1,2,3,4]. When the structural dimensions are comparable with the internal length-scales of the medium of interest, the validity of the classical theory of elasticity ceases to hold. To adequately describe the scale-effect phenomena, generalized elasticity theories equipped with intrinsic length-scales are introduced in the literature. Implementation of the generalized elasticity theories can enhance the description of the physical behavior of media with nano-structural feature, and accordingly has stimulated a great deal of interest in the modeling and analysis of nano-structures [5,6,7,8,9,10,11,12,13,14,15,16].

The influences of long-range inter-atomic and inter-molecular forces on the mechanical response of structures, in the regimes smaller than the classical elasticity model, can be properly realized in the framework of the nonlocal elasticity theory [17]. The nonlocal stress state at a reference point in the continuum is expressed as a weighted mean value in terms of the local strain state measured at all points within the structural domain. The nonlocal effects are described through a constitutive law of integral-type wherein the stress field is the output of an integral convolution between an averaging nonlocal kernel and the strain field. To nanoscopic study of the field quantities on unbounded domains, the kernel function of the nonlocal integral constitutive law is taken to coincide with the Green function of a Helmholtz differential equation in the nonlocal stress. The consequent differential formulation of the nonlocal elasticity model leads to paradoxical results as applied to bounded domains of nano-mechanics interest [18]. Several advanced remedies are introduced in the literature to effectively eliminate the inherent drawbacks of the nonlocal differential problem, such as the strain-difference based nonlocal elasticity [19, 20], nonlocal surface elasticity [21, 22], and higher order nonlocal gradient elasticity theory [23,24,25]. Both the integral and differential approaches associated with the nonlocal elasticity model are widely exploited to study diverse structural problems at nano-scale, where representative recent researches are addressed in Refs. [26,27,28,29,30,31,32,33,34,35,36,37,38].

Elastodynamic analysis of nano-sized structures can be advantageously exploited to characterize the mechanical response of materials with nano-structural features. Thick bar model, accounting for the lateral deformation, shear stiffness, and lateral inertia effect, is perhaps the most inclusive structural theory to examine the axial deformation of CNTs [39,40,41,42,43,44]. The present study provides an important insight into the dynamics of thick nano-bars in the framework of the nonlocal integral elasticity and offers necessary amendments for the previous contributions on the matter. The paper proceeds as follows. The local thick bar theory is evoked in Sect. 2 providing a thorough understanding on the mathematical and mechanical model of stubby bars via a novel approach. The nonlocal elasticity theory in the original integral-type framework is utilized to introduce the constitutive law of the thick nano-bar in Sect. 3. The equivalent differential problem of the nonlocal thick bar is closed by prescribing the suitable form of variationally consistent non-standard boundary conditions naturally stemmed from the variational framework. The established nonlocal thick bar model is demonstrated to result in well-posed problems, exempt from all the drawbacks associated with the nonlocal differential approach. The axial wave dispersion and free vibrational behavior of thick nano-bars are analytically examined in Sect. 4 by making recourse to a viable solution procedure. Section 4 is furthermore enriched by illustrating, collecting, and commenting upon the numerical results associated with elastodynamic analysis of nonlocal thick bars. The detected wave dispersion relation and natural frequencies consistently illustrate a remarkable softening feature of the nonlocal elasticity theory and properly confirm the smaller-is-softer phenomenon. Concluding remarks are outlined in Sect. 5.

2 Local thick bar model

An elastic thick bar of length \(L = b - a\) with the circular cross-section \(\Upsilon\) is considered, as depicted in Fig. 1. The bar ends, located at \(x = a\) and \(x = b\), are restrained to prevent any rigid-body motion. The material density of the bar is denoted by \(\rho\) and the elastic and shear moduli are, respectively, designated by E and \(\mu = E/2\left( {1 + \nu } \right)\) along with \(\nu\) being the Poisson’s ratio. The bar is referred to the cylindrical coordinate system \(\left( {x,r,\theta } \right)\) with the abscissa x taken along the bar longitudinal axis and orthogonal to the cross-section plane identified by the axes r and \(\theta\). The stubby bar is assumed to be subject to a distributed axial force f. Consistent with the kinematic assumptions of the thick bar theory, the dimension of the cross-section is considered to be small enough in comparison with the bar length. The radial displacement component can be accordingly determined via vanishing of the radial stress on the cross-section. The circumferential displacement component is also overlooked in consequence of assuming the axially symmetric state [45, 46]. The displacement field u, therefore, writes as:

$${\mathbf{u}} = u\left( {x,t} \right){\mathbf{e}}_{{\mathbf{x}}} - \nu r\partial_{x} u\left( {x,t} \right){\mathbf{e}}_{{\mathbf{r}}} ,$$
(1)

where u designates the axial displacement component and assumed to have a uniform distribution over the bar cross-section. For non-vanishing values of the Poisson’s ratio, the effect of lateral deformation, neglected in the slender bar model, is properly comprised in the kinematics of the thick bar. The kinematically compatible strain field is given by:

$${{\varvec{\upvarepsilon}}} = \varepsilon \left( {x,t} \right)\left( {{\mathbf{e}}_{{\mathbf{x}}} \otimes {\mathbf{e}}_{{\mathbf{x}}} } \right) - \nu \varepsilon \left( {x,t} \right)\left( {{\mathbf{e}}_{{\mathbf{r}}} \otimes {\mathbf{e}}_{{\mathbf{r}}} + {\mathbf{e}}_{{{\varvec{\uptheta}}}} \otimes {\mathbf{e}}_{{{\varvec{\uptheta}}}} } \right) - \frac{1}{2}\nu r\partial_{x} \varepsilon \left( {x,t} \right)\left( {{\mathbf{e}}_{{\mathbf{r}}} \otimes {\mathbf{e}}_{{\mathbf{x}}} + {\mathbf{e}}_{{\mathbf{x}}} \otimes {\mathbf{e}}_{{\mathbf{r}}} } \right),$$
(2)

where the axial strain component is defined by \(\varepsilon = \partial_{x} u\) and the standard dyadic product of arbitrary first-order tensors \({\mathbf{p}},{\mathbf{q}}\) is indicated by \({\mathbf{p}} \otimes {\mathbf{q}}\).

Fig. 1
figure 1

Coordinate system and configuration of an elastic thick bar

Full size image

The corresponding stress field in the thick rod model is then expressed by:

$${{\varvec{\upsigma}}} = E\varepsilon \left( {x,t} \right)\left( {{\mathbf{e}}_{{\mathbf{x}}} \otimes {\mathbf{e}}_{{\mathbf{x}}} } \right) - \mu \nu r\partial_{x} \varepsilon \left( {x,t} \right)\left( {{\mathbf{e}}_{{\mathbf{r}}} \otimes {\mathbf{e}}_{{\mathbf{x}}} + {\mathbf{e}}_{{\mathbf{x}}} \otimes {\mathbf{e}}_{{\mathbf{r}}} } \right),$$
(3)

where the radial and circumferential components of the stress field vanish over the cross-section in view of the fundamental hypotheses of the thick bar model. The kinetic energy \({\mathbb{T}}\) and the total elastic strain energy \({\mathbb{U}}\), for the elastic thick bar model under consideration, can be written as follows:

$$\begin{aligned} {\mathbb{U}} &= \int_{a}^{b} {\left[ {\iint_{\Upsilon } {\left( {\frac{1}{2}{{\varvec{\upsigma}}}:{{\varvec{\upvarepsilon}}}} \right)}{\text{d}}A - fu} \right]} {\text{d}}x \\ &= \int_{a}^{b} {\left[ {\frac{1}{2}A_{{\text{E}}} \varepsilon \left( {x,t} \right)^{2} + \frac{1}{2}\nu^{2} J_{\mu } \left( {\partial_{x} \varepsilon \left( {x,t} \right)} \right)^{2} - f\left( x \right)u\left( {x,t} \right)} \right]} {\text{d}}x \hfill \\ {\mathbb{T}} &= \int_{a}^{b} {} \left[ {\iint_{\Upsilon } {\left( {\frac{1}{2}\rho \partial_{t} {\mathbf{u}} \cdot \partial_{t} {\mathbf{u}}} \right)}{\text{d}}A} \right]{\text{d}}x \\ &= \frac{1}{2}\int_{a}^{b} {\left[ {A_{\rho } \left( {\partial_{t} u\left( {x,t} \right)} \right)^{2} + \nu^{2} I_{\rho } \left( {\partial_{xt} u\left( {x,t} \right)} \right)^{2} } \right]} {\text{d}}x, \hfill \\ \end{aligned}$$
(4)

where the standard single and double tensor contraction of arbitrary first-order tensors \({\mathbf{p}}_{{\mathbf{i}}} ,{\mathbf{q}}_{{\mathbf{j}}}\) are, correspondingly, defined by \({\mathbf{p}}_{{\mathbf{i}}} \cdot {\mathbf{q}}_{{\mathbf{j}}}\) and \(\left( {{\mathbf{p}}_{{\mathbf{1}}} \otimes {\mathbf{p}}_{{\mathbf{2}}} } \right):\left( {{\mathbf{q}}_{{\mathbf{1}}} \otimes {\mathbf{q}}_{{\mathbf{2}}} } \right) = \left( {{\mathbf{p}}_{{\mathbf{1}}} \cdot {\mathbf{q}}_{{\mathbf{1}}} } \right)\left( {{\mathbf{p}}_{{\mathbf{2}}} \cdot {\mathbf{q}}_{{\mathbf{2}}} } \right)\). Furthermore, the cross-sectional mass \(A_{\rho }\), mass polar moment of inertia \(I_{\rho }\), elastic axial stiffness \(A_{E}\), and elastic shear stiffness \(J_{\mu }\) are introduced as:

$$\begin{gathered} A_{E} = \iint_{\Upsilon } E{\text{d}}A, \, J_{\mu } = \iint_{\Upsilon } {\mu \left( {{\mathbf{r}} \cdot {\mathbf{r}}} \right)}{\text{d}}A \hfill \\ A_{\rho } = \iint_{\Upsilon } \rho {\text{d}}A, \, I_{\rho } = \iint_{\Upsilon } {\rho \left( {{\mathbf{r}} \cdot {\mathbf{r}}} \right)}{\text{d}}A. \hfill \\ \end{gathered}$$
(5)

The first-order variation of the corresponding Lagrangian functional \({\mathbb{L}} = {\mathbb{T}} - {\mathbb{U}}\), while applying the kinematic compatibility condition \(\varepsilon = \partial_{x} u\) and integrating by parts, is written as:

$$\begin{aligned} \delta {\mathbb{L}} &= \int_{a}^{b} {\left[ { - A_{\rho } \partial_{tt} u\left( {x,t} \right) + \nu^{2} I_{\rho } \partial_{xxtt} u\left( {x,t} \right) + f\left( x \right) }\right.} \hfill \\ &+ {\left.{\partial_{x} \left( {A_{E} \varepsilon \left( {x,t} \right) - \nu^{2} J_{\mu } \partial_{xx} \varepsilon \left( {x,t} \right)} \right)} \right]} \delta u{\text{d}}x \hfill \\ &\left. { - \left( {A_{E} \varepsilon \left( {x,t} \right) - \nu^{2} J_{\mu } \partial_{xx} \varepsilon \left( {x,t} \right)} \right)\delta u} \right|_{x = a}^{x = b} - \left. {\left( {\nu^{2} J_{\mu } \partial_{x} \varepsilon \left( {x,t} \right)} \right)\delta \varepsilon } \right|_{x = a}^{x = b} . \hfill \\ \end{aligned}$$
(6)

The axial force field N, the corresponding stress field in the elastic thick bar model, and associated higher order boundary conditions can be accordingly introduced in view of the detected variation of the Lagrangian functional while assuming arbitrary variation of the axial strain:

$$\begin{gathered} N\left( {x,t} \right) = A_{E} \varepsilon \left( {x,t} \right) - \nu^{2} J_{\mu } \partial_{xx} \varepsilon \left( {x,t} \right) \hfill \\ \left. {\nu^{2} J_{\mu } \partial_{x} \varepsilon } \right|_{x = a} = \left. {\nu^{2} J_{\mu } \partial_{x} \varepsilon } \right|_{x = b} = 0. \hfill \\ \end{gathered}$$
(7)

The constitutive law of the elastic thick bar equipped with higher order boundary conditions is appropriately defined in terms of the axial strain field and of its gradients. Noticeably, the classical constitutive model of the elastic slender bar can be recovered via vanishing of either the Poisson’s ratio or the shear stiffness effect.

Implementing the Hamilton’s variational principle, the differential and boundary conditions of dynamic equilibrium associated with the local thick bar are determined:

$$\begin{gathered} \partial_{x} N\left( {x,t} \right) + f\left( x \right) = A_{\rho } \partial_{tt} u\left( {x,t} \right) - \nu^{2} I_{\rho } \partial_{xxtt} u\left( {x,t} \right) \hfill \\ \left. {N\delta u} \right|_{x = a} = \left. {N\delta u} \right|_{x = b} = 0. \hfill \\ \end{gathered}$$
(8)

It is noticeably inferred from the detected boundary-value problem that the effects of lateral deformation, shear stiffness, and lateral inertia are consistently comprised in the elastic thick bar model. A consistent variational framework is therefore established to introduce the constitutive law of elastic thick bars along with corresponding higher order boundary conditions, while the differential and boundary conditions of dynamic equilibrium are also appropriately recovered.

3 Nonlocal integral elasticity of thick bars

To properly introduce the long-range nonlocality to the thick bar model, the nonlocal constitutive law is considered to be governed by the elastic potential functional \({\mathbb{F}}\) as:

$$\begin{aligned}{\mathbb{F}} &= \frac{1}{2}\int_{a}^{b} {\left[ {A_{E} \varepsilon \left( {x,t} \right)\int_{a}^{b} {\alpha \left( {x - \overline{x},\ell } \right)} \varepsilon \left( {\overline{x},t} \right) {\text{d}}\overline{x} }\right.} \\ &{\left.{+ \nu^{2} J_{\mu } \partial_{x} \varepsilon \left( {x,t} \right)\int_{a}^{b} {\alpha \left( {x - \overline{x},\ell } \right)\partial_{{\overline{x}}} } \varepsilon \left( {\overline{x},t} \right){\text{d}}\overline{x}} \right]} {\text{d}}x,\end{aligned}$$
(9)

with \(x,\overline{x}\) being the points of the structural domain. The averaging nonlocal kernel \(\alpha\), enriched with the nonlocal characteristic length \(\ell\), is also assumed to fulfill the positivity, symmetry, normalization, and limit impulsivity properties [18]. The nonlocal characteristic length, reflecting the size-effects in the nonlocal elasticity theory, is commonly introduced as \(\ell = e_{0} a_{0}\) with \(e_{0}\) and \(a_{0}\), respectively, standing for the nonlocal material constant and the internal characteristic length [17]. The constitutive law of the nonlocal thick nano-bar is then provided by the variational condition of equality of the directional derivative of the elastic potential functional \({\mathbb{F}}\) along a virtual strain field \(\delta \varepsilon\) (having compact support in the domain) and the virtual work of the nonlocal axial force field [40, 47]. Applying a standard localization procedure, the nonlocal axial force field N associated with the axial strain field \(\varepsilon\) is determined as:

$$\begin{aligned}N\left( {x,t} \right) &= A_{E} \int_{a}^{b} {\alpha \left( {x - \overline{x},\ell } \right)} \varepsilon \left( {\overline{x},t} \right){\text{d}}\overline{x} \\ &- \nu^{2} J_{\mu } \partial_{x} \int_{a}^{b} {\alpha \left( {x - \overline{x},\ell } \right)\partial_{{\overline{x}}} } \varepsilon \left( {\overline{x},t} \right){\text{d}}\overline{x}. \end{aligned}$$
(10)

To establish the equivalent nonlocal differential formulation, a suitable choice for the nonlocal kernel, commonly adopted in the nonlocal elasticity theory, is the bi-exponential kernel function:

$$\alpha \left( {x,\ell } \right) = \frac{1}{2\ell }\exp \left( { - \frac{\left| x \right|}{\ell }} \right).$$
(11)

Following the mathematical approach originally introduced in Ref. [48], the nonlocal integral constitutive model Eq. (10), endowed with the bi-exponential kernel Eq. (11), can be demonstrated to be equivalent to the nonlocal differential law:

$$\frac{1}{{\ell^{2} }}N\left( {x,t} \right) - \partial_{xx} N\left( {x,t} \right) = \frac{1}{{\ell^{2} }}A_{E} \varepsilon \left( {x,t} \right) - \frac{{\nu^{2} }}{{\ell^{2} }}J_{\mu } \partial_{xx} \varepsilon \left( {x,t} \right),$$
(12)

subject to the variationally consistent non-standard boundary conditions of:

$$\begin{gathered} \partial_{x} N\left( {a,t} \right) - \frac{1}{\ell }N\left( {a,t} \right) = \frac{{\nu^{2} }}{{\ell^{2} }}J_{\mu } \partial_{x} \varepsilon \left( {a,t} \right) \hfill \\ \partial_{x} N\left( {b,t} \right) + \frac{1}{\ell }N\left( {b,t} \right) = \frac{{\nu^{2} }}{{\ell^{2} }}J_{\mu } \partial_{x} \varepsilon \left( {b,t} \right). \hfill \\ \end{gathered}$$
(13)

Notably, the local constitutive law of the axial force field and the associated higher order boundary conditions Eq. (7) can be recovered in view of the limit impulsivity property of the nonlocal kernel. The closure of the nonlocal differential problem on bounded domains and, accordingly, the equivalence to the nonlocal integral law Eq. (10) are also assured via prescribing the non-standard boundary conditions Eq. (13). In contrast to the nonlocal model of the elastic slender bar, the introduced non-standard boundary conditions are non-homogenous, and, thus, do not conflict with the boundary conditions enforced by the equilibrium. The axial force field, as the solution of the nonlocal differential constitutive Eq. (12), can effectively meet the equilibrium requirements. The established size-dependent thick bar model is accordingly free from the inherent drawbacks of the nonlocal differential theory, and leads to consistent and well-posed elastodynamic problems, as put in evidence by rigorously examining the wave desperation and free vibrations of elastic thick bars with kinematic constraints of nano-mechanics interest.

The nonlocal differential law associated with the slender bar model can be deduced from the constitutive relations Eqs. (12, 13) via disregarding the effects of lateral deformation and shear stiffness. For a nonlocal slender bar, the conflict between the equilibrium and the constitutive requirements is apparent as the homogenous non-standard boundary conditions are compared with the equilibrium conditions. The nonlocal axial force field of the slender bar model generated as the output of the nonlocal constitutive law, therefore, cannot meet the equilibrium conditions. The similar ill-posedness issue is addressed in preceding studies with reference to inflected beams [18]. The local-nonlocal mixture constitutive model has been adopted in previous contributions [49,50,51] to overcome the inherent drawbacks of the nonlocal differential formulation. Implementation of the local–nonlocal mixture constitutive model is capable of assuring the existence of a solution; nevertheless, results in ill-posed nonlocal problems for small volume fractions of the local elastic model. Notably, the conceived nonlocal integral elasticity formulation of the thick bar model is exempt from the aforementioned drawbacks and can advantageously realize the smaller-is-softer phenomenon.

4 Elastodynamic analysis of nonlocal thick bars

The distributed axial loading f is allowed to vanish to study the elastodynamic response of nonlocal thick bars. The expression of the axial force field N is determined via applying the differential condition of equilibrium Eq. (8)1 to the nonlocal constitutive law Eq. (12) as:

$$\begin{aligned}\frac{1}{{\ell^{2} }}N\left( {x,t} \right) &= A_{\rho } \partial_{xtt} u\left( {x,t} \right) - \nu^{2} I_{\rho } \partial_{xxxtt} u\left( {x,t} \right) \\ &+ \frac{1}{{\ell^{2} }}A_{E} \varepsilon \left( {x,t} \right) - \frac{{\nu^{2} }}{{\ell^{2} }}J_{\mu } \partial_{xx} \varepsilon \left( {x,t} \right).\end{aligned}$$
(14)

The differential condition governing the dynamics of the nonlocal thick bar, applying the kinematic compatibility condition \(\varepsilon = \partial_{x} u\), is thus written as:

$$\begin{aligned} & \frac{1}{{\ell^{2} }}A_{E} \partial_{xx} u\left( {x,t} \right) - \frac{{\nu^{2} }}{{\ell^{2} }}J_{\mu } \partial_{xxxx} u\left( {x,t} \right) - \frac{1}{{\ell^{2} }}A_{\rho } \partial_{tt} u\left( {x,t} \right) + \frac{{\nu^{2} }}{{\ell^{2} }}I_{\rho } \partial_{xxtt} u\left( {x,t} \right) \\ & \quad + A_{\rho } \partial_{xxtt} u\left( {x,t} \right) - \nu^{2} I_{\rho } \partial_{xxxxtt} u\left( {x,t} \right) = 0. \\ \end{aligned}$$
(15)

Prior to performing the elastodynamic analysis of the nonlocal thick bar theory, let us examine the dynamics differential condition of the slender bar model. Overlooking the effects of lateral deformation, shear stiffness, and lateral inertia in Eq. (15) leads to a partial differential equation of second-order in x. The requirement to meet two types of standard boundary conditions Eq. (8)2 and non-standard boundary conditions Eq. (13) makes the problem over-constrained with no solution in general. The nonlocal formulation of the slender bar model, thus, leads to an ill-posed boundary-value problem. Contrary to the slender bar model, the established nonlocal elasticity theory of thick bars results in well-posed elastodynamic problems and is able to successfully capture the softening size-effects in nano-structured materials.

4.1 Wave dispersion

Studying of the wave dispersion can be efficiently applied to realize the softening/stiffening behavior of structures at nano-scale. Employing the inverse theory approach [52, 53], the wave dispersion analysis can be furthermore utilized for calibration of the characteristic parameters of the generalized elasticity theory in comparison with the numerical or experiment data [54,55,56,57].

The wave dispersion phenomenon is formulated on unbounded domains where vanishing of the non-standard boundary conditions is tacitly fulfilled. The solution of the nonlocal thick bar with steady waves dispersing along the axial direction x takes the form of:

$$u\left( {x,t} \right) = \overline{u}\exp \left( {ik\left( {x - ct} \right)} \right),$$
(16)

where \(i = \sqrt { - 1}\), and k and c, respectively, denote the wave number and the phase velocity along with \(\overline{u}\) designating the wave amplitude. Imposing the wave dispersion solution Eq. (16) to the differential condition of dynamic equilibrium Eq. (15), the dispersion relation of axial waves consistent with the nonlocal integral theory of thick bars is determined:

$$c = \sqrt {\frac{{A_{E} + \nu^{2} k^{2} J_{\mu } }}{{\left( {A_{\rho } + \nu^{2} k^{2} I_{\rho } } \right)\left( {1 + k^{2} \ell^{2} } \right)}}} .$$
(17)

The phase velocity of axial wave dispersion for a uniform homogenous nano-bar can be simplified as:

$$c = \sqrt {\frac{E}{\rho }} \sqrt {\frac{{1 + \frac{{\nu^{2} \gamma^{2} }}{{2\left( {1 + \nu } \right)}}k^{2} }}{{\left( {1 + \nu^{2} k^{2} \gamma^{2} } \right)\left( {1 + k^{2} \ell^{2} } \right)}}} ,$$
(18)

where \(\gamma = \sqrt {I_{\rho } /A_{\rho } }\) denotes the radius of gyration of the thick bar. The derived wave dispersion relation for a uniform homogenous nano-bar as Eq. (18) is identical to the one detected in Ref. [44] disregarding the strain gradient effects.

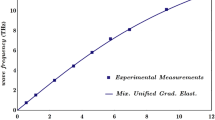
The established wave dispersion relation has been applied to simulate the X-ray scattering measurements of the monolayer graphene as reported in Refs. [58, 59] and recently addressed in other size-dependent elasticity approaches [49, 50]. The experimental data are graphically demonstrated in Fig. 2 and compared with the corresponding wave frequency \(kc\) associated with the nonlocal integral elasticity model. Applying the inverse theory approach [52, 53], the nonlocal characteristic length is identified as \(\ell = 5.9339 \times 10^{ - 2} {\text{nm}}\). The conceived nonlocal integral elasticity theory can accurately describe the axial wave dispersion in a wide range of wave numbers and effectively capture all the qualitative aspects of experimental measurements with excellent accuracy.

Fig. 2
figure 2

Wave dispersion frequency and comparison of X-ray scattering measurements with the nonlocal elasticity theory

Full size image

Nanoscopic effects of the nonlocal characteristic and geometrical parameter of the nonlocal thick bar on the phase dispersion response are graphically elucidated in Figs. 3 and 4. For consistency of illustrations, the non-dimensional form of the radius of gyration \(\overline{\gamma }\), nonlocal characteristic parameter \(\zeta\), wave number \(\overline{k}\), and phase velocity \(\overline{c}\) are introduced as:

$$\overline{\gamma } = \frac{1}{L}\sqrt {\frac{{I_{\rho } }}{{A_{\rho } }}} ,\quad \zeta = \frac{\ell }{L},\quad \, \overline{k} = kL,\quad \, \overline{c} = c\sqrt {\frac{{A_{\rho } }}{{A_{E} }}} .$$
(19)
Fig. 3
figure 3

Axial wave dispersion in a nonlocal thick nano-bar, effect of \(\zeta\) on \(\overline{c}\)

Full size image
Fig. 4
figure 4

Axial wave dispersion in a nonlocal thick nano-bar, effect of \(\overline{\gamma }\) on \(\overline{c}\)

Full size image

3-D variation of the phase velocity of the axial wave dispersion consistent with the nonlocal integral theory of elastic thick bars is exhibited in Figs. 3 and 4. Effect of the nonlocal characteristic parameter on the dispersion curve is studied for different values of the non-dimensional radius of gyration, wherein the logarithmic scaling of the non-dimensional wave number is utilized [60]. The nonlocal characteristic parameter \(\zeta\) is assumed to range in the interval \(\left] {0,0.5} \right]\), as the (logarithm of) non-dimensional wave number \(\overline{k}\) is ranging in the interval \(\left[ {10^{ - 1} ,10^{2} } \right]\). While the non-dimensional radius of gyration is prescribed as \(\overline{\gamma } = 0.3\) in Fig. 3, the phase dispersion response is demonstrated in Fig. 4 for two values of \(\overline{\gamma } = 0.1\) and \(\overline{\gamma } = 0.5\). In all illustrations, the value of the Poisson’s ratio \(\nu = 0.2\) is considered consistent with the elastic material properties of the \(\left( {10,10} \right)\) armchair CNT [56].

It is inferred from the illustrative results associated with the nonlocal integral approach that larger values of \(\zeta\) and \(\overline{\gamma }\) involve a smaller phase velocity, and accordingly, both the nonlocal characteristic parameter and the radius of gyration have the effect of decreasing the phase velocity of the axial wave dispersion. A softening response in terms of both the nonlocal characteristic parameter and the radius of gyration is, therefore, realized. The effect of nonlocality is, however, more pronounced in comparison with the gyration radius effect. This phenomenon is in contrast to the stiffening structural response associated with the gyration radius, as reported in the elastostatic study of nonlocal thick bars [40]. The phase dispersion response is not sensitive to the nano-structural material properties for large wavelengths, and consequently, the phase velocity remains unaffected for low wave numbers. The softening effect of the nonlocal parameter and the gyration radius is merely enhanced at higher wave numbers. As the nonlocal parameter tends to zero, the phase velocity of the axial wave dispersion consistent with the local thick bar model is inevitably recovered.

4.2 Free vibrational behavior

In view of the differential condition of dynamic equilibrium consistent with the nonlocal elastic thick bar, natural frequencies and mode shapes of axial vibrations can be determined by utilizing a standard procedure of separating spatial and time variables:

$$u\left( {x,t} \right) = \Psi \left( x \right)\exp \left( {i\omega t} \right),$$
(20)

with \(\Psi\) and \(\omega\) denoting the mode shape and the natural frequency of the axial vibration. The governing equation on the spatial coordinate function can be established, applying the separation of variables Eq. (20), as:

$$\begin{aligned}\nu^{2} &\left( { - \frac{{J_{\mu } }}{{\ell^{2} }} + I_{\rho } \omega^{2} } \right)\frac{{{\text{d}}^{4} }}{{{\text{d}}x^{4} }}\Psi \left( x \right) \\ &- \left( {\left( {A_{\rho } + \frac{{\nu^{2} }}{{\ell^{2} }}I_{\rho } } \right)\omega^{2} - \frac{1}{{\ell^{2} }}A_{E} } \right)\frac{{{\text{d}}^{2} }}{{{\text{d}}x^{2} }}\Psi \left( x \right) \\ &+ \frac{1}{{\ell^{2} }}A_{\rho } \omega^{2} \Psi \left( x \right) = 0.\end{aligned}$$
(21)

The analytical solution for the differential condition of spatial coordinate functions is written as:

$$\Psi \left( x \right) = U_{1} \sin \lambda_{1} x + U_{2} \cos \lambda_{1} x + U_{3} \sinh \lambda_{2} x + U_{4} \cosh \lambda_{2} x,$$
(22)

where unknown constants \(U_{1} , \ldots ,U_{4}\) have yet to be determined, along with:

$$\begin{aligned} \lambda_{1}^{2} &= \frac{{ - \left( {\left( {A_{\rho } + \frac{{\nu^{2} }}{{\ell^{2} }}I_{\rho } } \right)\omega^{2} - \frac{{A_{E} }}{{\ell^{2} }}} \right) }}{{2\nu^{2} \left( { - \frac{{J_{\mu } }}{{\ell^{2} }} + I_{\rho } \omega^{2} } \right)}}\\ & + \frac{{\sqrt {\left( {\left( {A_{\rho } + \frac{{\nu^{2} }}{{\ell^{2} }}I_{\rho } } \right)\omega^{2} - \frac{{A_{E} }}{{\ell^{2} }}} \right)^{2} - 4\frac{{A_{\rho } }}{{\ell^{2} }}\omega^{2} \nu^{2} \left( { - \frac{{J_{\mu } }}{{\ell^{2} }} + I_{\rho } \omega^{2} } \right)} }}{{2\nu^{2} \left( { - \frac{{J_{\mu } }}{{\ell^{2} }} + I_{\rho } \omega^{2} } \right)}}\\ \lambda_{2}^{2} &= \frac{{ + \left( {\left( {A_{\rho } + \frac{{\nu^{2} }}{{\ell^{2} }}I_{\rho } } \right)\omega^{2} - \frac{{A_{E} }}{{\ell^{2} }}} \right)}}{{2\nu^{2} \left( { - \frac{{J_{\mu } }}{{\ell^{2} }} + I_{\rho } \omega^{2} } \right)}}\\ &+ \frac{{\sqrt {\left( {\left( {A_{\rho } + \frac{{\nu^{2} }}{{\ell^{2} }}I_{\rho } } \right)\omega^{2} - \frac{{A_{E} }}{{\ell^{2} }}} \right)^{2} - 4\frac{{A_{\rho } }}{{\ell^{2} }}\omega^{2} \nu^{2} \left( { - \frac{{J_{\mu } }}{{\ell^{2} }} + I_{\rho } \omega^{2} } \right)} }}{{2\nu^{2} \left( { - \frac{{J_{\mu } }}{{\ell^{2} }} + I_{\rho } \omega^{2} } \right)}}. \hfill \\ \end{aligned}$$
(23)

In the framework of the nonlocal integral elasticity of thick bars, the spatial coordinate functions should fulfill the non-standard boundary conditions in addition to the standard boundary conditions, prescribed in the cantilever thick bar as:

$$\Psi \left( a \right) = N\left( b \right) = 0,$$
(24)

and in the fully fixed thick bar as:

$$\Psi \left( a \right) = \Psi \left( b \right) = 0.$$
(25)

A homogeneous fourth-order algebraic system in terms of the unknown constants \(U_{1} , \ldots ,U_{4}\) is formulated adopting the spatial base function Eq. (22) and enforcing two non-standard boundary conditions Eq. (13) together with two standard boundary conditions, Eqs. (24) or (25). The resulted system of algebraic equation should be singular to get a non-trivial solution for the natural frequency. A highly nonlinear characteristic equation is obtained, as a result of vanishing of the determinant of the coefficients of the homogeneous fourth-order system, which should be numerically solved.

Nano-scale effects of the nonlocality and the geometrical parameter (gyration radius) on the free vibrational behavior of the thick nano-bar are exhibited in Figs. 5 and 6. For the sake of generality, the non-dimensional fundamental frequency \(\overline{\omega }\) is defined by:

$$\overline{\omega }^{2} = \frac{{L^{2} A_{\rho } }}{{\pi^{2} A_{E} }}\omega^{2} .$$
(26)
Fig. 5
figure 5

Fundamental frequency of a nonlocal thick nano-bar with cantilever ends

Full size image
Fig. 6
figure 6

Fundamental frequency of a nonlocal thick nano-bar with fully-fixed ends

Full size image

Numerically detected fundamental frequencies are furthermore normalized applying the corresponding natural frequencies associated with the local slender bar model (LOC). 3-D variation of the normalized fundamental frequency of the cantilever and the fully fixed thick nano-bar associated with the nonlocal integral elasticity theory is, respectively, demonstrated in Figs. 5 and 6. While the nonlocal characteristic parameter \(\zeta\) is assumed to range in the same interval as the wave dispersion analysis, the non-dimensional radius of gyration is ranging in the interval \(\left[ {0.1,0.5} \right]\). The Poisson’s ratio is also set to \(\nu = 0.2\) consistent with the elastic material properties for the CNT of armchair \(\left( {10,10} \right)\).

It is noticeably deducible from the numerical illustrations that the fundamental frequency of the nonlocal thick bar decreases by increasing the nonlocal characteristic parameter, and accordingly, it exposes a softening response in terms of the nonlocal parameter \(\zeta\) for a given value of \(\overline{\gamma }\). The non-dimensional radius of gyration has also the effect of decreasing the fundamental frequency, i.e., a larger \(\overline{\gamma }\) involves a smaller fundamental frequency for a given value of \(\zeta\). Therefore, the fundamental frequency of the nonlocal thick bar reveals a softening behavior in terms of both the nonlocality and the gyration radius. The softening effects of the radius of gyration are, nevertheless, less conspicuous compared with the nonlocality. The size-dependent elastodynamic response of a fully-fixed thick nano-bar is found to be more affected by the nonlocality and the geometrical parameter. The fundamental frequency of the thick nano-bar detected in the framework of the nonlocal integral approach coincides with the fundamental frequency of the local thick bar, for vanishing of the nonlocal characteristic parameter. Tables 1 and 2 summarize the normalized fundamental frequencies of the nonlocal thick bar with cantilever and fully fixed ends for different values of the nonlocal characteristic parameter and the radius of gyration.

Table 1 Normalized fundamental frequencies of a cantilever nonlocal thick nano-bar
Full size table
Table 2 Normalized fundamental frequencies of a fully fixed nonlocal thick nano-bar
Full size table

5 Concluding remarks

There has been recently a great interest in the modeling and analysis of one-dimensional nano-structures due to their significant potential applications in advanced nano-systems. While the majority of investigations focus on the transverse vibrations of nano-beams, limited studies have been devoted to examine the elastodynamic response of thick nano-bars. An important insight into the dynamics of thick nano-bars in the framework of the nonlocal integral elasticity theory is provided in the present study. The elastic thick bar theory is evoked and the structural model of the thick bar is re-established in a consistent variational framework. The local constitute law of the axial force field and associated higher order boundary conditions are appropriately introduced and the differential and boundary conditions of dynamic equilibrium are restored. The proposed structural model suitably comprises the effects of lateral deformation, shear stiffness, and lateral inertia. The nonlocal constitutive law of the axial force field in the original integral-type framework is conceived. The integral convolutions of the constitutive law are substituted with the equivalent nonlocal differential model equipped with variationally consistent non-standard boundary conditions. The closure of the nonlocal constitutive problem on bounded domains is accordingly obtained. The introduced non-standard boundary conditions are demonstrated not to conflict with the equilibrium requirements as put in evidence by an accurate elastodynamic analysis of a nonlocal thick bar with kinematic constraints of nano-mechanics interest. As the boundary-value problem governing the nonlocal slender bar model is demonstrated to be ill-posed, the proposed size-dependent thick bar model is realized to be free from the inherent drawbacks of the nonlocal differential formulation and leads to consistent and well-posed elastodynamic problems. Previous contributions on the thick bar model are, therefore, amended to properly take into account the higher order and non-standard boundary conditions, correspondingly, associated with the local and nonlocal thick bar model.

The wave dispersion response and free vibrational behavior of the nonlocal thick bar are rigorously examined applying a viable analytical approach. Nanoscopic effects of the nonlocality and the geometrical parameter of the thick bar on the elastodynamic response are analytically detected, graphically illustrated, and thoroughly discussed. The conceived nonlocal integral elasticity theory is demonstrated to be capable of effectively capturing all the qualitative aspects of experimental measurements with excellent accuracy. The softening structural behavior in terms of the nonlocal characteristic length is properly confirmed. Contrary to the elastostatic analysis of nonlocal thick bars, a softening response is also realized for increasing the cross-sectional radius of gyration. A consistent variational framework to tackle the dynamics of nonlocal thick bars is introduced that can accurately recognize the smaller-is-softer phenomenon in the nonlocal mechanics.