1 Introduction

1.1 Literature survey

Carbon nanotubes (CNTs) demonstrated promising potential applications across a wide range of modern engineering fields and are widely employed as reinforcements in smart materials and nanocomposites. Due to the unique combination of physical characteristics, such as remarkable mechanical strength and high electrical and thermal conductivity, CNTs are well-suited for implications in nano-electro-mechanical-systems (NEMS) (Lamba et al. 2022; Iannacci and Tagliapietra 2022; Elishakoff et al. 2012). The main challenge that emerged in the literature is the accurate description of these significant physical features. The classical elasticity framework is well-known to be insufficient in the precise realization of the peculiar characteristics of structures at the ultra-small scale. Different schemes exist in the literature for nanoscopic analysis of the field quantities such as experimental measurements, atomistic-based numerical simulations, and augmented elasticity theories. Performing a robust experimental procedure at the nano-scale is too sophisticated and expensive. While advanced numerical techniques such as deep neural networks (Zhuang et al. 2021; Samaniego et al. 2020; Guo et al. 2019) and nonlocal operator method (Ren et al. 2020; Rabczuk et al. 2019) are presented in the recent literature, the implementation of numerical simulations leads to high-computational costs. The aforementioned deficiencies accompanied by the experimental approach and numerical simulations make them unsuitable strategies to realize the size-effects. To remedy such dilemmas, it is inevitable to restore to augmented elasticity frameworks as an efficient analytical approach to capture the size-dependent material behavior. A huge amount of recent literature is devoted to the study of the mechanical features of nanostructures; just to mention a few recent works refer to (Tornabene et al. 2023a, b; Abouelregal et al. 2023, 2021; Civalek and Avcar 2022; Faroughi et al. 2021; Uzun et al. 2021; Demir et al. 2018; Akgöz and Civalek 2017).

Nonlocality and gradient elasticity are perhaps well-recognized frameworks within the context of augmented elasticity theories. The nonlocality is founded on the concept of the weighted average value of the nanoscopic field in terms of the classical field variables at all points within the continuum domain (Eringen 2002). As a different line of thought, the gradient elasticity is established based on the main postulate of dependency of the constitutive model on the classical field variables along with the gradients of various order (Polizzotto 2014). These size-dependent elasticity theories have drawn much attention due to their inherent simplicity and are extensively adopted to capture the size-effects in a variety of structural problems at the ultra-small scale (Karamanli et al. 2023; Li and Zhang 2023; Xu et al. 2022; Civalek et al. 2022a; Akgöz and Civalek 2022; Akbas et al. 2021; Żur et al. 2020; Ouakad 2020; Uzun et al. 2020). Neither the nonlocal nor the gradient elasticity theory can cover the broad spectrum of material characteristics at the nano-scale. The desire to enhance the accuracy of the description of material response with nano-structural features turned the interest of recent investigations towards the unification of dissimilar size-dependent elasticity theories. The instances are the nonlocal strain gradient theory (Aifantis 2003, 2011), the nonlocal surface elasticity (Jiang et al. 2022; Li et al. 2020), and the mixture unified gradient theory (Faghidian et al. 2023a). Despite the fact that such unified size-dependent elasticity frameworks are nowadays in the spotlight, some serious challenges as how to enrich the associated boundary-value problem with non-standard boundary conditions, are posed (Faghidian et al. 2022a, 2023a).

The mixture unedified gradient theory is very recently introduced via integration of the size-effects associated with the stress gradient theory and the strain gradient elasticity with the classical elasticity theory. The most general intrinsic form of the mixture unified gradient theory is conceived within a consistent variational framework (Faghidian et al. 2023a). The constitute model is, accordingly, featured by the stress gradient and strain gradient characteristic length-scale parameters to, respectively, predict the softening and stiffening structural responses at the nano-scale. The effect of the classical elasticity theory is, furthermore, incorporated by the enrichment of the constitutive model with the mixture parameter. Efficacy of the mixture unified gradient theory is put into evidence in the nanoscopic analysis of the peculiar size-dependent behavior of field quantities in a variety of structural problems of interest in nano-mechanics (Faghidian and Elishakoff 2022, 2023; Faghidian et al. 2023b, 2022b; Faghidian and Tounsi 2022).

1.2 Novelty and outline

At the ultra-small scale, the van der Waals forces play a significant role in the interactions between nanostructures. The idealized boundary conditions of free and fixed ends are not precise enough to model the realistic state of CNTs embedded in elastic substrates. To appropriately present the structural model of CNTs, it is, therefore, necessary to take into consideration the van der Waals forces between CNTs and substrates. Indeed, CNTs that are bridged on the substrate at the end can be considered equivalent to a nano-sized structure with elastically restrained ends. A scrutiny of the literature reveals that much effort is given towards the analysis of nanostructures with idealized boundary conditions; nevertheless, some limited attempts exist to formulate the nano-sized structures with elastically restrained ends (Civalek et al. 2022b; Darban et al. 2022; Luciano et al. 2020; Jiang et al. 2017; Jiang and Wang 2017).

The present study provides an insight into the nanomechanics of bars with elastic boundary conditions, and hence, fruitfully bridges the gap between the structural model of nanobars with the idealized and elastic boundary conditions. The paper is organized as follows; the mixture unified gradient theory of elasticity is invoked in Sect. 2 to establish the size-dependent structural model of the nanobar with elastic boundary conditions. The differential condition of equilibrium is properly equipped with extra non-standard boundary conditions modified to take into account the elastically restrained end conditions of the nanobar. Section 3 is devoted to analytically addressing the mechanics of the mixture unified gradient bar and detecting a closed-form solution of the axial deformation of the nano-sized bar. Section 3 is, furthermore, enriched with numerical illustrations addressing the elastostatic size-dependent response of a mixture unified gradient bar with elastic boundary conditions. Both the idealized free and fixed end conditions are demonstrated to be retrieved as special cases of the elastically retrained boundary conditions under ad hoc assumptions. Concluding remarks are drawn in Sect. 4.

2 Mixture unified gradient elasticity for nanobar

2.1 Mechanics of classic bars with elastic ends

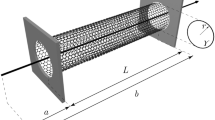
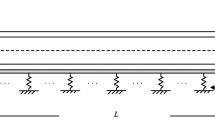
Let us preliminary recall the mechanics of an elastic bar subjected to an equilibrated axial load and terminal (quasi-static) forces as schematically demonstrated in Fig. 1. To this end, a straight bar of length \(L\) with a uniform cross-section \(\Omega\) is considered. The abscissa x is selected to coincide with the longitudinal axis of the bar while the position vector \({\mathbf{r}} = \left( {y,z} \right)\) represents an arbitrary cross-sectional point with respect to the bar centroid. The elasticity solution of the Saint–Venant problem can be properly utilized to determine the kinematics of beam-type structures (Faghidian 2016). Assuming the elastic bar to be adequately thin, the effects of the lateral deformation in the kinematics of the bar can be overlooked (Barretta et al. 2019). The displacement field, thus, \(\left( {u_{1} ,u_{2} ,u_{3} } \right)\) writes as

$$u_{1} = u\left( x \right), \, u_{2} = 0, \, u_{3} = 0$$
(1)

with u standing for the axial displacement of the bar. The nonvanishing component of the linear strain field consistent with the kinematically compatible deformation field is given by

$$\varepsilon \left( x \right) = \partial_{x} u\left( x \right)$$
(2)

with \(\varepsilon\) representing the axial strain field. The material is characterized by the elastic modulus E, and accordingly, it is practical to introduce the axial elastic stiffness \(A_{E}\) as

$$A_{E} = \int\limits_{\Omega } {E\left( {\mathbf{r}} \right)dA}$$
(3)

with \(A_{E}\) defined as the average of the elastic modulus over the cross-section. The mechanics of the elastic bar is attributed to an equilibrated force system \({\mathbf{P}}\) composed of the distributed axial loading p and the terminal concentrated forces \(\mathcal{P}_{0}\) and \(\mathcal{P}_{L}\) at the end cross-sections. The equilibrated stress in an elastic bar is an axial force field P. The principle of virtual work is employed to prescribe the equilibrium condition as

$$\begin{gathered} \left\langle {{\mathbf{P}},\delta {\mathbf{u}}} \right\rangle = \int_{0}^{L} {p\delta udx} + \left( {\mathcal{P}_{0} \delta u\left( 0 \right) + \mathcal{P}_{L} \delta u\left( L \right)} \right) \hfill \\ \, = \int_{0}^{L} {P\delta \varepsilon dx} \hfill \\ \end{gathered}$$
(4)

for any axial virtual displacement field \(\delta u\) fulfilling homogeneous kinematic boundary conditions. The scalar function \(\delta \varepsilon\) is the kinematically compatible axial strain associated with the axial virtual displacements \(\delta u\). The equilibrated axial force field P is also defined as the dual field of the axial strain field \(\varepsilon\). As a result of implementing a standard variational procedure, while performing integration by parts, the differential and classical boundary conditions associated with the introduced variational scheme are provided by

$$\begin{gathered} \partial_{x} P + p = 0 \hfill \\ \left. {\left( {P + \mathcal{P}_{0} } \right)\delta u} \right|_{x = 0} = \left. {\left( {P - \mathcal{P}_{L} } \right)\delta u} \right|_{x = L} = 0 \hfill \\ \end{gathered}$$
(5)
Fig. 1
figure 1

Configuration and coordinate system of a nanobar with the elastic boundary condition

Full size image

2.2 Mechanics of nanobars with elastic ends

Nanoscopic effects of the stress gradient theory and the strain gradient theory can be consistently integrated with the classical elasticity theory via the size-dependent elasticity framework of the mixture unified gradient theory. Motivated by the general intrinsic form of the stationary variational principle consistent with the mixture unified gradient theory and by virtue of the effects of the terminal forces, the associated variational functional \(\Pi\) is introduced as

$$\begin{gathered} \Pi = \int_{0}^{L} {\left( {P_{0} \left( x \right)\varepsilon \left( x \right) + P_{1} \left( x \right)\partial_{x} \varepsilon \left( x \right) - p\left( x \right)u\left( x \right) - \frac{1}{{2A_{E} }}\left( {P_{0} \left( x \right)} \right)^{2} - \frac{{\ell_{c}^{2} }}{{2A_{E} }}\left( {\partial_{x} P_{0} \left( x \right)} \right)^{2} } \right.} \hfill \\ \, \left. { - \frac{1}{{2A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)}}\left( {P_{1} \left( x \right)} \right)^{2} - \frac{{\ell_{c}^{2} }}{{2A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)}}\left( {\partial_{x} P_{1} \left( x \right)} \right)^{2} } \right)dx - \left( {\mathcal{P}_{0} \delta u\left( 0 \right) + \mathcal{P}_{L} \delta u\left( L \right)} \right) \hfill \\ \end{gathered}$$
(6)

where the axial resultant fields \(P_{0}\) and \(P_{1}\) are defined as the dual fields of the axial strain field \(\varepsilon\) and of its derivative along the bar longitudinal axis \(\partial_{x} \varepsilon\). To properly address the nanoscopic influence of the stress gradient theory and the strain gradient theory, the stress gradient characteristic length \(\ell_{c}\) and the strain gradient length-scale parameter \(\ell_{s}\) are, correspondingly, introduced. The contribution of the classical elasticity theory to the mixture unified gradient theory is furthermore integrated by the mixture parameter dented as \(0 \le \alpha \le 1\). Within the context of the stationary variational principles, it is well-established that all the kinematic and kinetic variables are selected as the primary variables subject to variation, and thus, all the field variables should be treated independent to each other. The virtual kinetic source field variables are, furthermore, assumed to have compact support on the nanobar domain. Performing the first variation of the introduced functional \(\Pi\), followed by integration by parts for the kinetic field variables, yields

$$\begin{gathered} \delta \Pi = \int_{0}^{L} {\left( {P_{0} \left( x \right)\delta \varepsilon \left( x \right) + P_{1} \left( x \right)\partial_{x} \delta \varepsilon \left( x \right) - p\left( x \right)\delta u\left( x \right)} \right.} \hfill \\ \, + \delta P_{0} \left( {\varepsilon \left( x \right) - \frac{1}{{A_{E} }}P_{0} \left( x \right) + \frac{{\ell_{c}^{2} }}{{A_{E} }}\partial_{xx} P_{0} \left( x \right)} \right) \hfill \\ \left. { \, + \delta P_{1} \left( {\partial_{x} \varepsilon \left( x \right) - \frac{1}{{A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)}}P_{1} \left( x \right) + \frac{{\ell_{c}^{2} }}{{A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)}}\partial_{xx} P_{1} \left( x \right)} \right)} \right)dx \hfill \\ \, - \left( {\mathcal{P}_{0} \delta u\left( 0 \right) + \mathcal{P}_{L} \delta u\left( L \right)} \right) \hfill \\ \, - \left. {\frac{{\ell_{c}^{2} }}{{A_{E} }}\partial_{x} P_{0} \left( x \right)\updelta P_{0} } \right|_{x = 0,L} - \left. {\frac{{\ell_{c}^{2} }}{{A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)}}\partial_{x} P_{1} \left( x \right)\updelta P_{1} } \right|_{x = 0,L} \hfill \\ \end{gathered}$$
(7)

By virtue of the heuristic assumption on the virtual kinetic source field variables to have compact support on the nanobar domain, i.e. \(\left. {\updelta P_{0} } \right|_{x = 0,L} = 0\) and \(\left. {\updelta P_{1} } \right|_{x = 0,L} = 0\), the boundary congruence conditions are released. Subsequent integration by parts for the kinematic field variables while applying the kinematic compatibility condition as \(\varepsilon = \partial_{x} u\), one may get

$$\begin{gathered} \delta \Pi = \int_{0}^{L} {\left( {\left( { - \partial_{x} P_{0} \left( x \right) + \partial_{xx} P_{1} \left( x \right) - p\left( x \right)} \right)\delta u\left( x \right)} \right.} \hfill \\ \, + \delta P_{0} \left( {\varepsilon \left( x \right) - \frac{1}{{A_{E} }}P_{0} \left( x \right) + \frac{{\ell_{c}^{2} }}{{A_{E} }}\partial_{xx} P_{0} \left( x \right)} \right) \hfill \\ \left. { \, + \delta P_{1} \left( {\partial_{x} \varepsilon \left( x \right) - \frac{1}{{A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)}}P_{1} \left( x \right) + \frac{{\ell_{c}^{2} }}{{A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)}}\partial_{xx} P_{1} \left( x \right)} \right)} \right)dx \hfill \\ \, + \left( {P_{0} \left( L \right) - \partial_{x} P_{1} \left( L \right) - \mathcal{P}_{L} } \right)\delta u\left( L \right) - \left( {P_{0} \left( 0 \right) - \partial_{x} P_{1} \left( 0 \right) + \mathcal{P}_{0} } \right)\delta u\left( 0 \right) \hfill \\ { + }P_{1} \left( L \right)\delta \varepsilon \left( L \right) - P_{1} \left( 0 \right)\delta \varepsilon \left( 0 \right) \hfill \\ \end{gathered}$$
(8)

The differential and boundary conditions of equilibrium associated with the elastic nanobar within the framework of the mixture stress gradient theory can be accordingly determined via prescribing the stationarity of the variational functional \(\delta \Pi = 0\) as

$$\begin{gathered} \partial_{x} P_{0} \left( x \right) - \partial_{xx} P_{1} \left( x \right) + p\left( x \right) = 0 \hfill \\ \left( {P_{0} \left( L \right) - \partial_{x} P_{1} \left( L \right) - \mathcal{P}_{L} } \right)\delta u\left( L \right) = 0 \hfill \\ \left( {P_{0} \left( 0 \right) - \partial_{x} P_{1} \left( 0 \right) + \mathcal{P}_{0} } \right)\delta u\left( 0 \right) = 0 \hfill \\ P_{1} \left( L \right) = P_{1} \left( 0 \right) = 0 \hfill \\ \end{gathered}$$
(9)

where the axial strain field on the nanobar ends is assumed to have arbitrarily variations. Taking into account the mathematical formula of the variation of the introduced functional, the physically motivated definition of the axial force field P, as a choice normally preferred within the framework of the augmented elasticity theory, is introduced as

$$P\left( x \right) = P_{0} \left( x \right) - \partial_{x} P_{1} \left( x \right)$$
(10)

The boundary-value problem of the equilibrium of the elastic nanobar consistent with the mixture unified gradient theory is, therefore, simplified as

$$\begin{gathered} \partial_{x} P\left( x \right) + p\left( x \right) = 0 \hfill \\ \left( {P\left( L \right) - \mathcal{P}_{L} } \right)\delta u\left( L \right) = 0 \hfill \\ \left( {P\left( 0 \right) + \mathcal{P}_{0} } \right)\delta u\left( 0 \right) = 0 \hfill \\ P_{1} \left( L \right) = P_{1} \left( 0 \right) = 0 \hfill \\ \end{gathered}$$
(11)

The physical characteristics of the elastic nanobar are well-known to depend on the structural boundary conditions. It is very often to simplify the realistic state of the boundary conditions as the idealized ones, i.e. perfectly free and fixed boundary conditions. The practical boundary conditions of a nano-sized bar are not so ideal, and hence, the prescription of the idealized boundary conditions is one of the main sources of error in the analysis of nanostructures. Indeed, CNTs are usually elastically restrained, and thus, the corresponding boundary conditions can be appropriately approximated by translational restraints at the boundaries. Deformable boundary conditions can be mathematically modeled with an axial spring for the nanoscopic structural analysis of elastic nanobars. Imposing the elastic boundary conditions, the ensued structural characteristics of nanobars are not restricted to the idealized boundary conditions and allow one to examine the more realistic response of nano-sized bars. Consistent with the assumed configuration as Fig. 1, the nanobar is bridged on the substrate at \(x = L\), and accordingly, the terminal concentrated forces \(\mathcal{P}_{0}\) and \(\mathcal{P}_{L}\) at the boundaries for the mixture unified gradient bar with elastic ends writes as

$$\mathcal{P}_{0} = 0, \, \mathcal{P}_{L} = - \kappa u\left( L \right)$$
(12)

with \(\kappa\) being the translational elastic spring constant. The corresponding differential and boundary conditions of equilibrium associated with the elastically restrained nanobar, therefore, is cast in the form

$$\begin{gathered} \partial_{x} P\left( x \right) + p\left( x \right) = 0 \hfill \\ \left( {P\left( L \right) + \kappa u\left( L \right)} \right)\delta u\left( L \right) = 0 \hfill \\ P\left( 0 \right)\delta u\left( 0 \right) = 0 \hfill \\ P_{1} \left( L \right) = P_{1} \left( 0 \right) = 0 \hfill \\ \end{gathered}$$
(13)

Notably, the elastic boundary conditions represent a set of general boundary conditions, i.e. the idealized boundary conditions of free and fixed ends can be retrieved by setting the elastic spring constant to be extremely small and extremely large, respectively.

The well-known privilege of implementing the stationary variational principle lies in the establishment of the constitutive model since all the governing equations are incorporated to a single variational functional \(\Pi\). Imposing the stationarity of the functional \(\delta \Pi = 0\), furthermore, results in the constitutive law of the axial resultant fields \(P_{0}\) and \(P_{1}\), cast as differential relations in the subsequent forms

$$\begin{gathered} A_{E} \varepsilon \left( x \right) = P_{0} \left( x \right) - \ell_{c}^{2} \partial_{xx} P_{0} \left( x \right) \hfill \\ A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)\partial_{x} \varepsilon \left( x \right) = P_{1} \left( x \right) - \ell_{c}^{2} \partial_{xx} P_{1} \left( x \right) \hfill \\ \end{gathered}$$
(14)

By virtue of the constitutive law of the axial resultant fields Eq. (14) accompanied by the definition of the axial force field Eq. (10), the sought constitutive model of the axial force field P is detected

$$A_{E} \varepsilon \left( x \right) - A_{E} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)\partial_{xx} \varepsilon \left( x \right) = P\left( x \right) - \ell_{c}^{2} \partial_{xx} P\left( x \right)$$
(15)

The introduced constitute model of the axial resultant fields is properly enriched with the stress gradient and strain gradient length-scale characteristic parameters to address the nanoscopic effects of the corresponding gradient elasticity theory. The effect of the classical elasticity theory is, furthermore, incorporated via consistently introducing the mixture parameter to the constitutive model. The mixture unified gradient theory, therefore, represents an apposite augmented elasticity framework to describe the peculiar size-dependent response of bar-type structures at the ultra-small scale.

The detected constitutive model of the axial force field within the context of the mixture unified gradient theory is of higher-order in comparison with the classical bar model, and therefore, to close the associated boundary-vale problem, suitable form of the extra non-standard boundary conditions should be prescribed. The consistent form of the extra non-standard boundary conditions within the framework of the presented size-dependent elasticity theory is introduced via vanishing of the axial resultant field \(P_{1}\) at both ends. Following some straightforward mathematics, the explicit constitutive relation of the axial resultant field \(P_{1}\) is detected as

$$P_{1} \left( x \right) = - \frac{{\ell_{c}^{2} \left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)}}{{\left( {1 - \alpha } \right)\ell_{c}^{2} - \ell_{s}^{2} }}p\left( x \right) - A_{E} \frac{{\left( {\alpha \ell_{c}^{2} + \ell_{s}^{2} } \right)^{2} }}{{\left( {1 - \alpha } \right)\ell_{c}^{2} - \ell_{s}^{2} }}\partial_{x} \varepsilon \left( x \right)$$
(16)

Various size-dependent elasticity frameworks can be recovered under ad hoc assumptions on the length-scale characteristic parameters. It is of notice that the retrieved augmented elasticity theories of the gradient-type are strictly related to the same differential and boundary conditions of equilibrium, while differ from each other in terms of the corresponding constitutive model. The constitutive model of the axial resultant fields consistent with the unified gradient theory of elasticity (Żur and Faghidian 2021) can be retrieved as the mixture parameter vanishes in Eqs. (14) and (15)

$$\begin{gathered} A_{E} \varepsilon \left( x \right) = P_{0} \left( x \right) - \ell_{c}^{2} \partial_{xx} P_{0} \left( x \right) \hfill \\ A_{E} \ell_{s}^{2} \partial_{x} \varepsilon \left( x \right) = P_{1} \left( x \right) - \ell_{c}^{2} \partial_{xx} P_{1} \left( x \right) \hfill \\ A_{E} \varepsilon \left( x \right) - A_{E} \ell_{s}^{2} \partial_{xx} \varepsilon \left( x \right) = P\left( x \right) - \ell_{c}^{2} \partial_{xx} P\left( x \right) \hfill \\ \end{gathered}$$
(17)

The constitutive model associated with the stress gradient theory (Polizzotto 2014) is recovered as the strain gradient length-scale parameter tends to zero in Eq. (17)

$$A_{E} \varepsilon \left( x \right) = P\left( x \right) - \ell_{c}^{2} \partial_{xx} P\left( x \right)$$
(18)

where the differential condition of equilibrium holds in the absence of the axial resultant field \(P_{1}\). Likewise, when the stress gradient characteristic length approaches zero in Eq. (17), one may obtain the constitutive relations corresponding to the strain gradient theory (Polizzotto 2015) as

$$\begin{gathered} A_{E} \varepsilon \left( x \right) = P_{0} \left( x \right) \hfill \\ A_{E} \ell_{s}^{2} \partial_{x} \varepsilon \left( x \right) = P_{1} \left( x \right) \hfill \\ A_{E} \varepsilon \left( x \right) - A_{E} \ell_{s}^{2} \partial_{xx} \varepsilon \left( x \right) = P\left( x \right) \hfill \\ \end{gathered}$$
(19)

The constitutive model consistent with the mixture stress gradient theory (Faghidian et al. 2022c) can be restored by vanishing the strain gradient length-scale parameter in Eqs. (14) and (15) as

$$\begin{gathered} A_{E} \varepsilon \left( x \right) = P_{0} \left( x \right) - \ell_{c}^{2} \partial_{xx} P_{0} \left( x \right) \hfill \\ A_{E} \left( {\alpha \ell_{c}^{2} } \right)\partial_{x} \varepsilon \left( x \right) = P_{1} \left( x \right) - \ell_{c}^{2} \partial_{xx} P_{1} \left( x \right) \hfill \\ A_{E} \varepsilon \left( x \right) - A_{E} \left( {\alpha \ell_{c}^{2} } \right)\partial_{xx} \varepsilon \left( x \right) = P\left( x \right) - \ell_{c}^{2} \partial_{xx} P\left( x \right) \hfill \\ \end{gathered}$$
(20)

The well-known constitute model of the classical elasticity theory \(A_{E} \varepsilon = P\) can be retrieved as either the stress gradient and the strain gradient characteristic lengths tend to zero or as the mixture parameter approaches to unity in the absence of the strain gradient length-scale parameter.

The conceived size-dependent elasticity framework of the mixture unified gradient theory is highly capable of accurate realization of the physical characteristics of nano-sized bars with elastic boundary conditions as put into evidence in Sect. 3.

3 Static characteristics of nanobars with elastic ends

3.1 Analytical solution of elastostatic response

To rigorously examine the static characteristics of a nano-sized bar with elastic boundary conditions, the axial deformation of a mixture unified gradient elastic bar is analytically addressed. The common choice usually preferred in the literature is to describe the differential conditions of equilibrium in terms of kinematics field variables, and subsequently, to solve the resulting higher-order differential equations. As a different school of thought, a viable methodology, founded on successive integration of differential equations of lower-order (Faghidian et al. 2022a, 2023a), is invoked here to address the analytical solution of the kinematics field variables.

The equilibrated axial force P is first determined by integrating the differential condition of equilibrium Eq. (13)1 up to an integration constant \({\mathbb{k} }_{1}\)

$$P\left( x \right) = - \int_{0}^{x} {p\left( \varsigma \right)d\varsigma } + {\mathbb{k} }_{1}$$
(21)

The differential equation of the constitutive law Eq. (15) is, subsequently, solved yielding the expression of the axial strain field \(\varepsilon\) in terms of integration constants \({\mathbb{k} }_{2} ,\,{\mathbb{k} }_{3}\)

$$\begin{aligned} \varepsilon \left( x \right) = & \,{\mathbb{k} }_{2} \exp \left( {\frac{x}{{\sqrt {\alpha \ell_{c}^{2} + \ell_{s}^{2} } }}} \right) + {\mathbb{k} }_{3} \exp \left( { - \frac{x}{{\sqrt {\alpha \ell_{c}^{2} + \ell_{s}^{2} } }}} \right) \\ - & \frac{1}{{2A_{E} \sqrt {\alpha \ell_{c}^{2} + \ell_{s}^{2} } }}\int_{0}^{x} {\exp \left( {\frac{x - \varsigma }{{\sqrt {\alpha \ell_{c}^{2} + \ell_{s}^{2} } }}} \right)\left( {P\left( \varsigma \right) - \ell_{c}^{2} \partial_{\varsigma \varsigma } P\left( \varsigma \right)} \right)d\varsigma } \\ + & \frac{1}{{2A_{E} \sqrt {\alpha \ell_{c}^{2} + \ell_{s}^{2} } }}\int_{0}^{x} {\exp \left( {\frac{\varsigma - x}{{\sqrt {\alpha \ell_{c}^{2} + \ell_{s}^{2} } }}} \right)\left( {P\left( \varsigma \right) - \ell_{c}^{2} \partial_{\varsigma \varsigma } P\left( \varsigma \right)} \right)d\varsigma } \\ \end{aligned}$$
(22)

Lastly, the axial deformation field of the mixture unified gradient elastic bar u is detected by integration of the differential condition of kinematic compatibility Eq. (2) up to an integration constant \({\mathbb{k} }_{4}\)

$$u\left( x \right) = \int_{0}^{x} {\varepsilon \left( \varsigma \right)d\varsigma } + {\mathbb{k} }_{4}$$
(23)

The axial deformation function u of the nanobar consistent with the mixture unified gradient theory should meet the classical boundary conditions Eq. (13)2,3 along with the extra no-standard boundary conditions Eq. (13)4. Prescribing the complete set of boundary conditions then closes the boundary-value problem associated with the equilibrium of nanobar, and accordingly, the unknown integration constants \(\left\{ {{\mathbb{k} }_{1} ,\,{\mathbb{k} }_{2} ,\,{\mathbb{k} }_{3} ,\,{\mathbb{k} }_{4} } \right\}\) will be determined. The exact analytical solution of the elastostatic deformation of the mixture unified gradient elastic bar is detected via successive integration of differential equations of lower-order. Addressing the analytical solution of the nanoscopic field variables is of practical importance in the calibration of the material length-scale parameters associated with the augmented elasticity theories utilizing the inverse theory approach (Faghidian 2017a, b) as evinced in (Faghidian et al. 2022a, 2023a). The important issue of the uncertainties within the framework of the inverse analysis can be addressed by applying the probabilistic sensitivity analysis (Zhuang et al. 2021; Samaniego et al. 2020; Guo et al. 2019) or the regularization theory (Faghidian et al. 2012).

To study the size-dependent static characteristics of nanobar within the context of the mixture unified gradient theory, the nano-sized elastic bar is assumed to be subjected to a uniformly distributed axial load of intensity \(\overline{p}\). For the sake of consistency, the non-dimensional form of the axial abscissa \(\overline{x}\), the stress gradient characteristic parameter \(\zeta_{c}\), the strain gradient characteristic parameter \(\zeta_{\ell }\), the stiffness of the elastic spring \(\overline{\kappa }\), and the axial displacement function \(\overline{u}\) are defined as

$$\overline{x} = \frac{x}{L}, \, \zeta_{c} = \frac{{\ell_{c} }}{L}, \, \zeta_{\ell } = \frac{{\ell_{s} }}{L}, \, \overline{\kappa } = \frac{\kappa L}{{A_{E} }}, \, \overline{u} = \frac{{A_{E} }}{{\overline{p}L^{2} }}u$$
(24)

For a nano-sized bar with elastic boundary conditions consistent with the size-dependent elasticity framework of the mixture unified gradient theory, the classical boundary conditions consist of vanishing the axial displacement function at the fixed end and substitution of the terminal concentrated force with the reaction force of the elastic spring at the other end of the nanobar. Furthermore, the extra non-standard boundary conditions involving the vanishing of the axial resultant field \(P_{1}\) at both the bar ends should be fulfilled. Applying the solution approach introduced above, the non-dimensional axial deformation function of a nano-bar with elastic boundary conditions, subjected to a uniformly distributed axial load, within the size-dependent elasticity framework of the mixture unified gradient theory can be expressed as

$$\begin{gathered} \overline{u}\left( {\overline{\kappa },\overline{x}} \right) = \overline{u}_{0} \left( {\overline{\kappa },\overline{x}} \right) \hfill \\ \, - 2\left( {\left( { - 1 + \alpha } \right)\zeta_{c}^{2} + \zeta_{\ell }^{2} } \right){\text{sech}} \left( {\frac{1}{{2\sqrt {\alpha \zeta_{c}^{2} + \zeta_{\ell }^{2} } }}} \right)\sinh \left( {\frac{{1 - \overline{x}}}{{2\sqrt {\alpha \zeta_{c}^{2} + \zeta_{\ell }^{2} } }}} \right)\sinh \left( {\frac{{\overline{x}}}{{2\sqrt {\alpha \zeta_{c}^{2} + \zeta_{\ell }^{2} } }}} \right) \hfill \\ \end{gathered}$$
(25)

where the classical non-dimensional axial deformation field of a bar with elastic boundary conditions \(\overline{u}_{0}\) is well-established to write as

$$\overline{u}_{0} \left( {\overline{\kappa },\overline{x}} \right) = \frac{{\overline{x}\left( {2 + \overline{\kappa } - \left( {1 + \overline{\kappa }} \right)\overline{x}} \right)}}{{2\left( {1 + \overline{\kappa }} \right)}}$$
(26)

A close examination of the detected axial deformation field reveals important circumstances regarding its asymptotic behavior. For large enough values of the non-dimensional stiffness of the elastic spring \(\overline{\kappa } \to \infty\), the axial deformation function of a mixture unified gradient bar is simplified as

$$\begin{gathered} \overline{u}\left( {\infty ,\overline{x}} \right) = \frac{1}{2}\left( { - 2\left( { - 1 + \alpha } \right)\zeta_{c}^{2} - 2\zeta_{\ell }^{2} + \overline{x} - \overline{x}^{2} } \right) \hfill \\ \, + \left( {\left( { - 1 + \alpha } \right)\zeta_{c}^{2} + \zeta_{\ell }^{2} } \right)\cosh \left( {\frac{{1 - 2\overline{x}}}{{2\sqrt {\alpha \zeta_{c}^{2} + \zeta_{\ell }^{2} } }}} \right){\text{sech}} \left( {\frac{1}{{2\sqrt {\alpha \zeta_{c}^{2} + \zeta_{\ell }^{2} } }}} \right) \hfill \\ \end{gathered}$$
(27)

which literally retrieves the axial deformation function of a nano-sized bar with fixed–fixed ends consistent with the mixture unified gradient theory (Faghidian et al. 2022b).

Likewise, the axial deformation function of a mixture unified gradient bar is simplified for infinitesimal values of the non-dimensional stiffness of the elastic spring \(\overline{\kappa } \to 0\) as

$$\begin{gathered} \overline{u}\left( {0,\overline{x}} \right) = - \left( { - 1 + \alpha } \right)\zeta_{c}^{2} - \zeta_{\ell }^{2} + \overline{x} - \frac{1}{2}\overline{x}^{2} \hfill \\ \, + \left( {\left( { - 1 + \alpha } \right)\zeta_{c}^{2} + \zeta_{\ell }^{2} } \right)\cosh \left( {\frac{{1 - 2\overline{x}}}{{2\sqrt {\alpha \zeta_{c}^{2} + \zeta_{\ell }^{2} } }}} \right){\text{sech}} \left( {\frac{1}{{2\sqrt {\alpha \zeta_{c}^{2} + \zeta_{\ell }^{2} } }}} \right) \hfill \\ \end{gathered}$$
(28)

which literally recovers the axial deformation function of a mixture unified gradient elastic bar with fixed-free ends (Faghidian et al. 2022b).

Asymptotic size-dependent response of a mixture unified gradient bar with elastically restrained ends, accordingly, retrieves the axial deformation field of the nanobar with fixed-free and fixed–fixed ends as the elastic spring constant approaches zero and infinity, respectively. The introduced elastic boundary conditions, therefore, represents a complete set of general boundary conditions.

For the sake of consistency of numerical illustration, the axial deformation function of the mixture unified gradient bar with elastic boundary conditions is determined at the nanobar mid-span and adopted as

$$\overline{u}\left( {\overline{\kappa },\frac{1}{2}} \right) = - \frac{1}{8} + \frac{{2 + \overline{\kappa }}}{{4\left( {1 + \overline{\kappa }} \right)}} - \left( { - 1 + \alpha } \right)\zeta_{c}^{2} - \zeta_{\ell }^{2} + \left( {\left( { - 1 + \alpha } \right)\zeta_{c}^{2} + \zeta_{\ell }^{2} } \right){\text{sech}} \left( {\frac{1}{{2\sqrt {\alpha \zeta_{c}^{2} + \zeta_{\ell }^{2} } }}} \right)$$
(29)

The derived analytical solution of the axial deformation function of nano-sized bar can efficaciously realize the size-effect at the ultra-small scale and accurately describe the peculiar size-dependent static characteristics of nanobars with elastic ends.

3.2 Numerical illustrations of elastostatic response

Nanoscopic effects of the characteristic length-scale parameters on the structural behavior of nano-sized bars with elastic boundary conditions are illustrated in Figs. 2, 3, 4 in comparison with the counterpart results associated with the nanobars with idealized boundary conditions of fixed–fixed and fixed-free ends. The size-effects of the stress gradient characteristic parameter and the non-dimensional stiffness of the elastic spring on the mid-span axial deformation of the nano-sized bar are demonstrated in Fig. 2. While the stress gradient characteristic parameter is assumed to range in the interval \(\left[ {0,1/2} \right]\) in Fig. 2, the strain gradient characteristic parameter and the mixture parameter are prescribed as \(\zeta_{\ell } = 1/3,\alpha = 1/4\). The 3D variation of the axial deformation of the nanobar at the mid-span is demonstrated in Fig. 3 in terms of the strain gradient characteristic parameter and the stiffness of the elastic spring. The ranging interval of the strain gradient characteristic parameter is considered as \(\left[ {0,1/2} \right]\) in Fig. 3 for given values of the stress gradient characteristic parameter and the mixture parameter as \(\zeta_{c} = 1/3,\alpha = 1/4\). The spatial variation of axial deformation of the nano-sized bar versus the non-dimensional abscissa \(\overline{x}\) is, moreover, studied in Fig. 4 in terms of the non-dimensional stiffness of the elastic spring. While the stress gradient and the strain gradient characteristic parameters are given as \(\zeta_{c} = 1/2,\zeta_{\ell } = 1/3\) in Fig. 4, three values of the mixture parameter as \(\alpha = 0,1/4,1\) are prescribed. In Fig. 4, the non-dimensional abscissa \(\overline{x}\) is, inevitably, ranging in the interval \(\left[ {0,1} \right]\). In all the ensuing numerical results, the ranging interval of the non-dimensional stiffness of the elastic spring is considered as \(\left[ {0,10} \right]\).

Fig. 2
figure 2

Nanoscopic effects of the stress gradient parameter on the mid-span axial deformation of the nanobar for prescribed characteristic parameters \(\zeta_{\ell } = 1/3,\alpha = 1/4\)

Full size image
Fig. 3
figure 3

Nanoscopic effects of the strain gradient parameter on the mid-span axial deformation of the nanobar for prescribed characteristic parameters \(\zeta_{c} = 1/3,\alpha = 1/4\)

Full size image
Fig. 4
figure 4

Effects of the elastic spring stiffness on the axial deformation of the nanobar for prescribed characteristic parameters \(\zeta_{c} = 1/2,\zeta_{\ell } = 1/3\)

Full size image

As inferable from the numerical illustrations, the axial deformation of the nano-sized bar associated with the mixture unified gradient theory increases with increasing the stress gradient characteristic parameter, i.e. a larger value of the stress gradient parameter \(\zeta_{c}\) involves a larger value of the mid-span axial deformation of the nanobar for given values of \(\alpha ,\zeta_{\ell }\). Within the context of the mixture unified gradient theory, a softening structural response in terms of the stress gradient parameter is, therefore, confirmed. On the contrary, the axial deformation of the mixture unified gradient elastic bar decreases with increasing the strain gradient characteristic parameter, i.e. a larger value of \(\zeta_{\ell }\) involves a smaller value of the mid-span axial deformation of the nano-sized bar for prescribed values of \(\alpha ,\zeta_{c}\). The mixture unified gradient theory, thus, can efficaciously capture the stiffening structural behavior in terms of the strain gradient parameter. The effects of classical elasticity theory are incorporated to the mixture unified gradient theory via the mixture parameter. As the mixture parameter continuously varies from zero to unity, the effect of the stress gradient theory reduced and replaced with the influence of the classical elasticity theory. The axial deformation of the nano-sized bar consistent with the framework of the mixture unified gradient theory decreased with increasing the mixture parameter for prescribed values of the gradient characteristic parameters \(\zeta_{c} ,\zeta_{\ell }\). The mixture unified gradient theory is, therefore, capable of efficiently realize the stiffening structural response in terms of the mixture parameter \(\alpha\). The axial deformation of the nano-sized bar coincides with the classical elastostatic response of the elastic bar as the gradient characteristic parameters approach zero, or otherwise, as the mixture parameter tends to unity in the absence of the strain gradient characteristic parameter. The expected nanoscopic features of the gradient characteristic parameters and the mixture parameter are, thus, confirmed in the numerical illustrations.

The structural behavior of the nano-sized bar is significantly affected by the elastic boundary conditions. The axial deformation of the nanobar with elastic boundary conditions is strictly higher than, and thus overestimates, the associated elastostatic response of the nano-sized bar with fixed–fixed ends. On the contrary, the axial deformation of the mixture unified gradient bar with elastic boundary conditions is less than or equal to the corresponding structural response of the nanobar with fixed-free ends. The axial deformation function of the nanobar with elastic boundary conditions decreases with increasing the stiffness of the elastic spring, i.e. a larger value of the elastic spring stiffness \(\overline{\kappa }\) involves a smaller value of the axial displacement of the nano-sized bar for prescribed values of the gradient characteristic parameter and the mixture parameter. A stiffening structural behavior in terms of the stiffness of the elastic spring \(\overline{\kappa }\) is, therefore, realized. The asymptotic structural responses of the nano-sized bar are noticeably demonstrated in the numerical illustrations. For infinitesimal values of the non-dimensional stiffness of the elastic spring, the axial deformation of a mixture unified gradient bar with elastic boundary conditions approaches the elastostatic structural response of the nanobar with fixed-free ends. Alternatively and for large enough values of the non-dimensional stiffness of the elastic spring, the axial deformation of a mixture unified gradient bar with elastic boundary conditions tends to the elastostatic structural response of the nano-sized bar with fixed–fixed ends. This issue is of practical importance in the inference of the experimental measurements. The inaccurate prescription of the idealized boundary conditions in the structural analysis of nanobars will inevitably lead to misleading interpretations of the size-dependent behavior of nano-sized bars.

The numerical values of the mid-span axial deformation of the nanobar with elastic boundary conditions within the framework of the mixture unified gradient theory is collected in Tables 1, 2, and 3 in terms of the stress gradient characteristic parameter, the strain gradient characteristic parameter, and the mixture parameter, respectively. The tabulated numerical results of the static structural response of the nanobar with elastic boundary conditions is, furthermore, enriched with the presentation of the axial deformation of the nano-sized elastic bar with fixed–fixed and fixed-free boundary conditions.

Table 1 Midspan axial deformation of an elastic nanobar, effects of the stress gradient characteristic parameter for prescribed parameters \(\alpha = 1/4,\zeta_{\ell } = 1/3\)
Full size table
Table 2 Midspan axial deformation of an elastic nanobar, effects of the strain gradient characteristic parameter for prescribed parameters \(\alpha = 1/4,\zeta_{c} = 1/3\)
Full size table
Table 3 Midspan axial deformation of an elastic nanobar, effects of the mixture parameter for prescribed characteristic parameters \(\zeta_{c} = 1/2,\zeta_{\ell } = 1/3\)
Full size table

4 Concluding remarks

The nanoscopic characteristics of CNTs are significantly affected by the type of boundary conditions employed in the structural analysis. To model the realistic state of the boundary conditions of CNTs embedded in elastic substrates, the atomistic-scale interactions between CNTs and substrates should be taken into account. The practical boundary conditions of CNTs are utterly dissimilar from the idealized boundary conditions commonly adopted in the literature. In the present study, CNTs that are bridged on the substrate at the end are modeled as a nano-sized bar with an elastically restrained end. The mixture unified gradient theory, within a variational consistent framework, is invoked to capture the size-effects at the ultra-small scale. The elastically retained boundary condition of the nanobar is modeled with an axial spring. Prescribing the elastic boundary conditions, the ensued structural features of nanobars are not restricted to the idealized boundary conditions and allow one to examine the more realistic structural response of nano-sized bars. The constitutive model of the nano-sized bar is properly enriched with the stress gradient characteristic length, the strain gradient length-scale parameter, and the mixture parameter to efficiently realize the size-effects. Explicit mathematical formulae of the extra non-standard boundary conditions, modified to take into account the elastically restrained end conditions of the nanobar, are introduced to appropriately close the associated boundary-value problem of equilibrium.

The static characteristics of a nano-sized bar with elastic boundary conditions are rigorously studied and the axial deformation of a mixture unified gradient elastic bar is analytically addressed. The closed-form exact solution of the kinematics field variable for a nanobar with elastic boundary conditions, subjected to a uniformly distributed axial load, is detected. The asymptotic size-dependent structural behavior of nanobars with the elastically restrained end is analytically examined under ad hoc assumptions on the elastic spring stiffness. The nanoscopic effects of the characteristic length-scale parameters on the structural characteristics of nano-sized bars with elastic boundary conditions are numerically illustrated and thoroughly discussed. The expected size-dependent features of the gradient characteristic parameters and the mixture parameter on the structural response of nanobars are numerically confirmed. The axial deformation of a mixture unified gradient bar with elastic boundary conditions is demonstrated to approach the elastostatic response of the nanobar with fixed-free and fixed–fixed ends for, respectively, infinitesimal and large enough values of the stiffness of the elastic spring. It is evinced that the inaccurate prescription of the idealized boundary conditions in the structural analysis of nanobars will inevitably yield a misleading inference of the size-dependent behavior of nanobars. The detected numerical benchmark can be advantageously implemented in the analysis and design of nanostructures with practical implications in NEMS.