1 Introduction

Over the years, functionally graded materials (FGMs) as new engineering materials have drawn the attention of many researchers. The primary purpose of making and expanding these materials is to increase the efficiency and different structural components and to control unwanted stresses and strains. Suitable properties of functional materials such as high strength, low weight, and appropriate resistance to chemical conditions and high temperatures have led to the development of the use of these materials in various fields. In these materials, the properties of each point are defined by a proper mixing law as a function of the component properties and their volume fraction at each point. Graded materials are mainly used in a combination of metal and ceramics. In recent years, the use of FGMs in high-temperature environments such as nuclear reactors, chemical plants and in the manufacture of high-speed vessels has become increasingly important. Also, a member with a metal-ceramic cross section has a higher bearing capacity than a material made of only a single metal or ceramic member and also with a larger cross-sectional area. Most engineers today are looking for efficient methods to help them reduce the weight of the structure. As a result, by combining different materials on a functional scale, the bearing capacity can be substantially increased, and the weight of the structure reduced at the same time. This is very important in terms of economic savings. In this study, we will analyze the vibrational analysis of local beam made of functionally graded materials.

Analysis of the natural frequency of the beam made of FGMs has a very much publication in engineering and academic research. In the literature, Sina et al. [1] considered a first-order shear deformation beam approach in combination with an analytical method to study vibrations of an FGM beam. Ke et al. [2] analyzed FGM beams based on nonlinear vibration studies using an analytical examination. They utilized the classical beam hypothesis and solved the achieved constitutive equation for three different boundary condition cases, namely hinged–hinged, fixed–hinged, and fixed–fixed. Hein and Feklistova [3] assumed FGM beams with the non-uniform geometrical section in a vibrational situation and a variety of edge conditions. They employed the Euler–Bernoulli beam model and solved their obtained relations with Haar wavelets numerical technique. Shooshtari and Rafiee [4] modeled nonlinear frequencies of an FGM beam with fixed edge conditions based on the outer excitations. The classical beam theory, in conjunction with the Galerkin solution method, gave numerical outcomes. Wattanasakulpong et al. [5] studied the thermal effects on an FGM beam besides resonant vibrations on the basis of a third-order shear deformation beam approach and solved the harvested vibrational relation based on the Ritz variational technique. In another work, Wattanasakulpong et al. [6], this time, employed experimental validation to compare with the numerical results of vibrations of an FGM beam with assuming the beam as a laminated composite as well. The used beam model in their theoretical part was a higher-order shear deformation one, and the obtained characteristic relation was solved with the Ritz method. They also applied various models of edge conditions and got good approval from their experiment with just 10 percent discrepancies between theoretical and experiments sections averaged for all boundary conditions. Thai and Vo [7] developed vibration analysis of FGM beams for different higher-order beam models. The constitutive equation of vibration was solved analytically, and the natural frequencies were computed using the Navier approach. Fallah and Aghdam [8] embedded an FGM beam with several edge conditions on a nonlinear elastic substrate and studied the vibrational response of the modeled system based on the temperature variations of the environment. The influences of the foundation were assumed as a linear transverse effect, shear, and nonlinear transverse impact. Pradhan and Chakraverty [9] investigated an FGM beam based on both classical and Timoshenko models and calculated the natural frequencies utilizing the Rayleigh–Ritz solution technique. Rahimi et al. [10] evaluated the response of an FGM beam to the vibrational condition based on the first-order shear deformation beam theory. The achieved governing equations were solved by imposing fixed and hinged edge conditions in accurate modal analysis. Vo et al. [11] numerically analyzed a sandwich FGM beam in both stability and vibrational states with the help of a higher-order shear deformation beam model. The numerical results were captured by applying various boundary conditions based on the finite element method. Kanani et al. [12] studied the effects of a nonlinear elastic matrix on an FGM beam placed in a vibrational state with considering large amplitudes. The characteristic relation was derived based on the classical beam approach and solved by a variational iteration technique. There also many published works on the FGM beams in various conditions, considering new deformation beam models [13], using dynamic stiffness solution technique [14], a two-parameter elastic medium [15], and geometrical non-uniformity as well [16]. Chen et al. [17], in a diverse study, investigated an FGM beam with some porosity imperfections. The constitutive relation was derived in the framework of the Timoshenko beam model, and the Ritz trial function helped them to compute excited frequencies. They evaluated two kinds of porosity and confirmed that the type of porosity affects fundamentally the frequencies. Jing et al. [18] combined the Timoshenko beam theory with finite element formulation to extract natural frequencies of an FGM beam. They considered three kinds of shear corrections factors to modify and refine the shear stresses along the thickness. Sedighi et al. [19,20,21] promoted various analytical approaches such as homotopy perturbation method with an auxiliary term, max–min approach (MMA), and iteration perturbation method (IPM) to study dynamical characteristics of structural elements. Esmaeili and Tadi Beni [22] analyzed dynamical characteristics of flexoelectric nanobeam composed of functionally graded materials.

Karami et al. [23] employed generalized DQM to investigate free vibration characteristics of two-dimensional FG tampered nanobeam exposed to thermal environment based on Timoshenko beam theory, while size-dependent behavior was captured by non-local strain gradient model. Again, Karami et al. [24] studied guided wave propagation of clamped–clamped FG nanoplate with porosity by utilizing the first-order shear deformation theory and non-local elasticity theory. In the pioneering works, She et al. studied nonlinear bending behavior [25] of curved nanotubes made up of FG porous material, while thermal snap-buckling [26] was carried out by using uniform temperature distributions across the thickness. Free vibration of FG porous nanoplate exposed to hygrothermal environment embedded in Kerr elastic foundation was studied by Karami et al. [27]. In the work [28], resonance behavior of Kirchhoff nanoplate made up of 3D-FG materials was analyzed by using Navier’s method and incorporating bi-Helmholtz non-local strain gradient theory. Karami et al. [29] employed second-order shear deformation theory in combination with non-local strain gradient model to study wave propagation analysis of FG porous nanoplate subjected to thermal and magnetic environment embedded in Winkler–Pasternak elastic foundation. Karami and Janghorban [30] utilized G-DQM to analyze free vibration of porous nanotube based on Timoshenko beam theory. The size-dependent behavior was studied by non-local strain gradient model, while the porosity of the nanotube was evenly distributed which was governed by modified power-law rule. Alimirzaei et al. [31] used finite element method to study static and dynamic analyses of viscoelastic micro-composite beam having geometrical imperfection. The microstructural effect was handled by the modified coupled stress theory. Karami et al. [32] used Galerkin’s approach to investigate buckling behavior of functional graded nanoplate using non-local strain gradient theory. Tounsi et al. [33] investigated static behavior of advanced functionally graded (AFG) ceramic-metal plates exposed to a nonlinear hygrothermo-mechanical load using a four-variable trigonometric integral shear deformation model placed in a two-parameter elastic foundation. Addou et al. [34] comprehensively studied the influence of different types of porosities on coupled vibration response of FG plates embedded in different types of elastic substrates using a quasi 3D HSDT. Chaabane et al. [35] analytically investigated the static and dynamic analyses of functionally graded beams resting on Winkler–Pasternak elastic foundation using hyperbolic shear deformation theory. Some other studies related to FG structures embedded in elastic foundations are discussed in [36, 37]. Kaddari et al. [38] used a quasi-3D model to investigate bending and free vibration of functionally graded plates having porosity. Bourada et al. [39] utilized a trigonometric deformation theory to investigate vibrational behavior of FG beam considering perfect and porosity condition for simply supported edge support. Khiloun et al. [40] analytically investigated static and dynamic analyses of FG plates using high-order shear and normal deformation theory. Bousahla et al. [41] used a novel integral first-order shear deformation theory to investigate the buckling and vibrational characteristics of the composite beam armed with single-walled carbon nanotubes resting on elastic foundation of Winkler–Pasternak type. Boussoula et al. [42] employed nth-order shear deformation theory to investigate the thermo-mechanical flexural behavior of sandwich plates composed of functionally graded material.

Paul and Das [43], in a new work, modeled pre-stresses into an FGM beam by taking the Timoshenko beam theory. They considered large deflections for various classic edge conditions. They, first, analyzed statically the problem and then studied the model dynamically with keeping the static stresses as pre-stressed in the beam. Wang and Li [44] discussed the vibration of an FGM beam based on the Levinson beam model. The simple–simple boundary conditions were gained by an approximate solution technique, and the accurate results were obtained in terms of natural frequencies by the aforementioned beam model. The finite element method, in conjunction with the first-order theory of shear deformation, was employed to attain natural frequencies of an FGM beam by Kahya and Turan [45]. Nguyen et al. [46] investigated the excited vibrational state of an FGM Timoshenko beam based on the two-directional functionality. Deng et al. [47] presented a double-FGM Timoshenko beams system with assuming the Winkler–Pasternak elastic matrix. The frequencies of this system were shown on the basis of the dynamics stiffness solution method for a variety of edge conditions. Celebi et al. [48] derived a complementary function method to study the natural frequencies of a hinged–hinged beam. Sinir et al. [49] studied nonlinearly excited and natural frequencies of an FGM Euler–Bernoulli beam model with considering a non-uniform cross section. Differential quadrature method was associated to discretize the frequency equation, and an eigenvalue solution made the results graphically. Banerjee and Ananthapuvirajah [50] in the framework of the dynamic stiffness method investigated the free vibration of an FGM classical beam. Karamanli [51] assumed bi-directional functionality for an FGM beam and presented natural frequencies of the beam for several boundary conditions based on a third-order of shear deformation theory. Fazzolari [52] examined three different higher-order shear deformation theories, namely trigonometric, polynomial, and exponential models, to investigate a laminated sandwich FGM beam. The porosity was taken into consideration as two types, and finally, the characteristic equation of vibration was solved on the basis of the Ritz solution approach. Cao and Gao [53] used an asymptotic development method to present natural frequencies of an FGM beam with taking non-uniformly geometry into account. The basic model of the beam, namely Euler–Bernoulli, was utilized, and a perturbation technique showed the numerical results.

As can be seen from the above literature, there is huge number of research to investigate the vibrational behavior of functionally graded porous beam, but only a few have employed higher-order shear deformation theory to examine the vibration characteristic of these materials. The porous FG beam is embedded in the Kerr elastic foundation, and the displacement field of the beam is governed by a refined higher-order shear deformation theory (RHSDT). Several classical boundary conditions such as HH, CH, CC, and CF boundary conditions have been taken into account by using the shifted Chebyshev polynomials Rayleigh–Ritz method. The advantage of the shifted Chebyshev polynomials is due to the orthogonal properties that makes the technique more computationally efficient by avoiding ill-conditioning for the higher number of terms of the polynomial. The results of this numerical method are also validated with the results of the Navier’s method for HH edge support. Further, a parametric study is also conducted to analyze the effects of various parameters such as power-law exponent, porosity volume fraction index, and elastic foundation on natural frequencies.

2 Mathematical formulation of the proposed model

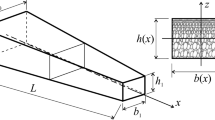
A functionally graded beam consisting of ceramic and metal components, having a length \(\left( L \right)\), breadth \(\left( b \right)\), and thickness \(\left( h \right)\), is considered in this study. It is assumed that the material composition at the top surface \(\left( {z = {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \right)\) is ceramic-rich and consistently varies to the metal-rich surface at the bottom \(\left( {z = {{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}} \right)\). In this analysis, the FG beam is presumed to have even porosity distribution with porosity volume fraction \(\psi\)\(\left( {\psi < < 1} \right)\), scattering equally throughout the metal and ceramic constituents, as illustrated in Fig. 1.

Fig. 1
figure 1

a Schematic representation of a rectangular FGM beam that rested on the Kerr elastic foundation in 3D, b schematic representation of the rectangular cross section of the FGM beam with evenly distributed porosity

Full size image

So, the modified rule of the mixture is stated as [54,55,56]

$$P = P_{\text{c}} V_{\text{c}} + P_{\text{m}} V_{\text{m}} - \frac{\psi }{2}\left( {P_{\text{c}} + P_{\text{m}} } \right)$$
(1)

Here, \(P_{\text{c}}\), \(V_{\text{c}}\) and \(P_{\text{m}}\), \(V_{\text{m}}\) are the material properties and volume fractions of the ceramic and metal components, respectively.

The volume fractions of the ceramic and metal constituents are given by [54,55,56]

$$V_{\text{c}} = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k}$$
(2)
$$V_{\text{m}} = 1 - \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k}$$
(3)

where \(k\) is the nonnegative parameter that determines the distribution of material all across the thickness of the beam, namely power-law exponent, and \(z\) is the distance from the mid-plane of the FG beam. Combining Eqs. (1), (2), and (3), the material properties of the FG beam with porosity can be expressed as [54,55,56]

$$P = \left( {P_{\text{c}} - P_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + P_{\text{m}} - \frac{\psi }{2}\left( {P_{\text{c}} + P_{\text{m}} } \right)$$
(4)

Therefore, Young’s modulus \(E\left( z \right)\), material density \(\rho \left( z \right)\), and Poisson’s ratio of the FG beam can be represented graphically as shown in Figs. 2, 3 and 4 and mathematically as [54,55,56]

Fig. 2
figure 2

Power-law variation of Young’s modulus

Full size image
Fig. 3
figure 3

Power-law variation of mass density

Full size image
Fig. 4
figure 4

Power-law variation of Poisson’s ratio

Full size image
$$E\left( z \right) = \left( {E_{\text{c}} - E_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + E_{\text{m}} - \frac{\psi }{2}\left( {E_{\text{c}} + E_{\text{m}} } \right)$$
(5a)
$$\rho \left( z \right) = \left( {\rho_{\text{c}} - \rho_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + \rho_{\text{m}} - \frac{\psi }{2}\left( {\rho_{\text{c}} + \rho_{\text{m}} } \right)$$
(5b)
$$\upsilon \left( z \right) = \left( {\upsilon_{\text{c}} - \upsilon_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + \upsilon_{\text{m}} - \frac{\psi }{2}\left( {\upsilon_{\text{c}} + \upsilon_{\text{m}} } \right)$$
(5c)

According to the refined higher-order shear deformation theory, the displacement field can be represented as [7, 57, 58]

$$u_{1} \left( {x,z,t} \right) = u\left( {x,t} \right) - z\left( {\frac{{\partial w_{\text{b}} }}{\partial x}} \right) - \left( {z - \frac{h}{\pi }\sin \left( {\frac{\pi }{h}z} \right)} \right)\left( {\frac{{\partial w_{\text{s}} }}{\partial x}} \right)$$
(6a)
$$u_{2} \left( {x,z,t} \right) = 0$$
(6b)
$$u_{3} \left( {x,z,t} \right) = w_{\text{b}} \left( {x,t} \right) + w_{\text{s}} \left( {x,t} \right)$$
(6c)

where \(u\), \(w_{\text{b}}\), and \(w_{\text{s}}\) are the axial displacement, bending, and shear components of transverse displacement on the mid-plane of the FG beam, respectively.

The normal and shear strains of the FG beam for this beam theory are stated as

$$\varepsilon_{xx} = \frac{{\partial u_{1} \left( {x,z,t} \right)}}{\partial x} = \frac{\partial u}{\partial x} - z\left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial x^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right) + \left( {\frac{h}{\pi }} \right)\sin \left( {\frac{\pi }{h}z} \right)\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}$$
(7)
$$\gamma_{xz} = \frac{{\partial u_{1} \left( {x,z,t} \right)}}{\partial z} + \frac{{\partial u_{3} \left( {x,z,t} \right)}}{\partial x} = \cos \left( {\frac{\pi }{h}z} \right)\frac{{\partial w_{\text{s}} }}{\partial x}$$
(8)

Considering that the material constituents of the FG beam comply with the generalized Hooke’s law, the stress components yield [9]

$$\sigma_{xx} = Q_{11} \varepsilon_{xx} = \left( {\frac{E\left( z \right)}{{1 - \upsilon \left( z \right)^{2} }}} \right)\,\varepsilon_{xx}$$
(9)
$$\sigma_{xz} = Q_{55} \gamma_{xz} = \left( {\frac{E\left( z \right)}{{2\left( {1 + \upsilon \left( z \right)} \right)}}} \right)\,\gamma_{xz}$$
(10)

2.1 Formulation of governing equations for Rayleigh–Ritz method

The strain energy \(\left( {S_{\text{e}} } \right)\) of the proposed model can be expressed as

$$\begin{aligned} S_{\text{e}} & = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\left( {\sigma_{xx} \varepsilon_{xx} + \sigma_{xz} \gamma_{xz} } \right){\text{d}}A{\text{d}}x} } \\ & \quad = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\left( {Q_{11} \varepsilon_{xx}^{2} + Q_{55} \gamma_{xz}^{2} } \right)} } {\text{d}}A{\text{d}}x \\ & \quad = \frac{1}{2}\int\limits_{0}^{L} {\left[ \begin{aligned} A_{11} \left( {\frac{\partial u}{\partial x}} \right)^{2} - 2B_{11} \left( {\frac{\partial u}{\partial x}} \right)\left( {\frac{{\partial^{2} w_{b} }}{{\partial x^{2} }}} \right) + D_{11} \left( {\frac{{\partial^{2} w_{b} }}{{\partial x^{2} }}} \right)^{2} + A_{\text{s}} \left( {\frac{{\partial w_{\text{s}} }}{\partial x}} \right)^{2} \hfill \\ \quad + 2D_{\text{s}} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial x^{2} }}} \right)\left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right) + H_{s} \left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right)^{2} - 2B_{\text{s}} \left( {\frac{\partial u}{\partial x}} \right)\left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right) \hfill \\ \end{aligned} \right]} {\text{d}}x \\ \end{aligned}$$
(11)

Here, \(\left( {A_{11} ,B_{11} ,D_{11} ,B_{\text{s}} ,D_{\text{s}} ,H_{\text{s}} } \right) = \int\limits_{A} {Q_{11} \left( {1,z,z^{2} ,f_{\text{e}} ,zf_{\text{e}} ,f_{\text{e}}^{2} } \right)} {\text{d}}A\), where \(f_{\text{e}} = z - \left( {\frac{h}{\pi }} \right)\sin \left( {\frac{\pi }{h}z} \right)\) and \(A_{\text{s}} = \int\limits_{A} {Q_{55} \cos^{2} \left( {\frac{\pi }{h}z} \right)} {\text{d}}A\).

The kinetic energy \(\left( {K_{\text{e}} } \right)\) can be stated as

$$\begin{aligned} K_{\text{e}} & = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\rho \left( z \right)\left[ {\left( {\frac{{\partial u_{1} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{2} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{3} }}{\partial t}} \right)^{2} } \right]} } {\text{d}}A{\text{d}}x \\ & \quad = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\rho \left( z \right)\left[ {\left( {\frac{\partial u}{\partial t} - z\left( {\frac{{\partial^{2} w_{\text{b}} }}{\partial x\partial t} + \frac{{\partial^{2} w_{\text{s}} }}{\partial x\partial t}} \right) + \left( {\frac{h}{\pi }} \right)\sin \left( {\frac{\pi }{h}z} \right)\left( {\frac{{\partial^{2} w_{\text{s}} }}{\partial x\partial t}} \right)} \right)^{2} + \left( {\frac{{\partial w_{\text{b}} }}{\partial t} + \frac{{\partial w_{\text{s}} }}{\partial t}} \right)^{2} } \right]} } {\text{d}}A{\text{d}}x \\ & \quad = \frac{1}{2}\int\limits_{0}^{L} {\left[ \begin{aligned} I_{0} \left( {\left( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{{\partial w_{\text{b}} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w_{\text{s}} }}{\partial t}} \right)^{2} + 2\left( {\frac{{\partial w_{\text{b}} }}{\partial t}} \right)\left( {\frac{{\partial w_{\text{s}} }}{\partial t}} \right)} \right) - 2I_{1} \left( {\frac{\partial u}{\partial t}} \right)\left( {\frac{{\partial^{2} w_{\text{b}} }}{\partial x\partial t}} \right) \hfill \\ \quad + I_{2} \left( {\frac{{\partial^{2} w_{\text{b}} }}{\partial x\partial t}} \right)^{2} - 2J_{1} \left( {\frac{\partial u}{\partial t}} \right)\left( {\frac{{\partial^{2} w_{\text{s}} }}{\partial x\partial t}} \right) + 2J_{2} \left( {\frac{{\partial^{2} w_{\text{b}} }}{\partial x\partial t}} \right)\left( {\frac{{\partial^{2} w_{\text{s}} }}{\partial x\partial t}} \right) + K_{2} \left( {\frac{{\partial^{2} w_{\text{s}} }}{\partial x\partial t}} \right)^{2} \hfill \\ \end{aligned} \right]} {\text{d}}x \\ \end{aligned}$$
(12)

where \(\left( {I_{0} ,I_{1} ,I_{2} ,J_{1} ,J_{2} ,K_{2} } \right) = \int\limits_{A} {\rho \left( z \right)\left( {1,z,z^{2} ,f_{\text{e}} ,zf_{\text{e}} ,f_{\text{e}}^{2} } \right)} {\text{d}}A\), where \(f_{\text{e}} = z - \left( {\frac{h}{\pi }} \right)\sin \left( {\frac{\pi }{h}z} \right)\).

The external work done \(\left( {W_{\text{e}} } \right)\) by the Kerr foundation can be expressed as [55, 59]

$$W_{\text{e}} = - \frac{1}{2}\int\limits_{0}^{L} {\left[ {\left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {w_{\text{b}} + w_{\text{s}} } \right)^{2} + \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {\frac{\partial }{\partial x}\left( {w_{\text{b}} + w_{\text{s}} } \right)} \right)^{2} } \right]} {\text{d}}x$$
(13)

Here, \(k_{\text{s}}\), \(k_{\text{u}}\), and \(k_{\text{l}}\) are shear, upper, and lower layers elastic parameters of the Kerr foundation, respectively.

Assuming the motion of the FG beam as sinusoidal, the displacement components can be represented as [9]

$$u\left( {x,t} \right) = U\left( x \right)\cos \left( {\omega t} \right),w_{\text{b}} \left( {x,t} \right) = W_{\text{b}} \left( x \right)\cos \left( {\omega t} \right),{\text{and}}\,w_{\text{s}} \left( {x,t} \right) = W_{\text{s}} \left( x \right)\cos \left( {\omega t} \right)$$
(14)

where \(U\left( x \right)\), \(W_{\text{b}} \left( x \right)\), and \(W_{\text{s}} (x)\) are the amplitudes of axial displacement, bending and shear components of transverse displacement, respectively, and \(\omega\) denotes the natural frequency of the proposed model.

Utilizing Eq. (14) into Eqs. (11), (12), and (13), the maximum strain energy \(\left( {S_{\text{e}}^{\text{Max}} } \right)\), kinetic energy \(\left( {K_{\text{e}}^{\text{Max}} } \right)\), and work done by Kerr foundation \(\left( {W_{\text{e}}^{\text{Max}} } \right)\) can be portrayed as

$$S_{\text{e}}^{\text{Max}} = \frac{1}{2}\int\limits_{0}^{L} {\left[ \begin{aligned} A_{11} \left( {\frac{{{\text{d}}U}}{{{\text{d}}x}}} \right)^{2} - 2B_{11} \left( {\frac{{{\text{d}}U}}{{{\text{d}}x}}} \right)\left( {\frac{{{\text{d}}^{2} W_{\text{b}} }}{{{\text{d}}x^{2} }}} \right) + D_{11} \left( {\frac{{{\text{d}}^{2} W_{\text{b}} }}{{{\text{d}}x^{2} }}} \right)^{2} + A_{\text{s}} \left( {\frac{{{\text{d}}^{2} W_{\text{s}} }}{{{\text{d}}x^{2} }}} \right)^{2} \hfill \\ \quad + 2D_{\text{s}} \left( {\frac{{{\text{d}}^{2} W_{\text{b}} }}{{{\text{d}}x^{2} }}} \right)\left( {\frac{{{\text{d}}^{2} W_{\text{s}} }}{{{\text{d}}x^{2} }}} \right) + H_{\text{s}} \left( {\frac{{{\text{d}}^{2} W_{\text{s}} }}{{{\text{d}}x^{2} }}} \right)^{2} - 2B_{\text{s}} \left( {\frac{{{\text{d}}U}}{{{\text{d}}x}}} \right)\left( {\frac{{{\text{d}}^{2} W_{\text{s}} }}{{{\text{d}}x^{2} }}} \right) \hfill \\ \end{aligned} \right]} {\text{d}}x$$
(15)
$$K_{\text{e}}^{\text{Max}} = \frac{{\omega^{2} }}{2}\int\limits_{0}^{L} {\left[ \begin{aligned} I_{0} \left( {U^{2} + W_{\text{b}}^{2} + W_{\text{s}}^{2} + 2W_{\text{b}} W_{\text{s}} } \right) - 2I_{1} \left( {U\frac{{{\text{d}}W_{\text{b}} }}{{{\text{d}}x}}} \right) + I_{2} \left( {\frac{{{\text{d}}W_{\text{b}} }}{{{\text{d}}x}}} \right)^{2} \hfill \\ \quad - 2J_{1} \left( {U\frac{{{\text{d}}W_{\text{s}} }}{{{\text{d}}x}}} \right) + 2J_{2} \left( {\frac{{{\text{d}}W_{\text{b}} }}{{{\text{d}}x}}} \right)\left( {\frac{{{\text{d}}W_{\text{s}} }}{{{\text{d}}x}}} \right) + K_{2} \left( {\frac{{{\text{d}}W_{\text{s}} }}{{{\text{d}}x}}} \right)^{2} \hfill \\ \end{aligned} \right]} {\text{d}}x$$
(16)
$$W_{\text{e}}^{\text{Max}} = - \frac{1}{2}\int\limits_{0}^{L} {\left[ {\left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {W_{\text{b}} + W_{\text{s}} } \right)^{2} + \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {\frac{\text{d}}{{{\text{d}}x}}\left( {W_{\text{b}} + W_{\text{s}} } \right)} \right)^{2} } \right]} {\text{d}}x$$
(17)

  • By removing the upper spring, the Kerr foundation will be changed into Winkler–Pasternak foundation and the maximum work done by the Winkler–Pasternak foundation can be stated as

    $$W_{\text{e}}^{\text{Max}} = - \frac{1}{2}\int\limits_{0}^{L} {\left[ {\left( {k_{\text{l}} } \right)\left( {W_{\text{b}} + W_{\text{s}} } \right)^{2} + \left( {k_{\text{s}} } \right)\left( {\frac{\text{d}}{{{\text{d}}x}}\left( {W_{\text{b}} + W_{\text{s}} } \right)} \right)^{2} } \right]} {\text{d}}x$$
    (18)

  • Likewise, if the upper spring and shear layer will be removed from the Kerr foundation, the model will be converted into Winkler elastic foundation and the maximum work done by the Winkler foundation can be modified as

    $$W_{\text{e}}^{\text{Max}} = - \frac{1}{2}\int\limits_{0}^{L} {\left[ {\left( {k_{\text{l}} } \right)\left( {W_{\text{b}} + W_{\text{s}} } \right)^{2} } \right]} {\text{d}}x$$
    (19)

2.2 Formulation of governing equations for Navier’s method

The variation in strain energy \(\left( {\delta S_{\text{e}} } \right)\) can be represented as

$$\begin{aligned} \delta S_{\text{e}} & = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\left( {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{xz} \delta \gamma_{xz} } \right){\text{d}}A{\text{d}}x} } \\ & \quad = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\left[ {\sigma_{xx} \left( {\frac{\partial \delta u}{\partial x} - z\frac{{\partial^{2} \delta w_{\text{b}} }}{{\partial x^{2} }} - f_{\text{e}} \frac{{\partial^{2} \delta w_{\text{s}} }}{{\partial x^{2} }}} \right) + \sigma_{xz} \left( {g\frac{{\partial \delta w_{\text{s}} }}{\partial x}} \right)} \right]{\text{d}}A{\text{d}}x} } \\ & \quad = \frac{1}{2}\int\limits_{0}^{L} {\left[ {\left( {N\frac{\partial \delta u}{\partial x} - M_{b} \frac{{\partial^{2} \delta w_{\text{b}} }}{{\partial x^{2} }} - M_{\text{s}} \frac{{\partial^{2} \delta w_{\text{s}} }}{{\partial x^{2} }} + Q\frac{{\partial \delta w_{\text{s}} }}{\partial x}} \right)} \right]{\text{d}}x} \\ & \quad = \frac{1}{2}\int\limits_{0}^{L} {\left[ {\left( { - \frac{\partial N}{\partial x}\delta u - \frac{{\partial^{2} M_{\text{b}} }}{{\partial x^{2} }}\delta w_{\text{b}} - \frac{{\partial^{2} M_{\text{s}} }}{{\partial x^{2} }}\delta w_{\text{s}} - \frac{\partial Q}{\partial x}\delta w_{\text{s}} } \right)} \right]{\text{d}}x} \\ \end{aligned}$$
(20)

Here, \(\left( {N,M_{\text{b}} ,M_{\text{s}} } \right) = \int\limits_{A} {\left( {1,z,f_{\text{e}} } \right)} \,\sigma_{xx} {\text{d}}A\), \(Q = \int\limits_{A} {g\sigma_{xz} dA}\), \(f_{\text{e}} = z - \left( {\frac{h}{\pi }} \right)\sin \left( {\frac{\pi }{h}z} \right)\), and \(g = \cos \,\left( {\frac{\pi }{h}z} \right)\)

Likewise, the variation in kinetic energy \(\left( {\delta K_{\text{e}} } \right)\) can be expressed as

$$\begin{aligned} \delta K_{\text{e}} & \quad = \int\limits_{0}^{L} {\int\limits_{A} {\rho \left( z \right)\left[ {\left( {\frac{{\partial u_{1} }}{\partial t}} \right)\left( {\frac{{\partial \delta u_{1} }}{\partial t}} \right) + \left( {\frac{{\partial u_{2} }}{\partial t}} \right)\left( {\frac{{\partial \delta u_{2} }}{\partial t}} \right) + \left( {\frac{{\partial u_{3} }}{\partial t}} \right)\left( {\frac{{\partial \delta u_{3} }}{\partial t}} \right)} \right]} } {\text{d}}A{\text{d}}x \\ & \quad = \int\limits_{0}^{L} {\int\limits_{A} {\rho \left( z \right)\left[ { - \left( {\frac{{\partial^{2} u_{1} }}{{\partial t^{2} }}} \right)\delta u_{1} - \left( {\frac{{\partial^{2} u_{2} }}{{\partial t^{2} }}} \right)\delta u_{2} - \left( {\frac{{\partial^{2} u_{3} }}{{\partial t^{2} }}} \right)\delta u_{3} } \right]} } {\text{d}}A{\text{d}}x \\ & \quad = \int\limits_{0}^{L} {\left[ \begin{aligned} \left( { - I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{3} w_{\text{b}} }}{{\partial x\partial t^{2} }} + J_{1} \frac{{\partial^{3} w_{\text{s}} }}{{\partial x\partial t^{2} }}} \right)\,\delta u + \left( \begin{aligned} - I_{0} \frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} - I_{0} \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} \hfill \\ \quad + I_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} + J_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} \hfill \\ \end{aligned} \right)\delta w_{\text{b}} \hfill \\ \quad + \left( { - I_{0} \frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} - I_{0} \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }} - J_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} + J_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} + K_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }}} \right)\delta w_{\text{s}} \hfill \\ \end{aligned} \right]} {\text{d}}x \\ \end{aligned}$$
(21)

where \(\left( {I_{0} ,I_{1} ,I_{2} ,J_{1} ,J_{2} ,K_{2} } \right) = \int\limits_{A} {\rho \left( z \right)\left( {1,z,z^{2} ,f_{\text{e}} ,zf_{\text{e}} ,f_{\text{e}}^{2} } \right)} {\text{d}}A\), where \(f_{\text{e}} = z - \left( {\frac{h}{\pi }} \right)\sin \left( {\frac{\pi }{h}z} \right)\).

The variation in external work done \(\left( {\delta W_{\text{e}} } \right)\) can be portrayed as [55, 59]

$$\delta W_{\text{e}} = - \int\limits_{0}^{L} {\left[ {\left( {\left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) - \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\frac{{\partial^{2} \left( {w_{\text{b}} + w_{\text{s}} } \right)}}{{\partial x^{2} }}} \right)\left( {\delta w_{\text{b}} + \delta w_{\text{s}} } \right)} \right]}$$
(22)

Substituting Eqs. (20–22) into the extended Hamilton’s principle \(\int\limits_{0}^{T} {\left( {\delta K_{\text{e}} - \delta S_{\text{e}} + \delta W_{\text{e}} } \right){\text{d}}t = 0}\) and collecting the coefficients of \(\delta u\), \(\delta w_{\text{b}}\), and \(\delta w_{\text{s}}\), we have

$$\frac{\partial N}{\partial x} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w_{\text{b}} }}{{\partial x\partial t^{2} }} - J_{1} \frac{{\partial^{3} w_{\text{s}} }}{{\partial x\partial t^{2} }}$$
(23)
$$\begin{aligned} \frac{{\partial^{2} M_{\text{b}} }}{{\partial x^{2} }} & = I_{0} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) + I_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - I_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} - J_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} \\ & \quad + \left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) - \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\frac{{\partial^{2} \left( {w_{\text{b}} + w_{\text{s}} } \right)}}{{\partial x^{2} }} \\ \end{aligned}$$
(24)
$$\begin{aligned} \frac{{\partial^{2} M_{\text{s}} }}{{\partial x^{2} }} + \frac{\partial Q}{\partial x} & = I_{0} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) + J_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - J_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} - K_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} \\ & \quad + \left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) - \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\frac{{\partial^{2} \left( {w_{\text{b}} + w_{\text{s}} } \right)}}{{\partial x^{2} }} \\ \end{aligned}$$
(25)

Using generalized Hooke’s law, the local stress resultants can be written as

$$N = A_{11} \left( {\frac{\partial u}{\partial x}} \right) - B_{11} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial x^{2} }}} \right) - B_{\text{s}} \left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right)$$
(26)
$$M_{\text{b}} = B_{11} \left( {\frac{\partial u}{\partial x}} \right) - D_{11} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial x^{2} }}} \right) - D_{\text{s}} \left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right)$$
(27)
$$M_{\text{s}} = B_{\text{s}} \left( {\frac{\partial u}{\partial x}} \right) - D_{\text{s}} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial x^{2} }}} \right) - H_{\text{s}} \left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right)$$
(28)
$$Q = A_{\text{s}} \left( {\frac{{\partial w_{\text{s}} }}{\partial x}} \right)$$
(29)

Combining Eqs. (23–25) and (26–29), the governing equations of motion in terms of displacements can be obtained as

$$A_{11} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right) - B_{11} \left( {\frac{{\partial^{3} w_{\text{b}} }}{{\partial x^{3} }}} \right) - B_{s} \left( {\frac{{\partial^{3} w_{\text{s}} }}{{\partial x^{3} }}} \right) = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w_{\text{b}} }}{{\partial x\partial t^{2} }} - J_{1} \frac{{\partial^{3} w_{\text{s}} }}{{\partial x\partial t^{2} }}$$
(30a)
$$\begin{aligned} & B_{11} \left( {\frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) - D_{11} \left( {\frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{4} }}} \right) - D_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{4} }}} \right) = I_{0} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) + I_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - I_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} \\ & \quad - J_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} + \left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) - \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\frac{{\partial^{2} \left( {w_{\text{b}} + w_{\text{s}} } \right)}}{{\partial x^{2} }} \\ \end{aligned}$$
(30b)
$$\begin{aligned} & B_{\text{s}} \left( {\frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) - D_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{4} }}} \right) - H_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{4} }}} \right) + A_{\text{s}} \left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right) = I_{0} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) + J_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} \\ & \quad - J_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} - K_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} + \left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) - \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\frac{{\partial^{2} \left( {w_{\text{b}} + w_{\text{s}} } \right)}}{{\partial x^{2} }} \\ \end{aligned}$$
(30c)

  • When the upper spring is removed into the Kerr foundation, the proposed model will be converted for Winkler–Pasternak foundation and the governing equations of motion can be given as

    $$A_{11} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right) - B_{11} \left( {\frac{{\partial^{3} w_{\text{b}} }}{{\partial x^{3} }}} \right) - B_{s} \left( {\frac{{\partial^{3} w_{\text{s}} }}{{\partial x^{3} }}} \right) = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w_{\text{b}} }}{{\partial x\partial t^{2} }} - J_{1} \frac{{\partial^{3} w_{\text{s}} }}{{\partial x\partial t^{2} }}$$
    (31a)
    $$\begin{aligned} & B_{11} \left( {\frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) - D_{11} \left( {\frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{4} }}} \right) - D_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{4} }}} \right) = I_{0} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) + I_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - I_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} \\ & \quad - J_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} + \left( {k_{\text{l}} } \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) - \left( {k_{\text{s}} } \right)\frac{{\partial^{2} \left( {w_{\text{b}} + w_{\text{s}} } \right)}}{{\partial x^{2} }} \\ \end{aligned}$$
    (31b)
    $$\begin{aligned} & B_{\text{s}} \left( {\frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) - D_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{4} }}} \right) - H_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{4} }}} \right) + A_{\text{s}} \left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right) = I_{0} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) + J_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} \\ & \quad - J_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} - K_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} + \left( {k_{\text{l}} } \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) - \left( {k_{\text{s}} } \right)\frac{{\partial^{2} \left( {w_{\text{b}} + w_{\text{s}} } \right)}}{{\partial x^{2} }} \\ \end{aligned}$$
    (31c)

  • If the upper spring and shear layer are detached from the Kerr foundation, the proposed model will be changed for Winkler foundation and the governing equations of motion can be depicted as

    $$A_{11} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right) - B_{11} \left( {\frac{{\partial^{3} w_{\text{b}} }}{{\partial x^{3} }}} \right) - B_{s} \left( {\frac{{\partial^{3} w_{\text{s}} }}{{\partial x^{3} }}} \right) = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w_{\text{b}} }}{{\partial x\partial t^{2} }} - J_{1} \frac{{\partial^{3} w_{\text{s}} }}{{\partial x\partial t^{2} }}$$
    (32a)
    $$\begin{aligned} & B_{11} \left( {\frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) - D_{11} \left( {\frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{4} }}} \right) - D_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{4} }}} \right) = I_{0} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) + I_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - I_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} \\ & \quad - J_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} + \left( {k_{\text{l}} } \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) \\ \end{aligned}$$
    (32b)
    $$\begin{aligned} & B_{\text{s}} \left( {\frac{{\partial^{3} u}}{{\partial x^{3} }}} \right) - D_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{4} }}} \right) - H_{\text{s}} \left( {\frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{4} }}} \right) + A_{\text{s}} \left( {\frac{{\partial^{2} w_{\text{s}} }}{{\partial x^{2} }}} \right) = I_{0} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) + J_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} \\ & \quad - J_{2} \frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} - K_{2} \frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} + \left( {k_{\text{l}} } \right)\left( {w_{\text{b}} + w_{\text{s}} } \right) \\ \end{aligned}$$
    (32c)

3 Solution methodology

In the present analysis, Navier’s method [60,61,62] and shifted Chebyshev polynomial-based Rayleigh–Ritz method [63] have been utilized to solve governing differential equations for free vibration of the FG beam. Navier’s technique has been exploited for hinged–hinged (HH) boundary condition, whereas the shifted Chebyshev polynomial-based Rayleigh–Ritz is adopted to solve hinged–hinged (HH), clamped–clamped (CC), clamped–hinged (CH), and clamped-free (CF) boundary conditions. Further descriptions of each approach are presented in the subsections below.

3.1 Implementation of Navier’s method

According to the Navier’s technique, the axial displacement \(u\,\left( {x,t} \right)\), bending \(w_{\text{b}} \left( {x,t} \right)\), and shear \(w_{\text{s}} \left( {x,t} \right)\) components of transverse the displacement endorse the solution as shown below [58]:

$$u\left( {x,t} \right) = \sum\limits_{m = 1}^{\infty } {u_{\text{m}} } \cos \left( {\frac{m\pi }{L}x} \right){\text{e}}^{i\omega t}$$
(33a)
$$w_{\text{b}} \left( {x,t} \right) = \sum\limits_{m = 1}^{\infty } {w_{bm} } \sin \left( {\frac{m\pi }{L}x} \right){\text{e}}^{i\omega t}$$
(33b)
$$w_{\text{s}} \left( {x,t} \right) = \sum\limits_{m = 1}^{\infty } {w_{sm} } \sin \left( {\frac{m\pi }{L}x} \right){\text{e}}^{i\omega t}$$
(33c)

where \(u_{m} ,\) \(w_{bm}\), and \(w_{sm}\) are arbitrary parameters and \(\omega\) is the natural frequency of vibration. Substituting Eq. (33) into the governing equations of motion, i.e., Equations (30), (31), (32), generalized eigenvalue problem for free vibration of Kerr, Winkler–Pasternak, and Winkler foundation, respectively, will take the form as given in Eq. (34). But, the results for Kerr foundation are only considered (except for comparison) in this investigation as other two foundations are the special cases of Kerr.

$$\left[ K \right]\left\{ X \right\} = \omega^{2} \left[ M \right]\left\{ X \right\}$$
(34)

Here \(\left[ K \right] = \left[ {\begin{array}{*{20}c} {k_{11} } & {k_{12} } & {k_{13} } \\ {k_{21} } & {k_{22} } & {k_{23} } \\ {k_{31} } & {k_{32} } & {k_{33} } \\ \end{array} } \right]\), \(\left[ M \right] = \left[ {\begin{array}{*{20}c} {m_{11} } & {m_{12} } & {m_{13} } \\ {m_{21} } & {m_{22} } & {m_{23} } \\ {m_{31} } & {m_{32} } & {m_{33} } \\ \end{array} } \right]\) and \(\left\{ X \right\} = \left[ {\begin{array}{*{20}c} {u_{m} } & {w_{bm} } & {w_{sm} } \\ \end{array} } \right]^{\text{T}}\)

$$\begin{aligned} k_{11} & = - A_{11} \left( {\frac{m\pi }{L}} \right)^{2} ,k_{22} = - D_{11} \left( {\frac{m\pi }{L}} \right)^{4} - \left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right) - \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {\frac{m\pi }{L}} \right)^{2} , \\ k_{12} & = k_{21} = B_{11} \left( {\frac{m\pi }{L}} \right)^{3} ,k_{23} = k_{32} = - D_{\text{s}} \left( {\frac{m\pi }{L}} \right)^{4} - \left( {\frac{{k_{\text{u}} k_{\text{l}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right) - \left( {\frac{{k_{\text{s}} k_{\text{u}} }}{{k_{\text{u}} + k_{\text{l}} }}} \right)\left( {\frac{m\pi }{L}} \right)^{2} , \\ k_{13} & = k_{31} = B_{\text{s}} \left( {\frac{m\pi }{L}} \right)^{3} ,k_{33} = - H_{\text{s}} \left( {\frac{m\pi }{L}} \right)^{4} - A_{\text{s}} \left( {\frac{m\pi }{L}} \right)^{2} . \\ \end{aligned}$$
$$\begin{aligned} m_{11} & = - I_{0} ,m_{12} = m_{21} = I_{1} \left( {\frac{m\pi }{L}} \right),m_{23} = m_{32} = - I_{0} - J_{2} \left( {\frac{m\pi }{L}} \right)^{2} , \\ m_{22} & = - I_{0} - I_{2} \left( {\frac{m\pi }{L}} \right)^{2} ,m_{13} = m_{31} = J_{1} \left( {\frac{m\pi }{L}} \right),m_{33} = - I_{0} - K_{2} \left( {\frac{m\pi }{L}} \right)^{2} . \\ \end{aligned}$$

3.2 Implementation shifted Chebyshev polynomial-based Rayleigh–Ritz method

In this study, the shifted Chebyshev polynomial of the first kind is considered as shape function over algebraic polynomials because of the fact that Chebyshev polynomials are the orthogonal polynomials which reduce the computational effort, and for the larger value of \(n\,\left( {n > 10} \right)\), the system avoids ill-conditioning. First few terms of shifted Chebyshev polynomials of the first kind can be expressed as [63],

$$\begin{aligned} \varphi_{0} \left( x \right) & = 1 \\ \varphi_{1} \left( x \right) & = 2x - 1 \\ \varphi_{n} \left( x \right) & = 2\left( {2x - 1} \right)\varphi_{n - 1} \left( x \right) - \varphi_{n - 2} \left( x \right),\quad n = 2,3, \ldots \\ \end{aligned}$$
(35)

The axial displacement \(u\,\left( {x,t} \right)\), bending \(w_{b} \,\left( {x,t} \right)\), and shear \(w_{s} \,\left( {x,t} \right)\) components of transverse displacement can be stated as [9, 63,64,65]

$$U\left( x \right) = x^{p} \left( {L - x} \right)^{q} \sum\limits_{i = 1}^{n} {c_{i} \varphi_{i - 1} (x)}$$
(36a)
$$W_{\text{b}} \left( x \right) = x^{p} \left( {L - x} \right)^{q} \sum\limits_{i = 1}^{n} {d_{i} \varphi_{i - 1} (x)}$$
(36b)
$$W_{\text{s}} \left( x \right) = x^{p} \left( {L - x} \right)^{q} \sum\limits_{i = 1}^{n} {e_{i} \varphi_{i - 1} (x)}$$
(36c)

Here, \(c_{i} '{\text{s}}\),\(d_{i} '{\text{s}}\), and \(e_{i} '{\text{s}}\) are unknown parameters, \(\varphi_{n} \left( x \right)\) is the shifted Chebyshev polynomial of index \(n\), \(x^{p} \left( {L - x} \right)^{q}\) is the admissible functions, and \(p\,\), \(q\) are the exponents that regulate the boundary conditions as shown in Table 1.

Table 1 \(p\,{\text{and}}\,q\) for different boundary conditions [9, 63, 65]
Full size table

Plugging Eq. (36) into maximum strain energy \(\left( {S_{\text{e}}^{\text{Max}} } \right)\), kinetic energy \(\left( {K_{\text{e}}^{\text{Max}} } \right)\), and work done by Kerr foundation \(\left( {W_{\text{e}}^{\text{Max}} } \right)\), i.e., Equations (15–17) and equating as \(S_{\text{e}}^{\text{Max}} + W_{\text{e}}^{\text{Max}} = K_{\text{e}}^{\text{Max}}\) and minimizing the natural frequency \(\left( {\omega^{2} } \right)\) with respect to the coefficients \(c_{i} '{\text{s}}\),\(d_{i} '{\text{s}}\), and \(e_{i} '{\text{s}}\),\(\,i = 1,\,2,\,3\, \ldots n\,\), yield the generalized eigenvalue problem as

$$\left[ K \right]\left\{ X \right\} = \omega^{2} \left[ M \right]\left\{ X \right\}$$
(37)

where \(\left\{ X \right\} = \left[ {c_{1} ,c_{2} ,c_{3} , \ldots c_{n} ,d_{1} ,d_{2} ,d_{3} , \ldots d_{n} ,e_{1} ,e_{2} ,e_{3} , \ldots e_{n} } \right]^{\text{T}}\), \(\left[ K \right]\) denotes the stiffness matrix, and \(\left[ M \right]\) represents the mass matrix.

4 Numerical results and discussion

In this study, the functionally graded beam is assumed to be composed of stainless steel (SUS304) as a metal constituent and silicon nitride (Si3N4) as a ceramic constituent with their mechanical properties as [66, 67]

Silicon nitride (Si3N4):\(E_{\text{c}} = 348.43\,{\text{GPa}}\), \(\rho_{\text{c}} = 2370\,{\text{kg}}\,{\text{m}}^{ - 3}\), and \(\upsilon_{\text{c}} = 0.24\)

Stainless steel (SUS304):\(E_{\text{m}} = 201.04\,{\text{GPa}}\), \(\rho_{\text{m}} = 8166\,{\text{kg}}\,{\text{m}}^{ - 3}\), and \(\upsilon_{\text{m}} = 0.3262\).

The dimension of the FG beam is taken as width \(\left( {b = 0.05\,{\text{m}}} \right)\) × thickness \(\left( {h = 0.0125\,{\text{m}}} \right)\) × length \(\left( {L = 1\,{\text{m}}} \right)\). Natural frequencies \(\left( \omega \right)\) for four essential boundary conditions such as hinged–hinged (HH), clamped–hinged (CH), clamped–clamped (CC), and clamped-free are taken into the investigation in this investigation by employing Navier’s technique for HH boundary condition and shifted Chebyshev polynomial-based Rayleigh–Ritz method for all the boundary conditions mentioned above.

4.1 Validation

Through this subsection, the present model is validated in two ways. Firstly, the current results are compared with other existing works present in the literature, in special cases. In this regard, the first three non-dimensional frequency parameters of the present model are compared with [7, 68] for different power-law index by neglecting the elastic foundation and porosity effect from the present investigation. For the validation purpose, all the parameters are kept the same as [7, 68], and the tabular results are depicted in Table 2. Secondly, natural frequencies of the first four modes of hinged–hinged boundary condition are computed by using an analytical method, i.e., Navier’s method and numerical method, such as shifted Chebyshev polynomial-based Rayleigh–Ritz method with porosity index \(\psi = 0.1\), \(k_{\text{u}} = k_{\text{l}} = 1\,{\text{GPa}}\), \(k_{\text{s}} = 1\,{\text{GN}}\) and other parameters are taken as given as above section. A comparison of the natural frequencies is demonstrated in Table 3. From these results, one may perceive that the current model goes well with other established outcomes.

Table 2 Validation of the present model for HH boundary condition with [7, 68] in special cases
Full size table
Table 3 Comparisons of results between Navier’s method and shifted Chebyshev polynomial-based Rayleigh–Ritz method for HH boundary condition
Full size table

4.2 Convergence

This subsection is dedicated to analyzing the convergence of natural frequencies of the first four modes of HH, CH, CC, and CF boundary conditions by employing the shifted Chebyshev polynomial-based Rayleigh–Ritz method. The use of shifted Chebyshev polynomial as a shape function makes the methods more efficient because of orthogonal properties and avoids the system from becoming an ill condition for the higher number of terms. This study is conducted by considering the power-law exponent \(\left( k \right) = 5\), porosity volume fraction \(\left( \psi \right) = 0.1\), \(k_{\text{u}} = k_{\text{l}} = 1\,{\text{GPa}}\), and \(k_{\text{s}} = 1\,{\text{GN}}\), and the graphical results are illustrated in Figs. 5, 6, 7 and 8. From these results, it is very much evident that the number of polynomials plays a very vital role in the convergence of frequencies. Lower-mode frequencies require less number of polynomials, whereas higher-mode frequencies need more number of terms. It is also observed that first- and second-mode frequencies are converging with \(n = 5\), while third and fourth modes are attending convergence at \(n = 6\), which is almost the same for all the boundary conditions mentioned in this study.

Fig. 5
figure 5

Convergence of natural frequency for HH boundary condition

Full size image
Fig. 6
figure 6

Convergence of natural frequency for CH boundary condition

Full size image
Fig. 7
figure 7

Convergence of natural frequency for CC boundary condition

Full size image
Fig. 8
figure 8

Convergence of natural frequency for CF boundary condition

Full size image

4.3 Effect of power-law exponent \(\left( k \right)\)

Through this subsection, the effect of the power-law index has been studied on the first four modes of natural frequencies of the FG beam considering HH, CH, CC, and CF boundary conditions. Both the tabular and graphical results are computed with porosity volume fraction \(\left( \psi \right) = 0.1\), \(k_{\text{u}} = k_{\text{l}} = 1\,{\text{GPa}}\), \(k_{\text{s}} = 1\,{\text{GN}}\), and power-law exponent are varied as 0, 0.2, 0.5, 1, 2, 3, 5, and 10, which are illustrated in Table 4 and Figs. 9, 10, 11 and 12. From this study, it is quite evident that with the rise in the power-law exponent, the natural frequencies of all the modes decrease and this reduction is more remarkable when \(k < 2\). This can be explained by the fact that at \(k = 0\), the beam is purely ceramic possesses the highest natural frequencies, while at \(k = \infty\), the beam is pure metal having the lowest natural frequencies, i.e., as we go on increasing the power-law exponent \(\left( k \right)\), Young’s modulus of the FG beam decreases which leads to higher flexibility and lower natural frequencies.

Table 4 Variation of natural frequencies \(\left( \omega \right)\) with power-law exponent \(\left( k \right)\)
Full size table
Fig. 9
figure 9

Variation of the natural frequency with the power-law index for HH boundary condition

Full size image
Fig. 10
figure 10

Variation of the natural frequency with power-law index for CH boundary condition

Full size image
Fig. 11
figure 11

Variation of the natural frequency with the power-law index for CC boundary condition

Full size image
Fig. 12
figure 12

Variation of the natural frequency with the power-law index for CF boundary condition

Full size image

4.4 Effect of porosity volume fraction \(\left( \psi \right)\)

In the present investigation, the FG beam is considered as a porous beam with evenly distributed porosity along the thickness of the beam. Graphical and tabular results (Figs. 13, 14, 15, 16; Table 5) are computed by considering \(k_{\text{u}} = k_{\text{l}} = 1\,{\text{GPa}}\), \(k_{\text{s}} = 1\,{\text{GN}}\) and by varying both the power-law index \(\left( k \right)\) and porosity volume fraction \(\left( \psi \right)\). From these results, it can be concluded that with the increase in porosity index \(\left( \psi \right)\), natural frequencies also increase when the FG beam is purely ceramic, i.e., at \(k = 0\). This is due to the fact that the beam becomes stiffer, which ultimately gives rise to the natural frequencies. On the other hand, for different values of power-law index, i.e., \(k = 1,\,2,\,10\), etc., this trend is completely opposite that means natural frequencies reduce with the rise in porosity volume fraction. Also, this trend is more significant in the case of higher values of \(k\). Based on these observations, it may be concluded that the rise or fall of natural frequencies depends upon the power-law index even if the porosity index follows an increasing or decreasing trend. Since the trend is similar for other boundary conditions, only results of HH edge support are exclusively provided in the study.

Fig. 13
figure 13

Variation of the natural frequency with porosity index for first mode

Full size image
Fig. 14
figure 14

Variation of the natural frequency with porosity index for second mode

Full size image
Fig. 15
figure 15

Variation of the natural frequency with porosity index for third mode

Full size image
Fig. 16
figure 16

Variation of the natural frequency with porosity index for fourth mode

Full size image
Table 5 Variation of natural frequencies \(\left( \omega \right)\) porosity volume fraction \(\left( \psi \right)\) for HH boundary condition
Full size table

4.5 Effect of elastic foundation

This subsection is aimed at analyzing the effect of the Kerr elastic foundation along with Winkler–Pasternak and Winkler foundations in special cases on the natural frequencies of HH, CH, CC, and CF boundary conditions. For the computational purpose, the power-law index \(\left( k \right)\) is taken as 0.5, and the porosity volume fraction \(\left( \psi \right)\) is considered as 0.1. For Kerr elastic foundation, the elastic moduli of upper and lower springs are equally varying as \(0,\,10^{3} ,\,10^{6} ,\,10^{9} ,\,10^{12}\) Pa, while the elastic modulus of shear layer is considered as \(0,\,10^{3} ,\,10^{6} ,\,10^{9} ,\,10^{12}\) N. Likewise, for the computation of Winkler–Pasternak model, elastic moduli of lower spring and shear layer are taken as \(0,\,10^{3} ,\,10^{6} ,\,10^{9} ,\,10^{12}\) Pa, and \(0,\,10^{3} ,\,10^{6} ,\,10^{9} ,\,10^{12}\) N, respectively. Finally, for Winkler foundation model, elastic moduli of lower spring are varies as \(0,\,10^{3} ,\,10^{6} ,\,10^{9} ,\,10^{12}\) Pa. The tabular results of all the above-mentioned boundary conditions are listed in Table 6. Based on this analysis, we conclude that, with the rise in elastic modulus of Kerr foundation, the natural frequencies of the FG beam display a mixed behavior that means natural frequencies decrease initially and then increase until the elastic moduli attain 1 GPa and then exhibit very less change in natural frequencies as we go on increasing elastic moduli. Also, for higher values of elastic constants, natural frequencies for the three types of elastic models are almost equal.

Table 6 Variation of natural frequencies \(\left( \omega \right)\) in kHz with various elastic foundations such as Kerr, Winkler–Pasternak, and Winkler elastic foundations
Full size table

5 Conclusion

In this investigation, the shifted Chebyshev polynomial-based Rayleigh–Ritz method is implemented to analyze the vibration characteristics of the FG beam placed on the Kerr foundation, having evenly distributed porosity along the thickness. Energy equations are developed for the use shifted Chebyshev polynomial-based Rayleigh–Ritz method, and Navier’s solution based model has also been implemented to solve the governing equations of motion in terms of displacement derived from Hamilton’s principle. A parametric analysis is also conducted, and the following are the main results:

  • Lower-mode frequencies such as first and second modes require number of polynomials \(n = 5\) for the convergence, while higher-mode frequencies, i.e., third and fourth modes, need more number of terms, i.e., \(n = 6\) for achieving the convergence.

  • With the increase in the power-law exponent \(\left( k \right)\), the natural frequencies of all the modes decrease, and this reduction is more remarkable when \(k < 2\). Also, at \(k = 0\), the beam purely ceramic possesses the highest value natural frequencies, while at \(k = \infty\), the beam is purely metallic with the lowest value natural frequencies.

  • With the rise of porosity volume \(\left( \psi \right)\), natural frequencies at \(k = 0\), i.e., purely ceramic, while for other values of the power-law index, i.e., \(k = 1,\,2,\,10\) etc., this trend is opposite that means natural frequencies reduce with the rise in porosity volume fraction.

  • With the increase in elastic modulus of Kerr foundation, the natural frequencies of the FG beam display a mixed behavior; natural frequencies decrease initially and then increase until the elastic moduli attain 1 GPa and then exhibit very less change toward the natural frequencies as we go on increasing elastic moduli. Also, for higher values of elastic constants, natural frequencies for the three types of elastic models are almost equal.