Development of a shell superelement for large deformation and free vibration analysis of composite spherical shells

Abstract

Finite element analysis of huge and/or complicated structures often requires long times and large computational expenses. Superelements are huge elements that exploit the deformation theory of a specific problem to provide the capability of discretizing the problem with minimum number of elements. They are employed to reduce the computational cost while retaining the accuracy of results in FEM analysis of engineering problems. In this research, a new shell superelement is presented to study linear/nonlinear static and free vibration analysis of spherical structures with partial or full spherical geometries that exist in many industrial applications. Furthermore, this study investigates the effects of changing the superelement size and its number of nodes on solution accuracy. The governing equations of composite spherical shells are derived based on the first-order shear deformation theory and considering large deformations. For solving the nonlinear governing equations, the tangent stiffness matrix has been extracted and the Newton–Raphson method is employed. The capability of the presented shell superelement is investigated in several problems under linear/nonlinear static and free vibration analysis. The results acquired by the presented shell superelements are compared with available results in the literature and conventional shell elements in a commercial software. Results comparisons reveal high accuracy at a reduced computational cost in the superelement model.

1 Introduction

Finite element method (FEM) has been widely used for analysis of engineering problems [1]. However, in some cases that the structure is huge or complicated, FEM requires tremendous computational costs [2]. This is mainly due to a large number of elements and nodes that should be considered for approximating the field variables in these problems. Recently, researchers have presented several approaches to overcome this shortcoming. In one approach, isogeometric analysis has been presented to eliminate the mesh generation process, which results in decreasing the solution time of engineering problems [3,4,5]. Another approach investigated in this study is the use of superelement, which considerably reduces the number of necessary elements and nodes, while providing an acceptable accuracy in the solution. Koko et al. [6, 7] analyzed stiffened plates using superelements. They used shear deformation theory and concluded that using superelements in nonlinear dynamic analysis of plates is highly efficient. Furthermore, they studied the vibration analysis of stiffened plates using their proposed superelement in Ref. [8]. Jiang et al. [9] studied static and dynamic analysis of stiffened cylindrical shells using superelements with considering geometric and material nonlinearities. Ahmadian et al. [10] investigated the free vibration analysis of composite plates using superelements.

In recent years, cylindrical, conical and spherical superelements have been introduced for static and vibration analysis of such structures. For instance, Bonakdar et al. [11] proposed a cylindrical superelement for static and dynamic analysis of multilayer composite cylinders. Also, Rezaei et al. [12] developed a tapered superelement to simulate tapered parts in the machine tools spindle. Furthermore, free vibration analysis of several FGM structures was studied by Torabi et al. [13] using a presented 3D superelement. The spherical superelement was initially presented by Nasiri et al. [14]. They studied static and free vibration analysis of the spherical structures using the presented superelement. Then, Shamloofard et al. [15] modified the spherical superelement designed in [14] and developed a thermo-elastic model of spherical and tapered superelements.

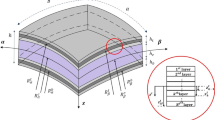
Laminated composite shells are frequently used in many structures, due to the high strength/weight ratio of composite structures [16, 17]. These structures are usually thin and are exposed to various and severe static and dynamic loads. Therefore, vibration behavior and deformation analysis of these structures are significantly important, and these issues have been recently discussed in many research studies. For instance, vibration characteristics of laminated doubly curved and spherical shells have been investigated by using different methods in Refs. [18,19,20,21,22,23,24,25,26,27,28,29]. In addition, deformation analysis of these shells has been studied by considering different approaches in Refs. [30,31,32,33,34,35,36,37,38,39].

The objective of this research study is to present a new shell superelement which is capable of discretizing complete and partial spherical shells and predicting linear/nonlinear static and free vibration behavior of composite spherical shells under local loads and boundary conditions. Moreover, this study recommends the optimum number of nodes in each shell superelement to achieve the best compromise between accuracy and computational cost. To the best of the authors’ knowledge, this subject has not been investigated for spherical, conical and cylindrical superelements which have been presented in the literature.

In what follows, the finite element equations for spherical shells are initially derived using first-order shear deformation theory (FSDT), next a spherical shell superelement is presented, and finally, through several problems, the results obtained from the proposed superelement are compared with the existing results in the literature and conventional shell elements in ANSYS software.

2 Background theory and governing equations

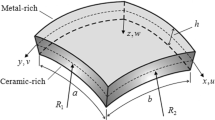
Based on FSDT and considering the spherical coordinate system, a displacement field $\left( {U_{\phi } , U_{\theta } ,W} \right)$ is related to displacements and rotations of mid-plane of the plate through the following equation [40]:

$$\begin{aligned} & U_{\phi } \left( {\phi ,\theta ,\xi } \right) = u_{\phi } \left( {\phi ,\theta } \right) + \xi \beta_{\phi } \left( {\phi ,\theta } \right) \\ & U_{\theta } \left( {\phi ,\theta ,\xi } \right) = u_{\theta } \left( {\phi ,\theta } \right) + \xi \beta_{\theta } \left( {\phi ,\theta } \right) \\ & W\left( {\phi ,\theta ,\xi } \right) = w\left( {\phi ,\theta } \right) \\ \end{aligned}$$

(1)

where $u_{\phi }$, $u_{\theta }$ and $w$ are the displacement components for points lying on the middle surface of the shell along with meridional, circumferential and normal directions, respectively. Also, $\beta_{\phi }$, $\beta_{\theta }$ and $\xi$ are normal-to-mid-surface rotations and distance from the mid-surface, respectively. Strain–displacement relations used in this paper are formulated based on the extension of the Sanders theory [41] and deal with the large deformation in the von Karman sense stated in Ref. [42]. For this case of geometric nonlinearity, small strains and moderate rotations are taken into consideration [40]. Using these assumptions as well as the FSDT for spherical shells with a radius of $R$, the strain–displacement equations are deduced as follows:

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{\varphi }^{{}} } \\ {\varepsilon_{\theta }^{{}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\varepsilon_{\varphi \xi }^{{}} } \\ {\varepsilon_{\theta \xi }^{{}} } \\ \end{array} } \\ {\varepsilon_{\varphi \theta }^{{}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{\varphi }^{0} } \\ {\varepsilon_{\theta }^{0} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\varepsilon_{\varphi \xi }^{0} } \\ {\varepsilon_{\theta \xi }^{0} } \\ \end{array} } \\ {\varepsilon_{\varphi \theta }^{0} } \\ \end{array} } \right\} + \xi \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\kappa_{\varphi } } \\ {\kappa_{\theta } } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\kappa_{\varphi \theta } } \\ \end{array} } \right\} \\ & \varepsilon_{\varphi }^{0} = \frac{1}{R}\left( {\frac{{\partial u_{\varphi } }}{\partial \varphi } + w} \right) + \frac{1}{2}\left( {\frac{1}{R}\frac{\partial w}{\partial \varphi }} \right)^{2} \\ & \varepsilon_{\theta }^{0} = \frac{1}{R\sin \left( \varphi \right)}\frac{{\partial u_{\theta } }}{\partial \theta } + \frac{\cot \left( \varphi \right)}{R}u_{\varphi } + \frac{w}{R} + \frac{1}{2}\left( {\frac{1}{R\sin \left( \varphi \right)}\frac{\partial w}{\partial \theta }} \right)^{2} \\ & \varepsilon_{\varphi \xi }^{0} = \frac{1}{R}\left( {\frac{\partial w}{\partial \varphi } - u_{\varphi } } \right) + \beta_{\varphi } \\ & \varepsilon_{\theta \xi }^{0} = \frac{1}{R\sin \left( \varphi \right)}\frac{\partial w}{{\partial \xi_{2} }} - \frac{{u_{\theta } }}{R} + \beta_{\theta } \\ & \varepsilon_{\varphi \theta }^{0} = \frac{1}{R}\frac{{\partial u_{\theta } }}{\partial \varphi } + \frac{1}{R\sin \left( \varphi \right)}\frac{{\partial u_{\varphi } }}{\partial \theta } {-}\frac{\cot \left( \varphi \right)}{R}v_{0} + \left( {\frac{1}{R}\frac{\partial w}{\partial \varphi }} \right)\left( {\frac{1}{R\sin \left( \varphi \right)}\frac{\partial w}{\partial \theta }} \right) \\ & \kappa_{\varphi } = \frac{1}{R}\frac{{\partial \beta_{\varphi } }}{\partial \varphi } \\ & \kappa_{\theta } = \frac{1}{R\sin \left( \varphi \right)}\left( {\frac{{\partial \beta_{\theta } }}{\partial \theta } + \frac{\cot \left( \varphi \right)}{R}\beta_{\varphi } } \right) \\ & \kappa_{\varphi \theta } = \frac{1}{R}\frac{{\partial \beta_{\theta } }}{\partial \varphi } + \frac{1}{R\sin \left( \varphi \right)}\frac{{\partial \beta_{\varphi } }}{\partial \theta } {-}\frac{\cot \left( \varphi \right)}{R}\beta_{\theta } \\ \end{aligned}$$

(2)

where the strains $\varepsilon_{\varphi }^{0}$, $\varepsilon_{\theta }^{0}$ and $\varepsilon_{\varphi \theta }^{0}$ are the in-plane meridional, circumferential and shearing components, $\varepsilon_{\varphi \xi }^{0}$ and $\varepsilon_{\theta \xi }^{0}$ are the transverse shearing strains, and $\kappa_{\varphi }$, $\kappa_{\theta }$ and $\kappa_{\varphi \theta }$ are the analogous curvature changes in the middle surface.

The relationship between stress resultants and couples with generalized strains and curvature variations on the middle surface can be summarized as:

$$\begin{aligned} & \left\{ {Q^{s} } \right\} = \left[ {A^{s} } \right]\left\{ \beta \right\} \\ & \left\{ N \right\} = \left[ A \right]\left\{ {\varepsilon^{0} } \right\} + \left[ B \right]\left\{ \kappa \right\} \\ & \left\{ M \right\} = \left[ B \right]\left\{ {\varepsilon^{0} } \right\} + \left[ D \right]\left\{ \kappa \right\}. \\ \end{aligned}$$

(3)

The strain vector $\left\{ {\varepsilon^{0} } \right\}$ is expressed as the sum of the two linear and nonlinear strain vectors:

$$\left\{ {\varepsilon^{0} } \right\} = \left\{ {\varepsilon^{0} } \right\}_{L} + \left\{ {\varepsilon^{0} } \right\}_{NL} .$$

(4)

Substituting Eq. (4) in Eq. (3) gives:

$$\left\{ N \right\} = \left[ A \right]\left\{ {\varepsilon^{0} } \right\}_{L} + \left[ A \right]\left\{ {\varepsilon^{0} } \right\}_{NL} + \left[ B \right]\left\{ \kappa \right\},\left\{ M \right\} = \left[ B \right]\left\{ {\varepsilon^{0} } \right\}_{L} + \left[ B \right]\left\{ {\varepsilon^{0} } \right\}_{NL} + \left[ D \right]\left\{ \kappa \right\}$$

(5)

where the components of the extensional stiffness A, bending extensional coupling stiffness B, bending stiffness D and transverse shear stiffness $A^{s}$ are defined as follows:

$$\begin{aligned} & \left( {A_{ij} \left( {\varphi ,\theta } \right), B_{ij} \left( {\varphi ,\theta } \right), D_{ij} \left( {\varphi ,\theta } \right)} \right) = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \bar{Q}_{ij} \left( {\varphi ,\theta } \right) \left( {1,\xi ,\xi^{2} } \right) {\text{d}}\xi \quad i,j = 1,2,6 \\ & A_{ij}^{s} \left( {\varphi ,\theta } \right) = K^{s} \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \bar{Q}_{ij} \left( {\varphi ,\theta } \right){\text{d}}\xi \quad i,j = 4,5 \\ \end{aligned}$$

(6)

where $h$ is the shell thickness and $K^{s}$ is the shear correction factor, which is usually set to 5/6 [43]. Also, $\bar{Q}_{ij}$ represents the transformed reduced stiffness which is computed for any arbitrary kth layer as follows:

$$\begin{aligned} & \bar{Q}_{11}^{\left( k \right)} = Q_{11}^{\left( k \right)} m^{4} + 2\left( {Q_{12}^{\left( k \right)} + 2Q_{66}^{\left( k \right)} } \right)n^{2} m^{2} + Q_{22}^{\left( k \right)} n^{4} \\ & \bar{Q}_{12}^{\left( k \right)} = \left( {Q_{11}^{\left( k \right)} + Q_{22}^{\left( k \right)} - 4Q_{66}^{\left( k \right)} } \right)n^{2} m^{2} + Q_{12}^{\left( k \right)} \left( {n^{4} + m^{4} } \right) \\ & \bar{Q}_{22}^{\left( k \right)} = Q_{11}^{\left( k \right)} n^{4} + 2\left( {Q_{12}^{\left( k \right)} + 2Q_{66}^{\left( k \right)} } \right)n^{2} m^{2} + Q_{22}^{\left( k \right)} m^{4} \\ & \bar{Q}_{66}^{\left( k \right)} = \left( {Q_{11}^{\left( k \right)} + Q_{22}^{\left( k \right)} - 2Q_{12}^{\left( k \right)} - 2Q_{66}^{\left( k \right)} } \right)n^{2} m^{2} + Q_{66}^{\left( k \right)} \left( {n^{4} + m^{4} } \right) \\ & \bar{Q}_{16}^{\left( k \right)} = \left( {Q_{11}^{\left( k \right)} - Q_{12}^{\left( k \right)} - 2Q_{66}^{\left( k \right)} } \right) n m^{3} + \left( {Q_{12}^{\left( k \right)} - Q_{22}^{\left( k \right)} + 2Q_{66}^{\left( k \right)} } \right)m n^{3} \\ & \bar{Q}_{26}^{\left( k \right)} = \left( {Q_{11}^{\left( k \right)} - Q_{12}^{\left( k \right)} - 2Q_{66}^{\left( k \right)} } \right)m n^{3} + \left( {Q_{12}^{\left( k \right)} - Q_{22}^{\left( k \right)} + 2Q_{66}^{\left( k \right)} } \right)n m^{3} \\ & \bar{Q}_{44}^{\left( k \right)} = Q_{44}^{\left( k \right)} m^{2} + Q_{55}^{\left( k \right)} n^{2} \\ & \bar{Q}_{55}^{\left( k \right)} = Q_{55}^{\left( k \right)} m^{2} + Q_{44}^{\left( k \right)} n^{2} \\ & \bar{Q}_{45}^{\left( k \right)} = \left( {Q_{44}^{\left( k \right)} - Q_{55}^{\left( k \right)} } \right)nm \\ & m = \cos \left( {\alpha_{1} } \right);\quad n = { \sin }\left( {\alpha_{1} } \right) \\ \end{aligned}$$

(7)

where $\alpha_{1}$ is the fiber orientation angle of the k^th lamina with respect to the shell coordinate system and elastic constants $Q_{ij}^{\left( k \right)}$ in each layer are given as follows:

$$\begin{aligned} & Q_{11}^{\left( k \right)} = \frac{{E_{1}^{\left( k \right)} }}{{1 - \nu_{12}^{\left( k \right)} \nu_{21}^{\left( k \right)} }},\quad Q_{22}^{\left( k \right)} = \frac{{E_{2}^{\left( k \right)} }}{{1 - \nu_{12}^{\left( k \right)} \nu_{21}^{\left( k \right)} }},\quad Q_{12}^{\left( k \right)} = \frac{{\nu_{12}^{\left( k \right)} E_{2}^{\left( k \right)} }}{{1 - \nu_{12}^{\left( k \right)} \nu_{21}^{\left( k \right)} }} \\ & Q_{66}^{\left( k \right)} = G_{12}^{\left( k \right)} ,\quad Q_{44}^{\left( k \right)} = G_{13}^{\left( k \right)} ,\quad Q_{55}^{\left( k \right)} = G_{23}^{\left( k \right)} \\ \end{aligned}$$

(8)

where $E_{1}^{\left( k \right)} ,E_{2}^{\left( k \right)} ,G_{12}^{\left( k \right)} ,G_{13}^{\left( k \right)} ,G_{23}^{\left( k \right)} ,\nu_{12}^{\left( k \right)}$ and $\nu_{21}^{\left( k \right)}$ are engineering parameters of the kth layer.

3 Finite element analysis

Based on FSDT, five degrees of freedom $u_{0}$, $v_{0}$, $w_{0}$, $\beta_{\varphi }$ and $\beta_{\theta }$ are considered for each node of the superelement. Displacements and rotations of an arbitrary point ($L$) are calculated as follows:

$$\begin{aligned} & u^{L} \left( {\varphi ,\theta } \right) = \mathop \sum \limits_{i = 1}^{npe} N_{i} \left( {\varphi ,\theta } \right)u_{i} \\ & v^{L} \left( {\varphi ,\theta } \right) = \mathop \sum \limits_{i = 1}^{npe} N_{i} \left( {\varphi ,\theta } \right)v_{i} \\ & w^{L} \left( {\varphi ,\theta } \right) = \mathop \sum \limits_{i = 1}^{npe} N_{i} \left( {\varphi ,\theta } \right)w_{i} \\ & \beta_{\varphi }^{L} \left( {\varphi ,\theta } \right) = \mathop \sum \limits_{i = 1}^{npe} N_{i} \left( {\varphi ,\theta } \right)\beta_{\varphi i} \\ & \beta_{\theta }^{L} \left( {\varphi ,\theta } \right) = \mathop \sum \limits_{i = 1}^{npe} N_{i} \left( {\varphi ,\theta } \right)\beta_{\theta i} \\ \end{aligned}$$

(9)

where $u_{i}$, $v_{i} ,w_{i}$, $\beta_{\theta i}$ and $\beta_{\varphi i}$ are displacements and rotations of the node $i$, N_i is the shape function of node $i$, and $npe$ is the number of nodes in each superelement. Equation (9) can also be described as the following equation:

$$\left\{ u \right\}_{5 \times 1} = \left[ N \right]_{5 \times 5npe} \left\{ U \right\}_{5npe \times 1}$$

$$[N] = \left[ {\begin{array}{*{20}l} {N_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & {N_{npe} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {N_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & {N_{npe} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {N_{1} } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & {N_{npe} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {N_{1} } \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {N_{npe} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {N_{1} } \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {N_{npe} } \hfill \\ \end{array} } \right]_{5 \times 5npe}$$

(10)

where $\left\{ U \right\}$ is the nodal displacement vector. Using Eq. (10), the relationship between nodal displacement vector with strain and curvature variations vectors can be deduced as below:

$$\begin{aligned} & \left\{ {\varepsilon^{0} } \right\}_{L} = \left[ {L_{m} } \right]\left[ N \right]\left\{ U \right\} = \left[ {B_{m} } \right]\left\{ U \right\} \\ & \left\{ \kappa \right\} = \left[ {L_{b} } \right]\left[ N \right]\left\{ U \right\} = \left[ {B_{b} } \right] \left\{ U \right\} \\ & \left\{ \beta \right\} = \left[ {L_{s} } \right]\left[ N \right]\left\{ U \right\} = \left[ {B_{s} } \right] \\ & \left\{ {\varepsilon_{NL}^{0} } \right\} = \left[ {L_{NL} } \right]\left[ N \right]\left\{ U \right\} = \left[ {B_{NL} } \right]\left\{ U \right\} \\ \end{aligned}$$

(11)

where $\left[ {B_{m} } \right],\left[ {B_{b} } \right],\left[ {B_{s} } \right]$ and $\left[ {B_{NL} } \right]$ are given in Appendix 1.

Following the finite element approach, the governing equation is concluded as follows:

$$\begin{aligned} & KU = F \\ & F = \mathop \sum \limits_{i = 1}^{ne} f_{i}^{\left( e \right)} ,K = \mathop \sum \limits_{i = 1}^{ne} K_{i}^{\left( e \right)} \\ & f^{\left( e \right)} = \mathop {\iint }\limits_{s}^{{}} \left[ N \right]^{T} \left\{ {f_{s} } \right\}{\text{d}}A + \sum \left[ N \right]^{T} \left\{ {f_{c} } \right\} \\ \end{aligned}$$

(12)

where $ne$, $F$, $f_{s}$, $f_{c}$ and $K$ are the number of superelements, total force vector, traction force, concentrated force and stiffness matrix computed as follows:

$$K^{\left( e \right)} = K_{1} + K_{2} + K_{3} + K_{4} + K_{5} + K_{6} + K_{7} + K_{8} + K_{9} + K_{10}$$

(13)

where $K_{1} ,K_{2} ,K_{3} , \ldots ,K_{10}$ are presented in Appendix 2.

The solution algorithm for solving the governing equations (Eq. (12)) is the iterative method of Newton–Raphson described in Appendix 3.

3.1 Free vibration analysis

For free vibration analysis, natural frequencies $\left( \omega \right)$ are calculated according to the eigenvalue equation in which $M$ is the mass matrix as follows:

$$\begin{aligned} & \left( {K - \omega^{2} M} \right)\lambda = 0 \\ & M^{\left( e \right)} = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ N \right]^{T} \left[ \rho \right]\left[ N \right] {\text{d}}A \\ & \left[ \rho \right] = \left[ {\begin{array}{*{20}c} {\rho_{0} } & 0 & 0 & {\rho_{1} } & 0 \\ 0 & {\rho_{0} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{0} } & 0 & 0 \\ {\rho_{1} } & 0 & 0 & {\rho_{2} } & 0 \\ 0 & 0 & 0 & 0 & {\rho_{2} } \\ \end{array} } \right] \\ \end{aligned}$$

(14)

where $\rho_{0}$, $\rho_{1}$ and $\rho_{2}$ are the normal, coupled normal-rotary and rotary inertial coefficients defined by:

$$\left( {\rho_{0} ,\rho_{1} ,\rho_{2} } \right) = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \rho \left( \xi \right) \left( {1,\xi ,\xi^{2} } \right){\text{d}}\xi .$$

(15)

4 Spherical shell superelement

The purpose of introducing this superelement is to present an element that can easily discretize spherical sectors with and without apex and complete spherical shells with fewer elements. Polynomial and circular shape functions are employed to obtain this spherical shell superelement in meridional and circumferential directions, respectively. Figures 1 and 2 show the arrangement of nodes in these directions.

Fig. 1

Arrangement of nodes in the meridional direction where three nodes are used in this direction

Fig. 2

Arrangement of nodes in the circumferential direction where 16 nodes are used in this direction

Along $\varphi$, Lagrange shape functions (polynomials) are utilized for approximating the field variables. By setting $M$ nodes in this direction, shape functions have the following form:

$$N_{i}^{\left( \varphi \right)} = A_{1} + A_{2} \varphi + \cdots + A_{M} \varphi^{M - 1} \quad i = 1,2,3, \ldots , M$$

(16)

where $A_{1} ,A_{2} , \ldots ,A_{M}$ are computed based on the definition of the shape functions as follows:

$$\begin{aligned} & N_{i}^{\left( \varphi \right)} = 1\,{\text{for}}\,\varphi = \varphi_{i} \\ & N_{i}^{\left( \varphi \right)} = 0\,{\text{for}}\,\varphi = \varphi_{1} ,\varphi_{2} , \ldots , \varphi_{i - 1} , \varphi_{i + 1} , \ldots , \varphi_{M} . \\ \end{aligned}$$

(17)

Along $\theta$, as stated earlier, circular shape functions are used according to [11, 15]. By selecting $N = 2^{n}$ nodes ($n$ is a positive integer parameter) in a circle, shape functions are obtained as:

$$\begin{aligned} & N_{j}^{\theta } = \frac{1}{{2^{n - 1} }}\cos \left( {2^{n - 2} \left( {\theta - \frac{{\left( {j - 1} \right)\pi }}{{2^{n - 1} }}} \right)} \right) \times \left[ {1 + \cos \left( {2^{n - 2} \left( {\theta - \frac{{\left( {j - 1} \right)\pi }}{{2^{n - 1} }}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2^{n - 3} \left( {\theta - \frac{{\left( {j - 1} \right)\pi }}{{2^{n - 1} }}} \right)} \right)} \right] \ldots \left[ {1 + \cos \left( {2^{0} \left( {\theta - \frac{{\left( {j - 1} \right)\pi }}{8}} \right)} \right)} \right],\quad j = 1,2,3, \ldots ,N. \\ \end{aligned}$$

(18)

Finally, shape functions for nodes of the superelement are calculated by multiplying Eqs. (16) and (18) as follows:

$$N_{i.j} \left( {\theta ,\varphi } \right) = N_{i}^{\varphi } \times N_{j}^{\theta } \quad i = 1,2,3, \ldots ,M;\quad j = 1,2,3, \ldots , N.$$

(19)

Equation (19) is implemented for all nodes except for those which are poles ($\varphi = 0, \pi$). Shape functions in polar nodes are achieved by setting $N_{j}^{\theta } = 1$ in Eq. (19) since these points are individually located in the circumferential direction

In the presented shell superelement, the number of nodes is computed as below:

$$\begin{array}{*{20}l} {npe = 1 + N *\left( {M - 1} \right)} \hfill & {{\text{Shell}}\,{\text{superelement}}\,{\text{including}}\,{\text{pole}}} \hfill \\ {npe = N *M} \hfill & {{\text{Shell}}\,{\text{superelement}}\,{\text{without}}\,{\text{a}}\,{\text{pole}}} \hfill \\ \end{array}.$$

(20)

Figures 3 and 4 depict the general form of the obtained spherical shell superelement with $M$ and $N$ nodes in meridional and circumferential directions. The shape functions of these superelements for cases (1) $M = 2, N = 16$ and (2) $M = 3, N = 16$ can be found in Appendix 4.

Fig. 3

$(M \times N$)-node superelement without a pole

Fig. 4

($1 + N *\left( {M - 1} \right)$)-node superelement including pole

By increasing the values of $M$ and $N$, converging to the solution will be more time-consuming. On the other hand, decreasing these values can deteriorate the accuracy of results. Therefore, the optimum values of $M$ and $N$ should be selected, which will be discussed in Sects. 5.1 and 5.2 for static and vibration analysis of the spherical shells.

Figures 5 and 6 display how the accuracy of the finite element solution could be increased using this superelement. In Figs. 5 and 6, the accuracy will be improved due to increasing (a) the number of superelements and (b) the number of nodes in each superelement, respectively.

Fig. 5

Increasing the number of superelements

Fig. 6

Increasing the number of circumferential nodes in each superelement

One of the most advantages of the presented superelement is that all axisymmetric shell structures can be discretized using this superelement. However, since the equations for spherical shells are presented in this study, this superelement is employed for analysis of the spherical shells.

4.1 Coordinate transformation

The governing equations derived in Sect. 3 have been presented in terms of the global coordinates $\left( {\varphi_{1} \le \varphi \le \varphi_{2} , 0 \le \theta \le 2\pi } \right)$. Since the numerical integration of the governing equations can be easily done using the local coordinate system ($- 1 \le \gamma ,\mu \le 1$), conversion of global coordinates to local ones should be determined. In this research, the linear transformation and isoparametric mapping are employed to convert the global coordinates to the local ones in the circumferential and meridional directions, respectively, as given below:

$$\begin{aligned} \theta = \pi \left( {\mu + 1} \right),\quad 0 \le \theta \le 2\pi ,\quad - 1 \le \mu \le 1 \hfill \\ \varphi = \mathop \sum \limits_{i = 1}^{npe} N_{i} \left( {\gamma ,\mu } \right)\bar{\varphi }_{i} ,\quad \varphi_{1} \le \varphi \le \varphi_{2} ,\quad - 1 \le \gamma \le 1. \hfill \\ \end{aligned}$$

(21)

Considering these mappings between global and local coordinates, the Jacobean matrix and infinitesimal area in the presented superelement are calculated as follows:

$$\begin{aligned} & J = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{\partial \varphi }{\partial \gamma }} & {\frac{\partial \theta }{\partial \gamma }} \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{\partial \varphi }{\partial \mu }} & {\frac{\partial \theta }{\partial \mu }} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} \left( {\gamma ,\mu } \right)}}{\partial \gamma }\bar{\varphi }_{i} } & 0 \\ {\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} \left( {\gamma ,\mu } \right)}}{\partial \mu }\bar{\varphi }_{i} } & \pi \\ \end{array} } \right] \\ & {\text{d}}A = R^{2} \sin \left( \varphi \right){\text{d}}\varphi {\text{d}}\theta = \det \left( J \right)R^{2} \sin \left( {\mathop \sum \limits_{i = 1}^{npe} N_{i} \left( {\gamma ,\mu } \right)\bar{\varphi }_{i} } \right){\text{d}}\gamma {\text{d}}\mu \\ \end{aligned}$$

(22)

where $\bar{\varphi }$ represents the nodal values of the superelement in the meridional coordinate.

5 Results

In this section, several examples are presented to investigate the accuracy of the presented shell superelement under various types of loadings. In these problems, the achieved results using the offered shell superelement model are compared to the results obtained by using four-node shell elements of ANSYS software and also available results in the literature. In problems 1 and 2, static analysis and free vibration behavior of the isotropic spherical shell are studied and the optimum number of nodes and elements in the superelement model is obtained. In the next problems, free vibration and linear/nonlinear static analysis of composite spherical shells will be numerically investigated.

5.1 Problem 1

In this problem, the internal pressure of $1\,{\text{MPa}}$ is applied to the hemispherical shell displayed in Fig. 7. The main objective of this problem is to find the optimum values of $N$ and $M$ (the number of nodes in the circumferential and meridional directions) in the presented shell superelement for static analysis of spherical shells. For this purpose, Figs. 8 and 9 illustrate the obtained radial displacements along $\varphi$ direction in paths #1 and 2 by two different methods: (1) using the presented spherical shell superelement with varied values of $N$ and (2) employing conventional shell elements of ANSYS software. Figures 8 and 9 show that setting $N = 4$ and 8 is not computationally accurate for this analysis, and the optimum value of $N$ to obtain the acceptable accuracy results is 16. Also, the effects of considering two different values of $M$ on the radial displacement at point A are investigated in Table 1. As presented in Table 1, $M = 2$ and $M = 3$ lead to a comparable accuracy, though setting $M = 3$ requires fewer elements and nodes. Therefore, this study recommends using the presented shell superelement with $N = 16$ and $M = 3$ for static analysis of spherical shells.

Fig. 7

The hemispherical shell in problem 1

Fig. 8

Comparison of radial displacements in path #1

Fig. 9

Comparison of radial displacements in path #2

Table 1 Comparison of radial displacement at point A in problem 1

5.2 Problem 2

Vibration analysis of the spherical shell depicted in Fig. 10 is presented. The aims of this problem are (1) to evaluate the performance of the spherical shell superelement in the prediction of natural frequencies, (2) to investigate the required number of nodes in each spherical shell superelement and (3) to study the effects of superelement size on the solution accuracy.

Fig. 10

The spherical shell in problem 2

Table 2 compares the natural frequencies obtained by conventional shell elements and different types of shell superelements. This table shows that using the spherical shell superelements with four and eight nodes in the $\theta$ direction cannot predict the natural frequencies of the studied shell accurately. On the other hand, although the accuracy of results cannot be meaningfully improved by employing N = 32, the solution time is significantly increased in this case. Therefore, similar to static analysis carried out in example 2, spherical shell superelements with $N = 16$ are selected for vibration analysis of the spherical shell. Furthermore, Table 3 compares the natural frequencies calculated by two different $M$ values. As can be seen in Table 3, less number of elements and nodes is required for setting $M = 3$, while retaining the same level of accuracy. Therefore, the optimum values of $N$ and $M$ that minimize the solution time and maximize the result accuracy are obtained by setting $N = 16$ and $M = 3$ for vibration analysis of the spherical shells.

Table 2 Comparison of the natural frequencies obtained by different $N$ values in problem 2

Table 3 Comparison of the natural frequencies obtained by different M values in problem 2

Figures 11 and 12 illustrate the dependency of the first and sixth natural frequencies of the studied shell to the number of conventional shell elements and shell superelements. As displayed in these figures, the number of required shell superelements for converging the solution is approximately 15 (481 nodes), while this number is about 4238 (4342 nodes) in the case of using conventional shell elements. Therefore, the number of required elements and nodes is significantly decreased when the problem is discretized via the presented shell superelement.

Fig. 11

Dependency of the first natural frequency to the number of conventional shell elements and shell superelements in problem 2

Fig. 12

Dependency of the sixth natural frequency to the number of conventional shell elements and shell superelements in problem 2

5.3 Problem 3

The main purpose of this problem is evaluating the performance of the composite spherical shell superelement in prediction of natural frequencies. For this purpose, free vibration analysis of a hemispherical shell ($R = 1000\,{\text{mm}}$) with the boundary conditions $u_{0} = v_{0} = w_{0} = \beta_{\varphi } = \beta_{\theta } = 0$ at the bottom edge and $u_{0} = v_{0} = \beta_{\theta } = 0$ at the apex is conducted for different shell thicknesses and fiber orientations. Material properties of this composite spherical shell are given in Table 4. In Table 5, fundamental natural frequency parameter ($\omega_{1} R\sqrt {\rho /E_{2} )}$ obtained by the composite spherical shell superelements is compared with the results presented in Refs. [18, 22] and conventional shell elements of ANSYS software. Results comparisons confirm the credibility of the composite spherical shell superelement in free vibration analysis.

Table 4 Material properties of the studied composite spherical shell

Table 5 Comparison of the fundamental frequency parameter for different shell thicknesses and fiber orientations among all approaches

5.4 Problem 4

The composite spherical shell displayed in Fig. 13 is subjected to the concentrated force ($F$). Material properties of this spherical shell are given in Table 4. Here, linear and nonlinear solutions are compared. Figure 14 shows the maximum deflection calculated by shell superelements and conventional shell elements for different values of $F$. As depicted in Fig. 14, by increasing the $F$ value, the difference between the results obtained by linear and nonlinear solutions grows significantly. The achieved results indicate that the same trend and proper consistency are observed between the conventional shell element of ANSYS software and the presented shell superelement model in both linear and nonlinear solutions. The solution procedure for the nonlinear equations is given in Appendix 3.

Fig. 13

The spherical shell in problem 4

Fig. 14

Variations of displacement under the load versus the magnitude of the force

5.5 Problem 5

The purpose of this problem is the linear static analysis of the composite spherical vessel shown in Fig. 15 with three different methods: using the proposed shell superelement, spherical superelements according to [15] and conventional shell elements of ANSYS software. Material properties of the used composite are given in Table 4. Since the spherical superelement developed in [15] is 3-dimensional, 3D elasticity equations are used to analyze the problem using this superelement. A total of 2524 shell elements in ANSYS, three spherical superelements with 228-node [15] and 16 spherical shell superelements with $N = 16$ and $M = 3$ of this work are employed to study this problem. Table 6 compares the maximum dimensionless radial displacement parameter ($\frac{{w_{ \hbox{max} } }}{h}$) obtained by these methods for different fiber orientations, shell radius-to-thickness ratios ($R/h$) and internal pressures ($q$). In all simulations, the radius of the vessel ($R$) and dimensionless parameter $Q = \left( {\frac{q}{{E_{2} }}} \right) \times \left( {\frac{R}{h}} \right)^{3}$ are set as $300\,{\text{mm}}$ and 50. Table 6 shows that high accuracy results are obtained in both superelement models. However, the required time for solving this problem using the proposed shell superelements is less, compared to 3D spherical superelements. This outcome is caused by the fewer Gaussian points in the presented shell superelements compared to the 3D spherical superelement. Therefore, by employing the presented shell superelement, the mechanical behavior of spherical vessels can be studied with a high level of accuracy and decreased computational cost.

Fig. 15

Pressure vessel in problem 5

Table 6 Comparing the maximum dimensionless radial displacement ($\frac{{w_{max} }}{h}$) in problem 5

It should be noted that the detailed information regarding the required number of Gaussian points in the spherical superelement can be found in Ref. [15].

5.6 Problem 6

The purpose of this problem is to evaluate the accuracy of the presented superelement model in comparison with the experimental results reported in Ref. [44]. In this problem, asymmetrical natural frequencies of a steel shallow spherical shell with clamped boundary conditions are studied. The material properties and geometry parameters of this spherical shell are given in Ref. [44]. Table 7 presents the asymmetrical natural frequencies resulted from experiment and the present shell superelement model. Comparisons of natural frequencies indicate the credibility of the superelement model, with the maximum error between the superelement model and experiment being around 3%.

Table 7 Comparison of natural frequencies in problem 6

6 Conclusions

In this paper, a new shell superelement for finite element analysis of spherical shell structures has been presented. This superelement deals with the first-order shear deformation theory and considering large deformation formulation. Comparing the results between the proposed shell superelement and conventional shell elements reveals that this superelement is capable of predicting structural, vibratory and nonlinear behavior of the spherical shell with high accuracy and decreased computational costs. Several significant properties obtained by the presented shell superelement are summarized as follows:

• The presented superelement can analyze partial spherical sectors with and without apex and complete spherical shells properly;

• For static and vibration analysis of spherical shells, the optimum number of nodes in each superelement is obtained by setting $M = 3$ and $N = 16$ resulting in 48-node superelement without apex and 33-node superelement with apex;

• In the mechanical analysis of the spherical vessels, employing the presented shell superelement is much more computationally efficient than that of the 3D spherical superelement presented in the literature, at the comparable level of accuracy;

• The presented superelement predicts the behavior of spherical shells under local loads and boundary conditions with acceptable level of accuracy.

Appendices

Appendix 1

$\left[ {B_{m} } \right],\left[ {B_{b} } \right],\left[ {B_{s} } \right]$ and $\left[ {B_{NL} } \right]$ are given as the following equations:

$$\begin{aligned} & \left[ {B_{m} } \right] \\ & \quad = \left[ {\begin{array}{*{20}l} {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }}} \hfill & 0 \hfill & {\frac{1}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }}} \hfill & 0 \hfill & {\frac{1}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill \\ {\frac{{\cot \left( \varphi \right)}}{R}N_{1} } \hfill & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} \hfill & {\frac{1}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & {\frac{{\cot \left( \varphi \right)}}{R}N_{i} } \hfill & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} \hfill & {\frac{1}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill \\ {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} \hfill & {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }} - \frac{{\cot \left( \varphi \right)}}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} \hfill & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }} - \frac{{\cot \left( \varphi \right)}}{R}N_{i} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] \\ & \left[ {B_{b} } \right] \\ & \quad = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }}} & 0 \\ 0 & 0 & 0 & {\frac{{\cot \left( \varphi \right)}}{R}N_{1} } & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} \\ 0 & 0 & 0 & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} & {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }} - \frac{{\cot \left( \varphi \right)}}{R}N_{1} } \\ \end{array} \begin{array}{*{20}c} \ldots & 0 & 0 & 0 & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }}} & 0 \\ \ldots & 0 & 0 & 0 & {\frac{{\cot \left( \varphi \right)}}{R}N_{i} } & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} \\ \ldots & 0 & 0 & 0 & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }} - \frac{{\cot \left( \varphi \right)}}{R}N_{i} } \\ \end{array} } \right] \\ & \left[ {B_{s} } \right] \\ & \quad = \left[ {\begin{array}{*{20}c} { - \frac{1}{R}N_{1} } & 0 & {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }}} & 1 & 0 \\ 0 & { - \frac{1}{R}N_{1} } & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} & 0 & 1 \\ \end{array} \begin{array}{*{20}c} {~~~ \ldots } & { - \frac{1}{R}N_{i} } & 0 & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }}} & 1 & 0 \\ {~~~ \ldots } & 0 & { - \frac{1}{R}N_{i} } & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} & 0 & 1 \\ \end{array} } \right] \\ & \left[ {B_{{NL}} } \right] = \left[ {\begin{array}{*{20}c} {B_{{NL}}^{{\left( 1 \right)}} } \\ {B_{{NL}}^{{\left( 2 \right)}} } \\ {B_{{NL}}^{{\left( 3 \right)}} } \\ \end{array} } \right] = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}\left\{ U \right\}^{T} ~\left\{ {\tilde{d}_{1} } \right\}^{T} \left\{ {\tilde{d}_{1} } \right\}} \\ {\frac{1}{2}\left\{ U \right\}^{T} ~\left\{ {\tilde{d}_{2} } \right\}^{T} \left\{ {\tilde{d}_{2} } \right\}} \\ {~~~\frac{1}{2}\left\{ U \right\}^{T} ~\left\{ {\tilde{d}_{1} } \right\}^{T} \left\{ {\tilde{d}_{2} } \right\}~} \\ \end{array} } \right\} \\ & [B_{{NL}} ] = \left[ {\begin{array}{*{20}c} {\frac{1}{{2R^{2} }}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{{\partial \varphi }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \varphi }}w_{i} \quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \frac{{\partial N_{{npe}} }}{{\partial \varphi }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \varphi }}w_{i} \quad 0\quad 0} \right\}} \\ {\frac{1}{{2R^{2} \sin ^{2} \left( \varphi \right)}}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{{\partial \theta }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \theta }}w_{i} \quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \frac{{\partial N_{{npe}} }}{{\partial \theta }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \theta }}w_{i} \quad 0\quad 0} \right\}} \\ {\frac{1}{{R^{2} \sin \left( \varphi \right)}}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{{\partial \theta }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \varphi }}w_{i} \quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \frac{{\partial N_{{npe}} }}{{\partial \theta }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \varphi }}w_{i} \quad 0\quad 0} \right\}.} \\ \end{array} } \right] \\ \end{aligned}$$

(23)

Appendix 2

$K_{1} ,K_{2} ,K_{3} , \ldots ,K_{10}$ are specified as the following equations:

$$\begin{aligned} K_{1} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{m} } \right]^{T} \left[ A \right]\left[ {B_{m} } \right]{\text{d}}A \\ K_{2} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{m} } \right]^{T} \left[ A \right]\left[ {B_{NL} } \right]{\text{d}}A \\ K_{3} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{m} } \right]^{T} \left[ B \right]\left[ {B_{b} } \right]{\text{d}}A \\ K_{4} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {\tilde{B}_{NL} } \right]^{T} \left[ A \right]\left[ {B_{m} } \right]{\text{d}}A \\ K_{5} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {\tilde{B}_{NL} } \right]^{T} \left[ A \right]\left[ {B_{NL} } \right]{\text{d}}A \\ K_{6} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {\tilde{B}_{NL} } \right]^{T} \left[ B \right]\left[ {B_{b} } \right]{\text{d}}A \\ K_{7} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{b} } \right]^{T} \left[ B \right]\left[ {B_{m} } \right] dA \\ K_{8} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{b} } \right]^{T} \left[ B \right]\left[ {B_{NL} } \right] dA \\ K_{9} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{b} } \right]^{T} \left[ D \right]\left[ {B_{b} } \right]{\text{d}}A \\ K_{10} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{s} } \right]^{T} \left[ {A_{s} } \right]\left[ {B_{s} } \right]{\text{d}}A. \\ \end{aligned}$$

(24)

In the above equation, $\left[ {\tilde{B}_{NL} } \right]$ is written as:

$$\begin{aligned} & \left[ {\tilde{B}_{NL} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{B}_{NL}^{\left( 1 \right)} } \\ {\tilde{B}_{NL}^{\left( 2 \right)} } \\ {\tilde{B}_{NL}^{\left( 3 \right)} } \\ \end{array} } \right] \\ & \tilde{B}_{NL}^{\left( 1 \right)} = \frac{1}{{R^{2} }}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{\partial \varphi }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \varphi }w_{i} \quad 0\quad 0\quad \cdots \quad \cdots 0\quad 0\quad \frac{{\partial N_{npe} }}{\partial \varphi }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \varphi }w_{i} \quad 0\quad 0} \right\} \\ & \tilde{B}_{NL}^{\left( 2 \right)} = \frac{1}{{R^{2} \sin^{2} \left( \varphi \right)}}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{\partial \theta }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \theta }w_{i} \quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \frac{{\partial N_{npe} }}{\partial \theta }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \theta }w_{i} \quad 0\quad 0} \right\} \\ & \tilde{B}_{NL}^{\left( 3 \right)} = \frac{1}{{R^{2} \sin \left( \varphi \right)}}\left\{ {0\quad 0\quad \left( {\frac{{\partial N_{1} }}{\partial \theta }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \varphi }w_{i} } \right) + \left( {\frac{{\partial N_{1} }}{\partial \varphi }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \theta }w_{i} } \right)\quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \left( {\frac{{\partial N_{npe} }}{\partial \theta }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \varphi }w_{i} } \right) + \left( {\frac{{\partial N_{npe} }}{\partial \varphi }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \theta }w_{i} } \right)\quad 0\quad 0} \right\}. \\ \end{aligned}$$

(25)

Appendix 3

This research uses the Newton–Raphson algorithm for solving the nonlinear governing equation as follows:

$$\begin{aligned} & \left[ {K^{t} \left( {\left\{ U \right\}^{r} } \right)} \right]\left\{ {\Delta U} \right\} = \left\{ F \right\} - \left[ {K \left( {\left\{ U \right\}^{r} } \right)} \right] \left\{ U \right\}^{r} \\ & \left\{ U \right\}^{r + 1} \,= \left\{ U \right\}^{r} + \left\{ {\Delta U} \right\} \\ \end{aligned}$$

(26)

where $K^{t}$ is the tangent stiffness matrix which is expressed as follows:

$$(K_{ij}^{t} )^{r} = K_{ik,j}^{r} U_{k}^{r} + K_{ij}^{r}$$

(27)

where

$$\begin{aligned} & K_{{ik,j}}^{r} = \left( {K_{2} } \right)_{{ik,j}}^{r} + \left( {K_{4} } \right)_{{ik,j}}^{r} + \left( {K_{5} } \right)_{{ik,j}}^{r} + \left( {K_{6} } \right)_{{ik,j}}^{r} + \left( {K_{8} } \right)_{{ik,j}}^{r} \\ & \left( {K_{2} } \right)_{{ik,j}}^{r} = \left( {B_{m} } \right)_{{pi}} ~\left( A \right)_{{pq}} ~\left( {B_{{NL}} } \right)_{{qk,j}} \\ & \left( {K_{4} } \right)_{{ik,j}}^{r} = \left( {\tilde{B}_{{NL}} } \right)_{{pi,j}} ~\left( A \right)_{{pq}} ~\left( {B_{m} } \right)_{{qk,j}} \\ & \left( {K_{5} } \right)_{{ik,j}}^{r} = \left( {\tilde{B}_{{NL}} } \right)_{{pi,j}} ~~~\left( A \right)_{{pq}} ~~~\left( {B_{{NL}} } \right)_{{qk}}^{r} + \left( {\tilde{B}_{{NL}} } \right)_{{pi}}^{r} ~~~\left( A \right)_{{pq}} ~~~\left( {B_{{NL}} } \right)_{{qk,j}} \\ & \left( {K_{6} } \right)_{{ik,j}} = \left( {\tilde{B}_{{NL}} } \right)_{{pi,j}} ~~~\left( B \right)_{{pq}} ~~~\left( {B_{b} } \right)_{{qk}} \\ & \left( {K_{8} } \right)_{{ik,j}} = \left( {B_{b} } \right)_{{pi}} ~~~\left( B \right)_{{pq}} ~~~\left( {B_{{NL}} } \right)_{{q,jk}} \\ & \quad i,j,k = 1:dof \times npe;\quad p,q = 1,2,3. \\ \end{aligned}$$

(28)

Nonzero terms of $\left( {B_{NL} } \right)_{pi,j}$ and $\left( {\tilde{B}_{NL} } \right)_{pi,j}$ matrices are defined as the following equations:

$$\left( {B_{NL} } \right)_{pi,j} = \left\{ {\begin{array}{*{20}c} {\left[ {B_{NL} } \right]_{1i,j} } \\ {\left[ {B_{NL} } \right]_{2i,j} } \\ {\left[ {B_{NL} } \right]_{3i,j} } \\ \end{array} } \right\},\left( {\tilde{B}_{NL} } \right)_{pi,j} = \left\{ {\begin{array}{*{20}c} {\left[ {\tilde{B}_{NL} } \right]_{1i,j} } \\ {\left[ {\tilde{B}_{NL} } \right]_{2i,j} } \\ {\left[ {\tilde{B}_{NL} } \right]_{3i,j} } \\ \end{array} } \right\}$$

(29)

where

$$\begin{aligned} & \left[ {B_{NL} } \right]_{1i,j} = \left[ {\begin{array}{*{20}c} {B_{1NLj}^{11} } & {B_{1NLj}^{12} } & \cdots & {B_{1NLj}^{1l} } \\ {B_{1NLj}^{21} } & {B_{1NLj}^{22} } & \cdots & {B_{1NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {B_{1NLj}^{k1} } & {B_{1NLj}^{k2} } & \cdots & {B_{1NLj}^{kl} } \\ \end{array} } \right],\quad \left[ {\tilde{B}_{NL} } \right]_{1i,j}= \left[ {\begin{array}{*{20}c} {\tilde{B}_{1NLj}^{11} } & {\tilde{B}_{1NLj}^{12} } & \cdots & {\tilde{B}_{1NLj}^{1l} } \\ {\tilde{B}_{1NLj}^{21} } & {\tilde{B}_{1NLj}^{22} } & \cdots & {\tilde{B}_{1NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{B}_{1NLj}^{k1} } & {\tilde{B}_{1NLj}^{k2} } & \cdots & {\tilde{B}_{1NLj}^{kl} } \\ \end{array} } \right] \\ & \left[ {B_{NL} } \right]_{2i,j} = \left[ {\begin{array}{*{20}c} {B_{2NLj}^{11} } & {B_{2NLj}^{12} } & \ldots & {B_{2NLj}^{1l} } \\ {B_{2NLj}^{21} } & {B_{2NLj}^{22} } & \ldots & {B_{2NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {B_{2NLj}^{k1} } & {B_{2NLj}^{k2} } & \ldots & {B_{2NLj}^{kl} } \\ \end{array} } \right],\quad \left[ {\tilde{B}_{NL} } \right]_{2i,j} = \left[ {\begin{array}{*{20}c} {\tilde{B}_{2NLj}^{11} } & {\tilde{B}_{2NLj}^{12} } & \cdots & {\tilde{B}_{2NLj}^{1l} } \\ {\tilde{B}_{2NLj}^{21} } & {\tilde{B}_{2NLj}^{22} } & \cdots & {\tilde{B}_{2NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{B}_{2NLj}^{k1} } & {\tilde{B}_{2NLj}^{k2} } & \cdots & {\tilde{B}_{2NLj}^{kl} } \\ \end{array} } \right] \\ & \left[ {B_{NL} } \right]_{3i,j} = \left[ {\begin{array}{*{20}c} {B_{3NLj}^{11} } & {B_{3NLj}^{12} } & \ldots & {B_{3NLj}^{1l} } \\ {B_{3NLj}^{21} } & {B_{3NLj}^{22} } & \ldots & {B_{3NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {B_{3NLj}^{k1} } & {B_{3NLj}^{k2} } & \ldots & {B_{3Lj}^{kl} } \\ \end{array} } \right] ,\quad \left[ {\tilde{B}_{NL} } \right]_{3i,j} = \left[ {\begin{array}{*{20}c} {\tilde{B}_{3NLj}^{11} } & {\tilde{B}_{3NLj}^{12} } & \cdots & {\tilde{B}_{3NLj}^{1l} } \\ {\tilde{B}_{3NLj}^{21} } & {\tilde{B}_{3NLj}^{22} } & \cdots & {\tilde{B}_{3NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{B}_{3NLj}^{k1} } & {\tilde{B}_{3NLj}^{k2} } & \cdots & {\tilde{B}_{3NLj}^{kl} } \\ \end{array} } \right] \\ & B_{1NLJ}^{kl} = \frac{1}{{2R^{2} }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\varphi } N_{l,\varphi } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad \tilde{B}_{1NLJ}^{kl} = \frac{1}{{R^{2} }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\varphi } N_{l,\varphi } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ & B_{2NLJ}^{kl} = \frac{1}{{2R^{2} \sin^{2} \left( \varphi \right)}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\theta } N_{l,\theta } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad \tilde{B}_{2NLJ}^{kl} = \frac{1}{{R^{2} \sin^{2} \left( \varphi \right)}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\theta } N_{l,\theta } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ & B_{3NLJ}^{kl} = \frac{1}{{R^{2} \sin \left( \varphi \right)}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\theta } N_{l,\varphi } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad \tilde{B}_{3NLJ}^{kl} = \frac{1}{{R^{2} \sin \left( \varphi \right)}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\theta } N_{l,\varphi } + N_{k,\varphi } N_{l,\theta } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]. \\ \end{aligned}$$

(30)

Appendix 4

Shape functions of the spherical shell superelement including pole in the local coordinate system are expressed as follows:

• (a) $M = 3, N = 16$:

  $$\begin{gathered} \begin{array}{*{20}c} {N_{i} = \frac{{\gamma \left( {\gamma - 1} \right)}}{2}} & {i = 1} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {N_{{2,i}} = \frac{{\left( {1 - \gamma } \right)\left( {1 + \gamma } \right)}}{4} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {i = 1 - 16} \hfill \\ {\quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right]} \hfill & {} \hfill \\ \end{array} \hfill \\ \begin{array}{*{20}l} {N_{{3,i}} = \frac{{\gamma \left( {\gamma + 1} \right)}}{8} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {i = 1 - 16} \hfill \\ {\quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right]} \hfill & {} \hfill \\ \end{array} \hfill \\ \end{gathered}$$

  (31)

• (b) $M = 2, N = 16$:

  $$\begin{gathered} \begin{array}{*{20}c} {N_{i} = \frac{{\left( {1 - \lambda } \right)}}{2}} & {i = 1} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {N_{{2,i}} = \frac{{\left( {1 + \lambda } \right)}}{{16}} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {i = 1 - 16} \hfill \\ {\quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right]} \hfill & {} \hfill \\ \end{array} \hfill \\ \end{gathered}$$

  (32)

Also, the shape functions of the spherical shell superelement without pole are given as follows:

• (a) $M = 3, N = 16$:

  $$\begin{array}{*{20}l} \begin{aligned} & N_{{1,{\text{i}}}} = \frac{{\gamma \left( {\gamma - 1} \right)}}{8} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16} \hfill \\ \begin{aligned} & N_{{2,{\text{i}}}} = \frac{{\left( {1 - \gamma } \right)\left( {1 + \gamma } \right)}}{4} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16} \hfill \\ \begin{aligned} & N_{{3,{\text{i}}}} = \frac{{\gamma \left( {\gamma + 1} \right)}}{8} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16} \hfill \\ \end{array}$$

  (33)

• (b) $M = 2, N = 16$:

  $$\begin{array}{*{20}l} \begin{aligned} & N_{{1,{\text{i}}}} = \frac{{\left( {1 - \lambda } \right)}}{{16}} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16} \hfill \\ \begin{aligned} & N_{{2,{\text{i}}}} = \frac{{\left( {1 + \lambda } \right)}}{{16}} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16~} \hfill \\ \end{array} .$$

  (34)