1 Introduction

Laminated composite structures falls into most active and revolutionary research fields in recent years. The reason for that is their suitability to be used for weight sensitive and high performance applications, as in civil, mechanical, aeronautical, automobile, petrochemical, naval and other engineering industries (Jones 1975; Fangueiro 2011). The laminated composite structures are exposed to unlike environmental condition both during manufacturing and their operational life. These structure experience small strain but large (finite) deformation due to combined action of hygro-thermo-mechanical loading. It is well known that, the combined hygrothermal load causes significant dimensional change in laminated structure and geometrical nonlinearity induce subsequently. Moreover, high temperature and moisture generally reduce the elastic moduli and degrade the strength of composites (Boukhoulda et al. 2006) due to the internal/residual stresses and the structure may lead to failure ultimately. In this regard, it is necessary to analyse the mechanical responses (bending/vibration/buckling etc.) of laminated structures carefully for the accurate prediction of responses for the final design. It is also true that the analytical and/or experimental analysis of such complex situation are not only tough but also hard to achieve in real life situation.

Finite element method (FEM) is proved to be the robust and versatile numerical tool for the modelling and analysis laminated structure of different geometries, support condition and complex loading by taking the effect of degraded material properties. Many theories have already been developed in past to analyse the laminated structure by taking with and/or without shear deformation into consideration such as classical laminate plate theory (CLPT), first order shear deformation theory (FSDT), higher order shear deformation theory (HSDT) and refined/layer wise theories (Reddy 2004; Tornabene et al. 2013; Khandan et al. 2012; Kant and Swaminathan 2001). It is also noted that the HSDT type of mid-plane kinematics is more accurate approximation for the transverse shear stress and strain in laminated structures and also useful to avoid shear correction factor (Khdeir et al. 1989).

In order to make the article self-standing few recent and earlier studies are discussed in the following line regarding the mid-plane kinematics (HSDT and FSDT), nonlinearity (Green–Lagrange and von-Karman) and/or degraded composite properties under combined hygro-thermo-mechanical load. Zhang and Kim (2006) developed two displacement based 4-noded quadrilateral elements (20 and 24 degrees of freedom) using the FSDT kinematics and von-Karman type nonlinearity to analyse the geometrical nonlinear bending behaviour of thin to moderately thick laminated composite plates. A simple C0 isoparametric finite element formulation based on the refined HSDT is developed to investigate the bending behaviour of laminated composite and sandwich plates by Tu et al. (2010). Baltacioglu et al. (2011) presented nonlinear static behaviour of rectangular laminated thick plates resting on elastic foundation using discrete singular convolution method in the framework of the FSDT and von-Karman nonlinear kinematics. Doxsee (1989) developed a HSDT model to investigate axisymmetric composite shells with and without soft core under hygrothermal load. Ram and Sinha (1991) examined the linear bending characteristics of laminated composite plates by considering hygrothermal dependent composite material properties using the FEM. Parhi et al. (2001) studied hygrothermal free vibration and the transient responses of multiple delaminated doubly curved composite shell using quadratic isoparametric finite element (FE) formulation based on the FSDT. Patel et al. (2002) presented FE solutions of static and dynamic behaviour of thick laminated composite plate based on the modified HSDT kinematics under hygrothermal load by taking the temperature and moisture dependent properties. Rao and Sinha (2004) developed a micro mechanics model to investigate the static behvaiour of multidirectional composites under temperature and moisture environments. Naidu and Sinha (2005) developed a mathematical model based on the FSDT and Green–Lagrange nonlinear kinematics to investigate the large deflection bending behaviour of laminated composite shell panel under hygrothermal environment. Kundu et al. (2007) analysed bending behaviour of laminated composite shells under hygrothermal environment using the FSDT mid-plane kinematics through geometrically nonlinear FE model. Lo et al. (2010) developed a global–local HSDT model to study the responses of laminated plate under hygrothermal environment by including temperature and moisture dependent material properties. Nanda and Pradyumna (2011) examined nonlinear dynamic behaviour of laminated shell panel under hygrothermal load by taking temperature and moisture dependent material properties. They have developed the numerical model based on the FSDT mid-plane kinematics and von-Karman type nonlinearity. Zenkour (2012) developed a refined (sinusoidal) shear deformation model to study the bending responses of angle-ply laminated composite plate subjected to hygrothermal loads by considering temperature and/or moisture-dependent material properties. Bending behaviour of multilayered composite and sandwich shells under hygrothermal environment has been analyzed by Brischetto (2013) using Carrera’s unified formulation. Sharma et al. (2013) presented analytical solutions of flexural behaviour of laminated composite doubly curved shell panel using FSDT mid-plane kinematics.

Few attempts have already been made in past by various researchers (Huang et al. 2004; Shi et al. 2014; Parhi and Singh 2014; Kumar et al. 2014; Shen 2001, 2002; Upadhyay et al. 2010; Lal et al. 2011) to investigate the structural responses (bending, vibration, buckling) of laminated composite plate/shell under the influence of coupled (hygro-thermo-mechanical) loading by taking the hygro-thermal dependent composite properties based on a micromechanical model approach. Thermal post-buckled vibration and thermal free vibration behaviour of single/doubly curved shell panel have been investigated using HSDT mid-plane kinematics and Green–Lagrange nonlinearity (Panda and Singh 2011; Panda and Mahapatra 2014) by taking temperature invariant composite properties. However, to the best of the authors’ knowledge, no study has been reported yet in open literature on the geometrically nonlinear flexural analysis of laminated composite doubly curved shell panel under combined hygro-thermo-mechanical loading by using HSDT mid-plane kinematics with Green–Lagrange nonlinearity and hygrothermal dependent composite material properties through a micromechanical model.

The motivation of the present study is to analyse the geometrically nonlinear bending behaviour of shear deformable laminated composite doubly curved shell panel under hygro-thermo-mechanical loading with temperature and/or moisture dependent material properties. A general nonlinear FE model for laminated composite doubly curved shell panel based on the HSDT mid-plane kinematics and Green–Lagrange type geometric nonlinearity under combined hygro-thermo-mechanical loading is developed for different shell geometries. The degraded composite material properties are included using a micromechanical model for the elevated temperature and moisture concentration. The material properties of the composite constituents are evaluated in terms of the **fibre and matrix properties and volume fractions of each constituent as well. In addition, all the nonlinear higher order terms are incorporated in the mathematical model to achieve the exact flexural behaviour of the structure under hostile environment. The system of governing equation is obtained through variational approach and discretised using nonlinear FEM steps. The desired nonlinear bending responses are computed through a direct iterative method. The convergence behaviour of the newly developed model has been checked and validated by comparing the responses with those available published results. Finally, effect of geometries, material properties and support conditions on the nonlinear flexural responses of laminated composite doubly curved shell panel under coupled hygro-thermo-mechanical loading are highlighted by solving several numerical illustrations.

2 General theoretical formulation

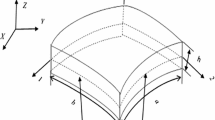
Figure 1 shows the geometry of typical laminated doubly curved shell panel with dimension say, length a, width b and thickness ‘h’. It is assumed that the panel is consist of ‘N’ number of uniformly thick layer and layer details as shown in the figure. In this present analysis, the laminated composite panel is assumed to be made of parallel fibres embedded in a matrix material. The composite constituents are considered as macroscopically homogeneous, orthotropic, and made of linearly elastic material. The fibres in each layer are assumed to be follow a constant angle with their coordinates. The intrinsic geometry of the shell is identical to its plane projection. Z k and Z k−1 are the top and bottom layer in the Z direction of any kth lamina. R 1 and R 2 are the principal radii of curvature defined at the mid-plane (z = 0) of the shell panel, which are considered to be constant throughout the analysis. The mid surface describe the geometries of various shell panel and defined based on the curvature say, spherical (R 1 = R 2 = R), cylindrical (R 1 = R; R 2 = ∞), elliptical (R 1 = 2R; R 2 = R), hyperboloid (R 1 = R and R 2 = −R), and flat (R 1 = R 2 = ∞). The present study also assume uniform hygrothermal load along with uniform lateral load on the shell panel.

Fig. 1
figure 1

Geometry of laminated doubly curved shell and layer details

Full size image

2.1 Displacement field and strain displacement relation

In order to derive present mathematical model, the HSDT type displacement field is considered, where the transverse shear strains are assumed to be parabolically distributed across the shell thickness. It is also possible to expand the displacement field in terms of the thickness coordinate up to any desired degree to achieve better accuracy. However, to avoid algebraic complexity and computational cost for very insignificant gain in accuracy, the present displacement field is assumed as follows (Szekrenyes 2014; Aragh et al. 2013):

$$ \begin{aligned} \bar{u}\left( {x,y,z} \right) & = u(x,y) + z\phi_{1} (x,y) + z^{2} \psi_{1} (x,y) + z^{3} \theta_{1} (x,y) \\ \bar{v}\left( {x,y,z} \right) & = v(x,y) + z\phi_{2} (x,y) + z^{2} \psi_{2} (x,y) + z^{3} \theta_{2} (x,y)\quad \left[ { - \frac{h}{2} \le z \le \frac{h}{2}} \right] \\ \bar{w}\left( {x,y,z} \right) & = w(x,y) \\ \end{aligned} $$
(1)

where, \( (\bar{u},\bar{v},\bar{w}) \) are the displacements of any point within the shell panel along x, y and z directions. \( \left( {u,v,w} \right) \) are displacements of any point in the mid-plane of the panel, \( \phi_{1} \) and \( \phi_{2} \) are the rotations of normal to the mid-plane in the directions of y and x-axis, respectively. The kinematic model also contain the functions \( \psi_{1} \), \( \psi_{2} \), \( \theta_{1} \) and \( \theta_{2} \), are the higher order terms of Taylor series expansion defined at the mid-plane and it account the parabolic distribution of shear stress.

2.2 Green–Lagrange strain–displacement relation

The Green–Lagrange strain–displacement relation is employed for the laminated composite doubly curved shell panel to compute the nonlinear distortion. The total strain corresponding to the displacement field is expressed as follows (Panda and Mahapatra 2014).

$$ \left\{ \varepsilon \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\bar{u}_{,x} } \hfill \\ {\bar{v}_{,y} } \hfill \\ {\left( {\bar{u}_{,y} + \bar{v}_{,x} } \right)} \hfill \\ {\left( {\bar{u}_{,z} + \bar{w}_{,x} } \right)} \hfill \\ {\left( {\bar{v}_{,z} + \bar{w}_{,y} } \right)} \hfill \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\left\{ {\left( {\bar{u}_{,x} } \right)^{2} + \left( {\bar{v}_{,x} } \right)^{2} + \left( {\bar{w}_{,x} } \right)^{2} } \right\}} \hfill \\ {\frac{1}{2}\left\{ {\left( {\bar{u}_{,y} } \right)^{2} + \left( {\bar{v}_{,y} } \right)^{2} + \left( {\bar{w}_{,y} } \right)^{2} } \right\}} \hfill \\ {\left\{ {\bar{u}_{,x} \bar{u}_{,y} + \bar{v}_{,x} \bar{v}_{,y} + \bar{w}_{,x} \bar{w}_{,y} } \right\}} \hfill \\ {\left\{ {\bar{u}_{,x} \bar{u}_{,z} + \bar{v}_{,x} \bar{v}_{,z} + \bar{w}_{,x} \bar{w}_{,z} } \right\}} \hfill \\ {\left\{ {\bar{u}_{,y} \bar{u}_{,z} + \bar{v}_{,y} \bar{v}_{,z} + \bar{w}_{,y} \bar{w}_{,z} } \right\}} \hfill \\ \end{array} } \right\} = \left\{ {\varepsilon_{L} } \right\} + \left\{ {\varepsilon_{NL} } \right\} $$
(2)

Now, using Eq. (1) in Eq. (2) the strain displacement relation of the laminated spherical shell is given by

$$ \begin{aligned} \varepsilon & = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\varepsilon_{xy}^{0} } \\ {\varepsilon_{xz}^{0} } \\ {\varepsilon_{yz}^{0} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{4} } \\ {\varepsilon_{y}^{4} } \\ {\varepsilon_{xy}^{4} } \\ {\varepsilon_{xz}^{4} } \\ {\varepsilon_{yz}^{4} } \\ \end{array} } \right\} + z\left[ {\left\{ {\begin{array}{*{20}c} {k_{x}^{1} } \\ {k_{y}^{1} } \\ {k_{xy}^{1} } \\ {k_{xz}^{1} } \\ {k_{yz}^{1} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {k_{x}^{5} } \\ {k_{y}^{5} } \\ {k_{xy}^{5} } \\ {k_{xz}^{5} } \\ {k_{yz}^{5} } \\ \end{array} } \right\}} \right] + z^{2} \left[ {\left\{ {\begin{array}{*{20}c} {k_{x}^{2} } \\ {k_{y}^{2} } \\ {k_{xy}^{2} } \\ {k_{xz}^{2} } \\ {k_{yz}^{2} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {k_{x}^{6} } \\ {k_{y}^{6} } \\ {k_{xy}^{6} } \\ {k_{xz}^{6} } \\ {k_{yz}^{6} } \\ \end{array} } \right\}} \right] \\ & \quad + z^{3} \left[ {\left\{ {\begin{array}{*{20}c} {k_{x}^{3} } \\ {k_{y}^{3} } \\ {k_{xy}^{3} } \\ {k_{xz}^{3} } \\ {k_{yz}^{3} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {k_{x}^{7} } \\ {k_{y}^{7} } \\ {k_{xy}^{7} } \\ {k_{xz}^{7} } \\ {k_{yz}^{7} } \\ \end{array} } \right\}} \right] + z^{4} \left\{ {\begin{array}{*{20}c} {k_{x}^{8} } \\ {k_{y}^{8} } \\ {k_{xy}^{8} } \\ {k_{xz}^{8} } \\ {k_{yz}^{8} } \\ \end{array} } \right\} + z^{5} \left\{ {\begin{array}{*{20}c} {k_{x}^{9} } \\ {k_{y}^{9} } \\ {k_{xy}^{9} } \\ {k_{xz}^{9} } \\ {k_{yz}^{9} } \\ \end{array} } \right\} + z^{6} \left\{ {\begin{array}{*{20}c} {k_{x}^{10} } \\ {k_{y}^{10} } \\ {k_{xy}^{10} } \\ {k_{xz}^{10} } \\ {k_{yz}^{10} } \\ \end{array} } \right\} \\ \end{aligned} $$
(3)

where

$$ \left\{ {\bar{\varepsilon }_{L} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{1}^{0} } & {\varepsilon_{2}^{0} } & {\varepsilon_{6}^{0} } & {\varepsilon_{5}^{0} } & {\varepsilon_{4}^{0} } & {k_{1}^{1} } & {k_{2}^{1} } & {k_{6}^{1} } & {k_{5}^{1} } & {k_{4}^{1} } \\ {k_{1}^{2} } & {k_{2}^{2} } & {k_{6}^{2} } & {k_{5}^{2} } & {k_{4}^{2} } & {k_{1}^{3} } & {k_{2}^{3} } & {k_{6}^{3} } & {k_{5}^{3} } & {k_{4}^{3} } \\ \end{array} } \right\}^{T} $$

and

$$ \left\{ {\bar{\varepsilon }_{NL} } \right\} = \frac{1}{2}\left\{ {\begin{array}{*{20}c} {\varepsilon_{1}^{4} } & {\varepsilon_{2}^{4} } & {\varepsilon_{6}^{4} } & {\varepsilon_{5}^{4} } & {\varepsilon_{4}^{4} } & {k_{1}^{5} } & {k_{2}^{5} } & {k_{6}^{5} } & {k_{5}^{5} } & {k_{4}^{5} } & {k_{1}^{6} } & {k_{2}^{6} } & {k_{6}^{6} } & {k_{5}^{6} } & {k_{4}^{6} } & {k_{1}^{7} } & {k_{2}^{7} } \\ {k_{6}^{7} } & {k_{5}^{7} } & {k_{4}^{7} } & {k_{1}^{8} } & {k_{2}^{8} } & {k_{6}^{8} } & {k_{5}^{8} } & {k_{4}^{8} } & {k_{1}^{9} } & {k_{2}^{9} } & {k_{6}^{9} } & {k_{5}^{9} } & {k_{4}^{9} } & {k_{1}^{10} } & {k_{2}^{10} } & {k_{6}^{10} } & {} \\ \end{array} } \right\}^{T} $$

are the linear and nonlinear mid-plane strain vectors, respectively.

The Eq. (3) can be rearranged in the following form:

$$ \left\{ \varepsilon \right\} = \left[ {\text{H}} \right]_{L} \left\{ {\bar{\varepsilon }_{L} } \right\} + \frac{1}{2}\left[ {\text{H}} \right]_{NL} \left\{ {\bar{\varepsilon }_{NL} } \right\} $$
(4)

where, \( \left[ {\text{H}} \right]_{L} \) and \( \left[ {\text{H}} \right]_{NL} \) are the linear and the nonlinear thickness coordinate matrices. \( \left\{ {\bar{\varepsilon }_{L} } \right\} \) and \( \left\{ {\bar{\varepsilon }_{NL} } \right\} \) are the mid-plane linear and nonlinear strains and functions of x and y only. The superscripts 0–3 and 4–10 are the extension, bending, curvature and higher order terms associated in the linear and the nonlinear strain vectors, respectively. The expanded form of each individual strain terms can be seen in Panda and Mahapatra (2014).

2.3 Hygro-thermo-elastic constitutive relation

In the present study, plane stress state is considered and both the temperature and moisture are assumed to be uniformly distributed over the panel geometry. In addition, the strains occurring due to temperature and moisture changes are assumed to be uncoupled. The hygro-thermo-elastic constitutive relation of any general kth composite lamina with arbitrary fibre orientation angle \( \theta \) under uniform hygrothermal load can be written as:

$$ \left\{ {\sigma_{ij} } \right\}^{k} = \left[ {\overline{{Q_{ij} }} } \right]^{k} \left\{ {\varepsilon_{ij} - \alpha_{ij}\Delta T - \beta_{ij} \Delta C} \right\}^{k} $$
(5)

where, \( \left\{ {\sigma_{ij} } \right\}^{k} = \left\{ {\begin{array}{*{20}c} {\sigma_{1} } & {\sigma_{2} } & {\sigma_{6} } & {\sigma_{5} } & \sigma \\ \end{array}_{4} } \right\}^{T} \) and \( \left\{ {\varepsilon_{ij} } \right\}^{k} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{1} } & {\varepsilon_{2} } & {\varepsilon_{6} } & {\varepsilon_{5} } & {\varepsilon_{4} } \\ \end{array} } \right\}^{T} \) are the stress and strain vectors respectively for any kth layer. \( \left[ {\overline{{Q_{ij} }} } \right]^{k} \) is transformed reduced stiffness matrix for any kth layer. \( \left\{ {\alpha_{ij} } \right\}^{k} = \left\{ {\begin{array}{*{20}c} {\alpha_{1} } & {\alpha_{2} } & {2\alpha_{12} } \\ \end{array} } \right\}^{T} \) is the thermal expansion/contraction coefficient vector and \( \left\{ {\beta_{ij} } \right\}^{k} = \left\{ {\begin{array}{*{20}c} {\beta_{1} } & {\beta_{2} } & {2\beta_{12} } \\ \end{array} } \right\}^{T} \) is the moisture expansion/contraction coefficient vector. Similarly, \( \Delta T \) and \( \Delta C \) are the temperature/weight percentage of moisture increments (difference between applied temperature/moisture, T/C to the reference temperature/moisture, T 0/C 0).

Now, Eq. (5) can be expanded as in the following form:

$$ \left\{ {\sigma_{ij} } \right\}^{k} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{16} } & 0 & 0 \\ {\overline{Q}_{21} } & {\overline{Q}_{22} } & {\overline{Q}_{26} } & 0 & 0 \\ {\overline{Q}_{16} } & {\overline{Q}_{26} } & {\overline{Q}_{66} } & 0 & 0 \\ 0 & 0 & 0 & {\overline{Q}_{55} } & {\overline{Q}_{54} } \\ 0 & 0 & 0 & {\overline{Q}_{45} } & {\overline{Q}_{44} } \\ \end{array} } \right]^{k} \left[ {\left\{ {\begin{array}{*{20}c} {\varepsilon_{1} } \\ {\varepsilon_{2} } \\ {\varepsilon_{6} } \\ {\varepsilon_{5} } \\ {\varepsilon_{4} } \\ \end{array} } \right\}_{l}^{k} - \left\{ {\begin{array}{*{20}c} {\alpha_{1} } \\ {\alpha_{2} } \\ {2\alpha_{12} } \\ 0 \\ 0 \\ \end{array} } \right\}^{k}\Delta T - \left\{ {\begin{array}{*{20}c} {\beta_{1} } \\ {\beta_{2} } \\ {2\beta_{12} } \\ 0 \\ 0 \\ \end{array} } \right\}^{k}\Delta C + \left\{ {\begin{array}{*{20}c} {\varepsilon_{1} } \\ {\varepsilon_{2} } \\ {\varepsilon_{6} } \\ {\varepsilon_{5} } \\ {\varepsilon_{4} } \\ \end{array} } \right\}_{nl}^{k} } \right] $$
(6)

2.4 Micromechanical model for property evaluation

The hygro-thermo-elastic properties of the composite lamina are influenced due to changes in temperature and/or moisture content and affect the final stiffness of the laminated structure. In order to include exact behaviour of laminated structure due to combined hygrothermal loading, the degraded material properties are evaluated based on the micromechanical model as in (Shen 2002). The individual parameter associated with composite properties are evaluated using the following relations.

The longitudinal and transverse thermal expansion coefficients are (Shen 2002):

$$ \begin{aligned} \alpha_{11} & = \frac{{V_{f} E_{f} \alpha_{f} + V_{m} E_{m} \alpha_{m} }}{{V_{f} E_{f} + V_{m} E_{m} }} \\ \alpha_{22} & = (1 + v_{f} )V_{f} \alpha_{f} + (1 + v_{m} )V_{m} \alpha_{m} - v_{12} \alpha_{11} ) \\ \end{aligned} $$
(7)

Similarly, the longitudinal and transverse coefficients of hygroscopic expansion of the composite lamina can be computed as:

$$ \begin{aligned} \beta_{11} & = \frac{{V_{f} E_{f} c_{fm} \beta_{f} + V_{m} E_{m} \beta_{m} }}{{E_{11} (V_{f} \rho_{f} c_{fm} + V_{m} \rho_{m} )}}\rho \\ \beta_{22} & = \frac{{V_{f} \left( {1 + v_{f} } \right)c_{fm} \beta_{f} + V_{m} \left( {1 + v_{m} } \right)\beta_{m} }}{{V_{f} \rho_{f} c_{fm} + V_{m} \rho_{m} }}\rho - v_{12} \beta_{11} \\ \end{aligned} $$
(8)

The \( \rho \), \( \rho_{f} \) and \( \rho_{m} \) are the mass densities of the composite lamina, fiber and matrix materials, respectively, and are related by simple rule of mixture (Voigt’s rule) as follows:

$$ \rho = V_{f} \rho_{f} + V_{m} \rho_{m} $$
(9)

The hygro-thermo elastic constants due to coupled temperature and moisture effect are evaluated as follows:

$$ \begin{aligned} E_{11} & = V_{f} E_{f} + V_{m} E_{m} \\ \frac{1}{{E_{22} }} & = \frac{{V_{f} }}{{E_{f} }} + \frac{{V_{m} }}{{E_{m} }} - V_{f} V_{m} \frac{{v_{f}^{2} E_{m} /E_{f} + v_{m}^{2} E_{f} /E_{m} - 2v_{f} v_{m} }}{{V_{f} E_{f} + V_{m} E_{m} }} \\ \frac{1}{{G_{12} }} & = \frac{{V_{f} }}{{G_{f} }} + \frac{{V_{m} }}{{G_{m} }} \\ v_{12} & = V_{f} v_{f} + V_{m} v_{m} \\ \end{aligned} $$
(10)

In Eqs. (7)–(10) volume fraction of each constituents have been utilized based on the following assumption:

$$ V_{f} + V_{m} = 1 $$
(11)

where, \( V \), E, G, \( v \), \( \alpha \) and \( c \) are volume, Young’s modulus, shear modulus, Poisson’s ratio, coefficient of thermal expansion, moisture concentration ratio. Similarly, \( \beta \) is the hygroscopic expansion coefficient and the subscripts “f” and “m” are used for fiber and matrix materials, respectively.

In the present analysis \( E_{m} \) is assumed to be function of temperature and weight percentage of moisture concentration, so that \( \alpha_{11} \), \( \alpha_{22} \), \( \beta_{11} \), \( \beta_{22} \), \( E_{11} \), \( E_{22} \), \( G_{12} \), \( G_{13} \) and \( G_{23} \) are also functions of temperature and moisture. The final constitutive equation as in Eq. (6) has been evaluated by using the Eqs. (7)–(11).

2.5 Strain energy of the shell panel

The strain energy of the doubly curved shell panel under combined hygro-thermo-mechanical loading can be expressed as

$$ U = \frac{1}{2}\iint {\left\{ {\sum\limits_{k = 1}^{N} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \varepsilon \right\}_{i}^{T} \left\{ {\sigma_{i} } \right\}dz} } } \right\}}dx\,dy $$
(12)

Now substituting the strain and resultant stress from Eqs. (4) and (5), the strain energy expression may be rewritten as

$$ \begin{aligned} U & = \frac{1}{2}\iint {\left\{ {\sum\limits_{k = 1}^{N} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \varepsilon \right\}_{i}^{T} \left[ {\bar{Q}} \right]\left\{ \varepsilon \right\}_{i} dz} } } \right\}}dx\,dy \\ & = \frac{1}{2}\iiint {\left\{ {\varepsilon_{L} + \varepsilon_{NL} } \right\}}^{T} \left[ {\bar{Q}} \right]\left\{ {\varepsilon_{L} + \varepsilon_{NL} } \right\}dx\,dy\,dz \\ \end{aligned} $$
(13)

Now, Eq. (13) can be further modified as

$$ \begin{aligned} U & = \frac{1}{2}\int_{A} {\left( {\left\{ {\varepsilon_{L} } \right\}_{i}^{T} \left[ {D_{1} } \right]\left\{ {\varepsilon_{L} } \right\}_{i} } \right)} dA \\ & \quad + \frac{1}{4}\int_{A} {\left( {\left\{ {\varepsilon_{L} } \right\}_{i}^{T} \left[ {D_{2} } \right]\left\{ {\varepsilon_{NL} } \right\}_{i} + \left\{ {\varepsilon_{NL} } \right\}_{i}^{T} \left[ {D_{3} } \right]\left\{ {\varepsilon_{L} } \right\}_{i} + \frac{1}{2}\left\{ {\varepsilon_{NL} } \right\}_{i}^{T} \left[ {D_{4} } \right]\left\{ {\varepsilon_{NL} } \right\}_{i} } \right)} dA \\ & = U_{L} + U_{NL} \\ \end{aligned} $$
(14)

where, \( \left[ {D_{1} } \right] = \sum\limits_{k = 1}^{N} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left[ H \right]_{L}^{T} \left[ {\bar{Q}} \right]\left[ H \right]_{L} dz} } \), \( \left[ {D_{2} } \right] = \sum\limits_{k = 1}^{N} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left[ H \right]_{L}^{T} \left[ {\bar{Q}} \right]\left[ H \right]_{NL} dz} } \), \( \left[ {D_{3} } \right] = \sum\limits_{k = 1}^{N} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left[ H \right]_{NL}^{T} \left[ {\bar{Q}} \right]\left[ H \right]_{L} dz} } \), \( \left[ {D_{4} } \right] = \sum\limits_{k = 1}^{N} {\int_{{z_{k - 1} }}^{{z_{k} }} {\left[ H \right]_{NL}^{T} \left[ {\bar{Q}} \right]\left[ H \right]_{NL} dz} } \).

2.6 Work done expression

Total work done due to the external applied uniformly distributed transverse static load q can be expressed as

$$ W = \int\limits_{A} {\left\{ \delta \right\}^{T} } qdA $$
(15)

where, the intensity of transverse static load is expressed in terms of the applied uniform lateral load as:

$$ q = \frac{{Qh^{4} E_{22} }}{{a^{4} }} $$
(16)

3 Solution methodology

3.1 Nonlinear finite element implementation

FEM is a versatile and powerful numerical tool and suitably adopted for the analysis of structure and/or structural component with complex geometry, material and loading conditions. The present nonlinear model is discretised using a nine noded isoparametric quadrilateral Lagrangian element with nine degrees of freedom per node \( \left( {u,v,w,\phi_{1} ,\phi_{2} ,\psi_{1} ,\psi_{2} ,\theta_{1} ,\theta_{2} } \right) \). The details of the element and the interpolation functions can be seen in (Cook et al. 2009).

The domain is discretized by employing the FEM steps and the displacement vector over each of the element may be expressed as follows:

$$ \begin{aligned} u & = \sum\limits_{i = 1}^{9} {N_{i} } u_{i} ,v = \sum\limits_{i = 1}^{9} {N_{i} } v_{i} ,w = \sum\limits_{i = 1}^{9} {N_{i} } w_{i} , \\ \phi_{1} & = \sum\limits_{i = 1}^{9} {N_{i} } \phi_{1i} ,\phi_{2} = \sum\limits_{i = 1}^{9} {N_{i} } \phi_{2i} , \\ \psi_{1} & = \sum\limits_{i = 1}^{9} {N_{i} } \psi_{1i} ,\psi_{2} = \sum\limits_{i = 1}^{9} {N_{i} } \psi_{2i} , \\ \theta_{1} & = \sum\limits_{i = 1}^{9} {N_{i} } \theta_{1i} ,\theta_{2} = \sum\limits_{i = 1}^{9} {N_{i} } \theta_{2i} \\ \end{aligned} $$
(17)

This equation can be rewritten in any general form as:

$$ \left\{ {\delta^{*} } \right\} = \left[ N \right]_{i} \left\{ \delta \right\}_{i} $$
(18)

where, \( \left[ N \right]_{i} \) and \( \left\{ \delta \right\}_{i} \) are the nodal shape function matrix and displacement field vector for any ith node, respectively. \( \left\{ {\delta^{*} } \right\} = \left\{ {\begin{array}{*{20}c} u & v & w & {\phi_{1} } & {\phi_{2} } & {\psi_{1} } & {\psi_{2} } & {\theta_{1} } & {\theta_{2} } \\ \end{array} } \right\}^{\text{T}} \) is the displacement vector for any general node.

Substituting the corresponding shape functions of the nodal displacement variable in the strain displacement relation of Eq. (4) and conceded as:

$$ \left\{ \varepsilon \right\} = \left[ {B_{i} } \right]\left\{ {\delta_{i} } \right\} $$
(19)

where, \( \left[ {B_{i} } \right] \) is the multiplication form of operator matrix and corresponding shape functions.

Now, substituting Eq. (19) into Eq. (14), the strain energy expression can be rewritten as:

$$ U = \frac{1}{2}\int_{A} {\left( {\begin{array}{*{20}l} {\left\{ {\delta^{*} } \right\}_{i}^{T} \left[ {B_{L} } \right]_{i}^{T} \left[ {D_{1} } \right]\left[ {B_{L} } \right]_{{{\kern 1pt} i}} \left\{ {\delta^{*} } \right\}_{i} } \hfill \\ { + \frac{1}{2}\left\{ {\delta^{*} } \right\}_{i}^{T} \left[ {B_{L} } \right]_{i}^{T} \left[ {D_{2} } \right]\left[ A \right]_{i} \left[ G \right]_{i} \left\{ {\delta^{*} } \right\}_{i} } \hfill \\ { + \frac{1}{2}\left\{ {\delta^{*} } \right\}_{i}^{T} \left[ G \right]_{i}^{T} \left[ A \right]_{i}^{T} \left[ {D_{3} } \right]\left[ {B_{L} } \right]_{i} \left\{ {\delta^{*} } \right\}_{i} } \hfill \\ { + \frac{1}{4}\left\{ {\delta^{*} } \right\}_{i}^{T} \left[ G \right]_{i}^{T} \left[ A \right]_{i}^{T} \left[ {D_{4} } \right]\left[ A \right]_{i} \left[ G \right]_{i} \left\{ {\delta^{*} } \right\}_{i} } \hfill \\ \end{array} } \right)} dA - \left\{ {F_{\Delta T} + F_{\Delta C} } \right\}_{i} $$
(20)

where, \( \left\{ {\varepsilon_{L} } \right\}_{i} = \left[ {B_{L} } \right]_{i} \left\{ {\delta^{*} } \right\}_{i} \), \( \left\{ {\varepsilon_{NL} } \right\}_{i} { = }\frac{1}{2}\left[ {B_{NL} \left( \delta \right)} \right]_{i} \left\{ {\delta^{*} } \right\}_{i} = \frac{1}{2}\left[ {A\left( \delta \right)} \right]_{i} \left[ G \right]_{i} \left\{ {\delta^{*} } \right\}_{i} \) and \( \left\{ {F_{{\Delta T}} + F_{{\Delta C}} } \right\}_{i} = \left[ D \right]\left[ {\left\{ \varepsilon \right\}_{i} - \left\{ \alpha \right\}\Delta T - \left\{ \beta \right\}\Delta C} \right] = \int_{A} {\left[ {B_{L} } \right]_{i}^{T} \left\{ {N_{\Delta T} + N_{\Delta C} } \right\}} dA \). \( \left[ {B_{L} } \right] \) and \( \left[ G \right] \) are the product form of the differential operator and nodal shape function matrices in the linear and the nonlinear strain terms, respectively. \( \left[ A \right] \) is the linearized form of the nonlinear strain matrix which is coupled with displacement terms and associated with nonlinear stiffness matrices. The expressions and individual terms of \( \left[ A \right] \) and \( \left[ G \right] \) can be seen in (Panda and Mahapatra 2014). \( \left\{ {F_{\Delta T} + F_{\Delta C} } \right\} \) is the hygrothermal load vector due to combined temperature and moisture effect.

3.2 System of governing equation and solution

The governing equation of laminated composite doubly curved shell panel under hygro-thermo-mechanical loading is obtained by minimizing the total energy expression. This results in

$$ \delta \,\Pi = 0 $$
(21)

where, Π = (U − W)

Using, Eqs. (15) and (20) in Eq. (21) the final system governing equation can be expressed as using the steps as in (Rajasekaran and Murray 1973):

$$ \left[ K \right]\left\{ \delta \right\} = \{ q\} \quad {\text{or}}\quad \left( {\left[ {K_{L} } \right] + \frac{1}{2}\left[ {K_{NL} } \right]_{1} + \frac{1}{3}\left[ {K_{NL} } \right]_{2} } \right)\left\{ \delta \right\} = \left\{ q \right\} $$
(22)

where, \( \left[ {K_{L} } \right] \) is the global linear stiffness matrix, \( \left[ {K_{NL} } \right]_{1} \) and \( \left[ {K_{NL} } \right]_{2} \) are the nonlinear coupled stiffness matrices which depend on the displacement vector linearly and quadratically, respectively.

Finally, Eq. (22) is solved through a direct iterative method (Reddy 2004) and the detailed solution steps are discussed in the following line:

Step-1 :

As a first step, stiffness matrices and force vectors over each element are evaluated by using the FEM concept.

Step-2 :

The elemental matrices are assembled and the global stiffness and force vector are calculated.

Step-3 :

By using the static equilibrium equation and dropping the nonlinear stiffness terms, linear response is obtained.

Step-4 :

The previous stiffness matrices are normalized and scaled up for finding and updating the nonlinear stiffness matrices.

Step-5 :

The iteration steps will be repeated until the two consecutive iterations achieve the tolerance limit (~10−3).

4 Results and discussion

A FE computer code has been developed in MATLAB environment using the proposed nonlinear model of laminated composite doubly curved shell panel under combined hygro-thermo-mechanical loading. Firstly, the model has been validated by comparing the responses with those available published result and subsequently the model is employed to compute new responses. The effect of different parameters on the nonlinear flexural behaviour of laminated composite doubly curved shell panel is highlighted. For the computational purpose, Graphite/epoxy composite properties have been utilized for throughout the analysis. The composite properties under unlike environmental condition are evaluated using the micromechanics model as discussed earlier by setting the initial properties (\( T_{0} \) = 25 °C and \( C_{0} \) = 0/wt% H2O) same as in (Shen 2002):

\( E_{f} \) = 230 GPa, \( G_{f} \) = 9.0 GPa, \( v_{f} \) = 0.203, \( v_{m} \) = 0.34, \( \alpha_{f} \) = −0.54 × 10−6/°C, \( \rho_{f} \) = 1750 kg/m3, \( \alpha_{m} \) = 45.0 × 10−6/°C, \( \rho_{m} \) = 1200 kg/m3, V f  = 0.6, \( c_{fm} \) = 0, \( \beta_{m} \) = 2.68 × 10−6/wt% H2O and \( E_{m} = (3.51 - 0.003T - 0.142C) \) GPa, where \( T = T_{0} +\Delta T \), and \( C = C_{0} +\Delta C \).

To avoid rigid body motion and to reduce the number of unknowns from final form of equation the following constraint conditions are used in the present analysis.

  1. (a)

    Simply support (SSSS):

    $$ \begin{aligned} & v = w = \varPhi_{2} = \varPsi_{2} = \theta_{2} = \, 0\;{\text{at}}\;x \, = \, 0,a\quad {\text{and}} \\ & u = w = \varPhi_{1} = \varPsi_{1} = \theta_{1} = \, 0\;{\text{at}}\;y \, = \, 0,b \\ \end{aligned} $$
  2. (b)

    Clamped condition (CCCC):

    $$ u = v = w = \varPhi_{1} = \varPhi_{2} = \varPsi_{1} = \varPsi_{2} = \theta_{1} = \theta_{2} = 0\;{\text{for}}\,{\text{both}}\quad x \, = \, 0,a\;{\text{and}}\;y = 0,b. $$
  3. (c)

    Hinged support (HHHH):

    $$ \begin{aligned} & u = v = w = \varPhi_{2} = \varPsi_{2} = \theta_{2} = \, 0\,{\text{at}}\,x = 0,a\quad {\text{and}} \\ & u = v = w = \varPhi_{1} = \varPsi_{1} = \theta_{1} = \, 0\,{\text{at}}\,y = 0,b \\ \end{aligned} $$

For the computation of new results five different load parameters (Q = 100, 200, 300, 400 and 500) are used in the present analysis. The linear/nonlinear transverse central deflections are nondimensionalised using the relations \( Q = (q/E_{2} )*(a/h)^{4} \) and \( w_{Central} = \frac{{w_{\hbox{max} } }}{h} \), respectively for throughout the analysis if not stated otherwise.

4.1 Convergence and comparison study

In this section, the convergence and comparison study of the present FE model has been established by solving some examples with different available geometries and support conditions. The convergence behaviour of flat/curved panels are computed for different mesh sizes are tabulated in Tables 1, 2 and 3. In addition to that, the results are also compared with those available references. The material and geometrical properties are taken to be same as the references for the computational purpose. Tables 1 and 2, present the nondimensional linear/nonlinear centre deflections of square anti-symmetric angle-ply ([±45°]2) and cross-ply ([0°/90°]2) laminated flat panels, respectively. The results are obtained for two different thickness ratios (a/h = 10 and a/h = 20), two support conditions (SSSS and CCCC), two sets of hygrothermal loads (ΔT = 300 °C, ΔC = 3 % and ΔT = 100 °C, ΔC = 1 %) and four mechanical load parameters (Q = 50, 100, 150, and 200) by setting V f  = 0.6. In addition, a square simply supported anti-symmetric angle-ply ([±45°]2) laminated composite spherical (R/a = 5) shell panel (a/h = 15, V f  = 0.5) under constant transverse load parameter (Q = 150) and two unlike hygrothermal load (ΔT = 50 °C, ΔC = 1 %; ΔT = 50 °C, ΔC = 1.5 %; ΔT = 100 °C, ΔC = 1 % and ΔT = 100 °C, ΔC = 1.5 %) is also examined and presented in Table 3. It is clear from the each table that, the present model is converging well with mesh refinement for all types of support conditions, combined loading and panel geometries. It is also observed that the nonlinear bending responses are in good agreement with that of the references. Based on the convergence, a (6 × 6) mesh is used to compute the responses for further analysis.

Table 1 Convergence and comparison study of nondimensional nonlinear central deflection of simply supported antisymmetric [45/-45]2 laminated composite flat panel (a/h = 10 and V f = 0.6)
Full size table
Table 2 Convergence and comparison behavior of linear/nonlinear central deflections of clamped cross ply [0/90]2 laminated composite flat panel (a/h = 20 and V f = 0.6)
Full size table
Table 3 Convergence and comparison behavior of linear/nonlinear central deflections of simply supported antisymmetric [45/-45]2 laminated composite spherical (R/a = 5, a/h = 15, Q = 150 and V f = 0.5)
Full size table

In order to build more confidence on the present nonlinear model few more comparison studies on flat and curved panels are discussed in this section. The nondimensional nonlinear central deflections of anti-symmetric angle-ply [±45°]2 laminated composite plate under different hygrothermal load and support conditions are computed and compared with those of the references (Kumar et al. 2014; Upadhyay et al. 2010). The material properties, geometrical parameters and volume fractions are taken same to be as in the references. The central deflections are plotted against two sets of transverse load parameter (Q = 100, 150 and 200 and Q = 0, 50, 100, 150 and 200) and presented Fig. 2a, b, respectively. The comparison study is further extended for one more simply supported square anti-symmetric angle-ply ([±45°]2) laminated spherical shell panel with R/a = 5, a/h = 15 and Q = 150 under combined hygrothermal environment. The responses are computed using the material and geometrical properties same as to be the reference (Lal et al. 2011) and presented in Table 4 for two volume fractions (V f = 0.4 and 0.6). It is clearly observed that the difference between the results increase as the volume fraction increases.

Fig. 2
figure 2

a, b Comparison study of nonlinear hygro-thermo-mechanical bending responses of laminated composite flat panels

Full size image
Table 4 Comparison study of nondimensional nonlinear bending behaviour of laminated composite spherical shell panel
Full size table

It is understood that the present model is converging well with mesh refinement and also well agreement with available analytical and/or numerical responses. The difference between the results indicate the effect of HSDT mid-plane kinematics with Green–Lagrange type nonlinearity instead of von-Karman nonlinear equations as adopted in all the references. The comparison study also reveals the effect and necessity of all the nonlinear higher order terms under combined action of loading in hostile environment of laminated structure with corrugated material properties.

4.2 Additional numerical illustrations

The present nonlinear model has been further extended to analyse the effect of geometrical and material parameters, hygrothermal conditions and support conditions on the bending behaviour of laminated composite doubly curved shell panel with degraded material properties through some numerical experimentation. For the computational purpose each of the ply of laminated shell is assumed to be of equal thickness by setting the total thickness as h = 5 mm. In addition, the panel is exposed to uniform rise in temperature and moisture concentration and through the thickness as well.

4.2.1 Effect of hygro-thermal conditions

The effect of percentage of moisture concentrations (ΔC = 0, 0.5, 1.0, 1.5, 2.0, 2.5 and 3.0 %) and uniform temperature increments (ΔT = 100 °C, ΔT = 200 °C and ΔT = 300 °C) on the nonlinear bending responses of single/doubly curved panel is presented in Fig. 3. The responses are computed for square simply supported anti-symmetric cross-ply laminated composite curved panel under uniform transverse load (Q = 400) by setting R/a = 40, a/h = 20 and V f = 0.6. It is observed that, the nondimensional nonlinear bending responses are decreasing monotonously with increase in temperature and moisture concentration for all types of shell geometries. This is due to the fact that the combined hygrothermal load not only induces high initial stress but also reduces the elastic strength of the laminated structure.

Fig. 3
figure 3

Effect of hygral and thermal loading on the nonlinear centre deflection of laminated composite doubly curved shell panel

Full size image

4.2.2 Effect of panel geometry

It is well known that, the shell panels are classified based on the curvature rather than their load bearing capacity. It is also true that the panel curvature regulate largely the membrane strength behaviour and play a key role in deformation analysis of curved panel structural component. The present example is to study the effect of various shell geometries on the nonlinear flexural behaviour of laminated composite shell panel under combined hygro-thermo-mechanical loading. For the present investigation, five different geometries (spherical, cylindrical, elliptical, hyperboloid and flat) of square simply supported antisymmetric cross ply ([0/90]2) laminated composite shell panel are analysed under four different hygrothermal loads (ΔT = 0 °C, ΔC = 0 %; ΔT = 100 °C, ΔC = 1 %; ΔT = 200 °C, ΔC = 2 % and ΔT = 300 °C, ΔC = 3 %) and five mechanical load parameters (Q = 100, 200, 300, 400 and 500) by setting a/h = 100, R/a = 40 and V f = 0.6. The responses are presented in Fig. 4a–d for all four sets of hygrothermal load in conjunction with the mechanical load. It is interesting to note that the nondimensional central deflection of each panel are increasing in a sequence of spherical, elliptical, cylindrical, hyperboloid and flat panel. It is also interesting to note that all the panels show soft spring type behaviour as the hygro-thermo-mechanical load increases.

Fig. 4
figure 4

a–d Effect of panel geometries and hygrothermal load on the nonlinear centre deflection of laminated composite doubly curved shell panel

Full size image

4.2.3 Effect of curvature ratio

In this present example, the effect of radius of curvature on the nonlinear bending responses of laminated composite doubly curved shell panel under hygro-thermo-mechanical load is examined. For the computation, clamped square anti-symmetric angle-ply ([±45°]2) laminated composite doubly curved shell panel (a/h = 80) under three distinct environmental conditions (ΔT = 0 °C, ΔC = 0 %; ΔT = 100 °C, ΔC = 1 %; and ΔT = 200 °C, ΔC = 2 %) are investigated for three curvature ratios (R/a = 10, 50 and 100). The responses are plotted in Fig. 5a–c for three different geometries (cylindrical, hyperboloid and elliptical) of shell panel and five different mechanical load parameters (Q = 100, 200, 300, 400 and 500). It is clear from the figures that the nondimensional central deflections of each panel increase with increase in curvature ratios and decreases as the hygrothermal load increases. It is also interesting to note that the responses are very distinct for each shell geometries for R/a = 10 and the differences very small for other two curvature ratios. It is important to note that the deflections are higher and lower for hyperboloid and elliptical panels, respectively whereas the cylindrical panel shows an in between value for each analysis.

Fig. 5
figure 5

a–c Effect of curvature ratio on the nonlinear centre deflection of laminated composite doubly curved shell panel

Full size image

4.2.4 Effect of thickness ratio

The effects of thickness ratio (a/h) on the nonlinear hygro-thermo-mechanical bending behaviour of square, symmetric cross-ply ([0°/90°]S) laminated composite doubly curved shell panel (R/a = 20) with CSCS support condition and V f = 0.6 is analysed in this present example. Figure 6 present bending responses of doubly curved shell panel against load parameters for three different thickness ratios (a/h = 10, 50 and 100). The nondimensional deflections are decreasing monotonously as the thickness ratio and the hygrothermal load parameters are increasing. It is also clearly observed that the thick shells are less sensitive to environmental effect in contrast to thin shell panel. In addition it is also noticed that the thin shell panels are showing soft spring type behaviour for each set of hygrothermal load.

Fig. 6
figure 6

a–c Effect of thickness ratio on the nonlinear centre deflection of laminated composite doubly curved shell panel

Full size image

4.2.5 Effect of aspect ratio

It is well known that the aspect ratio plays a vital role in design and analysis of the laminated structure and it inevitable when subjected to large deformation under hostile environment. In this example the effect of aspect ratio on nondimensional central deflection of symmetric angle-ply ([±45]S) laminated composite curved panel (a/h = 100, R/a = 50 and V f = 0.6) is examined. Numerical results are presented in Fig. 7a–c for three different geometries at three aspect ratios (a/b = 1, 1.5 and 2) and three sets of hygrothermal (ΔT = 0 °C, ΔC = 0 %; ΔT = 100 °C, ΔC = 1 %; and ΔT = 200 °C, ΔC = 2 %) load. It is observed that, the nonlinear central deflections decrease monotonically as the aspect ratio and hygrothermal load increases. It is because as the aspect ratio increases the load per unit area decreases subsequently and corresponding the structural strength increases. However, it is also observed that the nonlinearity is more pronounced in case of square panels instead of rectangular for each shell geometries (cylindrical, elliptical, hyperboloid) investigated in this example.

Fig. 7
figure 7

a–c Effect of aspect ratio on the nonlinear centre deflection of laminated composite doubly curved shell panel

Full size image

4.2.6 Effect of lamination scheme

It is well known that, the laminated structural stiffness properties tailored according to the lamination scheme through the orthotropic constitutive relation and which in turn affects the bending behaviour considerably. In this regard lamination scheme is one of the key factor in strength design while the elastic properties vary with unlike environmental condition. The nondimensional nonlinear centre deflection of fully clamped square, laminated doubly curved shell panel (R/a = 30, a/h = 60 and V f = 0.6) for four different lamination schemes (symmetric/anti-symmetric, cross-ply/angle-ply) under hygro-thermo-mechanical load are computed and presented in Fig. 8. It is observed that the symmetric laminations are less affected under hygrothermal loads in comparison to anti-symmetric laminations irrespective of the type of panel geometries. However, soft spring type of behaviour is also noticed for each lamination scheme in the present example.

Fig. 8
figure 8

a–d Effect of lamination scheme on the nonlinear centre deflection of laminated composite doubly curved shell panel

Full size image

4.2.7 Effect of support condition

Figure 9 present the effect of restrained conditions on the nondimensional nonlinear central deflection of square anti-symmetric angle-ply ([±45]2) laminated curved shell panel (R/a = 10, a/h = 20 and V f = 0.6) under combined hygro-thermo-mechanical load. The responses are computed for four different support conditions (SSSS, CCCC, SCSC and HHHH) under two sets of hygothermal load (ΔT = 0 °C, ΔC = 0 % and ΔT = 300 °C, ΔC = 3 %) and five mechanical load parameters (Q = 100, 200, 300, 400 and 500). It is noted that the nondimensional nonlinear central deflections are lower and higher for CCCC and SSSS support conditions, respectively. It is interesting to note that, the shell panel exhibit soft spring type behaviour for all support conditions irrespective of panel geometry except HHHH support at higher mechanical load parameter. The simply support conditions are following the same type of behavior as in HHHH at ambient condition.

Fig. 9
figure 9

a–c Effect of support conditions on the nonlinear centre deflection of laminated composite doubly curved shell panel

Full size image

4.2.8 Effect of volume fraction

It is true that the laminated structural strength is majorly governed by the fiber volume fraction and inevitable if the structure working under a hostile environment. In this present investigation the structural properties are evaluated through a micromechanics model by taking the matrix properties, fibre properties and fibre volume fractions to achieve a real life situation. The effect of fibre volume fraction on the linear/nonlinear bending behaviour of square simply supported anti-symmetric [±45]2 angle-ply laminated doubly curved shell panels (R/a = 15 and a/h = 50) under four sets of hygro-thermo-mechanical loading is analysed by taking Q = 300 and the responses are presented in Table 5. It is interesting to note that as the fibre volume fraction increases both the nondimensional linear and nonlinear bending responses (\( w_{l} \) and \( w_{nl} \)) decrease from V f  = 0.4–0.5 and then gradually increase up to V f  = 0.7. This is because of the fact that the structural strength greatly affected due to matrix dominant properties at lower fibre volume fraction (V f  = 0.4) and which in turn reduces the elastic strength of the composite.

Table 5 Effect of volume fraction on the linear/nonlinear centre deflection of laminated composite doubly curved shell panels under hygro-thermo-mechanical loading
Full size table

5 Conclusions

In this present article, the geometrical nonlinear flexural behaviour of single/doubly curved laminated composite shell panel is investigated using Green–Lagrange nonlinearity in the framework of HSDT kinematics under combined hygro-thermo-mechanical loading. In addition to that all the nonlinear higher order terms are included in the present model and a micromechanics model employed to incorporate the lamina degraded properties due to hygrothermal load. The nonlinear governing equation of laminated curved panel is obtained using variational principle and discretised using FE steps. The desired nonlinear solutions are computed using a direct iterative method and the comprehensive testing of the developed model has been checked with those available literature. Finally, the effect of hygrothermal conditions, the material properties, the support conditions, the aspect ratios, the thickness ratios, the curvature ratios and the fibre volume fractions on the nonlinear bending responses of laminated composite doubly curved shell panel have been highlighted through numerical experimentation. The specific conclusions are summarized in the following lines.

  1. (a)

    The flexural responses are significantly influenced by hygrothermal conditions and hygrothermal dependent thermal and mechanical properties irrespective of the geometry of the structure.

  2. (b)

    The nonlinear transverse central deflections increase with curvature ratios whereas, decrease with the thickness ratios and aspect ratios irrespective of the type of geometry, hygrothermal load and support conditions. However, the responses may not follow a monotonous trend for volume fractions of composite constituents.

  3. (c)

    It is understood from the support condition analysis that the nonlinear transverse central deflection decreases as the number of constraint increases monotonically. However, HHHH type of support does not follow the same trend under hygro-thermo-mechanical loading in contrast to other type of support conditions.

  4. (d)

    It is also seen that the symmetric laminations are less susceptible under hygrothermal load in comparison to the anti-symmetric laminations.

  5. (e)

    It is interesting to note that the spherical geometries are most efficient under combined hygro-thermo-mechanical load as compared to the other geometries and the strength of the panel decreases in a decline manner as elliptical, cylindrical, hyperboloid and flat.