1 Introduction

Engineering structural components such as domes, rocket motor casings, space vehicles, nuclear reactors, submarine hulls and pressure vessels experience sonic boom/blast pressure including the variable time-dependent loading during their service life. Hence, the designer’s quest is to evolve sophisticated methodologies for the modeling and analysis of the dynamic behavior of such components including the variable load pattern to imitate the actual cases. However, the improvement of the existing methodology and the introduction of new techniques are implemented every now and then to achieve a step closer to the exact case. The mathematical implementation of the exact profile of the time-dependent loading is not only complicated but also challenging to achieve the desired case. Additionally, the composite structural model with and without defect adds an extra amount of the complexity too. The fiber-reinforced composite structures are well known for their tailor-made orientational characteristics and can easily be altered according to the design requirement.

Further, to model the elastic and the deformation behavior of the layered structure under the influence of variable loading pattern, different theoretical models have been proposed in the past considering the effect of time and position. In this regard, the classical plate theory (CLPT), the first-order shear deformation theory (FSDT) [1,2,3,4,5,6] and the higher-order shear deformation theory (HSDT) [7,8,9,10] are proposed to model the mid-plane displacements. Similarly, a few solution techniques have also been proposed and implemented for the evaluation of desired responses namely, hyperbolic shear deformation beam theory [11], the 3D finite element analysis (FEA) [12], analytical methodologies [13,14,15], closed form [16] solutions. Additionally, the geometrical configuration including the structural distortion (large deformation) [17, 18] is modeled via either the von Karman strain–displacement relation [19, 20] or the Green–Lagrange strain kinematics [21, 22]. Subsequently, the research related to the large deformation analysis indicates that the von Karman strain–displacement relations [23] are unable to count the geometrical distortion (quadratic and cubic terms) correctly, since the kinematic theory assumed moderate rotation (\(10^\circ \ll\)) only. However, the Green–Lagrange strain is capable of modeling the layered structure appropriately including the full geometrical nonlinearity.

The review of research articles related to the displacement-based mid-plane theories and the nonlinear strain kinematics including the solution techniques was mainly for the intact layered structures. However, these structural components may be associated with the internal defect in the real condition, i.e., the debonding between the adjacent layers which may arise due to manufacturing defects such as air trapping and foreign particle insertions. It is important to note that the propagation of debonding between the layers during the service period may lead to the catastrophic failure of either the structural component or the full structure. Hence, the analysis of the layered structure without considering these common type of internal defect may not give a complete understanding. Therefore, a significant effort [24,25,26,27,28,29,30,31,32,33,34,35] has been made by different parts of the world related to the modeling of the laminated structure considering the debonded type of defect and unlike loading effect.

The review of research articles indicates that modeling of the laminated structure including the debonding defect and subsequent dynamic characteristics mainly utilized the FSDT type of mid-plane displacement kinematics. Additionally, the analysis of the curved panel composite structure including the effect of either single or the double curvature based on the HSDT kinematics has not yet been reported in the open literature. Moreover, von Karman type of strain kinematics is adopted by the majority to model the structural distortion instead of Green–Lagrange nonlinear strain for the evaluation of the large deformation performance. Hence, the authors of the current article made an effort for the first time to investigate the nonlinear dynamic behavior of the delaminated composite shell structures under blast/pulse loading using two types of the HSDT mid-plane theories and Green–Lagrange strain–displacement relations. The present generic model is derived considering the single (cylindrical) and double curvature (hyperboloid, elliptical and spherical) including all of the nonlinear higher-order terms. Also, the sub-laminate approach is adopted to model the inter-laminar debonding effect. The time-dependent structural responses are evaluated computationally with the help of an original MATLAB code by solving the equation of motion using the direct iterative technique including the average acceleration method (Newmark’s time integration) and the finite element (FE) steps. The convergence rate of the dynamic responses of the debonded structure including the model validity is established a priori. The effect of the loading amplitude and the loading time on the nonlinear dynamic responses of the delaminated structure including the geometrical configurations is computed via solving different numerical examples and discussed in detail.

2 Mathematical expression of structural panel

2.1 Geometrical configuration

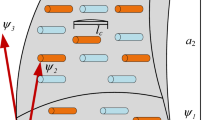
An orthogonal curvilinear coordinate system (\(\xi_{x} ,\xi_{y} ,\,\xi_{z}\)) is employed in the current work to define the pre-damaged composite curved panel structure (Fig. 1). The axis system is considered in such a way that, the \(\xi_{x} \,{\text{and}}\,\xi_{y}\) are lines of curvature on a surface \(\left( {\xi_{z} = 0} \right)\) and \(\xi_{z}\) is the line perpendicular to the surface \(\left( {\xi_{z} = 0} \right)\). The shell model is assumed to be composed of finite ‘N’ numbers of equally thick orthotropic laminas, oriented at an angle “\(\theta\)” with the corresponding coordinate axes. The length ‘a’; breadth ‘b’ and thickness ‘h’ are the parameters associated with the panel geometries along \(\xi_{x} ,\,\,\xi_{y} \,{\text{and}}\,\,\xi_{z} ,\) respectively. Similarly, \(r_{{\xi_{x} }} \,{\text{and}}\,r_{{\xi_{y} }}\) are the principal radii of curvature along the \(\xi_{x} \,{\text{and}}\,\xi_{y}\), respectively. In addition, the different geometries of the panel can be achieved by setting the appropriate radii of curvature as: \(\left( {r_{{\xi_{x} }} = \infty ,\,r_{{\xi_{y} }} = \infty } \right),\) plate; \(\left( {r_{{\xi_{x} }} = r,\,r_{{\xi_{y} }} = r} \right),\) spherical; \(\left( {r_{{\xi_{x} }} = r,\,\,r_{{\xi_{y} }} = \infty } \right),\) cylindrical; \(\left( {r_{{\xi_{x} }} = r,\,r_{{\xi_{y} }} = - r} \right),\) hyperboloid and \(\left( {r_{{\xi_{x} }} = r,\,r_{{\xi_{y} }} = 2r} \right),\) elliptical.

Fig. 1
figure 1

Geometry and layup sequence of the curved shallow shell structure

Full size image

The top view of the debonded panel including the zoomed view of the laminated and delaminated portions is presented in Fig. 2. The presence of delamination at a certain interface/plane divides the delaminated zone into upper and lower sub-laminates. Therefore, the entire laminate can be divided into three zones: (i) laminated zone, (ii) lower delaminated zone and (iii) upper delaminated zone. Now, all the zones, i.e., laminated, lower delaminated and upper delaminated are meshed separately via Element-I, Element-II and Element-III, respectively. It is important to discuss that Element-I, Element-II and Element-III are the same type of element, i.e., nine-noded isoparametric Lagrangian elements, but they have been given separate name zone-wise for the sake of brevity and better readability. Further, the mathematical expressions for the laminated and delaminated zones are derived separately and presented in the following lines.

Fig. 2
figure 2

Top view of the delaminated shell panel structure

Full size image

2.2 Displacement field kinematics

Two different types of higher-order mid-plane kinematics are used in the current work to model the displacement kinematics of the shell panel. The first (HSDT-I) and second (HSDT-II) kinematic models are associated with nine and ten space variables, respectively, as in the references [36, 37] for different kinematic models:

HSDT-I:

$$\left. \begin{aligned} & U_{x} \left( {\xi_{x} ,\xi_{y} ,\xi_{z} } \right) = u_{x} + \xi_{z} \alpha_{x} + \xi_{z}^{2} \,\psi_{x} + \xi_{z}^{3} \lambda_{x} \hfill \\ & U_{y} \left( {\xi_{x} ,\xi_{y} ,\xi_{z} } \right) = u_{y} + \xi_{z} \alpha_{y} + \xi_{z}^{2} \,\psi_{y} + \xi_{z}^{3} \lambda_{y} \hfill \\ & U_{z} \left( {\xi_{x} ,\xi_{y} ,\xi_{z} } \right) = u_{z} \hfill \\ \end{aligned} \right\}.$$
(1)

HSDT-II:

$$\left. \begin{aligned} & U_{x} \left( {\xi_{x} ,\xi_{y} ,\xi_{z} } \right) = u_{x} + \xi_{z} \alpha_{x} + \xi_{z}^{2} \,\psi_{x} + \xi_{z}^{3} \lambda_{x} \hfill \\ & U_{y} \left( {\xi_{x} ,\xi_{y} ,\xi_{z} } \right) = u_{y} + \xi_{z} \alpha_{y} + \xi_{z}^{2} \,\psi_{y} + \xi_{z}^{3} \lambda_{y} \hfill \\ & U_{z} \left( {\xi_{x} ,\xi_{y} ,\xi_{z} } \right) = u_{z} + \xi_{z} \alpha_{z} \hfill \\ \end{aligned} \right\},$$
(2)

where \(U_{x} ,\,U_{y}\) and \(U_{z}\) denote the displacement variable of any general point along the corresponding coordinate axes, i.e., \(\xi_{x} ,\xi_{y}\) and \(\xi_{z}\), respectively. In continuation to that, the other individual space variables associated with both the deformation kinematics are the displacements (\(u_{x} ,u_{y} \,{\text{and}}\,u_{z}\)), rotation of the transverse normal to the mid-plane (\(\alpha_{x} \,{\text{and}}\,\alpha_{y}\)) and the remaining (\(\alpha_{z} ,\,\psi_{x} ,\,\,\psi_{y} ,\,\,\lambda_{x} ,\,\,\lambda_{y}\)) are the higher-order terms defined on the mid-plane.

2.3 Stress–strain constitutive relations

The generalized form of the stress–strain relation for any kth lamina, oriented at an angle ‘\(\varphi\)’ about any arbitrary axis can be expressed mathematically as:

$$\left\{ {\begin{array}{*{20}l} {\sigma_{{\xi_{x} \xi_{x} }} } \\ \begin{aligned} \sigma_{{\xi_{y} \xi_{y} }} \hfill \\ \sigma_{{\xi_{z} \xi_{z} }} \hfill \\ \end{aligned} \\ {\sigma_{{\xi_{y} \xi_{z} }} } \\ {\sigma_{{\xi_{x} \xi_{z} }} } \\ {\sigma_{{\xi_{x} \xi_{y} }} } \\ \end{array} } \right\}^{k} = \left[ {\begin{array}{*{20}l} {\bar{Q}_{11} } & {\bar{Q}_{12} } & {\bar{Q}_{13} } & 0 & 0 & {\bar{Q}_{16} } \\ {\bar{Q}_{12} } & {\bar{Q}_{22} } & {\bar{Q}_{23} } & 0 & 0 & {\bar{Q}_{26} } \\ {\bar{Q}_{13} } & {\bar{Q}_{23} } & {\bar{Q}_{33} } & 0 & 0 & {\bar{Q}_{36} } \\ 0 & 0 & 0 & {\bar{Q}_{44} } & {\bar{Q}_{45} } & 0 \\ 0 & 0 & 0 & {\bar{Q}_{54} } & {\bar{Q}_{55} } & 0 \\ {\bar{Q}_{16} } & {\bar{Q}_{26} } & {\bar{Q}_{36} } & 0 & 0 & {\bar{Q}_{66} } \\ \end{array} } \right]^{k} \,\left\{ {\begin{array}{*{20}l} {\varepsilon_{{\xi_{x} \xi_{x} }} } \\ \begin{aligned} \varepsilon_{{\xi_{y} \xi_{y} }} \hfill \\ \varepsilon_{{\xi_{z} \xi_{z} }} \hfill \\ \end{aligned} \\ {\varepsilon_{{\xi_{y} \xi_{z} }} } \\ {\varepsilon_{{\xi_{x} \xi_{z} }} } \\ {\varepsilon_{{\xi_{x} \xi_{y} }} } \\ \end{array} } \right\}^{k} ,$$
(3)
$$\left\{ {\sigma_{ij} } \right\} = \left[ {\overline{Q}_{ij} } \right]\left\{ {\varepsilon_{ij} } \right\},$$
(4)

where \(\left\{ {\sigma_{ij} } \right\}\), \(\left[ {\overline{Q}_{ij} } \right]\) and \(\left\{ {\varepsilon_{ij} } \right\}\) are the stress tensor, the elastic property matrix, and the strain tensor, respectively. The elaborated form of the constitutive relation can be seen in Jones [38].

2.4 Strain–displacement relation

Further, the strain can be elaborated using the generalized strain–displacement relations for any material continuum via Green’s strain (Reddy [39]) for the inclusion of the geometrical distortion and their mathematical form can be presented as:

$$\left\{ {\begin{array}{*{20}l} {\varepsilon_{{\xi_{x} \xi_{x} }} } \\ \begin{aligned} \varepsilon_{{\xi_{y} \xi_{y} }} \hfill \\ \varepsilon_{{\xi_{z} \xi_{z} }} \hfill \\ \end{aligned} \\ {\varepsilon_{{\xi_{y} \xi_{z} }} } \\ {\varepsilon_{{\xi_{x} \xi_{z} }} } \\ {\varepsilon_{{\xi_{x} \xi_{y} }} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{x} }} + \frac{{U_{z} }}{{r_{{\xi_{x} }} }}} \right)} \\ \begin{aligned} \left( {\frac{{\partial U_{y} }}{{\partial \xi_{y} }} + \frac{{U_{z} }}{{r_{{\xi_{y} }} }}} \right) \hfill \\ \left( {\frac{{\partial U_{z} }}{{\partial \xi_{z} }}} \right) \hfill \\ \end{aligned} \\ {\left( {\frac{{\partial U_{y} }}{{\partial \xi_{z} }} + \frac{{\partial U_{z} }}{{\partial \xi_{y} }} - \frac{{U_{y} }}{{r_{{\xi_{y} }} }}} \right)} \\ {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{z} }} + \frac{{\partial U_{z} }}{{\partial \xi_{x} }} - \frac{{U_{x} }}{{r_{{\xi_{x} }} }}} \right)} \\ {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{y} }} + \frac{{\partial U_{y} }}{{\partial \xi_{x} }} + 2\frac{{U_{z} }}{{r_{{\xi_{x} \xi_{y} }} }}} \right)} \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\left\{ {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{x} }} + \frac{{U_{z} }}{{r_{{\xi_{x} }} }}} \right)^{2} + \left( {\frac{{\partial U_{y} }}{{\partial \xi_{x} }} + \frac{{U_{z} }}{{r_{{\xi_{x} \xi_{y} }} }}} \right)^{2} + \left( {\frac{{\partial U_{z} }}{{\partial \xi_{x} }} - \frac{{U_{x} }}{{r_{{\xi_{x} }} }}} \right)^{2} } \right\}} \\ {\frac{1}{2}\left\{ {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{y} }} + \frac{{U_{z} }}{{r_{{\xi_{x} \xi_{y} }} }}} \right)^{2} + \left( {\frac{{\partial U_{y} }}{{\partial \xi_{y} }} + \frac{{U_{z} }}{{r_{{\xi_{2} }} }}} \right)^{2} + \left( {\frac{{\partial U_{z} }}{{\partial \xi_{y} }} - \frac{{U_{y} }}{{r_{{\xi_{2} }} }}} \right)^{2} } \right\}} \\ {\frac{1}{2}\left[ {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{z} }}} \right)^{2} + \left( {\frac{{\partial U_{y} }}{{\partial \xi_{z} }}} \right)^{2} + \left( {\frac{{\partial U_{z} }}{{\partial \xi_{z} }}} \right)^{2} } \right]} \\ {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{y} }} + \frac{{U_{z} }}{{r_{{\xi_{x} \xi_{y} }} }}} \right)\left( {\frac{{\partial U_{x} }}{{\partial \xi_{z} }}} \right) + \left( {\frac{{\partial U_{y} }}{{\partial \xi_{y} }} + \frac{{U_{z} }}{{r_{{\xi_{y} }} }}} \right)\left( {\frac{{\partial U_{y} }}{{\partial \xi_{z} }}} \right) + \left( {\frac{{\partial U_{z} }}{{\partial \xi_{y} }} - \frac{{U_{y} }}{{r_{{\xi_{y} }} }}} \right)\left( {\frac{{\partial U_{z} }}{{\partial \xi_{z} }}} \right)} \\ {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{x} }} + \frac{{U_{z} }}{{r_{{\xi_{x} }} }}} \right)\left( {\frac{{\partial U_{x} }}{{\partial \xi_{z} }}} \right) + \left( {\frac{{\partial U_{y} }}{{\partial \xi_{x} }} + \frac{{U_{z} }}{{r_{{\xi_{x} \xi_{y} }} }}} \right)\left( {\frac{{\partial U_{y} }}{{\partial \xi_{z} }}} \right) + \left( {\frac{{\partial U_{z} }}{{\partial \xi_{x} }} - \frac{{U_{x} }}{{r_{{\xi_{x} }} }}} \right)\left( {\frac{{\partial U_{z} }}{{\partial \xi_{z} }}} \right)} \\ {\left( {\frac{{\partial U_{x} }}{{\partial \xi_{x} }} + \frac{{U_{z} }}{{r_{{\xi_{x} }} }}} \right)\left( {\frac{{\partial U_{x} }}{{\partial \xi_{y} }} + \frac{{U_{z} }}{{r_{{\xi_{x} \xi_{y} }} }}} \right) + \left( {\frac{{\partial U_{y} }}{{\partial \xi_{x} }} + \frac{{U_{z} }}{{r_{{\xi_{x} \xi_{x} }} }}} \right)\left( {\frac{{\partial U_{y} }}{{\partial \xi_{y} }} + \frac{{U_{z} }}{{r_{{\xi_{y} }} }}} \right) + \left( {\frac{{\partial U_{z} }}{{\partial \xi_{x} }} - \frac{{U_{x} }}{{r_{{\xi_{x} }} }}} \right)\left( {\frac{{\partial U_{z} }}{{\partial \xi_{y} }} - \frac{{U_{y} }}{{r_{{\xi_{y} }} }}} \right)} \\ \end{array} } \right\},$$
(5)
$$\left\{ {\varepsilon_{ij} } \right\} = \{ \varepsilon_{\text{l}} \} + \{ \varepsilon_{\text{nl}} \} ,$$
(6)

where \(\left\{ {\varepsilon_{\text{l}} } \right\}\) and \(\left\{ {\varepsilon_{\text{nl}} } \right\}\) are the linear and nonlinear strains, respectively. Now, the individual mid-plane strain terms are derived by substituting the corresponding displacement fields, i.e., Equations (1) and (2) into Eq. (5). For the sake of brevity, only the one case has been provided, i.e., the expanded form by substituting Eqs. (2) in (4) and conceded as:

$$\begin{aligned} \left\{ {\varepsilon_{ij} } \right\} = \underbrace {{\left\{ {\begin{array}{*{20}l} {\varepsilon_{{\xi_{x} \xi_{x} }}^{0} } \\ {\varepsilon_{{\xi_{y} \xi_{y} }}^{0} } \\ {\varepsilon_{{\xi_{z} \xi_{z} }}^{0} } \\ {\varepsilon_{{\xi_{y} \xi_{z} }}^{0} } \\ {\varepsilon_{{\xi_{x} \xi_{z} }}^{0} } \\ {\varepsilon_{{\xi_{x} \xi_{y} }}^{0} } \\ \end{array} } \right\} + \xi_{z} \left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{1} } \\ {k_{{\xi_{y} \xi_{y} }}^{1} } \\ 0 \\ {k_{{\xi_{y} \xi_{z} }}^{1} } \\ \begin{aligned} k_{{\xi_{x} \xi_{z} }}^{1} \hfill \\ k_{{\xi_{x} \xi_{y} }}^{1} \hfill \\ \end{aligned} \\ \end{array} } \right\} + \xi_{z}^{2} \left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{2} } \\ {k_{{\xi_{y} \xi_{y} }}^{2} } \\ 0 \\ {k_{{\xi_{y} \xi_{z} }}^{2} } \\ \begin{aligned} k_{{\xi_{x} \xi_{z} }}^{2} \hfill \\ k_{{\xi_{x} \xi_{y} }}^{2} \hfill \\ \end{aligned} \\ \end{array} } \right\} + \xi_{z}^{3} \left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{3} } \\ {k_{{\xi_{2} \xi_{2} }}^{3} } \\ 0 \\ {k_{{\xi_{y} \xi_{z} }}^{3} } \\ \begin{aligned} k_{{\xi_{x} \xi_{z} }}^{3} \hfill \\ k_{{\xi_{x} \xi_{y} }}^{3} \hfill \\ \end{aligned} \\ \end{array} } \right\}}}_{{\varepsilon_{\text{l}} }} + \frac{1}{2}\underbrace {{\left\{ {\begin{array}{*{20}l} {\varepsilon_{{\xi_{x} \xi_{x} }}^{{{\text{nl}}_{0} }} } \\ {\varepsilon_{{\xi_{y} \xi_{y} }}^{{{\text{nl}}_{0} }} } \\ {\varepsilon_{{\xi_{z} \xi_{z} }}^{{{\text{nl}}_{0} }} } \\ {2\varepsilon_{{\xi_{y} \xi_{z} }}^{{{\text{nl}}_{0} }} } \\ {2\varepsilon_{{\xi_{x} \xi_{z} }}^{{{\text{nl}}_{0} }} } \\ {2\varepsilon_{{\xi_{x} \xi_{y} }}^{{{\text{nl}}_{0} }} } \\ \end{array} } \right\} + \xi_{z} \frac{1}{2}\left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{{{\text{nl}}_{1} }} } \\ {k_{{\xi_{y} \xi_{y} }}^{{{\text{nl}}_{1} }} } \\ {k_{{\xi_{z} \xi_{z} }}^{{{\text{nl}}_{1} }} } \\ {2k_{{\xi_{y} \xi_{z} }}^{{{\text{nl}}_{1} }} } \\ \begin{aligned} 2k_{{\xi_{x} \xi_{z} }}^{{{\text{nl}}_{1} }} \hfill \\ 2k_{{\xi_{x} \xi_{y} }}^{{{\text{nl}}_{1} }} \hfill \\ \end{aligned} \\ \end{array} } \right\}}}_{{\varepsilon_{\text{nl}} }} \hfill \\ \underbrace {{ + \xi_{z}^{2} \frac{1}{2}\left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{{{\text{nl}}_{2} }} } \\ {k_{{\xi_{y} \xi_{y} }}^{{{\text{nl}}_{2} }} } \\ {k_{{\xi_{z} \xi_{z} }}^{{{\text{nl}}_{2} }} } \\ {2k_{{\xi_{y} \xi_{z} }}^{{{\text{nl}}_{2} }} } \\ \begin{aligned} 2k_{{\xi_{x} \xi_{z} }}^{{{\text{nl}}_{2} }} \hfill \\ 2k_{{\xi_{x} \xi_{y} }}^{{{\text{nl}}_{2} }} \hfill \\ \end{aligned} \\ \end{array} } \right\} + \xi_{z}^{3} \frac{1}{2}\left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{{{\text{nl}}_{3} }} } \\ {k_{{\xi_{y} \xi_{y} }}^{{{\text{nl}}_{3} }} } \\ {k_{{\xi_{z} \xi_{z} }}^{{{\text{nl}}_{3} }} } \\ {2k_{{\xi_{y} \xi_{z} }}^{{{\text{nl}}_{3} }} } \\ \begin{aligned} 2k_{{\xi_{x} \xi_{z} }}^{{{\text{nl}}_{3} }} \hfill \\ 2k_{{\xi_{x} \xi_{y} }}^{{{\text{nl}}_{3} }} \hfill \\ \end{aligned} \\ \end{array} } \right\} + \xi_{z}^{4} \frac{1}{2}\left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{{{\text{nl}}_{4} }} } \\ {k_{{\xi_{y} \xi_{y} }}^{{{\text{nl}}_{4} }} } \\ {k_{{\xi_{z} \xi_{z} }}^{{{\text{nl}}_{4} }} } \\ {k_{{\xi_{y} \xi_{z} }}^{{{\text{nl}}_{4} }} } \\ \begin{aligned} k_{{\xi_{x} \xi_{z} }}^{{{\text{nl}}_{4} }} \hfill \\ k_{{\xi_{x} \xi_{y} }}^{{{\text{nl}}_{4} }} \hfill \\ \end{aligned} \\ \end{array} } \right\} + \xi_{z}^{5} \frac{1}{2}\left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{{{\text{nl}}_{5} }} } \\ {k_{{\xi_{y} \xi_{y} }}^{{{\text{nl}}_{5} }} } \\ {k_{{\xi_{z} \xi_{z} }}^{{{\text{nl}}_{5} }} } \\ {2k_{{\xi_{y} \xi_{z} }}^{{{\text{nl}}_{5} }} } \\ \begin{aligned} 2k_{{\xi_{x} \xi_{z} }}^{{{\text{nl}}_{5} }} \hfill \\ 2k_{{\xi_{x} \xi_{y} }}^{{{\text{nl}}_{5} }} \hfill \\ \end{aligned} \\ \end{array} } \right\} + \xi_{z}^{6} \frac{1}{2}\left\{ {\begin{array}{*{20}l} {k_{{\xi_{x} \xi_{x} }}^{{{\text{nl}}_{6} }} } \\ {k_{{\xi_{y} \xi_{y} }}^{{{\text{nl}}_{6} }} } \\ 0 \\ \begin{aligned} 0 \hfill \\ 0 \hfill \\ \end{aligned} \\ \begin{aligned} 2k_{{\xi_{x} \xi_{y} }}^{{{\text{nl}}_{6} }} \hfill \\ \end{aligned} \\ \end{array} } \right\}}}_{{\varepsilon_{\text{nl}} }} \hfill \\ \end{aligned}$$
(7)
$${\text{or}}\;\left\{ \varepsilon \right\} = \left\{ {\varepsilon_{\text{l}} } \right\} + \left\{ {\varepsilon_{\text{nl}} } \right\} = \left[ {H_{\text{l}} } \right]\left\{ {\overline{{\varepsilon_{\text{l}} }} } \right\} + \left[ {H_{\text{nl}} } \right]\left\{ {\overline{{\varepsilon_{\text{nl}} }} } \right\},$$
(8)

where \(\left[ {H_{\text{l}} } \right]\) and \(\left[ {H_{\text{nl}} } \right]\) are used to represent the thickness coordinate matrices associated with the linear and nonlinear mid-plane strains. The complete details of the thickness coordinate matrices can be seen in the references [40, 41]. It is noteworthy to discuss that the present formulation has been derived for the FE model HSDT-II, while the necessary mathematical expression for another model HSDT-I can easily be derived by dropping the appropriate terms from the given expression (the displacement and the strain–displacement relation).

2.5 Energy equations

The total strain energy of the shell panel due to the time-dependent deflection of the panel is computed with the help of the stress and strain tensors and reported as:

$$U = \frac{1}{2}\iint {\left\{ {\sum\limits_{k = 1}^{N} {\int_{{\xi_{zk - 1} }}^{{\xi_{zk} }} {\left\{ {\varepsilon_{ij} } \right\}^{\text{T}} \left\{ {\sigma_{ij} } \right\}{\text{d}}\xi_{z} } } } \right\}}{\text{d}}\xi_{x} {\text{d}}\xi_{y} .$$
(9)

Similarly, the kinetic energy of the shell panel is obtained due to the mass density of the panel and expressed as:

$$V = \frac{1}{2}\iint {\left\{ {\sum\limits_{k = 1}^{N} {\int_{{\xi_{zk - 1} }}^{{\xi_{zk} }} {\rho^{k} \left\{ {\dot{\delta }} \right\}^{\text{T}} \left\{ {\dot{\delta }} \right\}{\text{d}}\xi_{z} } } } \right\}{\text{d}}\xi_{x} {\text{d}}\xi_{y} }$$
(10)

where the expression \(\rho\) and \(\left\{ {\dot{\delta }} \right\}\) denotes mass density and the velocity vector, respectively.

2.6 Introduction of finite element steps

The displacement type of FEM is introduced in the current analysis via the state space field variables to obtain the nonlinear algebraic equation from the derived governing equations for the mathematical simplification. The current intact and debonded shell structure domains are discretized with the help of a Lagrangian element (81 and 90 degrees of freedom per elements according to the type of kinematics models, i.e., HSDT-I and HSDT-II, respectively). Details about the nodal polynomial functions and implementation steps can be seen in Cook et al. [42]. The displacement vector over each element can be expressed as follows:

$$\left\{ \delta \right\} = \sum\limits_{i = 1}^{9} {\left[ {N_{i} } \right]} \left\{ {\delta_{i} } \right\},$$
(11)

where \(\left[ {N_{i} } \right]\) and \(\left\{ {\delta_{i} } \right\}\) are the nodal interpolating functions and nodal displacement vectors, respectively. The nodal displacement vectors for the proposed models, i.e., the HSDT-I and the HSDT-II are represented as \(\left\{ {\delta_{i} } \right\} = \left\{ {u_{{x_{i} }} u_{{y_{i} }} u_{{z_{i} }} \,\theta_{xi} \,\theta_{yi} \,\,\psi_{xi} \,\psi_{yi} \,\lambda_{xi} \,\lambda_{yi} } \right\}^{\text{T}}\) and \(\left\{ {\delta_{i} } \right\} = \left\{ {u_{{x_{i} }} u_{{y_{i} }} u_{{z_{i} }} \,\theta_{xi} \,\theta_{yi} \,\,\theta_{zi} \,\,\,\psi_{xi} \,\psi_{yi} \,\lambda_{xi} \,\lambda_{yi} } \right\}^{\text{T}}\), respectively.

After introducing the FE steps, the linear and nonlinear mid-plane strain vectors can be expressed further using the nodal displacement vectors and conceded to the following form:

$$\left\{ {\bar{\varepsilon }_{\text{l}} } \right\} \, = \, \left[ {B_{\text{l}} } \right]\left\{ {\delta_{i} } \right\},\,\,\,\,\left\{ {\bar{\varepsilon }_{\text{nl}} } \right\} \, = \, \left[ {B_{\text{nl}} } \right]\left\{ {\delta_{i} } \right\},$$
(12)

where \([B_{\text{l}} ]\;{\text{and}}\; \, [B_{\text{nl}} ]\) are the linear and nonlinear mid-plane strain–displacement expressions. Additionally, the nonlinear strain (\([B_{\text{nl}} ] = [A][G]\), where [A] is displacement dependent and [G] similar to the linear case) is linearized for the sake of mathematical simplification.

Now, the elemental stiffness ([k]) and the elemental mass ([m]) can be calculated as:

$$\begin{aligned} \, [k] = & \int\limits_{A} {\left( {\sum\limits_{k = 1}^{n} {\int\limits_{{\xi_{zk - 1} }}^{{\xi_{zk} }} {\left[ B \right]^{\text{T}} [D][B]{\text{d}}\xi_{z} } } } \right)} {\text{d}}A + \frac{1}{2}\int\limits_{A} {\left( {\sum\limits_{k = 1}^{n} {\int\limits_{{\xi_{zk - 1} }}^{{\xi_{zk} }} {\left[ B \right]^{\text{T}} [D_{2} ][A][G]{\text{d}}\xi_{z} } } } \right)} {\text{d}}A \\ & \quad + \int\limits_{A} {\left( {\sum\limits_{k = 1}^{n} {\int\limits_{{\xi_{zk - 1} }}^{{\xi_{zk} }} {[G]^{\text{T}} [A]^{\text{T}} [D_{3} ][B]{\text{d}}\xi_{z} } } } \right)} {\text{d}}A + \frac{1}{2}\int\limits_{A} {\left( {\sum\limits_{k = 1}^{n} {\int\limits_{{\xi_{zk - 1} }}^{{\xi_{zk} }} {\left[ G \right]^{\text{T}} \left[ A \right]^{\text{T}} [D_{4} ][A]\left[ G \right]{\text{d}}\xi_{z} } } } \right)} {\text{d}}A, \\ \end{aligned}$$
(13)
$$[k] = \underbrace {{\left[ {k_{\text{l}} } \right]}}_{{\,k_{\text{L}} }} + \underbrace {{\left[ {k_{{{\text{nl}}1}} } \right] + \left[ {k_{{{\text{nl}}2}} } \right] + \left[ {k_{{{\text{nl}}3}} } \right]}}_{{k_{\text{NL}} }},$$
(14)
$$[m] = \int\limits_{A} {\left( {\sum\limits_{k = 1}^{n} {\int\limits_{{\xi_{zk - 1} }}^{{\xi_{zk} }} {\left[ N \right]^{\text{T}} } [N]\rho {\text{d}}\xi_{z} } } \right){\text{d}}A} .$$
(15)

2.7 Mathematical model of debonded curved panel structure

The concept of modeling delamination is based on sub-laminate approach as described in the Ref. [43, 44]. First of all, the meshing/element numbering of the laminated section with lower delamination zone and upper delamination are provided in Fig. 3a, b, respectively. In the current investigation, three sizes of debonding are considered including the intact one and defined in a ratio of their side lengths c and a (c/a = 0, 0.25, 0.5 and 0.75), where c is the side length of the delamination. Further, the earlier provided mathematical expression is applicable for all elements except the element attached to the connecting boundary of the delaminated section (Kumar and Shrivastava [45]). These elements need to satisfy the continuity criteria. To derive the same two elements, Element-I and Element-II as in Fig. 4 are considered with the coordinate \(\left( {0,\xi_{x} ,\,\xi_{y} ,\,\xi_{z} } \right)\) and \(\left( {0^{\prime},\xi^{\prime}_{x} ,\,\xi^{\prime}_{y} ,\,\xi^{\prime}_{z} } \right)\), respectively. The displacements, as well as higher-order terms, can be written as:

Fig. 3
figure 3

a Element distribution in the laminated shell with lower delaminated section; b element distribution in the upper delaminated section

Full size image
Fig. 4
figure 4

Connectivity of the Element-I and Element-II

Full size image
$$\left. \begin{aligned} & u^{\prime}_{xi} = u_{xi} + E_{L} \theta_{xi} + E_{L}^{2} \psi_{xi} + E_{L}^{3} \lambda_{xi} \hfill \\ & u^{\prime}_{yi} = u_{yi} + E_{L} \theta_{yi} + E_{L}^{2} \psi_{yi} + E_{L}^{3} \lambda_{yi} \hfill \\ & u^{\prime}_{zi} = u_{zi} ;\,\,\theta^{\prime}_{xi} = \theta_{xi} ;\,\,\theta^{\prime}_{yi} = \theta_{yi} ;\,\,\theta^{\prime}_{zi} = \theta_{zi} ;\, \hfill \\ & \psi^{\prime}_{xi} = \psi_{xi} ;\,\psi^{\prime}_{yi} = \psi_{yi} ;\,\,\lambda^{\prime}_{xi} = \lambda_{xi} ;\,\,\lambda^{\prime}_{yi} = \lambda_{yi} \hfill \\ \end{aligned} \right\}\quad i = 1,4\,{\text{and}}\,8$$
(16)

where \(u^{\prime}_{xi} ,\,u^{\prime}_{yi} ,\,u^{\prime}_{zi} ,\,\theta^{\prime}_{xi} ,\,\,\theta^{\prime}_{yi} ,\,\theta^{\prime}_{zi} ,\psi^{\prime}_{xi} ,\psi^{\prime}_{yi} ,\,\lambda^{\prime}_{xi} ,\,\,\lambda^{\prime}_{yi}\) are the degrees of freedom associated with the delaminated element Element-II. Similarly, EL denotes the distance between mid-plane of laminate and lower delaminated section as shown in Fig. 4. The sign convention must be taken for the distance, as in the current case EL is negative.

Equation (16) can be further written as:

$$\left\{ {\delta_{i} } \right\}_{\text{L}}^{{\prime }} = [\eta_{\text{L}} ]\left\{ {\delta_{i} } \right\},$$
(17)

where

$$[\eta_{\text{L}} ] = \left[ {\begin{array}{*{20}l} 1 & 0 & 0 & {E_{\text{L}} } & 0 & 0 & {E_{\text{L}}^{2} } & 0 & {E_{\text{L}}^{3} } & 0 \\ 0 & 1 & 0 & 0 & {E_{\text{L}} } & 0 & 0 & {E_{\text{L}}^{2} } & 0 & {E_{\text{L}}^{3} } \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right].$$

The nodal displacement for the delaminated element Element-II can be expressed as:

$$\left\{ {\delta_{i} } \right\}_{\text{L}}^{{\prime }} = \left\{ {\delta^{\prime}_{1} \,\,\delta^{\prime}_{2} \,\delta^{\prime}_{3} \,\delta^{\prime}_{4} \,\delta^{\prime}_{5} \,\delta^{\prime}_{6} \,\delta^{\prime}_{7} \,\delta^{\prime}_{8} \,\delta^{\prime}_{9} } \right\}^{\text{T}} .$$
(18)

On substituting Eq. (16) into Eq. (17):

$$\left\{ {\delta_{i} } \right\}_{\text{L}}^{{\prime }} = \left\{ {\begin{array}{*{20}l} {\eta_{\text{L}} \delta_{1} } & {\delta^{\prime}_{2} \,} & {\delta^{\prime}_{3} } & {\eta_{\text{L}} \delta^{\prime}_{4} } & {\delta^{\prime}_{5} } & {\delta^{\prime}_{6} \,} & {\delta^{\prime}_{7} } & {\eta_{\text{L}} \delta^{\prime}_{8} \,} & {\delta^{\prime}_{9} } \\ \end{array} } \right\}^{\text{T}} ,$$
(19)
$$\left\{ {\delta_{i} } \right\}_{\text{L}}^{{\prime }} = {\text{diag}}[\eta_{\text{L}} \,I\,I\,\eta_{\text{L}} \,I\,I\,I{\kern 1pt} \,\eta_{\text{L}} \,I]\left\{ {\delta_{1} \,\,\delta^{\prime}_{2} \,\delta^{\prime}_{3} \,\delta_{4} \,\delta^{\prime}_{5} \,\delta^{\prime}_{6} \,\delta^{\prime}_{7} \,\delta_{8} \,\delta^{\prime}_{9} } \right\}^{\text{T}} ,$$
(20)
$$\left\{ {\delta_{i} } \right\}_{\text{L}}^{{\prime }} = [T_{\text{L}} ]\left\{ {\delta_{1} \,\,\delta^{\prime}_{2} \,\delta^{\prime}_{3} \,\delta_{4} \,\delta^{\prime}_{5} \,\delta^{\prime}_{6} \,\delta^{\prime}_{7} \,\delta_{8} \,\delta^{\prime}_{9} } \right\}^{\text{T}} ,$$
(21)

where I represents the identity matrix of (10 × 10). For HSDT-I, it will be reduced to a size of (9 × 9).

Further, the necessary transformation of elemental stiffness, as well as mass matrix for the delaminated element Element-II, can be written as:

$$[\bar{k}]_{\text{L}} = [T_{\text{L}} ]^{\text{T}} [k]_{\text{L}} [T_{\text{L}} ],$$
(22)
$$[\bar{m}]_{\text{L}} = [T_{\text{L}} ]^{\text{T}} [m]_{\text{L}} [T_{\text{L}} ].$$
(23)

Similar steps [from Eqs. (16 to 23)] can be applied to obtain the elemental stiffness and mass matrix for the delaminated element Element-III, except the distance EL. After obtaining the necessary elemental stiffness and mass matrix for lower and upper delaminated element, it can be used to obtain the desired global stiffness and mass matrices.

2.8 System governing equation

To obtain the time-dependent deflection of the panel structure, the governing equation of motion is derived from the Lagrangian equation of motion [46] and presented in the following form:

$$[M]\ddot{\delta } + [K]\delta = \left\{ F \right\},$$
(24)

where \(\left[ M \right]\), \(\left[ K \right]\) and {F} are the global mass matrix and global stiffness matrix and applied force vector, respectively. Similarly, \(\ddot{\delta }\) and \(\delta\) represent the acceleration and displacement vectors, respectively. The robust direct iterative technique is employed to solve Eq. (24). To get the desired nonlinear deflection, the following convergence criterion is adopted:\(\sqrt {(\delta_{n} - \delta_{n - 1} )^{2} /(\delta_{n} )^{2} } \le \varepsilon\) where \(\delta ,\,\,n\,\,{\text{and }}\varepsilon\) are the nondimensional deflection, number of iteration and convergence tolerance limit \(( \approx 10^{ - 3} )\), respectively. Further, the time-dependent deflection is obtained using the Newmark time integration scheme as presented in [47].

2.9 Constraints condition for the edges

The constraints condition used in the present article is as follows:

Simply support:

$$\begin{aligned} u_{y} = u_{z} = \theta_{y} = \theta_{z} = \psi_{y} = \lambda_{y} = 0\quad {\text{at}}\,\xi_{x} = 0\quad {\text{and}}\;a \hfill \\ u_{x} = u_{z} = \theta_{x} = \theta_{z} = \psi_{x} = \lambda_{x} = 0\,\quad {\text{at}}\,\xi_{y} = 0\quad {\text{and}}\;b \hfill \\ \end{aligned}$$
(25)

Clamped:

$$\begin{aligned} u_{x} = u_{y} = u_{z} = \theta_{x} = \theta_{y} = \theta_{z} = \psi_{x} = \psi_{y} = \lambda_{x} = \lambda_{y} = 0\;{\text{at}}\;\xi_{x} = 0\;{\text{and}}\;a;\;{\text{at}}\,\xi_{y} = 0\;{\text{and}}\;b. \hfill \\ \hfill \\ \end{aligned}$$
(26)

3 Results and discussion

An original MATLAB code is derived using the current nonlinear HSDT model for the numerical analysis. The required elastic properties of the layered structure utilized for the computational purpose are provided in Table 1. In general, Material-II is adopted throughout for the computation unless stated otherwise. Similarly, transient responses are obtained for two different types of loading: (i) uniformly distributed load (UDL) and (ii) sinusoidally distributed load (SDL) and the load distribution is provided mathematically in the following lines, i.e., in Eqs. (27) and (28), respectively. Additionally, the magnitude of both the loading configurations varies with time and the details are provided in Table 2. The symbols ‘t’ and ‘t1’ represent the instantaneous and total loading time. The value of ‘t1’, \(\gamma \,{\text{and}}\,\lambda\) is taken as 100 ms, 330 and 2, respectively, for the current computation. The time step ‘Δt’ is chosen as 0.1 ms throughout the study and the nondimensional central deflection is obtained using Eq. (29) unless stated otherwise. In continuation to that, all different sizes of delamination are considered at the center mid-plane of the layered composite panel unless stated otherwise. The delamination of size c/a = 0.5 and c/a = 0.25 is also considered in different positions (Fig. 5a) and locations (Fig. 5b), respectively, in a particular example and details are provided on the same.

Table 1 Material property
Full size table
Table 2 Different types of time-dependent loading
Full size table
Fig. 5
figure 5

a Positions of debonding. b Locations of debonding

Full size image
$$q = q_{0} ,$$
(27)
$$q = q_{0} \sin \left( {\frac{{\pi \xi_{x} }}{a}} \right)\sin \left( {\frac{{\pi \xi_{y} }}{b}} \right),$$
(28)
$$W = w/h.$$
(29)

3.1 Element sensitivity and validation study

The convergence statistics of the currently derived nonlinear FE solutions of the dynamic responses are computed for different element densities. In this regard, a simply supported three-layer (0°/90°/0°) cylindrical shell panel (a = b=0.5 m, a/h = 50, r/a = 40) structural example has been solved for two types of step loading (UDL and SDL) by considering the amplitude as q = 1 kN. The nondimensional nonlinear central displacement values are with respect to the dynamic loading evaluated using both the higher-order models and provided in Figs. 6a, b. The figure shows that the responses computed using both the models are converging well with each type of loading (UDL and SDL). Although, the deflection parameters are following a consistent behavior from the mesh refinement (6 × 6) onward, however, the mesh refinement (8 × 8) is utilized for the computation of new responses throughout the analysis.

Fig. 6
figure 6

Convergence study of a HSDT-I; b HSDT-II-nonlinear dynamic responses of cylindrical shell panel under UDL and SDL step load

Full size image

Now, the derived FE models are extended to check the validation behavior. In this regard, a clamped square (a = b=1.27 m and h = 0.0254 m) four-layer symmetric angle-ply [± 30°]s composite plate example is solved using the UDL type of blast load-II including the material (Material-I) and the associated parameter, i.e., \(t_{1} = 0.004\,{\text{s}},\)\(\lambda = 1.98,\)\(\,q = 68.95\,\,{\text{kPa}}\), time step Δt = 0.005 ms. The nondimensional time-dependent deflection parameter \(\left( {W = 100\,w\,E_{{\xi_{y} }} h^{3} /qa^{4} } \right)\) obtained using the current model and the source data is provided in Fig. 7. The present dynamic deflection values show good agreement with the reference data. However, the small differences between the response graph (Fig. 7) may arise due to the solution techniques adopted in the references, i.e., the element strip method (SEM) in Wang et al. [48]. and the generalized differential quadrature (GDQ) technique in Maleki et al. [49].

Fig. 7
figure 7

Validation study-linear time-dependent deflection of plate structure under UDL blast load-II

Full size image

After showing the validation behavior for the linear dynamic values, the models are extended to check the degree of accuracy for the nonlinear time-dependent central deflection values. For the comparison purpose, a simply supported cylindrical shell panel [0°/0°/30°/− 30°]s example is solved considering the geometrical parameter as: a = b=0.5 m, a/h = 50, r/a = 10 under the UDL \(\left( {q = 10^{4} \,{\text{Pa}}} \right)\) type of pressure step load including Material-II type of elastic properties. The present nondimensional deflection parameters \(\left( {W = w\,/h} \right)\) are obtained via both the higher-order nonlinear FE models including Kundu and Sinha [50] data provided in Fig. 8. The figure clearly indicates that the time-dependent deflection parameter computed using the current models follows a similar kind of path as in the reference with small variation between the amplitude values. The differences between the results may arise due to the type of kinematic theories and nonlinear strain–displacement adopted in the current models and the reference. The current results are computed using the HSDT type of displacement models and Green–Lagrange nonlinear strain instead of the FSDT and von Karman strain–displacement relations as in the reference. In general, the FSDT displacement field kinematics overestimates the structural deflection values and von Karman strain unable to count the exact structural flexure for the small (finite) strain and large deformation regime.

Fig. 8
figure 8

Validation study nonlinear central displacement of cylindrical shell panel subjected to UDL step load

Full size image

After completing the convergence and the subsequent comparison for the intact layered structure, the models are employed to show the validity of the delaminated structure. In this regard, the simply supported intact (c/a = 0) and the damaged (c/a = 0.25) plate structural example have been solved while subjected to a suddenly applied pulse load. The input geometrical parameters are taken as same as the reference, [51] i.e., a = b=0.5, a/h = 100, lamination scheme (0°/90°)10 and Material-III. The currently evaluated responses including the Ref. [51] data are provided in Fig. 9 for comparison purpose. The figure shows that the present responses are slightly higher than that of the reference time-deflection data as in the earlier case. It is because of the difference between the assumed displacement field theories adopted in the reference (FSDT) and the present case (HSDT).

Fig. 9
figure 9

Validation study—linear deflection of intact (c/a = 0) and damaged (c/a = 0.25) plate structure under uniform pressure load

Full size image

3.2 Additional numerical illustration

After a comprehensive check of the currently developed nonlinear FE models, i.e., the convergence and the subsequent validity, the models are extended to solve different kinds of numerical illustrations. The numerical examples are solved to compute the nonlinear dynamic responses of the debonded curved composite panel structure under the influence of the variable loading (pulse and blast) and the discussed in detail. In general, the responses are computed for the square panel (a = b=0.5 m) including the Material-II properties (refer Table 1) if not stated otherwise.

3.2.1 Effect of loading time

The time up to which the load is applied to the shell panel may affect the displacement profile. To have a clear understanding of the same, the example of simply supported symmetric eight-layer (0°/90°/45°/90°)s delaminated (c/a = 0.25) spherical shell panel (a/h = 60, r/a = 40) subjected to different (triangular, sine, blast-I and blast-II) time-dependent UDL (q = 1 kN) is examined. The nonlinear deflection is obtained via HSDT-I for different time-dependent loading (10, 20, 30, 50, 80 and 100 ms) and shown in Fig. 10. The figure indicates the gradual increase in the amplitude of nonlinear nondimensional displacement with the increase in loading time in most of the cases. However, in case of blast load-I, the displacements are almost identical for the entire range of loading time. It is important to discuss that the displacement amplitude at any instance purely depends on the amplitude of the load at that instant of time.

Fig. 10
figure 10

Effect of loading time on nonlinear dynamic responses of simply supported spherical shell panel under different pulse load

Full size image

3.2.2 Effect of size of debonding

This example presents the influence of the debonding sizes on nonlinear time-dependent central deflection responses. In this regard, a simply supported symmetrical angle-ply (0°/0°/30°/− 30°)s elliptical shell panel (a/h = 50 and r/a = 30) under the influence of the blast load-I type is analyzed. The values are obtained for the different sizes of square debonding (c/a = 0, 0.25, 0.5 and 0.75) as provided in Fig. 3a and the responses plotted in Fig. 11. The dynamic deflections computed via both the models (HSDT-I and HSDT-II) and the nondimensional nonlinear deflection amplitude values are shown to be comparatively small for the intact shell (c/a = 0) when compared with the debonded structure. Further, the dynamic deflection values follow an increasing trend with the debonding sizes, i.e., c/a = 0.25, 0.5 and 0.75. However, the response frequency follows a reverse trend, i.e., decreases with the increase in debonding sizes. This kind of behavior may be due to the decrease in overall stiffness of the panel along with increase in the size of debonding which further increases the deflection values.

Fig. 11
figure 11

Effect of debonding sizes on nonlinear dynamic responses of simply supported elliptical shell panel under UDL blast load-I

Full size image

3.2.3 Effect of debonding positions

Now, the debonding (c/a = 0.5) located at the center of the laminate is varied at different positions (P-I, P-II, P-III and P-IV as in Fig. 5 (a)) of the clamped hyperboloid shell panel (a/h = 40 and r/a = 50). The shell panel is composed of eight symmetric layers (0°/0°/30°/− 30°)s and subjected to the SDL triangular load (q = 10 kN). The nonlinear dynamic responses obtained using the proposed models and shown in Fig. 12, indicate that as the position changes from middle to outwards (P-I to P-II, P-III and P-IV), the nonlinear deflection response decreases irrespective of the models (HSDT-I and HSDT-II). From this analysis, it can be concluded that the middle position of the delamination is more severe in comparison to other positions as discussed in this example. This is due to the decrement of the overall stiffness at position P-I while compared to the other positions.

Fig. 12
figure 12

Effect of debonding positions on nonlinear time-dependent responses of clamped hyperboloid shell panel subjected to SDL triangular load

Full size image

3.2.4 Effect of debonding location

Figure 13 shows the nonlinear nondimensional deflection responses of all sides simply supported symmetric (0°/0°/30°/− 30°)s delaminated (c/a = 0.25) spherical shell panel with the geometrical configuration (a/h = 60 and r/a = 40). The shell panel is subjected to SDL blast load-II (10 kN). The dynamic deflection values are obtained via the derived higher-order models for different locations, i.e., A, B, C, D and E as provided in Fig. 5b. The amplitude of the central deflection is highest for the location C while compared to other locations (A, B, D and E). Further, the dynamic deflection values are identical for the pair of locations, i.e., A, B and D, E, respectively. From the computed results, it is understood that the central debonding affects the structural stiffness significantly in comparison to other locations.

Fig. 13
figure 13

Effect of debonding locations on nonlinear time-dependent responses of simply supported spherical shell panel under SDL blast load-II

Full size image

3.2.5 Effect of load amplitude

The influence of loading amplitude on the nonlinear deflection values is examined in this current example by solving a debonded (c/a = 0.5) clamped cylindrical shell panel (a/h = 60 and r/a = 30) problem. A quasi-isotropic symmetric (0°/45°/− 45°/90°)s panel under the influence of UDL type of sine load is computed for five different amplitudes (q = 1, 10, 20, 30 and 40 kN) and presented in Fig. 14. The figure indicates that the response frequency decrease and the deflection parameter increase, while the amplitude of the loading increases irrespective of the FE model types (HSDT-I and HSDT-II) and the results follow an expected trend. This is because of the proportionality relation between the load and the corresponding deflection values.

Fig. 14
figure 14

Effect of load amplitude on nonlinear time-dependent responses of clamped debonded cylindrical shell panel subjected to UDL sine load

Full size image

3.2.6 Effect of geometry

In this illustration, the influence of various geometrical configurations (plate, cylindrical, spherical, hyperboloid and elliptical) on nonlinear central deflection responses has been investigated. The analysis has been carried out using an eight-layer (0°/45°/− 45°/90°)s symmetric delaminated (c/a = 0.25)simply supported shell panel structure with the associated geometrical parameter (a/h = 65 and r/a = 50) under the influence of UDL type of blast load-II (q = 10 kN). The nonlinear nondimensional dynamic responses are evaluated using the nonlinear HSDT models (HSDT-I and HSDT-II) and plotted in Fig. 15. The figure infers that the highest deflection is for the plate and lowest deflection is for the spherical shell geometry irrespective of the FE models. It indicates that the spherical and plate geometries have the highest and lowest overall stiffnesses, respectively.

Fig. 15
figure 15

Effect of different shell geometry on nonlinear time-dependent responses of simply supported debonded shell panel under UDL blast load-II

Full size image

3.2.7 Effect of curvature ratio

This example investigates the influence of the curvature ratios on the time-dependent deflection responses of the curved shell panel structure. The symmetric clamped (0°/0°/30°/− 30°)s laminated composite cylindrical shell panel (a/h = 50) with a small delamination (c/a = 0.25) under the SDL triangular load (q = 10 kN) is examined for different curvature ratios (r/a = 10, 20, 30, 50, 70 and 100). The nonlinear nondimensional deflection values are presented in Fig. 16. The response figure indicates that the deflection values are shown to be smaller in amplitude for the lowest curvature ratio (r/a = 10) and increased further when the curvature ratio increased. It is because of the fact that the flatness of the panel increased while the curvature ratio increased by keeping the panel length (a) constant.

Fig. 16
figure 16

Effect of curvature ratio on nonlinear time-dependent responses of clamped delaminated cylindrical shell panel under SDL triangular load

Full size image

4 Conclusions

The nonlinear dynamic behavior of the debonded curved shell panel subjected to different time-dependent loading is analyzed in this present research article. The composite panel model including the internal defect has been modeled using two higher-order kinematics and the sub-laminate approach. The large deformation behavior of the debonded structure is modeled via Green–Lagrange strain and all of the nonlinear strain terms included for maintaining the required generality. The direct iterative method in association with Newmark’s integration technique and the FE steps is adopted for the numerical computation of the results. Further, to compute the dynamic responses, a customized computer code was developed in the MATLAB environment with the help of the currently developed mathematical model. The model consistency and the accuracy were checked by solving different types of numerical examples for the intact and debonded structures. Further, the influences of the individual or the combined effect of the different input parameters (loading amplitude, loading type and geometrical configuration) have been analyzed by solving different numerical illustrations. The final inferences on the dynamic deflection parameter are discussed in the following lines.

  • With reference to the convergence and comparison study, it can be concluded that the present models are stable and capable of solving the desired time-dependent deflections with adequate accuracy.

  • The presence of debonding affects (decrease) the overall integrity considerably. Hence, the overall integrity of the structural panel decreases while the debonding size increases, which, in turn, increases the deflection responses and decreases the response frequency simultaneously.

  • The results related to the position of debonding indicate that presence of debonding at the mid-plane of the laminate is severe in comparison to the other positions.

  • Similarly, the debonding located in the middle of the panel refers to the higher displacement amplitude compared to the other locations.

  • With increasing the load amplitude, the nonlinear dynamic responses also increase.

  • The spherical and the plate geometries show the lowest and the highest values in nonlinear time-dependent deflection, respectively, regardless of the kinematic theories adopted for the computational purpose.

  • The nonlinear deflection responses are higher for the HSDT-II in comparison to the HSDT-I for most of the cases. It is because the HSDT-II model has higher flexibility compared to the HSDT-I.