1 Introduction

Rock strength plays a significant role in any type of geotechnical projects such as slope and tunnels. The uniaxial compressive strength (UCS) of rock may be estimated directly with standard test method suggested by ISRM (International Society for Rock Mechanics) or ASTM (American Standards for Testing Materials). However, some impeding factors, such as obtaining standard intact rock samples especially in highly jointed faulted rock, exist in determination of UCS directly. Further, performing the direct test to measure the UCS of rock is relatively expensive and time consuming as well [1–3]. Due to that, an estimation of the UCS from simple index tests is economic and easier in present. For these purposes, several prediction methods have been developed and published in the literature [1, 4–10]. Some simple and multiple regression analysis techniques have been used for estimating the UCS of rocks [7, 11, 12].

Several researchers have been developed empirical relations to estimate UCS. New relationships between petrographical and engineering properties of granite were proposed in the study conducted by Tugrul and Zarif [4]. They used simple regression analysis to obtain the relationship between the UCS and other rock properties including sonic velocity, I s(50) and Brazilian tensile strength (BTS). Sharma and Singh [8] introduced empirical equations to estimate the impact strength index, slake durability index and UCS from V p. Yagiz [13] used non-destructive test, p-wave velocity, to estimate UCS, Schmidt hardness, modulus of elasticity, water absorption and effective porosity, slake durability index, saturated and dry density of rock. He stated that there is significant relationship between UCS and p-wave velocity of rocks. D’Andrea et al. [14] suggested a linear regression model for predicting UCS using I s(50). Cargill and Shakoor [15] performed test on five different rocks to evaluate the correlations between UCS and the Schmidt hammer, point load, the slake durability and the Los Angeles abrasion test values. Their results indicate that there is a strong correlation between the UCS and I s(50). Singh and Singh [16] obtained the relationship between I s(50) and UCS of quartzites. Kahraman [17] developed the relationship between UCS and some rock parameters like I s(50), Schmidt hammer, sound velocity tests. Young and Rosenbaum [18] developed a reliable model to control the strength and deformability of sandstone using some mineralogical properties. Kahraman and Gunaydin [19] obtained some correlation between the UCS and I s(50) for igneous, metamorphic and sedimentary rocks via regression analysis. Further, Basu and Kamran [20] examined the point load test on schistose rocks and its applicability for estimating UCS. Singh et al. [11] tested and verified the empirical relation between point load index and UCS for some Indian rocks. Empirical relationships to estimate UCS using P-wave velocity were suggested mainly for coal measure rocks in the studies carried out by Singh and Dubey [21] and Singh et al. [22]. Basu and Aydin [23] recommended an empirical relationship between UCS and point load index for Hong Kong Granite. Sharma et al. [24] established some statistical relationship between Schmidt hammer rebound numbers with impact strength index; slake durability index and p-wave velocity. Table 1 shows some published equations to estimate the UCS of rock.

Table 1 Lists of UCS correlations and their descriptions
Full size table

Various researchers have utilized soft computing methods to estimate UCS [10, 43–48] from some rock index properties including point load, p-wave velocity and Schmidt hammer hardness. Sarkar et al. [49] conducted artificial neural network model to predict the UCS and shear strength of different types of rocks using dynamic wave velocity, I s(50), slake durability index and density. Verma and Singh [50] proposed an ANFIS model for predicting p-wave velocity and they emphasized that neuro-fuzzy method shows a good potential to model complex, nonlinear and multivariate problems. Singh and Verma [51] performed a comparative analysis of intelligent algorithms to correlate strength and petrographic properties of some schistose rocks. Singh et al. [52] also published a comprehensive paper on the prediction of UCS by soft computing methods. Yagiz et al. [53] developed model to estimate uniaxial compressive strength of carbonate rock using slake durability and index properties of rocks. They stated that the slake durability index (I d4), p-wave velocity, density and Schmidt hammer values of rocks may be used for estimating the UCS of rocks. Table 2 presents several recent works on the UCS prediction using soft computing techniques.

Table 2 Recent works on UCS prediction using soft computing techniques
Full size table

In this study, several modeling techniques have been used for estimating the uniaxial compressive strength of rocks using various rock properties including Schmidt hardness, p-wave velocity and point load index of rocks. Furthermore, developed models have been discussed and the best model has been chosen to be used for engineering practices.

2 Data source and structure

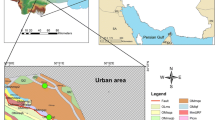
The Pahang–Selangor fresh water tunnel in Malaysia has been investigated to obtain the rock cores to gain the research goals. The tunnel that is crossed under the main mountain range between Pahang and Selangor states is constructed to transfer the fresh water from Pahang state to Selangor and Kuala Lumpur states in the Country. The tunnel is 44.6 km long with a diameter of 5.2 m and a longitudinal gradient of 1/1900. The tunnel is designed to operate under free flow conditions with the maximum 27.6 m3/s of fresh water discharge. 35 km of the tunnel was excavated using three different tunnel boring machines (TBMs), while the remaining tunnel was excavated using the drilling and blasting method. The mentioned TBMs were used to excavate different ground conditions, i.e., mixed ground, very hard ground and blocky ground in Pahang–Selangor fresh water tunnel. Geological map of tunnel site and sampling point along the tunnel is given in Fig. 1. The geological units include granite, metamorphic and some sedimentary rocks as seen in the geological map; however, the most of the rock which is excavated with TBMs and blasting method is composed of granite. To obtain the goal of the study, geotechnical investigation is conducted along the tunnel, and 124 granite block samples were taken from the face of the tunnel in different TBMs site to perform the planned rock testing program. These blocks were taken to the laboratory and the samples were prepared according to the International Society for Rock Mechanics [64]. In this study, representative rock blocks having no defect and discontinuities were collected from site to conduct laboratory tests as much as can be.

Fig. 1
figure 1

Geological map around the tunnel

Full size image

Afterwards, laboratory tests including Schmidt hammer rebound number (R n), point load index (I s(50)), p-wave velocity (V p) and UCS were carried out on those samples. If the samples were failed along the fractures or any defects, then this test result was extracted and not counted in the dataset since it may not characterize the intact rock strength. Results of the laboratory tests conducted in this study are shown in Table 3. As a result, the established datasets have been used for developing several models by performing different techniques and, then, introduced models are compared to each other for choosing the best model among them.

Table 3 Results of laboratory tests conducted in this study
Full size table

3 Model constructions

To predict the uniaxial compressive strength of rocks, several methods including simple regression, non-linear multiple regression (NLMR), artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS) have been utilized herein. The following sections describe modeling procedure of the aforementioned methods to predict the UCS of intact rock like granite. For this purpose, developed data set including R n, I s(50), and V p for 124 samples is used as inputs for purposed models. Afterward, estimated UCS values are compared with actual UCS values obtained from laboratory study.

3.1 Simple regression model and input selection

In this study, first of all, simple regression analyses were conducted to examine the weight of each parameter as input for purposed models. Relevant rock properties that were measured in the laboratory were analyzed to obtain new empirical relations to predict the UCS. In this regard, some equation types such as linear, exponential, power and logarithmic were examined for each predictor as tabulated in Table 4. In this table, values of R 2 were considered to evaluate the capacity performances of the developed empirical equations. In addition, selected equations for each predictor model are highlighted. As result, the best relationship was obtained as exponential, linear and power between the UCS and other rock properties including R n, I s(50), and V p, respectively. The obtained relationships between measured variables and the UCS of rock are given in Figs. 2, 3 and 4. The results revealed that the relationships between the relevant variables and the UCS are statistically meaningful and acceptable. Although gained results are relatively acceptable for predicting UCS, the multiple linear regression analysis was also performed to obtain the best estimation.

Table 4 Results of simple regression analyses for prediction of UCS
Full size table
Fig. 2
figure 2

Proposed equation for UCS prediction using Schmidt hammer rebound number

Full size image
Fig. 3
figure 3

Proposed equation for UCS prediction using point load index

Full size image
Fig. 4
figure 4

Proposed equation for UCS prediction using p-wave velocity

Full size image

3.2 Non-linear multiple regression model

Multiple regression techniques can be applied to obtain the best-fit equation when more than one input parameter was needed. In common, the objective of this estimation method is to develop a relationship between more than one inputs and outputs. There are two types of multiple regressions, namely linear and non-linear. Using linear multiple regression (LMR) technique, a linear relationship can be achieved between inputs and output parameters, while non-linear multiple regression (NLMR) is an approach to obtain a non-linear relationship between relevant parameters. Many researchers proposed both NLMR and LMR equations for predicting UCS of rock using different rock index properties [1, 10, 42, 48, 65, 66]. In the present study, considering the simple regression analysis, the NLMR equations were introduced and the process was performed via iteration algorithm. The NLMR models were constructed using statistical software package of SPSS version 16 [67] herein. For this purpose, all datasets were normalized using the following equation:

$$X_{\text{norm}} = (X - X_{\hbox{min} } )/(X_{\hbox{max} } - X_{\hbox{min} } )$$
(1)

where X min is the minimum value of the measured parameter, X max is the maximum value of the measured parameter, X and X norm are the measured and normalized values in the dataset, respectively. Furthermore, five different datasets were selected randomly for training and testing to develop non-linear models.

The idea behind using some datasets for testing is to check the performance capacity of each model to select the best one. Swingler [68] and Looney [69] suggested that the 20 and 25 % of the all datasets can be used for testing. Also, Nelson and Illingworth [70] stated that the 20 to 30 % of the whole datasets may be used for testing. Considering these suggestions in the literature, 20 % of the database was selected randomly for testing, whereas the remaining 80 % of data were used for training the constructed models. Random data selection for purposed models was performed utilizing the ANN code written by authors. Using the constructed datasets, five NLMR equations have been proposed as listed in Table 5. In these models, Schmidt hardness, point load index and p-wave velocity parameters were utilized as inputs and then the UCS of rock was estimated as function of the mentioned rock properties. While the regression coefficients (R 2) of training dataset that used for modeling were various from 0.747 and 0.789, testing datasets have regression coefficients ranges from 0.471 to 0.706 as in Table 5.

Table 5 NLMR equations for five randomly selected datasets
Full size table

3.3 ANN model

Artificial neural network (ANN) is a soft computing technique inspired by the human-brain information process. A typical ANN consists of three main constituents, namely learning rule, network architecture, and transfer function [71]. There are two major types of ANN: recurrent and feed-forward. Shahin et al. [72] stated that if there is no time-dependent parameter in the ANN, the feed-forward (FF) ANN can be employed. The multi-layer perceptron (MLP) neural network is one of the most well-known FF-ANNs [73]. MLP consists of several nodes or neurons in three layers (input, hidden and output) linked to each other by weights. Du et al. [74] and Kalinli et al. [75] reported on the high efficiency of MLP-ANNs in approximating various functions in high-dimensional spaces. Nevertheless, the ANN needs to be trained before interpreting the results. Among many kinds of learning algorithms to train MLP-FF, the back-propagation (BP) is the most extensively utilized algorithm (Dreyfus, 2005). In a BP-ANN, the imported data in the input layer start to propagate to hidden neurons through connection weights [76]. The input from each neuron in the previous layer, I i, is multiplied by an adjustable connection or weight, W ij . At each node, the sum of the weighted input signals is computed and then this value is added to a threshold value known as the bias value, B ij (Eq. 2). To create the output of the neuron, the combined input, J i , is passed through a non-linear transfer function f (J j ), such as a sigmoidal function (Eq. 3). However, in general, the output of each neuron provides the input to the next layer neuron. This procedure is continued until the output is generated. To achieve the error, the created output is checked against the desired output. The BP training can change the weights between the neurons iteratively in a way that minimizes the root mean square error (RMSE) of the system. More details of the BP algorithm can be seen in the classic artificial intelligence books [77].

$$J_{j} = \sum {(w_{ij} I_{i} ) + B_{j} }$$
(2)
$$y_{i} = f(J_{j} )$$
(3)

In ANN modeling procedure, the same datasets of the NLMR analyses were utilized. The parameters of ANN such as momentum coefficient and learning rate play an important role in the performance capacity of the ANN models. A brief review of the previous studies is required to determine the values of these parameters. If the selected learning rate is small, the training rate will be slow. Because minor changes to weights can be occurred when small values of learning rate are implemented [6, 78]. In addition, fluctuations may happen in the results of training phase caused using large values of learning rate [6, 65]. Different learning rate values have been proposed by several authors. Learning rates of 0.05 and 0.5 were suggested in the studies conducted by Jahed Armaghani et al. [42] and Choobbasti et al. [79], respectively. Yilmaz and Yuksek [56], Erzin and Cetin [80] and Momeni et al. [81] recommended the value of 0.01 for learning rate, while this value was suggested as 0.1 in the study conducted by Yagiz et al. [65]. Apart from learning rate, a steadying effect can be observed by momentum coefficient [82]. Various values have been recommended for momentum coefficient such as 0.95 by Yagiz et al. [65], 0.9 by Jahed Armaghani et al. [42], 0.0–1.0 by Hassoun [83] and Fu [84], 0.4–0.9 by Wyhthoff [85] and close to 1.0 by Henseler [86]. According to the above discussion, it seems that different values of learning rates and the momentum coefficients can be utilized to solve the engineering problems. To determine the proper learning rate and momentum coefficient, a series of sensitivity analyses were performed in this study. Considering the provided information by various researchers and the trial-and-error procedure performed in this study, values of 0.05 and 0.9 were chosen for learning rate and the momentum coefficient, respectively.

Besides, performance of ANN models also depends strongly on the suggested architecture of the network as mentioned in the studies conducted by Hush [87] and Kanellopoulas and Wilkinson [88]. Therefore, determination of the optimal architecture is required to design an ANN model. The network architecture is defined as the number of hidden layer(s) and the number of nodes in each hidden layer(s). According to various researchers (e.g., [89–91]) and considering the results of several studies (e.g., [92, 93]), one hidden layer can solve any complex function in a network. Hence, one hidden layer was chosen to construct the ANN models. In addition, determining neuron number(s) in the hidden layer is the most critical task of the ANN architecture as highlighted in the studies conducted by Sonmez et al. [6] and Sonmez and Gokceoglu [94]. Table 6 presents some proposed equations for determination of number of neuron by several scholars. As mentioned earlier, R n, I s(50), and V p were used as input parameters in the analyses of this study. Based on Table 6, considering three neurons in input layer (N i) and one neuron in output layer (N o), the numbers of neurons that should be used in the hidden layer are in the range of 1 and 7.

Table 6 The proposed equations for number of neurons in hidden layer
Full size table

To determine the optimum number of neurons in the hidden layer, using 5 randomly selected datasets, 35 ANN models were constructed using one hidden layer and number of hidden neurons of 1 to 7 as shown in Table 7. According to Table 7, considering average R 2 value of both training and testing datasets, model no. 5 with hidden neurons of 5 outperforms the other models. Hence, five was selected as number of hidden neurons in constructing ANN models. It should be noted that only results of R 2 are considered as performance criteria to select the best model. Performance indices of all models with 5 hidden neurons for training and testing datasets are presented in Table 9. Suggested ANN structure in this study is illustrated in Fig. 5. More discussions regarding the selection of the best ANN model to predict UCS will be given in results and discussion section.

Table 7 Several ANN models with different hidden nodes
Full size table
Fig. 5
figure 5

Suggested structure of the ANN model

Full size image

3.4 ANFIS model

ANFIS was developed by Jang [100] based on the Takagi–Sugeno fuzzy inference system (FIS). ANFIS is constructed by a set of if–then fuzzy rules with proper membership functions to produce the required output from the input data. As a universal predictor, ANFIS has the capability of estimating any real continuous functions [101]. In general, an FIS is established based on five functioning blocks:

  • Several if–then fuzzy rules

  • A database to define the membership functions

  • A decision-making element to conduct the inference operations on the rules

  • A fuzzification interface to convert the inputs utilizing linguistic values

  • A defuzzification interface to convert the fuzzy results into an output.

An ANFIS model offers the advantages of both ANN and FIS principles and presents all their benefits in a single framework. An adaptive ANN model involves numbers of nodes connected by directional links, where each node is designated using a node function with fixed or changeable parameters. In these networks, the ANN is employed to determine the unknown relationship between the parameters when the FIS is initialized. This process is called “adaptive”. An adaptive ANN model which involves premise and consequent parts is shown in Fig. 6a, which equates to an FIS (Fig. 6b).

Fig. 6
figure 6

a Sugeno fuzzy model with two rules, b equivalent ANFIS architecture [101]

Full size image

To describe the modeling procedure through an ANFIS model, it is supposed that the FIS under consideration is composed of two inputs (x, y) and one output (f) and the rule base includes a two fuzzy rule set “if–then” as below:

  • Rule I: if x is A 1 and y is B 1, then f 1 = p 1 x + q 1 y + r 1

  • Rule II: if x is A 2 and y is B 2, then f 2 = p 2 x + q 2 y + r 2

where p i , q i , and r i are the consequent parameters to be settled. According to Jang [100] and Jang et al. [101], an ANFIS model with two inputs, one output, five layers and two rules (see Fig. 6b) can be described as follows:

Layer 1: Each node i in layer 1 produces a membership grade of a linguistic label. For instance, the node function of the ith node is:

$$Q_{i}^{1} = \mu_{Ai} (x) = \frac{1}{{1 + \left[ {\left( {\frac{{x - v_{i} }}{{\sigma_{1} }}} \right)^{2} } \right]^{{b_{i} }} }}$$
(4)

in which Q 1 i and x are the membership function and input to node i, respectively. A i is the linguistic label related to node i and σ 1, v i , b i are parameters that make changes in the form of the membership functions. The existing parameters in this layer are related to the premise part, as shown in Fig. 6a.

Layer 2: Each node in layer 2 computes the firing strength of each rule through multiplication:

$$Q_{i}^{2} = w_{i} = \mu_{Ai} (x) \cdot \mu_{Bi} (y) \quad i = 1,2$$
(5)

Layer 3: The ratio of firing strength of the ith rule to the sum of firing strengths of all rules is obtained in this layer.

$$Q_{i}^{3} = W_{i} = \frac{{w_{i} }}{{\mathop \sum \nolimits_{j = 1}^{2} w_{j} }}\quad i = 1,2$$
(6)

Layer 4: Every node i in this layer is a node function whereas W i is the output of layer 3. Parameters of this layer are related to the consequent part.

$$Q_{i}^{4} = W_{i} f_{i} = W_{i} (p_{i} x + q_{i} y + r_{i} )$$
(7)

Layer 5: The incoming signals are summed in this layer and form the overall output.

$$Q_{i}^{5} = {\text{Overall output}} = \sum {W_{i} f_{i} } = \frac{{\mathop {\sum {w_{i} f_{i} } }\nolimits }}{{\mathop {\sum {w_{i} } }\nolimits }}$$
(8)

To develop an ANFIS model for prediction of the UCS of rock, results of three index tests including R n, I s(50), and V p were utilized as input parameters. Accordingly, the results of UCS tests were set as the output parameter. The modeling was conducted over a database consisting of 124 datasets. In ANFIS technique, similar to ANN modeling, the best architecture should be determined. To this aim, using a trial-and-error procedure, several ANFIS models were constructed to determine the number of fuzzy rules. The Gaussian, as a well-known membership function in fuzzy systems, was employed for this model [42]. Eventually, each input parameter with 4 fuzzy rules outperforms the other ANFIS models. Therefore, 64 fuzzy rules (4 × 4 × 4) show the best performance for UCS prediction of the rock. In determining the number of fuzzy rules, the results of RMSE were only considered. The linguistic variables for input parameters were set to very low (VL), low (L), high (H) and very high (VH). In this step, considering the suggested ANFIS structure and using randomly selected datasets, five ANFIS models were constructed as shown in Table 9. In addition, these models were checked using the data assigned for testing datasets. Figures 7, 8 and 9 show the normalized membership functions of the input parameters for the ANFIS model. For this model, the RMSE results were not decreased after epoch number of 17. The presented membership functions were assigned after training the system. Furthermore, for the output, a linear type of membership function was utilized. Table 8 shows ANFIS parameters and their values used in the modeling. It should be mentioned that all ANN and ANFIS models in this study were constructed using MatLab version 7.14.0.739 [102].

Fig. 7
figure 7

Membership functions assigned for Schmidt hammer rebound number

Full size image
Fig. 8
figure 8

Membership functions assigned for point load index

Full size image
Fig. 9
figure 9

Membership functions assigned for p-wave velocity

Full size image
Table 8 ANFIS parameters and their values
Full size table

4 Results of models performances

From simple regression results, it was found that the models with multi-input parameters may predict UCS with higher degree of accuracy. Therefore, various non-linear techniques namely NLMR, ANN and ANFIS were developed to predict UCS of rocks obtained from the face of the Pahang–Selangor fresh water tunnel in Malaysia. During the modeling process of this study, all 124 datasets were randomly selected to 5 different datasets including training and testing for development of non-linear models. Some performance indices including R 2, variance account for (VAF) and RMSE were computed to check the capacity performance of all predictive models:

$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} (y - y^{\prime})^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} (y - \tilde{y})^{2} }}$$
(9)
$${\text{VAF}} = \left[ {1 - \frac{{\text{var} (y - y^{\prime})}}{{\text{var} (y)}}} \right] \times 100$$
(10)
$${\text{RMSE}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} (y - y^{\prime})^{2} }$$
(11)

where y, y′ and \(\tilde{y}\) are the measured, predicted and mean of the y values, respectively, N is the total number of data and P is the number of predictors. Theoretically, the model will be excellent if the R 2 is one, VAF is 100 and RMSE is zero. Results of models performance indices (R 2, RMSE and VAF) for all randomly selected datasets based on training and testing are presented in Table 9. High performances of the training datasets indicate that the learning process of the predictive models is successful if those of testing datasets reveal that the models generalization ability is satisfactory. As seen in Table 9, selecting the best model for the UCS prediction is quite difficult. To overcome this difficulty, a simple ranking procedure suggested by Zorlu et al. [55] was used to select the best models. A ranking value was calculated and assigned for each training and testing dataset separately (Table 9). Total ranking of training and testing datasets for three non-linear models is shown in Table 10. According to this table, models 2 and 3 exhibited the best performances of UCS prediction for NLMR and ANN techniques, respectively, while model 3 yielded the best results among ANFIS models. When considering both training and testing datasets, the prediction performances of the ANFIS models are higher than those of ANN and NLMR models. The NLMR equation for model 2 is given as follows:

$${\text{UCS}} = 11.442{\text{e}}^{0.0297} R_{{\rm n}} + 0.001V_{\text{p}}^{1.178} + 22.297I_{{\rm s}(50)}-35.051$$
(12)
Table 9 Performance indices of each model and their rank values for all predictive approaches
Full size table
Table 10 Results of total rank for all predictive techniques obtained from five randomly selected datasets
Full size table

Utilizing the NLMR, ANN and ANFIS methods, the developed relationship between the estimated UCS of granitic rocks and the measured one is given in Figs. 10, 11 and 12 respectively. It is shown that the best prediction model is obtained using the ANFIS technique with regression coefficient of 0.951 and 0.956 for testing and training data in comparison with others including NLMR and ANN as shown in figures.

Fig. 10
figure 10

R 2 of measured and predicted values of UCS for training and testing datasets using NLMR technique

Full size image
Fig. 11
figure 11

R 2 of measured and predicted values of UCS for training and testing datasets using ANN technique

Full size image
Fig. 12
figure 12

R 2 of measured and predicted values of UCS for training and testing datasets using ANFIS technique

Full size image

5 Conclusions

To develop the purposed models, laboratory tests were performed on the rocks obtained from the face of the Pahang–Selangor fresh water tunnel in Malaysia herein. The dataset composed of Schmidt hammer rebound number, point load index, p-wave velocity and UCS properties of granitic rocks. Based on the dataset, several non-linear prediction models were developed for estimating the UCS of granitic rocks. The simple relationship between the UCS and input variables including R n, I s(50) and V p is acceptable and obtained regression coefficients between the UCS and each variable are acceptable. Afterward, non-linear multiple regression model, the ANN and ANFIS techniques were employed for developing the best accurate predictor for estimating the UCS of rocks. Further, the developed models are compared to each other for choosing the best model one. For selecting the best model, obtained regression coefficient and total rank for each model were computed and compared. As considering the testing datasets, the prediction performance of the ANFIS models (R 2 = 0.951) is higher than those of the ANN model (R 2 = 0.886) and NLMR (R 2 = 0.651). Also, considering the training datasets, similar results were also obtained (R 2 = 0.766; 0.867; 0.956, respectively). Further, it is found that the ANFIS model gives best result in comparison with other models according to the total rank method as discussed previously. As a result, it is concluded that each developed model can be used for predicting the UCS of granitic rocks; however, the most accurate result can be obtained using the ANFIS model; however, it is obvious that developed models should be used for similar type of rocks and it is open to be developed.