1 Introduction

Additive manufacturing (AM) technologies have undergone remarkable advancements over the past two decades, transitioning from their initial application in rapid prototyping to the production of functional end-use parts. These technologies have shown promising potential across various sectors, including aerospace, automotive, biomedical, and energy applications [1,2,3]. Forecasts indicate that these technologies are poised to evolve into a multi-billion dollar industry within the next decade [4]. These advancements have paved the way for the direct fabrication of end-use components employing a diverse array of metallic alloys, such as stainless steel, titanium alloys, and nickel-based superalloys [3, 5]. Selective laser melting (SLM) is one of the numerous most widely used additive manufacturing (AM) techniques for producing metallic components. Using SLM, it is possible to produce and to excel at creating intricate and functional parts with outstanding printing resolution, heightened density, and superior surface finish. Moreover, SLM significantly reduces the need for extensive post-processing, distinguishing it from alternative techniques, such as binder jetting [6].

At its core, SLM lies in employing a high-energy laser beam for the selective fusion of fine metallic powder particles, building functional parts layer by layer. The intricacy of this process is rooted in complex physical phenomena that transpire at each stage. These include rapid melting, evaporation, solidification, recoil, and reheating arising from the interaction between the laser beam and the material within a single layer or across successive layers [7, 8]. The intricate interplay of high thermal gradients and rapid cooling rates inherent in these phenomena can give rise to defects such as porosity and microcracks in the final manufactured parts [9]. These defects, in turn, exert detrimental effects on the mechanical properties of fabricated components [9, 10]. In addition, the current understanding of fundamental physical phenomena remains constrained, impeding our ability to anticipate the microstructure and properties of the resultant parts, which is a prerequisite for ensuring their alignment with prescribed design specifications.

Optimizing process parameters for metal selective laser melting (SLM) is challenging due to the complex physics involved and the large parameter space [8]. Conventional trial and error approaches and single-factor-at-a-time optimization strategies are insufficient and inefficient [3, 5, 11, 12]. More advanced multivariate techniques, such as the design of experiments (DoE), are required [13,14,15,16,17,18,19]. DoE has been used to optimize a variety of properties in AM, including porosity, surface roughness, fatigue life, and melt pool dimensions [20]. However, classical DoE methods have limited flexibility and efficiency, and they rely on statistical assumptions that may not always be guaranteed [21, 22]. Additionally, it is difficult to adapt classical DoE to multi-objective optimization, which is the case for AM [23].

Given the inherently multivariate and multi-objective nature of AM process optimization, many researchers have found an attractive solution by adopting surrogate modeling [24, 25]. Surrogate models (or data-driven models) can be used to approximate mathematical models that mimic the real model response within the experimental parameter space, and which are constructed using a data-driven bottom-up approach, even when the underlying physics of the AM process is not fully described. Many studies have used surrogate models in AM of metals. For example, Tapia et al. [24] used a Gaussian process (GP)-based surrogate model of the L-PBF process that predicts the melt pool depth in single-track experiments as a function of laser power, scan speed, and laser beam size combination. Similarly, Meng and Zhang [26] combined experimental and simulated data to predict remelted depths using GP. Surrogate models were also used to perform an MOO of AM. Li et al. [27] proposed a hybrid multi-objective optimization approach by combining an ensemble of metamodels (EM) and a non-dominated sorting genetic algorithm-II (NSGA-II) for optimization to generate optimal process parameters to improve energy consumption, the tensile strength, and the surface roughness of produced parts. Instead of EM, Meng et al. [28] used the response surface methodology in combination with NSGA-II to optimize the structure of a multilayer bio-inspired sandwich of Ti6Al4V. Padhye and Deb [26] carried out an MOO by considering the minimization of surface roughness and build time in the selective laser sintering (SLS) process using evolutionary algorithms, mainly NSGA‐II–II and multi-objective particle swarm optimizers (MOPSO). More recently, Chaudhry and Soulaimani [29] compared the performance of three optimization techniques, genetic algorithms (GA), particle swarm optimization (PSO), and differential evolution (DE), to optimize residual strains using Sobol sampled high-fidelity numerical simulations and deep neural networks (DNN) as a surrogate model since it was found to be much faster for prediction than the polynomial chaos expansion (PCE). One of the key criticisms facing surrogate models in AM is that they are basically “black-box” models without any physical basis, which may result in MOO procedures that can be described as “blindfolded”, as the optimization is executed without knowledge of the relationship between the input and the output. This lack of interpretability makes it difficult to gain scientific insight, which constrains the transferability of knowledge to other systems. Moreover, it also hinders the ability to gain insights into the underlying system or process being optimized, limiting transferability as well [30].

The optimization of additive manufacturing (AM) processes poses a formidable challenge due to their inherently multivariate and multi-objective nature [20, 27, 31]. Numerous process parameters interact in complex ways to influence multiple, often conflicting, quality characteristics [8, 20]. While surrogate modeling offers a computationally efficient alternative to direct optimization, traditional surrogate-based approaches often suffer from a lack of interpretability [30, 32, 33]. This “black box” nature obscures the underlying relationships between process inputs and outputs, hindering scientific understanding and limiting the transferability of optimization results [32]. Furthermore, challenges in designing efficient experiments for surrogate model construction and the lack of continuous improvement mechanisms within these frameworks highlight the need for novel paradigms. These paradigms should aim to optimize multiple facets of the AM process while providing deeper insights into the complex process dynamics.

The present study presents a novel surrogate model-based MOO framework for AM that addresses three critical challenges that have not been discussed in the literature [26,27,28,29]: inefficient experimental design, lack of model interpretability, and rigid optimization frameworks. The proposed framework addresses these challenges by (1) using a space-filling design for data collection that efficiently samples the design space and avoids leaving gaps or subsampling critical regions; (2) using explainable machine learning techniques that make the surrogate models more interpretable and transparent, thus allowing researchers and practitioners to gain deeper insights into the optimization process; and (3) by implementing Bayesian optimization, which allows for continuous process optimization, enabling the framework to refine the estimation of the objective function and potentially uncover a more optimal solution.

2 Modeling and optimization framework

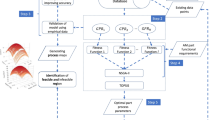
This section presents the proposed optimization framework for improving the AM processes. The framework can accommodate additional factors for a comprehensive evaluation of the design space and systematically covers the parameter space by using a space-filling design which provides a foundation for reliable predictions and optimization (space-filling design). The probabilistic modeling approach enables robust predictions and uncertainties during the optimization process, and utilizes an acquisition function to balance exploration and exploitation, making the optimization process more efficient and effective. The trade-offs between conflicting objectives are balanced by adapting a multi-objective paradigm that ensures that the optimization process considers various criteria. In addition, the iterative nature of the process and the robust testing and validation enable learning from previous evaluations, adapting the model, and refining the optimization approach over successive steps.

Figure 1 summarizes the optimization framework, which starts by (Section 2.1) identifying the most critical processing variables and sampling data points \(X=\{{x}_{1},{x}_{2},\dots ,{x}_{d}\}\) based on the specified space; \({x}_{i}\) is a controllable processing parameter and \(d\) is the number of variables. The variable space should be based on previous work. It should also avoid, if known, parameter combinations, such as high scan speeds with low power, which promote defects [10, 34,35,36,37,38] (such as a lack of fusion, porosity, or balling) for the specified alloy. Space-filling designs should be used to ensure that the design space is thoroughly explored and that the effect of each factor is equally represented and accurately captured [39,40,41,42]. This set of techniques attempts to achieve good coverage of the variable space with a limited number of experiments by distributing the experimental points as uniformly as possible without being biased toward a particular region or variable [43]. In addition, this type of experimental design can easily be accommodated in the processing map by actively constraining the data points [44]. Consequently, the surrogate model can better generalize the constrained design space. However, classical experimental design can also be used in this framework.

Fig. 1
figure 1

Proposed optimization framework for additive manufacturing

Full size image

The second step consists in manufacturing the samples at the given experimental design points and characterizing them. The dimensions and geometry of the pieces could be those of small test cubes if the goal is to optimize the process; however, genuine functional parts could also be used if the goal is to optimize the properties of the part. The characterization step could include many techniques and is set by the optimization objectives; for example, it is known that to improve the fatigue performance of AM parts, the key focus should be on minimizing crack initiation sites, mainly surface roughness and internal defects [12, 45]. In this case, therefore, both quantities of interest (QoI) must be added in the characterization step. It should be noted that the framework is sufficiently flexible to allow adding as many objectives and parameters as needed. In the case study, we used an example involving the optimization of the part density and surface roughness (\({R}_{a}\)); however, other properties could be added to the list of optimization objectives, depending on the application at hand.

After characterization (Section 2.2), each objective \(\{{Y}_{1},{Y}_{2},\dots ,{Y}_{m}\}\) is modeled using a Gaussian process (Kriging model). We assume that the true values differ from the predicted ones by additive noise that follows an independent, identical Gaussian distribution. However, measurement uncertainties exist, and then they can easily be added during training using heteroscedastic GP regression instead [46]. This step produces \(m\) models for each optimization objective. The trained models \(\{{f}_{1}, {f}_{2},\dots ,{f}_{m}\}\) are examined for generalizability using cross-validated metrics [47] and can be further inspected through train/test splits of the data points. These black-box models do not reveal the underlying functional relationship between the input and output. Although there are many techniques for interpreting the model, we opted for a variance-based global interpretation technique, known as the sensitivity analysis (SA) (Section 2.3), since it makes no assumptions regarding the functional form, it produces quantitative measurements that are relatively simple to report, and it is model-agnostic [48]. The SA result is a sensitivity index that describes each variable’s contribution to the model’s output. This index can also guide the optimization [49, 50] process in the following run.

The last step before optimization (Section 2.4) defines the objectives. It can include many other objectives than the modeled objectives \(Y\), for example. In addition to surface roughness and porosity, we can add energy consumption and laser speed as economic objectives, which allows the decision maker (DM) to assess the potential outcomes of different alternatives, given the materials, geometry, process, mechanical properties, and economic constraints. Finally, in Section 2.6, the optimization procedure is performed, and two types of results are obtained: the optimal processing parameters for each property \({Y}_{i}\) and the non-dominated set of solutions, which will be further explained in Section 2.2. These two types of results are used to inform the DM and can be employed to define the different trade-offs between different optimization objectives. If the optimization result does not meet the initial goal set by the DM, a Bayesian optimization procedure (Section 2.5) can be initiated using the acquisition function based on the fitted GP models, which allows for continuous refinement and improvements to achieve better results. This process can be iterated until the objective is met, or the number of the available experiments is exhausted.

The implementation of this framework is carried out using Python scripts by implementing several libraries: The space-filling design is implemented using the SciPy library [51] Latin hypercube function, the NumPy library [52] was used for general array manipulation and served as a communication link to pass the data from one element to another. The modeling aspect relied on the Gaussian process implementation of the scikit-learn library [53], the multiobjective optimization part used the NSGAII algorithm from the pymoo library [54], the acquisition function for the iterative process improvement used a custom function, and lastly, the sensitivity analysis was carried out using the SALib library [55].

2.1 Experimental design

The design of experiments plays a pivotal role in understanding complex systems, identifying causal relationships, and making informed decisions. Classical DoE involves several assumptions of independence, normality, and homogeneity of variance, and in some cases, a linear relationship is assumed between the variables and the response (e.g., response surface methodology) [56]. In addition, complex nonlinear physical phenomena often require the inclusion of higher-order terms, particularly interaction terms between factors. This is because these experiments aim to replicate intricate processes and capture the complexity of the actual physical system, which requires accounting for higher-order effects. Thus, as in factorial designs, relying solely on corner points would be inadequate for fully characterizing the response. Instead, space-filling (SF) designs should be used to obtain good coverage of the entire design space, allowing the fitting of various nonlinear models that can effectively explain the intricate nature of these systems [39, 57, 58].

One of the most commonly used SF designs is Latin hypercube (LHS) sampling [39]. This sampling technique provides improved sampling efficiency (compared to grid-based designs), reduces sampling bias, and is scalable to high-dimensional spaces [39, 41]. However, the direct implementation of an LHS for the optimization of laser-based AM should only be used for new materials, as this can result in a large amount of experimental waste because the LHS distributes the points uniformly in the selected regions, and a large portion of these points will be placed in regions where process defects are known to occur, as illustrated, see Fig. 2, including keyhole porosity, balling, and lack-of-fusion porosity. Other AM defects [59] can be added to further refine the processing region. In the case where the decision function that separates dense parts from parts with defects is known, instead of using a direct implementation of LHS, a constrained LHS design [44, 60] is more appropriate, where the constraints can be derived from already established processing maps [61] or by using regularized logistic regression on literature data for each major defects [62] to obtain the decision surface. The employed constraints should also be used during the MOO process by adding them as optimization constraints (see Section 2.5) and during the optimization of the acquisition function in the BO step (Section 2.6).

Fig. 2
figure 2

The proposed constrained LHS design to avoid common L-PBF defects and get defect-free parts (adapted from [63]); design constraints can also be used as constraints during the MOO procedure and during querying for the following design points during the sequential design step

Full size image

2.2 Surrogate modeling

Surrogate models are constructed by statistically relating the input data to the output data collected by evaluating the black-box function at a set of carefully selected sample points. They can be used for sensitivity analysis or optimization [64]. Overall, surrogate modeling is a valuable tool for the efficient and effective optimization of complex systems, and they continue to play an increasingly important role in a wide range of fields [24, 65,66,67,68,69].

2.2.1 Gaussian processes

In the present framework, a multitude of machine learning models can serve as surrogate models. However, we deliberately chose Gaussian processes (GP) for several compelling reasons, including flexibility (nonlinearity) and uncertainty estimation [70]. However, the most important feature is that this ML class can be easily implemented in a Bayesian optimization framework for adaptive sampling (see Section 2.5). GP modeling assumes that any finite collection of \(n\) observations is modeled as having a multivariate normal distribution [25, 70], which means that they can be described using a mean function \(m({\varvec{x}})\) and a covariance function \(k({\varvec{x}},{{\varvec{x}}}^{\boldsymbol{^{\prime}}})\):

$$m\left({\varvec{x}}\right)={\mathbb{E}}\left[f\left({\varvec{x}}\right)\right],$$
$$k\left({\varvec{x}},{{\varvec{x}}}^{\boldsymbol{^{\prime}}}\right)={\text{cov}}\left(f\left({\varvec{x}}\right),f\left({{\varvec{x}}}^{\boldsymbol{^{\prime}}}\right)\right)$$
(1)

The GP model can be expressed as follows:

$$f\left({\varvec{x}}\right)\sim \mathcal{G}\mathcal{P}(m\left({\varvec{x}}\right),k\left({\varvec{x}},{{\varvec{x}}}^{\boldsymbol{^{\prime}}}\right))$$
(2)

The mean function is typically set to zero [70]. The choice of the covariance function (also known as the kernel) is the most consequential part of GP modeling [70,71,72]. The covariance function expresses the underlying patterns of the data: smoothness, periodicity, linearity, and nonlinearity. It is an estimated function for the dependence of two points in variable space. In our study, we employed a squared exponential covariance function [70], also known as the radial basis function (RBF), because such functions are smooth, infinitely differentiable, and have a simple functional form that makes them well-suited for modeling smooth physical processes [72, 73], where the output changes gradually with the input. In addition, RBFs have only a few hyperparameters, making them easy to optimize and interpret. The RBF covariate function is expressed as follows:

$$k({\varvec{x}},{\varvec{x}}\mathbf{^{\prime}})={e}^{-\frac{{||{\varvec{x}}-{\varvec{x}}\mathbf{^{\prime}}||}^{2}}{2{l}^{2}}}$$
(3)

where \(l>0\) is a hyperparameter that controls the input length scale, and thus, therefore the prediction’s smoothness [70]. This hyperparameter was optimized by maximizing the log-marginal likelihood (LML) during fitting using the L-BFGS algorithm. The LML may have multiple local optima, and as a result, the optimizer is restarted several times during fitting.

The kernel matrix \(K\) can at times be ill-conditioned and particularly evident in cases where the foundational kernel displays a high degree of smoothness (such as with the RBF kernel) [74]. For example, this near-singularity becomes significant when the measurements are affected by measurement noise. To solve this, a noise variance parameter \({\sigma }^{2}\) is added to effectively implement a Tikhonov regularization by adding it to the diagonal of the kernel matrix. The noise parameter represents the global noise level in the datasets, using a single value or individual noise for each data point. This is beneficial for handling numerical instabilities during the optimization of the hyperparameters, which results in inconsistent or inaccurate parameter estimates [53, 75]. Another option is to include a white noise kernel component in the kernel [53, 70], which automatically estimates the global noise level from the data.

2.2.2 Model validation using LOOCV

To evaluate the model’s predictive ability, we used a cross-validation (CV) technique [47]. The main idea with this is to split the training data into training and validation sets and to then use the validation set to estimate the model performance. A variant of this method was used to avoid the drawback of training the model on only a fraction of the dataset. This variant is known as k-fold cross-validation, in which the training dataset is divided into k equally sized subsets (usually between 3 and 10). The model is trained on the union of \(k-1\) datasets and validated on one \(k\)-th dataset, and the process is repeated on every subgroup. Due to the scarcity of data in the current dataset, the \(k\)-fold CV was applied with the setting \(k = n\) (where \(n\) is the number of data points), which is known as leave-one-out cross-validation (LOO CV) [47, 76]. The model performance could then be evaluated using standard performance metrics such as R2 and \(MAPE\) (mean absolute percentage error). The model evaluation procedure is illustrated in Fig. 3.

Fig. 3
figure 3

Model validation using LOOCV and performance metrics

Full size image

2.3 Sensitivity analysis for model explanation

Explainable artificial intelligence (XAI) has emerged as an important field for enhancing the interpretability of surrogate models, particularly when utilizing advanced ML techniques such as neural networks and GP. XAI offers a range of model explanation techniques that aim to provide insights from various perspectives [32, 77]. One approach that has gained significant traction within the XAI community is the variance-based sensitivity analysis [48, 78]. This method has been widely used to evaluate critical systems, and is highly valued thanks to its rigorous theoretical foundation [33].

Sensitivity analysis [48, 79] is used as it offers valuable insight into which model input contributes the most to the variability of the model output. SA was applied to increase understanding of the relationship between model inputs and outputs, investigate variable interactions, and simplify the model by considering only high-impact model inputs and as a guiding tool for future experiments. There are two SA approaches available: local and global SA [80]. Local SA focuses on the impact of small perturbations of a single parameter on the model output. In contrast, in global SA, all parameters are varied simultaneously over the entire parameter range, which gives the relative contribution of the individual parameters and the contribution of each interaction parameter pair. There are several types of global sensitivity analyses, including the Sobol method, Fourier amplitude sensitivity analysis, multiparametric sensitivity analysis, and partial rank correlation [79, 81].

In the present work, we adopted the Sobol method due to its specific advantages [82, 83], which include evaluation efficiency, handling of nonlinear relationships, interaction detection, and incorporation of stochasticity. Sobol SA and SA, in general, have proven invaluable for surrogate MOO scenarios [49, 50, 83], aiding in dimensionality reduction by pinpointing influential variables, guiding objective balancing, and enhancing the model and optimization robustness. In addition, it allows for increased transparency and interpretability of surrogate models, potentially reducing computational costs, validating results, and fostering the creation of sensitivity-informed optimization strategies [49] that integrate sensitivity information into the optimization process to adaptively adjust the exploration of the input space based on identified sensitivities, and ultimately elevating the efficiency, reliability, and comprehensibility of the optimization process, especially in an MOO setting.

2.3.1 Sobol’s sensitivity analysis

Sobol’s method is based on the decomposition of the model output variance into additive variances of the input parameters in increasing dimensionality [81, 84]; this is intended to determine the contribution of each input (based on a single parameter or the interaction of different parameters) to the output variability [81]. Sobol’s analysis makes no assumption between model input and output; thus, it can be easily implemented for black-box models and allows to evaluate the full range of input parameters and their interactions. However, Sobol’s method can be computationally expensive, especially for high-dimensional problems, which can only be computed with efficient estimators [85]. The output variance can be attributed to individual input variables and their interactions [81]. These indices can accurately reveal the influence of the individual parameters and their interactions, and their interpretation is straightforward because they are strictly positive. A higher index value (closer to 1) indicates greater importance for the analyzed variables or interactions.

2.4 Multi-objective optimization

2.4.1 Multi-objective optimization and Pareto optimal solutions

An optimization problem with a single objective can be formulated as follows:

$${\varvec{x}}={\text{arg}\;}\underset{x\in S}{{\text{min}\;}}f\left({\varvec{x}}\right)$$
(4)

where \(f\) is the objective function and \(S=\{{\varvec{x}}\in {\mathbb{R}}^{m}:h\left({\varvec{x}}\right)=0, g\left({\varvec{x}}\right)\ge 0\}\) is a set of variable constraints, \(m\) denotes the dimensionality of the problem, and the \(h({\varvec{x}})\) and \(g\left({\varvec{x}}\right)\) functions are the equality and the inequality constraints applied during the optimization. These constraints can be used to (a) add range constraints to limit the optimization domain, because most ML models are essentially interpolation models with weak extrapolation capabilities, (b) enforce the optimization process to navigate only the defect-free region by adding defect constraints, and (c) enforce a certain productivity exigency by adding productivity constraints based on the processing variables.

Multi-objective optimization, on the other hand, takes into consideration many objectives, usually named performance metrics [86, 87], \(\left[{f}_{1}\left({\varvec{x}}\right),{f}_{2}\left({\varvec{x}}\right),\dots ,{f}_{n}\left({\varvec{x}}\right)\right] ,\) where\(n>1\). Under these considerations, the scalar concept of “optimality” cannot be applied here. Thus, we need to use the concept of Pareto optimality [87]. Other constraints can be added, depending on the desired composition of the optimization objective or other constraints related to the variables themselves [27, 31, 86, 88]. The shape of the Pareto front reveals the nature of the compromise between different objective functions. An example is illustrated in Fig. 4, where the set of points between points A and B defines the Pareto front. MOO problems usually have multiple Pareto optimal solutions; therefore, the selection is not as straightforward as compared to single-objective optimization. In this case, the optimal solution is subject to the decision-maker’s preferences, likes, or other non-included criteria (such as another consequence of the selected optimal solution). The selection of an optimal solution may be based on predetermined preferences. These methods are called a priori methods, and include the scalarization technique, for example. The selection may also be based on finding a representative set of Pareto optimal solutions after which a solution is chosen by the decision maker. Such methods are a posteriori method and include the non-dominated sorting genetic algorithm (NSGA-II).

Fig. 4
figure 4

Example of a Pareto curve of a bi-objective optimization problem

Full size image

2.4.2 Scalarization technique

The scalarization technique combines many objectives into a single one using a function \(g({f}_{1}\left({\varvec{x}}\right),{f}_{2}\left({\varvec{x}}\right),\dots ,{f}_{k}\left({\varvec{x}}\right);{\varvec{\theta}})\), where \({\varvec{\theta}}\) is a vector parameter. A simple and intuitive method is the linear scalarization, where the objective functions are weighted by \({w}_{i}\) and summed, and the MOO problem thus becomes a single objective of \({\sum }_{i=1}^{k}{w}_{i}{f}_{i}({\varvec{x}})\).

2.4.3 Nonlinear multiobjective optimization using NSGA II

NSGA-II (non-dominated sorting genetic algorithm II) [89, 90] is a multi-objective optimization algorithm widely used to solve problems with multiple conflicting objectives. This algorithm is based on the principles of evolutionary computing, specifically genetic algorithms. In NSGA-II, a population of candidate solutions is initialized randomly, and then each individual is evaluated for fitness based on their performance over multiple objectives [90]. These objectives can be conflicting or complementary, and the optimization goal is to find a set of solutions that is not dominated by any other solution in the search space. This set of solutions is called the Pareto set and represents the optimal trade-offs between the multiple objectives. To rank the solutions in the population, NSGA-II uses a non-dominated sorting procedure based on their dominance relationships.

NSGA-II incorporates elitism by always preserving the best solutions from the previous generation, which helps ensure that progress is made toward the optimal solution. The algorithm proceeds to the next generation by selecting parents based on their fitness, using a binary tournament selection scheme. Crossover and mutation operations are then applied to the selected parents to generate new offspring solutions. NSGA-II is highly effective in solving many real-world problems with multiple objectives [89], including engineering design, financial portfolio optimization, and environmental management.

2.5 Bayesian optimization

Bayesian optimization (BO) stands out as an iterative, sample-efficient optimization algorithm, making it particularly suitable for optimizing expensive black-box systems. In the present context, “black box” refers to objective functions lacking closed-form representations and function derivatives, allowing only pointwise evaluations. Although several optimization algorithms can handle black-box functions [43, 89, 91, 92], they are not explicitly designed for sample efficiency and require evaluating the function multiple times for optimization, which is very expensive in the case of AM. To reduce the number of evaluations needed, BO adopts a model-based (surrogate model) approach with an adaptive sampling strategy that minimizes the number of function evaluations. BO has been proven in many applications, including material design using physical models [93], laboratory experiments [94], and the discovery of new materials using multiple objectives [95].

Classical design of experiments (DOE) and space-filling designs suffer from a limitation where the sampling pattern is predetermined before measurements are taken and cannot adapt to emerging features during the experiment. In contrast, the concept of adaptive sampling [58, 96, 97] offers a sequential approach where a balance between two criteria guides the selection of the following sample location. Firstly, it focuses on sampling in unexplored regions (e.g., based on the distance from previous samples). Secondly, it places denser sampling in areas that exhibit interesting behaviors, such as rapid changes or nonlinearity.

Bayesian optimization (BO), a form of model-based global optimization (MBGO) [97], employs adaptive sampling to steer the experiment toward a global optimum. Unlike pure adaptive sampling, MBGO incorporates consideration of the optimal value predicted by the modeled objective when determining the sampling locations. BO has two main components [98]:

  • A Gaussian process (GP) model for point prediction and for measuring the uncertainty associated with that prediction.

  • An acquisition function, which identifies the most promising configuration for the next experiment, considering both the predicted mean and the associated uncertainty.

The GP was already discussed in Section 2.2. The acquisition functions are derived primarily from the mean \(\mu ({\varvec{x}})\) and uncertainty \(\sigma ({\varvec{x}})\) estimates of the GP model, and their computation is inexpensive. The acquisition function tries to achieve a balance between exploitation (sampling where the mean objective value \(\mu (\bullet )\) is high) and exploration (sampling where the uncertainty \(\sigma\)(·) is high), and its global maximum is selected as the following experimental setting. The design of acquisition functions aims to be significant in regions where potentially high values of the objective function exist. Commonly used acquisition functions include the probability of improvement PI, the expected improvement EI, and the upper confidence bond GP-UCB, each of which has its specific advantages [99]. We propose to use the EI criterion as it has been shown to be better behaved than PI, and unlike GP-UCB, it does not require parameter tuning [99]. The acquisition function can be sampled inexpensively and optimized. However, like the space-filling design, this should also be a constrained optimization to prevent the algorithms from exploring regions where process defects are known to occur.

3 Case study: optimizing surface roughness and part density

As stated in Section 1, this study aims to offer a MOO paradigm that utilizes surrogate models to efficiently optimize the processing parameters of AM and allow for continuous process improvement. In the following, we will leverage the main components to illustrate the applicability of this optimization framework using literature data [100].

The data uses a central composite design (CCD) [57] as an experimental design method and a response surface model to study the results. The CCD design is essentially a fractional factorial design with an augmented group of points to estimate the curvature; the distance of the augmented group is set to 1.682 to that of the first group. The independent variables are the laser’s power, scanning speed, and hatch spacing with this central point and the extreme points of the design are set to (225 ± 75 W,1000 ± 300 mm/s, {60,80,120} µm), respectively. The data is shown in Fig. 5.

Fig. 5
figure 5

Three-dimensional scatter plot of the experimental data; the color of the points represents the obtained part density

Full size image

For comparison, two models were fitted on the same data: a linear model (LM) using the least squares method with a second-order polynomial and interaction terms, and a surrogate model (SM) implemented using a Kriging model in the SMT python library [101] with a squared exponential kernel. The result of the fitting is shown in Fig. 6 with the actual versus predicted plots. Both models have high training scores and fit the data perfectly. The linear model benefited well from the chosen experimental design since the CCD is specifically designed to allow the estimation of the curvature of the response based on a quadratic function; the surrogate model, on the other hand, provides not only the predictions, but also the homoscedastic confidence intervals (CI) (represented by the error bars) for the uncertainty quantification. The CI interval contains the actual value, in almost all the parameters combinations.

Fig. 6
figure 6

Actual vs. predicted values of a porosity and b surface roughness using a linear model (LM) and GP regression as a surrogate model (SM); the green error bars represent the uncertainty in the GP predictions

Full size image

The two porosity and surface roughness models were visually inspected using contour plots (Fig. 7) across varying laser speeds: 700, 1000, and 1300 mm/s. The insightful contour plot effectively showcases the trade-off between achieving the finest surface roughness and achieving the ideal density. To achieve an optimal porosity, it was observed that higher laser speeds and reduced hatch distances were necessary, as opposed to the optimal surface roughness, which required lower scan speeds and increased hatch distance. This will later be demonstrated quantitatively using the proposed optimization algorithms.

Fig. 7
figure 7

Contour section plots of a porosity % (top row) and b surface roughness µm (bottom row) at different laser speeds: 700, 1000, and 1300 mm/s

Full size image

A sensitivity analysis was applied using a 1024 data point generated using Saltelli’s sampling scheme [102], including interactions and a resampling number of 100. We used the evaluation of the surrogate model for the sensitivity analysis and compared it to the standardized coefficients of the linear regression. The result of the study is summarized in Fig. 8. The total sensitivity indicates that the laser power and hatch distance contribute equally to the porosity variance. At the same time, the dominating factor for the surface roughness is the hatch distance, which is almost double the influence of the laser speed and power. This can be further confirmed by looking at the first-order sensitivity indices, which isolate the effect of a single variable, where the hatch distance has almost 2.5 times the impact of laser speed on surface roughness and has virtually double the influence of laser power. The contribution of \(P\), \(V\), and \(H\) on the porosity is similar. Second-order sensitivity indices show that the sensitivity due to the interactions of the laser power and laser speed is negligible (below the 0.05 threshold) for both the porosity and surface roughness; moreover, the interaction of the laser power with the hatch distance is also insignificant for the surface roughness, leaving the interaction of the laser speed and hatch distance as the sole significant interaction for the surface roughness. On the other hand, the porosity is influenced by the interaction of the pair laser power, hatch distance (P, H), and the laser speed and hatch distance (V, H) combination in near-equal measure.

Fig. 8
figure 8

Sensitivity analysis results: a total order, b first-order, and c second-order Sobol’s indices

Full size image

A regression analysis was done using the same data with a polynomial degree of two, and their interactions [100] confirmed the sensitivity analysis results, in which the interaction terms with negligible sensitivity indices were found nonsignificant in the regression analysis. This was due to either high p-value or small coefficients for the standardized linear regression.

The scalar optimization was applied to the linear and surrogate modes using the Powell method, and the optimization constraints were selected as the variable ranges (\(P, V, H\)). Table 1 summarizes the optimization results. The porosity optimization provided the same optimized value for both models, with a consistent process parameter value. However, the surface roughness optimization brought different values for the LM and SM models, with variances of up to 10%, and the process parameters did not coincide. This highlights the fact that although both models have a good fit on the data, the shape of the curve might still differ due to either model constraints or the selected experimental design. This also highlights the need for uncertainty analysis when it comes to modeling physical phenomena in additive manufacturing.

Table 1 Porosity and surface roughness scalar optimization results
Full size table

For the MOO using the scalarization techniques, the weights (\({w}_{1}\), \({w}_{2}\)) were set to 0.5 with settings similar to those in the previous single objective optimization. A more recent technique based on evolutionary algorithms is NSGA II. This technique is very efficient at exploring the design space while escaping suboptimal solutions, and is independent of the selected initial point. The NSGA II algorithm was set with a population size of 200 and 1000 generations, respectively, and a crossover probability of 0.9, while the offspring population was set to 10 as previous studies [103] have shown that reducing the offspring population and increasing the population size can improve the performance of the algorithm.

The NSGA II results in a set of non-dominated solutions. To narrow down the results into a single point, we use multi-criteria decision making (MCDM). First, we eliminate the effect of objective scales. This can be achieved using normalization, and to that end, we use min–max scaling \((x-{x}_{{\text{min}}})/({x}_{{\text{max}}}-{x}_{{\text{min}}})\) and employ a decomposition method like the achievement scalarizing function (ASF) [104]. Table 2 presents the results of using the scalarization technique and the NSGA II algorithm on the SM model. Both methods have consistent results, with a slight difference seen in the obtained porosity and surface roughness values, resulting from the different selected approaches. The scalarization technique linearly combines the two objectives into one without considering the scale effect between both. This is apparent in Fig. 9, where the solution of the scalarization technique is slightly biased in favor of the surface roughness. In contrast, the NSGA II tries to find the Pareto set of optimal solutions, which it then normalizes, and by using an ASF, it combines the two objectives.

Table 2 Results of multiobjective optimization using the scalarization technique and the NSGA II-based technique
Full size table
Fig. 9
figure 9

Contour plots of a porosity, b surface roughness, and c the combined objectives using weights of (0.5, 0.5) for both objectives. The contours are plotted by fixing the laser speed at the optimal solution V = 965.3 mm/s. The white star marker represents the optimal laser power and hatch distance

Full size image

Figure 10 shows the non-dominated solution set provided by the NSGA II algorithm with the interpolated change of design variables (\(P\),\(V\), and \(H\)) as a function of the objective functions (porosity and surface roughness). The non-dominated solutions show a typical Pareto curve with a compromise of approximately 3% and 12% between the porosity and surface porosity, respectively. The bottom right point represents the single objective optimal surface roughness values, and the top left point is the optimal porosity value; both points agree with the scalar optimization of SM presented in Table 3. The scale effect is present as the optimal solution using the scalarization favors optimizing the surface roughness. The NSGA II approach with the ASF method provides a more balanced solution as the optimal solution is closer to the ideal point (a reference point that represents, simultaneously, the best possible values for all objectives). Analyzing the effect of design variables on the two objectives reveals an interesting relationship. With respect to the Pareto, the porosity increases with increasing hatch distance and decreasing laser power and speed simultaneously; the opposite is true for the surface roughness, which increases with decreasing hatch distance and increasing laser power and speed. This observation qualitatively agrees with the sensitivity analysis results, as the hatch distance was the main contributing factor in the surface roughness.

Fig. 10
figure 10

Trade-off curve between porosity and surface roughness along with the scaled variables laser power (P), laser speed (V), and hatch distance (H)

Full size image
Table 3 Porosity and surface roughness training and cross-validation scores of linear and surrogate model
Full size table

The optimized processing parameters in Table 2 can be effectively set as the machine parameters for the next printing set-up. However, it should be considered that these parameters are dependent on the experimental data [105] and on the fitted model [106]; i.e., the optimized parameters are not absolute. In our case, the model is mainly controlled by the covariance function. Meanwhile, the data pose a significant challenge when optimizing the AM process due to the expensive experimental runs which results in data scarcity and can lead to model overfitting. In addition, a small dataset may only capture some of the variations and complexity of the problem. Although model validation using LOOCV and train/test splits can alleviate some of these problems, we should always strive to get more data. One way to do this efficiently is using adaptive sampling, which allows the model to actively select data points that are most uncertain or informative to improve its knowledge and reduce uncertainty by efficiently allocating the available resources. Using the prediction and the uncertainty of the two GP models, we can quantify the potential improvement of a candidate point in the design space over the current best solution using the EI acquisition function. The EI considers both the predicted value of the candidate point and the uncertainty associated with that prediction. This function can be optimized to find the best candidate having the most significant potential improvement for each model using the L-BFGS-B algorithm [107, 108]. This optimization step should be run multiple times using random starting, mainly when dealing with highly nonlinear predictions and uncertainties in Gaussian process (GP) models. This approach helps address the sensitivity to the initialization problem and assess the solution’s robustness.

Table 4 presents the selected candidates based on this approach. These candidate parameters were set based on their impact on surface roughness and porosity levels. In Fig. 11, the density plots of the predicted surface roughness and porosity, their relative uncertainty, and the expected improvement at fixed values of hatch distance are compared, and correspond to the candidate parameters. The density plots of the predicted values of the two models show expected behaviors that are typical when fitting an ML model to classical experimental design, in our case, the CCD design. The CCD design is a response surface methodology, in which the regression is typically quadratic. Thus, the fitted ML model will also assume a similar response. What is more interesting is the density plot of the uncertainty. We see in this plot that the closer we get to an initial design point (observed points), the less the model is uncertain about its prediction. The acquisition function uses this information to either explore new regions of the design space or exploit promising regions where improvements are expected. For the part density, the four points have relatively good coverage of the parameter space; this incites the acquisition function to exploit the domain to get the optimal candidate, whereas, for the surface roughness, a high laser power seems to produce parts with low porosity. Here, the acquisition function decides to explore this region further.

Table 4 Selected points for subsequent evaluation using surface roughness and porosity GP models
Full size table
Fig. 11
figure 11

Density plots of the predicted values of a surface roughness and d density and their b, e relative model uncertainty (standard deviation) and c, f the measured EI. The plots are a cutoff plane

Full size image

The proposed optimization framework, while comprehensive, is not without limitations. One key limitation is the expensiveness of the first optimization run, as this usually include a moderately large number of experiments due to the space filling design. Additionally, the effectiveness of the framework may be influenced by the quality and quantity of available data, and uncertainties during the measurement process; however, this can be overcome with the incorporation of heteroscedastic Gaussian process [46, 109] and robust property measurements. The current version of the framework also assumes that the excluded variables and the part geometry are fixed, and the transferability from one set of geometry to other ones may require further exploration of transfer learning techniques coupled with Bayesian optimization [110,111,112]. This can help reducing the number of initial experimental runs for other geometries. Lastly, the framework adapts a classical notion of multiobjective optimization where each objective is modeled separately, a modern Bayesian multiobjective optimization [113] using the expected hypervolume improvement acquisition function [114], can largely accelerate the optimization process.

To address these limitations and further enhance the optimization framework, future research could explore methods to transfer the knowledge gained from an optimization on a specific AM machine to other process. Additionally, exploring alternative surrogate modeling techniques could make the framework applicable to a broader range of additive manufacturing scenarios. Although the case study was carried out using custom python scripts, the overall framework can benefit from software design principle to construct a more coherent code. Continuous collaboration with industry and stakeholders can provide valuable insights, ensuring the framework remains relevant and effective in addressing emerging challenges in AM.

4 Conclusions

Building upon existing knowledge, this study presents an adaptable multi-objective optimization framework specifically designed for additive manufacturing (AM). This framework offers flexibility, as it accommodates diverse process variables and objectives, facilitating optimization of various AM processes. And adaptability where continuous process improvement is enabled through Bayesian optimization, leading to a data-driven learning process. Our investigation yielded valuable insights and recommendations:

  • Model selection: While initially comparable, Gaussian process models outperform simpler models like linear regressions with interactions in long-term AM optimization.

  • Sensitivity analysis: Hatch distance significantly influences surface roughness, emphasizing the need for precise control.

  • Multi-objective optimization: NSGA-II outperforms scalarization techniques in ensuring diverse optimal solutions and avoiding scaling effects.

Based on these findings, we recommend the following: utilizing GP models for AM optimization due to their superior long-term reliability compared to simpler models like linear regressions with interactions, prioritizing precise control of hatch distance for achieving desired surface roughness in AM processes, selecting NSGA-II over scalarization techniques for MOO to avoid potential biases and obtain a broader range of optimal solutions. This framework, along with the recommendations outlined, holds promising potential for advancing the optimization of diverse AM processes, leading to improved product quality and performance.