A sequential surrogate-based multiobjective optimization method: effect of initial data set

Abstract

Process optimization based on high-fidelity computer simulations or real experimentation is commonly expensive. Therefore, surrogate models are frequently used to reduce the computational or experimental cost. However, surrogate models need to achieve a maximum accuracy with a limited number of sampled points. Sequential sampling is a procedure in which sequentially surrogates are fitted and each surrogate defines the points that need to be sampled and used to fit the next model. For optimization purposes, points are sampled on regions of high potential for the optimal solutions. In this work, we first compared the effect of using different initial sets of points (experimental designs) in a sequential surrogate-based multiobjective optimization method. The optimization method is tested on five benchmark problems and the performance is quantified based on the total number of function evaluations and the quality of the final Pareto Front. Then an industrial applications on titanium welding is presented to show the use of the method. The case study is based on real experimental data.

1 Introduction

For manufacturing businesses to be successful in the global market, they must strive to deliver high quality products at the lowest possible cost. One approach to select the processing conditions to achieve these goals is to run experiments on the manufacturing floor. Such experimentation is usually costly and requires considerable amount of time and effort, which may not be feasible during production [1]. Alternatively, companies use advance computer simulations to represent their processes. Such computer simulations along side with optimization methods are used to identify the values of the processing conditions (variables) that optimize the relevant performance measures (objectives).

Joining simulation and optimization in a single framework for defining the best possible process parameters is an actual need in current engineering practice [2,3,4,5,6]. However, a major difficulty of optimizing engineering problems based on simulations is that each function evaluation requires a complete simulation run which is computationally expensive [7]. For many real world problems, a single simulation evaluation can take minutes to even days. Therefore, optimization methodologies for simulation outputs are typically based on surrogate models (or metamodels) which are mathematical models that try to mimic the behavior of the simulation model based on a limited number of observations [2, 8,9,10]. They help reduce the computational effort required to evaluate the performance measures at different processing conditions, as they are faster to evaluate than the simulation model [11, 12]. Surrogate models are also convenient for cases when it is only possible to use experimental data and a single process evaluation is expensive and time consuming, like the application presented here. Therefore, by utilizing surrogate models it is possible to use an optimization technique that requires the evaluation of the process at a high number of processing conditions. The most commonly used surrogate models are Response Surface, Kriging, Radial Basis Function (RBF), and Artificial Neural Networks. Reviews of surrogate models used in optimization via simulation can be found in [2, 8, 9, 13, 14].

Surrogate models are constructed based on a limited number of ’smart’ chosen data points. These points are typically chosen in one of two ways: (a) one stage or (b) sequential (adaptive) sampling. The one stage sampling approach selects a set of data points and a global surrogate model is fitted [15]. This method tries to locate the sampled points over the entire inputs space in one step. In contrast, sequential or adaptive sampling is an iterative procedure in which sequentially surrogates are fitted and each surrogate defines the points that are sampled for the next model. The accuracy of the model usually depends on the technique used to distribute the points [15]. Design of experiment techniques are commonly used to form the one-stage sample or the initial data set for the sequential sampling. Some of these techniques are Factorial and Central Composite designs, Latin Hypercube designs (LHD), Orthogonal arrays, Sobol sequences, among others [15].

On the other hand, there are several adaptive sampling approaches, [16] reviewed different methods such as entropy approach, maximin distance, Mean Squared Error (MSE) and cross validation. On the entropy method new sets of points are selected in such a way that the amount of information obtained with the new sampled set is maximized. On the maximin distance approach, the point that maximizes the minimum distance between any existent point is selected. In the MSE approach, the point with largest prediction error is selected. For cross validation, the idea is to leave out one or several points each time and fit a surrogate model based on the rest of the sampled points. Then the prediction error is estimated and the point with largest prediction error is selected. It is important to notice that techniques such as the entropy method or the MSE require the estimation of the prediction error at any given point, therefore metamodeling techniques such as Kriging models need to be used [17]. The authors also compared the sequential approaches with a one-stage approach. They found that there is no guarantee that sequential sampling will do better than the one stage approach, because it depends on the sampling and metamodeling technique used. However, sequential sampling requires less computer evaluations than the one-stage since they stop when the surrogate models are accurate enough. Recently, [18] compared the performance of different sampling and metamodeling techniques for process optimization. They found that none of the compared metamodeling techniques was best in all the quality criteria used. Hu et al. [19] compared different surrogate models using expected improvements to select one or several points sequentially. On the expected improvement approach, the solution(s) that maximize the expected improvement is (are) selected. The improvement function is based on the difference between the best-known objective value and the expected objective value at a given (unobserved) point.

Sequential sampling methods are used for two main purposes: accurately fit a global metamodel or metamodel based optimization. On the first case, samples are chosen at places were the models show poor fitting quality, and in the second case more points are assigned towards the region where the potential optimum could be [20]. The second type of methods are convenient for optimization purposes, where the goal is to find the optimum and not necessarily to map the complete surface. The underlying idea is that the approximated surrogate model should be more accurate at the region were the optimal solution is, while it can be less accurate far from the optimal [21].

Real manufacturing problems usually involve different performance measures (PMs) that exhibit conflicting behavior [22, 23]. For example, the processing conditions that provide the best quality product may not correspond to the lowest production cost. When multiple conflicting performance measures are involved, optimizing a single objective can result in solutions that perform poorly for other objectives. Thus, it is not the best approach to obtain a single solution but rather the set of solutions corresponding to the best compromises, known as Pareto solutions (see Definition 1), from which the decision maker can select the best one on a particular moment of the process.

Definition 1

A feasible solution ${\mathbf{x}}_1$ of the optimization problem minimize $(f_1({\mathbf{x}}),f_{2}({\mathbf{x}}),\ldots ,f_{m}({\mathbf{x}}))$ is said to dominate ${\mathbf{x}}_2$ if: $f_{j}({\mathbf{x}}_1)\le f_{j}({\mathbf{x}}_2)$ for, $j = 1,\ldots ,m$ and $f_{j}({\mathbf{x}}_1)<f_{j}({\mathbf{x}}_2)$ for some $j\in \{1,\ldots ,m\}$. The non-dominated solutions are known as Pareto solutions. The input values of the Pareto solutions are known as Pareto Set $(P_{{\textit{set}}})$ and the corresponding output values form the Pareto Front $(P_{{\textit{front}}})$.

Guodong et al. [24] and Kitayama et al. [25] proposed sequential surrogate-based multiobjective optimization methods based on RBFs. Guodong et al. [24] used multiobjective Genetic Algorithm (GA) to approximate the Pareto Front. Iteratively a trust region was established around the predicted Pareto Front, and new points were sampled on the trust region in such a way that a LHD is kept. On the other hand, [25] selected new solutions in three ways (1) Pareto optimal solutions from the response surface, (b) points in unexplored regions, and (3) the solution that minimizes a Pareto-fitness function. Yun et al. [26] proposed support vector regression (SVR) to represent the PMs and GA to solve the multiobjective optimization problem. Iteratively, new points were selected based on the sensitivity information of the SVR.

Most of the works found on the literature that focuses on comparing different sampling and/or metamodeling techniques used LHDs as initial samples. In this work, we preset the effect of the initial sample of data points (experimental design) on a sequential surrogate based optimization method with multiple objectives. The method is based on multiple linear regression models and uses the idea of minimum interpolation surface to select new points. In the minimum interpolation surface approach, a surrogate model is fitted based on a sample of data points, and the minimum of the response surface is identified and used as additional point to fit the next model. In our case, we do not have a unique solution but the set of best compromises between several surfaces. The optimization method is tested on five multiobjective benchmark problems and the performance is quantified based on the quality of the final Pareto Front and the total number of samples needed on the optimization. In addition, the performance of the sequential approach is compared with a non-sequential approach. Then an industrial applications is presented to illustrate the use of method. The case study is on titanium welding and it is based on real experiments.

The article is organized as follows: in Sect. 2, the sequential multiobjective optimization method is described. Section 3 presents the comparison of the performance of the method using different initial sets of points on several benchmark test problems. In Sect. 4, the optimization method is illustrated with an industrial case studies, and in Sect. 5 conclusions and future work are presented.

2 Sequential surrogate-based multiobjective optimization method

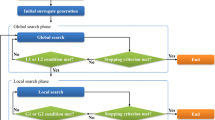
The sequential surrogate-based multiobjective optimization method used here is based on the method introduced by [27]. The method is schematically shown on Fig. 1 and it starts by performing an experimental design to collect a set of initial data points. At each design point, an experimental or simulation run is performed. Based on the initial set of data points, the set of best compromises between all performance measures is found using Definition 1, and it is called incumbent Pareto Front. Then, the current set of points is used to fit a metamodel for each performance measure. Subsequently, the metamodels are used to estimate the value of the performance measures for a large set of input combinations and the best compromises between all performance measures are identified. Such Pareto Front is called here predicted Pareto Front. The corresponding controllable variables settings are the predicted Pareto Set $({\tilde{P}}_{{\textit{set}}})$. Then, the predicted Pareto Set is evaluated using the physical process or simulation code. However, if the number of solutions on the Pareto Set is larger than the remaining number of runs allowed $(N_{{\textit{left}}})$, or it is larger than the maximum number of runs allowed per iteration $(N_{{\textit{max}}})$, a subset of $\min \{N_{{\textit{left}}},N_{{\textit{max}}}\}$ solutions is selected based on a Maximin distance criterion using the predicted Pareto Front. Now, with the new information available the incumbent Pareto Front (based on simulated/experimented data) is updated. Note that all available data points (Pareto efficient or not) are used in this step. Lastly, a series of stopping criteria are evaluated and if at least one is met, the method stops and the incumbent Pareto solutions are reported. Otherwise, the new evaluated points are added to the existing set of data points and a new iteration begins. Iteratively, the surrogate models are updated using the newly available data and new Pareto Sets are approximated. At each iteration, the updated models are able to obtain good approximations of the output responses near the Pareto Front.

Fig. 1

Sequential multiobjective optimization method

Villarreal-Marroquin et al. [27] showed that the sequential optimization method is able to approximate a set of Pareto solutions without having to evaluate a large number of simulations. In Villarreal-Marroquin et al. [28] the method was used to solve two injection molding case studies. Two initial data sets were used and the results were compared with a similar approach based on Gaussian process metamodels. The alternative method uses an expected improvement approach to iteratively search for new points. The results showed that both methods perform comparably. In Montalvo-Urquizo et al. [6] it was used to optimize a milling process using a small number of expensive simulations.

The key idea that makes sequential surrogate models efficient is that they become more accurate in the region of interest as the search progresses, rather than being equally accurate over the entire design space.

The following section presents a comprehensive comparison of the effect of the initial data set on the performance of the optimization method.

3 Effect of using different initial sets of points

In this section, the performance of the sequential multiobjective optimization approach presented before is compared using different initial sets of data points (design of experiments). The comparison was carried out using five benchmark multiobjective optimization test problems and fourth different initial design of experiments and a random set of the same size.

3.1 Multiobjective test problems

The multiobjective optimization test problems used here are shown in Table 1. Multi-Objective Problem (MOP) 1, 2 and 3 have 2 controllable variables and 2 PMs. MOP4 has 3 control variable and 3 PMs, while MOP5 has 4 control variables and 4 PMs. The second column of Table 1 shows the objective functions, all to be minimized; the last column indicates the inputs ranges. None of the problems has additional constraints other than the bounds on the inputs. $f_{1}$ in MOP1 is the global optimization test function Rastrigin and $f_{2}$ is the negative of the Six-hump Camel Back function. MOP2–MOP5 are test problems that can be found on the multiobjective literature [29]. The objective functions of MOP3 were originally developed by [30], for single objective optimization and were adapted later to multiobjective optimization (see [29] for further details). MOP4 and MOP5 are the test problem known as DTLZ2 (Deb, Thiele, Laumanns, Zitzler).

Table 1 Multiobjective optimization test problems

3.2 Initial data sets

The fourth experimental designs and the random set used as the initial set of data points for the optimization method are as follows: (1) an Inscribed Central Composite (CCI) Design which is a scaled down Central Composite Design (CCD) with each factor level divided by $\alpha$. Here an $\alpha =(2^k)^{1/4}$ (k, number of input variables) was used. The top plot of Fig. 2 is a CCI for $k=2$; (2) a Maximin Latin Hypercube Design (LHD) with the same number of points than a CCD with the same number of variables. The LHDs were generated using the Matlab built-in function lhsdesign with 1000 iterations. The middle-left plot of Fig. 2 shows 6 LHDs for $k=2$ and $n=9$ points; (3) a D-Optimal Design (D-Opt) which was generated using the Matlab built-in function cordexch with 10 tries. The initial designs are $3^k$ Full Factorial Designs; the initial models are the metamodels to be constructed on the first iteration of the optimization method; and the number of runs to be selected was set as the same number of the CCD. The middle-right plot of Fig. 2 is an example of a D-Optimal design for $k=2$ and $n=9$. As the initial designs are $3^k$, the resulted D-Optimal designs are Full or Fractional Factorial Designs with 3 levels; (4) a Uniform Random (Rand) set with the same number of points as the CCD, the low-left plot of Fig. 2 shows 6 examples of random sets for $k=2$ and $n=9$ points; and (5) a Sobol Sequence (Sobol-Seq) with the same number of points as the CCD. The Sobol sequences were generated using the Matlab built-in function sobolset on k-dimensions, no points were skipped from the sequence and the function scramble was used to apply a random linear scramble combined with a random digit shift. The low-right plot of Fig. 2 shows 6 examples of Sobol sequences for $k=2$ and $n=9$. Different examples are represented by a different color on each subplot of Fig. 2. In all cases the controllable variables were scaled between $[-1, 1]$.

Fig. 2

Examples of initial DOEs for $k=2$ and $n=9$. a CCI (o), b LHD (+), c D-Opt (x), d Rand ($*$), e Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, orange, yellow, olive) represent different examples of a particular DOE (Color figure online)

3.3 Comparison of results

The sequential multiobjective optimization method was solved 25 (5 problems $\times$ 5 initial samples) times. However, since several of the initial designs have a stochastic component, 3k repeats were made for the cases where a LHD, D-Opt (except for $k=2$), Rand and Sobol sequence are used. The following parameters were considered on the optimization method: (1) the maximum number of runs per iteration, $N_{{\textit{max}}} = 3m$ (m, number of PMs); (2) the total number of simulation (experiments) allowed, $N_{{\textit{total}}} = 15k$. The fitted metamodels for each performance measure were Generalized Linear Regression models (GLM) with one degree of freedom. This is, $N-1$ coefficient were estimated, where N is the number of data points used to fit the model. The stopping criteria used were: (1) stop if $N_{{\textit{total}}}$ is reached; (2) stop if $R^2$ (coefficient of determination) of all models is larger than $1- \varepsilon$, an $\varepsilon =0.05$ was considered; (3) stop if no new Pareto solutions are found.

3.3.1 Final Pareto Sets and Fronts

The final Pareto Sets and Fronts found using the optimization method are shown graphically on “Appendix A”. The true Pareto Set and Front for all the test problems is also shown. Figures 7, 8, 9, 10, 11, 12, 13 and 14 show the results for MOP1–MOP4. The plots are as follows: subplot (a) shows in light gray the input’s or output’s feasible regions, the dark gray regions represent the ’true’ Pareto Set or Front respectively. We used ’ ’ in true to indicate that the Pareto Set and Front is based on a fine grid of evaluations ($100^2$ for MOP1–MOP3, $50^3$ for MOP4 and $30^4$ for MOP5). Subplots (b) to (f) show the approximated Pareto Sets or Fronts using the 5 initial samples with different repeats shown in distinct colors(light blue, blue, purple, orange, yellow, and green). (b) is for CCI, (c) LHD, (d) D-Optima, (e) Random set and (f) Sobol sequence. Subplots (b) to (f) also show the true Pareto Set or Front in dark gray. Since MOP5 has 4 controllable variables and 4 objectives, it is not easy to visualize the final Pareto Sets and Fronts. The true Pareto Set of MOP4 is the plane at $x_{3}=0.5$ and for MOP5 the hyperplane at $x_{4}=0.5$, the corresponding Pareto Fronts are concave regions as shown on Fig. 14(a).

From the plots on Figs. 7, 8, 9, 10, 11, 12, 13 and 14 it can not easily be seen which initial sample of data points is more effective for the sequential multiobjective optimization method. Nevertheless, we can see that in most cases (except when started with a random set) the method was able to identify solutions close to the true Pareto Front with a very limited number of function evaluations ($\le 15k$). From these figures, it can also be noticed that the chosen initial data set makes a difference on the final Pareto Set, however the final Pareto Fronts are not very different. Our original goal was to identify, if possible, overall which initial sample design will work better on the optimization method. However from these figures it is difficult to choose an overall winner. Next we evaluate the performance of each case quantitatively.

3.3.2 Performance of multiobjective optimization method

When comparing the performance of multiobjective optimization methods three aspects are usually considered [31]:

• 1. Convergence, how close is the approximated Pareto Front from the true Pareto Front.

• 2. Spredness, how spread or distributed are the solutions on the approximated Pareto Front.

• 3. Number of solutions, how many solutions are on the Pareto Front.

• 4. Total number of runs, since the total number of simulation (experimental) runs is important for expensive experiments, we considered it as a fourth indicator.

3.3.2.1 Convergence

A natural way to compare two approximated Pareto Fronts is to see if one dominates the other, in which case the one that dominates is better. However, more often neither competing Pareto Fronts dominate the other. As an example, consider Fig. 3 which shows two approximated Pareto Fronts obtained hypothetically by Method A (red solid circles) and B (black open squares). From Fig. 3 it can be seen that solution 1B dominates 1A. However, solutions 2A, 2B, 3A, 3B, 4A and 4B cannot be compared. In this example, neither Pareto Front completely dominates the other.

Fig. 3

Illustration of two competing Pareto Fronts [A (red solid circles), B (black open squares)]. The shaded area is the hypervolume indicator of Pareto Front A with respect to the reference point (filled square). The star point is the utopia solution and the filled square represents the anti-utopia point (Color figure online)

Several methods have been proposed to compare approximated Pareto Fronts [32]. One popular measurement is the hypervolume indicator. Consider, first, a single approximation to a Pareto Front that consists of the 4 red solid circles in Fig. 3; assume that the black solid squared at the northeast corner of the graph is the vector with the worst solution of each individual performance measure (anti-utopia solution). Then, the solutions in the shaded red region are all dominated by approximate Pareto Front A. This area is known as the hypervolume indicator of the approximated Pareto Front. When comparing two approximated Pareto Fronts, the one that dominates the larger region of points relative to a reference point is considered better by the hypervolume indicator. Here, the hypervolume indicator is used to quantify the convergence of the approximated Pareto Fronts.

The hypervolume of each Pareto Front was approximated using a function inspired by the Matlab function hypervolume(PF, U, R, N). Where PF is the approximated Pareto Front, U is the utopia solution, R is the reference point, and N is a large number which indicates how many random samples are drawn in the hypercube defined by U and R. Here N was selected as $100^2$ for MOP1–MOP3, $50^3$ for MOP4 and $30^4$ for MOP5. The utopia point is the vector of the independent minimal of each objective function. The jth component of the reference vector for problem l, $l = 1, \ldots , 5$, $j = 1, \ldots , m$ is defined as follows:

$$\begin{aligned} R_j^l= \max \left\{ {P_{{\textit{front}}}}_j^l \right\} + 0.5 * {\hbox{range}} \left(f_j^l\right) \end{aligned}$$

(1)

This is, the reference point R is the maximal of the ’true’ Pareto Front plus half the range of the objective function values.

Since the algorithm used to approximate the hypervolume (HV) depends on the N generated random points, it was ran 10 independent times. In all cases, the standard deviation of the hypervolumes was less than 0.0068. It is important to notice that all objectives were scaled between [0, 1], so the maximum value of the hypervoulume is 1.

The relative hypervolume (RHV) is calculated as follows:

$$\begin{aligned} {\textit{RHV}}_l^o = \frac{\hbox{HV of problem}~l~\hbox{using design}~o}{\hbox{true HV of problem}~l} \end{aligned}$$

(2)

$o=1,\ldots ,5$.

Table 2 shows the mean RHV and standard deviation (in parenthesis) of each approximated Pareto Front. Each raw represents an optimization problem and each column different initial sampling sets. The instances without standard deviation are the cases where no repeats were performed as the initial DOE are always the same.

Table 2 Mean relative hypervolume and standard deviation (in parenthesis): comparative results for each problem and initial sample

These results give an idea how close, in terms of the hypervolume, the approximated Pareto Front is from the true one. For example, a hypervolume of 0.778 means that the hypervolume of the approximated Pareto Front covers 77.8% of the true hypervolume. Relative hypervolumes slightly lager than one means that the hypervolume of the approximated Pareto Front was a litter larger than the ’true’ one. This is possible since the ’true’ Pareto Front is a good discrete approximation of the true Pareto Front, but not necessary the global optimal.

As suggested by Demsar [33] and Garcia and Herrera [34] when comparing different methods over different data sets the Friedman’s test can be conducted to statistically compare the results. With a Friedman test it is possible to detect differences considering all methods; and if the test rejects the null hypothesis (a difference does not exist), a post-hoc test can be used to identify the pairwise comparisons that do differ. The Friedman’s test is a non parametric test equivalent to the Analysis of Variance (ANOVA) use to analyze unreplicated complete block designs. Here the groups/factors are the different methods (CCI, LHD, etc.) and the problems (MOP1, MOP2, ..., MOP5) are represented as blocks. The response is the average hypervoulme for each combination. The p-value of the Friedman’s test for the data on Table 2 is 0.0043. Since p-value is less than 0.05, we reject the null hypothesis that there is not a difference between the average ranks of the methods and conclude that a difference does exist. Therefore, a post-hoc test is performed to identify which methods do differ. As suggested by Garcia and Herrera [34], the Bergmann–Hommel’s procedure was used to adjust the p-values for the simultaneous pairwise comparisons.

Table 3 shows the none adjusted p-values (above diagonal) for the pairwise comparisons of ranked relative hypervolumes test and the adjusted p-values (below diagonal) using the Bergmann–Hommel’s procedure for the simultaneous comparisons. With a significance level $\alpha =0.05$, the hypothesis that the method performs the same when a CCI or a random set is used is rejected, therefore we conclude that a difference does exist. If a significance level of $\alpha =0.1$ is used it will be concluded that there is a significant different between the D-Opt and the Rand set too. For the remaining pairwise comparisons, the hypothesis that there is not a difference between the performance of the method using the different sample sets can not be rejected. We further investigated the difference between CCI and Rand and performed a Wilcoxon signed rank test with the alternative hypothesis: the difference is greater than 0. The obtained p-value $=$ 0.0312, therefore we reject the null hypothesis that there is not a difference between the average ranks of the methods and conclude that the difference is greater than 0, i.e. the optimization method performs better with a CCI design than a random set.

Detailed information on Friedman test, Wilcoxon test and Bergmann–Hommel procedure for adjusting p-values on simultaneous multiple comparison tests can be found in [33, 34].

Table 3 p-values for pairwise relative hypervolume comparison tests: none adjusted (above diagonal) and adjusted using Bergmann–Hommel’s procedure (below diagonal)

It is important to notice that the hypervolume indicator is impacted by the number of solutions on the Pareto Front, its distribution and the reference point [35]. Therefore, the hypervolume of two approximated Pareto Fronts with different number of solutions and different distribution could be biased. Thus, a second quality indicator, spreadnes, is used to further compare the results.

3.3.2.2 Spread (diversity)

Another criteria used to compare Pareto Fronts is how spread out or distributed are the solutions on the approximated Pareto Front with respect to all objectives. Here, the distance metric criteria proposed by Deb et al. [36] was used. The metric is shown in Eq. 3, $d_s$ is the Euclidean distance between consecutive points of the approximated Pareto Front (P) and ${\bar{d}}$ is the average of these distances. $d_j^e$ is the Euclidean distance between the extreme solution of the true Pareto Font and the extreme solution of the approximated Pareto Front corresponding to the jth objective function ($j=1,\ldots ,m$). The extreme solutions are the solutions with the smallest value per objective.

$$\begin{aligned} \Delta = \frac{\sum_{j=1}^{m} d_j^e +\sum_{i=1}^{|P|} | d_s - \bar{d}|}{\sum_{j=1}^{m} d_j^e + |P|\bar{d}} \end{aligned}$$

(3)

For problems with 2 objectives, |P| on Eq. 3 is replaced by $(|P|-1)$, as there are only $(|P|-1)$ consecutive solutions. For the cases with more than 2 objectives, $d_s$ is calculated as the average distance to the $2(m-1)$ nearest neighbors.

Small values of $\Delta$ indicate a more widely and uniformly spread set of solutions on the Pareto Front. Table 4 shows the mean and standard deviation (in parenthesis) of the distance metric calculations. To calculate the distances the data was normalize between 0 and 1.

Table 4 Mean spread metric ($\Delta$) and standard deviation (in parenthesis): comparative results for each problem and initial sample

As before, a Friedman rank test was performed to compare the results on Table 4. However, in this case the p-value is 0.1804. Therefore, their is not evidence to reject the null hypothesis that there is not a difference between the average ranks of the methods base on the spread metric. So, we concluded that the spreadnes of the solutions on the approximated Pareto Fronts is not statistically different if different initial data sets are used.

Next, the number of solutions on the approximated Pareto Fronts and the total number of function evaluations (simulation runs or physical experiments) are compared.

3.3.2.3 Number of approximated Pareto solutions and total number of function evaluations

Lastly, the number of approximated Pareto solutions and the total number of function evaluations (NFE) are compared. Tables 5 and 6 show the results. A large number of Pareto solutions and a low number of function evaluations is preferred. It is important to notice that a maximum number of evaluations is set on the optimization method, however it could stop before using all the runs. This is one of the advantage of using sequential design optimization methods versus one-stage methods. The number of function evaluations on the one-stage column corresponds to $N_{{\textit{total}}}$.

Table 5 Mean number of solutions on final Pareto Front and standard deviation (in parenthesis): comparative results for each problem and initial sample

Table 6 Mean number of function evaluations and standard deviation (in parenthesis): comparative results for each problem and initial sample

Using the results on Tables 5 and 6, 2 Friedman rank tests were performed. For the first test, comparison of total number of Pareto solutions, a p-value of 0.9417 was obtained. This result strongly suggest that despite the initial sample set used the total number of solutions on the approximated Pareto Front is not statistically different. On the second test, comparison of total number of function evaluations, a p-value of 0.3438 was obtained. As before, we do not have evidence to reject the null hypothesis that the number of function evaluation is the same using the different initial sets.

In summary, based on the 4 quality indicator used here, it seems like the initial sample of data points does not have a large effect on the quality of the approximated Pareto Front. However, since convergence and total number of function evaluations are the most important indicators, for further applications we recommend the use of CCI designs with the optimization method. Overall the method performed better, in terms of hypervolume, using a CCI than a Rand Set. Individually (per problem), when a CCI was used the mean hypervolume of the approximated Pareto Fronts of MOP1, 3, 4 and 5 were the largest, and for MOP2 it was the second largest.

Next, the sequential optimization method is compared with a one-stage approach.

3.3.3 Comparison of sequential versus one-stage multiobjective optimization method

To further compare the performance of the sequential multiobjective optimization method a comparison versus a one-stage approach is presented here. For the one stage approach the optimization algorithm was ran only one iteration. The number of points of the initial design is the maximum number of simulations allowed on the sequential approach minus $10$ to 20% of the points, which were left for validations. The initial designs were Full Factorial Designs with the following levels: $5$ (with 5 validation points) for MOP1–MOP3, $3\times 3\times 4$ (with 9 validation points) for MOP4, and $2\times 3\times 3\times 3$ (with 6 validation points) for MOP5. The surrogate models used here are complete 2nd order GLM. After the Pareto Fronts were approximated, some points (validation points) were selected based on the Maxmin distance criteria described before. The selected points were evaluated and used to update the incumbent Pareto Front.

The mean relative hypervolume, spread metric, number of solutions on the approximated Pareto Front and total number of function evaluations are shown on the last column of Tables 2, 4, 5 and 6 respectively. As can be noticed, the sequential design optimization performs slightly better than the one stage on all criteria. The sequential method required less function evaluations that the one-stage since it stops when the surrogate models are accurate enough. On the worst cases of each problem it used 40–50% less evaluations. Although, the one-stage approach computed more function evaluation it did not found more Pareto solutions than the sequential approach.

Finally, the multiobjetive optimization method is illustrated using an industrial case study.

4 Industrial case studies

This section presents the application of the sequential multiobjective optimization method shown on Sect. 2 using an industrial application. The case study is on welding of ferrous alloys and it is based on costly physical experimentation.

4.1 Optimization on titanium welding

The objective of this application is to identify the values of the process controllable variables of a gas tungsten arc welding (GTAW) of Titanium Ti6Al4V, which is frequently used in the aerospace industry. For the welding of this titanium alloys it is necessary that the mechanical properties like tensile strength, ductility (% elongation) and impact toughness are balanced in order to produce a joint capable to withstand the design loads and the crack growth. For this case study only physical experimental data, which is limited due to the high cost of the test, was used.

4.1.1 Problem description

Figure 4 is a flow diagram of the welding and mechanical testing processes. The process starts by designing and preparing the test coupons. After the coupons are ready and the process parameter set, the pieces are welded. After welded, one day is waited for steady state to be reached before the mechanical tests are performed. For testing, as can be seen on Fig. 4(e), different specimens are obtained from each welded piece flowing mechanical testing standards. Two mechanical test were performed here: (1) a tensile test and (2) an impact test. During the tensile test, tensile strain, tensile strength, yield strength and percentage elongation were measured. On the other hand, the impact test provides the amount of energy absorbed by a material during fracture. This is a measurement of the material’s notch toughness. A larger energy indicates a stronger weld that will withstand the growth of a crack. Further information related to process parameters and welding sequence can be found in [37, 38].

Fig. 4

Welding and mechanical testing flow diagram

The objective of this application is to identify the values of the process controllable variables of the GTAW process of Ti6Al4V plates that provide the best compromises between two performance measures. In the literature, different works that relate the controllable variables and performance measures of titanium welding have been presented. Junaid et al. [39] and Nandagopa and Kailasanathan [40], for example, found that the process variables that have a mayor effect on welding strength are welding velocity, feed rate and energy power. Several others have applied different optimization techniques to improve the welding process. Thepsonthi and Özel [41] used RSM and PSO methods for optimizing a micro-end milling process, [42] used genetic algorithms and particle swarm optimization to identified the best welding robot’s path. However, here we optimized the process considering multiple conflicting objectives simultaneously.

4.1.2 Optimization results

This optimization case study has 2 performance measures: maximize percentage elongation in 25mm and maximize energy absorbed at fracture (J); and 3 process controllable variables: voltage (V), amperage (A) and welding speed ($\hbox{mm min}^{-1}$). The range of the controllable variables are [9.5, 10], [121, 141], and [91.6, 108.4] respectively.

The following parameters were considered for the sequential multiobjective optimization algorithm: $N_{{\textit{max}}} = 3 \times 2$, $N_{{\textit{total}}} = 15 \times 3$ and the lower bound for $R^2$ was set at 95% $(\varepsilon =0.05)$.

Table 7 Initial experiment: welding case study

Fig. 5

Performance Measure values of initial experiment. Circled solutions are incumbent Pareto Front

Fig. 6

Prediction of surrogate models. Circled solutions are selected Predicted Pareto Front

Table 8 Iteration 1: evaluation of selected predicted Pareto solutions

The optimization procedure is as follows:

• 1. Run initial experimental design The first step of the method is to design and ran an experiment to get initial information: as suggested before a Central Composite Design is used. The initial data set used here is the results of the experiment performed by Cruz et al. [37] which is a CCI with $\alpha =1.68$ (when scaled between $-1$ and 1). The values of the controllable variables and corresponding performance measures are shown on Table 7. The experiment has 15 independent runs with 5 extra replicas at the center. The test coupons used here are schematically shown on Fig. 4(a), they are rectangular Ti6Al4V plates 5 mm thick, 60 mm width and 250 mm long. The joint has a bevel angel of $30^{\circ }$ for a groove angle of $60^{\circ }$. Here the pieces were cut and joined using a Fronius GO-FER III machine. In order to prevent bending or opening of the welded joint, the welding was carried out on both extremes of the joint. Since oxygen could contaminate the welding pool, causing embrittlement when it solidifies, argon supplied by the gun nozzle and backing jig was used during the welding cycle [38]. As mentioned before, the process performance measures are percentage elongation and the amount of energy absorbed during fracture. To measure the percentage of elongation a tensile test was performed. Here a electromechanical 100 kN Instron 4482 was used. The stress rate and the testing speed used were around $5~\hbox{MPa s}^{-1}$ and $10~\hbox{mm min}^{-1}$ respectively. For the tensile test, two specimens were fabricated following the ASTM E8/E8M standard. The specimens were obtained for each welded coupon following the procedures of the AWS D17.1 specification. The left zoom-in draw on Fig. 4(e) sketches the specimens. The outer dimensions of the test specimen are $102 \times 15$ mm and $42 \times 5$ mm on the interior section. A gauge length of 25 mm was used to calculate the elongation of the material. Percentage elongation is calculated by dividing the length of the gage section after fracture by its original gauge length multiplied by 100. Higher elongation means higher ductility. To measure the amount of energy absorb during fracture, a Charpy impact test was performed. For the impact test, 3 specimens were fabricated from each coupon and the average energy was reported. The test specimens are schematically shown on the right zoom-in draw of Fig. 4(e), they are 5 mm thick, 55 mm long, and 10 mm width, with a notch of $45^{\circ }$ angel and a 0.25 mm radio. The specimens were machined until their thickness reach 3.3 mm, then chemically etched to reveal heat affected zone. An automated tungsten carbide broach coated by TiN was used to machine the V notch until the final dimensions were reached. A go/no-go gauge was used to verify the notch quality. After quality assurance was compiled the specimens were tested on a $400~\hbox{J SATEC}^{\mathrm{TM}}$ Charpy machine.

• 2. Found incumbent Pareto Front After all data has been collected, the incumbent Pareto Front is identified. Figure 5 shows the values of the PMs graphically. The solution marked as ’center’ is the average of the 6 replication of the center points (solutions 2, 7, 11, 16, 17, and 20). The incumbent Pareto solutions are Solutions 4, 6, and 15, which are circled on Figure 5.

• 3. Form a surrogate model per performance measure Next, a surrogate model is fitted for each PM using all available experimental data. The fitted models are GLM with $n-1$ degree of freedom (n, current number of evaluated data points). The coefficient of determination $R^2$ of the surrogate models are 0.9020 and 0.6085 respectively.

• 4. Evaluate surrogate models at a uniform grid of input combinations The surrogate models were evaluated at a uniform grid of $7 \times 50 \times 50$ input combinations. Figure 6 shows the evaluation of the models.

• 5. Found approximated Pareto Set and Front Now, the Pareto Front of the predicted solutions is found. The predicted Pareto Front has 34 solutions. However, since the maximum number of simulation allowed per iteration is 6, 6 solutions were selected using a max–min distance criteria with 1000 iterations. The circled solutions on Fig. 6 are the selected predicted Pareto solutions.

• 6. Evaluate selected predicted Pareto solutions Table 8 shows the input and output values of the 6 new runs (step 5). The experiments were carried out as the initial experiment (step 1). From each welded coupon 3 specimens were cut to perform the impact test and 2 for the tensile test, the average is reported.

• 7. Update incumbent Pareto Front Now the incumbent Pareto Front is updated comparing the initial 15 independent runs and the new additional 6 runs. The new Pareto solutions are 4, 6, 15, and 22.

• 8. Evaluate Stopping Criteria Next the stopping criteria are evaluated. The criteria used are: (1) stop if $N_{{\textit{total}}}$ is reached; (2) stop if $R^2$ of all models is larger than $1- 0.05$; (3) stop if no new Pareto solutions are found. None of the stopping criteria were met, therefore the optimization algorithm will suggest to iterate again. However, since the cost of the test is expensive we were not able to do more experimentation.

• 9. Report final incumbent solutions The final Pareto solutions are shown on Table 9. From this table it can be noticed that in other to obtained a more ductile weld (higher elongation), the process needs to be set at a voltage of 9.75 V, Amperage of 131 A and weld speed of $108.41~\hbox{mm min}^{-1}$. To obtained a larger Energy (tougher piece), the process should be set at a voltage of 9.90 V, Amperage 125 A and weld speed of $97.45~\hbox{mm min}^{-1}$. Solutions 4 and 15 represent a compromise between maximum elongation and maximum energy.

Table 9 Final Pareto solutions

5 Conclusions

In summary, a sequential surrogate based multiobjective optimization method was used to solve five multiobjective optimization test problems using five different initial sample sets. The goal was to examine which initial set allows the optimization method to better approximate the Pareto Front of problems with different degrees of difficulty on the individual objective functions as well as on the form of the Pareto Set and Front.

In general, the method was able to identify solutions on or very close to the true Pareto Front in a modest number of evaluations, which is critical for the cases of interest where a single simulation or experimental run can be costly and time consuming. A paired wise comparison of 4 quality criteria of the approximated Pareto Fronts showed that there is not a statistical significant different when different initial data sets are used, except for one case (convergence). Therefore, regardless of the initial design used the method will do a good job approximating the Pareto Front. The fact that the method finds similar Pareto Fronts independent of the initial sample of points could be due to the fact that the method iteratively searches for solutions close to the true Pareto Front.

These results show that, as the works reported in sequential single optimization, the initial set of points does not have a high impact on the final solutions of the the multiobjective sequential optimization method used here. However, it is important to extend the analysis to other sequential multiobjective optimization methods.

In addition, to illustrate the method, a case study on titanium welding was used and a Pareto Front was approximated with only 26 experimental runs.

Appendix A

See the Figs. 7, 8, 9, 10, 11, 12, 13 and 14.

Fig. 7

Comparison of final Pareto Sets for MOP1: a True (dark gray), b CCI (o), c LHD (+), d D-Opt (x), e Rand ($*$), f Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, orange, yellow, green) represent the different repeats (Color figure online)

Fig. 8

Comparison of final Pareto Fronts for MOP1: a True (dark gray), b CCI (o), c LHD (+), d D-Opt (x), e Rand ($*$), f Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, orange, yellow, green) represent the different repeats (Color figure online)

Fig. 9

Comparison of final Pareto Sets for MOP2: a True (dark gray), b CCI (o), c LHD (+), d D-Opt (x), e Rand ($*$), f Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, orange, yellow, olive) represent the different repeats (Color figure online)

Fig. 10

Comparison of final Pareto Fronts for MOP2: a True (dark gray), b CCI (o), c LHD (+), d D-Opt (x), e Rand ($*$), f Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, orange, yellow, olive) represent the different repeats (Color figure online)

Fig. 11

Comparison of final Pareto Sets for MOP3: a True (dark gray), b CCI (o), c LHD (+), d D-Opt (x), e Rand ($*$), f Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, orange, yellow, olive) represent the different repeats (Color figure online)

Fig. 12

Comparison of final Pareto Fronts for MOP3: a True (dark gray), b CCI (o), c LHD (+), d D-Opt (x), e Rand ($*$), f Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, orange, yellow, olive) represent the different repeats (Color figure online)

Fig. 13

Comparison of final Pareto Sets for MOP4: a True (dark gray ($x_3=0.5$)), b CCI (o), c LHD (+), d D-Opt (x), e Rand ($*$), f Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, magenta, scarlet, orange, yellow, olive, green) represent different repeats (Color figure online)

Fig. 14

Comparison of final Pareto Fronts for MOP4: a True (dark gray), b CCI (o), c LHD (+), d D-Opt (x), e Rand ($*$), f Sobol-Seq ($\diamond$). Different colors (light blue, blue, purple, magenta, scarlet, orange, yellow, olive, green) represent different repeats (Color figure online)