Achievement scalarizing function sorting for strength Pareto evolutionary algorithm in many-objective optimization

Abstract

Multi-objective evolutionary algorithms (MOEAs) have proven their effectiveness in solving two or three objective problems. However, recent research shows that Pareto-based MOEAs encounter selection difficulties facing many similar non-dominated solutions in dealing with many-objective problems. In order to reduce the selection pressure and improve the diversity, we propose achievement scalarizing function sorting strategy to make strength Pareto evolutionary algorithm suitable for many-objective optimization. In the proposed algorithm, we adopt density estimation strategy to redefine a new fitness value of a solution, which can select solution with good convergence and distribution. In addition, a clustering method is used to classify the non-dominated solutions, and then, an achievement scalarizing function ranking method is designed to layer different frontiers and eliminate redundant solutions in the environment selection stage, thus ensuring the convergence and diversity of non-dominant solutions. The performance of the proposed algorithm is validated and compared with some state-of-the-art algorithms on a number of test problems with 3, 5, 8, 10 objectives. Experimental studies demonstrate that the proposed algorithm shows very competitive performance.

1 Introduction

Evolutionary algorithms (EAs) are a kind of population-based search heuristic algorithms that can obtain a set of candidate solutions in a single run. The multi-objective evolutionary algorithms (MOEAs) have experienced a boom development during the past two decades [1]. Most MOEAs perform well on multi-objective optimization problems (MOPs) with two or three objectives [2]. However, when MOEAs are adopted to tackle many-objective optimization problems (MaOPs) with more than three objectives [3], they will confront with substantial difficulties. As a result, there is growing interest in the development of MOEAs to address MaOPs.

One of the primary reasons is that when MOEAs solves MaOPs, almost all solutions in the population are not dominant as the number of objectives increases, which is attributed to the severe loss of selection pressure based on Pareto front (PF) [4, 5]. Another primary reason is that it is difficult for MOEAs to maintain good population diversity in high-dimensional objective space of MaOPs [6, 44, 45]. Due to the relatively sparse distribution of candidate solutions in the high-dimensional objective space, diversity management strategies widely used in MOEAs, such as crowded distance [7] or clustering operator [8], are confronted with great difficulties.

In order to enhance the performance of MOEAs in solving MaOPs, a lot of improved approaches have been proposed. In summary, the developing approaches can be roughly classified into three categories, including dominance-based, indicator-based and decomposition-based approaches [9].

The first category is dominance-based MOEAs. In order to increase the selection pressure toward the PF, the basic idea adopts various improved dominance relationships or novel diversified management strategies to select quality solutions. Example of some cross-sectional modified dominance relationships, such as $\epsilon$-dominance [10, 11], fuzzy Pareto dominance [12, 13] and grid dominance [14], have been proposed. Besides, another important role for the quality solutions is diversity selection mechanism. For example, in [15], a binary $\epsilon$-dominance is proposed to combined with dominance to speed up convergence of NSGA-II. SPEA2+SDE [16] presented a shift-based density estimation strategy, which punishes solutions with poor convergence by assigning a high density value on the basis of dominant comparison. In addition, a knee point evolutionary algorithm is also a new dominance-based method, aiming at dealing with MaOPs [17].

The second category is indicator-based MOEAs, which adopts solution quality measurement of performance indicators as selection criteria. Among the current available indicator, hypervolume (HV) and R2 indicator may be the most commonly used indicators in multi-objective search process [18]. For instance, SMS-EMOA [19] used $\textit{S}$ metric selection strategy to update population. HypE [20] proposed the uses of Monte Carlo simulation to estimate the HV contributions of the candidate solutions, which reduces the high complexity of HV computation. MOMOBI-II [21] designed a predefined binary indicator, HV indicator, GD and R2 indicator in the environmental selection. SRA [40] adopted the stochastic ranking algorithm to balance the search biases of $I_{\epsilon +}$ and $I_{\mathrm{SDE}}$ indicators.

The third category is decomposition-based MOEAs, which transforms a MOP into a set of single-objective optimization problems. Then, these single-objective problems are optimized simultaneously by evolving a set of solutions. MOEA/D [22] is a classical decomposition-based algorithm, which is an important turning point in the development of evolutionary algorithms. Since then, some improved algorithms based on decomposition methods have been proposed successively, such as [23, 24, 38, 39]. In addition, some researchers have made important breakthroughs in the algorithm for solving MaOPs based on dominance and decomposition methods. For example, MOEA/DD [25] proposed a method based on dominance and decomposition to balance the convergence and diversity of the algorithm. BCE-MOEA/D [26] proposed that dominance and decomposition work collaboratively to facilitate each other’s evolution. Besides, the study on the convergence and distribution of reference vectors is also the focus of investigators. For instance, RVEA [27] proposed that reference vectors can be used to clarify the user’s preferences, thus targeting a preferred subset of the entire Pareto front. RPEA [28] proposed the reference vectors-based approach to guide the evolution so as to strength the selection pressure toward the Pareto front and maintain the uniform distribution of solutions. Hence, a well-distributed reference vectors have been widely used to increase the convergence and diversity in solving many-objective optimization problems. Furthermore, the dominant relationship based on decomposition is also the main research direction. In NSGA-III [29], the authors proposed a clustering operator assisted by a set of well-distributed reference vectors to replace the crowding distance operator in NSGA-II. In RPD-NSGA-II [30], the authors proposed a new decomposition-based dominance relation to create a strict partial order on a set of non-dominating solutions using a well-distributed set of reference vectors. In $\theta$-NSGA-III [31], the authors proposed a new $\theta$-dominance relation-based non-dominant sorting to ensure convergence and diversity in the environmental selection. And in SPEA/R [32], the authors introduced a density estimator based on reference direction for handling both multi-objective and many-objective problems.

According to the above three methods, no matter which method is based on, it will make an important contribution to our future research. More recently, dominance-based and decomposition-based methods have been the focus of research when dealing with MaOPs in some literature [25, 31, 42, 43]. However, as highlighted in [26], dominance-based MOEAs present inferior performance in a high-dimensional objective space, while decomposition approaches have been performed suitable ability in solving different many-objective optimization problems [33]. Therefore, this observation greatly inspired us to adopt decomposition-based methods into dominance-based MOEAs so as to tackle with MaOPs.

SPEA2 [8] is the most typical Pareto dominance relationship implementation, but when dealing with MaOPs, there is not enough selection pressure as the number of non-dominant solutions increases. Hence, some effective strategy needs to be considered to improve the performance of SPEA2. In the existing studies, decomposition-based MOEAs seem to be quite straightforward since the reference vector can guide the solutions uniformly distribution. For example, NSGA-III [29] that is a reference-points-based many-objective evolutionary algorithm based on NSGA-II algorithm emphasized those non-dominant solutions closing to a set of provided reference points. MOMOBI-II [21] is R2 ranking-based algorithm, which introduce that the achievement scalarizing function value is consistent with the reference vector. Motivated by NSGA-III and MOMOBI-II, we suggest a reference-vectors-based many-objective evolutionary algorithm following SPEA2 framework. Compared with existing approaches, the main new contributions of this paper can be summarized as follows.

(1) A density estimation is adopted by the perpendicular distance from a solution to reference vector so as to redefine a new fitness value of a solution. In the proposed method, a set of reference vector is used to build the density distribution in the process of assignment fitness which can select solution with good distribution.

(2) A new achievement scalarizing function sorting algorithm in environmental selection. In this method, a clustering method is designed to classify the non-dominated solutions, and then, an achievement scalarizing function sort method is applied to layer different fronts and prune the redundant solutions, and then, we can ensure both convergence and diversity of non-dominated solutions entering the next generations.

The remainder of this paper is organized as follows: Sect. 2 presents the preliminaries of this paper. Section 3 introduces the proposed SPEA2+ASF algorithms. Section 4 describes experimental design including test problems, performance metrics and experimental setting. Section 5 provides the experimental results. Finally, the conclusion is given in Sect. 6.

2 Preliminaries

In this section, we give some basic definitions in multi-objective optimization. Then, we will briefly introduce the decomposition methods, which are the foundations of our proposed algorithm.

2.1 Basic definitions

In general, the multi-objective optimization problem (MOP) can be mathematically defined as:

$$\begin{aligned} {\mathrm{min}} \quad F( x )=(f_{1}(x),f_{2}(x),...,f_{m}(x) )^{T} \end{aligned}$$

(1)

$$\begin{aligned} s.t\ x\in \varOmega \end{aligned}$$

where $x=(x_{1},x_{2},...,x_{n} )^{T}$ is a n-dimensional decision variable, $\varOmega ^{n}$ is a feasible solution space for n decision variables, $F:\varOmega ^{n}\rightarrow R^{m}$ is the mapping from the decision space to the target space, m is the dimension of the objective space.

In multi-objective optimization, the following concepts have been well defined and widely applied.

Definition 1 (Pareto dominance) For two different decision variables x, y $\in \varOmega$, if $\forall {i=1,2,...,m}$, $f_{i}(x)\le f_{i}(y)$, and $\exists {i=1,2,...,m}$, $f_{i}(x)< f_{i}(y)$, then x is said to Pareto dominate y, denoted as $x \succ y$.

Definition 2 (Pareto optimal set ): For a solution $x^{*}\in \varOmega$, if there is no $x\in \varOmega$ satisfying $x \succ x^{*}$, $x^{*}$ is regarded as the Pareto optimal solution. So the Pareto optimal set (PS) is defined as:

$$\begin{aligned} {\text {PS}}=\{x\in \varOmega | x {\text { is the Pareto optimal solution}\}} \end{aligned}$$

(2)

Definition 3 (Pareto front): Pareto front (PF) is described as the image of Pareto optimal solution set on the objective space. The PF is defined as:

$$\begin{aligned} {\text {PF}}=\{f(x)\in R^{m}| x\in {\text {PS}\}} \end{aligned}$$

(3)

MOEAs have the powerful capacity for solving MOPs. The goal of MOEAs is to obtain the non-dominated solutions which is close to PF and evenly distributed over PF.

2.2 Decomposition methods

The decomposition method is used to transform the multi-objective problem into a set of single-objective optimization problems. There are several possible approaches such as Tchebycheff approach, penalty-based boundary intersection approach and achievement scalarizing function approach.

2.2.1 Tchebycheff approach

The Tchebycheff aggregate function with a non-negative weight vector w and reference point $z^{*}={\mathrm{min}}\left\{ f_{i}(x)\mid x\in \varOmega \right\}$ is written as follows:

$$\begin{aligned} minimize \quad g^{te}(x\mid w ,z^{*})=\displaystyle {\max _{1\le i \le m}}\left\{ w_{i}\mid f_{i}(x)-z^{*} \mid \right\} \end{aligned}$$

(4)

where $z^{*}=(z_{1}^{*},...,z_{m}^{*})$ is reference point, and the value of $z^{*}$ is set $z^{*}={\mathrm{min}}\left\{ f_{i}(x)\mid x\in \varOmega \right\}$, $i=1,2,...,m$.

2.2.2 Penalty-based Boundary intersection approach

Mathematically, penalty-based boundary intersection approach can be defined as follows:

$$\begin{aligned} minimize \quad g^{pbi}(x\mid w,z^{*})=d_{1}+\theta d_{2} \end{aligned}$$

(5)

where $\theta > 0$ is a penalty parameter. The $d_{1}$ represents the Euclidean distance between the fitness value and ideal point $z^{*}$, $d_{2}$ is the perpendicular distance between F(x) and w.

2.2.3 Achievement scalarizing function approach

Achievement scalarizing function (ASF) has been scarcely studied in MOEAs, and ASF is defined as:

$$\begin{aligned} minimize \quad g^{ASF}(x\mid w ,z^{*})=\displaystyle {\max _{1\le i \le m}}\left\{ \frac{1}{w_{i}}\mid f_{i}(x)-z^{*} \mid \right\} \end{aligned}$$

(6)

where the reference vectors is the reciprocal form because the method can make the contour lines of a solution consistent with the reference vector. To make it clear that achievement scalarizing function value is superior to Tchebycheff aggregate function value in calculation, we illustrate it with a two-dimensional example in Fig. 1.

Fig. 1

Illustrate the contour line with ASF and TCH with a two-dimensional example

In Fig. 1, we calculate the achievement scalarizing function values and Tchebycheff aggregate function values of solution A on $w_{i}$, $i=1,2,3$, respectively. According to Eq. 4, we can obtain $g^{te}(A,w_{1})=0.49$, $g^{te}(A,w_{2})=0.35$, $g^{te}(A,w_{3})=0.21$, and solution A is an optimal value on reference vector $w_{3}$. According to Eq. 6, we can obtain these values $g^{ASF}(A,w_{1})=1$, $g^{ASF}(A,w_{2})=\frac{7}{5}$, $g^{ASF}(A,w_{3})=\frac{7}{3}$, and solution A is an optimal value on reference vector $w_{1}$. Therefore, the calculated value of ASF not only has convergence performance, but also has better distribution performance than the TCH value in terms of the distribution property of the solution. Besides, the reason why we did not choose PBI method is that although PBI has good convergence and distribution performance in the calculation process, the $\theta$ value selected has a great impact on the results. So we consider ASF as the selection criterion in environmental selection.

3 The proposed SPEA2+ASF

3.1 Overview

The framework of the proposed SPEA2+ASF is described in Algorithm 1.

First, after setting the population size N, a set of N reference vectors is generated, which is denoted as $W=\{w_{1},w_{2},...,w_{N}\}$. So a m-objective reference vector is represented by $w_{j}=(w_{j,1},w_{j,2},...,w_{j,m})$, where $w_{j,i}\ge 0$, $\displaystyle {\sum\nolimits _{i=1}^{m}}w_{j,i}=1$, $i=1,2,...,m$, and $j=1,2,...,N$. Then, the initial population $P_{0}$ is randomly generated and the ideal point $z^{*}$ is initialized. Next, the algorithm enters the iteration until the termination condition is satisfied. In the iteration, we use the recombination operator to produce the offspring population $Q_{t}$. Next, population $R_{t}$ is composed of current population $P_{t}$ and offspring population $Q_{t}$. Then, we redefine the fitness of solutions according to the distance between the reference vector and solutions. Finally, a clustering operator and a new achievement scalarizing function sorting strategy are implemented for environmental selection. The non-dominated solutions in the final population $P_{t+1}$ is returned as the output when the iterative optimization is compete.

3.2 Generate reference vectors

In our algorithm, the decomposition-based approach consists of a systematic process that first generates a set of uniformly distributed reference vectors. In this paper, we use Das and Dennis’s [29] systematic approach to generate the evenly distributed reference vectors. The number of reference vectors (N) is defined as follows:

$$\begin{aligned} N=\left( \begin{array}{l} H+M-1 \\ \quad M-1 \\ \end{array} \right) \end{aligned}$$

(7)

where H is considered as divisions along each objective, M is the number of objective problem. In this case, the reference vectors are widely distributed on the entire normalized hyperplane. Therefore, the algorithm is likely to find widely distributed Pareto optimal solutions corresponding to the reference vectors.

3.3 Recombination operator

The selection of recombination operators plays an important role in population renewal, especially in high-dimensional objectives space. Because it is more likely to choose solutions that are far away from each other to recombine and generate poor-performing descendant solutions in a higher-dimensional objectives space. In the existing research, the two schemes of mating restriction and SBX operation with a large distribution index are the most widely used. As in NSGA-III [29], a careful elitist selection of solutions and maintaining diversity among solutions are applied by emphasizing the solutions closest to the reference line of each reference point. They do not employ any explicit reproduction operation for handling problems with box constraints only. In SPEA2+ASF, we also use a reference vector to lead selection strategy to maintain the diversity in solving many-objective optimization problems. Besides, we adopt a clustering method and ASF non-dominated sort method to layer the different fronts, which enhance not only the distribution but also the convergence. Therefore, we consider creating offspring solutions that is closer to parent solutions, such as NSGA-III [29]. Thereby, we employs SBX operation with a lager distribution index, where near-parent solutions are emphasized. During the recombination, two parent solutions are randomly selected from the current population $P_{t}$, and the offspring solutions are created using SBX operators with large distribution exponential and polynomial mutations.

3.4 Fitness assignment

In SPEA2 [8], after generating offspring population $Q_{t}$ by parent population $P_{t}$, a union population $R_{t}$ consists of $R_{t}$ and $Q_{t}$. Then, a fine-grained fitness assignment strategy is incorporated into density information in $R_{t}$. Each individual x is assigned a strength value S(x), indicating the number of solutions in which it dominates:

$$\begin{aligned} S(x)=|\{y|y\in R_{t} \wedge x\succ y\}| \end{aligned}$$

(8)

where $|\cdot |$ stands for the cardinality, $\cup$ signifies the union of parent population and offspring population, $\succ$ represents the Pareto dominance relation. Then, the raw fitness R(x) of an individual x is calculated:

$$\begin{aligned} R(x)=\displaystyle {\sum _{y\in R_{t}, y\succ x} S(y)} \end{aligned}$$

(9)

where $R(x)=0$ corresponds to a non-dominated solution, and a high R(x) value means that a solution x is dominated by many solutions.

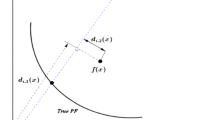
However, if the individuals do not dominate each other, the raw fitness value will be zero, and the fitness assignment will be meaningless. In order to avoid this case, we adopt an distance-based density estimation technique to discriminate between individuals and solutions having identical raw fitness values. Each solution has the unique distance value $d_{2}=(\overline{f}(x),w_{i})$, which is actually the perpendicular distance between $\overline{f}(x)$ and the associated reference vector $w_{i}$. The distance of $d_{2}$ is calculated as follows:

$$\begin{aligned} d_{1}(x)=\parallel \overline{f}(x)w_{i} \parallel /\parallel w_{i}\parallel \end{aligned}$$

(10)

$$\begin{aligned} d_{2}(x)=\parallel \overline{f}(x)-d_{1}(w_{i}/\parallel w_{i}\parallel ) \parallel \end{aligned}$$

(11)

where $\overline{f}(x)=(\overline{f_{1}}(x),\overline{f_{2}}(x),...,\overline{f_{m}}(x))$ is a transformed objective value of solution x. $w_{i}$ is an m-dimensional reference vector. The expressions for $d_{1}$ and $d_{2}$ in two dimensions are illustrated in Fig. 2.

Fig. 2

Illustrate the calculation of $d_{1}$ and $d_{2}$

In SPEA2 [8], the authors proposed that existing some individuals in current generation may do not dominate each other. Then, according to the partial order defined by the dominance relationship, there will be no information or little information. In this case, the use of density information can guide the search more effectively [8]. Therefore, density estimation method with an adaptation of the k-th nearest neighbor is designed in SPEA2+ASF. In this situation, we use the reciprocal of the distance to the k-th nearest neighbor as the density estimate. More specifically, we calculate the distance ($d_{2}$) between each solution x and all reference vectors, and then, all distances are sorted in increasing order. Then, the k-th nearest solution represents the desired distance, denoted as $\varrho _{x}{k}$. Therefore, the density D(x) is defined as follows:

$$\begin{aligned} D(x)=\frac{1}{\varrho _{x}^{k}+\theta _{x}} \end{aligned}$$

(12)

where k is the square root of the union population size, $k=\sqrt{2N}$. $\theta _{x}=2$ is designed to the denominator to ensure that its value is greater than zero and $D(i)<1$.

The redefined fitness of solution x is defined as:

$$\begin{aligned} F(x)=R(x)+D(x) \end{aligned}$$

(13)

This method can make solutions with better local diversity and convergence to have higher final fitness, which is of great benefit to the diversity and local convergence of subregions.

3.5 Achievement scalarizing function sorting-based environmental selection

Environmental selection plays a key role in the process of retaining the population into next generation. In SPEA2 [8], the truncation method prevents the deletion of boundary solutions, but it lacks convergence and distribution in the retention of solution sets, especially in solving high-dimensional multi-objective optimization problems.

In order to select the candidate solutions with good convergence and diversity from the union set $R_{t}$ when we tackle with MaOPs, we use $d_{2}$ clustering and ASF non-dominated sorting method to select these solutions that will be next generation parent population. The procedure of environmental selection is shown in Algorithm 2.

In environmental selection, we select these population which have a fitness lower than 1 to the next generation population. If the number of the selected population is less than or equal to the population size N, we will copy these best dominated solutions in the previous population to $P_{t+1}$ until meeting the population size according to the fitness ranking. However, when the number of population with fitness value greater than 1 exceeds N, more attention has been paid to the reduction strategies of the population. In order to obtain individuals with good convergence and diversity, we adopt a clustering operator method and ASF non-dominated sorting method in St. In this situation, a set of reference vector is designed to guide population toward Pareto front and reference vectors. Therefore, the convergence and diversity of population will be increased, the detailed procedures are described in Algorithm 3, Algorithm 4 and Fig. 3.

In the following, the clustering operator is illustrated in Algorithm 3.

Each objective value of St is then translated by subtracting objective $f_{i}(x)$ by $z_{i}^{\mathrm{min}}$ so that the ideal point of translated St becomes a zero vector. We denote this translated objective as $\overline{f}_{i}(x)=f_{i}(x)-z_{i}^{\mathrm{min}}$. After translating each objective of St in the objective space, we need to associate each population member with a reference vector. In the translated objective space, we calculate the perpendicular distance between each solution of St and each reference vector. Next, a solution with minimum distance is assigned into a cluster C. Then, an achievement scalarizing function sort is applied to select these population that will join the next generation. The procedure of ASF non-dominated sort is shown in Algorithm 4.

In Fig. 1, the ASF value is proved to be in the same direction as the reference vector and has both convergence and distribution. In addition, the smaller the ASF value is, the closer the corresponding solution is to the real frontier and the reference vector. So, we suggest a new sorting method based on clustering operator and achievement scalarizing function in environmental selection. To be precise, we calculate the ASF value in each cluster and sort these solutions in this cluster. Then, different fronts $[F_{1}, F_{2},\ldots ]$ in all clusters are obtained. Finally, these solutions from $F_{1}$ to $F_{i-1}$ fronts are copied into $P_{t+1}$, and $N-|P_{t+1}|$ solutions in the maximum front $F_{i}$ are put into $P_{t+1}$ according to randomly sorting.

To illustrate the process of achievement scalarizing function sorting strategy more clearly, we describe it with a two-dimensional example in Fig. 3.

Fig. 3

Illustrate the achievement scalarizing function sorting strategy with a two-dimensional example

We assume separately reference vectors $w_{1}=(0.2,0.8)$, $w_{2}=(0.4,0.6)$, $w_{3}=(0.5,0.5)$, $w_{4}=(0.6,0.4)$ and $w_{5}=(0.8,0.2)$. These solutions are set $a=(0.19,0.8)$, $b=(0.22,0.9)$, $c=(0.48,0.5)$, $d=(0.51,0.48)$, $e=(0.7,0.49)$, $f=(0.6,0.4)$, $g=(0.7,0.3)$ and $h=(0.8,0.18)$. In our paper, population size is same to the number of reference vectors. In this case, we should retain 5 solutions into the next generation. After performing the clustering operation according to Algorithm 3, we get the reference vector and the associated solution set such as $w_{1}$ and {a,b,c}, $w_{3}$ and {c,d,e}, $w_{4}$ and{f,g}, $w_{5}$ and {h}. Then, we carried out achievement scalarizing function in each cluster. Solutions {a,c,f,h} are classified into first front, {b,d,g} is sorted into second front, and {e} is layered into third front. Therefore, solutions {a,c,f,h} are reserved directly to the next generation of population, and then, the remaining solution is randomly selected in {b,d,g} to keep the number of solutions equal to the number of reference vectors. In addition, when the number of solutions in first fonts exceeds the population size N, we will select these solutions with the optimal ASF value in each cluster into the next parent population.

3.6 Computational complexity of SPEA2+ASF

The computational complexity of SPEA2+ASF is dominated in one generation by the clustering operator that is shown in Algorithm 3. In Algorithm 3, each solution x in $S_{t}$ need to be calculated the distances with N reference vectors, and the computational complexity of each distance calculation is O(m). Due to $\mid S_{t}\mid \le 2N$, the overall worst complexity of SPEA2+ASF in each generation is $O(mN^{2})$.

3.7 Discussions

It is worth noting that SPEA2+ASF algorithm is based on the SPEA2 framework and is partly inspired by NSGA-III and MOMOBI-II, but it is also different from these compared algorithms. These differences can be summarized as follows.

Both SPEA2+ASF and SPAE2 [8] employ the strength Pareto and assign fitness to execute the dominate relations. However, there are two major differences between the two algorithms. Firstly, SPEA2+ASF adopts a set of reference vector to build the density distribution in the process of assignment fitness, while SPEA2 adopts the distance between any two solutions for density distribution. Secondly, in order to deal with the scaled Pareto fronts, SPEA2+ASF adopts a set of reference vector to guide selection strategy to maintain the diversity, while SPEA2 only adopts the distance between solution x to its k-th nearest neighbor to select non-dominated solutions.

Both SPEA2+ASF and NSGA-III [29] adopt dominance relationships to converge populations and reference vectors to maintain diversity. But NSGA3 uses the NSGA2 method of fast non-dominant sorting, while SPEA2+ASF uses a strong dominant relationship based on fitness values. In addition, NSGA-III applies the correlation operation of the vertical distance between population and reference point and adopts the niche to retain the good candidate solutions, while SPEA2+ASF employs a clustering correlation operation and ASF non-dominated sorting method to preserve the quality solutions.

Both SPEA2+ASF and MOMOBI-II [21] use a reference vector to lead selection strategy to maintain the diversity in solving many-objective optimization problems. Nevertheless, SPEA2+ASF performs a clustering method and ASF non-dominated sort method to layer the different fronts, enhancing distribution and convergence. MOMOBI-II employs the fast R2 indicator ranking strategy in solving many-objective problems.

In summary, our major motivation is to exploit the merits of both a clustering method and ASF non-dominated sort guided approaches for enhancing the convergence and diversity in solving many-objective problems.

4 Experimental design

The experimental design introduced in this section investigates the performance of SPEA2+ASF. First, we give the test problems and performance metrics which are used in our experiments. Then, the experimental settings adopted are provided.

4.1 Test problems

In this comparison, thirteen test problems with different characteristics of the Pareto front are involved in the experiments. We assessed two test suits including Deb–Thiele–Laumanns–Zitzler (DTLZ1-DTLZ4) [34] and Walking Fish Group (WFG1-WFG9) [35]. All these problems can be extended to any number of objectives and decision variables. In this paper, we consider the number of objectives $m\in \{3,5,8,10\}$. For DTLZ1 test problems, the number of division is $m+k-1$, where m is the number of objectives and k is set to 5. However, k is set to 10 for DTLZ2-DTLZ4 as mentioned in [34]. As for WFG problems, the divisions is set to $k+l$, where $k=2*(m-1)$ and $l=20$ [35].

4.2 Performance metrics

The performance metrics are need to evaluate the quality of the proposed algorithm. In the multi-objective and many-objective optimization algorithms literature, the inverted generation distance (IGD) [36] is one of the most widely used metric, which can comprehensively reflect the convergence and diversity of solution sets.

IGD measures the average Euclidean distance from the uniformly distributed points across the Pareto front to the closet solution in its resulting solution set. Therefore, the situation where all the obtained solutions are concentrated to one point is avoided, which can well lead to convergence while the possibility of the algorithm at the same time. The lower value shows that the algorithm obtains a better performance. The formula of IGD is as follows:

$$\begin{aligned} IGD=\frac{\sum ^{|P|}_{i=1}d(P_{i},P^{*})}{|P|} \end{aligned}$$

(14)

where P is the number of groups on the true front ; $P^{*}$ is the Pareto solutions set for the multi-objective algorithm ; |P| is the population size of P; $d(P_{i},P^{*})$ represents the minimum between $P_{i}$ and $P^{*}$.

In addition, another performance metric (hypervolume) [20] is adopted to evaluate the population quality, which can measure both convergence and diversity. The hypervolume (HV) metric is defined as the volume of the hypercube enclosed in the objective space by the reference point and every vector in the Pareto approximation set A. This is mathematically defined as:

$$\begin{aligned} HV=\{\cup _{i}vol_{i}|vec_{i}\in A\} \end{aligned}$$

(15)

where $vec_{i}$ is a non-dominated vector from Pareto approximation set A, $vol_{i}$ is the volume from the hypercube formed by the reference point and the non-dominated vector $vec_{i}$, and reference point is $z^{ref}$ in the objective space.

The HV metric is suitable for accessing the convergence and maximum diffusion of solutions of Pareto approximation sets obtained by any multi-objective optimization algorithm. In addition, a larger value for this metric indicates that the solution is closer to the true Pareto frontier and that the solution covers a wider range of extensions.

Since IGD and HV can simultaneously evaluate the convergence and diversity of a given solution set, we consider the following two widely used performance metrics to evaluate the performance of each algorithm. The HV metric is calculated with respect to a given reference point $z^{ref}=(z_{1}^{ref}, z_{2}^{ref},\dots ,z_{m}^{ref})$. In our paper, we design $z^{ref}=(1,1,\ldots ,1)$ as the reference point for DTLZ1 and use $z^{ref}=(2,2,\ldots ,2)$ as the reference point for DTLZ2, DTLZ3 and DTLZ4. Besides, $z^{ref}=(3,5,\ldots ,2m+1)$ is applied as the reference point for WFG1-WFG9 problems.

4.3 Experimental setting

In this section, we describe in detail the different parameter setting between our proposed algorithm and these compared algorithms. In this paper, the parameter setting of each algorithm is consistent with original paper (SPEA2 [8], MOEA/D [22], MOMOBI-II [21] and NSGA-III [29]). Parameters are set as follows: neighborhood size $T=20$, probability of crossover $p_{c}=0.5$, probability of mutation $p_{m}=1/D$ (D is the division), probability of mutation $\eta _{c}=20$ and distribution index $\eta _{m}=20$.

Besides, in order to compare the results of the algorithm to some extent, we set the same parameters in the number of objectives, population size and maximum of the iterative generations of the five algorithms. The parameters are shown in Table 1.

Table 1 Setting of the population size and the maximum number of iterative generation in the experiments

5 Experimental results

In this section, the performance of SPEA2+ASF is to be validated to compare with SPEA2 [8], MOEA/D [22], MOMOBI-II [21] and NSGA-III [29]. The aim is to demonstrate the superiority of SPEA2+ASF implementation required for algorithm convergence and diversity in solving many-objective problems. We analyze the results of the proposed algorithm and the compared algorithms, respectively, from the data and the figures.

5.1 The analysis of data

During data processing, we run all the algorithms 20 times independently to indicate the comparative results for each test problems with different number of objectives. The statistical experimental results of IGD are summarized in Table 2, where the minimum IGD mean value and standard deviation are recorded. Moreover, the statistical experimental results of HV are summarized in Table 3, where the maximum HV mean value and the standard deviation are recorded. The mean value represents the optimal value, while the standard deviation represents the difference between most data and the mean value, with no other significance. In addition, the Wilcoxon rank sum test [37] at a significance level of 0.05 is recorded in tables. That is, if the p value is greater than 0.05, two algorithms show no significant difference. In our paper, we use +, = and − to represent that SPEA2+ASF is superior to, similar to and inferior to the compared algorithm. Besides, the bold black front represents the optimal value among the five algorithms. Bold italic font represents that the indicator value of the compared algorithm is superior to SPEA2+ASF when there is no significant difference between the two algorithms. In this case, we can consider that the proposed algorithm also has the optimal value.

Table 2 Statistical result (mean and standard deviation) of IGD values on DTLZ problems calculated by SPEA2, MOEA/D, MOMOB-II, NSGA-III and SPEA2+ASF

Table 3 Statistical result (mean and standard deviation) of HV values on DTLZ problems calculated by SPEA2, MOEA/D, MOMOB-II, NSGA-III and SPEA2+ASF

Tables 2 and 3 show the IGD and HV values obtained by the five algorithms, which can express the convergence and diversity of the algorithm simultaneously. In all the test problems, SPEA2+ASF algorithm has 22 optimal values in Table 2 and has 34 optimal values in Table  3, and the total number of optimal values is higher than other compared algorithms. Moreover, the proposed algorithm has stronger optimal value quantity advantage when compared with other algorithms alone. Since the performance indicators IGD [36] and HV [20] can simultaneously evaluate the population convergence and diversity, it can be shown from the data in Tables 2 and 3 that the SPEA2+ASF algorithm achieves better performance than the compared algorithms.

In addition, the proposed algorithm is analyzed in detail from each problem and the compared algorithms to further understand the performance of SPEA2+ASF algorithm on all problems. The detailed analysis is as follows.

DTLZ1 is characterized by linearity and multi-mode, and its biggest challenge is to have a number of local Pareto fronts. As can be observed in Tables 2 and 3, SPEA2+ASF achieves the best results for the four objectives on the DTLZ1 problem, which indicates the obvious competitiveness of the proposed algorithm. In addition, SPEA2+ASF algorithm shows the similar performance to NSGA-III for 3-, 5- and 8-objective, and similar performance to MOMOBI-II for 3- and 5-objective in HV data statistics. For DTLZ1, SPEA2+ASF is not inferior to the compared algorithms for the four objectives, which confirms the splendid performance of SPEA2+ASF in terms of both convergence and diversity for getting over the liner and multi-modal many-objective problem.

DTLZ2 is a relatively simple problem with concave PF. For the statistical results in Tables 2 and 3, SPEA2+ASF shows competitive performance in HV statistics for 3-, 5-, 8- and 10-objective than the compared algorithms, while there is no significant performance difference than MOMOBI-II. In addition, SPEA2+ASF performs slightly worse than MOMOBI-II in IGD statistics for 3- and 10-objective and NSGA-III for 3-objective, which indicates that decomposition-based method has certain advantages in dealing with concave problems in higher dimensions.

DTLZ3 is characterized by concave and multi-mode, where the challenge lies in how to get rid of local optimality. For the statistical results in Tables 2 and 3, the performance of SPEA2+ASF is better than other algorithms for 3- and 5-objective, but it has the obvious disadvantage over MOEA/D, MOMOBI-II and NSGA-III on 8- and 10-objectives. By contrast, SPEA2+ASF shows slight resemblance with SPEA2. From this result, the convergence of this algorithm in dealing with the concave problem of multi-mode is still to be improved.

The main challenge of DTLZ4 lies the biased solutions. As indicated by the statistical results in Tables 2 and 3, SPEA2+ASF shows competitive performance on 5-, 8- and 10-objective in terms of both IGD and HV values. SPEA2+ASF is able to achieve a good convergence and wide distribution of approximate PF. However, SPEA2+ASF performs the slightly worse than NSGA-III for 3-objective in IGD statistics and shows similar performance with MOMOBI-II for 3- and 5-objective.

WFG1 is recommended to test the ability of each algorithm to deal with mixed, biased and scaled PF. As shown by the statistical results in Tables 2 and 3, SPEA2+ASF behaves superior performance than SPEA2 and NSGA-III but inferior than MOEA/D and MOMOBI-II.

WFG2 is introduced to test optimizer’s ability to tackle convex, disconnected and non-separable PF. As shown in Tables 2 and 3, SPEA2+ASF shows slightly worse than NSGA-III only for 3-objective and manifests competitive performance than other algorithms for 3-, 5-, 8- and 10-objective. However, SPEA2+ASF shows a relatively poor performance than other algorithms in dealing with WFG3 characterized by linear, degenerate and non-separable.

Regarding WFG4, it introduces concave and multi-model characteristic in decision space. As shown by the statistical results in Tables 2 and 3, SPEA2+ASF performs better than other algorithms in HV statistics but only better than MOEA/D and MOMOBI-II in IGD statistics. Even though the results of the two statistical methods were different, SPEA2+ASF algorithm still shows a good advantage over the other algorithms.

Fig. 4

The representation of the optimal solutions obtained by each algorithm on the 3-objective DTLZ1(a)–(e) and DTLZ3(f)–(j)

Fig. 5

The representation of HV convergence trend by each algorithm on the 3-objective of partial functions

Fig. 6

The representation of the optimal solutions obtained by each algorithm on the 5-objective DTLZ3(a)-(e) and WFG8(f)-(j)

Fig. 7

The representation of HV convergence trend by each algorithm on the 5-objective of partial functions

WFG5 is a deceptive optimization problem with concave PF. As shown in Table 2, SPEA2+ASF performs superior than the compared algorithms but inferior than SPEA2 and NSGA-III for 5- and 8-objective. However, as shown in Table 3, SPEA2+ASF puts up competitive performance than compared algorithms but only shows slightly worse than NGSA-III for 10-objective.

For WFG6, non-separable and concave characteristics are introduced. SPEA2+ASF achieves better performance in HV statistical results than other algorithms. However, SPEA2 and NSGA-III perform better than the proposed algorithm SPEA2+ASF in Table 3 for 5-, 8- and 10-objective. WFG7 is designed to test the ability of each algorithm to deal with concave and biased feature. SPEA2+ASF performs relatively worse performance compared with the SPEA2 and NSGA-III for different objective space in Table 2 but shows the competitive performance in Table 3.

WFG8 is featured by concave, biased and non-sparable. As shown in Table 2, SPEA2+ASF displays slightly worse performance then NSGA-III in IGD values for 8- and 10-objective. However, SPEA2+ASF achieves competitive performance compared with algorithms for different objectives. As for WFG9, it is a difficult problem to solve, characterized by concave, biased, multi-modal, deceptive and non-separable. SPEA2+ASF realizes competitive performance for 5-, 8- and 10-objective in HV statistics, whereas SPEA2 has achieved no significantly different IGD value for 3- and 8-objective and performs superior to SPEA2+ASF for 5-objective.

Besides, the tables record not only the optimal value of the indicator average but also the standard deviation. In general, the standard deviation corresponding to the optimal value of average value is also optimal. However, there may be some poor values in the 20 independent operations, resulting in the standard deviation, and the optimal value is not uniform optimal. It can be seen from Tables 2 and 3 that SPEA2+ASF has the largest number of optimal values among the 52 functions, regardless of the optimal value or standard deviation. Finally, SPEA2+ASF and each algorithm are counted on 13 test problems with four different objective numbers in the last row of the table. Among the 52 functions, SPEA2+ASF algorithm has a certain advantage in the number of superior and similar than compared algorithms. In general, SEPA2+ASF algorithm achieves good convergence and distribution in solving high-dimensional many-objective optimization problems.

5.2 The analysis of figures

Data statistics show that the proposed algorithm has an overall advantage over the compared algorithms. However, figures are more intuitive to see the convergence and distribution of each algorithm on a certain function. In the following, we will analyze the front figures and HV convergence figures of the test problem for 3-, 5-, 8- and 10-objectives.

The convergence and diversity of the five algorithms show that the approximate Pareto optimal solution set converges to the position of the true Pareto front and can be uniformly distributed along the true Pareto front. As shown in Figs. 4, 6, 8 and 10, SPEA2+ASF algorithm obtains an approximate Pareto solution set with good convergence and distribution. In addition, the convergence trend of the performance indicator can also intuitively show the convergence accuracy and convergence speed of the algorithms. As further observed in Figs. 5, 7, 9, 11 and 12, SPEA2+ASF algorithm almost achieves the optimal or suboptimal convergence accuracy and convergence speed, which indicates that the proposed algorithm is competitive in solving high-dimensional problems.

Besides, the proposed algorithm is analyzed in detail with the compared algorithms to further understand the performance of the SPEA2+ASF algorithm on these problems with obvious characteristics. The specific analysis is as follows.

Fig. 8

The representation of the optimal solutions obtained by each algorithm on the 8-objective DTLZ2 (a)–(e) and WFG9 (f)–(j)

Fig. 9

The representation of HV convergence trend by each algorithm on the 8-objective of partial functions

Fig. 10

The representation of the optimal solutions obtained by each algorithm on the 10-objective DTLZ1 (a)–(e) and WFG2 (f)–(j)

Fig. 11

The representation of HV convergence trend by each algorithm on the 10-objective of partial functions

Fig. 12

The representation of IGD convergence trend by each algorithm on the 10-objective of partial functions

Figure 4 shows the representation of the optimal solutions obtained by each algorithm on the 3-objective DTLZ1 and DTLZ3, where Fig. 4 a–e represents DTLZ1 and Fig. 4 f–j represents DTLZ3. Three coordinates represent three objective functions. In Fig. 4, the five algorithms can converge to the true Pareto front on both test problems. However, SPEA2 and MOEA/D are obviously poorly distributed on the front, especially MOEA/D. The distribution of MOMOBI-II is relatively better, but the locations of extreme points on DTLZ1 are unevenly distributed, and the processing of boundary solutions on DTLZ2 needs to be improved. The NSGA-III frontier map is closest to SPEA2+ASF on DTLZ1, but it is not evenly distributed at the extreme points on DTLZ2.

Figure 5 shows the representation of HV convergence trend by each algorithm on the 3-objective of partial functions. In experiments, we use the number of iterations as the termination condition of the algorithm, which is the abscissa. In this paper, the ordinate of convergence trend is log10(HV) or log10(IGD), and this representation can make the convergence trend and accuracy more clear. As observed in Fig. 5, SPEA2+ASF obtains the best HV value on DTLZ1, DTLZ2, DTLZ3,WFG5 and WFG7. As for WFG2, WFG4 and WFG6, SPEA2+ASF performs the almost the same HV accuracy. According to Figs. 4 and 5, SPEA2+ASF demonstrates the good convergence and diversity for 3-objective problems.

Figure 6 shows the representation of the optimal solutions obtained by each algorithm on the 5-objective DTLZ3 (a)–(e) and WFG8 (f)–(j). In Fig. 6, SPEA2 obviously did not converge to the true front and MOEA/D performs the worst distribution on DTLZ3, while MOMOBI-II and NSGA-III show the similar Pareto front with good convergence and distribution of SPEA2+ASF. As further observed in Fig. 6f–j, MOEA/D and MOMOBI-II perform the worst distribution, while NSGA-III shows the almost similar Pareto front with SPEA2+ASF.

Figure 7 shows the representation of HV convergence trend by each algorithm on the 5-objective of partial functions. As further observed in Fig. 7, SPEA2+ASF obtains the best HV accuracy on DTLZ1, DTLZ4, WFG2, WFG4, WFG5, WFG6, WFG8 and WFG9. In this case, SPEA2+ASF shows the competitive performance of convergence and diversity for 5-objective test instances.

Figure 8 shows the representation of the optimal solutions obtained by each algorithm on the 8-objective DTLZ2 (a)–(e) and WFG9 (f)–(j). As for Fig. 8a, SPEA2 shows no convergence to the true Pareto front, which indicates the strength Pareto dominate fails to tackle with 8-objective DTLZ2. In addition, MOEA/D is poorly distributed although it converges to the true Pareto front. Besides, SPEA2+ASF performs the similar Pareto front with MOMOBI-II but superior to NSGA-III on 8-objective DTLZ2. As for Fig. 8f–j, SPEA2+ASF shows the superior distribution performance than SPEA2, MOWA/D and MOMOBI-II and shows the similar Pareto front with NSGA-III on 8-objective WFG9.

Figure 9 shows the representation of HV convergence trend by each algorithm on the 8-objective of partial functions. Since SPEA2 does not converge to the true Pareto front on DTLZ1, DTLZ2 and DTLZ3, only four algorithms of HV convergence figures are given in Fig. 9a, b and c. As further observed in Fig. 9, SPEA2+ASF performs the best HV accuracy on DTLZ1, DTLZ2, DTLZ4, WFG2, WFG4, WFG5, WFG6 and WFG9. Although SPEA2 + ASF cannot guarantee that all of these test problems converge fastest, the final accuracy is indeed optimal.

Figure 10 shows the representation of the optimal solutions obtained by each algorithm on the 10-objective DTLZ1 (a)–(e) and WFG2 (f)–(j). Fig. 10a shows that SPEA2 does no converge to the true Pareto front. MOEA/D and MOMOBI-II are only able to obtain some partial true Pareto front due to the biased distribution of the non-dominated solutions. Fig. 10d displays that NSGA-III performs relatively good convergence and distribution, but some solutions have not converged to the true Pareto front. However, Fig. 10e shows that SPEA2+ASF manifests better than the compared algorithms. This is because the clustering and scalarizing function method in SPEA2+ASF can well balance the convergence and distribution in the high-dimensional target space. As further observed in Fig. 10f–j, all five algorithms converge to the true Pareto front, but the distribution of non-dominated solutions is different. MOEA/D and MOMOBI-II obtain some true Pareto front of partial biased distribution. The non-dominant solutions obtained by NSGA-III are difficult to meet the distribution requirements of the frontier when they are clustered in the middle space. Fig. 10f shows that SPEA2 performs better than MOEA/D, MOMOBI-II and NSGA-III. However, the non-dominant solution obtained by SPEA2 is not nearly as good as that obtained by SPEA2+ASF. As can be seen from Fig. 10f–j, SPEA2+ASF achieves competitive performance of distribution in high-dimensional objective spaces for WFG2.

Figure 11 shows the representation of HV convergence trend by each algorithm on the 10-objective of partial functions. As can be seen from Fig. 11, the convergence precision of SPEA2+ASF is the highest on WFG2, WFG6 and WFG9 relative to the compared algorithms. However, NSGA-III performs the similar HV accuracy with SPEA2+ASF on 10-objective WFG4, superior than SPEA2, MOEA/D and MOMOBI-II. In addition, the IGD convergence figure of some test instances is to show that SPEA2+ASF is competitive in dealing with 10-objective test problems. As further observed in Fig. 12, SPEA2+ASF obtains the best IGD accuracy on DTLZ1, DTLZ4, WFG2 and WFG8. Therefore, Figs. 11 and 12 show that SPEA2+ASF is suitable to tackle with many-objective problems.

Through the analysis of data and graphs, we can obtain the potential ability of SPEA2 + ASF in dealing with multi-objective and high-dimensional problems. In addition, according to the law of no free lunch [41], SPEA2+ASF algorithm cannot guarantee that all test problems are better than other algorithms. From the data and figures, it can be seen SPEA2+ASF algorithm manifests a better performance of convergence and distribution, which indicates that SPEA2+ASF algorithm can achieve good convergence and distribution in high dimensional space.

6 Conclusion

In this paper, an achievement scalarizing function sorting method is proposed in strength Pareto evolutionary algorithm, namely SPEA2+ASF, for many-objective optimization. This algorithm adopts the perpendicular distance from a solution to reference vector as the density estimation. Then, we redefine the fitness of a solution to be different from SPEA2, which increases the diversity of non-dominated solutions. In the process of SPEA2+ASF, a clustering method has been adopted to classify the non-dominated solutions. In addition, an achievement scalarizing function sorting methods are applied to layer different fronts and prune the redundant solutions.

According to the empirical experimental results, the proposed algorithm SPEA2+ASF has shown the competitive performance of convergence and distribution on the thirteen benchmark problems up to ten objectives in compared with four state-of-the-art algorithms, namely SPEA2, MOEA/D, MOMOBI-II and NSGA-III.

In the future, we would like to discuss further how to modify the proposed SPEA2+ASF to improve the ability to solve problems such as DTLZ3, WFG1 and WFG7. In addition, constraints and large-scale multi-objective optimization problems may also be our future research direction.