1 Introduction

The aim of reliability-based design optimization (RBDO) is to obtain the safe and reliable optimal solution by considering the uncertainties stemming from manufacturing tolerances, loadings, material properties, boundaries and initial conditions, etc. For the constraints in RBDO are usually implicit and highly nonlinear, several analytical reliability approaches have been received extensive attentions. Among these approaches, the first-order reliability method (FORM) is widely used due to its simplicity and efficiency (Du 2008b; Yao et al. 2013). And the second-order reliability method (SORM) (Zhao and Ono 1999) is developed to improve the accuracy of FORM. Based on FORM and SORM, the reliability index approach (RIA) (Tu et al. 1999) is applied in the uncertainty design optimization. RIA evaluates the reliability by calculating the reliability index, and compares the result with the reliability index βT corresponding to the predetermined reliability requirements, to determine whether the reliability constraint is met. Another method is the performance measure approach (PMA) (Tu et al. 2001). The optimization problem of PMA is to construct an inverse problem of the problem in FORM. To find the inverse most probable point (iMPP), PMA only need to determine the minimum unit vector direction of the constraints function in U space on the hypersphere which is determined by βT. In addition, many methods have been developed to solve the optimization problem of PMA, including the advanced mean value method (AMV) (Wu et al. 1990), the conjugate mean value method (CMV) and the hybrid mean value method (HMV) (Youn et al. 2003).

However, solving RBDO problems requires double loops in conventional techniques, including the loop of design optimization and the loop of reliability assessment. Both RIA and PMA require expensive computational cost because of these double loops, in which the reliability analysis (inner loop) is nested in design optimization process (outer loop). For the nested structure, the efficiency of the double loop method is low. So, the integration strategies of reliability analysis and optimization also have great influence on the accuracy and efficiency of RBDO (Valdebenito and Schuëller 2010). To improve the efficiency of RBDO, single-loop method (Agarwal et al. 2007; Chen et al. 1997; Kharmanda et al. 2002; Kirjner-Neto et al. 1998; Kogiso et al. 2012; Li et al. 2013; Liang et al. 2004; Shan and Wang 2008) and decoupled-loop method (Chen et al. 2013a, b; Cheng et al. 2006; Ching and Hsu 2008; Cho and Lee 2011; Royset et al. 2001; Yi et al. 2008) are proposed. Single-loop method is very efficient for the linear and mild nonlinear problems, but is inaccurate for highly nonlinear problems. In decoupled-loop method, the optimization and reliability assessment are decoupled from each other in each cycle, so this method has a good balance between the accuracy and efficiency in solving RBDO problems.

The sequential optimization and reliability assessment method (SORA) (Du and Chen 2004) is proposed. This method decouples the double loops by employing a single loop strategy with a serial of cycles of deterministic optimization and reliability assessment. And the efficiency of searching the solution to a probabilistic design can be improved significantly. To further improve the computational efficiency for RBDO, some enhanced SORA methods are proposed (Du 2008a; Huang et al. 2012).

In engineering design, probabilistic constraints are generally implicit and highly nonlinear, so the process of RBDO is usually a trade-off between efficiency and accuracy. To reduce the computational cost during optimization and reliability evaluating process, response surface method, such as Kriging (Hyeon Ju and Chai Lee 2008; Mourelatos 2005; Pretorius et al. 2004), and some efficient sampling techniques, such as Latin Hypercube sampling and importance sampling (Cadini et al. 2014; Zhao et al. 2015), are introduced into the RBDO process. On the other hand, considering the complexity of the RBDO problem, accurate response surfaces of constraint boundaries are valuable for obtaining accurate result in RBDO process.

To make sure the space-filling sampling is effective in case of fitting response surfaces used in reliability analysis, efficient global reliability analysis (EGRA) (Bichon et al. 2008) and constraint boundary sampling (CBS) (Lee and Jung 2008) are proposed. The response surfaces constructed by EGRA method will be required to be locally accurate only in the regions of the component limit states that contribute to system failure. And the CBS method can guarantee the accuracy of the response surfaces by sampling on boundaries of feasible region sequentially. Based on the accuracy of EGRA and CBS, extensional researches (Bichon et al. 2010, 2011) of these methods are proposed. However, these methods use global sampling technique and the response surfaces are constructed in the whole design space. In fact, the results of RBDO usually depend on the constraint boundaries in a local range that contains optimal RBDO design point. So, the global sampling method may spend much more computational cost on locating sample points in unrelated areas, which may contribute little to the accuracy of RBDO results. It is clear that determining local range and building response surfaces in the local range can validly avoid selecting sample points in unrelated areas, and will be helpful to reduce evaluate cost and improving efficiency of RBDO. In such a situation, adaptive response surface method may be a good solution to solve this problem (Roussouly et al. 2013; Zou et al. 2003).

Although Kriging-model-based RBDO is an effective method to overcome the huge computational cost when RBDO is used in practical applications, the accuracy of Kriging model depends directly on how to select the sample points. Several advanced sampling strategies have been developed: Bect et al. proposed the sequential design of computer experiments for the estimation of a probability of failure (Bect et al. 2012). Echard et al. presented an active learning reliability method combining Kriging and Monte Carlo simulation (Echard et al. 2011), and combined importance sampling and kriging reliability method to solve the small failure probabilities with time-demanding numerical models (Echard et al. 2013).

Zhuang and Pan proposed a new sequential sampling strategy to improve the RBDO with implicit constraint functions (Zhuang and Pan 2012). Picheny et al. introduced the adaptive designs of experiments for accurate approximation of a target region (Picheny et al. 2010). Huang and Chan presented a modified efficient global optimization algorithm for maximal reliability in a probabilistic constrained space (Huang and Chan 2010). Lee et al. (2011) introduced a sampling-based RBDO using the stochastic sensitivity analysis and dynamic kriging method (Lee et al. 2011). Zhao et al. proposed a conservative surrogate model using weighted kriging variance for sampling-based RBDO (Zhao et al. 2013). Chen et al. introduced an important boundary sampling method for RBDO using kriging model (Chen et al. 2015), and proposed a local adaptive sampling method which has a significant importance in improving the efficiency of RBDO (Chen et al. 2014). Li et al. presented a new local approximation method using MPP for RBDO (Li et al. 2016).

To deal with the complexity of the RBDO problem, some artificial intelligence techniques, such as support vector machine (SVM), are also introduced into the RBDO process. For example, SVM is combined with subset simulation to assess small failure probabilities (Bourinet et al. 2011). By sequentially placing training points in the random variables space, SVM classifiers are built as accurate surrogates for y-threshold intermediate limit-state. In another SVM-based RBDO method, SVM is used to create a surrogate model of the limit-state function at the MPP with the gradient information in the reliability analysis (Wang et al. 2015). It can make sure that the surrogate model not only pass through the MPP but also be tangent to the limit-state function at the MPP.

In this research, a new RBDO process is proposed based on the local range sampling method to improve the efficiency of RBDO. Because the local range plays a key role to the RBDO process, the proposed method is named based on local range (LR), and the proposed RBDO process is named local range RBDO (LR-RBDO) process. The proposed approach includes two phases. In the first phase, new samples are selected by using SVM and mean squared error to determine the local range. In the second phase, new samples are required to be located on the constraint boundaries within the local range to refine the adaptive response surfaces of constraint functions. The location and the size of the local range are adaptively defined by the current RBDO design point and the current DOP. A generalized flowchart of LR-RBDO process is also proposed. In terms of efficiency and accuracy, the superiority of the proposed approach is demonstrated with numerical examples of highly nonlinear constraints, and engineering problems that are treated as black-box problems. The analysis and conclusion are also provided to make a comparison between different methods.

This paper is organized with six sections. After conventional methods are briefly reviewed in the Section 1, commonly used methods in RBDO are introduced in the Section 2. The principle of using the SVM in this research is explained in Section 3. The methodology and flowchart of the proposed method are presented in Section 4. The accuracy and efficiency of the proposed method are demonstrated by some illustrative examples in Section 5. Finally, conclusions are drawn in the last section.

2 Commonly used methods in RBDO

2.1 Kriging model

Kriging model, first proposed by a South African geostatistician Krige (Krige 1994), is a high precision interpolation model.

The response of the Kriging model at a certain sample point is affected by both the design parameters and the points in its neighbourhood. In addition, the spatial correlation between design points is also considered (Zhuang and Pan 2012).

Assuming that the current design points are x = [x1,…,xm]T, and the corresponding values are y = [y1,…,ym]T. The Kriging approximations of function y(x) are denoted as

$$ \widehat{y}\left(\mathbf{x}\right)={\displaystyle \sum_j^k{\beta}_j{f}_j\left(\mathbf{x}\right)}+z\left(\mathbf{x}\right) $$
(1)

This function has two parts. The first part is the regression model which consists of a series of regression functions. β is the trend coefficient vector. The second part, Z(x), is the stochastic process which is assumed to have a zero mean and a variance σ2. The spatial covariance function between Z(x) and Z(w) is expressed as

$$ Cov\left[Z(x),Z(w)\right]={\sigma}_Z^2R\left(\theta, x,w\right) $$
(2)

where w is a point different from the point x; σ is the process variance; R is the correlation function; and θ is the key parameter of the correlation function (Kim et al. 2009). By adjusting θ, the correlation function can be defined adaptively. There exist several models to define the correlation function (Bichon et al. 2008; Rasmussen 2004). Based on this correlation function, Kriging model can provide a smooth and infinitely differentiable surrogate surface, so it is a suitable model for modelling computer experiments (Lophaven et al. 2002).

In the Kriging model, the approximation function is regarded as a random function, and the mean square error (MSE) is defined to find the smallest linear unbiased estimation (Lophaven et al. 2002).

$$ MSE(x)=E\left[{\left(\widehat{y}(x)-y(x)\right)}^2\right] $$
(3)

The mean square error of Kriging prediction is equal to zero exactly at the training point, and increases highly at the testing point which is away from the training point.

Kriging model has a good fitting effect when dealing with low and middle dimension problems and highly nonlinear problems. With its high precision, Kriging model is applied in many studies and engineering problems. In order to obtain good RBDO results, in this paper, Kriging model is used to construct the surrogate model.

2.2 Latin hypercube sampling

Latin Hypercube sampling (LHS) is a multi-dimensional stratified sampling method. It is the most commonly used method to construct initial surrogate model in the adaptive optimization process (McKay et al. 2000). LHS method can flexibly adapt to different sample size. Its characteristics can ensure each dimension of the variables to be evenly divided into some levels. So LHS method is especially suitable for computer design test.

2.3 RBDO problem model

The general expression for the RBDO problem is typically formulated as follows:

$$ \begin{array}{l}\mathrm{find}\kern1em \boldsymbol{d}\\ {} \min \kern1.5em f\left(\boldsymbol{d}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern2.1em \mathrm{prob}\left[{g}_i\left(\boldsymbol{X}\right)\le 0\right]\le \boldsymbol{\varPhi} \left[-{\upbeta}_{\mathrm{T}}^i\right],\kern0.5em i=1,2,\cdots, N\\ {}{\boldsymbol{d}}^{Lower}\le \boldsymbol{d}\le {\boldsymbol{d}}^{Upper},\kern0.5em {\boldsymbol{X}}^{Lower}\le \boldsymbol{X}\le {\boldsymbol{X}}^{Upper}\end{array} $$
(4)

where d is the vector of the deterministic design variables; X is the vector of random design variables; f(d) is the objective function; prob[g i (X) ≤ 0] denotes the probability of satisfying the ith constraint function g i (X); βT denotes the target reliability index; Φ(−β iT ) denotes the desired design probability of satisfying the ith constraint function.

2.4 Reliability analysis methods RIA and PMA

RIA searches the most probable point (MPP) on the limit state function. MPP is the point on the limit state function with maximum probability density. The RIA problem is given by (Tu et al. 1999; Youn and Choi 2004; Youn et al. 2003)

$$ \begin{array}{l}\mathrm{find}\kern1em \boldsymbol{u}\\ {} \min \kern1.2em \left\Vert \boldsymbol{u}\right\Vert \\ {}\mathrm{s}.\mathrm{t}.\kern1.6em G\left(\boldsymbol{u}\right)=0\end{array} $$
(5)

where u is the vector of the random variables in the standard normal space; G(u) is the probabilistic constraint in the standard normal space.

Random variables do not usually obey normal distributions, so it is needed to transform the random variables in the original space into independent random variables with standard normal distribution in the standard normal space. The transformation can be implemented by Rosenblatt transformation (Rosenblatt 1952). Based on this transformation, the probabilistic constraint g(X) becomes G(u). Then the result of the RIA problem in the standard normal space is the minimum distance from the origin to the constraints.

PMA searches the minimum value of the constraint function under the condition of satisfying the target reliability index. The PMA problem is given by (Tu et al. 1999; Youn and Choi 2004; Youn et al. 2003)

$$ \begin{array}{l}\underset{\mathbf{u}}{ \min}\kern1.5em G\left(\boldsymbol{u}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern2.5em \left\Vert \boldsymbol{u}\right\Vert ={\upbeta}_{\mathrm{T}}\end{array} $$
(6)

In fact, this optimization problem is an inverse problem of solving the MPP in RIA. The result of this problem is called the inverse most probable point (iMPP). To solve this problem, we just need to search the minimum unit vector of G(u) on the hypersphere which is determined by the constraints. So this approach is more simple than solving the MPP directly. There are three methods to solve this problem by iterative computation, including AMV,CMV and HMV.

The iterative model of AMV is (Youn and Choi 2004; Youn et al. 2003):

$$ \begin{array}{l}{\boldsymbol{u}}_{\mathrm{AMV}}^{(1)}={\upbeta}_{\mathrm{T}}\left(-\frac{\nabla G\left(\boldsymbol{0}\right)}{\left\Vert \nabla G\left(\boldsymbol{0}\right)\right\Vert}\right)\\ {}for\kern0.5em k\ge 1,\kern1em {\boldsymbol{u}}_{\mathrm{AMV}}^{\left(k+1\right)}={\upbeta}_{\mathrm{T}}\mathbf{n}\left({\boldsymbol{u}}_{\mathrm{AMV}}^{(k)}\right),\kern0.5em \mathbf{n}\left({\boldsymbol{u}}_{\mathrm{AMV}}^{(k)}\right)=-\frac{\nabla G\left({\boldsymbol{u}}_{\mathrm{AMV}}^{(k)}\right)}{\left\Vert \nabla G\left({\boldsymbol{u}}_{\mathrm{AMV}}^{(k)}\right)\right\Vert}\end{array} $$
(7)

The iterative model of CMV is (Youn and Choi 2004; Youn et al. 2003)

$$ \begin{array}{l}{\boldsymbol{u}}_{\mathrm{CMV}}^{(0)}=0,\kern1em {\boldsymbol{u}}_{\mathrm{CMV}}^{(1)}={\boldsymbol{u}}_{\mathrm{CMV}}^{(1)},\kern1em {\boldsymbol{u}}_{\mathrm{CMV}}^{(2)}={\boldsymbol{u}}_{\mathrm{CMV}}^{(2)}\\ {}for\kern0.5em k\ge 2,\kern1em {\boldsymbol{u}}_{\mathrm{CMV}}^{\left(k+1\right)}={\upbeta}_{\mathrm{T}}\frac{\mathbf{n}\left({\boldsymbol{u}}_{\mathrm{CMV}}^{(k)}\right)+\mathbf{n}\left({\boldsymbol{u}}_{\mathrm{CMV}}^{\left(k-1\right)}\right)+\mathbf{n}\left({\mathbf{u}}_{\mathrm{CMV}}^{\left(k-2\right)}\right)}{\left\Vert \mathbf{n}\left({\boldsymbol{u}}_{\mathrm{CMV}}^{(k)}\right)+\mathbf{n}\left({\boldsymbol{u}}_{\mathrm{CMV}}^{\left(k-1\right)}\right)+\mathbf{n}\left({\mathbf{u}}_{\mathrm{CMV}}^{\left(k-2\right)}\right)\right\Vert}\\ {}\mathbf{n}\left({\boldsymbol{u}}_{\mathrm{CMV}}^{(k)}\right)=-\frac{\nabla G\left({\boldsymbol{u}}_{\mathrm{CMV}}^{(k)}\right)}{\left\Vert \nabla G\left({\boldsymbol{u}}_{\mathrm{CMV}}^{(k)}\right)\right\Vert}\end{array} $$
(8)

The HMV method will judge the convex or non-convex properties in each iteration based on the expression that is given by (Youn and Choi 2004; Youn et al. 2003)

$$ {\varsigma}^{\left(k+1\right)}=\left({\mathbf{n}}^{\left(k+1\right)}-{\mathbf{n}}^{(k)}\right)\bullet \left({\mathbf{n}}^{(k)}-{\mathbf{n}}^{\left(k-1\right)}\right) $$
(9)

When ς (k + 1) is positive, it means the constraint function is a convex function on the current iteration point u (k + 1)HMV , AMV method is adopted in the current iteration to solve the iMPP; otherwise ς (k + 1) is negative, and CMV method is adopted. In this work, HMV is adopted in SORA process, and the iteration process stops when the error of consecutive result values is less than a small positive number (i.e., 1e−3).

2.5 Sequential optimization and reliability assessment (SORA)

The main purpose of SORA is to decouple the reliability assessment from the outer optimization. SORA method constitutes a serial of single cycles in which deterministic optimization and reliability analysis are performed sequentially. The typical optimization problem in SORA process is given by (Du and Chen 2004):

$$ \begin{array}{l}\mathrm{find}\kern1em {\boldsymbol{\upmu}}_{\mathbf{x}}^k\\ {} \min \kern1.5em f\left({\boldsymbol{\upmu}}_{\mathbf{x}}^k\right)\\ {}\mathrm{s}.\mathrm{t}.\kern2em g\left({\boldsymbol{\upmu}}_{\mathbf{x}}^k-{\mathbf{s}}^k\right)\ge 0\\ {}\kern3em {\mathbf{s}}^k={\boldsymbol{\upmu}}_{\mathbf{x}}^{k-1}-{\mathbf{X}}_{iMPP}^{k-1}\\ {}{\boldsymbol{\upmu}}_{\mathbf{x}}^{Lower}\le {\boldsymbol{\upmu}}_{\mathbf{x}}\le {\boldsymbol{\upmu}}_{\mathbf{x}}^{Upper}\end{array} $$
(10)

Where X iMPP is the inverse MPP that is calculated by (6). In this way, SORA transforms the reliability optimization to a deterministic optimization. In each iteration, SORA shifts the constraint function to the feasible region by the vector s k and locates the iMPP in the feasible region or on the limit state boundary. In the next iteration, the shifted constraint function will be the deterministic constraint condition in the optimization. To start the process of SORA, an starting point is needed. Then in each cycle, the DOP of the previous cycle is taken as the starting point of the optimization of current cycle. When the difference of the objective function between two consecutive cycles is small enough and all the reliability requirements are satisfied, SORA method stops.

3 Support vector machine (SVM)

As an artificial intelligence technique, SVM is a machine-learning method for the data classification in pattern recognition. There are two kinds of SVM, the support vector classification machine (SVC) (Hsu et al. 2003; Suykens and Vandewalle 1999) for classification problems and the support vector regression machine (SVR) (Smola and Schölkopf 2004) for regression problems. For there are two kinds of state in the reliability analysis, safety or failure, both kinds of SVM are applicable to the RBDO problem. The most important feature is that SVM can be used as a classifier to define a highly nonlinear explicit boundary that optimally separates two classes of samples into feasible or infeasible. Recently, studies which use these approaches to construct explicit boundaries have shown several advantages (Basudhar et al. 2012; Song et al. 2013).

For given N samples that are distributed within a design space, SVM equation is given by (Wang et al. 2015)

$$ s\left(\boldsymbol{X}\right)=b+{\displaystyle \sum_{i=1}^N{\lambda}_i{y}_iK\left({\boldsymbol{X}}_i,\boldsymbol{X}\right)} $$
(11)

where X i is the i th training sample; b is the bias; λ i is the Lagrange multiplier; y i is the class that can take values +1 or −1 responding to success and failure respectively; and K is the kernel function. For each sample point X i , it is associated with one of two class values, and the classification is predicted by the sign of s(X) in (11). Because the Lagrange multiplier λ i will be strictly positive only when the corresponding sample is the support vector, the value of s(X) depends only on support vectors. Thus, there are two parallel hyperplanes passing through support vectors with a margin which is the region between the two hyperplanes given by s(X) = ±1. The SVM does not allow any samples to exist in the margin.

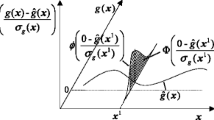
To get accurate results of RBDO, samples are hoped to be located only in the vicinity of the constraint function. Because the constraint function is usually implicit or even a black-box function, initial samples are usually uneven distributed at both sides of it. As shown in the Fig. 1, initial samples are separated into two different sample sets by the SVM decision function. Uneven distribution of these initial samples makes a great bias from the SVM decision function to the true constraint function. The reason leading to the error is that the samples hold a unequal distribution proportion in the space on both sides of the true constraint function. This phenomenon can also be described very vividly as the big data bully the small data. The sample set with fewer samples has a smaller opportunity to locate samples close enough to the true constraint function. In order to reduce the error and refine the prediction of the SVM, new samples are hoped to be located in the margin.

Fig. 1
figure 1

SVM with uneven distributed samples

Full size image

In addition, there are commonly no information of the true constraint function in the initial phase of the RBDO. In this work, the next new sampling point is added onto the SVM decision function in each iteration to predict the true constraint function. An example of the refinement process is shown in picture (a), (b) and (c) of Fig. 2. After a sampling point is added to the sample set based on the SVM decision function, a new classification standard is built based on the updated sample set. Then a new SVM decision function is constructed by the extended sample set. And a series of new hyperplanes will pass through new support vectors. It is clear that new samples and the SVM decision function are getting more and more close to the true constraint function, and the margin between hyperplanes is getting more and more narrow during the iteration process. So, with a small error, the prediction of the true constraint function will become more accurate.

Fig. 2
figure 2

Depiction of the refinement process of SVM

Full size image

4 RBDO process with an efficient local adaptive sampling method

In this paper, the LR-RBDO method is proposed to solve the problem with parameter uncertainty. In this case, the uncertainty exists in the design variable. Based on SORA method, RBDO process is decoupled into two parts, the uncertainty analysis and the deterministic optimization. Then the uncertainty can be separated from the design variable and treated separately. In this way, the uncertainty analysis is solved in SORA process. Excepting the uncertainty analysis, other optimizations in RBDO can all be regarded as deterministic optimizations. Generally, the random uncertainty has the normal distribution form, so the design variable in fact is the mean value of the random design variable in the probabilistic constraint.

In general, the LR-RBDO adopts two kinds of effective strategies. Firstly, SVM is used to guide the RBDO to a right direction with high efficiency and avoid the local minima solutions. Secondly, a new type of local range is defined to make the optimization focused on the most important region rather than other unrelated area. So the efficiency of the LR-RBDO process is improved greatly.

A brief introduction of the LR-RBDO process has been presented in Section 1. This section provides a more detailed description of the efficient local adaptive sampling method and the steps in the LR-RBDO process.

The flowchart of the LR-RBDO process is simply shown in Fig. 3. As already mentioned in Section 1, this process includes two phases. The purpose of the first phase is to construct a SVM model which is precise enough to determine a margin that probably contains the true constraint function. Besides, a local range should be constructed to make a preliminary judgment of where the optimal RBDO design point will be located. Although the accurate results could not be found, the phase 1 may provide much more valuable information about the RBDO problem with an efficient way, and guide the next phase of the RBDO process to a possible direction with the cost as fewer as possible. The phase 1 is also named coarse search process.

Fig. 3
figure 3

Flowchart of the LR-RBDO process

Full size image

In the second phase, additional samples are selected within the local range to refine the response surfaces of the constraint functions locally. The optimum result of the RBDO problem will be more and more accurate. So, the Phase 2 is named fine search process. With the preliminary prediction of the Phase 1, new samples selected in the Phase 2 will avoid locating in the unrelated area. And the response surfaces will become more and more accurate in the local range. In the worst situation, uneven distribution of initial samples may lead to an inaccurate prediction of the local range, the local range may not cover the area in which the true optimum of the RBDO is located. However, due to the supplementary treatment that the local range could be refined based on the updated response surfaces, the accurate optimal RBDO design point is found in the end.

There often exist local minima solutions in many problems. It is hard to obtain the global minima, because there often exists no appropriate feasible initial point to start optimization algorithm and guide it to a right direction.

In order to obtain a more accurate DOP, SVM is adopted based on its better prediction effect. Due to the robustness of the SVM model, the optimum point calculated by the SVM model is reliable, and it is generally closer to the global minima compared to other local minima. So in the first phase, the initial point is replaced by the optimum point which is calculated based on the SVM model. In this way, the optimization process can effectively avoid to fall into most of local minima solutions. In the second phase, the RBDO design point obtained in the first stage is chosen as the initial point to start the optimization in the second stage.

4.1 Phase 1-the coarse search process

The flowchart of the Phase 1 is simply shown in Fig. 4. The detail information of the steps is provided as below.

Fig. 4
figure 4

The flowchart of the Phase 1

Full size image

  • Step 1: Initialize the design variable and the sample set. In order to obtain a more uniform distribution, Latin Hypercube sampling (LHS) method is adopted, and at least 2(n+1) samples generated by LHS are taken as initial sampling points for the problem with n dimensions.

  • Step 2: Evaluate constraint functions at each sample, and construct/update Kriging models for all constraint functions. Because uncertain parameters are independently exist in the constraint, surrogate models of constraints are in fact constructed based on random design variables.

  • Step 3: Construct/update the SVM model. The SVM model is constructed to form a surface in the design space to divide all samples into two classes: feasible points and infeasible points. The SVM model contains the SVM decision function according to s(X) = 0 and parallel hyperplanes according to s(X) = ±1 in (11).

  • Step 4: Obtain the optimum point calculated by the SVM model.

This optimum point is obtained by the optimization problem as follow:

$$ \left\{\begin{array}{l} \min \kern1em f\left(\boldsymbol{X}\right)\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1.3em \boldsymbol{s}\left(\boldsymbol{X}\right)=0\hfill \end{array}\right. $$
(12)

where f(X) is the objective function, and s(X) = 0 is the SVM decision function. There often exists no appropriate initial point to start the optimization of (12), so this problem is calculated by genetic algorithm.

The current Kriging models of constraints are used to judge whether this optimum point is a feasible point. If it is a feasible point, the initial point will be replaced by this optimum point, otherwise, the initial point will not be changed. And this initial point will be used to start the algorithm in the next step.

  • Step 5: In some malignant case, local minima points are quite far away in the physical space but very close in terms of objective function. Furthermore the global minimum of the RBDO problem would be outside of the trust region around the deterministic optimum. Using MSC based on current RBDO design point will allowed the searching jump out the current trust region to avoid the local optimum within the local range and find the global optimum in the whole design space more reliable.

Take the current initial point as the mean point, and using Monte Carlo simulation (MSC) to generate a series of new points. In order to ensure the reliability of the calculation results, the sampling size of MSC is 105. Select out new feasible points based on current Kriging models of constraint functions.

Take these new feasible points as the start points to start the deterministic optimization to obtain a series of DOPs based on current kriging models. The optimization problem is given by:

$$ \left\{\begin{array}{l} \min \kern1em f\left(\boldsymbol{X}\right)\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1.3em {\widehat{\boldsymbol{g}}}_{\boldsymbol{i}}\left(\boldsymbol{X}\right)\le 0\kern2em i=1,\cdots, N\hfill \end{array}\right. $$
(13)

where ĝ i (X) are current Kriging models of constraint functions. Because the Kriging models have been built, sequence quadratic program (SQP) method can be used in the optimization to improve the computational efficiency. Then, a series of DOPs are obtained separately corresponding to different initial points.

  • Step 6: Obtain RBDO design point by SORA method. The DOPs obtained in Step 5 is taken as the initial points to start the SORA process. And the performance measure approach (PMA) is used in the reliability analysis. It is worth noting that the DOP and the corresponding RBDO design point always appear in pairs. The RBDO design point with the minimum objective function value and the corresponding DOP will be the final results in current iteration. DOP will be helpful for predicting the location where the optimal RBDO design point exists, so it is added to the sample set.

  • Step 7: Check whether the stopping criterion is met. If not, go to Step 8; otherwise go to Step 9.

The purpose of the Phase 1 is only to determine a local range which probably contains the optimal RBDO design point of the RBDO problem. When two consecutive RBDO design points are very close, the surrogate models are considered to be accurate enough. Then the refinement process in the Phase 2 will be started. The key region is a circle that takes the RBDO design point as the center, and its radius corresponds to the reliability index. So we only need to consider the relationship between these circles. In other words, as two consecutive circles overlapping each other, the distance between two corresponding RBDO design points is less than two times the radius, the Phase 1stops. Then, the stopping criterion of the Phase 1 is given by:

$$ \left\Vert {\boldsymbol{d}}_i-{\boldsymbol{d}}_{i-1}\right\Vert \le 2R $$
(14)

where d i means the optimal RBDO design point of the current Kriging models in the iteration i. R is the radius that corresponds to the target reliability index. When the (14) is satisfied, the RBDO design point will be very close to the RBDO design point of the previous iteration, so Kriging models are accurate enough to start the further fine search in Phase 2.

  • Step 8: Select a new sample by using mean square error (MSE) and SVM decision function, and add this new sample to the sample set. Then go to Step 2.

In this step, a sampling criterion is used to select a new sample:

$$ \left\{\begin{array}{l} \max \kern1em {\displaystyle \sum_{i=1}^N\sqrt{MS{E}_i\left(\boldsymbol{X}\right)}\bullet D}\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1.7em s\left(\boldsymbol{X}\right)=0\hfill \end{array}\right. $$
(15)

where D is the minimal distance from the current sample point to the existing sample points. N is the number of the constraints. MSE is the mean square error of Kriging prediction (Lophaven et al. 2002). The equation s(X) = 0 is the SVM decision function. The objective function of the sampling criterion contains two parts. The purpose of the first part, mean square error, is to improve the precision of the Kriging model. The purpose of the second part, D, is to make a uniform distribution of samples. And the purpose of the constraint of the sampling criterion is to ensure that the new sample is located at the SVM decision function. So, maximizing the objective function of the sampling criterion will greatly refine the response surfaces of the constraints of the RBDO. And satisfying the SVM decision function will ensure the new sample is always located in the margin which is decided by SVM hyperplans and becomes narrower in each iteration. At the same time, new samples are definitely located in the vicinity of the true constraint function, rather than other unrelated area.

GA is employed to solve (15), because there is no feasible initial design variable and surrogate models to start gradient-based optimization algorithms conveniently.

With this sample adding method, we have a new way to guide the RBDO process. A series of new samples selected by this criterion will be helpful for refining Kriging models efficiently.

  • Step 9: Construct a local range based on the RBDO design point and the corresponding DOP.

The local range is defined as a hypercube which contains two β-spheres. DOP and RBDO design point are two centers of these β-spheres. And the distance between each center and the boundary of the hypercube is 2R. The radius of the β-sphere is R that corresponds to the target reliability index. The trust region of the local range is shown in Fig. 5.

Fig. 5
figure 5

The trust region of the local range

Full size image

In this step, the local range is built and adaptively updated based on the RBDO design point and the DOP of current constraints Kriging models. In other words, the location and the size of the local range will change in each iteration. As mentioned above, the results of RBDO depend on the constraint boundaries in the local range which contains the RBDO design point. In the SORA process, the DOP obtained based on current Kriging models is also taken as the initial point to calculate the RBDO design point.

In the trust region, there are two β-spheres with the same radius. According to the target reliability index, the radius of the β-sphere is set as R. The centers of these two spheres are the DOP and the RBDO design point. The DOP is the result of the deterministic optimization based on Kriging models of the constraints. The RBDO design point is the result of the reliability analysis by SORA method. To include the nearby constraint boundaries that may impact calculate results, the trust region of the local range is slightly extended by R from the edge of these two β-spheres at the direction of each dimension.

4.2 Phase 2-the fine search process

After the local range is constructed, the fine search process begins. Different from the purpose of the Phase 1, the Phase 2 is to create constraint boundaries accurately. Therefore, it is necessary to make a trade-off between the efficiency and the accuracy. The flowchart of the Phase 2 is shown in Fig. 6.

Fig. 6
figure 6

The flowchart of Phase 2

Full size image

  • Step 1: Select a new sample based on the constraint boundary sampling (CBS) criterion within the current local range, and add this new sample to the sample set.

In this step, the CBScriterion is used to select a new sample in the local range. This criterion was proposed by Lee and Jung in 2008 (Lee and Jung 2008). The priority of this method is employing the probability density function to measure the error of the Kriging prediction to the constraint. We use this criterion in the local range, and the modified sampling criterion is defined as follows:

$$ \left\{\begin{array}{l} \max \kern1em {\displaystyle \sum_{i=1}^N\boldsymbol{\varPhi} \left(\frac{{\widehat{g}}_i\left(\boldsymbol{X}\right)}{\sqrt{MS{E}_i\left(\boldsymbol{X}\right)}}\right)\bullet D}\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1.5em \boldsymbol{X}\in LR\hfill \end{array}\right. $$
(16)

where Φ is the probability density function. ĝ i (X) are the Kriging models of constraint boundaries. LR is the adaptive local range according to current Kriging models of the constraints. And MSE, D and N have the same meaning as them in (15). With this sampling criterion, Kriging models of the constraints are refined within the local range in each iteration.

GA is employed to solve (16), because there are no feasible initial design variables and surrogate models to start gradient-based optimization algorithms conveniently.

  • Step 2: Evaluate the new sample which is obtained in the Step 1. And update Kriging models of constraints based on all samples.

  • Step 3: If the optimization problem is highly nonlinear, there may still exists local minimum in the local range. In this case, the Monte Carlo simulation and SORA method are integrated to avoid the local optima within the local range.

Take the current initial point as the mean point, and using Monte Carlo simulation (MSC) to generate a series of new points. In order to ensure the reliability of the calculation results, the sampling size of MSC is 105. And select out new feasible points based on current Kriging models of constraint functions.

Take these new feasible points as the start points to start the deterministic optimization based on (13). In Phase 2, the precision of the Kriging models is high. Using gradient-based optimization algorithm can improve the efficiency of obtaining the DOP. So SQP is preferred to solve this deterministic optimization problem. Then, a series of DOPs are obtained separately corresponding to different initial points.

  • Step 4: Obtain RBDO design point by SORA method. The DOPs obtained in Step 3 is taken as the initial points to start the SORA process. The RBDO design point with the minimum objective function value and the corresponding DOP will be the final results in current iteration. And replace the initial point by this RBDO design point.

  • Step 5: Calculate the distance between the DOPs of two successive iterations. When the value of the distance is large than 2R, it means that Kriging models have a large change in this iteration. Then, the current DOP is treated as a new sample. On the other hand, a small value of the distance means a little change of the Kriging models. In order to save calculation cost and improve efficiency, the new DOP will not be added to the sample set.

  • Step 6: Update the local range based on the DOP and the corresponding RBDO design point.

In the worst case, the local range determined in the Phase 1 may not contain the optimal RBDO design point of the RBDO problem. To overcome this drawback, an adaptive local range should be updated to always tracking the current DOP. Just like the same definition in the Phase 1, the local range is always updated according to current Kriging models. In this way, the local range will always have a tendency to contain the optimal RBDO design point.

  • Step 7: Check whether the stopping criterion is met or the iteration number achieves the maximum. If not, go back to Step 1; otherwise the Phase 2 stops.

With a series of new samples, Kriging models will be more and more accurate in the local range. When two consecutive optimal RBDO design points are close enough, new samples are nearly useless to improve the accuracy of the RBDO problem results. So we define the termination criterion as follows:

$$ \left\Vert {\boldsymbol{d}}_i-{\boldsymbol{d}}_{i-1}\right\Vert \le \boldsymbol{\varepsilon} $$
(17)

where ε is a small positive number (i.e., 1e−3); d i is the optimal RBDO design point of the iteration i.

5 Examples

In order to demonstrate the accuracy and efficiency of the proposed LR-RBDO process, Some examples are adopt to make tests and comparisons with different sampling methods. All of the constraints in the RBDO problem are approximated by Kriging models which are constructed by using sampling method, include Latin Hypercube sampling (LHS), constraint boundary sampling (CBS) and the local range based method proposed in this work. In all methods, the SORA method is used to execute an efficient probabilistic design with the performance measure approach to perform reliability analysis. In order to quantify the accuracy of the results of the proposed RBDO process, the reliability of design points obtained by different RBDO methods are assessed by Monte Carlo simulation with 105 sampling size.

5.1 Example 1

This example is the modified Haupt example (Lee and Jung 2008), which has two random design variables and two probabilistic constraints. The RBDO problem of the modified Haupt example is formulated as follows:

$$ \begin{array}{l}\mathrm{find}\kern1em \boldsymbol{d}=\left[{d}_1,{d}_2\right]\\ {} \min \kern1.5em f\left(\boldsymbol{d}\right)={\left({d}_1-3.7\right)}^2+{\left({d}_2-4\right)}^2\\ {}\mathrm{s}.\mathrm{t}.\kern1.8em \mathrm{prob}\left[{g}_i\left(\boldsymbol{X}\right)<0\right]\le \boldsymbol{\varPhi} \left(-{\upbeta}_{\mathrm{T}}^i\right)\kern0.5em ,\kern0.5em i=1,2\\ {}\kern3.1em g{}_1\left(\boldsymbol{X}\right)=-{X}_1 \sin \left(4{X}_1\right)-1.1{X}_2 \sin \left(2{X}_2\right)\\ {}\kern3.1em {g}_2\left(\boldsymbol{X}\right)={X}_1+{X}_2-3\\ {}\kern3.1em 0.0\le {d}_1\le 3.7\kern0.5em ,\kern0.5em 0.0\le {d}_2\le 4.0\kern0.5em \\ {}\kern3.1em {\upbeta}_{\mathrm{T}}^1={\upbeta}_{\mathrm{T}}^2=2.0\\ {}\kern3.1em {\boldsymbol{d}}^{(0)}={\left[2.5,2,5\right]}^{\mathrm{T}}\\ {}\kern3.1em {X}_n\sim N\left({d}_n,{0.1}^2\right)\kern0.5em ,\kern0.5em n=1,2\end{array} $$
(18)

In this example, all the random variables are statistically independent and normal distributed. The target reliability index is βT = 2.0, and the standard deviation is σ = 0.1. As shown in Fig. 7, the simple quadratic objective function decreases from lower left to upper right, and denoted by dotted lines. A simple straight line constraint and a highly nonlinear function of the first constraint are denoted by dotted lines. Based on constraints, the feasible region is shown as the shaded region. The DOP and the RBDO design point based on the analytical method which directly calls the true functions are also shown in this figure. In order to clearly display these points in the figure, the DOP is expressed as Xopt, and the RBDO design point is expressed as Xd.

Fig. 7
figure 7

Graphical representation of the true constraint boundaries of modified Haupt example

Full size image

Two classical space sampling methods are studied in this example. As shown in Fig. 8, constraint boundary sampling (CBS) method and Latin Hypercube sampling (LHS) method are selected to construct Kriging models.

Fig. 8
figure 8

Graphical representation of CBS method (a) and LHS method (b) of example 1

Full size image

In Fig. 8a, we fit Kriging models by using CBS method. At the beginning, initial Kriging models are constructed by nine initial samples which are denoted by ‘▫’. Note that with the CBS method, new samples are tend to locate closely along constraint boundaries. These new samples are denoted by ‘×’. As shown in Fig. 8a, Kriging models of the constraints are constructed with a very high accuracy around the feasible region, but inaccurate in the infeasible region especially the lower left of the design space. In this way, we can construct Kriging models and obtain the optimal RBDO design point with higher accuracy. But, in terms of the efficiency, more samples are located far away from the vicinity of the optimal RBDO design point. So theses samples are not exploited enough to improve the efficiency and the accuracy of results.

Based on the same number of sampling points, we fit Kriging models by LHS method to approximate the two constraints to compare with CBS method. As shown Fig. 8b, Kriging models are denoted by dotted line, the true constraints are denoted by solid lines, and new samples are denoted by ‘×’. Note that all samples are randomly distributed in the entire design space. These samples are not close enough to the constraints, and most of them are distributed in large unrelated areas, even in the infeasible region that include the lower left corner and upper right corner of the design space. So, Kriging models are not accurate enough to predicate the first constraint in the region around the optimal RBDO design point. The optimal RBDO design point according to the LHS method and the optimal RBDO design point of the RBDO based on the analytical method are both displayed in this picture.

The LR-RBDO process of example 1 and the results are shown in Fig. 9. As seen in Fig. 9, the local range is found and be displayed with a red rectangle. The Kriging models of the constraints are denoted by pink dotted lines. To make a comparison, the original functions of the constraints are shown as green lines. All of the samples are separated into two classes which include the +1 class denoted by red spots and the -1class denoted by blue spots. The SVM decision function is denoted by black lines. Parallel hyperplanes given by s(X) = ±1 are denoted by red lines and blue lines separately. Support vectors are passed through by hyperplanes, and each of them are denoted by the sample with a circle. The current RBDO design point is shown with a yellow circle to represent the β sphere.

Fig. 9
figure 9

Graphical representation of the LR-RBDO process of example 1

Full size image

The process of Phase 1 is shown from Fig. 9a. to c. At the beginning, nine initial samples are added by Latin hypercube sampling method to build initial SVM model and initial Kriging models. As seen in Fig 9a, the initial local range has a large error to predict the optimal RBDO design point. However, SVM model and Kriging models are updated in each iteration, the local range moves to the optimal design point gradually, and the margin of SVM is getting narrower especially within the local range. By comparing with the Fig. 7, it can be seen that RBDO design points obtained in each iteration are gradually close to the optimal RBDO design point. And the local range has covered the vicinity of the DOP and the optimal RBDO design point.

Then, based on the sampling criterion of Phase 2, a series of samples are selected in the local range, and marked as ‘×’ in Fig. 9c. These sample points tend to locate closely along constraint boundaries within the local range.

Figure 9d graphically represents the results of Phase 2. For the local range is updated by adding new samples, the size of the local range has changed when the new optimal RBDO design point is obtained. And accurate Kriging models can be constructed within the current local range. At the same time, there may exists a very large error of Kriging models outside the local range. It means that more samples are selected to construct the adaptive response surfaces to predict accurately only in the local range. In this way, the efficiency of the RBDO process will be improved significantly by avoiding unnecessary samples in the unimportant area.

Some further tests of example 1 based on the LR-RBDO process are shown in Table 1. A total of 10 tests are conducted to get some details. Because of the randomness of the initial samples which are selected by LHS, there exists a slight bias among the results. The calculation results, including the mean values of the sample sizes and the errors, are listed at the end of Table 1.

Table 1 Test results of the LR-RBDO process for example 1
Full size table

To make a comparison, all results of above methods are presented in the Table 2. In this table, ORI-RBDO is the RBDO process which directly calls the true original functions based on SORA method, CBS-RBDO is the RBDO process based on CBS method, LHS-RBDO is the RBDO process based on LHS method, and LR-RBDO is the proposed RBDO process based on LR method. All the methods in this table are used in conjunction with SORA method to obtain the results of the RBDO problem. The results of LR-RBDO correspond to the mean values which are presented at the end of Table 1.

Table 2 Summary of the RBDO results for example 1
Full size table

As seen in Table 2, a good result is obtained by using CBS method. And with the same sample size, the error is much greater by using LHS method only. Compared with CBS-RBDO, LR-RBDO reduces the error by 33.82%, shrinks the sample size by 36.36%, and slightly improves the accuracy of the objective function value. So, it is clear that the efficiency and the accuracy of the RBDO process can all be improved by using LR method.

The reliability indexes of the RBDO results assessed by Monte Carlo simulation are shown in Table 2. β1 and β2 are two reliability index according to the constraints in (18). It can be seen that the reliability index β1 of LR-RBDO is very close to 2.0, so the target reliability index βT is satisfied well.

5.2 Example 2

In order to demonstrate the ability of LR-RBDO process when dealing with the problem with local minima, the second constraint function in example 1 is modified. The RBDO problem of the modified Haupt example is formulated as follows:

$$ \begin{array}{l}\mathrm{find}\kern1em \boldsymbol{d}=\left[{d}_1,{d}_2\right]\\ {} \min \kern1.2em f\left(\boldsymbol{d}\right)={\left({d}_1-3.7\right)}^2+{\left({d}_2-4\right)}^2\\ {}\mathrm{s}.\mathrm{t}.\kern1.5em \mathrm{prob}\left[{g}_i\left(\boldsymbol{X}\right)<0\right]\le \boldsymbol{\varPhi} \left(-{\upbeta}_{\mathrm{T}}^i\right)\kern0.5em ,\kern0.5em i=1,2\\ {}\kern2.7em g{}_1\left(\boldsymbol{X}\right)={X}_1 \sin \left(4{X}_1\right)+1.1{X}_2 \sin \left(2{X}_2\right)\\ {}\kern2.7em {g}_2\left(\boldsymbol{X}\right)={\left({X}_1-2\right)}^2+{\left({X}_2-2.5\right)}^2-0.3\\ {}\kern2.7em 0.0\le {d}_1\le 3.7\kern0.5em ,\kern0.5em 0.0\le {d}_2\le 4.0\kern0.5em \\ {}\kern2.7em {\upbeta}_{\mathrm{T}}^1={\upbeta}_{\mathrm{T}}^2=2.0\\ {}\kern2.7em {\boldsymbol{d}}^{(0)}={\left[1.0,2,5\right]}^{\mathrm{T}}\\ {}\kern2.7em {X}_n\sim N\left({d}_n,{0.1}^2\right)\kern0.5em ,\kern0.5em n=1,2\end{array} $$
(19)

As seen in Fig. 10, in the design space of this example, the feasible region is divided into two parts by a circle constraint. It is clear to see that there exist two local minima points, local minima 1 and local minima 2. In addition, the initial point is modified to [1.0, 2.5], so it is located in the left feasible region. In this situation, inappropriate initial point in the left feasible region will make the optimization result stick to the local minima.

Fig. 10
figure 10

Graphical representation of the true constraint boundaries of modified Haupt example

Full size image

The LR-RBDO process of example 2 and the results are shown in Fig. 11. It is clear that the LR-RBDO process has not been affected by the circle constraint. The results reveal that the new initial point obtained by SVM model can guide the optimization to the global minima, and effectively avoid the optimization result stick to the local minima.

Fig. 11
figure 11

Graphical representation of the LR-RBDO process of example 2 (a) and the results (b)

Full size image

Ten test results of example 2 are shown in Table. 3. The results of example 2 are quite similar with the results of example 1. So it is clear that LR-RBDO can obtain the global minima even if there exist local minima.

Table 3 Test results of the LR-RBDO process for example 2
Full size table

The results of LHS-RBDO and CBS-RBDO are also presented in the Table 4. As seen in this table, with the same sample size, CBS-RBDO can get a smaller error than LHS-RBDO. However, compared with CBS-RBDO, LR-RBDO can reduce the error more, and shrink the sample size significantly. In terms of the reliability index, the Monte Carlo simulation result of LR-RBDO can also satisfied the target reliability index well.

Table 4 Summary of the RBDO results for example 2
Full size table

5.3 Example 3

This example is the modified Choi example with two random design variables and three probabilistic constraints (Lee and Jung 2008). In order to clearly show how the proposed method treats local minima, the objective function and the second constraint function are modified to construct a malignant case. In this example, all of the random variables are statistically independent and normal distributed. The target reliability index and the standard deviation are βT = 1.0 and σ = 0.6 respectively. The RBDO problem of the modified Choi example is formulated as follows:

$$ \begin{array}{l}\mathrm{find}\kern1em \boldsymbol{d}={\left[{d}_1,{d}_2\right]}^{\mathrm{T}}\\ {} \min \kern1.2em f\left(\boldsymbol{d}\right)={d}_2-0.4{d}_1\\ {}\mathrm{s}.\mathrm{t}.\kern1.4em \mathrm{prob}\left[{g}_i\left(\boldsymbol{X}\right)<0\right]\le \varPhi \left(-{\upbeta}_{\mathrm{T}}^i\right)\kern0.5em ,\kern0.5em i=1,2,3\\ {}\kern2.5em g{}_1\left(\boldsymbol{X}\right)={X}_1^2{X}_2/20-1\\ {}\kern2.5em {g}_2\left(\boldsymbol{X}\right)={\left({X}_1-6.5\right)}^2+8\left({X}_2-3\right)\\ {}\kern2.5em g{}_3\left(\boldsymbol{X}\right)=80/\left({X}_1^2+8{X}_2+5\right)-1\\ {}\kern2.5em 0.0\le {d}_1\le 10.0\kern0.5em ,\kern0.5em 0.0\le {d}_2\le 10.0\kern0.5em \\ {}\kern2.5em {\upbeta}_{\mathrm{T}}^1={\upbeta}_{\mathrm{T}}^2={\upbeta}_{\mathrm{T}}^3=1.0\\ {}\kern2.5em {\boldsymbol{d}}^{(0)}={\left[3.0,3.0\right]}^{\mathrm{T}}\\ {}\kern2.5em {X}_n\sim N\left({d}_n,{0.6}^2\right)\kern0.5em ,\kern0.5em n=1,2\end{array} $$
(20)

As shown in Fig. 12, the objective function, which is denoted by dotted lines, decreases from upper left to lower right in the design space. Surrounded by the three constraints, the feasible region is shown as a shaded region. The DOP and the RBDO design point, which are obtained based on the analytical method by directly calling the true functions, are also marked as Xopt and Xd separately in this figure.

Fig. 12
figure 12

Graphical representation of the true constraint boundaries of modified Haupt example

Full size image

In this malignant case, the local minima and the global minima are far away in the design space but very close in terms of objective function. With normal optimization method, different optimum results may be obtained separately corresponding to different initial points. As shown in Fig. 12a, when the initial point X0 is placed at [3.0, 3.0], the local optimization results are placed at Xopt = [3.3622, 1.7693] and Xd = [3.4764, 2.5891], and the value of the objective function at point Xd is 1.1985. As shown in Fig. 12b, when the initial point X0 is placed at [5.0, 5.0], the global optimization results are placed at Xopt = [7.1731, 2.9434] and Xd = [6.1105,3.5832], and the value of the objective function at point Xd is 1.1390.

To verify that the proposed RBDO process can appropriately handle situations where there are multiple optima or optima that are very close in terms of objective function. The initial point in this example is set at [3.0, 3.0].

The LR-RBDO process of example 3 and the results are shown in Fig. 13. At the beginning, we also select nine initial sample points to construct the initial Kriging models and the SVM models of the constraints. In Fig. 13a, a series of new samples are selected to refine Kriging models based on CBS method. When the local range rectangle emerging in the lower right corner of the design space, there still exists a large predict error, and the DOP and the optimal RBDO design point of the RBDO process are located in the local range. Then, based on the local range sampling method in the Phase 2, new samples are mostly located in the feasible region within the local range. So, as we can see in Fig. 13b, accurate Kriging models of the constraints within the local range are constructed, despite the fact that there is a large error outside the local range, especially in the upper left corner and the lower right corner.

Fig. 13
figure 13

Graphical representation of the LR-RBDO process of example 3 (a) and the results (b)

Full size image

The LR-RBDO process of example 3 and the results can clearly verify that the LR-RBDO process has not been affected by inappropriate initial point. Based on the integration of MCS and SORA, the new initial point obtained by LR-RBDO in each iteration can adjust the search direction to the global optimum gradually, and effectively avoid the optimization result stick to the local minima.

The results of ten further tests of example 3 based on LR-RBDO process are shown in Table 5. And the comparison between all above methods is presented in Table 6. To obtain the global optima, the initial point is set at [5.0, 5.0] in CBS-RBDO and LHS-RBDO. Based on the comparison results of example 3, we can draw a conclusion that is similar to example 1, CBS is more accurate and efficient than LHS based on the same sample size. Among these three methods, the result of LR-RBDO is most close to the result of ORI-RBDO.

Table 5 Test results of the LR-RBDO process for example 3
Full size table
Table 6 Summary of the RBDO results for example 3
Full size table

Compared with CBS-RBDO, the LR-RBDO can avoid the local optima effectively when the initial point is placed at point [3.0, 3.0]. The error of LR-RBDO and the sample size is reduced significantly. It means that LR-RBDO is more accurate and efficient. The assessment results of the reliability index of LR-RBDO can also satisfied the target reliability index on every constraint.

5.4 Example 4

In this section, the applicability of the proposed RBDO process is demonstrated by a thin-walled box beam example.

As shown in the left picture of Fig. 14, the left end of the box beam is fixed and the other end is free. The length of the box beam is denoted by L which is a constant and equals to 1000 mm. The cross-section is shown in the right picture of Fig. 14. There are two variables, the side length X 1 and the thickness of the box beam X 2, determine the area of the cross section. With a vertical load Y = 500kN and a horizontal load Z = 500kN, which are added at the free end of the box beam, the objective of this example is to minimize the weight of the box beam. There are two implicit black-box constraints, including the bending stress constraint and the displacement constrains with the thresholds of σ1 = 24000kN and σ2 = 60 mm respectively. It can be inferred that the maximum value of the displacement will take place on the free end of the beam, and the maximum value of the bending stress will take place on the fixed end. The optimization problem of this example is defined as follows:

$$ \begin{array}{l}\mathrm{find}\kern1em \boldsymbol{d}=\left[{d}_1,{d}_2\right]\\ {} \min \kern1em weight\left({d}_1,{d}_2,L\right)\\ {}s.t.\kern1.3em \mathrm{prob}\left[{\boldsymbol{\sigma}}_1<24000\mathrm{k}\mathrm{N}\right]\le \boldsymbol{\varPhi} \left(-{\upbeta}_{\mathrm{T}}^1\right)\kern0.5em \\ {}\kern2.5em \mathrm{prob}\left[{\boldsymbol{\sigma}}_2<60\mathrm{mm}\right]\le \boldsymbol{\varPhi} \left(-{\upbeta}_{\mathrm{T}}^2\right)\kern1em \\ {}\kern2.5em 30\le {d}_1\le 50\kern0.5em ,\kern0.1em 1\le {d}_2\le 7\kern0.5em \\ {}\kern2.5em {\upbeta}_{\mathrm{T}}^1={\upbeta}_{\mathrm{T}}^2=2.0\\ {}\kern2.5em {\boldsymbol{d}}^{(0)}={\left[40,4\right]}^{\mathrm{T}}\\ {}\kern2.5em {X}_1\sim N\left({d}_1,0{.3}^2\right),\kern0.5em {X}_2\sim N\left({d}_2,0{.3}^2\right)\end{array} $$
(21)
Fig. 14
figure 14

A thin-walled box beam and the cross-section

Full size image

In this example, the parametric geometry is modelled in ProE 4.0, and the finite element model is built and calculated in ANSYS 12.0. Since the material is assumed to be isotropic in each iteration of the RBDO process, the finite element analysis (FEA) is calculated based on the same condition. The material’s elastic modulus is set as E = 2.9 × 107 psi, the Poisson’s ratio is set as 0.3, and the grid number of the finite element model is set as 100 in the L direction. To perform RBDO process, the standard deviation is set as σ = 0.3, and the target reliability index is set as βT = 2.0.

A graphical representation of the two phases of the RBDO process and the results are presented in Fig. 15a and b. And some detail information of the results is provided in Table 7. There are nine initial samples selected by LHS. Based on these initial samples, FEA computer experiments are executed to construct the initial Kriging models of the constraints. Followed by 4 new samples selected by the sampling method in this work, the local range is determined to predict the area where the optimal RBDO design point is located. Because the Kriging models are very accurate in the end of Phase 1, there is only one new point selected by the CBS method within the local range to meet the stopping criterion. The results of Monte Carlo simulation also indicate that the design point of LR-RBDO can meet the target reliability index of every constraint.

Fig. 15
figure 15

Graphical representation of the LR-RBDO process (a) and the results (b) of thin-walled box beam

Full size image
Table 7 Summary of the results of the LR-RBDO process for thin-walled box beam example
Full size table

This example demonstrates the applicability of the LR-RBDO process in the optimization problem based on CAE method which is widely used in real engineering problems. In this example, the bending stress constraint and the displacement constraint are seen as black box constraint functions. When the geometric parameters has been changed, the output value of these constraints can only be calculated by FEA process. Then the results indicate that the LR-RBDO process can be used to solve black box problems and to provide accurate optimal solutions, even if the constraint functions of RBDO are black box functions.

5.5 Example 5

This example is a long cylinder pressure vessel for compressed natural gas. As shown in Fig. 16, this vessel has five continuous random design variables. These variables are all geometric parameters of the vessel. h1 is the height of the end part, r1 is the inside diameter of the end part, t1 is the thickness of the end part, r2 is the inside diameter of the body part, and t2 is the thickness of the body part. All these variables follow the normal distribution with σ = 0.2. And the range of the design variables are listed in Table 8. The cylinder pressure vessel is subjected to a uniformly distributed load P = 23 MPa. The Young’s modulus is E = 207GPa and the Poisson’s ratio is u = 0.3. The maximum allowable stress and the minimum volume are σ al  = 250 MPa and V low  = 0.63 m3 respectively.

Fig. 16
figure 16

The cylinder pressure vessel

Full size image
Table 8 The range of the design variables
Full size table

The objective of this example is to minimize the weight of the cylinder pressure vessel. The reliability index is βT = 2.0. The RBDO problem of this example is defined as follows:

$$ \begin{array}{l}\mathrm{find}\kern1em \boldsymbol{d}=\left[{h}_1,{r}_1,{t}_1,{r}_2,{t}_2\right]\\ {} \min \kern1.1em f\left({h}_1,{r}_1,{t}_1,{r}_2,{t}_2\right)\\ {}s.t.\kern1.3em \mathrm{prob}\left[{\boldsymbol{\sigma}}_s\le {\boldsymbol{\sigma}}_{al}\right]\le \boldsymbol{\varPhi} \left(-{\upbeta}_{\mathrm{T}}^1\right)\kern0.5em \\ {}\kern2.5em \mathrm{prob}\left[V\ge \kern0.5em {V}_{low}\right]\le \boldsymbol{\varPhi} \left(-{\upbeta}_{\mathrm{T}}^2\right)\kern1em \\ {}\kern2.5em 280\le {h}_1\le 320,\kern0.2em 40\le {r}_1\le 50\kern2.5em \\ {}\kern2.5em 19\le {t}_1\le 27,\kern0.3em 165\le {r}_2\le 205\kern3.5em \\ {}\kern2.5em 13\le {t}_2\le 23\\ {}\kern2.5em {\upbeta}_{\mathrm{T}}^1={\upbeta}_{\mathrm{T}}^2=2.0\\ {}\kern2.5em {X}_1\sim N\left({h}_1,0{.1}^2\right),\kern0.2em {X}_2\sim N\left({r}_1,0{.1}^2\right)\\ {}\kern2.5em {X}_3\sim N\left({t}_1,0{.1}^2\right),\kern0.2em {X}_4\sim N\left({r}_2,0{.1}^2\right)\\ {}\kern2.5em {X}_5\sim N\left({\mathrm{t}}_2,0{.1}^2\right)\end{array} $$
(22)

where V is the volume of the cylinder pressure vessel, and f is the total consumption of the manufacturing material. V and f are calculated by using following equations:

$$ \begin{array}{l}V=\boldsymbol{\pi} {r}_2^2\left(6000-{h}_1-\sqrt{r_2^2-{t}_1^2}\right)\\ {}\kern3em +2\boldsymbol{\pi} {h}_1{r}_1^2+\boldsymbol{\pi} \left({r}_1^2+{r}_2^2\right)\sqrt{r_2^2-{r}_1^2}\\ {}\kern3em +\frac{1}{3}\boldsymbol{\pi} {\left(\sqrt{r_2^2-{r}_1^2}\right)}^3\end{array} $$
(23)
$$ \begin{array}{l}f=\boldsymbol{\pi} \left[{\left({t}_2+{r}_2\right)}^2-{r}_2^2\right]\left(6000-{h}_1-\sqrt{r_2^2-{r}_1^2}\right)\\ {}\kern3em +2\boldsymbol{\pi} {h}_1\left[{\left({t}_1+{r}_1\right)}^2-{r}_1^2\right]+\frac{1}{3}\boldsymbol{\pi} \left\{3\right[{\left({t}_1+{r}_1\right)}^2\\ {}\kern3em +{\left({t}_2+{r}_2\right)}^2\Big]\sqrt{{\left({t}_2+{r}_2\right)}^2-{\left({t}_1+{r}_1\right)}^2}\\ {}\kern3em +{\left[\sqrt{{\left({t}_2+{r}_2\right)}^2-{\left({t}_1+{r}_1\right)}^2}\right]}^3\\ {}\kern3em -3\left({r}_2^2+{r}_1^2\right)\sqrt{r_2^2-{r}_1^2}-{\left(\sqrt{r_2^2-{r}_1^2}\right)}^3\Big\}\end{array} $$
(24)

In this example, the parametric geometry model and the finite element model are built and calculated in ANSYS 12.0. The finite element model with Hexahedral meshes and the stress simulation analysis result are depicted in Fig. 17.

Fig. 17
figure 17

The finite element model (a) and the stress simulation analysis results (b) of pressure vessel

Full size image

In the LR-RBDO process of this example, 64 initial samples are selected by LHS. By calling the proposed LR-RBDO process, 36 new samples are selected in Phase 1 and 26 new samples are selected in Phase 2. The results are shown in Table 9.

Table 9 Summary of the results of the LR-RBDO process for pressure vessel example
Full size table

From Table 9, we can see that the calculation results of the design variable can satisfy the probabilistic constraint with the reliability index. The results of Monte Carlo simulation indicate that the LR-RBDO results can meet the target reliability requirements, although the stress constraint is a black box function. In summary, the LR-RBDO provides an accurate RBDO solutions.

6 Conclusions and future work

In this paper, we proposed a new LR-RBDO process which includes two phases to solve RBDO problems. In this process, Kriging models are used to approximate the constraint functions of RBDO. To improve the efficiency and the accuracy, the purpose of Phase 1 is to find a local range based on SVM and mean squared error, and the purpose of Phase 2 is to construct accurate Kriging models within the local range. So new samples are located in the vicinity of the optimal RBDO design point, rather than unrelated areas in the design space. Because the trust region of the local range is updated in each iteration based on the current DOP of the deterministic optimization and the RBDO design point according to current Kriging models, so we can refine the local range in a high efficient way even the initial local range does not contain the optimal RBDO design point of the RBDO problem. Then the optimal RBDO design point will be obtained based on accurate local Kriging models.

Several examples are studied to make a comparison between RBDO process with different typical sampling methods. The results show that LR-RBDO process has the most accurate objective value with the least samples. Thus, the proposed LR-RBDO process improves both efficiency and accuracy.

However, there still exists some room for improvement. Such as the sampling method based on SVM to determine the local range, if we had some information of the distribution of design variables, we could modify the sampling density function of the importance sampling, and use it to select new samples within the SVM margin. In addition, in this work, we use the support vector classification machine to predict the local range, and use Kriging models to calculate the RBDO results. If the accuracy of the support vector machine can be improved effectively, we can use it to replace Kriging models. Then the LR-RBDO process may be more simple.