SBSC+SRU: an error-guided adaptive Kriging method for expensive system reliability analysis

Abstract

In this paper, SBSC+SRU: an error-guided adaptive Kriging modeling method is proposed for the system reliability analysis with multiple failure modes. Therein, the accuracies of Kriging models will be improved by a novel learning function, in which the magnitude of Component Limit State Functions (CLSFs), uncertainties of Kriging models, and the coupling relationships among CLSFs are considered to identify the location and component index of the new sample. Then, the maximum estimated relative error of predicted failure probability is derivated by quantifying the probability of wrong sign prediction of samples. To be specific, the highly uncertain samples are first defined, after that the probability of wrong sign prediction of each highly uncertain sample is deduced combining the predictions of Kriging models and coupling relationship among all CLSFs. Therefore, the proposed approach knows the real-time estimated error and could terminate the adaptive updating process under the accuracy requirement. Three numerical examples including parallel and series system problems and an engineering case concerning the system reliability analysis of a stiffened cylindrical shell are studied to validate the performance of the proposed method. Results demonstrate that the proposed method converges to the required estimated accuracy while saving considerable computational burdens compared with state-of-the-art approaches.

1 Introduction

System reliability analysis (SRA) motivates to evaluate the failure probability of a system under multiple failure modes considering various uncertainties such as structural parameters, materials, loadings, and so on. Each failure mode is controlled by a so-called Component Limit State Function (CLSF), in which the Component Limit State (CLS) separates the design space into safety and failure regions (Teixeira et al. 2021). All CLSFs are usually highly nonlinear, implicit, and expensive because of the high complexity of the engineering system. To obtain the result of system failure probability, the approximation paradigms were firstly adopted, which substitute the CLSFs with low-order Taylor expansions, then employ optimization algorithms to search for the most probable point (MPP). In this regard, the First-/Second-Order Reliability analysis Methods (FORM/SORM) (Du and Hu 2012; Jiang et al. 2016) are two representative approaches, which may yield extremely inaccurate estimations when encountering problems with high-order or multiple MPPs. If more accurate results are expected, the simulation-based approaches such as Monte Carlo Simulation (MCS) (Tamimi et al. 1989), Subset Simulation (SS) (Au and Beck 2001), Importance Sampling (IS) (Yun et al. 2021; Zhang et al. 2020b), etc. are better alternatives. However, tremendous samples are the prerequisite for those simulation-based approaches to obtain credible results, which prevent their further application on complex engineering systems due to unaffordable computational costs (Zhou et al. 2020a).

Over the past decade, researchers found that surrogate models show incredible excellence in imitating the expensive input–output relationships of CLSFs with a few samples. (Forrester et al. 2008; Li and Xiu 2010; Peherstorfer et al. 2018). Diverse surrogate models including Radial Basis Function (RBF) model (Li et al. 2018), Support Vector Machine (SVM) model (Bourinet et al. 2011), Polynomial Chaos Expansion (PCE) model (Marelli and Sudret 2018), Kriging model (Hu et al. 2020), and so forth have demonstrated their effectiveness and efficiency in tackling reliability analysis issues. Generally, most of the reported surrogate-based reliability analysis approaches are based on the adaptive updating process because of significant computational cost savings compared with static methods(Peherstorfer et al. 2018) Therein, the Kriging model (Gaussian process model) gained much attention because of extra estimated variance prediction (Kleijnen 2009; Liu et al. 2020; Yang et al. 2019; Yin et al. 2019). Moreover, it was confirmed that an excellent adaptive Kriging-based reliability analysis method should integrate an efficient learning function and an effective stopping criterion. In this regard, two typical adaptive-Kriging based methods, efficient global reliability analysis (EGRA) method (Bichon et al. 2008) and Active-learning Kriging combining Monte Carlo Simulation (AK-MCS) method (Echard et al. 2011) showed excellent performance at the very beginning via their learning functions, i.e., the efficient feasibility function (EFF) and learning function U, respectively. Recently, dozens of learning functions such as H (Lv et al. 2015), LIF (Sun et al. 2017), REIF (Zhang et al. 2019), and so on were developed from different aspects of considerations. Regarding the stopping criteria, traditional stopping criteria depend on the values of learning functions, for example, the stopping criteria employed in EGRA and AK-MCS are $\max \left\{ {EF\left( {x} \right)} \right\} < 0.001$ and $\min \left\{ {U\left( {x} \right)} \right\} > 2$ respectively, where $EF\left( {x} \right)$ and $U\left( {x} \right)$ are the learning functions for EGRA and AK-MSC respectively. It is difficult to determine problem-independent thresholds of for traditional stopping criteria, which may lead the adaptive updating process to pre-mature or late-mature. To address this shortage, several error-based stopping criteria (Menz et al. 2020; Wang and Shafieezadeh 2019a, b; Yi et al. 2020; Zhang et al. 2020a) are proposed by derivating the maximum relative error of estimated failure probability which could halt the adaptive updating process under a pre-determined error threshold. However, the above-mentioned methods are component reliability analysis-oriented approaches that only concern one failure mode, whose efficiency and effectiveness will be hurt tremendously if they are applied to the SRA directly.

Designing effective adaptive Kriging-based system reliability analysis methods is a non-trivial process because several Kriging models should be updated collaboratively according to different system types. The EGRA and AK-MCS methods were extended to the system scenario, those were so-called EGRA-SYS (Bichon et al. 2011) and AK-SYS methods (Fauriat and Gayton 2014). Learning functions for EGRA-SYS and AK-SYS methods have the abilities not only to quantify the efficient feasibilities of samples of each CLSF but also to identify the contributions of different CLSFs to the failure state under different system types. Yun et al. (Yun et al. 2018) introduced the AK-SYSi approach by revising the learning functions of AK-SYS to guarantee the right component index to be identified. Yang et al. (2018, 2019) proposed a method based on truncated candidate regions to avoid the influence of magnitudes of different CLSFs. Hu et al. (2017) utilized the Singular Value Decomposition (SVD) to consider the coupling relationship among CLSFs so that the number of Kriging models could be reduced, i.e., the computational burden could be alleviated. The EEK-SYS method proposed by Jiang et al. (2020) extended the component maximum relative error to the system reliability scenario by derivating the system wrong sign predicted probability for each sample. More publications concerned SRA based on other metamodels refer to Li et al. (2020), Wu et al. (2020), Zhou et al. (2020b). To summarize, many attempts were made to design effective adaptive kriging-based system reliability analysis methods, but efforts could be further made to improve the efficiency of those methods both on the learning function and the stopping criterion.

To resolve this conflict, a novel error-guided adaptive kriging-based system reliability analysis method will be introduced in this work, in which a novel learning function and an error-based stopping criterion are fabricated. Regarding the learning function, the Reliability-based Lower Confidence Bonding (RLCB) for CRA proposed in our previous work had confirmed its superiority since it considers both Kriging predicted uncertainty and statistical features of random design variables (Yi et al. 2020). Therefore, it is incorporated as the core part of the new learning function for SRA where magnitudes of CLSFs, initial uncertainties of Kriging models, and system types will also be considered in ascertaining the new sample and corresponding component index. The proposed error-based stopping criterion focuses on the highly uncertain samples instead of all the MCS population to alleviate the computational burden. Moreover, the bootstrap method is employed to obtain a more robust estimation of confidence intervals of safety and failure samples, i.e., the maximum relative error of system failure probability. To validate the performance of the proposed approach, three numerical examples with different system types and an engineering case evaluating the system failure probability of an underwater cylindrical shell with variable ribs are investigated. Results indicate the proposed approach has significant superiority compared with state-of-the-art approaches.

The remaining parts will be organized as follows: Sect. 2 introduces two basic system types and classic adaptive kriging-based system reliability analysis methods; details of the proposed approach will be elaborated in Sect. 3; Sect. 4 demonstrates the performance of the proposed approach; the conclusions and expected future works will be finally drawn in Sect. 5.

2 Classic system analysis methods via adaptive Kriging model

2.1 Set up of system reliability analysis problem

According to different coupling relationships of components, structural systems can be divided into the series system, the parallel system, and the hybrid system. Usually, the hybrid system consists of several sub-series and sub-parallel systems, in this case, the process of obtaining failure probability of hybrid system combines the processes of series and parallel systems. To this end, the failure probability evaluation processes of series and parallel systems are elaborated as follows.

For a series system, if one component fails, the series system will collapse. Therefore, the failure probability of the series system is defined by:

$$ P_{f}^{series} = P\left\{ {\mathop \cup \limits_{i = 1}^{k} g_{i} \left( {x} \right) < 0} \right\} = P\left\{ {\mathop {\min }\limits_{i = 1}^{k} g_{i} \left( {x} \right) < 0} \right\} $$

(1)

where $k$ is the number of components, $g_{i} ({x})$ is limit state function of i-th the CLSF.

It is difficult to obtain the analytical solution of $P_{f}^{series}$ via Eq. (1) because of the high-order integral. Usually, the MCS method (Tamimi et al. 1989) is employed, by which $P_{f}^{series,mcs}$ is given:

$$ P_{f}^{series,mcs} = \frac{1}{{N^{mcs} }}\sum\limits_{i = 1}^{{N^{mcs} }} {I^{series} ({x}_{i} )} $$

(2)

where

$$ I^{series} \left( {x} \right) = \left\{ {\begin{array}{lll} 1 & { \, \exists \, g_{i} (x) < 0} \\ 0 & {\forall \, g_{i} (x) \ge 0} \\ \end{array} } \right. $$

(3)

Regarding the parallel system, the failure event requires all components in failure mode. Failure probability is described as

$$ P_{f}^{parallel} = P\left\{ {\mathop \cap \limits_{i = 1}^{k} g_{i} \left( {x} \right) < 0} \right\} = P\left\{ {\mathop {\max }\limits_{i = 1}^{k} g_{i} \left( {x} \right) < 0} \right\} $$

(4)

Failure probability calculated by the MCS method is given by:

$$ P_{f}^{parallel,mcs} = \frac{1}{{N^{mcs} }}\sum\limits_{i = 1}^{{N^{mcs} }} {I^{parallel} ({x}_{i} )} $$

(5)

where

$$ I^{parallel} \left( {x} \right) = \left\{ {\begin{array}{lll} 1 & { \, \forall \, g_{i} (x) < 0} \\ 0 & {\exists \, g_{i} (x) \ge 0} \\ \end{array} } \right. $$

(6)

It is worth mentioning that the number of MCS samples $N^{mcs}$ has to satisfy the following condition so that the estimated failure probability is trustworthy.

$$ Cov = \sqrt {\frac{{1 - P_{f}^{mcs} }}{{N^{mcs} P_{f}^{mcs} }}} < 0.05 $$

(7)

where $P_{f}^{mcs}$ represents $P_{f}^{series,mcs}$ or $P_{f}^{parallel,mcs}$ to simplify notations. Basically, the range of $P_{f}^{mcs}$ is $10^{ - 2} \sim 10^{ - 4}$, in this case, approximately $10^{4} \sim 10^{6}$ samples should be evaluated for a system.

2.2 Short review of several adaptive Kriging methods

Generally, adaptive Kriging methods for system reliability analysis are based on an iterative process. For different methods, the main differences are the learning functions and the stopping criteria. In this section, details of those methods, which will be compared in Sect. 4 including the AK-SYS method (Fauriat and Gayton 2014), AK-SYSi method (Yun et al. 2018), and the EEK-SYS method (Jiang et al. 2020) are shortly reviewed.

2.2.1 AK-SYS method

Kriging model is constructed for each CLSF, and the Kriging prediction (Lophaven et al. 2002) for arbitrary CLSF is given by

$$ \hat{f}\left( {x} \right) \sim N\left[ {\hat{g}\left( {x} \right),\hat{s}^{2} \left( {x} \right)} \right] $$

(8)

where $\hat{g}\left( {x} \right)$ and $\hat{s}_{{}}^{2} \left( {x} \right)$ are the predicted value and Kriging variance respectively.

The learning functions for series and parallel systems are different. The failure event of a series system is $\min \left\{ {g_{i} ({x})} \right\} < 0$. Thereby, the CLSF with minimum value should be identified. For this reason, system learning function U for the series system reads

$$ \begin{array}{lll} {U_{s}^{series} \left( {x} \right) = \left| {\frac{{\hat{g}_{m} ({x}) - \overline{z}_{m} }}{{\hat{s}_{m} \left( {x} \right)}}} \right|} & {m = \arg \mathop {\min }\limits_{i = 1\ldots k} \{ \hat{g}_{i} ({x})\} } \\ \end{array} $$

(9)

On the other hand, the CLSF with maximum value should be identified for the parallel system whose failure event is $\max \left\{ {g_{i} ({x})} \right\} < 0$. The learning function U for the parallel system is given by

$$ \begin{array}{lll} {U_{s}^{parallel} \left( {x} \right) = \left| {\frac{{\hat{g}_{m} ({x}) - \overline{z}_{m} }}{{\hat{s}_{m} \left( {x} \right)}}} \right|} & {m = \arg \mathop {\max }\limits_{i = 1\ldots k} \{ \hat{g}_{i} ({x})\} } \\ \end{array} $$

(10)

During the adaptive updating process, the location and component index could be determined by searching for the minimum value of Eqs. (9) or (10) among the MCS population. Note that, for Eqs. (9) and (10), if $k = 1$, the learning function will degenerate to the situation, i.e., $U(x) = \left| {{{\hat{g}(x) - \overline{z}} \mathord{\left/ {\vphantom {{\hat{g}(x) - \overline{z}} {\hat{s}(x)}}} \right. \kern-\nulldelimiterspace} {\hat{s}(x)}}} \right|$, that could only deal with one component. The iterative process of the AK-SYS method stops when the condition $\min \left( {U_{s} \left( {x} \right)} \right) \ge 2$ is satisfied (Fauriat and Gayton 2014).

The AK-SYS method opened the gate to solve the system reliability analysis problems by adaptive Kriging methods, in which the location and component index of updated samples could be identified by the system-level learning function U. However, the learning functions from Eqs. (9) and (10) may treat some components as useless to the system when their CLSFs are poorly approximated which will deduce a huge discrepancy in the failure probability estimation (Li et al. 2020). Moreover, the threshold of the stopping criteria is hard to determine because the values of the learning function are problem-dependent.

2.2.2 AK-SYSi method

The AK-SYSi method aims to refine the learning functions presented by Eq. (9) or (10) by classifying the situations of different samples in different ways when evaluating their improvements to the system limit state. Their expressions are more complex compared with Eq. (9) or (10) which are given by (Yun et al. 2018)

$$ U_{s,refined}^{series} ({x}) = \left\{ {\begin{array}{lll} {\mathop {\min }\limits_{i = 1\ldots ,k} U_{i} ({x})} & {\hat{g}_{i} (x) > 0,\forall i = 1,\ldots ,k} & {w = \arg \mathop {\min }\limits_{i = 1\ldots ,k} U_{i} ({x})} \\ {\mathop {\max }\limits_{{i = 1\ldots ,k^{\prime}}} U_{i} ({x})} & {\hat{g}_{i} (x) < 0,\exists i = 1,\ldots ,k^{\prime}} & {w = \arg \mathop {\max }\limits_{{i = 1\ldots ,k^{\prime}}} U_{i} ({x})} \\ \end{array} } \right. $$

(11)

$$ U_{s,refined}^{parallel} ({x}) = \left\{ {\begin{array}{lll} {\mathop {\min }\limits_{i = 1\ldots ,k} U_{i} ({x})} & {\hat{g}_{i} (x) < 0,\forall i = 1,\ldots ,k} & {w = \arg \mathop {\min }\limits_{i = 1\ldots ,k} U_{i} ({x})} \\ {\mathop {\max }\limits_{{i = 1\ldots ,k^{\prime}}} U_{i} ({x})} & {\hat{g}_{i} (x) > 0,\exists i = 1,\ldots ,k^{\prime}} & {w = \arg \mathop {\max }\limits_{{i = 1\ldots ,k^{\prime}}} U_{i} ({x})} \\ \end{array} } \right. $$

(12)

By the refined learning functions, the adaptive updating process could select the correct component to update automatically for series and parallel systems by minimizing Eqs. (11) and (12) respectively, even at the start of the iterative process where the accuracies of Kriging models are at low levels. However, for the AK-SYSi method, the stopping criterion also adopts the same one as the AK-SYS method, which is a critical shortcoming.

2.2.3 EEK-SYS method

The EEK-SYS method (Jiang et al. 2020) utilized the wrong sign prediction probability function as the infill strategy to select the new sample during the active-learning process. The learning function for the series system is given by

$$ \begin{aligned} {x}_{new} = {x}_{mcs}^{m} ,m = \arg \mathop {\max }\limits_{{j_{s} ,j_{f} }} \left( {p_{s,wsc}^{series} \left( {{x}_{mcs}^{{j_{s} }} } \right),p_{f,wsc}^{series} \left( {{x}_{mcs}^{{j_{f} }} } \right)} \right) \\ Index = \left\{ {\begin{array}{lll} {\mathop {\max }\limits_{i = 1\ldots ,k} p_{wsc,i} \left( {{x}_{new}^{{}} } \right)} & {\hat{g}_{i} (x) > 0,\forall i = 1,\ldots ,k} & {} \\ {\mathop {\min }\limits_{{i = 1\ldots ,k^{\prime}}} p_{wsc,i} ({x}_{new}^{{}} )} & {\hat{g}_{i} (x) < 0,\exists i = 1,\ldots ,k^{\prime}} & {} \\ \end{array} } \right. \\ \end{aligned} $$

(13)

where ${x}_{mcs}^{m}$ donates the m^th MCS samples. The value of $m$ is determined by maximum the system level probabilities of wrong sign prediction among all MCS samples, those are $p_{s,wsc}^{series} \left( {{x}_{mcs}^{{}} } \right)$ and $p_{f,wsc}^{series} \left( {{x}_{mcs}^{{}} } \right)$. Moreover, the index of the component should be updated is determined by choosing the component with the largest probability of wrong sign prediction.

Similarly, the learning function for the parallel system is given by

$$ \begin{aligned} {x}_{new} = {x}_{mcs}^{m} , \, m = \arg \mathop {\max }\limits_{{j_{s} ,j_{f} }} \left( {p_{s,wsc}^{parallel} \left( {{x}_{mcs}^{{j_{s} }} } \right),p_{f,wsc}^{parallel} \left( {{x}_{mcs}^{{j_{f} }} } \right)} \right) \hfill \\ Index = \left\{ {\begin{array}{lll} {\mathop {\max }\limits_{i = 1\ldots ,k} p_{wsc,i} \left( {{x}_{new}^{{}} } \right)} & {\hat{g}_{i} (x) > 0,\forall i = 1,\ldots ,k} & {} \\ {\mathop {\min }\limits_{{i = 1\ldots ,k^{\prime}}} p_{wsc,i} ({x}_{new}^{{}} )} & {\hat{g}_{i} (x) < 0,\exists i = 1,\ldots ,k^{\prime}} & {} \\ \end{array} } \right. \hfill \\ \end{aligned} $$

(14)

where $p_{s,wsc}^{parallel} \left( {{x}_{mcs}^{{_{{}} }} } \right)$ and $p_{f,wsc}^{parallel} \left( {{x}_{mcs}^{{}} } \right)$ are the system level probabilities of wrong sign prediction of the parallel system.

It is noted that the essence of calculating those probabilities of wrong sign prediction is multiplication operations based on probabilities of wrong sign prediction of each component. The derivations are complicated to be expressed clearly by one or two equations, therefore if the reader wants a more detailed explanation, please refer to (Jiang et al. 2020). Furthermore, the learning function will mislead the adaptive updating process because the effectiveness of the wrong sign prediction probability will deteriorate when the number of components is large. (Zhan and Xing 2020, 2021).

The EEK-SYS method (Jiang et al. 2020) derivated the real-time estimated relative error of the failure probability which is regarded as the stopping criterion for the adaptive updating process. The real-time relative error estimator is given by

$$ \hat{\varepsilon }_{r}^{{}} = \left| {\frac{{\hat{N}_{f} }}{{\hat{N}_{f} - \hat{N}_{{_{f} }}^{s} + \hat{N}_{s}^{f} }} - 1} \right| \le \varepsilon_{r}^{given} $$

(15)

where $\hat{N}_{f}$ is the number of samples predicted failure among MCS population S, $\hat{N}_{{_{f} }}^{s}$ is the number of MCS samples predicted failure while actual safe, $\hat{N}_{s}^{f}$ is the number of MCS samples predicted safe while actual failure. The values of $\hat{N}_{{_{f} }}^{s}$ and $\hat{N}_{s}^{f}$ are derivated based on those system and component levels probabilities of wrong sign prediction.

The EEK-SYS method could terminate the active-learning process under a pre-determined accuracy level $\varepsilon_{r}^{given}$. It provides an effective way to balance the accuracy and computational burden. If a more accurate estimation is required, a strict threshold could be used while more computational burden is consumed. However, EEK-SYS employs the Normal distribution and Poisson distribution to calculate the confidence intervals of safety and failure samples respectively. This hypothesis is regarded unsound because the number of samples in safety and failure regions will fluctuate, moreover, the failure samples are rare.

3 The proposed SBSC+SRU method

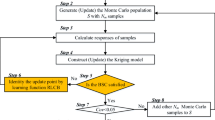
Strictly speaking, the prototype of the SBSC+SRU method is the BSC+RLCB (adaptive Kriging-based reliability analysis method combining Bootstrap-based Stopping Criterion ‘BSC’ and Reliability-based Lowering Confidence Bounding ‘RLCB’ function) method whose superiority had demonstrated in our previous work for CRA (Yi et al. 2020). However, the BSC+RLCB method could not be used to solve the SRA problem because of several critical drawbacks. To this end, the RLCB for CRA is extended to be a system version (abbreviated as SRU) to choose update samples for SRA firstly. Subsequently, the BSC is also revised into a system one (abbreviated as SBSC) to terminate the adaptive updating process under the desired estimated accuracy. First of all, the flowchart of the SBSC+SRA method is shown in Fig. 1 and the contributions of this work compared with other active-learning methods are highlighted in orange. Then, the details of the main contributions, i.e., the learning function SRU and stopping criterion SBSC for SRA, will be drawn in Sects. 3.1 and 3.2 respectively.

Fig. 1

The flowchart of the proposed approach

3.1 System reliability-based lowering confidence bounding function

3.1.1 Reminder of the learning function RLCB

The learning function RLCB is short reviewed because it is the foundation of the new learning function SRU. Learning function RLCB can be given by

$$ RLCB({x}) = \left| {\hat{g}({x}) - \overline{z}} \right| - \eta ({x})\hat{s}({x}) + d({x}) $$

(16)

where $\overline{z}$ represents the CLS, other terms could be expressed as

$$ \begin{aligned} \eta ({x}) = \phi \left( {\frac{{\hat{g}\left( {x} \right) - \overline{z}}}{{\hat{s}\left( {x} \right)}}} \right) \\ d({\varvec{x}}) = \left\{ {\begin{array}{lll} 0 & {if \, l({\varvec{x}}) > \overline{l} \, } \\ {{\text{Inf}}} & {else} \\ \end{array} } \right. \\ l({\varvec{x}}) = \min \left( {\sqrt {({\varvec{x}} - {\varvec{x}}_{i} )^{T} ({\varvec{x}} - {\varvec{x}}_{i} )} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,\ldots ,N) \\ \overline{l} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{1}}{{2}}\min \left( {\sqrt {({\varvec{x}}_{i} - {\varvec{x}}_{j}^{{}} )^{T} ({\varvec{x}}_{i} - {\varvec{x}}_{j}^{{}} )} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,\ldots ,N;j = 1,2,\ldots ,i - 1,i + 1,\ldots ,N) \\ \end{aligned} $$

(17)

According to Eqs. (16) and (17), $\eta ({x})$ is a PDF-based weight function that combines the Kriging predictions and statistic information of design variables to assign a unique weight factor for every sample. In this case, the RLCB has excellent performance on the balance of global exploration and local exploitation. $d({\varvec{x}})$ is a distance function to prevent clustering of samples.

3.1.2 Extention of learning function RLCB to system-level: SRU

Although it was demonstrated that the learning function RLCB shows outstanding performance in dealing with component reliability analysis problems, it can not be used to solve system reliability analysis problems directly. First, learning function RLCB will deduce bias on the comparison of the efficient feasibilities of two components by replacing $\left| {{{\left( {\hat{g}({x}) - \overline{z}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat{g}({x}) - \overline{z}} \right)} {\hat{s}\left( {x} \right)}}} \right. \kern-\nulldelimiterspace} {\hat{s}\left( {x} \right)}}} \right|$ in Eqs. (9) and (10) with $RLCB({x})$ because learning function RLCB has a dimensional quantity. For example, if a system consists of two CLSFs which are used to describe two different quantities of interests such as displacement and stress of a cantilever beam, then the dimensions of displacement and stress are also attached to the corresponding learning function. To circumvent this bottleneck, RLCB is transformed to a new form called RU to eliminate the magnitude effect, which is expressed as:

$$ RU({x}) = \frac{{\left| {\hat{f}({x}) - \overline{z}} \right|}}{{\eta ({x})\hat{s}({x})}} + d({x}) $$

(18)

According to Eq. (18), the values $RU({x})$ are nondimensionalized because the dimension quantities in $\hat{f}({x})$ and $\hat{s}({x})$ will be eliminated by the division operation. To show the difference between $RLCB({x})$ and $RU({x})$, Fig. 2 shows the values of these two learning functions based on a simple one-dimensional example.

Fig. 2

Illustrations of the difference between RLCB and RU based on one-dimensional functions

The illustrated example consists of two CLSFs where $G_{1} ({x}) = (6x - 1)^{2} \sin (12x - 4) + 2$ and $G_{2} ({x}) = 10G_{1} ({x})$. Essentially, those two CLSFs should have the same importance to the system because $G_{2} ({x})$ is a linear transformation of $G_{1} ({x})$ by multiplying 10. However, as shown in \* MERGEFORMAT Fig. 2. (a), their values of $RLCB({x})$ are different. On the other side, the learning function RU values the same for $G_{1} ({x})$ and $G_{2} ({x})$, which indicates that RU could eliminate the magnitude effect among the CLSFs.

The second part of the extension is to find a proper way so that the new learning function could handle multiple CLSFs simultaneously. Theoretically, by replacing $\left| {{{\left( {\hat{g}({x}) - \overline{z}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat{g}({x}) - \overline{z}} \right)} {\hat{s}\left( {x} \right)}}} \right. \kern-\nulldelimiterspace} {\hat{s}\left( {x} \right)}}} \right|$ in Eqs. (9) and (10) with $RU({x})$, two learning functions for series and parallel systems expected with higher effectiveness could be obtained. However, the initial uncertainties of Kriging models have critical impacts on the effectiveness of learning function, which have not been considered in Eq. (9) or (10). For instance, if the activated CLSF has great uncertainty which may be regarded as the least important component. Several more iterations will be required to correct the bias, which deduces extra computational burden. The learning function SRU aims to avoid this shortage by evaluating the efficient feasibilities of a sample in line with their safe and failure statements. Specifically, the way of choosing one component among a k-dimensional vector $\left[ {RU_{1} ({x}),RU_{2} ({x}),\ldots ,RU_{k} ({x})} \right]$ for updating should be different for safe and failure statements under different system types (Yun et al. 2018). For the series system, the SRU reads:

$$ SRU_{{}}^{series} ({x}) = \left\{ {\begin{array}{lll} {\mathop {\min }\limits_{i = 1\ldots ,k} RU_{i} ({x})} & {\hat{g}_{i} (x) > 0,\forall i = 1,\ldots ,k} & {w = \arg \mathop {\min }\limits_{i = 1\ldots ,k} RU_{i} ({x})} \\ {\mathop {\max }\limits_{{i = 1\ldots ,k^{\prime}}} RU_{i} ({x})} & {\hat{g}_{i} (x) < 0,\exists i = 1,\ldots ,k^{\prime}} & {w = \arg \mathop {\max }\limits_{{i = 1\ldots ,k^{\prime}}} RU_{i} ({x})} \\ \end{array} } \right. $$

(19)

According to Eq. (19), if it is reported safe, the component with the smallest $RU({x})$ will be identified for updating. From the definition of RU in Eq. (18), a smaller value of $RU({x})$ indicates smaller ${{\left| {\hat{f}({x}) - \overline{z}} \right|} \mathord{\left/ {\vphantom {{\left| {\hat{f}({x}) - \overline{z}} \right|} {\eta ({x})\hat{s}({x})}}} \right. \kern-\nulldelimiterspace} {\eta ({x})\hat{s}({x})}}$, which means a larger probability of wrong sign prediction. By this operation, the component with the largest probability of wrong sign prediction will be selected because this one has a critical impact on the safe and failure statements. In terms of the predicted failure sample, SRU selects the component with the largest $RU({x})$ among the $\hat{g}({x}) < 0$ CLSFs for updating. Under this case, if the component with the smallest probability of wrong sign prediction still fails, other components seem unimportant since this design scheme definitely fails.

Similarly, regarding the parallel system, the SRU is given by

$$ SRU_{{}}^{parallel} ({x}) = \left\{ {\begin{array}{lll} {\mathop {\min }\limits_{i = 1\ldots ,m} RU_{i} ({x})} & {\hat{g}_{i} (x) < 0,\forall i = 1,\ldots ,m} & {w = \arg \mathop {\min }\limits_{i = 1\ldots ,m} RU_{i} ({x})} \\ {\mathop {\max }\limits_{{i = 1\ldots ,m^{\prime}}} RU_{i} ({x})} & {\hat{g}_{i} (x) > 0,\exists i = 1,\ldots ,m^{\prime}} & {w = \arg \mathop {\max }\limits_{{i = 1\ldots ,m^{\prime}}} RU_{i} ({x})} \\ \end{array} } \right. $$

(20)

Compared with Eq. (19), Eq. (20) for the parallel system selects the component with the smallest $RU({x})$ when it is predicted failure to identify the component with the largest probability deducing wrong sign prediction. Meanwhile, for the sample predicted safe, the component with the largest $RU({x})$ among the $\hat{g}({x}) > 0$ CLSFs will be identified for the reason of verifying the safe statement.

During the adaptive updating process, the location and component index of the new sample for series and the parallel system could be ascertained by minimizing Eqs. (19) and (20) respectively.

3.2 System bootstrap-based stopping criterion

3.2.1 Reminder of the BSC stopping criterion

The maximum estimated relative error of failure probability for CRA (Yi et al. 2020) was derived according to the extra uncertainty prediction of Kriging. Specifically, the prediction of a sample located in the design space obeys binomial distribution with a probability of wrong sign prediction $P_{{}}^{wsp} \left( {x} \right) = \Phi \left( {{{(\hat{g}\left( {x} \right) - \overline{z})} \mathord{\left/ {\vphantom {{(\hat{g}\left( {x} \right) - \overline{z})} {\hat{s}\left( {x} \right)}}} \right. \kern-\nulldelimiterspace} {\hat{s}\left( {x} \right)}}} \right)$ and the probability of right sign prediction is $1 - P_{{}}^{wsp} \left( {x} \right)$. Then, the maximum estimated relative error of failure probability of component is determined based on bootstrap resampling technology and the highly uncertain samples.

The highly uncertain samples are defined by

$$ \begin{aligned} {\mathbf{X}}_{f} = \{ \left. {x} \right|\hat{g}({x}) < \overline{z};\hat{g}({x}) + a\hat{s}({x}) > \overline{z}\} \hfill \\ {\mathbf{X}}_{s} = \{ \left. {x} \right|\hat{g}({x}) > \overline{z};\hat{g}({x}) - a\hat{s}({x}) < \overline{z}\} \hfill \\ \end{aligned} $$

(21)

where samples in ${\mathbf{X}}_{f}$ are predicted failure while maybe actually safe to a great extent; samples in ${\mathbf{X}}_{s}$ belong to the opposite situation; $a$ is used to control the confidence level.

The maximum estimated relative error of failure probability is given by

$$ \varepsilon_{r}^{\max } = \max \left\{ {\left| {\frac{{\hat{N}_{f} }}{{\hat{N}_{f} - (\hat{N}_{f}^{s} )^{u} }} - 1} \right|,\left| {\frac{{\hat{N}_{f} }}{{\hat{N}_{f} + (\hat{N}_{s}^{f} )^{u} }} - 1} \right|} \right\} $$

(22)

where

$$ \begin{aligned} \hat{N}_{f}^{s} = \sum\nolimits_{i = 1}^{{N_{{{\mathbf{X}}_{f} }} }} {P_{{}}^{wsp} \left( {{x}^{i} } \right)} \hfill \\ \hat{N}_{s}^{f} = \sum\nolimits_{i = 1}^{{N_{{{\mathbf{X}}_{s} }} }} {P_{{}}^{wsp} \left( {{x}^{i} } \right)} \hfill \\ \end{aligned} $$

(23)

$(\hat{N}_{f}^{s} )^{u}$ and $(\hat{N}_{s}^{f} )^{u}$ are the corresponding upper bound of the confidence interval of $\hat{N}_{f}^{s}$ and $\hat{N}_{s}^{f}$ respectively, which can be obtained by bootstrap confidence estimation (Yi et al. 2020). To give a better intuition of the bootstrap confidence estimation, suppose that we have 5 MCS samples located in ${\mathbf{X}}_{f}$ and corresponding probabilities of wrong sign prediction are [0.182, 0.95,0.12,0.211, 0.102]^T. To this end, one could obtain the value of $\hat{N}_{f}^{s}$ by

$$ \hat{N}_{f}^{s} = 0.182 + 0.95 + 0.12 + 0.211 + \, 0.102 = 1.5665 $$

(24)

The essence of bootstrap resampling is to regenerate a vector of probabilities of wrong sign prediction based on the original vector by resampling. To this end, B times (supposed that B = 1000) resampling could be executed, whose information is listed in Table 1.

Table 1 Illustration of bootstrap resampling

According to Table 1, 1000 estimations of $\hat{N}_{f}^{s}$ are obtained, and the confidence interval of $\hat{N}_{f}^{s}$ can be obtained by sorting those values of $\hat{N}_{f}^{s}$ by ascending order. The orders of lower and higher bound are

$$ k_{1} = \left[ {B \times \frac{\alpha }{2}} \right],k_{2} = \left[ {B \times (1 - \frac{\alpha }{2})} \right] $$

(25)

where $\alpha$ is the significant level (note the confidence level is $1 - \alpha$). For this illustration case, the 95% confidence interval of $\hat{N}_{f}^{s}$ is $[0.644,3.181]$ (the value of $(\hat{N}_{f}^{s} )^{u}$ is 3.181).

From this illustration example, it is observed that the bootstrap confidence interval estimation does not rely on any assumption, and it is suitable for a vector with any length. The only factor that would influence its accuracy is the resampling times B, with larger B, the estimated results will get closer to the ground truth. In this paper, the value of B is set to be 1000 to guarantee the credibility of bootstrap confidence estimation.

3.2.2 Determination of highly uncertain samples and probability of wrong sign prediction

The conception of the maximum estimated relative error in Eq. (22) is also powerful for SRA. Whereas, how to ascertain the highly uncertain samples and their probabilities of wrong sign prediction are two vital problems for SRA due to its failure modes controlled by multiple CLSFs. To begin with, the highly uncertain sample sets take the union of all ${\mathbf{X}}^{i}_{f}$ and ${\mathbf{X}}^{i}_{s}$, which are expressed by

$$ \begin{aligned} {\mathbf{X}}_{f}^{system} = \bigcup\limits_{i = 1}^{k} {{\mathbf{X}}_{f}^{i} } ,{\text{ for }}i = 1,\ldots ,k \hfill \\ {\mathbf{X}}_{s}^{system} = \bigcup\limits_{i = 1}^{k} {{\mathbf{X}}_{s}^{i} } ,{\text{ for }}i = 1,\ldots ,k \hfill \\ \end{aligned} $$

(26)

It is worth mentioning that $a = 1.96$ in Eq. (21) guarantees the 95% confidence level for CRA. In terms of SRA, the value of $a$ has to be adjusted according to different system types. In detail, the value of $a$ is determined by combining the number of CLSFs of the series system and the PDF of Normal distribution. Because if $a = 1.96$ is adopted for each CLSF, the confidence level for series system becomes $(95\% )^{k}$ which is significantly smaller than 95% with the number of components increasing. For the parallel system, $a = 1.96$ is still utilized for the confidence level equals $\left( {1 - (5\% )^{k} } \right) \ge 95\%$. In this situation, the parallel system is more stable with more components.

Because there are $k$ CLSFs among a system, a vector of component probabilities of wrong sign prediction ${P}^{wsp} = \left[ {P_{{1}}^{wsp} \left( {x} \right),P_{{2}}^{wsp} \left( {x} \right),\ldots ,P_{m}^{wsp} \left( {x} \right)} \right]$ exists for a system design scheme. Similar to the learning function, the system probabilities of wrong sign prediction are organized in different manners for different systems. If a sample of a series system is predicted safe, wrong sign prediction occurred in one CLSF will lead the whole system to be misjudged. It is cumbersome to calculate the system probability of wrong sign prediction for tremendous combinations of wrong sign prediction situations while calculating the probability of right sign prediction is more convenient.

$$ P_{series}^{rsp} \left( {x} \right) = \prod\limits_{i = 1}^{k} {\left( {1 - P_{i}^{wsp} \left( {x} \right)} \right)} $$

(27)

Because the statement prediction of a system obeys Poisson distribution, the probability of wrong sign prediction could be obtained by

$$ P_{{X_{s} }}^{wsp} \left( {x} \right) = 1 - P_{series}^{rsp} \left( {x} \right) = 1 - \prod\limits_{i = 1}^{m} {\left( {1 - P_{i}^{wsp} \left( {x} \right)} \right)} $$

(28)

If a sample of a series system is predicted failure, the wrong sign prediction of this sample needs all CLSFs predicted failure being misjudged, and the predictions of all CLSFs predicted safe are correct. Suppose there are $k_{1}$ and $k_{2}$ CLSFs predicted failure and safety respectively, where $k_{1} + k_{2} = k$. The probability of wrong sign prediction can be analytically given by

$$ P_{{X_{f} }}^{wsp} \left( {x} \right) = \prod\limits_{{i_{1} = 1}}^{{k_{1} }} {\left( {P_{{i_{1} }}^{wsp} \left( {x} \right)} \right)} \prod\limits_{{i_{2} = 1}}^{{k_{2} }} {\left( {1 - P_{{i_{2} }}^{wsp} \left( {x} \right)} \right)} $$

(29)

Similarly, if a sample of a parallel system is predicted safe, the wrong sign prediction of this sample needs all CLSFs predicted safe being misjudged, and predictions of all CLSFs predicted failure are correct. Suppose $k_{1}$ and $k_{2}$ are the number of components predicted safe and failure respectively, where $k_{1} + k_{2} = k$. The probability of wrong sign prediction is given by

$$ P_{{X_{s} }}^{wsp} \left( {x} \right) = \prod\limits_{{i_{1} = 1}}^{{k_{1} }} {\left( {1 - P_{{i_{1} }}^{wsp} \left( {x} \right)} \right)} \prod\limits_{{i_{2} = 1}}^{{k_{2} }} {\left( {P_{{i_{2} }}^{wsp} \left( {x} \right)} \right)} $$

(30)

If a sample of a parallel system is predicted failure, the sign will be wrong predicted even if only one CLSF is misjudged. The probability of right sign prediction is calculated by

$$ P_{parallel}^{rsp} \left( {x} \right) = \prod\limits_{i = 1}^{k} {\left( {1 - P_{i}^{wsp} \left( {x} \right)} \right)} $$

(31)

Because the state of failure statement obeys Poisson distribution, the probability of wrong sign prediction could be obtained by

$$ P_{{X_{f} }}^{wsp} \left( {x} \right) = 1 - P_{parallel}^{rsp} \left( {x} \right) = 1 - \prod\limits_{i = 1}^{k} {\left( {1 - P_{i}^{wsp} \left( {x} \right)} \right)} $$

(32)

3.2.3 Stopping condition for the adaptive updating process

The maximum estimated relative error of series system failure probability $\varepsilon_{r,series}^{\max }$ could be obtained based on Eqs. (22), (23), (26), (28), and (29). The stopping criterion for the series system is expressed as

$$ \varepsilon_{r,series}^{\max } = \max \left\{ {\left| {\frac{{\hat{N}_{f} }}{{\hat{N}_{f} - (\hat{N}_{f}^{s} )^{u} }} - 1} \right|,\left| {\frac{{\hat{N}_{f} }}{{\hat{N}_{f} + (\hat{N}_{s}^{f} )^{u} }} - 1} \right|} \right\} \le \varepsilon_{r,series}^{given} $$

(33)

where $\varepsilon_{r,series}^{given}$ is the pre-determined error threshold.

The same as the series system, the stopping criterion for the parallel system is defined by

$$ \varepsilon_{r,parallel}^{\max } = \max \left\{ {\left| {\frac{{\hat{N}_{f} }}{{\hat{N}_{f} - (\hat{N}_{f}^{s} )^{u} }} - 1} \right|,\left| {\frac{{\hat{N}_{f} }}{{\hat{N}_{f} + (\hat{N}_{s}^{f} )^{u} }} - 1} \right|} \right\} \le \varepsilon_{r,parallel}^{given} $$

(34)

For reasons of concise notation, $\varepsilon_{r,system}^{\max }$ and $\varepsilon_{r,system}^{given}$ are used to express the maximum estimated relative error and pre-determined threshold of both series and parallel systems. Generally, the value of $\varepsilon_{r,system}^{given}$ could be set to 0.03 or 0.02 that are basic enough for most system reliability analysis problems.

4 Cases studies and results discussions

To validate the performance of the proposed SBSC+SRU method, four cases with different complexities are investigated compared with the methods reviewed in Sect. 2.2. As for the comparison with the AK-SYS method and AK-SYSi method, the case of the SBSC+SRU method with similar accuracy is adopted where their computational cost difference will be detailed analyzed to show the efficiency of the proposed method. Moreover, $\varepsilon_{r,system}^{given} = \left[ {0.05,0.04,0.03,0.02,0.01} \right]$ are adopted to further compare the effectiveness and efficiency of the EEK-SYS method and the SBSC+SRU method under different stopping conditions. Taking into account the randomness of the initial samples, each method repeats independently 30 times where the initial samples of different methods with same run order are the same, and then the statistical results are recorded and analyzed.

4.1 Four branches function

The four branches function is a series system composed of three CLSFs, which was modified by Hu et al. (Hu et al. 2017) from the classic component four branches function. It reads:

$$ \begin{aligned} g_{1} ({x}) = \left\{ {\begin{array}{lll} {3 + \frac{{\left( {x_{1} - x_{2} } \right)^{2} }}{10} \pm \frac{{\left( {x_{1} + x_{2} } \right)}}{\sqrt 2 }} \\ {\frac{6}{\sqrt 2 } \pm \left( {x_{1} - x_{2} } \right)} \\ \end{array} } \right. \hfill \\ g_{2} ({x}) = 7\left( {x_{2}^{{}} { + }3} \right)_{{}}^{2} - 5x_{1}^{2} + \left( {x_{1}^{2} + \left( {x_{2}^{{}} + 3} \right)^{2} } \right)^{2} + 1 \hfill \\ g_{3} ({x}) = 2\left( {x_{1}^{{}} { + 2}} \right)_{{}}^{2} - 4\left( {x_{2}^{{}} - 1} \right) + \left( {\left( {x_{1}^{{}} + 2} \right)^{2} + \left( {x_{2}^{{}} - 1} \right)^{2} } \right)^{2} + 1 \hfill \\ \end{aligned} $$

(35)

where the two independent design variables obey standard normal distribution.

4.1.1 Visualization of the fitting situation of SBSC+SRU method

In this subsection, to intuitively show the fitting performance of SBSC+SRU method, the contour plots of the real system limit state and the approximated one by the final Kriging models under $\varepsilon_{r,system}^{given} = 0.02$ are depicted in Fig. 3.

Fig. 3

Visualization of the fitting situation of SBSC+SRU method on Four branches function

It can be observed from Fig. 3a, four branches function has four failure regions shaded by orange. Most of the system limit state is governed by $g_{1}$, while $g_{2}$ and $g_{3}$ increase the degree of non-linearity on the system limit state that brings difficulty on the fitting of SBSC+SRU method. In Fig. 3b, the black line represents real system limit state, while the pink, blue, and sky blue lines indicate predicted CLS of $g_{1} ,g_{2} ,g_{3}$ respectively. SBSC+SRU method achieves the convergence with 29, 24, and 25 samples respectively in $g_{1} ,g_{2} ,g_{3}$. The new samples are distributed normally around the corresponding CLS, which confirms the excellent performance of the SRU learning function. In terms of the approximated accuracy, the predicted CLSs of $g_{2} ,g_{3}$ almost coincide with the real ones. $g_{1}$ takes majority parts of the CLS, while it has little discrepancies on the corners of the CLS. However, the $\varepsilon_{r,system}^{{}}$ equals $0.0156$ (that is smaller than the given stopping threshold) on this trial, which shows the effectiveness of SBSC+SRU method.

4.1.2 Comparison between different advanced approaches

In comparison with other approaches, 10 initial samples are sampled through OLHS (Garud et al. 2017) for each CLSF. Table 2 provides the statistical results of the four branches function under $\varepsilon_{r,system}^{given} = \left[ {0.05,0.04,0.03,0.02,0.01} \right]$.

Table 2 Results of the four branches function with different methods and $\varepsilon_{r,system}^{given}$

As shown in Table 2, $N_{call} (g_{i} ),i = 1,2,3$ are the numbers of calls of each CLSF and $N_{call} (G)$ the summation of $N_{call} (g_{i} ),i = 1,2,3$. The reference $P_{f}^{mcs} = 1.398 \times 10^{ - 3}$ is obtained through $3 \times 10^{6}$ MCS samples. The AK-SYS and AK-SYSi methods spend 135.29 and 129.00 samples respectively to obtain the convergence, where the $\varepsilon_{r,system}^{{}}$ of those two methods are 0.0193 and 0.0011 respectively. To achieve the same accuracy level, the EEK-SYS method and SBSC+SRU method could save tremendous computational burden. Taking $\varepsilon_{r,system}^{given} = 0.01$ for example, the accuracies of EEK-SYS and SBSC+SRU methods are comparable with that of the AK-SYSi method, while their computational burden, especially their $N_{call} (g_{1} )$ are significantly smaller than that of the AK-SYSi method. One could find that both EEK-SYS method and SBSC+SRU methods converge to the pre-determined $\varepsilon_{r,system}^{given}$, which confirms the superiority of error-guided approaches compared with the traditional approaches that terminate the adaptive updating process through values of learning functions. The computational burden will increase while the accuracies of EEK-SYS method and SBSC+SRU method with the values of $\varepsilon_{r,system}^{given}$ decrease. It is also observed from Table 2 that the value of $\varepsilon_{r,system}^{{}}$ SBSC+SRU method is closer to the pre-determined $\varepsilon_{r,system}^{given}$ in comparison with EEK-SYS method. It demonstrates the effectiveness of the proposed SBSC stopping criterion. In terms of $N_{call} (G)$ between EEK-SYS and SBSC+SRU methods, the SBSC+SRU method reduces about 10 samples compared with EEK-SYS method under the same $\varepsilon_{r,system}^{given}$. Specifically, about 3 ~ 4 samples could be saved in $g_{1}$, and about 2 ~ 3 samples could be reduced in $g_{2}$ and $g_{3}$.

To illustrate the performance difference between EEK-SYS and SBSC+SRU methods more specifically, Fig. 4 gives the boxplots of two concerning metrics $N_{call} (G)$ and $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$.

Fig. 4

Boxplots of $N_{call} (G)$ and $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$ of four branches function under different $\varepsilon_{r,system}^{given}$

One could found from Fig. 4a that the superiority of the SBSC+SRU method compared with the EEK-SYS method is significant since there is a prominent negative slope between the means of the two methods under same $\varepsilon_{r,system}^{given}$. Furthermore, the variation of the SBSC+SRU method on $N_{call} (G)$ is also better than that of EEK-SYS method because the length of the box of SBSC+SRU method is shorter, which shows the robustness of $N_{call} (G)$ to different initial DoEs. Regarding $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$, the mean that is closer to zero and shorter length of the box indicates better convergence to $\varepsilon_{r,system}^{given}$ and robustness to different DoEs. According to Fig. 4b, the robustnesses of both approaches decrease with the larger value of $\varepsilon_{r,system}^{given}$. Although the performance of SBSC+SRU method on $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$ is slightly worse than that of the EEK-SYS method, the SBSC+SRU method still converges to the pre-set $\varepsilon_{r,system}^{given}$.

4.2 Two-dimensional parallel function with disconnected failure regions

The two-dimension parallel function is utilized by Yun et al. (2018) to verify the performance of the AK-SYSi method, which is analytically defined by

$$ \begin{aligned} g_{1} ({x}) = \left( {{ - 4 - 2}{\text{.1}}x_{{1}}^{2} { + }\frac{{x_{{1}}^{{4}} }}{{3}}} \right)x_{{1}}^{2} - x_{1}^{{}} x_{2} + \left( { - 4 + 4x_{2}^{2} } \right)x_{2}^{2} + 0.8 \hfill \\ g_{2} ({x}) = 100\left( {{ - 4 - 2}{\text{.1}}x_{{1}}^{2} { + }\frac{{x_{{1}}^{{4}} }}{{3}}} \right)x_{{1}}^{2} - 100x_{1}^{{}} x_{2} + 100\left( { - 4 + 4x_{2}^{2} } \right)x_{2}^{2} + 60 \hfill \\ g_{3} ({x}) = 500\left( {{ - 4 - 2}{\text{.1}}x_{{1}}^{2} { + }\frac{{x_{{1}}^{{4}} }}{{3}}} \right)x_{{1}}^{2} - 500x_{1}^{{}} x_{2} + 500\left( { - 4 + 4x_{2}^{2} } \right)x_{2}^{2} + 250 \hfill \\ \end{aligned} $$

(36)

The statistical information of the random design variables is listed in Table 3.

Table 3 Statistical information of design variables of the parallel function

4.2.1 Visualization of the fitting situation of SBSC+SRU method

The setting of the SBSC+SRU method is the same as the former example to show the effectiveness of the adaptive updating process for the parallel system. Similarly, Fig. 5 illustrates the contour plots of real system limit state and predicted one by SBSC+SRU method.

Fig. 5

Visualization of the fitting situation of the SBSC+SRU method on parallel function

It can be observed from Fig. 5. (a) that the parallel function has two sub-regions of failure that are the intersection of all component failure regions. Moreover, the system failure mode is mainly controlled by $g_{1}$, which means small predicted errors on $g_{1}$ will lead to wrong sign prediction. According to Fig. 5. (b), 35, 16, and 12 samples are consumed for the three CLSFs respectively to obtain convergence. Herein, majority of new samples are utilized to refine component $g_{1}$, therefore the estimation contour of $g_{1}$ almost coincides with the real one. On the contrary, only 6 and 2 new samples are supplemented for $g_{2} ,g_{3}$ respectively. In this case, the prediction contour of $g_{2}$ has some discrepancies compared with the real one, while that of $g_{3}$ predicts the two separate sub failure regions in a series one. However, it has little influence on the judgment of the safe/failure state of each design scheme according to Fig. 5. (b). In summary, the SBSC+SRU method could recognize the CLSFs that are more important to the $P_{f}^{mcs}$, then it utilizes the majority computational burden to refine those CLSFs. For those CLSFs that are less important, the proposed approach will spend less computational burden to achieve the accuracy level that will not influence the safe/failure state prediction. In this way, the SBSC+SRU method could maximize the efficiency of each sample and reduce the consumption of computational burden.

4.2.2 Comparison between different advanced approaches

The same as the four branches function, the statistical results compared with state-of-the-art methods are recorded in Table 4. Meanwhile, the boxplots of $N_{call} (G)$ and $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$ are shown in Fig. 6 to compare the EEK-SYS and SBSC+SRU methods intuitively.

Table 4 Results of the parallel function with different methods and $\varepsilon_{r,system}^{given}$

Fig. 6

Boxplots of $N_{call} (G)$ and $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$ of parallel function under different $\varepsilon_{r,system}^{given}$

Combining Table 4 and Fig. 6, as the $\varepsilon_{r,system}^{given}$ decreases, the $\varepsilon_{r,system}^{{}}$ of both EEK-SYS and SBSC+SRU methods will decrease and their computational burden will increase. Besides, the $N_{call} (G)$ of SBSC+SRU method is less than that of EEK-SYS method under same $\varepsilon_{r,system}^{given}$, which confirms the superiority of the proposed SBSC+SRU method on the parallel system. The robustness of the SBSC+SRU method on $N_{call} (G)$ is better than that of EEK-SYS method for the shorter length of boxes. Concerning $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$ illustrated in Fig. 6. (b), their robustnesses of both approaches increase with smaller $\varepsilon_{r,system}^{given}$, which reveals more sound results could be obtained through stricter stopping conditions. The ability to eliminate the influence of initial samples of the SBSC+SRU method is slightly worse than that of the EEK-SYS method because the variation of $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$ of SBSC+SRU method is larger. However, the SBSC+SRU method converges to the $\varepsilon_{r,system}^{given}$ with less computational burden, in this case, slight robustness loss on $\varepsilon_{r,system}^{\max } - \varepsilon_{r,system}^{{}}$ is reasonable.

4.3 Roof truss system

The roof truss system is a series system consisting of three CLSFs(Jiang et al. 2020; Yun et al. 2018), which reads

$$ \begin{aligned} g_{1} ({x}) = 0.030 - \frac{{ql^{2} }}{2}\left( {\frac{3.81}{{A_{c} E_{c} }} + \frac{1.13}{{A_{s} E_{s} }}} \right) \hfill \\ g_{2} ({x}) = f_{c} A_{c} - 1.185ql \hfill \\ g_{3} ({x}) = f_{s} A_{s} - 0.75ql \hfill \\ \end{aligned} $$

(37)

According to Eq. (37), the roof truss system has 8 random design variables whose statistical information is recorded in Table 5.

Table 5 The parameters of random design variables of the roof truss structure

Table 6 Results of the roof truss system with different methods and $\varepsilon_{r,system}^{given}$

Figure 7 gives the schematic diagram plot of the roof truss structure, in which two materials are utilized to fabricate the roof truss. In detail, the bottom chords and the tension bars are made up of steel. The material of the top chords and the compression bars is reinforced concrete. The normally distributed load q on the top of the roof truss could be transformed into the nodal forces applied to $D,C,F$ where $P = {{ql} \mathord{\left/ {\vphantom {{ql} 4}} \right. \kern-\nulldelimiterspace} 4}$.

Fig. 7

The schematic diagram plot of the roof truss structure

Combining Eq. (37), Table 5, and Fig. 7, the first CLSF monitors the reliability performance of the displacement of node $C$. To be specific, it is regarded as failure when the displacement of node $C$ exceeds 0.03. As for $g_{2}$ and $g_{3}$, they consider the strength performance of the roof truss. Specifically, the $g_{2}$ concerns the internal force of the $AD$ bar, where its value $1.185ql$ could not exceed its ultimate stress $f_{c} A_{c}$. If the internal force of $EC$ bar $0.75ql$ is larger than the ultimate stress $f_{s} A_{s}$, it triggers the failure mode of $g_{3}$. The comparison results with state-of-the-art methods under different $\varepsilon_{r,system}^{given}$ are provided in Table 5.

As listed in Table 5, the EEK-SYS and SBSC+SRU methods could reach the same accuracy level as the AK-SYS and AK-SYSi methods, whereas the $N_{call} (G)$ of EEK-SYS and SBSC+SRU methods reduce more 43.40 samples such as in the case of $\varepsilon_{r,system}^{given} = 0.01$. It indicates the performance advantages of the error-guided approaches are more significant in the case with higher complexity. The AK-SYS method spends 38.98 samples to refine $g_{1}$, while for other approaches almost no new samples are consumed. Moreover, the $N_{call} (g_{2} )$ and $N_{call} (g_{3} )$ also significantly more than other listed approaches, which shows the effectiveness of the traditional learning function encountered problems with complex issues. The AK-SYSi method could save $N_{call} (g_{1} )$ and $N_{call} (g_{3} )$, but its $N_{call} (g_{2} )$ is comparable with that of the AK-SYS method. The EEK-SYS and SBSC+SRU method could overcome this shortage because about half of $N_{call} (g_{2} )$ is eliminated. In comparison with EEK-SYS and SBSC+SRU methods, the observations are the same as other tested cases, those are the $\varepsilon_{r,system}^{given}$ could strictly control the adaptive updating process to halt under the designer’s willingness. Meanwhile, better accuracy means more computational burden. The SBSC+SRU method reduces about 7 sample consumption compared with the EEK-SYS method under the same $\varepsilon_{r,system}^{given}$, which confirms the superiority of the proposed method.

4.4 Engineering application: system reliability analysis of cylindrical shell with variable ribs

In this section, the SRA of an underwater cylindrical shell with variable ribs whose structural profile is shown in Fig. 8 is investigated to demonstrate the applicability of the SBSC+SRU method in realistic cases.

Fig. 8

The structural diagram plot of the stiffened cylindrical shell with variable ribs

The reliability performance of the stiffened cylindrical shell with variable ribs is controlled by five CLSFs considering strength and stability requirements. All CLSFs are expressed as

$$ \begin{aligned} g_{1} ({x}) = 1 - \frac{{\sigma_{1} }}{{k_{1} \sigma_{s} }},g_{2} ({x}) = 1 - \frac{{\sigma_{2} }}{{k_{2} \sigma_{s} }},g_{3} ({x}) = 1 - \frac{{\sigma_{3} }}{{k_{3} \sigma_{s} }} \hfill \\ g_{4} ({x}) = \frac{{P_{cr1} }}{{k_{4} P_{c} }} - 1,g_{5} ({x}) = \frac{{P_{cr2} }}{{k_{5} P_{c} }} - 1 \hfill \\ \end{aligned} $$

(38)

where $g_{1}$, $g_{2}$, and $g_{3}$ are the CLSFs to control the failure modes of strength, in which $\sigma_{1} \sim \sigma_{3}$ are the mid-span midplane stress of the shell, longitudinal stress on the inner surface at the rib, and rib stress respectively; $P_{cr1}$ and $P_{cr2}$ in $g_{4}$ and $g_{5}$ are the local and global buckling pressures respectively to evaluate the stability performance of the cylindrical shell. Besides, $\sigma_{s} = 650{\text{MPa}}$ and $P_{c} = 3.6{\text{MPa}}$ are the yield limit of material and computational pressure respectively. $k_{1} \sim k_{5}$ are factors to control allowable stress and critical pressure whose values are 0.85, 1.10, 0.60, 1.00, and 1.20 according to the engineering experience Jiang et al. (2016) (Table 6). The information of design variables is listed in Table 7 and the fixed parameters are recorded in Table 8.

Table 7 Design parameters of cylindrical shell with variable ribs

Table 8 Fixed parameter values of cylindrical shell with variable ribs

The values of $\sigma_{1} ,\sigma_{2} ,\sigma_{f} ,P_{cr2}$ (Note that $P_{cr1}$ could be determined by the classic formula, which is effortless (Zhou et al. 2019)) are determined by the time-consuming simulation processes via ANSYS 18.2. in which the mesh grids for strength and stability analyses are more than 200,000 and 30,000 respectively. 4 × 10 initial samples are used to construct the initial Kriging models for the time-consuming CLSFs, then they will be refined via different strategies. Results of the cylindrical shell with variable ribs compared with different approaches are provided in Table 8.

As summarized in Table 9, 145 and 203 samples are costed for the AK-SYS and AK-SYSi methods to get accurate estimations with $\varepsilon_{r,system}^{{}} = 0.006$. Most of the new samples are supplemented to $g_{1}$ and $g_{5}$, and no new samples are allocated to $g_{2}$. To figure out the reason, the failure probability of failure mode governed by $g_{2}$ is calculated via MCS, results show that no failure will be caused by $g_{2}$. The Kriging model of $g_{2}$ of SBSC+SRU method is not updated under all $\varepsilon_{r,system}^{given}$, which shows the effectiveness of the learning function SRU when dealing with real problems. In terms of the estimated accuracies of the two error-guided approaches, they both get good estimations whose $\varepsilon_{r,system}^{{}} \le \varepsilon_{r,system}^{given}$. However, the advantages on the computational burden of the SBSC+SRU method compared with the EEK-SYS method is more remarkable with stricter stopping condition. For instance, 7, 11, 42, 55, and 75 samples could be reduced in the cases of $\varepsilon_{r,system}^{given} = \left[ {0.05,0.04,0.03,0.02,0.01} \right]$ compared with EEK-SYS method. More specifically, in the case of $\varepsilon_{r,system}^{given} = 0.05$, the samples of the EEK-SYS and SBSC+SRU methods are 53 and 46 respectively, the computational reduction is about 13.2%. In the case of $\varepsilon_{r,system}^{given} = 0.01$, the samples of EEK-SYS method is 134 that is double more than that of SBSC+SRU method. Results confirm that the proposed method has incredible potential to solve complicated engineering SRA problems.

Table 9 Results of the cylindrical shell with variable ribs with different methods and $\varepsilon_{r,system}^{given}$

The proposed SBSC+SRU method shows excellent performance among the listed cases, while it still has some limitations. Many reported publications had indicated that the Kriging model will lose its merits when handling high-dimensional problems(Bhosekar and Ierapetritou 2018; Fuhg et al. 2020; Teixeira et al. 2021; Zhan and Xing 2020) because of the “curse of dimensionality”. The SBSC+SRU method has to construct multiple Kriging models simultaneously, in this case, the computational cost for constructing Kriging models and predicting responses could not be neglected, and even becomes costly. Besides, the effectiveness of the SBSC+SRU method will decrease when the number of components is large. Because the derivation of the maximum estimated relative error is based on the product of probabilities of wrong sign prediction whose values are range from zero to one. In this case, the values of system probability of wrong sign prediction of all samples will be extremely small, and even difficult to distinguish contributions of two samples.

5 Conclusions

This paper discusses how to solve system reliability analysis problems efficiently through the adaptive kriging-based system reliability analysis approach, in which multiple kriging models have to be updated collaboratively. To further improve the efficiency of state-of-the-art methods, the presented SBSC+SRU method introduces novel strategies to overcome the bottleneck of choosing new samples and termination of the adaptive updating process. Specifically, the new learning function SRU is based on learning function RLCB for component reliability analysis, then many factors that may hurt the effectiveness of SRA including magnitudes of CLSFs, initial uncertainties of Kriging models, and system types are integrated properly in the proposed method. As a result, the proposed SRU could locate the new sample and corresponding component index for updating automatically and objectively. The stopping criterion focuses on highly uncertain samples in the MCS population firstly, then derivates a sound estimated maximum relative error by quantifying the probability of wrong sign prediction governed by multiple CLSFs and the bootstrap estimation.

Results of three numerical examples with different system types and one engineering case demonstrate the effectiveness and efficiency of the proposed approach compared with recently reported methods. Firstly, the SBSC+SRU method could converge to the preset stopping threshold with regard to both series and parallel systems. Moreover, with stricter stopping thresholds, the estimated accuracy improves, but more computational burdens are required. Secondly, during the adaptive updating process, the proposed approach could refine the Kriging model on purpose, that is to say, the SBSC+SRU method could allocate computational burden for different CLSFs via evaluating their contributions to the system automatically. Finally, the superiority of the SBSC+SRU method is more significant when dealing with complex problems.

The presented SBSC+SRU method is promising in low-dimensional structural systems, however, with the complexity of structural systems rising, the dimension of system reliability analysis problems also increases. As for the high-dimensional component/system reliability analysis problems, it remains a challenge for this research domain, more attention could be focused on high-dimension problems.