A novel single-loop meta-model importance sampling with adaptive Kriging for time-dependent failure probability function

Abstract

To learn the effect of interested distribution parameter, also the design variable of random input vector, on time-dependent failure probability, and to decouple time-dependent reliability-based design optimization (T-RBDO), estimating time-dependent failure probability function (T-FPF), a relation of time-dependent failure probability varying with the distribution parameter in interested design region, is necessary. However, estimating T-FPF is time-consuming and a challenge at present. Thus, this paper proposes a novel single-loop meta-model importance sampling with adaptive Kriging model (SL-Meta-IS-AK) to estimate T-FPF efficiently. In SL-Meta-IS-AK, for estimating the T-FPF by single-loop simulation, an optimal importance sampling probability density function (IS-PDF), which can envelope the interested distribution parameter region and be free of the distribution parameter, is constructed by an integral operation. After the Kriging model is adaptively constructed for time-dependent performance function to approach optimal IS-PDF for T-FPF by quasi-optimal one, a simple sampling strategy is designed to extract the samples of quasi-optimal IS-PDF, and a time-dependent misclassification probability function is derived to update the Kriging model adaptively until it can accurately recognize the states of all extracted samples, on which the T-FPF at the whole interested distribution parameter region can be estimated as a byproduct. Due to the single-loop simulation aided by the IS-PDF covering the interested distribution parameter region but free of the distribution parameter, the efficiency of estimating T-FPF is improved by the proposed SL-Meta-IS-AK, which is verified by presented numerical and aviation engineering examples including a wing structure and a turbine shaft structure.

1 Introduction

Under universal uncertainty environment in engineering application, the safety degree of structure should be quantified by reliability and failure probability, in order to improve the performance of structure under ensuring the reliability of structure. The reliability-based design optimization (RBDO) (Chaudhuri et al. 2020; Cheng et al. 2021; Gasser and Schuëller 1997; Enevoldsen and Sørensen 1994) is proposed to replace the traditional deterministic design optimization in past decades. In RBDO, reliability constraint analysis is coupled in design variable optimization, and the design variable, which is varying in the designable region determined by manufacturing capability, or assembly limitation, etc., is generally the interested distribution parameter of the random input vector. Due to the coupling of the interested distribution parameter, i.e., the design variable, parameter optimization and reliability constraint evaluation in RBDO, solving RBDO is more time-consuming than solving the traditional deterministic optimization. To reduce the computational cost of solving RBDO, researchers developed lots of decoupling methods, among which estimating the failure probability function (FPF), a relation of failure probability varying with the interested distribution parameter ${\varvec{\theta}}$ in the interested design region $[{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$, in advance of solving RBDO is a direct decoupling method. In fact, estimating FPF not only helps to simplify the solution of RBDO (Yuan 2013; Ling et al. 2020; Yuan 2020), but also provides the effect of the interested distribution parameter on structure failure probability; therefore, it is worth studying. Actually, due to the working environment, the applied load, the material properties and the structural geometries affected by fatigue and corrosion during the service, etc. are time dependent; time-dependent reliability is more universal than the time-independent one. Thus, in order to decouple the design variable optimization and time-dependent reliability constraint evaluation in the time-dependent RBDO (T-RBDO) (Jiang et al. 2017; Yu and Wang 2019; Shi et al. 2020) for reducing the computational complexity of solving T-RBDO, and to learn about the effect of the interested distribution parameter on the time-dependent failure probability, it should study efficient algorithm for estimating the time-dependent FPF (T-FPF). Because T-FPF is more difficult to be estimated than time-independent FPF, and there lacks efficient estimation, this paper focuses on the algorithm of efficiently estimating T-FPF.

At present, several methods are developed to solve the time-independent FPF, among which the most direct method is double-loop Monte Carlo simulation (DLMCS). In DLMCS, the time-independent FPF is obtained by interpolating the pairs of distribution parameter and corresponding failure probability estimated by MCS one by one. Obviously, the computational cost of DLMCS is unaffordable for engineering application with time-demanding performance function. In order to reduce the computational cost of estimating FPF by DLMCS, Gasser and Schuëller (1997) proposed to use quadratic function to approximate the logarithmic FPF, and Jensen (2005) adopted a linear function to approximate the FPF. When estimating the failure probability at the interpolation point, efficiently adaptive Kriging model methods can be used; for example, a moving-zone renewal strategy-based adaptive Kriging combined with truncated importance sampling method proposed by Zhang et al. (2022a) can be used to estimate the failure probability, and an active Kriging model combined with reducing candidate sample pool and adaptive importance sampling method (Zhang et al. 2023) can also be employed to estimate the failure probability. It should be noted that these methods of estimating FPF need select a fixed interpolation function form; thus, the flexibility of these interpolation-based methods is limited. Au (2005) proposed a single-loop method to estimate the FPF based on Bayes inference. In this method, the FPF is transformed into the ratio of the product of augmented failure probability and conditional probability density function (PDF) of distribution parameter on failure domain to an assigned prior PDF of distribution parameters. Based on the sample information produced in estimating the augmented failure probability, the conditional PDF of distribution parameter in the method of Au (2005) can be obtained by use of histogram (Au 2005) or maximum entropy principle (Ching and Hsieh 2007). Thus, the Bayes inference-based method for estimating FPF only needs one reliability analysis for estimating the augmented failure probability. It should be noted that the Bayes inference-based method needs failure sample information for estimating the required conditional PDF of distribution parameter; thus, it should use numerical simulation to estimate the augmented failure probability and produce failure sample to fit the conditional PDF of distribution parameter. In order to improve the efficiency of estimating the augmented failure probability by numerical simulation and finally improve the efficiency of estimating FPF, Ling et al. (2020) combined adaptive Kriging model with MCS to estimate the augmented failure probability and to obtain the FPF finally. Yuan (2013) proposed some weighted methods to rewrite the failure probability and then effectively estimate FPF, and Yuan et al. (2020) also proposed an augmented space integral method to obtain the FPF. Li et al. (2020) proposed an estimation method to solve FPF based on Bayes theorem and copula. Dang et al. (2021) proposed an active learning-augmented probabilistic integration.

The above studies are mainly concerning the time-independent FPF. Comparing with estimating the time-independent FPF, estimating the T-FPF is more time-consuming due to the time factor increases the computational cost. Similar to the time-independent FPF, T-FPF is defined as the relation of the time-dependent failure probability varying with the distribution parameter in the interested region. Several methods are developed to solve the time-dependent reliability analysis, such as single-loop Kriging model (Hu and Mahadevan 2016), equivalent stochastic process transformation method (Wang and Chen 2016), the nested extreme value response surface method (Wang and Wang 2015), the active extremum Kriging-based multi-level linkage method (Zhang et al. 2022b), etc. However, there are few methods to study T-FPF. It is inefficient to use the double-loop strategy directly with the existing time-dependent reliability analysis methods to estimate T-FPF. To improve the efficiency of estimating T-FPF, based on Bayes inference similarly used in estimating time-independent FPF, Feng et al. (2019) proposed an adaptive Kriging model combined with conditional PDF fitting method (AK-MCS-Bay) to estimate the T-FPF. However, the common conditional PDF fitting methods required by AK-MCS-Bay generally have the defects of low precision at the edges of the interested distribution parameter region. Moreover, the PDF fitting precision decreases as the dimensionality increasing of the distribution parameter, which results this kind method to be difficultly applied to the case of multidimensional distribution parameter. The other disadvantage of existing AK-MCS-Bay is that the direct MCS based on the PDF of random input vector is used to analyze the augmented time-dependent failure probability. Since AK-MCS-Bay is based on the joint PDF in the augmented space spanned by the random input and the interested distribution parameter, the sampling efficiency is low and a large size of candidate sample pool is required to get a convergent estimation of augmented time-dependent failure probability, which sequentially affects the efficiency of estimating T-FPF.

In order to improve the computational efficiency of solving T-FPF, a novel single-loop meta-model importance sampling combined with adaptive Kriging (SL-Meta-IS-AK) method is proposed in this paper. In SL-Meta-IS-AK, the theoretical optimal importance sampling PDF (IS-PDF) is used to replace the joint PDF in AK-MCS-Bay, which improves the efficiency of estimating T-FPF due to the variance reduction resulted by the importance sampling. For extracting the samples of IS-PDF, an adaptive Kriging model of the time-dependent performance function is constructed for approaching the optimal IS-PDF by the quasi-optimal one, and a simple sampling strategy can be employed to extract the samples of the quasi-optimal IS-PDF by designing an acceptance domain. In this step of SL-Meta-IS-AK, the main novelty is constructing the quasi-optimal IS-PDF, and it is free of the distribution parameter but enveloping the whole interested region of the distribution parameter. It is even more important to emphasize that the introduced quasi-optimal IS-PDF in this paper improves the sampling efficiency and avoids the PDF fitting required by AK-MCS-Bay. This novelty of SL-Meta-IS-AK makes it applicable to arbitrary dimensionality and region size of the distribution parameter. After the samples of the quasi-optimal IS-PDF are extracted, a misclassification probability function is derived to adaptively update the Kriging model to converge, on which it can complete the T-FPF estimation at any realization of the distribution parameter by same group sample of the quasi-optimal IS PDF.

The main contributions of this work can be summarized as follows:

• ① By constructing an approximate optimal importance sampling probability density function (IS-PDF), this paper proposes an importance sampling strategy combining with adaptive Kriging model to reduce the estimation variance of the time-dependent failure probability function (T-FPF).

• ② By introducing an integral operation with respect to the concerned distribution parameter in the interested region, the IS-PDF, which is free of the distribution parameter and envelopes the whole interested region of the distribution parameter, is constructed to efficiently estimate the T-FPF in the proposed SL-Meta-IS-AK.

• ③ Due to the property of the IS-PDF being free of the distribution parameter and enveloping the whole interested range, the information of the same group sample of the IS-PDF can be shared to simultaneously estimate the T-FPF at arbitrary distribution parameter realization in the whole interested region.

• ④ By introducing the Kriging model of time-dependent performance function and designing a simple sampling strategy, the difficulty of efficiently extracting the sample of the constructed IS-PDF is solved in the proposed SL-Meta-IS-AK.

The rest of the paper is organized as follows. Section 2 introduces the definition of T-FPF. Section 3 gives the basic theory and the detailed implementation steps of the proposed SL-Meta-IS-AK method. Section 4 provides several examples to verify the effectiveness of the SL-Meta-IS-AK, and Sect. 5 gives the conclusion.

2 Definition of the T-FPF

For a general time-dependent performance function $g_{{{\varvec{\alpha}}{ - }{\varvec{\beta}}{ - }t}} ({\varvec{\alpha}},{\varvec{\beta}}(t),t)$ including random variable vector ${\varvec{\alpha}}$, stochastic process vector ${\varvec{\beta}}(t)$ and time $t$, the spectral representation method (Li and Der Kiureghian 1993; Zhang and Ellingwood 1994; Huang et al. 2001) is usually used to transform ${\varvec{\beta}}(t)$ into a series of independent random variables and time. In this paper, the expansion optimal linear estimation (EOLE) (Li and Der Kiureghian 1993) is used to transform ${\varvec{\beta}}(t)$ by Eq. (1),

$$\hat{\beta }(t) = \mu_{\beta } (t) + \sigma_{\beta } (t)\sum\limits_{k}^{r} {\frac{{\xi_{k} }}{{\sqrt {\lambda_{k} } }}{\varvec{\phi}}_{k}^{T} {\varvec{\rho}}_{{t,t_{k} }} (t)}$$

(1)

where $r$ is the number of eigenvalues used to represent the stochastic process. $\lambda_{k}$ and ${\varvec{\phi}}_{k} (k = 1,2, \cdots ,r)$ are the eigenvalues and eigenvectors of the correlation matrix of $\beta (t)$, respectively. $\xi_{k} (k = 1,2, \cdots ,r)$ are independent standard normal random variables. $\mu_{\beta } (t)$ and $\sigma_{\beta } (t)$ are the mean function and the standard deviation function of the stochastic process, respectively. ${\varvec{\rho}}_{{t,t_{k} }} (t) = \{ \rho (t,t_{0} ),\rho (t,t_{1} ), \cdots ,\rho (t,t_{p} )\}^{T}$ is the correlation coefficient vector, and $p$ is the number of the time realizations.

After the transformation of Eq. (1), the time-dependent performance function $g_{{{\varvec{\alpha}}{ - }{\varvec{\beta}}{ - }t}} ({\varvec{\alpha}},{\varvec{\beta}}(t),t)$ including stochastic process can be transformed into $g({\varvec{\alpha}},{\varvec{\xi}},t) = g({\varvec{X}},t)$ without stochastic process, where ${\varvec{X}} = [{\varvec{\alpha}},{\varvec{\xi}}]^{T}$. According to the transformed time-dependent performance function $g({\varvec{X}},t)$ with n-dimension random input vector ${\varvec{X}} = (X_{1} ,X_{2} ,,X_{n} )^{T}$, the time-dependent failure probability $P_{ft}$ within the interested time interval $[t_{0} ,t_{e} ]$ can be given as follows:

$$\begin{gathered} P_{ft} = {\text{P}}\{ g({\varvec{x}},t) \le 0,\exists t \in [t_{0} ,t_{e} ]\} = {\text{P}}\{ F_{{t \in [t_{0} ,t_{e} ]}} \} = \int_{{F_{{t \in [t_{0} ,t_{e} ]}} }} {f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}})d{\varvec{x}}} \\ = \int {I_{{F_{t} }} ({\varvec{x}})f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}})d{\varvec{x}}} \\ \end{gathered}$$

(2)

where $F_{{t \in [t_{0} ,t_{e} ]}} = \{ {\varvec{x}}|g({\varvec{x}},t) \le 0,\exists t \in [t_{0} ,t_{e} ]\}$ represents the time-dependent failure domain; $I_{{F_{t} }} ({\varvec{x}}) = \left\{ \begin{gathered} 0,\forall t \in [t_{0} ,t_{e} ] \, g({\varvec{x}},t) > 0 \hfill \\ 1,\exists t \in [t_{0} ,t_{e} ] \, g({\varvec{x}},t) \le 0 \hfill \\ \end{gathered} \right.$ is the indicator function of time-dependent failure domain $F_{{t \in [t_{0} ,t_{e} ]}}$. ${\text{P}}\{ \cdot \}$ is the probability operator. $f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}})$ is the joint PDF of the random input vector at given ${\varvec{\theta}}$, and ${\varvec{\theta}} = (\theta_{1} ,\theta_{2} , \cdots ,\theta_{m} )^{T}$ is the concerned $m$-dimensional distribution parameter vector.

From Eq. (2), it can be observed that $P_{ft}$ varies with the distribution parameter vector ${\varvec{\theta}}$, and it is named as T-FPF and denoted by $P_{ft} ({\varvec{\theta}})$, i.e., $P_{ft} ({\varvec{\theta}}) = \int {I_{{F_{t} }} ({\varvec{x}})f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}})d{\varvec{x}}}$.

The basic idea of solving the T-FPF $P_{ft} ({\varvec{\theta}})$ by Monte Carlo simulation (MCS) is employing the double-loop MCS to estimate the time-dependent failure probability at each discrete point of ${\varvec{\theta}}$ one by one. The discrete points are generated by discretizing the distribution parameter vector ${\varvec{\theta}}$ in the interested region $[{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$ uniformly. The computational cost of the direct double-loop MCS is usually unaffordable for engineering application with time-consuming time-dependent performance function, especially for the small T-FPF at the interested distribution parameter region. Although it can improve the computational efficiency by replacing direct MCS with some advanced time-dependent reliability analysis methods, such as single-loop Kriging model (Hu and Mahadevan 2016), equivalent stochastic process transformation method (Wang and Chen 2016), the nested extreme value response surface method (Wang and Wang 2015), etc., to estimate the time-dependent failure probability at the realization ${\varvec{\theta}}_{i}$ of ${\varvec{\theta}} \in [{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$, it cannot change the property of double-loop analysis for T-FPF and may result the computational cost far away from the ideal state. To complete the T-FPF with the single-loop simulation and reduce the computational cost as much as possible, the following section proposes a method abbreviated as SL-Meta-IS-AK to efficiently estimate T-FPF, in which not only the double-loop simulation is replaced by the single-loop one, but also the importance sampling technique based on the meta-model is organized into the proposed method to improve the sampling efficiency and reduce the T-FPF estimation variance.

3 The SL-Meta-IS-AK for solving the T-FPF

The basic idea of SL-Meta-IS-AK is introducing an IS-PDF $h_{{\varvec{X}}} ({\varvec{x}})$ for estimating the T-FPF. By the introduced $h_{{\varvec{X}}} ({\varvec{x}})$, T-FPF can be rewritten in Eq. (3), and the value of T-FPF corresponding to arbitrary realization ${\varvec{\theta}}_{j} \in {\varvec{S}}_{{\varvec{\theta}}}$ can be simultaneously estimated by the $N$-size sample set ${\varvec{S}}_{{\varvec{x}}}^{h} = \{ {\varvec{x}}_{1}^{h} ,{\varvec{x}}_{2}^{h} , \cdots ,{\varvec{x}}_{N}^{h} \}^{T}$ of $h_{{\varvec{X}}} ({\varvec{x}})$ in Eq. (4).

$$P_{ft} ({\varvec{\theta}}) = \int {\frac{{I_{{F_{t} }} ({\varvec{x}})f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}})}}{{h_{{\varvec{X}}} ({\varvec{x}})}}h_{{\varvec{X}}} ({\varvec{x}})d{\varvec{x}}}$$

(3)

$$\hat{P}_{ft} ({\varvec{\theta}}_{j} ) = \frac{1}{N}\sum\limits_{i = 1}^{N} {\frac{{I_{{F_{t} }} ({\varvec{x}}_{i}^{h} )f_{{\varvec{X}}} ({\varvec{x}}_{i}^{h} |{\varvec{\theta}}_{j} )}}{{h_{{\varvec{X}}} ({\varvec{x}}_{i}^{h} )}}}$$

(4)

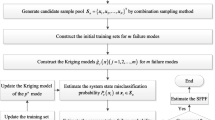
From Eq. (4), it can be observed that the introduced IS-PDF $h_{{\varvec{X}}} ({\varvec{x}})$ should satisfy the following requirements. Firstly, $h_{{\varvec{X}}} ({\varvec{x}})$ should be free of the distribution parameter but enveloping the interested region of the distribution, which is the basic condition that the proposed SL-Meta-IS-AK realizes the single-loop simulation of estimating T-FPF. Secondly, $h_{{\varvec{X}}} ({\varvec{x}})$ should be selected to reduce the variance of T-FPF estimation as much as possible. To satisfy these two requirements for improving the efficiency under acceptable precision, the proposed SL-Meta-IS-AK starts from the optimal IS-PDF $h_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}^{*} )$ for estimating the time-dependent failure probability $P_{ft} ({\varvec{\theta}}^{*} )$ at the realization ${\varvec{\theta}}^{*}$ of the distribution parameter; then, an integral operation for $h_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}^{*} )$ over the interested region $[{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$ is carried out to construct the IS-PDF $h_{{\varvec{X}}} ({\varvec{x}})$ for estimating T-FPF. Since the optimal IS-PDF $h_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}^{*} )$ concerns the time-dependent performance function, usually in an implicit state, and T-FPF also needs estimating $I_{{F_{t} }} ({\varvec{x}}_{i}^{h} )$ $(i = 1,2, \cdots ,N)$ in Eq. (4) for finally estimating T-FPF, the meta-model is used to help dealing with the computational cost resulted from implicit time-dependent performance function. The concept schematic flow chart of the proposed SL-Meta-IS-AK method is shown in Fig. 1.

Fig. 1

Concept schematic flow chart of SL-Meta-IS-AK

3.1 Strategy for constructing IS-PDF for T-FPF

The optimal IS-PDF $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ for T-FPF can be constructed by the integration shown in Eq. (5) over the interested region $[{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$ of distribution parameter ${\varvec{\theta}}$,

$$h_{X}^{{opt}} (\varvec{x}) = \int {h_{X}^{{opt}} (\varvec{x}|\varvec{\theta })\varphi _{{\mathbf{\Theta }}} (\varvec{\theta })d\varvec{\theta }} ,$$

(5)

where $\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})$ is the assigned PDF of the distribution parameter ${\varvec{\theta}}$ over $[{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$ and $\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})$ is usually selected as uniform distribution in $[{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$. ${h_{X}^{{opt}} (\varvec{x}|\varvec{\theta })}$ is the optimal IS-PDF for estimating time-dependent failure probability at distribution parameter realization ${\varvec{\theta}}$.

Theoretically, it is well known that optimal IS-PDF ${h_{X}^{{opt}} (\varvec{x}|\varvec{\theta })}$, which can minimize the variance of the estimated time-dependent failure probability $\hat{P}_{ft} ({\varvec{\theta}})$ at ${\varvec{\theta}}$, can be derived by Eq. (6) (Dubourg et al. 2013).

$$h_{X}^{opt} (\varvec{x}|\varvec{\theta }) = \frac{{I_{{F_{t} }} (\varvec{x})f_{X} (\varvec{x}|\varvec{\theta })}}{{P_{ft} (\varvec{\theta })}}.$$

(6)

Since time-dependent failure probability $P_{ft} ({\varvec{\theta}})$ at ${\varvec{\theta}}$ is unknown and $I_{{F_{t} }} ({\varvec{x}})$ is generally related to the implicit time-dependent performance function $g({\varvec{x}},t)$. It is difficult to obtain $h_{{\varvec{X}}}^{opt} (\varvec{x|\theta })$ analytically and generate the sample of $h_{{\varvec{X}}}^{opt} (\varvec{x|\theta })$ in Eq. (6). In order to solve the difficulty of sampling $h_{{\varvec{X}}}^{opt} (\varvec{x|\theta })$ and further sampling $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ in Eq. (5), the Kriging model $g_{K} ({\varvec{x}},t)$ is established for the time-dependent performance function $g({\varvec{x}},t)$, on which a quasi-optimal IS-PDF $h_{{\varvec{X}}} (\varvec{x|\theta })$ shown in Eq. (7) can be constructed to replace $h_{{\varvec{X}}}^{opt} (\varvec{x|\theta })$ at distribution parameter realization ${\varvec{\theta}}$.

$$h_{{\varvec{X}}} (\varvec{x|\theta }) = \frac{{\pi_{{F_{t} }} (\varvec{x|\theta })f_{{\varvec{X}}} (\varvec{x|\theta })}}{{\hat{P}_{ft} ({\varvec{\theta}})}}$$

(7)

where $\pi_{{F_{t} }} (\varvec{x|\theta })$ is the probability classification function of time-dependent failure domain determined by $g_{K} ({\varvec{x}},t)$, and it is shown in Eq. (8). $\hat{P}_{ft} ({\varvec{\theta}})$ is named as an extended time-dependent failure probability at ${\varvec{\theta}}$ for normalization shown in Eq. (9).

$$\pi _{{F_{t} }} (\varvec{x|\theta }) = {\text{P}}\left\{ {\mathop {{\text{min}}}\limits_{{t \in \varvec{S}_{t} }} g_{K} (\varvec{x},t) \le 0} \right\}$$

(8)

$$\hat{P}_{ft} ({\varvec{\theta}}) = \int {\pi_{{F_{t} }} (\varvec{x|\theta })f_{{\varvec{X}}} (\varvec{x|\theta })d{\varvec{x}}}$$

(9)

By substituting $h_{{\varvec{X}}} (\varvec{x|\theta })$ in Eq. (7) to replace $h_{{\varvec{X}}}^{opt} (\varvec{x|\theta })$ into Eq. (5), the quasi-optimal IS-PDF denoted as $h_{{\varvec{X}}} ({\varvec{x}})$ for estimating T-FPF can be expressed in Eq. (10).

$$h_{{\varvec{X}}} ({\varvec{x}}) = \int {\frac{{\pi_{{F_{t} }} (\varvec{x|\theta })f_{{\varvec{X}}} (\varvec{x|\theta })}}{{\hat{P}_{ft} ({\varvec{\theta}})}}\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})d{\varvec{\theta}}}$$

(10)

After the quasi-optimal IS-PDF $h_{{\varvec{X}}} ({\varvec{x}})$ is obtained by Eq. (10), the following work is how to adaptively update $g_{K} ({\varvec{x}},t)$ for approaching $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ by $h_{{\varvec{X}}} ({\varvec{x}})$ and extracting sample of $h_{{\varvec{X}}} ({\varvec{x}})$ as well as how to use the samples of $h_{{\varvec{X}}} ({\varvec{x}})$ to finally complete T-FPF estimation, and these two following works are illustrated, respectively, in Subsects. 3.2 and 3.3.

3.2 Strategy of updating $g_{K} ({\varvec{x}},t)$ for approaching $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ by $h_{{\varvec{X}}} ({\varvec{x}})$ and extracting samples of $h_{{\varvec{X}}} ({\varvec{x}})$

In this subsection, an initial Kriging model $g_{K} ({\varvec{x}},t)$ is firstly constructed for $g({\varvec{x}},t)$ to obtain the quasi-optimal IS-PDF $h_{{\varvec{X}}} ({\varvec{x}})$ and extract the sample of $h_{{\varvec{X}}} ({\varvec{x}})$. Since the initial $g_{K} ({\varvec{x}},t)$ may not represent $g({\varvec{x}},t)$ well to approach $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ by $h_{{\varvec{X}}} ({\varvec{x}})$, it is necessary to adaptively update $g_{K} ({\varvec{x}},t)$ to get the aim of approximating $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ with $h_{{\varvec{X}}} ({\varvec{x}})$ as accurately as possible. Thus, the following parts illustrate the strategy of extracting sample of $h_{{\varvec{X}}} ({\varvec{x}})$ based on $g_{K} ({\varvec{x}},t)$ and that of adaptively updating $g_{K} ({\varvec{x}},t)$. About the basic theory of Kriging (Echard et al. 2011), it is given in Appendix 1.

3.2.1 Strategy of constructing initial $g_{K} ({\varvec{x}},t)$ for $g({\varvec{x}},t)$ and the numerical solution of $h_{{\varvec{X}}} ({\varvec{x}})$

To obtain the quasi-optimal IS-PDF $h_{{\varvec{X}}} ({\varvec{x}})$ for estimating T-FPF, the initial $g_{K} ({\varvec{x}},t)$ should be constructed for the time-dependent performance function $g({\varvec{x}},t)$. For ensuring the initial $g_{K} ({\varvec{x}},t)$ representing $g({\varvec{x}},t)$ over ${\varvec{\theta}} \in [{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$ and $t \in [t_{0} ,t_{e} ]$, an $N_{{\varvec{T}}}$-size initial training set ${\varvec{S}}_{{\varvec{x}}}^{{\varvec{T}}} = \{ {\varvec{x}}_{1}^{{\varvec{T}}} ,{\varvec{x}}_{2}^{{\varvec{T}}} , \cdots ,{\varvec{x}}_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} \}^{T}$ of the random input vector ${\varvec{X}}$ is randomly generated by $f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}})$ with ${\varvec{\theta}} \in [{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$, i.e., ${\varvec{x}}_{i}^{{\varvec{T}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\varvec{T}}}$ is generated from the PDF $\int {f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}})\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})d{\varvec{\theta}}}$, where $\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})$ is usually an assigned PDF of ${\varvec{\theta}} \in [{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$, and $\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})$ is taken as uniform distribution over the interested region $[{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$. About the $N_{{\varvec{T}}}$-size initial training set ${\varvec{S}}_{t}^{{\varvec{T}}} = \{ t_{1}^{{\varvec{T}}} ,t_{2}^{{\varvec{T}}} , \cdots ,t_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} \}^{T}$ of the time variable $t$, $t_{i}^{{\varvec{T}}} \in {\varvec{S}}_{t}^{{\varvec{T}}}$ is uniformly generated in the interested time interval $[t_{0} ,t_{e} ]$. By evaluating $g({\varvec{x}}_{i}^{{\varvec{T}}} ,t_{i}^{{\varvec{T}}} )$, the initial training set ${\varvec{T}}$ can be formed as follows:

$${\varvec{T}} = \left\{ {\left( {({\varvec{x}}_{1}^{{\varvec{T}}} ,t_{1}^{{\varvec{T}}} ),g({\varvec{x}}_{1}^{{\varvec{T}}} ,t_{1}^{{\varvec{T}}} )} \right),\left( {({\varvec{x}}_{2}^{{\varvec{T}}} ,t_{2}^{{\varvec{T}}} ),g({\varvec{x}}_{2}^{{\varvec{T}}} ,t_{2}^{{\varvec{T}}} )} \right), \cdots ,\left( {({\varvec{x}}_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} ,t_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} ),g({\varvec{x}}_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} ,t_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} )} \right)} \right\}^{T}$$

(11)

By the training set ${\varvec{T}}$, the Kriging model $g_{K} ({\varvec{x}},t)$ of $g({\varvec{x}},t)$ can be established, and $g_{K} ({\varvec{x}},t)$ follows Gaussian distribution with prediction mean $\mu_{{g_{K} }} ({\varvec{x}},t)$ and prediction variance $\sigma_{{g_{K} }}^{2} ({\varvec{x}},t)$, i.e.,

$$g_{K} ({\varvec{x}},t)\sim N(\mu_{{g_{K} }} ({\varvec{x}},t),\sigma_{{g_{K} }}^{2} ({\varvec{x}},t))$$

(12)

Based on $g_{K} ({\varvec{x}},t)$, the numerical simulation solution of $h_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$(${\varvec{\theta}}_{k} \in {\varvec{S}}_{{\varvec{\theta}}}$) and $h_{{\varvec{X}}} ({\varvec{x}})$ can be given by $\hat{h}_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$ and $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$, respectively, as follows:

$$\hat{h}_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{k} ) = \frac{{\pi_{{F_{t} }} ({\varvec{x}}|{\varvec{\theta}}_{k} )f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{k} )}}{{\hat{P}_{ft} ({\varvec{\theta}}_{k} )}}$$

(13)

$$\hat{h}_{{\varvec{X}}} ({\varvec{x}}) = \frac{1}{{N_{{\varvec{\theta}}} }}\sum\limits_{k = 1}^{{N_{{\varvec{\theta}}} }} {\hat{h}_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{k} )} = \frac{1}{{N_{{\varvec{\theta}}} }}\sum\limits_{k = 1}^{{N_{{\varvec{\theta}}} }} {\frac{{\pi_{{F_{t} }} ({\varvec{x}}|{\varvec{\theta}}_{k} )f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{k} )}}{{\hat{P}_{ft} ({\varvec{\theta}}_{k} )}}}$$

(14)

where $N_{{\varvec{\theta}}}$ is the size of the sample ${\varvec{\theta}}_{k} (k = 1,2, \cdots ,N_{{\varvec{\theta}}} )$ extracted from $\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})$. $\hat{P}_{ft} ({\varvec{\theta}}_{k} )$ is the estimation of the extended time-dependent failure probability at ${\varvec{\theta}}_{k}$ based on the current $g_{K} ({\varvec{x}},t)$, and it can be estimated as follows,

$$\hat{P}_{ft} ({\varvec{\theta}}_{k} ) = \frac{1}{{N_{\varepsilon } }}\sum\limits_{i = 1}^{{N_{\varepsilon } }} {\pi_{{F_{t} }} ({\varvec{x}}_{i}^{f} \varvec{|\theta }_{k} )}$$

(15)

where ${\varvec{x}}_{i}^{f} \varvec{|\theta }_{k}$ is the $i$-th element of ${\varvec{S}}_{{\varvec{x}}}^{{f|{\varvec{\theta}}_{k} }} = \{ {\varvec{x}}_{1}^{f} |{\varvec{\theta}}_{k} ,{\varvec{x}}_{2}^{f} |{\varvec{\theta}}_{k} , \cdots ,{\varvec{x}}_{{N_{\varepsilon } }}^{f} |{\varvec{\theta}}_{k} \}^{T}$, an $N_{\varepsilon }$-size candidate sample set extracted from $f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{k} )$.

Since $g_{K} ({\varvec{x}},t)$ follows Gaussian distribution with prediction mean $\mu_{{g_{K} }} ({\varvec{x}},t)$ and prediction variance $\sigma_{{g_{K} }}^{2} ({\varvec{x}},t)$, $\pi_{{F_{t} }} ({\varvec{x}}_{i}^{f} \varvec{|\theta }_{k} ) = {\text{P}}\{ \mathop {\min }\limits_{t} g_{K} ({\varvec{x}}_{i}^{f} \varvec{|\theta }_{k} ,t) \le 0\}$ can be approximately estimated by Eq. (16).

$$\pi_{{F_{t} }} ({\varvec{x}}_{i}^{f} \varvec{|\theta }_{k} ) = \Phi \left( { - \frac{{\mu_{{g_{K} }} ({\varvec{x}}_{i}^{f} \varvec{|\theta }_{k} ,t_{i}^{f} \varvec{|\theta }_{k} )}}{{\sigma_{{g_{K} }} ({\varvec{x}}_{i}^{f} \varvec{|\theta }_{k} ,t_{i}^{f} \varvec{|\theta }_{k} )}}} \right)$$

(16)

where $t_{i}^{f} \varvec{|\theta }_{k}$ is approximated by $t_{i}^{f} \varvec{|\theta }_{k} = \arg \mathop {\min }\limits_{{t \in {\varvec{S}}_{t} }} \mu_{{g_{K} }} ({\varvec{x}}_{i}^{f} \varvec{|\theta }_{k} ,t)$, and ${\varvec{S}}_{t} = \{ t_{1} ,t_{2} , \cdots ,t_{{N_{t} }} \}$ is an $N_{t}$-size candidate sample set extracted from the interested interval $[t_{0} ,t_{e} ]$ of $t$. $\Phi ( \cdot )$ is the cumulative distribution function (CDF) of a standard normal distribution.

3.2.2 Extracting samples of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ and $\hat{h}_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$ based on the current $g_{K} ({\varvec{x}},t)$

Based on the current Kriging model $g_{K} ({\varvec{x}},t)$ of $g({\varvec{x}},t)$, an acceptance domain $\Omega$ shown in Eq. (17) can be employed to filter the sample of $f_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$ to obtain the sample of $\hat{h}_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$. It can be proved theoretically that the sample screened from those of $f_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$ by $\Omega$ accurately follows PDF $\hat{h}_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$, i.e., the sample screened from those of $f_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$ by $\Omega$ are definitely the sample of $\hat{h}_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$ shown in Eq. (13).

$$\Omega = \left\{ {p - c\pi _{{F_{t} }} (\varvec{x}|\varvec{\theta }_{k} ) \le 0} \right\},$$

(17)

where $p\sim {\text{U}}[0,1]$ is a standard uniform random variable. $c$ is a constant that should satisfy inequality ${0} \le c\pi_{{F_{t} }} (\varvec{x|\theta }_{k} ) \le {1}$, and $c = 1$ satisfies the inequality due to $0 \le \pi_{{F_{t} }} (\varvec{x|\theta }_{k} ) \le 1$.

Appendix 2 lists the proof that the sample screened from that of $f_{{\varvec{X}}} (\varvec{x|\theta }_{k} )$ by the acceptance domain in Eq. (17) follows the PDF $\hat{h}_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{k} )$. The detailed steps of extracting the sample of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ can be organized as follows based on the sample of $\hat{h}_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{k} )$.

Firstly, generate $N_{{\hat{h}}}$-size sample ${\varvec{\theta}}_{i} (i = 1,2, \cdots ,N_{{\hat{h}}} )$ ($N_{{\hat{h}}}$ is the preset number of the sample of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$) by $\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})$. Secondly, generate one sample ${\varvec{x}}_{i}^{{\hat{h}}}$ of $\hat{h}_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{i} )$ corresponding to each ${\varvec{\theta}}_{i}$$(i = 1,2, \cdots ,N_{{\hat{h}}} )$ by using the acceptance domain $\Omega$ in Eq. (17) to screen the sample of $f_{{\varvec{X}}} ({\varvec{x}}|{\varvec{\theta}}_{i} )$. Finally, an $N_{{\hat{h}}}$-size sample set ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}} = \{ {\varvec{x}}_{1}^{{\hat{h}}} ,{\varvec{x}}_{2}^{{\hat{h}}} , \cdots ,{\varvec{x}}_{{N_{{\hat{h}}} }}^{{\hat{h}}} \}^{T}$ of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ can be constructed by ${\varvec{x}}_{i}^{{\hat{h}}}$$(i = 1,2, \cdots ,N_{{\hat{h}}} )$ taken from the $N_{{\hat{h}}}$-size sample pair set $({\varvec{\theta}}_{i} ,{\varvec{x}}_{i}^{{\hat{h}}} )$$(i = 1,2, \cdots ,N_{{\hat{h}}} )$.

3.2.3 Strategy of adaptively updating g _K(x, t) to approach $h_{\varvec{X}}^{opt} ({\varvec{x}})$ by $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$

Since the initial Kriging model $g_{K} ({\varvec{x}},t)$ may not approach $g({\varvec{x}},t)$ well, the sample set ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ obtained by the initial $g_{K} ({\varvec{x}},t)$ may not well approximate that of the optimal IS-PDF for estimating T-FPF either. Thus, $g_{K} ({\varvec{x}},t)$ needs to be updated adaptively to make $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ close to the theoretical optimal IS-PDF $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ as much as possible.

In order to realize the purpose of approaching $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ by $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ based on $g_{K} ({\varvec{x}},t)$ with preset precision, the center points obtained from the cluster analysis with respect to ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ should be added to the training set ${\varvec{T}}$ for updating the Kriging model $g_{K} ({\varvec{x}},t)$ adaptively. By K-means (Zhu et al. 2020) clustering the sample in ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ iteratively and adding the clustering center points to the training set to update $g_{K} ({\varvec{x}},t)$, the quasi-optimal IS-PDF $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ based on $g_{K} ({\varvec{x}},t)$ can gradually approach $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$. For constructing the convergence criterion of adaptively updating $g_{K} ({\varvec{x}},t)$ to approach $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$, the convergence index $\alpha_{acc}$ in Eq. (18) may be introduced. $\alpha_{acc}$ expresses the accuracy of the current Kriging model $g_{K} ({\varvec{x}},t)$ predicting the time-dependent failure domain indicator function $I_{{F_{t} }} ({\varvec{x}})$.

$$\alpha_{acc} = \frac{{I_{{F_{t} }} ({\varvec{x}})}}{{\pi_{{F_{t} }} ({\varvec{x}})}}$$

(18)

According the cross-validation method (Stone 1974), the estimated value $\hat{\alpha }_{accL}$ of $\alpha_{acc}$ can be given in Eq. (19) by the leave-one method.

$$\hat{\alpha }_{accL} = \frac{1}{{N_{{\varvec{T}}} }}\sum\limits_{i = 1}^{{N_{{\varvec{T}}} }} {\frac{{I_{{F_{t} }} ({\varvec{x}}_{i} )}}{{\pi_{{F_{t} ,{\varvec{T}}/{\varvec{x}}_{i}^{{\varvec{T}}} }} ({\varvec{x}}_{i} )}}} = \frac{1}{{N_{{\varvec{T}}} }}\sum\limits_{i = 1}^{{N_{{\varvec{T}}} }} {\frac{{I_{{F_{t} }} ({\varvec{x}}_{i} )}}{{{\text{Prob}}\left\{ {\mathop {{\text{min}}}\limits_{{t_{i} \in {\varvec{S}}_{t} }} g_{{K,{\varvec{T}}/{\varvec{x}}_{i}^{{\varvec{T}}} }} ({\varvec{x}}_{i} ,t_{i} ) \le 0} \right\}}}}$$

(19)

where $N_{{\varvec{T}}}$ is the size of the training set ${\varvec{T}}$. $\pi_{{F_{t} ,{\varvec{T}}/{\varvec{x}}_{i}^{{\varvec{T}}} }} ( \cdot )$ represents the probability classification function established by the Kriging model $g_{{K,{\varvec{T}}/{\varvec{x}}_{i}^{{\varvec{T}}} }} ({\varvec{x}},t)$, where ${\varvec{T}}/{\varvec{x}}_{i}^{{\varvec{T}}}$ means the corresponding Kriging model $g_{{K,{\varvec{T}}/{\varvec{x}}_{i}^{{\varvec{T}}} }} ({\varvec{x}},t)$ is constructed by the training set ${\varvec{T}}$ without the $i$ th training point $(({\varvec{x}}_{i}^{{\varvec{T}}} ,t_{i}^{{\varvec{T}}} ),g({\varvec{x}}_{i}^{{\varvec{T}}} ,t_{i}^{{\varvec{T}}} ))$.

In this paper, $\hat{\alpha }_{accL} \in [0.1,10]$ is taken as the convergence criterion according to Refs. (Dubourg et al. 2013; Zhu et al. 2020). After the Kriging model $g_{K} ({\varvec{x}},t)$ satisfies $\hat{\alpha }_{accL} \in [0.1,10]$, it is considered that $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ can approach $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ with the preset precision. Then the work of adaptively updating $g_{K} ({\varvec{x}},t)$ for approaching $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ by $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ and extracting the sample of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ is completed. The following task is estimating T-FPF by using the sample set ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$.

3.3 Strategy of estimating T-FPF based on ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$

According to Eq. (4), it is shown that the whole T-FPF at arbitrary realization of ${\varvec{\theta}}$ can be simultaneously estimated by the same candidate sample set ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$, after the time-dependent failure domain indicator function $I_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$ with ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ is estimated accurately. The task of accurately estimating $I_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$ with ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ can be efficiently completed by sequentially updating Kriging model $g_{K} ({\varvec{x}},t)$ in ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$.

For adaptively updating $g_{K} ({\varvec{x}},t)$ to be convergent for accurately and efficiently estimating $I_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$ with ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$, this paper proposes a time-dependent misclassification probability ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$ learning function to adaptively select the training point to update $g_{K} ({\varvec{x}},t)$. ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$ is proposed to measure the capability of the candidate point ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ to improve the accuracy of $g_{K} ({\varvec{x}},t)$ predicting $I_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$, and ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$ is defined as the probability of the sign of the minimum prediction $g_{K\min } {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} = \mathop {{\text{min}}}\limits_{{t \in {\varvec{S}}_{t} }} g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t)$ of the time-dependent Kriging model $g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t)$ is different from the sign of the minimum prediction mean $\mu_{{g_{K\min } }} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} = E\left[ {\mathop {{\text{min}}}\limits_{{t \in {\varvec{S}}_{t} }} g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t)} \right]$ at ${\varvec{x}}_{i}^{{\hat{h}}}$, i.e.,

$${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} = {\text{P}}\left\{ {{\text{sign}}[g_{K\min } {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}] \ne {\text{sign}}[\mu_{{g_{K\min } }} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}]} \right\}$$

(20)

Since $\mu_{{g_{K\min } }} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} = E\left[ {\mathop {{\text{min}}}\limits_{{t \in {\varvec{S}}_{t} }} g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t)} \right]$ is used to recognize the structure state at ${\varvec{x}}_{i}^{{\hat{h}}}$, i.e., $\mu_{{g_{K\min } }} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} > 0$ indicating safety state with $I_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} ) = 0$ and $\mu_{{g_{K\min } }} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} \le 0$ meaning failure state with $I_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} ) = 1$, the event of $\left\{ {{\text{sign}}[g_{K\min } {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}] \ne {\text{sign}}[\mu_{{g_{K\min } }} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}]} \right\}$ represents that the time-dependent Kriging model $g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t)$ misclassifies the structure state at ${\varvec{x}}_{i}^{{\hat{h}}}$. Thus, the larger the misclassification probability ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$ at the candidate sample ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ is, the larger the contribution of adding ${\varvec{x}}_{i}^{{\hat{h}}}$ to the training set is to improve precision of the time-dependent Kriging model $g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t)$ predicting the time-dependent failure domain indicator.

Since the misclassification probability ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$ is defined by Eq. (20), ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$ can be estimated by Eq. (21).

$${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} = \left\{ \begin{gathered} {\text{P}}\left\{ {g_{K\min } {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} > 0} \right\} \, \mu_{{g_{K\min } }} ({\varvec{x}}_{i}^{{\hat{h}}} ) < 0 \hfill \\ {\text{P}}\left\{ {g_{K\min } {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} \le 0} \right\} \, \mu_{{g_{K\min } }} ({\varvec{x}}_{i}^{{\hat{h}}} ) \ge 0 \hfill \\ \end{gathered} \right.$$

(21)

In order to estimate ${\text{P}}\left\{ {g_{K\min } (x_{i}^{{\hat{h}}} ) > 0} \right\}$ and ${\text{P}}\left\{ {g_{K\min } {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} \le 0} \right\}$ to obtain ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$, the following derivation is given by use of the property of the time-dependent Kriging model $g_{K} ({\varvec{x}},t)$.

$$\begin{gathered} {\text{P}}\left\{ {g_{K\min } {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} > 0} \right\} = {\text{P}}\left\{ {\bigcap\limits_{{t_{j} \in {\varvec{S}}_{t} }} {[g_{K} {(}{\varvec{x}}_{i}^{{\hat{h}}} ,t_{j} {)} > 0]} } \right\} \\ = \underbrace {{\int_{0}^{ + \infty } \cdots }}_{{N_{t} {\text{ layer}}}}\int_{0}^{ + \infty } {\varphi_{{\varvec{\rm N}_{t} }} ({\varvec{\mu}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}}),{\varvec{\varSigma}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}}))dt_{1} dt_{2} \cdots dt_{{N_{t} }} } \\ \end{gathered}$$

(22)

where $\varphi_{{\varvec{\rm N}_{t} }} ({\varvec{\mu}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}}),{\varvec{\varSigma}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}}))$ is an $N_{t}$-dimensional normal PDF with mean vector ${\varvec{\mu}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}})$ and covariance matrix ${\varvec{\varSigma}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}})$ as follows:

$${\varvec{\mu}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}}) = [\mu_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{1} ),\mu_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{2} ), \cdots ,\mu_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{{N_{t} }} )]^{T}$$

(23)

$${\varvec{\varSigma}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}}) = \left[ \begin{array} {cccc}\sigma_{{g_{K} }}^{2} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{1} ) & \prod\limits_{k = [1,2]} {\sigma_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{k} )\rho_{{t_{1} t_{2} }} } \, & \cdots & \prod\limits_{{k = [1,N_{t} ]}} {\sigma_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{k} )\rho_{{t_{1} t_{{N_{t} }} }} } \hfill \\ \prod\limits_{k = [2,1]} {\sigma_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{k} )\rho_{{t_{2} t_{1} }} } & \sigma_{{g_{K} }}^{2} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{2} ) & \cdots & \prod\limits_{{k = [2,N_{t} ]}} {\sigma_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{k} )\rho_{{t_{2} t_{{N_{t} }} }} } \hfill \\ \vdots & \vdots & & \vdots \hfill \\ \prod\limits_{{k = [N_{t} ,1]}} {\sigma_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{k} )\rho_{{t_{{N_{t} }} t_{1} }} } & \prod\limits_{{k = [N_{t} ,2]}} {\sigma_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{k} )\rho_{{t_{{N_{t} }} t_{2} }} } & \cdots & \sigma_{{g_{K} }}^{2} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{{N_{t} }} ) \hfill \end{array} \right]$$

(24)

where $\rho_{{t_{i} t_{j} }}$$(i \ne j,i,j = 1,2, \cdots ,N_{t} )$ is the correlation coefficient of $g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{i} )$ and $g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t_{j} )$ in ${\varvec{\varSigma}}_{{g_{K} }} ({\varvec{x}}_{i}^{{\hat{h}}} ,{\varvec{t}})$, and $\rho_{{t_{i} t_{j} }}$ can be provided by the current $g_{K} ({\varvec{x}}_{i}^{{\hat{h}}} ,t)$.

All terms concerned in Eqs. (23) and (24) for solving ${\text{P}}\left\{ {g_{K\min } {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} > 0} \right\}$ can be given by the DACE toolbox based on the current $g_{K} ({\varvec{x}},t)$. So far, the misclassification probability ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$ at ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ can be obtained, and the training point ${\varvec{x}}^{*}$ of the random input vector can be adaptively selected by Eq. (25).

$${\varvec{x}}^{*} = \arg \mathop {\max }\limits_{{{\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}} }} {\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$$

(25)

The training point $t^{*}$ of the time variable can be selected by U-learning function $U_{{g_{K} }} {(}{\varvec{x}}^{*} ,t{)}$ (Echard et al. 2011) at ${\varvec{x}}^{*}$ as follows:

$$t^{*} = \arg \mathop {\min }\limits_{{t \in {\varvec{S}}_{t} }} U_{{g_{K} }} {(}{\varvec{x}}^{*} ,t{)} = \arg \mathop {\min }\limits_{{t \in {\varvec{S}}_{t} }} \frac{{|\mu_{{g_{K} }} {(}{\varvec{x}}^{*} ,t{)|}}}{{\sigma_{{g_{K} }} {(}{\varvec{x}}^{*} ,t{)}}}$$

(26)

Then, the training set ${\varvec{T}}$ can be updated as:

$${\varvec{T}} = {\varvec{T}} \cup \{ (({\varvec{x}}^{*} ,t^{*} ),g({\varvec{x}}^{*} ,t^{*} ))\}$$

(27)

Update the training set until the average misclassification probability satisfies the inequality in Eq. (28), then $g_{K} ({\varvec{x}},t)$ is considered to be convergent to accurately estimate $I_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$ at ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$.

$$\frac{{1}}{{N_{{\hat{h}}} }}\sum\limits_{i = 1}^{{N_{{\hat{h}}} }} {{\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}} \le 5{\raise0.5ex\hbox{$\scriptstyle 0$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 0$}}$$

(28)

After the convergent $g_{K} ({\varvec{x}},t)$ can accurately identify the time-dependent failure domain indicator function $I_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$ with ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$, the T-FPF $P_{ft} ({\varvec{\theta}})$ can be estimated by $\hat{P}_{ft} ({\varvec{\theta}})$ in Eq. (29).

$$\hat{P}_{ft} ({\varvec{\theta}}) = \frac{{1}}{{N_{{\hat{h}}} }}\sum\limits_{i = 1}^{{N_{{\hat{h}}} }} {\frac{{\hat{I}_{F} ({\varvec{x}}_{i}^{{\hat{h}}} )f_{{\varvec{X}}} ({\varvec{x}}_{i}^{{\hat{h}}} |{\varvec{\theta}})}}{{\hat{h}_{{\varvec{X}}} ({\varvec{x}}_{i}^{{\hat{h}}} )}}}$$

(29)

where ${\varvec{\theta}}$ can take any realization in the interested region $[{\varvec{\theta}}^{{\text{L}}} ,{\varvec{\theta}}^{{\text{U}}} ]$, and $\hat{I}_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$ is the time-dependent failure domain indicator function estimated by the convergent $g_{K} ({\varvec{x}},t)$ as follows:

$$\hat{I}_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} ) = \left\{ \begin{gathered} {0 }\mu_{{g_{K\min } }} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} > 0 \hfill \\ {1 }\mu_{{g_{K\min } }} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)} \le 0 \hfill \\ \end{gathered} \right.$$

(30)

3.4 Detailed steps of the SL-Meta-IS-AK for analyzing T-FPF

According to the above demonstration, the detailed steps of SL-Meta-IS-AK analyzing T-FPF are given as follows, and the corresponding flow chart is shown in Fig. 2.

Fig. 2

Flow chart of the SL-Meta-IS-AK

• Step 1 Construct an initial time-dependent Kriging model $g_{K} ({\varvec{x}},t)$.

• Step 2 Generate an $N_{T}$-size initial training point set ${\varvec{S}}_{{\varvec{x}}}^{{\varvec{T}}} = \{ {\varvec{x}}_{1}^{{\varvec{T}}} ,{\varvec{x}}_{2}^{{\varvec{T}}} , \cdots ,{\varvec{x}}_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} \}^{T}$ and an $N_{T}$-size one ${\varvec{S}}_{t}^{{\varvec{T}}} = \{ t_{1}^{{\varvec{T}}} ,t_{2}^{{\varvec{T}}} , \cdots ,t_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} \}^{T}$ for random input vector ${\varvec{X}}$ and time variable $t$, respectively, by $\int {f_{{\varvec{X}}} (\varvec{x|\theta })\varphi_{{\varvec{\varTheta}}} ({\varvec{\theta}})d{\varvec{\theta}}}$ and uniformly discretizing $[t_{0} ,t_{e} ]$.

• Step 3 Construct the training set ${\varvec{T}}$ as follows by estimating $g({\varvec{x}},t)$ at ${\varvec{x}} \in {\varvec{S}}_{{\varvec{x}}}^{{\varvec{T}}}$ and $t \in {\varvec{S}}_{t}^{{\varvec{T}}}$.

  $${\varvec{T}} = \left\{ {\left( {({\varvec{x}}_{1}^{{\varvec{T}}} ,t_{1}^{{\varvec{T}}} ),g({\varvec{x}}_{1}^{{\varvec{T}}} ,t_{1}^{{\varvec{T}}} )} \right),\left( {({\varvec{x}}_{2}^{{\varvec{T}}} ,t_{2}^{{\varvec{T}}} ),g({\varvec{x}}_{2}^{{\varvec{T}}} ,t_{2}^{{\varvec{T}}} )} \right), \cdots ,\left( {({\varvec{x}}_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} ,t_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} ),g({\varvec{x}}_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} ,t_{{N_{{\varvec{T}}} }}^{{\varvec{T}}} )} \right)} \right\}^{T}$$

• Step 4 Construct the initial Kriging model $g_{K} ({\varvec{x}},t)$ of $g({\varvec{x}},t)$ by ${\varvec{T}}$.

• Step 5 Update $g_{K} ({\varvec{x}},t)$ to approach $h_{{\varvec{X}}}^{opt} ({\varvec{x}})$ and extract IS-PDF candidate sample pool ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$.

• Step 6 Generate the IS-PDF candidate sample pool ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}} = \{ {\varvec{x}}_{1}^{{\hat{h}}} ,{\varvec{x}}_{2}^{{\hat{h}}} , \cdots ,{\varvec{x}}_{{N_{{\hat{h}}} }}^{{\hat{h}}} \}^{T}$ of $\hat{h}_{{\varvec{X}}} ({\varvec{x}})$ by the current $g_{K} ({\varvec{x}},t)$ and the designed acceptance domain $\Omega$ in Eq. (17).

• Step 7 Execute the K-means clustering analysis, and estimate $\hat{\alpha }_{accL}$ by Eq. (19).

• Step 8 If $\hat{\alpha }_{accL} \in [0.1,10]$ and the size $N_{{\varvec{T}}}$ of the training set is greater than 30 (Zhu et al. 2020), the Kriging model $g_{K} ({\varvec{x}},t)$ can be viewed as convergence and execute step 3. Otherwise, add the center points of K-mean clustering into the training set ${\varvec{T}}$ to update the Kriging model $g_{K} ({\varvec{x}},t)$, and return to Step 2.1.

• Step 9 Update $g_{K} ({\varvec{x}},t)$ in ${\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ to identify $\hat{I}_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$ and estimate T-FPF.

• Step 10 Generate an $N_{t}$-size candidate sample set ${\varvec{S}}_{t} = \{ t_{1} ,t_{2} , \cdots ,t_{{N_{t} }} \}^{T}$ by uniformly discretizing $t \in [t_{0} ,t_{e} ]$.

• Step 11 Estimate the misclassification probability ${\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}$ at ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ according to Eq. (21), and find the new training point ${\varvec{x}}^{*}$ and $t^{*}$ by Eqs. (25) and (26), respectively.

• Step 12 If the average misclassification probability satisfies $\frac{{1}}{{N_{{\hat{h}}} }}\sum\limits_{i = 1}^{{N_{{\hat{h}}} }} {{\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}} \le 5{\raise0.5ex\hbox{$\scriptstyle 0$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 0$}}$, the Kriging model $g_{K} ({\varvec{x}},t)$ can be viewed as convergence to identify $\hat{I}_{{F_{t} }} ({\varvec{x}}_{i}^{{\hat{h}}} )$ with ${\varvec{x}}_{i}^{{\hat{h}}} \in {\varvec{S}}_{{\varvec{x}}}^{{\hat{h}}}$ accurately and T-FPF can be accurately estimated. If $\frac{{1}}{{N_{{\hat{h}}} }}\sum\limits_{i = 1}^{{N_{{\hat{h}}} }} {{\text{P}}_{e} {(}{\varvec{x}}_{i}^{{\hat{h}}} {)}} > 5{\raise0.5ex\hbox{$\scriptstyle 0$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 0$}}$, add $({\varvec{x}}^{*} ,t^{*} )$ into the training set ${\varvec{T}}$ to update the Kriging model $g_{K} ({\varvec{x}},t)$, and return to Step 3.2.

4 Case study

In this section, the SL-Meta-IS-AK is used to estimate T-FPF of several examples, in which other three methods including the Monte Carlo simulation (MCS), the single-loop Kriging model (SILK) (Hu and Mahadevan 2016) and the adaptive Kriging-MCS combined with Bayes formula (AK-MCS-Bay) (Feng et al. 2019) are compared with the SL-Meta-IS-AK under the similar variation coefficient of the T-FPF estimation. In the MCS and SILK, the region of the design parameter ${\varvec{\theta}}$ is discretized as ${\varvec{\theta}}_{i}$$(i = 1,2, \cdots ,N_{{\varvec{\theta}}} )$ at first. Then, the double-loop Monte Carlo simulation and the single-loop Kriging model are employed, respectively, in the MCS and SILK to estimate the time-dependent failure probability for each discrete point ${\varvec{\theta}}_{i}$$(i = 1,2, \cdots ,N_{{\varvec{\theta}}} )$, on which the T-FPF can be obtained by the interpolation method. In the AK-MCS-Bay, the Bayes formula is employed to transform the T-FPF into three components, i.e., the assigned PDF of ${\varvec{\theta}}$, the conditional PDF of ${\varvec{\theta}}$ on the time-dependent failure domain, and the augmented time-dependent failure probability in the space spanned by the random input vector and distribution parameter. Then, the T-FPF can be obtained by constructing a single-loop Kriging model to estimate the augmented time-dependent failure probability and obtain the conditional PDF by the kernel density estimation on the basis of the failure samples provided in estimating the augmented time-dependent failure probability.

In order to compare the accuracy of three compared methods in estimating T-FPF, the mean relative error (MRE) is defined as follows,

$${\text{MRE}} = \frac{{1}}{{N_{{\varvec{\theta}}} }}\sum\limits_{i = 1}^{{N_{{\varvec{\theta}}} }} {\frac{{|\hat{P}_{f}^{(i)} - P_{f}^{(i)} |}}{{P_{f}^{(i)} }}}$$

(31)

where $N_{{\varvec{\theta}}}$ is the number of discrete points of ${\varvec{\theta}}$. $P_{f}^{(i)}$ represents the failure probability estimated by the MCS method, and $\hat{P}_{f}^{(i)}$ represents the failure probability estimated by three compared methods including the SILK, the AK-MCS-Bay and SL-Meta-IS-AK.

4.1 Numerical example

Consider the following time-dependent performance function $g({\varvec{X}},t)$.

$$g({\varvec{X}},t) = X_{1}^{2} X_{2} - 5X_{1} t + (X_{2} + 1)t^{2} - 20$$

(32)

where $t$ is the time variable. $X_{1}$ and $X_{2}$ are two independent random inputs with normal distribution, i.e., $X_{1} \sim N{(}\mu_{{X_{1} }} {,0}{\text{.4}}^{2} {)}$ and $X_{2} \sim N{(}4{,0}{\text{.4}}^{2} {)}$. The mean value of $X_{1}$ is taken as the concerned distribution parameter in $[3.5,4.5]$, i.e., ${\varvec{\theta}} = \mu_{{X_{1} }} \in [3.5,4.5]$. The interval of the design parameter $\mu_{{X_{1} }}$ is discretized uniformly into 10 points. The interested interval of $t$ is taken as $t \in [0,5]$, and the interval of $t$ is discretized uniformly into 500 points.

At first, MCS is employed to estimate the T-FPF, and 10 time-dependent reliability analyses at the discrete point of $\mu_{{X_{1} }}$ are needed in estimating T-FPF. In each time-dependent reliability analysis, the size of the input vector sample set is ${10}^{{5}}$. Thereof, the total number of model evaluations for MCS in estimating the T-FPF is $5 \times 10^{{8}}$. Then, SILK, AK-MCS-Bay and SL-Meta-IS-AK are employed to estimate T-FPF. The size of the initial training sample sets of these methods is 10. The size of the candidate sample pool of SILK and AK-MCS-Bay is ${10}^{{5}}$, and the total numbers of model evaluations for SILK and AK-MCS-Bay are 43 and 40, respectively. The size of the importance sample pool of SL-Meta-IS-AK is 500, and the total number of model evaluations for SL-Meta-IS-AK is 30. The extreme limit states of Kriging model constructed by SILK, AK-MCS-Bay and SL-Meta-IS-AK compared with the real extreme limit state are shown in Fig. 3, respectively. From Fig. 3, it can be seen that the real extreme limit state and the extreme limit states of Kriging model constructed by SILK, AK-MCS-Bay and SL-Meta-IS-AK are almost superposed, while only 30 times of the model evaluations are required to construct the convergent Kriging model in SL-Meta-IS-AK. The T-FPF curves and the variation coefficient curves, respectively, obtained by MCS, SILK, AK-MCS-Bay and SL-Meta-IS-AK method are shown in Fig. 4. The MRE and computational cost of several compared methods are listed in Table 1.

Fig. 3

Extreme limit states of Kriging model compared with the real extreme limit state

Fig. 4

T-FPF curves and the variation coefficient curves of numerical example

Table 1 MRE and computational cost of the four compared methods of numerical example

From Fig. 4, it is shown that the T-FPF curve estimated by SL-Meta-IS-AK is consistent with the T-FPF curve estimated by MCS method under the similar variation coefficient, while the T-FPF curve estimated by AK-MCS-Bay method has a large error at both ends of the concerned distribution parameter region. The error of AK-MCS-Bay method is caused by the low accuracy of PDF fitting. In addition, it can be concluded from Table 1 that SL-Meta-IS-AK is more efficient than the two existing meta-models in estimating T-FPF under the similar T-FPF estimation precision. Since SILK has to estimate the time-dependent failure probability at each distribution parameter realization, more number of model evaluation is needed; the efficiency of SILK is lower than others.

4.2 Rack-and-pinion steering linkage

A rack-and-pinion steering linkage (Huang and Zhang 2010) shown in Fig. 5a is employed to verify the effectiveness of the SL-Meta-IS-AK in engineering application with one concerned distribution parameter. The motion behavior of the mechanism is represented by the simplified model shown in Fig. 5b. $L_{a} = L_{{1}} = L_{{4}}$ is the length of the steering arms (1) and (4). $L_{t} = L_{{2}} = L_{{3}}$ is the length of the steering linkages (2) and (3). $W_{t}$ is the length of the wheel track, and $H$ is the distance between the front axle ($X$ axle) and rack axis (5). As shown in Fig. 5a, the horizontal displacement of the frame shaft $D \in [ - 50,50]$ mm is viewed as time variable, and the rotation degrees $\phi_{1}$ and $\phi_{4}$ of the left and right steering arm, respectively, are viewed as the time-dependent output. Regard ${\varvec{X}} = (L_{a} ,L_{t} ,W_{t} ,H)^{T}$ as the random input vector, and the distribution parameters are shown in Table 2.

Fig. 5

Structure and the model of the rack-and-pinion steering linkage

Table 2 Distribution parameters of the rack-and-pinion steering linkage

${\varvec{\phi}} = (\phi_{1} ,\phi_{2} ,\phi_{3} ,\phi_{4} )^{T}$ shown in Fig. 5b is the output vector. The closed-loop equation of the mechanism is obtained from Fig. 5b as,

$$\left\{ \begin{gathered} L_{a} \cos \phi_{1} + L_{t} \cos \phi_{2} - W_{t} /2 - D = 0 \hfill \\ L_{a} \sin \phi_{1} + L_{t} \sin \phi_{2} - H = 0 \hfill \\ ( - W_{t} /2 + D) + L_{t} \cos \phi_{3} - L_{a} \cos \phi_{4} = 0 \hfill \\ H + L_{a} \sin \phi_{3} - L_{t} \sin \phi_{4} = 0 \hfill \\ \end{gathered} \right.$$

(33)

in which $\phi_{1}$ is the concerned output, and its expression is given as follows,

$$y({\varvec{X}},D) = \phi_{1} = 2\arctan \frac{{ - B \pm \sqrt {B^{2} - 4AC} }}{2A}$$

(34)

where $A = \left( {\frac{{W_{t} }}{2} + D + L_{a} } \right)^{2} + H^{2} - L_{t}^{2}$, $B = - 4HL_{a}$, $C = \left( {\frac{{W_{t} }}{2} + D - L_{a} } \right)^{2} + H^{2} - L_{t}^{2}$. When taking the time-dependent $y({\varvec{\mu}}_{{\varvec{X}}} ,D)$ at the mean vector ${\varvec{\mu}}_{{\varvec{X}}}$ of ${\varvec{X}}$ as the ideal one, the time-dependent performance function of this mechanism can be expressed as:

$$g({\varvec{X}},D) = y({\varvec{X}},D) - y({\varvec{\mu}}_{{\varvec{X}}} ,D) + \varepsilon$$

(35)

where $\varepsilon = 0.4^{ \circ }$ is the allowable threshold of the difference between $y({\varvec{X}},D)$ and its ideal $y({\varvec{\mu}}_{{\varvec{X}}} ,D)$.

The mean of $L_{a}$ is taken as the concerned distribution parameter at the interested region, i.e., ${\varvec{\theta}} = \mu_{{L_{a} }} \in [106,110]$. The interval of $\mu_{{L_{a} }}$ is discretized uniformly into 10 points. The interested interval of the time variable $t$, i.e., $D$, is taken as $t = D \in [ - 50,50]$, and the interval of $t$ is discretized uniformly into 100 points.

Firstly, MCS is used to estimate the T-FPF, and the size of the input variables set is ${10}^{{7}}$ in estimating T-FPF. The total number of model evaluations for MCS in estimating the T-FPF is $10^{{{10}}}$. Next, SILK, AK-MCS-Bay and SL-Meta-IS-AK are employed to estimate T-FPF. The size of the candidate sample pool of SILK and AK-MCS-Bay is ${10}^{{7}}$. The total number of model evaluations for SILK is 63, i.e., 12 initial samples and 51 updating samples. As for AK-MCS-Bay, the initial sample size is 12 and the updating samples 47. The size of the importance sample pool of SL-Meta-IS-AK is 1000, and the total number of model evaluations for SL-Meta-IS-AK is 34, i.e., 12 initial samples and 22 updating samples. The T-FPF curves and the variation coefficient curves, respectively, obtained by MCS, SILK, AK-MCS-Bay and SL-Meta-IS-AK method are shown in Fig. 6. The MRE and computational cost of several compared methods are listed in Table 3. From Fig. 6, it can be seen that the T-FPF curve estimated by SL-Meta-IS-AK is almost coincides to that by MCS method. The accuracy of SL-Meta-IS-AK is the highest among the compared methods since the MRE of the SL-Meta-IS-AK is the smallest one, which is listed in Table 3. From Table 3, it can be observed that the efficiency of SL-Meta-IS-AK is highest and the computational time is shortest among the compared methods, which verifies the accuracy and efficiency of the proposed SL-Meta-IS-AK.

Fig. 6

T-FPF curves and the variation coefficient curves of the rack-and-pinion steering linkage

Table 3 MRE and computational cost of the four compared methods

4.3 Wing structure

A typical wing structure (Ling et al. 2019) shown in Fig. 7 is considered to verify the effectiveness of the proposed SL-Meta-IS-AK in engineering application with two concerned distribution parameters. The cross section of the wing is shown in Fig. 7a, where $T$ is the thickness, $h$ is the height of the wing, and $c$ is the chord length. The top view of the wing is shown in Fig. 7b, where $b = 40{\text{m}}$ is the wingspan of the wing. The load distribution on the wing is given in Fig. 7c. In Fig. 7c, it is shown that the position on the $x$ axis is regarded as the time variable $t$ in this example, and $t \in [0,b/2]{\text{m}} = [0,20]{\text{m}}$ is the interested interval of $t$. Regard ${\varvec{X}} = [P_{r} ,\sigma_{f} ,c_{r} ,c_{0} /c_{r} ,h/c,T]^{T}$ as the random input vector, and the distribution types and parameters are shown in Table 4. The time-dependent performance function of the wing structure is shown as follows:

$$g({\varvec{X}},t) = \sigma_{f} - \frac{{M({\varvec{X}},t)(h({\varvec{X}},t)/2)}}{{I_{Z} ({\varvec{X}},t)}}$$

(36)

where $M({\varvec{X}},t) = 4P_{r} c_{r} b\left[ {\left( {\frac{{c_{0} }}{{c_{r} }}} \right)\frac{{t^{4} }}{{12b^{2} }} + \left( {1 - 2\frac{{c_{0} }}{{c_{r} }}} \right)\frac{{t^{5} }}{{20b^{3} }} + \left( {\frac{{c_{0} }}{{c_{r} }} - 1} \right)\frac{{t^{6} }}{{30b^{4} }}} \right]$ denotes the moment. $P_{r}$ denotes the distributed load. $I_{Z} ({\varvec{X}},t) = \frac{1}{2}c({\varvec{X}},t)Th^{2} ({\varvec{X}},t)$ represents the rotational inertia. $c({\varvec{X}},t) = c_{r} \left[ {\left( {\frac{{c_{0} }}{{c_{r} }}} \right) + \left( {1 - \frac{{c_{0} }}{{c_{r} }}} \right)\frac{t}{b/2}} \right]$ is the chord length. $h({\varvec{X}},t) = c_{r} \frac{h}{c}\left[ {\left( {\frac{{c_{0} }}{{c_{r} }}} \right) + \left( {1 - \frac{{c_{0} }}{{c_{r} }}} \right)\frac{t}{b/2}} \right]$ is the wing height. $\sigma_{f}$ represents the threshold of the stress.

Fig. 7

Wing structure

Table 4 Distribution parameters of the wing structure

The mean values of $c_{r}$ and $T$ are taken as the concerned distribution parameters, i.e., ${\varvec{\theta}} = [\mu_{{c_{r} }} ,\mu_{T} ]$, and their interested regions are, respectively, $\mu_{{c_{r} }} \in [6,8]$, and $\mu_{T} \in [8.7 \times 10^{{ - 3}} ,9.1 \times 10^{{ - 3}} ]$. Each parameter is discretized into 10 points. The interested interval of $t$ is taken as $[0,20]$, and the interval is discretized into 100 points. The T-FPF surfaces obtained by MCS and SL-Meta-IS-AK are, respectively, shown in Fig. 8a, and the T-FPF curves estimated by the four methods are shown in Fig. 8b (for visualization comparison, a diagonal line of the T-FPF surface is selected to illustrate the accuracy of the compared methods). The MRE and computational cost are listed in Table 5.

Fig. 8

T-FPF surface and T-FPF curve of wing structure

Table 5 MRE and computational cost of the four compared methods of the wing structure

At first, MCS is adopted to estimate the T-FPF, and the size of the input variables set is ${10}^{{6}}$ in estimating T-FPF. The total number of model evaluations for MCS in estimating the T-FPF is $10^{{{10}}}$. In SILK and AK-MCS-Bay, the size of the candidate sample pool is ${10}^{{6}}$. The total number of model evaluations for SILK is 172 including 25 initial samples and 147 updating samples. As for AK-MCS-Bay, the initial samples are 25 and the updating samples 116. The size of the importance sample pool of SL-Meta-IS-AK is 5000, and the total number of model evaluations for SL-Meta-IS-AK is 103. From Table 5, it is obviously that SL-Meta-IS-AK takes least computation time than other compared methods, which shows the efficiency of the proposed SL-Meta-IS-AK. It can be seen from Fig. 8a that the T-FPF surface estimated by the proposed SL-Meta-IS-AK is consistent with that by MCS method, which verifies the accuracy of the proposed SL-Meta-IS-AK. From the T-FPF diagonals obtained by the four methods shown in Fig. 8b, it can be seen that the T-FPF curve of proposed SL-Meta-IS-AK method coincides with that of MCS, while the T-FPF results at both ends of the interested distribution parameter regions by AK-MCS-Bay are inaccurate due to the error of density fitting.

4.4 A corroded bending beam involving stochastic load

A corroded bending beam (Hu and Du 2015) shown in Fig. 9 is employed to verify the effectiveness of the proposed SL-Meta-IS-AK in engineering application including stochastic process with four distribution parameters. The time-dependent performance function is defined as follows:

$$g({\varvec{X}},Y(t),t) = \frac{{(a_{0} - 2kt)(b_{0} - 2kt)^{2} \sigma_{u} }}{4} - \left( {\frac{F(t)L}{4} + \frac{{\rho_{st} a_{0} b_{0} L^{2} }}{8}} \right)$$

(37)

where ${\varvec{X}} = (\sigma_{u} ,a_{0} ,b_{0} )^{T}$ is the random input vector. $\sigma_{u}$ denotes the ultimate strength, $a_{0}$ is the width of the beam, and $b_{0}$ is the height of the beam. $\rho_{st} = 7.84 \times 10^{4} {\text{kg/m}}^{{3}}$ is the density. $k = 5 \times 10^{ - 5} {\text{m/year}}$ is the corrosion coefficient. $L = 5{\text{m}}$ is the length of the beam. $F(t)$ is a stochastic process modeled by,

$$F(t) = 6500 + \sum\limits_{i = 1}^{7} {\xi_{i} \left( {\sum\limits_{j = 1}^{7} {a_{ij} \sin (b_{ij} t + c_{ij} )} } \right)}$$

(38)

where $\xi_{i} (i = 1,2, \cdots ,7)$ are seven independent random variables, and $a_{ij}$, $b_{ij}$, $c_{ij} (\forall i,j = 1,2, \cdots ,7)$ are the coefficients of the sine wave basis functions, i.e.,

$$a = \left[ \begin{gathered} 0.13 \, 0.36 \, 0.14 \, 3.07 \, 0.17 \, 0.13 \, 0.12 \hfill \\ 0.02 \, 0.18 \, 0.09 \, 0.13 \, 0.69 \, 0.04 \, 0.27 \hfill \\ 0.08 \, 0.29 \, 0.14 \, 3.09 \, 0.05 \, 0.37 \, 0.13 \hfill \\ 0.03 \, 0.06 \, 0.01 \, 0.04 \, 0.63 \, 0.30 \, 0.06 \hfill \\ 0.03 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \hfill \\ 0.01 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \hfill \\ 0.01 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \hfill \\ \end{gathered} \right]$$

(39)

$$b = \left[ \begin{gathered} 0.06 \, 0.31 \, 0.15 \, 0.28 \, 0.24 \, 0.44 \, 0.48 \hfill \\ 0.38 \, 0.15 \, 0.40 \, 0.06 \, 0.42 \, 0.09 \, 0.01 \hfill \\ 0.10 \, 0.33 \, 0.03 \, 0.29 \, 0.11 \, 0.26 \, 0.38 \hfill \\ 0.28 \, 0.07 \, 0.59 \, 0.55 \, 0.42 \, 0.23 \, 0.29 \hfill \\ 0.52 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \hfill \\ 0.77 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \hfill \\ 0.91 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \, 0.00 \hfill \\ \end{gathered} \right]$$

(40)

$$c = \left[ \begin{array} {rrrrrrr} \, 2.91 & - 2.34 & - 2.43 & - 2.82 & - 2.15 & 0.47 & 2.90 \\ - 2.91 & 2.21 & - 0.97 & 0.98 & - 1.03 & - 3.81 & - 0.35 \\ 1.25 & 0.52 & 2.62 & 0.23 & 0.91 & - 1.39 & - 2.45 \\ 0.73 & 0.00 & - 0.45 & - 0.50 & 1.93 & - 3.64 & - 3.00 \\ 0.18 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 \\ - 1.71 & 0.00&0.00 & 0.00 & 0.00 & 0.00 & 0.00 \\ - 2.46 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 \end{array} \right]$$

(41)

Fig. 9

Corroded bending beam

By transforming the input stochastic process $F(t)$ into Eq. (38), time-dependent performance function is transformed into $g({\varvec{X}},t)$, and ${\varvec{X}}$ is enlarged to a 10-dimensional random input vector with distribution parameters listed in Table 6.

Table 6 Distribution parameters of the corroded bending beam

The mean values of $\sigma_{u}$, $a_{0}$, $b_{0}$ and the standard deviation of $\sigma_{u}$ are taken as four concerned distribution parameters, i.e., ${\varvec{\theta}} = [\mu_{{\sigma_{u} }} ,\mu_{{a_{0} }} ,\mu_{{b_{0} }} ,\sigma_{{\sigma_{u} }} ]$, and their interested regions are $\mu_{{\sigma_{u} }} \in [2.25 \times 10^{8} ,2.35 \times 10^{8} ]$, $\mu_{{a_{0} }} \in [0.15,0.25]$, $\mu_{{b_{0} }} \in [0.04,0.05]$, and $\sigma_{{\sigma_{u} }} \in [0.04,0.06]$, respectively. The region of each parameter is uniformly discretized into 10 points. The interested interval of $t$ is taken as $[0,35]$, and the interval is uniformly discretized into 350 points. Since the density fitting method is difficult to apply in this 4-dimensional problem, only MCS method and SILK are used as the methods compared with the proposed method. Note that the T-FPF is the function of the four-dimensional distribution parameters which can be estimated by the proposed method but cannot be visualized by the diagram. We only visualize in Fig. 10 the T-FPF with respect to each parameter by keeping the residual 3 concerned distribution parameters at their midpoint of the interested ranges. The MRE and computational cost of different methods are listed in Table 7.

Fig. 10

T-FPF curves of the corroded bending beam

Table 7 MRE and computational cost of the three compared methods of the corroded bending beam

Firstly, MCS is used to estimate the T-FPF, and the total number of model evaluations for MCS in estimating the T-FPF is ${3}{\text{.5}} \times 10^{{{13}}}$. Next, SILK is employed to estimate T-FPF and the size of the candidate sample pool of SILK is ${10}^{{7}}$. The total number of model evaluations for SILK is 403, i.e., 50 initial samples and 353 updating samples. As for SL-Meta-IS-AK, the size of the importance sample pool of SL-Meta-IS-AK is 10000, and the total number of model evaluations for SL-Meta-IS-AK is 175 including 50 initial samples and 125 updating samples. From the T-FPF curves in Fig. 10(a)-(d), respectively, it can be seen that T-FPF obtained by SL-Meta-IS-AK coincides with that of MCS. The estimation efficiency of SL-Meta-IS-AK is higher than that of SILK, as the SL-Meta-IS-AK only needs 2.40 days and SILK needs 15.39 days to obtain the result. The result indicates the accuracy and efficiency applicability of the proposed SL-Meta-IS-AK to multiple distribution parameters including the mean and the standard deviation.

4.5 Turbine shaft structure

A turbine shaft shown in Fig. 11a is used to verify the effectiveness of the proposed SL-Meta-IS-AK in engineering application with finite element model determining the time-dependent performance function. The finite element model of the turbine shaft is shown in Fig. 11b and it includes connecting holes, grooves, splines, vents, flanges, etc. The factors that affect the turbine shaft including the radius $r$ of hole at the spline, the distance $h$ between the hole and the bottom of the spline, the diameter $D$ of the inner wall of the spline, the elastic modulus $E$ of the turbine shaft, and the Poisson's ratio $\gamma$ and rotational speed $\omega$ are assumed as independent random variables. The torque $T(t)$ is independent stochastic process. The distribution parameters of these inputs are given in Table 8, and the time interval of interest is $t \in [0,24]$.

Fig. 11

Turbine shaft structure

Table 8 Distribution parameters of the turbine shaft

The failure state of the turbine shaft corresponds to the maximum displacement $\Delta_{\max }$ exceeds the given threshold $\Delta_{{{\text{allow}}}} = 0.415{\text{mm}}$. The displacement nephogram of the turbine shaft analyzed by finite element analysis in ABAQUS at the random input vector taking their mean vector is shown in Fig. 12.

Fig. 12

Result of the finite element analysis

The mean values of $r$ and $D$ are taken as the concerned distribution parameters, i.e., ${\varvec{\theta}} = [\mu_{r} ,\mu_{D} ]$, and their interested regions are, respectively, $\mu_{r} \in [0.7,0.8]$, and $\mu_{D} \in [38,40]$. The region of each parameter is uniformly discretized into 10 points. The interested interval of $t$ is taken as $[0,24]$, and the interval is uniformly discretized into 500 points. The T-FPF curves obtained by SILK, AK-MCS-Bay and SL-Meta-IS-AK method are, respectively, shown in Fig. 11. Note that the T-FPF with respect to one distribution parameter is shown at the other one is fixed at the midpoint value of the interested region. Computational cost of several compared methods is listed in Table 9.

Table 9 Computational cost of the three compared methods of the turbine shaft

Since the computational cost by MCS is huge, it is hard to obtain the result by the MCS. Figure 13 and Table 9 only give the results obtained by the SILK, AK-MCS-Bay and the SL-Meta-IS-AK. In this example, the results obtained by the SILK at the discrete points of ${\varvec{\theta}}$ can be viewed as the reference solution. At first, SILK is adopted to estimate the T-FPF, and the size of the candidate sample pool is ${5} \times {10}^{{5}}$ in estimating T-FPF. The total number of model evaluations for SILK is 217 including 50 initial samples and 167 updating samples, and it costs 21.28 days to obtain the T-FPF from Table 9. In AK-MCS-Bay, the size of the candidate sample pool is ${5} \times {10}^{{5}}$. The total number of model evaluations for AK-MCS-Bay is 176 including 50 initial samples and 126 updating samples, and it costs 5.69 days to obtain the T-FPF. As for the proposed SL-Meta-IS-AK, the size of the importance sample pool is 2000, and the total number of model evaluations is only 109 including 50 initial samples and 59 updating samples. Besides, it only costs 2.81 days for the proposed SL-Meta-IS-AK to obtain the T-FPF. From Fig. 13, it can be seen that in results of SILK and those of SL-Meta-IS-AK are close to each other. This example verifies the accuracy and efficiency of the proposed method SL-Meta-IS-AK in solving the T-FPF of engineering application with the complex finite element determined performance function and stochastic process input.

Fig. 13

T-FPF curves of the turbine shaft

5 Conclusion

In order to efficiently estimate the time-dependent failure probability function (T-FPF), this paper proposes a novel single-loop meta-model importance sampling with adaptive Kriging model (SL-Meta-IS-AK) method. In SL-Meta-IS-AK, an optimal importance sampling probability density function (IS-PDF) is constructed to estimate T-FPF. Since the constructed IS-PDF includes variance reduction technique, and it envelopes the interested distribution parameter region and is free of the distribution parameter, the T-FPF can be estimated by single-loop analysis efficiently. For alleviating the difficulty of extracting the samples of the constructed IS-PDF, an adaptive Kriging model of the time-dependent performance function is constructed for approaching the optimal IS-PDF by the quasi-optimal one, and a simple sampling strategy is designed to extract the samples of quasi-optimal IS-PDF. After the samples are extracted for the IS-PDF, the Kriging model of the time-dependent performance function is updated sequentially by an analytically derived time-dependent misclassification probability function until it can accurately recognize the states of all extracted IS-PDF samples, on which the T-FPF at arbitrary realization of the distribution parameter in the whole interested region can be estimated simultaneously by the same group of the IS-PDF samples.

Numerical and complex aviation engineering examples are introduced to verify the effectiveness of the proposed SL-Meta-IS-AK. The results illustrate that the proposed SL-Meta-IS-AK possesses high computational efficiency under the acceptable precision, and it has no limits on the dimensionality or interested region of the concerned distribution parameter vector. However, due to the limitation of Kriging model suffering from the curse of random input dimensionality, the concerned distribution parameter dimensionality of the random input vector is limited dependently.

Appendices

Appendix 1: Kriging surrogate model

Select training set ${\varvec{T}} = \{ ({\varvec{x}}_{1} ,g({\varvec{x}}_{1} )),({\varvec{x}}_{2} ,g({\varvec{x}}_{2} )), \cdots ,({\varvec{x}}_{{N_{t} }} ,g({\varvec{x}}_{{N_{t} }} ))\}^{T}$ ($N_{t}$ is the size of the training set) by a design of experiment (DOE) for performance function $Y = g({\varvec{x}})$. Then, the Kriging model $g_{K} ({\varvec{x}})$ of $g({\varvec{x}})$ can be established by Kriging toolbox as:

$$g_{K} ({\varvec{x}}) = {\varvec{f}}^{T} ({\varvec{x}}){\varvec{\beta}} + Z({\varvec{x}})$$

(42)

where ${\varvec{f}}^{T} ({\varvec{x}}){\varvec{\beta}}$ is the regression model. ${\varvec{f}}({\varvec{x}}) = [f_{1} ({\varvec{x}}),f_{2} ({\varvec{x}}), \cdots ,f_{n} ({\varvec{x}})]^{T}$ is the basis vector of the regression function, and $n$ represents the number of basis functions. ${\varvec{\beta}} = (\beta_{1} ,\beta_{2} , \cdots ,\beta_{n} )^{T}$ is the coefficient vector of the regression function. $Z({\varvec{x}})$ is a Gaussian process with a mean of zero and a standard deviation of $\sigma$. Its covariance matrix is:

$$Cov[Z({\varvec{x}}_{i} ),Z({\varvec{x}}_{j} )] = \sigma^{2} R({\varvec{x}}_{i} ,{\varvec{x}}_{j} )$$

(43)

where $R({\varvec{x}}_{i} ,{\varvec{x}}_{j} )$ is the correlation function of any two sample points, and it has many expressions. In this paper, the following Gaussian form is adopted,

$$R({\varvec{x}}_{i} ,{\varvec{x}}_{j} ,{\varvec{\xi}}) = \exp \left( { - \sum\limits_{k = 1}^{n} {{\varvec{\xi}}_{k} \left| {x_{i}^{(k)} - x_{j}^{(k)} } \right|^{2} } } \right)$$

(44)

where $x_{i}^{(k)}$ represents the $k$-dimensional component of the sample ${\varvec{x}}_{i}$. ${\varvec{\xi}} = (\xi_{1} ,\xi_{2} , \cdots ,\xi_{n} )^{T}$ is an unknown correlation parameter vector, and it can be obtained by maximum likelihood estimation as follows,

$$\hat{\varvec{\xi }} = \arg \mathop {\min }\limits_{{\varvec{\xi}}} \left[ {\left| {\varvec{R}} \right|^{{1/N_{t} }} \hat{\sigma }^{2} } \right]$$

(45)

The regression coefficient vector ${\varvec{\beta}}$ and the variance $\sigma^{2}$ of the Gaussian process can be obtained from the training points shown in Eqs. (46) and (47), respectively,

$$\hat{\varvec{\beta} } = \left( {\varvec{F}^{T} \varvec{R}^{ - 1} \varvec{F}} \right)^{ - 1} \varvec{F}^{T} \varvec{R}^{ - 1}\varvec{ y}$$

(46)

$$\hat{\sigma }^{2} = \frac{1}{{N_{t} }}\left( {\varvec{y} - \varvec{F}\hat{\varvec{\beta} }} \right)^{T} \varvec{R}^{ - 1} \left( {\varvec{y} - \varvec{F}\hat{\varvec{\beta} }} \right)$$

(47)

where ${\varvec{F}}$ is an $N_{t} \times n$ regression matrix shown as follows:

$$\varvec{F = }\left[ \begin{gathered} f_{1} ({\varvec{x}}_{1} ) f_{2} ({\varvec{x}}_{1} ) \cdots f_{n} ({\varvec{x}}_{1} ) \\ f_{1} ({\varvec{x}}_{2} ) f_{2} ({\varvec{x}}_{2} ) \cdots f_{n} ({\varvec{x}}_{2} ) \\ \vdots \vdots \ddots \vdots \\ f_{1} ({\varvec{x}}_{{N_{t} }} ) f_{2} ({\varvec{x}}_{{N_{t} }} ) \cdots f_{n} ({\varvec{x}}_{{N_{t} }} ) \\ \end{gathered} \right]$$

(48)

${\varvec{R}}$ is an $N_{t} \times N_{t}$ correlation matrix in Eq. (49).

$$\varvec{R = }\left[ \begin{gathered} R({\varvec{x}}_{1} ,{\varvec{x}}_{1} ) R({\varvec{x}}_{1} ,{\varvec{x}}_{2} ) \cdots R({\varvec{x}}_{1} ,{\varvec{x}}_{{N_{t} }} ) \\ R({\varvec{x}}_{2} ,{\varvec{x}}_{1} ) R({\varvec{x}}_{2} ,{\varvec{x}}_{2} ) \cdots R({\varvec{x}}_{2} ,{\varvec{x}}_{{N_{t} }} ) \\ \vdots \vdots \ddots \vdots \\ R({\varvec{x}}_{{N_{t} }} ,{\varvec{x}}_{1} ) R({\varvec{x}}_{{N_{t} }} ,{\varvec{x}}_{2} ) \cdots R({\varvec{x}}_{{N_{t} }} ,{\varvec{x}}_{{N_{t} }} ) \\ \end{gathered} \right]$$

(49)

According to the principle of Kriging model, the predicted value at any untried point ${\varvec{x}}$ follows the Gaussian distribution with a mean of $\hat{\mu }_{{g_{K} }} ({\varvec{x}})$ and a variance of $\hat{\sigma }_{{g_{K} }}^{2} ({\varvec{x}})$; namely, $\hat{g}({\varvec{x}}) \sim N\left( {\hat{\mu }_{{g_{K} }} ({\varvec{x}}),\hat{\sigma }_{{g_{K} }}^{2} ({\varvec{x}})} \right)$. $\hat{\mu }_{{g_{K} }} ({\varvec{x}})$ and $\hat{\sigma }_{{g_{K} }}^{2} ({\varvec{x}})$ are shown in Eqs. (50) and (51), respectively,

$$\hat{\mu }_{{g_{K} }} (\varvec{x}) = \varvec{f}^{T} (\varvec{x})\hat{\varvec{\beta} } + \varvec{r}^{T} (\varvec{x})\varvec{R}^{ - 1} (\varvec{y} - \varvec{F}\hat{\varvec{\beta} })$$

(50)

$$\hat{\sigma }_{{g_{K} }}^{2} (\varvec{x}) = \hat{\sigma }^{2} [1 + \varvec{u}^{T} (\varvec{x})(\varvec{F}^{T} \varvec{R}^{ - 1} \varvec{F})^{ - 1} \varvec{u}(\varvec{x}) - \varvec{r}^{T} (\varvec{x})R^{ - 1} \varvec{r}(\varvec{x})]$$

(51)

where ${\varvec{r}}({\varvec{x}})$ is the correlation coefficient vector between training sample and predicted points. ${\varvec{r}}({\varvec{x}})$ and ${\varvec{u}}({\varvec{x}})$ are shown in Eqs. (52) and (53), respectively.

$${\varvec{r}}({\varvec{x}}) = [R({\varvec{x}},{\varvec{x}}_{1} ),R({\varvec{x}},{\varvec{x}}_{2} ), \cdots ,R({\varvec{x}},{\varvec{x}}_{{N_{t} }} )]^{T}$$

(52)

$$\varvec{u}(\varvec{x}) = \varvec{F}^{T} \varvec{R}^{ - 1} \varvec{r}(\varvec{x}) - \varvec{f}(\varvec{x})$$

(53)

Appendix 2: the proof of the importance samples

Suppose that the cumulative distribution function of the random vector ${\varvec{X}}$ is $F_{{\varvec{X}}} ({\varvec{a}}) = P\{ X_{1} \le a_{1} ,X_{2} \le a_{2} , \cdots ,X_{n} \le a_{n} \} = P\{ {\varvec{X}} < {\varvec{a}}\}$. Then,

$$F_{{\varvec{X}}} ({\varvec{a}}) = P\{ {\varvec{X}} < {\varvec{a}}\} = \int_{{ - {\mathbf{\infty }}}}^{{\varvec{a}}} { \cdots \int {\hat{h}_{{\varvec{X}}} (\varvec{x|\theta })d{\varvec{x}}} } = \frac{{\int_{{ - {\mathbf{\infty }}}}^{{\varvec{a}}} { \cdots \int {\pi_{{F_{t} }} (\varvec{x|\theta })f_{{\varvec{X}}} (\varvec{x|\theta })d{\varvec{x}}} } }}{{P_{ft\varepsilon } ({\varvec{\theta}})}}$$

(54)

Under the condition of the acceptance domain of $\Omega = \{ p - c\pi_{{F_{t} }} (\varvec{x|\theta }) \le 0\}$, where $p\sim U[0,1]$, $\varvec{x\sim }f_{{\varvec{X}}} (\varvec{x|\theta })$ and $c\pi_{{F_{t} }} (\varvec{x|\theta }) \le 1$, the conditional CDF $F_{{{\varvec{X}}|\Omega }} ({\varvec{a}}) = P\{ {\varvec{X}} < {\varvec{a}}|p < c\pi_{{F_{t} }} (\varvec{x|\theta })\}$ of vector ${\varvec{X}}$ on $\Omega$ can be estimated as follows:

$$\begin{gathered} F_{{{\varvec{X}}|\Omega }} ({\varvec{a}}) = P\{ {\varvec{X}} < {\varvec{a}}|p < c\pi_{{F_{t} }} (\varvec{x|\theta })\} \\ = \frac{{P\{ {\varvec{X}} < {\varvec{a}},p < c\pi_{{F_{t} }} (\varvec{x|\theta })\} }}{{P\{ p < c\pi_{{F_{t} }} (\varvec{x|\theta })\} }} \\ = \frac{{\int_{{ - {\mathbf{\infty }}}}^{{\varvec{a}}} { \cdots \int {\int_{0}^{{c\pi_{{F_{t} }} ({\varvec{a}})}} {f_{P} (p)f_{{\varvec{X}}} (\varvec{x|\theta })dpd{\varvec{x}}} } } }}{{\int_{{ - {\mathbf{\infty }}}}^{{ + {\mathbf{\infty }}}} { \cdots \int {\int_{0}^{{c\pi_{{F_{t} }} ({\varvec{a}})}} {f_{P} (p)f_{{\varvec{X}}} (\varvec{x|\theta })dpd{\varvec{x}}} } } }} = \frac{{\int_{{ - {\mathbf{\infty }}}}^{{\varvec{a}}} { \cdots \int {\pi_{{F_{t} }} (\varvec{x|\theta })f_{{\varvec{X}}} (\varvec{x|\theta })d{\varvec{x}}} } }}{{\int_{{ - {\mathbf{\infty }}}}^{{ + {\mathbf{\infty }}}} { \cdots \int {\pi_{{F_{t} }} (\varvec{x|\theta })f_{{\varvec{X}}} (\varvec{x|\theta })d{\varvec{x}}} } }} \\ = \frac{{\int_{{ - {\mathbf{\infty }}}}^{{\varvec{a}}} { \cdots \int {\pi_{{F_{t} }} (\varvec{x|\theta })f_{{\varvec{X}}} (\varvec{x|\theta })d{\varvec{x}}} } }}{{P_{ft\varepsilon } ({\varvec{\theta}})}} \\ \end{gathered}$$

(55)

where $f_{P} (p) = \left\{ \begin{gathered} 1, \, 0 \le p \le 1 \hfill \\ 0, {\text{else}} \hfill \\ \end{gathered} \right.$ is PDF of the standard uniform random variable $p$.

According to Eqs. (54) and (55), it is obvious that $F_{{\varvec{X}}}^{{\tilde{h}}} ({\varvec{a}}) = F_{{{\varvec{X}}|\Omega }}^{f} ({\varvec{a}})$. Therefore, the samples generated from the acceptance domain $\Omega$ are those generated from $\hat{h}_{{\varvec{X}}} (\varvec{x|\theta })$.