Bayes theorem–based and copula-based estimation for failure probability function

Abstract

The failure probability function (FPF), aiming to decouple the nested-loop reliability-based design optimization solution into a single-loop optimization problem, has attracted a great deal of interest from designers and researchers. It is defined as a function of failure probability with respect to the design parameter. Among the estimation methods for the FPF, the Bayes theorem based on probability distribution function methods is competitive. It transforms the FPF as the estimation of the conditional joint probability density function (PDF) of design parameters on the failure event and the augmented failure probability. The augmented failure probability can be estimated by Monte Carlo simulation, while for the joint multi-dimensional PDF, the existing estimation methods are unavailable. To alleviate this issue, a novel FPF estimation method is proposed by Bayes theorem and copula. In the proposed method, the FPF is derived as a product of the conditional copula density and the augmented failure probability, in which the vine copula is employed to disassemble the multi-dimensional conditional copula density into several bivariate copula density functions, and they can be completed by the existing PDF estimation methods. In contrast to the existing Bayes theorem–based estimation methods for the FPF, the proposed method interprets the FPF as the dependence function between design parameters and the augmented failure probability in terms of copula, which involuntarily breaks the limitation of the multi-dimensional design parameters. In addition, the adaptive Kriging surrogate model is embedded in the proposed method to improve the efficiency of the proposed method. The presented examples demonstrate the efficiency and accuracy of the proposed method.

1 Introduction

A typical reliability-based design optimization (RBDO) solution is a nested-loop approach, i.e., the candidate optimal solutions are first acquired in the outer loop which is followed by the evaluation of reliability constraints in the inner loop. To decouple the nested loop for the RBDO, the failure probability function (FPF) P_F(θ), defined as a function of failure probability varying with the design parameter vector θ = (θ₁, θ₂, ..., θ_m) (m is the dimension), has been proposed (Jensen 2005; Ching and Hsieh 2007a, b; Zou and Mahadevan 2006). If the function P_F(θ) can be obtained beforehand, the inner reliability analysis is transformed into an ordinary constraint, so the nested-loop problem of the RBDO is decoupled into a single-loop optimization problem (Xiukai 2013).

Estimating the function P_F(θ) is a challenging problem in real applications, and it has received great attention. Lots of estimation methods have been proposed to calculate the FPF. One strategy of these direct solutions is the interpolation method, i.e., after obtaining the numerous failure probabilities at the predefined interpolation points in the space of the design parameters, the FPF is approximated by the interpolation techniques. This solution is adopted by Jensen (2005), where a linear function of θ is used to calculate the function log[P_F(θ)], and at least m reliability analyses are required to determine the corresponding coefficients of the linear function. Gasser and Schueller (1997) proposed to employ a quadratic function of θ to replace the linear function to locally approximate log[P_F(θ)]. The minimum required number of reliability analyses is equal to m + m(m + 1)/2. Other competitive methods are based on the Bayes theorem. Au (2005) has proposed a novel augmenting the idea that only a single loop is needed to estimate the FPF P_F(θ). The design parameter θ is regarded as a predefined random variable, and Bayes theorem is used to transform the function P_F(θ) into a combination including the three parts, i.e., the joint probability density function (PDF) f_θ(θ), the conditional joint PDF f_θ(θ|F) on the failure event F, and the augmented failure probability P(F) of the failure event F. In these three parts, f_θ(θ) is predefined and P(F) can be estimated by the classification of the Monte Carlo simulation (MCS) samples; thus, f_θ(θ|F) is pivot for estimating the FPF P_F(θ). There are several PDF estimation methods, such as the maximum entropy method (Ormoneit and While 1999; Zhang and Pandey 2013) and the kernel density estimation (KDE) (Botev et al. 2010; Resenblatt 1956). However, for the multi-dimensional (m > 2) design parameters, the maximum entropy method and KDE method are infeasible. There is a strong need to estimate the multi-dimensional conditional joint PDF which is the most critical part of the FPF P_F(θ) based on Bayes theorem.

Recently, in the uncertainty analysis field, copula theory has been found widespread application for investigating the correlations of random variables. Copula function that fully defined the multivariate distribution of random variables links the joint distributions functions of random variables to their univariate marginal distributions (Nelsen 2006; Sklar 1959). A most remarkable feature of copula is that it retains all information of the dependence among the random variables (Montes and Heredia 2016). In recent years, the copula theory has been applied to reliability analysis widely. For example, Tang et al. (2013a, b) studied the impact of copula for modeling bivariate distributions on system reliability. Jiang et al. (2014) researched structural reliability analysis using copula-based evidence and used vine copula to process the multi-dimensional correlation for the structural reliability analysis (Jiang et al. 2015). In the engineering system with multiple failure modes, the correlations among the failure modes are investigated in Wu (2015) and He et al. (2018). Therefore, it is hopeful that a more universal reliability analysis strategy can be developed based on copula.

In this paper, FPF P_F(θ) is firstly interpreted as a dependence function between the design parameters and the augmented failure probability in terms of copula. According to the transforming the joint PDF to the copula density function, P_F(θ) is derived as a product of the conditional copula density function on the failure event and the augmented failure probability. Then, vine copula is used to disassemble the multi-dimensional conditional copula density functions into several bivariate copula density functions which can be obtained by the existing PDF estimations. Additionally, in order to improve the efficiency for classification of the conditional samples and estimating the augmented failure probability, the adaptive Kriging (AK) is embedded into the proposed method.

The rest of this paper is outlined as follows. In Section 2, we briefly review the formulations of the FPF and copula. Section 3 proposes a novel method based on Bayes theorem and copula, it derives the FPF as a product of the conditional copula density function and the augmented failure probability, and then, vine copula can be used to disassemble the multi-dimensional copula density functions into several bivariate copula density functions. Section 4 develops the solution for estimating the FPF by the proposed method, and the AK model is embedded to improve the efficiency of the proposed method. In Section 5, examples are given to illustrate the effectiveness of the proposed method. Section 6 draws some conclusions.

2 Review of basic definitions and formulations

2.1 Formulations of the FPF

Consider a performance function represented by Y = g(X) where X = (X₁, X₂, ..., X_n) denotes the n-dimensional random input vector, and there is m-dimensional design parameter vector θ = (θ₁, θ₂, ..., θ_m) of the m input variables. The FPF P_F(θ) under the given θ is described as:

$$ {P}_F\left(\boldsymbol{\theta} \right)=P\left(F\left|\boldsymbol{\theta} \right.\right)=\int {I}_F(x){f}_X\left(x\left|\boldsymbol{\theta} \right.\right) dx $$

(1)

where the failure event F is defined by g(x) as F = {g(x) ≤ 0} and f_X(x|θ) denotes the conditional PDF of the random input vector X on the given design parameter vector θ. I_F(x) represents the indicator function of failure domain. If g(x) ≤ 0, I_F(x) = 1; otherwise, I_F(x) = 0.

Based on the Bayes theory and Au’s idea (Au 2005), the design parameters θ can be treated as the random variables, and the PDF f_θ(θ) is assigned a prior PDF of θ subjectively. In this work, θ is assigned to be independent and follows the uniform distribution within the design space [θ^L, θ^U], where θ^U and θ^L represent the upper bound and lower bound, respectively. Hence, the FPF in (1) is derived as

$$ {P}_F\left(\boldsymbol{\theta} \right)=P\left(F\left|\boldsymbol{\theta} \right.\right)=\frac{f_{\theta}\left(\boldsymbol{\theta} \left|F\right.\right)P(F)}{f_{\theta}\left(\boldsymbol{\theta} \right)} $$

(2)

In which, f_θ(θ|F) represents the PDF of θ conditioned on the failure event F. The augmented failure probability P(F) of the failure event F is the probability the failure when both X and θ are considered to be random variables, and it is estimated as follows:

$$ P(F)=\int {I}_F(x){f}_X\left(x\left|\boldsymbol{\theta} \right.\right){f}_{\theta}\left(\boldsymbol{\theta} \right) dxd\theta $$

(3)

According to the expression of FPF in (2), the joint PDF f_θ(θ) is usually assigned beforehand, so it can be evaluated without computational cost. The augmented failure probability P(F) can be obtained by the traditional MCS in which both X and θ are considered to be random variables. Thus, the estimating for the conditional PDF f_θ(θ|F) is the key to the FPF. Among the existing PDF estimation methods, the maximum entropy method (Ormoneit and While 1999; Zhang and Pandey 2013) is only available for estimating one-dimensional PDF. The KDE method (Botev et al. 2010; Resenblatt 1956) is useable only for one-dimensional PDF or two-dimensional joint PDF estimation. Therefore, the existing methods based on Bayes theorem for estimating the FPF in (2) are limited for the solution to the multi-dimensional design parameters.

2.2 Definition of copula

It is well known that copula is a function that links the multivariate joint cumulative distribution function (CDF) with its one-dimensional marginal CDFs. By Sklar theory (Nelsen 2006; Sklar 1959), if two marginal CDFs ${F}_{\theta_i}\left({\theta}_i\right)$ and ${F}_{\theta_j}\left({\theta}_j\right)$ are continuous, and ${F}_{\theta_i{\theta}_j}\left({\theta}_i,{\theta}_j\right)$ is the joint CDF of θ_i and θ_j, then there is only one unique copula $C\left({F}_{\theta_i}\left({\theta}_i\right),{F}_{\theta_j}\left({\theta}_j\right)\right)$ to combine ${F}_{\theta_i{\theta}_j}\left({\theta}_i,{\theta}_j\right)$ with marginal ${F}_{\theta_i}\left({\theta}_i\right)$ and ${F}_{\theta_j}\left({\theta}_j\right)$. It is defined as:

$$ C\left({F}_{\theta_i}\left({\theta}_i\right),{F}_{\theta_j}\left({\theta}_j\right)\right)={F}_{\theta_i{\theta}_j}\left({\theta}_i,{\theta}_j\right) $$

(4)

Let ${u}_i={F}_{\theta_i}\left({\theta}_i\right)$ and ${u}_j={F}_{\theta_j}\left({\theta}_j\right)$, ${F}_{\theta_i}\left({\theta}_i\right)$ and ${F}_{\theta_j}\left({\theta}_j\right)$ are the CDFs of the ith and the jth variables respectively, then the copula function C(u_i, u_j) of θ_i and θ_j is a joint CDF with uniform marginal distribution in [0, 1]².

Accordingly, the copula density c(u_i, u_j) is given as:

$$ c\left({u}_i,{u}_j\right)=\frac{\partial^2C\left({u}_i,{u}_j\right)}{\partial {u}_i\partial {u}_j} $$

(5)

Subsequently, joint probability density function of θ_i and θ_j is derived as

$$ {\displaystyle \begin{array}{c}{f}_{\theta_i,{\theta}_j}\left({\theta}_i,{\theta}_j\right)=\frac{\partial^2{F}_{\theta_i,{\theta}_j}\left({\theta}_i,{\theta}_j\right)}{\partial {\theta}_i\partial {\theta}_j}\\ {}=\frac{\partial^2C\left({u}_i,{u}_j\right)}{\partial {u}_i\partial {u}_j}\frac{d{u}_j}{d{\theta}_j}\frac{d{u}_i}{d{\theta}_i}\\ {}=c\left({u}_i,{u}_j\right)\cdot {f}_{\theta_j}\left({\theta}_j\right)\cdot {f}_{\theta_i}\left({\theta}_i\right)\end{array}} $$

(6)

where ${f}_{\theta_i}\left({\theta}_i\right)=\frac{d{u}_i}{d{\theta}_i}$ and ${f}_{\theta_j}\left({\theta}_j\right)=\frac{d{u}_j}{d{\theta}_j}$ are marginal densities of θ_i and θ_j, respectively.

3 Bayes theorem–based and copula-based method for estimating the FPF

3.1 Expression of FPF based on Bayes theorem and copula

By use of the definition of copula in (4) and the copula density in (6), the conditional PDF f_θ(θ|F) can be derived as:

$$ {\displaystyle \begin{array}{c}{f}_{\theta}\left(\boldsymbol{\theta} \left|F\right.\right)=\frac{d{F}_{\boldsymbol{\theta}}\left(\boldsymbol{\theta} \left|F\right.\right)}{d\theta}\\ {}=\frac{d{C}_U\left(u\left|F\right.\right)}{d u}\cdot \frac{d u}{d\theta}\\ {}={c}_U\left(u|v\le {v}^{\ast}\right)\cdot {f}_{\theta}\left(\boldsymbol{\theta} \right)\end{array}} $$

(7)

where u = F_θ(θ) and v = F_Y(y), and for the special point y = 0 in the whole CDF of the model output, v^∗ = F_Y(0) = P(Y ≤ 0) holds, i.e., the augmented failure probability P(F) = v^∗.

Substituting (7) into (2), the FPF P_F(θ) can be derived as follows:

$$ {P}_F\left(\boldsymbol{\theta} \right)=P\left(F\left|\boldsymbol{\theta} \right.\right)=\frac{f_{\theta}\left(\boldsymbol{\theta} \left|F\right.\right)\cdot P(F)}{f_{\theta}\left(\boldsymbol{\theta} \right)}={c}_U\left(u|v\le {v}^{\ast}\right)\cdot {v}^{\ast } $$

(8)

Equation (8) indicates that the FPF P_F(θ) equals the product of the conditional copula density c_U(u|v ≤ v^∗) and the augmented failure probability v^∗. It also implies that P_F(θ) can be regarded as the dependence function of u and v with respect to the copula. In contrast to the existing Bayes theorem–based estimation methods limited for the one- or two-dimensional design parameters, the novel expression of FPF in terms of copula can involuntarily break the limitation of the multi-dimensional design parameters by use of the vine copula.

3.2 Vine copula processing multi-dimensional design parameters

For multi-design parameters in (8), multi-dimensional conditional copula density estimation is the key to the FPF. Since the core of a vine copula is to disassemble the joint PDF of multi-dimensional random variables into several bivariate copula functions related to the margin PDF and their conditional CDFs, vine copula (Shemyakin and Kniazev 2017; Czado 2010; Frederik and Scherer 2014; Bedford and Cooke 2001) is employed to process the multivariate correlations.

For m ≥ 3 random variables θ₁, θ₂, ..., θ_m, with continuous marginal distribution functions F₁(θ₁), F₂(θ₂), ..., F_m(θ_m), this is a unique copula function C_{1, 2, ..., m} expressed as

$$ {F}_{1,2,...,m}\left({\theta}_1,{\theta}_2,\cdots {\theta}_m\right)={C}_{1,2,...,m}\left({F}_1\left({\theta}_1\right),{F}_2\left({\theta}_2\right),...,{F}_m\left({\theta}_m\right)\right) $$

(9)

And copula density function c_{1, 2, ..., m} is derived as

$$ {\displaystyle \begin{array}{c}{c}_{1,2,...,m}\left({F}_1\left({\theta}_1\right),{F}_2\left({\theta}_2\right),\cdots, {F}_m\left({\theta}_m\right)\right)=\frac{\partial^m{C}_{1,2,...,m}\left({F}_1\left({\theta}_1\right),{F}_2\left({\theta}_2\right),\cdots, {F}_m\left({\theta}_m\right)\right)}{\partial {F}_1\left({\theta}_1\right)\partial {F}_2\left({\theta}_2\right)\cdots \partial {F}_m\left({\theta}_m\right)}\\ {}=\frac{f_{1,2,...,m}\left({\theta}_1,{\theta}_2,...,{\theta}_m\right)}{f_1\left({\theta}_1\right){f}_2\left({\theta}_2\right)...{f}_m\left({\theta}_m\right)}\end{array}} $$

(10)

In order to illustrate the construction of vine copula, the construction of a 3-dimensional vine copula is explained. For the three-dimensional design parameter vector θ = (θ₁, θ₂, θ₃), its joint PDF f(θ₁, θ₂, θ₃) can be decomposed as outlined below:

$$ f\left({\theta}_1,{\theta}_2,{\theta}_3\right)={f}_1\left({\theta}_1\right){f}_{2\left|1\right.}\left({\theta}_2\left|{\theta}_1\Big)\right.{f}_{3\left|1,2\right.}\right({\theta}_3\left|{\theta}_1,{\theta}_2\Big)\right. $$

(11)

where f_2|1(θ₂|θ₁) and f_{3|1, 2}(θ₃|θ₁, θ₂) are the corresponding conditional PDF.

Based on the theory of vine copulas, in a case with three variables, the joint PDF f_{1, 2, 3}(θ₁, θ₂, θ₃) is disassembled by D-vine as follows:

$$ {\displaystyle \begin{array}{ll}{f}_{1,2,3}\left({\theta}_1,{\theta}_2,{\theta}_3\right)& ={f}_1\left({\theta}_1\right)\cdot {f}_2\left({\theta}_2\right)\cdot {f}_3\left({\theta}_3\right)\\ {}& \cdot {c}_{1,2}\left({F}_1\left({\theta}_1\right),{F}_2\left({\theta}_2\right)\right)\cdot {c}_{2,3}\left({F}_2\left({\theta}_2\right),{F}_3\left({\theta}_3\right)\right)\\ {}& \cdot {c}_{1,3\mid 2}\left({F}_{1\mid 2}\left({\theta}_1\left|{\theta}_2\right.\right)\cdot {F}_{3\mid 2}\left({\theta}_3\left|{\theta}_2\right.\right)\right)\end{array}} $$

(12)

i.e.,

$$ {\displaystyle \begin{array}{ll}{c}_{1,2,3}\left({F}_1\left({\theta}_1\right),{F}_2\left({\theta}_2\right),{F}_3\left({\theta}_3\right)\right)& ={c}_{1,2}\left({F}_1\left({\theta}_1\right),{F}_2\left({\theta}_2\right)\right)\cdotp {c}_{2,3}\left({F}_2\left({\theta}_2\right),{F}_3\left({\theta}_3\right)\right)\\ {}& \cdotp {c}_{1,3\mid 2}\left({F}_{1\mid 2}\left({\theta}_1\left|{\theta}_2\right.\right)\cdotp {F}_{3\mid 2}\left({\theta}_3\left|{\theta}_2\right.\right)\right)\end{array}} $$

(13)

where

$$ {\displaystyle \begin{array}{l}{F}_{1\mid 2}\left({\theta}_1\left|{\theta}_2\right.\right)=\frac{\partial {C}_{1,2}\left({F}_1\left({\theta}_1\right)\cdot {F}_2\left({\theta}_2\right)\right)}{\partial {F}_2\left({\theta}_2\right)}\\ {}{F}_{3\mid 2}\left({\theta}_3\left|{\theta}_2\right.\right)=\frac{\partial {C}_{3,2}\left({F}_3\left({\theta}_3\right)\cdot {F}_2\left({\theta}_2\right)\right)}{\partial {F}_2\left({\theta}_2\right)}\end{array}} $$

(14)

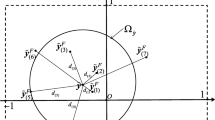
Figure 1 illustrates the principle of constructing a 3-dimensional vine copula by D-vine. It consists of (m − 1) = 2 trees T_j(j = 1, 2). In tree 1, three uniform distributed in [0,1] random variables F₁(θ₁),F₂(θ₂)_, and F₃(θ₃) are given and their pairwise dependences are represented by the bivariate copulas C₁₂ and C₂₃. In tree 2, there are two conditional CDFs F_1|2 and F_2|3 obtained by partial differentiation for the bivariate copulas C₁₂ and C₂₃ respectively, and the pairwise dependence between the two conditional CDFs is described by the conditional copula C_13|2.

Fig. 1

Construction of a 3-dimensional vine copula

In the case with three design variables θ = (θ₁, θ₂, θ₃), let u|v ≤ v^∗ = u^∗, i.e., ${u}^{\ast }=\left({u}_1^{\ast },{u}_2^{\ast },{u}_3^{\ast}\right)$. The FPF P_F(θ) with three design variables is derived as

$$ {\displaystyle \begin{array}{ll}{P}_F\left({\theta}_1,{\theta}_2,{\theta}_3\right)& =c\left(u\left|v\le {v}^{\ast}\right.\right)\cdot {v}^{\ast}\\ {}& =c\left(\left({u}_1,{u}_2,{u}_3\right)\left|v\le {v}^{\ast}\right.\right)\cdot {v}^{\ast}\\ {}& =c\left({u}_1^{\ast },{u}_2^{\ast },{u}_3^{\ast}\right)\cdot {v}^{\ast}\\ {}& ={c}_{12}\left({u}_1^{\ast },{u}_2^{\ast}\right)\cdot {c}_{23}\left({u}_2^{\ast },{u}_3^{\ast}\right)\cdot {c}_{13\left|2\right.}\left({u}_{1\left|2\right.}^{\ast },{u}_{3\left|2\right.}^{\ast}\right)\cdot {v}^{\ast}\end{array}} $$

(15)

where ${u}_{1\left|2\right.}^{\ast }={F}_{1\left|2\right.}\Big(\left({\theta}_1\left|F\Big)\right.\left|\Big({\theta}_2\left|F\Big)\right.\right.\right)$ and ${u}_{3\left|2\right.}^{\ast }={F}_{3\left|2\right.}\Big(\left({\theta}_3\left|F\Big)\right.\left|\Big({\theta}_2\left|F\Big)\right.\right.\right)$.

Similarly, in the case with four design variables θ = (θ₁, θ₂, θ₃, θ₄), P_F(θ) with four design variables is derived as

$$ {\displaystyle \begin{array}{ll}{P}_F\left({\theta}_1,{\theta}_2,{\theta}_3,{\theta}_4\right)& =c\left(u\left|v\le {v}^{\ast}\right.\right)\cdot {v}^{\ast}\\ {}& =c\left(\left({u}_1,{u}_2,{u}_3,{u}_4\right)\left|v\le {v}^{\ast}\right.\right)\cdot {v}^{\ast}\\ {}& =c\left({u}_1^{\ast },{u}_2^{\ast },{u}_3^{\ast },{u}_4^{\ast}\right)\cdot {v}^{\ast}\\ {}& ={c}_{12}\left({u}_1^{\ast },{u}_2^{\ast}\right)\cdot {c}_{23}\left({u}_2^{\ast },{u}_3^{\ast}\right)\cdot {c}_{34}\left({u}_3^{\ast },{u}_4^{\ast}\right)\\ {}& \cdot {c}_{13\left|2\right.}\left({u}_{1\left|2\right.}^{\ast },{u}_{3\left|2\right.}^{\ast}\right)\cdot {c}_{24\left|3\right.}\left({u}_{2\left|3\right.}^{\ast },{u}_{4\left|3\right.}^{\ast}\right)\\ {}& \cdot {c}_{14\left|23\right.}\left({u}_{1\left|23\right.}^{\ast },{u}_{4\left|23\right.}^{\ast}\right)\cdot {v}^{\ast}\end{array}} $$

(16)

where ${u}_{2\left|3\right.}^{\ast }={F}_{2\left|3\right.}\Big(\left({\theta}_2\left|F\Big)\right.\left|\Big({\theta}_3\left|F\Big)\right.\right.\right)$, ${u}_{4\left|3\right.}^{\ast }={F}_{4\left|3\right.}\Big(\left({\theta}_4\left|F\Big)\right.\left|\Big({\theta}_3\left|F\Big)\right.\right.\right)$, ${u}_{1\left|23\right.}^{\ast }={F}_{1\left|23\right.}\Big(\left({\theta}_1\left|F\Big)\right.\left|\Big({\theta}_2\left|F,\right.{\theta}_3\left|F\Big)\right.\right.\right)$, and${u}_{4\left|23\right.}^{\ast }={F}_{4\left|23\right.}\Big(\left({\theta}_4\left|F\Big)\right.\left|\Big({\theta}_2\left|F,\right.{\theta}_3\left|F\Big)\right.\right.\right)$.

Through the above analysis, it can be found that the FPF P_F(θ) with multi-dimensional design parameters is fully determined by the augmented failure probability v^∗ and several bivariate copula density functions disassembled from multivariate copula density. Therefore, based on the vine copula, the existing estimation methods based on Bayes theorem for the FPF P_F(θ) can be extended to the multi-dimensional design parameters.

4 Solutions for estimating the FPF-based copula

Based on the novel expression of the FPF in terms of copula in (8), it implies that the FPF P_F(θ) is fully determined by several bivariate copula density functions and the augmented failure probability v^∗, which can be estimated by a group of MCS samples. For estimating these bivariate copula density functions, generally, there are two categories for this purpose: the parametric estimation and the nonparametric estimation. Comparing with the former, because it does not need to assume any specific family for copula function, the nonparametric estimation is more general and flexible (Bedford and Cooke 2002; Cherubini and Luciano 2004; Scaille and Fermanian 2002). Many nonparametric methods can be employed to estimate the bivariate copula density. In this paper, a widely used two-dimensional KDE method (Botev et al. 2010) is employed to evaluate these bivariate copula density functions.

4.1 Strategy of estimating the conditional CDFs

In the construction of the vine copula, it should be noted that the corresponding conditional CDFs are required for estimating the bivariate copula density functions. Although there are several nonparametric methods (Gijbels et al. 2011; Gijbels et al. 2012; Kauermann and Schellhase 2014; Nagler and Czado 2016) for estimating these CDFs, they require the complicated estimation of the weights, integral or other operators. In order to reduce the complexity of estimation, in this work based on Bayes theorem, a strategy of estimating the conditional CDFs proposed in Li et al. (2019) is employed, and the conditional CDFs are derived as

$$ {\displaystyle \begin{array}{ll}{C}_{V\mid U}\left(v|u\right)& ={F}_{Y\mid X}\left(y|x\right)\\ {}& =P\left\{Y\le y|X=x\right\}\\ {}& =\frac{f_X\left(x|Y\le y\right)P\left\{Y\le y\right\}}{f_X(x)}\\ {}& ={c}_U\left(u|V\le v\right)v\end{array}} $$

(17)

$$ {\displaystyle \begin{array}{ll}{C}_{W\mid UV}\left(w|u,v\right)& ={F}_{Z\mid XY}\left(z|x,y\right)\\ {}& =P\left\{Z\le z|Y=y,X=x\right\}\\ {}& =\frac{f_{X,Y}\left(x,y|Z\le z\right)}{f_{X,Y}\left(x,y\right)}P\left\{Z\le z\right\}\\ {}& ={c}_{UV}\left(u,v|W\le w\right)w\end{array}} $$

(18)

where F_X(x) = U, F_Y(y) = V, and F_Z(z) = W, c_U is denoted as the copula density of U, f_{X, Y}(x, y) is the joint PDF of X and Y, and f_{X, Y}(x, y| Z ≤ z) and c_UV(u, v| W ≤ w) are the conditional joint PDF of X and Y and conditional copula density on the event {Z ≤ z}, respectively.

In the vine copula, two kinds of conditional CDFs are needed, such as ${u}_{1\left|2\right.}^{\ast }={F}_{1\left|2\right.}\Big(\left({\theta}_1\left|F\Big)\right.\left|\Big({\theta}_2\left|F\Big)\right.\right.\right)$ and ${u}_{1\left|23\right.}^{\ast }={F}_{1\left|23\right.}\Big(\left({\theta}_1\left|F\Big)\right.\left|\Big({\theta}_2\left|F,\right.{\theta}_3\left|F\Big)\right.\right.\right)$. Based on (17) and (18) derived in Li et al. (2019), the two kinds of conditional CDFs can be derived as

$$ {u}_{1\left|2\right.}^{\ast }={F}_{1\mid 2}\left({\theta}_1^{\ast}\left|{\theta}_2^{\ast}\right.\right)={c}_{12}\left({u}_2^{\ast}\left|{U}_1^{\ast}\right.\le {u}_1^{\ast}\right)\cdot {u}_1^{\ast } $$

(19)

$$ {\displaystyle \begin{array}{ll}{u}_{1\left|23\right.}^{\ast }& ={F}_{1\left|23\right.}\left(\Big({\theta}_1\left|F\Big)\right.\left|\Big({\theta}_2\left|F,\right.{\theta}_3\left|F\Big)\right.\right.\right)\\ {}& ={F}_{1\left|23\right.}\left(\left({\theta}_1^{\ast}\left|\Big({\theta}_2^{\ast },{\theta}_3^{\ast}\right.\right)\right.\\ {}& ={c}_{23}\left({u}_2^{\ast },{u}_3^{\ast}\left|{U}_1^{\ast}\right.\le {u}_1^{\ast}\right)\cdot {u}_1^{\ast}\end{array}} $$

(20)

where ${\theta}_i^{\ast }={\theta}_i\mid F\ \left(i=1,2,...,m\right)$ denotes the design parameter falling into the failure domain.

According to (19) and (20), the conditional CDFs in vine copula can be obtained by the one- or two-dimensional KDE.

4.2 Estimation procedure of the proposed method

The FPF P_F(θ) in (8) can be estimated by a group of MCS samples. The detailed steps of the proposed method are generalized as follows:

• Step 1. Generate N-samples of the margin CDF u of design parameters θ, N-samples of the design parameters θ and the corresponding input variables X. The detailed process is given as follows:

  • i. Produce N-size sample set A = {u₁, u₂, ..., u_N} of the m-dimensional random variables following the uniformly distributed in the interval [0, 1], where u_j = (u_1j, u_2j, ...u_mj) (j = 1, 2, ..., N).

  • ii. Obtain N-samples of the m-dimensional design parameters by ${\boldsymbol{\theta}}_j={F}_{\theta_j}^{-1}\left({u}_j\right)$, where each of design parameters θ is assigned to be independent and follow uniform distribution with the upper bound θ^U and the lower bound θ^L, i.e., θ ∼ U(θ^L, θ^U).

  • iii. For one sample point of design parameters θ, generate one corresponding input variable X. Thus, obtain N-size sample set S = {x₁, x₂, ..., x_N} of the m-dimensional input variables by f_X(X|θ), where x_j = (x_1j, x_2j, ...x_mj) (j = 1, 2, ..., N).

• Step 2. Compute the model output for all the samples of input variables in S by (21), then obtain a vector of model output of dimension N × 1:

$$ \boldsymbol{y}=g\left(\boldsymbol{S}\right) $$

(21)

• Step 3. Screen the failure samples from A, and denote ${\boldsymbol{A}}_F=\left\{{u}_1^{\ast },{u}_2^{\ast },...,{u}_{N_F}^{\ast}\right\}$ as the failure sample set, where N_F is the number of the failure samples and ${\boldsymbol{u}}_j^{\ast }=\left\{{u}_{1j}^{\ast },{u}_{2j}^{\ast },...,{u}_{mj}^{\ast}\right\}\ \left(j=1,2,...,{N}_F\right)$.

• Step 4. Estimate the augmented failure probability v^∗ by

$$ {v}^{\ast}\approx \frac{N_F}{N} $$

(22)

• Step 5. Use the D-vine construction of vine copula to disassemble the multi-dimensional copula density ${c}_{U_1,{U}_2,...{U}_m}\left({u}_1^{\ast },{u}_2^{\ast },...,{u}_m^{\ast}\right)$ into a product of several bivariate copula density functions and marginal PDFs.

• Step 6. Estimate the conditional CDFs disassembled from vine copula by use of the strategy of estimating the conditional CDFs introduced in Section 4.1.

• Step 7. Estimate the bivariate copula density functions disassembled from vine copula by use of two-dimensional KDE method.

• Step 8. Estimate the FPF P_F(θ) based on (8).

Apparently, for estimating the FPF P_F(θ), a set of N samples of the design parameters and input variables is needed. Thus, the computational cost is free of the dimensionality of the design variables. However, the computational burden of the proposed method with N times of the actual performance function evaluations is still unacceptable for some complex engineering problems requiring time-consuming finite element analysis. In order to enhance its applicability of the proposed method, the AK surrogate model based on U-learning function (Echard et al. 2011) is embedded in the proposed method to improve the efficiency.

4.3 The implementation of combining the proposed method with the AK model for estimating FPF

Based on the estimation procedure of the proposed method in Section 4.2, it can be found that the computational cost for estimating FPF by the proposed method is mainly consumed in classifying the samples set into the safety sample set and the failure sample set to estimating the augmented failure probability v^∗, while the copula density ${c}_{U_1,{U}_2,...{U}_m}\left({u}^{\ast}\right)$ is the byproduct of estimating v^∗. Therefore, the AK surrogate model can be employed to replace the actual performance function for classification of the samples based on U-learning function. The detailed introduction to the AK surrogate model (Echard et al. 2011) is given in the Appendix. And the detailed steps of the proposed method combining with the AK model are generalized as follows:

• Step 1. Generate N-size sample set A = {u₁, u₂, ..., u_N} of the m-dimensional random variables following the uniformly distributed in the interval [0, 1], where u_j = (u_1j, u_2j, ...u_mj) (j = 1, 2, ..., N).

• Step 2. Obtain N-samples of the m-dimensional design parameters by ${\boldsymbol{\theta}}_j={F}_{\theta_j}^{-1}\left({u}_j\right)$, where each of design parameters θ is assigned to be independent and follow uniform distribution with the upper bound θ^U and the lower bound θ^L, i.e., θ ∼ U(θ^L, θ^U).

• Step 3. For one sample point of design parameters θ, generate one corresponding input variable X. Thus, obtain N-size sample set S = {x₁, x₂, ..., x_N} of the m-dimensional input variables by f_X(X|θ), where x_j = (x_1j, x_2j, ...x_mj) (j = 1, 2, ..., N).

• Step 4. Select N₀-size initial sample points from S and calculate their outputs by the actual performance function, denoted as S₀ and g₀ respectively, and then collect them to the training sample set {S₀, g₀} to build the initial AK model g_K(x).

• Step 5. Select the new training sample point x_u by the following U-learning function:

$$ U\left({x}_j\right)=\frac{\left|{\mu}_{g_K}\left({x}_j\right)\right|}{\sigma_{g_K}\left({x}_j\right)} $$

(23)

where ${\mu}_{g_K}\left({x}_j\right)$ and ${\sigma}_{g_K}\left({x}_j\right)$ are respectively the prediction value and standard deviation of the current AK model g_K(x) at x_j ∈ S. And the new training sample point x_u is obtained by

$$ {x}_u=\arg\ \underset{x_j\in S}{\mathit{\min}}\left[U\left({x}_j\right)\right] $$

(24)

• Step 6. Judge the convergence of the current AK model:

  • i. If U(x_u) < 2, it indicates that the current g_K(x) does not converge, the training sample set {S₀, g₀} should be updated as {S₀ ∪ x_u, g₀ ∪ g(x_u)}. Then, g_K(x) should be updated by use of the updated training sample set and return to step 5.

  • ii. If U(x_u) ≥ 2, it indicates that the current g_K(x) is convergent, and it can correctly distinguish the symbols of the outputs at the sample points in S with 1 − Φ(−2) = 97.7% probability, where Φ(⋅) denotes the calculative distribution function of a standard normal variable. Then, execute step 7.

• Step 7. Screen the failure sample points from A by the convergent AK model g_K(x), and collect the failure sample points to the failure sample set ${\boldsymbol{A}}_F=\left\{{u}_1^{\ast },{u}_2^{\ast },...,{u}_{N_F}^{\ast}\right\}$, where N_F is the number of the failure samples and ${\boldsymbol{u}}_j^{\ast }=\left\{{u}_{1j}^{\ast },{u}_{2j}^{\ast },...,{u}_{mj}^{\ast}\right\}\ \left(j=1,2,...,{N}_F\right)$.

• Step 8. Estimate the augmented failure probability v^∗ by

$$ {v}^{\ast}\approx P\left({g}_K(x)\le 0\right)\approx \frac{N_F}{N} $$

(25)

• Step 9. Use vine copula to disassemble the multi-dimensional copula density ${c}_{U_1,{U}_2,...{U}_m}\left({u}_1^{\ast },{u}_2^{\ast },...,{u}_m^{\ast}\right)$ into a product of several bivariate copula density functions and marginal PDFs.

• Step 10. Estimate the conditional CDFs disassembled from vine copula by use of the strategy of estimating the conditional CDFs introduced in Section 4.1.

• Step 11. Estimate the bivariate copula density functions disassembled from vine copula by use of two-dimensional KDE method.

• Step 12. Estimate the FPF P_F(θ) based on (8).

Based on the estimation steps above, in order to construct the convergent AK model, N₀ + N_t times of model evaluations are acquired, where N_t is the size of the final new training sample points selected by (24). Generally, N₀ + N_t < < N. Therefore, the efficiency of the proposed method combining with the AK is improved greatly. Since the convergent AK model can correctly distinguish the performance function g(X) signs of samples in S with 1 − Φ(−2) = 97.7% probability based on U-learning function defined by (23), the precision of the proposed method embedding AK model can keep almost same as that of the proposed method without AK model, while the computational cost can be greatly reduced.

Figure 2 demonstrates the procedure of the proposed method for estimating the FPF.

Fig. 2

The flowchart of the proposed method for estimating the FPF

5 Illustrative examples

In this section, comparing with the traditional MCS with ${N}_{\theta_1}\cdot {N}_{\theta_2}\cdot ...,\cdot {N}_{\theta_m}\cdot N$ times of the performance function evaluations (where ${N}_{\theta_i}\ \left(i=1,2,...,m\right)$ denotes the number of the design parameter θ_i required at the predefined interpolation points, in this work, we discretize uniformly each design parameter space into 10 points, i.e., ${N}_{\theta_i}=10$, N is the number of performance function runs for estimating failure probability), three examples are analyzed to demonstrate the effectiveness of the proposed method by Bayes theorem and copula. The results obtained by the traditional MCS are regarded as the reference values.

5.1 Example 1: An automobile front axle

In the automobile engineering, the front axle supporting the weight of the front part of the vehicle is one of the most important structures, where the I-beam structure is general in the design of the front axle due to its high bend strength and light weight. As shown in Fig. 3, the dangerous location appears in cross section. And σ = M/W_x denotes the maximum normal stress and τ = T/W_ρ represents the shear stress, where M, T, W_x, and W_ρ are the bending moment, torque, section factor, and polar section factor, respectively. W_x and W_ρ are evaluated as follows:

$$ {W}_x=a{\left(h-2C\right)}^3/6h+B\left[{h}^3-{\left(h-2C\right)}^3\right]/6h $$

(26)

$$ {W}_{\rho }=0.8B{C}^2+0.4{a}^3\left(h-2C\right)/C $$

(27)

Fig. 3

Automobile front axle structure

To check the strength of the front axle, the output of the model is expressed by (28)

$$ g={\sigma}_s-\sqrt{\sigma^2+3{\tau}^2} $$

(28)

where σ_s is the yield strength and σ_s = 460 MPa. The geometry variables of I-beam including a, B, C, and h shown in Fig. 3 and the load variables including M and T are mutually independent with normal distribution. The distribution parameters are listed in Table 1.

Table 1 Distribution parameters of input variables for example 1

5.1.1 Case 1: One design parameter

Suppose the mean value of B be the single design parameter, i.e., θ = μ_B and μ_B ∈ [55, 75]. The interval of the design parameter μ_B is discretized uniformly into 10 points. The results of FPF P_F(θ) estimated by the MCS, the proposed method based on the Bayes theorem and copula, and the proposed method combining with AK are shown in Fig. 4. In the MCS, for estimating failure probability at each sample point of the design parameter μ_B, 10⁶ sample points of input random variable are needed, i.e., 10⁷ times of the model evaluations are required for these 10 sample points of μ_B. For the sake of fairness, the samples of input variables for the proposed method are same to 10⁶ at each sample point of the design parameter. However, Bayes theorem–based method is a single loop; 10⁶ times of model runs are required for all of the 10 sample points of the design parameter by the proposed method. In the proposed method combining with the AK model, only 233 times of the model runs are required to construct the convergent AK model for classification of the conditional samples and estimating the augmented failure probability, which improves the efficiency dramatically. Because the convergent AK model can identify the symbols of the output in sample pool correctly, the accuracy of the proposed method combining with AK is same as that of the proposed method without embedding AK.

Fig. 4

The estimates of FPF of case 1

As shown in Fig. 4, we can see that three curves plotted by the traditional MCS, the proposed method without embedding AK, and the proposed method combining with AK model are almost superposed, which indicates that the results estimated by the two proposed methods are consistent with those obtained by the traditional MCS.

In order to check the accuracy of the proposed method, the maximum relative error (MAXRE) is defined by

$$ MAXRE=\underset{j=1}{\overset{N_{\theta }}{\mathit{\operatorname{Max}}}}\left\{\frac{\left|{P}_{Fj}\left(\boldsymbol{\theta} \right)-{\hat{P}}_{Fj}\left(\boldsymbol{\theta} \right)\right|}{{\hat{P}}_{Fj}\left(\boldsymbol{\theta} \right)}\right\} $$

(29)

where N_θ is the number of design parameter θ required at the predefined interpolation points and P_Fj(θ) and ${\hat{P}}_{Fj}\left(\boldsymbol{\theta} \right)$ represent the failure probability estimated by the proposed method and that obtained by the MCS, respectively. Figure 5 demonstrates the MAXRE curve of FPF obtained by the proposed method vs sample size. It can be found that the MAXRE of results gradually decreases with the increase of sample size.

Fig. 5

The MAXREs estimated by the proposed method vs sample size in case 1

5.1.2 Case 2: Two design parameters

Suppose the mean value of a and B be the design parameters, i.e., θ = (μ_a, μ_B), and μ_a ∈ [10, 14] and μ_B ∈ [55, 75]. For each design parameters, we still discretize them into 10 points. Thus, 10 × 10 × 10⁶ model evaluations are needed by the traditional MCS, where for each sample of 10 × 10 design points, 10⁶ samples of input variables are employed for reliability analysis. While in the proposed method, as analyzed above in case 1, only a set of 10⁶ samples are enough; thus, the computational cost of the proposed method is free of the dimensionality of the design parameters. In order to construct the AK model to identify the sample points falling into the failure domain in samples pool with 10⁶ input variable samples, 100 initial samples and 149 training samples are needed. Therefore, the total number of model evaluating is only 249 in the proposed method combining with AK model.

The results of FPF in the diagonal of the whole design space are illustrated in Fig. 6. From Fig. 6, it can be seen that the curves obtained by the proposed method and that combining with AK model are in good agreement with that plotted by the traditional MCS. The MAXRE curve of results obtained by the proposed method and those estimated by MCS is plotted in Fig. 7. The MAXRE is generally smaller as the size of samples increasing, and when the sample size is 10⁸, the MAXRE is smaller than 0.1.

Fig. 6

The estimates of FPF of case 2

Fig. 7

The MAXREs estimated by the proposed method vs sample size in case 2

5.1.3 Case 3: Three design parameters

Suppose the mean value of a, B, and h be the design parameters, i.e., θ = (μ_a, μ_B, μ_h), where μ_a ∈ [10, 14], μ_B ∈ [55, 75], and μ_h ∈ [75, 95]. The region of each design parameter is uniformly discretized into 10 points. Thus, in the whole space of design parameters, 10 × 10 × 10 × 10⁶ model evaluations are required by the traditional MCS, where 10⁶ sample points are employed to estimate the failure probability at each design point. For this problem with three design parameters, vine copula is needed to decompose the joint conditional PDF to several bivariate copula densities. Because of the Bayes theorem, only a single loop with a set of 10⁶ samples is needed by the proposed method. While for the proposed method combining with AK model, 246 samples are enough for constructing the AK model to estimate the augmented failure probability. The efficiency of the methods for example 1 is listed in Table 2.

Table 2 The efficiency of the methods for example 1

The results of FPF at the edges of the whole design space are plotted in Fig. 8. As demonstrated in Fig. 8, the curves obtained by the proposed two methods are consistent with each other. There is very small difference between the results evaluated by the proposed methods and those obtained by MCS. Figure 9 demonstrates the MAXRE of the results vs the sample size. It can be found that the bigger the sample size, the smaller the MAXRE, and it indicates that the proposed method is accurate for estimating FPF when the size of samples is big enough.

Fig. 8

The estimates of FPF of case 3

Fig. 9

The MAXREs estimated by the proposed method vs sample size in case 3

5.2 Example 2: An aero engine turbine disk

Turbine disk (Yun et al. 2018), which plays a big role in supporting, connecting, and transmitting torque and power, and meanwhile, undergoes the complex loads, is a very important part in engine turbine. Because of the complex structural shape, the stress concentration easily takes place in some parts during the working process, such as tongue, groove bottom, and pin hole. After working for a period of time, some cracks may appear. Figure 10 shows the crack of an aero engine turbine disk.

Fig. 10

Crack of an aero engine turbine disk

The load applied on an aero engine turbine disk is F = Cω²/2π + 2ρω²J, in which ρ, C, ω, and J are the mass density, coefficient, rotation angular velocity, and moment of inertia, respectively. And ω = 2πn, n is the rotational frequency. The performance function of the structure is

$$ g\left({\sigma}_s,\rho, C,A,J,n\right)={\sigma}_sA-F $$

(30)

where σ_s is the ultimate strength and A is the sectional area.

The distribution types and parameters of input variables are listed in Table 3.

Table 3 Distribution parameters of input variables for example 2

Suppose the mean value of σ_s, ρ, C, and n be the design parameters, i.e., $\boldsymbol{\theta} =\left({\mu}_{\sigma_s},{\mu}_{\rho },{\mu}_C,{\mu}_n\right)$, and ${\mu}_{\sigma_s}\in \left[0.6\times {10}^9,1.6\times {10}^9\right]$, μ_ρ ∈ [4000, 12000], μ_C ∈ [2.67, 8.67], and μ_n ∈ [150, 250]. With 10 points uniformly discretized for each design parameter in the design space, 10 × 10 × 10 × 10 × 10⁶ times of model evaluations are needed by the traditional MCS, where 10⁶ times of computational cost are used for each reliability analysis at each sample point of the design parameters. The computational burden of MCS with 10¹⁰ numbers of model runs is very heavy. In the proposed method, vine copula is employed to process four-dimensional design parameters by (16), and 10⁶ times of model runs are enough for estimating the augmented failure probability. Combining with AK model with 100 initial samples and 106 training samples, the computational cost is only 206. Because the convergent AK model can recognize all symbols of outputs at all samples in the sample pool, the calculation accuracy of the proposed method combining with AK keeps as same as that of the proposed method without embedding AK, but the former efficiency is greatly higher. The efficiency of the methods for example 2 is listed in Table 4.

Table 4 The efficiency of the methods for example 2

The curves of FPF at the edges of the design space are plotted in Fig. 11. As illustrated in Fig. 11, we can see that the curves of the FPF obtained by the proposed two methods are mostly in agreement with those estimated by the traditional MCS.

Fig. 11

The estimates of FPF of the aero engine turbine disk with four design parameters

5.3 Example 3: A flap structure

In this example, a flap structure with four parts, including moveable wings, fixed wing, the control mechanism, and beams subjected to an aerodynamic load F, is investigated (Wei et al. 2013). One of the main failure modes is that the maximum displacement Δ_max of the flap exceeds the threshold Δ_D. Here, Δ_D = 0.4 m_. Based on the finite element analysis (the model is built by ANSYS 14 software in this work, as shown in Fig. 12), the performance function for the flap structure is:

$$ g\left({t}_1,{t}_2,{t}_3,{E}_1,{G}_1,{E}_2,{G}_2,F\right)={\varDelta}_D-{\varDelta}_{\mathrm{max}} $$

(31)

where t₁, t₂, and t₃ are the thickness of beams, respectively. E₁ and E₂ denote Young’s modulus of the skin and the frame, respectively. And G₁ and G₂ correspond to the shear modulus, respectively. These input variables are assumed to be independent and follow the normal distribution. Their distribution parameters are listed in Table 5.

Fig. 12

Finite element model of the flap structure

Table 5 Distribution parameters of the flap

In this example, five design parameters including the mean values of t₁, t₂, t₃, G₁, and G₂ are considered design parameters, i.e., $\theta =\left({\mu}_{t_1},{\mu}_{t_2},{\mu}_{t_3},{\mu}_{G_1},{\mu}_{G_2}\right)$, and ${\mu}_{t_1}\in \left[1.9,2.1\right]$, ${\mu}_{t_2}\in \left[1.9,2.1\right]$, ${\mu}_{t_3}\in \left[3.8,4.2\right]$, ${\mu}_{G_1}\in \left[2.5\times {10}^4,2.7\times {10}^4\right]$, and ${\mu}_{G_2}\in \left[2.6\times {10}^4,2.8\times {10}^4\right]$. The region of each design parameter is uniformly discretized into 10 points. Thus, in the whole space of design parameters, 10⁵ × 10⁶ model evaluations are required by the traditional MCS, where 10⁶ sample points are employed to estimate the failure probability at each design point. As mentioned by other examples, only a set of 10⁶ samples is needed for the proposed method. While in the proposed method combining with AK model, 416 times of model runs are required to construct the convergent AK model for FPF, which improves the efficiency greatly. The efficiency of the methods for example 3 is listed in Table 6.

Table 6 The efficiency of the methods for example 3

The results of FPF at the edges of the whole design space are plotted in Fig. 13. Figure 13 shows the curves obtained by proposed methods are almost consistent with those obtained by the MCS.

Fig. 13

The estimates of FPF of example 3 with five design parameters

6 Conclusion

The FPF is defined as a failure probability function with respect to the design parameters of the random inputs, which can be used to decouple the nested-loop reliability-based design optimization solution into a single-loop optimization problem. In this paper, based on Bayes theorem and copula, a novel FPF estimation method is proposed. In the proposed method, FPF is derived as a product of the conditional copula density and the augmented failure probability, in which the vine copula can be used to disassemble the multi-dimensional conditional copula density into several bivariate copula density functions which can be estimated by the two-dimensional KDE method. Additionally, a novel strategy of estimating the conditional CDFs is used in vine copula. In contrast to the existing Bayes theorem–based methods for FPF, the novel method can be extended to multi-dimensionality. In order to further improve the efficiency for complex and time-consuming performance function to meet engineering requirements, the AK model based on U-learning function is embedded in the proposed method to estimate the augmented failure probability.

An automobile front axle, an aero engine turbine disk, and a planar 10-bar structure have been introduced for validating the proposed methods. Two main conclusions can be drawn. First, the proposed method can be used to estimate the FPF with multi-dimensional design parameters accurately. Second, the proposed method combining with AK model can dramatically reduce the computational burden to meet the requirement of the engineering application.

Appendix

To construct a Kriging surrogate model, the output of the model Y = g(X) can be considered a realization of stochastic process represented in Zheng et al. (2017) and Hu et al. (2017)

$$ {g}_K(X)={\beta}_0+Z(X) $$

(32)

where β₀ is the mean value and Z(X) represents a stationary Gaussian process with zero mean and a covariance between two samples x⁽ⁱ⁾ and x^(j), the covariance is defined by

$$ Cov\left[Z\left({x}^{(i)}\right),\kern0.5em Z\left({x}^{(j)}\right)\right]={\sigma}^2R\left({x}^{(i)},{x}^{(j)}\right) $$

(33)

where σ² is the process variance of Z(⋅), R is the spatial correlation function, which is only dependent on the spatial distance between x⁽ⁱ⁾ and x^(j). In this paper, the widely used Gaussian correlation is employed.

Therefore, for the arbitrary sample x, the Kriging model g_K(x) is a Gaussian random process, i.e., ${g}_K(x)\sim N\left({\mu}_{g_K}(x),{\sigma}_{g_K}^2(x)\right)$, where ${\mu}_{g_K}(x)$ and ${\sigma}_{g_K}^2(x)$ are the Kriging prediction mean and variance respectively. More details can be obtained in Zheng et al. (2017) and Hu et al. (2017).

In order to construct a convergent adaptive Kriging (AK) model for the output of model and to identify the input samples falling into the failure domain, a sample pool and an active learning strategy are required. Firstly, a sample pool of input variables is built as S = {x₁, x₂, ..., x_N}. Subsequently, N₀ initial samples are selected to establish the initial Kriging model. Then, an active learning function is employed to select new training sample with the most contribution to the prediction quality to refine the initial Kriging model. For the failure problem, a widely used learning function, named as U-learning function (Echard et al. 2011), is adopted and it is denoted as

$$ U(x)=\frac{\left|{\mu}_{g_K}(x)\right|}{\sigma_{g_K}(x)} $$

(34)

The U-learning function implies a reliability index of misjudging the sign of g(x) by g_K(x), i.e.,

$$ \varPhi \left(-U(x)\right)=\varPhi \left(-\frac{\left|{\mu}_{g_K}(x)\right|}{\sigma_{g_K}(x)}\right) $$

(35)

where Φ(⋅) denotes the calculative distribution function of a standard normal variable. Thus, the new training sample can be found in the sample pool by

$$ {x}_u=\arg\ \underset{x\in S}{\mathit{\min}}\left[U(x)\right] $$

(36)

When U(x) = 2, it indicates that there is Φ(−2) = 0.0228 probability to misjudge the sign of g(x). Then, the stop criterion of selecting the new training point in the sample pool S to update the current Kriging model is given as

$$ \underset{x\in S}{\mathit{\min}}\left[U(x)\right]\ge 2 $$

(37)

The flowchart of the AK model based on U-learning function is shown in Fig. 14.

Fig. 14

Flowchart of the AK model based on U-learning function

Replication of results

The original codes of examples in Section 5.1 including 3 folders are available in the Supplementary materials. The results can be replicated by running codes directly.