Design sensitivity analysis for transient responses of viscoelastically damped systems using model order reduction techniques

Abstract

Design sensitivity analysis (DSA) of transient responses, which are indispensable in gradient-based time domain optimization, often requires excessive computational resources for viscoelastically damped systems to directly differentiate and integrate the full-order model (FOM). In this paper, an efficient model-order reduction (MOR)–based DSA framework is developed for capturing the 1st- and 2nd-order derivatives of the transient responses and response functions for viscoelastically damped systems. The damping force is represented by a non-viscous damping model, which depends on the past history of motion via convolution integrals over suitable kernel functions. The direct differentiation method (DDM) is used to derive the DSA. Three robust modal reduction bases, namely multi-model (MM) method, modal strain energy modified by displacement residuals (MSER) method and improved approximation method (IAM) are introduced to reduce the system dimension. Based on a generalized damping model in expression of fraction formula, a reduced state-space formulation without convolution integral term is derived. The 1st- and 2nd-order derivatives of the transient responses and response functions are calculated using a modified precise integration method and the DDM on the reduced stage. The computational efficiency and accuracy of the presented methods are illustrated and compared by two examples. The results indicate that the computational time is significantly reduced by the proposed MOR methods maintaining fairly good accuracy. Among these methods, the MM method represents the most compromise between precise and efficiency and would be the best candidate to be the reduction basis for calculating the time domain DSA of large-scale viscoelastically damped systems.

1 Introduction

Design sensitivity analysis (DSA) is the study of how the measurable outputs of a model change with respect to changes in its design variables (Martins and Hwang 2013). It plays a key role in gradient-based optimization (Zhang and Kang 2014; Xiao et al. 2020), model-updating (Machado et al. 2018), uncertainty quantification (Wang et al. 2019) and structural reliability (Chen et al. 2020). However, the majority of DSA studies remain focused on undamped or viscously damped systems, with only a few papers deal with the viscoelastically damped systems. Viscoelastic materials have been extensively utilized in controlling vibration and noise of engineering structures because of their favourable characteristics in energy dissipation. The non-viscous damping model, which assumes that the dissipative forces depend on the past history of motion via convolution integrals over suitable kernel functions (Adhikari 2013), provides an effective method to represent the viscous and elastic character of the viscoelastic materials. It has been considered to be the most general damping model within the scope of linear system (Woodhouse 1998). Currently, the DSA studies of the non-viscously damped systems are limited mostly to their eigensolution (Adhikari and Friswell 2006; Li et al. 2012; Lin et al. 2020) and frequency response function (FRF) (de Lima et al. 2010b; Lewandowski and Łasecka-Plura 2016; Xie et al. 2019) problems, the corresponding DSA methods for transient responses are less concerned. But in practice, the viscoelastically damped systems are often subjected to transient excitations, which may cause severe undesired vibrations and noises. Therefore, there is a great desire to develop accurate and efficient DSA methods that are capable of predicting the dynamic properties of the non-viscously damped systems during transient simulations.

In general, approaches for DSA can be divided into three broad categories (Kang et al. 2006): finite difference method (FDM), adjoint variable method (AVM) and direct differentiation method (DDM). The FDM uses numerical perturbation of design variables and is easy to be implemented. However, it suffers from subtractive cancelation and truncation errors at small and large perturbation values, respectively. Besides, a complete reanalysis is needed for each design variable, which is extremely time-consuming. It has been proved in Alberdi et al. (2018) that, when the number of design variables is larger than the number of response functions, e.g., topology optimization, the AVM is a more computationally efficient way to calculate sensitivity than the DDM. However, for transient problems, the AVM requires a reverse transient analysis to obtain the adjoint variables. This may result in storage problems for large-scale systems since the time integration has to be performed sequentially (Hooijkamp and van Keulen 2018). Hence, the DSA for transient problems is often performed using the DDM (Callejo et al. 2015; Dopico et al. 2018; Callejo and Dopico 2019). For the DSA of viscoelastically damped systems, Li et al. (2013) derived both AVM and DDM formulations of the transient responses for the non-viscously damped systems based on the discrete Fourier transform and inverse Fourier transform algorithms. Kai and Waisman (2015) proposed a time-dependent discretize-then-differentiate AVM in their viscoelastic topology optimization framework and proved the importance of accounting for viscoelastic effects in structural optimization algorithms (Kai and Waisman 2016). Yun and Youn (2017) developed a DSA method of transient responses for generalized Maxwell model based on the discretize-then-differentiate AVM and the implicit Newmark’s time integration scheme. Ding et al. (2018c) proposed a differentiate-then-discretize AVM and a DDM (Ding et al. 2019), successively, for transient DSA of non-viscously damped systems and conducted a comparative study by considering computational accuracy, efficiency and implementation of each method.

However, the introduction of viscoelastic effects described by the non-viscous damping models significantly increase the system dimension, since extra dissipation coordinates or internal variables are included for analyzing, especially for large-scale problems. Particularly, when considering transient responses, one must utilize direct integration methods to obtain transient solutions at each time point. This can leave a massive computational cost when applying the DSA. Model order reduction (MOR) techniques, which aims at finding a lower-dimensional system with relative high-quality approximation, are ideal choice to improve the computational efficiency and reduce the storage requirement. The MOR techniques, such as mode displacement methods, Krylov subspace–based methods and Ritz vector methods, are widely used in modal analysis and dynamic response calculations (Besselink et al. 2013). Similarly, they also can be used to decrease the computational cost and storage of DSA. Yoon (2010) applied three MOR schemes, namely mode superposition method (MSM), Ritz vector method and quasi-static Ritz vector (QSRV) method in the framework of topology optimization for FRF problem. Kang et al. (2012) developed an undamped eigenmode-based MOR to reduce the system dimension of state space formulation when calculating the harmonic response sensitivities of non-proportional damping system using the AVM. Recently, Koh et al. (2020) further developed a multi-substructure multi-frequency QSRV method to compute the dynamic responses and sensitivity values. Later, Liu et al. (2015) conducted a MOR-based topology optimization to harmonic responses based on mode displacement method (MDM) and mode acceleration method (MAM), respectively. Zhao and Wang (2016) extended the MDM and MAM to the time domain response problems and investigated the effectiveness within the framework of density-based topology optimization. Zhao et al. (2020) proposed an adaptive hybrid expansion method for efficient structural topology optimization by using the MSM and Neumann expansion.

Most of the abovementioned MOR-DSA studies consider undamped or viscously damped systems. These MOR techniques give good results when the structure is lightly damped, but cannot directly incorporate the frequency-dependent behavior exhibited by certain highly damped materials. Trindade (2006) proposed a complex-based modal reduction method for viscoelastically damped beams through internal variables projection. de Lima et al. (2010a) developed a robust enriched Ritz approach for viscoelastically damped structures and applied it into the component mode synthesis method. Li et al. (2014) derived three projection bases for viscoelastically damped systems by considering higher order modes, which aims at eliminating the modal truncation problem in FRF problem. Xie et al. (2018) presented a MOR technique based on second-order Arnoldi algorithm for solving the frequency-dependent damping systems and applied it to the topology optimization procedure for efficiently calculating the structural response and sensitivity analyses (Xie et al. 2019). Recently, Rouleau et al. (2017) evaluated a variety of modal projection-based MOR techniques for structures with frequency-dependent damping and drawn some instructive conclusions by comparing their computational accuracy and efficiency.

Although the MOR techniques have been well established for viscoelastically damped systems of harmonic responses, few attentions have been paid to their counterparts of transient responses. Park et al. (1999) proposed an internal balancing based MOR method for Golla-Hughes-McTavish (GHM) model without the need to increase the dimension of original model. Zghal et al. (2015) reviewed some MOR methods for viscoelastic sandwich structures represented by the GHM model and calculated the transient responses using the Newmark’s integration method. Ding et al. (2018b) developed two robust modal reduction bases, namely multi-model (MM) method and modal strain energy by first-order correction (MSEC) method, to solve the transient responses of structural systems with multiple damping models. Kuether (2019) presented a two-tier MOR procedure along with Newmark-β method to perform numerical time integration for viscoelastically damped finite element models.

The overarching goal of this paper is to develop an efficient MOR-DSA method for transient responses of viscoelastically damped systems. Greene and Haftka (1989) reduced the system dimension using the traditional basis of vibration modes and performed the DSA using the forward difference procedure, central difference procedure and DDM. Han (2013) developed an efficient MOR method to calculate the approximation of both transient responses and their sensitivities. The projection matrix is generated from Krylov basis vectors instead of the traditional eigenvectors or Ritz vectors. However, both methods are limited to viscously damped systems and adopted the Newmark’s integration method to obtain the transient responses. It has been pointed out in Greene and Haftka (1989) that any numerical error associated with the numerical solutions of the transient responses would have a significant effect on the accuracy of derivatives. When computing the transient responses of viscoelastically damped systems, a modified precise integration method (MPIM) has been proofed much more accurate than the Newmark’s implicit and explicit methods (Ding et al. 2018a). In this paper, three different modal-projection bases are presented to improve the efficiency and accuracy of the approximated solutions of the sensitivity results. It is hoped that this study will clarify which modal-projection basis yields the best trade-off between efficiency and accuracy for computing the sensitivities of transient responses and their response functions for viscoelastically damped systems. To this end, the DDM is used to conduct the DSA for its high numerical stability, mathematically easy to understand and, most importantly, accessible to obtain second-order derivatives.

The remainder of this paper is organized as follows: Section 2 gives theoretical background on viscoelastically damped systems and problem description on DSA methods, whereas Section 3 presents three projection-bases for reducing the system dimension of the viscoelastically damped systems. Section 4 develops the DSA framework based on the MOR and MPIM techniques and derives the detailed expressions of the first- and second-order sensitivities for the transient responses and response functions. Section 5 applies the developed methods to two numerical examples and demonstrates their efficiency and accuracy under various conditions and parameters on calculating sensitivity values. Finally, Section 6 finishes with some important conclusions.

2 Theoretical background and problem description

2.1 Governing equation of viscoelastically damped systems

The equations of motion of an N degree-of-freedom (DOF) linear system with viscoelastic constitutive models, which assume that the dissipative forces depend on the past history of motion via convolution integrals over suitable kernel functions, can be expressed in time domain as (Cook et al. 2007; Kuether 2019)

$$ \begin{array}{@{}rcl@{}} &&\mathbf{M}\ddot{\mathbf{x}}(t) + {{\mathbf{C}}_{0}}\dot{\mathbf{x}}(t) + {{\mathbf{K}}_{K}}{{\int}_{0}^{t}} {{g_{K}}(t - \tau )} \dot{\mathbf{x}}(\tau )d\tau \\&& + {{\mathbf{K}}_{G}}{{\int}_{0}^{t}} {{g_{G}}(t - \tau )} \dot{\mathbf{x}}(\tau )d\tau+ {{\mathbf{K}}_{E}}{\mathbf{x}}(t) = {\mathbf{f}}(t) \end{array} $$

(1)

together with the initial conditions

$$ {\mathbf{x}}(t = 0) = {{\mathbf{x}}_{0}} \in \mathbb{R}^{N},\dot{\mathbf{x}}(t = 0) = {\dot{\mathbf{x}}_{0}} \in \mathbb{R}^{{N}}, $$

(2)

where t denotes time, τ is retardation time, and M, C₀ and K_E $\in \mathbb {R}^{{N \times N}}$ are mass, viscous damping and elastic stiffness matrix, respectively (real and symmetric in this paper). K_K and K_G $\in \mathbb {R}^{{N \times N}}$ are viscoelastic bulk and shear stiffness matrix, respectively. g_K(t) and g_G(t) are the corresponding kernel functions for the bulk and shear moduli. ${\mathbf {x}}(t), \dot {\mathbf {x}}(t), \ddot {\mathbf {x}}(t) \in \mathbb {R}^{{N}}$ are displacement, velocity and acceleration vectors, ${\mathbf {f}}(t) \in \mathbb {R}^{{N}}$ is forcing vector.

From the mathematical point of view, (1) can be further transformed into a more general form

$$ \mathbf{M}\ddot{\mathbf{x}}(t) + {{\mathbf{C}}_{0}}\dot{\mathbf{x}}(t) + \sum\limits_{k = 1}^{n} {{{\mathbf{C}}_{k}}{{\int}_{0}^{t}} {{g_{k}}(t - \tau )} \dot{\mathbf{x}}(\tau )d\tau } + {{\mathbf{K}}_{E}}{\mathbf{x}}(t) = {\mathbf{f}}(t), $$

(3)

where ${{\mathbf {C}}_{k}} \in \mathbb {R}^{{N \times N}}$ is k th frequency-dependent coefficient damping matrix and g_k(t) is the corresponding kernel function. This coupled integro-differential equation has been widely used in non-viscous damping systems, which the dissipative forces depend on any quantity other than the instantaneous generalized velocities (Adhikari 2013). Besides, (3) is also able to account for structural systems with multiple damping models (Cortés et al. 2009; Ding et al. 2018a; Ding et al. 2018b). For large engineering structure, where the damping behavior varies due to differing geometric and/or material properties, each damping material and component is partially distributed in the whole system. Therefore, the coefficient matrix C_k is not always of full rank and can be decomposed into rank-revealing form

$$ {\mathbf{C}}_{k} = {\mathbf{L}}_{k}{\mathbf{R}}_{k}^{T}, $$

(4)

where ${\mathbf {L}}_{k}, {\mathbf {R}}_{k} \in \mathbb {R}^{{N \times {r_{k}}}}$ are full column rank and r_k denotes the rank of matrix C_k. Some efficient rank-revealing methods can be found in Li and Zeng (2005). Equation (3) can be equivalently transformed into Laplace domain with zero initial conditions as

$$ \left( {{s^{2}}{\mathbf{M}} + s\left( {{{\mathbf{C}}_{0}} + \sum\limits_{k = 1}^{n} {{G_{k}}(s){{\mathbf{C}}_{k}}} } \right) + {{\mathbf{K}}_{E}}} \right){\mathbf{X}}(s) = {\mathbf{F}}(s), $$

(5)

where ${\mathbf {X}}(s) = L\left [ {{\mathbf {x}}(t)} \right ],{{G}}(s) = L\left [ {{{g}}(t)} \right ],{\mathbf {F}}(s) = L\left [ {{\mathbf {f}}(t)} \right ]$ and $L\left [ \bullet \right ]$ denotes Laplace transform. In context of this paper, s is the Laplace parameter and has the relationship s = iω, where ${\mathrm {i}} = \sqrt { - 1}$ and $\omega \in \mathbb {R}{^{+}}$ denotes the circle frequency.

2.2 Review of kernel function and eigenvalue problem

The kernel function G(s) is also known as retardation function, heredity function, relaxation function or after-effect function in other subjects. Mathematically, any causal model that makes the energy dissipation functional non-negative could be a possible candidate for a non-viscous damping model (Adhikari 2013). Therefore, a wide range of choices are possible. These kernel functions can be obtained either based on a physics-based approach, or by a mathematical approach (for example, by priori selecting a model and fitting its parameters from experiments).

The constitutive relationship of the physics-based approach is derived from a combination of springs and dashpots, such as Maxwell model, Voigt model and generalized Maxwell model. Other kernel functions based on the mathematical approach are also promising and had been used by many authors, such as Biot model, exponential damping model, GHM model, Anelastic Displacement Field (ADF) model and fractional derivative model. The detailed expressions and comparisons can be found in Adhikari (2013), Ding et al. (2019), and Mukhopadhyay et al. (2019) for further reading.

The generalized eigenvalue problem associated with (5) gives

$$ \begin{array}{@{}rcl@{}} &&\left( {{\lambda_{j}^{2}}{\mathbf{\mathbf{M}}} + {\lambda_{j}}{{\mathbf{C}}_{0}} + {\lambda_{j}}\sum\limits_{k = 1}^{n} {{G_{k}}({\lambda_{j}}){{\mathbf{C}}_{k}} + {{\mathbf{K}}_{E}}}} \right){{\boldsymbol{\varphi }}_{j}} = {\mathbf{0}}, \\ && \forall j = 1,2, \cdot\cdot\cdot J, \end{array} $$

(6)

where λ_j is the j th complex eigenvalue, φ_j represents the corresponding j th complex eigenvector and J is the order of the eigenvalue problem. It is worthy noting that the order of an N DOF eigenvalue problem for the viscoelastically damped systems usually results in more than 2N

$$ J = 2N + p,\quad \quad p \ge 0. $$

(7)

In above equations, the N complex conjugated pairs are called elastic modes and the rest $p = \sum \limits _{k = 1}^{n} {{r_{k}}}$ eigenvalues are called viscoelastic modes or auxiliary modes. For a stable passive system, the p extra modes are negative real number, which represent over-critically damped modes and have no oscillatory behavior. Clearly, the order of the eigenvalue is closely related to the rank of each coefficient matrix (the distribution of each damping material).

The eigenvalue problem associated with (7) is nonlinear, and until now, the efficient resolution of nonlinear eigenvalue problem remains a challenge. There are mainly two ways to deal with this task. The first one is the iterative-based method (Singh 2016; Lin and Ng 2019), which gives satisfactory results but in the meantime, can be computationally expensive. Therefore, the iterative-based method may not be suitable for large-scale systems.

The second approach is built on the state-space formulation (Adhikari and Wagner 2004; Cortés and Elejabarrieta 2006). By introducing a series of internal variables, the nonlinear eigen-problem can be transformed into a linear eigen-problem. But the state-space method usually develops based on specific damping models, such as the exponential damping model, resulting in a loss of generality. Although the existing viscoelastic damping models differ in physical significance, the majority of the kernel functions can be mathematically represented by a fraction formula. Ding et al. (2016) proposed a general damping model (GDM) to uniformly express the frequency-dependent damping models as

$$ G_{k}(s) = \frac{{{c_{{p_{k}}}}{s^{{p_{k}}}} + {c_{{p_{k - 1}}}}{s^{{p_{k - 1}}}} + {\cdots} + {c_{0}}}}{{{d_{{q_{k}}}}{s^{{q_{k}}}} + {d_{{q_{k - 1}}}}{s^{{q_{k - 1}}}} + {\cdots} + {d_{0}}}} = {\mathbf{P}}_{k}^{T}{({{\mathbf{E}}_{k}} - s{{\mathbf{W}}_{k}})^{- 1}}{{\mathbf{Q}}_{k}}, $$

(8)

where ${{\mathbf {P}}_{k}} = \left \{ {\begin {array}{c} {{c_{{q_{k}} - 1}} - {d_{{q_{k}} - 1}}{c_{{q_{k}}}}}\\ {{c_{{q_{k}} - 2}} - {d_{{q_{k}} - 2}}{c_{{q_{k}}}}}\\ {\vdots } \\ {{c_{0}} - {d_{0}}{c_{{q_{k}}}}} \end {array}} \right \}\left ({\forall j > {p_{k}},{c_{j}} = 0} \right ),{{\mathbf {E}}_{k}} = \left [ {\begin {array}{cccc} { - {d_{{q_{k}} - 1}}}& {\cdots } &{ - {d_{1}}}&{ - {d_{0}}}\\ 1&{\mathbf {0}}&0&0\\ {\mathbf {0}}& {\ddots } &{\mathbf {0}}& {\vdots } \\ 0&{\mathbf {0}}&1&0 \end {array}} \right ],{{\mathbf {W}}_{k}} = {{\mathbf {I}}_{{q_{k}}}},{{\mathbf {Q}}_{k}} = \left \{ {\begin {array}{c} { - 1}\\ 0\\ {\vdots } \\ 0 \end {array}} \right \}$ and ${{\mathbf {E}}_{k}}, {{\mathbf {W}}_{k}} \in \mathbb {R} {^{{q_{k}} \times {q_{k}}}}$, ${{\mathbf {P}}_{k}}, {{\mathbf {Q}}_{k}} \in \mathbb {R} {^{{q_{k}}}}$. In the context, I stands for the identity matrix with its corresponding size. It is assumed that the numerator and the denominator have no common factor and the order of the denominator is no less than the numerator (p_k ≤ q_k). If p_k,q_k = 0, (8) reduces to the viscous damping model. When p_k,q_k = 1, by adopting various relaxation parameters, (8) can be reduced to the Biot model or the ADF model. Specially, when p_k,q_k = 2, the GHM damping model can be obtained. Therefore, based on the GDM model, a general state-space method for calculating the eigensolutions of structural systems with various viscoelastic damping models can be derived.

However, this state-space method may significantly enlarge the size of the system matrices if different viscoelastic damping components involved. This fact restricts its application for large-scale systems. In order to reduce the computational cost, modal projection–based reduction techniques are often introduced. Hence, the displacement vector X(s) can be approximated in a reduced dimension spanned by the columns of a reduction basis ${\mathbf {T}} \in \mathbb {R} {^{{N} \times {Nm}}}$:

$$ {\mathbf{X}}(s) = {\mathbf{Tp}}, $$

(9)

where ${\mathbf {p}} \in \mathbb {R} {^{{Nm}}}$ is a generalized coordinate representing the approximate solution and Nm is the number of column dimension which is usually much smaller than N. A modal truncation augmentation method (MTAM) has been proposed by using the normal modes of the undamped system corresponding to (6)

$$ \left( {{{\mathbf{K}}_{E}} - {\omega_{k}^{2}}{\mathbf{M}}} \right){{\boldsymbol{\phi }}_{k}} = {\mathbf{0}}, $$

(10)

where ω_k and ϕ_k are respectively the eigenfrequency and eigenvector for the undamped system. The projection basis T_MTAM of the MTAM is

$$ {{\mathbf{T}}_{MTAM}} = \left[ {{{\mathbf{X}}_{cor}},{{\boldsymbol{\phi }}_{1}}, {\cdots} ,{{\boldsymbol{\phi }}_{n}}} \right], $$

(11)

where X_cor is the static correction and constructed by the normal modes of eigensolutions, load vector and the stiffness matrix

$$ {{\mathbf{X}}_{cor}} = \left( {{{{\mathbf{K}}_{E}}^{- 1}} - \sum\limits_{j = 1}^{N} {\frac{{{{\boldsymbol{\phi }}_{j}}{\boldsymbol{\phi }}_{j}^{T}}}{{{\omega_{j}^{2}}}}} } \right){\mathbf{F}}. $$

(12)

Obviously, the computational accuracy of the approximated results rely on the choice of the modal projection basis. The normal mode–based projection basis, which neglects the contributions of the viscoelastic kernel function terms, may lead to significant errors for highly damped structures. The appropriate modal-projection bases for viscoelastically damped system will be discussed in next section.

2.3 DSA of transient responses

Design optimization problems are typically formulated as an integral of general response function H, which depends on the transient responses and the design parameters of the system

$$ {\boldsymbol{\psi}}={\int}_{{t_{0}}}^{{t_{F}}} {{\mathbf{H}}\left( {{\mathbf{x}},\dot{\mathbf{x}},\ddot{\mathbf{x}},p,t} \right)} {\mathrm{d}}t, $$

(13)

where ${\boldsymbol {\psi }},{\mathbf {H}} \in \mathbb {R} {^{o}}$ are column vectors of o scalar object functions, and o is the number of target point. t₀, t_F are the start and end response time point. The sensitivity of the integral general response function with respect to the design variable p is

$$ {\boldsymbol{\psi }}^{\prime}={\int}_{{t_{0}}}^{{t_{F}}} {\left( {\frac{{\partial {\mathbf{H}}}}{{\partial p}} + \frac{{\partial {\mathbf{H}}}}{{\partial {\mathbf{x}}}}{\mathbf{x}}^{\prime} + \frac{{\partial {\mathbf{H}}}}{{\partial \dot{\mathbf{x}}}}\dot{\mathbf{x}}^{\prime} + \frac{{\partial {\mathbf{H}}}}{{\partial \ddot{\mathbf{x}}}}\ddot{\mathbf{x}}^{\prime}} \right)} {\text{d}}t, $$

(14)

where prime symbol $\left (\bullet \right )^{\prime }$ represents total derivatives with respect to the design variable, that is, ${\mathrm {d}}\left (\bullet \right )/{\text {d}}p$ and $\partial \left (\bullet \right )$ denotes partial derivatives with respect to some implicit dependencies. As can be seen in (14), the partial derivatives of the response function H with respect to the design parameter p and the transient response vectors x are easy to be determined. The only undetermined terms are the derivatives of the transient response vectors ${\mathbf {x}}^{\prime },\dot {\mathbf {x}}^{\prime },\ddot {\mathbf {x}}^{\prime }$.

The DSA of the transient responses and their response functions can be calculated by the FDM, the AVM and the DDM. This paper aims to provide clarity on which presented modal projection basis yields the best trade-off between accuracy and efficiency for computing the 1st- and 2nd-order derivatives of transient responses for viscoelastically damped systems. Therefore, the DDM is adopted in this paper for its high numerical stability, mathematically easy to understand and, most importantly, accessible to obtain second-order derivatives.

2.4 Cut-off criterion of projection basis

Assuming that the force vector f(t) can be equivalently expressed by a boolean matrix ${\mathbf {H}} \in \mathbb {R}^{{N}}$ and a dimensionless scalar force function f(t)

$$ {\mathbf{f}}(t) = {\mathbf{H}}f(t). $$

(15)

If the column vector of the reduction basis T is denoted by T_i, the approximated column vector H_Nm gives

$$ {{\mathbf{H}}_{Nm}} = \sum\limits_{i = 1}^{Nm} {{{\mathbf{T}}_{i}}{{\mathbf{H}}^{T}}{\mathbf{M}}{{\mathbf{T}}_{i}}}. $$

(16)

Hence, the error e_m of the boolean matrix H and its approximated result H_Nm is evaluated by

$$ {{\mathbf{e}}_{m}} = {\mathbf{H}} - {{\mathbf{H}}_{Nm}}. $$

(17)

The cut-off criterion ε_Nm associated with the number of projection bases can be defined as

$$ {\varepsilon_{Nm}} = \frac{{\left| {{{\mathbf{H}}^{T}}{{\mathbf{e}}_{m}}} \right|}}{{{{\mathbf{H}}^{T}}{\mathbf{H}}}}. $$

(18)

Therefore, the following inequality relationship of the required number of projection bases ε_Nm should be satisfied

$$ {\varepsilon_{Nm}} \le {\varepsilon_{R}}, $$

(19)

where ε_R is a pre-given error tolerance by experience to avoid localized design sensitivities.

3 Modal projection bases of viscoelastically damped systems

Up to now, extensive literatures studied the modal projection–based reduction technique for structures with frequency-dependent damping. The simplest one may be the modal strain energy (MSE) method proposed by Johnson and Kienholz (1982), which constructs the projection basis by combination of the normal modes corresponding to the viscoelastically damped system. The projection basis is defined as

$$ {{\mathbf{T}}_{MSE}} = \left[ {{{\mathbf{X}}_{cor}},{{\boldsymbol{\phi }}_{1}}(0), {\cdots} ,{{\boldsymbol{\phi }}_{n}}(0)} \right], $$

(20)

where ϕ_n(0) denotes the pseudo-normal modes, which are real and solution of

$$ \left( {{{\mathbf{K}}_{0}} - {\lambda_{k}^{2}}{\mathbf{M}}} \right){{\boldsymbol{\phi }}_{k}} = {\mathbf{0}}. $$

(21)

In above equation, ${{\mathbf {K}}_{0}} = {{\mathbf {K}}^{*}}\left ({\omega {\text { = 0}}} \right )$ is the static stiffness matrix. For the viscoelastically damped system reduced by the real modes, it is assumed that the damping introduced by the viscoelastic component is generally much more important than that of the elastic structure, and thus the structural damping will be ignored for simplicity (Xie et al. 2018). Under such condition, the frequency-dependent damping matrix and the elastic stiffness could be approximated as:

$$ {{\mathbf{K}}^{*}}(\omega ) = \sum\limits_{k = 1}^{n} {{G_{s}}^{\prime}(\omega ){{\mathbf{C}}_{k}} + {{\mathbf{K}}_{E}}}, $$

(22)

where ${{G_{s}}^{\prime }(\omega )}$ is the purely real components of the kernel function. The detailed expression of the Prony series model can be found in Kuether (2019). The expression of ${{G_{s}}^{\prime }(\omega )}$ for other damping models can be obtained after some mathematical manipulations. When the structure is lightly damped, the modal-projection basis T_MSE gives good results. However, for highly damped systems, the projection basis derived by (21) may not be representative of the normal modes, and hence leads to significant errors in the approximations.

Some modified approaches are developed to improve the accuracy of the approximated results by adding some corrective terms to the MSE basis. These projection bases can be classified into real modal–based and complex modal–based methods. The latter one is generally reaches higher approximation results than the former one for viscoelastically damped systems. But the complex modal based method suffers from heavy computational burden, since it is still challenging and inefficient to directly solve the complex eigenvalue problem of (6).

The majority of existing studies focus on their performances in frequency domain problems for viscoelastically damped systems (Zghal et al. 2015; Rouleau et al. 2017). There is no sufficient research to provide clarity on which modal-projection basis yields the best trade-off between efficiency and accuracy for transient response problems, especially for sensitivity analyses. In this paper, three modal projection–based reduction techniques of viscoelastically damped systems (MM, MESR, IAM) are adopted to investigate their effectiveness for calculating the transient response sensitivities.

3.1 MM method

The MM method is firstly derived from Takani-Sugeno fuzzy model that is used to represent nonlinear dynamic systems (Takagi and Sugeno 1985). Then, Balmès (1996) extended this approach to built a real-valued based projection basis formulated from the corresponding viscoelastically damped system. The projection basis of the MM method T_MM is a combination of static correction X_cor and several modal bases ${{\mathbf {T}}_{{p_{j}}}}$:

$$ {{\mathbf{T}}_{MM}} = \left[ {{{\mathbf{X}}_{cor}},{{\mathbf{T}}_{{p_{1}}}}, {\cdots} ,{{\mathbf{T}}_{{p_{m}}}}} \right]. $$

(23)

For each modal basis ${{\mathbf {T}}_{{p_{j}}}}$, it is constructed by the pseudo-normal mode solutions of the eigenvalue problem

$$ \left( {{{\mathbf{K}}^{*}}({\omega_{{p_{j}}}}) - \lambda_{k}^{*2}({\omega_{{p_{j}}}}){\mathbf{M}}} \right){\boldsymbol{\phi }}_{k}^{*}({\omega_{{p_{j}}}}) = {\mathbf{0}}, $$

(24)

where ${{\omega _{{p_{j}}}}}$ is a priori chosen value related to the frequency range of interest and $\lambda _{k}^{*}$, ${\boldsymbol {\phi }}_{k}^{*}$ are the k th normal eigensolutions when the priori imposed frequency is ${{\omega _{{p_{j}}}}}$. It is verified that good approximation results of the dynamic responses of highly damped structures could be obtained when the projection bases evaluated at the minimum and the maximum frequency range of interest are included (Balmès 1996; Rouleau et al. 2017). If the computational accuracy is still unsatisfactory, the projection bases calculated at other frequency points can be added, such as the average frequency of the frequency range of interest (Kuether 2019). The initially obtained projection basis T_MM need the use of a Gram-Schmidt orthonormalisation algorithm to improve the robustness of the projection basis.

3.2 MSER method

The MSER method aims to increase the accuracy of the approximation by iteratively seeking a better projection basis. The projection basis T_MSER is enriched by adding displacement residuals ${\mathbf {R}}_{d}^{*}$ to the T_MSE:

$$ {{\mathbf{T}}_{MSER}} = \left[ {{{\mathbf{T}}_{MSE}},{\mathbf{R}}_{d}^{*}} \right]. $$

(25)

The displacement residuals are derived from the static response to load residuals ${\mathbf {R}}_{f}^{*}$:

$$ {\mathbf{R}}_{f}^{*}(\omega ) = \left( {{{\mathbf{K}}^{*}}(\omega ) - {\omega^{2}}{\mathbf{M}}} \right){\mathbf{X}}_{r}^{*}(\omega ) - {\mathbf{F}}, $$

(26)

where ${\mathbf {X}}_{r}^{*}(\omega )$ is the approximation of the dynamic response calculated by using the projection basis T_MSER (the initial projection basis is T_MSE and the robustness of the updated projection basis increases as the displacement residuals are added). The displacement residuals are obtained by using of the static stiffness matrix ${{\mathbf {K}}_{0}} = {{\mathbf {K}}^{*}}\left ({\omega {\text { = 0}}} \right )$ and the load residuals ${\mathbf {R}}_{f}^{*}$, which are given by

$$ {\mathbf{R}}_{d}^{*}(\omega ) = {\mathbf{K}}_{0}^{- 1}{\mathbf{R}}_{f}^{*}(\omega ). $$

(27)

The residuals are calculated at each eigenfrequencies λ_k of the undamped eigenvalue problem of (21) and added to the projection basis T_MSER. The iterative procedure will be stopped until the chosen error criterion ε_tol is satisfied

$$ {\varepsilon_{R}} = \frac{{{{\left\| {{\mathbf{R}}_{d}^{*H}{{\mathbf{K}}_{0}}{\mathbf{R}}_{d}^{*}} \right\|}_{2}}}}{{{{\left\| {{\mathbf{X}}_{r}^{*H}{{\mathbf{K}}_{0}}{\mathbf{X}}_{r}^{*}} \right\|}_{2}}}} < {\varepsilon_{tol}}, $$

(28)

where ε_R is the error estimate of the displacement residuals. The procedure of constructing the projection basis T_MSER is indicated in Algorithm 1 (Rouleau et al. 2017).

3.3 IAM

The projection basis T_IAM is enriched by complex modes, which aims to reduce the error of the modal truncation problem for viscoelastically damped systems. The projection matrix T_IAM is built on a modified MSE basis and three perturbation bases (T₁, T₂ and T₃)

$$ {{\mathbf{T}}_{IAM}} = \left[ {{{\mathbf{T}}_{MMSE}},{{\mathbf{T}}_{\text{1}}},{{\mathbf{T}}_{2}},{{\mathbf{T}}_{3}}} \right], $$

(29)

where the modal projection basis T_MMSE is defined as

$$ {{\mathbf{T}}_{MMSE}} = \left[ {{{\mathbf{X}}_{cor}},{{\boldsymbol{\phi }}_{1}}({\omega_{{p_{j}}}}), {\cdots} ,{{\boldsymbol{\phi }}_{n}}({\omega_{{p_{j}}}})} \right]. $$

(30)

For the modal basis T_MMSE, the equivalent stiffness matrix is ${{{\mathbf {K}}^{*}}(\omega ={\omega _{{p_{j}}}})}$. While for the T_MSE, the equivalent stiffness matrix is ${{\mathbf {K}}^{*}}\left ({\omega {\text { = 0}}} \right )$. The first perturbation basis T₁ considers the contribution of the lower available modes and is given by

$$ {{\mathbf{T}}_{\text{1}}}=\sum\limits_{j = 1}^{L} {\frac{{{\boldsymbol{\varphi }}_{j}^{T}{\mathbf{F}}(s){{\boldsymbol{\varphi }}_{j}}}}{{(s - {\lambda_{j}}){\theta_{j}}}}}, $$

(31)

where ${\theta _{j}} = {\boldsymbol {\varphi }}_{j}^{T}\left ({2{\lambda _{j}}{\mathbf {M}} + {\mathbf {G}}({\lambda _{j}}) + {\lambda _{j}}{{\left . {\frac {{\partial {\mathbf {G}}(s)}}{{\partial s}}} \right |}_{s = {\lambda _{j}}}}} \right ){{\boldsymbol {\varphi }}_{j}}$ and ${\mathbf {G}}(s) = \sum \limits _{k = 1}^{n} {{G_{k}}(s){{\mathbf {C}}_{k}}}$.

The second perturbation basis T₂ represents the first-order approximate contribution of the higher truncated modes and is expressed by using the first term of the Neumann expansion of the contribution of the higher unavailable modes

$$ {{\mathbf{T}}_{2}}=\sum\limits_{j = 1}^{L} {\frac{{{\boldsymbol{\varphi }}_{j}^{T}{\mathbf{F}}(s){{\boldsymbol{\varphi }}_{j}}}}{{{\lambda_{j}}{\theta_{j}}}}} + {{\mathbf{K}}^{- 1}}{\mathbf{F}}(s). $$

(32)

The last perturbation basis T₃ stands for the second-order approximate contribution of the higher truncated modes and is given by

$$ {{\mathbf{T}}_{3}}=\sum\limits_{j = 1}^{L} {\frac{{{\boldsymbol{\varphi }}_{j}^{T}{\mathbf{F}}(s){{\boldsymbol{\varphi }}_{j}}}}{{{\lambda_{j}^{2}}{\theta_{j}}}}} - {{\mathbf{K}}^{- 1}}{{\mathbf{G}}_{0}}{{\mathbf{K}}^{- 1}}{\mathbf{F}}(s), $$

(33)

where ${{\mathbf {G}}_{0}} = \underset {s \to 0}{\lim \limits } {\mathbf {G}}(s)$. The projection basis T_IAM is complex value based. And to avoid the strong collinearity between these modal bases, a Gram-Schmidt orthonormalisation procedure is also needed.

4 Modal projection–based reduction technique of DSA for transient responses of viscoelastically damped systems

The performances of the modal projection–based reduction method of DSA for transient responses mainly depend on the following issues (Greene and Haftka 1989): (1) numerical errors of the transient and sensitivity results associated with the integration method, (2) selection of the step size, (3) convergence of the modal projection and (4) computational cost of the sensitivity calculation method. In order to investigate the influences of different modal bases on the performance of the DSA, the numerical errors of the transient responses for viscoelastically damped systems generated by the integration method should be limited to the least. Herein, the MPIM method (Ding et al. 2018a) rather than the Newmark’s integration method is used to calculate the transient responses and their derivatives, since the former method is more accurate and has simpler expressions for viscoelastically damped systems. These advantages can minimize the impact of issue (1) and (4) on the performances for sensitivity calculations.

4.1 MOR for transient responses of viscoelastically damped systems

Substituting (9) into (5) and pre-multiplying from the left side by T^T yields the reduced-order viscoelastically damped system in Laplace domain:

$$ \left( {{s^{2}}{\bar{\mathbf{M}}} + s{{\bar{\mathbf{C}}}_{0}} + s\sum\limits_{k = 1}^{n} {{G_{k}}(s)} {{\bar{\mathbf{C}}}_{k}} + {\bar{\mathbf{K}}}} \right){\mathbf{p}} = {\bar{\mathbf{F}}}(s), $$

(34)

where ${\bar {\mathbf {M}}} = {{\mathbf {T}}^{T}}{\mathbf {MT}},{{\bar {\mathbf {C}}}_{0}} = {{\mathbf {T}}^{T}}{{\mathbf {C}}_{0}}{\mathbf {T}},{{\bar {\mathbf {C}}}_{k}} = {{\mathbf {T}}^{T}}{{\mathbf {C}}_{k}}{\mathbf {T}},{\bar {\mathbf {K}}} = {{\mathbf {T}}^{T}}{{\mathbf {K}}_{E}}{\mathbf {T}} \in \mathbb {R} {^{{Nm} \times {Nm}}},{\bar {\mathbf {F}}}(s) = {{\mathbf {T}}^{T}}{\mathbf {F}}(s) \in \mathbb {R} {^{{Nm}}}$. The reduced coefficient matrix of damping ${{\bar {\mathbf {C}}}_{k}}$ can be decomposed into rank-revealing form

$$ {{\bar{\mathbf{C}}}_{k}} = {{\bar{\mathbf{L}}}_{k}}{\bar{\mathbf R}}_{k}^{T}, $$

(35)

where ${{\bar {\mathbf {L}}}_{k}},{{\bar {\mathbf R}}_{k}} \in {^{Nm \times {{\bar r}_{k}}}}$ and ${{{\bar r}_{k}}}$ represents the rank of the matrix ${{\bar {\mathbf {C}}}_{k}}$.

Combining (8) and (35) gives the following expression

$$ \begin{array}{@{}rcl@{}} \sum\limits_{k = 1}^{n} {{G_{k}}(s)} {{\bar{\mathbf{C}}}_{k}} &=&\sum\limits_{k = 1}^{n} {{{\bar{\mathbf{L}}}_{k}}{{\left( {{{\mathbf{I}}_{{{\bar{r}}_{k}}}} \otimes {{\mathbf{P}}_{k}}} \right)}^{T}}\cdot{{\left( {{{\mathbf{I}}_{{{\bar{r}}_{k}}}} \otimes {{\mathbf{E}}_{k}} - s{{\mathbf{I}}_{{{\bar{r}}_{k}}}} \otimes {{\mathbf{W}}_{k}}} \right)}^{- 1}}}\\ &&{\cdot\left( {{{\mathbf{I}}_{{{\bar{r}}_{k}}}} \otimes {{\mathbf{Q}}_{k}}} \right){\bar{\mathbf R}}_{k}^{T}}, \end{array} $$

(36)

where ⊗ represents the kronecker product. The above equation can be further simplified as

$$ \sum\limits_{k = 1}^{n} {{G_{k}}(s)} {{\bar{\mathbf{C}}}_{k}} = {\bar{\mathbf{L}}}{\left( {{\bar{\mathbf E}} - s{\bar{\mathbf W}}} \right)^{- 1}}{{\bar{\mathbf R}}^{T}}. $$

(37)

The specific expressions of ${\bar {\mathbf {L}}},{\bar {\mathbf E}},{\bar {\mathbf W}}$ and ${\bar {\mathbf R}}$ can be seen in Appendix A. Substituting (37) into (34) gives

$$ \left( {{s^{2}}{\bar{\mathbf{M}}} + s{{\bar{\mathbf{C}}}_{0}} + s{\bar{\mathbf{L}}}{{({\bar{\mathbf E}} - s{\bar{\mathbf W}})}^{- 1}}{{{\bar{\mathbf R}}}^{T}} + {\bar{\mathbf{K}}}} \right){\mathbf{p}} = {\bar{\mathbf{F}}}(s) $$

(38)

Denoting that ${\mathbf {Y}}(s) = s{({\mathbf {E}} - s{\mathbf {W}})^{- 1}}{{\bar {\mathbf R}}^{T}}{\mathbf {p}} \in \mathbb {R}^{{\bar {p}}}$ and using the inverse Laplace transformation, (38) can be rewritten in time domain as

$$ {\bar{\mathbf{M}}\ddot{\mathbf{p}}}(t) + {{\bar{\mathbf{C}}}_{0}}{\dot{\mathbf p}}(t) + {\bar{\mathbf{K} \mathbf{p}}}(t) + {\bar{\mathbf Ly}}(t) = {\bar{\mathbf f}}(t). $$

(39)

Pre-multiplying both sides of ${\mathbf {Y}}(s) = s{({\mathbf {E}} - s{\mathbf {W}})^{- 1}}{{\bar {\mathbf R}}^{T}}{\mathbf {p}}$ by matrix $\left ({{\bar {\mathbf E}} - s{\bar {\mathbf W}}} \right )$ and rearranging the matrices lead to the expression:

$$ {\bar{\mathbf Ey}}(t) = {\bar{\mathbf{W}}\dot{\mathbf{y}}}(t) + {{\bar{\mathbf R}}^{T}}{\dot{\mathbf p}}(t). $$

(40)

Here, an identical equation is introduced to built some state-space vectors:

$$ {{\mathbf{I}}_{Nm}}{\dot{\mathbf p}}(t) - {{\mathbf{I}}_{Nm}}{\dot{\mathbf p}}(t) = {\mathbf{0}}. $$

(41)

Finally, by combining (39)–(41), a state-space formulation expressed by the reduced matrices and vectors can be obtained as

$$ \left[ {\begin{array}{ccc} {\mathbf{0}}&{ - {{\mathbf{I}}_{Nm}}}&{\mathbf{0}}\\ {{\bar{\mathbf{K}}}}&{{{\bar{\mathbf{C}}}_{0}}}&{{\bar{\mathbf{L}}}}\\ {\mathbf{0}}&{{{{\bar{\mathbf R}}}^{T}}}&{ - {\bar{\mathbf E}}} \end{array}} \right]\left\{ {\begin{array}{c} {{\mathbf{p}}(t)}\\ {{\dot{\mathbf p}}(t)}\\ {{\mathbf{y}}(t)} \end{array}} \right\} + \left[ {\begin{array}{ccc} {{{\mathbf{I}}_{Nm}}}&{\mathbf{0}}&{\mathbf{0}}\\ {\mathbf{0}}&{{\bar{\mathbf{M}}}}&{\mathbf{0}}\\ {\mathbf{0}}&{\mathbf{0}}&{{\bar{\mathbf W}}} \end{array}} \right]\left\{ {\begin{array}{c} {{\dot{\mathbf p}}(t)}\\ {{\ddot{\mathbf p}}(t)}\\ {{\dot{\mathbf y}}(t)} \end{array}} \right\} = \left\{ {\begin{array}{c} {\mathbf{0}}\\ {{\bar{\mathbf f}}(t)}\\ {\mathbf{0}} \end{array}} \right\}. $$

(42)

Since the matrices ${\bar {\mathbf {M}}}$ and ${\bar {\mathbf W}}$ are nonsingular, (42) can be further simplified as:

$$ {\dot{\mathbf z}}(t) = {\mathbf{Az}}(t) + {\mathbf{r}}(t) $$

(43)

where ${\mathbf {A}} = \left [ {\begin {array}{ccc} {\mathbf {0}}&{{{\mathbf {I}}_{Nm}}}&{\mathbf {0}}\\ { - {{{\bar {\mathbf {M}}}}^{- 1}}{\bar {\mathbf {K}}}}&{ - {{{\bar {\mathbf {M}}}}^{- 1}}{{\bar {\mathbf {C}}}_{0}}}&{ - {{{\bar {\mathbf {M}}}}^{- 1}}{\bar {\mathbf {L}}}}\\ {\mathbf {0}}&{ - {{{\bar {\mathbf W}}}^{- 1}}{{{\bar {\mathbf R}}}^{T}}}&{{{{\bar {\mathbf W}}}^{- 1}}{\bar {\mathbf E}}} \end {array}} \right ] \in \mathbb {R}^{{\bar J \times \bar J}}, {\mathbf {z}}(t) = \left [ {\begin {array}{c} {{\mathbf {p}}(t)}\\ {{\dot {\mathbf p}}(t)}\\ {{\mathbf {y}}(t)} \end {array}} \right ] \in \mathbb {R}^{{\bar J}},{\mathbf {r}}(t) = \left [ {\begin {array}{c} {\mathbf {0}}\\ { {{{\bar {\mathbf {M}}}}^{- 1}}{\bar {\mathbf f}}(t)}\\ {\mathbf {0}} \end {array}} \right ] \in \mathbb {R}^{\bar J}$.

In above expressions, $\bar J = 2Nm + \bar {p}$ represents the dimension of the reduced state-space formulation. The dynamic responses of (43) can be expressed in a recurrence formula

$$ {{\mathbf{z}}_{k + 1}} = {\mathbf{T}}({{\varDelta}} t){{\mathbf{z}}_{k}} + {\int}_{{t_{k}}}^{{t_{k + 1}}} {\exp (({t_{k + 1}} - \tau ){\mathbf{A}})} {\mathbf{r}}(\tau )d\tau, $$

(44)

where

$$ {\mathbf{T}}({{\varDelta}} t) = \exp({{\varDelta}} t{\mathbf{A}}). $$

(45)

The matrix exponential function of (45) can be approximated by using the precise integration method (Zhong 2004). The integral term in (44) can be calculated by using the Gauss-Legendre quadrature approximation (Wang and Au 2006). Therefore, the final step-by-step integral recurrence formula of solution vector z_k+ 1 from vector z_k is

$$ {{\mathbf{z}}_{k + 1}}= {\mathbf{T}}({{\varDelta}} t){{\mathbf{z}}_{k}} + \frac{{{{\varDelta}} t}}{2}\sum\limits_{j = 1}^{gm} {{w_{j}}} {\mathbf{T}}\left( {\frac{{{{\varDelta}} t}}{2}(1 - {\xi_{j}})} \right){\mathbf{r}}\left( {{t_{k}} + \frac{{{{\varDelta}} t}}{2}(1 + {\xi_{j}})} \right), $$

(46)

where ω_j,ξ_j are respectively weight coefficients and locations of each Gauss quadrature points gm. The detailed derivations for the MPIM can be found in Ding et al. (2018a). The transient responses of the displacement and velocity are obtained in the generalized coordinate by using (46), which could be transformed into the original coordinate by the expression:

$$ {\mathbf{x}}({t_{k}}) = {\mathbf{Tp}}({t_{k}}), \quad \dot{\mathbf{x}}({t_{k}}) = {\mathbf{T}{\dot{\mathbf p}}} ({t_{k}}). $$

(47)

If required, the accelerations of the system can also be calculated according to the relationship in (9) and (39):

$$ \ddot{\mathbf{x}}({t_{k}}) = {\mathbf{T}} \cdot {{\mathbf{M}}^{- 1}}\left[ {{\bar{\mathbf f}}({t_{k}}) - {{\bar{\mathbf{C}}}_{0}}{\dot{\mathbf p}}({t_{k}}) - {\bar{\mathbf Kp}}({t_{k}}) - {\bar{\mathbf Ly}}({t_{k}})} \right] $$

(48)

4.2 First-order sensitivity of transient responses based on DDM of reduced system

The first-order sensitivities for transient responses of viscoelastically damped system are derived based on reduced model using the DDM. Noting the force vector r(t) is independent from design variable and differentiating (46) with respect to the design variable p_i gives

$$ \begin{array}{@{}rcl@{}} \frac{{\partial {{\mathbf{z}}_{k{\text{ + 1}}}}}}{{\partial {p_{i}}}}&=& \frac{{\partial {\mathbf{T}}({{\varDelta}} t)}}{{\partial {p_{i}}}}{{\mathbf{z}}_{k}} + {\mathbf{T}}({{\varDelta}} t)\frac{{\partial {{\mathbf{z}}_{k}}}}{{\partial {p_{i}}}}\\&&+ \frac{{{{\varDelta}} t}}{2}\sum\limits_{i = 1}^{gm} {{w_{i}}\frac{{\partial {\mathbf{T}}\left( {\frac{{{{\varDelta}} t}}{2}(1 - {\xi_{i}})} \right)}}{{\partial {p_{i}}}}{\mathbf{r}}\left( {{t_{k}} + \frac{{{{\varDelta}} t}}{2}(1 + {\xi_{i}})} \right)}.\\ \end{array} $$

(49)

In above equation, when calculating the first-order sensitivity of the dynamic responses at time point (k + 1)Δt, it is assumed that the transient responses z_k and their 1st-order sensitivity ${{\partial {{\mathbf {z}}_{k}}} \left / {\partial {p_{i}}}\right .}$ at time point kΔt are already known (the initial values of z₀ and ${{\partial {{\mathbf {z}}_{0}}} \left /{\partial {p_{i}}}\right .}$ will be given as initial conditions). Therefore, the only unknown term in (49) is the first derivative of the matrix exponential function ${\partial {\mathbf {T}}({{\varDelta }} t)} \left / { {\partial {p_{i}}}}\right .$, which can be calculated by

$$ \frac{{\partial {\mathbf{T}}({{\varDelta}} t)}}{{\partial {p_{i}}}} = \frac{{\partial {\text{e}^{{\mathbf{A}}{{\varDelta}} t}}}}{{\partial {p_{i}}}} = {\text{e}^{{\mathbf{A}}{{\varDelta}} t}}{{\varDelta}} t\frac{{\partial {\mathbf{A}}}}{{\partial {p_{i}}}}. $$

(50)

Differentiating the amplification matrix A with respect to the design variable p_i, one can obtain that

$$ \frac{{\partial {\mathbf{A}}}}{{\partial {p_{i}}}} = \left[ {\begin{array}{ccc} {\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}}\\ {\frac{{\partial \left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{\bar{\mathbf{K}}}} \right)}}{{\partial {p_{i}}}}}&{\frac{{\partial \left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}}} \right)}}{{\partial {p_{i}}}}}&{\frac{{\partial \left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{\bar{\mathbf{L}}}} \right)}}{{\partial {p_{i}}}}}\\ {\mathbf{0}}&{\frac{{\partial \left( { - {{{\bar{\mathbf W}}}^{- 1}}{{{\bar{\mathbf R}}}^{\mathbf{T}}}} \right)}}{{\partial {p_{i}}}}}&{\frac{{\partial \left( {{{{\bar{\mathbf W}}}^{- 1}}{\bar{\mathbf E}}} \right)}}{{\partial {p_{i}}}}} \end{array}} \right]. $$

(51)

The first-order sensitivity term ${{\partial \left ({ - {{{\bar {\mathbf {M}}}}^{- 1}}{\bar {\mathbf {K}}}} \right )} \left / {\partial {p_{i}}}\right .}$ is derived here (the specific expressions of other terms in (51) are listed in Appendix B) and can be expressed by

$$ \frac{{\partial \left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{\bar{\mathbf{K}}}} \right)}}{{\partial {p_{i}}}} = {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}{\bar{\mathbf{K}}} - {{\bar{\mathbf{M}}}^{-1}}\frac{{\partial {\bar{\mathbf{K}}}}}{{\partial {p_{i}}}}. $$

(52)

By assuming that the projection basis T in (9) can be treated as constant with respect to the design variable p_i (Greene and Haftka 1989; Han 2013), i.e., ${{\partial {\mathbf {T}}} \left / {\partial {p_{i}}}\right .} = {\mathbf {0}}$ yields

$$ \frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}} = \frac{{\partial {{\mathbf{T}}^{T}}}}{{\partial {p_{i}}}}{\mathbf{MT}} + {{\mathbf{T}}^{T}}\frac{{\partial {\mathbf{M}}}}{{\partial {p_{i}}}}{\mathbf{T}} + {{\mathbf{T}}^{T}}{\mathbf{M}}\frac{{\partial {\mathbf{T}}}}{{\partial {p_{i}}}}{\text{ }} \to {\text{ }}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}} = {{\mathbf{T}}^{T}}\frac{{\partial {\mathbf{M}}}}{{\partial {p_{i}}}}{\mathbf{T}} $$

(53)

with similar expressions for the derivatives of ${{\bar {\mathbf {K}}}}$ and ${{{\bar {\mathbf {C}}}_{0}}}$. Substituting (81) into (52), one has

$$ \frac{{\partial \left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{\bar{\mathbf{K}}}} \right)}}{{\partial {p_{i}}}} = {{\bar{\mathbf{M}}}^{- 1}}{{\mathbf{T}}^{T}}\frac{{\partial {\mathbf{M}}}}{{\partial {p_{i}}}}{\mathbf{T}}{{\bar{\mathbf{M}}}^{- 1}}{\bar{\mathbf{K}}} - {{\bar{\mathbf{M}}}^{- 1}}{{\mathbf{T}}^{T}}\frac{{\partial {\mathbf{K}}}}{{\partial {p_{i}}}}{\mathbf{T}}. $$

(54)

By substituting the derivatives derived in Appendix B into (49), one can obtain the first-order sensitivities of transient responses ${{\partial {{\mathbf {z}}_{k}}} \left / {\partial {p_{i}}}\right .}$ using the DDM in the generalized coordinate. The first-order sensitivities of transient responses in the original coordinate can be obtained by

$$ \frac{{\partial {{\mathbf{x}}_{k}}}}{{\partial {p_{i}}}} = \frac{{\partial {\mathbf{T}}}}{{\partial {p_{i}}}}{{\mathbf{p}}_{k}} + {\mathbf{T}}\frac{{\partial {{\mathbf{p}}_{k}}}}{{\partial {p_{i}}}}{\text{ }} \to {\text{ }}\frac{{\partial {{\mathbf{x}}_{k}}}}{{\partial {p_{i}}}} = {\mathbf{T}}\frac{{\partial {{\mathbf{p}}_{k}}}}{{\partial {p_{i}}}} $$

(55)

with similar expressions for the derivatives ${{\partial {{\dot {\mathbf {x}}}_{k}}} \left / {\partial {p_{i}}}\right .}$ and ${{\partial {{\ddot {\mathbf {x}}}_{k}}} \left / {\partial {p_{i}}}\right .}$ according to (47) and (48).

4.3 Second-order sensitivity of transient responses based on DDM of reduced system

Further differentiating (49) with respect to the design variable p_j gives

$$ \begin{array}{@{}rcl@{}} \frac{{{\partial^{2}}{{\mathbf{z}}_{k{\text{ + 1}}}}}}{{\partial {p_{i}}\partial {p_{j}}}} &=& \frac{{{\partial^{2}}{\mathbf{T}}({{\varDelta}} t)}}{{\partial {p_{i}}\partial {p_{j}}}}{{\mathbf{z}}_{k}} + \frac{{\partial {\mathbf{T}}({{\varDelta}} t)}}{{\partial {p_{i}}}}\frac{{\partial {{\mathbf{z}}_{k}}}}{{\partial {p_{j}}}} + \frac{{\partial {\mathbf{T}}({{\varDelta}} t)}}{{\partial {p_{j}}}}\frac{{\partial {{\mathbf{z}}_{k}}}}{{\partial {p_{i}}}} + {\mathbf{T}}({{\varDelta}} t)\frac{{{\partial^{2}}{{\mathbf{z}}_{k}}}}{{\partial {p_{i}}\partial {p_{j}}}} \\&& + \frac{{{{\varDelta}} t}}{2}\sum\limits_{i = 1}^{gm} {{w_{i}}\frac{{{\partial^{2}}{\mathbf{T}}\left( {\frac{{{{\varDelta}} t}}{2}(1 - {\xi_{i}})} \right)}}{{\partial {p_{i}}\partial {p_{j}}}}{\mathbf{r}}\left( {{t_{k}} + \frac{{{{\varDelta}} t}}{2}(1 + {\xi_{i}})} \right)}. \end{array} $$

(56)

In (56), the only unknown term is the second-order derivative of exponential matrix function with respect to design variables ${{{\partial ^{2}}{\mathbf {T}}({{\varDelta }} t)} \left / {\partial {p_{i}}\partial {p_{j}}}\right .}$. By further differentiating (50), one obtains

$$ \frac{{{\partial^{2}}{\mathbf{T}}({{\varDelta}} t)}}{{\partial {p_{i}}\partial {p_{j}}}} = \frac{{\partial {\mathbf{T}}({{\varDelta}} t)}}{{\partial {p_{j}}}}{{\varDelta}} {t}\frac{{\partial {\mathbf{A}}}}{{\partial {p_{i}}}} + {\text{e}^{{\mathbf{A}}{{\varDelta}} t}}{{\varDelta}} t\frac{{{\partial^{2}}{\mathbf{A}}}}{{\partial {p_{i}}\partial {p_{j}}}}, $$

(57)

where

$$ \frac{{{\partial^{2}}{\mathbf{A}}}}{{\partial {p_{i}}\partial {p_{j}}}} = \left[ {\begin{array}{ccc} {\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}}\\ {\frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{\bar{\mathbf{K}}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}}}&{\frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}}}&{\frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{\bar{\mathbf{L}}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}}}\\ {\mathbf{0}}&{\frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf W}}}^{- 1}}{{{\bar{\mathbf R}}}^{\mathbf{T}}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}}}&{\frac{{{\partial^{2}}\left( {{{{\bar{\mathbf W}}}^{- 1}}{\bar{\mathbf E}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}}} \end{array}} \right]. $$

(58)

The specific expressions of the second-order sensitivities in (58) are derived and shown in Appendix C. The second-order sensitivities of the transient responses should be also transformed from the reduced generalized coordinate into the original coordinate by

$$ \frac{{{\partial^{2}}{{\mathbf{x}}_{k}}}}{{\partial {p_{i}}\partial {p_{j}}}} = {\mathbf{T}}\frac{{{\partial^{2}}{{\mathbf{p}}_{k}}}}{{\partial {p_{i}}\partial {p_{j}}}},\frac{{\partial {{\dot{\mathbf{x}}}_{k}}}}{{\partial {p_{i}}}} = {\mathbf{T}}\frac{{{\partial^{2}}{{{\dot{\mathbf p}}}_{k}}}}{{\partial {p_{i}}\partial {p_{j}}}}. $$

(59)

4.4 Summary of the DDM-based MOR-DSA method

To better understand and code up the methods proposed above, the proposed methods for calculating the first- and second-order derivatives for transient responses of reduced viscoelastically damped systems based on the DDM are summarized as follows:

• (1) Calculate the mass matrix M, the stiffness matrix K of the full system and their first and second derivatives with respect to all design variables.

• (2) Choose one of the projection bases proposed in Section 3 and construct the corresponding reduction basis T.

• (3) Construct the reduced system matrices and vectors ${\bar {\mathbf {M}}}, {{\bar {\mathbf {C}}}_{0}}, {{\bar {\mathbf {C}}}_{k}}, {\bar {\mathbf {K}}}, {\bar {\mathbf {F}}}(s), {{\bar {\mathbf {L}}}_{k}}, {{\bar {\mathbf R}}_{k}}$ by using (34) and (35), respectively.

• (4) Obtain matrices ${\bar {\mathbf E}},{\bar {\mathbf W}},{\bar {\mathbf {L}}},{\bar {\mathbf R}}$ according to (66)–(69).

• (5) Compute the inverse matrices ${{\bar {\mathbf {M}}}^{- 1}}$ and ${{\bar {\mathbf W}}^{- 1}}$.

• (6) Obtain the state-space amplification matrix A of the reduced structural system by (43) and its first and second derivatives with respect to the design variables by solving (51) and (58), respectively.

• (7) Select an appropriate time step Δt, a bisection order N_e, a truncation order L and a number of Guass points gm as required computational accuracy.

• (8) Calculate the matrix exponential functions T(Δt), ${{\mathbf {T}}\left ({\frac {{{{\varDelta }} t}}{2}(1 - {\xi _{i}})} \right )}$ by using the PIM and their first and second derivatives ${{\partial {\mathbf {T}}({{\varDelta }} t)} \left /{\partial {p_{i}}}\right .}$, ∂²T(Δt)/∂p_i∂p_j by solving (50) and (57), respectively.

• (9) For each k = 0,1,2,⋯, solve the dynamic responses z_k+ 1 from vector z_k by (46), the first derivatives of dynamic responses with respect to the design variable ${{\partial {{\mathbf {z}}_{k{\text { + 1}}}}} \left / {\partial {p_{i}}}\right .}$ by (49) and the second derivatives of dynamic responses with respect to the design variable ${{{\partial ^{2}}{{\mathbf {z}}_{k{\text { + 1}}}}} \left / {\partial {p_{i}}\partial {p_{j}}}\right .}$ by (56) (z₀, ${{\partial {{\mathbf {z}}_{\text {0}}}} \left / {\partial {p_{i}}}\right .}$, ${{{\partial ^{2}}{{\mathbf {z}}_{\text {0}}}} / {\partial {p_{i}}\partial {p_{j}}}}$ are the given initial conditions).

• (10) Transform the calculated sensitivities from the reduced generalized coordinate to their full original coordinate by (55) and (59).

5 Numerical examples and discussions

In this section, two numerical examples are investigated to show and compare the performances of each presented method. All computations are performed on a laptop computer with a Windows 10, 64 bit operating system and a Intel Core i7-8565U CPU (2.00 GHz) with 8.00 GB random-access memory.

5.1 A fixed-free axially vibrating rod with exponential damping models

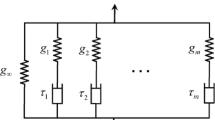
In this case, a fixed-free axially vibrating rod with two exponential damping models shown in Fig. 1 is considered. The rod example is derived from (Adhikari and Wagner 2004) and can be discretized into N elements according to different mesh sizes. The equation of motion of the axially vibrating rod with two exponential damping models can be expressed as

$$ \mathbf{M}\ddot{\mathbf{x}}(t) + {{\int}_{0}^{t}} {\left[ {{\mu_{1}}{e^{- {\mu_{1}}(t - \tau )}}{{\mathbf{C}}_{1}} + {\mu_{2}}{e^{- {\mu_{2}}(t - \tau )}}{{\mathbf{C}}_{2}}} \right]} \dot{\mathbf{x}}(\tau )d\tau + {\mathbf{Kx}}(t) = {\mathbf{f}}(t), $$

(60)

where M and K are global mass and stiffness matrices and can be easily deduced using the finite element assembly procedure. Besides, C₁, C₂ are the damping coefficient matrices, which are assumed to be proportional to the global mass and stiffness matrices

$$ {{\mathbf{C}}_{1}} = \alpha {\mathbf{M}},\quad {{\mathbf{C}}_{2}} = \beta {\mathbf{K}}, $$

(61)

where

$$ \alpha = 2\xi \frac{{{\omega_{1}}{\omega_{2}}}}{{{\omega_{1}} + {\omega_{2}}}},\beta = 2\xi \frac{1}{{{\omega_{1}} + {\omega_{2}}}}. $$

(62)

Fig. 1

Diagram of the fixed-free axial rod example with two exponential damping models

The related geometrical and physical data of the rod example are listed in Table 1.

Table 1 Geometrical and physical parameters of axially vibrating rod

As can be seen from Fig. 1, the element number of the rod is changeable. Therefore, the computational performances against the element number N of various methods can be investigated in this example. Since the damping coefficient matrices C₁, C₂ are of full-rank, an N DOF rod example in this case results in a 4N × 4N system matrix in the state-space formulation. The dynamic responses, response functions and their 1st- and 2nd-order sensitivities of the rod will be approximated by the presented modal-projection bases. The reference values of the dynamic responses and the response functions are calculated by using the MPIM (Ding et al. 2018a). For the sensitivity results, the FDM is adopted based on the reference values of the transient response. The central difference method of 0.01% perturbation with respect to the design variable is used.

5.1.1 Computational accuracy

In order to investigate the computational accuracy of each method, the rod is firstly discretized into 500 elements (N = 500 and the system dimension is 2000). A forced vibration problem is considered. As illustrated in Fig. 1, an impact force shown in Fig. 2 is firstly exerted on the tip of the free end (Zhang and Kang 2014). An initial velocity condition is considered, that is ${{\mathbf {x}}_{0}} = {\mathbf {0}},{\dot {\mathbf {x}}_{0}} = {\left \{ {0.0001,0, {\ldots } ,0} \right \}^{T}}$.

Fig. 2

Impact force applied to the axially vibrating rod

The first-order sensitivities and their relative errors of the tip displacement with respect to ρ and E are calculated by the MM (${\omega _{{p_{1}}}} = 0$), MSER (ε_tol = 1E − 8) and IAM (${\omega _{{p_{1}}}} = 0$) methods with the same time step (Δt = 1.5 × 10^− 5s) and the retained lower-order modes (Nm = 25) for constructing T_MSE. The first 0.012 s is considered and the results are shown in Fig. 3. The relative errors in this paper are defined by

$$ \varepsilon = \left| {\frac{{{\boldsymbol{\psi}^{\prime}}\left( {t,p,{{\varDelta}} t} \right) - {{\boldsymbol{\psi }}_{r}}^{\prime} \left( {t,p,{{\varDelta}} t} \right)}}{{{{\boldsymbol{\psi }}_{r}}^{\prime} \left( {t,p,{{\varDelta}} t} \right)}}} \right|, $$

(63)

where ${\boldsymbol {\psi }^{\prime }}$ is the sensitivity calculated by the proposed method and ${{\boldsymbol {\psi }}_{r}}^{\prime }$ is the sensitivity of the reference value.

Fig. 3

1st-order sensitivities and their relative errors of the tip displacement using three different methods (Δt = 1.5 × 10^− 5s, Nm = 25): a-b $\frac {{\partial {\mathbf {x}}(t)}}{{\partial \rho }}$ and c–d $\frac {{\partial {\mathbf {x}}(t)}}{{\partial E}}$

As can be seen from Fig. 3a, c, the first-order sensitivities of the tip displacement responses calculated by the presented three methods all match well with the reference value. The relative errors shown in Fig. 3b, d indicate that the computational accuracy of the MSER and the MM are almost the same. And the IAM method performs better than the former two methods on this condition. It can be also found that, although the retained modes of the T_MSE are the same, the final reduced system dimensions of each method are different. The final reduced system dimensions of the MM and the IAM methods can be determined when the projection bases are adopted. However, the final reduced system dimension of the MSER is affected by the chosen error tolerance.

The second-order sensitivities and their relative errors of the tip displacement with respect to ρE are also investigated by the presented methods and shown in Fig. 4. All methods give satisfactory results for the second-order sensitivity calculations. The relative errors of the 2nd-order sensitivities for each method show the same tendency with their 1st-order sensitivity calculations. However, by considering the amplitudes, the relative errors of the 2nd-order sensitivity are slightly higher than their corresponding 1st-order sensitivity for all methods.

Fig. 4

a 2nd-order sensitivities with respect to $\frac {{{\partial ^{2}}{\mathbf {x}}(t)}}{{\partial \rho \partial E}}$ and b their relative errors of three different method (Δt = 1.5 × 10^− 5s, Nm = 25)

Since the correction term T_MSE is included in all presented projection bases for viscoelastically damped system, the dimension Nm of correction basis has a great influence on the computational accuracy of each method. The required number of Nm can be determined using the cut-off criterion in Section 2.4. Besides the non-harmonic load shown in Fig. 2, a harmonic excitation force $f(t) = 500,000\sin \limits (500\pi t)$ is also considered. The relative errors of the 1st-order tip displacement sensitivity of different methods under both harmonic and non-harmonic loads, which differ in dimension number (Nm = 25,35,45 and 55), are shown in Fig. 5.

Fig. 5

Relative errors of different reduction basis dimensions for the 1st-order sensitivities with various methods (Δt = 1.5 ×10^{- 5} s): a–c $\frac {{\partial {\mathbf {x}}(t)}}{{\partial \rho }}$ under non-harmonic load and d–f $\frac {{\partial {\mathbf {x}}(t)}}{{\partial \rho }}$ under harmonic load

It can be seen that all methods obtain satisfactory results on calculating the first-order transient sensitivities under both harmonic and non-harmonic loadings. With the increase of the number of the retained mode Nm, the relative errors of tip displacement sensitivities for all methods decrease significantly when the loads are exerted (for example, the first 0.0024 s in Fig. 5a–c and all time histories in Fig. 5d–f). And for decayed transient responses, the improved accuracy by taking into account more Nm is not that obvious than the previous condition. It should also be mentioned that the final reduced dimensions of the MSER method for harmonic and non-harmonic loads are different. This is because the minimum error tolerance of the MSER method to ensure convergence for different excitations are different (ε_tol = 1E − 8 for non-harmonic case and ε_tol = 1E − 15 for harmonic case).

The relative errors of the 2nd-order tip displacement sensitivities with different Nm are displayed in Fig. 6 for each method. With the increase of Nm, the relative errors of each method generally decrease. Unlike their corresponding results of the 1st-order sensitivity, the relative errors shown in Fig. 6e–f of the MSER and the IAM obtained by Nm = 55 are slightly bigger than those obtained by Nm = 45. It indicates that the number of the retained mode Nm is not the only factor to affect the computational accuracy of the sensitivities. Other parameters, such as the time step, the priori chosen frequency point and error criterion of each method, should be also investigated.

Fig. 6

Relative errors of different reduction basis dimensions for the 2nd-order sensitivities $\frac {{{\partial ^{2}}{\mathbf {x}}(t)}}{{\partial \rho \partial E}}$ with various methods (Δt = 1.5 ×10^{- 5} s): a–c under non-harmonic load and d–f under harmonic load

5.1.2 Computational efficiency

As evidenced in Figs. 5 and 6, increasing the dimension of the projection basis will generally improve the computational accuracy. However, in the mean time, the computational time of the sensitivity computations is also increased. Figure 7 displays the distribution of computational time for evaluation of the dynamic response sensitivities using each modal-projection basis and the FOM. Two cases are considered (DOF = 1500 and 2000). Other computational parameters are fixed: Δt = 1.5 ×10^{- 5} s for all methods, Nm = 50 for MOR methods, ${\omega _{{p_{1}}}} = 0$ for T_MM, T_IAM and ε_tol = 1E − 15 for T_MSER.

Fig. 7

Distribution of computational time for evaluation of the transient response sensitivities using each modal-projection based reduction technique: a DOF= 1500 and b DOF= 2000 (Δt = 1.5 ×10^{- 5} s,Nm = 50)

As shown in Fig. 7, the computational time for calculating the sensitivities by using the FOM is very time-consuming. When DOF = 1500 and 2000, it requires almost 14,942 s and 33,833 s, respectively. The computational efficiency is unacceptable in practical engineering optimization for viscoelastically damped systems. However, by using the presented modal-projection based reduction techniques, the computational time can be significantly reduced. The computational time for the MM method is only 0.16% (DOF= 1500) and 0.24% (DOF= 2000) of the FOM.

The computational time of the reduced-order method can be divided into projection bases construction part (for both static correction and other vectors) and dynamic response sensitivities calculation part. It can be found that most of the computational time for the reduced-order method is dedicated to the evaluation of the projection bases. For the MM and MSER methods, the most time-consuming part is the construction for static correction terms. While for the IAM method, the construction for other vectors is the most time-consuming part. This is because for the IAM method, the complex eigenvalue problem needs to be solved. Once the system is reduced, the time required to calculate the sensitivity is low and is directly related to the size of the reduction basis.

In an attempt to find the best compromise between precision and efficiency, the computational time and relative error of presented methods against the increase of DOF (N = 500,1000,1500 and 2000) with a fixed time step Δt = 1.5 ×10^{- 5}s and retained modes (Nm = 25) are investigated. Two response functions are considered

$$ {{\boldsymbol{\psi }}_{1}} = {{\int}_{0}^{T}} {{\mathbf{x}}_{{\text{target}}}^{2}dt} ,\quad{{\boldsymbol{\psi }}_{2}} = {{\int}_{0}^{T}} {{\mathbf{x}}_{{\text{target}}}^{T}{\mathbf{F}}(t)} dt. $$

(64)

Figure 8 confronts the relative errors of sensitivities of different methods (MM, MSER and IAM) as a function of their relative computational time for two response functions ψ₁ and ψ₂. The reference values of the sensitivities given in this case are calculated by the DDM using the FOM instead of the FDM. Both 1st- and 2nd-order sensitivities are calculated.

Fig. 8

Relative errors of the displacement sensitivities as function of the relative computational time for two response functions: a 1st-order sensitivities and b 2nd-order sensitivities (Δt = 1.5 ×10^{- 5}s,Nm = 25)

As can be seen, the computational time of the MM is less than the MSER for the 1st- and 2nd-order sensitivity calculations. And the former two methods are much more efficient than the IAM. Conversely, the computational errors of the IAM is much lower than the MM method and almost the same with the MSER method for both 1st- and 2nd-order sensitivity calculations. Therefore, the MSER yields good trade-off between computational accuracy and efficiency among the presented methods when only one modal basis is added to build T_MM, T_IAM (${\omega _{{p_{1}}}} = 0$). However, the computational time of the MSER is influenced by the error criterion ε_tol. The results computed by the MSER may be sometimes not converged if the error criterion is not appropriately given.

In order to investigate the performances of various methods with different parameters (${\omega _{{p_{i}}}}$, ε_tol) and time steps Δt, the relative error and computational time of the sensitivity calculations for the response function ψ₁ are listed in Table 2. The DOF is 1000 and the number of the retained modes is Nm = 25 for all reduced methods.

Table 2 Relative error and computational time of the sensitivities calculating the response function ψ₁ for various methods (Nm = 25) with different parameters and time steps

With the decrease of the time step, the computational time of the FOM dramatically improves. When Δt = 1.5 × 10^− 6s, the computational time of the FOM is about 51,967 s (14.7 h). On the contrary, the computational time can be largely reduced by the MOR techniques. With the decrease of the time step, although the computational time of each method increase, the imcrement can be ignored compared with the FOM. Particularly, for the MSER method, there is no obvious relationship between the time step and its computational time. This is because the computational time of the MSER is influenced by both time step and chosen error criteria. When the error criteria is set too small, the results of the MSER may be not converged. Besides, it can also be concluded that both the number and value of the priori chosen frequency will affect the computational accuracy and has no obvious influence on the computational time for all methods.

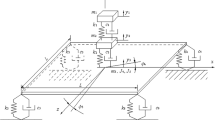
5.2 A two stage floating raft isolation system with multiple damping models

In this case, a simplified two stage floating raft isolation system with multiple damping models is considered. The diagram of the example is shown in Fig. 9. The floating raft system contains a foundation plate, a raft plate and two machines (m₁, m₂). All sides of the raft plate and two long sides of the foundation plate are free. Two short sides of the foundation plate are clamped. The connections of the foundation, raft plate and two machines are modelled by the spring-damp element. In order to better approximate the actual characteristics of the dynamic performances, the damping models between these two connections are assumed to be different. The viscoelastic spring-damp elements g₁(t) between the raft plate and two machines are defined by the Biot model, while the connections g₂(t) between the foundation and the raft plate are the exponential model. Since two viscoelastic damping models are included in this example, some special difficulties may be encountered in analyzing the corresponding structural system. By using the presented formulations with the GDM, the sensitivity analysis for structural systems with multiple damping models can be solved. The related geometrical and physical data of the floating raft example are listed in Table 3.

Fig. 9

Diagram of the two stage floating-raft system with multiple damping models

Table 3 Geometrical and physical parameters of floating raft system

The two stage floating raft system is discretized into 7202 DOFs. Unlike the previous axially vibrating rod example, the dampers of this example are distributed, so the damping coefficient matrices are not of full-rank. The actual dimension of the system matrix is 7262. A forced vibration with non-zero initial conditions is considered. The initial displacement conditions of m₁, m₂ are set to 0.02 m and 0.01 m, respectively. The excitation force is applied on m₁ and assumed to be $f(t) = 5\sin \limits (0.5\pi t)$. Both geometry and meshed finite element models are generated from HYPERMESH. The mass and stiffness matrices are exported from the BDF file. Based on these system matrices, the sensitivities with respect to damping parameters can be explicitly derived and computed in MATLAB. If other geometry and material parameters are studied, the system matrices should be derived by the finite element procedure, which would be more complicated than obtained from the BDF file.

The first-order displacement and velocity sensitivities and their relative errors of the target point m₂ (in Z direction) with respect to damping coefficient b₁ are computed by the MM (${\omega _{{p_{1}}}} = 0$), MSER (ε_tol = 1E − 10) and IAM (${\omega _{{p_{1}}}} = 0$) methods. The time step Δt = 0.01s and the retained lower-order modes Nm = 45 are the same for all methods. The first 6 s is considered and the results are shown in Fig. 10.

Fig. 10

1st-order sensitivities and their relative errors of the dynamic responses using three different methods (Nm = 45): a–b $\frac {{\partial {\mathbf {x}}(t)}}{{\partial {b_{1}}}}$ and c–d $\frac {{\partial \dot {\mathbf {x}}(t)}}{{\partial {b_{1}}}}$

As can be observed, the 1st-order displacement and velocity sensitivities are all in good agreement with the FOM. The results obtained by the MSER method match well with the reference values, which show obvious advantageous on accuracy over the MM and IAM methods. It can be founded that although the initial obtained modes of each reduced-order method are the same (Nm = 45), the final dimension of the MSER method is much more than the other two methods. This is the reason for the MSER method give better results on this condition.

The second-order displacement and velocity sensitivities as well as their relative errors are also investigated using the same parameters. The design variables are b₁a₁ and the results are shown in Fig. 11. The performances and relative errors of the presented methods show the same tendency with their 1st-order sensitivity calculations. However, the amplitude of the relative error for the 2nd-order sensitivities is much higher than their corresponding 1st-order results.

Fig. 11

2nd-order sensitivities and their relative errors of the dynamic responses using three different methods (Nm = 45): a–b $\frac {{\partial {\mathbf {x}}(t)}}{{\partial {b_{1}}{a_{1}}}}$ and c–d $\frac {{\partial \dot {\mathbf {x}}(t)}}{{\partial {b_{1}}{a_{1}}}}$

In order to investigate the performances of the presented methods on different parameters and orders of retained modes (Nm = 20,40,60,80), the relative sensitivity errors of the response functions ψ₂, ψ₃ for each presented method are calculated and shown in Figs. 12, 13, 14. The expression of the response function ψ₃ is

$$ {{\boldsymbol{\psi }}_{3}} = {{\int}_{0}^{T}} {\left( {0.5{{\mathbf{x}}^{2}} + 0.5{{\dot{\mathbf{x}}}^{2}}} \right)} dt. $$

(65)

Fig. 12

Relative sensitivity errors of the response functions for the floating raft system computed by the MM with different parameters and orders of retained modes (Δt = 0.01s)

Fig. 13

Relative sensitivity errors of the response functions for the floating raft system computed by the MSER with different parameters and orders of retained modes (Δt = 0.01s)

Fig. 14

Relative sensitivity errors of the response functions for the floating raft system computed by the IAM with different parameters and orders of retained modes (Δt = 0.01s)

In Fig. 12, with the increase of the order of reduced bases, the relative errors of the 1st-order sensitivities for all cases generally decreased, while the relative errors of the 2nd-order sensitivity are not stable for each case. Besides, the relative error of ${\omega _{{p_{1}}}} = 2000$ is much less than that of ${\omega _{{p_{1}}}} = 0$ for both 1st- and 2nd-order sensitivity calculations. When multiple priori frequency points are chosen (${\omega _{{p_{1}}}} = 0,{\omega _{{p_{2}}}} = 2000$), it performs better than simple frequency point case. Therefore, for the MM method, it is better to choose more than one frequency point to construct the reduced basis. The number of retained modes for each frequency point can be equally divided.

For the MSER method shown in Fig. 13, when the time step is fixed, with the decease of the error criterion, the accuracy of both 1st- and 2nd-order sensitivity improves. However, small error criterion may lead to convergence problem.

As to the IAM method, when the priori chosen frequency ${\omega _{{p_{j}}}} \ne 0$, the sensitivity results obtained is much more accurate than that of when ${\omega _{{p_{j}}}} = 0$. But the value of the non-zero ${\omega _{{p_{j}}}}$ seems has no influence on the accuracy.

Table 4 lists the sensitivity results of different methods with respect to various damping coefficients. The retained modes Nm = 40 and the time step Δt = 0.01s. The parameters adopted for each method are their corresponding best performances in above analyses. For the 1st-order sensitivity calculations, all methods show good agreement with the reference value. However, as to the 2nd-order sensitivity results, the relative errors for each method increase rapidly.

Table 4 The sensitivities and relative errors of different methods with respect to various design variables (Nm = 40,Δt = 0.01s)

The relative error and computational time of the sensitivity calculations for response functions ψ₂, ψ₃ with different time steps are listed in Table 5. The number of the retained modes is Nm = 40 for all reduced methods. With the decrease of the time step, the computational time for the FOM improves significantly, while the computational time for the reduced-order methods has no obvious increment. Compared with the FOM, the computational time of all reduced methods is greatly reduced. When the time step is big (Δt = 0.1s), the relative errors of the reduced methods are relatively larger, especially for the 2nd-order sensitivities. However, when the time step is too small (Δt = 0.005s), the relative errors of response function ψ₂ are even larger than those with bigger time-steps. This is because ψ₂ is associated with the excitation forces. The approximations of the excitation terms may also affect the relative error of the sensitivity analyses.

Table 5 Relative errors and computational time of the sensitivities calculating the response functions (ψ₂, ψ₃) for various methods with different time steps (Nm = 40)

In order to investigate the performances of presented methods on the excitation frequency, several excitation forces with various excitation frequencies are exerted on m₁. The force amplitude, tim step and other computational parameters are fixed. The response function ψ₂ is considered and the target point is m₂. Table 6 lists the computational errors of 1st- and 2nd-order sensitivities of ψ₂ with various excitation frequencies. The results indicate that the computational accuracy of all reduced methods, including the MM method, the MSER method and the IAM method, is influenced by the excitation frequency. Besides, the accuracy of 1st-order sensitivity calculations is much more accurate than the 2nd-order sensitivity results.

Table 6 The computational errors of different methods with various excitations with respect to b₁, b₁a₁ (Nm = 40,Δt = 0.1s)

6 Conclusions

This paper develops an efficient design sensitivity analysis (DSA) method for transient responses and response functions of viscoelastically damped systems based on model order reduction (MOR) techniques. The energy dissipation behaviors of the viscoelastic materials are represented by non-viscous damping models. However, the introduction of non-viscous damping models significantly increase the system dimension, because extra coordinates and internal variables are needed for obtaining their dynamic solutions. This would leave a massive computational burden, particularly when performing the DSA of transient responses. Traditional MOR techniques have been well-developed for undamped or viscously damped systems on frequency responses, but they cannot be directly applied into the viscoelastically damped systems for transient responses, especially for calculating the sensitivity. The difficulty lies in the fact that both the projection matrix and system matrices are frequency-dependent, which is rather challenging. In order to alleviate these problems, several modal-projection bases are developed for viscoelastically damped systems to ease the burden and efficiently calculate the sensitivities of the transient responses.

By introducing three robust modal-projection bases, namely multi-model (MM) method, modal strain energy modified by displacement residuals (MSER) method and improved approximation method (IAM), the matrices of the viscoelastically damped systems are dramatically reduced. Then, a reduced state-space expression without convolution integral term is derived by using a generalized damping model of fraction formula. Based on this, the first- and second-order derivatives of the transient responses and response functions are deduced in the framework of a modified precise integration method using direct differentiation method (DDM). The computational efficiency and accuracy of the presented MOR-DDM methods are studied and compared via two numerical examples under various parameters. Important conclusions are drawn as follows:

• The assumption that the projection bases are treated as constant with respect to the design variables is reasonable and the proposed MOR-DDM can obtain satisfactory results on calculating the first- and second-order derivatives of the transient responses and the response functions for viscoelastically damped systems. However, it is noted that one needs to choose a relative small time step size to ensure the accuracy of the second-order transient response sensitivities.

• The computational time is significantly reduced by using both real and complex mode based projection bases and the MOR-DDM gives fairly accurate approximations of DSA compared to those from the FOM. The results show that the real mode based projection basis yields better trade-off between accuracy and efficiency, which is more suitable for large-scale systems.

• Both the MM and the MSER methods represent a good compromise between accuracy and computational time compared with the IAM. However, the computational time and accuracy are highly built on the appropriate choice of tolerance for the MSER. Therefore, the MM is more stable than the MSER, which would be the best choice to be the reduction basis for capturing the time domain DSA of large-scale viscoelastically damped systems.

• For the MM method, by considering both computational accuracy and efficiency, it is recommended that two or more priori frequency points are chosen to generate the projection bases. To obtain higher accuracy, the adopted frequency points can be near the normal modes of the corresponding undamped system for the viscoelastically damped system.

In future work, it is valuable to develop a MOR-DSA method for transient responses using adjoint variable method. Besides, some robust modal-projection bases and their proper assumptions of derivatives are needed to improve the computational accuracy on calculating the second-order derivatives of the transient responses for viscoelastically damped systems.

Appendices

Appendix A:: Specific expressions of some matrices in Section 4.1

The expressions of the relative reduced matrices in (37) are

$$ {\bar{\mathbf E}} = diag({{\mathbf{I}}_{{{\bar{r}}_{1}}}} \otimes {{\mathbf{E}}_{1}},{{\mathbf{I}}_{{{\bar{r}}_{2}}}} \otimes {{\mathbf{E}}_{2}}, {\cdots} ,{{\mathbf{I}}_{{{\bar{r}}_{n}}}} \otimes {{\mathbf{E}}_{n}})\in \mathbb{R}^{{\bar{p} \times \bar{p}}}, $$

(66)

$$ {\bar{\mathbf W}} = diag({{\mathbf{I}}_{{{\bar{r}}_{1}}}} \otimes {{\mathbf{W}}_{1}},{{\mathbf{I}}_{{{\bar{r}}_{2}}}} \otimes {{\mathbf{W}}_{2}}, {\cdots} ,{{\mathbf{I}}_{{{\bar{r}}_{n}}}} \otimes {{\mathbf{W}}_{n}})\in \mathbb{R}^{{\bar{p} \times \bar{p}}}, $$

(67)

$$ {\bar{\mathbf{L}}} = \left[ {{{\bar{\mathbf{L}}}_{1}}{{({{\mathbf{I}}_{{{\bar{r}}_{1}}}} \otimes {{\mathbf{P}}_{1}})}^{T}},{{\bar{\mathbf{L}}}_{2}}{{({{\mathbf{I}}_{{{\bar{r}}_{2}}}} \otimes {{\mathbf{P}}_{2}})}^{T}}, {\cdots} ,{{\bar{\mathbf{L}}}_{n}}{{({{\mathbf{I}}_{{{\bar{r}}_{n}}}} \otimes {{\mathbf{P}}_{n}})}^{T}}} \right] \in \mathbb{R}^{{Nm \times \bar{p}}}, $$

(68)

$$ {\bar{\mathbf R}} = \left[ {{{\bar{\mathbf R}}_{1}}{{({{\mathbf{I}}_{{{\bar{r}}_{1}}}} \otimes {{\mathbf{Q}}_{1}})}^{T}},{{\bar{\mathbf R}}_{2}}{{({{\mathbf{I}}_{{{\bar{r}}_{2}}}} \otimes {{\mathbf{Q}}_{2}})}^{T}}, {\cdots} ,{{\bar{\mathbf R}}_{n}}{{({{\mathbf{I}}_{{{\bar{r}}_{n}}}} \otimes {{\mathbf{Q}}_{n}})}^{T}}} \right] \in \mathbb{R}^{{Nm \times \bar{p}}}, $$

(69)

$$ \bar{p} = \sum\limits_{k = 1}^{n} {{{\bar{r}}_{k}}{q_{k}}}. $$

(70)

Appendix B:: The first-order sensitivity derivatives in (51)

As defined in (8) and Appendix A, the matrices ${\bar {\mathbf {L}}},{\bar {\mathbf W}},{\bar {\mathbf R}},{\bar {\mathbf E}}$ are related to the viscoelastic damping model involved, which are composed of the relaxation parameters, the order of the damping models and the identity matrix. If the design variable p_i is not related to the damping relaxation parameters, the first-order derivatives of ${\bar {\mathbf {L}}},{\bar {\mathbf W}},{\bar {\mathbf R}},{\bar {\mathbf E}}$ are all zero. On the contrary, when the damping model parameters are chosen to be the design variable, the first-order derivatives of ${\bar {\mathbf {L}}},{\bar {\mathbf W}},{\bar {\mathbf R}},{\bar {\mathbf E}}$ should be considered. As defined in (35), ${{\bar {\mathbf {L}}}_k},{{\bar {\mathbf R}}_k}$ are the full column rank of the reduced viscoelastic damping coefficient matrix. It describes the distribution of the damping materials, which is independent of the parameters of the damping models. Besides, W_k,Q_k are also independent of any design parameters. Therefore, we have

$$ \frac{{\partial {{{\bar{\mathbf{L}}}}_{k}}}}{{\partial {p_{i}}}} = {\mathbf{0}},{\text{ }}\frac{{\partial {{{\bar{\mathbf R}}}_{k}}}}{{\partial {p_{i}}}} = {\mathbf{0}},\frac{{\partial {{\mathbf{W}}_{k}}}}{{\partial {p_{i}}}} = {\mathbf{0}},\frac{{\partial {{\mathbf{Q}}_{k}}}}{{\partial {p_{i}}}} = {\mathbf{0}},\frac{{\partial {{\bar{\mathbf{C}}}_{0}}}}{{\partial {p_{i}}}} = {\mathbf{0}}. $$

(71)

Substituting (71) into (66)–(69), one can derive the first-order derivatives of the ${\bar {\mathbf {L}}},{\bar {\mathbf W}},{\bar {\mathbf R}},{\bar {\mathbf E}}$:

$$ \begin{array}{l} \frac{{\partial {\bar{\mathbf{L}}}}}{{\partial {p_{i}}}} = \left[ {{{{\bar{\mathbf{L}}}}_{1}}{{({{\mathbf{I}}_{{{\bar r}_{1}}}} \otimes \frac{{\partial {{\mathbf{P}}_{1}}}}{{\partial {p_{i}}}})}^{T}},{{{\bar{\mathbf{L}}}}_{2}}{{({{\mathbf{I}}_{{{\bar r}_{2}}}} \otimes \frac{{\partial {{\mathbf{P}}_{2}}}}{{\partial {p_{i}}}})}^{T}}, {\cdots} ,{{{\bar{\mathbf{L}}}}_{N}}{{({{\mathbf{I}}_{{{\bar r}_{n}}}} \otimes \frac{{\partial {{\mathbf{P}}_{n}}}}{{\partial {p_{i}}}})}^{T}}} \right],\\ \frac{{\partial {\bar{\mathbf E}}}}{{\partial {p_{i}}}} = \left[ {{{\mathbf{I}}_{{{\bar r}_{1}}}} \otimes \frac{{\partial {{\mathbf{E}}_{1}}}}{{\partial {p_{i}}}},{{\mathbf{I}}_{{{\bar r}_{2}}}} \otimes \frac{{\partial {{\mathbf{E}}_{2}}}}{{\partial {p_{i}}}}, {\cdots} ,{{\mathbf{I}}_{{{\bar r}_{n}}}} \otimes \frac{{\partial {{\mathbf{E}}_{n}}}}{{\partial {p_{i}}}}} \right],\\ \frac{{\partial {\bar{\mathbf W}}}}{{\partial {p_{i}}}} = {\mathbf{0}},\frac{{\partial {\bar{\mathbf R}}}}{{\partial {p_{i}}}} = {\mathbf{0}}, \end{array} $$

(72)

where $\frac {{\partial {{\mathbf {P}}_k}}}{{\partial {p_i}}},\frac {{\partial {{\mathbf {E}}_k}}}{{\partial {p_i}}}$ can be easily obtained from (8). Therefore, the specific expressions of the terms in (51) are

$$ \begin{array}{@{}rcl@{}} \frac{{\partial \left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}}} \right)}}{{\partial {p_{i}}}} & = {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}} - {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {{\bar{\mathbf{C}}}_{0}}}}{{\partial {p_{i}}}}{\text{ }} \to \\& {\text{ }}\frac{{\partial \left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}}} \right)}}{{\partial {p_{i}}}} = {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}}, \end{array} $$

(73)

$$ \frac{{\partial \left( { - {{{\bar{\mathbf{M}}}}^{{\text{ - 1}}}}{\bar{\mathbf{L}}}} \right)}}{{\partial {p_{i}}}} = {{\bar{\mathbf{M}}}^{{\text{ - 1}}}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{{\text{ - 1}}}}{\bar{\mathbf{L}}} - {{\bar{\mathbf{M}}}^{{\text{ - 1}}}}\frac{{\partial {\bar{\mathbf{L}}}}}{{\partial {p_{i}}}}, $$

(74)

$$ \begin{array}{@{}rcl@{}} \frac{{\partial \left( { - {{{\bar{\mathbf W}}}^{- 1}}{{{\bar{\mathbf R}}}^{T}}} \right)}}{{\partial {p_{i}}}} &= {{\bar{\mathbf W}}^{- 1}}\frac{{\partial {\bar{\mathbf W}}}}{{\partial {p_{i}}}}{{\bar{\mathbf W}}^{- 1}}{{\bar{\mathbf R}}^{T}} - {{\bar{\mathbf W}}^{- 1}}\frac{{\partial {{{\bar{\mathbf R}}}^{T}}}}{{\partial {p_{i}}}}{\text{ }} \to \\& {\text{ }}\frac{{\partial \left( { - {{{\bar{\mathbf W}}}^{- 1}}{{{\bar{\mathbf R}}}^{T}}} \right)}}{{\partial {p_{i}}}} = {\mathbf{0}}, \end{array} $$

(75)

$$ \begin{array}{@{}rcl@{}} \frac{{\partial \left( {{{{\bar{\mathbf W}}}^{- 1}}{\bar{\mathbf E}}} \right)}}{{\partial {p_{i}}}} & = - {{\bar{\mathbf W}}^{- 1}}\frac{{\partial {\bar{\mathbf W}}}}{{\partial {p_{i}}}}{{\bar{\mathbf W}}^{- 1}}{\bar{\mathbf E}} + {{\bar{\mathbf W}}^{- 1}}\frac{{\partial {\bar{\mathbf E}}}}{{\partial {p_{i}}}}{\text{ }} \to \\& {\text{ }}\frac{{\partial \left( {{{{\bar{\mathbf W}}}^{- 1}}{\bar{\mathbf E}}} \right)}}{{\partial {p_{i}}}} = {{\bar{\mathbf W}}^{- 1}}\frac{{\partial {\bar{\mathbf E}}}}{{\partial {p_{i}}}}. \end{array} $$

(76)

Appendix C:: The second-order sensitivity derivatives in (58)

The second-order derivatives of (58) are as follows:

$$ \begin{array}{@{}rcl@{}} \frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{\bar{\mathbf{K}}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}} &=& \frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{j}}}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}{\bar{\mathbf{K}}} + {{\bar{\mathbf{M}}}^{- 1}}\frac{{{\partial^{2}}{\bar{\mathbf{M}}}}}{{\partial {p_{i}}\partial {p_{j}}}}{{\bar{\mathbf{M}}}^{- 1}}{\bar{\mathbf{K}}} \\&& +{{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}\frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{j}}}}{\bar{\mathbf{K}}} + {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{K}}}}}{{\partial {p_{j}}}}\\&&- \frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{j}}}}\frac{{\partial {\bar{\mathbf{K}}}}}{{\partial {p_{i}}}} - {{\bar{\mathbf{M}}}^{- 1}}\frac{{{\partial^{2}}{\bar{\mathbf{K}}}}}{{\partial {p_{i}}\partial {p_{j}}}}, \end{array} $$

(77)

$$ \begin{array}{@{}rcl@{}} \frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}}&=& \frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{j}}}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}} + {{\bar{\mathbf{M}}}^{- 1}}\frac{{{\partial^{2}}{\bar{\mathbf{M}}}}}{{\partial {p_{i}}\partial {p_{j}}}}{{\bar{\mathbf{M}}}^{- 1}}{{\bar{\mathbf{C}}}_{0}} \\&& + {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}\frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{j}}}}{{\bar{\mathbf{C}}}_{0}}, \end{array} $$

(78)

$$ \begin{array}{@{}rcl@{}} \frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf{M}}}}^{- 1}}{\bar{\mathbf{L}}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}} &= &\frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{j}}}}{{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}{\bar{\mathbf{L}}} + {{\bar{\mathbf{M}}}^{- 1}}\frac{{{\partial^{2}}{\bar{\mathbf{M}}}}}{{\partial {p_{i}}\partial {p_{j}}}}{{\bar{\mathbf{M}}}^{- 1}}{\bar{\mathbf{L}}} \\&&+ {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}\frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{j}}}}{\bar{\mathbf{L}}} + {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{L}}}}}{{\partial {p_{j}}}} \\&&- \frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{j}}}}\frac{{\partial {\bar{\mathbf{L}}}}}{{\partial {p_{i}}}} - {{\bar{\mathbf{M}}}^{- 1}}\frac{{{\partial^{2}}{\bar{\mathbf{L}}}}}{{\partial {p_{i}}\partial {p_{j}}}}, \end{array} $$

(79)

$$ \frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf W}}}^{- 1}}{{{\bar{\mathbf R}}}^{T}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}} = {\mathbf{0}},\frac{{{\partial^{2}}\left( { - {{{\bar{\mathbf W}}}^{- 1}}{\bar{\mathbf E}}} \right)}}{{\partial {p_{i}}\partial {p_{j}}}} = {{\bar{\mathbf W}}^{- 1}}\frac{{{\partial^{2}}{\bar{\mathbf E}}}}{{\partial {p_{i}}\partial {p_{j}}}}, $$

(80)

where

$$ \frac{{\partial {{{\bar{\mathbf{M}}}}^{- 1}}}}{{\partial {p_{i}}}} = - {{\bar{\mathbf{M}}}^{- 1}}\frac{{\partial {\bar{\mathbf{M}}}}}{{\partial {p_{i}}}}{{\bar{\mathbf{M}}}^{- 1}}, $$

(81)

$$ \frac{{{\partial^{2}}{\bar{\mathbf{M}}}}}{{\partial {p_{i}}\partial {p_{j}}}} = {{\mathbf{T}}^{T}}\frac{{{\partial^{2}}{\mathbf{M}}}}{{\partial {p_{i}}\partial {p_{j}}}}{\mathbf{T}},\quad\frac{{{\partial^{2}}{\bar{\mathbf{K}}}}}{{\partial {p_{i}}\partial {p_{j}}}} = {{\mathbf{T}}^{T}}\frac{{{\partial^{2}}{\mathbf{K}}}}{{\partial {p_{i}}\partial {p_{j}}}}{\mathbf{T}}, $$

(82)

$$ \frac{{{\partial^{2}}{\bar{\mathbf{L}}}}}{{\partial {p_{i}}\partial {p_{j}}}} = \left[ {{{{\bar{\mathbf{L}}}}_{1}}{{({{\mathbf{I}}_{{{\bar r}_{1}}}} \otimes \frac{{{\partial^{2}}{{\mathbf{P}}_{1}}}}{{\partial {p_{i}}\partial {p_{j}}}})}^{T}}, {\cdots} , {{{\bar{\mathbf{L}}}}_{N}}{{({{\mathbf{I}}_{{{\bar r}_{n}}}} \otimes \frac{{{\partial^{2}}{{\mathbf{P}}_{n}}}}{{\partial {p_{i}}\partial {p_{j}}}})}^{T}}} \right], $$

(83)

$$ \frac{{{\partial^{2}}{\bar{\mathbf E}}}}{{\partial {p_{i}}\partial {p_{j}}}} = \left[ {{{\mathbf{I}}_{{{\bar r}_{1}}}} \otimes \frac{{{\partial^{2}}{{\mathbf{E}}_{1}}}}{{\partial {p_{i}}\partial {p_{j}}}},{{\mathbf{I}}_{{{\bar r}_{2}}}} \otimes \frac{{{\partial^{2}}{{\mathbf{E}}_{2}}}}{{\partial {p_{i}}\partial {p_{j}}}}, {\cdots} ,{{\mathbf{I}}_{{{\bar r}_{n}}}} \otimes \frac{{{\partial^{2}}{{\mathbf{E}}_{n}}}}{{\partial {p_{i}}\partial {p_{j}}}}} \right]. $$

(84)