1 Introduction

Topology optimization for dynamics problems has been extensively studied since the early 1990s (Díaaz and Kikuchi 1992; Ma et al. 1993; Bendsøe and Sigmund 2003; Deaton and Grandhi 2014). The existing research generally falls into three categories: eigenfrequency problems (Díaaz and Kikuchi 1992; Pedersen 2000; Du and Olhoff 2007; Yi and Youn 2016), frequency response problems (Ma et al. 1993; Olhoff and Du 2005; 2016; Shu et al. 2011; Kang et al. 2012; Li et al. 2018), and dynamic response problems (Min et al. 1999; Jang et al. 2012; Zhang and Kang 2014a; Zhao and Wang 2016; Yan et al. 2016; Zhao and Wang 2017; Behrou and Guest 2017). Solutions to the first kind of problems aim to improve the inherent characteristics of the structure, while the goal of addressing the latter two kinds of problems is to improve the dynamic responses, such as displacement, velocity, acceleration, and stress, generated by the structure under external loads. It is worth noting that there are also some researches on topology optimization driven to control of structures, either for active or passive problems. Interested readers are referred to the published works (Gonçalves et al. 2016, 2017; Padoin et al. 2019; Zhang and Kang 2014a, b; Zhang et al. 2018) and the references therein. This work focuses on topology optimization for frequency response problems.

Topology optimization for frequency response problems has been studied based on the homogenization method (Ma et al. 1993), density-based approach (Olhoff and Du 2005; Yoon 2010; Olhoff and Du 2016), level-set-based approach (Shu et al. 2011; Li et al. 2018), and evolutionary structural optimization method (Vicente et al. 2015). Ma et al. (1993) proposed a dynamic compliance minimization formulation for topology optimization problems under harmonic force excitation. Jog (2002) developed a density-based approach to minimize the average input power and displacement amplitude under periodic loads. Tcherniak (2002) formulated a topology optimization problem to maximize the magnitude of the steady-state response of resonating structures. Olhoff and Du (2005) proposed an incremental frequency method for minimizing dynamic compliance subject to harmonic force excitation. Olhoff and Du (2016) further developed a generalized incremental frequency method. Shu et al. (2011) presented a level-set-based approach to minimize frequency response at the specific points or surfaces on the structure. Kang et al. (2012) investigated the optimal distribution of damping material in vibrating structures subject to harmonic excitation. Niu et al. (2018) compared some commonly used objective functions in topology optimization for frequency response problems. Silva et al. (2019) performed a critical analysis for using the dynamic compliance as the objective function for topology optimization of one-material structures under harmonic excitation. Most of these studies only considered the excitation for a given frequency; however, the structural responses over a specific frequency interval also need to be considered for many practical applications (Wijker 2008; Yu et al. 2013; Zhu et al. 2016; Liu et al. 2019).

When solving topology optimization problems under harmonic excitation over a specific frequency interval, a practical issue is that the frequency response analysis required at each iteration would be computationally intensive when the number of excitation frequencies is large, especially for large-scale problems. Many prior efforts have been devoted to finding a way to cope with this challenge. Ma et al. (1993) applied the mode displacement method (MDM) to solve the frequency response topology optimization problems within the homogenization design framework. Tcherniak (2002) employed the mode acceleration method (MAM) to compute the frequency responses of the structure. Jensen (2007) employed the Padé approximants to represent the frequency responses over a given frequency interval. Yoon (2010) investigated the effectiveness of the MDM, the Ritz vector method (RVM), and the quasi-static Ritz vector method (QSRVM) for evaluating the frequency response functions within the density-based topology optimization framework. Liu et al. (2015a) performed a comparative study among the MDM, MAM, and the full method for structural topology optimization under harmonic excitation, and found that the MAM is preferable when multiple excitation frequencies are considered due to its balance between efficiency and accuracy.

Although it has been shown that some model-order reduction methods, such as the MAM, RVM, and QSRVM, are effective for solving frequency response topology optimization problems, there still exist some issues that may affect their performance. During topology optimization, the structure may evolve dramatically and its eigenfrequencies and eigenmodes also may change substantially. Therefore, the MAM and RVM may not always be able to ensure the accuracy of the responses at all iterations with a fixed number of lower-order eigenfrequencies or Ritz vectors (Zhao et al. 2018; Gu et al. 2000). In addition, the centering frequency of the QSRVM may be close to or may even coincide with some eigenfrequency of the structure at some iteration; this is disadvantageous for generating the quasi-static Ritz vectors. Recently, Wu et al. (2015, 2016) developed a combined method of modal superposition and model-order reduction for efficient frequency response analysis of proportionally damped systems. This combined method can adaptively determine the number of lower-order eigenfrequencies and eigenmodes to be computed, and compensates for the contribution of other unknown higher-order eigenmodes through the use of a model-order reduction method. This combined method has been employed to solve (concurrent) topology optimization problems for frequency responses (Zhao et al. 2018, 2019). However, a reliable criterion for determining the number of basis vectors for the model-order reduction method is still lacking. Actually, it can be observed from their examples that the relative residual error usually is larger than the given error tolerance (e.g., see Fig. 6 in Zhao et al. (2018), where the given error tolerance is ε = 10− 8). This drives the research interest in adaptively determining the number of eigenfrequencies and eigenmodes to be computed for efficient frequency response analysis in topology optimization.

Assuming Rayleigh damping, this study develops a hybrid expansion for the displacement vector, where the contributions of the lower-order modes and higher-order modes are given by the modal superposition and Neumann expansion, respectively. A simple expression for the residual error of the approximate displacement vector provided by the truncated hybrid expansion is derived. Key factors affecting the convergence rate of the truncated hybrid expansion series are uncovered. Finally, an adaptive hybrid expansion method (AHEM) is proposed, where the number of lower-order eigenfrequencies and eigenmodes to be computed can be determined using the Strum sequence (Bathe 2014), while the number of terms to be preserved in the truncated Neumann expansion can be determined according to the given error tolerance. The performance of the proposed AHEM and its effectiveness for solving topology optimization problems under harmonic force excitation are demonstrated by studying several 2D and 3D numerical examples.

The rest of this paper is organized as follows. Section 2 gives a brief review of the topology optimization problem under harmonic excitation. Section 3 presents the theory and computational procedure for the adaptive hybrid expansion method. Section 4 gives three numerical examples to demonstrate the performance of the proposed AHEM and its effectiveness for solving topology optimization problems. Finally, the conclusions of this work are outlined in Section 5.

2 Frequency response topology optimization problems

This section briefly reviews topology optimization and solution methods for minimizing frequency responses (more details can be found in the relevant literature (Yoon 2010; Liu et al. 2015a)).

2.1 Density-based approach and material interpolation scheme

The density-based approach is employed to perform topology optimization in this work. Assume that the design domain is meshed into Ne elements, then a design variable ηe is assigned to the e th element to indicate if it is full of material or void. To obtain clear designs, the SIMP (solid isotropic material with penalization) model (Bendsøe 1989; Zhou and Rozvany 1991) is applied for material interpolation as

$$ \begin{array}{l} {\mathbf{{D}}_{e}} = g({{\eta}_{e}}){\mathbf{{D}}_{\mathrm{s}}}\\ {\rho_{e}} = {{\eta}_{e}}{\rho_{\mathrm{s}}} \end{array} $$
(1)

where Ds and ρs are the elasticity matrix and structural density of the solid material, respectively. To alleviate the appearance of localized modes in topology optimization of dynamics problems, the following polynomial interpolation function (Zhu et al. 2009) is used in this work.

$$ g({{\eta}_{e}}) = \alpha {{{\eta}_{e}^{p}}} + (1 - \alpha ){{\eta}_{e}} $$
(2)

where p > 1 is a penalty exponent and 0 < α < 1 is used to prevent the ratio ηe/g(ηe) from becoming too large when ηe approaches zero. In numerical implementation, p = 3 and α = 15/16 are typically used.

2.2 Formulation of frequency response minimization

The semi-discrete momentum equation of a damped structure under an external load can generally be written as

$$ \mathbf{M}{\ddot{\mathbf{u}}}(t) + \mathbf{C}{\dot{\mathbf{u}}}(t) + \mathbf{K}\mathbf{u}(t) = \mathbf{{f}}(t) $$
(3)

where M, C, and K are the global mass, damping, and stiffness matrices, respectively; f(t) is the global force vector corresponding to the load applied to the structure; and u(t), \({\dot {\mathbf {u}}}(t)\), and \({\ddot {\mathbf {u}}}(t)\) are the time-dependent displacement, velocity, and acceleration vectors, respectively.

When harmonic excitation is considered, the response is also harmonic and has the same frequency as the excitation frequency, but with different phases. By letting f(t) = Re(Feiωt) and u(t) = Re(Ueiωt), it is obtained that

$$ (- {\omega^{2}}\mathbf{M} + i\omega \mathbf{C} + \mathbf{K})\mathbf{U} = \mathbf{F} $$
(4)

where \(i = \sqrt { - 1} \) is the complex unit. The global stiffness matrix K and mass matrix M can be obtained by assembling the corresponding element stiffness and mass matrices, respectively. The element stiffness matrix ke and mass matrix me can be computed as

$$ {\mathbf{{k}}_{e}} = g({{\eta}_{e}})\mathbf{{k}}_{e}^{0}, {\mathbf{{m}}_{e}} = {{\eta}_{e}}\mathbf{{m}}_{e}^{0} $$
(5)

where

$$ \mathbf{{k}}_{e}^{0} = {\int}_{{\varOmega_{e}}} {{\mathbf{B}^{\mathrm{T}}}\mathbf{D}_{\mathrm{s}}\mathbf{B}d\varOmega} $$
(6)
$$ \mathbf{{m}}_{e}^{0} = {\rho_{\mathrm{s}}}{\int}_{{\varOmega_{e}}} \mathbf{N}^{\mathrm{T}}\mathbf{N}d\varOmega $$
(7)

with N being the matrix of shape functions and B the matrix of shape function derivatives.

In addition, Rayleigh damping C = αrM + βrK is assumed in this work, and the coefficients αr and βr are considered to be design-independent. Furthermore, it is also assumed that the load vector F has no spatial dependency on the excitation frequency ω.

Finally, topology optimization for minimizing the frequency response of structures under an external harmonic force excitation can be formulated as

$$ \begin{array}{ll} \mathop {\min }\limits_{{\boldsymbol{\eta }}} &:J_{\mathrm{d}} = \frac{1}{{{\omega_{\mathrm{b}}} - {\omega_{\mathrm{a}}}}}{\int}_{{\omega_{\mathrm{a}}}}^{{\omega_{\mathrm{b}}}} {J(\omega ,{\boldsymbol{\eta }},\mathbf{U},{\bar{\mathbf{U}}})} d\omega \\ s.t.&:(- {\omega^{2}}\mathbf{M} + i\omega \mathbf{{C}} + \mathbf{K})\mathbf{U} = \mathbf{F},\omega \in [{\omega_{\mathrm{a}}},{\omega_{\mathrm{b}}}]\\ &:{G_{0}} = \left( \sum\limits_{e = 1}^{{N_{e}}} {{{\eta}_{e}}v_{e}}\right) - \varsigma V \le 0\\ &:0 \le {{\eta}_{e}} \le 1,1 \le e \le {N_{e}} \end{array} $$
(8)

As discussed in many previous works (Ma et al. 1993; Yoon 2010; Shu et al. 2011; Liu et al. 2015b; Zhu et al. 2018), the mean value Jd of a target response \(J(\omega ,{\boldsymbol {\eta }},\mathbf {U},{\bar {\mathbf {U}}})\) over a frequency interval is taken as the objective function; ωa and ωb are the lower and upper bounds of the frequency interval, respectively; \({\bar {\mathbf {U}}}\) is the conjugate of displacement vector U; ve is the volume of the e th element; V is the volume of the design domain; and ς is the prescribed volume fraction of the design domain.

2.3 Solution method

2.3.1 Calculation of the objective function

In order to perform topology optimization, the objective function and its sensitivities need to be calculated at each iteration. As described in Section 2.2, the objective function is defined as an integration of the target response, which is an implicit function of ω, over a given frequency interval. When applying a numerical quadrature technique to evaluate the value of the objective function, it can be approximated as

$$ {J_{\mathrm{d}}} = \sum\limits_{n = 1}^{{N_{f}}} {{w_{n}}J(\omega_{n},{\boldsymbol{\eta}},\mathbf{U}_{n},{\bar{\mathbf{U}}}_{n})} $$
(9)

where Nf is the number of integration points, ωn and wn are the corresponding frequency points and weights for numerical integration, and Un and \({\bar {\mathbf {U}}}_{n}\) denote the displacement vector and its conjugate corresponding to the n th frequency points.

It is well known that the frequency response curves usually have sharp peaks around the resonant frequencies. Therefore, usually a large number of integration points are needed to accurately calculate the value of the objective function when the frequency interval [ωa, ωb] contains some resonant frequencies (Yoon 2010; Liu et al. 2015a; Allaire and Michailidis 2018). Noting that the displacement vectors corresponding to each integration point have to be computed, efficient frequency response analysis is desired.

2.3.2 Sensitivity analysis

To solve topology optimization problems, sensitivity analysis is an indispensable step to quantify the influence of each design variable on the structural performance (Sigmund 2011). For convenience, we denote the dynamic stiffness matrix as S = −ω2M + iωC + K in the following discussion. According to the adjoint method (Yoon 2010), we can obtain the following equation:

$$ \frac{{dJ}}{{d{{\eta}_{e}}}} = \frac{{\partial J}}{{\partial {{\eta}_{e}}}} + 2{\text{Re}} \left( {{\boldsymbol{\lambda }}^{\mathrm{T}}}\left( \frac{{\partial \mathbf{{S}}}}{{\partial {{\eta}_{e}}}}\mathbf{U}-\frac{{\partial \mathbf{F}}}{{\partial {{\eta}_{e}}}}\right)\right) $$
(10)

where

$$ \frac{\partial \mathbf{S}} {\partial {\eta}_{e}}= - {\omega^{2}}\frac{{\partial \mathbf{M}}}{{\partial {{\eta}_{e}}}} + i\omega \frac{{\partial \mathbf{{C}}}}{{\partial {{\eta}_{e}}}} + \frac{{\partial \mathbf{K}}}{{\partial {{\eta}_{e}}}} $$
(11)

The adjoint displacement vector λ satisfies

$$ \mathbf{{S}\boldsymbol{\lambda }}= - {\left( {\frac{{\partial J}}{{\partial \mathbf{U}}}} \right)^{\mathrm{T}}} $$
(12)

Since this work only considers the case of design-independent loads, ∂F/∂ηe = 0, consequently (10) is simplified to

$$ \frac{{dJ}}{{d{{\eta}_{e}}}} = \frac{{\partial J}}{{\partial {{\eta}_{e}}}} + 2{\text{Re}} \left( {{\boldsymbol{\lambda }}^{\mathrm{T}}}\frac{{\partial \mathbf{{S}}}}{{\partial {{\eta}_{e}}}}\mathbf{U}\right) $$
(13)

Applying (13) for every frequency ωn(n = 1,⋯,Nf) can obtain the adjoint displacement vectors λn(n = 1,⋯,Nf). Consequently, the sensitivity of the objective function can be obtained as:

$$ \frac{{d{J_{\mathrm{d}}}}}{{d{{\eta}_{e}}}} =\sum\limits_{n = 1}^{{N_{f}}} {{w_{n}}} {\left. {\frac{{\partial J}}{{\partial {{\eta}_{e}}}}} \right|_{\omega = {\omega_{n}}}}+2{\text{Re}} \left( \sum\limits_{n = 1}^{{N_{f}}} {{w_{n}}} {\boldsymbol{\lambda}}_{n}^{\mathrm{T}}\frac{{\partial {{\mathbf{S}}_{n}}}}{{\partial {{\eta}_{e}}}}{\mathbf{U}_{n}}\right) $$
(14)

It can be seen from (12) that the adjoint problem can also be treated as a frequency response analysis problem, and Nf adjoint displacement vectors need to be obtained for sensitivity analysis. For self-adjoint problems, the adjoint displacement vectors can be obtained by scaling the corresponding displacement vectors; therefore, little extra computation effort is needed. In contrast, for non-self-adjoint problems, the adjoint displacement vectors have to be solved via (12) for each frequency; thus, an efficient frequency response analysis method is also desired for the calculation of the adjoint displacement vectors.

2.4 Numerical procedure

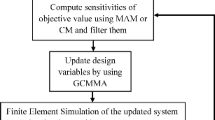
Once the sensitivity information is obtained, the design variables can be updated by using the MMA (Svanberg 1987). The flowchart for solving topology optimization problems under harmonic force excitation is shown in Fig. 1. The most time-consuming steps at each iteration are the computations of the displacement and adjoint displacement vectors; therefore, efficient frequency response analysis is the key to reduce the huge overall computational cost.

Fig. 1
figure 1

Flowchart of topology optimization for minimizing frequency responses

Full size image

3 A novel approach for efficient frequency response analysis: adaptive hybrid expansion method

This section presents a novel approach for efficient frequency response analysis, namely adaptive hybrid expansion method (AHEM). The AHEM can make the frequency response analysis adaptive, thereby enabling efficient computation. Suppose that F = F0h(ω), where F0 and h(ω) represent the spatial distribution and frequency-dependence of force excitation, respectively. In this case, it is only necessary to solve the equations SU0 = F0; then, the displacement vector U can be obtained as U = U0h(ω).

3.1 A hybrid expansion of the displacement vector

Suppose that \(0 < {{\omega _{1}^{2}}} \le {{\omega _{2}^{2}}} \le {\cdots } \le {{\omega _{N}^{2}}}\) are the eigenvalues of the structure and ϕ1, ϕ2,⋯ϕN are the corresponding eigenvectors. These eigenvectors are normalized by the mass matrix; thus, they satisfy

$$ \begin{array}{l} {{\boldsymbol{\Phi}}^{\mathrm{T}}}{\mathbf{M}{\boldsymbol{\Phi}}}= \mathbf{{I}}\\ {{\boldsymbol{\Phi}}^{\mathrm{T}}}{\mathbf{K}{\boldsymbol{\Phi}}}=\boldsymbol{{\Lambda}} \end{array} $$
(15)

where Φ = [ϕ1, ϕ2,⋯ϕN], and \(\boldsymbol {{\Lambda }}=\text {diag}({{\omega _{1}^{2}}},{{\omega _{2}^{2}}},\cdots ,{{\omega _{N}^{2}}})\).

According to the modal superposition method, the response of the structure can be expressed by a linear combination of all the eigenvectors as

$$ \mathbf{U}_{0} = \mathbf{\Phi }\mathbf{{q}}={{\boldsymbol{\Phi}}_{\mathrm{L}}}{\mathbf{{q}}_{\mathrm{L}}}+{{\boldsymbol{\Phi}}_{\mathrm{H}}}{\mathbf{{q}}_{\mathrm{H}}} $$
(16)

with

$$ \begin{array}{@{}rcl@{}} {\boldsymbol{\Phi}}_{\mathrm{L}}&=&[\mathbf{{\phi}}_{1},\mathbf{{\phi}}_{2}, {\cdots} \mathbf{{\phi}}_{l}]\\ {\boldsymbol{\Phi}}_{\mathrm{H}}&=&[\mathbf{{\phi}}_{l+1},\mathbf{{\phi}}_{l+2}, {\cdots} \mathbf{{\phi}}_{N}]\\ {\mathbf{{q}}_{\mathrm{L}}} &=& {[(- {\omega^{2}} + i{\alpha_{\mathrm{r}}}\omega){\mathbf{{I}}_{\mathrm{L}}} +(i{\beta_{\mathrm{r}}}\omega + 1){\boldsymbol{{\Lambda}}_{\mathrm{L}}}]^{ - 1}}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}}\mathbf{F}_{0}\\ {\mathbf{{q}}_{\mathrm{H}}} &=& {[(- {\omega^{2}} + i{\alpha_{\mathrm{r}}}\omega){\mathbf{{I}}_{\mathrm{H}}} +(i{\beta_{\mathrm{r}}}\omega + 1){\boldsymbol{{\Lambda}}_{\mathrm{H}}}]^{ - 1}}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0} \end{array} $$
(17)

where the number l of lower-order modes will be determined later. The matrices involved in (17) are defined as

$$ \begin{array}{@{}rcl@{}} {\mathbf{{I}}_{\mathrm{L}}} &=& {\mathbf{{I}}_{l \times l}}\\ {\mathbf{{I}}_{\mathrm{H}}} &=& {\mathbf{{I}}_{{(N-l)} \times {(N-l)}}}\\ \boldsymbol{{\Lambda}}_{\mathrm{L}}&=&\text{diag}({{\omega_{1}^{2}}},{{\omega_{2}^{2}}},\cdots,{{\omega_{l}^{2}}})\\ \boldsymbol{{\Lambda}}_{\mathrm{H}}&=&\text{diag}({\omega_{l+1}^{2}},{\omega_{l+1}^{2}},\cdots,{{\omega_{N}^{2}}}) \end{array} $$
(18)

Since it is expensive or impossible to compute all the eigenvalues and eigenvectors, here, we develop a hybrid expansion for the displacement response, where the lower-order response is computed by the modal superposition method, while the higher-order response is given by a Neumann expansion.

The higher-order response can be given as

$$ \begin{array}{@{}rcl@{}} {{\boldsymbol{\Phi}}_{\mathrm{H}}}{\mathbf{{q}}_{\mathrm{H}}} &=& {{\boldsymbol{\Phi}}_{\mathrm{H}}}{[(i{\beta_{\mathrm{r}}}\omega + 1){\boldsymbol{{\Lambda}}_{\mathrm{H}}}({\mathbf{{I}}_{\mathrm{H}}} + \frac{{ - {\omega^{2}} + i{\alpha_{\mathrm{r}}}\omega }}{{i{\beta_{\mathrm{r}}}\omega + 1}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-1})]^{- 1}}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}\\ &=&\frac{1}{{i{\beta_{\mathrm{r}}}\omega + 1}}{{\boldsymbol{\Phi}}_{\mathrm{H}}}{({\mathbf{{I}}_{\mathrm{H}}} - \gamma \boldsymbol{{\Lambda}}_{\mathrm{H}}^{-1})^{- 1}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0} \end{array} $$
(19)

where γ = (ω2 − iαrω)/(iβrω + 1).

When the spectral radius \(\rho (\gamma \boldsymbol {{\Lambda }}_{\mathrm {H}}^{-1}) < 1\), according to the Neumann expansion theorem, we have

$$ {({\mathbf{{I}}_{\mathrm{H}}} - \gamma \boldsymbol{{\Lambda}}_{\mathrm{H}}^{-1})^{- 1}}=\sum\limits_{n = 0}^{+ \infty } {{\gamma^{n}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{- n}} $$
(20)

Substituting (20) into (19) yields

$$ \begin{array}{@{}rcl@{}} (i{\beta_{\mathrm{r}}}\omega + 1){{\boldsymbol{\Phi}}_{\mathrm{H}}}{\mathbf{{q}}_{\mathrm{H}}}&=&{{\boldsymbol{\Phi}}_{\mathrm{H}}}\left( \sum\limits_{n = 0}^{+ \infty } {{\gamma^{n}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{- n}}\right)\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}\\ &=&\sum\limits_{n = 1}^{+ \infty } {{\gamma^{n-1}}{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-n}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}}_{0}\\ &=&\sum\limits_{n = 1}^{+ \infty } {{\gamma^{n-1}}{\mathbf{{u}}_{\mathrm{{H}},n}}} \end{array} $$
(21)

where

$$ {\mathbf{{u}}_{\mathrm{{H}},n}}={{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-n}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0} $$
(22)

Both ΦH and ΛH in (22) are unknown. However, notice that

$$ {\mathbf{K}^{- 1}}={{\boldsymbol{\Phi}}_{\mathrm{L}}}\boldsymbol{{\Lambda}}_{\mathrm{L}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}}+{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}} $$
(23)

thus, we have

$$ {\mathbf{{u}}_{\mathrm{{H}},1}}=({\mathbf{K}^{- 1}} - {{\boldsymbol{\Phi}}_{\mathrm{L}}}\boldsymbol{{\Lambda}}_{\mathrm{L}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}})\mathbf{F}_{0}\\ $$
(24)

and when n ≥ 2,

$$ \begin{array}{@{}rcl@{}} {\mathbf{{u}}_{\mathrm{{H}},n}}&=&{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-n}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}\\ &=&{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-(n - 1)}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}\\ &=& {{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{M}{\mathbf{{u}}_{\mathrm{{H}},n - 1}}\\ &=& ({\mathbf{K}^{- 1}} - {{\boldsymbol{\Phi}}_{\mathrm{L}}}\boldsymbol{{\Lambda}}_{\mathrm{L}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}})\mathbf{M}{\mathbf{{u}}_{\mathrm{{H}},n - 1}} \end{array} $$
(25)

Premultiply (24) and (25) by K and noticing that KΦL = MΦLΛL, we further have

$$ \mathbf{K}{\mathbf{{u}}_{\mathrm{{H}},1}}=(\mathbf{{I}} - \mathbf{K}{{\boldsymbol{\Phi}}_{\mathrm{L}}}\boldsymbol{{\Lambda}}_{\mathrm{L}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}})\mathbf{F}_{0}= (\mathbf{{I}} - \mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{L}}}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}})\mathbf{F}_{0} $$
(26)

and when n ≥ 2,

$$ \begin{array}{@{}rcl@{}} \mathbf{K}{\mathbf{{u}}_{\mathrm{{H}},n}}&=&(\mathbf{{I}} - \mathbf{K}{{\boldsymbol{\Phi}}_{\mathrm{L}}}\boldsymbol{{\Lambda}}_{\mathrm{L}}^{-1}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}})\mathbf{M}{\mathbf{{u}}_{\mathrm{{H}},n - 1}}\\ &=&(\mathbf{{I}} - \mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{L}}}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}})\mathbf{M}{\mathbf{{u}}_{\mathrm{{H}},n - 1}} \end{array} $$
(27)

Equations (26) and (27) imply that the vectors uH,n(n = 1,2,⋯ ) can be obtained iteratively by solving a series of static problems sharing the same stiffness matrix.

By substituting (21) into (16), it can be found that

$$ \mathbf{U}_{0}={{\boldsymbol{\Phi}}_{\mathrm{L}}}{\mathbf{{q}}_{\mathrm{L}}}+\frac{1}{{(i{\beta_{\mathrm{r}}}\omega + 1)}}\sum\limits_{n = 1}^{+ \infty } {{\gamma^{n - 1}}}{\mathbf{{u}}_{\mathrm{{H}},n}} $$
(28)

For practical computation, usually only a finite number of terms can be used to compute the response. By only preserving the first q terms for the higher-order response in (28), a truncated hybrid expansion of the displacement response can be obtained as

$$ \mathbf{U}_{\mathrm{a}}={{\boldsymbol{\Phi}}_{\mathrm{L}}}{\mathbf{{q}}_{\mathrm{L}}}+\frac{1}{{(i{\beta_{\mathrm{r}}}\omega + 1)}}\sum\limits_{n = 1}^{q} {{\gamma^{n-1}}}{\mathbf{{u}}_{\mathrm{{H}},n}} $$
(29)

The truncated hybrid expansion usually converges very fast because, in addition to the lower-order effect being taken account by the terms ΦLqL, the higher-order effect of the load F0 is also considered when constructing the vectors uH,n (hereafter referred to as basis vectors). When solving topology optimization problems under harmonic excitation, the frequency response analysis needs to be performed automatically at each iteration; thus, it is desired to develop an adaptive method to automatically determine how many eigenmodes and basis vectors need to be involved in the truncated hybrid expansion.

It is noteworthy that, because of the mass-orthogonality of the lower-order and higher-order eigenmodes (i.e., \({\boldsymbol {\Phi }}_{\mathrm {L}}^{\mathrm {T}}\mathbf {M}{{\boldsymbol {\Phi }}_{\mathrm {H}}}=\mathbf {{0}}\)), it can be found that

$$ {\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}}\mathbf{M}{\mathbf{{u}}_{\mathrm{{H}},n}}={\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}}\mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-n}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}=\mathbf{{0}} $$
(30)

Thus, the basis vectors uH,n are mass-orthogonal to the lower-order eigenmodes.

3.2 Computation of the residual error for the truncated hybrid expansion

This subsection develops an efficient method for computing the residual error of the truncated hybrid expansion in (29). The error of the displacement vector is

$$ \mathbf{U}_{0}-\mathbf{U}_{\mathrm{a}}=\frac{1}{{(i{\beta_{\mathrm{r}}}\omega + 1)}}\sum\limits_{n = q+1}^{+ \infty } {{\gamma^{n - 1}}} {\mathbf{{u}}_{\mathrm{{H}},n}} $$
(31)

Consequently, the residual of the force vector is

$$ \begin{array}{@{}rcl@{}} \mathbf{F}_{0}-\mathbf{{SU}}_{\mathrm{a}}&=&\mathbf{{S}}(\mathbf{U}_{0}-\mathbf{U}_{\mathrm{a}})\\ &=&(-\gamma \mathbf{M} + \mathbf{K})\left( \sum\limits_{n = q + 1}^{+ \infty } {{\gamma^{n-1}}} {\mathbf{{u}}_{\mathrm{{H}},n}}\right) \end{array} $$
(32)

Substituting (22) into (32) and noticing that KΦH = MΦHΛH, we have, when q ≥ 1,

$$ \begin{array}{@{}rcl@{}} \mathbf{F}_{0}-\mathbf{{S}}{\mathbf{U}_{\mathrm{a}}}&=&(-\gamma \mathbf{M}+\mathbf{K})\left( \sum\limits_{n = q + 1}^{+ \infty } {{\gamma^{n - 1}}} {{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{- n}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}\right)\\ &=&-\sum\limits_{n = q + 1}^{+ \infty } {{\gamma^{n}}} \mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-n}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}\\ &&+ \sum\limits_{n = q + 1}^{+ \infty } {{\gamma^{n - 1}}} \mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-(n - 1)}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}\\ &=&{\gamma^{q}}\mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-q}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}\\ &=&{\gamma^{q}}\mathbf{M}{\mathbf{{u}}_{\mathrm{{H}},q}} \end{array} $$
(33)

Therefore,

$$ ||\mathbf{F}_{0}-\mathbf{{SU}}_{\mathrm{a}}||_{2} = |\gamma {|^{q}}||\mathbf{M}{\mathbf{{u}}_{\mathrm{{H}},q}}||_{2} $$
(34)

Since M and uH,q are independent of the excitation frequency ω, and |γ|q is monotonic increasing with respect to the increasing of the excitation frequency, (34) implies that the residual norm is also monotonic increasing with respect to the increasing of the excitation frequency and attains its maximum at ω = ωb. Thus, only the residual error at ω = ωb needs to be computed to evaluate the accuracy of the truncated hybrid expansion.

Furthermore, according to (32), we also have

$$ \begin{array}{@{}rcl@{}} ||\mathbf{F}_{0}-\mathbf{{S}}{\mathbf{U}_{\mathrm{a}}}|{|_{2}} &=&|\gamma {|^{q}} ||\mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{H}}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-q}{\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}|{|_{2}}\\ &=& ||\mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{H}}}(|\gamma {|^{q}}\boldsymbol{{\Lambda}}_{\mathrm{H}}^{-q}){\boldsymbol{\Phi}}_{\mathrm{H}}^{\mathrm{T}}\mathbf{F}_{0}|{|_{2}} \end{array} $$
(35)

Noticing that \(\rho (|\gamma {|^{q}}\boldsymbol {{\Lambda }}_{\mathrm {H}}^{-q}) =(\rho (\gamma \boldsymbol {{\Lambda }}_{\mathrm {H}}^{-1}))^{q}\) and \(\rho (\gamma \boldsymbol {{\Lambda }}_{\mathrm {H}}^{-1}) =|\gamma |/\omega _{l + 1}^{2}< 1\), thus, the residual norm usually decreases very fast as q increases. This also explains why usually preserving only a few terms in the truncated hybrid expansion would be sufficient to achieve accurate results.

3.3 An adaptive hybrid expansion method for efficient frequency response analysis

This subsection newly proposes an adaptive hybrid expansion method (AHEM) for efficient frequency response analysis. Here, we only consider the case of frequency-independent excitations (i.e., h(ω) is a constant); however, there is no difficulty to generalize the proposed procedure for solving problems involving frequency-dependent excitations. To make the frequency response analysis method adaptive, two issues have to be addressed. The first issue is how many lower-order eigenpairs are required; the second one is how many terms need to be preserved in the truncated hybrid expansion.

To address the first issue, note that the convergence condition of the Neumann expansion is that \(\rho (\gamma \boldsymbol {{\Lambda }}_{\mathrm {H}}^{-1}) =|\gamma |/\omega _{l + 1}^{2}< 1\), and \(|\gamma |=\sqrt {\frac {{\omega ^{4} + \alpha _{\mathrm {r}}^{2}\omega ^{2}}}{{\beta _{\mathrm {r}}^{2}\omega ^{2} + 1}}}\) attains its maximum \(|\gamma _{\mathrm {b}}|=\sqrt {\frac {{\omega _{\mathrm {b}}^{4} + \alpha _{\mathrm {r}}^{2}\omega _{\mathrm {b}}^{2}}}{{\beta _{\mathrm {r}}^{2}\omega _{\mathrm {b}}^{2} + 1}}}\) at ω = ωb; thus \(\omega _{l + 1}^{2} \) should be larger than |γb|. To address the second issue, the analysis in Section 3.2 reveals that only the residual norm corresponding to ω = ωb needs to be computed to determine whether the current truncation of the hybrid expansion is accurate enough. If not, more terms can be computed until the given accuracy is satisfied.

Furthermore, the overflow issue may occur when (29) is directly employed to calculate the displacement vector Ua because the coefficient \(\gamma _{\mathrm {b}}^{n - 1}\) grows exponentially when γb > 1 (which happens often in practical applications because \({\gamma _{\mathrm {b}}} \approx \omega _{\mathrm {b}}^{2}\)). Here, we propose a simple method to alleviate this issue: normalizing all basis vectors by the mass matrix M, so that not only \(\mathbf {{\phi }}_{i}^{T}\mathbf {M}{\mathbf {{\phi }}_{i}} = 1(i = 1, {\cdots } ,l)\), but also \(\mathbf {{v}}_{\mathrm {{H}},n}^{T}\mathbf {M}{\mathbf {{v}}_{\mathrm {{H}},n}} = 1(n = 1,2, {\cdots } )\), where vH,n denotes the normalized basis vectors.

Now a robust and adaptive computational procedure for efficient frequency response analysis can be formulated as:

  1. 1.

    Calculate the truncation frequency \(\omega _{\mathrm {f}}={\max \limits } ({\omega _{\mathrm {b}}},\sqrt {|{\gamma _{\mathrm {b}}}|}/\tau )\), where τ ≤ 1 is a constant.

  2. 2.

    Determine the number l of eigenfrequencies in [0,ωf] using the Strum sequence.

  3. 3.

    Obtain the first l lowest eigenfrequencies ω1,⋯,ωl and the mass-orthogonal eigenvectors ϕ1,⋯,ϕl through generalized eigenvalue analysis.

  4. 4.

    Compute the modal coordinates qL for the lower-order eigenmodes at ω = ωb.

  5. 5.

    Compute the approximate displacement vector Ua = ΦLqL at ω = ωb.

  6. 6.

    Compute the force residual

    $$ {\Delta} \mathbf{F}=\mathbf{F}_0-(- {\omega_{\mathrm{b}} ^2}\mathbf{M} + i\omega_{\mathrm{b}} \mathbf{{C}} + \mathbf{K})\mathbf{U}_{\mathrm{a}}. $$
  7. 7.

    Calculate the relative residual error δ = ||ΔF||2/||F0||2 and set q = 0.

  8. 8.

    While δ ≥ ε do:

    • (a) q = q + 1.

    • (b) Obtain the vector \({{\bar {\mathbf {v}}}_{\mathrm {{H}},q}}\) by solving the equation \({\mathbf {K}\bar {\mathbf {v}}}=\mathbf {{r}}_q\), where

      $$ {\mathbf{{r}}_{q}} = \left\{ {\begin{array}{*{20}{c}} {(\mathbf{{I}} - \mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{L}}}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}})\mathbf{F}_{0},}& \text{{if}} {q = 1}\\ {(\mathbf{{I}} - \mathbf{M}{{\boldsymbol{\Phi}}_{\mathrm{L}}}{\boldsymbol{\Phi}}_{\mathrm{L}}^{\mathrm{T}})\mathbf{M}{\mathbf{{v}}_{\mathrm{{H}},q - 1}},}& \text{{if}} {q \ge 2} \end{array}} \right. $$
      (36)

    • (c) Compute \({\beta _q} = \sqrt {{\bar {\mathbf {v}}}_{\mathrm {{H}},q}^T\mathbf {M}{{{\bar {\mathbf {v}}}}_{\mathrm {{H}},q}}}\) and the normalized basis vector \({\mathbf {{v}}_{\mathrm {{H}},q}}={{\bar {\mathbf {v}}}_{\mathrm {{H}},q}}/{\beta _q}\).

    • (d) Compute the coefficient cq as

      $$ {c_{q}} = \left\{ {\begin{array}{*{20}{c}} {{\beta_{1}}/(i{\beta_{r}}{\omega_{\mathrm{b}}} + 1),}&{q = 1}\\ {{\gamma_{\mathrm{b}}}{\beta_{q}}{c_{q - 1}},}&{q \ge 2} \end{array}} \right. $$
      (37)

    • (e) Update the approximate displacement vector

      $$\mathbf{U}_{\mathrm{a}}=\mathbf{U}_{\mathrm{a}}+{c_{q}}{\mathbf{{v}}_{\mathrm{{H}},q}}.$$

    • (f) Update the force residual

      $$ {\Delta} \mathbf{F}=\mathbf{F}-(- {\omega_{\mathrm{b}} ^2}\mathbf{M} + i\omega_{\mathrm{b}} \mathbf{{C}} + \mathbf{K})\mathbf{U}_{\mathrm{a}}. $$

    • (g) Calculate the relative residual norm

      $$ \delta = ||{\Delta} \mathbf{F}|{|_{2}}/||\mathbf{F}_{0}||_{2}. $$
  9. 9.

    For each frequency of interest ω in [ωa, ωb]:

    • (a) Compute the modal coordinates qL for the lower-order eigenmodes.

    • (b) Compute the coefficients for the normalized basis vectors

      $$ {c_{n}} = \left\{ {\begin{array}{*{20}{c}} {{\beta_{1}}/(i{\beta_{r}}{\omega} + 1),}&{n = 1}\\ {{\gamma}{\beta_{n}}{c_{n - 1}},}&{2 \le n \le q} \end{array}} \right. $$
      (38)

    • (c) Obtain the displacement vector as \(\mathbf {U}_{\mathrm {a}}={{\boldsymbol {\Phi }}_{\mathrm {L}}}{\mathbf {{q}}_{\mathrm {L}}}+\sum \limits _{n = 1}^{q} {{c_{n}}} {\mathbf {{v}}_{\mathrm {{H}},n}}\).

Here, in Step 1, we set ωf ≥ ωb because the information of all the resonant eigenfrequencies in [ωa, ωb] is necessary for some numerical quadrature techniques (Liu et al. 2015a). The parameter τ ≤ 1 is introduced to accelerate the possible slow convergence of the Neumann expansion because (35) reveals that if \(|{\gamma _{\mathrm {b}}}|/\omega _{l + 1}^{2} \approx 1.0\), the residual norm would converge very slow; thus, many basis vectors would have to be generated. It can be seen that \(|{\gamma _{\mathrm {b}}}|/\omega _{l + 1}^{2} < |{\gamma _{\mathrm {b}}}|/\omega _{\mathrm {f}}^{2} \le {\tau ^{2}}|{\gamma _{\mathrm {b}}}|/|{\gamma _{\mathrm {b}}}| = {\tau ^{2}}\); thus, the convergence rate of the residual norm will be at least of the order τ2. Notice that only the residual force corresponding to ω = ωb needs to be computed when constructing the basis vectors; thus, the residual norm is computationally inexpensive.

From the computational procedure of the proposed AHEM, it can be found that for frequency response analysis under many load vectors, the lower-order eigenfrequencies and eigenmodes can be shared when computing the displacement vectors, while only the basis vectors need to be generated for each load vector. This is the case for non-self-adjoint topology optimization problems, where both the displacement and adjoint displacement vectors need to be computed at each iteration. It is worth pointing out that when employing the AHEM, the lower-order eigenfrequencies and eigenmodes can be shared when computing the displacement and adjoint displacement vectors. Therefore, the modal analysis does not need to be performed again when computing the adjoint displacement, only the basis vectors need to be calculated according to the adjoint force.

We note here that the development of the hybrid expansion method for harmonic analysis of undamped systems can be dated back at least to Liu et al. (1993, 1994), where the Neumann expansion was also employed to represent the higher-order responses. In addition, Qu (2000) and Qu and Selvam (2000) also developed a hybrid expansion method for frequency response analysis of undamped and viscously damped systems, respectively. Li et al. (2014) proposed a hybrid expansion method for frequency response analysis of non-proportionally damped systems. However, only qualitative discussion about the performance of the hybrid expansion method was presented in these works; thus, they are insufficient to be employed for solving topology optimization problems. One important contribution of the present work is that a simple (yet accurate) expression for the residual of the truncated hybrid expansion (i.e., (33)) is derived. Furthermore, (34) reveals the very important property of the residual form, and (35) uncovers the key factors affecting the convergence rate of the truncated hybrid expansion, which can provide a helpful guide for parameter setting.

4 Numerical examples

This section presents three numerical examples to demonstrate the performance of the AHEM and its effectiveness for solving topology optimization problems under harmonic excitation. The code for all examples was implemented by MATLAB R2018b. The first example investigates the effects of the key parameters on the performance of the AHEM; the second example minimizes the compliance response of a 2D MBB beam and its modified version under harmonic loads of various excitation frequency intervals; the third example minimizes the compliance response of a 3D cantilever beam under harmonic loads of various frequency intervals. The MBB beam problem not only demonstrates the effectiveness of the AHEM for solving topology optimization problems, but also exhibits that asymmetrical optimal designs may be obtained even in the situation where the design domain, the boundary condition, and the load condition are all symmetric.

For all the examples, the Young’s modulus, Poisson’s ratio, and structural density of the material are assumed to be 70 GPa, 0.35, and 2700 kg/m3, respectively. In addition, the linear density filter (Bruns and Tortorelli 2001; Bourdin 2001) together with the threshold projection method (Wang et al. 2011) is employed when solving the topology optimization problems. Details can be found in Zhao et al. (2019). The method of moving asymptotes (MMA) (Svanberg 1987) is employed to update the design variables.

4.1 Case study 1: Frequency response analysis of a 2D cantilever beam under harmonic force excitation

In this subsection, a 2D cantilever beam under harmonic force excitation is studied to demonstrate the computational efficiency of the AHEM for frequency response analysis. As illustrated in Fig. 2, the length, width, and thickness of the beam structure are 2.0 m, 1.0 m, and 0.01 m, respectively. The structure is fixed at its left edge and a harmonically varying concentrated force of magnitude 3 kN is vertically applied at its lower right corner. For Rayleigh damping, \({\alpha _{\mathrm {r}}} = 20.15 {\text {{s}}^{- 1}}\) and βr = 1.5762 × 10− 6 s are assumed. Here, the displacement response of the degree of freedom (DOF) where the external load is applied is considered.

Fig. 2
figure 2

Problem definition of a 2D cantilever beam under harmonic force excitation

Full size image

In order to perform frequency response analysis, the structure is meshed into Ne = 200 × 100 bilinear square elements. The displacement response of the target DOF computed by the full method is presented in Fig. 3a. It can be observed that among the six eigenfrequencies, f = 175.64 Hz, 640.04 Hz, 665.73 Hz, 1392.76 Hz, 1775.09 Hz, and 1843.79 Hz, in the frequency interval [0,2000] Hz, there are four resonant frequencies, 175.64 Hz, 665.73 Hz, 1392.76 Hz, and 1775.09 Hz. These four resonant frequencies correspond to the four peaks in the frequency response curve, respectively. It should also be noted from Fig. 3b that, due to the presence of rounding errors, the relative residual error can achieve the order of 10− 11 even when the full method is employed to compute the frequency responses.

Fig. 3
figure 3

a, b Frequency response analysis results obtained by the full method, f ∈ [0,2000] Hz

Full size image

In order to show the influence of the error tolerance ε, the number of required basis vectors against the tolerance level (where τ = 0.8) is plotted in Fig. 4a. It can be seen that the expressions \(||\gamma _{\mathrm {u}}^{q}\mathbf {M}{\mathbf {{u}}_{\mathrm {H},q}}|{|_{2}}/||\mathbf {F}|{|_{2}}\) and ||SUa −F||2/||F||2 yield the same result when ε ≥ 10− 12; otherwise, different values are obtained because of the rounding errors. The relative residual errors for all the excitation frequencies in the interval [0,2000] Hz for different error tolerances are shown in Fig. 4b. It can be observed that the maximum relative residual errors indeed occur at f = 2000 Hz when ε > 10− 10. It can also be found that the relative residual error is not monotonically increasing with respect to the increasing of the excitation frequency, as indicated by our method. This disagreement should be attributed to the rounding errors similar to those presented in Fig. 3b. Actually, Fig. 5 reveals that when the number of involved basis vectors is small (e.g., q = 1), the truncation errors dominate the relative residual error curve and the relative residual error is indeed monotonically increasing with respect to the increasing of the excitation frequency. Conversely, when the number of involved basis vectors is large (e.g., q = 30), the truncation error will be eliminated, but the rounding errors still exist and dominate the relative residual error curve. It can also be observed that with the increasing of the number of involved basis vectors, the truncation errors for low-frequency responses vanish first; then, those corresponding to high-frequencies gradually disappear. This is reasonable, as indicated by our theory that the spectral radius \(\rho (\gamma \boldsymbol {{\Lambda }}_{\mathrm {H}}^{-1}) =|\gamma |/\omega _{l + 1}^{2}\) is monotonically increasing with respect to the increasing of the excitation frequency. Thus, the lower the excitation frequency, the faster the truncated hybrid expansion series converges. All four cases shown in Fig. 5 demonstrate that for the frequency interval where the truncation error is not eliminated, the relative residual error is monotonically increasing with respect to the increasing of the excitation frequency, which is in a good agreement with our theoretical analysis.

Fig. 4
figure 4

a, b Relative residual errors of the displacement vectors obtained by the AHEM (τ = 0.8), f ∈ [0,2000] Hz

Full size image
Fig. 5
figure 5

a–d Relative residual errors when different numbers of basis vectors are involved in the AHEM

Full size image

To demonstrate the necessity of introducing the parameter τ, the convergence histories of the relative residual error for four different frequency intervals, [0,100] Hz, [0,650] Hz, [0,1000] Hz, and [0,2000] Hz, with three different values of τ, 1.0, 0.9, and 0.8, are presented in Fig. 6, where ε is set to 10− 8. It can be seen from Fig. 6b that for the case of f = [0,650] Hz and τ = 1.0, the relative residual error decreases very slowly. The reason is that for this case \(\rho (\gamma _{\mathrm {b}} \boldsymbol {{\Lambda }}_{\mathrm {H}}^{-1}) =|\gamma _{\mathrm {b}} |/{\omega _{3}^{2}} = 0.953 \approx 1.0\). If τ = 0.9 or 0.8, ω3 < ωf < ω4, then \(\rho (\gamma _{\mathrm {b}} \boldsymbol {{\Lambda }}_{\mathrm {H}}^{-1}) =|\gamma _{\mathrm {b}} |/{\omega _{4}^{2}} = 0.218 \ll 1\). This also explains why the relative residual errors decrease very fast for the cases of τ = 0.9 and 0.8. Figure 6a and d show the influence of the value of τ on the number of required basis vectors for the cases of [0,100] Hz and [0,2000] Hz, respectively. Usually, a small value of τ implies a small number of basis vectors to be generated at a possible price of one or more additional eigenpairs to be computed. Figure 6c presents a special case where the three values, 0.8, 0.9, and 1.0, of τ yield the same convergence rate. This can be well understood because when 0.718 < τ ≤ 1.0, \(\omega _{3}<\omega _{\mathrm {f}}={\max \limits } ({\omega _{\mathrm {b}}},\sqrt {|{\gamma _{\mathrm {b}}}|}/\tau ) < \omega _{4}\), thus \(\rho (\gamma _{\mathrm {b}} \boldsymbol {{\Lambda }}_{\mathrm {H}}^{-1}) =|\gamma _{\mathrm {b}} |/{\omega _{4}^{2}} = 0.718^{2} = 0.5155\); this implies that the introduction of the parameter τ in this case does not affect the converge process. However, as discussed before, in order to make the frequency response analysis adaptive and efficient, τ < 1 is recommended.

Fig. 6
figure 6

a–d Influence of the value of τ on the number of required basis vectors in the AHEM

Full size image

4.2 Case study 2: Topology optimization of a 2D MBB beam under harmonic force excitation

This subsection presents a numerical example of topology optimization for minimizing the dynamic compliance of a 2D MBB beam. The design domain, boundary condition, and loading condition are illustrated in Fig. 7a. The length, width, and thickness of the design domain are 2.4 m, 0.4 m, and 0.01 m, respectively. The lower left and right corners of the design domain are fixed and simply supported, respectively. A harmonically varying concentrated force of magnitude 300 N is vertically applied at the top middle of the design domain. The prescribed volume fraction is 0.4. Four excitation frequency intervals f = [0,10] Hz, [0,250] Hz, [0,400] Hz, and [0,500] Hz are considered to demonstrate the effectiveness of the AHEM as well as the effects of the dynamic load on the optimum design.

Fig. 7
figure 7

a, b Definition of the 2D MBB beam design problem and the static design

Full size image

To perform topology optimization, the design domain is meshed into 480 × 80 bilinear square elements. The filter radius is set to 0.04 m. Initially, the material is uniformly distributed into the design domain. For Rayleigh damping, the coefficients αr and βr are calculated by assuming that the damping ratios of the initial structure satisfy ζ1 = ζ10 = 1%. The trapezoidal integration scheme with equally spaced abscissas is employed to compute the objective function and its sensitivity (Yoon 2010). The interval between two adjacent abscissas is set as Δf = 0.5 Hz.

The optimum designs for different excitation frequency intervals obtained by the full method and AHEM (τ = 0.8 and ε = 10− 8) are shown in Fig. 8. It can be seen that the optimum designs obtained by the two methods for the same excitation frequency interval are either the same or only have a slight difference. The iterative histories of the objective function presented in Fig. 9 and the values of the objective function summarized in Table 1 show that although there might be a slight difference during the optimization process, the values of the objective function for the optimum designs obtained by the two methods have little difference for the same excitation frequency interval.

Fig. 8
figure 8

a–h Dynamic designs of the 2D MBB beam

Full size image
Fig. 9
figure 9

a–d Iteration histories of the objective and constraint functions for the 2D MBB beam problem

Full size image
Table 1 Computational costs for topology optimization of the 2D MBB beam design problem
Full size table

The numbers of eigenmodes and basis vectors required by the AHEM in each iteration, as well as the history of the relative residual error, are plotted in Fig. 10. At least two conclusions can be drawn: (1) The relative residual error is strictly no larger than the given error tolerance in all the iterations for all cases and (2) The number of eigenmodes and basis vectors can be determined adaptively according to the given error tolerance; no redundant eigenmodes and basis vectors need to be computed. Consequently, the AHEM is efficient. The efficiency advantage of the AHEM over the full method can be found from the data listed in Table 1. Here we point out that to reduce the CPU time, the parfor function provided by matlab was employed with 8 workers when using the full method to perform frequency response analysis. However, the AHEM still needs much less CPU time compared with the full method.

Fig. 10
figure 10

a–d Performance of the AHEM for the 2D MBB beam design problem

Full size image

The frequency response curves of the initial and optimum designs are shown in Fig. 11. It can be found that for the case of f = [0,250] Hz, the frequency response curves corresponding to the two optimum designs have some obvious discrepancies; however, the values of the objective function listed in Table 2 prove that the two optimum designs have the same dynamic performance in terms of the mean dynamic compliance.

Fig. 11
figure 11

a–d Frequency response curves for the initial and optimum designs of the 2D MBB beam problem

Full size image
Table 2 Comparison of the values of objective function for initial and optimum designs of the 2D MBB beam design problem
Full size table

A very interesting phenomenon can be seen from Fig. 8; specifically, when the excitation frequency is low (e.g., f = [0,10] Hz), the optimum dynamic design is very close to the static design, as shown in Fig. 7b; and it is symmetric about the middle vertical line of the design domain. However, when the excitation frequency is high (e.g., f = [0,250] Hz), the optimum dynamic designs become asymmetric. The optimum dynamic designs with enforced geometric symmetry constraints for different excitation frequency intervals are shown in Fig. 12, and the values of the objective function are listed in Table 2. It can be found that the optimum design with an enforced geometric symmetry constraint has the same or a larger objective function value compared with their counterpart that has no enforced geometric symmetry constraint. This means that the optimum dynamic design of the MBB beam problem is not necessarily symmetric, as is that of the static design (Andreassen et al. 2011). This can be well understood because although the design domain and the load condition are symmetric, the boundary condition is not completely symmetric; therefore, the optimum dynamic designs might be asymmetric.

Fig. 12
figure 12

a–h Dynamic designs of the 2D MBB beam with enforced geometric symmetry constraint

Full size image

In order to further study the influence of the harmonic loading on the optimum design, the MBB beam problem is modified so that the lower right corner of the design domain is also fixed, as illustrated in Fig. 13. Thus, the design domain, boundary condition, and loading condition are all symmetric about the middle vertical line of the design domain. This is referred to as the symmetric situation (Stolpe 2010). The optimum dynamic designs for different excitation frequency intervals are shown in Fig. 14. Surprisingly, when the excitation frequency is high (e.g., f = [0,400] Hz), the optimum dynamic designs again become asymmetric. The optimum dynamic designs obtained by imposing the geometric symmetry constraint are shown in Fig. 15. The values of the objective function of the optimum designs listed in Table 3 prove that the optimum designs obtained without the enforced geometric symmetry constraint are indeed better than their counterparts that enforce the geometric symmetry constraint. This demonstrates that even for problems under the symmetric situation, the optimum dynamic designs might be asymmetric. In addition, the computational costs listed in Table 4 again demonstrate the efficiency advantage of the AHEM over the full method.

Fig. 13
figure 13

a, b Definition of the 2D MBB beam design problem with modified boundary conditions and its static design

Full size image
Fig. 14
figure 14

a–h Dynamic designs of the 2D MBB beam with modified boundary conditions

Full size image
Fig. 15
figure 15

a–h Dynamic designs of the 2D MBB beam with modified boundary conditions and enforced geometric symmetry constraint

Full size image
Table 3 Comparison of the values of objective function for initial and optimum designs of the 2D MBB beam design problem with modified boundary conditions
Full size table
Table 4 Computational costs for topology optimization of the 2D MBB beam design problem with modified boundary conditions
Full size table

To reduce the computational cost, a widely used strategy for solving topology optimization problems with symmetric conditions, such as the (modified) MBB beam design problem, is to perform topology optimization on part of the design domain with appropriate boundary and loading conditions (Andreassen et al. 2011). However, this example reminds us that it would be better to use the whole design domain to perform topology optimization for dynamics problems to reduce the risk of obtaining sub-optimal designs. A somewhat counter-intuitive result discovered by White and Voronin (2019) shows that asymmetric designs can be better than symmetric designs in certain regions of the problem space even for the classical minimum compliance design problems in the symmetric situation. Here, it is found that when the excitation frequency is high, asymmetric design may be obtained even the initial design is symmetric. In theory, if an asymmetric design D* is optimum, the same will be true for its mirror design D**. Since it has been found that the symmetric design is not optimum, the path of the topology optimization process will bifurcate at some intermediate design and the bifurcation is triggered by numerical errors (e.g., f = [0,400] Hz, as shown in Fig. 16, the initial design is completely symmetric, the design at iteration 25 is almost symmetric, the design at iteration 35 is slightly asymmetric, and gradually the topology optimization process converged to an asymmetric design. For completeness, the first four mode shapes of some intermediate designs are shown in Figs. 17, 18, 19, 20). Because the numerical errors may be produced by the solver (as is demonstrated in Fig. 3b) somewhat randomly, which optimum design will be obtained is also somewhat random. This can be seen from the case of f = [0,250] Hz as shown in Fig. 14c and d, where the two small holes in the designs are different and two optimum designs are almost mirror to each other. This is similar to the static problems presented in White and Voronin (2019), where “noise” is added to the finite element solution to avoid obtaining symmetric design when started from a symmetric initial design. Due to the purpose of this work, a further study on symmetry and non-uniqueness in topology optimization is not carried out here. More examples and in-depth discussion can be found in the published literatures (Bendsøe and Sigmund 2003; Stolpe 2010; Rozvany 2011; Cheng and Liu 2011; White and Voronin 2019).

Fig. 16
figure 16

a–l Intermediate designs of the 2D MBB beam problem with modified boundary conditions, f ∈ [0,400]Hz

Full size image
Fig. 17
figure 17

a–d Mode shapes of the initial design of the 2D MBB beam with modified boundary conditions

Full size image
Fig. 18
figure 18

a–d Mode shapes of the design of the 2D MBB beam at iteration 25 with modified boundary conditions

Full size image
Fig. 19
figure 19

a–d Mode shapes of the design of the 2D MBB beam at iteration 35 with modified boundary conditions

Full size image
Fig. 20
figure 20

a–d Mode shapes of the final design of the 2D MBB beam with modified boundary conditions

Full size image

4.3 Case study 3: Topology optimization of a 3D cantilever beam under harmonic force excitation

This subsection presents a numerical example of topology optimization for minimizing the dynamic compliance of a 3D cantilever beam. The design domain and boundary and load conditions are illustrated in Fig. 21a. The length, width, and thickness of the design domain are 1.0 m, 0.5 m, and 0.1 m, respectively. The left edge of the design domain is fixed. Nine harmonically varying concentrated loads of each magnitude 1 kN are simultaneously and uniformly applied on the lower right edge of the design domain. The prescribed volume fraction is 0.4. Four excitation frequency intervals f = [0,30] Hz, [0,200] Hz, [0,300] Hz, and [0,600] Hz are considered.

Fig. 21
figure 21

a, b Definition of the 3D cantilever beam design problem and its static design

Full size image

The optimum designs for different excitation frequency intervals are shown in Fig. 22. Here, only the results obtained by the AHEM are provided because the use of the full method becomes impractical due to the huge computational cost. The iteration histories of the objective function and volume fraction for different excitation frequency intervals are shown in Fig. 23. The frequency response curves for the initial and optimum designs are shown in Fig. 24. It can be observed from Fig. 23 that for all cases the optimization process is converged and the constraint is always satisfied. It can be seen from Fig. 22 that for all cases clear designs are obtained. When the excitation frequency is low (e.g., f = [0,30] Hz and [0,200] Hz), the optimum dynamic design is similar to the static design. For the case of f = [0,30] Hz, no eigenfrequency of the initial design is contained in the excitation frequency interval. During the topology optimization process, the eigenfrequencies become larger and the first resonant eigenfrequency of the structure is driven away from the excitation frequency interval. For the case of f = [0,200] Hz, there are three eigenfrequencies, f = 38.5 Hz, 146.5 Hz, and 160.8 Hz in the excitation frequency interval. Among these three eigenfrequencies, only the frequency of 160.8 Hz is a resonant eigenfrequency; it corresponds to the peak value presented in the frequency response curve of the initial design. During topology optimization, this resonant eigenfrequency is driven away from the excitation frequency interval. When the excitation frequency is high (e.g., f = [0,300] Hz and [0,600] Hz), the dynamic design is quite different from the static design, and the optimum designs for different excitation intervals are also different from each other. In addition, as shown in Fig. 24, the frequency responses have been reduced substantially by redistributing the materials in the design domain although one or more resonant eigenfrequencies of the optimum designs remain in the excitation frequency interval for the cases of f = [0,300] Hz and [0,600] Hz. The values of the objective function listed in Table 5 also demonstrate the substantial improvement of the dynamic performance of the optimum designs over the initial design.

Fig. 22
figure 22

a–d Dynamic designs of the 3D cantilever beam

Full size image
Fig. 23
figure 23

a–d Iteration histories of dynamic designs of the 3D cantilever beam

Full size image
Fig. 24
figure 24

a–d Frequency response curves for the initial and optimum designs of the 3D cantilever beam problem

Full size image
Table 5 Comparison of the values of objective function for initial and optimum designs of the 3D Cantilever beam design problem
Full size table

The numbers of eigenmodes and basis vectors required by the AHEM in each iteration, as well as the history of the relative residual error, are presented in Fig. 25. Again, it can be observed that the relative residual error is below the given error tolerance in the iterations of all cases. In addition, the AHEM can determine adaptively the number of eigenmodes and basis vectors to be computed for the given error tolerance. It is noted that for the case of f = [0,30] Hz, no eigenmode is needed at all iterations, and the number of basis vectors to be computed is also very small. For the case of f = [0,600] Hz, the number of eigenmodes that need to be computed is usually less than 10, and the number of involved basis vectors is less than 30. It can be thus concluded that the AHEM is efficient for solving topology optimization problems under harmonic excitation.

Fig. 25
figure 25

a–d Performance of the AHEM for the 3D cantilever beam design problem

Full size image

5 Concluding remarks

This study developed an efficient frequency response analysis method, namely adaptive hybrid expansion method (AHEM), for structural topology optimization under harmonic force excitation over a given frequency interval. When solving such problems, one main challenge is how to accurately and efficiently compute the displacement and adjoint displacement vectors for a large number of excitation frequencies in the frequency response analysis. Assuming Rayleigh damping, a hybrid expansion for frequency response is developed, where the contributions of the lower-order and higher-modes are given by the modal superposition and Neumann expansion, respectively. The number of lower-order eigenpairs that need to be computed can be determined using the Strum sequence. Meanwhile, a simple expression for the relative residual error of the truncated hybrid expansion is provided. This expression indicates that the relative residual error is monotonically increasing with respect to the increasing of the excitation frequency. Thus, efficient computation of the residual norm for every excitation frequency in the given interval is enabled. The key factors affecting the convergence rate of the hybrid expansion method are also uncovered; thus, the number of terms that need to be preserved in the truncated Neumann expansion can also be determined adaptively. Finally, the performance of the AHEM is numerically studied in detail, and its effectiveness for solving structural topology optimization problems under harmonic force excitation is demonstrated by 2D and 3D numerical examples.

In addition, it is found that the optimum dynamic design of structures under a symmetric situation (i.e., the design domain, boundary condition, and load condition are all symmetric) might be asymmetric. Thus, the widely used strategy to reduce the huge computational cost by employing only part of the design domain with appropriate boundary conditions is risky because it may obtain sub-optimal designs. Thus, it is better to solve the original topology optimization problems with the whole design domain and original boundary conditions, even under a symmetric situation. From this point of view, the proposed AHEM not only is computationally efficient, but it is also helpful for reducing the risk of obtaining sub-optimal designs.