1 Introduction

Design sensitivity analysis (DSA) involves the determination of the rate change of performance measures with respect to a set of design variables. Sensitivity analysis plays an important role in structural optimization and system identification (Haftka and Adelman 1989). It can also be applicable in many fields such as model updating (Mottershead et al. 2011), structural reliability (Xiao et al. 2011) and damage detection (Yan and Ren 2011). In general, there are three approaches to sensitivity analysis: the finite difference method, the direct differentiation method and the adjoint method (Komkov et al. 1986). The finite difference method is a direct and simple approach. However, the finite difference method suffers from computational inefficiency. Therefore, the direct differentiation method (DDM) or the adjoint variable method (AVM) are generally preferred despite their relative complexity. The efficiency of these methods depends on the number of design variables and the number of active constraints. When the number of design variable is large, e.g., topology optimization problems, then AVM is preferred (Ryu et al. 1985; Kang et al. 2006).

Design sensitivity analysis of dynamic responses has been widely studied by several authors. The steady-state response of mechanical and structural system is of interest in design problems which are subject to harmonic loadings caused by rotating machines such as fans, electric motors and reciprocating engines. Choi and Lee (Choi and Lee 1992) developed the sensitivity analysis method of dynamic frequency response using the adjoint variable and direct differentiation methods for viscously damped systems. Based on mode superposition method, Qu developed the sensitivities of undamped system (QU 2000) and viscously damped system (QU and SELVAM 2000). Lewandowski and Łasecka-Plura (Lewandowski and Łasecka-Plura 2016) presented a design sensitivity analysis of structures with viscoelastic dampers.

The above studies addressed frequency responses under harmonic loadings. However, transient responses of dynamic systems are important when structures are subject to sudden loadings e.g. impact, shock and seismic loadings. The design sensitivity analysis of linear transient problem has been also studied by many authors (van Keulen et al. 2005; Kang et al. 2006). In most studies on linear dynamic problems, the sensitivities are computed via the differentiate-then-discretize adjoint method (Kang et al. 2006; Zhao and Wang 2015; Zhang and Kang 2014; Dahl et al. 2008). Another approach is developed to produce consistent sensitivities by differentiating the discretized response, which is called the discretize-then-differentiate method (Le et al. 2012). Jensen et al. (Jensen et al. 2013) discussed consistency issues of the two above approaches. The discretize-then-differentiate approach is extended to nonlinear problems (Nakshatrala and Tortorelli 2015).

The above-mentioned studies of transient problems consider only viscously damped systems. However, the viscous damping is rarely physically present in most systems (Adhikari and Woodhouse 2003). Woodhouse (Woodhouse 1998) presented the general damping model via convolution integrals. This model is commonly referred to as non-viscous (viscoelastic) damping model. In the non-viscously damped system, the damping force depends on the past history of motion, which causes time- and history-dependent behavior. Thus, the response sensitivity at a given time depends on the response and the response sensitivities at all previous times in consequence of the history-dependent behavior (Vidal and Haber 1993). Therefore, design sensitivity analysis for transient responses is a challenging task in the non-viscously damped system. Compared to the above-mention publications on viscous damping systems, very limited research has been carried out on the design sensitivity analysis of the non-viscously damped dynamic systems. Poldneff and Arora (Poldneff and Arora 1996) addressed design sensitivity for coupled thermoviscoelasticity systems by utilizing the semi-analytical method. Li et al. (Li et al. 2013) presented the sensitivity analysis of non-viscously damped system using inverse Fourier transform. However, these methods require approximate methods for calculating the sensitivity of transient responses. The approximate methods may lead to inaccurate or inconsistent sensitivities.

In this paper, a consistent sensitivity analysis method is developed for non-viscously damped systems. The transient responses are evaluated with an implicit time integration scheme. The adjoint variable method is employed based on the discretize-then-differentiate approach. The accuracy and the consistency of the proposed method are demonstrated by several numerical examples.

The rest of the paper is organized as follows; in Section 2, the equations of motion and the time integration method are introduced. In Section 3, the procedure to obtain the design sensitivity is described in detail. In Section 4, the usage of the proposed method is demonstrated by several numerical examples. The calculated sensitivities are compared with analytical solutions or the finite difference ones. Finally, conclusions are presented in Section 5.

2 Dynamics of non-viscously damped system

2.1 Non-viscous damping model

In a non-viscous damping model, the damping force depends on the past history of motion (Adhikari and Woodhouse 2003). From the Boltzmann superposition principle (Christensen 1982), the non-viscous damping force f d(t) is expressed in terms of the past history of velocities via convolution integrals over suitable kernel functions.

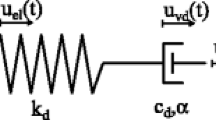
$$ {f}^{\mathrm{d}}(t)={\displaystyle {\int}_0^tg\left(t-s\right)\frac{\partial u(s)}{\partial s}}ds $$
(1)

Where u is the displacement, and s is any arbitrary time between time 0 and t. The kernel function g (t) is also called retardation function, heredity function and relaxation function. The viscous damping model is a special case of the non-viscous damping model when the kernel function becomes a delta function (i.e., g(t − s) = Cδ(t − s) where C is a damping coefficient). Then, the damping force becomes \( {f}^{\mathrm{d}}(t)=C\frac{\partial u(t)}{\partial t} \), and thus has no memory (Adhikari and Woodhouse 2001). The kernel function g (t) of the non-viscous damping force is typically modelled by the generalized Maxwell model as shown in Fig. 1.

Fig. 1
figure 1

Generalized Maxwell model

Full size image

The model consists of several spring-dashpot Maxwell elements in parallel and an isolated spring. This type of model results in a Prony series expression as follows.

$$ g(t)={g}_{\infty }+{\displaystyle \sum_{j=1}^m{g}_j{e}^{-t/{\tau}_j}} $$
(2)

Where m is the number of Maxwell elements, and g ∞ is the long-term elastic stiffness coefficient when the Maxwell elements are totally relaxed. The parameters g j and τ j are the Prony coefficient and relaxation time, respectively.

Using (2) in (1), the damping force is split into elastic and non-viscous parts.

$$ {f}^{\mathrm{d}}(t)={g}_{\infty }u(t)-{g}_{\infty }u(0)+{\displaystyle {\int}_0^t{\displaystyle \sum_{j=1}^m{g}_j{e}^{-\left(t-s\right)/{\tau}_j}\frac{\partial u(s)}{\partial s}}ds} $$
(3)

For simplicity, it is convenient to introduce an auxiliary history variable h j t .

$$ {h}_t^j={\displaystyle {\int}_0^t{g}_j{e}^{-\left(t-s\right)/{\tau}_j}\frac{\partial u(s)}{\partial s}}ds $$
(4)

Then, the damping force becomes

$$ {f}^{\mathrm{d}}(t)={g}_{\infty }u(t)-{g}_{\infty }u(0)+{\displaystyle \sum_{j=1}^m{h}_t^j} $$
(5)

2.2 Equations of motion

The equations of motion for linear non-viscously damped system can be written in the following form (Adhikari 2002; Li et al. 2013).

$$ \mathbf{Ma}(t)+{\displaystyle {\int}_{-\infty}^t\mathbf{G}\left(t-s\right)\frac{\partial \mathbf{u}(s)}{\partial s}}ds+\mathbf{K}\mathbf{u}(t)={\mathbf{f}}^{\mathrm{ext}}(t) $$
(6)

Where M, G and K are mass, non-viscous damping and stiffness matrices, respectively. Moreover, a(t), u(t) and f ext(t) denote the acceleration vector, the displacement vector and forcing vector, respectively. In general, the motion starts at t = 0. Therefore, taking u(t) = 0 for t < 0, and imposing the following the initial conditions

$$ \mathbf{u}\left(t=0\right)={\mathbf{u}}_0\kern0.5em \mathrm{and}\kern1em \mathbf{v}\left(t=0\right)={\mathbf{v}}_0 $$
(7)

The equations of motion becomes

$$ \mathbf{Ma}(t)+\mathbf{G}(t)\mathbf{u}(0)+{\displaystyle {\int}_0^t\mathbf{G}\left(t-s\right)\frac{\partial \mathbf{u}(s)}{\partial s}}ds+\mathbf{K}\mathbf{u}(t)={\mathbf{f}}^{\mathrm{ext}}(t) $$
(8)

where the damping matrix G(t) is given by

$$ \mathbf{G}(t)={\mathbf{G}}_{\infty }+{\displaystyle \sum_{j=1}^m{\mathbf{G}}_j{e}^{-t/{\tau}_j}} $$
(9)

where G ∞ is the stiffness matrix consists of the long-term elastic stiffness g ∞ in (2), and G j is the stiffness matrix of the Prony series coefficient g j in (2).

2.3 Implicit time integration

In this paper, the Newmark-β algorithm (Newmark 1959) is used for the time discretization of the equations of motion. The time-discrete displacement vector is represented by u n  = u(t n ) for t 1, t 2, …, t N where N is the number of time steps. Then, the equations of motion become

$$ \mathbf{M}{\mathbf{a}}_n+{\mathbf{G}}_n{\mathbf{u}}_0+{\mathbf{f}}_n^{\mathrm{d}}+\mathbf{K}{\mathbf{u}}_n={\mathbf{f}}_n^{\mathrm{ext}} $$
(10)

where a n , f d n , u n and f ext n denote the acceleration, damping force, displacement and external force vectors at time t n . The time domain is divided into N equally-sized time steps. Then the Newmark time integration procedure involves the following equations with the time step Δt = t n  − t n − 1.

$$ {\mathbf{u}}_n={\mathbf{u}}_{n-1}+\varDelta t{\mathbf{v}}_{n-1}+\varDelta {t}^2\left(\left(\frac{1}{2}-\beta \right){\mathbf{a}}_{n-1}+\beta {\mathbf{a}}_n\right) $$
(11)
$$ {\mathbf{v}}_n={\mathbf{v}}_{n-1}+\varDelta t\left(\left(1-\gamma \right){\mathbf{a}}_{n-1}+\gamma {\mathbf{a}}_n\right) $$
(12)

Where β and γ are the Newmark stability parameters. The initial displacement u 0 and velocity v 0 are prescribed, and the initial acceleration a 0 is obtained via Ma 0 + G 0 u 0 + Ku 0 = f ext0 . From (5), the damping force vector f d n is given by

$$ {\mathbf{f}}_n^{\mathrm{d}}={\mathbf{G}}_{\infty }{\mathbf{u}}_n-{\mathbf{G}}_{\infty }{\mathbf{u}}_0+{\displaystyle \sum_{j=1}^m{\mathbf{H}}_n^j} $$
(13)

where H j n is a history variable vector at time t n . In order to evaluate the history variable, the history variable is approximately divided into discrete variables.

$$ {\mathbf{H}}_n^j={e}^{-\left({t}_n-{t}_{n-1}\right)/{\tau}_j}{\displaystyle {\int}_0^{t_{n-1}}{e}^{-\left({t}_{n-1}-s\right)/{\tau}_j}{\mathbf{G}}_j\frac{\partial \mathbf{u}(s)}{\partial s}}ds+{\displaystyle {\int}_{t_{n-1}}^{t_n}{e}^{-\left({t}_n-s\right)/{\tau}_j}{\mathbf{G}}_j\frac{\partial \mathbf{u}(s)}{\partial s}}ds $$
(14)

The history variable H j n is calculated from the previous history variable using the following recursive equation.

$$ {\mathbf{H}}_n^j={e}^{-\varDelta t/{\tau}_j}{\mathbf{H}}_{n-1}^j+{\displaystyle {\int}_{t_{n-1}}^{t_n}{e}^{-\left({t}_n-s\right)/{\tau}_j}{\mathbf{G}}_j\frac{\partial \mathbf{u}(s)}{\partial s}ds} $$
(15)

It is assumed that ∂/∂s[u(s)] is constant for s ∈ [t n − 1, t n ]. Then, (15) becomes

$$ {\mathbf{H}}_n^j\cong {e}^{-\varDelta t/{\tau}_j}{\mathbf{H}}_{n-1}^j+{\mathbf{G}}_j\frac{{\mathbf{u}}_n-{\mathbf{u}}_{n-1}}{\varDelta t}{\displaystyle {\int}_{t_{n-1}}^{t_n}{e}^{-\left({t}_n-s\right)/{\tau}_j}ds} $$
(16)

The exponential term is integrated analytically. Then, the history variable is given by

$$ {\mathbf{H}}_n^j={e}^{-\varDelta t/{\tau}_j}{\mathbf{H}}_{n-1}^j+{A}_j{\mathbf{G}}_j\left({\mathbf{u}}_n-{\mathbf{u}}_{n-1}\right) $$
(17)

where A j is defined as

$$ {A}_j=\frac{1-{e}^{-\varDelta t/{\tau}_j}}{\varDelta t/{\tau}_j} $$
(18)

The recursive formula can also be expressed in terms of the past history of displacement.

$$ {\mathbf{H}}_n^j={\displaystyle \sum_{i=1}^n{e}^{-\left({t}_n-{t}_i\right)/{\tau}_j}}{A}_j{\mathbf{G}}_j\left({\mathbf{u}}_i-{\mathbf{u}}_{i-1}\right) $$
(19)

Finally, the damping force of the system is defined as

$$ {\mathbf{f}}_n^{\mathrm{d}}={\mathbf{G}}_{\infty }{\mathbf{u}}_n-{\mathbf{G}}_{\infty }{\mathbf{u}}_0+{\displaystyle \sum_{i=1}^n{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_n-{t}_i\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\left({\mathbf{u}}_i-{\mathbf{u}}_{i-1}\right)}} $$
(20)

Then, the discretized equations of motion of the non-viscously damped system is given by

$$ \mathbf{M}{\mathbf{a}}_n+{\mathbf{G}}_n{\mathbf{u}}_0+{\mathbf{G}}_{\infty }{\mathbf{u}}_n-{\mathbf{G}}_{\infty }{\mathbf{u}}_0+{\displaystyle \sum_{i=1}^n{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_n-{t}_i\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\left({\mathbf{u}}_i-{\mathbf{u}}_{i-1}\right)}}+\mathbf{K}{\mathbf{u}}_n={\mathbf{f}}_n^{\mathrm{ext}} $$
(21)

Rewriting the above equation, it becomes

$$ \mathbf{M}{\mathbf{a}}_n+{\mathbf{G}}_n{\mathbf{u}}_0-{\mathbf{G}}_{\infty }{\mathbf{u}}_0+{\mathbf{K}}_{\mathrm{T}}{\mathbf{u}}_n-{\mathbf{K}}_{\mathrm{hist}}{\mathbf{u}}_{n-1}+{\displaystyle \sum_{i=1}^{n-1}{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_n-{t}_i\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\left({\mathbf{u}}_i-{\mathbf{u}}_{i-1}\right)}}={\mathbf{f}}_n^{\mathrm{ext}} $$
(22)

where \( {\mathbf{K}}_{\mathrm{T}}=\left({\mathbf{G}}_{\infty }+{\displaystyle \sum_{j=1}^m{A}_j{\mathbf{G}}_j+\mathbf{K}}\right) \) and \( {\mathbf{K}}_{\mathrm{hist}}={\displaystyle \sum_{j=1}^m{A}_j{\mathbf{G}}_j} \). Using the Newmark relation in (11) and (12), the a-form of the Newmark method can be written as

$$ \begin{array}{l}\tilde{\mathbf{M}}{\mathbf{a}}_n={\mathbf{f}}_n^{\mathrm{ext}}-{\mathbf{G}}_n{\mathbf{u}}_0+{\mathbf{G}}_{\infty }{\mathbf{u}}_0-{\mathbf{K}}_{\mathrm{T}}\left({\mathbf{u}}_{n-1}+\varDelta t{\mathbf{v}}_{n-1}+\varDelta {t}^2\left(\frac{1}{2}-\beta \right){\mathbf{a}}_{n-1}\right)+{\mathbf{K}}_{\mathrm{hist}}{\mathbf{u}}_{n-1}\\ {}-{\displaystyle \sum_{i=1}^{n-1}{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_n-{t}_i\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\left({\mathbf{u}}_i-{\mathbf{u}}_{i-1}\right)}}\end{array} $$
(23)

where \( \tilde{\mathbf{M}}=\left(\mathbf{M}+{\mathbf{K}}_{\mathrm{T}}\varDelta {t}^2\beta \right) \). Then, the acceleration vector a n at time t n is obtained by solving (23) based on velocity v n − 1, acceleration a n − 1 at the previous time step, and the past history of displacement u i . Once a n is computed, the displacement u n and velocity v n at the current time step are computed from (11) and (12), respectively.

3 Design sensitivity analysis

The transient response of the non-viscously damped system depends on the past history of motion. Therefore, the response sensitivity at any given time also depends on the response and the response sensitivities at all previous times. In this paper, the design sensitivity analysis method of the history-dependent system is developed using the adjoint variable method (AVM) (Haftka and Adelman 1989; Adelman and Haftka 1986). The discretize-then-differentiate AVM approach (Jensen et al. 2013; Le et al. 2012; Nakshatrala and Tortorelli 2016) is adopted for deriving discrete adjoint equations. For the design sensitivity analysis, a general response function f is considered which depends on displacement u, velocity v, acceleration a and the design parameter d.

$$ f=f\left(d,{\mathbf{a}}_N,{\mathbf{a}}_{N-1},\dots, {\mathbf{a}}_0,{\mathbf{v}}_N,{\mathbf{v}}_{N-1},\dots, {\mathbf{v}}_0,{\mathbf{u}}_N,{\mathbf{u}}_{N-1},\dots, {\mathbf{u}}_0\right) $$
(24)

where t N is the terminal time in the simulation. Then, the sensitivity of the response function is obtained from the derivative with respected to design parameter d.

$$ {f}^{\prime }=\frac{\partial f}{\partial d}+{\displaystyle \sum_{i=0}^N\left(\frac{\partial f}{\partial {\mathbf{a}}_i}{\mathbf{a}}_i^{\prime }+\frac{\partial f}{\partial {\mathbf{v}}_i}{\mathbf{v}}_i^{\prime }+\frac{\partial f}{\partial {\mathbf{u}}_i}{\mathbf{u}}_i^{\prime}\right)} $$
(25)

It is difficult to compute the response derivative, since it contains implicit derivatives of the acceleration, velocity and displacement. The strategy to obtain the sensitivity is to evaluate the sensitivity of the acceleration (i.e., \( {\mathbf{a}}_i^{\prime } \)) prior to evaluating the sensitivities of both the velocity and the displacement (i.e., \( {\mathbf{v}}_i^{\prime } \) and \( {\mathbf{u}}_i^{\prime } \)), since both the velocity and the displacement depend on the acceleration. To obtain the sensitivity of the acceleration, the residual equations are considered. From the equations of motion in (23), there are N + 1 residual equations corresponding at each time t i .

$$ \begin{array}{l}{\mathbf{R}}_i=\tilde{\mathbf{M}}{\mathbf{a}}_i+{\mathbf{G}}_i{\mathbf{u}}_0-{\mathbf{G}}_{\infty }{\mathbf{u}}_0+{\mathbf{K}}_{\mathrm{T}}\left({\mathbf{u}}_{i-1}+\varDelta t{\mathbf{v}}_{i-1}+\varDelta {t}^2\left(\frac{1}{2}-\beta \right){\mathbf{a}}_{i-1}\right)-{\mathbf{K}}_{\mathrm{hist}}{\mathbf{u}}_{i-1}\\ {}+{\displaystyle \sum_{k=1}^{i-1}{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_i-{t}_k\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\left({\mathbf{u}}_k-{\mathbf{u}}_{k-1}\right)}}-{\mathbf{f}}_i^{\mathrm{ext}}=\mathbf{0}\end{array} $$
(26)

Rewriting (11) and (12), the displacement u and the velocity v can be expressed in recursive forms as follows.

$$ {\mathbf{u}}_i={\mathbf{u}}_0+\varDelta ti{\mathbf{v}}_0+\varDelta {t}^2\left(\frac{1}{2}-\beta \right){\mathbf{a}}_0+\varDelta {t}^2\left(1-\gamma \right)\left(i-1\right){\mathbf{a}}_0+{\displaystyle \sum_{k=1}^{i-1}\varDelta {t}^2\left(i+\gamma -k-\frac{1}{2}\right)}{\mathbf{a}}_k+\varDelta {t}^2\beta {\mathbf{a}}_i $$
(27)
$$ {\mathbf{v}}_i={\mathbf{v}}_0+\left(1-\gamma \right)\varDelta t{\mathbf{a}}_0+\varDelta t{\displaystyle \sum_{k=1}^{i-1}{\mathbf{a}}_k}+\varDelta t\gamma {\mathbf{a}}_i $$
(28)

Note that the above recursive equations only depend on the acceleration. Substituting these recursive equations into the residual equations (26), and rearranging the involved terms, the residual equation can be expressed in terms of the past history of the accelerations (29).

$$ \begin{array}{l}{\mathbf{R}}_i=\tilde{\mathbf{M}}{\mathbf{a}}_i+{\mathbf{G}}_i{\mathbf{u}}_0-{\mathbf{G}}_{\infty }{\mathbf{u}}_0+\left({\mathbf{K}}_{\mathrm{T}}-{\mathbf{K}}_{\mathrm{hist}}\right)\left({\mathbf{u}}_0+\varDelta t\left(i-1\right){\mathbf{v}}_0+\varDelta {t}^2\left(\frac{1}{2}-\beta \right){\mathbf{a}}_0+\varDelta {t}^2\left(1-\gamma \right)\left(i-2\right){\mathbf{a}}_0\right)\\ {}+\left({\mathbf{K}}_{\mathrm{T}}\left(\frac{1}{2}+\gamma \right)-{\mathbf{K}}_{\mathrm{hist}}\beta \right)\varDelta {t}^2{\mathbf{a}}_{i-1}+{\mathbf{K}}_{\mathrm{T}}\left\{\varDelta t{\mathbf{v}}_0+\left(1-\gamma \right)\varDelta {t}^2{\mathbf{a}}_0\right\}+{\displaystyle \sum_{k=1}^{i-2}\varDelta {t}^2\left\{\left({\mathbf{K}}_{\mathrm{T}}-{\mathbf{K}}_{\mathrm{hist}}\right)\left(i+\gamma -k-\frac{3}{2}\right)+{\mathbf{K}}_{\mathrm{T}}\right\}}{\mathbf{a}}_k\\ {}+{\displaystyle \sum_{k=1}^{i-1}{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_i-{t}_k\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\left(\varDelta t{\mathbf{v}}_0+\varDelta {t}^2\left(1-\gamma \right){\mathbf{a}}_0+\varDelta {t}^2\left(\gamma -\beta +\frac{1}{2}\right){\mathbf{a}}_{k-1}+\varDelta {t}^2\beta {\mathbf{a}}_k+{\displaystyle \sum_{l=1}^{k-2}\varDelta {t}^2{\mathbf{a}}_l}\right)}}-{\mathbf{f}}_i^{\mathrm{ext}}\end{array} $$
(29)

Then, each residual is expressed as a function of the acceleration history.

$$ {\mathbf{R}}_i={\mathbf{R}}_i\left(d,{\mathbf{a}}_i,{\mathbf{a}}_{i-1},\dots,, {\mathbf{a}}_1,{\mathbf{a}}_0\right)=\mathbf{0}\kern1em \mathrm{f}\mathrm{o}\mathrm{r}\kern1em i=0,1,2,\dots, N $$
(30)

However, the derivative of the acceleration in Equation (25) remains an implicit quantity. To resolve the implicit derivative, adjoint variable λ is introduced (Haug and Arora 1978), and then multiplied by each residual to annihilate the implicit derivative.

$$ {\mathbf{a}}_i={\mathbf{a}}_i+{\displaystyle \sum_{k=0}^i{\boldsymbol{\uplambda}}_k^T{\mathbf{R}}_k} $$
(31)

where the multiplier λ k is the adjoint variable corresponding each residual equation. Then, the sensitivity is obtained by taking the derivative of the acceleration a i with respect to d.

$$ {\mathbf{a}}_i^{\prime }={\mathbf{a}}_i^{\prime }+{\displaystyle \sum_{k=0}^i{\boldsymbol{\uplambda}}_k^T}\frac{\partial {\mathbf{R}}_k}{\partial d}+{\displaystyle \sum_{k=0}^i{\boldsymbol{\uplambda}}_k^T\left({\displaystyle \sum_{l=0}^k\frac{\partial {\mathbf{R}}_k}{\partial {\mathbf{a}}_l}{\mathbf{a}}_l^{\prime }}\right)} $$
(32)

Rearranging (32) yields

$$ {\mathbf{a}}_i^{\prime }={\displaystyle \sum_{k=0}^i{\boldsymbol{\uplambda}}_k^T}\frac{\partial {\mathbf{R}}_k}{\partial d}+\left(\mathbf{I}+{\boldsymbol{\uplambda}}_i^T\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_i}\right){\mathbf{a}}_i^{\prime }+{\displaystyle \sum_{k=0}^{i-1}\left({\displaystyle \sum_{l=\mathrm{k}}^i{\boldsymbol{\uplambda}}_l^T}\frac{\partial {\mathbf{R}}_l}{\partial {\mathbf{a}}_k}\right){\mathbf{a}}_k^{\prime }} $$
(33)

In the above equation, the adjoint variable λ i is arbitrary. To vanish the implicit derivatives of the acceleration at the last time step \( {\mathbf{a}}_i^{\prime } \), the multiplier of the last residual equation is assigned by

$$ {\boldsymbol{\uplambda}}_i=-{\left[\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_i}\right]}^{-1} $$
(34)

Also, the implicit derivatives of the previous acceleration should vanish. Expanding the last summation in (33), it becomes

$$ \begin{array}{l}{\mathbf{a}}_i^{\prime }={\displaystyle \sum_{k=0}^i{\boldsymbol{\uplambda}}_k^T}\frac{\partial {\mathbf{R}}_k}{\partial d}+\left(\mathbf{I}+{\boldsymbol{\uplambda}}_i^T\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_i}\right){\mathbf{a}}_i^{\prime}\hfill \\ {}+\left({\boldsymbol{\uplambda}}_0^T\frac{\partial {\mathbf{R}}_0}{\partial {\mathbf{a}}_0}+{\boldsymbol{\uplambda}}_{\mathrm{l}}^T\frac{\partial {\mathbf{R}}_1}{\partial {\mathbf{a}}_0}+\cdots +{\boldsymbol{\uplambda}}_i^T\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_0}\right){\mathbf{a}}_0^{\prime}\hfill \\ {}+\left({\boldsymbol{\uplambda}}_1^T\frac{\partial {\mathbf{R}}_1}{\partial {\mathbf{a}}_1}+{\boldsymbol{\uplambda}}_2^T\frac{\partial {\mathbf{R}}_2}{\partial {\mathbf{a}}_1}+\cdots +{\boldsymbol{\uplambda}}_i^T\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_1}\right){\mathbf{a}}_1^{\prime}\hfill \\ {}\cdots \hfill \\ {}+\left({\boldsymbol{\uplambda}}_{i-1}^T\frac{\partial {\mathbf{R}}_{i-1}}{\partial {\mathbf{a}}_{i-1}}+{\boldsymbol{\uplambda}}_i^T\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_{i\hbox{-} 1}}\right){\mathbf{a}}_{i-1}^{\prime}\hfill \end{array} $$
(35)

In order to annihilate the implicit derivatives, the adjoint problem is defined by

$$ \begin{array}{l}{\boldsymbol{\uplambda}}_{i-1}^T\frac{\partial {\mathbf{R}}_{i-1}}{\partial {\mathbf{a}}_{i-1}}+{\boldsymbol{\uplambda}}_i^T\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_{i-1}}=\mathbf{0}\\ {}\kern4.25em \cdots \kern2.25em =\mathbf{0}\\ {}{\boldsymbol{\uplambda}}_1^T\frac{\partial {\mathbf{R}}_1}{\partial {\mathbf{a}}_1}+{\boldsymbol{\uplambda}}_2^T\frac{\partial {\mathbf{R}}_2}{\partial {\mathbf{a}}_1}+\cdots +{\boldsymbol{\uplambda}}_i^T\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_1}=\mathbf{0}\\ {}{\boldsymbol{\uplambda}}_0^T\frac{\partial {\mathbf{R}}_0}{\partial {\mathbf{a}}_0}+{\boldsymbol{\uplambda}}_1^T\frac{\partial {\mathbf{R}}_1}{\partial {\mathbf{a}}_0}+\cdots +{\boldsymbol{\uplambda}}_i^T\frac{\partial {\mathbf{R}}_i}{\partial {\mathbf{a}}_0}=\mathbf{0}\end{array} $$
(36)

Rewriting the above equation, the multipliers of previous steps are given by

$$ {\boldsymbol{\uplambda}}_k={\left[\frac{\partial {\mathbf{R}}_k}{\partial {\mathbf{a}}_k}\right]}^{-1}\left(-{\displaystyle \sum_{l=k+1}^i{\boldsymbol{\uplambda}}_l^T\frac{\partial {\mathbf{R}}_l}{\partial {\mathbf{a}}_k}}\right)\kern0.5em \mathrm{f}\mathrm{o}\mathrm{r}\kern0.75em k=i-1,i-2, \dots, 1,0 $$
(37)

where λ i at time t i is the multiplier given in (34). The derivatives of the residuals with respect to the acceleration is given by

$$ \begin{array}{l}\frac{\partial {\mathbf{R}}_l}{\partial {\mathbf{a}}_k}={\delta}_{l,k}\tilde{\mathbf{M}}+\left({\mathbf{K}}_{\mathrm{T}}\left(\frac{1}{2}+\gamma \right)-{\mathbf{K}}_{\mathrm{hist}}\beta \right)\varDelta {t}^2{\delta}_{l-1,k}\\ {}\kern2.5em +\varDelta {t}^2\left\{\left({\mathbf{K}}_{\mathrm{T}}-{\mathbf{K}}_{\mathrm{hist}}\right)\left(l+\gamma -k-\frac{3}{2}\right)+{\mathbf{K}}_{\mathrm{T}}\right\}\\ {}\kern2.5em +{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_l-{t}_{k+1}\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\left(\varDelta {t}^2\left(\gamma -\beta +\frac{1}{2}\right)\right)}+{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_l-{t}_k\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\left(\varDelta {t}^2\beta \right)}\\ {}\kern2.5em +{\displaystyle \sum_{k=1}^{l-1}{\displaystyle \sum_{j=1}^m{e}^{-\left({t}_l-{t}_k\right)/{\tau}_j}{A}_j{\mathbf{G}}_j\varDelta {t}^2}}\end{array} $$
(38)

Then, the derivative of the acceleration a i with respect to the density d is given by

$$ {\mathbf{a}}_i^{\prime }={\displaystyle \sum_{k=0}^i{\boldsymbol{\uplambda}}_k^T\frac{\partial {\mathbf{R}}_k}{\partial d}} $$
(39)

This procedure may be considered as an extension of the time-dependent adjoint method (James and Waisman 2015) to dynamic problems. After obtaining the sensitivity of the acceleration, the sensitivities of the velocity and the displacement with respect to the design variables d are easily obtained by the chain rule.

$$ {\mathbf{v}}_i^{\prime }={\displaystyle \sum_{k=0}^i\frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{a}}_k}{\mathbf{a}}_k^{\prime }}\kern1em \mathrm{and}\kern1em {\mathbf{u}}_i^{\prime }={\displaystyle \sum_{k=0}^i\frac{\partial {\mathbf{u}}_i}{\partial {\mathbf{a}}_k}{\mathbf{a}}_k^{\prime }} $$
(40)

The derivatives of the velocity and the displacement with respect to the acceleration are obtained by differentiating (27) and (28).

$$ \frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{a}}_k}=\varDelta t+{\delta}_{i,k}\varDelta t\gamma $$
(41)
$$ \frac{\partial {\mathbf{u}}_i}{\partial {\mathbf{a}}_k}=\varDelta {t}^2\left(i+\gamma -k-\frac{1}{2}\right)+{\delta}_{i,k}\varDelta {t}^2\beta $$
(42)

Then, the sensitivity of the response function f can be obtained by inserting (39) and (40) into (25).

The entire procedure of the sensitivity analysis is illustrated in Fig. 2. The sensitivity analysis loop is started with the transient responses (i.e., a i , v i and u i ) obtained by the Newmark method (23). In the loop, the adjoint equations are solved to evaluate the adjoint variable λ ((34) and (37)). The derivative of the residual equations can be obtained by modifying the residual equations as a-form residual equations which are derived by using the recurrence formulas of the velocity and the displacement ((27) and (28)). Then, the sensitivity of the acceleration vector at time t i is evaluated using the adjoint variables. The sensitivities of the velocity and the displacement are obtained by applying the chain rule ((41) and (42)). These steps are repeated until the time step reaches the final time step. Finally, the sensitivity of the response function is calculated by using the transient responses and the response sensitivities (25). Note that the response function f is the most general form. Therefore, any type of function (e.g., ∫ T0 f(a, v, u)dt and f = u 2 N ) can be treated. The sensitivities of various response functions are demonstrated in the next section.

Fig. 2
figure 2

Flow chart of the proposed sensitivity analysis method

Full size image

4 Numerical examples

In this section, three numerical examples are presented to demonstrate the validity of the proposed method. The first example is a single-dof non-viscously damped system under free vibration. In this simple example, the sensitivity analysis results are compared with the analytical solutions. The second example is a single-dof system subject to a transient loading. The last example is a three-dof dynamic vibration absorber subject to a dynamic loading with non-zero initial condition. All examples are solved using unconditionally stable implicit second-order scheme (i.e., the Newmark approach with β = 1/4 and γ = 1/2).

4.1 Free response of a single-dof system

In the first example, a single dof non-viscously damped system shown in Fig. 3 is considered. There is no external force acting on the mass, and non-zero initial conditions are prescribed. In this example, the mass m = 27 kg, the non-viscous damper g(t) = 0.2 + 8e − t N/m and the stiffness k = 0.8 N/m are assumed. The initial conditions are chosen as initial displacement u 0 = 0.1 m and velocity v 0 = 0 m/s.

Fig. 3
figure 3

Single-dof non-viscously damped system

Full size image

For the single-dof non-viscously damped system, an analytic solution can be obtained by employing the Laplace transformation of the equations of motion. Taking the Laplace transform of the equations of motion (6) gives

$$ \mathbf{U}(s)=\frac{\mathbf{F}(s)+{\mathbf{M}\mathbf{v}}_0+s{\mathbf{M}\mathrm{u}}_0}{s^2\mathbf{M}+s\mathbf{G}(s)+\mathbf{K}} $$
(43)

where G(s) is the Laplace transform of the generalized Maxwell model given by

$$ \mathbf{G}(s)=\frac{{\mathbf{G}}_{\infty }}{s}+{\displaystyle \sum_{j=1}^m\frac{{\mathbf{G}}_j}{s+\frac{1}{\tau_j}}} $$
(44)

Then, the displacement in the time domain can be obtained by taking inverse Laplace transformation u(t) = ℒ− 1{U(s)}. The sensitivity of the displacement can also be obtained by taking inverse Laplace transformation of the following equation.

$$ {\mathbf{u}}^{\prime }(t)={\mathrm{\mathcal{L}}}^{-1}\left\{{\mathbf{U}}^{\prime }(s)\right\} $$
(45)

For different time step sizes, the displacement and its sensitivities are compared with the exact ones. Figure 4 shows the accuracy of the displacement response. The accuracy is low when a relatively large time increment (i.e., Δt = 1) is considered. The discrepancy between the approximate displacement and the exact one gradually decreases as the time increment size decreases. In the sensitivity calculation, the mass m and the stiffness k are chosen as the design variables. The sensitivity results for different time steps are shown in Figs 5 and 6. The discrepancies between the calculated sensitivities and the exact ones also decrease as the time increment size decreases. However, these discrepancies are inherent in time discretization. The errors might be negligible when a small enough time step is considered.

Fig. 4
figure 4

Displacement of the single dof system for different time steps

Full size image
Fig. 5
figure 5

The sensitivity of the displacement with respect to mass m for different time steps

Full size image
Fig. 6
figure 6

The sensitivity of the displacement with respect to stiffness k for different time steps

Full size image

In this example, the consistency of the sensitivity is demonstrated by introducing a response function. For transient problems, a quadratic function of time integral of displacement or velocity is often chosen as a response function (Yan et al. 2016; Jensen et al. 2013).

$$ f={\displaystyle {\int}_0^T\left(\alpha {u}^2+\left(1-\alpha \right){v}^2\right)dt} $$
(46)

where α is the weighting parameter. In this example, the weighting parameter is set as α = 0.5. The response function is integrated over T = 50 s. To demonstrate the consistency of the sensitivity, the response function and its sensitivity are compared with exact solutions. For numerical integration over the time interval, the response function and its sensitivity can be approximately evaluated by the trapezoidal summation.

$$ f\approx {\displaystyle \sum_{n=0}^N{\omega}_nf\left({t}_n\right)\kern0.52em \mathrm{and}\ {f}^{\prime}\approx {\displaystyle \sum_{n=0}^N{\omega}_n{f}^{\prime}\left({t}_n\right)}} $$
(47)

where N is the number of time steps, and the weighting factors of the trapezoidal rule are

$$ 2{\omega}_0={\omega}_1={\omega}_2=\dots ={\omega}_{N-1}=2{\omega}_N=\varDelta t $$
(48)

The relative errors of the objective function and its sensitivity are evaluated by comparing with analytic solutions. The accuracy of the discrete approximation for the response function and its sensitivity is depicted in Fig. 7. In the figure, the difference is normalized by the analytical solutions.

Fig. 7
figure 7

The accuracy of the discrete approximation for the response function and sensitivity versus the number of time steps

Full size image

Figure 7 shows the convergence rate of the response function (blue line) and its sensitivities (yellow and red lines). As already mentioned, a second-order accurate algorithm is used to integrate the equations of motion. Therefore, the response function (blue line) naturally shows second-order convergence rate. Note that both the sensitivities (yellow and red lines) also show same second-order convergence rate. It demonstrates that the sensitivities are consistent with those of the time-discretized solutions.

4.2 Forced response of a single-dof system

To demonstrate the proposed method under general transient loads, a single-dof system is considered with zero initial condition. The non-viscous damper is expressed with 3-term Prony series, i.e., g(t) = 3 + 4e − t/0.1 + 2e − t/1 + 1e − t/10 N/m. The mass m = 5 kg and the stiffness k = 10 N/m are considered. When an arbitrary load is applied at the system, unlike the previous example, the solution cannot be obtained analytically even for simple single dof system. That is, the Laplace transform in (42) cannot be inverted analytically. The time history of the applied load is shown in Fig. 8. The time step used in the time integration is Δt = 0.1 s (Fig. 9).

Fig. 8
figure 8

Applied loading of the single-dof system

Full size image
Fig. 9
figure 9

Forced responses of the single-dof system

Full size image

To illustrate the accuracy of the sensitivities, the sensitivities are compared with the results from the finite difference method. (i.e., the approximated sensitivity is \( f^{\prime } \approx \left(f\left(d+\varDelta d\right)-f(d)\right)/\varDelta d \). Figure 10 shows the accuracy of sensitivities for the transient responses with respect to the mass m compared to the results from the finite difference method with Δm = 0.5 (10% perturbation) and Δm = 0.005 (0.1% perturbation). The sensitivities analysis results show good agreements with the results from the finite difference method. The sensitivities with respect to the stiffness k are shown in Fig. 11. The sensitivities obtained by the proposed method also show good agreements with the results approximated by the finite difference method. Therefore, it is verified that the proposed method is also applicable to non-viscously damped systems under general transient loads.

Fig. 10
figure 10

The sensitivities of the transient responses with respect to mass m obtained by the proposed method and finite difference method; (a) acceleration; (b) velocity; (c) displacement

Full size image
Fig. 11
figure 11

The sensitivities of the transient responses with respect to stiffness k obtained by the proposed method and finite difference method; (a) acceleration; (b) velocity; (c) displacement

Full size image

4.3 Dynamic vibration absorber

A practical application is considered to demonstrate the proposed approach in the multi-dof system, which is represented in Fig. 12. The dynamic vibration absorber generally consists of springs and non-viscous dampers, which are connected to a primary system. For the non-viscous damping materials, rubbers are typically used for vibration control in real engineering applications.

Fig. 12
figure 12

Schematic of a dynamic vibration absorber system

Full size image

The objective of the absorber is to mitigate transient vibrations of the primary system. In this system, m 1, k 1 and g 1(t) represent mass, spring and non-viscous damper of the primary system. Two dynamic absorbers (i.e., m 2 and m 3) are connected to the primary system m 1 by springs and non-viscous dampers in parallel.

The system matrices of the equations of motion are given by

$$ \mathbf{M}=\left[\begin{array}{ccc}\hfill {m}_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {m}_2\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {m}_3\hfill \end{array}\right],\kern0.24em \mathbf{K}=\left[\begin{array}{ccc}\hfill {k}_1+{k}_2+{k}_3\hfill & \hfill -{k}_2\hfill & \hfill -{k}_3\hfill \\ {}\hfill -{k}_2\hfill & \hfill {k}_2\hfill & \hfill 0\hfill \\ {}\hfill -{k}_3\hfill & \hfill 0\hfill & \hfill {k}_3\hfill \end{array}\right],\; and\kern0.24em {\mathbf{F}}^{ext}=\left[\begin{array}{c}\hfill f(t)\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\right] $$

with the damping matrix

$$ \mathbf{G}(t)=\left[\begin{array}{ccc}\hfill {g}_{\infty}^1+{g}_{\infty}^2+{g}_{\infty}^3+{\displaystyle \sum_{j=1}^m\left({g}_j^1+{g}_j^2+{g}_j^3\right)}{e}^{-t/{\tau}_j}\hfill & \hfill -{g}_{\infty}^2-{\displaystyle \sum_{j=1}^m{g}_j^2{e}^{-t/{\tau}_j}}\hfill & \hfill -{g}_{\infty}^3-{\displaystyle \sum_{j=1}^m{g}_j^3{e}^{-t/{\tau}_j}}\hfill \\ {}\hfill -{g}_{\infty}^2-{\displaystyle \sum_{j=1}^m{g}_j^2{e}^{-t/{\tau}_j}}\hfill & \hfill {g}_{\infty}^2+{\displaystyle \sum_{j=1}^m{g}_j^2{e}^{-t/{\tau}_j}}\hfill & \hfill 0\hfill \\ {}\hfill -{g}_{\infty}^3-{\displaystyle \sum_{j=1}^m{g}_j^3{e}^{-t/{\tau}_j}}\hfill & \hfill 0\hfill & \hfill {g}_{\infty}^3+{\displaystyle \sum_{j=1}^m{g}_j^3{e}^{-t/{\tau}_j}}\hfill \end{array}\right] $$

For the numerical calculation, it is assumed that m 1 = 5 kg, m 2 = 2 kg, m 3 = 1 kg, k 1 = 10 N/m, k 2 = 15 N/m and k 3 = 5 N/m. The prony series coefficients of the non-viscous dampers are given in Table 1. In the table, the terms in brackets denote the relaxation times.

Table 1 Prony series coefficients of the non-viscous dampers.
Full size table

4.3.1 Sensitivity analysis of the transient response

The sensitivities of the displacement and the velocity are calculated. The initial conditions are u 0 = [ 0.2 0.1 0 ]T m and v 0 = [ 0 0 0.1 ]T m/s. It is assumed that the primary system m 1 is excited by a transient external load f(t) shown in Fig. 13.

Fig. 13
figure 13

Applied loading of the three-dof dynamic absorber

Full size image

The transient responses can be obtained by solving the equations of motion. The time step used in the time integration is Δt = 0.1 s. The displacements and the velocities of each dof are illustrated in Fig. 14. In the initial stage, each mass oscillates due to the initial conditions. Then, the responses also depend on the excited load after t = 1.0 s. These conditions are the most general condition in dynamic problems since the dynamic responses depend on both initial conditions and excited loads. In this general condition, the sensitivities of the displacement and the velocity of each dof are verified.

Fig. 14
figure 14

Displacements and velocities of the vibration absorber

Full size image

The sensitivities of the displacement of the velocity with respect to mass of primary system m 1 are shown in Fig. 15. The sensitivities of the responses of both the primary system and the dynamic absorbers are compared with the results from the finite difference method. Figure 16 shows the sensitivities with respect to the stiffness of the primary system k 1. The results are also compared with the results from the finite difference method. In both cases, the results from the finite difference method are obtained using 0.1% perturbation of each design variable. The results show excellent agreements with the results from the finite difference method.

Fig. 15
figure 15

Sensitivity of the displacement and the velocity with respect to mass m 1

Full size image
Fig. 16
figure 16

Sensitivity of the displacement and the velocity with respect to stiffness k 1

Full size image

4.3.2 Sensitivity analysis of response functions

In the time-domain dynamic problems, various types of response functions may be considered (Zhao and Wang 2015; Zhang and Kang 2014). Among them, two different kinds of response functions are considered as follows. Firstly, the mean squared displacement of a target dof during the whole time interval is chosen as the response function.

$$ f={\displaystyle {\int}_0^T{u}_{\mathrm{target}}^2(t)dt} $$
(49)

The squared displacement can be considered as vibration response in the time interval. The second one is the mean dynamic compliance during the whole time interval. It is defined as the work done by the external force F(t) against the corresponding displacements.

$$ f={\displaystyle {\int}_0^T{\mathbf{u}}^T(t)\mathbf{F}(t)dt} $$
(50)

In this example, a pulse-like input excitation is applied to the primary system assuming zero initial conditions.

$$ f(t)=\left\{\begin{array}{c}\hfill \sin \left(\pi t\right),\kern1em 0\le t\le 1\hfill \\ {}\hfill \kern1em 0,\kern2.25em 1<t\le 5\hfill \end{array}\right. $$
(51)

The terminal time is T = 5.0 s and the time step used in the time integration is Δt = 0.1 s.

The sensitivity analysis results are given in Table 2. The sensitivity analysis results are compared with the results from the finite difference method (consider a 0.01% perturbation). The errors are evaluated as the relative difference between the two sensitivities which are normalized by the results from the finite difference method. There are good agreements between calculated sensitivities and the results from the finite difference method. In this result, the mass of the second dynamic vibration absorber m 2 is found out to be the most sensitive design variable in both response funtions. Therefore, both the dynamic mean compliance and the vibration response can be effectively reduced with the increase of the mass of the second vibration absorber. Also, the obtained sensitivities are applicable to design optmization problems.

Table 2 Sensitivity analysis results of the vibration absorber
Full size table

5 Conclusions

The design sensitivity analysis method is developed for transient response of non-viscously damped dynamic systems. It is assumed that the non-viscous damping force depends on the past history of velocities via convolution integrals with the kernel function. The kernel function is modeled by the Generalized Maxwell model, which has been widely used for interpreting experimental data. The transient response is calculated with the Newmark time integration scheme in time domain. The sensitivity depends on the past history of the response and the response sensitivity, since the non-viscous damping force depends on the past history motion. To resolve this problem, the sensitivity analysis method is developed using the adjoint variable method (AVM). The discretize-then-differentiate approach is adopted for deriving discrete adjoint equations. The accuracy and the consistency are demonstrated by comparing with analytic sensitivity for the single dof system. The proposed method is also applied to the analysis of the multi-dof system, and the accuracy of the sensitivities obtained by the proposed method are confirmed by the results from the finite difference method. The proposed method may easily be extended to large-dof systems or finite element models.