1 Introduction

Switched systems have received increasing investigations by scholars in the past two decades [5, 7, 16] since they may describe a variety of physical plants in engineering applications, such as chemical processes [29], aero-engine systems [28], and electric circuits [19]. By far, many accomplishments have been conducted in the study of switched systems in a non-networked context [30, 34].

Modern industrial applications are usually controlled via communication networks due to the advancement of spatially distributed systems. This class of control systems termed NCS has attracted growing attention as they present various advantages [2, 12, 14], including low installation cost, reduced wiring, and ease of maintenance. However, some severe issues, such as network-induced delay, transmission packet loss, and cyber-attacks, arise and may affect the system’s performance and stability. For more details, see [8, 31] and references therein. Therefore, the study of the dynamic behaviors and control design of switched systems in networked environments, known as networked switched systems (NSS), brings more intriguing problems and requires difficult mathematical formulation [13, 15]. In [15], authors have studied the resilient optimal controller design of networked switched systems against denial-of-service attack using dynamic programming principles. Also, a genetic algorithm is adopted to search for the optimal switching signal, while [13] has proposed an adaptive sliding mode controller to deal with actuator/sensor faults, in which the obtained results were applied to a mechanical system example.

In the traditional control framework, transmitted data of switched systems over digital communication channels are based on a time-triggered scheme with a fixed sampling rate. Nevertheless, the periodic approach may lead to a waste of network energy consumption since some unnecessary information updates are transmitted even when they do not significantly change the system dynamics. To overcome this problem, an alternate scheme of control referred to as event-triggered control (ETC) has been developed [6, 22]. This kind of aperiodic communication strategy can significantly save power consumption and mitigate the obstacle of redundant data transmission while achieving desirable closed-loop performance in terms of stability.

From an engineering point of view, most modern control systems deal with transient behavior over finite-time intervals instead of traditional Lyapunov stability. This last one is not satisfactory in some practical applications, where stability should be guaranteed in a short time [24]. The new idea of finite-time stability ensures that the system trajectories do not exceed a given unacceptably large value during the prescribed fixed finite-time interval, which is more practically meaningful than classical Lyapunov stability. In the past few years, many researchers have widely addressed the finite-time event-driven control issue for numerous types of practical systems, including networked systems [11] and switched systems [4]. Some interesting achievements have also been made regarding the new-appearing class of NSS [3, 18, 23, 33]. The practical limitation of exogenous disturbance is mainly found in most engineering switched and networked systems, which necessitates specific analysis tools [4, 18, 23, 33]. In [4], the event-triggered finite-time \(H_\infty \) filtering of the time-varying delay switched linear system was studied. Authors in [18] addressed the problem of finite-time boundedness and input–output finite-time stability for networked switched linear systems with asynchronous switching. Using the convex hull technique, [33] was concerned with the problem of finite-time \(H_\infty \) control of state-saturated switched systems in the presence of network-induced delays and external disturbances, where an event-driven policy is used to reduce the transmission frequency. In addition, [23] presented a switched time-delay system and discussed the relevant problem of event-based finite-time \(H_\infty \) boundedness of the reformulated system under the quantization effect. The finite-time extended dissipative problem of the closed-loop networked switched systems was studied in [3] by solving the \(H_\infty \), \(L_2 - L_\infty \), passivity and (Q, S, R)-dissipativity performance.

Generally, the above-mentioned studies do not consider that the full system state is inaccessible. Therefore, an observer needs to be incorporated into the control loop to generate an estimate of the unmeasured state. Furthermore, it should be noted that most of the results of observer design use a time-triggered sampling approach and assume that the sensor is collocated with the observer at the same node of the networked control loop [10, 27]. Nevertheless, a novel event-triggered observer design idea is suggested where the sampled-data output measurements are sent to the remote observer only when an event condition is violated. As a consequence, redundant output transmissions and observer energy consumption are reduced [20, 21]. This work provides additional answers to the literature on networked switched systems and motivates our research on the subject of event-triggered observer-based finite-time \(H_\infty \) control. The main contributions of this paper can be summarized as follows:

  1. 1.

    An event-triggered observation scheme is constructed, which involves Lyapunov parameter to decide when the output measurements are sent over the communication network.

  2. 2.

    The Lyapunov–Krasovskii functional technique and the average dwell time provide several sufficient LMIs conditions for the observer-based finite-time boundedness and the disturbance attenuation control performance.

  3. 3.

    We have shown the effect of the triggering threshold \(\eta \) on the transmission rate. We have also verified the exclusion of the Zeno phenomenon.

This paper is organized as follows. In Sect. 2, the problem of finite-time event-triggered observer design of network-based switched systems is formulated. Some definitions and lemmas are also introduced. Section 3 provides sufficient conditions for the finite-time boundedness and \(H_\infty \) control design. An illustrative example is given in Sect. 4 to verify the proposed results. Finally, Sect. 5 presents the conclusion of this study.

Notations. Throughout this paper, we denote by \({\mathbb {N}}\) the set of natural numbers. Given a square matrix \(X,\; X^{-1}\) and \(X^\textrm{T}\) are the inverse and the transpose of X, respectively. \(\lambda _{\max }(X)\) and \(\lambda _{\min }(X)\) stand for its minimum and maximum eigenvalue. The symmetric terms within a symmetric matrix are represented by the asterisk \(\star \), and the block-diagonal matrix by \({\text {diag}}\{\cdots \}\). \({\mathcal {L}}_2[0,\infty [\) is the space of square-integrable functions over the interval \([0,\infty [\).

2 Problem Formulation

2.1 Switched System and Event-Triggered Observer

Consider the switched nonlinear system defined by:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}(t)=A_{i} x(t)+B_{i} u(t)+ f_{i}(x(t))+D_{i} \omega (t),\\ y(t)=C_{i} x(t), \\ z(t)=C_{1i} x(t) +D_{1i} \omega (t), \end{array}\right. \end{aligned}$$
(1)

where \(x(t) \in {\mathbb {R}}^{n}\) is the state vector, \(u(t) \in {\mathbb {R}}^{m}\) is the control input, \(y(t) \in {\mathbb {R}}^{p}\) is the measurable output, \(z(t) \in {\mathbb {R}}^{q}\) is the controlled output, \(w(t) \in {\mathbb {R}}^{m}\) which belongs to \({\mathcal {L}}_2[0, \infty [\) is the external disturbance input satisfying \(\int _{t_0}^{T_f} w^\textrm{T}(t) w(t) {\text {d}}t \le d_{w}, \quad d_{w} \ge 0\), and \(\left[ t_{0}, T_f\right] \) is the finite-time interval. The function \(\sigma :[t_{0}, \infty [ \rightarrow {\mathbb {I}}=\{1,2, \ldots , N\}\) denotes the switching signal where N stands for the number of subsystems. Its corresponding switching sequence can be given by \(\Sigma = \left\{ \left( i_{0}, t_{0}\right) ,\left( i_{1}, t_{1}\right) , \ldots ,\left( i_{s}, t_{s}\right) \ldots \mid i_{s} \in {\mathbb {I}}, s \in {\mathbb {N}} \right\} \), which means that the \(i_s\)-th subsystem is activated when \(t \in [t_{s}, t_{s+1}[\). For  \(\sigma (t)=i \in {\mathbb {I}}; \; A_{i},\; B_{i}, \; C_{i}, \; C_{1i}, \; D_{i}\), and \(D_{1i}\) are constant matrices with appropriate dimensions. Moreover, \(f_i: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) are known Lipschitz nonlinear functions.

In practice, the state is not available. Therefore, a state observer needs to be implemented. In this framework, an event-based Luenberger observer is designed to obtain the state and synthesize the corresponding controller. In what follows, the network-based event-triggered observer reported in [26] can be used:

$$\begin{aligned} \left\{ \begin{aligned} \dot{\hat{x}}(t)=&A_{i} \hat{x}(t)+B_{i} u(t) + L_{i}(\bar{y}(t)-C_{i} \hat{x}(t))+ f_{i}(\hat{x}(t)),\\ \hat{y}(t)=&C_{i} \hat{x}(t), \end{aligned}\right. \end{aligned}$$
(2)

where \(\hat{x}(t) \in {\mathbb {R}}^{n}\) is the observer state, and \(\hat{y}(t) \in {\mathbb {R}}^{p}\) is the observer output, while \(\bar{y}(t)\) is the event-triggered holded output between two consecutive events. \(L_i\) is the sub-observer gain matrix.

2.2 Event-Triggered Observation Scheme

We propose in this subsection a network-based event-triggered observation and control scheme as depicted in Fig. 1. Therefore, we know the following:

  1. 1.

    The system output y(t) is sampled periodically as \(y(v h), \; v \in {\mathbb {N}}\) and \(h>0\) being the sampling period.

  2. 2.

    An event generator will check a well-designed event-triggered condition to decide when the output measurements should be transmitted.

  3. 3.

    \(\bar{y}(t)=y\left( t_{k}h\right) \) is the triggered output to be transmitted to the observer via a zero-order hold (ZOH) at time instants \(t_{k}h, \; k \in {\mathbb {N}}, \; \left\{ t_0, t_1, t_2, \ldots , t_k \right\} \subseteq {\mathbb {N}}\).

Fig. 1
figure 1

A network-based event-triggered observer architecture

Full size image

In networked environments, transmission delays are unavoidable. Then, successfully transmitted data reach the remote observer at time instants \(t_k h+d_{k}\) and remain constant until the next event at \(t_{k+1}h+d_{k+1}\), that is:

$$\begin{aligned} \bar{y}(t)=y\left( t_k h\right) , \; t \in [t_k h+d_k, t_{k+1}h+d_{k+1}[ \end{aligned}$$
(3)

where \(d_{k}\) is the network-induced delay.

The event-triggered observation condition proposed in this paper is relatively inspired by [10, 17] as below:

$$\begin{aligned} t_{k+1} h=t_k h+\min _{v \in {\mathbb {N}}}\left\{ v h \mid e_k^\textrm{T}(t) \Phi _i e_k(t) \ge \eta \; y^\textrm{T}\left( t_k h+v h\right) y\left( t_k h+v h\right) \right\} \end{aligned}$$
(4)

where \(\Phi _i\) is a symmetric positive-definite matrix to be given and the parameter \(\eta > 0\) is a constant threshold, and \(e_k(t) =y\left( t_k h\right) -y\left( t_k h+v h\right) , v \in \left\{ 1,2, \cdots , t_{k+1} -t_k -1\right\} \) is the measurement error between the current sampled output \(y\left( t_k h+v h\right) \) and the last transmitted triggered output \(y\left( t_k h\right) , t \in [t_k h+d_k, t_{k+1} h+d_{k+1}[\). We assume that \(t_0=0\). To control the switched system (1), an observer-based control law is applied:

$$\begin{aligned} u(t)=K_i \hat{x}(t), \; \forall \; t \in \left[ 0, T_f\right] \end{aligned}$$
(5)

where \(K_i\) is the feedback gain of appropriate dimension.

Next, we partition the holding interval of the ZOH into subintervals,

$$\begin{aligned}{}[t_k h + d_k, t_{k+1} h + d_{k+1}[=\bigcup _{v=0}^{T_k} [l_{k, v}, l_{k, v+1}[ \end{aligned}$$
(6)

where \(T_k=t_{k+1}-t_k -1, l_{k,v}=[t_kh+vh+d_{k,v}[\), and \(d_{k,v}\) are the corresponding time delays. Define \(d(t) = t - t_k h - vh, t \in [l_{k,v},l_{k,v+1}[\), which satisfies \( \text {min}\left\{ d_{k,v}\right\} =d_m< d(t) < d_M = h + \text {max}\left\{ d_{k,v}\right\} \). Resorting to the definition of \(e_k(t)\) and d(t), the triggered output (3) becomes:

$$\begin{aligned} \bar{y}(t)=y(t-d(t))+e_k\left( t\right) \quad \forall t \in [l_{k, v}, l_{k, v+1}[ \end{aligned}$$
(7)

Remark 1

We can easily verify the exclusion of the Zeno behavior based on the event-triggered scheme (4), where it is clear that the inter-event period is always greater than the sampling period, \(t_{k+1}h-t_{k}h \ge h\).

Remark 2

In this paper, the results are developed under the assumption \(\text {max}\left\{ d_{k,v}\right\} <h\). However, when \(\text {max}\left\{ d_{k,v}\right\} \ge h\), packet disorder may occur, which will necessitate other modeling and analysis techniques.

2.3 Modeling of the Networked Switched System

By defining \(\tilde{x}(t)=\hat{x}(t) - x(t)\) as the observation error, and combining equations (1)-(2), (5), and (7), we get the following system dynamics:

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}(t)=&(A_{i}+B_{i}K_i)x(t)+B_{i}K_i \tilde{x}(t)+ f_{i}(x(t))+D_{i} \omega (t) \\ \dot{\hat{x}}(t)=&(A_{i}+B_{i}K_i) \hat{x}(t)+ L_{i}C_i(x(t-d(t))-\hat{x}(t)) + f_{i}(\hat{x}(t)) \\ {}&+L_i e_k(t) \\ \dot{{\tilde{x}}}(t)=&(A_{i}-L_{i}C_i)\tilde{x}(t) - L_{i} C_i x(t) + L_{i} C_i x(t-d(t)+f_{i}(\hat{x}(t)) \\ {}&- f_{i}(x(t)) -D_{i} \omega (t) +L_i e_k(t)\\ x(s)=&\phi (s), \quad s \in \left[ -d_M, 0\right] \\ \end{aligned}\right. \end{aligned}$$
(8)

where \(\phi (s)\) is a continuous initial function on \(\left[ -d_M, 0\right] \).

From the above closed-loop system, an augmented time-delay switched system can be established by using the same technique as in [18]:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\xi }}(t)=\bar{A}_{i}\xi (t)+\bar{A}_{di}\xi (t-d(t))+\bar{f}_{i}(\xi (t))+\bar{D}_{i} \omega (t) +\bar{L}_i e_k(t)\\ z(t)=\bar{C}_{1i} \xi (t) +D_{1i} \omega (t) \end{array}\right. \end{aligned}$$
(9)

where

$$\begin{aligned} \begin{aligned} \xi (t)&=\left[ \begin{array}{l} x(t) \\ \tilde{x}(t) \end{array}\right] , \quad \bar{A}_{i}=\left[ \begin{array}{cc} A_{i}+B_i K_i &{} B_i K_i \\ -L_i C_i &{} A_{i}-L_i C_i \end{array}\right] , \quad \bar{A}_{di} =\left[ \begin{array}{cc} 0 &{} 0 \\ L_i C_{i} &{} 0 \end{array}\right] \\ \bar{f}_{i}(\xi (t))&=\left[ \begin{array}{c} f_i(x(t)) \\ f_i(\hat{x}(t))-f_i(x(t)) \end{array}\right] , \; {\bar{D}}_i=\left[ \begin{array}{r} D_i \\ -D_i \end{array}\right] , \;{\bar{L}}_i=\left[ \begin{array}{c} 0 \\ L_i \end{array}\right] , \; {\bar{C}}_{1i}=\left[ \begin{array}{cc} C_{1i}&0 \end{array}\right] \end{aligned} \end{aligned}$$

In the sequel, we will recall some assumptions, definitions, and technical lemmas, which will facilitate the establishment of the major results.

Assumption 1

Given weighting matrices \(F_i \in {\mathbb {R}}^{n \times n}, \forall i \in {\mathbb {I}}\), the known nonlinear functions \(f_i\) satisfy:

$$\begin{aligned} \begin{aligned} \left\| f_i(\hat{x}(t))-f_i(x(t))\right\| \le&\left\| F_i (\hat{x}(t)-x(t))\right\| , \;\\ {}&\forall \; \hat{x}(t), \; x(t) \in {\mathbb {R}}^n \end{aligned} \end{aligned}$$
(10)

Assumption 2

For full-row rank matrices \(C_i\), the singular value decomposition (SVD) of \(C_i\) is defined as follows:

$$\begin{aligned} C_i=U_i\left[ \begin{array}{ll}C_{0i}&0\end{array}\right] V_i^\textrm{T} \end{aligned}$$
(11)

where \(V_i \in {\mathbb {R}}^{n \times n}\) and \(U_i \in {\mathbb {R}}^{p \times p}\) are unitary matrices and \(C_{0i} \in {\mathbb {R}}^{p \times p}\) are diagonal matrices with positive elements.

Definition 1

[4] For given constants \(c_1, c_2, T_f, d_M\), and \(d_w\), where \(c_1<c_2\), a positive-definite matrix R, and a switching signal \(\sigma \), the closed-loop switched system (9) is observer-based finite-time bounded (OB-FTB) with respect to \(\left( c_1, c_2, T_f, d_M, d_w, R, \sigma \right) \), if

$$\begin{aligned} \begin{aligned} \max _{-d_M \le s \le 0} \left\{ \xi ^\textrm{T}(s) R \xi (s)\right\}<&c_1 \Rightarrow \xi (t)^\textrm{T} R \xi (t)<c_2, \; \forall t \; \in \left[ 0, T_f\right] \end{aligned} \end{aligned}$$
(12)

When \(\omega (t)=0\), the switched system (9) is said to be observer-based finite-time stabilizable (OB-FTS).

Definition 2

[4] For given constants \(c_1, c_2, T_f, d_M, d_\omega \), and \(\gamma \), where \(c_1<c_2\), a positive-definite matrix R, and a switching signal \(\sigma \), then under zero initial conditions, the closed-loop system (9) is observer-based \(H_\infty \) finite-time bounded (OB \(H_\infty \) FTB) with respect to \(\left( c_1, c_2, T_f, d_M, d_w, \gamma , R, \sigma \right) \), if the following conditions are verified:

  1. 1.

    Closed-loop switched system (9) is OB-FTB.

  2. 2.

    The output z(t) satisfies

    $$\begin{aligned} \int _0^{T_f} z^\textrm{T}(t) z(t) {\text {d}} t<\gamma ^2 \int _0^{T_f} \omega ^\textrm{T}(t) \omega (t) {\text {d}}t, \quad \forall t \; \in \left[ 0, T_f\right] \end{aligned}$$
    (13)

where \(\gamma >0\) is a prescribed noise attenuation index.

Lemma 1

[9] For a given matrix \(C \in {\mathbb {R}}^{p \times n}\) with \({\text {rank}}(C)=p\), assume that \(X_1 \in {\mathbb {R}}^{n \times n}\) is a symmetric matrix, then there exists a matrix \(\hat{X}_1 \in {\mathbb {R}}^{p \times p}\) such that \(C X_1=\hat{X}_1 C\), if and only if

$$\begin{aligned} X_1=V\left[ \begin{array}{ll} \hat{X}_{11} &{} \\ &{} \hat{X}_{22} \end{array}\right] V^\textrm{T} \end{aligned}$$
(14)

where \(\hat{X}_{11} \in {\mathbb {R}}^{p \times p}\) and \(\hat{X}_{22} \in {\mathbb {R}}^{(n-p) \times (n-p)}\). V is defined in Assumption 2.

3 Main Results

To guarantee the OB-FTB and \(H_\infty \) control performance, we provide some sufficient conditions for the control synthesis of the switched delayed system (9) under the above-mentioned event-driven observation strategy (4), external disturbance, and network-induced delays.

3.1 Observer-Based Finite-Time Boundedness

Firstly, we present sufficient conditions for the closed-loop switched system (9) to be OB-FTB.

Theorem 1

Consider the time-delay closed-loop switched system (9), for given positive parameters \(c_1, c_2, T_f, d_M, d_w, h, \eta , \lambda , \mu \ge 1\), and symmetric positive-definite matrices \(\Phi _i\), \(R={\text {diag}}\left\{ R_{1}, R_{2}\right\} \), if for any consecutive \(i, j \in {\mathbb {I}}, i \ne j\), there exist symmetric positive-definite matrices \(X_i>0, S_i>0, W_i>0\), and matrices \(Y_i, Z_i\) of appropriate dimensions such that:

$$\begin{aligned} \Theta _i= \left[ \begin{array}{cc} \Theta _{i}^{11} &{} \Theta _{i}^{12} \\ \star &{} \Theta _{i}^{22} \end{array}\right] <0 \end{aligned}$$
(15)
$$\begin{aligned} X_{j} \le \mu X_{i}, \quad S_{j} \le \mu S_{i} \end{aligned}$$
(16)
$$\begin{aligned} c_1\left( \rho _1+\rho _3 \rho _M \right) +\rho _\omega d_\omega <c_2 \rho _2 e^{-\lambda T_f} \end{aligned}$$
(17)

then the system (9) is OB-FTB with respect to \((c_1, c_2, T_f, d_M, d_\omega , R, \sigma )\), with switchings satisfying:

$$\begin{aligned} \tau _a>\tau _a^{\star }=\frac{T_f \ln \mu }{\ln \left( c_2 \rho _2\right) -\ln \left( c_1 \rho _1+c_1 \rho _3 \rho _M +\rho _\omega d_\omega \right) -\lambda T_f} \end{aligned}$$
(18)

Moreover, the corresponding observer-based controller gains are given by:

$$\begin{aligned} K_i = Y_iX_{1i}^{-1},\quad L_i = Z_i U_i C_{0i}\hat{X}^{-1}_{11i}C_{0i}^{-1}U_i^\textrm{T} \end{aligned}$$
(19)

where

$$\begin{aligned} \Theta _{i}^{11}= & {} \left[ \begin{array}{ccccc} \psi _{i}^{11} &{}\quad \psi _{i}^{12} &{}\quad 0 &{}\quad 0 &{}\quad D_{i} \\ \star &{}\quad \psi _{i}^{22} &{}\quad \psi _{i}^{23} &{}\quad 0 &{}\quad - D_{i} \\ \star &{}\quad \star &{}\quad \psi _{i}^{33} &{}\quad 0 &{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \psi _{i}^{44} &{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -W_i \end{array}\right] ,\\ \Theta _{i}^{12}= & {} \left[ \begin{array}{ccccccc} X_{1i} &{}\quad X_{1i} F_i^\textrm{T} &{}\quad X_{1i} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad X_{1i} &{}\quad X_{1i} F_i^\textrm{T} &{}\quad X_{1i} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \sqrt{\eta } X_{1i} C_i^\textrm{T} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array}\right] ,\\ \Theta _{i}^{22}= & {} {\text {diag}}\left\{ -S_{1i},-I,-I,-S_{2i},-I,-I,-I\right\} \end{aligned}$$

where

$$\begin{aligned} \psi ^{11}_{i}= & {} A_i X_{1i}+ X_{1i} A_i^\textrm{T} + B_i Y_i + Y_i^\textrm{T} B_i^\textrm{T} -\lambda X_{1i} + I\\ \psi ^{12}_{i}= & {} B_i Y_i - C_i^\textrm{T} Z_i^\textrm{T}\\ \psi ^{22}_{i}= & {} A_i X_{1i}+ X_{1i} A_i^\textrm{T} - Z_i C_i - C_i^\textrm{T} Z_i^\textrm{T}- \lambda X_{1i} + I\\ \psi ^{23}_{i}= & {} Z_i C_i\\ \psi ^{33}_{i}= & {} e^{\lambda d_M} S_{1i} -2 e^{\lambda d_M} X_{1i}\\ \psi ^{44}_{i}= & {} -e^{\lambda d_M}S_{2i} \end{aligned}$$

and

$$\begin{aligned} \rho _1= & {} \max _{i \in {\mathbb {I}}}\left\{ \lambda _{\max }\left( {\bar{X}}^{-1}_i\right) \right\} , \rho _2=\min _{i \in {\mathbb {I}}}\left\{ \lambda _{\min }\left( {\bar{X}}^{-1}_i\right) \right\} , \\ \rho _3= & {} \max _{i \in {\mathbb {I}}}\left\{ \lambda _{\max }\left( {\bar{S}}^{-1}_i\right) \right\} , \rho _\omega =\max _{i \in {\mathbb {I}}}\left\{ \lambda _{\max }\left( W_i\right) \right\} , \rho _M=\frac{e^{\lambda d_M}-1 }{\lambda }\\ {\bar{X}}_i= & {} R^{1 / 2} X_i R^{1 / 2}, {\bar{S}}_i=R^{1 / 2} S_i R^{1 / 2},\\ X_i= & {} {\text {diag}}\left\{ X_{1i}, X_{1i}\right\} , S_i={\text {diag}}\left\{ S_{1i}, S_{2i}\right\} \\ C_i X_{1i}= & {} \hat{X}_{1i}C_i \end{aligned}$$

Proof

We choose the following Lyapunov–Krasovskii function for the i-th subsystem:

$$\begin{aligned} V_{i}(t)=\xi ^\textrm{T}(t) P_i \xi (t)+\int _{t-d(t)}^t e^{\lambda (t-s)} \xi ^\textrm{T}(s) Q_i \xi (s) \textrm{d} s \end{aligned}$$
(20)

where \(P_i={\text {diag}}\left\{ P_{1i}, P_{1i}\right\} \), \(Q_i={\text {diag}}\left\{ Q_{1i}, Q_{2i}\right\} \) are symmetric positive-definite matrices, and \(\lambda >0 \) is a constant parameter. For \(t \in [t_{s}, t_{s+1}[\), the derivative of (20) along the trajectories of the system (9) can be obtained as below:

$$\begin{aligned} \begin{aligned} {\dot{V}}_{i}(t) -\lambda V_i(t)&=\xi ^\textrm{T}(t) P_{i} {\dot{\xi }}(t)+{\dot{\xi }}^\textrm{T}(t) P_{i} \xi (t) \\ {}&-e^{\lambda d(t)} \xi ^\textrm{T}(t-d(t)) Q_{i} \xi (t-d(t)) \\ {}&- \lambda \xi ^\textrm{T}(t) P_{i} \xi (t) + \xi ^\textrm{T}(t) Q_{i} \xi (t) \end{aligned} \end{aligned}$$
(21)

Expanding (21) using the augmented closed-loop system (9), we can get

$$\begin{aligned} \begin{aligned} {\dot{V}}_i(t)-\lambda V_i(t)&\le \xi ^\textrm{T}(t)\left( {P}_i {\bar{A}}_i + {\bar{A}}_i^\textrm{T} {P}_i+ {Q}_i-\lambda {P}_i\right) \xi (t)\\&\quad +\xi ^\textrm{T}(t) {P}_i {\bar{A}}_{di} \xi \left( t-d(t)\right) +\xi ^\textrm{T}\left( t-d(t)\right) {\bar{A}}_{di}^\textrm{T} {P}_i \xi (t) \\&\quad +\xi ^\textrm{T}(t) P_i {\bar{f}}_i(\xi (t)) +{\bar{f}}^\textrm{T}_i(\xi (t)) P_i \xi (t)\\&\quad +\xi ^\textrm{T}(t) P_i {\bar{D}}_i \omega (t) +\omega ^\textrm{T}(t) {\bar{D}}_i^\textrm{T} P_i \xi (t)+\xi ^\textrm{T}(t) P_i {\bar{L}}_i e_k(t) \\&\quad +e_k^\textrm{T}(t) {\bar{L}}_i^\textrm{T} P_i \xi (t) - e^{\lambda d_M} \xi ^\textrm{T}\left( t-d(t)\right) Q_i \xi \left( t-d(t)\right) \end{aligned} \end{aligned}$$
(22)

By setting \(\bar{F}_i={\text {diag}}\left\{ F_{i}, F_{i}\right\} \), then under Assumption 1, we obtain

$$\begin{aligned} \begin{aligned} \xi ^\textrm{T}(t) P_i \bar{f}_{i}(\xi (t))+\bar{f}_{i}^\textrm{T}(\xi (t)) P_i \xi (t)&\le \xi ^\textrm{T}(t) P_i P_i \xi (t) + \bar{f}_{i}^\textrm{T}(\xi (t))\bar{f}_{i}(\xi (t)) \\&\le \xi ^\textrm{T}(t) ( P_i P_i + \bar{F}^\textrm{T}_{i} \bar{F}_{i}) \xi (t) \end{aligned} \end{aligned}$$
(23)

Also, it is obvious that

$$\begin{aligned} \begin{aligned} \xi ^\textrm{T}(t) P_i {\bar{L}}_i e_k(t) +e_k^\textrm{T}(t) {\bar{L}}_i^\textrm{T} P_i \xi (t) \le&\xi ^\textrm{T}(t) \xi (t) + e_{k}^\textrm{T}(t)\bar{L}^\textrm{T}_{i}P_i P_i \bar{L}_{i} e_k(t) \end{aligned} \end{aligned}$$
(24)

Combining (23)–(24) with (22), we have

$$\begin{aligned} \begin{aligned} {\dot{V}}_i(t)-\lambda V_i(t)&\le \xi ^\textrm{T}(t)\left( {P}_i {\bar{A}}_i + {\bar{A}}_i^\textrm{T} {P}_i+ {Q}_i-\lambda {P}_i + P_i P_i + \bar{F}_i^\textrm{T} \bar{F}_i + I \right) \xi (t) \\&\quad +\xi ^\textrm{T}(t) {P}_i {\bar{A}}_{di} \xi \left( t-d(t)\right) +\xi ^\textrm{T}\left( t-d(t)\right) {\bar{A}}_{di}^\textrm{T} {P}_i \xi (t) \\&\quad +\xi ^\textrm{T}(t) P_i {\bar{D}}_i \omega (t) +\omega ^\textrm{T}(t) {\bar{D}}_i^\textrm{T} P_i \xi (t)+e_k^\textrm{T}(t) {\bar{L}}_i^\textrm{T} P_i P_i {\bar{L}}_i e_k(t) \\&\quad -e ^{\lambda d_M} \xi ^\textrm{T}\left( t-d(t)\right) Q_i \xi \left( t-d(t)\right) \end{aligned} \end{aligned}$$
(25)

Notice from (7) that \(y(t_k h+v h)=y(t-d(t))=C_i x(t-d(t))\), and set \(\Phi _i=L_i^\textrm{T} P_{1i}P_{1i} L_i\) in (4). Then, between two triggering instants, it holds that

$$\begin{aligned} e_k^\textrm{T}(t) L_i^\textrm{T} P_{1i}P_{1i} L_i^\textrm{T} e_k(t) < \eta \; x^\textrm{T}\left( t-d(t)\right) C^\textrm{T}_i C_i x\left( t-d(t)\right) \end{aligned}$$
(26)

By substituting \(\bar{A}_i, \bar{A}_{di}, \bar{D}_i, \bar{F}, \bar{L}_i, P_i\), \(Q_i\), equation (26) in (25), and subtracting \(\omega ^\textrm{T}(t) W_{i} \omega (t)\), we get

$$\begin{aligned} \begin{aligned} {\dot{V}}_i(t)-\lambda V_i(t) - \omega ^\textrm{T}(t) W_{i} \omega (t)\le \zeta ^\textrm{T}(t) \Psi _i \zeta (t) \end{aligned} \end{aligned}$$
(27)

where   \(\zeta (t) = \left[ x^\textrm{T}(t) \quad \hat{x}^\textrm{T}(t) \quad x^\textrm{T}(t-d(t)) \quad \hat{x}^\textrm{T}(t-d(t)) \quad \omega ^\textrm{T}(t) \right] ^\textrm{T}\)

and

$$\begin{aligned} \Psi _i= \left[ \begin{array}{ccccc} \Psi _{i}^{11} &{}\quad \Psi _{i}^{12} &{}\quad 0 &{}\quad 0 &{}\quad P_{1i}D_{i} \\ \star &{}\quad \Psi _{i}^{22} &{}\quad \Psi _{i}^{23} &{}\quad 0 &{}\quad - P_{1i}D_{i} \\ \star &{}\quad \star &{}\quad \Psi _{i}^{33} &{}\quad 0 &{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \Psi _{i}^{44} &{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -W_i \end{array}\right] <0, \end{aligned}$$
(28)

with

$$\begin{aligned} \Psi ^{11}_{i}= & {} P_{1i}(A_i+B_iK_i)+(A_i+B_iK_i)^\textrm{T} P_{1i}-\lambda P_{1i}+Q_{1i}+P_{1i}P_{1i}+F^\textrm{T}_{i}F_{i}+I\\ \Psi ^{12}_{i}= & {} P_{1i}B_{i}K_{i}-C_{i}^\textrm{T} L_{i}^\textrm{T} P_{1i}\\ \Psi ^{22}_{i}= & {} P_{1i}(A_i-L_iC_i)+(A_i-L_iC_i)^\textrm{T} P_{1i}-\lambda P_{1i}+Q_{2i}+P_{1i}P_{1i}+F^\textrm{T}_{i}F_{i}+I \\ \Psi ^{23}_{i}= & {} P_{1i}L_{i}C_{i}\\ \Psi ^{33}_{i}= & {} -\text {e}^{\lambda d_M}Q_{1i} + \eta C_i^\textrm{T} C_i\\ \Psi ^{44}_{i}= & {} -\text {e}^{\lambda d_M}Q_{2i} \end{aligned}$$

Setting \(\Pi ={\text {diag}}\left\{ P_{1i}^{-1}, P_{1i}^{-1}, P_{1i}^{-1}, Q_{2i}^{-1}, I\right\} \), pre- and post-multiplying the matrix inequality (15) by \(\Pi ^\textrm{T}\) and \(\Pi \), we have

$$\begin{aligned} \bar{\Psi }_{i}=\Pi ^\textrm{T} \; \Psi \; \Pi = \left[ \begin{array}{ccccc} \bar{\Psi }_{i}^{11} &{}\quad \bar{\Psi }_{i}^{12} &{}\quad 0 &{}\quad 0 &{}\quad D_{i} \\ \star &{}\quad \bar{\Psi }_{i}^{22} &{}\quad \bar{\Psi }_{i}^{23} &{}\quad 0 &{}\quad D_{i} \\ \star &{}\quad \star &{}\quad \bar{\Psi }_{i}^{33} &{}\quad 0 &{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \bar{\Psi }_{i}^{44} &{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -W_i \end{array}\right] <0, \end{aligned}$$
(29)

where

$$\begin{aligned} \bar{\Psi }^{11}_i= & {} (A_i+B_iK_i)P_{1i}^{-1}+P_{1i}^{-1}(A_i+B_iK_i)^\textrm{T}-\lambda P_{1i}^{-1}+ P_{1i}^{-1} Q_{1i} P_{1i}^{-1} \\{} & {} \quad +I + P_{1i}^{-1} F^\textrm{T}_i F_i P_{1i}^{-1}+P_{1i}^{-1}P_{1i}^{-1}\\ \bar{\Psi }^{12}_{i}= & {} B_{i}K_{i}P_{1i}^{-1}-P_{1i}^{-1} C_{i}^\textrm{T} L_{i}^\textrm{T}\\ \bar{\Psi }^{22}_i= & {} (A_i-L_iC_i)P_{1i}^{-1}+P_{1i}^{-1} (A_i-L_iC_i)^\textrm{T} -\lambda P_{1i}^{-1}+P_{1i}^{-1}Q_{2i}P_{1i}^{-1}\\{} & {} \quad +I+P_{1i}^{-1}F^\textrm{T}_{i}F_{i}P_{1i}^{-1}+P_{1i}^{-1}P_{1i}^{-1}\\ \bar{\Psi }^{23}_{i}= & {} L_{i}C_{i}P_{1i}^{-1}\\ \bar{\Psi }^{33}_{i}= & {} -e^{\lambda d_M}P_{1i}^{-1}Q_{1i}P_{1i}^{-1} + \eta P_{1i}^{-1}C_i^\textrm{T} C_iP_{1i}^{-1}\\ \bar{\Psi }^{44}_{i}= & {} -\text {e}^{\lambda d_M}Q_{2i}^{-1} \end{aligned}$$

By defining \(X_i=P_i^{-1},\; S_i=Q_i^{-1}, \; Y_i=K_iP^{-1}_{1i}, \; Z_i=L_i \hat{X}_{1i}\), and resorting to Lemma 1, the condition \(C_i X_{1i}=\hat{X}_{1i}C_i\) holds, if there exist matrices \(V_i\) such that:

$$\begin{aligned} X_{1i}=V_{i}\left[ \begin{array}{ll} \hat{X}_{11i} &{} \\ &{} \hat{X}_{22i} \end{array}\right] V_{i}^\textrm{T} \end{aligned}$$
(30)

Also, since \(X_{1i}\) and \(S_{1i}\) are positive-definite matrices, we can get

$$\begin{aligned} e^{\lambda d_M}(S_{1i}-X_{1i})^\textrm{T} S_{1i}^{-1} (S_{1i}-X_{1i}) \ge 0 \end{aligned}$$
(31)

Therefore, we can deduce that

$$\begin{aligned} -e^{\lambda d_M} X_{1i} S_{1i}^{-1} X_{1i} \le e^{\lambda d_M} S_{1i} -2e^{\lambda d_M} X_{1i} \end{aligned}$$
(32)

It is easy to see that condition (29) is a nonlinear matrix inequality. Hence, by substituting (32) into (29) and applying the Schur complement lemma [1], the LMI (15) is satisfied. Thus, we come into

$$\begin{aligned} {\dot{V}}_i(t)<\lambda V_i(t)+\omega ^\textrm{T}(t) W_{i} \omega (t) \end{aligned}$$
(33)

Employing the comparison lemma to (33) yields

$$\begin{aligned} V_i(t)<e^{\lambda \left( t-t_s\right) } V_i\left( t_s\right) +\int _{t_s}^t e^{\lambda (t-s)} \omega ^\textrm{T}(s) W_i \omega (s) {\text {d}} s \end{aligned}$$
(34)

Suppose that the state does not jump, that is, \(\sigma \left( t_s\right) =i_s\) and \(\sigma \left( t_s^{-}\right) =\sigma \left( t_{s-1}\right) =i_{s-1}\) at switching instants. Then, according to (16) and (20), it holds that

$$\begin{aligned} V_{i_{s}}\left( t_{s}\right) \le \mu V_{i_{s-1}}\left( t_{s}^{-}\right) , \quad \forall i_{s}, i_{s-1} \in {\mathbb {I}} \end{aligned}$$
(35)

Then, based on (34), (35), with the average dwell definition in [7], it can be deduced that

$$\begin{aligned} \begin{aligned} V_{i}(t)&< \mu ^{N_{\sigma }(t, 0)} e^{\lambda t} V_{i_0}(0)+\mu ^{N_{\sigma }(t, 0)} \int _0^{t_1} e^{\lambda (t-s)} \omega ^\textrm{T}(s) W_{i_0} \omega (s) {\text {d}}s\\&\quad +\mu ^{N_{\sigma }(t, t_1)} \int _{t_1}^{t_2} e^{\lambda (t-s)} \omega ^\textrm{T}(s) W_{i_1} \omega (s) {\text {d}}s \\&\quad +\cdots +\int _{t_s}^t e^{\lambda (t-s)} \omega ^\textrm{T}(s) W_{i_s} \omega (s) {\text {d}} s \\&=\mu ^{N_{\sigma }(t, 0)} e^{\lambda t} V_{i_0}(0)+\int _0^t \mu ^{N_\sigma (t,s)} e^{\lambda (t-s)} \omega ^\textrm{T}(s) W_{\sigma (s)} \omega (s) {\text {d}} s \end{aligned} \end{aligned}$$
(36)

It is easy to notice that \(N_{\sigma }(T_f, 0) \le T_f / \tau _a\), and then, we can get

$$\begin{aligned} \begin{aligned} V_{i}(t)&< \mu ^{N_{\sigma }(T_f, 0)} e^{\lambda T_f} \left( V_{i_0}(0)+d_\omega \max _{i \in {\mathbb {I}}}\left\{ \lambda _{\max }\left( W_{\sigma (s)}\right) \right\} \right) \\&< e^{\lambda T_f} \mu ^{T_f / \tau _a}\left( V_{i_0}(0)+\rho _\omega d_\omega \right) \end{aligned} \end{aligned}$$
(37)

Additionally, it can be derived that

$$\begin{aligned}{} & {} \begin{aligned} V_i(t)&\ge \xi ^\textrm{T}(t) P_i \xi (t) \ge \min _{i \in {\mathbb {I}}}\left\{ \lambda _{\min }\left( {\bar{P}}_i\right) \right\} \xi ^\textrm{T}(t) R \xi (t) =\rho _2 \xi ^\textrm{T}(t) R \xi (t) \end{aligned} \end{aligned}$$
(38)
$$\begin{aligned}{} & {} \begin{aligned} V_{i_0}(0)&\le \xi ^\textrm{T}(0) P_{i_0} \xi (0)+\int _{-d_M}^0 e^{-\lambda s }\xi ^\textrm{T}(s) Q_{i_0} \xi (s) {\text {d}} s \\&\le \lambda _{\max }\left( {\bar{P}}_{i_0}\right) \xi ^\textrm{T}(0) R \xi (0) +\frac{e^{\lambda d_M }-1}{\lambda } \lambda _{\max }\left( {\bar{Q}}_{i_0}\right) \max _{-d_M \le s \le 0}\left\{ \xi ^\textrm{T}(s) R \xi (s)\right\} \\&\le \left( \rho _1+\rho _M \rho _3 \right) c_1 \end{aligned}\nonumber \\ \end{aligned}$$
(39)

Combining (37)–(39), we conclude that

$$\begin{aligned} \begin{aligned} \xi ^\textrm{T}(t) R \xi (t)&\le \frac{V(t)}{\rho _2}<\frac{V_{i_0}(0)+\rho _\omega d_\omega }{\rho _2} e^{\lambda T_f} \mu ^{T_f / \tau _a} \\&<\frac{c_1\left( \rho _1+\rho _M \rho _3\right) +\rho _\omega d_\omega }{\rho _2} e^{\lambda T_f} \mu ^{T_f / \tau _a} \end{aligned} \end{aligned}$$
(40)

If \(\mu =1\), then from (17), we obtain

$$\begin{aligned} \begin{aligned} \xi ^\textrm{T}(t) R \xi (t)&<\frac{c_1\left( \rho _1+\rho _M \rho _3\right) +\rho _\omega d_\omega }{\rho _2} e^{\lambda T_f} < c_2 \end{aligned} \end{aligned}$$
(41)

If \(\mu >1\), then from (18), we have

$$\begin{aligned} \frac{T_f}{\tau _a}<\frac{\ln \left( c_2 \rho _2\right) -\ln \left( c_1 \rho _1+c_1 \rho _3 \rho _M +\rho _\omega d_\omega \right) -\lambda T_f}{\ln \mu } \end{aligned}$$
(42)

Substituting (42) into (40) yields

$$\begin{aligned} \xi ^\textrm{T}(t) R \xi (t) < c_2 \end{aligned}$$
(43)

According to the aforementioned change of variable, it can be obtained that \(K_i = Y_iX_{1i}^{-1},\; L_i = Z_i \hat{X}_{1i}^{-1}\). In order to get the matrices \(\hat{X}_{1i}\), we combine equations (11) and (30) with the condition \(C_i X_{1i}=\hat{X}_{1i}C_i\). Then, the matrices \(L_{i}\) are achieved as below:

$$\begin{aligned} L_{i}=Z_i U_i C_{0i} \hat{X}_{11i}^{-1} C_{0i}^{-1} U^\textrm{T}_i \end{aligned}$$
(44)

Consequently, the observer-based controller gain matrices (19) are obtained.

Hence, in light of Definition 1, the closed-loop switched system (9) is OB-FTB with respect to \((c_1, c_2, T_f, d_M, d_\omega , R, \sigma )\). This ends the proof. \(\square \)

Remark 3

The finite-time boundedness analysis could be obtained with \(K_i\) and \(L_i\) given in advance in such a way that \(A_i + B_i K_i\) and \(A_i - L_i C_i\) are Hurwitz, and the remaining design variables are derived by solving a finite set of LMIs. This method does not allow us to get an ideal design solution. In Theorem 1, more design freedom was given, where the observer-based controller gains were obtained for the closed-loop switched time-delay system (9) to be OB-FTB under the event-triggered mechanism (4).

3.2 Observer-Based Finite-Time \(H_\infty \) Controller Design

This subsection provides sufficient conditions that ensure the prescribed finite-time \(H_\infty \) performance of the switched closed-loop time-delay system (9).

Theorem 2

Consider the time-delay closed-loop switched system (9) under the event-triggered observation scheme (4), for given positive parameters \(c_1, c_2, T_f, d_M, d_w, h\), \(\eta , \lambda , \gamma , \mu \ge 1\), and symmetric positive-definite matrices \(\Phi _i\), \(R={\text {diag}}\left\{ R_{1}, R_{2}\right\} \), if for any consecutive \(i, j \in {\mathbb {I}}, i \ne j\), there exist symmetric positive-definite matrices \(X_i>0, S_i>0\), and matrices \(Y_i, Z_i\) of appropriate dimensions such that:

$$\begin{aligned} \Lambda _i= & {} \left[ \begin{array}{cc} \Lambda _{i}^{11} &{} \Lambda _{i}^{12} \\ \star &{} \Lambda _{i}^{22} \end{array}\right] <0, \end{aligned}$$
(45)
$$\begin{aligned} X_{j}\le & {} \mu X_{i}, \quad S_{j} \le \mu S_{i} \end{aligned}$$
(46)
$$\begin{aligned} \gamma ^2 d_w< & {} c_2 \rho _2 e^{-\lambda T_f}, \end{aligned}$$
(47)

then the system (9) is OB \(H_\infty \) FTB with respect to \((c_1, c_2, T_f, d_M, d_\omega , \gamma , R, \sigma )\), with a prescribed performance index \(\gamma \) and switchings satisfying the following condition:

$$\begin{aligned} \tau _a>\tau _a^{\star }=\frac{T_f \ln \mu }{\ln \left( c_2 \rho _2\right) -\ln \left( \gamma ^2 d_w\right) -\lambda T_f} \end{aligned}$$
(48)

The corresponding observer-based controller gains are given by (19) in Theorem 1.

where

$$\begin{aligned} \Lambda _{i}^{11}= & {} \left[ \begin{array}{ccccc} \chi _{i}^{11} &{}\quad \chi _{i}^{12} &{}\quad 0 &{}\quad 0 &{}\quad \chi _{i}^{15} \\ \star &{}\quad \chi _{i}^{22} &{}\quad \chi _{i}^{23} &{}\quad 0 &{}\quad \chi _{i}^{25} \\ \star &{}\quad \star &{}\quad \chi _{i}^{33} &{}\quad 0 &{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \chi _{i}^{44} &{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \chi _{i}^{55} \end{array}\right] ,\\ \Lambda _{i}^{12}= & {} \left[ \begin{array}{cccccccc} X_{1i} &{}\quad X_{1i} F_i^\textrm{T} &{}\quad X_{1i} &{}\quad X_{1i} C_{1i}^\textrm{T} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad X_{1i} &{}\quad X_{1i} F_i^\textrm{T} &{}\quad X_{1i} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \sqrt{\eta } X_{1i} C_i^\textrm{T} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array}\right] ,\\ \Lambda _{i}^{22}= & {} {\text {diag}}\left\{ -S_{1i},-I,-I,-I,-S_{2i} -I,-I,-I\right\} \end{aligned}$$

where

$$\begin{aligned} \chi ^{11}_{i}= & {} A_i X_{1i}+ X_{1i} A_i^\textrm{T} + B_i Y_i + Y_i^\textrm{T} B_i^\textrm{T} -\lambda X_{1i} + I\\ \chi ^{12}_{i}= & {} B_i Y_i - C_i^\textrm{T} Z_i^\textrm{T}\\ \chi ^{15}_{i}= & {} D_i + X_{1i} C_{1i}^\textrm{T} D_{1i}\\ \chi ^{22}_{i}= & {} A_i X_{1i}+ X_{1i} A_i^\textrm{T} - Z_i C_i - C_i^\textrm{T} Z_i^\textrm{T}- \lambda X_{1i} + I\\ \chi ^{23}_{i}= & {} Z_i C_i\\ \chi ^{25}_{i}= & {} - D_i\\ \chi ^{33}_{i}= & {} e^{\lambda d_M} S_{1i} -2 e^{\lambda d_M} X_{1i}\\ \chi ^{44}_{i}= & {} -e^{\lambda d_M}S_{2i}\\ \chi _{i}^{55}= & {} -\gamma ^2 I + D_{1i}^\textrm{T} D_{1i} \end{aligned}$$

and

$$\begin{aligned} \rho _2= & {} \min _{i \in {\mathbb {I}}}\left\{ \lambda _{\min }\left( {\bar{X}}^{-1}_i\right) \right\} ,\\ {\bar{X}}_i= & {} R^{1 / 2} X_i R^{1 / 2}, {\bar{S}}_i=R^{1 / 2} S_i R^{1 / 2},\\ X_i= & {} {\text {diag}}\left\{ X_{1i}, X_{1i}\right\} , S_i={\text {diag}}\left\{ S_{1i}, S_{2i}\right\} \\ C_i X_{1i}= & {} \hat{X}_{1i}C_i \end{aligned}$$

Proof

The proof of Theorem 2 will not be covered since it is similar to the proof of Theorem 1. Hence, we obtain

$$\begin{aligned} {\dot{V}}_i(t) - \lambda V_i(t)+z^\textrm{T}(t) z(t)-\gamma ^2 \omega ^\textrm{T}(t) \omega (t) < 0 \end{aligned}$$
(49)

By letting \(W_i=\gamma ^2 I\) and noticing that \(z^\textrm{T}(t)z(t)>0\), the conditions of Theorem 1 and Theorem 2 are equivalent. Hence, the switched system (9) is FTB. We now show that the condition (13) is satisfied. According to LMI (45), it is assumed that \(\Lambda _i<0\). By setting \(\Delta (s)=\gamma ^2 \omega ^\textrm{T}(s) \omega (s)-z^\textrm{T}(s) z(s)\), we integrate (49) from \(t_s\) to t

$$\begin{aligned} V_i(t)<e^{\lambda \left( t-t_s\right) } V_i\left( t_s\right) +\int _{t_s}^t e^{\lambda (t-s)} \Delta (s) {\text {d}} s \end{aligned}$$
(50)

Using the same method as in (36), it holds that

$$\begin{aligned} V_{i}(t) < \mu ^{T_f / \tau _a} e^{\lambda T_f} V_{i_0}(0)+\mu ^{T_f / \tau _a} e^{\lambda T_f} \int _0^t \Delta (s) {\text {d}} s \end{aligned}$$
(51)

For zero initial conditions, \(V_{i_0}(0)=0\), it follows that

$$\begin{aligned} 0 \le V_i(t)<\mu ^{T_f / \tau _a} e^{\lambda T_f} \int _0^{T_f} \Delta (s) {\text {d}} s \end{aligned}$$
(52)

Therefore, the condition (13) is verified. As a result, in light of Definition 2, the closed-loop switched system (9) is OB \(H_\infty \) FTB with respect to \(\left( c_1, c_2, T_f, d_M, d_w, \gamma , R, \sigma \right) \), with a prescribed performance index \(\gamma \). This concludes our proof. \(\square \)

4 Example

This section gives a simulation example to verify the theoretical results. We consider the switched system (1) with the following matrices:

Subsystem 1:

$$\begin{aligned} A_{1}=\left[ \begin{array}{cc} -1.5 &{} -1 \\ 0.8 &{} -2.5 \end{array}\right] , \; B_{1}=\left[ \begin{array}{c} 1 \\ 0.5 \end{array}\right] , \; C_1=\left[ \begin{array}{c} -1 \\ 2 \end{array}\right] ^\textrm{T}, \; D_{1}=\left[ \begin{array}{c} 0 \\ 0.2 \end{array}\right] \end{aligned}$$

Subsystem 2:

$$\begin{aligned} A_{2}=\left[ \begin{array}{cc} -2 &{} -1 \\ 1.5 &{} -1.8 \end{array}\right] , \; B_{2}=\left[ \begin{array}{c} 0.5 \\ 1 \end{array}\right] , \; C_2=\left[ \begin{array}{c} -2 \\ 1 \end{array}\right] ^\textrm{T}, \; D_{2}=\left[ \begin{array}{c} 0.1 \\ 0 \end{array}\right] \end{aligned}$$

The nonlinear functions \(f_i(x(t))\) are given as below:

$$\begin{aligned} f_{1}(x(t))=\left[ \begin{array}{c} 0.1 \sin \left( x_1(t)\right) \\ 0.1 x_2(t) \end{array}\right] ,\quad f_{2}(x(t))=\left[ \begin{array}{c} 0.2 x_1(t) \\ 0.2 \sin \left( x_2(t)\right) \end{array}\right] \end{aligned}$$

According to Assumption 1, the Lipschitz matrices are given by

$$\begin{aligned} F_{1}=\left[ \begin{array}{cc} 0.1 &{} 0 \\ 0 &{} 0.1 \end{array}\right] , \quad F_{2}=\left[ \begin{array}{cc} 0.2 &{} 0 \\ 0 &{} 0.2 \end{array}\right] \end{aligned}$$

The initial state of the system and the observer is chosen as \(x(s)=[-0.15,0.1]^\textrm{T}\), \(\hat{x}(s)=[-0.2,0.15]^\textrm{T},\; s \in \left[ -d_M, 0\right] \), respectively. Set \(c_1=0.1, \; c_2=20, \; T_f=1\,s, \; h= 1\, ms, \; d_M=1.9\,ms\) and \(R={\text {diag}}\left\{ I, I\right\} \). Also, other adjustable parameters are set as \(\lambda =4, \eta =5 \times 10^{-3}\), and \(\mu =1.3\). For a predefined external disturbance input \(\omega (t) = 0.2e^{-t}\), we choose \(d_\omega = 0.03\).

By solving LMIs of Theorem 1 using the MATLAB LMI control toolbox, we can obtain the following feasible solutions:

$$\begin{aligned} K_1=\left[ \begin{array}{ll} 0.2242&0.2825 \end{array}\right] , \quad L_{1}=\left[ \begin{array}{c} 0.0310 \\ -0.1047 \end{array}\right] \\ K_2=\left[ \begin{array}{ll} 0.1537&0.2876 \end{array}\right] , \quad L_{2}=\left[ \begin{array}{c} 0.0999 \\ -0.0485 \end{array}\right] \end{aligned}$$

Besides, based on (18), the average dwell time satisfies \(\tau _a=0.3\,s> \tau _a^{\star }=0.28\,s\).

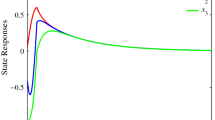
Figures 2, 3, 4, 5, 6 and 7 provide the simulation results of the closed-loop switched system (9) for the given initial conditions. The system state and the observer state time responses are plotted in Fig. 2. Therefore, we conclude that the real state can successfully be estimated using the designed event-triggered observer. Figure 3 shows the switching signal with the event-based observation instants. Figure 4 displays the system output and the event-triggered output, while the evolution of the triggering error norm \(\Vert P_{1i} L_i e_k(t)\Vert ^{2}\) compared to the output-based bound \(\eta \Vert y(t-d(t))\Vert ^{2}\) is illustrated in Fig. 5. Meanwhile, under the event-triggered condition (4), the event-triggered instants and the inter-event times are depicted in Fig. 6 with a minimum inter-event interval MIET=\(0.033\, s\). Figure 7 presents the trajectory of \(\xi ^\textrm{T}(t)R\xi (t)\), which indicates that under the designed event-triggered observer-based controller, the condition \(\xi ^\textrm{T}(t)R\xi (t)<c_2\) is satisfied in the finite-time interval [0, 1]. Thus, the switched system is OB-FTB with respect to \((0.1, 20, 1, 0.0019, 0.03, I, \sigma )\).

The system output generates 1000 sampled data within the finite-time interval [0, 1]. Meanwhile, under the event-triggered observation mechanism (4), only 14 triggered data are sent to the observer for state reconstruction and control design. Accordingly, just 1.5% of sensing information is transmitted over the communication network while maintaining satisfactory finite-time control performance of the switched system. Hence, the developed event-triggered observation strategy can effectively mitigate the burden of communication networks and save a certain proportion of the observer’s computational resources in the presence of practical limitations, that is to say, the network-induced delays and the external disturbance input.

In order to review the effect of the triggering threshold on the transmission rate, the comparison in Table 1 shows the number of event-based transmitted data and the inter-event time intervals for different values of \(\eta \). We remark that less output data are triggered for a larger triggering parameter \(\eta \). However, it is necessary to point out that LMIs in Theorem 1 are not feasible for \(\eta =10\). Consequently, the system state may exceed the prescribed bound and even be unstable. Additionally, Table 1 verifies that any inter-event interval is strictly greater than the sampling interval h. Namely, no Zeno behavior has occurred.

Table 1 Comparison between number of events and MIET
Full size table
Fig. 2
figure 2

State trajectories of the system and the observer

Full size image
Fig. 3
figure 3

Switching signal \(\sigma (t)\)

Full size image
Fig. 4
figure 4

Output and event-triggered output signals

Full size image
Fig. 5
figure 5

The event-triggered condition evolution

Full size image
Fig. 6
figure 6

Event-instants and inter-event time interval

Full size image
Fig. 7
figure 7

Trajectory of \(\xi ^\textrm{T}(t)R\xi (t)\)

Full size image

5 Conclusion

In this paper, we investigated the issue of robust finite-time observer-based control for a class of networked switched systems with exogenous disturbances via an event-triggered observation scheme. Owing to the network-based event-triggered output measurements used to estimate the unmeasured state, the overall system is modeled as a switched time-delay system. On the basis of Lyapunov–Krasovskii functions and the average dwell time technique, novel LMI-based theorems have been developed to obtain a restrictive average dwell time condition and to derive the observer-based sub-controller gains in order to guarantee the finite-time \(H_\infty \) boundedness of the resulting closed-loop switched system. Finally, through a simulation example, we have verified that the obtained results can reduce the communication network burden and optimize the network resources while ensuring satisfactory finite-time event-triggered control performance. With the help of [25, 32], additional investigations on the problem of quantization and packet dropout may improve the effectiveness of the proposed approach.