Robust Fault Detection Filter Design for Nonlinear Networked Control Systems with Time-Varying Delays and Packet Dropout

Abstract

This paper deals with the problem of detecting faults in nonlinear networked control systems. The considered system is the state space models of time-varying systems in which the upper and lower bounds of delay are known. Sector-bounded condition is exploited to overcome the nonlinear term. It is assumed that data packet dropouts occur during data transmission, which here is modeled as Bernoulli-distributed white sequences. For fault detection, an $H_{-} /H_{\infty }$ performance index is utilized to design an observer such that the residual signal is much sensitive to faults and less sensitive to disturbance. The Lyapunov–Krasovskii approach is exploited to ensure the stability of the designed observer. The obtained results for observer design are modeled as linear matrix inequalities. Finally, a numerical example and a practical example of engineering systems are adopted to illustrate the effectiveness of the proposed approach.

1 Introduction

During the last 2 decades, the application of networked control systems (NCSs) in industries is growing. Compared to traditional point-to-point control systems, the NCSs have benefited from advantages such as low cost, system safety, and ease of diagnosing and maintenance [22, 23, 30]. However, using networks for data transmission instead of wires has been resulted in many issues such as delay, data packet dropout and quantization problems [10, 17, 18, 34]. System stabilization is an important issue in the practical and theoretical systems. Besides, the occurrence of delay and data packet dropout impacts stability, and therefore, these issues should be considered in the controller design [3, 14,15,16, 31, 33].

The existence of nonlinear terms in networked control systems result in many mathematical issues. There are several methods to analyze nonlinear systems, for example, utilizing Takagi–Sugeno fuzzy model is an appropriate method to design stabilizing controllers and observers for nonlinear systems [7, 13, 19, 29, 30, 32]. Sum of squares (SOS) method is another approach that is used to investigate the stability of nonlinear NCSs. For example in [4], the SOS method is exploited to analyze a nonlinear system with time-varying delay and transition intervals. In many studies, sector-bounded nonlinearity condition is utilized to analyze the stability of nonlinear systems [24, 25, 35]. A gain-scheduled algorithm for controller design in discrete-time systems with randomly nonlinear disturbance, which satisfy sector-bounded condition is studied in [26], where the random variable is represented by Bernoulli-distributed sequence.

Due to increased demands for safety, reliability and performance, fault detection methods have received much attention in the last decades [5, 11]. In the fault detection process for NCSs, transmission delays and data packet dropouts cause many challenges. In several studies, delays or data packet dropouts are considered, for example in [12, 20, 24] transmission delays, and in [9, 21] data packet dropout is studied. The aim of this paper is fault detection by designing a stable observer, and computing and evaluating the residual signal using the observer. Comparing the residual evaluation signal with a predefined threshold can detect faults [8, 27, 28].

Moreover, the mathematical model of systems suffers from uncertainty as well as disturbance that can cause inappropriate effects in the residual signal. In other words, incipient fault cannot be detected in the presence of modeling uncertainty and disturbances; therefore, a robust ${{H}_{-}}/{{H}_{\infty }}$ strategy can be adopted to improve the process of fault detection. This performance index is the combination of ${{H}_{-}}$ and ${{H}_{\infty }}$ indexes in which the ${{H}_{\infty }}$ index reduces the effect of disturbance and the ${{H}_{-}}$ index increases the faults impact on the residual signal [1, 2, 6, 11]. Despite the clear advantages of ${{H}_{-}}/{{H}_{\infty }}$ performance index, to the best of our knowledge, it has not been used for the fault detection of networked control systems.

Thus, our goal, in current work, is to design a stable observer using a robust fault detection approach, in which the residual signal is sensitive to fault, while it is robust against disturbance. To this end, ${{H}_{-}}/{{H}_{\infty }}$ performance index is exploited to achieve the optimal fault detection filter. It is assumed that the system model includes a class of nonlinearity, which can be handled using a sector-bounded nonlinearity condition technique. This work aims to design a robust fault detection scheme, where data transmission from sensors to the observer is subjected to data packet dropout. This phenomenon is modeled as Bernoulli-distributed white sequences. Finally, a numerical example and a practical example of engineering systems are studied to show the effectiveness of the proposed approach.

The rest of this paper is organized as follows: In Sect. 2, the structure of the system including observer is described. In Sect. 3, three theorems are derived, in the first theorem, ${{H}_{\infty }}$ index is used to reduce the impact of disturbance on the residual signal, in the second theorem, ${{H}_{-}}$ index is used to increase the effect of fault on the residual signal, and finally third theorem makes use of model matching technique to obtain observer gain. In Sect. 4, a numerical example and in Sect. 5 a practical example of engineering systems is adopted to show the efficiency of the proposed approach. Finally, the paper is concluded in Sect. 6.

Notations The notations used throughout this paper are as follows. $E\left\{ . \right\}$ denotes the expectation, ||.|| denotes the standard ${{l}_{2}}$ norm, $\Pr ob\left\{ . \right\}$ denotes occurrence probability, $\hbox {diag}\left\{ . \right\}$ denotes a block diagonal matrix, $*$ illustrates a symmetrical transpose. I and 0 are an identity and zero matrices with appropriate dimensions.

2 Problem Statement

Consider a dynamic system that is described by:

$$\begin{aligned} \begin{aligned} x(k+1)&=(A+\Delta A)x(k)+({{A}_{h}}+\Delta {{A}_{h}})x(k-h(k)) +Ng(x(k))\\&\quad +{{M}_{1}}w(k)+{{F}_{1}}f(k) \\ y(k)&=Cx(k) \end{aligned} \end{aligned}$$

(1)

where $x(k)\in {\mathbb {R}^{n}}$ is the state vector, $g(x(k))\in {\mathbb {R}^{n}}$ is the nonlinear term that depends on system state, $y(k)\in {\mathbb {R}^{m}}$ is the output vector, $w(k)\in {\mathbb {R}^{w}}$ is disturbance that belongs to $L_{2}\left( 0\,,\,\infty \right) \,$, $f(k)\in {\mathbb {R}^{f}}$ denotes the faults. $A,\,\,{{A}_{h}},\,\,N,\,\,{{M}_{1}},\,\,{{F}_{1}},\,\,C$ are predefined matrices with appropriate dimensions, h(k) is a positive value for delay with upper and lower bounds ${{\tau }_{m}}<h(k)<{{\tau }_{M}}$, where ${{\tau }_{m}},\,\,{{\tau }_{M}}$ are positive known scalars. $\Delta A(k)$ and $\Delta {{A}_{h}}(k)$ are time-varying uncertainties of the matrices A and ${{A}_{h}}$ where:

$$\begin{aligned} \begin{aligned} \left[ \begin{matrix} \Delta A &{} \Delta {{A}_{h}} \\ \end{matrix} \right] =LF(k)\left[ \begin{matrix} {{E}_{1}} &{} {{E}_{2}} \\ \end{matrix} \right] \end{aligned} \end{aligned}$$

(2)

$L,\,\,{{E}_{1}},\,{{E}_{2}}$ are known matrices and F(k) is a time-varying matrix that satisfies ${{F}^\mathrm{T}}(k)F(k)<I$.

It is assumed that for the nonlinear term, the following sector-bounded nonlinearity condition is satisfied:

$$\begin{aligned} \begin{aligned} {{\left[ g(x(k))-{{S}_{1}}x(k) \right] }^\mathrm{T}}\left[ g(x(k))-{{S}_{2}}x(k) \right] \le 0\,\,\,\,\,\,\forall x(k)\in {{\mathbb {R} }^{n}} \end{aligned} \end{aligned}$$

(3)

and $g(0)=0$ for some constant real matrices ${{S}_{1}},\,\,{{S}_{2}}$ with appropriate dimensions, in which $({{S}_{2}}-{{S}_{1}})>0$.

The structure of fault detection filter for considered NCS is shown in Fig. 1. This figure shows that the network is used for data transmission from the plant to the fault detection filter.

Fig. 1

The structure of networked control systems

Considering data packet dropout, the input of the fault detection filter is:

$$\begin{aligned} \begin{aligned} \hat{y}(k)=\alpha (k)Cx(k)+{{M}_{2}}w(k)+{{F}_{2}}f(k) \end{aligned} \end{aligned}$$

(4)

where ${{M}_{2}},\,\,{{F}_{2}}$ are known matrices, and stochastic variable $\alpha (k)$ is assumed to be a Bernoulli-distributed white sequence defined as follows:

$$\begin{aligned} \begin{aligned}&\hbox {Prob}\left\{ \alpha (k)=1 \right\} =E\left\{ \alpha (k) \right\} =\bar{\alpha } \\&\hbox {Prob}\left\{ \alpha (k)=0 \right\} =1-E\left\{ \alpha (k) \right\} =1-\bar{\alpha } \\&\hbox {Var}\left\{ \alpha (k) \right\} =E\left\{ {{\left( \alpha (k)-\bar{\alpha } \right) }^{2}} \right\} =\bar{\alpha }(1-\bar{\alpha })={{{\bar{\beta }}}^{2}} \end{aligned} \end{aligned}$$

(5)

where $\bar{\alpha }$ is the expected value of $\alpha (k)$ and ${{\bar{\beta }}^{2}}$ is the variance of $\alpha (k)$.

Fault detection system considers a full-order filter as follows:

$$\begin{aligned} \begin{aligned} \hat{x}(k+1)&={{A}_{c}}\hat{x}(k)+{{B}_{c}}\hat{y}(k) \\ r(k)&=V(\hat{y}(k)-C\hat{x}(k)) \end{aligned} \end{aligned}$$

(6)

where $\hat{x}(k)\in {{\mathbb {R} }^{n}}$ is an auxiliary vector for the observer, $r(k)\in {{\mathbb {R} }^{m}}$ is the residual signal, ${{A}_{c}},\,{{B}_{c}}$, and V are the observer parameters.

Considering new augmented vector $\eta (k)={{\left[ \begin{matrix} {{x}^\mathrm{T}}(k)&{{{\hat{x}}}^\mathrm{T}}(k) \end{matrix} \right] }^\mathrm{T}}$, the overall system can be represented as:

$$\begin{aligned} \begin{aligned} \eta (k+1)=&{{{\tilde{A}}}_{\Delta }}\eta (k)+\left( \alpha (k)-\bar{\alpha } \right) {{{\tilde{A}}}_{\alpha }}\eta (k)+{{{\tilde{A}}}_{\Delta h}}\eta (k-h(k))+\tilde{N}g(H\eta (k))\\&+{{{\tilde{M}}}_{1}}w(k)+{{{\tilde{F}}}_{1}}f(k) \\ r(k)=V\tilde{C}&\eta (k)+\left( \alpha (k)-\bar{\alpha } \right) V{{{\tilde{C}}}_{\alpha }}\eta (k)+V{{{\tilde{M}}}_{2}}w(k)+V{{{\tilde{F}}}_{2}}f(k) \end{aligned} \end{aligned}$$

(7)

where:

$$\begin{aligned} \begin{aligned}&{{{\tilde{A}}}_{\Delta }}=\left[ \begin{array}{cc} A+\Delta A &{} 0 \\ \bar{\alpha }{{B}_{c}}C &{} {{A}_{c}} \\ \end{array} \right] ,{{{\tilde{A}}}_{\alpha }}=\left[ \begin{array}{cc} 0 &{} 0 \\ {{B}_{c}}C &{} 0 \\ \end{array} \right] , {{{\tilde{A}}}_{\Delta h}}=\left[ \begin{array}{cc} {{A}_{h}}+\Delta {{A}_{h}} &{} 0 \\ 0 &{} 0 \\ \end{array} \right] , {\tilde{N}=\left[ \begin{array}{c} {N}\\ {0}\\ \end{array}\right] },\\&{{{\tilde{M}}}_{1}}=\left[ \begin{array}{c} {{M}_{1}} \\ {{B}_{c}}{{M}_{2}} \\ \end{array} \right] , {{{\tilde{F}}}_{1}}=\left[ \begin{array}{c} {{F}_{1}} \\ {{B}_{c}}{{F}_{2}} \\ \end{array} \right] , \tilde{C}=\left[ \begin{array}{ll} \bar{\alpha }C &{} -C \\ \end{array} \right] , {{{\tilde{C}}}_{\alpha }}=\left[ \begin{array}{ll} C &{} 0 \\ \end{array} \right] , {{{\tilde{M}}}_{2}}={{M}_{2}},\\&{{{\tilde{F}}}_{2}}={{F}_{2}},H=\left[ \begin{array}{ll} I &{} 0 \\ \end{array} \right] \end{aligned} \end{aligned}$$

Moreover, term $g(H\eta (k))$ in Eq. (7) can be rewritten using Eq. (3) as:

$$\begin{aligned} \begin{aligned}&{{\left[ g(H\eta (k))-{{{\tilde{S}}}_{1}}\eta (k) \right] }^\mathrm{T}}\left[ g(H\eta (k))-{{{\tilde{S}}}_{2}}\eta (k)) \right] \le 0 \\&{{{\tilde{S}}}_{1}}=\left[ \begin{matrix} {{S}_{1}} &{} 0 \\ \end{matrix} \right] ,\,\,{{{\tilde{S}}}_{2}}=\left[ \begin{matrix} {{S}_{2}} &{} 0 \\ \end{matrix} \right] \end{aligned} \end{aligned}$$

(8)

By simple arrangement of the above equation, one can obtain:

$$\begin{aligned} \begin{aligned} {{\left[ \begin{array}{c} \eta (k) \\ g(H\eta (k)) \\ \end{array} \right] }^\mathrm{T}}\left[ \begin{array}{cc} \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2} &{} -\frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2} \\ -\frac{\tilde{S}_{1}^{{}}+\tilde{S}_{2}^{{}}}{2} &{} I \\ \end{array} \right] \left[ \begin{array}{c} \eta (k) \\ g(H\eta (k)) \\ \end{array} \right] \le 0 \end{aligned} \end{aligned}$$

(9)

Our aim is to use ${{H}_{-}}/{{H}_{\infty }}$ performance index to design a fault detection filter that maximizes the effect of fault while minimizes the effect of disturbance on the residual signal; in other words:

$$\begin{aligned} \begin{aligned}&||r(k)||<\lambda ||w(k)|| \\&||r(k)||>\gamma ||f(k)|| \end{aligned} \end{aligned}$$

(10)

To this end, a reference system is defined as:

$$\begin{aligned} \begin{aligned} {{\eta }_{r}}(k+1)&= {{{\tilde{A}}}^{*}}{{\eta }_{r}}(k)+\left( \alpha (k)-\bar{\alpha } \right) {{{\tilde{A}}}^{*}}_{\alpha }{{\eta }_{r}}(k)+{{{\tilde{A}}}_{h}}{{\eta }_{r}}(k-h(k)) \\&\quad +\tilde{N}g(H{{\eta }_{r}}(k))+\tilde{M}_{1}^{*}w(k)+\tilde{F}_{1}^{*}f(k)\\ {{r}_{r}}(k)&={{V}^{*}}\tilde{C}{{\eta }_{r}}(k)+\left( \alpha (k)-\bar{\alpha } \right) {{V}^{*}}{{{\tilde{C}}}_{\alpha }}{{\eta }_{r}}(k)+{{V}^{*}}{{{\tilde{M}}}_{2}}w(k)+{{V}^{*}}{{{\tilde{F}}}_{2}}f(k)\\ \end{aligned} \end{aligned}$$

(11)

where:

$$\begin{aligned} \begin{aligned}&{{\tilde{A}}^{*}}=\left[ \begin{matrix} A &{} 0\\ \bar{\alpha }B_{c}^{*}C &{} A_{c}^{*}\\ \end{matrix} \right] ,{{\tilde{A}}^{*}}_{\alpha }=\left[ \begin{matrix} 0 &{} 0\\ B_{c}^{*}C &{} 0\\ \end{matrix} \right] ,{{\tilde{A}}_{h}}=\left[ \begin{matrix} {{A}_{h}} &{} 0\\ 0 &{} 0\\ \end{matrix} \right] ,\\&{\tilde{N}=\left[ \begin{matrix} {N}\\ {0} \end{matrix}\right] }, {{\tilde{M}}^{*}}_{1}=\left[ \begin{matrix} {{M}_{1}}\\ B_{c}^{*}{{M}_{2}} \\ \end{matrix} \right] , {{\tilde{F}}^{*}}_{1}=\left[ \begin{matrix} {{F}_{1}} \\ B_{c}^{*}{{F}_{2}} \\ \end{matrix}\right] , \end{aligned} \end{aligned}$$

By defining ${{r}_{e}}(k)=r(k)-{{r}_{r}}(k)$, and introducing new augmented matrices $\xi (k)=\left[ \begin{matrix} {{x}^\mathrm{T}}(k) &{} {{{\eta }}^\mathrm{T}_{r}}(k) \\ \end{matrix} \right.$${{\left. {{{\hat{x}}}^\mathrm{T}}(k) \right] }^\mathrm{T}}$ and $d(k)={{\left[ \begin{matrix} {{f}^\mathrm{T}}(k) &{} {{w}^\mathrm{T}}(k) \\ \end{matrix} \right] }^\mathrm{T}}$, we have:

$$\begin{aligned} \begin{aligned} \xi (k+1)=&\,(\bar{A}+\Delta \bar{A})\xi (k)+\left( \alpha (k)-\bar{\alpha } \right) {{{\bar{A}}}_{\alpha }}\xi (k)+({{{\bar{A}}}_{h}}+\Delta {{{\bar{A}}}_{h}})\xi (k-h(k))\\&+\bar{N}g(\bar{H}\xi (k))+{{{\bar{D}}}_{1}}d(k) \\ {{r}_{e}}(k)=&\,\bar{C}\xi (k)+\left( \alpha (k)-\bar{\alpha } \right) {{{\bar{C}}}_{\alpha }}\xi (k)+{{{\bar{D}}}_{2}}d(k) \\ \end{aligned} \end{aligned}$$

(12)

where:

$$\begin{aligned} \begin{aligned}&\bar{A}=\left[ \begin{matrix} A &{} 0 &{} 0 \\ \bar{\alpha }B_{c}^{*}C &{} A_{c}^{*} &{} 0 \\ \bar{\alpha }{{B}_{c}}C &{} 0 &{} {{A}_{c}} \\ \end{matrix} \right] ,{{{\bar{A}}}_{\alpha }}=\left[ \begin{matrix} 0 &{} 0 &{} 0 \\ B_{c}^{*}C &{} 0 &{} 0 \\ {{B}_{c}}C &{} 0 &{} 0 \\ \end{matrix} \right] , {{{\bar{A}}}_{h}}=\left[ \begin{matrix} {{A}_{h}} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{matrix} \right] , {{{\bar{D}}}_{1}}=\left[ \begin{matrix} {{F}_{1}} &{} {{M}_{1}} \\ B_{c}^{*}{{F}_{2}} &{} B_{c}^{*}{{M}_{2}} \\ {{B}_{c}}{{F}_{2}} &{} {{B}_{c}}{{M}_{2}} \\ \end{matrix} \right] , \\&{{{\bar{D}}}_{2}}=\left[ \begin{matrix} (V-{{V}^{*}}){{F}_{2}} &{} (V-{{V}^{*}}){{M}_{2}} \\ \end{matrix} \right] , \bar{C}=\left[ \begin{matrix} (V-{{V}^{*}})\bar{\alpha }C &{} {{V}^{*}}C &{} -VC \\ \end{matrix} \right] , \\&{{{\bar{C}}}_{\alpha }}=\left[ \begin{matrix} (V-{{V}^{*}})C &{} 0 &{} 0 \\ \end{matrix} \right] , \bar{H}=\left[ \begin{matrix} I &{} 0 &{} 0 \\ \end{matrix} \right] \\&\Delta \bar{A}=\left[ \begin{matrix} \Delta A &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{matrix} \right] ,\Delta {{{\bar{A}}}_{h}}=\left[ \begin{matrix} \Delta {{A}_{h}} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{matrix} \right] ,\bar{N}=\left[ \begin{matrix} N \\ 0 \\ 0 \\ \end{matrix} \right] , \end{aligned} \end{aligned}$$

Considering Eq. (2), uncertain terms $\Delta \bar{A}$ and $\Delta {{\bar{A}}_{h}}$ can be obtained as:

$$\begin{aligned} \begin{aligned}&\Delta \bar{A}={{\left[ \begin{matrix} {{L}^\mathrm{T}} &{} 0 &{} 0 \\ \end{matrix} \right] }^\mathrm{T}}F(k)\left[ \begin{matrix} {{E}_{1}} &{} 0 &{} 0 \\ \end{matrix} \right] =\bar{L}F(k){{{\bar{E}}}_{1}} \\&\Delta {{{\bar{A}}}_{h}}={{\left[ \begin{matrix} {{L}^\mathrm{T}} &{} 0 &{} 0 \\ \end{matrix} \right] }^\mathrm{T}}F(k)\left[ \begin{matrix} {{E}_{2}} &{} 0 &{} 0 \\ \end{matrix} \right] =\bar{L}F(k){{{\bar{E}}}_{2}} \\ \end{aligned} \end{aligned}$$

(13)

Sector-bounded condition for nonlinear term, $g(\bar{H}\xi (k))$, in the new structure can be rewritten as:

$$\begin{aligned} \begin{aligned}&{{\left[ g(\bar{H}\xi (k))-{{{\bar{S}}}_{1}}\xi (k) \right] }^\mathrm{T}}\left[ g(\bar{H}\xi (k))-{{{\bar{S}}}_{2}}\xi (k)) \right] \le 0 \\&{{{\bar{S}}}_{1}}=\left[ \begin{matrix} {{S}_{1}} &{} 0 &{} 0 \\ \end{matrix} \right] ,\,\,{{{\bar{S}}}_{2}}=\left[ \begin{matrix} {{S}_{2}} &{} 0 &{} 0 \\ \end{matrix} \right] \end{aligned} \end{aligned}$$

(14)

By a simple arrangement, it can be reformulated as:

$$\begin{aligned} \begin{aligned} {{\left[ \begin{array}{c} \xi (k) \\ g(\bar{H}\xi (k)) \\ \end{array} \right] }^\mathrm{T}}\left[ \begin{array}{cc} \frac{\bar{S}_{1}^\mathrm{T}{{{\bar{S}}}_{2}}+\bar{S}_{2}^\mathrm{T}{{{\bar{S}}}_{1}}}{2} &{} -\frac{\bar{S}_{1}^\mathrm{T}+\bar{S}_{2}^\mathrm{T}}{2} \\ -\frac{\bar{S}_{1}^{{}}+\bar{S}_{2}^{{}}}{2} &{} I \\ \end{array} \right] \left[ \begin{array}{c} \xi (k) \\ g(\bar{H}\xi (k)) \\ \end{array} \right] \le 0 \end{aligned} \end{aligned}$$

(15)

The following ${{H}_{\infty }}$ performance index is considered for the system (12) to minimize the deviation of the residual dynamics from the reference dynamics:

$$\begin{aligned} \begin{aligned} ||{{r}_{e}}(k)||<\kappa ||d(k)||. \end{aligned} \end{aligned}$$

(16)

To detect faults, the residual evaluation function and the threshold are defined as:

$$\begin{aligned} \begin{aligned}&J(k)={{\left\{ \sum \limits _{s=1}^{s=k}{{{r}^\mathrm{T}}(s)r(s)} \right\} }^{1/2}} \\&{{J}_{\mathrm{th}}}=\underset{f(k)=0}{\mathop {\sup \left\{ J(k) \right\} }}\, \\ \end{aligned} \end{aligned}$$

(17)

A fault can be detected by comparing the residual evaluation with the threshold by resorting to the following rules:

$$\begin{aligned} \begin{aligned}&J(k)>{{J}_{\mathrm{th}}}\Rightarrow \hbox {fault has occurred} \\&J(k)\le {{J}_{\mathrm{th}}}\Rightarrow \hbox {fault free} \\ \end{aligned} \end{aligned}$$

(18)

Lemma 1

Consider real matrices ${{\psi }_{1}},{{\psi }_{2}},{{\psi }_{3}}$ with appropriate dimensions and assume that $\psi _{3}^\mathrm{T}{{\psi }_{3}}\le I$, and then following equation is satisfied:

$$\begin{aligned} \begin{aligned} {{\psi }_{1}}{{\psi }_{3}}{{\psi }_{2}}+\psi _{2}^\mathrm{T}\psi _{3}^\mathrm{T}\psi _{1}^\mathrm{T}\le \vartheta {{\psi }_{1}}\psi _{1}^\mathrm{T}+{{\vartheta }^{-1}}\psi _{2}^\mathrm{T}{{\psi }_{2}}\,\,\,\,\,\,\,\,\,\,\forall \vartheta >0 \end{aligned} \end{aligned}$$

3 Main Results

The objective of this section is to design a fault detection filter for nonlinear networked control systems. The residual signal is designed in a way that it is the most sensitive to fault, and robust against disturbances and uncertainties. In the first step, define ${{r}_{rf}}(k),\,\,{{r}_{rw}}(k)$ as the sum of reference residual signal. Our goal is to increase the effect of fault in ${{r}_{rf}}(k)$, and to reduce the impact of disturbance in ${{r}_{rw}}(k)$, in the other words:

$$\begin{aligned} \begin{aligned}&||{{r}_{rw}}(k)||<\lambda ||w(k)|| \\&||{{r}_{rf}}(k)||>\gamma ||f(k)|| \\ \end{aligned} \end{aligned}$$

(19)

The first two Theorems are proposed to achieve ${{r}_{rw}}(k)$ and ${{r}_{rf}}(k)$, respectively. The observer gain is obtained from the third theorem by means of a model matching approach.

Theorem 1

For any positive matrices $P={{P}^\mathrm{T}}=\hbox {diag}({{P}_{11}},\,{{P}_{22}})>0,\,\,Q={{Q}^\mathrm{T}}>0$, and matrices $\tilde{R},\,\,\tilde{S},\,\,{{Z}^{*}}$ with appropriate dimensions, positive scalar $\varepsilon >0$ and ${{H}_{\infty }}$ gain $\lambda >0$ that satisfies (19), if the following LMI is satisfied:

$$\begin{aligned} \begin{aligned} \left[ \begin{matrix} {{\varPsi }_{11}} &{} 0 &{} 0 &{} {{\varPsi }_{14}} &{} {{\left( \tilde{A}_{p}^{*} \right) }^\mathrm{T}} &{} {{{\tilde{C}}}^\mathrm{T}}{{Z}^{*}} &{} \bar{\beta }{{\left( \tilde{A}_{P\alpha }^{*} \right) }^\mathrm{T}} &{} \bar{\beta }\tilde{C}_{\alpha }^\mathrm{T}{{Z}^{*}} \\ * &{} -Q &{} 0 &{} 0 &{} \tilde{A}_{h}^\mathrm{T}P &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\lambda I &{} 0 &{} {{\left( \tilde{M}_{P1}^{*} \right) }^\mathrm{T}} &{} \tilde{M}_{2}^\mathrm{T}{{Z}^{*}} &{} 0 &{} 0 \\ * &{} * &{} * &{} -\varepsilon I &{} {{{\tilde{N}}}^\mathrm{T}}P &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} -P &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} -{{Z}^{*}} &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} -P &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} -{{Z}^{*}} \\ \end{matrix} \right] <0 \end{aligned} \end{aligned}$$

(20)

where

$$\begin{aligned} \begin{aligned}&{{\varPsi }_{11}}=-P+({{\tau }_{M}}-{{\tau }_{m}}+1)Q-\varepsilon \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2} \\&{{\varPsi }_{14}}= \varepsilon \frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2}\\&\tilde{A}_{p}^{*}=\left[ \begin{matrix} {{P}_{11}}A &{} 0 \\ \bar{\alpha }\tilde{R}C &{} {\tilde{S}} \\ \end{matrix} \right] ,\,\,\,\tilde{A}_{p\alpha }^{*}=\left[ \begin{matrix} 0 &{} 0 \\ \tilde{R}C &{} 0 \\ \end{matrix} \right] ,\,\,\,\tilde{M}_{p1}^{*}=\left[ \begin{matrix} {{P}_{11}}{{M}_{1}} \\ \tilde{R}{{M}_{2}} \\ \end{matrix} \right] , \end{aligned} \end{aligned}$$

system (21) is asymptotically stable,

$$\begin{aligned} \begin{aligned} {{\eta }_{rw}}(k+1)&={{{\tilde{A}}}^{*}}{{\eta }_{rw}}(k)+\left( \alpha (k)-\bar{\alpha } \right) {{{\tilde{A}}}^{*}}_{\alpha }{{\eta }_{rw}}(k)+{{{\tilde{A}}}_{h}}{{\eta }_{rw}}(k-h(k))\\&\quad +\tilde{N}g(H({{\eta }_{rw}}(k))+\tilde{M}_{1}^{*}w(k) \\ {{r}_{rw}}(k)&={{V}^{*}}\tilde{C}{{\eta }_{rw}}(k)+\left( \alpha (k)-\bar{\alpha } \right) {{V}^{*}}{{{\tilde{C}}}_{\alpha }}{{\eta }_{rw}}(k)+{{V}^{*}}{{{\tilde{M}}}_{2}}w(k) \end{aligned} \end{aligned}$$

(21)

Then, the observer gain is achieved by:

$$\begin{aligned} \begin{aligned} B_{c}^{*}={{\left( {{P}_{22}} \right) }^{-1}}\tilde{R},\,A_{c}^{*}\,={{\left( {{P}_{22}} \right) }^{-1}}\tilde{S},\,\,{{V}^{*}}={{\left( {{Z}^{*}} \right) }^{1/2}} \end{aligned} \end{aligned}$$

Proof

Consider the following Lyapunov–Krasovskii (LK) functional:

$$\begin{aligned} \begin{aligned} V(k)=\eta _{rw}^\mathrm{T}(k)P\,{{\eta }_{rw}}(k)+\sum \limits _{i=k-\tau (k)}^{k-1}{\eta _{rw}^\mathrm{T}(i)Q{{\eta }_{rw}}(i)}\, +\sum \limits _{j=-{{\tau }_{M}}+1}^{-{{\tau }_{m}}}{\,\,\sum \limits _{i=k+j}^{k-1}{\eta _{rw}^\mathrm{T}(i)Q\,{{\eta }_{rw}}(i)}} \end{aligned} \end{aligned}$$

(22)

and the following criterion:

$$\begin{aligned} \begin{aligned} J_{\infty }^{l}=\sum \limits _{k=0}^{l-1}{\left( r_{rw}^\mathrm{T}(k){{r}_{rw}}(k)-\lambda {{w}^\mathrm{T}}(k)w(k) \right) } \end{aligned} \end{aligned}$$

(23)

where l is an arbitrary positive integer. For any initial condition ${{\eta }_{rw}}(0)=0$, then:

$$\begin{aligned} \begin{aligned} J_{\infty }^{l}=\sum \limits _{k=0}^{l-1}{\left( r_{rw}^\mathrm{T}(k){{r}_{rw}}(k)-\lambda {{w}^\mathrm{T}}(k)w(k)-\Delta V(k) \right) }+V(k) \end{aligned} \end{aligned}$$

(24)

With attention to the LK functional (22) and the inequality (9) for the nonlinear term, the system (21) is stable with the ${{H}_{\infty }}$ performance, if:

$$\begin{aligned} E[&\Delta V(k)]<E\left[ (r_{rw}^\mathrm{T}(k){{r}_{rw}}(k))-\lambda {{w}^\mathrm{T}}(k)w(k) \right. \nonumber \\&+\left. \eta _{rw}^\mathrm{T}(k+1)P\,{{\eta }_{rw}}(k+1) \right] \nonumber \\&-\eta _{rw}^\mathrm{T}(k)P {{\eta }_{rw}}(k)+({{\tau }_{M}}-{{\tau }_{m}}+1)\eta _{rw}^\mathrm{T}(k)Q\,{{\eta }_{rw}}(k) \nonumber \\&-\eta _{rw}^\mathrm{T}(k-\tau (k))Q{{\eta }_{rw}}(k-\tau (k))\nonumber \\&-\varepsilon {{\left[ \begin{array}{c} {{\eta }_{rw}}(k) \\ g(H{{\eta }_{rw}}(k)) \\ \end{array} \right] }^\mathrm{T}}\left[ \begin{array}{cc} \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2} &{} -\frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2} \\ -\frac{\tilde{S}_{1}^{{}}+\tilde{S}_{2}^{{}}}{2} &{} I \\ \end{array} \right] \left[ \begin{array}{c} {{\eta }_{rw}}(k) \\ g(H{{\eta }_{rw}}(k)) \\ \end{array} \right] <0 \end{aligned}$$

(25)

By the substituting system (21) into Eq. (25), then:

$$\begin{aligned}&{{\left( {{V}^{*}}\tilde{C}{{\eta }_{rw}}(k)+{{V}^{*}}{{\tilde{M}}_{2}}w(k) \right) }^\mathrm{T}}\times \,\left( {{V}^{*}}\tilde{C}{{\eta }_{rw}}(k)+{{V}^{*}}{{\tilde{M}}_{2}}w(k) \right) -\lambda {{\omega }^\mathrm{T}}(k)\omega (k)\nonumber \\&\quad +\left( {{{\tilde{A}}}^{*}}{{\eta }_{rw}}(k)+{{{\tilde{A}}}_{h}}{{\eta }_{rw}}(k-h(k)) \right. {{\left. +\tilde{N}g(H{{\eta }_{rw}}(k))+\tilde{M}_{1}^{*}w(k) \right) }^\mathrm{T}}P\nonumber \\&\quad \left( {{{\tilde{A}}}^{*}}{{\eta }_{rw}}(k)+{{{\tilde{A}}}_{h}}{{\eta }_{rw}}(k-h(k))\right. \nonumber \\&\quad \left. +\tilde{N}g(H{{\eta }_{rw}}(k))+\tilde{M}_{1}^{*}w(k) \right) +({{\tau }_{M}}-{{\tau }_{m}}+1)\eta _{rw}^\mathrm{T}(k)Q{{\eta }_{rw}}(k)\nonumber \\&\quad -\eta _{rw}^\mathrm{T}(k-\tau (k))Q{{\eta }_{rw}}(k-\tau (k)) +{{\bar{\beta }}^{2}}\eta _{rw}^\mathrm{T}(k){{\left( {{{\tilde{C}}}_{\alpha }} \right) }^\mathrm{T}}{{Z}^{*}}\left( {{{\tilde{C}}}_{\alpha }} \right) {{\eta }_{rw}}(k)\nonumber \\&\quad +{{{\bar{\beta }}}^{2}}\eta _{rw}^\mathrm{T}(k){{\left( {{{\tilde{A}}}^{*}}_{\alpha } \right) }^\mathrm{T}}P\left( {{{\tilde{A}}}^{*}}_{\alpha } \right) {{\eta }_{rw}}(k) -\varepsilon {{\left[ \begin{array}{c} {{\eta }_{rw}}(k) \\ g(H{{\eta }_{rw}}(k)) \\ \end{array} \right] }^\mathrm{T}}\left[ \begin{array}{cc} \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2} &{} -\frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2} \\ -\frac{\tilde{S}_{1}^{{}}+\tilde{S}_{2}^{{}}}{2} &{} I \\ \end{array} \right] \nonumber \\&\quad \left[ \begin{array}{c} {{\eta }_{rw}}(k) \\ g(H{{\eta }_{rw}}(k)) \\ \end{array} \right] <0 \end{aligned}$$

(26)

Now, consider augmented matrix $\psi (k)=\Big [ \begin{matrix} \eta _{rw}^\mathrm{T}(k)&\eta _{rw}^\mathrm{T}(k-\tau (k))&{{w}^\mathrm{T}}(k)\end{matrix} \begin{matrix}{{g}^\mathrm{T}}(H({{\eta }_{rw}}(k)) \\ \end{matrix} \Big ]$, Eq. (26) can be reformulated as:

$$\begin{aligned} \begin{aligned} {{\psi }^\mathrm{T}}(k) \varXi \psi (k)<0 \end{aligned} \end{aligned}$$

(27)

where:

$$\begin{aligned} \varXi =&\left[ \begin{matrix} {{\varXi }_{11}} &{} {{\varXi }_{12}} &{}{{\varXi }_{13}} &{} {{\left( {{{\tilde{A}}}^{*}} \right) }^\mathrm{T}}P\tilde{N}+\varepsilon \frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2} \\ * &{} {{\varXi }_{22}} &{} \tilde{A}_{h}^\mathrm{T}P{{{\tilde{M}}}^{*}_{1}} &{} \tilde{A}_{h}^\mathrm{T}P\tilde{N} \\ * &{} * &{} {{\varXi }_{33}} &{} {{\left( \tilde{M}_{1}^{*} \right) }^\mathrm{T}}P\tilde{N} \\ * &{} * &{} * &{} {{\varXi }_{44}} \\ \end{matrix} \right] \\ {{\varXi }_{11}}=&-P+({{\tau }_{M}}-{{\tau }_{m}}+1)Q+{{\left( {{{\tilde{A}}}^{*}} \right) }^\mathrm{T}}P{{{\tilde{A}}}^{*}}+{{{\bar{\beta }}}^{2}}{{\left( \tilde{A}_{\alpha }^{*} \right) }^\mathrm{T}}P\tilde{A}_{\alpha }^{*}\\&-\varepsilon \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2}+{{{\tilde{C}}}^\mathrm{T}}{{Z}^{*}}\tilde{C}+{{{\bar{\beta }}}^{2}}\left( \tilde{C}_{\alpha }^{{}} \right) {{Z}^{*}}\tilde{C}_{\alpha }^{{}}\\ {{\varXi }_{12}}=&\,{{\left( {{{\tilde{A}}}^{*}} \right) }^\mathrm{T}}P{{{\tilde{A}}}_{h}}; {{\varXi }_{13}}=\, {{{\tilde{C}}}^\mathrm{T}}{{Z}^{*}}{{{\tilde{M}}}_{2}}+{{\left( {{{\tilde{A}}}^{*}} \right) }^\mathrm{T}}P\tilde{M}_{1}^{*}\\ {{\varXi }_{22}}=&-Q+\tilde{A}_{h}^\mathrm{T}P{{{\tilde{A}}}_{h}}; {{\varXi }_{33}}=-\lambda I+\tilde{M}_{2}^\mathrm{T}{{Z}^{*}}{{{\tilde{M}}}_{2}}+{{\left( \tilde{M}_{1}^{*} \right) }^\mathrm{T}}P{{{\tilde{M}^{*}}}_{1}}\\ {{\varXi }_{44}}=&\,{{{\tilde{N}}}^\mathrm{T}}P\tilde{N}-\varepsilon I \end{aligned}$$

The system (21) is stable if $\varXi <0$. Now using the Schur complement, and defining:

$$\begin{aligned} \begin{aligned}&{{Z}^{*}}={{\left( {{V}^{*}} \right) }^\mathrm{T}}{{V}^{*}},\,\,P=\hbox {diag}({{P}_{11}},\,{{P}_{22}}), \\&\tilde{R}={{P}_{22}}B_{c}^{*},\,\,\,\tilde{S}={{P}_{22}}A_{c}^{*}, \\&\tilde{A}_{p}^{*}=P{{{\tilde{A}}}^{*}},\,\,\tilde{A}_{p\alpha }^{*}=P{{{\tilde{A}}}_{\alpha }}^{*},\,\,\tilde{M}_{p1}^{*}=P{{{\tilde{M}^{*}}}_{1}} \end{aligned} \end{aligned}$$

(28)

to overcome the nonlinear terms, the LMI (20) can be obtained. $\square$

Theorem 2

For any positive matrices $P={{P}^\mathrm{T}}=\hbox {diag}({{P}_{11}}\,{{P}_{22}})>0,\,\,Q={{Q}^\mathrm{T}}>0$, matrices $\tilde{R},\,\,\tilde{S},\,\,{{Z}^{*}}$ with appropriate dimensions, positive scalars $\varepsilon ,\,\,\delta ,\,\,e>0$ and the ${{H}_{-}}$ gain $\gamma >0$ that satisfies (19), if the following LMI satisfied:

$$\begin{aligned} \begin{aligned} \left[ \begin{matrix} {{\varLambda }_{11}} &{} 0 &{} {\varLambda }_{13} &{} \varepsilon \frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2} &{} {{\left( \tilde{A}_{p}^{*} \right) }^\mathrm{T}} &{} \bar{\beta }{{\left( \tilde{A}_{P\alpha }^{*} \right) }^\mathrm{T}} \\ * &{} {{\varLambda }_{22}} &{} 0 &{} 0 &{} \tilde{A}_{h}^\mathrm{T}P &{} 0 \\ * &{} * &{} {{\varLambda }_{33}} &{} 0 &{} {{\left( \tilde{F}_{P1}^{*} \right) }^\mathrm{T}} &{} 0 \\ * &{} * &{} * &{} -\varepsilon I &{} {{{\tilde{N}}}^\mathrm{T}}P &{} 0 \\ * &{} * &{} * &{} * &{} -P &{} 0 \\ * &{} * &{} * &{} * &{} * &{} -P \\ \end{matrix} \right] <0 \end{aligned} \end{aligned}$$

(29)

where

$$\begin{aligned} \begin{aligned}&{{\varLambda }_{11}}=-P+({{\tau }_{M}}-{{\tau }_{m}}+1)Q-\varepsilon \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2}-{{{\tilde{C}}}^\mathrm{T}}{{Z}^{*}}\tilde{C}-{{{\bar{\beta }}}^{2}}\tilde{C}_{\alpha }^\mathrm{T}{{Z}^{*}}\tilde{C}_{\alpha }^{{}}+I+\delta I \\&{\varLambda }_{13} = -{{{\tilde{C}}}^\mathrm{T}}{{Z}^{*}}{{{\tilde{M}}}_{2}},\\&{{\varLambda }_{22}}= -Q+I+\delta I , {{\varLambda }_{33}}=\gamma I-\tilde{F}_{2}^\mathrm{T}{{Z}^{*}}{{{\tilde{F}}}_{2}}-{{e}^{2}}\delta I\\&\tilde{A}_{p}^{*}=\left[ \begin{matrix} {{P}_{11}}A &{} 0 \\ \bar{\alpha }\tilde{R}C &{} {\tilde{S}} \\ \end{matrix} \right] ,\,\,\,\tilde{A}_{p\alpha }^{*}=\left[ \begin{matrix} 0 &{} 0 \\ \tilde{R}C &{} 0 \\ \end{matrix} \right] ,\,\,\,\tilde{F}_{p1}^{*}=\left[ \begin{matrix} {{P}_{11}}{{F}_{1}} \\ \tilde{R}{{F}_{2}} \\ \end{matrix} \right] \end{aligned} \end{aligned}$$

system (30) is asymptotically stable:

$$\begin{aligned} \begin{aligned} {{\eta }_{rf}}(k+1)&={{{\tilde{A}}}^{*}}{{\eta }_{rf}}(k)+\left( \alpha (k)-\bar{\alpha } \right) {{{\tilde{A}}}^{*}}_{\alpha }{{\eta }_{rf}}(k) +{{{\tilde{A}}}_{h}}{{\eta }_{rf}}(k-h(k))+\tilde{N}g({{x}_{rf}}(k)) \\&\quad +\tilde{F}_{1}^{*}f(k)\\ {{r}_{rf}}(k)&= {{V}^{*}} \tilde{C}{{\eta }_{rf}}(k)+\left( \alpha (k)-\bar{\alpha } \right) {{V}^{*}}{{{\tilde{C}}}_{\alpha }}{{\eta }_{rf}}(k)+{{V}^{*}}{{{\tilde{F}}}_{2}}f(k) \end{aligned} \end{aligned}$$

(30)

and the observer gain can be achieved by:

$$\begin{aligned} \begin{aligned} B_{c}^{*}={{\left( {{P}_{22}} \right) }^{-1}}\tilde{R},\,A_{c}^{*}\,={{\left( {{P}_{22}} \right) }^{-1}}\tilde{S},\,\,{{V}^{*}}={{\left( {{Z}^{*}} \right) }^{1/2}} \end{aligned} \end{aligned}$$

Proof

Consider the following Lyapunov–Krasovskii functional:

$$\begin{aligned} \begin{aligned} V(k)=&\,\eta _{rf}^\mathrm{T}(k)P\,{{\eta }_{rf}}+\sum \limits _{i=k-\tau (k)}^{k-1}{\eta _{rf}^\mathrm{T}(i)Q{{\eta }_{rf}}(i)}\\&+\sum \limits _{j=-{{\tau }_{M}}+1}^{-{{\tau }_{m}}}{\,\,\sum \limits _{i=k+j}^{k-1}{\eta _{rf}^\mathrm{T}(i)Q\,{{\eta }_{rf}}(i)}} \end{aligned} \end{aligned}$$

(31)

and the following criterion:

$$\begin{aligned} \begin{aligned} J_{-}^{l}=\sum \limits _{k=0}^{l-1}{\left( r_{rf}^\mathrm{T}(k){{r}_{rf}}(k)-\gamma {{f}^\mathrm{T}}(k)f(k) \right) } \end{aligned} \end{aligned}$$

(32)

where l is an arbitrary positive integer. For any initial condition ${{\eta }_{rf}}(0)=0$, Eq. (32) can be rewritten as:

$$\begin{aligned} \begin{aligned} J_{-}^{l}=\sum \limits _{k=0}^{l-1}{\left( r_{rf}^\mathrm{T}(k){{r}_{rf}}(k)-\gamma {{f}^\mathrm{T}}(k)f(k)-\Delta V(k) \right) }+V(k) \end{aligned} \end{aligned}$$

(33)

With attention to LK functional (31) and inequality (9) for the nonlinear term, system (30) is stable with the ${{H}_{-}}$ performance, if:

$$\begin{aligned}&E\{\Delta V(k)\}<E\left\{ - \right. r_{rf}^\mathrm{T}(k){{r}_{rf}}(k)+\gamma {{f}^\mathrm{T}}(k)f(k) \nonumber \\&\quad +\eta _{rf}^\mathrm{T}(k+1)P{{\eta }_{rf}}(k+1)-\eta _{rf}^\mathrm{T}(k)P{{\eta }_{rf}}(k) \nonumber \\&\quad \left. \eta _{rf}^\mathrm{T}(k+\tau (k))Q{{\eta }_{rf}}(k+\tau (k)) \right\} \nonumber \\&\quad -\gamma {{\omega }^\mathrm{T}}(k)\omega (k)+\left( {{{\tilde{A}}}^{*}}{{\eta }_{rw}}(k)+{{{\tilde{A}}}_{h}}{{\eta }_{rw}}(k-h(k)) \right. \nonumber \\&\quad {{\left. +\tilde{N}g(H{{\eta }_{rw}}(k))+\tilde{M}_{1}^{*}w(k) \right) }^\mathrm{T}}P\left( {{{\tilde{A}}}^{*}}{{\eta }_{rw}}(k) \right. \nonumber \\&\quad \left. +{{{\tilde{A}}}_{h}}{{\eta }_{rw}}(k-h(k))+\tilde{N}g(H{{\eta }_{rw}}(k))+\tilde{M}_{1}^{*}w(k) \right) \nonumber \\&\quad +({{\tau }_{M}}-{{\tau }_{m}}+1)\eta _{rf}^\mathrm{T}(k)Q{{\eta }_{rf}}(k)\nonumber \\&\quad -\varepsilon {{\left[ \begin{array}{c} {{\eta }_{rf}}(k) \\ g(H{{\eta }_{rf}}(k)) \\ \end{array} \right] }^\mathrm{T}} \left[ \begin{array}{c} \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2} \\ -\frac{{{{\tilde{S}}}_{1}}+{{{\tilde{S}}}_{2}}}{2} \\ \end{array} \right. \left. \begin{array}{c} -\frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2} \\ I \\ \end{array} \right] \left[ \begin{array}{c} {{\eta }_{rf}}(k) \\ g(H{{\eta }_{rf}}(k)) \\ \end{array} \right] <0 \end{aligned}$$

(34)

By substituting system (30) into (34), we have:

$$\begin{aligned}&-{{\left( {{V}^{*}}\tilde{C}{{\eta }_{rf}}(k)+{{V}^{*}}{{{\tilde{F}}}_{2}}f(k) \right) }^\mathrm{T}}\,\left( {{V}^{*}}\tilde{C}{{\eta }_{rf}}(k)+{{V}^{*}}{{{\tilde{F}}}_{2}}f(k) \right) \nonumber \\&\quad +\gamma {{f}^\mathrm{T}}(k)f(k)+\left( {{{\tilde{A}}}^{*}}{{\eta }_{rf}}(k)+{{{\tilde{A}}}_{h}}{{\eta }_{rf}}(k-h(k)) \right. \nonumber \\&\quad \left. +\tilde{N}g({{x}_{rf}}(k))+\tilde{F}_{1}^{*}f(k) \right) P \left( {{{\tilde{A}}}^{*}}{{\eta }_{rf}}(k)+{{{\tilde{A}}}_{h}}{{\eta }_{rf}}(k-h(k))\right. \nonumber \\&\quad \left. +\tilde{N}g({{x}_{rf}}(k))+\tilde{F}_{1}^{*}f(k) \right) \nonumber \\&\quad -\eta _{rf}^\mathrm{T}(k)P\,{{\eta }_{rf}}(k)\,({{\tau }_{M}}-{{\tau }_{m}}+1)\eta _{rf}^\mathrm{T}(k)Q\,{{\eta }_{rf}}(k)\nonumber \\&\quad -\eta _{rf}^\mathrm{T}(k-\tau (k))Q{{\eta }_{rf}}(k-\tau (k)) \\&\quad -\eta _{rf}^\mathrm{T}(k){{{\bar{\beta }}}^{2}}{{\left( {{{\tilde{C}}}_{\alpha }} \right) }^\mathrm{T}}{{Z}^{*}}\left( {{{\tilde{C}}}_{\alpha }} \right) \,{{\eta }_{rf}}(k)\nonumber \\&\quad +\eta _{rf}^\mathrm{T}(k){{{\bar{\beta }}}^{2}}{{\left( {{{\tilde{A}}}^{*}}_{\alpha } \right) }^\mathrm{T}}P\left( {{{\tilde{A}}}^{*}}_{\alpha } \right) \,{{\eta }_{rf}}(k)\nonumber \\&\quad \,-\varepsilon {{\left[ \begin{array}{c} {{\eta }_{rf}}(k) \nonumber \\ g(H{{\eta }_{rf}}(k))\nonumber \\ \end{array} \right] }^\mathrm{T}}\left[ \begin{array}{cc} \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2} &{} -\frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2} \\ -\frac{\tilde{S}_{1}^{{}}+\tilde{S}_{2}^{{}}}{2} &{} I \\ \end{array} \right] \left[ \begin{array}{c} {{\eta }_{rf}}(k) \\ g(H{{\eta }_{rf}}(k)) \\ \end{array} \right] <0\nonumber \end{aligned}$$

(35)

Consider the augmented vector $\chi (k)=\Big [ \begin{matrix} \eta _{rf}^\mathrm{T}(k)&\eta _{rf}^\mathrm{T}(k-\tau (k))&{{f}^\mathrm{T}}(k)\end{matrix} \begin{matrix} {{g}^\mathrm{T}}(H({{\eta }_{rf}}(k)) \\ \end{matrix} \Big ]$, then:

$$\begin{aligned} \begin{aligned} {{\chi }^\mathrm{T}}(k)\varOmega \chi (k)<0 \end{aligned} \end{aligned}$$

(36)

where:

$$\begin{aligned} \varOmega =&\left[ \begin{matrix} {\varOmega }_{11} &{} {{\left( {{{\tilde{A}}}^{*}} \right) }^\mathrm{T}}P{{{\tilde{A}}}_{h}} &{} {\varOmega }_{13} &{} {\varOmega }_{14} \\ * &{} {\varOmega }_{22} &{} \tilde{A}_{h}^\mathrm{T}P{{{\tilde{M}}}_{1}} &{} \tilde{A}_{h}^\mathrm{T}P\tilde{N} \\ * &{} * &{} {\varOmega }_{33} &{} {{\left( \tilde{F}_{1}^{*} \right) }^\mathrm{T}}P\tilde{N} \\ * &{} * &{} * &{} -\varepsilon I+{{{\tilde{N}}}^\mathrm{T}}P\tilde{N} \\ \end{matrix} \right] \\ {{\varOmega }_{11}}=&-P+({{\tau }_{M}}-{{\tau }_{m}}+1)Q+{{\left( {{{\tilde{A}}}^{*}} \right) }^\mathrm{T}}P{{{\tilde{A}}}^{*}}+{{{\bar{\beta }}}^{2}}\left( \tilde{A}_{\alpha }^{*} \right) P\tilde{A}_{\alpha }^{*} \\&-\varepsilon \frac{\tilde{S}_{1}^\mathrm{T}{{{\tilde{S}}}_{2}}+\tilde{S}_{2}^\mathrm{T}{{{\tilde{S}}}_{1}}}{2}-{{{\tilde{C}}}^\mathrm{T}}{{Z}^{*}}\tilde{C}-{{{\bar{\beta }}}^{2}}\tilde{C}_{\alpha }^\mathrm{T}{{Z}^{*}}\tilde{C}_{\alpha }^{{}}\\ {\varOmega }_{13}=&-{{{\tilde{C}}}^\mathrm{T}}{{Z}^{*}}{{{\tilde{M}}}_{2}}+{{\left( {{{\tilde{A}}}^{*}} \right) }^\mathrm{T}}P\tilde{F}_{1}^{*} , {\varOmega }_{14}={{\left( {{{\tilde{A}}}^{*}} \right) }^\mathrm{T}}P\tilde{N}+\varepsilon \frac{\tilde{S}_{1}^\mathrm{T}+\tilde{S}_{2}^\mathrm{T}}{2}\\ {\varOmega }_{22}=&-Q+\tilde{A}_{h}^\mathrm{T}P{{{\tilde{A}}}_{h}}, {\varOmega }_{33}=\gamma I-\tilde{F}_{2}^\mathrm{T}{{Z}^{*}}{{{\tilde{F}}}_{2}}+{{\left( \tilde{F}_{1}^{*} \right) }^\mathrm{T}}P\tilde{F}_{1}^{*} \end{aligned}$$

System (30) is stable and satisfies the ${{H}_{-}}$ performance index, if $\varOmega <0$. Moreover, it is clear that in $\varOmega$ the value $\gamma$ depends on $-\tilde{F}_{2}^\mathrm{T}{{Z}^{*}}{{\tilde{F}}_{2}}+{{\left( \tilde{F}_{1}^{*} \right) }^\mathrm{T}}P\tilde{F}_{1}^{*}$; therefore, one can use S-procedure Lemma to reduce the dependence of $\gamma$. Consequently, the following S-procedure equations are used:

$$\begin{aligned} \begin{aligned}&||{{\eta }_{rf}}(k)|{{|}^{2}}+{{\left\| {{\eta }_{rf}}(k-h(k)) \right\| }^{2}}\ge 0 \\&||{{\eta }_{rf}}(k)|{{|}^{2}}+{{\left\| {{\eta }_{rf}}(k-h(k)) \right\| }^{2}}\ge {{e}^{2}}{{\left\| \bar{f}(k) \right\| }^{2}} \end{aligned} \end{aligned}$$

(37)

Now, using the S-procedure Lemma and the Schur complement, LMI (29) can be obtained. The proof of the second Theorem is completed. $\square$

Then, our aim is to find reference residual that is much sensitive to fault and insensitive to disturbance. Therefore, there is a need for the simultaneous use of the both Theorems.

Remark 1

Our aim is to obtain reference residual to reach $\inf \frac{\lambda }{\gamma }$, for this purpose, first $\lambda$ and $\gamma$ are initialized, in the next step, $\,\gamma$ is increased and $\,\lambda$ is decreased, as much as possible, while Theorem 1 and Theorem 2 are feasible.

Remark 2

Our aim is to select $\lambda$ as small as possible and $\gamma$ as large as possible. This might lead to a big value for ${{Z}^{*}}$. Therefore, we can limit the ${{Z}^{*}}$ by selecting a design parameter ${{\mu }_{Z}}$ as follows:

$$\begin{aligned} \begin{aligned} {{Z}^{*}}-{{\mu }_{Z}}I<0 \end{aligned} \end{aligned}$$

where ${{\mu }_{z}}$ is a positive scalar.

Using both theorems, we can obtain $A_{c}^{*},\,\,B_{c}^{*},$ and ${{V}^{*}}$. Now a model matching technique has been used to find the observer gain; therefore, in Theorem 3, the ${{H}_{\infty }}$ performance index (16) has been used to decrease the difference between the residual and the reference residual.

Theorem 3

System (12) is robust and asymptotically stable, which satisfies the ${{H}_{\infty }}$ performance index (16), if for any positive matrices $P={{P}^\mathrm{T}}=\hbox {diag}({{P}_{11}},\,{{P}_{22}},\,{{P}_{33}})>0,\,\,Q={{Q}^\mathrm{T}}>0$, matrices $\bar{S},\,\,\bar{R},\,\,V$ with appropriate dimensions, and positive scalars $\varepsilon ,\,v,\,\kappa >0$ the following LMI is satisfied:

$$\begin{aligned} \begin{aligned} \left[ \begin{matrix} \varGamma _{11} &{} 0 &{} 0 &{} \varGamma _{14} &{} {{{\bar{A}}}_{P}}^\mathrm{T} &{} {{{\bar{C}}}^\mathrm{T}} &{} \bar{\beta }\bar{A}_{P\alpha }^\mathrm{T} &{} \bar{\beta }\bar{C}_{\alpha }^\mathrm{T} &{} 0 \\ * &{} \varGamma _{22} &{} 0 &{} 0 &{} \bar{A}_{h}^\mathrm{T}P &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\kappa I &{} 0 &{} \bar{D}_{P1}^\mathrm{T} &{} \bar{D}_{2}^\mathrm{T} &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} -\varepsilon I &{} {{{\bar{N}}}^\mathrm{T}}P &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} -P &{} 0 &{} 0 &{} 0 &{} P\bar{L} \\ * &{} * &{} * &{} * &{} * &{} -I &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} -P &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} -I &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} -v \\ \end{matrix} \right] <0 \end{aligned} \end{aligned}$$

(38)

where:

$$\begin{aligned}&\varGamma _{11} =-P+({{\tau }_{M}}-{{\tau }_{m}}+1)Q-\varepsilon \frac{\bar{S}_{1}^\mathrm{T}{{{\bar{S}}}_{2}}+\bar{S}_{2}^\mathrm{T}{{{\bar{S}}}_{1}}}{2}+\bar{E}_{1}^\mathrm{T}v{{{\bar{E}}}_{1}}\\&\varGamma _{14}=\varepsilon \frac{\bar{S}_{1}^\mathrm{T}+\bar{S}_{2}^\mathrm{T}}{2}, \varGamma _{22} = -Q+\bar{E}_{2}^\mathrm{T}v{{{\bar{E}}}_{2}}\\&{{{\bar{A}}}_{p}}=\left[ \begin{matrix} {{P}_{11}}A &{} 0 &{} 0 \\ \bar{\alpha }{{P}_{22}}B_{c}^{*}C &{} {{P}_{22}}A_{c}^{*} &{} 0 \\ \bar{\alpha }\bar{R}C &{} 0 &{} {\bar{S}} \\ \end{matrix} \right] ,\,{{{\bar{A}}}_{p\alpha }}=\left[ \begin{matrix} 0 &{} 0 &{} 0 \\ {{P}_{22}}B_{c}^{*}C &{} 0 &{} 0 \\ \bar{R}C &{} 0 &{} 0 \\ \end{matrix} \right] , \\ {}&{{{\bar{D}}}_{p1}}=\left[ \begin{matrix} {{P}_{11}}{{F}_{1}} &{} {{P}_{11}}{{M}_{1}} \\ {{P}_{22}}B_{c}^{*}{{F}_{1}} &{} {{P}_{22}}B_{c}^{*}{{M}_{1}} \\ \bar{R}{{F}_{1}} &{} \bar{R}{{M}_{1}} \\ \end{matrix} \right] , \end{aligned}$$

Thus, the observer gain can be obtained by:

$$\begin{aligned} {{A}_{c}}={{\left( {{P}_{33}} \right) }^{-1}}\bar{S},\,\,\,{{B}_{c}}={{\left( {{P}_{33}} \right) }^{-1}}\bar{R} \end{aligned}$$

Proof

Consider the following Lyapunov–Krasovskii functional:

$$\begin{aligned} \begin{aligned} V(k)&={{\xi }^\mathrm{T}}(k)P\xi (k)+\sum \limits _{i=k-\tau (k)}^{k-1}{{{\xi }^\mathrm{T}}(i)Q\,\xi (i)}\,\\&\quad +\sum \limits _{j=-{{\tau }_{M}}+1}^{-{{\tau }_{m}}}{\,\,\sum \limits _{i=k+j}^{k-1}{{{\xi }^\mathrm{T}}(i)Q\,\xi (i)}} \end{aligned} \end{aligned}$$

(39)

and the following criterion:

$$\begin{aligned} \begin{aligned} J_{\infty }^{l}=\sum \limits _{k=0}^{l-1}{\left( {{r}_{e}}^\mathrm{T}(k){{r}_{e}}(k)-\kappa {{d}^\mathrm{T}}(k)d(k) \right) } \end{aligned} \end{aligned}$$

(40)

where l is an arbitrary positive integer. For any initial condition $\xi (0)=0$, we have:

$$\begin{aligned} \begin{aligned} J_{\infty }^{l}=\sum \limits _{k=0}^{l-1}{\left( {{r}_{e}}^\mathrm{T}(k){{r}_{e}}(k)-\kappa {{d}^\mathrm{T}}(k)d(k)-\Delta V(k) \right) }+V(k) \end{aligned} \end{aligned}$$

(41)

With attention to LK functional (39) and inequality (15) for the nonlinear term, system (12) is stable with the ${{H}_{\infty }}$ performance index, if:

$$\begin{aligned}&E\left\{ {{r}_{e}}^\mathrm{T}(k){{r}_{e}}(k)+{{\xi }^\mathrm{T}}(k+1)P\,\xi (k+1) \right\} -{{\xi }^\mathrm{T}}(k)P\xi (k) \nonumber \\&\quad +({{\tau }_{M}}-{{\tau }_{m}}+1){{\xi }^\mathrm{T}}(k)Q\,\eta (k)\nonumber \\&\quad \,-{{\xi }^\mathrm{T}}(k-\tau (k))Q\xi (k-\tau (k))-\kappa {{d}^\mathrm{T}}(k)d(k)\, \nonumber \\&\quad -\varepsilon {{\left[ \begin{array}{c} \xi (k) \\ g(\bar{H}\xi (k)) \\ \end{array} \right] }^\mathrm{T}}\left[ \begin{array}{cc} \frac{\bar{S}_{1}^\mathrm{T}{{{\bar{S}}}_{2}}+\bar{S}_{2}^\mathrm{T}{{{\bar{S}}}_{1}}}{2} &{} -\frac{\bar{S}_{1}^\mathrm{T}+\bar{S}_{2}^\mathrm{T}}{2} \\ -\frac{\bar{S}_{1}^{{}}+\bar{S}_{2}^{{}}}{2} &{} I \\ \end{array} \right] \left[ \begin{array}{c} \xi (k) \\ g(\bar{H}\xi (k)) \\ \end{array} \right] <0 \end{aligned}$$

(42)

By substituting system (12) into Eq. (42), and considering an augmented matrix $\bar{\psi }(k)=\left[ {{\xi }^\mathrm{T}}(k) \right.$${{\left. \begin{matrix} {{\xi }^\mathrm{T}}(k-h(k)) &{} {{d}^\mathrm{T}}(k) &{} {{g}^\mathrm{T}}(\bar{H}\xi (k)) \\ \end{matrix} \right] }^\mathrm{T}}$, then:

$$\begin{aligned} \begin{aligned} {{\bar{\psi }}^\mathrm{T}}(k)\varPi \bar{\psi }(k)<0 \end{aligned} \end{aligned}$$

(43)

where:

$$\begin{aligned} \begin{aligned} \varPi =&\left[ \begin{matrix} {{\varPi }_{11}} &{} {{\varPi }_{12}} &{} {{\varPi }_{13}} &{} {{\varPi }_{14}} \\ * &{} {{\varPi }_{22}} &{} {{\varPi }_{23}} &{} {{\varPi }_{24}} \\ * &{} * &{} {{\varPi }_{33}} &{} \bar{D}_{1}^\mathrm{T}P\bar{N} \\ * &{} * &{} * &{} -\varepsilon I+{{{\bar{N}}}^\mathrm{T}}P\bar{N} \\ \end{matrix} \right] \\ {{\varPi }_{11}}=&-P+({{\tau }_{M}}-{{\tau }_{m}}+1)Q-\varepsilon \frac{\bar{S}_{1}^\mathrm{T}{{{\bar{S}}}_{2}}+\bar{S}_{2}^\mathrm{T}{{{\bar{S}}}_{1}}}{2}\\&+{{\left( \bar{A}+\Delta \bar{A} \right) }^\mathrm{T}}P\left( \bar{A}+\Delta \bar{A} \right) +{{{\bar{C}}}^\mathrm{T}}\bar{C}+{{{\bar{\beta }}}^{2}}\bar{C}_{\alpha }^\mathrm{T}{{{\bar{C}}}_{\alpha }}+{{{\bar{\beta }}}^{2}}\bar{A}_{\alpha }^\mathrm{T}P{{{\bar{A}}}_{\alpha }} \\ {{\varPi }_{12}}=&\,{{\left( \bar{A}+\Delta \bar{A} \right) }^\mathrm{T}}P\left( {{{\bar{A}}}_{h}}+\Delta {{{\bar{A}}}_{h}} \right) \\ {{\varPi }_{13}}=&\,{{{\bar{C}}}^\mathrm{T}}{{{\bar{D}}}_{2}}+{{\left( \bar{A}+\Delta \bar{A} \right) }^\mathrm{T}}P{{{\bar{D}}}_{1}}\\ {{\varPi }_{14}}=&\,{{\left( \bar{A}+\Delta \bar{A} \right) }^\mathrm{T}}P\bar{N}+\varepsilon \frac{\bar{S}_{1}^\mathrm{T}+\bar{S}_{2}^\mathrm{T}}{2}\\ {{\varPi }_{22}}=&\,-Q+{{\left( {{{\bar{A}}}_{h}}+\Delta {{{\bar{A}}}_{h}} \right) }^\mathrm{T}}P\left( {{{\bar{A}}}_{h}}+\Delta {{{\bar{A}}}_{h}} \right) \\ {{\varPi }_{23}}=&\,{{\left( {{{\bar{A}}}_{h}}+\Delta {{{\bar{A}}}_{h}} \right) }^\mathrm{T}}P{{{\bar{D}}}_{1}} \\ {{\varPi }_{24}}=&\,{{\left( {{{\bar{A}}}_{h}}+\Delta {{{\bar{A}}}_{h}} \right) }^\mathrm{T}}P\bar{N} \\ {{\varPi }_{33}}=&\,-\kappa +\bar{D}_{2}^\mathrm{T}{{{\bar{D}}}_{2}}+\bar{D}_{1}^\mathrm{T}P{{{\bar{D}}}_{1}} \end{aligned} \end{aligned}$$

System (12) is stable if $\varPi <0$. Now, Lemma 1 is used for uncertain terms, and the Schur complement is used to achieve a LMI. However, some slack matrices should be defined to overcome the nonlinear terms, as follows:

$$\begin{aligned} \begin{aligned}&P=\hbox {diag}\left( \begin{matrix} {{P}_{11}} &{} {{P}_{22}} &{} {{P}_{33}} \\ \end{matrix} \right) \\&\bar{S}={{P}_{33}}{{A}_{c}},\,\,\bar{R}={{P}_{33}}{{B}_{c}} \\&{{{\bar{A}}}_{p}}=P\bar{A},\,\,{{{\bar{A}}}_{p\alpha }}=P{{{\bar{A}}}_{\alpha }},\,\,{{{\bar{D}}}_{p1}}=P{{{\bar{D}}}_{1}} \end{aligned} \end{aligned}$$

(44)

Then, LMI (38) is obtained. The proof of the third Theorem is completed. $\square$

Remark 3

The observer gains obtained from Theorem 3 might be very small; therefore, one can define design parameters for the model matching section as follows:

$$\begin{aligned} \begin{aligned} {{P}_{33}}<{{\mu }_{P}}I,\,\,\,\bar{S}>{{\mu }_{S}}I \end{aligned} \end{aligned}$$

(45)

where ${{\mu }_{p}}$ and ${{\mu }_{s}}$ are positive scalars.

Remark 4

With the aim of the proposed method, the effect of fault in the residual signal is increased while the disturbance effect is minimized at the same time. Accordingly, in the residual evaluation signal the effect of fault is more clear, and therefore, the fault can be detected at the early stages. However, it should be noted that developed theorems present sufficient conditions, which may be difficult to obtain a feasible solution.

4 Numerical Example

Consider a class of nonlinear NCS represented by (1), in which:

$$\begin{aligned} \begin{aligned}&A=\left[ \begin{array}{cc} {0}{.6} &{} {0}{.2} \\ 0 &{} {0}{.7} \\ \end{array} \right] ,\,{{A}_{h}}=\left[ \begin{array}{cc} {0}{.03} &{} 0 \\ 0.{02} &{} {0}{.03} \\ \end{array} \right] {,}\,N=\left[ \begin{array}{cc} -0.1 &{} 0 \\ 0 &{} 0.1 \\ \end{array} \right] {,}\,\\&{{{M}}_{1}}=\left[ \begin{array}{c} {0}{.8} \\ {0}{.3} \\ \end{array} \right] ,\,{{{F}}_{1}}=\left[ \begin{array}{c} {-1} \\ {0}{.6} \\ \end{array} \right] C=\left[ \begin{array}{cc} {0}{.2} &{} {-0}{.1} \\ {0}{.3} &{} {-0}{.2} \\ \end{array} \right] ,\,{{{M}}_{2}} =\left[ \begin{array}{c} {0}{.6} \\ {0}{.7} \\ \end{array} \right] ,\\&{{{F}}_{2}}=\left[ \begin{array}{c} {-0}{.9} \\ {0}{.3} \\ \end{array} \right] ,\, L=\left[ \begin{array}{c} {0}{.1} \\ {0}{.2} \\ \end{array} \right] ,\,{{{E}}_{{1}}}=\left[ \begin{array}{cc} -0.1 &{} 0.1 \\ \end{array} \right] {,} \\&{{{E}}_{{2}}}=\left[ \begin{array}{cc} {0}{.2} &{} 0 \\ \end{array} \right] , {{\tau }_{M}}=2,\,{{\tau }_{m}}=1,\,F(k)=\,0.4\sin (\pi /6k). \end{aligned} \end{aligned}$$

The nonlinear term is considered as [25]:

$$\begin{aligned} \begin{aligned} g(x(k))=\left[ \begin{matrix} -0.1{{x}_{1}}(k)+0.15{{x}_{2}}(k)+\frac{0.1{{x}_{2}}(k)\sin ({{x}_{1}}(k))}{\sqrt{x_{1}^{2}(k)+x_{2}^{2}(k)+10}} \\ -0.05{{x}_{1}}(k)+0.05{{x}_{2}}(k) \end{matrix} \right] \end{aligned} \end{aligned}$$

With attention to equation (3), ${{S}_{1}},\,\,{{S}_{2}}$ is obtained as:

$$\begin{aligned} \begin{aligned} {{S}_{1}}=\left[ \begin{array}{cc} {-0}{.4} &{} 0 \\ {-0}{.2} &{} {-0}{.3} \\ \end{array} \right] ,\,\,{{S}_{2}}=\left[ \begin{array}{cc} {0}{.2} &{} {0}{.3} \\ {0}{.1} &{} {0}{.4} \\ \end{array} \right] \end{aligned} \end{aligned}$$

Data packet modeled as Bernoulli-distributed white sequences:

$$\begin{aligned} \begin{aligned} E\left\{ \alpha (k) \right\} = {\left\{ \begin{array}{ll} &{}0.8\alpha (k)=1 \\ &{} 0.2\alpha (k)=0 \end{array}\right. } \end{aligned} \end{aligned}$$

It is clear that $\bar{\alpha }=0.8$ and $\bar{\beta }=0.16$. As mentioned in the previous section, our aim is to obtain a minimum value for $\lambda ,\,\,e$ and a maximum value for $\gamma$ such that Theorems 1 and 2 are feasible. The best values for these parameters are obtained as follows:

$$\begin{aligned} \lambda =0.1,\,\,\gamma =10,\,\,e=2 \end{aligned}$$

where design parameter is ${{\lambda }_{z}}=37$. Obtained reference gain is used in Theorem 3 to achieve observer gain. Consider ${{H}_{\infty }}$ gain $\kappa =0.15$ and model matching designing parameter ${{\mu }_{P}}=50,\,\,{{\mu }_{S}}=1$; therefore, the observer gain is achieved as:

$$\begin{aligned} \begin{aligned}&{{A}_{c}}=\left[ \begin{array}{cc} {0}{.3565} &{} {0}{.0176} \\ {0}{.0175} &{} {0}{.3508} \\ \end{array} \right] ,\,\,{{B}_{c}}=\left[ \begin{array}{cc} {0}{.0073} &{} {-0}{.0044} \\ {-0}{.0043} &{} {0}{.0195} \\ \end{array} \right] ,\\&V=\left[ \begin{array}{cc} {4}{.2288} &{} {-2}{.7685} \\ {-2}{.7685} &{} {1}{.9421} \\ \end{array} \right] \end{aligned} \end{aligned}$$

Disturbance is assumed to be a random variable in interval [0, 0.75] for $1<k<100$, and also fault is an abrupt signal that occurs between 50 to 70, as follows:

$$\begin{aligned} \begin{aligned} f(k)= {\left\{ \begin{array}{ll} &{} 1,50<k<70 \\ &{} 0, \hbox {otherwise} \end{array}\right. } \end{aligned} \end{aligned}$$

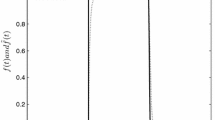
With the aim of designed observer, residual signal is computed. The results of the proposed observer are compared with the presented approach in [25]. If an abrupt fault occurs in the system, the response of residual signal considering the initial conditions ${x(0)}=[\pi {/8,0}]^{\mathrm{T}},\,\hat{x}(0)={{[0,0]}^\mathrm{T}}$ is illustrated in Fig. 2. It is clear that using the proposed approach the effect of fault is more clear in the residual signal. The threshold after 1000 Monte Carlo run is computed ${{J}_{\mathrm{th}}}{=}\,{6.8645}$. Residual evaluation signal is shown in Fig. 3. By comparing the residual evaluation signal with the threshold ${{J}_{\mathrm{th}}}$ in Fig. 3, it is clear that the fault can be detected in the first step. In other words, the proposed ${{H}_{-}}/{{H}_{\infty }}$ approach can make an earlier alarm by increasing the fault effect, while the disturbance effect is minimized in the residual signal.

Fig. 2

Residual signals of the proposed method and method of [25]

Fig. 3

Residual evaluation signal of the proposed method and method of [25]

5 Practical Example

In this section, a mass–spring system with two masses and two springs as explained in [24] is considered. In terms of nonlinear networked control system represented by (1), the parameters are obtained as follows:

$$\begin{aligned}&A=\left[ \begin{array}{cccc} {0.5172} &{} {0.2290}&{}{0.5316} &{} {0.0562}\\ {0.4017} &{} {0.5734}&{}{0.1123} &{} {0.452} \\ {-0.9509} &{} {0.4193}&{}{0.2524} &{} {0.1728}\\ {0.6658} &{} {-0.7781}&{}{0.3456} &{} {0.1281}\\ \end{array} \right] ,\, {{{M}}_{1}}=\left[ \begin{array}{c} {0.2663} \\ {0.2507} \\ {0.5878} \\ {0.5575} \\ \end{array} \right] ,\,\\&{{{F}}_{1}}=\left[ \begin{array}{c} {0.1} \\ {0.2} \\ {0.15} \\ {0.2} \\ \end{array} \right] N=\left[ \begin{array}{cccc} {-0.1} &{} {0}&{}{0} &{} {0}\\ {0} &{} {-0.085}&{}{0} &{} {0}\\ {0} &{} {0}&{}{0.125} &{} {0}\\ {0} &{} {0}&{}{0} &{} {-0.15} \end{array} \right] ,{{{M}}_{2}}=\left[ \begin{array}{c} {0.1} \\ {0.1} \\ {0.1} \\ \end{array} \right] ,\\&C=\left[ \begin{array}{ccc} {1} &{} {0} &{} {0} \\ {0} &{} {1}&{}{0} \\ {0}&{}{0} &{} {1} \\ \end{array} \right] ,\,{{{M}}_{2}}=\left[ \begin{array}{c} {0}{.1} \\ {0}{.1} \\ {0}{.1} \\ \end{array} \right] , {{{F}}_{2}}=\left[ \begin{array}{c} {0.2} \\ {-0.3} \\ {0.2} \\ \end{array} \right] .\, \end{aligned}$$

Suppose:

$$\begin{aligned} \begin{aligned}&L=\left[ \begin{array}{c} {0.1} \\ {0.2} \\ \end{array} \right] ,\,{{{E}}_{{1}}}=\left[ \begin{array}{cc} -0.1 &{} 0.1 \\ \end{array} \right] ,F(k)=\,0.4\sin (\pi /6k). \end{aligned} \end{aligned}$$

The nonlinear term is considered as:

$$\begin{aligned} \begin{aligned} g(x(k))=\left[ \begin{matrix} -0.7 {{x}_{1}}(k)+0.05{{x}_{2}}(k)+0.05{{x}_{3}}(k)\\ -0.05{{x}_{1}}(k)+0.85{{x}_{2}}(k)\\ -0.05{{x}_{1}}(k)-0.47{{x}_{2}}(k)+\frac{{{x}_{3}}(k)\sin ({{x}_{1}}(k))}{\sqrt{x_{1}^{2}(k)+x_{2}^{2}(k)+20}} \\ 0 \end{matrix} \right] \end{aligned} \end{aligned}$$

With attention to equation (3), ${{S}_{1}}$ and ${{S}_{2}}$ are obtained as:

$$\begin{aligned} \begin{aligned} {{S}_{1}}=\left[ \begin{array}{cccc} {-0.9} &{} 0 &{} 0.1&{}0\\ {-0.1} &{} {0.8}&{}0&{}0 \\ 0 &{} 0&{} {-0.75}&{}0 \\ 0&{} 0&{}0&{}0 \\ \end{array} \right] ,\,\,{{S}_{2}}=\left[ \begin{array}{cccc} {-0.5} &{}{0.1} &{} 0&{}0\\ 0 &{} {0.9}&{}0&{}0 \\ {-0.1} &{} 0&{} {-0.2}&{}0 \\ 0&{} 0&{}0&{}0 \\ \end{array} \right] \end{aligned} \end{aligned}$$

Here, data packet dropout is assumed to be a Bernoulli-distributed white sequences:

$$\begin{aligned} \begin{aligned} E\left\{ \alpha (k) \right\} = {\left\{ \begin{array}{ll} &{}0.9\alpha (k)=1 \\ &{} 0.1\alpha (k)=0 \end{array}\right. } \end{aligned} \end{aligned}$$

It is clear that $\bar{\alpha }=0.9$ and $\bar{\beta }=0.09$. As mentioned in the previous section, our aim is to obtain a minimum value for $\lambda$, and e, and a maximum value for $\gamma$ such that Theorems 1 and 2 are feasible. The best values for these parameters are obtained as follows:

$$\begin{aligned} \begin{aligned} \lambda =2,\,\,\gamma =6,\,\, e=4 \end{aligned} \end{aligned}$$

The design parameter is obtained ${{\lambda }_{z}}=37$. The obtained reference gain is used in Theorem 3 to achieve observer gain. Assume ${{H}_{\infty }}$ attenuation level $\kappa =0.25$ and model matching design parameters ${{\mu }_{P}}=50,\,\,{{\mu }_{S}}=1$, and therefore, the observer gain is achieved as:

$$\begin{aligned} \begin{aligned}&{{A}_{c}}=\left[ \begin{array}{cccc} {0.1078} &{} {0.0840} &{} {0.0855} &{} {0.0834} \\ {0.0705} &{} {0.0930} &{} {0.0725} &{} {0.0704} \\ {0.1370} &{} {0.1386} &{} {0.1557} &{} {0.1324} \\ {0.1902} &{} {0.1913} &{} {0.1885} &{} {0.2085} \\ \end{array} \right] , \,\,{{B}_{c}}=\left[ \begin{array}{ccc} {0.0239} &{} {-0.0011} &{} {0.0054} \\ {-0.0011} &{} {0.0227} &{} {0.0109} \\ {0.0017} &{} {0.0023} &{} {0.0244} \\ {0.0016} &{} {0.0014} &{} {-0.0052} \\ \end{array} \right] ,\\&V=\left[ \begin{array}{ccc} {2.1709} &{} {-1.4668}&{} {-0.4179} \\ {-1.4668} &{} {1.2980}&{} {0.3275} \\ {-0.4179} &{} {0.3275}&{} {0.6116} \\ \end{array} \right] \end{aligned} \end{aligned}$$

Disturbance is supposed to be a random variable in interval [0, 0.5] for $1<k<100$. Moreover, a fault with an abrupt behavior that occurs between 50 to 70 is considered as follows:

$$\begin{aligned} \begin{aligned} f(k)= {\left\{ \begin{array}{ll} &{} 1,50<k<70 \\ &{} 0, \hbox {otherwise} \end{array}\right. } \end{aligned} \end{aligned}$$

With the aim of designed observer, residual signal is computed. If an abrupt fault occurs in the system, the response of residual signal considering the initial conditions $x(0)= {[0,0,0,0]}^{\mathrm{T}},\,\hat{x}(0)={{[0,0,0,0]}^\mathrm{T}}$ is illustrated in Fig. 4. It is clear that the effect of fault appears in the residual signal. The threshold after 1000 Monte Carlo run is computed ${{J}_{\mathrm{th}}}=\,\,{0.5753}$. Residual evaluation signal is shown in Fig. 5. By comparing the residual evaluation signal with the predefined threshold ${{J}_{\mathrm{th}}}$ in Fig. 5, the fault can be clearly detected in the first steps. Accordingly, the proposed ${{H}_{-}}/{{H}_{\infty }}$ filter can detect faults in the incipient stages by increasing the fault effect and decreasing the disturbance effect in the residual signal. This ability introduces it as an appropriate approach for fault detection of nonlinear networked control systems.

Fig. 4

Residual signal

Fig. 5

Residual evaluation signal

6 Conclusions

In this paper, the problem of robust ${{H}_{-}}/{{H}_{\infty }}$ fault detection for nonlinear networked control systems with data packet dropout has been investigated. The sector-bounded condition is used to analyze the nonlinear terms. Data packet dropout, in data transmission, is considered as a Bernoulli-distributed white sequences. ${{H}_{-}}/{{H}_{\infty }}$ performance index is exploited to maximize the effect of fault, and minimize the effect of disturbance in the residual signal. One advantage of using Lyapunov–Krasovskii functional is that the results are developed as LMIs. Finally, the effectiveness of the proposed approach is studied using numerical and practical examples.

As a future work, delay and packet dropout can be modeled by Markov process, and the proposed approach can be developed for the Markovian jump system.