1 Introduction

Control systems utilizing a real-time network to exchange information among system components (sensors, actuators, controllers, etc.) are known as networked control systems (NCSs) [1, 2]. Owing to the advantages of quick and easy maintenance and low power consumption, NCSs have been applied widespread in manufacture plants, vehicles, aircraft, and so on [2–5]. Thus, numerous research results about NCSs are given in [6–12]. Regarding the data sampling method, it is noted that the time-driven mechanism is adopted in most of these works. In this paradigm, the sampled data are transmitted with a fixed rate, which is simplified for system analysis and implementation. However, once the adjacent transmission signals change marginally, it could lead to over-occupation of limited network bandwidth. To release the overloaded bandwidth, event-driven control has gained more and more attention and interests [13].

In event-driven communication mechanism, the signal transmission is determined by a predesigned-driven condition (also called event) instead of time. Consequently, this mechanism could mitigate the unnecessary data. As such, fruitful results based on different event-driven schemes are made in [5, 14–19]. Concretely speaking, in [14], a continuous triggered scheme is defined by calculating the error between the latest triggered state and the current state continuously. This manner is also used in output feedback systems [15, 16]. Nevertheless, this scheme needs a specialized hardware with a very high frequency to measure the system information. To cope with this deficiency, a discrete event-driven mechanism is developed in [5, 17]. With this mechanism, the system data are sampled periodically and the triggered condition is tested only at each sampling instant. Alternatively, by using the current system information to predict the next triggered time, the self-triggered scheme is proposed in [18, 19]. Based on the aforementioned mechanisms, most of them are focused on stability analysis and synthesis [15, 17, 20, 21], network-induced time delay and packet dropout [17, 22, 23], and network quantization [14, 24, 25]. Noticeably, a common hypothesis is that all system states are accessible. Unfortunately, this hypothesis is hard to realize since only system outputs or part of system states are accessible. Stimulated by this point, event-driven-based output feedback control has been a fascinated topic [15, 26–28]. For given dynamic output feedback controller, depending on the provided decentralized triggered mechanism, conditions for stability analysis and \({\mathcal {L}}_\infty \) performance are discussed in [26]. [27] develops a framework of dynamic-output-based event-driven control for uncertain NCSs with quantization. Event-triggered static output feedback \(H_{\infty }\) control with time-varying sampling is studied in [28]. The issue of event-triggered observer-based output feedback control of continuous-time linear systems is delivered in [15]. It is to note that the methods for controller synthesis in these results are nonconvex. Moreover, the driven threshold in some of them still has room for further improvement.

Inspired by the above discussions, the event-triggered observer-based output feedback control of NCSs is further investigated in this paper. Motivated by [15], an extended event-driven threshold is exploited firstly. The extended triggered threshold is regulated by a tuning parameter and a weighting matrix. Due to the weighting matrix, it is feasible to do the co-design of the event-driven scheme and observer-based output controller. Then the event-driven closed-loop system is expressed by a delay approach. To derive the event-driven controllers and observers via a convex way, a constructive approach [29] is employed to separate the coupling of control matrix and other variables. With the help of these strategies, a sufficient condition for the resulted closed-loop system to be the global uniform ultimate boundedness is established in the framework of linear matrix inequalities. Based on the established condition, some special cases are also discussed. Finally, a numerical example is presented to show the validity of the proposed method.

The structure of this paper is as follows: The problem statement and some preliminaries are formulated in Sect. 2. The event-driven observer-based output control is elaborated in Sect. 3. Section 4 provides a numerical example to illustrate the effectiveness of the proposed approach. Lastly, Sect. 5 concludes the paper.

Notation

Throughout the paper, the notation \(M{>}0\) \(({<}0)\) is used to represent that M is symmetric and positive (negative) definite. \({\mathbb {R}}^n\) is the n-dimensional Euclidean space, and \({\mathbb {R}}^{n\times m}\) is the set of all \(n\times m\) real matrices. The transpose of M is denoted by \(M^\mathrm{T}\). \(*\) stands for the entries of matrices implied by symmetry. The symbol \(\Vert \bullet \Vert \) represents the Euclidean norm. Then, \((M+M^\mathrm{T})\) is denoted by He(M). \(I_n\) and \(0_{n\times m}\) mean the identity block matrix and zero block matrix with appropriate dimensions, respectively. What is more, matrices, if not explicitly stated, are assumed to have compatible dimensions.

2 Problem statement and preliminaries

Consider the following linear system

$$\begin{aligned} \left\{ {\begin{array}{lll}\dot{x}(t)&{}=&{}Ax(t)+Bu(t)\\ y(t)&{}=&{}Cx(t)\end{array}}\right. \end{aligned}$$
(1)

where \(x(t)\,{\in }\,{\mathbb {R}}^n\) is the state vector, \(u(t)\,{\in }\, {\mathbb {R}}^m\) is control input, \(y(t)\,{\in }\,{\mathbb {R}}^q\) is the system output, and A, B, and C are system matrices with appropriate dimensions. Assume that system (1) is controlled over a network.

Due to the fact that only partial system state is accessible in practical engineering, a state observer is used to estimate the system state x(t) with the measured output y(t) modeled as below

$$\begin{aligned}&\dot{\hat{x}}(t)=A\hat{x}(t)+Bu(t)+L(y(i_kh)-C\hat{x}(i_kh)),\nonumber \\&\quad t\in [t_kh+\tau _{t_k}, t_kh+\tau _{t_k+1}) \end{aligned}$$
(2)

where \(\hat{x}(t)\,{\in }\,{\mathbb {R}}^n\) means the observer state, L is the observer gain to be designed, and \(\tau _{t_k}\) is the communication delay.

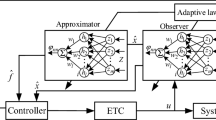
Thus, taking the limited capacity of the communication channels into account, an event-driven transmitter based on the estimated state, as depicted in Fig. 1, is constructed as

$$\begin{aligned} t_{k+1}h=t_kh+\min _{l}\{lh|e^T(i_kh)\Phi e(i_kh)\geqslant \gamma ^2(t)\} \end{aligned}$$
(3)

where \(e(i_kh)\,{=}\,\hat{x}(i_kh)-\hat{x}(t_kh)\) denotes the error between the observer state at the current sampling time \(i_kh\,{=}\,t_kh+lh (l\,{\in }\, {\mathbb {N}})\) and the observer state at the latest triggered time \(t_kh\); \(\Phi \) is a symmetric positive-definite weighting matrix; \(\gamma (t)\,{=}\,\sqrt{\beta \varepsilon ^{-\alpha t}+\varepsilon _0}\) is the error threshold with \(\varepsilon \,{>}\,1\), \(\beta \,{>}\,0\), \(0\,{\leqslant }\,\alpha \,{<}\,1\), \(\varepsilon _0\,{\geqslant }\,0\); and h denotes the sampling period.

Fig. 1
figure 1

Framework of an event-triggered NCS

Full size image

Remark 1

The proposed event-driven mechanism (3) is an extended version of the scheme in [15]. On the one hand, a tuning parameter \(\beta \) related to \(\alpha \) is added to the exponent term as coefficient. The benefit could be obvious once \(\alpha \) is small. On the other hand, a weighting matrix \(\Phi \) is introduced to enable the co-design of the triggered mechanism and the desired controllers.

Then, an event-driven observer-based state feedback control law is formed as

$$\begin{aligned} u(t)=K\hat{x}(t_kh), \quad t\in \Omega \end{aligned}$$
(4)

where K is the control gain matrix to be designed later.

Until the novel triggered signal arrives at the actuator, the control input is generated by a zero-order holder (ZOH) with the holding time interval \(\Omega \,{=}\,[t_kh+\tau _{t_k}, t_kh+\tau _{t_k+1})\). The following section provides a detailed statement of the holding time \(\Omega \) of ZOH, which is divided into subsets \(\Omega _l\,{=}\,[i_kh+\tau _{i_k}, i_kh+h+\tau _{i_k+1})\), i.e., \(\Omega \,{=}\,\cup \,\Omega _l\), where \(i_kh\,{=}\,t_kh+lh\), \(l=0,\ldots ,t_{k+1}-t_k-1\) represents sampling time from the current triggered time \(t_kh\) to the next triggered time \(t_{k+1}h\). For \(l\,{=}\,t_{k+1}-t_k-1\), then \(\tau _{i_k+1}\,{=}\,\tau _{t_{k+1}}\), otherwise \(\tau _{i_k}\,{=}\,\tau _{t_k}\). Define \(\tau (t)\,{\triangleq }\, t-i_kh\) and \(\dot{\tau }(t)\,{=}\,1\), \(t\,{\in }\,\Omega _l\). Note that \(0\,{<}\,\tau (t)\,{<}\,h+\bar{\tau }\,{\triangleq }\, \tau _m\), where \(\bar{\tau }\) means the maximum allowable upper transmission delay bound.

Combing the state observer (2), control law (4), and ZOH, the resulted closed-loop system is described as

$$\begin{aligned} \left\{ {\begin{array}{lll} \dot{x}(t)&{}=&{}Ax(t)+BKx(t-\tau (t))\\ &{}&{}-BK\tilde{x}(t-\tau (t))-BKe(i_kh)\\ \dot{\tilde{x}}(t)&{}=&{}A\tilde{x}(t)-LC\tilde{x}(t-\tau (t)), \quad t\in \Omega _l\end{array}}\right. \end{aligned}$$
(5)

where \(\tilde{x}(t)\,{=}\,x(t)-\hat{x}(t)\) is the estimation error.

Defining \(\xi ^T(t)\,{=}\,\left[ {\begin{array}{c} x^T(t)\quad \tilde{x}^T(t)\end{array}} \right] ^T\), an augmented closed-loop system is obtained

$$\begin{aligned} \dot{\xi }(t)= & {} \bar{A}_1\xi (t)+\bar{A}_2\xi (t-\tau (t))+\bar{B}e(i_kh),\quad t\in \Omega _l\nonumber \\ \end{aligned}$$
(6)

where \(\bar{A}_1\,{=}\,\left[ {\begin{array}{cc} A &{} 0\\ 0 &{} A\end{array}} \right] \), \(\bar{A}_2\,{=}\,\left[ {\begin{array}{cc}BK &{} -BK\\ 0 &{} -LC\end{array}} \right] \), and \(\bar{B}\,{=}\left[ {\begin{array}{cc} -BK\\ 0 \end{array}} \right] \).

This study aims at designing an event-driven observer-based controller (4) such that the system (6) is global uniform ultimate boundedness. To this end, some technical lemmas are presented as follows.

Lemma 1

[30] For given positive integers p, q, a scalar \(\delta \) in the interval (0, 1), a given positive matrix R in \({\mathbb {R}}^{p}\), two matrices \(M_1\) and \(M_2\) in \({\mathbb {R}}^{p\times q}\), define, for all vector \(\vartheta \) in \({\mathbb {R}}^{q}\), the function \(\mathfrak {I}(\delta ,R)\) given by:

$$\begin{aligned} \mathfrak {I}(\delta ,R)=\frac{1}{\delta } \,\vartheta ^TM_1^TRM_1\vartheta +\frac{ 1}{1-\delta }\,\vartheta ^TM_2^TRM_2\vartheta . \end{aligned}$$
(7)

Then, if there exists a matrix U in \({\mathbb {R}}^{p\times p}\) such that \(\left[ {\begin{array}{cc} R &{} U^{T}\\ * &{} R\end{array}} \right] ^{{\phantom {\frac{1}{1}}}}>0\), the following inequality holds

$$\begin{aligned} \min _{\delta \in (0,1)}\mathfrak {I}(\delta ,R)\geqslant \left[ {\begin{array}{cc} M_1\vartheta \\ M_2\vartheta \end{array}} \right] ^{T}\left[ {\begin{array}{cc} R &{} U^T\\ * &{} R\end{array}} \right] \left[ {\begin{array}{cc} M_1\vartheta \\ M_2\vartheta \end{array}} \right] . \end{aligned}$$
(8)

Lemma 2

[31] Given matrices D, E(t), and F of appropriate dimensions with E(t) satisfying \(E^T(t)E(t){\leqslant }\, I\), for any \(\epsilon \,{>}\,0\) the following inequality holds

$$\begin{aligned} DE(t)F+F^TE^T(t)D^T\leqslant \epsilon DD^T+\epsilon ^{-1}F^TF. \end{aligned}$$
(9)

Lemma 3

[32] The following two inequalities are equivalent:

  1. (a)

    There exists a symmetric and positive-definite matrix P satisfying

    $$\begin{aligned} \left[ {\begin{array}{cc} -P &{} A^T\\ A &{} -P^{-1}\end{array}} \right] <0; \end{aligned}$$
    (10)
  2. (b)

    There exists a symmetric and positive-definite matrix P and matrix Y satisfying

    $$\begin{aligned} \left[ {\begin{array}{cc} -P &{} (YA)^T\\ YA &{} He(-Y)+P\end{array}} \right] <0. \end{aligned}$$
    (11)

3 Main results

In Sect. 3, a sufficient condition for the closed-loop system (6) is established to guarantee the considered NCSs to be global uniform ultimate boundedness in the framework of linear matrix inequalities firstly. Based on the obtained main result, some special cases are presented subsequently.

Theorem 1

Consider the closed-loop system (6) under the driven scheme (3) with \(\varepsilon \), \(\alpha \), \(\beta \), \(\tau _m\,{>}\,0\). For given decay rate \(\sigma \), if there exist matrices \(P_1\,{>}\,0\), \(P_2\,{>}\,0\), \(\Phi \,{>}\,0\), \(R_1\,{>}\,0\), \(\Psi \,{>}\,0\), J and \(U_i\ (i=1,2,3,4)\), matrices Z, N, Q with appropriate dimensions such that

$$\begin{aligned}&\left[ {\begin{array}{cccc} \Delta _{11}+J &{} \Delta _{12} &{} 0 &{} 0\\ * &{} \Delta _{22} &{} \Delta _{23} &{} 0\\ * &{} * &{} He(-B^TBZ) &{} \Delta _{34}\\ * &{} * &{} * &{} -J \end{array}} \right] <0, \end{aligned}$$
(12)

where

$$\begin{aligned} \Delta _{11}= & {} \left[ {\begin{array}{cccccc} \bar{\Delta }_{11} &{} 0 &{} U^T_1 &{} U^T_3 &{} \sqrt{\tau _m}(R_1A)^T &{} 0 \\ * &{} \bar{\Delta }_{22} &{} U^T_2 &{} U^T_4 &{} 0 &{} \sqrt{\tau _m}(P_2A)^T\\ * &{} * &{} -\varphi R_1 &{}0 &{} 0 &{} 0 \\ * &{} * &{} * &{} -\varphi P_2 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} -R_1 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} -P_2 \end{array}} \right] ,\\ \varphi= & {} \frac{\mathrm{e}^{-\sigma \tau _m}}{\tau _m},\\ \bar{\Delta }_{11}= & {} He(P_1A)-\varphi R_1+\sigma P_1,\\ \bar{\Delta }_{22}= & {} He(P_2A)-\varphi P_2+\sigma P_2,~~~~~~~~~~~~~~~~~~\\ \Delta _{12}= & {} \left[ {\begin{array}{ccc} -BN &{} BN-U^T_1+\varphi R_1 &{} -BN-U_3^T\\ 0 &{} -U^T_2 &{} -QC-U^T_4+\varphi P_2\\ 0 &{} \varphi R_1-U_1 &{} -U_2 \\ 0 &{} -U_3 &{} \varphi P_2-U_4\\ -\sqrt{\tau _m}BN &{} \sqrt{\tau _m}BN &{} -\sqrt{\tau _m}BN\\ 0 &{} 0 &{} -\sqrt{\tau _m}QC\end{array}} \right] ,\\ \Delta _{22}= & {} \left[ {\begin{array}{ccc} - \Phi &{} 0 &{} 0\\ * &{} -2\varphi R_1+He(U_1) &{} U_2+U^T_3\\ * &{} * &{} -2\varphi P_2+He(U_4) \end{array}} \right] ,\\ \Delta _{23}= & {} \left[ {\begin{array}{c} -(B^TBN)^T \\ (B^TBN)^T \\ -(B^TBN)^T\end{array}}\right] ,~~~~~~~~~~~~ \Psi =\left[ {\begin{array}{cccc} R_1 &{} 0 &{} U^T_1 &{} U^T_3 \\ * &{} P_2 &{} U^T_2 &{} U^T_4 \\ * &{} * &{} R_1 &{} 0\\ * &{} * &{} * &{} P_2 \end{array}} \right] ,\\ \Delta _{34}= & {} \left[ {\begin{array}{cccccc} (P_1B-BZ)^T&0&0&0&\sqrt{\tau _m}(R_1B-BZ)^T&0\end{array}} \right] , \end{aligned}$$

then the closed-loop system (6) is global uniform ultimate bounded and exponentially converges to the bounded region

$$\begin{aligned} B _d(\varepsilon _0)=\left\{ \xi (t)|\Vert \xi (t)\Vert \leqslant \sqrt{\frac{\varepsilon _0}{\sigma \lambda _{min}(P_1)}}\right\} . \end{aligned}$$
(13)

Moreover, the state feedback controller gain is \(K\,{=}Z^{-1}N\) and the observer gain is \(L\,{=}\,P_2^{-1}Q\).

Proof

Choose a Lyapunov function as

$$\begin{aligned} V(t)= & {} \xi ^T(t)P\xi (t)\nonumber \\&+\,(\tau _m-\tau (t))\int ^{t}_{t-\tau _m}\mathrm{e}^{\sigma (s-t)}\dot{\xi }^T(s)R\dot{\xi }(s){\text{ d }}s\nonumber \\ \end{aligned}$$
(14)

where \(P=\left[ {\begin{array}{cc}P_1 &{} 0\\ 0 &{} P_2\end{array}} \right] \), \(R=\left[ {\begin{array}{cc}R_1 &{} 0\\ 0 &{} P_2\end{array}} \right] \).

Taking the time derivative of (14) with \(\dot{\tau }(t)\,{=}\,1\) yields

$$\begin{aligned} \dot{V}(t)= & {} 2\xi ^T(t)P\dot{\xi }(t)-\int ^t_{t-\tau _m}{\text{ e }}^{\sigma (s-t)}\dot{\xi }^T(s)R\dot{\xi }(s){\text{ d }}s\nonumber \\&+\,(\tau _m-\tau (t))\dot{\xi }^T(t)R\dot{\xi }(t) \nonumber \\&-\,(\tau _m-\tau (t)){\text{ e }}^{-\sigma \tau _m}\dot{\xi }^T(t-\tau _m)R\dot{\xi }(t-\tau _m)\nonumber \\&-\,\sigma (\tau _m-\tau (t))\int ^t_{t-\tau _m}{\text{ e }}^{\sigma (s-t)}\dot{\xi }^T(s)R\dot{\xi }(s){\text{ d }}s\nonumber \\&+\,{\text{ e }}^T(i_kh)\Phi e(i_kh)-{\text{ e }}^T(i_kh)\Phi e(i_kh). \end{aligned}$$
(15)

Based on (3), it leads to

$$\begin{aligned}&\dot{V}(t)+\sigma V(t) \leqslant 2\xi ^T(t)P\dot{\xi }(t)\nonumber \\&\qquad -\int ^t_{t-\tau _m}{\text{ e }}^{\sigma (s-t)} \dot{\xi }^T(s)R\dot{\xi }(s){\text{ d }}s \nonumber \\&\qquad +\,(\tau _m-\tau (t))\dot{\xi }^T(t)R\dot{\xi }(t)\nonumber \\&\qquad -\,(\tau _m-\tau (t)){\text{ e }}^{-\sigma \tau _m}\dot{\xi }^T(t-\tau _m)R\dot{\xi }(t-\tau _m)\nonumber \\&\qquad +\,\sigma \xi ^T(t)P\xi (t)-{\text{ e }}^T(i_kh)\Phi e(i_kh)+\gamma ^2 (t)\nonumber \\&\quad \leqslant 2\xi ^T(t)P\dot{\xi }(t)-{\text{ e }}^{-\sigma \tau _m}\int ^t_{t-\tau _m}\dot{\xi }^T(s)R\dot{\xi }(s){\text{ d }}s\nonumber \\&\qquad +\, \tau _m\dot{\xi }^T(t)R\dot{\xi }(t)\nonumber \\&\qquad +\,\sigma \xi ^T(t)P\xi (t)-{\text{ e }}^T(i_kh)\Phi e(i_kh)+\gamma ^2 (t).\nonumber \\ \end{aligned}$$
(16)

The following step separates the integral term \(-{\text{ e }}^{-\sigma \tau _m}\int ^t_{t-\tau _m}\dot{\xi }^T(s)R\dot{\xi }(s){\text{ d }}s\) into two parts taken over the intervals \([t- \tau (t), t]\) and \([t-\tau _m, t-\tau (t)]\). Utilizing Jensen’s inequality [33], one has

$$\begin{aligned}&-{\text{ e }}^{-\sigma \tau _m}\int ^{t}_{t-\tau _m}\dot{\xi }^T(s)R\dot{\xi }(s){\text{ d }}s\nonumber \\&\quad \leqslant -\frac{{\text{ e }}^{-\sigma \tau _m}}{\tau _m-\tau (t)}\eta ^T(t)e_1^T R e_1 \eta (t)\nonumber \\&\qquad -\,\frac{{\text{ e }}^{-\sigma \tau _m}}{\tau (t)}\eta ^T(t)e_2^T R e_2\eta (t) \end{aligned}$$
(17)

where

$$\begin{aligned} \eta ^T(t)= & {} \left[ {\begin{array}{ccc} \xi ^T(t)&\xi ^T(t-\tau _m)&\xi ^T(t-\tau (t)) \end{array}} \right] ,\\ e_1= & {} \left[ {\begin{array}{ccc} 0&-I&I \end{array}} \right] ,\quad e_2 = \left[ {\begin{array}{ccc} I&0&-I \end{array}}\right] . \end{aligned}$$

For a matrix \(U\,{=}\,\left[ {\begin{array}{cc} U_1 &{} U_2\\ U_3 &{} U_4\end{array}} \right] \) satisfying \(\Psi \,{>}\,0\), Lemma 1 guarantees that

$$\begin{aligned}&-{\text{ e }}^{-\sigma \tau _m}\int ^{t}_{t-\tau _m}\dot{\xi }^T(s)R\dot{\xi }(s){\text{ d }}s \nonumber \\&\quad \leqslant -\eta ^T(t)\left[ {\begin{array}{ccc}-\varphi R &{} U^T &{} \varphi R-U^T\\ * &{} -\varphi R &{} \varphi R-U \\ * &{} * &{} -2\varphi R +He(U) \end{array}}\right] \eta (t)\nonumber \\ \end{aligned}$$
(18)

where \(\varphi \,{=}\, \frac{{\text{ e }}^{-\sigma \tau _m}}{\tau _m}\).

Substituting (18) into (16) yields

$$\begin{aligned} \dot{V}(x(t))+\sigma V(x(t))&\leqslant \zeta ^T(t)(\Pi +\Upsilon ^TR^{-1} \Upsilon )\zeta (t)\nonumber \\&\quad +\gamma ^2(t) \end{aligned}$$
(19)

where

$$\begin{aligned}&\zeta ^T(t) = \left[ {\begin{array}{cc} \eta ^T(t)&{\text{ e }}^T(i_kh) \end{array}} \right] ,\\&\Pi =\left[ {\begin{array}{cccc} \Pi _{11} &{} U^T &{} \Pi _{13} &{} P\bar{B} \\ * &{} -\varphi R &{} \varphi R-U &{} 0 \\ * &{} * &{} -2\varphi R+He(U) &{}0\\ * &{} * &{} * &{}-\Phi \end{array}} \right] ,\\&\Pi _{11}=He(P\bar{A}_1)-\varphi R+\sigma P,\\&\Pi _{13}=P\bar{A}_2+\varphi R-U^T,\\&\Upsilon =\left[ {\begin{array}{cccc} \sqrt{\tau _m}R\bar{A}_1&0&\sqrt{\tau _m}R\bar{A}_2&\sqrt{\tau _m}R\bar{B} \end{array}} \right] . \end{aligned}$$

On the other hand, applying Schur complement to (12) leads to

$$\begin{aligned} \left[ {\begin{array}{ccc} \Delta _{11}+J &{} \Delta _{12} &{} 0 \\ * &{} \Delta _{22} &{} \Delta _{23} \\ * &{} * &{} He(-B^TBZ)+\Delta _{34}J^{-1}\Delta ^T_{34} \end{array}} \right] <0.\nonumber \\ \end{aligned}$$
(20)

In terms of Lemma 3, (20) can be rewritten as

$$\begin{aligned} \left[ {\begin{array}{ccc} \Delta _{11}+J &{} \Delta _{12} &{} 0 \\ * &{} \Delta _{22} &{} \Theta _{23} \\ * &{} * &{} -\left( \Delta _{34}J^{-1}\Delta ^T_{34}\right) ^{-1} \end{array}} \right] <0 \end{aligned}$$
(21)

where \(\Theta _{23}\,{=}\,\left[ {\begin{array}{ccc} -Z^{-1}N&Z^{-1}N&-Z^{-1}N \end{array}}\right] ^T.\)

Using Schur complement to (21) once more time, one can get

$$\begin{aligned} \left[ {\begin{array}{cc} \Delta _{11}+J &{} \Delta _{12} \\ * &{} \Delta _{22}\end{array}} \right] +\left[ {\begin{array}{c} 0 \\ \Theta _{23} \end{array}} \right] \Delta _{34}J^{-1}\Delta ^T_{34}\left[ {\begin{array}{cc} 0&\Theta ^T_{23} \end{array}} \right] <0\nonumber \\ \end{aligned}$$
(22)

which is also equivalent to

$$\begin{aligned}&\left[ {\begin{array}{cc} \Delta _{11} &{} \Delta _{12} \\ * &{} \Delta _{22} \end{array}} \right] +\left[ {\begin{array}{c} I_6 \\ 0_{3\times 6}\end{array}} \right] J\left[ {\begin{array}{c} I_6 \\ 0_{3\times 6}\end{array}} \right] ^T\nonumber \\&\quad +\left[ {\begin{array}{c} 0 \\ \Theta _{23} \end{array}} \right] \Delta _{34}J^{-1}\Delta ^T_{34}\left[ {\begin{array}{cc} 0&\Theta ^T_{23} \end{array}} \right] <0. \end{aligned}$$
(23)

Based on Lemma 2, the following inequality holds

$$\begin{aligned}&\left[ {\begin{array}{c} I_6 \\ 0_{3\times 6}\end{array}} \right] J\left[ {\begin{array}{c} I_6 \\ 0_{3\times 6}\end{array}} \right] ^T+\left[ {\begin{array}{c} 0_{6\times 1} \\ \Theta _{23} \end{array}} \right] \Delta _{34}J^{-1}\Delta ^T_{34}\left[ {\begin{array}{cc} 0_{1\times 6}&\Theta ^T_{23} \end{array}} \right] \nonumber \\&\quad \geqslant He\left( \left[ {\begin{array}{c} I_6 \\ 0_{3\times 6}\end{array}} \right] \left[ {\begin{array}{c} P_1B-BZ \\ 0 \\ 0 \\ 0 \\ \sqrt{\tau _m}(R_1B-BZ)\\ 0\end{array}} \right] Z^{-1}N \left[ {\begin{array}{cccc}0_{1\times 6}&-I&I&-I\end{array}} \right] \right) .\nonumber \\ \end{aligned}$$
(24)

From the above fact and \(L\,{=}\,P_2^{-1}Q\), (23) is reformed as

$$\begin{aligned} \left[ {\begin{array}{ccccc} \Pi _{11} &{} U^T &{} \sqrt{\tau _m}(R\bar{A}_{1})^{T} &{} P\bar{B} &{} \Pi _{13}\\ * &{} -\varphi R &{} 0 &{} 0 &{} \varphi R-U\\ * &{} * &{} -R &{} \sqrt{\tau _m}(R\bar{B}) &{} \sqrt{\tau _m}(R\bar{A}_2)\\ * &{} * &{} * &{}-\Phi &{} 0\\ * &{} * &{} * &{} * &{}-2\varphi R+He(U)\end{array}} \right] <0. \end{aligned}$$
(25)

Left- and right-multiplying (25) with \(\Lambda \) and \(\Lambda ^T\), one has

$$\begin{aligned} \left[ {\begin{array}{ccccc} \Pi _{11} &{} U^T &{} \Pi _{13} &{} P\bar{B} &{} \sqrt{\tau _m}(R\bar{A}_1)^T\\ * &{} -\varphi R &{} \varphi R-U &{} 0 &{} 0\\ * &{} * &{} -2\varphi R+He(U) &{} 0 &{} \sqrt{\tau _m}(R\bar{A}_2)^T\\ * &{} * &{} * &{}-\Phi &{} \sqrt{\tau _m}(R\bar{B})^T\\ * &{} * &{} * &{} * &{} -R \end{array}} \right] <0 \end{aligned}$$
(26)

where

$$\begin{aligned} \Lambda =\left[ {\begin{array}{ccccc} I &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} I &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} I\\ 0 &{} 0 &{} 0 &{} I &{} 0\\ 0 &{} 0 &{} I &{} 0 &{} 0 \end{array}} \right] . \end{aligned}$$

Thus, (26) implies that \(\zeta ^T(t)(\Pi +\Upsilon ^TR^{-1} \Upsilon )\zeta (t)\,{<}\,0\) holds for any nonzero \(\zeta (t)\), which combined with (19) gives that

$$\begin{aligned} \dot{V}(t)+\sigma V(t)\leqslant \gamma ^2(t). \end{aligned}$$
(27)

Applying comparison lemma [34] to (27) leads to

$$\begin{aligned} V(t) \leqslant {\text{ e }}^{-\sigma t} V(0)+\int ^t_0{\text{ e }}^{-\sigma (t-s)}\gamma ^2(s){\text{ d }}s. \end{aligned}$$
(28)

Noting that \(\gamma ^2(t)\,{=}\,\beta \varepsilon ^{-\alpha t}+\varepsilon _0\,{=}\,\beta {\text{ e }}^{-(\alpha \ln \varepsilon )t}+\varepsilon _0\), (28) is rewritten as

$$\begin{aligned} V(t)\leqslant & {} {\text{ e }}^{-\sigma t} V(0)+{\text{ e }}^{-\sigma t}\int ^t_0{\text{ e }}^{(\sigma -\alpha \ln \varepsilon )t}{\text{ d }}s\\&+\,\varepsilon _0\int ^t_0{\text{ e }}^{-\sigma (t-s)}{\text{ d }}s\\= & {} {\text{ e }}^{-\sigma t} \left( V(0)-\frac{\varepsilon _0}{\sigma }\right) +\frac{\varepsilon _0}{\sigma }\\&+\,\beta {\text{ e }}^{-\sigma t} \int ^t_0{\text{ e }}^{(\sigma -\alpha \ln \varepsilon )t}{\text{ d }}s. \end{aligned}$$

The following three cases will be taken into account.

If \(\sigma -\alpha \ln \varepsilon \,{=}\,0\), one has

$$\begin{aligned} V(t)\leqslant & {} {\text{ e }}^{-\sigma t} \left( V(0)-\frac{\varepsilon _0}{\sigma }+\beta t\right) +\frac{\varepsilon _0}{\sigma }. \end{aligned}$$

If \(\sigma -\alpha \ln \varepsilon \,{>}\,0\), one can get

$$\begin{aligned} V(t)\leqslant & {} {\text{ e }}^{-\sigma t} \left( V(0)-\frac{\varepsilon _0}{\sigma }\right) \\&+\frac{\beta {\text{ e }}^{-\sigma t}}{\sigma -\alpha \ln \varepsilon }\left( {\text{ e }}^{(\sigma -\alpha \ln \varepsilon )t}-1 \right) \\= & {} {\text{ e }}^{-\sigma t} \left( V(0)-\frac{\varepsilon _0}{\sigma }-\frac{\beta }{\sigma -\alpha \ln \varepsilon }\right) \\&+\,\frac{\varepsilon _0}{\sigma }+\frac{\beta \varepsilon ^{-\alpha t}}{\sigma -\alpha \ln \varepsilon }. \end{aligned}$$

If \(\sigma -\alpha \ln \varepsilon \,{<}\,0\), thus, \({\text{ e }}^{(\sigma -\alpha \ln \varepsilon )t}\,{<}\,1\), we have

$$\begin{aligned} V(t)\leqslant & {} {\text{ e }}^{-\sigma t} \left( V(0)-\frac{\varepsilon _0}{\sigma }-\frac{\beta }{\sigma -\alpha \ln \varepsilon }\right) \\&+\,\frac{\varepsilon _0}{\sigma }+\frac{\beta \varepsilon ^{-\alpha t}}{\alpha \ln \varepsilon -\sigma }. \end{aligned}$$

Summarizing the above three cases, one can see that the global uniform ultimate boundedness of the closed-loop system (6) is satisfied and the states exponentially converge to the bounded region (13). \(\square \)

Remark 2

Compared with [15], this paper utilizes not only \(\xi (t-\tau (t))\) but also \(\xi (t-\tau _m)\) to get the obtained result more effective. Further, the upper bound of transmission delay in [15] is defined as the sampling period h, but it could be optimized without the constraint of h in the proposed method.

Remark 3

To get the closed-loop system (6) to be global uniform ultimate bounded, in [15], the state feedback controller gain and the observer gain are required to be given in advance. Therefore, they are independent on the driven scheme. Nevertheless, with the introduced weighting matrix, a co-design of the event-triggered mechanism and observer-based controller is given in Theorem 1 by a convex method.

Once system states are available, the event-driven scheme and the resulting closed-loop system are reformulated, respectively, as

$$\begin{aligned} t_{k+1}h= & {} t_kh+\min _{l}\{lh|{\text{ e }}^T(i_kh)\Phi e(i_kh)\nonumber \\\ge & {} \gamma ^2(t)\},\, e(i_kh)=x(i_kh)-x(t_kh); \end{aligned}$$
(29)
$$\begin{aligned} \dot{x}(t)= & {} Ax(t)+BKx(t-\tau (t))-BKe(i_kh),\nonumber \\&\quad t\in \Omega _l. \end{aligned}$$
(30)

Based on the obtained result given in Theorem 1, the corresponding result is given below.

Corollary 1

Consider the closed-loop system (30) under the trigger scheme (29) with \(\varepsilon \), \(\alpha \), \(\beta \), \(\tau _m>0\). For given decay rate \(\sigma \), if there exist matrices \(P_1>0\), \(\Phi >0\), \(R_1>0\), \(\left[ {\begin{array}{cc} R_1 &{} U_1\\ U_1^T &{} R_1 \end{array}} \right] >0\), \(J_1\) and \(U_1\), matrices Z, N with appropriate dimensions such that

$$\begin{aligned} \left[ {\begin{array}{cccc} \Xi _{11}+J_1 &{} \Xi _{12} &{} 0 &{} 0\\ * &{} \Xi _{22} &{} \Xi _{23} &{} 0\\ * &{} * &{} He(-B^TBZ) &{} \Xi _{34}\\ * &{} * &{} * &{} -J_1 \end{array}} \right] <0, \end{aligned}$$
(31)

where

$$\begin{aligned} \Xi _{11}= & {} \left[ {\begin{array}{ccc} He(P_1A)-\varphi R_1+\sigma P_1 &{} U_1^T &{} \sqrt{\tau _m}(R_1A)^T \\ * &{} -\varphi R_1 &{}0 \\ * &{} * &{} -R_1 \end{array}} \right] ,\\ \Xi _{12}= & {} \left[ {\begin{array}{cc} -BN &{} BN-U_1^T+\varphi R_1\\ 0 &{} \varphi R_1-U_1 \\ -\sqrt{\tau _m}BN &{} \sqrt{\tau _m}BN \end{array}} \right] ,\\ \Xi _{22}= & {} \left[ {\begin{array}{cc} - \Phi &{} 0,\\ * &{} -2\varphi R_1+He(U_1) \end{array}} \right] ,\\ \Xi _{23}= & {} \left[ {\begin{array}{c} -(B^TBN)^T \\ (B^TBN)^T \end{array}}\right] ,\\ \Xi _{34}= & {} \left[ {\begin{array}{ccc} (P_1B-BZ)^T&0&\sqrt{\tau _m}(R_1B-BZ)^T \end{array}} \right] , \end{aligned}$$

then the solutions of system (30) with the state feedback gain \(K=Z^{-1}N\) are globally uniformly ultimately bounded and exponentially converge to the region

$$\begin{aligned} B _d(\varepsilon _0)=\left\{ x(t)|\Vert x(t)\Vert \leqslant \sqrt{\frac{\varepsilon _0}{\sigma \lambda _{min}(P_1)}}\right\} . \end{aligned}$$
(32)

Assuming that all system states are known, the event-triggered level is chosen as

$$\begin{aligned} t_{k+1}h= & {} t_kh+\min _{l}\{lh|{\text{ e }}^T(i_kh)\Phi e(i_kh)\nonumber \\\ge & {} \delta x^T(i_kh)\Phi x(i_kh)\}, ~~~ \delta \in [0,1) \end{aligned}$$
(33)

which can be obtained by replacing \(\gamma ^2(t)\) in (29) with \(\delta x^T(i_kh)\Phi x(i_kh)\). In this scenario, the driven level is the same as that of [21]. Adopting the similar derivation, a sufficient condition for the system (30) to be asymptotically stable is derived in the following corollary.

Corollary 2

Consider the closed-loop system (30) under the trigger scheme (33) with \(\delta \,{\in }\,[0,1)\), \(\tau _m\,{>}\,0\). For given decay rate \(\sigma \), if there exist matrices \(P_1\,{>}\,0\), \(\Phi \,{>}\,0\), \(R_1\,{>}\,0\), \(\left[ {\begin{array}{cc} R_1 &{} U_1\\ U_1^T &{} R_1 \end{array}} \right] \,{>}\,0\), \(J_1\) and \(U_1\), matrices Z, N with appropriate dimensions such that

$$\begin{aligned} \left[ {\begin{array}{cccc} \Sigma _{11}+J_1 &{} \Sigma _{12} &{} 0 &{} 0\\ * &{} \Sigma _{22} &{} \Sigma _{23} &{} 0\\ * &{} * &{} He(-B^TBZ) &{} \Sigma _{34}\\ * &{} * &{} * &{} -J_1 \end{array}} \right] <0 \end{aligned}$$
(34)

where

$$\begin{aligned} \Sigma _{11}= & {} \left[ {\begin{array}{ccc} He(P_1A)-\varphi R_1+\sigma P_1 &{} U_1^T &{} \sqrt{\tau _m}(R_1A)^T \\ * &{} -\varphi R_1 &{}0 \\ * &{} * &{} -R_1 \end{array}} \right] ,\\ \Sigma _{12}= & {} \left[ {\begin{array}{cc} -BN &{} BN-U_1^T+\varphi R_1\\ 0 &{} \varphi R_1-U_1 \\ -\sqrt{\tau _m}BN &{} \sqrt{\tau _m}BN \end{array}} \right] ,\\ \Sigma _{22}= & {} \left[ {\begin{array}{cc} - \Phi &{} 0,\\ * &{} \delta \Phi -2\varphi R_1+He(U_1) \end{array}} \right] ,\\ \Sigma _{23}= & {} \left[ {\begin{array}{c} -(B^TBN)^T \\ (B^TBN)^T \end{array}}\right] ,\\ \Sigma _{34}= & {} \left[ {\begin{array}{ccc} (P_1B-BZ)^T&0&\sqrt{\tau _m}(R_1B-BZ)^T \end{array}} \right] , \end{aligned}$$

then the system (30) with state feedback control gain \(K\,{=}\,Z^{-1}N\) is asymptotically stable.

4 Numerical example

Example 1

Consider system (1) with

$$\begin{aligned}&A=\left[ {\begin{array}{cc} 0.2 &{} 0.1 \\ 0.2 &{} -0.5\end{array}} \right] , \quad B=\left[ {\begin{array}{c} 1 \\ 1\end{array}} \right] , \quad C=\left[ {\begin{array}{cc} 1&1\end{array}} \right] . \end{aligned}$$

Controller gain K, observer gain L, \(\tau _m\), and weighting matrix \(\Phi \) calculated by Theorem 1 are shown in Table 1. Based on Table 1, one can see that the derived \(\tau _m\) decreases as the given \(\sigma \) increases.

Thus, for given \(\tau _m\,{=}\,0.5\), \(\sigma \,{=}\,0.2\), the controller and observer gains and weighting matrix are also obtained as \(K\,{=}\,[-0.4702\, -0.2108]\), \(L\,{=}\,[0.7743\,0.2886]^T\), and \(\Phi \,{=}\,\left[ {\begin{array}{cc} 10.3975 &{} 1.3896\\ 1.3896 &{} 7.9191\end{array}} \right] \). Via the obtained parameters, the simulation is performed with the initial state \(x(0)\,{=}\,[1;\,-1]\), \(\varepsilon \,{=}\,e\), \(\alpha \,{=}\,0.5\), \(\beta \,{=}\,1\), \(\varepsilon _0\,{=}\,0.01\), and \(h\,{=}\,0.01\)s. Therefore, the corresponding the closed-loop system state trajectories, \(\Vert \Phi ^{1/2} e(i_kh)\Vert \), and transmission intervals are depicted in Figs. 2, 3, and 4, respectively. From these figures, it is obvious that the closed-loop system is global uniform ultimate bounded and converges to the prescribed threshold. It is also found that, for a given \(\sigma \), minor changes of system states could lead to less triggered transmission.

Fig. 2
figure 2

Closed-loop state responses

Full size image
Fig. 3
figure 3

\(\Vert \Phi ^{1/2} e(i_kh)\Vert \)

Full size image
Fig. 4
figure 4

Transmission intervals

Full size image
Table 1 Controller gain K, observer gain L, \(\tau _m\) and weighting matrix \(\Phi \)
Full size table

To show the effectiveness of the proposed triggered threshold, under the initial state \(x(0)\,{=}\,[1\,-1]^T\) and the same K, L, \(\Phi \) calculated by \(\tau _m\,{=}\,0.5\), \(\sigma \,{=}\,0.2\), and \(\varepsilon \,{=}\,e\), \(\alpha \,{=}\,0.06\), \(\varepsilon _0\,{=}\,0.01\), three driven levels are considered by choosing \(\beta \,{=}\,1\) and \(\Phi \,{=}\,I\) in [15] (Case I) and \(\beta \,{=}\,0.3\) in scheme (3) (Case II) and \(\beta \,{=}\,0.01\) in scheme (3) (Case III). Then, the closed-loop system state responses, \(\Vert \Phi ^{1/2} e(i_kh)\Vert \), and transmission intervals of the three cases are shown in Figs. 5, 6, 7, 8.

Fig. 5
figure 5

State responses of \(x_1(t)\) for three cases

Full size image
Fig. 6
figure 6

State responses of \(x_2(t)\) for three cases

Full size image
Fig. 7
figure 7

Curves of \(\Vert \Phi ^{1/2} e(i_kh)\Vert \) for three cases

Full size image
Fig. 8
figure 8

Transmission intervals for three cases

Full size image

Figures 5 and 6 show that the smaller the \(\beta \) is, the better the system performance will be. Figures 7 and 8 demonstrate that the smaller the \(\beta \), the more the cost consumed. Therefore, these figures also verify the fact a trade-off should be made between system performance and cost. Namely, if the goal is to obtain better performance, one just needs to decrease \(\beta \). If the attention is paid on saving cost, this goal can be realized by increasing \(\beta \).

5 Conclusions

This paper is concerned with the event-driven observer-based output control of NCSs. An extended triggered scheme is proposed, and a sufficient condition for the closed-loop system to be global uniform ultimate boundedness is established in the framework of linear matrix inequalities. The validity of the proposed method is verified by a numerical example. How to balance the triggered level and system performance will be studied in future.