Finite-time stability and observer-based control for nonlinear uncertain discrete-time switched system

Abstract

This paper investigates finite-time stability and observer-based finite-time control for nonlinear uncertain switched discrete-time system. Firstly, sufficient conditions are given to ensure that a class of switched nonlinear uncertain discrete-time system is finite-time stable under arbitrary switching. The observer-based controller is constructed. By constructing the switched Lyapunov function, sufficient conditions are derived to ensure the resulting closed-loop system is finite-time stable via observer-based control. The observer-based controller is designed to guarantee a switched nonlinear discrete-time system is finite-time stabilized. Finally, two numerical examples are given to illustrate the effectiveness of the proposed results.

1 Introduction

In recent years, the study of switched systems has attracted much research attention in control theory and practice. A switched system is a class of hybrid systems consisting of a family of subsystems, which are described by continuous or discrete-time dynamics, and a rule that orchestrates the switching between these subsystems. Switched system appears in many engineering applications, such as automatic engineering control, network control system, robot control system, motor engine control and so on (Cheng 2004; Lu et al. 2018; Balluchi et al. 1997; Bishop and Spong 1998).

It is well-known that stability is the primary consideration in system analysis and synthesis. The stability in Lyapunov sense describes the asymptotic behavior of the state trajectory of the system when time approaches infinity. In the current literature, most results on the stability of switched systems mainly focus on Lyapunov sense stability (Liberzon and Morse 1999; Liu et al. 2017; Kundu and Chatterjee 2017). However, in many practical systems, we need to pay attention to the behavior of the system in a limited time interval. The concept of finite-time stability was proposed in Dorato (1961). In recent years, finite-time stability and finite-time stabilization have gained importance as research topics due to their practical significance, and many results have been reported in Zuo et al. (2013), Zang et al. (2019), Chen and Jiao (2010), Xiang and Xiao (2011), Dong et al. (2021), Hu et al. (2015), Kheloufi et al. (2016). Zuo et al. (2013) considered the finite-time stability for linear discrete-time systems with time-varying delay. In Chen and Jiao (2010) finite-time stability theorem for stochastic nonlinear systems was presented. In Xiang and Xiao (2011), H_∞ finite-time control for switched nonlinear discrete-time systems with norm-bounded disturbance was investigated. Dong et al. (2021) considered the robust observer-based finite-time H_∞ control designs for discrete time delay nonlinear systems.

Usually, the design of state feedback control is achieved with the assumption that the system states are available. However, this unrealistic assumption is not always verified. Hence a state observer is proposed to estimate the unknown states. In recent years, observer based control has attracted the attention of researchers, and some control design methods have been proposed in Dong et al. (2021), Kheloufi et al. (2016), Dong et al. (2014) and Ahmad and Rehan (2016). Kheloufi et al. (2016) proposed a robust H_∞ observer-based stabilization method for uncertain nonlinear systems. Dong et al. (2014) investigated the problem of observer-based feedback control for discrete-time nonlinear time-delay systems. In Ahmad and Rehan (2016), the observer-based control for one-sided Lipschitz system was considered. However, so far, the problem of observer-based finite-time stabilization for uncertain nonlinear discrete-time switched system has not been addressed, which is the focus of our research.

In this paper, we address the finite-time stability and finite-time stabilization for nonlinear discrete switched systems with parameter uncertainty. Firstly, we derive new sufficient conditions which ensure that a class of switched nonlinear uncertain discrete-time system is finite-time stable under arbitrary switching. We construct an observer-based controller. By observer-based control, and utilizing sector-bounded conditions, the sufficient conditions of finite-time stabilization for nonlinear uncertain discrete-time systems are established in terms of matrices inequality. The design methods of controller and observer gain matrix are provided. Finally, two numerical examples are given to confirm the effectiveness and less conservatism of the proposed method.

The paper is organized as follows. Some preliminaries and the problem statement are introduced in Sect. 2. The main results, finite-time stable analysis and finite-time stabilization via observer-based control are given in Sect. 3. Two numerical examples are presented in Sect. 4. Conclusions are drawn in Sect. 5.

Notations: Throughout this paper, the superscript T denotes the transpose of a matrix. $X > Y(X < Y)$ denotes the matrix $X - Y$ is a positive definite (negative definite) symmetric matrix. $\lambda_{\max } ({\text{P}})$ and $\lambda_{\min } (P)$ denotes the maximum eigenvalue and minimum eigenvalue of a matrix P, respectively. ${\mathbb{N}}$ denotes the non-negative integer set. $A \otimes B$ denotes the Kronecker product of two matrices A and B. $*$ denotes the symmetric block in symmetric matrix. Diag $( \cdots )$ denotes a block-diagonal matrix.

2 Problem formulation

Consider the following nonlinear uncertain discrete-time switched system

$$ \left\{ \begin{gathered} x(k + 1) = (A_{\sigma (k)} +\Delta A_{\sigma (k)} )x(k) + B_{\sigma (k)} u(k) + G_{\sigma (k)} f(x(k)), \hfill \\ y(k) = C_{\sigma (k)} x(k), \hfill \\ \end{gathered} \right. $$

(1)

where $x(k) \in R^{n}$ is the state vector; $u(k) \in R^{m}$ is the control input; $y(k) \in R^{p}$ is the measured output, $\sigma (k):{\mathbb{Z}}^{ + } \to \Gamma = \{ 1,2, \cdots ,N\}$ is a piecewise constant function of discrete time $k$, called switching law or switching signal, which takes its value in finite set $\Gamma .$ $N > 0$ is the number of subsystems. For simplicity, at any arbitrary discrete time $k \in {\mathbb{Z}}^{ + }$, the switching signal $\sigma (k)$ is denoted by $\sigma .$$A_{i} ,B_{i} ,C_{i} ,G_{i} ,i \in \{ 1,2, \cdots ,N\}$ are appropriate dimension constant matrices. Assume that $\Delta A_{\sigma (k)}$ are unknown matrices representing time-varying parameter uncertainties and are assumed to be of the following form:

$$\Delta A_{\sigma (k)} = D_{\sigma } F_{\sigma } (k)N_{\sigma } , $$

(2)

where, for each $\sigma \in \Gamma ,$ the uncertainty $F_{\sigma } (k)$ is the unknown time-varying matrix-valued function subject to the following condition:

$$ F_{\sigma }^{T} (k)F_{\sigma } (k) \le I. $$

(3)

$D_{i} ,N_{i} ,i \in \{ 1,2, \cdots ,N\} ,$ are constant matrices. The nonlinear functions $f( \cdot )$ are assumed to be continuous with $f(0) = 0,$ and satisfy the following sector-bounded conditions:

$$ [f(x) - f(y) - H_{1} (x - y)]^{T} [f(x) - f(y) - H_{2} (x - y)] \le 0,\quad \forall x,y \in R^{n} , $$

(4)

where $H_{1} ,H_{2}$ are real matrices of appropriate dimensions.

Remark 1

The parameter uncertain structure in (2) appears in many uncertain systems (Ji et al. 2010; Dong et al. 2020; Dong and Wang 2020). It comprises the ‘matching conditions’ and many physical systems can be either exactly modeled in this manner or overbounded by (3).

Remark 2

As in Wang et al. (2008), the nonlinear function $f$ is said to belong to sectors. In other words, the nonlinearities are bounded by sectors. The nonlinear description in (4) is more general than the usual sigmoid functions and the commonly used Lipschitz conditions.

Remark 3

In this paper, we assume that the switching rule $\sigma$ is not known a priori, but it is available in real time, i.e. the activated subsystems is explicity known at each switching instant and the corresponding controller can be activated immediately.

Before presenting the main results, some useful definition and lemmas are given.

Definition 1

(Finite-time stability) Given a positive integer $M,$ two positive scalars $c_{1}$, $c_{2}$ with $0 < c_{1} \le c_{2}$, and a positive definite matrix $R,$ switched system (1) with $u(k) = 0$ is said to be finite-time stable with respect to $(c_{1} ,c_{2} ,R,M)$, if

$$ x^{T} (0)Rx(0) \le c_{1} \;\; \Rightarrow x^{T} (k)Rx(k) < c_{2} , \, \forall k \in \left\{ {1,2, \cdots ,M} \right\}. $$

Remark 4

The concept of finite-time stability is quite different from asymptotic stability. These are two independent concepts. Finite-time stability concerns the state trajectory of the system over the finite interval $[0,M],M \in {\mathbb{Z}}^{ + }$ with respect to given initial condition. A system satisfying finite-time stability may be not asymptotic stable, and vice versa (Xiang and Xiao 2011).

Problem 1

Given nonlinear switched system (1) with $u(k) = 0,$ find sufficient conditions ensuring the system finite-time stable with respect to $(c_{1} ,c_{2} ,R,M)$.

We construct an observer-based controller for system (1) as follows

$$ \left\{ \begin{aligned} &\hat{x}(k + 1) = A_{\sigma (k)} \hat{x}(k) + B_{\sigma (k)} u(k) + G_{\sigma (k)} f(\hat{x}(k)) + L_{\sigma (k)} (y(k) - C_{\sigma (k)} \hat{x}(k)), \\ & y(k) = C_{\sigma (k)} \hat{x}(k), \\ &u(k) = K_{\sigma (k)} \hat{x}(k), \end{aligned} \right. $$

(5)

where $\hat{x}(k) \in R^{n}$ is the estimated state vector; $K_{i}$ and $L_{i}$ are controller gain and observer gain, respectively. Let $e(k) = x(k) - \hat{x}(k).$ The error dynamic system is

$$ e(k + 1) = (A_{\sigma (k)} - L_{\sigma (k)} C_{\sigma (k)} )e(k) +\Delta A_{\sigma (k)} x(k) + G_{\sigma (k)} [f(x(k)) - f(\hat{x}(k))]. $$

(6)

Denoting $\overline{x}(k) = \left[ {\begin{array}{*{20}c} {x^{T} (k)} & {e^{T} (k)} \\ \end{array} } \right]^{T} ,$ then by (1) and (6), we get the following closed-loop system

$$ \overline{x}(k + 1) = \tilde{A}_{\sigma (k)} \overline{x}(k) + \overline{G}_{\sigma (k)} \overline{f}(\overline{x}(k)), $$

(7)

where

$$ \tilde{A}_{i} { = }\left[ {\begin{array}{*{20}c} {A_{i} { + }\Delta A_{i} + B_{i} K_{i} } & { - B_{i} K_{i} } \\ {\Delta A_{i} } & {A_{i} - L_{i} C_{i} } \\ \end{array} } \right],{\overline{\text{G}}}_{i} = \left[ {\begin{array}{*{20}c} {G_{i} } & 0 \\ 0 & {G_{i} } \\ \end{array} } \right],\quad \overline{f}(\overline{x}(k)) = \left[ {\begin{array}{*{20}c} {f(x(k))} \\ {f(x(k)) - f(\hat{x}(k))} \\ \end{array} } \right]. $$

(8)

Definition 2

Given a positive integer $M,$ two positive scalars $c_{1} ,c_{2}$, with $0 < c_{1} \le c_{2}$, and a positive definite matrix $\overline{R},$ switched system (1) is said to be finite-time stabilized with respect to $(c_{1} ,c_{2} ,\overline{R},M)$, if there exists an observer-based controller (5), such that the resulting closed-loop system (7) is finite-time stable with respect to $(c_{1} ,c_{2} ,\overline{R},M).$

Problem 2

Given nonlinear switched system (1), find the observer-based controllers to ensure the closed-loop system (7) is finite-time stable with respect to $(c_{1} ,c_{2} ,\overline{R},M).$

Lemma 1

(Kheloufi et al. 2016). Let $S_{1} ,S_{2}$, and $S_{3}$ be three real matrices of appropriate dimension such that $S_{1} = S_{1}^{T}$ and $S_{3} = S_{3}^{T} .$ Then $S_{3} < 0$ and $S_{1} - S_{2} S_{3}^{ - 1} S_{2}^{T} < 0$ if and only if

$$ \left( {\begin{array}{*{20}c} {S_{1} } & {S_{2} } \\ {S_{2}^{T} } & {S_{3} } \\ \end{array} } \right) < 0. $$

Lemma 2

(Ban et al. 2018). Let $D,F,N$ are real matrices of appropriate dimension with $F$ satisfying $F^{T} F \le I$. Then, for any scalar $\varepsilon > 0$.

$$ DFN + (DFN)^{T} \le \varepsilon^{ - 1} DD^{T} + \varepsilon N^{T} N. $$

3 Main results

In this section, Problems 1 and 2 are taken into consideration. We will first give the finite-time stability condition for nonlinear switched discrete-time system (1) with $u(k) = 0$. Then, we design the stabilizing observer-based controllers for the system (1).

Define the indicator function $\alpha (k) = [\alpha_{1} (k), \cdots ,\alpha_{N} (k)]^{T} ,$ where

$$ \alpha_{i} (k) = \left\{ \begin{gathered} 1,\;\;\;\text{when the switched system is described by the }i\text{th\,mode, } \hfill \\ 0,\;\;\;\text{otherwise,} \hfill \\ \end{gathered} \right.\quad \quad i \in \Gamma . $$

(9)

Then, the nonlinear switched system (1) with $u(k) = 0$ can be written as

$$ \left\{ \begin{gathered} x(k + 1) = \sum\limits_{i = 1}^{N} {\alpha_{i} (k)} [(A_{i} +\Delta A_{i} )x(k) + G_{i} f(x(k))], \hfill \\ y(k) = \sum\limits_{i = 1}^{N} {\alpha_{i} (k)} C_{i} x(k). \hfill \\ \end{gathered} \right. $$

(10)

3.1 Finite-time stability analysis

In this subsection, we give sufficient conditions which guarantee that the switched system (1) with $u(k) = 0$ is finite-time stable.

Theorem 1

The nonlinear switched system (1) with $u(k) = 0$ is finite-time stable with respect to $(c_{1} ,c_{2} ,R,M),$ if there exist positive-definite matrices $P_{i} ,i \in \Gamma ,$ and scalars $\mu \ge 0,$ $\varepsilon > 0$,$\gamma > 0$ such that the following conditions are satisfied $\forall (i,j) \in \Gamma \times \Gamma :$

$$ \left[ {\begin{array}{*{20}c} { - (1 + \mu )P_{i} - \gamma \tilde{H}_{1} } & { - \gamma \tilde{H}_{2} } & {A_{i}^{T} P_{j} } & 0 & {N_{i}^{T} } \\ * & { - \gamma I} & {G_{i}^{T} P_{j} } & 0 & 0 \\ * & * & { - P_{j} } & {P_{j} D_{i} } & 0 \\ * & * & * & { - \varepsilon I} & 0 \\ * & * & * & * & { - (2 - \varepsilon )I} \\ \end{array} } \right] < 0, $$

(11)

$$ (1 + \mu )^{M} \overline{\lambda }c_{1} - \underline{\lambda } c_{2} < 0, $$

(12)

where

$$ \begin{gathered} \tilde{H}_{1} = {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} \mathord{\left/ {\vphantom {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} 2}} \right. \kern-0pt} 2}, \, \tilde{H}_{2} = {{(H_{1} + H_{2} )} \mathord{\left/ {\vphantom {{(H_{1} + H_{2} )} 2}} \right. \kern-0pt} 2},{\kern 1pt} \; \hfill \\ \overline{\lambda } = \mathop {\sup }\limits_{i \in \Gamma } \{ \lambda_{\max } (R^{{ - \frac{1}{2}}} P_{i} R^{{ - \frac{1}{2}}} )\} , \underline{\lambda } = \mathop {\inf }\limits_{i \in \Gamma } \{ \lambda_{\min } (R^{{ - \frac{1}{2}}} P_{i} R^{{ - \frac{1}{2}}} )\} . \hfill \\ \end{gathered} $$

Proof

Construct the switched Lyapunov function candidate

$$ V(k) = x^{T} (k)P(\alpha (k))x(k) = x^{T} (k)\left( {\sum\limits_{l = 1}^{N} {\alpha_{l} (k)P_{l} } } \right)x(k), \, $$

(13)

where $P_{1} ,P_{2} , \cdots ,P_{N}$ are symmetric positive-definite matrices. We have

$$ \begin{aligned}\Delta V(k) & = V(k + 1) - V(k)\\ & = x^{T} (k + 1)P(\alpha (k + 1))x(k + 1) - x^{T} (k)P(\alpha (k))x(k) \\ & = [(A(\alpha (k)) +\Delta A(\alpha (k)))x(k) + G(\alpha (k))f(x(k))]^{T} P(\alpha (k + 1)) \\ & \quad \times [(A(\alpha (k)) +\Delta A(\alpha (k)))x(k) + G(\alpha (k))f(x(k))] - x^{T} (k)P(\alpha (k))x(k). \\ \end{aligned} $$

As this has to be satisfied under arbitrary switching laws, it follows that $\alpha_{i} (k) = 1, \,\alpha_{l \ne i}\, (k) = 0,$ $\alpha_{j} (k + 1) = 1,\,\alpha_{l \ne j} (k + 1) = 0.$ Then

$$ \begin{aligned}\Delta V(k) & = \left[ {\sum\limits_{l = 1}^{N} {\alpha_{l} (k)((} A_{l} (k) +\Delta A_{l} (k))x(k) + G_{l} (k)f(x(k)))} \right]^{T} \sum\limits_{l = 1}^{N} {\alpha_{l} (k + 1)} P_{l} \\ &\quad \times \left[ {\sum\limits_{l = 1}^{N} {\alpha_{l} (k)((} A_{l} (k) +\Delta A_{l} (k))x(k) + G_{l} (k)f(x(k)))} \right] - x^{T} (k)\sum\limits_{l = 1}^{N} {\alpha_{l} (k)} P_{l} (k)x(k) \\ & = [(A_{i} +\Delta A_{i} )x(k) + G_{i} f(x(k))]^{T} P_{j} [(A_{i} +\Delta A_{i} )x(k) + G_{i} f(x(k))] - x^{T} (k)P_{i} x(k) \\ & = x^{T} (k)(A_{i} +\Delta A_{i} )^{T} P_{j} (A_{i} +\Delta A_{i} )x(k) + x^{T} (k)(A_{i} +\Delta A_{i} )^{T} P_{j} G_{i} f(x(k)) \\ & \qquad {\kern 1pt} + f^{T} (x(k))G_{i}^{T} P_{j} (A_{i} +\Delta A_{i} )x(k) + f^{T} (x(k))G_{i}^{T} P_{j} G_{i} f(x(k)) - x^{T} (k)P_{i} x(k). \\ \end{aligned} $$

(14)

From Eq. (4), we have

$$ \left[ {\begin{array}{*{20}c} {x(k)} \\ {f(x(k))} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {\tilde{H}_{1} } & {\tilde{H}_{2} } \\ {\tilde{H}_{2}^{T} } & I \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(k)} \\ {f(x(k))} \\ \end{array} } \right] \le 0, $$

(15)

where $\tilde{H}_{1} = {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} \mathord{\left/ {\vphantom {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} 2}} \right. \kern-0pt} 2}, \, \tilde{H}_{2} = {{(H_{1} + H_{2} )} \mathord{\left/ {\vphantom {{(H_{1} + H_{2} )} 2}} \right. \kern-0pt} 2}.$

From (14) and (15), it follows that

$$ \begin{aligned}\Delta V(k) &\le x^{T} (k)(A_{i} +\Delta A_{i} )^{T} P_{j} (A_{i} +\Delta A_{i} )x(k) + x^{T} (k)(A_{i} +\Delta A_{i} )^{T} P_{j} G_{i} f(x(k)) \\ & + f^{T} (x(k))G_{i}^{T} P_{j} (A_{i} +\Delta A_{i} )x(k) + f^{T} (x(k))G_{i}^{T} P_{j} G_{i} f(x(k)) - x^{T} (k)P_{i} x(k) \\ &- \gamma \left[ {\begin{array}{*{20}c} {x(k)} \\ {f(x(k))} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {\tilde{H}_{1} } & {\tilde{H}_{2} } \\ {\tilde{H}^{T}_{2} } & I \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(k)} \\ {f(x(k))} \\ \end{array} } \right] \\ &= \xi^{T} (k)\Phi \xi (k), \\ \end{aligned} $$

(16)

where

$$ \xi (k){ = }\left[ {\begin{array}{*{20}c} {x^{T} (k)} & {f^{T} (x(k))} \\ \end{array} } \right]^{T} , \quad \Phi = \left[ {\begin{array}{*{20}c} {\Phi_{11} } & {\Phi_{12} } \\ * & {\Phi_{22} } \\ \end{array} } \right], $$

(17)

$$ \begin{aligned}&\Phi_{11} = (A_{i} +\Delta A_{i} )^{T} P_{j} (A_{i} +\Delta A_{i} ) - P_{i} - \gamma \tilde{H}_{1} ,\\ &\Phi_{12} = (A_{i} +\Delta A_{i} )^{T} P_{j} G_{i} - \gamma \tilde{H}_{2} , \, \quad \Phi_{22} = G_{i}^{T} P_{j} G_{i} - \gamma I\end{aligned}. $$

Let

$$ \Lambda = \Phi - \left[ {\begin{array}{*{20}c} {\mu P_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\Lambda_{11} } & {\Phi_{12} } \\ * & {\Phi_{22} } \\ \end{array} } \right], $$

(18)

where $\Lambda_{11} = (A_{i} +\Delta A_{i} )^{T} P_{j} (A_{i} +\Delta A_{i} ) - (1 + \mu )P_{i} - \gamma \tilde{H}_{1} .$

$\Lambda$ can be rewritten as

$$ \Lambda = \Lambda_{1} { + }\Lambda_{2} , $$

(19)

where

$$ \Lambda_{1} { = }\left[ {\begin{array}{*{20}c} { - (1{ + }\mu )P_{i} - \gamma \tilde{H}_{1} } & { - \gamma \tilde{H}_{2} } \\ * & { - \gamma I} \\ \end{array} } \right], \, \Lambda_{2} = \left[ {\begin{array}{*{20}c} {(A_{i} +\Delta A_{i} )^{T} P_{j} } \\ {G_{i}^{T} P_{j} } \\ \end{array} } \right]P_{j}^{ - 1} \left[ {\begin{array}{*{20}c} {P_{j} (A_{i} +\Delta A_{i} )} & {P_{j} G_{i} } \\ \end{array} } \right]. $$

From (18)–(19) and Lemma 1, $\Lambda < 0$ is equivalent to

$$ \Psi = \left[ {\begin{array}{*{20}c} { - (1{ + }\mu )P_{i} - \gamma \tilde{H}_{1} } & { - \gamma \tilde{H}_{2} } & {(A_{i} +\Delta A_{i} )^{T} P_{j} } \\ * & { - \gamma I} & {G_{i}^{T} P_{j} } \\ * & * & { - P_{j} } \\ \end{array} } \right] < 0. $$

(20)

$\Psi$ can be written as:

$$ \Psi = \hat{\Psi } +\Delta \Psi , $$

(21)

where

$$ \begin{gathered} \hat{\Psi }{ = }\left[ {\begin{array}{*{20}c} { - (1 + \mu )P_{i} - \gamma \tilde{H}_{1} } & { - \gamma \tilde{H}_{2} } & {A_{i}^{T} P_{j} } \\ * & { - \gamma I} & {G_{i}^{T} P_{j} } \\ * & * & { - P_{j} } \\ \end{array} } \right], \, \quad \hfill \\\Delta \Psi = \left[ {\begin{array}{*{20}c} 0 & 0 & {\Delta A_{i}^{T} P_{j} } \\ * & 0 & 0 \\ * & * & 0 \\ \end{array} } \right] = DF_{i} (k)N + N^{T} F_{i}^{T} (k)D^{T} , \, \hfill \\ D = \left[ {\begin{array}{*{20}c} 0 & 0 & {D_{i}^{T} P_{j} } \\ \end{array} } \right]^{T} , \, N = \left[ {\begin{array}{*{20}c} {N_{i} } & 0 & 0 \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

By Lemma 2, one can have:

$$\Delta \Psi \le \varepsilon^{ - 1} DD^{T} + \varepsilon N^{T} N. $$

(22)

For any $\varepsilon > 0,$ we have

$$ - \varepsilon^{ - 1} I < - (2 - \varepsilon )I. $$

(23)

By applying Lemma 1 and (11), it can be seen that $\Psi < 0,$ which implies that $\Lambda < 0.$ Then it follows that

$$ \begin{aligned}\Delta V(k) & \le \xi^{T} (k)\Phi \xi (k) \\ & = \xi^{T} (k)(\Lambda + \left[ {\begin{array}{*{20}c} {\mu P_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right])\xi (k) \\ & < \xi^{T} (k)\left[ {\begin{array}{*{20}c} {\mu P_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right]\xi (k) \\ &= \mu V(k). \\ \end{aligned} $$

(24)

From (24), we get

$$ V(k + 1) \le (1 + \mu )V(k), $$

(25)

which implies that

$$ \begin{aligned} V(k) & \le (1 + \mu )V(k - 1) \\ & \le \cdots \\ & \le (1 + \mu )^{k} V(0). \\ \end{aligned} $$

(26)

From (13), we know that for $\forall i \in \Gamma , \, \forall {k} \in \{ 1,2, \cdots ,M\}$

$$ \begin{aligned} (1 + \mu )^{k} V(0) & \le (1 + \mu )^{k} \mathop {\sup }\limits_{i \in \Gamma } \{ \lambda_{\max } (R^{{ - \frac{1}{2}}} P_{i} R^{{ - \frac{1}{2}}} )\} x^{T} (0)Rx(0) \\ & \le (1 + \mu )^{k} \overline{\lambda }c_{1} , \\ \end{aligned} $$

(27)

$$ \begin{aligned} V(k) & \ge \mathop {\inf }\limits_{i \in \Gamma } \{ \lambda_{\min } (R^{{ - \frac{1}{2}}} P_{i} R^{{ - \frac{1}{2}}} )\} x^{T} (k)Rx(k) \\ & = \underline{\lambda } x^{T} (k)Rx(k), \\ \end{aligned} $$

(28)

where $\overline{\lambda } = \mathop {\sup }\limits_{i \in \Gamma } \{ \lambda_{\max } (R^{{ - \frac{1}{2}}} P_{i} R^{{ - \frac{1}{2}}} )\} ,\quad \underline{\lambda } = \mathop {\inf }\limits_{i \in \Gamma } \{ \lambda_{\min } (R^{{ - \frac{1}{2}}} P_{i} R^{{ - \frac{1}{2}}} )\} .$

So, from (25)–(28), we have $\, \forall {k} \in \{ 1,2, \cdots ,M\}$

$$ \begin{aligned} \underline{\lambda } x^{T} (k)Rx(k) & \le (1 + \mu )^{k} V(0) \\ & \le (1 + \mu )^{k} \overline{\lambda }c_{1} \\ & \le (1 + \mu )^{M} \overline{\lambda }c_{1} , \\ \end{aligned} $$

(29)

From (12) and (29), we get that

$$ x^{T} (k)Rx(k) < c_{2} , $$

which means that system (1) with $u(k) = 0$ is finite-time stable with respect to $(c_{1} ,c_{2} ,R,M)$. This completes the proof.

Corollary 1

The nonlinear switched system (1) with $u(k) = 0$ and $\Delta A_{\sigma (k)} = 0$ is finite-time stable with respect to $(c_{1} ,c_{2} ,R,M),$ if there exist positive-definite matrices $P_{i} ,i \in \Gamma ,$ and scalars $\mu \ge 0,$ $\varepsilon > 0,$ $\gamma > 0$ such that the following conditions are satisfied $\forall (i,j) \in \Gamma \times \Gamma :$

$$ \begin{gathered} \left[ {\begin{array}{*{20}c} { - (1 + \mu )P_{i} - \gamma \tilde{H}_{1} } & { - \gamma \tilde{H}_{2} } & {A_{i}^{T} P_{j} } \\ * & { - \gamma I} & {G_{i}^{T} P_{j} } \\ * & * & { - P_{j} } \\ \end{array} } \right] < 0, \hfill \\ (1 + \mu )^{M} \overline{\lambda }c_{1} - \underline{\lambda } c_{2} < 0, \hfill \\ \end{gathered} $$

where

$$ \begin{aligned} \tilde{H}_{1} &= {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} \mathord{\left/ {\vphantom {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} 2}} \right. \kern-0pt} 2}, \, \tilde{H}_{2} = {{(H_{1} + H_{2} )} \mathord{\left/ {\vphantom {{(H_{1} + H_{2} )} 2}} \right. \kern-0pt} 2},{\kern 1pt} \\ \overline{\lambda } &= \mathop {\sup }\limits_{i \in \Gamma } \{ \lambda_{\max } (R^{{ - \frac{1}{2}}} P_{i} R^{{ - \frac{1}{2}}} )\} ,\;\underline{\lambda } = \mathop {\inf }\limits_{i \in \Gamma } \{ \lambda_{\min } (R^{{ - \frac{1}{2}}} P_{i} R^{{ - \frac{1}{2}}} )\} .\end{aligned} $$

Proof

The proof is similar to that for Theorem 1 and is omitted here.$\hfill\square$

3.2 Finite-time stabilization

The closed-loop system (7) can be written as

$$ \overline{x}(k + 1) = \sum\limits_{i = 1}^{N} {\alpha_{i} (k)} [\tilde{A}_{i} \overline{x}(k) + \overline{G}_{i} \overline{f}(\overline{x}(k))], $$

(30)

Next, sufficient conditions are proposed to guarantee discrete-time switched system (7) is finite-time stable via observer-based control.

Theorem 2

The nonlinear discrete-time switched system (1) is finite-time stabilized with respect to $(c_{1} ,c_{2} ,\overline{R},M),$ if there exists symmetric matrices $0 < \overline{S}_{i} = diag(\begin{array}{*{20}c} {S_{i} } & {S_{i} } \\ \end{array} ) \in R^{2n \times 2n} ,$ scalars $\mu \ge 0, \, \varepsilon > 0, \, \gamma > 0$, and any matrices $\overline{K}_{i} , \, \overline{L}_{i} ,\;i \in \Gamma ,$ such that the following conditions are satisfied $\forall (i,j) \in \Gamma \times \Gamma :$

$$ \left[ {\begin{array}{*{20}c} { - (1 + \mu )\overline{S}_{i} + \gamma (\overline{H}_{1}^{ - T} - 2\overline{S}_{i} )} & { - \gamma \overline{S}_{i} \overline{H}_{2} } & {\Theta_{13} } & 0 & {\overline{S}_{i} \overline{N}_{i}^{T} } \\ * & { - \gamma I} & {G_{i}^{T} } & 0 & 0 \\ * & * & { - \overline{S}_{j} } & {\overline{D}_{i} } & 0 \\ * & * & * & { - \varepsilon I} & 0 \\ * & * & * & * & { - (2 - \varepsilon )I} \\ \end{array} } \right] < 0, $$

(31)

$$ (1 + \mu )^{M} \lambda_{1} c_{1} - \lambda_{2} c_{2} < 0, $$

(32)

$$ S_{i} C_{i}^{T} = C_{i}^{T} \hat{S}_{i} , $$

(33)

where

$$ \begin{gathered} \, \Theta_{13} = \left[ {\begin{array}{*{20}c} {S_{i} A_{i}^{T} + \overline{K}_{i} B_{i}^{T} } & 0 \\ { - \overline{K}_{i} B_{i}^{T} } & {S_{i} A_{i}^{T} - C_{i}^{T} \overline{L}_{i} } \\ \end{array} } \right],\;\;\overline{G}_{i} = \left[ {\begin{array}{*{20}c} {G_{i} } & 0 \\ 0 & {G_{i} } \\ \end{array} } \right],\;\;\overline{N}_{i} = \left[ {\begin{array}{*{20}c} {N_{i} } & 0 \\ \end{array} } \right],\;\;\overline{D}_{i} = \left[ {\begin{array}{*{20}c} {D_{i}^{T} } & {D_{i}^{T} } \\ \end{array} } \right]^{T} , \hfill \\ \overline{H}_{1} = I \otimes [{{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} \mathord{\left/ {\vphantom {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} 2}} \right. \kern-0pt} 2}],\quad \;\;\overline{H}_{2} = - I \otimes [{{(H_{1} + H_{2} )} \mathord{\left/ {\vphantom {{(H_{1} + H_{2} )} 2}} \right. \kern-0pt} 2}],\quad \quad \overline{P}_{i}^{ - 1} = \overline{S}_{i} ,\quad \hfill \\ \end{gathered} $$

$$ \lambda_{1} { = }\mathop {\sup }\limits_{i \in \Gamma } \{ \lambda_{\max } (\overline{R}^{{ - \frac{1}{2}}} \overline{P}_{i} \overline{R}^{{ - \frac{1}{2}}} )\} ,\quad \lambda_{2} { = }\mathop {\inf }\limits_{i \in \Gamma } \{ \lambda_{\min } (\overline{R}^{{ - \frac{1}{2}}} \overline{P}_{i} \overline{R}^{{ - \frac{1}{2}}} )\} . $$

Furthermore, if the conditions (31)–(33) have feasible solutions, the controller gain and observer gain can be given by

$$ L_{i} = \overline{L}_{i}^{T} \hat{S}_{{\text{i}}}^{ - T} ,\;\quad K_{i} = \overline{K}_{i}^{T} S_{i}^{ - T} ,\quad \forall i \in \Gamma . $$

Proof

Construct the Lyapunov function for system (30)

$$ V(k) = \overline{x}^{T} (k)\overline{P}(\alpha (k))\overline{x}(k) = \overline{x}^{T} (k)\left( {\sum\limits_{l = 1}^{N} {\alpha_{l} (k)\overline{P}_{l} } } \right)\overline{x}(k), \, \forall l \in \Gamma , $$

(34)

where $\overline{P}_{i} = diag\left( {\begin{array}{*{20}c} {P_{i} } & {P_{i} } \\ \end{array} } \right) > 0$ and $\alpha_{i} (k) = 1,\,{\alpha}_{l \ne i} (k) = 0,\,{\alpha}_{j} (k{ + }1) = 1,{\alpha}_{l \ne j} (k{ + }1) = 0.$ Then the difference of $V(k)$ along the solution of the closed-loop system (30) is given by

$$ \begin{aligned}\Delta V(k) & = V(k + 1) - V(k) \\ & = \overline{x}^{T} (k + 1)\overline{P}(\alpha (k + 1))\overline{x}(k + 1) - \overline{x}^{T} (k)\overline{P}(\alpha (k))\overline{x}(k) \\ & = \left[ {\tilde{A}(\alpha (k))\overline{x}(k) + \overline{G}(\alpha (k))\overline{f}(\overline{x}(k))} \right]^{T} \overline{P}(\alpha (k + 1))\left[ {\tilde{A}(\alpha (k))\overline{x}(k) + \overline{G}(\alpha (k))\overline{f}(\overline{x}(k))} \right] \\ {\kern 1pt} {\kern 1pt}& \quad - \overline{x}^{T} (k)\overline{P}(\alpha (k))\overline{x}(k) \\ & = \left[ {\sum\limits_{l = 1}^{N} {\alpha_{l} (k)} (\tilde{A}_{l} \overline{x}(k) + \overline{G}_{l} \overline{f}(\overline{x}(k)))} \right]^{T} \sum\limits_{l = 1}^{N} {\alpha_{l} (k + 1)} \overline{P}_{l} \left[ {\sum\limits_{l = 1}^{N} {\alpha_{l} (k)} (\tilde{A}_{l} \overline{x}(k) + \overline{G}_{l} \overline{f}(\overline{x}(k)))} \right] \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} & \quad - \sum\limits_{l = 1}^{N} {\alpha_{l} (k)} \overline{x}^{T} (k)\overline{P}_{l} \overline{x}(k) \\ & = [\tilde{A}_{i} \overline{x}(k) + \overline{G}_{i} \overline{f}(\overline{x}(k))]^{T} \overline{P}_{j} [(\tilde{A}_{i} \overline{x}(k) + \overline{G}_{i} \overline{f}(\overline{x}(k))] - \overline{x}^{T} (k)\overline{P}_{i} \overline{x}(k). \\ \end{aligned} $$

(35)

From Eq. (4), we have

$$ \left[ {\begin{array}{*{20}c} {\overline{x}(k)} \\ {\overline{f}(\overline{x}(k))} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {\overline{H}_{1} } & {\overline{H}_{2} } \\ {\overline{H}_{2}^{T} } & I \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\overline{x}(k)} \\ {\overline{f}(\overline{x}(k))} \\ \end{array} } \right] \le 0, $$

(36)

where $\overline{H}_{1} = I \otimes [{{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} \mathord{\left/ {\vphantom {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} 2}} \right. \kern-0pt} 2}], \, \overline{H}_{2} = - I \otimes [{{(H_{1} + H_{2} )} \mathord{\left/ {\vphantom {{(H_{1} + H_{2} )} 2}} \right. \kern-0pt} 2}].$

From (35) and (36), we get

$$ \begin{aligned}\Delta V(k) & \le [\tilde{A}_{i} \overline{x}(k) + \overline{G}_{i} \overline{f}(\overline{x}(k))]^{T} \overline{P}_{j} [(\tilde{A}_{i} \overline{x}(k) + \overline{G}_{i} \overline{f}(\overline{x}(k))] - \overline{x}^{T} (k)\overline{P}_{i} \overline{x}(k) \\ & \quad - \gamma \left[ {\begin{array}{*{20}c} {\overline{x}(k)} \\ {\overline{f}(\overline{x}(k))} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {\overline{H}_{1} } & {\overline{H}_{2} } \\ {\overline{H}^{T}_{2} } & I \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\overline{x}(k)} \\ {\overline{f}(\overline{x}(k))} \\ \end{array} } \right] \\ & = \varsigma^{T} (k)\Pi \varsigma (k). \\ \end{aligned} $$

where

$$ \varsigma (k) = [\begin{array}{*{20}c} {\overline{x}^{T} (k)} & {\overline{f}^{T} (\overline{x}(k))} \\ \end{array} ]^{T} , \, \quad \Pi { = }\left[ {\begin{array}{*{20}c} {\tilde{A}_{i}^{T} \overline{P}_{j} \tilde{A}_{i} - \overline{P}_{i} - \gamma \overline{H}_{1} } & {\tilde{A}_{i}^{T} \overline{P}_{j} \overline{G}_{i} - \gamma \overline{H}_{2} } \\ * & {\overline{G}^{T}_{i} \overline{P}_{j} \overline{G}_{i} - \gamma I} \\ \end{array} } \right]. $$

Let

$$ \begin{aligned} \Xi &= \Pi - \left[ {\begin{array}{*{20}c} {\mu \overline{P}_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right] \\ & \quad = \left[ {\begin{array}{*{20}c} { - (1 + \mu )\overline{P}_{i} - \gamma \overline{H}_{1} } & { - \gamma \overline{H}_{2} } \\ * & { - \gamma I} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\tilde{A}^{T}_{i} \overline{P}_{j} } \\ {\overline{G}^{T}_{i} \overline{P}_{j} } \\ \end{array} } \right]\overline{P}_{j}^{ - 1} \left[ {\begin{array}{*{20}c} {\overline{P}_{j} \tilde{A}_{i} } & {\overline{P}_{j} \overline{G}_{i} } \\ \end{array} } \right], \\ \end{aligned} $$

(37)

By Lemma 1, we have that $\Xi < 0$ is equivalent to

$$ \tilde{\Pi }{ = }\left[ {\begin{array}{*{20}c} { - (1 + \mu )\overline{P}_{i} - \gamma \overline{H}_{1} } & { - \gamma \overline{H}_{2} } & {\tilde{A}_{i}^{T} \overline{P}_{j} } \\ * & { - \gamma I} & {\overline{G}^{T}_{i} \overline{P}_{j} } \\ * & * & { - \overline{P}_{j} } \\ \end{array} } \right] < 0, $$

(38)

where

$$ \begin{aligned} \tilde{A}_{i}& = \overline{A}_{i} +\Delta \overline{A}_{i} \\ & = \left[ {\begin{array}{*{20}c} {A_{i} + B_{i} K_{i} } & { - B_{i} K_{i} } \\ 0 & {A_{i} - L_{i} C_{i} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\Delta A_{i} } & 0 \\ {\Delta A_{i} } & 0 \\ \end{array} } \right]. \\ \end{aligned} $$

Then Eq. (38) can be written to

$$ \tilde{\Pi }{ = }\Pi_{1} + \Pi_{2} < 0, $$

(39)

where

$$ \begin{gathered} \Pi_{1} = \left[ {\begin{array}{*{20}c} { - (1 + \mu )\overline{P}_{i} - \gamma \overline{H}_{1} } & { - \gamma \overline{H}_{2} } & {\overline{A}_{i}^{T} \overline{P}_{j} } \\ * & { - \gamma I} & {\overline{G}_{i}^{T} \overline{P}_{j} } \\ * & * & { - \overline{P}_{j} } \\ \end{array} } \right],\quad \\ \Pi_{2} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\Delta \overline{A}_{i}^{T} \overline{P}_{j} } \\ * & 0 & 0 \\ * & * & 0 \\ \end{array} } \right] = {\rm O}F(k)Y + ({\rm O}F(k)Y)^{T} , \\ {\rm O} = \left[ {\begin{array}{*{20}c} 0 & 0 & {(\overline{P}_{j} \overline{D}_{{\text{i}}} )^{T} } \\ \end{array} } \right]^{T} , \, Y = \left[ {\begin{array}{*{20}c} {\overline{N}_{i} } & 0 & 0 \\ \end{array} } \right], \\ \overline{G}_{i} = \left[ {\begin{array}{*{20}c} {G_{i} } & 0 \\ 0 & {G_{i} } \\ \end{array} } \right],\;\;\overline{N}_{i} = \left[ {\begin{array}{*{20}c} {N_{i} } & 0 \\ \end{array} } \right],\;\;\overline{D}_{i} = \left[ {\begin{array}{*{20}c} {D_{i}^{T} } & {D_{i}^{T} } \\ \end{array} } \right]^{T} . \\ \end{gathered} $$

Applying Lemma 2, we have that $\tilde{\Pi } < 0$ if

$$ \Pi_{1} + \varepsilon^{ - 1} OO^{T} + \varepsilon Y^{T} Y < 0. $$

(40)

By Lemma 1, (40) is satisfied if and only if

$$ \hat{\Pi } = \left[ {\begin{array}{*{20}c} { - (1 + \mu )\overline{P}_{i} - \gamma \overline{H}_{1} } & { - \gamma \overline{H}_{2} } & {\overline{A}_{i}^{T} \overline{P}_{j} } & 0 & {\overline{N}_{i}^{T} } \\ * & { - \gamma I} & {G_{i}^{T} \overline{P}_{j} } & 0 & 0 \\ * & * & { - \overline{P}_{j} } & {\overline{P}_{j} \overline{D}_{i} } & 0 \\ * & * & * & { - \varepsilon I} & 0 \\ * & * & * & * & { - \varepsilon^{ - 1} I} \\ \end{array} } \right] < 0, $$

(41)

Setting $\overline{S}_{i} = \overline{P}_{i}^{ - 1}$, pre and post multiplying (41) by $T = diag\left( {\overline{S}_{i} ,I,\overline{S}_{j} ,I,I} \right)$, we have

$$ \overline{\Pi }{ = }\left[ {\begin{array}{*{20}c} { - (1 + \mu )\overline{S}_{i} - \gamma \overline{S}_{i} \overline{H}_{1} \overline{S}_{i} } & { - \gamma \overline{S}_{i} \overline{H}_{2} } & {\overline{S}_{i} \overline{A}_{i}^{T} } & 0 & {\overline{S}_{i} \overline{N}_{i}^{T} } \\ * & { - \gamma I} & {\overline{G}_{i}^{T} } & 0 & 0 \\ * & * & { - \overline{S}_{j} } & {\overline{D}_{i} } & 0 \\ * & * & * & { - \varepsilon I} & 0 \\ * & * & * & * & { - \varepsilon^{ - 1} I} \\ \end{array} } \right] < 0. $$

(42)

From (23) and $- \gamma \overline{S}_{i} \overline{H}_{1} \overline{S}_{i} \le \gamma (\overline{H}_{1}^{ - T} - 2\overline{S}_{i} ),$ we get that $\overline{\Pi } < 0$ if

$$ \left[ {\begin{array}{*{20}c} { - (1 + \mu )\overline{S}_{i} + \gamma (\overline{H}_{1}^{ - T} - 2\overline{S}_{i} )} & { - \gamma \overline{S}_{i} \overline{H}_{2} } & {\overline{S}_{i} \overline{A}_{i}^{T} } & 0 & {\overline{S}_{i} \overline{N}_{i}^{T} } \\ * & { - \gamma I} & {\overline{G}_{{\text{i}}}^{T} } & 0 & 0 \\ * & * & { - \overline{S}_{j} } & {\overline{D}_{i} } & 0 \\ * & * & * & { - \varepsilon I} & 0 \\ * & * & * & * & { - (2 - \varepsilon )I} \\ \end{array} } \right] < 0. $$

(43)

Let $S_{i} = P_{i}^{ - 1} ,\overline{K}_{i} = S_{i} K_{i}^{T} ,\overline{L}_{{\text{i}}} = \hat{S}_{i} L_{i}^{T} .$ From (31) and (33), we get that $\Xi < 0.$ Then

$$ \begin{aligned}\Delta V & \le \varsigma^{T} (k)\left( {\Xi + \left[ {\begin{array}{*{20}c} {\mu \overline{P}_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right]} \right)\varsigma (k) \\ & < \varsigma^{T} (k)\left[ {\begin{array}{*{20}c} {\mu \overline{P}_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right]\varsigma (k) \\ & = \mu V(k), \\ \end{aligned} $$

i.e.

$$ V(k + 1) \le (1 + \mu )V(k), $$

(44)

which implies that

$$ V(k) \le (1 + \mu )V(k - 1) \le \cdots \le (1 + \mu )^{k} V(0). $$

(45)

From (34), we know that for $\forall i \in \Gamma , \, \forall {k} \in \{ 1,2, \cdots ,M\} ,$

$$ \begin{aligned} (1 + \mu )^{k} V(0) & \le (1 + \mu )^{k} \mathop {\sup }\limits_{i \in \Gamma } \{ \lambda_{\max } (\overline{R}^{{ - \frac{1}{2}}} \overline{P}_{i} \overline{R}^{{ - \frac{1}{2}}} )\} \overline{x}^{T} (0)\overline{R}\overline{x}(0) \\ & \le (1 + \mu )^{k} \lambda_{1} c_{1} , \\ \end{aligned} $$

(46)

$$ V(k) \ge \mathop {\inf }\limits_{i \in \Gamma } \left\{ {\lambda_{\min } \left( {\overline{R}^{{ - \frac{1}{2}}} \overline{P}_{i} \overline{R}^{{ - \frac{1}{2}}} } \right)} \right\} = \lambda_{2} \overline{x}^{T} (k)\overline{R}\overline{x}(k), $$

(47)

where $\lambda_{1} { = }\mathop {\sup }\limits_{i \in \Gamma } \{ \lambda_{\max } (\overline{R}^{{ - \frac{1}{2}}} \overline{P}_{i} \overline{R}^{{ - \frac{1}{2}}} )\} ,$$\lambda_{2} { = }\mathop {\inf }\limits_{i \in \Gamma } \{ \lambda_{\min } (\overline{R}^{{ - \frac{1}{2}}} \overline{P}_{i} \overline{R}^{{ - \frac{1}{2}}} )\} .$

From (45)–(47), it follows that

$$ \begin{aligned} \lambda_{2} \overline{x}^{T} (k)\overline{R}\overline{x}(k) & \le (1 + \mu )^{k} V(0) \\ & \le (1 + \mu )^{k} \lambda_{1} c_{1} \\ & \le (1 + \mu )^{M} \lambda_{1} c_{1} . \\ \end{aligned} $$

(48)

From (32), we get that

$$ \overline{x}^{T} (k)\overline{R}\overline{x}(k) < c_{2} . $$

This completes the proof of the theorem.

Corollary 2

The nonlinear discrete-time switched system (1) with $\Delta A_{\sigma (k)} = 0$ is finite-time stabilizable with respect to $(c_{1} ,c_{2} ,\overline{R},M),$ if there exists symmetric matrices $0 < \overline{S}_{i} = diag(\begin{array}{*{20}c} {S_{i} } & {S_{i} } \\ \end{array} ) \in R^{2n \times 2n} ,$ scalars $\mu \ge 0,$ $\gamma > 0,$ and any matrices $\overline{K}_{i} , \, \overline{L}_{i} ,\forall i \in \Gamma ,$ such that the following conditions are satisfied $\forall (i,j) \in \Gamma \times \Gamma :$

$$ \left[ {\begin{array}{*{20}c} { - (1 + \mu )\overline{S}_{i} + \gamma (\overline{H}_{1}^{ - T} - 2\overline{S}_{i} )} & { - \gamma \overline{S}_{i} \overline{H}_{2} } & {\Theta_{13} } \\ * & { - \gamma I} & {G_{i}^{T} } \\ * & * & { - \overline{S}_{j} } \\ \end{array} } \right] < 0, $$

(49)

$$ (1 + \mu )^{M} \lambda_{1} c_{1} - \lambda_{2} c_{2} < 0, $$

(50)

$$ S_{i} C_{i}^{T} = C_{i}^{T} \hat{S}_{i} , $$

(51)

where

$\begin{gathered} \, \Theta_{13} = \left[ {\begin{array}{*{20}c} {S_{i} A_{i}^{T} + \overline{K}_{i} B_{i}^{T} } & { - \overline{K}_{{\text{i}}} B_{i}^{T} } \\ * & {S_{i} A_{i}^{T} - C_{i}^{T} \overline{L}_{i} } \\ \end{array} } \right],{\kern 1pt} \;\overline{G}_{i} = \left[ {\begin{array}{*{20}c} {G_{i} } & 0 \\ 0 & {G_{i} } \\ \end{array} } \right],\;\;\overline{H}_{1} = I \otimes [{{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} \mathord{\left/ {\vphantom {{(H_{1}^{T} H_{2} + H_{2}^{T} H_{1} )} 2}} \right. \kern-0pt} 2}],\; \hfill \\ \overline{H}_{2} = - I \otimes [{{(H_{1} + H_{2} )} \mathord{\left/ {\vphantom {{(H_{1} + H_{2} )} 2}} \right. \kern-0pt} 2}],\;\;\lambda_{1} { = }\mathop {\sup }\limits_{i \in \Gamma } \{ \lambda_{\max } (\overline{R}^{{ - \frac{1}{2}}} \overline{P}_{i} \overline{R}^{{ - \frac{1}{2}}} )\} ,\;\;\lambda_{2} { = }\mathop {\inf }\limits_{i \in \Gamma } \{ \lambda_{\min } (\overline{R}^{{ - \frac{1}{2}}} \overline{P}_{i} \overline{R}^{{ - \frac{1}{2}}} )\} ,\overline{P}_{i}^{ - 1} = \overline{S}_{i} . \hfill \\ \end{gathered} \break$Furthermore, if the conditions (31)–(33) have feasible solutions, the controller gain and observer gain can be given by

$$ L_{i} = \overline{L}_{i}^{T} \hat{S}_{{\text{i}}}^{ - T} ,\;K_{i} = \overline{K}_{i}^{T} S_{i}^{ - T} ,\quad \forall i \in \Gamma . $$

Proof

The proof is similar to that for Theorem 2 and is omitted here. $\hfill\square$

4 Numerical examples

In this section, two numerical examples are presented to show the application of the developed theory.

Example 1

Consider the uncertain discrete-time switched system (1) with $u(k) = 0$ and the following parameters:

$$ \begin{gathered} A_{1} = \left[ {\begin{array}{*{20}c} { - 0.1} & {0.1} \\ {0.2} & { - 0.1} \\ \end{array} } \right],\;\;C_{1} = \left[ {\begin{array}{*{20}c} {0.2} & {0.1} \\ {0.1} & {0.2} \\ \end{array} } \right], \, G_{1} = \left[ {\begin{array}{*{20}c} {0.1} & 0 \\ 0 & { - 0.2} \\ \end{array} } \right],{D}_{1} = \left[ {\begin{array}{*{20}c} { - 0.1} & {0.2} \\ 0 & {0.2} \\ \end{array} } \right], \, \\ {N}_{1} = \left[ {\begin{array}{*{20}c} {0.1} & {0.2} \\ {0.1} & {0.2} \\ \end{array} } \right],\;\;A_{2} = \left[ {\begin{array}{*{20}c} { - 0.2} & {0.02} \\ {0.02} & { - 0.2} \\ \end{array} } \right], \, C_{2} = \left[ {\begin{array}{*{20}c} {0.2} & 0 \\ 0 & {0.3} \\ \end{array} } \right],{G}_{2} = \left[ {\begin{array}{*{20}c} {0.02} & 0 \\ 0 & { - 0.3} \\ \end{array} } \right],\; \\ \;D_{2} = \left[ {\begin{array}{*{20}c} { - 0.2} & {0.1} \\ 0 & {0.1} \\ \end{array} } \right],{N}_{2} = \left[ {\begin{array}{*{20}c} {0.2} & {0.1} \\ {0.1} & {0.1} \\ \end{array} } \right],F_{1} (k) = \left[ {\begin{array}{*{20}c} {0.8\delta } & 0 \\ 0 & {0.8\delta } \\ \end{array} } \right], \, F_{2} (k) = \left[ {\begin{array}{*{20}c} {0.9\delta } & 0 \\ 0 & {0.9\delta } \\ \end{array} } \right],\;\;\left| \delta \right| \le 1, \\ \;H_{1} = \left[ {\begin{array}{*{20}c} {0.7} & 0 \\ 0 & {0.7} \\ \end{array} } \right],{\kern 1pt} \;\;H_{2} = \left[ {\begin{array}{*{20}c} {0.3} & 0 \\ 0 & {0.1} \\ \end{array} } \right],\;\;f(x(k)) = \left[ {\begin{array}{*{20}c} {0.5x_{1} + 0.2\sin (x_{1} )} \\ {0.4x_{2} + 0.3\sin (x_{2} )} \\ \end{array} } \right]{\kern 1pt} . \\ \end{gathered} $$

Take $\mu = 0.5, \, \gamma = 0.4, \, \varepsilon = 0.2,{c}_{1} = 0.25,{R} = {I}_{2} , \, M = 10.$ By using Matlab LMI Toolbox to solve inequalities (11) and (12), we can get a set of feasible solution as follows:

$$ P_{1} = P_{2} = \left[ {\begin{array}{*{20}c} {1.1461} & { - 0.0006} \\ { - 0.0006} & {1.1358} \\ \end{array} } \right],\quad c_{2} = 14.55. $$

According to Theorem 1, system (1) with $u(k) = 0$ is finite-time stable with respect to $(0.25,14.55,I_{2} ,10)$. Figure 1 shows the simulation results of the state trajectory $x(k)$ with $\;\delta { = }1$. Figure 2 shows the evolution of $x^{T} (k)Rx(k)$ for an initial value $x(0) = \left[ {\begin{array}{*{20}c} { - 0.25} & {0.3} \\ \end{array} } \right]^{T} .$ It can be seen that, the state responses satisfy

$$ x^{T} (k)Rx(k) \le 14.55,\quad k \in \{ 1,2, \cdots ,10\} . $$

Fig. 1

State response of the system in Example 1

Fig. 2

Trajectory of $x^{T} (k)Rx(k)$ in Example 1

For $\mu = 0.5,\gamma = 0.4,\varepsilon = 0.2,R = I_{2} ,$ $c_{1} = 0.25$ and $M \in \left\{ {2,5,8,10} \right\},$ the smallest eligible value of the parameter $c_{2}$ is computed by using Theorem 1, and the obtained results are listed in Table 1. From Table 1, it can be seen that the smallest eligible value of the parameter $c_{2}$ increases as M increases.

Table 1 The smallest eligible value of the parameter ${\text{c}}_{2}$

Example 2

Consider the nonlinear switched system (1) with the following parameters and two modes ($i = 1,{\kern 1pt} \;2$):

$$\begin{gathered} A_{1} = \left[ {\begin{array}{*{20}c} { - 0.1} & {0.02} \\ {0.01} & { - 0.2} \\ \end{array} } \right],{B}_{1} = \left[ {\begin{array}{*{20}c} {0.1} & {0.2} \\ {0.2} & { - 0.1} \\ \end{array} } \right],\;C_{1} = \left[ {\begin{array}{*{20}c} {0.1} & 0 \\ 0 & {0.2} \\ \end{array} } \right],\;\;{G}_{1} = \left[ {\begin{array}{*{20}c} {0.02} & 0 \\ 0 & { - 0.3} \\ \end{array} } \right], \, \;D_{1} = \left[ {\begin{array}{*{20}c} { - 0.2} & {0.1} \\ 0 & {0.1} \\ \end{array} } \right], \\ {N}_{1} = \left[ {\begin{array}{*{20}c} {0.2} & {0.1} \\ {0.1} & {0.2} \\ \end{array} } \right],\;A_{2} = \left[ {\begin{array}{*{20}c} { - 0.1} & {0.01} \\ {0.02} & { - 0.1} \\ \end{array} } \right],\;{B}_{2} = \left[ {\begin{array}{*{20}c} {0.1} & {0.1} \\ {0.2} & { - 0.3} \\ \end{array} } \right],{C}_{2} = \left[ {\begin{array}{*{20}c} {0.2} & {0.1} \\ {0.1} & {0.2} \\ \end{array} } \right], \, G_{2} = \left[ {\begin{array}{*{20}c} {0.01} & {0.1} \\ {0.1} & { - 0.1} \\ \end{array} } \right],\; \\ \, \quad {D}_{2} = \left[ {\begin{array}{*{20}c} { - 0.1} & {0.2} \\ 0 & {0.2} \\ \end{array} } \right],{N}_{2} = \left[ {\begin{array}{*{20}c} {0.1} & {0.2} \\ {0.1} & {0.2} \\ \end{array} } \right],\;F_{1} (k) = \left[ {\begin{array}{*{20}c} {0.85\delta } & 0 \\ 0 & {0.85\delta } \\ \end{array} } \right],\;F_{2} (k) = \left[ {\begin{array}{*{20}c} {0.95\delta } & 0 \\ 0 & {0.95\delta } \\ \end{array} } \right],\,\,\,\left| \delta \right| \le 1,\quad \\ \;H_{1} = \left[ {\begin{array}{*{20}c} {0.5} & 0 \\ 0 & {0.7} \\ \end{array} } \right],\quad H_{2} = \left[ {\begin{array}{*{20}c} {0.1} & 0 \\ 0 & {0.3} \\ \end{array} } \right],\quad f(x(k)) = \left[ {\begin{array}{*{20}c} {0.3x_{1} + 0.2\sin (x_{1} )} \\ {0.5x_{2} + 0.2\sin (x_{2} )} \\ \end{array} } \right]. \\ \end{gathered}$$

Take $\mu = 0.5, \, \gamma = 0.2, \, \varepsilon = 0.3, \, c_{1} = 0.8,{\overline{R}} = {I}_{4} , \, M = 10.$ By using Matlab LMI Toolbox to solve inequalities (31) and (32), we can get a set of feasible solution as follows:

$$ \begin{gathered} \overline{S}_{1} = \left[ {\begin{array}{*{20}c} {0.8410} & {0.0061} & 0 & 0 \\ {0.0061} & {0.8427} & 0 & 0 \\ 0 & 0 & {0.8410} & {0.0061} \\ 0 & 0 & {0.0061} & {0.8427} \\ \end{array} } \right],{\kern 1pt} \; \hfill \\ \overline{K}_{1} = \left[ {\begin{array}{*{20}c} {0.0465} & {0.1833} \\ {0.1833} & { - 0.1540} \\ \end{array} } \right],\;\overline{L}_{1} = \left[ {\begin{array}{*{20}c} { - 0.8362} & {0.0793} \\ {0.0793} & { - 0.9370} \\ \end{array} } \right], \hfill \\ \end{gathered} $$

$$ \overline{S}_{2} = \left[ {\begin{array}{*{20}c} {0.9507} & {0.0059} & 0 & 0 \\ {0.0059} & {0.9527} & 0 & 0 \\ 0 & 0 & {0.9507} & {0.0059} \\ 0 & 0 & {0.0059} & {0.9527} \\ \end{array} } \right], $$

$$ \begin{gathered} \; \hfill \\ \overline{K}_{2} = \left[ {\begin{array}{*{20}c} {0.1681} & {0.1298} \\ {0.1298} & { - 0.0757} \\ \end{array} } \right],\;\;\overline{L}_{2} = \left[ {\begin{array}{*{20}c} { - 0.7173} & {0.4640} \\ {0.4640} & { - 0.7401} \\ \end{array} } \right],\quad c_{2} = 52.85. \hfill \\ \end{gathered} $$

The controller gain matrices are

$$ K_{1} = \left[ {\begin{array}{*{20}c} {0.0537} & {0.2172} \\ {0.2193} & { - 0.1844} \\ \end{array} } \right],\quad \, K_{2} = \left[ {\begin{array}{*{20}c} {0.1759} & {0.1353} \\ {0.1370} & { - 0.0804} \\ \end{array} } \right], $$

and the observer gain matrices are

$$ L_{1} = \left[ {\begin{array}{*{20}c} { - 0.9957} & {0.0978} \\ {0.1106} & { - 1.1124} \\ \end{array} } \right], \, \quad {L}_{2} = \left[ {\begin{array}{*{20}c} { - 0.7574} & {0.4925} \\ {0.4924} & { - 0.7805} \\ \end{array} } \right]. $$

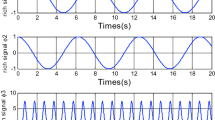
According to Theorem 2, system (1) is finite-time stabilized with respect to $(0.8,52.85,I_{4} ,10)$ via an observer-based control (28). Figures 3 and 4 show the states and estimate states of the closed-loop system with $\;\delta { = }1.$ Figure 5 shows the evolution of $\overline{x}^{T} (k)\overline{R}\overline{x}(k)$. In addition, it can be seen that, the state responses satisfy

$$ \overline{x}^{T} (k)\overline{R}\overline{x}(k) \le 52.85,\quad k \in \{ 1,2, \cdots ,10\} . $$

Fig. 3

Responses of state $x_{1} (k)$ and the estimate of $x_{1} (k)$ in Example 2

Fig. 4

Responses of state $x_{2} (k)$ and the estimate of $x_{2} (k)$ in Example 2

Fig. 5

The trajectory of $\overline{x}^{T} (k)\overline{R}\overline{x}(k)$ in Example 2

For $\mu = 0.5,\gamma = 0.2,\varepsilon = 0.3,\overline{R} = I_{4} ,$$c_{1} = 0.8$ and $M \in \left\{ {2,5,8,10} \right\},$ the smallest eligible value of the parameter $c_{2}$ is computed by using Theorem 2, and the obtained results are listed in Table 2.

Table 2 The smallest eligible value of the parameter ${\text{c}}_{2}$

From Table 2, it can be seen that the smallest eligible value of the parameter $c_{2}$ increases as M increases.

5 Conclusions

Unlike most existing research results focusing on Lyapunov stability property of switched system, this paper studies the finite-time stability for uncertain nonlinear switched discrete-time system. As the main contribution of this paper, for a class of nonlinear switched discrete-time system with uncertain under arbitrary switching, sufficient conditions of finite-time stability have been given by constructing the Lyapunov function. Then using the matrix inequality technique, and based on the analysis result, the sufficient conditions to guarantee that the closed-loop system is finite-time stability via observer-based control are derived. Finally, two numerical examples are given to demonstrate the validity of the proposed results. It should be also pointed out that how to extend the main results to the observer-based $H_{\infty }$ finite-time control for discrete-time switched systems with time delays and nonlinear disturbance, are very meaningful topics that deserves further exploration.