A Compact Low-Loss 6-bit DMTL Phase Shifter Using a Novel Three-State Unit Cell

Abstract

In this paper, a novel small-size, low-loss 6-bit MEMS phase shifter is designed, analyzed, and simulated. The proposed structure includes 17 unit cells, and each unit cell can generate three different phase shifts (i.e., 5.625-, 11.25-, and 22.5-degree phase shifts). The designed unit cell consists of a coplanar waveguide transmission line, a MEMS, and two-pair metal–air–metal bridges. The bridge capacitors are electrically in series and are actuated in three different modes. In each mode, the distributed capacitance of the transmission line and the phase velocity are changed to achieve a phase shift. As the novelty of this design, the number of unit cells is reduced from 64 (which is the case in a conventional 6-bit phase shifter) to only 17. Therefore, the total length of the 6-bit phase shifter is considerably reduced. The designed structure is simulated using Ansoft HFSS and IntelliSuite. Based on the simulation results, the lateral size of the phase shifter is only 8.5 mm; the root-mean-square (RMS) phase error is 1.35, and the average loss is 1.2 dB. A step-by-step fabrication process is also proposed for designing the DMTL phase shifter. The designed phase shifter can be easily scaled to other frequencies for radar and satellite applications that require more bits.

1 Introduction

Microelectromechanical systems (MEMS) technology is used in micron and submicron devices that use standard integrated circuit fabrication processes, such as photolithography, etching, and bonding. This technology makes it possible to fabricate small-size devices with high functionality, precision, and performance. Based on these properties, MEMS devices and systems are found in many applications such as automobiles, aerospace, medicine, and telecommunication. Radiofrequency (RF) MEMS is one of the critical areas which deals with communication devices and systems. Low-loss performance at high frequencies (up to 100 GHz), high isolation capability, low DC power consumption, and high linearity are the main advantages of RF MEMS devices and systems. These features make RF MEMS devices suitable for special applications such as radar, phased array antennas, satellite communication, and military systems. The main challenge of the RF MEMS devices is their large size [25].

RF MEMS phase shifters are the main component of phased array systems and a key element for modern radar and communication systems. Phase shifters are generally classified into two main groups: analog and digital. Analog phase shifters use either semiconductor varactors [21] or MEMS counterparts [26] and can continuously change the phase from 0° to 360°. Digital phase shifters use either FET or MMIC switches [19, 20] or MEMS switches [22] which provide a discrete set of phase shifts. However, due to the limited control on bridge height before the bridge snap, analog phase shifters have relatively small phase shifts. Digital MEMS phase shifters have resolved this problem. Hence, based on their large phase shift capability and simple operation, digital MEMS phase shifters have been investigated in many research papers. MEMS phase shifters are generally designed and fabricated in four basic types, i.e., reflected type [12, 23, 29], switched line [11, 24], loaded line [18, 30], and distributed MEMS transmission line (DMTL) [5, 6, 8, 9, 14, 27].

Many studies have focused on DMTL phase shifters because of their simple modeling, very wideband performance, and high-frequency operation. This method is based on the capacitive loading of the transmission line (e.g., by using coplanar waveguide) in a periodical manner using a MEMS switch by controlling the switch height. Hence, the distributed capacitance on the transmission line and the phase velocity are varied so that the desired phase shift is achieved. For the first time, DMTL analog phase shifters were introduced by Barker and Rebeiz in 1998 [4]. Their structure includes a coplanar waveguide (CPW) transmission line and a MEMS bridge located on top of the signal line. The bridge displacement changes the line capacitance, and the desired phase shift can be achieved.

Recently, the low-loss compact size designs of MEMS phase shifters have been the main challenge for designers. To fabricate a compact phase shifter, it is necessary to have a significant phase shift per unit cell, which is only possible by increasing the capacitance ratio of the phase shifter. However, a high capacitance ratio increases the return loss and degrades matching. During the past few years, different methods have been utilized to design small-size low-loss DMTL phase shifters. Employing metal–air–metal (MAM) capacitors [15], space-filling curves technique [7], and glass substrates instead of high resistive silicon (HRS) counterparts [13] has been a significant effort to reduce the losses of DMTL phase shifters. Using both capacitors and inductors in DMTL phase shifters around the resonance frequency is another way to obtain a significant phase shift per unit cell [1, 2]. A miniature DMTL phase shifter that uses both tunable capacitors and inductors was reported by F. Ling [17]. This phase shifter consists of two series ohmic contact switches, a MEMS shunt switch, and two MAM capacitors. When the cell capacitance under the actuation condition is increased to obtain a significant phase shift, the value of the tunable inductor also increases. This keeps the down impedance matched to the port impedance as the phase is further shifted.

To achieve high accuracy in digital phase shifters, DMTL phase shifters with more bits (e.g., with 5 or 6 bits) are required. However, in more-bit phase shifters, the number of unit cells is dramatically increased. Hence, the large size of this type of phase shifter is their main drawback. A small-size, two-state 6-bit phase shifter is proposed by Afrang et al. [3]. Their structure consists of a standard CPW, a MEMS bridge, two additional electrodes near the centerline under the bridge, and two MAM static capacitors; the phase shifter is only 12.8 mm and includes only 32 phase states. The MEMS bridge is actuated twice to create two states (5.625 and 11.25 degrees) in a unit cell. The configuration of two states in a unit cell can reduce the size and loss simultaneously.

Producing a significant phase shift per unit cell is another technique, which is used to decrease the number of unit cells [10]. In this technique, instead of using identical unit cells, three different types of MEMS switches, which can perform various phase shifts, are used. This structure includes only 29 switches instead of 64 switches in a 6-bit phase shifter.

In this paper, a new design of a three-state compact DMTL phase shifter with low actuation voltage and high reliability is proposed. The design is based on three individual switches in a small-size unit cell, which can produce three-phase states per unit cell and reduce the number of unit cells from 64 to 17.

The structure of the designed phase shifter is identical to that of universal DMTL phase shifters if the MAM bridges are excluded. The only difference is the MAM bridges, which are added to the conventional structure to obtain a three-state phase shift using one unit cell. Therefore, this is one of the innovations of the designed structure in which the one-state unit cell has become a three-state unit cell without adding complexity.

The three-state unit cell in the present study has been implemented more quickly than in Ref. [3]. In [3], implanting a stopper increases the fabrication process steps. One of the innovations of our unit cell is its similarity to one-state conventional DMTL phase shifters, so there is no complexity in this design. The only difference is in the number of bridges and actuation voltage. A three-state unit cell can create a phase shift of 22.5°, enabling us to design a compact 6-bit DMTL phase shifter. A universal one-state DMTL phase shifter consists of one MEMS bridge and two static MAM capacitors. When the MEMS bridge is actuated, the desired phase shift is achieved. In two- and three-state unit cells, a significant phase shift can be obtained by the same unit cell size or small increases in the unit cell size. At a particular operating frequency, a large unit cell is required to achieve a significant phase shift. This leads to the rise in the Bragg frequency and hence a reduction in the phase shifter linearity. Therefore, there is a trade-off between the Bragg frequency and the phase shift linearity. In an appropriate design, the unit cell size is selected so that the linearity of the phase shifter is maintained. In three-state unit cells with a phase shift of 22.5°, the ratio of the Bragg frequency to the operating frequency is 1.97. This ratio for two-state unit cells is 2.4. Hence, the Bragg frequency is one of the challenges in three-state unit cells.

The remainder of this paper includes four sections: The structure of DMTL is presented in Sect. 2. Section 3 consists of the analysis of the proposed structure. Simulation results and the fabrication process of the proposed phase shifter are presented in Sects. 4 and 5, respectively. Finally, the concluding remarks are given in the last section.

2 DMTL Phase Shifter

2.1 Unit Cell Design

A DMTL phase shifter consists of a CPW T-line and several MEMS switches periodically on top of the signal line. When the switches are actuated, they move downward, and the loading capacitance of the transmission line is changed; therefore, the phase velocity is varied, and a phase shift is achieved. The relationship between phase shift and the loading capacitance in a DMTL phase shifter is expressed in Eq. (1) [25]:

$$ \Delta \varphi = \frac{{360 \times s \times f \times {Z_0} \times \sqrt {{\varepsilon_{{\text{reff}}}}} }}{c}\left( {\frac{1}{{Z_d}} - \frac{1}{{Z_u}}} \right)$$

(1)

where s is the distance between the MEMS bridges, Z₀ is the characteristic impedance of the CPW t-line, f is the operating frequency, and c is the light velocity; Z_d and Z_u are the line impedance in, respectively, down- and up-state of the switches.

When a switch is actuated, the line loading capacitance and the line impedance change (Eq. 2).

$$ {Z_{{\text{load}}}} = \sqrt {\frac{{s{L_t}}}{{s{C_t} + {C_{{\text{load}}}}}}} \times \sqrt {1 - {{(\frac{f}{{f_B}})}^2}} $$

(2)

where L_t, C_t, C_load, and, f_B are the line inductance per unit length, line capacitance per unit length, loading capacitance, and Bragg frequency, respectively.

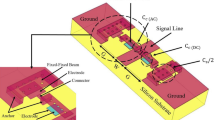
The main challenge in digital DMTL phase shifters is their large size, i.e., requiring more unit cells, especially in those with more bits. To realize a compact DMTL phase shifter, either the size or the number of unit cells should be decreased. However, based on Eq. (1), if the unit cell size (s) is reduced, the phase shift decreases; furthermore, for a given phase shift, the number of unit cells increases, and the overall size of the device becomes large. To resolve this problem, we proposed a novel three-state unit cell, which is shown in Fig. 1.

Fig. 1

Proposed unit cell for DMTL phase shifter

According to Fig. 1, the proposed structure includes a CPW T-line, a MEMS bridge on the centerline, and two-pair metal–air–metal (MAM) bridges. One pair of MAM bridges is located on a glass substrate (MAM-2), and another pair is near the ground line (MAM-1). This design employs three different loading capacitances of the transmission line, which produce three other phase states (5.625, 11.25, and 22.5 degrees). This three-state unit cell is used to design a small-size 6-bit DMTL phase shifter. Generally, 64 one-state unit cells are required to realize a 6-bit DMTL phase shifter. In the proposed structure, the number of unit cells needed to implement a 6-bit phase shifter is decreased to 17, so the total length of the phase shifter is considerably reduced (more than 35%). Furthermore, because of using fewer unit cells, the loss of the phase shifter also reduces. Based on our knowledge, the designed 6-bit DMTL phase shifter is the smallest capacitive-type DMTL phase shifter that has been studied so far and is very suitable for phased array antenna applications.

The equivalent circuit of the proposed unit cell is shown in Fig. 2. In this figure, R_t, L_t, and C_t represent the transmission line electrical characteristics; C_b, C_MAM-1, and C_MAM-2 denote the capacitances of the MEMS bridge, MAM-1, and MAM-2, respectively. These three capacitances are electrically in series and change the line loading capacitance based on the actuation sequence.

Fig. 2

Equivalent circuit of the proposed unit cell for DMTL phase shifter

2.2 Operating Principle

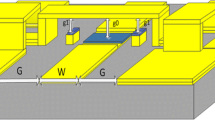
The three-state unit cell proposed in this study provides three different phase shifts. For a phase shift of 5.625°, the MAM-1 switch is actuated. When the MEMS switch is actuated, a phase shift of 11.25° is achieved, and to realize a phase shift of 22.5°, both MEMS and MAM-2 bridges are actuated. Phase shifters with more bits (5- and 6-bit phase shifters) require more switches. Our designed 6-bit phase shifter consists of only 17 unit cells. Unit cells U1 and U17 provide only 5.625° and 11.25° phase shifts, while U2 to U16 create only 11.25° and 22.5° shifts. Hence, the corresponding switches are only actuated to achieve the desired phase shift.

Figure 3 shows the operating principle of the designed unit cell for different phase states.

Fig. 3

Operating principle of the proposed DMTL phase shifter. a Up-state, b 5.625 degrees, c 11.25 degrees, and d 22.5 degrees

As shown in Fig. 3a, when the bridges are in the up-states, the phase shifter is in the primary state, called the 0-degree state. In this state, the loading capacitance is C_up:

$$ {C_{up}} = {\left( {\frac{1}{{C_b}} + \frac{1}{{{C_{MAM - 1}}}} + \frac{1}{{{C_{MAM - 2}}}}} \right)^{ - 1}} $$

(3)

when MAM-1 bridges are actuated, 5.625-degree phase shift is achieved (Fig. 3b). The loading capacitance is the series combination of the two other bridges capacitances (Eq. 4).

$$ {C_{{\text{down}}1}} = {\left( {\frac{1}{{C_b}} + \frac{1}{{{C_{\text{MAM - 2}}}}}} \right)^{ - 1}} $$

(4)

To achieve an 11.25-degree phase shift, only the MEMS bridge is actuated, and the loading capacitance is the series combination of capacitors MAM-1 and MAM-2 (Fig. 3c).

$$ {C_{{\text{down2}}}} = {\left( {\frac{1}{{{C_{{\text{MAM}} - 1}}}} + \frac{1}{{{C_{\text{MAM - 2}}}}}} \right)^{ - 1}}$$

(5)

When both MAM-2 and MEMS bridges are actuated, the third state of the designed unit cell is realized, and a 22.5-degree phase shift is obtained (Fig. 3d).

$$ {C_{{\text{down3}}}} = {\left( {\frac{1}{{{C_{{\text{MAM}} - 1}}}}} \right)^{ - 1}} $$

(6)

2.3 The Design Process of the Proposed Structure

Generally, in a capacitive-type DMTL phase shifter, when the capacitance of a loaded line increases, the impedance of the transmission line decreases. Hence, the unloaded impedance of the line must be greater than the highest load impedance. Accordingly, we assume that the designed phase shifter operates in a 50 Ω system. The loaded impedance of the DMTL in this system can be calculated by [23]:

$$ {Z_{{\text{line}}}} = 50 \times \sqrt {\frac{{1 \pm {\Gamma_{{\text{in}}}}}}{{1 \mp {\Gamma_{{\text{in}}}}}}} ,\;\left( {{Z_u} = 50 \times \sqrt {\frac{{1 + {\Gamma_{{\text{in}}}}}}{{1 - {\Gamma_{{\text{in}}}}}}} \,\,\,,\,\,\,\,{Z_d} = 50 \times \sqrt {\frac{{1 - {\Gamma_{{\text{in}}}}}}{{1 + {\Gamma_{{\text{in}}}}}}} } \right) $$

(7)

where Γ_in is the input return loss and is defined as:

$$ {\Gamma_{in}} = {10^{\frac{{R{L_{{\text{max}}}}}}{20}}}$$

(8)

where RL_max denotes the maximum return loss. Table 1 presents the loaded impedances of the up- and down-state positions (Z_u and Z_d) for a given return loss. For an ideal condition, Γ_in = 0, the system and the loaded transmission line are matched.

Table 1 Up- and down-state line impedances for different return losses

To achieve a significant phase shift per unit cell and a low return loss characteristic, we assume RL_max = -14 dB, so the up-state and down-state loading impedances are 61.2 and 40.8 Ω, respectively. According to Table 1, when we choose RL_max = − 14 dB, the largest phase shift corresponds to a unit cell with a significant reflected power loss at the input.

Assuming that the maximum phase shift per unit cell equals 22.5 degrees, the Bragg frequency is 1.97 times the operating frequency based on Eq. (9):

$$ \frac{{f_B}}{f} = \sqrt {{{\left( {\frac{{360\left( {{Z_u} - {Z_d}} \right)}}{{\pi \Delta \varphi {Z_u}}}} \right)}^2} + 1} \simeq \frac{{360\left( {{Z_u} - {Z_d}} \right)}}{{\pi \Delta \varphi {Z_u}}} $$

(9)

Equation 1 is used to calculate the unit cell size (s), operating frequency (f), and characteristic impedance of the line (Z₀). For a capacitive-type DMTL phase shifter, when the capacitance of a loaded line increases, the impedance of the transmission line decreases. Consequently, the unloaded impedance of the line (Z₀) must be greater than the highest load impedance (Z_u). A glass substrate is selected for this design because of its excellent phase shift/loss property [20]. Assuming s = 500 µm and f = 30 GHz, the characteristic impedance (Z₀) is calculated as 99 Ω. Since the proposed unit cell can produce three different phase shifts of 5.625, 11.25, and 22.5 degrees, based on Eq. (1), the loaded impedances of the 5.625° and 11.25° phase shifts are 54 Ω and 49 Ω, respectively.

To determine the capacitance of the loaded line in all states of the proposed unit cell, we consider Eqs. (10)–(14):

$$ {f_B} = \frac{1}{{\pi \sqrt {s{L_t}\left( {s{C_t} + {C_b}} \right)} }} $$

(10)

$$ {C_u} = \frac{{\left( {Z_0^2 \times {x^2} - Z_{up}^2} \right){Z_{d3}}}}{{Z_0^2Z_u^2\pi \,{f_B}}} $$

(11)

$$ {C_{d1}} = \frac{{\left( {Z_0^2 \times {x^2} - Z_{d1}^2} \right){Z_{d3}}}}{{Z_0^2Z_{d1}^2\pi \,{f_B}}} $$

(12)

$$ {C_{d2}} = \frac{{\left( {Z_0^2 \times {x^2} - Z_{d2}^2} \right){Z_{d3}}}}{{Z_0^2Z_{d2}^2\pi \,{f_B}}} $$

(13)

$$ {C_{d3}} = \frac{{Z_0^2 \times {x^2} - Z_{d3}^2}}{{Z_0^2{Z_{d3}}\pi \,{f_B}}} $$

(14)

where $x = \sqrt {1 - {{(\frac{f}{{f_B}})}^2}}$; C_u is the capacitance of the loaded line in the up-state position; C_d1, C_d2, and C_d3 are the capacitances of the loaded line for 5.625°, 11.25°, and 22.5° phase shifts, respectively. Table 2 shows the results of the loaded line capacitance.

Table 2 Calculation results of the loaded capacitance of the proposed unit cell

Based on Table 2 and Eqs. (3)–(6), the capacitances of MEMS, MAM-1, and MAM-2 bridges are 56, 88, and 140 fF, respectively (Table 3). Considering Fig. 1 and Z₀ = 99 Ω, the dimensions of the CPW transmission line are selected at 130/120/130 µm.

Table 3 Calculation results of the bridge capacitances

3 Analysis of the Proposed DMTL Phase Shifter

3.1 Frequency Analysis

In this section, the scattering parameters and the phase shift of the designed phase shifter are calculated using MATLAB. For this purpose, the ABCD matrix method is employed. Figure 4 shows the circuit for obtaining the S₁₁ of a lossy transmission line. In this figure, Z₀₁ is the characteristic impedance of the lossy transmission line and Z₀₂ is the matched transmission line impedance. For the matched transmission line, S₁₁ can be calculated using ABCD matrix parameters as follows [28]:

$${S_{11}} = \frac{{A + {Y_{02}}.B - {Z_{02}}.C + D}}{{A + {Y_{02}}.B + {Z_{02}}.C + D}}$$

(15)

Fig. 4

Circuit model for calculating S₁₁

The ABCD matrix of a loaded lossy transmission line is calculated as:

$$ \left[ \begin{gathered} A\,\,\,\,\,\,\,\,\,\,\,\,\,\,B \hfill \\ C\,\,\,\,\,\,\,\,\,\,\,\,\,D \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \cosh (\gamma .s)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{Z_{01}}.\sinh (\gamma .s) \hfill \\ \frac{1}{{{Z_{01}}}}\,.\sinh (\gamma .s)\,\,\,\,\,\,\,\,\,\,\,\,\cosh (\gamma .s)\, \hfill \\ \end{gathered} \right]\,\, \times \left[ \begin{gathered} 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \hfill \\ \frac{1}{{Z_l}}\,\,\,\,\,\,\,\,\,\,1 \hfill \\ \end{gathered} \right]$$

(16)

where Z_l is the loaded impedance, s is the unit cell length, and γ is the complex propagation constant that is expressed as:

$$ \gamma = \alpha + j\beta = \frac{{s{R_t}}}{{2{Z_{01}}}} + j\frac{\omega }{{\nu_p}} $$

(17)

$$ {\nu_p} = \frac{s}{{\sqrt {s{L_t}(s{C_t} + {C_b})} }} $$

(18)

where α is the attenuation constant, β is the propagation constant, Rt is the transmission line resistance per unit length, and νp is the propagation velocity.

The inductance per unit length and capacitance per unit length of the CPW transmission line are calculated using Eqs. (19) and (20), respectively; the loaded impedance of the transmission line is calculated from Eq. (21):

$$ {L_t} = \frac{{{Z_0} \times \sqrt {{\varepsilon_{{\text{reff}}}}} }}{c} $$

(19)

$$ {C_t} = \frac{{\sqrt {{\varepsilon_{{\text{reff}}}}} }}{{{Z_0}\,c}} = \frac{{L_t}}{Z_0^2} $$

(20)

$$ {Z_{01}} = {Z_l} = \sqrt {\frac{{s{L_t}}}{{s{C_t} + {C_{{\text{load}}}}}}}$$

(21)

Figure 5 shows a circuit model for calculating S₂₁. To calculate S₂₁ from ABCD matrix parameters in Fig. 5, Eq. (22) can be used.

$$ {S_{21}} = \frac{2}{{A + {Y_{02}}.B + {Z_{02}}.C + D}}$$

(22)

Fig. 5

Circuit model for calculating S₂₁

The phase shift is calculated using the difference between the phase angles of S₂₁ in the up- and down-state positions (Eq. 23).

$$ {\text{Phase}}\,\,\,{\text{Shift}}\, = \,{\text{Phase}}\,({S_{21}})\left| {_{\text{Up - state}}\, - } \right.{\text{Phase}}\,({S_{21}})\left| {_{\text{Down - state}}} \right. $$

(23)

A 6-bit DMTL phase shifter can be implemented using six building blocks, including 5.625°, 11.25°, 22.5°, 45°, 90°, and 180° blocks. The 45°, 90°, and 180° blocks can be realized using 2, 4, and 8 unit cells, respectively. Hence, to implement a 6-bit digital phase shifter, 17 unit cells are required, and the lateral size of the phase shifter is only 8.5 mm.

Figures 6, 7, and 8 illustrate the calculation results of the return loss, insertion loss, and phase shift of the six building blocks of the 6-bit phase shifter.

Fig. 6

Calculation results of the return loss of six building blocks of the proposed phase shifter

Fig. 7

Calculation results of the insertion loss of six building blocks of the proposed phase shifter

Fig. 8

Calculation results of the phase shift of six building blocks of the proposed phase shifter

As shown in Figs. 6 and 7, the calculated insertion loss and return loss of the proposed structure are better than − 10.1 and 0.47 dB, respectively. Moreover, the phase shift is in good agreement with ideal states.

3.2 Electrostatic Analysis

The actuation voltage of the MEMS and MAM bridges is calculated in this section. Generally, the pull-in voltage of a MEMS switch is presented by Eq. (24):

$$ {V_{\text{Pull - in}}} = \sqrt {\frac{8k}{{27{\varepsilon_0}A}}\,.{g_0}^3} $$

(24)

where k is the spring constant of the structure, A is the overlapping area of the electrodes, g₀ is the gap between the two electrodes, and ε₀ is the air permittivity. The proposed structure includes three fixed–fixed cantilever bridges (Fig. 9) for which the spring constant can be expressed as [25]:

$$ k = 32Ew{\left( \frac{t}{l} \right)^3} \times \frac{1}{{8{{\left( \frac{x}{l} \right)}^3} - 20{{\left( \frac{x}{l} \right)}^2} + 14\left( \frac{x}{l} \right) - 1}} $$

(25)

where E, w, t, and l are, respectively, Young’s modulus, width, thickness, and length of the cantilever beam.

Fig. 9

Fixed–fixed cantilever switch

Two factors determine the dimensions of the MEMS and MAM parallel plate capacitors: pull-in voltage and fringing effect. Pull-in voltage is directly proportional to the bridge length and width. It is inversely proportional to the bridge thickness, so these parameters are considered in designing MEMS and MAM bridges.

The fringing effect is considered for the bridges in the up-state. The fringing field capacitance of MEMS and MAM capacitors accounts for a substantial portion of the total capacitance. This has a lower impact on bridges that are wider and have a narrower air gap. For a capacitor with a width of 100 µm and an air gap of 4 µm, the fringing capacitance is about 60% of the initial capacitance, while for an air gap of 1.5 µm, this percentage is less than 20% [251]. In our design, the fringing effect is about 10%. The bridges’ dimensions are presented in Table 4 and Fig. 10.

Table 4 Mechanical and electrical properties of MEMS and MAM bridges

Fig. 10

a Dimensions of the proposed three-state unit cell (all sizes are in µm), b parallel-plate capacitor, and c fringing effect in parallel-plate capacitors

Based on Eq. (25) and Table 4, the spring constants of the MEMS, MAM-1, and MAM-2 bridges are 1.964, 0.77, and 1.16 N/m, respectively. Using Eq. (24), the pull-in voltages of these bridges are 3.3, 2.51, and 2.34 V, respectively.

4 Simulation of the Proposed 6-bit DMTL Phase Shifter

The structure of the proposed DMTL phase shifter is simulated in this section. The scattering parameters, phase shift, and bridges pull-in voltage are calculated in this simulation. To verify the calculations, frequency simulation is carried out using ANSOFT HFSS, and electrostatic simulation is performed using IntelliSuite.

4.1 Frequency Simulation

Generally, there are two different methods to implement a 6-bit phase shifter: the bit-level and unit-cell-level methods. The bit-level method, also known as the binary-weighted method, is mainly used by designers due to its simplicity in actuating electronic circuits. In this method, six building blocks, i.e., 5.625°, 11.25°, 22.5°, 45°, 90°, and 180°, are connected to form a 6-bit phase shifter. These six building blocks are actuated based on the binary-weighted phase states. Based on the designed three-state unit cell, the 5.625°, 11.25°, and 22.5° blocks can be implemented using three individual unit cells. The 45°, 90°, and 180° blocks consist of 2, 4, and 8 unit cells, respectively (Fig. 11).

Fig. 11

Bit-level actuation for 6-bit DMTL phase shifter using the proposed three-state unit cell

Each unit cell in these large phase shift blocks acts in the third state (22.5°). Accordingly, the 6-bit DMTL phase shifter based on the bit-level method consists of only 17 unit cells with an 8.5 mm lateral size, which is considerably small. The return loss, insertion loss, and phase shift simulation results of the six building blocks are shown in Figs. 12 and 13. According to Fig. 12, each of these blocks has good performance. For 64 states of the 6-bit phase shifter, when the blocks with large phase shift unit cells (22.5°, 45°, 90°, and 180°) are actuated to obtain the desired phase shift, the return loss is degraded, and a significant phase shift error occurs. This unwanted problem is the lack of proper impedance matching between the larger block and its side blocks (mainly when the larger block is actuated and its side block is in an un-actuated state). If the three-state unit cell size increases, the impedance matching will be better, and the mentioned problem can be resolved. However, this would contradict the primary goal of our design, which is achieving a compact 6-bit phase shifter. It should be mentioned that in 6-bit phase shifters that use one-state unit cells (5.625° cells) or two-state unit cells (11.25° cells), the impedance matching between the building blocks is easily achieved. However, due to a large number of unit cells (64 unit cells in one-state and 32 in two-state designs), the total size is large.

Fig.12

Simulation results of the return loss and insertion loss of six building blocks of the proposed 6-bit DMTL phase shifter

Fig. 13

Simulation results of phase shift of six building blocks of the proposed phase shifter

In the present study, the unit-cell-level method is used (instead of the binary-weighted method) to achieve appropriate return losses for all 64 states and increase the accuracy of phase shifts by maintaining the same number of cells (17 cells). In this method, to implement each of 64 states of the 6-bit phase shifter, the unit cells are used first in minor phase shift modes (5.625° and 11.25°). Unit cells U1 and U17 are only actuated in 5.625° and 11.25° phase shift modes, and the other unit cells (U2 to U16) are actuated in 11.25° and 22.5° modes (Fig.14). Table 5 shows the sequence for unit cells actuation. In this table, the subscripts 1, 2, and 3 indicate, respectively, 5.625°, 11.25°, and 22.5° phase shifts of a unit cell.

Fig. 14

Unit-cell-level actuation for the proposed 6-bit DMTL phase shifter using three-state unit cells

Table 5 Unit cell actuation sequence for 64 phase states

To obtain an appropriate impedance matching between unit cells and hence a low return loss and low phase shift error for the designed phase shift, the priority of unit cells U2-U16 is to provide a 11.25º phase shift. A phase shift of 22.5° is the second priority of unit cells to achieve the desired phase state (Table 5). For example, to implement phase state no. 6 (28.125°), we can use two 11.25° and one 5.625° unit cells instead of one 22.5° and one 5.625° unit cells. As another example, for obtaining a 45° shift, four 11.25° unit cells are implemented instead of two 22.5° unit cells, so a good impedance matching is realized. Table 6 compares some phase states of a 6-bit phase shifter using the two different methods.

Table 6 Comparison of different implementations of phase states

The proposed 6-bit DMTL phase shifter is simulated using ANSOFT HFSS to investigate frequency response. Figure 15 shows the insertion loss and return loss of the 64 states of the 6-bit phase shifter. The phase shift errors for various cases are given in Table 7, and the RMS phase error is shown in Fig. 16. Based on the frequency simulation results, the average loss is 1.2 dB, and the RMS phase error is 1.35°.

Fig. 15

Scattering parameters of 64 states of the proposed 6-bit DMTL phase shifter. a Return loss, b insertion loss

Table 7 Phase shift error of 64 states of the proposed 6-bit DMTL phase shifter

Fig. 16

Phase shift error of 64 states of the proposed 6-bit DMTL phase shifter

4.2 Electrostatic Simulation

An electrostatic simulation is performed in IntelliSuite to verify the pull-in voltage results calculated for the MEMS and MAM bridges of the designed unit cell. Table 8 presents the mechanical and electrical properties of the bridges.

Table 8 Comparison of the results of electrostatic calculation and simulation of bridges

The three bridges used in the designed three-state unit cell are clamped–clamped microbeams that are located on the substrate. For better illustration, the bridges are simulated, and anchors specify the boundary conditions. The pull-in voltage, stress distribution, and charge density of the MEMS, MAM-1, and MAM-2 bridges are shown in Figs. 17, 18, and 19, respectively. Based on the simulation results, the maximum stress distribution on the bridges is significantly smaller than the maximum yield stress of the bridge material (gold). The electrostatic simulation results are compared with the calculation results in Table 8.

Fig. 17

Electrostatic simulation results of the MEMS bridge. a Charge density, b pull-in voltage, and c stress distribution

Fig. 18

Electrostatic simulation results of the MAM-1 bridge. a Charge density, b pull-in voltage, and c stress distribution

Fig. 19

Electrostatic simulation results of the MAM-2 bridge. a Charge density, b pull-in voltage, and c stress distribution

Table 9 compares the performance of the proposed DMTL phase shifter and the previous state-of-the-art DMTL phase shifters. Based on our knowledge, the designed 6-bit DMTL phase shifter is the smallest phase shifter that has been designed so far.

Table 9 Comparison of the proposed DMTL phase shifter and the current state-of-the-art phase shifters

5 Fabrication Process

Usually, there are two mismatches in MEMS phase shifters. The first mismatch is desired and creates a significant phase shift. The second mismatch is due to MEMS process variations, including different unit cells and unsuitable bridge air gap. The mismatch between different unit cells can be resolved using an appropriate actuation voltage. The air gap of the bridge determines the loading capacitance and phase shift accuracy. Any mismatch in the air gap leads to a significant phase error in MEMS phase shifters. In practice, to resolve this problem, the air gap is considered a little larger than required. Therefore, an offset voltage is first applied to the bridge to adjust the air gap at the desired value. Then, the bridge is ready for the actuation to create a phase shift. This issue is considered in the present paper. The structure of the designed three-state unit cell is similar to conventional DMTL phase shifters, and the only difference is in the number of bridges and pull-in voltage. Therefore, there are no more mismatch cases in the designed structure compared to general structures.

The MEMS technology has fully matured and evolved in recent years. Therefore, by following the fabrication process presented in this section, the measurement results will undoubtedly agree with the analysis and the simulation results [16]. The proposed fabrication process of the designed unit cell for the DMTL phase shifter is shown in Fig. 20. In the first step, a 0.2-µm SiCr layer was sputtered on a glass substrate using a lift-off process to conform the biased lines for three bridges (Fig. 20a). Next, to define the CPW lines, MAM lower electrodes and bridge anchors, first, a 1000Å thin Cr layer and, then, a 3000 Å thin gold layer were sputtered and patterned using the lift-off process (Fig. 20b). To form a dielectric layer on the bottom plate of the MAM and MEMS bridges, 0.1-µm Si₃N₄ was deposited and patterned using plasma-enhanced chemical vapor deposition (PECVD) (Fig. 20c). The next step was to increase the height of the MAM and MEMS bridges, which was done by defining and then electroplating (Fig. 20d). Then, the photoresist was deposited and patterned as the sacrificial layer to create the gap of MAM and MEMS capacitors (Fig. 20e). To build the bridges, 300/1000/1000 Å Cr/Au/Ti seed layer was first deposited and patterned, followed by 1 µm Au electroplating (Fig. 20f). The final step was to remove the sacrificial layer by isotropic plasma etching (Fig. 20g).

Fig. 20

Proposed fabrication process of the designed unit cell for the DMTL phase shifter

6 Conclusion

A novel three-state unit cell for a compact, low-loss 6-bit DMTL phase shifter was designed, analyzed, and simulated in this study. The designed unit cell structure consisted of a coplanar waveguide transmission line, a MEMS, and two-pair metal–air–metal bridges. The bridge capacitors were electrically in series and were actuated in three different modes; in each mode, the distributed capacitance on the transmission line and the phase velocity were changed to achieve a phase shift. The novelty of this design is that the number of unit cells is reduced from 64 (which is the case in a conventional 6-bit phase shifter) to only 17. Therefore, the overall size of the 6-bit phase shifter is considerably reduced. Due to the very small size of the proposed phase shifter, the loss also decreases. The designed structure was simulated using Ansoft HFSS and IntelliSuite. Based on the simulation results, the lateral size of the phase shifter is only 8.5 mm; the root-mean-square (RMS) phase error is 1.35°, and the average loss is 1.2 dB. The main advantages of the designed MEMS phase shifter are its compact size, low RMS phase error, low loss, and low pull-in voltage. A step-by-step fabrication process was also proposed for designing the DMTL phase shifter. This means that the feasibility of the proposed design was investigated using the proposed fabrication process. Based on the fact that MEMS technology has fully matured characteristics, in the case of measuring, the results will certainly be in good agreement with the analysis and simulation results.