1 Introduction

Radio frequency micro-electro-mechanical-system is an emerging sub-area of MEMS technology which offers wide range of benefits. It enables radar, sensors and broadband communication devices for various military and commercial applications. RF MEMS phase shifters are essential components in phased array antennas for telecommunications and radar applications. Depending on the application, design approach of phase shifter is classified into two categories viz., analog and digital. In analog approach, continuously varying phase shift is obtained from 0° to 360° and fabricated using MEMS varactors while in digital approach, discrete set of phase delays are obtained and fabricated using MEMS switches.

There are mainly four kinds of MEMS shifters: reflect-line (Lee et al. 2004), switched-line (Kim et al. 2001; Nordquist et al. 2006), loaded line (Lou et al. 2010) and distributed MEMS transmission line (Barker and Rebeiz 1998; Hayden and Rebeiz 2003; Lakshminarayanan and Weller 2007; Afrang and Yeop Majlis 2008; Afrang 2013; Palei et al. 2005; CHEN et al. 2013; Liu et al. 2000; Sengar et al. 2013; Hung et al. 2004; Ling et al. 2014). Due to the true-time-delay and broad-band operation properties, many papers on the DMTL have been published since it was proposed by Barker and Rebeiz. The DMTL usually consists of a high impedance coplanar waveguide (CPW) transmission line that is periodically loaded by MEMS switches.

As a main component of phased-array antennas, microwave and millimeter-wave phase shifters are required to be low loss, widely tunable (broadband), low power, small size, and fast. In addition, phase shifters are required to handle high RF powers when used in the transmit channels or in radars for beam-forming applications.

All kinds of the MEMS phase shifters have large size compared to solid state phase shifters. It is essential that the area of RF MEMS phase shifter be reduced. The advantages of reduced size are many: easier in hermetic packaging, much higher part count per wafer, and much lower cost and loss.

Initially, the primary DMTL phase shifters were large in size. For example Hayden and Rebeiz designed 2 bit Ka-band DMTL phase shifter. The structure was consisted of a high impedance line capacitively loaded by the periodic placement of series MEMS switches and MIM or MAM capacitors. The structure was fabricated with 21 MEMS switches and 400 μm spacing. The total length was 8.4 mm and produced 360° phase shift. The digital DMTL phase shifter was developed by Lakshminarayanan and Weller to minimize the insertion loss and size, using impedance-matched slow-wave structure. One bit structure was fabricated with 10 unit cells and 476 μm spacing at 50 GHz. The total length was 4.6 mm and produced 360° phase shift.

Larger phase shift per unit cell, decreases the size of the phase shifters. To have a large phase shift per unit cell, it is needed to increase the capacitance ratio of a cell. It means one should increase the capacitance of the cell in the actuated condition. The penalty paid is to increase the return loss in the actuated position. To solve the problem Afrang and Yeop Majlis presented a new concept of DMTL phase shifter using both capacitors and inductors. Based on their proposed structure and around the resonance frequency it is possible to achieve large phase shift together with reasonable return loss.

Recently, Feng lin et al. reported on a miniature DMTL phase shifter using both tunable capacitors and inductors. Based on their proposed structure when increasing capacitance of the cell in the actuated condition to obtain a large phase shift, the value of tunable inductor is also increased, keeping Zdown matched to the port impedance while further increasing the phase shift.

For the DMTL phase shifters with more bits and consequently with small LSB (least significant bit), the size of the phase shifter will be large. To decrease the size of the phase shifter, a new design of MEMS switch is proposed. The proposed switch is a two step switch. Each step produces one phase state. Therefore, by considering two steps for each switch, two phase states are produced in a unit cell. The size of phase shifter with such switch decreases to half.

2 Design of proposed DMTL phase shifter

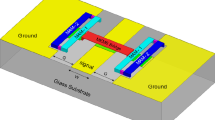
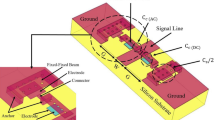
The schematic of the proposed unit cell DMTL phase shifter is shown in Fig. 1. The structure consists of a coplanar waveguide (CPW) line, a MEMS capacitive switch together with two additional electrodes near the center line under the bridge, and two static MAM capacitors connected to the ends of the bridge. The height of the additional electrodes is more than the lower electrode of the switch. The initial gap between the bridge with center line and additional electrodes is G0 and G1 respectively. Figure 2 shows the equivalent circuit of the proposed unit cell DMTL phase shifter. In this circuit, the distributed parameters for the transmission line have been used where Lt, Ct and Rt are per unit length inductance, capacitance and resistance of the transmission line respectively, and “S” is the periodic separation between MEMS switches. As represented in the equivalent circuit, the design is composed of an unloaded line loaded with MEMS switch in series with lumped element capacitors (Cs/2).

Fig. 1
figure 1

The schematic of the proposed unit cell DMTL phase shifter (not drown to scale)

Full size image
Fig. 2
figure 2

The unit cell lumped model of the proposed DMTL phase shifter

Full size image

The additional electrodes in the proposed structure, introduce additional phase state for the phase shifter. By using these additional electrodes it is possible to create two phase states in a unit cell.

Figure 3 shows MEMS switch in the up state position. In the initial condition and with no applied voltage, there is an ac capacitor between the bridge and ground planes via center line. In this condition the corresponding capacitance and impedance is named by Clu and Zlu respectively.

Fig. 3
figure 3

MEMS switch in the up state position

Full size image

When the actuation voltage of V1 is applied between the bridge and additional electrodes, the bridge moves down and makes required contact with the additional electrodes as shown in Fig. 4.

Fig. 4
figure 4

MEMS switch in the first step of down state position

Full size image

In this condition the corresponding capacitance and impedance between the bridge and ground plane is named by Cld1 and Zld1 respectively. When the actuation voltage of V2 is applied between the bridge and center line, the bridge moves down and makes required contact with the center line as shown in Fig. 5. In this condition the corresponding capacitance and impedance is named by Cld2 and Zld2 respectively. Therefore, by using additional electrodes and two different actuation voltages it is possible to achieve three different capacitances and impedances, and consequently two different phase states in the proposed unit cell.

Fig. 5
figure 5

MEMS switch in the second step of down state position

Full size image

In the capacitor type MEMS phase shifters the bridge capacitor serves to lower the impedance in the up and down state position. Therefore the unloaded impedance of the transmission line must be greater than the highest load impedance. Consider the DMTL is placed within a 50 Ω system. The desired DMTL loaded impedances in terms of the maximum desired reflection coefficient is obtained by:

$$Z_{l} = 50\sqrt {\frac{{1 \pm \Gamma_{in} }}{{1 \mp \Gamma_{in} }}}$$
(1)

where, \(\Gamma_{in}\) is the input return loss of the structure. The solution to this equation for maximum return loss of −17.5 dB gives Zlu = 57.15 and Zld = 43.7. These impedances are the optimal load impedances at the design frequency to maximize phase shift while keeping the reflected power loss at the input of the DMTL to a design specified minimum. These impedances represent the maximum (Zlu) and minimum (Zld) impedances of the DMTL in the up and down states of the MEMS bridge, respectively. The proposed structure is suitable for the phase shifters with smaller least significant bit and consequently with more bits. For the design, a six bit, Ka-band (30 GHz) MEMS phase shifter is considered.

The following expressions, combined with the Bragg frequency are solved to develop closed-form design equations for two phase states in a unit cell of the DMTL phase shifter:

$${\text{s}} = \frac{{{\text{Z}}_{{{\text{ld}}2}} {\text{C}}}}{{\pi {\text{f}}_{\text{B}} {\text{Z}}_{\text{o}} \sqrt {\varepsilon_{{{\text{r}},{\text{eff}}}} } }} \,\, {\text{meters}}$$
(2)
$${\text{C}}_{\text{lu}} = \frac{{\left( {{\text{Z}}_{0}^{2} - {\text{Z}}_{\text{lu}}^{2} } \right){\text{Z}}_{{{\text{ld}}2}} }}{{{\text{Z}}_{0}^{2} {\text{Z}}_{\text{lu}}^{2} \pi {\text{f}}_{\text{B}} }} \,\, {\text{farads}}$$
(3)
$${\text{C}}_{{{\text{ld}}1}} = \frac{{\left( {{\text{Z}}_{0}^{2} - {\text{Z}}_{\text{lu}}^{2} } \right){\text{Z}}_{{{\text{ld}}2}} }}{{{\text{Z}}_{0}^{2} {\text{Z}}_{{{\text{ld}}1}}^{2} \pi {\text{f}}_{\text{B}} }} \,\, {\text{farads}}$$
(4)
$${\text{C}}_{{{\text{ld}}2}} = \frac{{\left( {{\text{Z}}_{0}^{2} - {\text{Z}}_{{{\text{ld}}2}}^{2} } \right)}}{{{\text{Z}}_{0}^{2} {\text{Z}}_{{{\text{ld}}2}} \pi {\text{f}}_{\text{B}} }} \,\, {\text{farads}}$$
(5)
$$\Delta \varphi_{1} = \frac{{360^{ \circ } s\omega Z_{o} \sqrt {\varepsilon_{r,eff} } }}{C}\left( {\frac{1}{{Z_{lu} }} - \frac{1}{{Z_{ld1} }}} \right) \frac{degree}{section}$$
(6)
$$\Delta \varphi_{2} = \frac{{360^{ \circ } s\omega Z_{o} \sqrt {\varepsilon_{r,eff} } }}{C}\left( {\frac{1}{{Z_{lu} }} - \frac{1}{{Z_{ld2} }}} \right) \frac{degree}{section}$$
(7)

In this study, the Bragg frequency is selected to be approximately 2.4 times the design frequency at 30 GHz. The CPW line dimensions are 100/100/100 μm (Zo = 96Ω, εr = 3.75) with corresponding separation of 400 μm at 30 GHz. On the other hand, the maximum and minimum impedances of the DMTL in the up and down states of the MEMS bridge (Zlu = 57.15, Zld2 = 43.7) with Zld1 = 49.5 satisfy the phase states of 11.25° and 5.625° respectively at 30 GHz. Finally, the corresponding load capacitances in the up, first step and second step of down state position are Clu = 38.2 fF, Cld1 = 57 fF and Cld2 = 80.25 fF respectively.

From Fig. 5 it is clear that the capacitance in the second step of down state position (Cld2) is the series combination of static capacitor (Cs) and the capacitor named by Cbd (bridge capacitance in the second step of down state position). The capacitance of the Cbd is on the order of 1–3 pF. So, the capacitance in the second step of down state position is dominated by static capacitor, Cs (Cs ≈ Cld2 = 80.25 fF). From Fig. 4, the upper surface of the dielectric layer and lower surface of the bridge together with air-gap between them make the capacitor named by Cg1. The series combination of this capacitor with the capacitance in the second step of down state position (Cld2) determines the load capacitance in the first step of down state position. The air gap height of the Cg1, together with dielectric layer thickness determines the height of additional electrodes. Finally, from Fig. 3 the upper surface of the dielectric layer and lower surface of the bridge together with air-gap between them make the capacitor named by Cg0. The series combination of this capacitor with the capacitance in the second step of down state position (Cld2) determines the up state load capacitance.

3 Ka band six bit calculations and simulations

In order to verify the proposed phase shifter, all phase states of the structure are calculated and simulated using MATLAB and HFSS softwares, respectively.

3.1 Simulation based on HFSS software

A 6-bit phase shifter is based on the 5.625/11.25/22.5/45/90/180° set of delay networks and can be provided by 1/1/2/4/8/16 cells, respectively. Figure 6 shows the whole structure of proposed phase shifter. The whole structure including 32 cells is simulated using HFSS software.

Fig. 6
figure 6

The whole structure of proposed phase shifter

Full size image

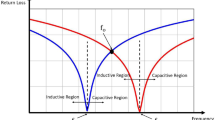
Figure 7a–c show simulation results of the return loss, insertion loss and phase shift for the phase states of 5.625/11.25/22.5/45/90/180°. As it is seen from Fig. 7a, b the return loss and insertion loss at 30 GHz for all six bit is better than −16 dB and −0.8 dB, respectively. From Fig. 7c the phase error for all phase states is smaller than 1°.

Fig. 7
figure 7

Simulation results of a return loss, b insertion loss and c phase shift, for the phase states of 5.625/11.25/22.5/45/90/180°

Full size image

3.2 Calculation based on MATLAB software

The scattering parameters of the structure can be conveniently analyzed using ABCD matrix. To derive S11 in terms of ABCD-parameters, the equivalent circuit in Fig. 8 is used. In this circuit, ZO2 is a matched transmission line. ZO1 is the characteristic impedance of the lossy transmission line. The length of the lossy transmission line determines the periodic separation. The structure is placed over this line. The term Zl is the shunt load.

Fig. 8
figure 8

Circuit for derivation of S11

Full size image

S11 in terms of ABCD-parameters of the structure and matched transmission line ZO2 is as following (Wolff 1988):

$$S_{11} = \frac{{A + B.Y_{O2} - C.Z_{O2} - D}}{{A + B.Y_{O2} + C.Z_{O2} + D}}$$
(8)

The ABCD matrix of the lossy transmission line is given by:

$$\left[ \begin{aligned} A \hfill \\ C \hfill \\ \end{aligned} \right.\left. \begin{aligned} B \hfill \\ D \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} &\cosh (\gamma .s) \hfill \\ &Y_{O1} .\sinh (\gamma .s) \hfill \\ \end{aligned} \right.\left. \begin{aligned} &Z_{O1} .\sin (\gamma .s) \hfill \\ &\cosh (\gamma .s) \hfill \\ \end{aligned} \right]$$
(9)
$$\gamma \, = \, \alpha \, + {\text{ j}}\beta$$
(10)

where, γ, α and β are the complex propagation constant, attenuation and the phase constant of the transmission line respectively. α and β are as following:

$$\alpha = \frac{{sR_{t} }}{{2Z_{o} }}$$
(11)
$$\beta = \frac{\omega }{{v_{p} }}$$
(12)
$$v_{p} = \frac{1}{{\sqrt {\left( {sL_{t} } \right)(sC_{t} )} }}$$
(13)

The per unit length inductance and capacitance of a transmission line are determined to be:

$$L_{t} = \frac{{\sqrt {\varepsilon_{\,eff} } Z_{o} }}{c}$$
(14)
$$C_{t} = \frac{{\sqrt {\varepsilon_{eff} } }}{{Z_{o} c}}$$
(15)

where, εeff is the effective dielectric constant of the unloaded line. The effective dielectric constant is approximated by assuming half of the fields are present in the air above the metallization and the other half is in the substrate.

$$\varepsilon_{eff} = \frac{{\varepsilon_{r} + 1}}{2}$$
(16)

The ABCD matrix of the shunt load is given by:

$$\left[ \begin{aligned} A \hfill \\ C \hfill \\ \end{aligned} \right.\left. \begin{aligned} B \hfill \\ D \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} 1 \hfill \\ 1/Z_{l} \hfill \\ \end{aligned} \right.\left. \begin{aligned} 0 \hfill \\ 1 \hfill \\ \end{aligned} \right]$$
(17)

The overall ABCD matrix of the structure is obtained as:

$$\left[ \begin{aligned} A \hfill \\ C \hfill \\ \end{aligned} \right.\left. \begin{aligned} B \hfill \\ D \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} &\cosh (\gamma .s) \hfill \\ &Y_{O1} .\sinh (\gamma .s) \hfill \\ \end{aligned} \right.\left. \begin{aligned} &Z_{O1} .\sinh (\gamma .s) \hfill \\ &\cosh (\gamma .s) \hfill \\ \end{aligned} \right] \bullet \left[ \begin{aligned} &1 \hfill \\ &1/Z_{l} \hfill \\ \end{aligned} \right.\left. \begin{aligned} &0 \hfill \\ &1 \hfill \\ \end{aligned} \right]$$
(18)

To derive S21 in terms of ABCD-parameters, the equivalent circuit in Fig. 9 is used.

Fig. 9
figure 9

Circuit for derivation of S21

Full size image

The source impedance Z O2 must be included in the calculation to separate incident and reflected waves. S21 in terms of ABCD-parameters is as following:

$$S_{21} = \frac{2}{{A + B.Y_{O2} + C.Z_{O2} + D}}$$
(19)

Finally, the phase angle of S21 determines the phase of the structure in the up, first step and second step of down state position. The phase difference between up, first step and second step of down state position at a given frequency determines the phase shift of the structure.

Figure 10a–c shows calculation results of the return loss, insertion loss and phase shift for the phase states of 5.625/11.25/22.5/45/90/180°. As it is seen from Fig. 10a, b the return loss and insertion loss at 30 GHz for all six bit is better than −9.5 dB and −2.2 dB, respectively. From Fig. 7c the phase error for all phase states is smaller than −2.2 dB.

Fig. 10
figure 10

Calculation results of a return loss, b insertion loss and c phase shift, for the phase states of 5.625/11.25/22.5/45/90/180°

Full size image

Table 1 shows the DMTL phase shifter performance comparison with the previously published phase shifters. This comparison indicates a significantly higher figure of merit-phase shift per area of the new design.

Table 1 Comparison of current state of the art DMTL phase shifters
Full size table

4 Electromechanical considerations

The additional electrodes change the electromechanical specifications of the proposed switch in comparison with a universal MEMS capacitive switch. Therefore, it is needed to consider electromechanical analysis including, pull in, stress, and switching speed analysis.

4.1 Spring constant and pull-in analysis

The first step in understanding the mechanical operation of proposed MEMS switch is to derive the spring constant of the fixed–fixed beam. In the proposed two step switch, two different loads are applied to two different portions of the beam. As a result of these loads, there are two different spring constants. To calculate the beam spring constant, the Eqs. (20), (21) and (22) are used (Rebeiz 2003).

$${\text{y}} = \frac{1}{\text{EI}}\mathop \int \limits_{0}^{\text{l}} \frac{\xi }{48}\left( {{\text{l}}^{3} - 6{\text{l}}^{2} {\text{a}} + 9{\text{la}}^{2} - 4{\text{a}}^{3} } \right){\text{da}}$$
(20)
$$I = \frac{{wt^{3} }}{12}$$
(21)
$$k = - \frac{P}{y}$$
(22)

where y is the deflection of the beam at the beam center, ξ is the load per unit length, P is the total load, and E, w, t and l are young’s modulus, width, thickness and length of the beam, respectively.

In the first step of down state position, as shown in Fig. 4, the load, p = ξ2(x2 − x1), is applied at the sides of the beam. Since the structure is symmetric, the integral is evaluated from x1 to x2 and multiplied by 2. The general expression for this spring constant is:

$$K_{1} = 4Ew\left( {\frac{t}{l}} \right)^{3} \frac{1}{{\frac{{\left( {x_{2}^{2} + x_{1}^{2} } \right)(x_{2} + x_{1} )}}{{l^{3} }} - 3\frac{{(x_{2}^{2} + x_{1}^{2} + x_{2} x_{1} )}}{{l^{2} }} + 3\frac{{x_{2} + x_{1} }}{l} - 1}}$$
(23)

In the second step of down state position, as shown in Fig. 5, the load, p = ξ2(x − l/2), is distributed over the center portion of the bridge. Since the structure is symmetric, the integral is evaluated from x1 = l/2 to x2 = x and multiplied by 2. The general expression for this spring constant is:

$$K_{2} = 32Ew\left( {\frac{t}{l}} \right)^{3} \frac{1}{{8\left( {\frac{x}{l}} \right)^{3} - 20\left( {\frac{x}{l}} \right)^{2} + 14\left( {\frac{x}{l}} \right) - 1}}$$
(24)

The general expression for pull in voltage is:

$$V_{pull - in} = \sqrt {\frac{8K}{{27\varepsilon_{0} Ww}}g_{0}^{3} }$$
(25)

Material and geometrical parameters of the switch is indicated in Table 2.

Table 2 Material and geometrical parameters of the switch
Full size table

In order to verify the proposed equations, the calculation results of pull in voltage are compared with intellisuite software results. Figures 11 and 12 show simulation result of beam displacement, and beam displacement versus applied voltage in the first step of down state position, respectively.

Fig. 11
figure 11

MEMS switch in the first step of down state position (not to scale)

Full size image
Fig. 12
figure 12

Beam displacement versus applied voltage in the first step of down state position

Full size image

Figures 13 and 14 show simulation result of beam displacement, and beam displacement versus applied voltage in the second step of down state position, respectively.

Fig. 13
figure 13

MEMS switch in the second step of down state position

Full size image
Fig. 14
figure 14

Beam displacement versus applied voltage in the second step of down state position

Full size image

Calculation and simulation results of pull in analysis are shown in Table 3. As it is seen the percent of error between calculation and simulation results in the first step of down state position is 20 %, whereas, this error in the second step of down state position is 10 %.

Table 3 Calculation and simulation results of pull in analysis
Full size table

4.2 Switching time analysis

To achieve switching time, calculation and simulation analysis is done. The switching time for beams with a small damping coefficient is obtained using Eq. 26 and is defined when y = g0.

$$m\frac{{d^{2} y}}{{dt^{2} }} + Ky = - \frac{1}{2}\frac{{\varepsilon_{0} AV^{2} }}{{g_{0}^{2} }}$$
(26)

The solution is

$$t_{s} \cong 3.67\frac{{V_{p} }}{{V_{s} \omega_{0} }}$$
(27)

where,

$$\omega_{0} = \sqrt {\frac{K}{m}}$$
(28)

As it is seen, the switching time is determined by the mechanical resonance frequency. For the proposed switch with two different spring constant, there are two different resonance frequencies and consequently two different switching times. On the other hand, to calculate resonance frequencies it is needed to determine the effective mass in the first and second step of down state position. It is noted that the effective mass of the beam is not equal to the actual mass of the beam since only a portion of the beam is moving. For the universal MEMS switches, when the load is applied to the center portion of the beam (second step of down state position in the proposed switch), the effective mass is considered to be about the thirty-five percent of total mass. On the other hand, as it is seen from Fig. 15, the moving portion of the beam in the first step of down state position is about two times greater than moving part in the second step of down state position.

Fig. 15
figure 15

Beam position in the a first and b second step, of down state position (not to scale)

Full size image

In order to verify the calculation analysis, the calculation results of resonance frequency and switching time are compared with COMSOL multiphysics software results. Figure 16 show simulation result of resonance frequency of both first and second step of down state position, respectively. As it is seen from this figure, the results for both steps are the same.

Fig. 16
figure 16

Resonance frequency of beam for both first and second step, of down state position

Full size image

Figure 17 shows simulation result of switching time in the first and second step of down state position, respectively.

Fig. 17
figure 17

Switching time of beam in the a first and b second step, of down state position

Full size image

Calculation and simulation results of resonance frequency and switching time analysis are shown in Table 4. As it is seen the percent of error between calculation and simulation results in the first and second step of down state position is negligible.

Table 4 Calculation and simulation results of resonance frequency and switching time analysis
Full size table

4.3 Reliability considerations

There are two cases of failure in capacitive actuation. The first one is the dielectric charging, and the second failure mechanism is due to mechanical failure. Charge injection results in the beam remaining in the down-state position when the actuation voltage is removed. The dielectric charging problem can be minimized by using PECVD silicon dioxide as the dielectric layer. Another solution to the dielectric charging problem is to design low actuation voltage. Both solutions are considered in the design. Mechanical failure is due to fatigue or fracture. Fatigue is a problem that can affect any part or component that moves. There are three basic factors necessary to cause fatigue: (1) a maximum tensile stress of sufficiently high value, (2) a large enough variation or fluctuation in the applied stress, and (3) a sufficiently large number of cycles of the applied stress. The fatigue strength (also referred to as the endurance limit) is the stress below which failure does not occur. As the applied stress level is decreased, the number of cycles to failure increases. Figure 18 shows the stress analysis of beam in the (a) first and (b) second step, of down state position.

Fig. 18
figure 18

Stress analysis of beam in the a first and b second step, of down state position

Full size image

As it is seen from these figures, maximum stress occurs in the first step of down state position. This stress is five times smaller than yield strength of gold. The stress is increased by shifting the electrodes to the sides of the anchors.

5 Fabrication process

The fabrication process starts by deposition and patterning of a 0.2 μm SiCr on a glass substrate using lift-off process (Fig. 19a). CPW line, lower plates of MAM capacitors, bridge and MAM capacitor anchors and additional electrodes are defined in the second step using liftoff process by sputtering a 3000-Å layer of Au (Fig. 19b). Next step is to increase the height of additional electrodes, anchors and CPW line (Fig. 19c). It is done by defining and then electroplating of the mentioned area. In forth step only the height of anchors is increased. Again, it is done by defining and then electroplating of the mentioned area (Fig. 19d). The fifth step is to deposit and then define the PECVD silicon dioxide layer on the additional electrodes and lower electrode of the switch (Fig. 19e). To create the gap under the bridge it is needed to deposit and then pattern photoresist as a sacrificial layer. On the other hand the bridge will be rough due to the additional electrodes. Therefore, before creating the sacrificial layer, to planarize the bridge, another photoresist is deposited and patterned (Fig. 19f). The bridge is defined first by deposition and patterning of 300/1000/1000-Å Cr/Au/Ti seed layer and then Au is electroplated (Fig. 19g). Finally, isotropic plasma ashing is used to remove sacrificial layer (Fig. 19h).

Fig. 19
figure 19

Fabrication process sequence formation of a bias line, b CPW line, lower electrodes of MAM capacitors, bridge and MAM capacitor anchors and additional electrodes, c increased height of additional electrodes, anchors and CPW line, d dielectric layer on the additional electrodes and lower electrode of the switch, e increased anchor height, f sacrificial layer into steps, g bridge, h final structure using bridge releasing

Full size image

6 Conclusion

A new small size six bit DMTL phase shifter was introduced. The design was based on two step MEMS switch. Each switch introduced two phase states. For all conditions, the design resulted in a return loss better than -11 dB, phase error smaller than 2.1°, and total length of 12.8 mm at 30 GHz. Electromechanical analysis including, pull in, stress, and switching speed analysis was done and general expression for corresponding spring constant of the switch steps was extracted. Calculated and simulated results of proof-of-concept devices were in good reasonable. The same concept can be applied to implement more than six bit phase shifters using more than two steps in a MEMS switch.