1 Introduction

Micro-electro-mechanical systems (MEMS) are used in various commercial and industrial applications (Mishra et al. 2019). BioMEMS devices are widely used in medical sciences such as disease detection and drug delivery (Çağlayan et al. 2020; Rotake et al. 2020). Micro-Electro-Mechanical Converters (MEMC) are one of the most utilized MEMS devices. They are designed to convert mechanical energy (or vibrations) into electrical one (Dragunov et al. 2022). One of the interesting fields of MEMS technology is the Radio-Frequency Micro-Electro-Mechanical-Systems (RF MEMS) which offer many advantages to design and fabricate high-performance devices and systems such as filters (Dey and Koul 2020; Entesari and Rebeiz 2005), phase shifters (Daw et al. 2008; McFeetors et al. 2004; Fernandez-Bolanos et al. 2008; Jin et al. 2008; Lacroix et al. 2008; Shafai et al. 2003; Cpw et al. 2007), and other broadband communication applications (Rebeiz 2004). Switches, inductors, and capacitors are the main elements used in RF MEMS-based devices. The phase shifters are one of the RF MEMS-based devices.

Phase shifters in general are mainly used in phased array systems.

Phased array systems, in turn, are widely used in civilian applications such as radars, 5G MIMO for cell phones (Nishimura et al. 2022; Bharadwaj et al. 2020), and communication systems to achieve electronic beam forming and fast beam scanning. The phased array principle is also used in acoustics (Qin et al. 2021), and phased arrays of acoustic transducers are used in medical ultrasound imaging scanners (Elloian 2021; Allevato et al. 2019).The phase shifter design is a major issue in building phased arrays, especially at millimeter-wave frequencies.

Phase shifters based on ferroelectric materials (Flaviis et al. 1997; Kazakov et al. 2010), PIN diodes (Yang and Yang 2011; Trinh et al. 2022), or field-effect transistors switches (Medina-Rull et al. 2020; Maruhashi et al. 1998) have lower switching times as an advantage and higher insertion loss as a defect compared to RF MEMS-based phase shifters. MEMS phase shifters are mainly divided into four types: reflect-line (Li et al. 2019), switched line (Jian et al. 2006; Du et al. 2013a; Huang et al. 2015), loaded line (Lou et al. 2010), and Distributed MEMS Transmission Line (DMTL) (Afrang et al. 2017; Du et al. 2010, 2013b; Puri et al. 2013; Sengar et al. 2013; Dey and Koul 2015; Afrang and Majlis 2008; Chen et al. 2013; Ramli and Arslan 2017). In the DMTL phase shifters, MEMS switches and static or variable capacitors are periodically loaded in the Transmission line (T-Line). The phase shift is done by changing the impedance of the structure. The mentioned phase shifters are classified into two types: analog and digital. Barker and Rebeiz (2000) introduced an analog DMTL phase shifter. In this approach, phase changes continuously varied from 0° to 360° using MEMS varactors. In the Digital phase shifters, a discrete set of phase delays are obtained using MEMS switches. In 2000 Borgioli (Liu et al. 2022) introduced a digital phase shifter using MEMS switches together with Metal–Insulator–Metal (MIM) capacitors. Later, Hayden and Rebeiz (2003) and Hayden (2002) introduced Metal-Air-Metal (MAM) capacitors in the digital phase shifter.

Recently, Teymoori et al. (2020) and Chakraborty et al. (2017) have introduced new DMTL phase shifters. The phase shifter introduced by Teymoori et al. is a small size six-bit DMTL phase shifter at 32 GHz. In their proposed structure, the first three bits is used in a cell. The size of the structure is 8.5 mm with 17 switches. Chakraborty et al. have presented a new DMTL phase shifter based on miniature switched capacitors for phased array radar applications. Their proposed structure has a 30-degree phase shift with three similar capacitive switches periodically located on CPW for each unit-cell and 660-µm spacing. Furthermore, the maximum lateral dimension of their structure is 4 mm at k-band (22 GHz).

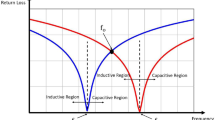
The main challenge in the MEMS-based phase shifters is the large size of the device compared to the other phase shifters. Hence, designing a small-size phase shifter is required. Results show that the small-size phase shifters have some advantages over bigger ones, such as a much higher part count per wafer and lower loss and cost. Obtaining a large phase shift together with lower spacing per unit cell is the solution. Therefore, we need to have a higher capacitance ratio. Note that a higher capacitance ratio causes higher return loss. This paper proposes two and six-bit capacitive DMTL phase shifters with a significant size reduction and appropriate return loss. Adjusting the quiescent point around the return loss peak solves the problem, and the desired phase shifts together with acceptable return loss are achieved. To prove our goal, we calculate the parameters from the related equations, and then calculate them in MATLAB software to achieve optimum values. Finally, to verify the best values are simulated in the structure-based software (HFSS).

2 Schematic design and calculation of two-bit DMTL phase shifter

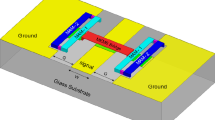
Figure 1 indicates the schematic of the proposed unit cell DMTL phase shifter on the High Resistance Silicon (HRS) substrate. The structure in Fig. 1 is a general form of a unit cell used in capacitive DMTL phase shifters. The key point in this research is to present a new approach to this type of phase shifter. The result of the new approach is a large reduction in cell length compared to other similar types. It should be noted that some changes are made to reduce the switching voltage compared to other similar structures. In this way, two cantilever beam switches are used instead of a fixed–fixed beam switch.

Fig. 1
figure 1

The schematic of the proposed unit cell of the two-bit DMTL phase shifter

Full size image

Generally, RF-MEMS-based structures are modeled as an electric circuits. The equivalent electrical circuit of the proposed structure in the up and down-state position is shown in Fig. 2a, b, respectively. The components in Fig. 2 are extracted from Fig. 1. The existed components in the structure are inductor, capacitors, and connectors.

Fig. 2
figure 2

One cell equivalent circuit of the proposed structure in the a up and b down-state position

Full size image

Inductor: The only inductor in the structure is due to the conductor line indicated by the "signal line". As it is known in electrical engineering, the equivalent circuit of the metal wire or line is indicated by the inductor. This inductor is named by "\({\mathrm{sL}}_{\mathrm{t}}\)", where "s" means the length of the line.

Capacitors: The capacitors in the structure are made of two metal layers with a dielectric interface layer. There are two types of capacitors in the structure. One type is a parallel plate capacitor, and another is a coplanar capacitor. The metal layers of coplanar type are signal line planes together with ground planes. The dielectric layer of this type on the upside is the air and on the downside is the silicon wafer. This capacitor is named "\({\mathrm{sC}}_{\mathrm{t}}\)," where "s" indicates the length of one side of the related metal layers. There are three types of parallel plate capacitors in the structure. They are named AC capacitor of cantilever switch "\({\mathrm{C}}_{\mathrm{c }(\mathrm{AC})}\)," DC capacitor of cantilever switch "\({\mathrm{C}}_{\mathrm{c }(\mathrm{DC})}\)," and static MAM capacitor "\({\mathrm{C}}_{\mathrm{s}}/2\)" The capacitor "\({\mathrm{C}}_{\mathrm{c }(\mathrm{AC})}\)," consists of the overlap area of the metal signal line layer and the end of the metal cantilever. The dielectric layer between these layers is air in this capacitor. This layer is an interface between the mentioned layers. The capacitor "\({\mathrm{C}}_{\mathrm{c }(\mathrm{DC})}\)," consists of the overlap area of the metal cantilever and metal layer named "Electrode." There are two dielectrics between the mentioned layers. These interfaces are \({\mathrm{SiO}}_{2}\) and air. Finally, the capacitor "\({\mathrm{C}}_{\mathrm{s}}/2\)" consists of the overlap area between the metal electrode and the fixed–fixed metal beam. The fixed–fixed metal beam is connected to the metal ground layer through a metal interface named "Anchor." The dielectric layer between the mentioned metal layers is air. This layer is an interface between the mentioned layers.

Connectors: The metal anchor layers in the structure act as a connector. The metal connector connects the cantilever beam anchor to the metal electrode.

As shown in Fig. 1, the structure is designed on a Co-Planar Waveguide (CPW) line with two MEMS cantilever type DC contact shunt switches. These switches are in series with "\({\mathrm{C}}_{\mathrm{s}}/2\)" and "\({\mathrm{C}}_{\mathrm{c }(\mathrm{AC})}\)," capacitors. One electrode is located under each cantilever. When the voltage is applied between these electrodes and corresponding cantilevers, the state of the switches is changed simultaneously.

One cell equivalent circuit of the proposed structure in the up and down-state position is shown in Fig. 2a, b, respectively.

This circuit is only valid for the frequencies in the linear region. In the linear region, the Bragg frequency is around three or more than three times the quiescent frequency. The ohmic and leakage resistance is not considered in the equivalent circuit. The effect of this simplification in the phase shift and return loss is negligible, except, the attenuation of return loss in the resonance points. From the Figures, \({\mathrm{sL}}_{\mathrm{t}}\) and \({\mathrm{sC}}_{\mathrm{t}}\) are the T-line inductance and capacitance of the unit cell, respectively. Each MEMS cantilever switch is in series with \({\mathrm{C}}_{\mathrm{s}}/2\) at one end and an AC capacitor at the other end in the up-state position. The overlap area between the cantilever end and signal line makes the mentioned AC capacitor (\({\mathrm{C}}_{\mathrm{C }(\mathrm{AC})})\). When the voltage is applied the free end of the cantilever moves downward and makes DC contact with the signal line. As a result, there is no AC capacitor between the plates in the down-state position.

The proposed structure aims to determine a frequency that satisfies a given phase shift and appropriate return loss with a small size. The computational method achieves the desired frequency by considering the assumptions and thus limitations. The assumption and thus limitation of the model is the working in a special area (around resonance frequency). This area limits the range of quiescent frequency. By calculating, the phase shifter can be adjusted for the desired frequencies. The device will not work outside the specified frequency. The desired phase shift per cell is obtained from Eq. (1) (Hayden 2002).

$$\mathrm{\Delta \phi }=\frac{360{\mathrm{sfZ}}_{0}\sqrt{{\upvarepsilon }_{\mathrm{r},\mathrm{eff}}}}{\mathrm{c}}\left(\frac{1}{{\mathrm{Z}}_{\mathrm{d}}}-\frac{1}{{\mathrm{Z}}_{\mathrm{u}}}\right) \mathrm{Degrees}/\mathrm{section}$$
(1)

where, s, f, Z0, \(\sqrt {\varepsilon_{r,eff} }\) and c are unit cell length (spacing), quiescent frequency, characteristic impedance effective dielectric constant, and speed of light, respectively. In this equation, \({\mathrm{Z}}_{\mathrm{u}}\) and \({\mathrm{Z}}_{\mathrm{d}}\) are the impedances in the up and down-state position, respectively.

The unit cell length indicated by "s" determines the size of the proposed structure. As is clear from Eq. (1), the phase shift of the structure is size-dependent, and as will be shown in the remaining Eqs. (2)–(27), all other parameters, including return loss, resonance frequencies, \({\mathrm{Z}}_{\mathrm{u}}\), \({\mathrm{Z}}_{\mathrm{d}}\), etc. are size-dependent. Our target is to obtain a high phase shift together with a small spacing and reasonable return loss in a unit cell. According to Eq. (1), small spacing decreases the phase shift, therefore to achieve the high phase shift, it is needed to increase the other parameters of Eq. (1), including the relative permittivity of the substrate, characteristic impedance, and impedance difference in the up and down-state position. We assume silicon (\(\varepsilon_{r}\) = 11.9) as a substrate because of its high relative permittivity. Considering the substrate type and T-line loss, the characteristic impedance is 70 \(\Omega\) (Hayden 2002). We also assume 200 μm and 35 GHz, for the spacing, and quiescent frequency, respectively. To achieve high phase shift, a higher impedance difference is needed. As it is known, higher impedance difference results in higher impedance mismatching with respect to port impedance. This high mismatching results in high return loss (higher than −10 dB). This problem appears when we use one cell due to the lack of any resonance peak. Multi-cells result in multi resonance frequencies in the return loss diagram. The return loss around these resonance frequencies is improved. Therefore, it is possible to have a high phase shift with acceptable return loss around the resonance frequencies.

For LSB design (90\(^\circ\)), we consider different cell states. In the first state, the 90\(^\circ\) is done using only one cell. To achieve such a high phase shift by only one cell, the impedance in the down-state position should be very low. This low impedance results in a high return loss. Due to the lack of resonance peak in the return loss diagram, it is impossible to obtain a reasonable return loss. In spite of peak resonance existing in the two-cell return loss diagram, due to very low down-state impedance, the return loss is not acceptable except only in the resonance frequency. To know the return loss behavior of the three-cell, it is needed to calculate the return loss resonance peaks. From Z11, we can find the return loss behavior of the three-cell circuit. The poles of \({\mathrm{Z}}_{11}\) indicate the resonance frequencies in the return loss diagram. Figure 3 shows the equivalent circuit of the three-cell.

Fig. 3
figure 3

Equivalent circuit of the three-cell

Full size image

The corresponding input impedance Z11(ω) of Fig. 3 as a function of ω and related poles are as follow:

$${\mathrm{Z}}_{11}\left(\upomega \right)=\frac{{\upomega }^{6}{\mathrm{L}}^{3}{\mathrm{C}}^{3}-5{\upomega }^{4}{\mathrm{L}}^{2}{\mathrm{C}}^{2}+6{\upomega }^{2}\mathrm{LC}-1}{{\upomega }^{5}{\mathrm{L}}^{2}{\mathrm{C}}^{3}-4{\upomega }^{3}{\mathrm{LC}}^{2}+3\mathrm{\omega C}}\Omega$$
$${\upomega }_{1}=0, {\upomega }_{2}=\frac{1}{\sqrt{\mathrm{LC}}}, {\upomega }_{3}=\frac{\sqrt{3}}{\sqrt{\mathrm{LC}}}$$
(2)

where C represents the equivalent capacitance including \({\mathrm{sC}}_{\mathrm{t}}\), \({\mathrm{C}}_{\mathrm{C }(\mathrm{AC})}\) and \({\mathrm{C}}_{\mathrm{S}}\) in the up/down-state position and L is the T-line inductance. The corresponding frequencies related to the poles \({\upomega }_{2}\) and \({\upomega }_{3}\) are \({\mathrm{f}}_{2}\) and \({\mathrm{f}}_{3}\), respectively. These frequencies are resonance frequencies. The input impedance at these frequencies is high. It means the return loss of the structure at these frequencies is in the best condition.

According to Eq. (1), the impedance in the down-state position should be very low to obtain a high phase shift considering the small unit cell size. However, low impedance in the down-state position results in high mismatching with respect to port impedance and consequently high return loss. Hence the quiescent frequency of the proposed three-cell in the down state position should be equal to one of the corresponding frequencies related to poles of the Eq. (2) due to better return loss around these poles. The selected resonance frequency should be compared with the Bragg frequency. The Bragg frequency is the frequency at which the line impedance becomes zero and is as follow (Hayden 2002):

$${\upomega }_{\mathrm{Bragg}}=2\uppi {\mathrm{f}}_{\mathrm{Bragg}}=\frac{2}{\sqrt{{\mathrm{sL}}_{\mathrm{t}}{\mathrm{C}}_{\mathrm{down}}}}$$
(3)

As mentioned before, the linear region requires the Bragg frequency very higher than the quiescent frequency. The Bragg frequency is two times \({\mathrm{f}}_{2}\) and 1.15 times \({\mathrm{f}}_{3}\). It means the resonance frequency "\({\mathrm{f}}_{3}\)" of the three-cell is around the Bragg frequency. Therefore, it is impossible to consider the "\({\mathrm{f}}_{3}\)" as a quiescent frequency, and our only choice is the resonance frequency "\({\mathrm{f}}_{2}\)" as a quiescent frequency in the down state position to have appropriate return loss, as shown in Eq. (4).

$${\mathrm{f}}_{2}=\frac{1}{2\uppi \sqrt{{\mathrm{sL}}_{\mathrm{t}}{\mathrm{C}}_{\mathrm{down}}}}=\frac{1}{2\uppi \sqrt{{\mathrm{sL}}_{\mathrm{t}}({\mathrm{sC}}_{\mathrm{t}}+{\mathrm{C}}_{\mathrm{S}})}} \mathrm{GHz}$$
(4)

In Eq. (4), \({\mathrm{L}}_{\mathrm{t}}\) and \({\mathrm{C}}_{\mathrm{t}}\) are as follow:

$${\mathrm{L}}_{\mathrm{t}}=\frac{\sqrt{{\upvarepsilon }_{\mathrm{eff}}}{\mathrm{ Z}}_{0}}{\mathrm{c}} \mathrm{H}/\mathrm{m}$$
(5)
$${\mathrm{C}}_{\mathrm{t}}=\frac{\sqrt{{\upvarepsilon }_{\mathrm{eff}}}}{{\mathrm{Z}}_{0}\mathrm{c}} \frac{\mathrm{F}}{\mathrm{m}}$$
(6)

The calculation is continued by extracting the capacitance (\({\mathrm{C}}_{\mathrm{S}}\)) from the Eq. (4).

The next step is to find the down-state impedance from Eq. (7) (Hayden 2002):

$${\mathrm{Z}}_{\mathrm{d}}=\sqrt{\frac{{\mathrm{sL}}_{\mathrm{t}}}{{\mathrm{sC}}_{\mathrm{t}}+{\mathrm{C}}_{\mathrm{S}}}}\Omega$$
(7)

Now we can find up-state impedance using Eq. (1). Assuming three cells, Δϕ for LSB design in this equation is 30 degrees. The AC capacitance of cantilever \({\mathrm{C}}_{\mathrm{C }(\mathrm{AC})}\) is extracted from up-state impedance.

$${\mathrm{Z}}_{\mathrm{u}}=\sqrt{\frac{{\mathrm{sL}}_{\mathrm{t}}}{{\mathrm{sC}}_{\mathrm{t}}+2{\mathrm{C}}_{\mathrm{c }(\mathrm{AC})}{\mathrm{C}}_{\mathrm{s}}/({2\mathrm{C}}_{\mathrm{c }(\mathrm{AC})}+{\mathrm{C}}_{\mathrm{s}})} }\Omega$$
(8)

The values of two-bit calculated parameters are shown in Table 1

Table 1 Two-bit calculated parameters
Full size table

From Table 1, the unit cell up-state impedance is 54.6 Ω, which means the mismatch with respect to port impedance is low. Therefore, the return loss in quiescent frequency will be in the appropriate condition. The extracted \({\mathrm{C}}_{\mathrm{down}}\) from Eq. (4) is applied to the related \({\mathrm{f}}_{3}\) formula in Eq. (2). The extracted \({\mathrm{f}}_{3}\) is 60.6 GHz.

For MSB design (180-degree), we use three-cell LSB as a unit cell. Therefore, six-cell is needed to obtain a 180-degree phase shift. Due to repeating three-cell in 180-degree phase shift, three-cell poles is appeared in the six-cell input impedance. As a result, it is possible to simplify the denominator of the Z11. The corresponding input impedance Z11(ω) of six-cell as a function of ω and related poles are as follow:

$${\mathrm{Z}}_{11}\left(\omega \right)=\frac{{\upomega }^{12}{\mathrm{L}}^{6}{\mathrm{c}}^{6}-11{\upomega }^{10}{\mathrm{L}}^{5}{\mathrm{c}}^{5}+45{\upomega }^{8}{\mathrm{L}}^{4}{\mathrm{c}}^{4}-84{\upomega }^{6}{\mathrm{L}}^{3}{\mathrm{c}}^{3}+70{\upomega }^{4}{\mathrm{L}}^{2}{\mathrm{c}}^{2}-21{\upomega }^{2}\mathrm{LC}+1}{({\upomega }^{5}{\mathrm{L}}^{2}{\mathrm{C}}^{3}-4{\upomega }^{3}{\mathrm{LC}}^{2}+3\mathrm{\omega C})({\upomega }^{6}{\mathrm{L}}^{3}{\mathrm{C}}^{3}-6{\upomega }^{4}{\mathrm{L}}^{2}{\mathrm{C}}^{2}+{9\upomega }^{2}\mathrm{LC}-2)}\Omega$$
(9)
$${\upomega }_{1}=0, {\upomega }_{2}=\frac{\sqrt{2-\sqrt{3}}}{\sqrt{\mathrm{LC}}}, {\upomega }_{3}=\frac{1}{\sqrt{\mathrm{LC}}}, {\upomega }_{4}=\frac{\sqrt{2}}{\sqrt{\mathrm{LC}}}, {\upomega }_{5}=\frac{\sqrt{3}}{\sqrt{\mathrm{LC}}}, {\upomega }_{6}=\frac{\sqrt{2+\sqrt{3}}}{\sqrt{\mathrm{LC}}}$$

The corresponding resonance frequencies \({\mathrm{f}}_{3}\) and \({\mathrm{f}}_{5}\) in the six-cell are the same as the resonance frequencies \({\mathrm{f}}_{2}\) and \({\mathrm{f}}_{3}\) in the three-cell. The choice in the six-cell in the down-state position is the resonance frequency \({\mathrm{f}}_{3}\) in the input impedance equation as the quiescent frequency.

The resonance frequencies of Eq. (9) in the down-state position are also calculated considering the unit cell inductance and capacitance in Table 1. The calculated results are shown in Table 2.

Table 2 The resonance frequencies extracted from the Eq. (9) in the down state position
Full size table

The final step for achieving a two-bit DMTL phase shifter is the combining the LSB and MSB. In the proposed two-bit DMTL phase shifter, three-cell as a unit cell is repeated three times. As a result, all three-cell poles are found in nine-cell poles. One of these poles in the down-sate position is the desired pole as the quiescent frequency.

The calculated parameters from the Eqs. (1)–(9) are verified using ABCD matrix-based scattering parameters in MATLAB software. The inputs of these equations are the calculated parameters (inductance and capacitances) shown in Table 1.

To derive unit cell ABCD parameters, the equivalent circuit in Fig. 4 is used. In this circuit, \({\mathrm{Z}}_{\mathrm{o}1}\), is the characteristic impedance. The length of the lossy T-line determines the periodic separation. The structure is placed over this line. The term (GL + jBL) is the shunt load.

Fig. 4
figure 4

Equivalent circuit of the three-cell of ABCD parameter of the unit cell

Full size image

The ABCD matrix of the lossy T-line is given by Pozar (2011):

$$\left[\begin{array}{cc}{\mathrm{A}}_{\mathrm{T}-\mathrm{line}}& {\mathrm{B}}_{\mathrm{T}-\mathrm{line}}\\ {\mathrm{C}}_{\mathrm{T}-\mathrm{line}}& {\mathrm{D}}_{\mathrm{T}-\mathrm{line}}\end{array}\right]=\left[\begin{array}{cc}\mathrm{cosh}(\upgamma .\mathrm{s})& {\mathrm{Z}}_{\mathrm{o}1}.\mathrm{sinh}(\upgamma .\mathrm{s})\\ {\mathrm{Y}}_{\mathrm{o}1}.\mathrm{sinh}(\upgamma .\mathrm{s})& \mathrm{cosh}(\upgamma .\mathrm{s})\end{array}\right]$$
(10)
$$\upgamma =\mathrm{\alpha }+\mathrm{j\beta }$$
(11)

where, γ, α and β are the complex propagation constant, attenuation and the phase constant of the T-line respectively. α, β and phase velocity (vp) are as follow:

$$\mathrm{\alpha }=\frac{{\mathrm{sR}}_{\mathrm{t}}}{2{\mathrm{Z}}_{01}}$$
(12)
$$\upbeta =\frac{\upomega }{{\mathrm{v}}_{\mathrm{p}}}$$
(13)
$${\mathrm{v}}_{\mathrm{p}}=\frac{1}{\mathrm{s}\sqrt{{\mathrm{L}}_{\mathrm{t}}{\mathrm{C}}_{\mathrm{t}}}}$$
(14)

The ABCD matrix of the shunt load is given by:

$$\left[\begin{array}{cc}{\mathrm{A}}_{\mathrm{L}}& {\mathrm{B}}_{\mathrm{L}}\\ {\mathrm{C}}_{\mathrm{L}}& {\mathrm{D}}_{\mathrm{L}}\end{array}\right]=\left[\begin{array}{cc}1& 0\\ {\mathrm{G}}_{\mathrm{L}}+{\mathrm{jB}}_{\mathrm{L}}& 1\end{array}\right]$$
(15)

As mentioned before, the ohmic and leakage resistance is not considered in this research. Hence, α = GL = 0 is considered. The susceptance of the shunt load is as follow:

$${\mathrm{B}}_{\mathrm{L}}=\upomega .{\mathrm{C}}_{\mathrm{L}}$$
(16)

The ABCD matrix of the unit cell is obtained by multiplying the matrices Eqs. (10) and (15).

The proposed structure includes multi cells, is shown in Fig. 5.

Fig. 5
figure 5

Proposed multi-cell structure

Full size image

The overall ABCD matrix of the structure is as follow:

$$\left[\begin{array}{cc}\mathrm{A}& \mathrm{B}\\ \mathrm{C}& \mathrm{D}\end{array}\right]=\left[\begin{array}{cc}{\mathrm{A}}_{1}& {\mathrm{B}}_{1}\\ {\mathrm{C}}_{1}& {\mathrm{D}}_{1}\end{array}\right]\times \left[\begin{array}{cc}{\mathrm{A}}_{2}& {\mathrm{B}}_{2}\\ {\mathrm{C}}_{2}& {\mathrm{D}}_{2}\end{array}\right]\times \dots . \times \left[\begin{array}{cc}{\mathrm{A}}_{\mathrm{n}}& {\mathrm{B}}_{\mathrm{n}}\\ {\mathrm{C}}_{\mathrm{n}}& {\mathrm{D}}_{\mathrm{n}}\end{array}\right]$$
(17)

In Eq. (17), the n equals 3, 6, and 9 correspond to LSB (90-degree), MSB (180-degree), and two-bit DMTL phase shifter design, respectively.

S11 and S21 in terms of ABCD parameters of LSB, MSB, and two-bit DMTL phase shifter connected to a line with port impedance (Z0 = 50Ω) are as follow (Pozar 2011):

$${\mathrm{S}}_{11=}\frac{\mathrm{A}+\mathrm{B}.{\mathrm{Y}}_{0}-\mathrm{C}{.\mathrm{Z}}_{0}-\mathrm{D}}{\mathrm{A}+\mathrm{B}.{\mathrm{Y}}_{0}+\mathrm{C}{.\mathrm{Z}}_{0}+\mathrm{D}}$$
(18)
$${\mathrm{S}}_{21}=\frac{2}{\mathrm{A}+\mathrm{B}.{\mathrm{Y}}_{0}+\mathrm{C}{.\mathrm{Z}}_{0}+\mathrm{D}}$$
(19)

Finally, the 3-cell 90-degree, 6-cell 180-degree, and two-bit return loss and phase shift are also obtained using Eqs. (20) and (21), respectively.

$$\mathrm{RL}=20\mathrm{ log}({\mathrm{S}}_{11}) \mathrm{ dB}$$
(20)
$$\Delta \mathrm{\varphi }=\mathrm{phase}\left({\mathrm{S}}_{21}\right){|}_{\mathrm{down\, state}}-\mathrm{phase}\left({\mathrm{S}}_{21}\right){|}_{\mathrm{up\, state }}\mathrm{ Degrees}$$
(21)

The MATLAB results in Fig. 6a, b show return loss and phase of the three-cell (90-degree) in the up and down-state position, respectively. Figure 6a verifies the calculated resonance frequencies of Table 1.

Fig. 6
figure 6

Calculated results of a return loss and b phase of the 90° in the up and down-state position

Full size image

As it is seen, the phase shift at 35 GHz is slightly higher than the calculated results. It is due to the non-linear behavior of the structure. The linearity of the structure is related to the amount of Bragg frequency (Hayden 2002). Considering Eqs. (3), and (4) in the proposed structure, the Bragg frequency is two times the resonance frequency. The exact linear condition occurs when the Bragg frequency is around three or more than three times the resonance frequency.

To be more linear, we move the quiescent point slightly to the lower frequencies. In the three-cell structure, the linearity and consequently proper phase shift occur in the 34 GHz. In Fig. 6a, b return loss in the up and down-state position and phase shift at 34 GHz are −25.22 dB, −21.75 dB, and 91.96°, respectively.

We continue this procedure to six-cell (180°). The MATLAB results in Fig. 7a, b show the return loss and phase in the up and down-state position, respectively. Figure 7a verifies the calculated resonance frequencies of Table 2.

Fig. 7
figure 7

Calculated results of a return loss and b phase of the 180° in the up and down-state position

Full size image

In Fig. 7a, b return loss in the up and down-state position and phase shift at 34 GHz are −35.09 dB, −15.90 dB, and 184.15°, respectively.

Finally, nine-cell two-bit phase shifter is calculated in MATLAB software. The nine-cell total size by considering the unit cell size (200 μm) is 1.8 mm. It is the smallest size in the two-bit DMTL phase shifters. Figure 8a, b show the return loss and phase shift of the 4-state (i.e., 0°, 90°, 180°, and 270°), respectively. According to Fig. 8a, the two resonance frequencies of the three-cell as a unit cell are repeated in the two-bit phase shifter with exact values in 270° and slightly different in 90° and 180° states. In the 270° all cells are in the same condition (all in down-state position) and are matched with three-cell as a unit cell. In states 90° and 180°, some cells are in the up-state position. These cells are different from the mentioned three-cell as a unit cell. As a result, the resonance frequency is moved to the left or right. In the Figures, the worst return loss is -12.47 dB, and phase shift at 34 GHz for 4-state (i.e., 0°, 90°, 180°, and 270°) are 0°, 91.85°, 183.44°, and 276.1°, respectively.

Fig. 8
figure 8

Calculated results of a return loss and b phase shift of the four-state two-bit DMTL phase shifter

Full size image

3 Two-bit DMTL phase shifter simulation results

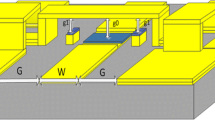
The final step is reconfirming calculated results using a Finite Element Method (FEM) named by HFSS software. This step uses the parameters extracted from the Eqs. (1)–(9). The proposed structure is simulated using HFSS software to verify the calculated results. Figure 9 shows the schematic of the top view of the two-bit phase shifter. The cells are the same as in Fig. 1.

Fig. 9
figure 9

The schematic of the top view of the two-bit DMTL phase shifter

Full size image

The dimensions and material properties are shown in Table 3:

Table 3 Dimensions and material properties
Full size table

There are some considerations in modeling the MAM capacitors. The MAM capacitor is located inside the cut ground plane. The cut ground plane adds capacitance to the MAM capacitor (Hayden 2002). Another parameter that affects the MAM capacitor is the fringing field. By considering these two items, the MAM capacitor is modeled. The simulation is also done by considering the fabrication process condition, including perforated capacitors and cantilever beams, and also the same MAM capacitor and cantilever beam air gaps.

Figure 10a, b show the return loss in the up and down-state position and phase shift at 34 GHz for 4-state (i.e., 0°, 90°, 180°, and 270°), respectively. From the Figures, the worst return loss is −12.30 dB, and phase shift at 34 GHz for 4-state (i.e.,0°, 90°, 180°, and 270°) are 0°, 89.97°, 179.21°, and 276°, respectively.

Fig. 10
figure 10

Simulated results of a return loss and b phase shift of the four-states two-bit DMTL phase shifter

Full size image

4 Electromechanical considerations

Until now, all the switches used in the DMTL phase shifters are based on fixed–fixed type beams. The spring constant of these beams is high. High spring constant results in high switching voltage. The residual stress in the fixed–fixed type beam also increases the switching voltage. The cantilever beam, due to its low spring constant and zero residual stress, is the appropriate candidate to use in the integrated circuits. The conventional MEMS switch used in DMTL phase shifters is a capacitive fixed–fixed beam-type switch in each cell. In this research, each cell consists of two cantilever-type DC contact switches. The material and geometrical parameters of the switch are indicated in Table 3.

Figure 11 shows the simulation result of cantilever beam displacement versus voltage using IntelliSuite software. From this Figure, the first contact voltage is 3.8 V. At this voltage, the cantilever end edge touches the signal line, and contact is imperfect. Figure 12a shows mentioned condition. The desired and perfect contact is between the cantilever AC capacitor plates, as shown in Fig. 12b. In such condition, the applied voltage is 4.25 V.

Fig. 11
figure 11

Simulation result of cantilever beam displacement versus voltage

Full size image
Fig. 12
figure 12

Switch in the down state position a imperfect b perfect contact

Full size image

5 Schematic design and calculation of six-bit DMTL phase shifter

Figure 13 shows the schematic of the unit cell structure of the six-bit DMTL phase shifter. It is the modified structure of the unit cell indicated in Fig. 1. As seen from the Figure, the two cantilever beam switches are changed to one fixed–fixed DC contact shunt switch. One cell equivalent circuit of the proposed structure in the up and down-state position is shown in Fig. 14a, b, respectively.

Fig. 13
figure 13

The schematic of the proposed unit cell of the six-bit DMTL phase shifter

Full size image
Fig. 14
figure 14

One cell equivalent circuit of the proposed structure in the a up and b down-state position

Full size image

The used design method in a two-bit phase shifter is again used in the design of the six-bit DMTL phase shifter. The small size is the main goal of the paper. As mentioned before, around the resonance frequency, it is possible to have a high phase shift and small size together with acceptable return loss. This procedure is applied to 45°, 90°, and 180° bits in the six-bit phase shifter design.

To change the quiescent frequency, it is needed to change the resonance frequency. The resonance frequency is changed by the capacitance load and the number and length of the cells. In the two-bit design and for 90°, the minimum cells with reasonable return loss and small size is three cells at 35 GHz. If one cell is added, the first resonance frequency is decreased. In the design of the six-bit DMTL phase shifter, it is assumed 200 μm and 25 GHz, for the spacing and quiescent frequency, respectively. Therefore, in 90°, four cells are considered.

The corresponding input impedance Z11(ω) of four cells as a function of ω and related poles are as follow:

$${\mathrm{Z}}_{11}\left(\upomega \right)=\frac{{\upomega }^{8}{\mathrm{L}}^{4}{\mathrm{C}}^{4}-7{\upomega }^{6}{\mathrm{L}}^{3}{\mathrm{C}}^{3}+15{\upomega }^{4}{\mathrm{L}}^{2}{\mathrm{C}}^{2}-10{\upomega }^{2}\mathrm{LC}+1}{{\upomega }^{7}{\mathrm{L}}^{3}{\mathrm{C}}^{4}-6{\upomega }^{5}{\mathrm{L}}^{2}{\mathrm{C}}^{3}+{10\upomega }^{3}{\mathrm{LC}}^{2}-4\mathrm{\omega C}}\Omega$$
(22)
$${\upomega }_{1}=0, {\upomega }_{2}=\frac{\sqrt{2-\sqrt{2}}}{\sqrt{\mathrm{LC}}}, {\upomega }_{3}=\frac{\sqrt{2}}{\sqrt{\mathrm{LC}}} , {\upomega }_{4}=\frac{\sqrt{2+\sqrt{2}}}{\sqrt{\mathrm{LC}}}$$

Same as the design procedure of 90° bit in two-bit, due to the high mismatch with respect to port impedance in the down-sate position, the quiescent frequency in this state should be equal to one of the resonance frequencies in the Eq. (22). These frequencies should be compared with the Bragg frequency. From Eq. (3) the Bragg frequency is 2.6 times the frequency \({\mathrm{f}}_{2}\), 1.4 times the frequency \({\mathrm{f}}_{3}\) and 1.08 times the frequency \({\mathrm{f}}_{4}\). The resonance frequencies \({\mathrm{f}}_{3}\) and \({\mathrm{f}}_{4}\) are around the Bragg frequency. Therefore it is impossible to consider them as the desired \(\mathrm{quiescent}\) frequency, and our only choice is the frequency \({\mathrm{f}}_{2}\).

$${\mathrm{f}}_{2}=\frac{\sqrt{2-\sqrt{2}}}{2\uppi \sqrt{{\mathrm{sL}}_{\mathrm{t}}{\mathrm{C}}_{\mathrm{down}}}}=\frac{\sqrt{2-\sqrt{2}}}{2\uppi \sqrt{{\mathrm{sL}}_{\mathrm{t}}({\mathrm{sC}}_{\mathrm{t}}+{\mathrm{C}}_{\mathrm{S}})}} \mathrm{GHz}$$
(23)

As mentioned before, the two cantilever beam switches are changed to one fixed–fixed DC contact shunt switch. Therefore, the equivalent circuit and impedance in the up-state position are changed. Equation (24) shows the up-state impedance of the unit cell of the proposed six-bit DMTL phase shifter.

$${\mathrm{Z}}_{\mathrm{u}}=\sqrt{\frac{{\mathrm{sL}}_{\mathrm{t}}}{{\mathrm{sC}}_{\mathrm{t}}+\frac{{\mathrm{C}}_{\mathrm{b }(\mathrm{AC})}{\mathrm{C}}_{\mathrm{s}}}{{\mathrm{C}}_{\mathrm{b }(\mathrm{AC})}{ +\mathrm{C}}_{\mathrm{s}}}}}\Omega$$
(24)

The Eqs.  (1), (5)–(7), and (22)–(24), are used to extract the parameters of 90° bit. The values of calculated parameters are shown in Table 4.

Table 4 Calculated parameters for the unit cell of each bit of the six-bit DMTL phase shifter
Full size table

In 180° design, four-cell (90°) is as a unit cell. Therefore, eight-cell is needed to obtain a 180° phase shift. Due to repeating four-cell in 180° phase shift, four-cell poles of Eq. (22) appear in the eight-cell input impedance poles.

In the 45° bit design, six cells are needed to drag the second pole or first resonance frequency to around the desired frequency (25 GHz). The corresponding input impedance Z11(ω) of six cells as a function of ω and related poles are the same as Eq. (9). The Eqs.  (1), (5)–(7), (9) and (24) are used to extract the parameters. The values of calculated parameters are shown in Table 4.

The three remaining bits require a small phase shift per cell. The return loss of such a small phase shift per cell is acceptable. Therefore, there is no need to have resonance peaks around the desired frequency. The design procedure and equations of the three remaining bits are as follow (Hayden 2002):

$${\Gamma }_{\mathrm{in}}={10}^{{\mathrm{RL}}_{\mathrm{max}}/20}$$
(25)
$${\mathrm{Z}}_{\mathrm{L}}=50\sqrt{\frac{1\pm {\Gamma }_{\mathrm{in }}}{1\mp {\Gamma }_{\mathrm{in}} }\Omega }$$
(26)

The Eqs. (25) and (26) indicate the relation between load impedance and return loss.

The design starts by considering the appropriate return loss of the cells in the up and down-state position. The return loss is directly proportional to the phase shift of the unit cell. The return loss of −25 dB is possible due to the small phase shift of LSB in the up-state position. The corresponding up-state impedance from Eqs. (25) and (26) is 53 Ω. Then, the down state impedance is extracted from Eq. (1). This impedance is 41.5Ω. Therefore, the corresponding down state return loss from Eq. (25) is −15 dB. Now, it is possible, calculate the \({\mathrm{C}}_{\mathrm{S}}\) and \({\mathrm{C}}_{\mathrm{b }(\mathrm{AC})}\) using Eqs. (7) and (24). These capacitor capacitances are 44.5 fF and, 30.5 fF respectively. This procedure is used to calculate, up state impedance, down-state impedance, \({\mathrm{C}}_{\mathrm{b }(\mathrm{AC})}\), and \({\mathrm{C}}_{\mathrm{S}}\), respectively, for 11.25° and 22.5° bits. The calculated results are shown in Table 4. The phase shift of the 11.25° bit is designed the same as the 5.625° bit using only one cell. Due to the higher phase shift, the corresponding return loss of 11.25° bit is higher than LSB. Therefore, the return loss of −15 dB is considered.

It is not possible to consider only one cell to 22.5° bit due to its high return loss. Therefore it is needed to use more cells. There are two options considering the desired return loss. One option is creating resonance peak around the desired frequency. The second option is dividing the 22.5° to small phase shift using more cells. As it is known, a small phase shift per cell improves the return loss. In the design, the second choice is used, and using five cells with 4.5° for each cell; it is possible to have −25 dB return loss. If the first option is used, it requires more than five cells to drag the resonance peak around the desired resonance frequency.

In the next step, same as the two-bit, and to verify, the calculated parameters from Table 4 are applied to Eqs. (10)–(21) and (27) related to ABCD matrix-based scattering parameters in MATLAB software.

The MATLAB results in Fig. 15a, b shows return loss in the up and down-state position and phase shift of the six main bits, respectively. Each bit in these Figures is independent and separate from the rest of the bits.

Fig. 15
figure 15

Calculated results of a return loss in the up and down-state position and b phase shift of six independent bits

Full size image

The next step is the connecting the six independent bits to achieve the six-bit phase shifter. Figure 16 shows the complete model of the proposed six-bit DMTL phase shifter. As is seen in Fig. 16, the extracted ABCD matrices of six independent bits in Eq. (17) are multiplied to achieve the six-bit DMTL phase shifter.

Fig. 16
figure 16

Proposed model of the six-bit DMTL phase shifter

Full size image

Equation (27) is used to derive the ABCD parameters of the proposed six-bit DMTL phase shifter.

$$\left[\begin{array}{cc}{\mathrm{A}}_{6-\mathrm{bit}}& {\mathrm{B}}_{6-\mathrm{bit}}\\ {\mathrm{C}}_{6-\mathrm{bit}}& {\mathrm{D}}_{6-\mathrm{bit}}\end{array}\right]=\left[\begin{array}{cc}{\mathrm{A}}_{22.5^\circ }& {\mathrm{B}}_{22.5^\circ }\\ {\mathrm{C}}_{22.5^\circ }& {\mathrm{D}}_{22.5^\circ }\end{array}\right]\times \left[\begin{array}{cc}{\mathrm{A}}_{11.25^\circ }& {\mathrm{B}}_{11.25^\circ }\\ {\mathrm{C}}_{11.25^\circ }& {\mathrm{D}}_{11.25^\circ }\end{array}\right]\times \left[\begin{array}{cc}{\mathrm{A}}_{90^\circ }& {\mathrm{B}}_{90^\circ }\\ {\mathrm{C}}_{90^\circ }& {\mathrm{D}}_{90^\circ }\end{array}\right]\times \left[\begin{array}{cc}{\mathrm{A}}_{180^\circ }& {\mathrm{B}}_{180^\circ }\\ {\mathrm{C}}_{180^\circ }& {\mathrm{D}}_{180^\circ }\end{array}\right]\times \left[\begin{array}{cc}{\mathrm{A}}_{5.625^\circ }& {\mathrm{B}}_{5.625^\circ }\\ {\mathrm{C}}_{5.625^\circ }& {\mathrm{D}}_{5.625^\circ }\end{array}\right]\times \left[\begin{array}{cc}{\mathrm{A}}_{45^\circ }& {\mathrm{B}}_{45^\circ }\\ {\mathrm{C}}_{45^\circ }& {\mathrm{D}}_{45^\circ }\end{array}\right]$$
(27)

The total 25 cells size considering the unit cell size of 200 μm is 5 mm. It is the smallest size in the six-bit DMTL phase shifters. Figure 17a, b show the return loss and phase shift for all 64 states, respectively. As it is seen from Fig. 17a, b, due to acceptable return loss between the frequencies 24.5 GHz and 25.5 GHz, the phase shift is approximately linear. From Fig. 17a the worst return loss is −11.62 dB.

Fig. 17
figure 17

Calculated results of a the return loss and b phase shift of all 64 states

Full size image

The final step is the reconfirming calculated results using FEM by HFSS software. This step uses the calculated parameters from Table 4. It is done in the next section.

6 Six-bit DMTL phase shifter simulation results

The proposed structure is simulated using HFSS software to verify the calculated results. Figure 18 shows the schematic of the top view of the six-bit DMTL phase shifter. The CPW line dimension and silicon thickness and resistance are the same as the two-bit structure. The capacitors plate area of all bits is shown in Table 5. The air gap of all capacitors is the same and equal to 1.5 µm. Figure 19a, b show the return loss and phase shift at 25 GHz for all 64-state, respectively. From the figures, the worst return loss is −11.62 dB.

Fig. 18
figure 18

The schematic of the top view of the six-bit DMTL phase shifter

Full size image
Table 5 Capacitors plate area of six-bit phase shifter
Full size table
Fig. 19
figure 19

Simulated results of a return loss and b phase shift of the 64 states of the six-bit DMTL phase shifter at 25 GHz

Full size image

7 Comparison

Table 6 presents a comparison between the state-of-the-art RF MEMS-based DMTL phase shifters and the current study. It is evident from the table that the proposed two and six-bit design results in better total length, and also two-bit design requires lower actuation voltage as compared to previously published research works. Reduction in the lateral dimension of two and six-bit phase shifter has minimized substrate area wastage which generates cost-effective output. Based on Table 6 and in comparison with our proposed phase shifter, the nearest six-bit phase shifter length is 8.5 mm. The actuation mechanism of the mentioned phase shifter is based on the unit cell level. It means that the number of input control is proportional to the number of cells. It should be noted that the actuation mechanism of the proposed phase shifter is based on bit-level actuation as it is in the conventional phase shifters.

Table 6 Comparison of the present work with the state-of-the-art RF MEMS based phase shifters
Full size table

8 Conclusion

A very small size Ka-band two-bit and K-band six-bit DMTL phase shifter was introduced in this research work. The improvement in size became possible by analyzing the return loss behavior in all frequencies. The calculated results showed that it is possible to have a small size, high phase shift, and reasonable return loss of unit cell for the frequencies near the resonance frequencies. The extracted two-bit and six-bit phase shifters lengths are 1.8 mm and 5 mm, respectively. These lengths are the smallest size among two-bit and six-bit DMTL phase shifters. The worst return loss in the two-bit and six-bit is −12.3 dB and −11.62 dB, respectively. The cantilever beam used in the two-bit phase shifter switches decreased the perfect contact voltage to 4.25 V. To verify, calculated results were then calculated and simulated using MATLAB and HFSS software, respectively.